Keywords

1 Introduction

Cardiovascular diseases are undergoing a rapid increase in the death of humans all over the world, according to the WHO updated risk chart, an estimated 17.9 million people died from CVDs (due to some risk factors such as diabetes, hypertension, blockage, thinning, and dilations of the blood cells) [1]. According to hematology, the blood vessels, including arteries, capillaries, and arterioles, execute some biotic functions such as supplying oxygen, waste products, and some essential nutrients to all the parts of the body and removing catabolic products [2,3,4]. Hence, the research works in the numerical simulation of blood rheology growing continuously for diagnosis, prevention, and the cure of cardiovascular diseases with the increase of computational power, for deeper study of the complexity of hemodynamic of blood and geometric parameters effect of CVDs [5,6,7,8,9]. The motivation behind this is to exert more and more effort in the development of these physiological methods and blood flow simulations because a computational tool could enable the development of alternative methods for clinical doctors to obtain some detection of cardiovascular disease in a non-invasive way.

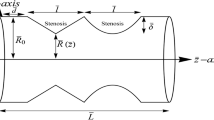
The function of the carotid artery is to supply blood as well as other nutrients to the brain, face, and neck of the human body. The carotid arteries are located on both sides of the neck. Internal carotid artery (ICA) and external carotid artery (ECA) are the two divisions that may be used to categorize carotid artery [10,11,12,13]. Figure 1 shows that the internal carotid artery is larger in diameter than the external carotid artery. The internal carotid artery supplies blood to the brain, whereas the external carotid artery supplies blood to the face and neck.

When predicting the flow pattern within an artery and monitoring the onset and evolution of plaque on the arterial wall, a computational fluid dynamics (CFD) model is a useful tool [14,15,16]. The application of CFD to 2-D artery geometries with plaque forms offers a priceless simulation of complicated geometry. The results produced by computational approaches are more accurate and cost-effective, and they are simple to mimic. In this current study, we use the methods that necessitated the foundations for the development of convoluted mathematics and physics. Consequently, the cardiovascular system modelling is limited to the parameters and boundary conditions that are available. So the computationally finite volume method for this system is prohibitive, and hence we used the coupled parameters to compromise. Therefore, this research simplified the area of interest for the 2D cardiovascular system model. Although only a few researchers have conducted a comprehensive study of hemodynamics on the 2D cardiovascular system model, [17,18,19].

In this study, we analyse the velocity of fluid in the constructed carotid artery by using the Navier-Stokes equation (NSE) as the governing equation of the motion of the fluid. The Navier-Stokes equation is a sequence of continuity and momentum equations that describe the flow in the large vascular domain and is coupled with the structural equation for simulation with the multi-dimensional structure. The objective of this research is to develop a simple simulation implementation that realistically describes the hemodynamics 2D constructed geometry of the vascular system using the axisymmetric Navier-Stokes equation.

2 Material and Methods

2.1 Elastic Model

Blood is a suspension of cells-red blood cells, white blood cells, platelets, and plasma-in a liquid solution, which consists of about 7% of protein and 90% of water. The elastic properties of the red blood cell membrane are responsible for the viscoelastic fluid behaviour of blood. The nature of the flow of blood determines whether the blood is Newtonian or non-Newtonian [20, 21]. Usually, the flow of blood is considered Newtonian in the large blood vessels. In this study, Blood is considered as the Newtonian fluid with the blood properties density and dynamic viscosity of \(1060\, \mathrm{kg/m^{3}}\) and 0.04 Pa.s respectively. [22].

This section of the study dealt with the spatial discretization of the Navier-Stokes equations for incompressible Newtonian fluids as the governing equations. The two-dimensional Navier-Stokes equations for incompressible Newtonian fluids consist of the momentum equation and the continuity equation with \(\Omega \) as the reference domain and the \(\tau \) as the boundary of the domain. The Cartesian form of the 2D Navier-stokes equation is given as follows [1, 11, 22, 23];

$$\begin{aligned} \frac{\partial u (x,t)}{\partial t}+u(x,t)\frac{\partial u (x,t)}{\partial x}+v(x,t)\frac{\partial u (x,t)}{\partial y}=-\frac{1}{\rho }\frac{\partial p}{\partial x}+\frac{\mu }{\rho }\left( \frac{\partial ^{2}u(x,t)}{\partial x^{2}}+\frac{\partial ^{2}u(x,t)}{\partial y^{2}}\right) \end{aligned}$$
(1)
$$\begin{aligned} \frac{\partial v (y,t)}{\partial t}+u(x,t)\frac{\partial v(y,t)}{\partial x}+v(x,t)\frac{\partial v (y,t)}{\partial y}=-\frac{1}{\rho }\frac{\partial p}{\partial y}+\frac{\mu }{\rho }\left( \frac{\partial ^{2}v(y,t)}{\partial x^{2}}+\frac{\partial ^{2}v(y,t)}{\partial y^{2}}\right) \end{aligned}$$
(2)

And the continuity equation,

$$\begin{aligned} \frac{\partial u (x,t)}{\partial x}+ \frac{\partial v (x,t)}{\partial y}=0 \end{aligned}$$
(3)

Where \(\rho \) is the density of fluid, u and v are velocity components along the x-axis and y-axis respectively with the pressure p and \(\upmu \) is the dynamic viscosity [24]. Taking into account the fluid velocity and pressure, Eq. (1) and (2) 2D the Navier-Stokes equations are discretized with the explicit method, as stated by the following equation:

$$\begin{aligned}{} & {} \frac{ u_{i,j}^{n+1}-u_{i,j}^{n}}{\bigtriangleup t}+u\frac{ u_{i,j}^{n}-u_{i-1,j}^{n}}{\bigtriangleup x}+v\frac{ u_{i,j}^{n}-u_{i-1,j}^{n}}{\bigtriangleup y}= - \frac{1}{\rho }\frac{ p_{i,j}^{n+1}-p_{i-1,j}^{n}}{\bigtriangleup x}\nonumber \\ {}{} & {} \quad + \frac{\mu }{\rho }\left( \frac{u_{i+1,j}^{n}-2u_{i,j}^{n}+u_{i-1,j}^{n}}{\triangle x^{2}} +\frac{u_{i+1,j}^{n}-2u_{i,j}^{n}+u_{i-1,j}^{n}}{\triangle y^{2}}\right) \end{aligned}$$
(4)
$$\begin{aligned}{} & {} \frac{ v_{i,j}^{n+1}-v_{i,j}^{n}}{\triangle t}+u\frac{ v_{i,j}^{n}-v_{i-1,j}^{n}}{\triangle x}+v\frac{ v_{i,j}^{n}-v_{i-1,j}^{n}}{\triangle y}= -\frac{1}{\rho }\frac{ p_{i,j}^{n+1}-p_{i-1,j}^{n}}{\triangle y}\nonumber \\ {}{} & {} \quad +\frac{\mu }{\rho }\left( \frac{v_{i+1,j}^{n}-2v_{i,j}^{n}+v_{i-1,j}^{n}}{\triangle x^{2}}+\frac{v_{i+1,j}^{n}-2v_{i,j}^{n}+v_{i-1,j}^{n}}{\triangle y^{2}}\right) \end{aligned}$$
(5)

2.2 Spatial Discretization

On the staggered grid space, the spatial discretization is performed with the velocity u on the horizontal cell interfaces, velocity v placed on the vertical cell interfaces, and the pressure p in the cell midpoint. For the staggered grid taking,

$$\begin{aligned} \triangle x = \triangle y =h \end{aligned}$$
(6)

and

$$\begin{aligned} \dfrac{\mu }{\rho }=\gamma , and {\dfrac{p}{\rho }=P} \end{aligned}$$
(7)

Using the Eq. (6), and (7), discrete form of Navier-stokes Eq. (4), and (5) are generalized to,

$$\begin{aligned}{} & {} \frac{u_{i,j}^{n+1}-u_{i,j}^{n}}{\triangle t} =-\frac{1}{h}((u^2)_{i,j}^{n}-(u^2)_{i-1,j}^{n}+(uv)_{i,j}^{n}-(uv)_{i,j-1}^{n})-\dfrac{1}{h} (P_{i,j}^{n}-P_{i-1,j}^{n})\nonumber \\ {}{} & {} +\frac{\gamma }{h^2} (u_{i+1,j}^{n}+ u_{i-1,j}^{n}+ u_{i,j+1}^{n}+u_{i,j-1}^{n}-4u_{i,j}^{n}) \end{aligned}$$
(8)
$$\begin{aligned}{} & {} \frac{v_{i,j}^{n+1}-v_{i,j}^{n}}{\triangle t} =-\frac{1}{h}((v^2)_{i,j}^{n}-(v^2)_{i,j-1}^{n}+(uv)_{i,j}^{n}-(uv)_{i-1,j}^{n})-\dfrac{1}{h} (P_{i,j}^{n}-P_{i-1,j}^{n})\nonumber \\ {}{} & {} +\frac{\gamma }{h^2} (v_{i+1,j}^{n}+ v_{i-1,j}^{n}+ v_{i,j+1}^{n}+v_{i,j-1}^{n}-4v_{i,j}^{n}) \end{aligned}$$
(9)

or,

$$\begin{aligned} \frac{u_{i,j}^{n+1}-u_{i,j}^{n}}{\triangle t} =-(a_{1})-\frac{1}{h}(P_{i,j}^{n}-P_{i-1,j}^{n})+(a_{2}+a_{3}) \end{aligned}$$
(10)
$$\begin{aligned} \frac{v_{i,j}^{n+1}-v_{i,j}^{n}}{\triangle t} =-(b_{1})-\frac{1}{h}(P_{i,j}^{n}-P_{i-1,j}^{n})+(b_{2}+b_{3}) \end{aligned}$$
(11)

where,

figure a

In vector notation to the velocity correction equation read as,

$$\begin{aligned} \boldsymbol{\frac{U_{i,j}^{n+1}-U_{i,j}^{n}}{\triangle t}=-G_{i,j}^{n}-\bigtriangledown _{h} P_{i,j}+F_{i,j}^{n}} \end{aligned}$$
(12)

where,

                        \(\boldsymbol{U_{i,j}^{n+1}= \left[ \begin{array}{c} u_{i,j}^{n+1} \\ u_{i,j}^{n+1} \end{array} \right] , U_{i,j}^{n}=\left[ \begin{array}{c} u_{i,j}^{n} \\ u_{i,j}^{n} \end{array} \right] }\)

                 \(\boldsymbol{G_{i,j}^{n}= \left[ \begin{array}{c} a_{1} \\ a_{1} \end{array} \right] , P_{i,j}= \left[ \begin{array}{c} P_{i,j}^{n}-P_{i-1,j}^{n}\\ P_{i,j}^{n}-P_{i,j-1}^{n} \end{array} \right] ,F_{i,j}^{n}= \left[ \begin{array}{c} b_{1} \\ 2_{1} \end{array} \right] }\),

The spatial discretize form of continuity Eq. (3) as,

$$\begin{aligned} \frac{u_{i,j}^{n}-u_{i-1,j}^{n}}{\triangle x}+\frac{v_{i,j}^{n}-v_{i,j-1}^{n}}{\triangle y}=0 \end{aligned}$$
(13)

As grid space is, \(\triangle x = \triangle y =h \)

$$\begin{aligned} u_{i,j}^{n}-u_{i-1,j}^{n}+v_{i,j}^{n}-v_{i,j-1}^{n} \end{aligned}$$
(14)

Write Eq. (14) as one vector equation for constraint on velocity,

$$\begin{aligned} \boldsymbol{\triangle _{h}u_{i,j}^{n+1}=0} \end{aligned}$$
(15)

Split the Eq. (12) with adding the temporary velocity into,

$$\begin{aligned} \frac{U_{i,j}^{t}-U_{i,j}^{n}}{\triangle t}=-G_{i,j}^{n}+F_{i,j}^{n} \end{aligned}$$
(16)
$$\begin{aligned} U_{i,j}^{t}=U_{i,j}^{n}+{\triangle t}(-G_{i,j}^{n}+F_{i,j}^{n}) \end{aligned}$$
(17)

Evaluating \(U_{i,j}^{n+1}\) from Eq. (17) with the advection and the diffusion terms.

$$\begin{aligned} \frac{U_{i,j}^{n+1}-U_{i,j}^{t}}{\triangle t}=-\bigtriangledown _{h} P_{i,j} \end{aligned}$$
(18)

On applying the divergence on the both side of Eq. (18),its becomes

$$\begin{aligned} \bigtriangledown _{h}U_{i,j}^{n+1}=\bigtriangledown _{h}U_{i,j}^{t}-\triangle t \bigtriangledown _{h}.\bigtriangledown _{h} P_{i,j} \end{aligned}$$
(19)

From Eq. (15) the right-hand side of (19) become vanish and the pressure needed to enforce the velocity becomes incompressible. Hence, it is obtained by solving the linear system.

$$\begin{aligned} \bigtriangledown _{h}^{2}P_{i,j}=\frac{1}{\triangle _{h}}\bigtriangledown _{h}U_{i,j}^{t} \end{aligned}$$
(20)

Update the velocity field by adding the pressure

$$\begin{aligned} U_{i,j}^{n+1}=U_{i,j}^{t}-\triangle t \bigtriangledown _{h}. P_{i,j} \end{aligned}$$
(21)

2.3 Boundary Conditions for the Tangential Velocity

Wall velocity is,

$$\begin{aligned} U_{w}=0 \end{aligned}$$
(22)

i.e. have no slip condition. Then, interpolate the \(U_{w}\) velocity linearly by adding the ghost \(u_{i,2}\),

$$\begin{aligned} \frac{u_{i,2}+u_{j,1}}{2}=U_{w} \end{aligned}$$
(23)
$$\begin{aligned} u_{i,2}=2U_{w}-u_{j,1} \end{aligned}$$
(24)

If \(U_{w}=0\), then Eq. (24) becomes,

$$\begin{aligned} u_{i,1}=-u_{i,2} \end{aligned}$$
(25)

This represents the reflection technique.

2.4 Solve for the Pressure

Here, the pressure at the boundary of the domain is obtained through solving the continuity Eq. (14) and Eq. (21), then using the presented method, rearranging for pressure, obtain a numerical scheme for boundary condition exactly in the form presented in [23].

$$\begin{aligned} P_{i+1,j}+P_{i-1,j}+P_{i,j+1}+P_{i,j-1}-4P_{i,j}=\frac{h}{\triangle x}(u_{i+1,j}^{t}-u_{i-1,j}^{t}+v_{i,j+1}^{t}-v_{i,j-1}^{t}) \end{aligned}$$
(26)

For the pressure at the boundary, the velocity \(v_{i,j-1}^{t}\) become vanish at the boundary of the domain, therefore Eq. (26)

$$\begin{aligned} P_{i+1,j}+P_{i-1,j}+P_{i,j+1}+P_{i,j-1}-3P_{i,j}=\frac{h}{\triangle x}(u_{i+1,j}^{t}-u_{i-1,j}^{t}+v_{i,j+1}^{t}) \end{aligned}$$
(27)

where, for the boundary nodes except corner (Table 1),

\(i=2;\) \(i=nx;\) and \(j=2;\) \(i=ny;\)

Table 1. Array dimension
Full size table

3 Result and Discussions

In this section, we discussed the numerical results of the regular and irregular flow patterns of fluid in a constructed carotid artery and bifurcation area. Fluid was incompressible, Newtonian, laminar flow having the blood properties density and dynamic viscosity \(1060\,\mathrm{kg/m^3}\) and 0.04 Pa. s respectively. An analysis of the result, the time impedance was considered \(t=0\). At the inlet, the initial time-averaged reference velocity, \(v_0\), was assumed to be \(0.3\,\mathrm{m/s}\). At the carotid bifurcation area, where there is a narrowing of the artery, the fluid velocities were found to be relatively high. In the tubular area before the bifurcation, the flow pattern of blood is regular, while after the bifurcation, with the change in dimensions near the sinus from dilation, the blood flow pattern is irregular.

The anatomical pathologies of the carotid artery shown in Fig. 1 are highly receptive due to bifurcation, high turbulence, or reverse flow. Because anatomical pathologies can affect blood flow, they contribute to the development of atherosclerosis. The spline and center-line geometry descriptions of the standard carotid artery are shown in Table 2 and is created using the outline listed in the literature [5, 6, 24, 25].

The meshing of the carotid artery is shown in Fig. 3 and the number of nodes and elements is given in Table 2, the size of elements being \(0.2\,\mathrm{m/s}\) (Fig. 2),

Table 2. Meshing details
Full size table
Fig. 1.
figure 1

Two-dimensional idealized geometric specification of Carotid artery: CAA, ICA and ECA

Full size image
Fig. 2.
figure 2

Two-dimensional idealized geometric specification of Carotid artery: CAA, ICA and ECA

Full size image

The blood velocity was found to be lower in the enlargement area while reaching a maximum velocity field of \(0.4556\,\mathrm{m/s}\) in the narrowing area. The flow pattern of continuity was obtained alternately between the internal and external carotid artery models. The wall and boundaries where the velocity was found to be at its maximum indicate the deformation of the wall of the reference geometry (Figs. 4 and 5).

The flow pattern of the blood is regular in the tubular areas while irregular in areas with changes in dimensions, as in the sinus, i.e., turbulent flow. More recirculation of blood flow is found in the sinus area (Table 3).

Fig. 3.
figure 3

Streamline simulated blood velocity field around the bifurcation of carotid artery at different time steps at t = 0.2 and t = 0.4

Full size image
Fig. 4.
figure 4

Contour velocity field around the bifurcation of carotid artery at different time steps at t = 0.2 and t = 0.4

Full size image
Fig. 5.
figure 5

Pressure Contour around the bifurcation of carotid artery at different time steps at t = 0.2 and t = 0.4

Full size image

Arteries with maximum pressures of 20.88 Pa.s are more widely recirculated in the region. At the dividing wall of an artery, pressure is higher than at the non-dividing wall, and at the point of bifurcation, pressure is at its maximum, due to the force exerted by the blood on the artery.

Table 3. Geometry specification of vessel diameter and the location
Full size table

The regular and irregular blood flow patterns were analysed in the rectangular tube and in vasodilation, respectively, for incompressible fluid in the subparts of the carotid artery. This regular and irregular have been done to determine the behaviour of blood flow patterns in the uniform and dilation areas. The density and the dynamic viscosity of blood were used as \(1060\,\mathrm{kg/m^3}\) and 0.04 Pa.s respectively. The inflow boundary condition was considered as parabolic, and the outlet boundary condition was set to zero external force. Laminar flow occurs where there is a uniform flow, as shown in Fig. 6a. The turbulent flow occurs in the area where there is an irregular flow due to the blockage and constrictions. The turbulent flow generally produces a non-parabolic velocity profile because, in turbulent flow, the stream of fluid mixes both types radially and axially. These flow models were analysed using the same parameters and presented in Fig. 6 (Fig 7).

Fig. 6.
figure 6

Blood velocity profile with regular and irregular flow pattern (6a) Laminar flow in Tubular domain, (6b) vasodilation

Full size image
Fig. 7.
figure 7

Parabolic velocity profile at inlet and out of Tubular domain

Full size image

4 Conclusion

The objective of this research is to present a simplified model for the cardiovascular system. The analysis of the blood flow profile in 2D using the Navier-Stokes equation as the governing equations for the incompressible Newtonian fluid. The blood flow pattern was computed in the idealised geometry of tubular and dilation, which leads to analysis in the carotid artery’s idealised 2D geometry. The idealised 2D carotid artery geometry parameters were taken from [11, 26]. Based on the results, we concluded that the numerical study of the generalised Newtonian 2D model of blood flow can be solved very well. In this model, the blood flow is determined by dividing the flow analysis into two different patterns, which are regular and irregular blood flow patterns analysed in the rectangular tube and in vasodilation, respectively, and the existence of reverse flow in the area of the internal carotid artery near the non-dividing wall. In the simulation of flow velocity in a rectangular tube domain, laminar flow was obtained, with a maximum velocity field of \(9.688 \times 10^{-4}\,\mathrm{m/s}\). In the simulation of vasodilation, we obtained the irregular flow pattern, and the maximum velocity was found \(1.384\,\mathrm{m/s}\) for the vasodilation prototype simulation. The blood flow pattern simulation about the bifurcation in the carotid artery was done at the inlet by using the same fluid quantities of blood, parabolic velocity profile, and boundary conditions. There was no external force considered at the outlet of the both external carotid artery and the internal carotid artery. The determination of the convergence of the solution was crucial on account of the boundary value problem and the complexity of the equation. In general, this paper shows quite good qualitative agreement with the nonlinearity of the problem and the multi-scale modelling based on the initial point. The modeling around the bifurcation of the carotid artery was done using ANSYS 19.1 CAD software and numerically solved to produce a valid simulation of flow. This research work is only the initial point for the bigger project with the biological parameters and 3D realistic geometry reconstructed from the patient-specific medical images. We could also work on the detection of possible multiplaque formation regions by computing the WSS and the blood flow behaviour.