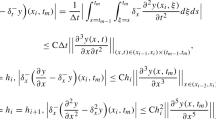NIPG Method on Shishkin Mesh for Singularly Perturbed Convection-Diffusion Problem with Discontinuous Convection Coefficient

Abstract

In this paper, we investigate the convergence of discontinuous Galerkin finite element method (DGFEM) for singularly perturbed convection-diffusion problem with discontinuous convection coefficient. Due to the discontinuity in the convection coefficient, the problem typically shows a weak interior layer. We develop a kind of DGFEM, the non-symmetric discontinuous Galerkin finite element method with interior penalties (NIPG) to handle the layer setbacks. With the use of a typical Shishkin mesh, the domain is discretized and uniform error estimate is obtained and theoretically we have obtained the convergence of order $\mathcal {O}(N^{-1} \ln N)$. The numerical outcome backs up our theoretical conclusions.

1 Introduction

In this article we consider a singularly perturbed convection-diffusion problem of the type

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathcal {L}u(x):=-\varepsilon u'' + b(x)u'(x) + c(x)u(x) = f(x), \qquad \text {in}~x\in \varOmega = (0, 1), \\ u(0) = u(1) = 0, \end{array}\right. } \end{aligned}$$

(1)

where, $\varepsilon$ is the perturbation parameter satisfies $0<\varepsilon \ll 1$ and b(x) has jump discontinuity at $x = d \in \varOmega$. We define $\varOmega _{1} = (0, d)$ and $\varOmega _{2} = (d, 1)$ where d is a point of discontinuity of b(x). Let us assume b, c and f belong to the class $C^{2}(\varOmega _{1} \cup \varOmega _{2})$ and the function satisfy

$$\begin{aligned} c(x) - \frac{1}{2} b'(x) \ge \gamma ^{2} >0. \qquad \text {on}~\varOmega _{1} \cup \varOmega _{2} \end{aligned}$$

(2)

Here, $\gamma$ is some fixed positive constant. Moreover the following conditions hold good,

$$\begin{aligned} \beta _{1}^{\star }> b(x)> \beta _{1}> 0,~x<d,~~-\beta _{2}^{\star }< b(x)< -\beta _{2} < 0,~x>d,~~c(x)\ge 0 \qquad x \in \overline{\varOmega }, \end{aligned}$$

and

$$\begin{aligned} |[b](d) |\le C, \qquad |[c](d) |\le C, \qquad |[f](d) |\le C, \end{aligned}$$

(3)

where, $\beta _{1}$, $\beta _{1}^{\star }$, $\beta _{2}$ and $\beta _{2}^{\star }$ are positive constants. In the close vicinity of $x= d$ in the solution u(x) of problem (1), exhibits layer of width $\mathcal {O}(\varepsilon \ln (1/\varepsilon ))$. We refer the layer as an interior layer.

There is a large number of papers in the literature dealing with a singular perturbation problem with continuous coefficients and source terms, see [10, 12] for a survey. Problem of type (1) with discontinuous right hand side are considered in [1, 12], whereas problem with discontinuous coefficient is considered in [3, 20]. In these articles, authors have proved second order and first order convergence, respectively. In [8] authors have proved first order $\varepsilon$-uniform convergence on Shishkin mesh of finite difference scheme for reaction-diffusion problem with discontinuous source term.

Except these literature review some of these are [16] in which, Singh et.al. presented an algorithms for approximate solution of nonlinear Lane-Emden type equations. Convergence analysis and stability result are also provided. Also Singh has applied Chebyshev’s spectral collocation method for Bratu’s type, Troesch’s and nonlocal elliptic boundary value problems in [14]. Moreover, Majid et.al. has established the convergence result for solution of nonlinear Lane-Emden type equations. Pandey et. al. has established the convergence of Bratu’s equation by means of Chebyshev polynomials [15]. Some other equations and physical models are investigated numerically in [4,5,6]. In these articles authors established the existence using Banach fixed point theory and convergence of numerical schemes are also investigated.

The idea to use non-symmetric Galerkin method with interior penalty (NIPG) method is not new in the literature. The interest in the non-symmetric Galerkin method with interior penalty (NIPG) method and singular perturbation problem is beneficial due to the presence of penalty terms which fulfill the requirement of additional stabilization. The non-symmetric Galerkin method with interior penalty (NIPG) method has the advantage to be very flexible in the sense of adaptivity; moreover it can be applied for the case $\varepsilon = 0$ if the solution is not smooth. In [10, 21] authors have proved first order convergence for convection-diffusion problem with turning point and continuous coefficients, respectively. This method is preferred like streamline diffusion finite element method (SDFEM) [17] over the classical finite element methods because of their potential in approximating globally rough solutions, their possible definition (additionally jump and penalization parameter) on unstructured meshes, their potential for error control and mesh adaptation, etc. There are other variants of DGFEM like symmetric interior penalty Galerkin (SIPG) method and incomplete interior penalty Galerkin (IIPG) method in which, we have to choose penalty parameters so that the method could be stable and convergent, besides these properties establishment of coercivity property is not an easy task. In addition to the aforementioned privilege to non-symmetric interior penalty Galerkin (NIPG) method. Drawbacks of this method is its much larger number of degree of freedom as compared to standard Galerkin finite element method. Another disadvantage of the method is adjoint consistency which is better in SIPG technique that appears in sketching optimal $L^{2}$ error or to apply duel weighted residual (DWR) technique.

In this paper, we adopt to the non-symmetric Galerkin method with interior penalty (NIPG) method for problem (1). As a result of discontinuity in convection coefficient, interior layer is present in the solution. Interior layer usually present due to turning point or discontinuity in the coefficients. In [11], authors have established the first order convergence up to logarithmic factor for non-symmetric interior penalty Galerkin (NIPG) method for one dimensional singular perturbation problem with discontinuous source term. We have shown the uniform convergence of the method on usual Shishkin mesh. Simplifying our analysis and using piecewise linear element on $\varOmega$, in Theorem 4 we prove that the finite element method (FEM) leads to the convergence result $\mathcal {O}(N^{-1} \ln N)$ and finally we get the result of same order in Theorem 5.

The article is arranged in the following way: Sect. 2 describes the existence, stability properties of the solution, opportunistically we have included decomposition of the solution in this section too. In Sect. 3, we have discussed the Shishkin mesh, the non-symmetric Galerkin method with interior penalty (NIPG) method and existence of solution. Section 4 dealt with the error analysis on the given mesh. Uniform convergence of the given FEM is described in Sect. 5 and the last Sect. 6 provides the numerical result that supports our theoretical findings. Section 7 is all about the summary of the article and last but not the least the original contribution in this article is described in Sect. 8.

2 Stability and Solution Decomposition

We propose some necessary notations. For any function v(x), the jump at d is denoted by [v](d) and defined by $[v](d) = v(d^{+}) - v(d^{-})$. C is a generic constant (sometimes subscripted) is free from perturbation parameter $\varepsilon$ and mesh parameter N. An arbitrary subinterval $[x_{j-1}, x_{j}]$ is represented by $I_{j}$ with interval height $h_{j} = x_{j} - x_{j-1}$.

Now the theorem given below guarantees the existence of solution to the problem (1).

Theorem 1

Let u(x) is the solution of (1) that belongs to the class of function $C^{0}(\overline{\varOmega }) \cap C^{1}(\varOmega ) \cap C^{2}(\varOmega _{1} \cup \varOmega _{2})$.

Proof

The detailed proof can be similar as in [20].    $\blacksquare$

Lemma 1

Suppose the problem (1) has a solution u(x) that belongs to the class of functions $C^{0}(\overline{\varOmega }) \cap C^{1}(\varOmega ) \cap C^{2}(\varOmega _{1} \cup \varOmega _{2})$, which satisfies the bound

$$\begin{aligned} \left\| u(x)\right\| _{L^{\infty }(\varOmega )} \le \frac{1}{\lambda } \left\| f(x)\right\| _{L^{\infty }(\varOmega )}, \end{aligned}$$

where $\lambda = \min \{\beta _{1}/d, \beta _{2}/(1-d)\}$.

Proof

Put $\psi (x) = -\frac{x\left\| f(x)\right\| _{L^{\infty }(\varOmega )}}{\lambda d} + u(x)$, $x<d$ and $\psi (x) = -\frac{(1-x)\left\| f(x)\right\| _{L^{\infty }(\varOmega )}}{\lambda (1-d)} + u(x)$, $x>d$.

Therefore, we have $\psi (x)\in C^{0}(\overline{\varOmega })$ and $\psi (0)\le 0$, $\psi (1)\le 0$.

For each $x \in \varOmega _{1} \cup \varOmega _{2}$,

$$\begin{aligned} \mathcal {L}\psi (x) \ge 0. \end{aligned}$$

Furthermore, since $u(x) \in C^{1}(\varOmega )$

$$\begin{aligned}{}[\psi ](d) = [u](d) = 0 \qquad \text {and} \qquad [\psi '](d) = \frac{\left\| f\right\| _{L^{\infty }(\varOmega )}}{\lambda d} + \frac{\left\| f\right\| _{L^{\infty }(\varOmega )}}{\lambda (1-d)} \ge 0. \end{aligned}$$

Hence, following comparison principle in Lemma 2 [7] that $\psi (x) \le 0$ for all $x \in \overline{\varOmega }$. Which determines the desired bound for the solution u(x).

Let us consider the decomposition $u = v + w$ into smooth component v and interior layer component w. We take two discontinuous function $v_{0}$ and $v_{1}$ such that

$$\begin{aligned} bv_{0}'= & {} f, \qquad x \in \varOmega _{1} \cup \varOmega _{2}\\ v_{o}(0)= & {} u(0), \qquad v_{0}(1) = u(1),\\ bv_{1}'= & {} -v_{0}'' ,\\ v_{1}(0)= & {} 0, \qquad v_{1}(1) = 0. \end{aligned}$$

Now we define smooth component of the solution v such that

$$\begin{aligned} \mathcal {L} v&= f,\quad x \in \varOmega _{1} \cup \varOmega _{2}\end{aligned}$$

(4a)

$$\begin{aligned} v(0)&= u(0), \qquad v(d^{-}) = v_{0}(d^{-}) + \varepsilon v_{1}(d^{-}),\end{aligned}$$

(4b)

$$\begin{aligned} v(d^{+})&= v_{0}(d^{+}) + \varepsilon v_{1}(d^{+}), \qquad v(1) = u(1). \end{aligned}$$

(4c)

Note that it is discontinuous function. Further, we have layer part of the solution w which is also discontinuous and given by the set of following equation

$$\begin{aligned} \mathcal {L} w&= 0, \quad x \in \varOmega _{1} \cup \varOmega _{2}\end{aligned}$$

(5a)

$$\begin{aligned} w(0)&= w(1) = 0, \qquad [w](d) = -[v](d), \qquad [w'](d) = -[v'](d). \end{aligned}$$

(5b)

Hence, we get $w(d^{-}) = u(d^{-})-v(d^{-})$ and $w(d^{+}) = u(d^{+})-v(d^{+})$. We note that the solution $u = v + w$ is unique to the problem (1). It is merited consideration that v and w are discontinuous at $x = d$, but their sum u is in $C^{1}(\varOmega )$ by (5b). It is called stability property for the exact solution of (1).    $\blacksquare$

It is crucial to deduce the bounds for different components of the solution in order to obtain the convergence result in the finite element method. The same is addressed in the below mentioned theorem.

Theorem 2

Let (3) holds true. Assume that $b, c, f \in C^{2}(\varOmega _{1} \cup \varOmega _{2})$, we have

$$\begin{aligned} \left\| b^{m}(x)\right\| _{L^{\infty }(\varOmega _{1}\cup \varOmega _{2})} \le C, \quad \left\| c^{m}(x)\right\| _{L^{\infty }(\varOmega _{1}\cup \varOmega _{2})} \le C, \quad \left\| f^{m}(x)\right\| _{L^{\infty }(\varOmega _{1}\cup \varOmega _{2})} \le C, \end{aligned}$$

$m = 0, 1, 2$ and we are able to derive the decomposition of solution to the problem (1) and in this way we find the smooth part S and layer part E satisfy $\mathcal {L}S = f$ and $\mathcal {L}E = 0$, respectively and their bound could be

$$\begin{aligned} \left\| S^{i}(x)\right\| _{L^{\infty }(\varOmega _{1}\cup \varOmega _{2})} \le C, \qquad |[S](d)|\le C, \qquad |[S'](d)|\le C. \nonumber \\ |E^{i}(x)|\le {\left\{ \begin{array}{ll} C \varepsilon ^{-i}e^{(x-d)\beta _{1}/\varepsilon }, \qquad x \in \varOmega _{1},\\ C \varepsilon ^{-i}e^{-(x-d)\beta _{2}/\varepsilon },\qquad x \in \varOmega _{2}. \end{array}\right. } \end{aligned}$$

(6)

$i = 0, 1, 2$.

Proof

The proof is same as it has been done in [20], so we omit the proof here.

   $\blacksquare$

3 Piecewise Equidistant Mesh and NIPG Method

3.1 Shishkin Mesh

For the domain discretization, a most practicable Shishkin mesh is considered. Let $N \in \mathbb {N}$, where $N\ge 4$ and N is a multiple of 4. Layer in the vicinity of d has been considered and any possibility of layer at the boundary is completely ruled out. Therefore the mesh can be generated in the following way: Following [19], we take transition points $\lambda _{1} = d - \frac{\rho \varepsilon }{\beta _{1}}\ln N$ and $\lambda _{2} = d +\frac{\rho \varepsilon }{\beta _{2}}\ln N$ where $\rho \ge 2$, with the help of these two transition points we make the division of $\overline{\varOmega }$ into four subintervals

$$\begin{aligned} \overline{\varOmega } = [0, \lambda _{1}] \cup [\lambda _{1}, d] \cup [d, \lambda _{2}] \cup [\lambda _{2}, 1] \end{aligned}$$

such that $d - \lambda _{1} \le d/2$ and $\lambda _{2}-d \le (1-d)/2$. Furthermore we assume that each subintervals are distributed into N/4 intervals, where grid points satisfy $x_{N/4} = \lambda _{1}$, $x_{N/2} = d$ and $x_{3N/4} = \lambda _{2}$.

Remark 1

Throughout our analysis we take $\varepsilon \le C N^{-1}$, which is reasonable in practice.

3.2 The NIPG Method: Procedure and Properties

The Shishkin mesh defined in Subsect. 3.1 partitioning the domain $\varOmega$ into subintervals $I_{j} = [x_{j-1}, x_{j}]$, $j = 1, 2, ..., N$. Denote these collections by $\mathcal {T}_{N}$. We introduce with some essential notations: For every $I_{j} \in \mathcal {T}_{N}$, define broken Sobolev space of order k

$$\begin{aligned} H^{k}(\varOmega , \mathcal {T}_{N}) = \big \{v\in L^{2}(\varOmega ): v\big |_{I_{j}} \in H^{k}(I_{j}),~\forall I_{j} \in \mathcal {T}_{N}\big \} \end{aligned}$$

and corresponding broken Sobolev norm and seminorm defined by

$$\begin{aligned} \left\| v\right\| _{s, \mathcal {T}_{N}} = \bigg (\sum _{j=1}^{N}\left\| v\right\| ^{2}_{s,I_{j}}\bigg )^{1/2}, \qquad |v|_{s,\mathcal {T}_{N}} = \bigg (\sum _{j=1}^{N}|v|^{2}_{s,I_{j}}\bigg )^{1/2}, \end{aligned}$$

respectively. Define $V^N$ as a finite element space related to the collection $\mathcal {T}_{N}$ of Shishkin meshes

$$\begin{aligned} V^{N} = \big \{v \in L^{2}(\varOmega ): v\big |_{I_{j}} \in P^{1}(I_{j}),~\forall I_{j} \in \mathcal {T}_{N}\big \}, \end{aligned}$$

where $P^{1}(I_{j})$ denotes the space of polynomial of degree at most one in each $I_{j}$. Moreover, the functions in $V^N$ are completely discontinuous on the boundaries of the subintervals in $\mathcal {T}_{N}$. That is we are considering the non-confirming finite element.

The NIPG formulation [10] of (1) reads as: Find $u_{N} \in V^{N}$ such that

$$\begin{aligned} B(u_{N}, v_{N}) = L(v_{N}), \qquad \text {for all}~v_{N} \in V^{N} \end{aligned}$$

(7)

where

$$\begin{aligned} B(u, v)&= B_{1}(u, v) + B_{2}(u, v),\end{aligned}$$

(8a)

$$\begin{aligned} B_{1}(u, v)&= \sum _{j=1}^{N} \int _{I_{j}} \varepsilon u' v' dx + \sum _{j=0}^{N} \varepsilon \bigg ([u(x_{j})]\{v'(x_{j})\} - [v(x_{j})]\{u'(x_{j})\}\bigg ) \end{aligned}$$

(8b)

$$\begin{aligned}&+ \sum _{j=0}^{N} \sigma _{j}[u(x_{j})][v(x_{j})], \nonumber \\ B_{2}(u, v)&= \sum _{j=1}^{N} \int _{I_{j}}(bu' + cu)v dx + \sum _{j=0}^{N-1}b(x_{j})[u(x_{j})]v(x_{j}^{+}),\end{aligned}$$

(8c)

$$\begin{aligned} L(v)&= \sum _{j=1}^{N} \int _{I_{j}}f v dx. \end{aligned}$$

(8d)

Here $\sigma _{j}(j = 0, 1, \cdots , N)$ are the discontinuous-penalization parameters that are closely related to each nodes $x_{j}$. These are user-defined parameters, in the sequel, we will provide the exact choice of these parameters. The construction of bilinear form inspired us to introduce the DG norm as follows: For any $v \in H^{2}(\varOmega , \mathcal {T}_{N})$,

$$\begin{aligned} \left\| v\right\| ^{2}_{DG} = \sum _{j=1}^{N} \big (\varepsilon \left\| v'\right\| ^{2}_{L^{2}(I_{j})} + \left\| \gamma v\right\| ^{2}_{L^{2}(I_{j})}\big ) + \sum _{j=0}^{N} \big (\frac{1}{2}b(x_{j}) + \sigma _{j}\big )[v(x_{j})]^2. \end{aligned}$$

(9)

Lemma 2

Let u and $u_{N}$ are the exact solution to the problem (1) and discretized solution to the weak formulation (7), respectively. Then the bilinear form provided by (7) satisfies,

$$\begin{aligned} B(u - u_{N}, v_{N})&= 0 \qquad \mathrm {for\ all }\ v_{N} \in V^N, \quad \mathrm {(Galerkin\ orthogonality)}\end{aligned}$$

(10a)

$$\begin{aligned} B(v_{N}, v_{N})&= \left\| v_{N}\right\| ^{2}_{DG} \qquad \mathrm {for\ all }\ v_{N} \in V^N, \quad \mathrm {(coercivity)} \end{aligned}$$

(10b)

Proof

Both the properties in (10a) and (10b) in the above Lemma 2 can be followed from [10] in Lemma 3.1 and equation (3.5).    $\blacksquare$

4 Error Estimations: Sharp Bound on Shishkin Mesh

In this section, we present piecewise linear interpolation $u^{I}$ of the exact solution u and their properties. There are numerous results on interpolation error in the literature (see [2]). We introduce an estimation on interpolation error which is useful in the derivation of error estimation.

Lemma 3

[18]: The special interpolant has the following properties:

$$\begin{aligned} |u - u^{I}|_{m, \mathcal {N}}&\le C h_{\mathcal {N}}^{j+1 - m}|u|_{j+1, \mathcal {N}}, \quad m = 0, 1, \cdots , j+1,~\forall ~u \in H^{j+1}(\mathcal {N}),\end{aligned}$$

(11a)

$$\begin{aligned} \left\| u \right\| _{L^{\infty }(\mathcal {N})}&\le Ch_{\mathcal {N}}^{j+1} |u|_{j+1,\infty ,\mathcal {N}}, \qquad \forall u \in W^{j+1, \infty }(\mathcal {N}), \end{aligned}$$

(11b)

where $\mathcal {N}$ is an element in the partition $\mathcal {T}_{N}$ of the domain $\varOmega$ and $h_{\mathcal {N}}$ is the length of element $\mathcal {N}$.

4.1 Interpolation Error

Lemma 4

On the Shishkin mesh, we have the following properties:

$$\begin{aligned} \left\| S-S^{I}\right\| _{L^2[0, \lambda _{1}]} + \left\| u-u^{I}\right\| _{L^2[0, \lambda _{1}]}&\le C N^{-2},\end{aligned}$$

(12a)

$$\begin{aligned} \left\| E-E^{I}\right\| _{L^2[\lambda _{1}, d]} + \left\| u-u^{I}\right\| _{L^2[\lambda _{1}, d]}&\le C \varepsilon ^{1/2}(N^{-1}\ln N)^{2},\end{aligned}$$

(12b)

$$\begin{aligned} \left\| (E-E^{I})'\right\| _{L^2[0, d]} + \left\| (u-u^{I})'\right\| _{L^2[0, d]}&\le C \varepsilon ^{-1/2}N^{-1}\ln N. \end{aligned}$$

(12c)

Proof

To estimate $\left\| S-S^{I}\right\| _{L^2[0, \lambda _{1}]}$, we use classical interpolation theory given by (11a) with $m = 0$ and $j=1$

$$\begin{aligned} \left\| S-S^{I}\right\| _{L^2(I_{j})} \le C h_{\mathcal {N}}^{2} \left\| S''\right\| _{L^2(I_{j})} \le C N^{-2}. \end{aligned}$$

Now

$$\begin{aligned} \left\| E-E^{I}\right\| _{L^2(I_{j})} \le C \left\| E\right\| _{L^2(I_{j})} + \left\| E^{I}\right\| _{L^2(I_{j})} \le C N^{-2}. \end{aligned}$$

combining the above two estimates, we get (12a). For (12b), we use the interpolation result from (11a).

Now we will estimate (12c)

$$\begin{aligned} \left\| (E-E^{I})'\right\| _{L^{2}[0, \lambda _{1}]}\le & {} \left\| E'\right\| _{L^{2}[0, \lambda _{1}]} + \left\| (E^{I})'\right\| _{L^{2}[0, \lambda _{1}]}, \nonumber \\\le & {} \left\| E'\right\| _{L^{2}[0, \lambda _{1}]} + C N \left\| (E^{I})\right\| _{L^{2}[0, \lambda _{1}]}. \end{aligned}$$

(13)

Here we have used inverse inequality and stability property for interpolant (see Lemma 3.3, [21]).

$$\begin{aligned} \left\| E'\right\| _{L^{2}[0, \lambda _{1}]} \le C \varepsilon ^{-1/2} N^{-2}, \quad \left\| E^{I}\right\| _{L^{2}[0, \lambda _{1}]} \le C \varepsilon ^{1/2} N^{-2}. \end{aligned}$$

(14)

(11a) give us

$$\begin{aligned} \left\| (E-E^{I})'\right\| _{L^{2}[\lambda _{1}, d]} \le C \varepsilon ^{-1/2} N^{-1} \ln N \end{aligned}$$

(15)

and finally

$$\begin{aligned} \left\| (S-S^{I})'\right\| _{L^{2}[0, d]} \le C \varepsilon N^{-1} \ln N. \end{aligned}$$

(16)

Combining (13)–(16), we get (12c).    $\blacksquare$

Remark 2

Bound for the estimations in Lemma 4 on the interval [d, 1] can be achieved easily. Hence, we have

$$\begin{aligned} \left\| S-S^{I}\right\| _{L^2[\lambda _{2}, 1]} + \left\| u-u^{I}\right\| _{L^2[\lambda _{2}, 1]}\le & {} C N^{-2},\\ \left\| E-E^{I}\right\| _{L^2[d, \lambda _{2}]} + \left\| u-u^{I}\right\| _{L^2[d, \lambda _{2}]}\le & {} C \varepsilon ^{1/2}(N^{-1}\ln N)^{2},\\ \left\| (E-E^{I})'\right\| _{L^2[d, 1]} + \left\| (u-u^{I})'\right\| _{L^2[d, 1]}\le & {} C \varepsilon ^{-1/2}N^{-1}\ln N. \end{aligned}$$

To cover error analysis we need multiplicative trace inequality which is referred as

Lemma 5

[9]. For $w \in H^{1}(I_{j})$

$$\begin{aligned} |w(x_{s})|^{2} \le 2\big (h_{j}^{-1} \left\| w\right\| ^{2}_{L^{2}(I_{j})} + \left\| w\right\| _{L^{2}(I_{j})} \left\| w'\right\| _{L^{2}(I_{j})}\big ), \qquad s \in \{j-1, j\}. \end{aligned}$$

(17)

Proof

For any $w \in H^{1}(0, 1)$, we set $v(t) = w^{2}(t)(t - 1/4)$. Now we just verify the inequality in (17) for $t = 3/4$ and proof at another point will be similar,

$$\begin{aligned} v'(t) = w^{2}(t) + 2 w(t) w'(t)(t-1/4). \end{aligned}$$

Using the definition of v(t) we see that $v(3/4) = \int _{1/4}^{3/4} v'(t) dt$.

$$\begin{aligned} |v(3/4) |\le & {} \int _{1/4}^{3/4} |v'(t)|dt,\\\le & {} \int _{1/4}^{3/4} |w^{2}(t) |dt + \int _{1/4}^{3/4} |2 w(t) w'(t)(t-1/4) |dt. \end{aligned}$$

Therefore,

$$\begin{aligned} |v(3/4) |\le & {} \int _{0}^{3/4} |w^{2}(t) |dt + \int _{0}^{3/4} |2 w(t) w'(t)(t-1/4) |dt,\\\le & {} \left\| w(t) \right\| ^{2}_{L^{2}[0,3/4]} + 2 \max _{t \in [0,3/4]} |t-1/4 |\left\| w(t) \right\| _{L^{2}[0,3/4]} \left\| w'(t) \right\| _{L^{2}[0,3/4]},\\\le & {} \left\| w(t) \right\| ^{2}_{L^{2}[0,3/4]} + \left\| w(t) \right\| _{L^{2}[0,3/4]} \left\| w'(t) \right\| _{L^{2}[0,3/4]}. \end{aligned}$$

Hence for all the points it can be shown similarly by changing in the definition of v(t). So, scaling argument tells us the consequences leads to the validation of the result given in the Lemma 5.    $\blacksquare$

Lemma 6

On the Shishkin mesh given in Subsect. 3.1, take $\rho = 2$ and $\eta = u - u^{I}$, we have the following bounds for $\{\eta '\}$

$$\begin{aligned} \{\eta '(x_{j})\}^{2}\le {\left\{ \begin{array}{ll} C \varepsilon ^{-2} (N^{-1}\ln N)^{2} \qquad j= N/4 + 1, \cdots , N/2~\text {and}~j= 3N/4 + 1, \cdots , N,\\ C \varepsilon ^{-2} N^{-3} \qquad j= 0, \cdots , N/4~\text {and}~j= N/2 + 1, \cdots , 3N/4.\\ \end{array}\right. } \end{aligned}$$

(18)

Proof

The proof of this lemma is quite similar as the Lemma 3.6 has been proved in [21]. So we leave the steps of the proof.    $\blacksquare$

Theorem 3

Let the assumption in Remark 1 holds, then the following result on Interpolation error holds true

$$\begin{aligned} \left\| u - u^{I}\right\| _{DG} \le C N^{-1} \ln N \end{aligned}$$

(19)

Proof

Recall that $\eta$ is continuous on interelement boundaries we have, $[\eta (x_{j})] = 0$. Using coercivity property in Lemma 2, we have

$$\begin{aligned} \left\| \eta \right\| _{DG}^{2} = \sum _{j=1}^{N} \bigg (\varepsilon \left\| \eta ' \right\| ^{2}_{L^{2}(I_{j})} + \gamma ^{2} \left\| \eta \right\| ^{2}_{L^{2}(I_{j})}\bigg ) \end{aligned}$$

Now bounds can be obtained from the estimations in Lemma 3 and Remark 2.    $\blacksquare$

5 Uniform Convergence

In this section, we deduce bound for error $u - u_{N}$, which will be free from $\varepsilon$. The obtained bound in this section relies on a priori estimate of the exact solution u and an special interpolant first introduced in [18].

Theorem 4

We introduce $\chi = u^{I} - u_{N}$. Applying Galerkin orthogonality and coercivity properties from (10a) and (10b) of Lemma 2, respectively, we have

$$\begin{aligned} \left\| \chi \right\| _{DG} \le C N^{-1} \ln N. \end{aligned}$$

(20)

Proof

Consider,

$$\begin{aligned} \left\| \chi \right\| _{DG}^{2}= & {} B(\chi , \chi ) = B(\eta , \chi ),\\= & {} B_{1}(\eta , \chi ) + B_{2}(\eta , \chi ). \end{aligned}$$

Since $\eta$ is continuous on $\varOmega$ which implies that $[\eta ]_{j} = 0$, for $j = 0, 1, \cdots , N$. Therefore,

$$\begin{aligned} B_{1}(\eta , \chi ) = \sum _{j=1}^{N} \int _{I_{j}} \varepsilon \eta ' \chi ' dx - \sum _{j=0}^{N} \varepsilon \big ( [\chi (x_{j})]\{\eta '(x_{j})\}\big ) = I_{1} + I_{2}, \end{aligned}$$

and

$$\begin{aligned} B_{1}(\eta , \chi ) = \sum _{j=1}^{N} \int _{I_{j}}(b\eta ' + c\eta )\chi dx. \end{aligned}$$

Making the use of Cauchy-Schwarz inequality, Eq. (12c) and Remark 2, we obtain,

$$\begin{aligned} |I_{1}|\le \bigg (\sum _{j=1}^{N} \int _{I_{j}}\varepsilon (\eta ')^{2} dx \bigg )^{1/2} \bigg (\sum _{j=1}^{N} \int _{I_{j}}\varepsilon (\chi ')^{2} dx \bigg )^{1/2} \le C N^{-1} \ln N \left\| \chi \right\| _{DG}. \end{aligned}$$

(21)

Now we have to make a bound for $I_{2}$. In this case the path of approach will be different,

$$\begin{aligned} |I_{2}|\le & {} \bigg (\sum _{j=0}^{N} \frac{\varepsilon ^2}{\sigma _{j}} \{\eta '(x_{j})\}^{2}\bigg )^{1/2} \bigg (\sum _{j=0}^{N} \sigma _{j} [\chi (x_{j})]^{2}\bigg )^{1/2},\\\le & {} \bigg (\sum _{j=0}^{N/4} \frac{\varepsilon ^2}{\sigma _{j}} \varepsilon ^{-2} N^{-3} + \sum _{j=N/4 + 1}^{N/2} \frac{\varepsilon ^2}{\sigma _{j}} \varepsilon ^{-2} N^{-2}\ln ^{2}N\\+ & {} \sum _{j=N/2 + 1}^{3N/4} \frac{\varepsilon ^2}{\sigma _{j}} \varepsilon ^{-2} N^{-3} + \sum _{j=3N/4 + 1}^{N} \frac{\varepsilon ^2}{\sigma _{j}} \varepsilon ^{-2} N^{-2}\ln ^{2}N\bigg )^{1/2} \left\| \chi \right\| _{DG}. \end{aligned}$$

In this procedure we take the exact choice of discontinuity-penalization parameter,

$$\begin{aligned} \sigma _{j} = N \quad \text {for all}~j = 0, 1, \cdots , N \end{aligned}$$

Meanwhile, $I_{2}$ can be estimated as,

$$\begin{aligned} |I_{2}|\le C N^{-1} \ln N \left\| \chi \right\| _{DG}. \end{aligned}$$

(22)

Collecting (21) and (22), we get

$$\begin{aligned} B_{1}(\eta , \chi ) \le C N^{-1}\ln N \left\| \chi \right\| _{DG}. \end{aligned}$$

(23)

It only remains to bound $B_{2}(\eta , \chi )$ and our purpose will be served. To bound the estimation one can refer [20] which also gives the bound

$$\begin{aligned} |B_{2}(\eta , \chi )|\le C N^{-1} \ln N \left\| \chi \right\| _{DG}. \end{aligned}$$

(24)

Therefore (23) and (24) together gives us (20) in Theorem 4.    $\blacksquare$

Theorem 5

Let u is the exact solution of (1) and $u_{N}$ is the discretized solution of the NIPG formulation 7 on the Shishkin mesh introduced in Subsect. 3.1. Then the discretization error obeys the following bound

$$\begin{aligned} \left\| u - u_{N}\right\| _{DG} \le C N^{-1} \ln N. \end{aligned}$$

Proof

From the estimations obtained in Theorem 3, Theorem 4 followed by triangular inequality we get the desired result.    $\blacksquare$

6 Numerical Result and Implementation

In this section, we present numerical result for a test problem to illustrate the theoretical results that has been established in Sect. 5.

Example 1

$$\begin{aligned} - \varepsilon u'' + b(x) u'(x) + 7 u(x)= & {} x,\\ u(0) = u(1)= & {} 0. \end{aligned}$$

where

$$\begin{aligned} b(x) = {\left\{ \begin{array}{ll} 3 x^{2} + 2 \quad x\le d,\\ 0.5x \qquad x > d, \end{array}\right. } \end{aligned}$$

and $d = 0.7$.

The test problem in Example 1 is taken similar to the test problems in Example 7.1 and 7.2 in [11]. Solution of the test problem given in Example 1 exhibits an interior layer at $x = d$. The curve of computed solution along with exact solution is sketched in Fig. 1 with $N = 1024$ and $\varepsilon = 10^{-7}$ for Example 1. The solution curve is showing interior layer at $x = d$ where d is a point of discontinuity of convection coefficient b inside the domain depends on the user choice. The exact choice of discontinuous-penalization parameters $\sigma _{j}$’s has been presented in Sect. 5.

Error and convergence rate are examined for various value of N and $\varepsilon$ with respect to DG-norm, $\left\| \cdot \right\| _{\text {DG}}$. In the present Example (1) do not have exact solution, so we apply double mesh principle to find out errors in the numerical solution and their convergence rates. We determine errors for DG-norm by $\left\| u_{N} - u_{2N} \right\| _{\text {DG}}$. The rate of convergence using double mesh principle can be calculated by the following expression

$$\begin{aligned} R_{\varepsilon }^{N} = \log _{2}\bigg (\frac{\left\| u_{N} - u_{2N} \right\| _{\text {DG}}}{\left\| u_{2N} - u_{4N} \right\| _{\text {DG}}}\bigg ) \end{aligned}$$

The error and rate of convergence calculated in DG-norm for the above example are provided by Table 1 and Table 2, respectively. It can be easily seen that the solution converges with desired order, which is free from perturbation parameter $\varepsilon$. It is presented in Table 2, which reflects the first order convergence in $\varepsilon$ weighted norm introduced by the bilinear form (9) that supports our theoretical findings. Hence, the numerical solution approximates the exact solution very well. All the calculations have been performed using FENICS library for finite element method and CPU run time was approximately two minutes.

Table 1. $\left\| u_N-u_{2N}\right\| _{\text {DG}}$ errors for Example 1.

Table 2. Convergence rates $R^N_{\varepsilon }$ for Example 1.

Fig. 1.

Computed and Exact solution for Example 1 for $N = 1024$ and $\varepsilon = 10^{-7}$.

7 Conclusion

The singularly perturbed convection-diffusion problem with discontinuous coefficient is investigated in this paper. In order to find the numerical approximation when the perturbation parameter $\varepsilon$ goes to zero, we apply NIPG method on piecewise uniform Shishkin mesh and convergence result is established. Numerical results are provided to defend our analytical findings. It is a singular perturbation problem with single perturbation parameter with discontinuities. We can extend this work to two parametric perturbation problem with discontinuities caused layer phenomenon at both boundaries points and some of the interior points as well. Not only this, but these problems can be extended to its $2-D$ limitations, in which we can discuss the uniform convergence of continuous/discontinuous Galerkin methods in $\varepsilon$-weighted norm and usual $L^{2}$-norm. So many cases can be there, like discontinuous coefficients, problem with two perturbation parameters and turning point, etc. In these conditions, solution may have boundary and interior layers simultaneously. Domain discretization also matter for these problem, for ex; if one discretize the domain by Bakhvalov mesh or more than that by exponential mesh gives the sharper convergence than the mesh discretization by Shishkin mesh.

8 Discussion

The literature contains a large number of studies that discuss the continuous/discontinuous Galerkin technique for singular perturbation problem (SPP). There are several papers in the literature which discussed the convergence of NIPG method for instance, one can see ([10, 11, 13, 21]). In first three papers authors deduced the first order convergence, while the last one reflects superconvergence of the solution. Except [11] all other deals with the discontinuous Galerkin method for SPP with continuous coefficients and source term but the former has convergence result for the problem with discontinuous source term. Furthermore, so many articles in the literature which we have already discussed in Sect. 1 that have analysis of SPP with discontinuous coefficient or source term. But there are not a single paper that analyze NIPG method for SPP with discontinuous source term ever before. That’s why this paper is elaboration of first order convergence up to logarithmic factor of NIPG method on usual Shishkin mesh where discontinuity of jump type occurs in convection coefficient.