Keywords

1 Introduction

Structural analysis and structural health monitoring are two essential issues in structural engineering from nano size to macro size [1,2,3,4,5,6,7,8,9,10]. The objective of structural health monitoring is to prevent the failure of structures [11,12,13,14]. As a result, structural health monitoring prevents additional costs for repairing and reconstruction of damaged structures [15,16,17]. In this regard, vibration-based analysis of damaged structures plays an essential role in structural health monitoring [18,19,20,21,22]. Generally, there are two main types of analysis of damaged structures: Forward analysis and inverse analysis [23,24,25,26,27,28].

The forward analysis deals with modeling damages to provide modal characteristics of structures such as mode shapes and their corresponding natural frequencies [29,30,31,32]. Also, the forward analysis may use to obtain dynamic responses of the damaged structures [33,34,35,36]. In this field, much research has been conducted.

In reverse analysis, on the other hand, the goal is to obtain the position or extent of the damage by having the vibrational properties of the system. So far, much research has been done in this area. Some of these approaches are based on optimization, a part of them are based on the mode shapes, the others are based on machine learning algorithms. In this research, one of the machine learning algorithms called the artificial neural network algorithm is used to detect horizontal cracks in steel beams, including a vertical crack. In this way, first, the modeling of finite components of horizontal cracks in steel beams is described in the next section. Then the artificial neural network is introduced, the technique proposed in this paper, and then numerical examples and results are presented, and finally, conclusions are presented.

2 Basic Mathematical Formulations

2.1 Geometry

In order to investigate the damage identification problem, a thin isotropic beam of length \(L\) with a rectangular cross-sectional area \(A\), width \(b\), and thickness \(h\) is modeled in the same procedure as [37]. As shown in Fig. 1-b, the damaged beam is modeled by the combination of four intact sub-beams, which is separated by a through-the-width horizontal crack of length \({L}_{2}\) which is located at the midplane and a distance \({L}_{1}\) from the left end of the beam. In this manner, each sub-beam has a length and thickness of \({L}_{i}\times {h}_{i} (i=1-4)\) where \(i\) represents the number of sub-beams, \({h}_{1}={h}_{4}=h\), \({L}_{2}={L}_{3}\), and \({L}_{4}=L-{L}_{1}-{L}_{2}\).

Fig. 1.
figure 1

a. The geometry of isotropic beam, b. Representation of beam into four sub-beams.

Full size image

2.2 Finite Element Modeling

To study the vibration analysis of the presented beam, in this paper, the Euler-Bernoulli beam theory is adopted to establish vibration equations. Therefore, a higher-order beam element as demonstrated in Fig. 2 with three nodes and six degrees of freedom, including vertical displacement \(\mathrm{w}\) and slope \(w^{\prime}\) is introduced.

Fig. 2.
figure 2

(a) Higher-order beam element. (b) intrinsic coordinate of the element

Full size image

The displacement field equation for the higher-order beam element can be interpolated via the Hermite interpolation function and in terms of the intrinsic coordinate as:

$${w}=\sum_{{i}=1}^{3}\left[{{w}}_{2{i}-1}\left(\eta \right){{w}}_{{i}}+{\Lambda }_{2{i}}(\eta ){{w}}_{{i}}^{{^{\prime}}}\right]=\left[\Lambda \right]\left\{{d}\right\}$$
(1)

where \(\eta \) is the intrinsic coordinate, i.e. \(\eta =\frac{{x}}{{{L}}_{{e}}}\) and \({{L}}_{{e}}\) is the length of the respective element. As well, \(\left\{{d}\right\}\) indicates the vector of DOFs and \({\Lambda }_{{i}}\left(\eta \right)\) are the shape functions associated with \({i}\) th degrees of freedom which are given as:

$${\Lambda }_{1}\left(\eta \right)=1-23{\eta }^{2}+66{\eta }^{3}-68{\eta }^{4}+24{\eta }^{5}$$
$${\Lambda }_{2}\left(\eta \right)={{L}}_{{e}}(\eta -6{\eta }^{2}+13{\eta }^{3}-12{\eta }^{4}+4{\eta }^{5})$$
$${\Lambda }_{3}\left(\eta \right)=16{\eta }^{2}-32{\eta }^{3}+16{\eta }^{4}$$
$${\Lambda }_{4}\left(\eta \right)={{L}}_{{e}}(-8{\eta }^{2}+32{\eta }^{3}-40{\eta }^{4}+16{\eta }^{5})$$
$${\Lambda }_{5}\left(\eta \right)=7{\eta }^{2}-34{\eta }^{3}+52{\eta }^{4}-24{\eta }^{5}$$
$${\Lambda }_{6}\left(\eta \right)={{L}}_{{e}}\left(-{\eta }^{2}+5{\eta }^{3}-8{\eta }^{4}+4{\eta }^{5}\right)$$
(2)
$$\{ d\} = \{ w_{1} \,w_{1}^{\prime } \;w_{2} \;w_{2}^{\prime } \;w_{2} \;w_{3}^{\prime } \}$$
(3)

The energy approach is utilized to obtain the element stiffness and mass matrices, which is not described in detail here [38, 39]. Hence, the potential and kinetic energy of an element can be stated in terms of displacement vector as follows [40]:

$${{U}}_{{e}}=\frac{1}{2}{\left\{{d}\right\}}^{{T}}\left[{{K}}_{{e}}\right]\left\{{d}\right\}$$
(4)
$${{T}}_{{e}}=\frac{1}{2}{\left\{\dot{{d}}\right\}}^{{T}}\left[{{M}}_{{e}}\right]\left\{\dot{{d}}\right\}$$
(5)

Thus, the element stiffness matrix can be obtained as:

$$\left[{{K}}_{{e}}\right]={\int }_{0}^{1}{\left({EI}\right)}_{{e}}{\left[{\varLambda }_{,{xx}}\right]}^{{T}}\left[{\varLambda }_{,{xx}}\right]{{L}}_{{e}}{d\eta }$$
(6)

Likewise, the element mass matrix can be expressed as follows:

$$\left[{{M}}_{{e}}\right]={\int }_{0}^{1}{{m}}_{{e}}{\left[\varLambda \right]}^{{T}}\left[\varLambda \right]{{L}}_{{e}}{d\eta }$$
(7)

In which, \({{m}}_{{e}}\) and \({\left({EI}\right)}_{{e}}\) are the density and flexural stiffness of the typical element, respectively.

Equations (6) and (7) give the element stiffness and mass matrices of each sub-beams. To obtain the total corresponding matrices \(\left[{K}\right]\) and \(\left[\mathrm{M}\right]\), the stiffness and mass matrices are assembled. To do this, the displacement continuity conditions have been established at the junction of sub-beams (1-2-3) and (2-3-4). Regarding Fig. 3, the deflection and slope of the connecting nodes at the tips of the crack are equal. Therefore, the corresponding entries of the stiffness and mass matrices of connected sub-beams are superposed to constitute the whole beam's total stiffness and mass matrices.

Fig. 3.
figure 3

Delamination boundaries

Full size image

2.3 Solution Method

The free vibrations equation of motion for the entire structure is acquired as follows:

$$\left[{M}\right]\left\{\ddot{\Delta }\right\}+\left[{K}\right]\left\{\Delta \right\}=\left\{0\right\}$$
(8)

where \(\left[\Delta \right]\) Indicates the nodal DOFs of the whole model. Considering a general solution of \(\left\{\Delta \right\}=\left\{{\Delta }_{0}\right\}{{e}}^{\widehat{{i}}{\omega t}}\) for Eq. (8), and assuming \(\uplambda ={\upomega }^{2}\) yields eigenvalue problem as:

$$\left(\left[{K}\right]-\uplambda \left[{M}\right]\right)\left\{{\Delta }_{0}\right\}=\left\{0\right\}$$
(9)

Which gives natural frequency \(\upomega \) and corresponding mode shapes of the system \(\left\{\Delta \right\}\).

2.4 Artificial Neural Network

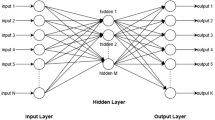
This study uses a feed-forward ANN to localize damage levels in beams with horizontal cracks. Figure 4 indicates that our MLP contains the input, hidden, and output layers. Nodes in hidden and output layers utilize a non-linear function.

The weighted sum of input data is calculated as following [41]:

$${{input}}_{{k}}={\sum }_{{i},{k}=1}^{{n},{m}}{{b}}_{{k}}+{{w}}_{{ik}}*{{x}}_{{i}};{ k}=\left(1:{m}\right);{ i}=(1:{ n})$$
(10)

where \({{w}}_{{ik}}\) show weight between the \({{i}}^{{th}}\) neurons and the \({{k}}^{{th}}\) neurons, \({{b}}_{{k}}\) indicates the bias ratio of hidden layers and inputs; \({{x}}_{{i}}\) show the output in \({{i}}^{{th}}\) neurons in the input layer; m and n are the number of the neurons in hidden layer and input layer, respectively. Furthermore, \({{input}}_{{k}}\) are the input of \({{k}}^{{th}}\) neurons in the hidden layer.

Fig. 4.
figure 4

Architecture of an MLP [41]

Full size image

In this article, after calculating the \({\mathrm{input}}_{\mathrm{k}}\) of a neuron on a layer, the nonlinear function is applied through the following relation to compute the output for the \({\mathrm{j}}^{\mathrm{th}}\) neuron [41]:

$${{ouput}}_{{j}}=\left(\frac{2}{1+\frac{1}{{{e}}^{2{{input}}_{{q}}}}}\right)-1$$
(11)

The function is called the Tan-Sigmoid transfer function. The diagram of such a function is shown in Fig. 5.

Fig. 5.
figure 5

Tan-Sigmoid activation function [41]

Full size image

Note that, in Eq. (11), \({\mathrm{input}}_{\mathrm{q}}\) is input of \({\mathrm{q}}^{\mathrm{th}}\) neuron in the output layer, and \({\mathrm{ouput}}_{\mathrm{j}}\) denotes \({\mathrm{j}}^{\mathrm{th}}\) neuron related to the output layer.

3 Proposed Approach

The current study uses a machine learning-based approach to damage detection in steel beam structures with a horizontal crack. Figure 6 shows the flowchart of the proposed technique used in the present study. As seen, the finite element method performs problem modeling using the equivalence technique of a damaged beam with a horizontal crack approximated with four intact beams. A database is then created to perform the interpolation by the Artificial Neural Network.

Fig. 6.
figure 6

Flowchart of the proposed technique used in the present study

Full size image

In this way, the artificial neural network inputs are the first five natural frequencies. The artificial neural network output is the location of the horizontal crack of the desired size in the considered steel beam. In the next section, results are presented.

4 Results and Discussion

The results of this study is presented in this section. The characterisitcs of the considered beam are presented in Table 1. Three hundred samples of the first five natural frequencies and their corresponding crack positions are used as databases to evaluate the method's performance presented in this paper.

Table 1. The characterisitcs of the considered beam
Full size table

The distribution of the Artificial Neural Network outputs (horizontal crack positions) is shown in Fig. 7. As can be seen, the distribution of artificial neural network outputs used in this research is uniform. Also, the horizontal crack length of the beam in this research is 0.3 cm, which is small enough to detect damage.

Fig. 7.
figure 7

The distribution of artificial neural network outputs

Full size image
Fig. 8.
figure 8

Result of training process of ANN

Full size image

Result of training process is shown in Fig. 8. Also, Result of test process is shown in Fig. 9.

Fig. 9.
figure 9

Result of training process of ANN

Full size image

Figures 8 and 9 show that the regression indices for training and testing processes are 0.954 and 0.979, respectively, demonstrating our predicting model's good approximation and efficiencies. Figure 10 shows the accuracy of the model created in this research.

Fig. 10.
figure 10

The accuracy of the model created in this research

Full size image
Fig. 11.
figure 11

Seventeen damage scenarios for evaluating the accuracy of the predictive ANN model

Full size image

Figure 11 presents the accuracy of the predictive ANN model for seventeen damage scenarios. As can be seen, ANN identifies the approximate location of the damages with sufficient certainty for the considered damages.

Also, to imagine the quantified numerical differences between the actual location of the crack and the location of crack detected by ANN, Table 2 is presented.

Table 2. The quantified numerical differences between the actual location of the crack and the location of crack detected by ANN
Full size table

As listed in Table 2, the location of cracks detected by ANN is well compatible with the actual location of cracks.

5 Conclusions

Structural health monitoring is one of the most critical efforts to prevent the failure of the structures before it occurs. Various methods have been proposed to monitor the structure's health, many of which are considered non-destructive tests. One of the most popular non-destructive tests is vibration-based non-destructive tests. These tests are also known as vibration-based damage detection techniques. In this research, the detection of damage to steel beams with a horizontal crack is investigated using artificial neural networks. In this way, first, a beam is equated with a horizontal crack with four intact beams. In this way, the finite element method is used. After modeling, they are using the finite element method, databases consisting of the first five natural frequencies and the position of the horizontal crack in the steel beam are created and fed to the artificial neural network. The results of this study show that the neural network created in this paper can predict the crack position with acceptable accuracy by having the first five natural frequencies.