Keywords

9.1 Introduction

Issues related to the strength study include static/dynamic materials tests and consideration of different physical fields interaction. This is due to various modern structures and different conditions of their operation. It is often necessary to consider the interaction between mechanical, diffusion, temperature and other fields in applied calculations.

Experimental study of the interaction between mechanical and diffusion fields began in the 20s of the twentieth century. Many scientific theories have been formed that allow describing the coupled mechanical, diffusion and other fields in a solid medium. Among the most recent works are [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]. Various aspects of mechanodiffusion processes modelling are considered here: beginning with initial–boundary problem formulation and ending with a description of methods for solving these problems. Here are stationary [4, 11, 12] and unsteady problems [1,2,3, 5,6,7,8, 13,14,16].

The main complexity is the Laplace inverse transform when solving mechanodiffusion problems analytically. It is often used in solving initial–boundary problems. The Durbin method [2, 3, 7, 8, 14] or similar algorithms based on the fact that the Mellin integral is expressed through the inverse Fourier transform are used here. Special quadrature formulas [1, 5, 15] allow to calculate the integral. These methods have proven themselves in calculating the originals in a certain class of functions. However, these algorithms are not suitable for Green’s functions because they belong to the generalized function class, and it is difficult to use numerical integration methods in this case.

Numerical algorithms based on finite difference methods [6, 13] and the finite element methods [16] are an alternative to analytical methods. In addition, numerical methods are the only way to solve the boundary value problem in some cases. A disadvantage of numerical methods is that solution comes to a discrete set of values, which is difficult to analyse and investigate later. A rather complicated mathematical problem is the question of algorithm stability and convergence.

This article proposes an analytical method for solving the unsteady mechanodiffusion problem for a rectangular plate. The method implies the Laplace transform and Fourier series expansion in eigenfunctions of the elastic diffusion operator. This approach has been tested for one-dimensional problems of elastic diffusion and thermoelastic diffusion [17, 18].

9.2 Problem Formulation

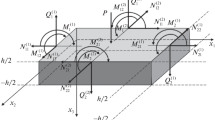
We considered a multicomponent rectangular plate under the action of unsteady longitudinal forces. The resulting mass transfer and diffusion flux relaxations are taken into account inside the plate.

The mathematical model describing two-dimensional elastic diffusion processes for a homogeneous orthotropic medium in the rectangular Cartesian coordinate system [19, 20]:

$$\begin{aligned} \begin{array}{c} {\frac{\partial ^{2} u_{1}}{\partial x_{1}^{2}} +C_{66} \frac{\partial ^{2} u_{1} }{\partial x_{2}^{2} } +C_{0} \frac{\partial ^{2} u_{2} }{\partial x_{1} \partial x_{2} } =\ddot{u}_{1} +\displaystyle {\sum _{j=1}^{N}}\alpha _{1}^{j} \frac{\partial \eta _{j} }{\partial x_{1} } ,} \\ {C_{0} \frac{\partial ^{2} u_{1} }{\partial x_{2} \partial x_{1} } +C_{66} \frac{\partial ^{2} u_{2} }{\partial x_{1}^{2} } +C_{22} \frac{\partial ^{2} u_{2} }{\partial x_{2}^{2} } =\ddot{u}_{2} +\displaystyle {\sum _{j=1}^{N}}\alpha _{2}^{j} \frac{\partial \eta _{j} }{\partial x_{2} } ,} \end{array} \end{aligned}$$
$$\begin{aligned} \begin{array}{c} {D_{1}^{q} \frac{\partial ^{2} \eta _{q} }{\partial x_{1}^{2} } +D_{2}^{q} \frac{\partial ^{2} \eta _{q} }{\partial x_{2}^{2} } =\dot{\eta }_{q} +\tau _{q} \ddot{\eta }_{q} +\Lambda _{11}^{q} \frac{\partial ^{3} u_{1} }{\partial x_{1}^{3} } +\Lambda _{21}^{q} \frac{\partial ^{3} u_{1} }{\partial x_{2}^{2} \partial x_{1} } +} \\ {+\Lambda _{12}^{q} \frac{\partial ^{3} u_{2} }{\partial x_{1}^{2} \partial x_{2} } +\Lambda _{22}^{q} \frac{\partial ^{3} u_{2} }{\partial x_{2}^{3} } ,\,\,\, \eta _{N+1} =-\displaystyle {\sum _{j=1}^{N}}\eta _{j} \,\, \left( q=\overline{1,N}\right) ;} \end{array} \end{aligned}$$
(9.1)
$$\begin{aligned} \begin{array}{c} {\left. u_{2} \right| _{x_{1} =0} =f_{111} \left( x_{2} ,\tau \right) ,\,\, \left. \eta _{q} \right| _{x_{1} =0} =f_{q+2,11} \left( x_{2} ,\tau \right) ,} \\ {\left. u_{1} \right| _{x_{2} =0} =f_{121} \left( x_{1} ,\tau \right) ,\,\, \left. \eta _{q} \right| _{x_{2} =0} =f_{q+2,21} \left( x_{1} ,\tau \right) ,} \\ {\left. \left( \frac{\partial u_{1} }{\partial x_{1} } +C_{12} \frac{\partial u_{2} }{\partial x_{2} } -\displaystyle {\sum _{j=1}^{N}}\alpha _{1}^{j} \eta _{j} \right) \right| _{x_{1} =0} =f_{211} \left( x_{2} ,\tau \right) ,} \\ {\left. \left( C_{12} \frac{\partial u_{1} }{\partial x_{1} } +C_{22} \frac{\partial u_{2} }{\partial x_{2} } -\displaystyle {\sum _{j=1}^{N}}\alpha _{2}^{j} \eta _{j} \right) \right| _{x_{2} =0} =f_{221} \left( x_{1} ,\tau \right) ,} \end{array} \end{aligned}$$
(9.2)
$$\begin{aligned} \begin{array}{c} {\left. u_{2} \right| _{x_{1} =l_{1} } =f_{112} \left( x_{2} ,\tau \right) ,\,\, \left. \eta _{q} \right| _{x_{1} =l_{1} } =f_{q+2,12} \left( x_{2} ,\tau \right) ,} \\ {\left. u_{1} \right| _{x_{2} =l_{2} } =f_{122} \left( x_{1} ,\tau \right) ,\,\, \left. \eta _{q} \right| _{x_{2} =l_{2} } =f_{q+2,22} \left( x_{1} ,\tau \right) ,} \\ {\left. \left( \frac{\partial u_{1} }{\partial x_{1} } +C_{12} \frac{\partial u_{2} }{\partial x_{2} } -\displaystyle {\sum _{j=1}^{N}}\alpha _{1}^{j} \eta _{j} \right) \right| _{x_{1} =l_{1} } =f_{212} \left( x_{2} ,\tau \right) ,} \\ {\left. \left( C_{12} \frac{\partial u_{1} }{\partial x_{1} } +C_{22} \frac{\partial u_{2} }{\partial x_{2} } -\displaystyle {\sum _{j=1}^{N}}\alpha _{2}^{j} \eta _{j} \right) \right| _{x_{2} =l_{2} } =f_{222} \left( x_{1} ,\tau \right) .} \end{array} \end{aligned}$$

Here, all quantities are dimensionless. Their relation to their dimensional counterparts (when written the same way, they are indicated with a dash) is defined as follows:

$$\begin{aligned} \begin{array}{c} {x_{i} =\frac{x'_{i} }{L} ,\,\, u_{i} =\frac{u'_{i} }{L} ,\,\, \tau =\frac{Ct}{L} ,\,\, C_{ij} =\frac{C'_{ij} }{C'_{11} } ,\,\, C^{2} =\frac{C'_{11} }{\rho } ,\,\, \alpha _{\alpha }^{q} =\frac{\alpha _{\alpha \alpha }^{\left( q\right) } }{C'_{11} } ,} \\ {D_{\alpha }^{q} =\frac{D_{\alpha \alpha }^{\left( q\right) } }{CL} ,\,\, \Lambda _{\alpha \beta }^{q} =\frac{m^{\left( q\right) } D_{\alpha \alpha }^{\left( qq\right) } \alpha _{\beta \beta }^{\left( q\right) } n_{0}^{\left( q\right) }}{\rho RT_{0}CL },\,\, l_{i} =\frac{l_{i}^{*} }{L} ,\,\, \tau _{q} =\frac{C\tau ^{\left( q\right) } }{L} ,} \end{array} \end{aligned}$$
(9.3)
$$\begin{aligned} \begin{array}{c} C_{0} =C_{66} +C_{12},\,\, C'_{11} =C_{1111} ,\,\, C'_{22} =C_{2222} ,\,\, C'_{66} =C_{1212} ,\,\, C'_{12} =C_{1122} ,\\ f_{1kl} \left( x_{1} ,\tau \right) =\frac{f_{1kl}^{*} \left( x_{1} ,t\right) }{L} ,\,\, f_{q+2,kl} \left( x_{1} ,\tau \right) =f_{q+2,kl}^{*} \left( x_{1} ,t\right) ,\,\, f_{2kl} \left( x_{1} ,\tau \right) =\frac{f_{2kl}^{*} \left( x_{1} ,\tau \right) }{C_{1111} }, \end{array} \end{aligned}$$

where t is a time parametr; \(x_{i}^{*} \) is a rectangular Cartesian coordinate; \(u_{i}^{*} \) is a displacement vector component; L is the diagonal size of the plate having dimensions \(l_{1}^{*} \times l_{2}^{*} \); \(\eta _{q} \) is the concentration increment of “q”th component in \(N+1\)-component medium; \(n_{0}^{\left( q\right) } \) is the initial concentration of “q”th component; \(C_{ijkl} \) is the component of elastic constants tensor; \(\rho \) is a mass density; \(\alpha _{ij}^{\left( q\right) } \) is a coefficient characterizing the volume change of the medium due to diffusion; \(D_{ij}^{\left( q\right) } \) is a diffusion coefficient; R is the universal gas constant; \(T_{0} \) is an average temperature; \(m^{\left( q\right) } \) is a molar mass of “q”th component, \(f_{klm}^{*} \) is an external perturbation; \(\tau ^{\left( q\right) } \) is the relaxation time of the diffusion flux.

We assume the initial conditions are zero.

9.3 Integral Representation of the Solution

The solution to the problem is sought in the integral form as follows:

$$\begin{aligned} \begin{array}{c} {\left\{ \begin{array}{c} {u_{1} \left( x_{1} ,x_{2} ,\tau \right) } \\ {u_{2} \left( x_{1} ,x_{2} ,\tau \right) } \\ {\eta _{q} \left( x_{1} ,x_{2} ,\tau \right) } \end{array}\right\} =\displaystyle {\sum _{k=1}^{N+2}\int _{0}^{\tau }\int _{0}^{l_{2} }}\left\{ \begin{array}{c} {G_{1k1} \left( x_{1} ,x_{2} ,\zeta ,t \right) } \\ {G_{2k1} \left( x_{1} ,x_{2} ,\zeta ,t \right) } \\ {G_{q+2,k1} \left( x_{1} ,x_{2} ,\zeta ,t \right) } \end{array}\right\} f_{k11} \left( \zeta ,\tau -t \right) d\zeta dt +} \\ {+\displaystyle {\sum _{k=1}^{N+2}\int _{0}^{\tau }\int _{0}^{l_{2} }}\left\{ \begin{array}{c} {-G_{1k1} \left( l_{1} -x_{1} ,x_{2} ,\zeta ,t \right) } \\ {G_{2k1} \left( l_{1} -x_{1} ,x_{2} ,\zeta ,t \right) } \\ {G_{q+2,k1} \left( l_{1} -x_{1} ,x_{2} ,\zeta ,t \right) } \end{array}\right\} f_{k12} \left( \zeta ,\tau -t \right) d\zeta dt+} \\ { +\displaystyle {\sum _{k=1}^{N+2}\int _{0}^{\tau }\int _{0}^{l_{1} }}\left\{ \begin{array}{c} {G_{1k2} \left( x_{1} ,x_{2} ,\xi ,t \right) } \\ {G_{2k2} \left( x_{1} ,x_{2} ,\xi ,t \right) } \\ {G_{q+2,k2} \left( x_{1} ,x_{2} ,\xi ,t \right) } \end{array}\right\} f_{k21} \left( \xi ,\tau -t \right) d\xi dt +} \\ {+\displaystyle {\sum _{k=1}^{N+2}\int _{0}^{\tau }\int _{0}^{l_{1} }}\left\{ \begin{array}{c} {G_{1k2} \left( x_{1} ,l_{2} -x_{2} ,\xi ,t \right) } \\ {-G_{2k2} \left( x_{1} ,l_{2} -x_{2} ,\xi ,t \right) } \\ {G_{q+2,k2} \left( x_{1} ,l_{2} -x_{2} ,\xi ,t\right) } \end{array}\right\} f_{k22} \left( \xi ,\tau -t \right) d\xi dt ,} \end{array} \end{aligned}$$
(9.4)

where \(G_{mkl} \) are Green’s functions, which satisfy the following initial–boundary value problem (initial conditions are zero):

$$\begin{aligned} \begin{array}{c} {\frac{\partial ^{2} G_{1kl} }{\partial x_{1}^{2} } +C_{66} \frac{\partial ^{2} G_{1kl} }{\partial x_{2}^{2} } +C_{0} \frac{\partial ^{2} G_{2kl} }{\partial x_{1} \partial x_{2} } =\ddot{G}_{1kl} +\displaystyle {\sum _{j=1}^{N}}\alpha _{1}^{j} \frac{\partial G_{j+2,kl} }{\partial x_{1} } ,} \\ {C_{0} \frac{\partial ^{2} G_{1kl} }{\partial x_{2} \partial x_{1} } +C_{66} \frac{\partial ^{2} G_{2kl} }{\partial x_{1}^{2} } +C_{22} \frac{\partial ^{2} G_{2kl} }{\partial x_{2}^{2} } =\ddot{G}_{2kl} +\displaystyle {\sum _{j=1}^{N}}\alpha _{2}^{j} \frac{\partial G_{j+2,kl} }{\partial x_{2} } ,}\\ {D_{1}^{q} \frac{\partial ^{2} G_{q+2,kl} }{\partial x_{1}^{2} } +D_{2}^{q} \frac{\partial ^{2} G_{q+2,kl} }{\partial x_{2}^{2} } =\dot{G}_{q+2,kl} +\tau _{q} \ddot{G}_{q+2,kl} +\Lambda _{11}^{q} \frac{\partial ^{3} G_{1kl} }{\partial x_{1}^{3} } +}\\ {+\Lambda _{21}^{q} \frac{\partial ^{3} G_{1kl} }{\partial x_{2}^{2} \partial x_{1} } +\Lambda _{12}^{q} \frac{\partial ^{3} G_{2kl} }{\partial x_{1}^{2} \partial x_{2} } +\Lambda _{22}^{q} \frac{\partial ^{3} G_{2kl} }{\partial x_{2}^{3} } \,\, \left( q=\overline{1,N}\right) ;} \end{array} \end{aligned}$$
(9.5)
$$\begin{aligned} \begin{array}{c} {\left. \left( \frac{\partial G_{1kl} }{\partial x_{1} } +C_{12} \frac{\partial G_{2kl} }{\partial x_{2} } -\displaystyle {\sum _{j=1}^{N}}\alpha _{1}^{j} G_{j+2,kl} \right) \right| _{x_{1} =0} =\delta _{1k} \delta _{1l} \delta \left( x_{2} -\zeta \right) \delta \left( \tau \right) ,} \\ {\left. \left( C_{12} \frac{\partial G_{1kl} }{\partial x_{1} } +C_{22} \frac{\partial G_{2kl} }{\partial x_{2} } -\displaystyle {\sum _{j=1}^{N}}\alpha _{2}^{j} G_{j+2,kl} \right) \right| _{x_{2} =0} =\delta _{2k} \delta _{2l} \delta \left( x_{1} -\xi \right) \delta \left( \tau \right) ,}\\ {\left. \left( \frac{\partial G_{1kl} }{\partial x_{1} } +C_{12} \frac{\partial G_{2kl} }{\partial x_{2} } -\displaystyle {\sum _{j=1}^{N}}\alpha _{1}^{j} G_{j+2,kl} \right) \right| _{x_{1} =l_{1} } =0,}\\ {\left. \left( C_{12} \frac{\partial G_{1kl} }{\partial x_{1} } +C_{22} \frac{\partial G_{2kl} }{\partial x_{2} } -\displaystyle {\sum _{j=1}^{N}}\alpha _{2}^{j} G_{j+2,kl} \right) \right| _{x_{2} =l_{2} } =0,}\\ {\left. G_{2kl} \right| _{x_{1} =0} =\delta _{2k} \delta _{1l} \delta \left( x_{2} -\zeta \right) \delta \left( \tau \right) ,\,\, \left. G_{q+2,kl} \right| _{x_{1} =0} =\delta _{q+2,k} \delta _{1l} \delta \left( x_{2} -\zeta \right) \delta \left( \tau \right) ,}\\ {\left. G_{1kl} \right| _{x_{2} =0} =\delta _{1k} \delta _{2l} \delta \left( x_{1} -\xi \right) \delta \left( \tau \right) ,\,\, \left. G_{q+2,kl} \right| _{x_{2} =0} =\delta _{q+2,k} \delta _{2l} \delta \left( x_{1} -\xi \right) \delta \left( \tau \right) ,}\\ {\left. G_{2kl} \right| _{x_{1} =l_{1} } =0,\,\, \left. G_{q+2,kl} \right| _{x_{1} =l_{1} } =0,\,\, \left. G_{1kl} \right| _{x_{2} =l_{2} } =0,\,\, \left. G_{q+2,kl} \right| _{x_{2} =l_{2} } =0.} \end{array} \end{aligned}$$
(9.6)

9.4 Algorithm for Green’s Functions

To find the Green’s functions, we apply the Laplace transform to (9.5) and (9.6) and then represent the unknown functions as a double Fourier series. Let’s multiply the first equation in (9.5) by \(\cos \mu _{m} x_{1} \sin \lambda _{n} x_{2} \), the second by \(\sin \mu _{m} x_{1} \cos \lambda _{n} x_{2} \), and the rest by \(\sin \lambda _{n} x_{1} \sin \mu _{n} x_{2} \) (\(\mu _{m} =\pi m/l_{1} \), \(\lambda _{n} =\pi n/l_{2} \)). Then we integrate into the rectangle \(\left[ 0,l_{1} \right] \times \left[ 0,l_{2} \right] \) and obtain the following system of linear algebraic equations:

$$\begin{aligned} \begin{array}{c} {k_{1mn} \left( s\right) G_{1klmn}^{L} \left( \xi ,\zeta ,s\right) +C_{0} \lambda _{n} \mu _{m} G_{2klmn}^{L} \left( \xi ,\zeta ,s\right) +}\\ {+\mu _{m} \displaystyle {\sum _{j=1}^{N}}\alpha _{1}^{j} G_{j+2,klmn}^{L} \left( \xi ,\zeta ,s\right) =F_{1mn} \left( \xi ,\zeta ,s\right) ,} \\ {C_{0} \mu _{m} \lambda _{n} G_{1klmn}^{L} \left( \xi ,\zeta ,s\right) +k_{2mn} \left( s\right) G_{2klmn}^{L} \left( \xi ,\zeta ,s\right) +}\\ {+\lambda _{n} \displaystyle {\sum _{j=1}^{N}}\alpha _{2}^{j} G_{j+2,klmn}^{L} \left( \xi ,\zeta ,s\right) =F_{2mn} \left( \xi ,\zeta ,s\right) ,} \\ {-\mu _{m} K_{qmn} G_{1klmn}^{L} \left( \xi ,\zeta ,s\right) -\lambda _{n} M_{qmn} G_{2klmn}^{L} \left( \xi ,\zeta ,s\right) +} \\ {+k_{q+2,mn} \left( s\right) G_{q+2,klmn}^{L} \left( \xi ,\zeta ,s\right) =F_{q+2,mn} \left( \xi ,\zeta ,s\right) ;} \end{array} \end{aligned}$$
(9.7)
$$\begin{aligned} \begin{array}{c} {F_{1mn} \left( \xi ,\zeta ,s\right) =\frac{4}{l_{1} l_{2} } \left[ C_{66} \lambda _{n} \delta _{1k} \left( \delta _{1l} \cos \lambda _{n} \zeta + \delta _{2l} \cos \mu _{m} \xi \right) -\delta _{2k} \delta _{1l} \sin \lambda _{n} \zeta \right] ,} \\ {F_{2mn} \left( \xi ,\zeta ,s\right) =\frac{4}{l_{1} l_{2} } \left[ \mu _{m} C_{66} \delta _{1k} \left( \delta _{1l} \cos \lambda _{n} \zeta + \delta _{2l} \cos \mu _{m} \xi \right) -\delta _{2k} \delta _{2l} \sin \mu _{m} \xi \right] ,} \\ {F_{q+2,mn} \left( \xi ,\zeta ,s\right) =\frac{4}{l_{1} l_{2} } \lambda _{n} \mu _{m} \delta _{1k} \left( \delta _{2l} \Lambda _{2q} \cos \mu _{m} \xi +\delta _{1l} \Lambda _{1q} \cos \lambda _{n} \zeta \right) +} \\ {+\frac{4}{l_{1} l_{2} } \mu _{m} \delta _{1l} \left( D_{1}^{q} \delta _{q+2,k} -\Lambda _{11}^{q} \displaystyle {\sum _{j=1}^{N}}\alpha _{1}^{j} \delta _{j+2,k}- \Lambda _{11}^{q}\delta _{2k} \right) \sin \lambda _{n} \zeta +} \\ {+\frac{4}{l_{1} l_{2} } \lambda _{n} \delta _{2l} \left( D_{2}^{q} \delta _{q+2,k} -\frac{\Lambda _{22}^{q} }{C_{22} } \displaystyle {\sum _{j=1}^{N}}\alpha _{2}^{j} \delta _{j+2,k} -\frac{\Lambda _{22}^{q} }{C_{22} }\delta _{2k} \right) \sin \mu _{m} \xi ,}\\ {k_{1mn} \left( s\right) =s^{2} +\mu _{m}^{2} +C_{66} \lambda _{n}^{2} ,\,\, k_{2mn} \left( s\right) =s^{2} +C_{66} \mu _{m}^{2} +C_{22} \lambda _{n}^{2} ,} \\ {k_{q+2,mn} \left( s\right) =s+\tau _{q} s^{2} +D_{1}^{q} \mu _{m}^{2} +D_{2}^{q} \lambda _{n}^{2} ,\,\, \Lambda _{1q} =\Lambda _{12}^{q} -\Lambda _{11}^{q} C_{12} ,}\\ {\Lambda _{2q} =\Lambda _{21}^{q} -\frac{\Lambda _{22}^{q} }{C_{22} } C_{12} ,\,\, K_{qmn} =\Lambda _{11}^{q} \mu _{m}^{2} +\Lambda _{21}^{q} \lambda _{n}^{2} ,\,\, M_{qmn} =\Lambda _{12}^{q} \mu _{m}^{2} +\Lambda _{22}^{q} \lambda _{n}^{2};} \end{array} \end{aligned}$$
(9.8)
$$\begin{aligned} G_{rkl}^{L} \left( x_{1} ,x_{2} ,\xi ,\zeta ,s\right) =\displaystyle {\int _{0}^{\infty }}G_{rkl} \left( x_{1} ,x_{2} ,\xi ,\zeta ,\tau \right) e^{-s\tau } d\tau , \end{aligned}$$
$$\begin{aligned} \begin{array}{c} {G_{1kl}^{L} \left( x_{1} ,x_{2} ,\xi ,\zeta ,s\right) =\displaystyle {\sum _{m=0}^{\infty }\sum _{n=1}^{\infty }}G_{1klmn}^{L} \left( \xi ,\zeta ,s\right) \cos \mu _{m} x_{1} \sin \lambda _{n} x_{2},} \\ {G_{2kl}^{L} \left( x_{1} ,x_{2} ,\xi ,\zeta ,s\right) =\displaystyle {\sum _{m=1}^{\infty }\sum _{n=0}^{\infty } }G_{2klmn}^{L} \left( \xi ,\zeta ,s\right) \sin \mu _{m} x_{1} \cos \lambda _{n} x_{2},}\\ {G_{q+2,kl}^{L} \left( x_{1} ,x_{2} ,\xi ,\zeta ,s\right) =\displaystyle {\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }}G_{q+2,klmn}^{L} \left( \xi ,\zeta ,s\right) \sin \mu _{m} x_{1} \sin \lambda _{n} x_{2},} \end{array} \end{aligned}$$
(9.9)
$$\begin{aligned} \begin{array}{c} {G_{1klmn}^{L} \left( \xi ,\zeta ,s\right) =\frac{4}{l_{1} l_{2} } \displaystyle {\int _{0}^{l_{1} }}\cos \mu _{m} x_{1} dx_{1} \int _{0}^{l_{2} }G_{1kl}^{L} \left( x_{1} ,x_{2} ,\xi ,\zeta ,s\right) \sin \lambda _{n} x_{2} dx_{2} ,} \\ {G_{1kl0n}^{L} \left( \xi ,\zeta ,s\right) =\frac{2}{l_{1} l_{2} } \displaystyle {\int _{0}^{l_{1} }dx_{1} \int _{0}^{l_{2} }}G_{1kl}^{L} \left( x_{1} ,x_{2} ,\xi ,\zeta ,s\right) \sin \lambda _{n} x_{2} dx_{2} ,}\\ {G_{2klmn}^{L} \left( \xi ,\zeta ,s\right) =\frac{4}{l_{1} l_{2} } \displaystyle {\int _{0}^{l_{1} }}\sin \mu _{m} x_{1} dx_{1} \int _{0}^{l_{2} }G_{2kl}^{L} \left( x_{1} ,x_{2} ,\xi ,\zeta ,s\right) \cos \lambda _{n} x_{2} dx_{2} ,} \\ {G_{2klm0}^{L} \left( \xi ,\zeta ,s\right) =\frac{2}{l_{1} l_{2} } \displaystyle {\int _{0}^{l_{1}} }\sin \mu _{m} x_{1} dx_{1} \displaystyle {\int _{0}^{l_{2}} }G_{2kl}^{L} \left( x_{1} ,x_{2} ,\xi ,\zeta ,s\right) dx_{2} ,} \\ {G_{q+2,klmn}^{L} \left( \xi ,\zeta ,s\right) =\frac{4}{l_{1} l_{2} } \displaystyle {\int _{0}^{l_{1} }}\sin \mu _{m} x_{1} dx_{1} \displaystyle {\int _{0}^{l_{2} }}G_{q+2,kl}^{L} \left( x_{1} ,x_{2} ,\xi ,\zeta ,s\right) \sin \lambda _{n} x_{2} dx_{2}.} \end{array} \end{aligned}$$

Below are the systems of equations for the zero harmonics:

$$\begin{aligned} \begin{array}{c} {k_{10n} \left( s\right) G_{1kl0n}^{L} \left( \xi ,\zeta ,s\right) =F_{10n} \left( \xi ,\zeta ,s\right) ,} \\ {k_{2m0} \left( s\right) G_{2klm0}^{L} \left( \xi ,\zeta ,s\right) =F_{2m0} \left( \xi ,\zeta ,s\right) ,}\\ {F_{10n} \left( \xi ,\zeta ,s\right) =\frac{2}{l_{1} l_{2} } \left[ C_{66} \lambda _{n} \delta _{1k} \left( \delta _{1l} \cos \lambda _{n} \zeta + \delta _{2l}\right) -\delta _{2k} \delta _{1l} \sin \lambda _{n} \zeta \right] ,} \\ {F_{2m0} \left( \xi ,\zeta ,s\right) =\frac{2}{l_{1} l_{2} } \left[ \mu _{m} C_{66} \delta _{1k} \left( \delta _{1l} + \delta _{2l} \cos \mu _{m} \xi \right] -\delta _{2k} \delta _{2l} \sin \mu _{m} \xi \right] .} \end{array} \end{aligned}$$
(9.10)

The solution of the systems (9.7) and (9.10) has the following form:

$$\begin{aligned} \begin{array}{c} G_{1kl0n}^{L} \left( \xi ,\zeta ,s\right) =\frac{2}{l_{1} l_{2} } \frac{C_{66} \lambda _{n} \delta _{1k} \left( \delta _{1l} \cos \lambda _{n} \zeta + \delta _{2l}\right) -\delta _{2k} \delta _{1l} \sin \lambda _{n} \zeta }{k_{1} \left( 0,\lambda _{n} ,s\right) },\\ G_{2klm0}^{L} \left( \xi ,\zeta ,s\right) =\frac{2}{l_{1} l_{2} } \frac{\mu _{m} C_{66} \delta _{1k} \left( \delta _{1l} + \delta _{2l} \cos \mu _{m} \xi \right) -\delta _{2k} \delta _{2l} \sin \mu _{m} \xi }{k_{2} \left( \mu _{m} ,0,s\right) }; \end{array} \end{aligned}$$
(9.11)
$$\begin{aligned} \begin{array}{c} {G_{iklmn}^{L} \left( \xi ,\zeta ,s\right) =\frac{P_{iklmn} \left( \xi ,\zeta ,s\right) }{P_{mn} \left( s\right) } \,\, \left( i=1,2\right) ,} \\ {G_{q+2,klmn}^{L} \left( \xi ,\zeta ,s\right) =\hat{G}_{q+2,klmn}^{L} \left( \xi ,\zeta ,s\right) +\frac{P_{q+2,klmn} \left( \xi ,\zeta ,s\right) }{Q_{qmn} \left( s\right) } ;} \end{array} \end{aligned}$$
(9.12)
$$\begin{aligned} \begin{array}{c} {\hat{G}_{q+2,21mn}^{L} \left( \xi ,\zeta ,s\right) =-\frac{4}{l_{1} l_{2} } \frac{\Lambda _{11}^{q} \mu _{m} }{k_{q+2,mn} \left( s\right) } \sin \lambda _{n} \zeta ,}\\ {\hat{G}_{q+2,12mn}^{L} \left( \xi ,\zeta ,s\right) =\frac{4}{l_{1} l_{2} } \frac{\Lambda _{2q} \lambda _{n} \mu _{m} }{k_{q+2,mn} \left( s\right) } \cos \mu _{m} \xi ,}\\ {\hat{G}_{q+2,11mn}^{L} \left( \xi ,\zeta ,s\right) =\frac{4}{l_{1} l_{2} } \frac{\Lambda _{1q} \lambda _{n} \mu _{m} }{k_{q+2,mn} \left( s\right) } \cos \lambda _{n} \zeta ,}\\ {\hat{G}_{q+2,22mn}^{L} \left( \xi ,\zeta ,s\right) =-\frac{4}{l_{1} l_{2} C_{22} } \frac{\Lambda _{22}^{q} \lambda _{n} }{k_{q+2,mn} \left( s\right) } \sin \mu _{m} \xi ,}\\ \hat{G}_{q+2,p+2,1mn}^{L} \left( \xi ,\zeta ,s\right) =\frac{4D_{1jq} \mu _{m} }{l_{1} l_{2} } \frac{\sin \lambda _{n} \zeta }{k_{q+2,mn} \left( s\right) } ,\\ \hat{G}_{q+2,p+2,2mn}^{L} \left( \xi ,\zeta ,s\right) =\frac{4D_{2qp} \lambda _{n} }{l_{1} l_{2} } \frac{\sin \mu _{m} \xi }{k_{q+2,mn} \left( s\right) }, \end{array} \end{aligned}$$
(9.13)

where

$$\begin{aligned} \begin{array}{c} {P_{mn} \left( s\right) =\left[ k_{1mn} \left( s\right) k_{2mn} \left( s\right) -\mu _{m}^{2} \lambda _{n}^{2} C_{0}^{2} \right] \Pi _{mn} \left( s\right) -}\\ {-\lambda _{n}^{2} \displaystyle {\sum _{j=1}^{N}}S_{1mn} \left( s\right) \Pi _{jmn} \left( s\right) M_{jmn} -\mu _{m}^{2} \displaystyle {\sum _{j=1}^{N}}S_{2mn} \left( s\right) \Pi _{jmn} \left( s\right) K_{jmn} +}\\ {+\mu _{m}^{2} \lambda _{n}^{2} \displaystyle {\sum _{i=1}^{N}\sum _{j=1}^{N}}\textrm{A} _{ij} K_{imn} M_{jmn} \Pi _{ijmn} \left( s\right) ,} \\ {Q_{qmn} \left( s\right) =k_{q+2,mn} \left( s\right) P_{mn} \left( s\right) ,} \end{array} \end{aligned}$$
(9.14)
$$\begin{aligned} \begin{array}{c} {P_{121mn} \left( \xi ,\zeta ,s\right) =-\frac{4}{l_{1} l_{2} }k_{2mn}\left( s\right) \Pi _{mn}\left( s\right) \sin \lambda _{n} \zeta -}\\ {-\frac{4}{l_{1} l_{2} } \displaystyle {\sum _{j=1}^{N}}\left[ \mu _{m}^{2} \Lambda _{11}^{j} S_{2mn} \left( s\right) +\alpha _{2}^{j} \lambda _{n}^{2} M_{jmn} \right] \Pi _{jmn} \left( s\right) \sin \lambda _{n} \zeta +}\\ +{\frac{4}{l_{1} l_{2} } \mu _{m}^{2} \lambda _{n}^{2} \displaystyle {\sum _{j=1}^{N}}\Lambda _{11}^{j} \displaystyle {\sum _{i=1}^{N}}\textrm{A} _{ji} M_{imn} \Pi _{ijmn} \left( s\right) \sin \lambda _{n} \zeta }, \end{array} \end{aligned}$$
$$\begin{aligned} \begin{array}{c} {P_{112mn} \left( \xi ,\zeta ,s\right) =\frac{4}{l_{1} l_{2} } C_{66} \lambda _{n} \left( k_{2mn} \left( s\right) -\mu _{m}^{2} C_{0} \right) \Pi _{mn} \left( s\right) \cos \mu _{m} \xi +} \\ {+\frac{4}{l_{1} l_{2} } \lambda _{n} \displaystyle {\sum _{j=1}^{N}}\left[ C_{66} B_{jmn} M_{jmn} +\mu _{m}^{2} \Lambda _{2j} S_{2mn} \left( s\right) \right] \Pi _{jmn} \left( s\right) \cos \mu _{m} \xi -} \\ {-\frac{4}{l_{1} l_{2} } \lambda _{n}^{3} \mu _{m}^{2} \displaystyle {\sum _{j=1}^{N}}\Lambda _{2j} \displaystyle {\sum _{i=1}^{N}}\textrm{A} _{ji} M_{imn} \Pi _{ijmn} \left( s\right) \cos \mu _{m} \xi ,} \end{array} \end{aligned}$$
$$\begin{aligned} \begin{array}{c} {P_{111mn} \left( \xi ,\zeta ,s\right) =\frac{4}{l_{1} l_{2} } C_{66} \lambda _{n} \left( k_{2mn} \left( s\right) -C_{0} \mu _{m}^{2} \right) \Pi _{mn} \left( s\right) \cos \lambda _{n} \zeta +} \\ {+\frac{4}{l_{1} l_{2} } \lambda _{n} \displaystyle {\sum _{j=1}^{N}}\left[ C_{66} B_{jmn} M_{jmn} +\mu _{m}^{2} \Lambda _{1j} S_{2mn} \left( s\right) \right] \Pi _{jmn} \left( s\right) \cos \lambda _{n} \zeta -} \\ {-\frac{4}{l_{1} l_{2} } \lambda _{n}^{3} \mu _{m}^{2} \displaystyle {\sum _{j=1}^{N}}\Lambda _{1j} \displaystyle {\sum _{i=1}^{N}}\textrm{A} _{ji} M_{imn} \Pi _{ijmn} \left( s\right) \cos \lambda _{n} \zeta ,} \end{array} \end{aligned}$$
$$\begin{aligned} \begin{array}{c} {P_{122mn} \left( \xi ,\zeta ,s\right) =\frac{4}{l_{1} l_{2} } \lambda _{n} \mu _{m} C_{0} \Pi _{mn} \left( s\right) \sin \mu _{m} \xi +}\\ {+\frac{4}{l_{1} l_{2} } \mu _{m} \lambda _{n} \displaystyle {\sum _{j=1}^{N}}\left[ \alpha _{1}^{j} M_{jmn} \left( s\right) -\frac{\Lambda _{22}^{j} }{C_{22} } S_{2mn} \left( s\right) \right] \Pi _{jmn} \left( s\right) \sin \mu _{m} \xi +} \\ {+\frac{4}{l_{1} l_{2} } \mu _{m} \lambda _{n}^{3} \displaystyle {\sum _{j=1}^{N}}\frac{\Lambda _{22}^{j} }{C_{22} } \displaystyle {\sum _{i=1}^{N}}\textrm{A} _{ji} M_{imn} \Pi _{ijmn} \left( s\right) \sin \mu _{m} \xi ,} \end{array} \end{aligned}$$
$$\begin{aligned} \begin{array}{c} {P_{221mn} \left( \xi ,\zeta ,s\right) =\frac{4}{l_{1} l_{2} } \mu _{m} \lambda _{n} C_{0} \Pi _{mn} \left( s\right) \sin \mu _{m} \zeta +}\\ {+\frac{4}{l_{1} l_{2} } \mu _{m} \lambda _{n} \displaystyle {\sum _{j=1}^{N}}\left[ \alpha _{2}^{j} K_{jmn} -\Lambda _{11}^{j} S_{1mn} \left( s\right) \right] \Pi _{jmn} \left( s\right) \sin \lambda _{n} \zeta +} \\ {+\frac{4}{l_{1} l_{2} } \mu _{m}^{3} \lambda _{n} \displaystyle {\sum _{j=1}^{N}}\Lambda _{11}^{j} \displaystyle {\sum _{i=1}^{N}}\textrm{A} _{ji} K_{imn} \Pi _{ijmn} \left( s\right) \sin \lambda _{n} \zeta ,} \end{array} \end{aligned}$$
$$\begin{aligned} \begin{array}{c} {P_{212mn} \left( \xi ,\zeta ,s\right) =\frac{4}{l_{1} l_{2} } C_{66} \mu _{m} \left( k_{1mn} -C_{0} \lambda _{n}^{2} \right) \Pi _{mn} \left( s\right) \cos \mu _{m} \xi +} \\ {+\frac{4}{l_{1} l_{2} } \mu _{m} \displaystyle {\sum _{j=1}^{N}}\left[ -C_{66} B_{jmn} K_{jmn} +\lambda _{n}^{2} \Lambda _{2j} S_{1mn} \left( s\right) \right] \Pi _{jmn} \left( s\right) \cos \mu _{m} \xi -} \\ {-\frac{4}{l_{1} l_{2} } \lambda _{n}^{2} \mu _{m}^{3} \displaystyle {\sum _{j=1}^{N}}\Lambda _{2j} \displaystyle {\sum _{i=1}^{N}}\textrm{A} _{ji} K_{imn} \Pi _{ijmn} \left( s\right) \cos \mu _{m} \xi ,} \end{array} \end{aligned}$$
$$\begin{aligned} \begin{array}{c} {P_{211mn} \left( \xi ,\zeta ,s\right) =\frac{4}{l_{1} l_{2} } C_{66} \mu _{m} \left( k_{1mn} \left( s\right) -C_{0} \lambda _{n}^{2} \right) \Pi _{mn} \left( s\right) \cos \lambda _{n} \zeta +} \\ {+\frac{4}{l_{1} l_{2} } \mu _{m} \displaystyle {\sum _{j=1}^{N}}\left[ -C_{66} B_{jmn} K_{jmn} +\lambda _{n}^{2} \Lambda _{1j} S_{1mn} \left( s\right) \right] \Pi _{jmn} \left( s\right) \cos \lambda _{n} \zeta -} \\ {-\frac{4}{l_{1} l_{2} } \lambda _{n}^{2} \mu _{m}^{3} \displaystyle {\sum _{j=1}^{N}}\Lambda _{1j} \displaystyle {\sum _{i=1}^{N}}\textrm{A} _{ji} K_{imn} \Pi _{ijmn} \left( s\right) \cos \lambda _{n} \zeta ,} \end{array} \end{aligned}$$
$$\begin{aligned} \begin{array}{c} {P_{222mn} \left( \xi ,\zeta ,s\right) =-\frac{4}{l_{1} l_{2} } k_{1mn} \left( s\right) \Pi _{mn} \left( s\right) \sin \lambda _{n} \xi -}\\ {-\frac{4}{l_{1} l_{2} } \displaystyle {\sum _{j=1}^{N}}\left[ \frac{\Lambda _{22}^{j} }{C_{22} } \lambda _{n}^{2} S_{1mn} \left( s\right) +\mu _{m}^{2} \alpha _{1}^{j} K_{jmn} \right] \Pi _{jmn} \left( s\right) \sin \mu _{m} \xi +} \\ {+\frac{4}{l_{1} l_{2} } \mu _{m}^{2} \lambda _{n}^{2} \displaystyle {\sum _{j=1}^{N}}\frac{\Lambda _{22}^{j} }{C_{22} } \displaystyle {\sum _{i=1}^{N}}\textrm{A} _{ji} K_{imn} \Pi _{ijmn} \left( s\right) \sin \mu _{m} \xi ,} \end{array} \end{aligned}$$
$$\begin{aligned} \begin{array}{c} {P_{1,q+2,1mn} \left( \xi ,\zeta ,s\right) =\frac{4}{l_{1} l_{2} } \mu _{m}^{2} \displaystyle {\sum _{j=1}^{N}}D_{1jq} S_{2mn} \left( s\right) \Pi _{jmn} \left( s\right) \sin \lambda _{n} \zeta -}\\ {-\frac{4}{l_{1} l_{2} } \mu _{m}^{2} \lambda _{n}^{2} \displaystyle {\sum _{j=1}^{N}}D_{1jq}\displaystyle {\sum _{r=1}^{N}}\textrm{A} _{jr} M_{rmn} \Pi _{rjmn} \left( s\right) \sin \lambda _{n} \zeta ,} \\ {P_{1,q+2,2mn} \left( \xi ,\zeta ,s\right) =\frac{4}{l_{1} l_{2} } \mu _{m} \lambda _{n} \displaystyle {\sum _{j=1}^{N}}D_{2jq} S_{2mn} \left( s\right) \Pi _{jmn} \left( s\right) \sin \mu _{m} \xi -} \\ {-\frac{4}{l_{1} l_{2} } \mu _{m} \lambda _{n}^{3} \displaystyle {\sum _{j=1}^{N}}D_{2jq} \displaystyle {\sum _{r=1}^{N}}\textrm{A} _{jr} M_{rmn} \Pi _{rjmn} \left( s\right) \sin \mu _{m} \xi ,} \end{array} \end{aligned}$$
$$\begin{aligned} \begin{array}{c} {P_{2,q+2,1mn} \left( \xi ,\zeta ,s\right) =\frac{4}{l_{1} l_{2} } \lambda _{n} \mu _{m} \displaystyle {\sum _{j=1}^{N}}D_{1jq} S_{1mn} \left( s\right) \Pi _{jmn} \left( s\right) \sin \lambda _{n} \zeta -}\\ {-\frac{4}{l_{1} l_{2} } \mu _{m}^{3} \lambda _{n} \displaystyle {\sum _{j=1}^{N}}D_{1jq} \displaystyle {\sum _{r=1}^{N}}\textrm{A} _{jr} K_{rmn} \Pi _{rjmn} \left( s\right) \sin \lambda _{n} \zeta ,} \end{array} \end{aligned}$$
$$\begin{aligned} \begin{array}{c} {P_{2,q+2,2mn} \left( \xi ,\zeta ,s\right) =\frac{4}{l_{1} l_{2} } \lambda _{n}^{2} \displaystyle {\sum _{j=1}^{N}}D_{2jq} S_{1mn} \left( s\right) \Pi _{jmn} \left( s\right) \sin \mu _{m} \xi -}\\ {-\frac{4}{l_{1} l_{2} } \mu _{m}^{2} \lambda _{n}^{2} \displaystyle {\sum _{j=1}^{N}}D_{2jq} \displaystyle {\sum _{r=1}^{N}}\textrm{A} _{jr} K_{rmn} \Pi _{rjmn} \left( s\right) \sin \mu _{m} \xi ,} \end{array} \end{aligned}$$
$$\begin{aligned} P_{q+2,klmn} \left( \xi ,\zeta ,s\right) =\mu _{m} K_{qmn} P_{1klmn} \left( \xi ,\zeta ,s\right) +\lambda _{n} M_{qmn} P_{2klmn} \left( \xi ,\zeta ,s\right) , \end{aligned}$$
$$\begin{aligned} \begin{array}{c} {\Pi _{mn} \left( s\right) =\displaystyle {\prod _{j=1}^{N}}k_{j+2,mn} \left( s\right) ,\,\, \Pi _{qmn} \left( s\right) =\displaystyle {\prod _{j=1,j\ne q}^{N}}k_{j+2,mn} \left( s\right) } ,\,\, {\Pi _{qpmn} \left( s\right) =\displaystyle {\prod _{j=1,j\ne q,p}^{N}}k_{j+2,mn} \left( s\right) ,} \\ {S_{1mn} \left( s\right) =\alpha _{1}^{j} C_{0} \mu _{m}^{2} -\alpha _{2}^{j} k_{1mn} \left( s\right) ,\,\, S_{2mn} \left( s\right) =\alpha _{2}^{j} C_{0} \lambda _{n}^{2} -\alpha _{1}^{j} k_{2mn} \left( s\right) ,} \\ {\textrm{A} _{ji} =\alpha _{1}^{j} \alpha _{2}^{i} -\alpha _{2}^{j} \alpha _{1}^{i} ,\,\, B_{jmn} =\alpha _{2}^{j} \lambda _{n}^{2} -\mu _{m}^{2} \alpha _{1}^{j} ,}\\ {D_{1jq} =D_{1}^{j} \delta _{qj} -\Lambda _{11}^{j} \alpha _{1}^{q} ,\,\, D_{2jq} =D_{2}^{j} \delta _{qj} -\frac{\Lambda _{22}^{j} }{C_{22} } \alpha _{2}^{q}. } \end{array} \end{aligned}$$

The transition to the original domain is done by residues and tables of operational calculus as follows [21]:

$$\begin{aligned} \begin{array}{c} G_{1kl0n} \left( \xi ,\zeta ,\tau \right) =\frac{2\sqrt{C_{66} } }{l_{1} l_{2} } \left[ \delta _{1k} \left( \delta _{1l} +\delta _{2l} \right) -\frac{\delta _{2k} \delta _{1l} \sin \lambda _{n} \zeta }{\lambda _{n} {C_{66} } }\right] \sin \left( \lambda _{n} \sqrt{C_{66} } \tau \right) ,\\ G_{2klm0}^{sc} \left( \xi ,\zeta ,\tau \right) =\frac{2\sqrt{C_{66} } }{l_{1} l_{2} } \left[ \delta _{1k} \left( \delta _{1l} +\delta _{2l} \right) - \frac{\delta _{2k} \delta _{2l} \sin \mu _{m} \xi }{\mu _{m} {C_{66} } } \right] \sin \left( \mu _{m} \sqrt{C_{66} } \tau \right) ; \end{array}\end{aligned}$$
(9.15)
$$\begin{aligned} \begin{array}{c} {G_{iklmn} \left( \xi ,\zeta ,\tau \right) =\displaystyle {\sum _{j=1}^{2N+4}}A_{iklmn}^{\left( j\right) } \left( \xi ,\zeta \right) e^{s_{jmn} \tau } \,\, \left( i=1,2\right) ,} \\ {G_{q+2,klmn}\left( \xi ,\zeta ,\tau \right) =\hat{G}_{q+2,klmn} \left( \xi ,\zeta ,\tau \right) +\displaystyle {\sum _{j=1}^{2N+6}}A_{q+2,klmn}^{\left( j\right) } \left( \xi ,\zeta \right) e^{s_{jmn} \tau },} \\ {A_{iklmn}^{\left( j\right) } \left( \xi ,\zeta \right) =\frac{P_{iklmn} \left( \xi ,\zeta , s_{jmn} \right) }{P'_{mn} \left( s_{jmn} \right) } ,\,\, A_{q+2,klmn}^{\left( j\right) } \left( \xi ,\zeta \right) =\frac{P_{q+2,klmn} \left( \xi ,\zeta , s_{jmn} \right) }{Q'_{qmn} \left( s_{jmn} \right) } ,} \end{array} \end{aligned}$$
(9.16)
$$\begin{aligned} \begin{array}{c} {\hat{G}_{q+2,21mn} \left( \xi ,\zeta ,\tau \right) =-\frac{4}{l_{1} l_{2} } \Lambda _{11}^{q} \mu _{m} \sin \lambda _{n} \zeta \displaystyle {\sum _{j=1}^{2}}\frac{e^{\chi _{jmn} \tau } }{k'_{q+2,mn} \left( \chi _{jmn} \right) } ,} \\ {\hat{G}_{q+2,12mn} \left( \xi ,\zeta ,\tau \right) =\frac{4}{l_{1} l_{2} } \Lambda _{2q} \lambda _{n} \mu _{m} \cos \mu _{m} \xi \displaystyle {\sum _{j=1}^{2}}\frac{e^{\chi _{jmn} \tau } }{k'_{q+2,mn} \left( \chi _{jmn} \right) } ,} \\ {\hat{G}_{q+2,11mn} \left( \xi ,\zeta ,\tau \right) =\frac{4}{l_{1} l_{2} } \Lambda _{1q} \lambda _{n} \mu _{m} \cos \lambda _{n} \zeta \displaystyle {\sum _{j=1}^{2}}\frac{e^{\chi _{jmn} \tau } }{k'_{q+2,mn} \left( \chi _{jmn} \right) } ,} \\ {\hat{G}_{q+2,22mn} \left( \xi ,\zeta ,\tau \right) =-\frac{4}{l_{1} l_{2} } \frac{\Lambda _{22}^{q} \lambda _{n} }{C_{22} } \sin \mu _{m} \xi \displaystyle {\sum _{j=1}^{2}}\frac{e^{\chi _{jmn} \tau } }{k'_{q+2,mn} \left( \chi _{jmn} \right) }.} \end{array} \end{aligned}$$

9.5 Calculation Example

Let us take a three-component material (\(N=2\), independent components, zinc and copper, diffusing into aluminium) with the following characteristics [22]:

$$\begin{aligned} \begin{array}{c} {C'_{12} =5.11\cdot 10^{10} \frac{\text{ N }}{{\text{ m }}^{2} } ,\,\, C'_{66} =2.63\cdot 10^{10} \frac{\text{ N }}{{\text{ m }}^{2} } ,\,\, T_{0} =700\; K ,\,\, \rho =2700\frac{\text{ kg }}{{\text{ m }}^{3} } ,}\\ {\alpha _{11}^{\left( 1\right) } =\alpha _{22}^{\left( 1\right) } =6.55\cdot 10^{7} \frac{\text{ J }}{\text{ kg }} ,\,\, \alpha _{11}^{\left( 2\right) } =\alpha _{22}^{\left( 2\right) } =6.14\cdot 10^{7} \frac{\text{ J }}{\text{ kg }}, \,\, l=10^{-2} \; {\text{ m }},} \end{array} \end{aligned}$$
$$\begin{aligned} \begin{array}{c} {D_{11}^{\left( 1\right) } =D_{22}^{\left( 1\right) } =2.62\cdot 10^{-12} \frac{{\text{ m }}^{2} }{\text{ s }} ,\,\, D_{11}^{\left( 2\right) } =D_{22}^{\left( 2\right) } =2.89\cdot 10^{-15} \frac{{\text{ m }}^{2} }{\text{ s }} ,} \\ {n_{0}^{\left( 1\right) } =0.01,\,\, n_{0}^{\left( 2\right) } =0.045,\,\, {{m}}^{\left( 1\right) } =0.065\; \frac{\text{ kg }}{\text{ mol }} ,\,\, {{m}}^{\left( 2\right) } =0.064\; \frac{\text{ kg }}{\text{ mol }}.} \end{array} \end{aligned}$$

Assume that the plate is under the action of tensile forces applied to the boundaries \(x_{1} =0\) and \(x_{1} =l_{1} \):

$$\begin{aligned} f_{211} \left( x_{2} ,\tau \right) =f_{212} \left( x_{2} ,\tau \right) =H\left( \tau \right) \sin \frac{\pi x_{2} }{l_{2} }, \end{aligned}$$

where \(H\left( \tau \right) \) is the Heaviside function.

All other load parameters in the boundary conditions (9.2) are assumed to be zero. Calculating the convolutions (9.4), we obtain

$$\begin{aligned} \begin{array}{c} {u_{1} \left( x_{1} ,x_{2} ,\tau \right) =\displaystyle {\int _{0}^{l_{2} }}G_{121} \left( x_{1} ,x_{2} ,\zeta ,\tau \right) *f_{211} \left( \zeta ,\tau \right) d\zeta -}\\ { -\displaystyle {\int _{0}^{l_{2} }}G_{121} \left( l_{1} -x_{1} ,x_{2} ,\zeta ,\tau \right) *f_{212} \left( \zeta ,\tau \right) d\zeta =} \\ {=l_{2} \sin \lambda _{1} x_{2} \displaystyle {\sum _{m=1}^{\infty }}\left( -1\right) ^{m+1} \sin \left[ \mu _{m} \left( \frac{l_{1} }{2} -x_{1} \right) \right] \displaystyle {\sum _{j=1}^{2N+4}}\tilde{A}_{121m1}^{\left( j\right) } \frac{e^{s_{jm1} \tau } -1}{s_{jm1} },} \end{array} \end{aligned}$$
$$\begin{aligned} \begin{array}{c} {u_{2} \left( x_{1} ,x_{2} ,\tau \right) =\displaystyle {\int _{0}^{l_{2} }}G_{221} \left( x_{1} ,x_{2} ,\zeta ,\tau \right) *f_{211} \left( \zeta ,\tau \right) d\zeta +}\\ {+\displaystyle {\int _{0}^{l_{2}} }G_{221} \left( l_{1} -x_{1} ,x_{2} ,\zeta ,\tau \right) *f_{212} \left( \zeta ,\tau \right) d\zeta =} \\ {=l_{2} \cos \lambda _{1} x_{2} \displaystyle {\sum _{m=1}^{\infty }}\left( -1\right) ^{m+1} \cos \left[ \mu _{m} \left( \frac{l_{1} }{2} -x_{1} \right) \right] \displaystyle {\sum _{j=1}^{2N+4}}\tilde{A}_{221m1}^{\left( j\right) } \frac{e^{s_{jm1} \tau } -1}{s_{jm1} },} \end{array} \end{aligned}$$
$$\begin{aligned} \begin{array}{c} {\eta _{q} \left( x_{1} ,x_{2} ,\tau \right) =\displaystyle {\int _{0}^{l_{2}} }G_{q+2,21} \left( x_{1} ,x_{2} ,\zeta ,\tau \right) *f_{211} \left( \zeta ,\tau \right) d\zeta +}\\ {+\displaystyle {\int _{0}^{l_{2} }}G_{q+2,21} \left( l_{1} -x_{1} ,x_{2} ,\zeta ,\tau \right) *f_{212} \left( \zeta ,\tau \right) d\zeta =}\\ {=\frac{4}{l_{1} } \sin \lambda _{1} x_{2} \displaystyle {\sum _{m=1}^{\infty }}\left( -1\right) ^{m+1} \cos \left[ \mu _{m} \left( \frac{l_{1} }{2} -x_{1} \right) \right] \displaystyle {\sum _{j=1}^{2}}\frac{\Lambda _{1q} \lambda _{1} \mu _{m} }{k'_{q+2,m1} \left( \chi _{jm1} \right) } \frac{e^{\chi _{jm1} \tau } -1}{\chi _{jm1} } +} \\ {+l_{2} \sin \lambda _{1} x_{2} \displaystyle {\sum _{m=1}^{\infty }}\left( -1\right) ^{m+1} \cos \left[ \mu _{m} \left( \frac{l_{1} }{2} -x_{1} \right) \right] \displaystyle {\sum _{j=1}^{2N+6}}\tilde{A}_{q+2,21m1}^{\left( j\right) } \frac{e^{s_{jm1} \tau } -1}{s_{jm1} },} \end{array} \end{aligned}$$
$$\begin{aligned} \tilde{A}_{k21mn}^{\left( j\right) } =\frac{A_{k21mn}^{\left( j\right) } \left( \zeta \right) }{\sin \lambda _{1} \zeta }. \end{aligned}$$

The calculation results are shown in the Figs. 9.1, 9.2, 9.3, 9.4, 9.5, 9.6, 9.7 and 9.8. Figures 9.1, 9.2, 9.3 and 9.4 show dependences of longitudinal displacements \(u_{i}\) on time and coordinates. Calculations show that diffusion processes at the initial stages of deformation do not affect the displacement field. At initial times, the elastic and elastic diffusion displacements coincide.

Fig. 9.1
figure 1

Displacement \(u_{1} \left( x_{1} ,x_{2} ,\tau \right) \) at \(x_{2} ={l_{2}/ 2} \)

Full size image
Fig. 9.2
figure 2

Displacement \(u_{1} \left( x_{1} ,x_{2} ,\tau \right) \) at \(x_{1} ={l_{1}/ 4} \)

Full size image
Fig. 9.3
figure 3

Displacement \(u_{2} \left( x_{1} ,x_{2} ,\tau \right) \) at \(x_{2} ={l_{2}/ 4} \)

Full size image
Fig. 9.4
figure 4

Displacements \(u_{2} \left( x_{1} ,x_{2} ,\tau \right) \) at \(x_{1} ={l_{1}/ 2} \)

Full size image

Figures 9.5 and 9.6 show the zinc and copper concentration increments, respectively, caused by longitudinal deformations.

Fig. 9.5
figure 5

Zinc concentration increment \(\eta _{1} \left( x_{1} ,x_{2} ,\tau \right) \) at \(x_{1} ={l_{1}/ 2} \)

Full size image
Fig. 9.6
figure 6

Copper concentration increment \(\eta _{2} \left( x_{1} ,x_{2} ,\tau \right) \) at \(x_{1} ={l_{1}/ 2} \)

Full size image

The influence of relaxation effects on the mass transfer kinetics is shown in Figs. 9.7 and 9.8. Here, different lines show zinc concentration increments for models with a finite and infinite speed of diffusion fluxes. The relaxation effects manifest themselves at some finite interval of time and then disappear. Thus, in Fig. 9.8, corresponding to the time \(\tau =10^{9} \), both curves already coincide.

Fig. 9.7
figure 7

Zinc concentration increment \(\eta _{1} \left( x_{1} ,x_{2} ,\tau \right) \). The solid line corresponds to the time \(\tau ^{\left( q\right) } =200\) s, the dotted line to \(\tau ^{\left( q\right) } =0\)

Full size image
Fig. 9.8
figure 8

Zinc concentration increment \(\eta _{1} \left( x_{1} ,x_{2} ,\tau \right) \). The solid line corresponds to the time \(\tau ^{\left( q\right) } =200\) s, the dotted line to \(\tau ^{\left( q\right) } =0\)

Full size image

9.6 Conclusions

We propose a mathematical model describing the effects of the interaction between mechanical and diffusion fields during a rectangular orthotropic plate deformation. The algorithm is developed for finding Green’s functions based on Laplace transform and decomposition into trigonometric Fourier series. It allows us to reduce the general problem of Laplace transform inversion to the problem of rational function inversion. Originals of Green’s functions are found using residues and tables of operational calculus. As a result, it is possible to obtain the solution in analytical form, which provides ample opportunities for various kinds of numerical experiments.

The effect of interaction between the mechanical and diffusion fields is demonstrated by the example of a rectangular plate under the action of tensile forces. Unsteady loads initiate the process of mass transfer. At the same time, the relaxation diffusion processes reduce with time. The kinetics of mass transfer at significant times can be described by classical mechanodiffusion with the infinite speed of diffusion fluxes. All results are presented in analytical and graphical forms.