Keywords

1 Introduction

Microcantilever based microresonators are very demanding and widely used in MEMS for varieties of applications such as, Atomic Force Microscope (AFM) [1], temperature and pressure measurement sensors, [2], biomedical sensors [3], vertical comb-drives [4, 5] and accelerometers [6, 7] due to its capability of tuning the resonance frequencies, sensitivity and, excellent resolution in dynamic operations. Besides, microcantilevers are easy to fabricate by bulk micromachining, surface micromachining and SoI-based processes. In addition, Metal-assisted Chemical Etching (MaCEtch) is explored for the fabrication of microstructures in recent works [8, 9] and can be extended for the development of the microcantilevers and other microstructures in MEMS.

Several authors reported the prismatic microcantilever beam for the study of quality factor (Q factor), damping ratios and other dynamic performance parameter of MEMS resonators. The performance of the microresonators is greatly affected by the damping mechanisms named as; squeezed film damping (SFD), thermoelastic damping (TED), anchor loss and surface loss. Out of the aforesaid damping mechanisms, SFD is found to be responsible for the losses associated with damping in majority of cases in MEMS [10]. SFD is affected by the several parameters such as, operating pressure, temperature, relative humidity, squeezing media (air, or any other gas) and degree of rarefaction. Bao and Yang [10] have contributed in the SFD analysis of MEMS and proposed the damping models with perforation and without perforation. Veijola [11] have developed the SFD model with effective viscosity method and is widely accepted for the damping analysis in MEMS. COMSOL Multiphysics also uses Veijola’s effective viscosity method for SFD analysis. The effects of environmental factors i.e. temperature, humidity and pressure on Q factors is studied by Nguyen et al. [12]. Martin et al. [13] have studied the different geometries of MEMS resonators and corrected the existing models of SFD by calculating the damping factors theoretically and experimentally. SFD coefficients and dynamic response of higher flexural mode is reported by Pandey and Pratap [14] for the MEMS cantilever resonators. They have compared the analytical response of damping at higher modes for different MEMS cantilever beams with the experimental results. Ashok et al. [15] have studied recently the tuning of wideband frequency and Q factors by coupling the non-uniform microbeam arrays. They reported the eigenfrequency and Q factor variation with tapering parameter for converging and diverging microbeams in atmosphere (1.01325 bar) and vacuum (8 × 10–3 mbar) operating conditions. From the best of our knowledge, Q factor and eigenfrequency analysis with wide pressure variation (105 Pa to 0.1 Pa) for the trapezoidal microcantilever beam is not yet reported in the literature.

In the present study, we have focused on the trapezoidal microcantilever beam to broaden the applicability of microresonators with variable cross sections in MEMS. The usefulness of the variable cross section of trapezoidal beam lies with the uniform distribution of stress along its length. The methodology developed in the present study using finite element method (FEM) for SFD analysis will be extended for the estimation of Q factor, damping ratio and other related dynamic parameters of MEMS-based vertical-comb drive microactuator in torsion at different pressure levels.

2 Squeezed Film Damping

In the MEMS, air remains trapped between the moving and fixed microstructures and acts as a thin film. On actuation, microstructures squeeze the thin film of air (or fluid) between the moving and fixed microstructures and exerts a back pressure or force on the walls of the microstructures. The back pressure dampens the movement and results in higher dissipation of energy per cycle. This phenomenon is known as squeezed film damping or SFD [10]. SFD depends on the various environmental factors i.e. pressure, temperature and humidity along with the boundary conditions and mode of actuation [16]. Pressure is one of the dominating factors in estimating the damping characteristics of the microresonators. The operating pressure flow regimes i.e. continuum, slip, transition and molecular flow, are defined by the Knudsen no. (Kn = λ/h0) where λ is the mean free path of surrounding media and h0 is the thickness of air gap between the moving and fixed microstructures and given in Table 1. The atmospheric pressure is considered as 105 Pa instead of 1.013 × 105 Pa for the calculations in the current study.

Table 1. Flow regimes based on Kn and operating pressure
Full size table

The modified Reynolds equation to calculate the pressure distribution in the SFD analysis for different flow regime is given by Eq. (1).

$$ \frac{{h_{0}^{3} }}{{12\mu_{eff} }}\left( {\frac{{\partial^{2} p}}{{\partial x^{2} }} + \frac{{\partial^{2} p}}{{\partial y^{2} }}} \right) = \frac{{h_{0} }}{{p_{a} }}\frac{\partial p}{{\partial t}} + \frac{\partial w}{{\partial t}} $$
(1)

where, p is the pressure distribution due to SFD, pa is the ambient pressure, w is the transverse deflection and µeff is the effective viscosity of the air and given by Eq. (2):

$$ \mu_{eff} = \frac{\mu }{{1 + 9.638K_{n}^{1.159} }} $$
(2)

here, µ is the dynamic viscosity of air.

Effective viscosity method [11] is used to solve the modified Reynolds equation (refer Eq. (1)) for the continuum, slip, transition and molecular flow regimes.

Total Q factor (Qtotal) and damping ratio (ζ) in the SFD analysis are given by Eqs. (4) and (5), respectively.

$$ \frac{1}{{Q_{total} }} = \frac{1}{{Q_{SFD} }} + \frac{1}{{Q_{TED} }} + \frac{1}{{Q_{anchor} }} $$
(3)
$$ \zeta = \frac{1}{{2Q_{total} }} $$
(4)

In microcantilever based resonators, Qtotal is governed by the SFD, thermoelastic damping (TED), and anchor loss. In the present study, only SFD is considered to calculate the Q factor and damping ratio for the microcantilever beam. TED and anchor loss are neglected due to the absence of temperature and simpler clamping at the fixed end of the trapezoidal microcantilever beam.

3 FEM Analysis

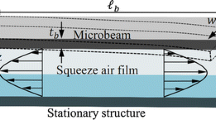
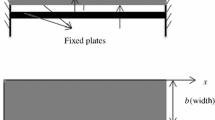
Schematic diagram of trapezoidal microcantilever beam is shown in Fig. 1. The width at distance x from the fixed end can be given by Eq. (5). Length and thickness of microcantilever beam are 150 µm and 5 µm, respectively. The width of microcantilever beam at fixed end (w0) is 50 µm whereas at free end (wl) is varying from 50 to 20 µm.

Fig. 1.
figure 1

Schematic diagram of trapezoidal microcantilever beam showing the dimensional parameters and variation of the width along the length

Full size image

Solid mechanics physics with eigenfrequency study is used in COMSOL Multiphysics to evaluate the SFD of microcantilever. Tetrahedral element is used to discretize the domain and serendipity approach is used to define the shape functions. Mesh convergence is done in order to determine the optimum size of the mesh element. The verification of eigen frequency and damping ratio is done with the literature [14] to validate the formulation in FEM.

$$ w_{x} = w_{0} - \left( {\frac{{w_{l} - w_{0} }}{l}} \right)x $$
(5)

3.1 Verification of FEM Model

The verification of FEM formulation is done using COMSOL Multiphysics for a known problem from the literature [14]. The microcantilever with different configurations are simulated at atmospheric pressure and the results are compared. From Table 2, it can be seen that FEM results of the current work are in good agreement with the simulation and experimental results of Pandey and Pratap [14].

Table 2. Verification and comparison of damping ratio and eigen frequencies with the literature [14] and current work in COMSOL Multiphysics 6.0
Full size table

Besides the verification of FEM model of SFD for microcantilevers at atmospheric pressure, the accuracy of the developed model is further verified using microcantilever beam of uniform length (lb) 150 µm, width (wb) 50 µm and thickness (tb) 5 µm for varying pressures (105–0.1 Pa). For verification, the analytical solution of damping ratio (ζ) (refer Eq. (6)) for the first mode of microcantilever beam of uniform cross section is used from the literature [14]. Various coefficients σ, χ, φ, ρ, ωn and b can be found from literature [14]. It is found that the analytical and FEM results of Q factor and damping ratio (ζ) are in good agreement for the pressures varying from 105 to 0.1 Pa and given in Table 3.

$$ \zeta_{d} = \frac{{384\mu_{eff} w_{b}^{2} }}{{\phi t_{b} \rho \omega_{n} h_{0}^{3} \pi^{6} }}\left( {\frac{{(4 + \chi^{2} )b^{2} }}{{(4 + \chi^{2} ) + (\sigma^{2} /4\pi^{4} )}}} \right) $$
(6)
Table 3. Verification of FEM model with analytical model of Q factors and damping ratio of microcantilever beam of uniform cross section at varying pressures (105–0.1 Pa)
Full size table

4 Results and Discussions

The variation of Q factor, from atmospheric pressure (105 Pa) to vacuum (0.1 Pa) is shown in Fig. 2 for variable width (50 µm to 20 µm) of free end of the trapezoidal beam. The Q factor decreases sharply from 0.1 to 103 Pa and changes its slope at 103 and 104 Pa. This is due to the fact that at lower pressure, mean free path of the gas molecules increase and energy losses gets minimized in successive collisions whereas at higher pressure mean free path of the gas molecules decreases and dissipates more energy in each collision, results in decrease in Q factor. Q factors for the proposed trapezoidal microcantilever beam are ranging from 3.7 × 107 at 0.1 Pa to 88.8 at 105 Pa and 1.2 × 108 at 0.1 Pa to 287.92 at 105 Pa for 50 and 20 µm width at free end, respectively. It can be observed that during the operation from atmospheric pressure to vacuum (0.1 Pa) the Q factor changes by nearly an order of 106 for different configurations of the microcantilever beam which signifies the huge loss of energy in operating the MEMS at atmospheric pressure in comparison to vacuum.

Figure 3 shows the variation of damping ratio with pressure. The damping ratio is inversely proportional to Q factor as shown in Eq. (4) and increases with the increase in pressure. The damping ratio varies from 1.35 × 10–8 at 0.1 Pa to 0.0056 at 105 Pa and 4.18 × 10–9 at 0.1 Pa to 0.0017 at 105 Pa for 50 µm and 20 µm width at free end, respectively.

Fig. 2.
figure 2

Q factors variation with operating pressure for trapezoidal microcantilever beam with varying cross section width 50–20 µm at free end

Full size image
Fig. 3.
figure 3

Damping ratio variation with operating pressure for trapezoidal microcantilever beam with varying cross section width 50–20 µm at free end

Full size image

Figure 4 shows the behavior of Q factor with varying width of free end of the trapezoidal beam at pressures 0.1, 10, 103 and 105 Pa. It can be seen that with the increase in width and pressure, Q factor is decreasing. The Q factor is minimum for 50 µm width at 105 Pa and maximum for 20 µm width at 0.1 Pa. The increase of width results in enhancement of losses due to SFD. It can be concluded that the losses due to damping can be minimized by the critical consideration of the design parameters in MEMS.

Fig. 4.
figure 4

Q factor variation with the variable width at free end of the trapezoidal microcantilever beam

Full size image

5 Conclusions

In the present paper, a methodology for the SFD analysis in COMSOL Multiphysics for trapezoidal microcantilever based resonator is developed to calculate the dynamic performance parameters i.e., Q factors and damping ratio for pressure varying from atmospheric pressure (105 Pa) to vacuum (0.1 Pa). The verification of FEM formulation for eigen frequencies and damping ratio is done at atmospheric pressure (105 Pa) in COMSOL Multiphysics and the simulation results are in good agreement with the literature. The proposed methodology for Q factor and damping ratio (ζ) is further verified with the analytical model at varying pressures from 105 to 0.1 Pa for the uniform microcantilever beam. In this way the correctness of the methodology for FEM simulation is authenticated and extended to analyze the trapezoidal microcantilever beam. It is observed that Q factors and damping ratio of trapezoidal microcantilever based resonator changes by an order of 106 when pressure varies from atmospheric (105 Pa) to vacuum (0.1 Pa).

The effects of SFD on Q factor and damping ratio are analyzed in the present study and will be extended to the other MEMS-based devices such as vertical comb-drives, accelerometers and micromotors.