Keywords

1 Introduction

Magnetic contactless suspension is a device that works on the principle of magnetic levitation [1, 2]. As a result, the moving part of the suspension becomes mechanically contactless, which leads to reduce the deterioration of the structural units due to the absence of mechanical friction, loss of mechanical energy, etc.

Magnetic levitation [3] of micro- and nano-suspensions [4, 5] is based on the law of electromagnetic induction [6]. The moving part of this device loses mechanical contact with the stationary part of the structure and gain a sufficiently large (theoretically infinite) sensitivity [7], which allows to use it as a sensor that registers the smallest deviations of motion relative to the initial equilibrium position of the device [7]. To demonstrate how the device works, let’s assume that the suspension works as an acceleration sensor. In the simplest case, the accelerometer can be described by a transfer function of a linear oscillator [7]:

$$ \frac{Y\left( p \right)}{{A\left( p \right)}} = \frac{1}{{p^{2} + \frac{\mu }{m}p + \frac{c}{m}}} , $$
(1)

where \(Y\left( p \right)\) is the mapping of the motion of the levitating part of the suspension, \(A\left( p \right)\) is the effective transport acceleration, \(p\) is the Laplace transform variable, \(m\) is the inertial mass, \(\mu\) is the viscous friction coefficient of the environment, \(c\) is the rigidity of the suspension.

The static sensitivity of the accelerometer is written as [7]

$$ \frac{Y\left( p \right)}{{A\left( p \right)}} = \frac{m}{c} . $$
(2)

As the suspension stiffness \(c \to 0\) decreases, the sensitivity of the accelerometer, defined by Eq. (2), increases indefinitely and becomes infinite [7]. The transfer function (1) in this case will take the following form

$$ \frac{Y\left( p \right)}{{A\left( p \right)}} = \frac{1}{{p\left( {p + \frac{\mu }{m}} \right){ }}} . $$
(3)

It is noted in works [7, 8] that the integration of acceleration takes place in the absence of the stiffness parameter \(c\). Thus, with the technological possibility of excluding the mechanical stiffness from the model, it is possible to obtain a device with infinite (very large) sensitivity and, consequently, the perspective of measuring arbitrarily small external accelerations. To exclude stiffness, a combination of magnetic and electric suspension is usually used to evaluate the total stiffness of the system to zero for certain parameters of the electric and magnetic parts of the structure. This approach is considered in work [7] when designing an electromagnetic suspension in the case of a disk-like mass, considering only the axial motions of the levitating mass. In works [8, 9] the dynamic equations of the levitating mass with additional consideration of angular displacements due to the appearance of magnetic moments are obtained. In works [10] general conditions for the stable motion of a levitating mass were considered.

The main purpose of this work is an analytical study of the magnetic part of the electromagnetic suspension and obtaining conditions for finding the equilibrium position and stability of vibrations of a levitating object near its equilibrium. The magnetic stiffness of the magnetic suspension is also evaluated. It is shown that in this formulation, it has a harmonic character, which should be considered when adjusting the electrical part of the system to eliminate the magnetic stiffness of the system.

2 Mathematical Model

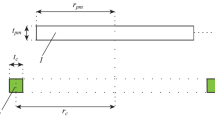
A contactless magnetic suspension (see Fig. 1) in the simplest case is a system consisting of two basic elements - an inductor coil, to which an alternating current is applied, and a proof levitating mass (PM) made of a conductive material. Due to the law of electromagnetic induction, currents are induced in the PM when current flows in the coil, and an electromagnetic force arises between the parts of the structure. Due to this effect, it is possible to use the PM, for example, as a stand or support for engineering and other structures.

Fig. 1.
figure 1

Scheme of magnetic suspension

Full size image

The energy of the magnetic field \(W\) of the coil of radius \(r_{c}\) and thickness \(t_{c}\) powered by alternating current \(\imath_{1}\) and the disc-shaped proof mass (PM) of the thickness \(t_{pm}\), radius \(r_{pm}\) with induced eddy current \(\imath_{2}\) is

$$ W = \frac{1}{2}L_{1} \imath_{1}^{2} + M_{12} \left( y \right)\imath_{1} \imath_{2} + \frac{1}{2}L_{2} \imath_{2}^{2} , $$
(4)

where \(L_{1}\) and \(L_{2}\) are the self-inductance of coil and PM, respectively [9].

$$ L_{1} = {\upmu }_{0} r_{c} w^{2} \left( {{\text{ln}}\frac{{8r_{c} }}{{t_{c} }} - 2 } \right), L_{2} = {\upmu }_{0} r_{pm} \left( {ln\frac{{16r_{pm} }}{{t_{pm} }} - 2 } \right), $$
(5)

where \(w\) is the number of turns of coil, \(M_{12} \left( y \right)\) is the mutual inductance, \(\mu_{0} \) is the magnetic permeability of free space, \((^{.}) = \frac{d}{dt}\), \(t\) is the time, \(y\) is the distance between coil and PM.

In general case, the mutual inductance \(M_{12 } \left( y \right)\) is a complex non-analytic function. This represents the main difficulty for analytical investigation of the magnetic suspension model [7]. However, it is possible to consider some features of the micro-machine suspension device, which allow the application of the mutual inductance approximation formula [11]. These simplifications consist in the assumption that the linear dimensions of the coil and PM are much larger than the height of the levitation equilibrium position \(y_{0}\). It is also assumed that the induced eddy current \(i_{2}\) is distributed along the levitated control mass such that a contour corresponding to the maximum eddy current density can be identified [7].

The eddy current contour is geometrically defined as a circle having the same diameter as the reference mass [7]. Due to the above features of the device, the force interaction in the vertical direction is reduced to the interaction between the eddy current and the levitating coil current [12]. In the case of considering PM and the induced current as circles, the mutual inductance between the PM and the eddy current can be described by the Maxwell formula [11] as follows:

$$ M_{12} \left( {\upkappa } \right) = \mu_{0} \sqrt {r_{c} r_{pm} } \left[ {\left( {\frac{2}{\kappa } - {\upkappa }} \right)K\left( {\upkappa } \right) - \frac{2}{\kappa }E\left( {\upkappa } \right)} \right], {\upkappa }^{2} \left( y \right) = \frac{{4r_{c} r_{pm} }}{{\left( {r_{c} + r_{m} } \right)^{2} + y^{2} }}, $$
(6)

where \(K\left( {\upkappa } \right)\) and \(E\left( {\upkappa } \right)\) are complete eliptic integrals of the first and second kind, \({\upkappa }\left( y \right)\) is the elliptic modulus.

In deriving the equations of dynamics of PM, we consider the dynamics of its center of gravity. From this assumptions potential \({\Pi }\) and kinetic \(T\) energies of the PM are:

$$ {\Pi } = \tilde{m}gy, T = \frac{1}{2}\tilde{m}\dot{y}^{2} , $$
(7)

where \(\tilde{m}\) is the mass of the PM, \(g\) is the gravity acceleration.

The dissipation function of the system \({\Psi }\) can be written as follow:

$$ {\Psi } = \frac{1}{2}{\text{R}}_{2} \imath_{2}^{2} + \frac{1}{2}{\upmu }\dot{y}^{2} , $$
(8)

where \(R_{2}\) is PM’s electrical resistance, \({\upmu }\) is the coefficient of mechanical friction between PM and external gas environment.

We assume that the current \(\imath_{1}\) generated in the coil by the current generator has the following form

$$ \imath_{1} = \imath_{{\text{a}}} \sin {\omega t}, $$
(9)

where \(\imath_{a}\) and \({\upomega }\) are the amplitude and the high frequency of the current \(\imath_{1}\), correspondingly.

We use the Lagrange-Maxwell equations to write equation of motion of the upper ring. The displacement \(y\) and the current \(\imath_{2}\) are taken as generalized coordinates:

$$ \begin{aligned} & \frac{d}{dt}\frac{\partial W}{{\partial \imath_{2} }} + \frac{{\partial {\Psi }}}{{\partial \imath_{2} }} = 0, \\ & \frac{d}{dt}\frac{\partial T}{{\partial \dot{y}}} + \frac{{\partial \left( {{\Pi } - T} \right)}}{\partial y} + \frac{{d{\Psi }}}{{d\dot{y}}} = 0. \\ \end{aligned} $$
(10)

Substituting Eqs. (5)–(9) into Eq. (10), we obtain

$$ \begin{aligned} & L_{2} \dot{\imath }_{2} + \frac{{dM_{12} \left( y \right)}}{dy}\dot{y}\imath_{a} \sin {\upomega }t + M_{12} \left( y \right)\imath_{a} {\upomega }\cos \omega t + R_{2} i_{2} = 0, \\ & \tilde{m}\ddot{y} + {\upmu }\dot{y} - \frac{{dM_{12} \left( y \right)}}{dy}\imath_{2} \imath_{a} \sin {\upomega }t + \tilde{m}g = 0. \\ \end{aligned} $$
(11)

We introduce the nondimensional quantities as [13]

$$ \begin{aligned} & {\upxi } = \frac{y}{{2r_{c} }},a = \frac{{r_{pm} }}{{r_{c} }},{\upbeta } = \frac{{{\upmu }_{0} r_{c} }}{{L_{1} }},{\upgamma } = \frac{{t_{c} }}{{t_{pm} }},\quad j_{1} = \frac{{\imath_{1} }}{{\imath_{a} }}\quad j_{2} = \frac{{\imath_{2} }}{{\imath_{a} }},r = \frac{{R_{2} }}{{L_{1} {\upomega }}}, \\ & m_{12} = \frac{{M_{12} }}{{L_{1} }},l = \frac{{L_{2} }}{{L_{1} }},{\uptau } = {\upomega }t,{\upvarepsilon } = \frac{g}{{2{\upomega }^{2} r_{c} }},{\upalpha } = \frac{{L_{1} \imath_{a}^{2} }}{{2\tilde{m}gr_{c} }},{\uplambda } = \frac{{\upmu }}{{\tilde{m}{\upomega }}}. \\ \end{aligned} $$
(12)

and rewrite Eq. (11) in nondimensional form as

$$ \begin{aligned} lj_{2}^{{\prime}} + rj_{2} & = - \frac{{dm_{12} \left( {\upxi } \right)}}{{d{\upxi }}}{{\upxi^{\prime}sin\uptau }} - m_{12} \left( {\upxi } \right){{{\text{cos}}\uptau }}, \\ {{\upxi^{\prime\prime}}} + {{\uplambda \xi^{\prime}}} & = {\upvarepsilon }\left( {{\upalpha }\frac{{dm_{12} \left( {\upxi } \right)}}{{d{\upxi }}}j_{2} {{{\text{sin}}\uptau }} - 1} \right). \\ \end{aligned} $$
(13)

where the prime indicates the derivative with respect to \({\uptau }\). The small nondimensional quantity \(\upvarepsilon \upalpha = \frac{{L_{1} i_{a}^{2} }}{{4r_{c}^{2}\upomega ^{2} }}\) defines the ratio between magnetic and electrical energies.

For further study of the system (13) we find its equilibrium position \(\left( {j_{2} ,{\upxi }} \right) = \left( {j_{20} ,{\upxi }_{0} } \right)\), where \(j_{20} = j_{20} \left( {\uptau } \right);{\upxi }_{0}\) is the constant.

3 Equilibrium

WE assume the condition under which the PM reaches an average value \({\upxi }_{0} = \frac{{y_{0} }}{{2r_{c} }}\) \((y_{0}\) is the dimensional average equilibrium point) over the period of change in coil current \(\imath_{1}\). In other words, due to the harmonicity of the excitation current \(\imath_{1}\), the magnetic force acting on the PM is also harmonic, which leads to a steady-state oscillatory process of the PM relative to some average value \({\upxi }_{0}\). When the magnetic force changes, the equilibrium point changes, which corresponds to the equilibrium of the gravity force and the Ampere force also acting on the PM in the considered formulation. Moreover, in the general case, a variable magnetic field forms a variable magnetic stiffness, as will be shown later.

$$ \begin{aligned} & j_{20}^{{\prime}} + rj_{20} = - \frac{{m_{12} \left( {{\upxi }_{0} } \right)}}{2}e^{{i{\uptau }}} + c.c, \\ & \frac{{i{\upalpha }}}{2}\frac{{dm_{12} \left( {{\upxi }_{0} } \right)}}{{d{\upxi }}}j_{20} e^{{i{\uptau }}} + \frac{1}{2} + c.c = 0, \\ \end{aligned} $$
(14)

where \(c.c\) is the complex conjugate value of equation [14].

Solving first equation in (14), we obtain the steady-state soultion for the current \(j_{20}\) as

$$ j_{20} = \frac{{im_{12} \left( {{\upxi }_{0} } \right)}}{{2\sqrt {r^{2} + l^{2} } }}e^{{i\left( {{\uptau } + \phi } \right)}} + c.c, $$
(15)

where \(\cos \phi = \frac{l}{{\sqrt {l^{2} + r^{2} } }}, \sin \phi = \frac{r}{{\sqrt {l^{2} + r^{2} } }}\), \(i^{2} = - 1\).

Substituting Eq. (15) in the second equation in (14), we integrate the current \(j_{20}\) within \({\uptau } \in \left[ {0,{\uppi }} \right]\) and obtain the expression for the average equilibrium \({\upxi }_{0}\).

$$ m_{12} \left( {{\upxi }_{0} } \right)\frac{{dm_{12} \left( {{\upxi }_{0} } \right)}}{{d{\upxi }}} = - \frac{{2\left( {r^{2} + l^{2} } \right)}}{{{\upalpha }l}}, $$
(16)

Figures 2 and 3 show the dependence of the value of the equilibrium position \({\upxi }_{0}\) on the physical parameters of the system.

Fig. 2.
figure 2

Dependence of the integral position of the frame equilibrium \({\upxi }_{0}\) on the parameter \(\upalpha \) with \(\left( {r = 500\,\upmu ; \,2\,{\text{m}};\,4\,{\text{m}};\, 5\,{\text{m}}} \right)\)

Full size image
Fig. 3.
figure 3

Dependence of the integral equilibrium position \({\upxi }_{0}\) on the parameter \(r\) \(\left( {\upalpha = 8.7;11.7;14.6;17.5;20.4} \right)\)

Full size image

Figures 2 and 3 show that with increasing parameter \({\upalpha }\) (which corresponds to increasing current \(\imath_{a}\) the value \({\upxi }_{0}\) increases, which is associated with an increase in electromagnetic force of the ring and, therefore, Ampere force. When the parameter \(r\) increases (which corresponds to a decrease in frequency \({\upomega }\)), the equilibrium position \({\upxi }_{0}\) takes smaller values, which is caused by an increase in reactance.

After finding the condition on the integral position of the suspension equilibrium, it is interesting to estimate the magnetic stiffness for its subsequent compensation by including an electric field, which is studied in the papers [7].

4 Magnetic Spring Constant of the Suspension

Let us study the behavior of the PM near to the equilibrium point \({\upxi }_{0}\). It is assumed that the linear displacement of the PM \({\upxi }\) is small in comparison with \({\upxi }_{0}\), hence the following inequality

$$ \frac{{\upxi }}{{{\upxi }_{0} }} \ll 1, $$
(17)

Because of (17), the function of the mutual inductance \(m_{12} \left( {\upxi } \right)\) can be extended by a Taylor series at the point \({\upxi }_{0}\) in the form can be written as follow

$$ m_{12} \left( {\upxi } \right) = m_{12} \left( {{\upxi }_{0} } \right) + m_{12}^{{\prime}} \left( {{\upxi }_{0} } \right)\left( {{\upxi } - {\upxi }_{0} } \right) + m_{12}^{{\prime\prime}} \left( {{\upxi }_{0} } \right)\left( {{\upxi } - {\upxi }_{0} } \right)^{2} , $$
(18)

Substituting (18) into the last equation of set (10) and considering (16) the differential equation of the linear displacement of the PM near to the equilibrium point can be written as

$$ {{\upxi^{\prime\prime}}} + {{\uplambda \xi^{\prime}}} + c_{m} {\upxi } = F_{{\upxi }} , $$
(19)

where \(F_{{\upxi }}\) is generalized force acting on the PM, \(c_{m}\) is the spring constant of the magnetic suspension

$$ c_{m} = \frac{\varepsilon \alpha }{l}\left( {m_{12}^{{\prime}} \left( {{\upxi }_{0} } \right)} \right)^{2} {\text{cos}}\phi {\text{ cos}}2\phi {{ {\text{sin}}\uptau }}\sin \left( {\tau + \phi } \right). $$
(20)

Equation (20) show that the magnetic stiffness has a periodic character and, in the general case, is sign-variable, which means an oscillatory mode of PM levitation near the integral equilibrium position. For a more detailed study of the dependence of the stiffness \(c_{m}\) on the system parameter, consider the average value of the stiffness \(c_{m} = \frac{1}{{\uppi }}\int_{0}^{{\uppi }} {c_{m} \left( {\uptau } \right)d{\uptau }}\)

$$ c_{m} = \frac{{\alpha \varepsilon l\left( {l^{2} - r^{2} } \right)}}{{2\left( {r^{2} + l^{2} } \right)^{2} }}\left( {m_{12}^{{\prime}} \left( {{\upxi }_{0} } \right)} \right)^{2} . $$
(21)

The Eq. (21) shows that the average value of the magnetic stiffness is always positive. The only possible problem is related to the sign-variability of the initial stiffness (20), which should be considered in the modes of operation associated with the compensation of magnetic stiffness by adding electrodes to the system and creating a negative electric stiffness, which is done, for example, in the paper [7].

5 Conclusion

In this paper, a magnetic suspension consisting of an inductance coil and a levitating disk was considered. When the coil is energized by alternating current, it is shown that in this case the character of the equilibrium position has an alternating harmonic form. If the equilibrium position comes to the same point during the coil current period, an estimate of the integral mean value of this quantity was given. An expression for the magnetic stiffness of the suspension is obtained and it is shown that it also has a periodic form, which should be considered in the construction of devices of this type.