Keywords

1 Introduction

The aim of the Math-Key program described in this chapter is to open mathematical minds through the use of open tasks. The program rationale is based on the position that intellectual openness determines the future of individuals and of society, determines learning motivation and curiosity, and advances technological and scientific progress as well as equity in a multicultural and highly heterogeneous society. We believe that mathematics in general and open mathematical tasks in particular are tools for the advancement of intellectual openness, flexibility, and creativity and that they promote collaborative skills. We suggest systematic integration of the Math-Key instructional approach in teaching and learning mathematics. The Math-Key program is designed for junior-high school mathematics as a problem-solving path designed to complement the regular curricular instructional activities. It can be used though integration in the regular lessons or as an enrichment program.

The goal of the Math-Key program is the development of mathematical creativity and mental flexibility along with the advancement of mathematical knowledge and skills. Of equal importance, it is aimed at making mathematics lessons enjoyable and attainable for all students. This is done by piquing their curiosity by exposing them to a variety of problem-solving strategies applied to a particular mathematical problem or a variety of solution outcomes attained.

The openness of Math-Key tasks determines their mathematical challenge. To allow regulation of mathematical challenges with respect to students’ mathematical potential, the majority of Math-Key tasks are accompanied by dynamic applets (DA) that allow regulation of the level of mathematical challenge embedded in the tasks. The applets are open to allow students to investigate the situation given in the task, to support their understanding of the mathematical structure of the task and, if needed, to simplify the situation through experimentation. Teaching with Math-Key tasks requires changing the classroom culture and requires flexibility and openness to ideas of students on the part of the teachers. In what follows, we characterize the mathematical challenge embedded in Math-Key tasks, with a focus on its association with task openness. Then we turn to the characterization of the dynamic applets integrated into Math-Key tasks as a major tool for various mathematical challenges.

2 Openness of Math-Key Tasks

One of the well-advertised instructional approaches to teaching and learning mathematics is solving open problems. Open mathematical tasks are broadly discussed in mathematics education and are accompanied by strong arguments about their effectiveness for the development of knowledge and creativity (Pehkonen, 1995; Silver, 1995; Leikin, 2018). However, open tasks are seldom used in mathematics classrooms and are rarely included in mathematics textbooks. The Math-Key program makes open tasks available for systematic use in mathematics classes.

Math-Key tasks are of several types:

  • Multiple Solution-Strategies Tasks (MSTs) that explicitly require solving a mathematical problem in multiple ways (using multiple strategies). MSTs are open-start tasks, the openness of which is linked to the possibility of producing different individual solution-strategies spaces.

  • Multiple Outcomes Tasks (MOTs) are associated with solving problems that have multiple solution outcomes independently of the solution-strategy used. MOTs are usually ill defined (cf., Krutetskii, 1976). In order to solve the problems, participants are required to change/ choose/add problem givens. MOTs can be either be complete-ended tasks or open-ended tasks.

    • Complete-ended tasks require finding a complete set of solution outcomes. The challenge is in examining the completeness of the set of solution outcomes of an ill-defined problem.

    • Open-ended tasks allow finding multiple outcomes, without attaining a complete set of solutions.

  • Combined open-start and open-ended tasks are both MSTs and MOTs that can be solved using different solution strategies and have multiple solution outcomes that do not have a complete solution set. Examples of such tasks are problem-posing tasks and investigation tasks.

2.1 Examples of Math-Key Tasks

This section presents examples of Math-Key tasks. The tasks are analyzed according to the type of openness, spaces of possible solution strategies, and types of solution outcomes. The solution outcome spaces can be composed of finite or infinite, discreet or continuous sets of outcomes. The solution strategies can differ in representations, frequency, conventionality, and insight imbedded in the solution.

2.1.1 Task 1: Birthday Party

Tal and Limor both have a birthday. Tal plans to invite five friends to her birthday party. Limor invites seven friends. They decide to celebrate their birthdays together. How many children will be at the party?Solution strategies:

  1. 1.

    Venn Diagram;

  2. 2.

    Trying different cases;

  3. 3.

    Insight about min-max-all between;

  4. 4.

    Algebraic: sum of inequalities.

Solution outcomes: {8, 9, 10, 11, 12, 13, 14}

The task is based on a task presented in Verschaffel et al. (1994). Its solution presumes students’ understanding that the two groups of friends can have common participants. In the term used by Krutetskii (1976) this problem is an ill-defined task since there is missing information in the givens, i.e., the number of common friends in the two groups is unknown. The complexity of the solution is related to the requirement of completing the missing information. Additional complexity is related to the unconventionality of the solution outcome, which is a set of numbers and not one particular number as is usually attained when solving textbook word problems.

2.1.2 Task 2: Distance from School

This task is based on a problem presented in Verschaffel et al. (1997). There is a missing given about the exact placement of the houses. An infinite number of correct solution outcomes is possible as related to the two circles around the school which depict loci of the houses’ positions. The solution outcome is an inequality which is rarely the format for an answer to a word problem.

Distance from schoolEran’s house is 100 meters from his school, and Alex’s house is 300 meters from the school. What is the distance (S) between Eran’s house and Alex’s house?Solution strategies:

  1. 1.

    Numerical.

  2. 2.

    Insight about min-max-all between.

  3. 3.

    Diagram.

Solution outcomes: Real numbers S: 100 ≤ S ≤ 500

2.1.3 Task 3: Car Speed

A motorcycle leaves Haifa at 10:00, traveling to Ashdod at 50 km/h. The length of the road between Haifa and Ashdod is 150 km. A car leaves Haifa at 10:30, following the same route as the motorcycle. How fast does the car need to be travelling in order to catch up with the motorcycle before reaching Ashdod? Solve the problem in multiple ways.Solution strategies:

  1. 1.

    Numerical.

  2. 2.

    Algebraic.

  3. 3.

    Graphical.

Solution outcomes: 60 < v ≤ 110

In the car speed task, the speed of the car that travels from Haifa to Ashdod is missing and, thus, the problem is ill defined and requires students to consider different conditions as in Tasks 1 and 2. Speed limitation by law, not given in the problem, is a constraint that the solvers have to take into account. The task enables solving the problem in multiple ways: using numerical or algebraic expressions, and using graphs of functions. The solution outcome is an interval of real numbers, the outcome of which is very rare for school algebra.

2.1.4 Task 4: Polygon from Two Squares

This task asks us to find possible polygons constructed of two squares, while the sizes and orientation of the two given squares are unknown. A finite number of n-corner polygons (with various infinite rotated figures) can solve the task. The task can be solved in multiple ways. The complete set of natural numbers {4, 5, 6, 7, 8, 9, 10, 11, 13, 16} presents the number of corners in the resulting polygons. However, this task is open-ended because for the same n in this set there is an infinite number of polygons that can be attained.

Polygon from two squaresFor which values of n can n-corner polygons be constructed of two squares?Solution strategies:

  1. 1.

    Using manipulatives

  2. 2.

    Paper and pencil

  3. 3.

    Using dynamic geometry

Solution outcomes: {4, 5, 6, 7, 8, 9, 10, 11, 13, 16} examples of polygons:

A rectangular block is classified into different values of n. When n = 4, 6, and 8, rectangular boxes are attached and overlapped side by side. When n = 6, 7, 9, 10, 11, 13, and 16, boxes are attached in an inclined way.

2.1.5 Task 5: Average Test Grade

A class has 24 students. All of the students took a math test. The teacher graded the tests and found that the average was 74.5. Below are the grades: 79, 80, 82, 63, 70, 70, 80, 80, 82, 63, 56, 76, 82, 90, 56, 44, 90, 90, 82, 82, 72, and 70. The next day, the teacher discovered that she had forgotten to grade two tests. She added the two missing tests to the list and found that the average did not change. What could be the grades of the two tests she added? Explain.Solution strategies:

  1. 1.

    Numerical – Trial and error

  2. 2.

    Algebraic

  3. 3.

    Using Excel

Solution outcomes: 36 (non-ordered) pairs of scores: (100, 49), (99, 50), (98, 51), …, (75, 74).

This task requires solvers to complete the missing test grades to attain the given average score. Multiple combinations of pairs of grades constitute solutions of the problem. Multiple solution strategies include numerical, algebraic, and graphical solutions. The completeness of the solution is determined by the constraints of the highest (100) and the lowest (0) school grades.

2.1.6 Task 6: Tiles on a Square

Find different ways to calculate the number of (colored) tiles on the perimeter of the square (a) Square 6 × 6 (b) Square n × nSolution strategies:

  1. 1.

    Numerical (counting)

  2. 2.

    Graphical (coloring)

  3. 3.

    Generalization of numerical expressions for n × n (from (a) to (b))

  4. 4.

    Substitution of numbers in the algebraic expressions (from (b) to (a))

Solution outcomes:

  1. (a)

    Set of numerical expressions

    (for specific n, e.g. n = 6)

    4(6 − 1);

    2 ∙ 6 + 2(6 − 2);

    4 ∙ 6 − 4;

    62 − (6 − 2)2;

    4 + 4(6 − 2).

  2. (b)

    Set of algebraic expressions:

    4(n − 1); 2n + 2(n − 2);

    4n − 4; n2 − (n − 2)2; 4 + 4(n − 2).

The openness of the “tiles on a square” task is linked to the requirement to solve the tiles problem in multiple ways. The task is both open-start and open-ended. The task’s outcomes are numerical (or algebraic) expressions that reflect the way the problem is solved. Moreover, while numerical solutions can be used as generic examples to attain generalized solutions, when starting from an algebraic solution, numerical solutions can be attained by substitution of concrete numbers in algebraic expressions.

2.1.7 Task 7: Expressions of Parabolas

The expressions of parabolas tasks requires the translation of a set of mutually related graphs of quadratic functions into a set of algebraic expressions. The openness from the start is related both to the possibility of solving the problem in multiple ways and with the need to decide the values of the intercepts of the graphs with the x-axis and the min values of the given functions, which are not given in the task. Among multiple solution strategies, representation of functions as a product of two linear expressions is the most elegant way. Thus, an infinite number of solutions is possible and can be generalized using parametric representation of the functions.

Expressions of parabolasWrite expressions for the parabolas pictured. Find at least two more possible expressions for the parabolas.Solution strategies:

  1. 1.

    Paper-pencil solution

  2. 2.

    Solution using dynamic software

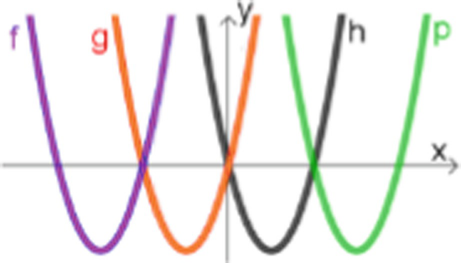
    A graph in x y coordinate system has 4 upward opening parabolic curves of f, g, h, and p. f intersects g, g intersects h, and h intersects p.

Solution outcomes:

  1. (a)

    Mutually related function equations,

    e.g.,

    f(x) = 2(x + 6)(x + 3);

    g(x) = 2x(x + 3);

    h(x) = 2x(x − 3);

    p(x) = 2(x − 6) (x − 3).

  2. (b)

    Generalized solution: Infinite number of mutually related algebraic expressions for functions f(x), g(x), h(x), p(x)

    For: a > 0, d > 0:

    f(x) = a(x + 2d) (x + d);

    g(x) = ax(x + d);

    h(x) = ax(x − d);

    p(x) = a(x − 2d) (x − d).

Table 6.1 summarizes the task analysis presented above. As described, the openness of Math-Key tasks increases the complexity of the tasks. These tasks require a high level of cognitive demand, which is linked to the mental flexibility needed to relate to the multiplicity of solutions and the novelty of mathematical reasoning necessary to complete the missing givens of the problems. To make these tasks accessible to students at different levels, we design dynamic diagrams (applets).

Table 6.1 Characterization of the openness of Math-Key tasks
Full size table

2.2 Solution Spaces and Mathematical Challenges Embedded in Math-Key Program Tasks

Solving Math-Key tasks is a fundamentally creativity-directed activity: Using different problem-solving strategies requires and develops mental flexibility and opens opportunities for using original strategies. Through task exploration, solvers search for data or knowledge they have acquired and build new structures that are matched with the task‘s information, learn new mathematical concepts, and develop new skills (Cai, 2010; Leikin, 2014; Nohda, 1995; Silver, 1995, 1997; Vale et al., 2018). Solving open tasks involves divergent and convergent thinking, decision-making, mathematical reasoning and critical reasoning.

Solving Math-Key tasks provides multiple opportunities for the development of social skills through cooperative learning and group competition directed at finding original solutions. Solving these tasks usually evokes surprises since different students can find different solutions. Positive affect is associated with surprise and “Aha!” moments when solving Math-Key tasks lead to the development of students’ mathematical curiosity and motivation to learn mathematics (Boaler, 2015; NCTM, 2014). Due to the openness of the tasks, solving Math-Key tasks also leads to the development of students’ self-regulated learning skills, self-esteem, and other twenty-first century skills (Kim et al., 2019; Leikin, 2018; Pellegrino & Hilton, 2012). Moreover, solving open tasks transforms mathematical instruction, and leads to enhanced classroom discussions in which students share different approaches and ideas as well as difficulties and successes that they have experienced (Peled & Leikin, 2017).

Figure 6.1 depicts the main components of the Math-Key program with the emphasis on typical goals, activities, conditions, and tools (cf. Leontiev’s (1978) Activity Theory). Additionally it draws attention to the construct of solution spaces and their transformation that promote students’ intellectual development. There are two kinds of solution spaces for Math-Key tasks: Spaces of Solution Strategies and Spaces of Solution Outcomes. We distinguish between individual and collective solution spaces. Due to the multiplicity of solution strategies and solution outcomes, individual solution spaces differ from one another and can be broadened by exposure to collective solution spaces (Leikin, 2007). Through broadening spaces of solution strategies, students develop problem-solving skills. Classroom discussion focuses on the elegance of the solutions, the level of complexity of the solutions, and their originality. Broadening the spaces of solution outcomes leads to either complete solution spaces or to the consideration of the quality of solution outcomes and their originality.

Fig. 6.1
A component diagram of the 2-dimensional plane with respect to spaces of solution strategies and outcomes has the factor challenge at the center surrounded by 4 major factors namely goals, tools, activities, and conditions.

Main components of the Math-Key activities

Full size image

When solving Math-Key tasks, upon finding a suitable strategy or outcome, the solvers have to search for a different strategy or outcome that fits the situation of the displayed problem (Dorfman et al., 2008; Lin & Lien, 2013). The inhibition process requires mental effort on the part of the solvers. Thus, high-level students usually display higher creativity capabilities than lower-level students (Kattou et al., 2013; Levav-Waynberg & Leikin, 2012). Usually, teachers state that MOTs and ITs are more difficult to solve than MSTs since higher cognitive skills are required. In these problems, various strategies have to be considered, as well as different outcomes (Klein & Leikin, 2020). Moreover, sometimes, during the problem-solving process, solvers experience an “Aha!” moment like a missing piece of a puzzle that falls into place, and are suddenly inspired to solve the problem (Liljedahl, 2013; Presmeg, 2018; Vale et al., 2018).

To summarize, Math-Key tasks are inherently challenging (Fig. 6.1). The challenge is associated with five main characteristics of the problem-solving process. The required multiplicity of the solutions induces activation of

  1. (a)

    Math-Key tasks requiring broader mathematical knowledge and advanced mathematical skills

  2. (b)

    Inhibition, which is essential for inhibiting a particular way of thinking which led to an already performed solution

  3. (c)

    Mathematical flexibility, which is necessary for finding a different solution strategy

  4. (d)

    Critical reasoning needed for the evaluation of the significance of differences between the strategies used or when examining the completeness of the space of solution outcomes

  5. (e)

    Novel thinking, which is entailed in the solver’s search for

    • New (for the solver) solution strategies

    • New (still unknown) solution outcomes (when solving open multiple-outcomes tasks)

    • Additional solution outcomes when completeness of the solution set is required (due to the unconventionality of the completeness criterion).

As mentioned in the introduction, dynamic applets are specially designed to allow the regulation of mathematical challenge with respect to students’ mathematical potential. The applets allow investigation of the situation given in the task, support students’ understanding of the mathematical structure of the tasks, and, if needed, simplify the situation through experimentation. In the next section, we characterize the dynamic applets that complement the Math-Key tasks and are a major tool for varying the mathematical challenge therein.

3 Varying Mathematical Challenge with Dynamic Applets

3.1 Math-Key Applets

In recent years, different types of technological tools have been developed to support teaching and learning practices. These tools have a wide variety of applications with respect to mathematical focus and didactical functionality. The notion of didactical functionality is a compound of a set of characteristics of the tool, a specific educational goal exploiting these characteristics, and a set of modalities of employing the tool in a teaching/learning process referred to the chosen educational goal (Cerulli et al., 2005). Dynamic diagrams are among the most popular technological tools used in teaching and learning mathematics.

Yerushalmi (2005) defined “a dynamic diagram” as a pre-constructed software application (often called an applet) built around an example or a problem. She distinguished between different types of diagrams: Illustrating diagrams usually offer a single graphic representation with relatively simple actions, such as viewing an animated example. Elaborating diagrams present occurrences relevant to the problem, to be explored while working on the task. Narrating diagrams are the principal delivery channel of the activity’s message.

Barzel et al. (2005) defined the four dimensions for structuring and categorizing dynamic diagrams linked to the availability of technological tools in learning and problem solving in mathematics. We apply these dimensions to Math-Key applets as follows: Math-key applets are explorative. They allow students to express and develop their ideas while exploring the mathematical relations and structures embedded in the applets. They are also Math-Key user driven. A user, not the applet, makes decisions about what to do with the applet and how. Math-Key applets are open to work with applets in different ways and find multiple solution outcomes. These Math-Key applets are specific since they are designed for use with concrete Math-Key tasks.

Implementation of Math-Key tasks accompanied by the Math-Key applets is performed according to the following principles suggested by Drijvers et al. (2010): The implementation of the Math-Key tasks requires didactic configuration based on the choice teachers make to use specific tools in order to create the desired learning outcome. Math-Key tasks support an exploitation mode of teaching by choosing how the task is presented to the students and the expected solution process needed for developing the students’ knowledge. Finally, Math-Key tasks support teachers’ didactical performance while expected results are attained by combinations of the technological tool, teaching method, and the potential of students.

Math-key applets are designed to help students to discover the structure of problems. The use of GeoGebra software simulates the situation of a given task and helps students explore it. Employing technology during math lessons is considered by some of the students as a game and not as study (Kebritchi et al., 2010). This may reduce mathematical anxiety, contribute to a positive atmosphere, and increase motivation to discover strategies and solutions. Furthermore, the applets enable the refinement of concepts and the relationships between them. When looking for solutions, sometimes the applets reveal options that students did not think of. Additionally, low-level students can reach solutions more easily using the applets, while high-level students can verify their answers. The applets can also be used as a summary tool to review the subjects studied. In conclusion, Math-Key applets make the problems displayed more approachable for students. Additionally, they make teaching more effective because mathematical concepts and structures are discovered by students through exploration of tasks with Math-Key applets.

3.2 Examples of Math-Key Applets

In this section we describe applets developed for the Math-Key tasks described above. The applets are analyzed from the point of view of applets’ functions: (a) technological features used: dragging, measuring, coloring, animation, slider, translation between representations, counting, writing expressions, value substitution; (b) focus of investigation: comparing, analyzing specific cases, observing regularity, searching for generalization. As mentioned above, all the applets are user driven, explorative, task directed, and ready to use.

3.2.1 Applet for Task 1: Birthday Party Applet

The birthday party applet (Fig. 6.2a) displays two disjoint groups of icons, representing the girls at the party, marked in two different colors. Each group is framed by a rectangle of a matching color. One of the groups is static (the number of girls icon for Tal’s group is constant). The second (Limor’s) group is dynamic, i.e., the rectangle can be dragged (Fig. 6.2b), and the number of icons can be changed (Fig. 6.2c). By dragging Limor’s rectangle, a solver can change the overall number of icons while the icons of different colors overlap. By dragging on the slider (1 ≤ n ≤ 10), the number of icons that represent Limor’s friends changes. The applet provides a dynamic illustration of the task’s structure. The dragging enables the users to focus on specific cases by creating additional solutions (including a situation where the number of participants is minimal), and as a result, enables them to analyze the outcomes. The applet enables the users to explore the situation and investigate the number of the participants at the party. The applet employs a Venn diagram with dynamic features that displays the minimal and the maximal numbers of party participants as well as all the numbers between. Changes in givens allow generalization using parameters for the invited people (Fig. 6.2).

Fig. 6.2
An illustration depicts the interrelation between the birthday applet when participants are 12, 9, and 10 with respect to the number of girls invited by Limor and the remaining by Tal.

Birthday party applet

Full size image

3.2.2 Applet for Task 2: Distance from School

This applet enables the students to visualize the task structure by visualizing the mutual position of two houses relative to the school. By continuous dragging, the students can observe the whole range of solution outcomes. The users can drag two points on the circles and understand that there is an infinite number of solutions to the problem. The applet has two versions. In one version, it does not display distances between the school and the houses; in the other version, the numerical values are displayed (Fig. 6.3).

Fig. 6.3
A diagram shows four hollow circles and points namely school, Eran, and Alex with a minimum distance of 100 meters, less than 100 and greater than 500 meters, and a maximum distance of 500 meters.

Distance from school applet – solution space (including the extremes)

Full size image

3.2.3 Applet for Task 3: Car Speed

The car speed applet includes animations of the motion of the car. Students can observe specific cases using the applet. The clock tracks the time that elapses from the beginning of the movement and can track the motion of the vehicles. They can stop the motion by clicking on the “stop” button in order to estimate the moment the vehicles meet. Additionally, two graphs of distance correspond to the speed of the vehicles and are displayed simultaneously with the animations. The applet enables students to understand the connections between numerical (car’s speed, clock’s time), algebraic (graph), and visual (animation) representations (Fig. 6.4).

Fig. 6.4
Four graphs of distance versus time illustrate the relative velocity of the scooter and the car speed at the initial default situation and when the car starts the motion at 10.30.

Car speed applet

Full size image

3.2.4 Applet for Task 4: Polygons from Two Squares

The polygon from two squares applet displays as a default two congruent squares. The squares can be rotated and dragged. The sliders enable changing the side length of each square to create incongruent squares. The dragging in the applet allows changing the positions of the squares. The users can focus on specific cases and analyze the outcomes. They can understand that there is an infinite number of polygons that can be created, while the number of vertices varies from four to sixteen (Fig. 6.5).

Fig. 6.5
A set of 2 diagrams in which the first depicts 2 conjoined rectangular boxes with 4 external points and the second depicts the overlapping of 2 boxes and external points form asymmetric angles.

Polygon from two squares applet: congruent and incongruent squares

Full size image

3.2.5 Applet for Task 5: Average Grades

The applet of this task makes use of an excel table with students’ grades that enables the calculation of the mean score. Students can add and then change grades, to see how the average changes. The applet displays the constraints of the task helping students to understand the structure of the givens of the task, to focus on specific cases, and to analyze the outcomes. Conclusions that are related to the sum of the missing grades can be reached as well conclusions regarding whether or not the order of the paired available set of scores is important (Fig. 6.6).

Fig. 6.6
A table of columns namely N and grade lists the original grades with 24 N values in which the average grade is 74.5 and the reset option is shown at the left bottom.

Average grades applet

Full size image

3.2.6 Applet for Task 6: Tiles on a Square

The tiles on a square applet depicts a square with the possibility of painting the tiles using different colors. The number of colored tiles can be displayed according to the user’s requirements. The default situation displayed is a 6x6 square. Users can change the length of the square’s sides (1 ≤ n ≤ 11). Coloring the tiles enables users to focus on specific cases and different patterns that reflect different numerical patterns. Changes of the square’s size, for which similar numerical patterns that express the number of tiles on the perimeter of the square allow geberalisation (Fig. 6.7).

Fig. 6.7
Four diagrams depict different square tiles within grids according to 5 colors of blocks. Restart, up, and down options are given with 36 0 in the first, and 36 20 in the second through last.

Tiles on a square applet

Full size image

3.2.7 Applet 7: Expressions of Parabolas

The applet for the expressions of parabolas task depicts a set of parabolas in a coordinate system. The scale on the axes is missing. The values and gridlines allow students to use specific cases. The applet allows users to write expressions for the functions and depicts corresponding graphs of parabolas. The applet allows students to check if the functions are correct by visual examination and also by using the checkbox. The correct connections between the functions are marked in blue. If there is a mistake, the incorrect connection between functions will appear in red (Fig. 6.8).

Fig. 6.8
Two graphs depict 4 upward parabolic curves on the x and y axis intersecting on a 2-dimensional plane with f, g, h, and p values in the first and deflection in the h curve and their values in the second with check work and start buttons.

Expressions of parabolas applet (right side)

Full size image

The users can focus on specific cases, find connections between numerical, algebraic, and visual representations, analyze the outcomes, and discover the regularity of the expressions. Using the applet, students can think of different solution strategies. For instance, they can start the solution process by focusing on the function that looks most familiar, and use it as a building block for the other functions. A student who chooses the function h(x) may notice that this is a function of the form h(x) = ax(x − d) for each value of d > 0, a > 0, and decide on values for a and d. The students may determine whether the algebraic expression they wrote matches the graph of the given function. This is done by conducting a visual comparison between the parabola appearing in the upper window and the original image of parabolas, and by doing calculations. How do they proceed? The students may note that every function in the given image meets the following conditions: (i) The graph of each function intersects the x-axis at two points; (ii) All of the functions are horizontal translations of the function h(x), respectively: (x) = a(x − 2d)(x − d), g(x) = ax(x + d), f(x) = a(x + 2d)(x + d). Students are familiar with the three forms of a parabola (standard, vertex, and factored form) with transitions between them, and with the significance of the parameters. They may decide which form to use in order to find an algebraic representation of the functions: First, they can focus on a specific instance with chosen parameters, and then they can try to generalize and to discuss the family of functions that fill the conditions given in the task. Some students may notice the symmetry between the functions with respect to the y-axis: g(x) = h(−x) and f(x) = p(−x).

3.3 Math-Key Applets Characteristics

Math-key applets have different goals related to each task, such as focusing on specific cases, connections between numerical, algebraic, and visual representations, discovery of regularity (expression / function), and visualization of the structure of task givens, analyzing the outcomes, and sorting (Fig. 6.9).

Fig. 6.9
A component diagram of solution strategies and outcomes in the 2 D plane has the factors, actions and challenge, in the center surrounded by 4 major factors namely goals, tools, activities, and conditions.

Main components of the Math-Key program

Full size image

Additionally, the goals of the applets can be reached by diverse functionalities of different types of dragging (continuous or discrete values; measurement; with or without change in objects’ size), coloring, animation, writing expressions or numerical values that match constraints. Moreover, each Math-Key applet is user driven – in each case, the student decides what strategy to choose.

Table 6.2 summarizes several aspects of the applets of each of the Math-Key examples discussed in this paper. These include (a) functionality of changing/transforming (through dragging, sliding, animation, and coloring) and investigations by means of measurement, writing, and substitution of values; (b) strategies used in the applets, as part of the students’ mental processing to solve the tasks (via focusing on specific cases, visualization, connections between representations, generalization, trial and error, and getting feedback from the applet); (c) the structure of the applets (user driven, explorative, open, and specific to the displayed problem); (d) the mathematical domain that the applet was built for (algebra, geometry, and statistics).

Table 6.2 Type of applets’ goals, functioning, structure, and mathematical domains according to Math-Key open tasks
Full size table

4 Summary

In conclusion, technology in mathematics classrooms has great potential to develop students’ knowledge. Coping with the challenge of Math-Key tasks using their dynamic applets is a key element in providing positive experiences, developing student knowledge, and increasing their motivation to learn. The applets provide a comfortable environment to discuss different solution strategies, produce different outcomes, and connect mathematical concepts and structures through visualization. This type of technology provides opportunities both for teachers and students through an exciting and enjoyable learning process, and should be further developed.

The variability of solution strategies and outcomes results in significant changes in classroom culture. In contrast to common instructional practices, students arriving at different solutions is acceptable and even desirable. The constructs of collective solution spaces – spaces of solution strategies and spaces of solution outcomes – are central for monitoring mathematics lessons.