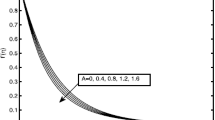Mathematical and Computational Analysis of MHD Viscoelastic Fluid Flow and Heat Transfer Over Stretching Surface Embedded in a Saturated Porous Medium

Abstract

The study of MHD flow and heat transfer over a stretching sheet in presence of saturated porous media with the effect of space and temperature dependent internal heat source/sink. Two different heating process has been considered namely, Prescribed surface temperature (PST) and Prescribe heat flux (PHF). The nonlinear boundary layer equations of momentum, which are nonlinear partial differential equations are converted into nonlinear ordinary differential equations by means of suitable similarity transformation. Similarly, the heat transfer equations, which are partial differential equations, are converted into ordinary differential equations introducing a similarity transformation. The resultant flow and heat transfer has been solved analytically. The effects of viscoelastic parameter, porous parameter, Magnetic field, suction, space and temperature dependent heat source/sink on both flow and heat transfer characteristics are presented graphically.

1 Introduction

The  study of continuously moving surface in a laminar boundary layer of non-Newtonian fluids is an important type of flow that occurs in various technological processes. Examples of practical applications include aerodynamic extrusion of plastic sheets, endless sheet metal cooling along cooling paths showing electrolyte crystal growth, boundary layers of liquid layers in the condensation process, compression by continuous deformation of mold or filament polymer sheets. Glass blowing, continuous casting, and fiber shearing are associated with flux as the surface stretches. There are a number of practical applications in the metallurgical and chemical industries, such as materials produced by extrusion and heat-treated materials, which move between a feed roller and a coil roller, or run on a conveyor belt with a continuously moving surface. And also in the polymer industry, where plastic films and man-made fibers are drawn, which rise from almost zero at the opening to a maximum value at which they remain stable. The moving fiber boundary layer creates a flow in the surrounding medium. Eventually, the fiber cools, and this affects the final product of the yarn.

Flow through a porous fluid saturated medium is important in many technological applications, and its importance increases with the growing interest in the problems of geothermal energy and astrophysics. Certain other applications can also benefit from an understanding of the basics of mass, energy and momentum transfer in porous media, namely cooling of nuclear reactors and underground disposal of nuclear waste, oil tank operations, building insulation, food processing, casting and welding, manufacturing processes and etc. Heat transfer in a porous medium plays a key role in these applications, so the books by Ingham and Pop  [7], Nild and Bejan  [20] have shown that flow in porous media is becoming a classic topic where previous developments have been confirmed by a large number of subsequent research.

Most studies of the thermal conductivity of porous media have been considered for liquids in environments with constant physical properties. However, it is well known that the viscosity of a liquid changes significantly with temperature and this affects the change in velocity and temperature caused by the flow. Therefore, when used for practical heat transfer problems where there is a large temperature difference between the surface and the liquid, continuous assimilation of ownership can lead to significant errors. For example, the viscosity of water decreases by about 240% when the temperature rises from 10 to $500\,^{\circ }$C, the effect of changing properties on heat transfer is a very difficult task for several reasons. Firstly, variations in temperature properties differ from one liquid to another, sometimes it is impossible to express them analytically. However, for practical applications, a reliable and suitable correlation equation based on the assumption of a constant property can be used so that it can be used when the influence of a variable property becomes important. Mahapatra et al. [8] studied the heat transfer and MHD stagnation point flow of a viscoelastic fluid over a stretching sheet. When the sheet is stretched on its own plane, the speed is proportional to the distance from the stagnation point. Babaelahi et al. [3] analyzed the viscoelastic magnetohydrodynamic flow and heat transfer overa stretching sheet and taken into account of ohmic and viscous dissipation. Hsiao [6] studied the heat and mass transfer of mixed convection magnetohydrodynamic viscoelastic fluid flow over a stretching sheet in presence of ohmic dissipation. Aiboud et al. [1] analyzed the second law of thermodynamics to MHD viscoelastic flow over a stretching sheet. The entropy analysis highly influenced the visco-elastic parameter and internal heating heat source/sink parameter.

The magnetic field was also used to clean molten metals from non-metallic inclusions. Numerous studies have been reported on the flow and heat transfer of electrically conductive fluids over an elongated surface in the presence of a magnetic field. Turkyilmazoglu [27, 28] studied the viscoelastic electrical conducting fluid of slip flow over a stretching surface. The key is to look at the structure of the solutions analytically and determine the thresholds above which multiple solutions exist. In various embodiments, the closed form formulas of the flow boundary layer equations are shown in two different cases, such as second class liquid B fluids and Walter. The heat transfer analysis is also performed for two different cases, such as the surface temperature of the required secondary power law and the heat flux of the required secondary power law. Rushi Kumar et al. [23] studied the viscoelastic electrically conducting fluid flow, heat and mass transfer over a vertical cone and flat plate taken into account of variable viscosity, viscous dissipation and chemical reaction. Turkyilmazoglu [29] investigated the three dimensional viscoelastic magnetohydrogynamic flow and heat transfer over a porous stretching and shrinking surface. Eswaramoorthi et al. [5] studied the three diemensional viscoelastic electrically conducting convective flow and heat transfer over a stretching surface in presence of thermal radiation and internal heating. Nayak et al. [18] studied the vicoelastic electrically conducting fluid, heat and mass transfer over a porous surface taken in to account of viscous dissipation, thermal radiation and chemical reaction. Metri et al. [9] studied the mathematical and computational analysis of viscoelastic electrically conducting mixed convection flow over a porous stretching surface considered the effects of viscous dissipation and non-uniform heat source/sink. Nayak [19] studied the heat and mass transfer of viscoelastic MHD flow over a stretching sheet embedded in a porous medium, considered the effects of thermal radiation and chemical reaction. Metri et al. [10, 11] studied the heat and mass transfer over a nonlinear stretching surface in presence of viscous dissipation. Tawade et al. [26] studied the effects of thermal radiation on electrically conducting fluid flow over a unsteady stretching surface with internal heating. Umavathi et al. [30] studied the linear stability of Maxwell nano fluid in a saturated porous medium, when the porous walls of the porous layers are subjected to periodic temperature modulation. A modified Darcy-Maxwell model is used to describe the movement of fluids. Metri et al. [12, 13] studied the MHD nanoliquid flow and heat transfer over an unsteady stretching surface. Pratap Kumar et al. [21] studied the effect of chemical reaction on magneto hydrodynamic flow in a vertical double passage channel. Baag et al. [2] analyzed the second law of thermodynamics for viscoelastic electrically conducting fluid flow, heat and mass transfer over a porous stretching surface. Metri et al. [14] Metri, P. G., studied the Lie symmetry analysis for magnetohydrodynamic flow over a stretching surface in presence of viscous dissipation and internal heating. Metri et al. [15] studied the analytical solution for magnetohydronamic nanoliquid flow over an unsteady stretching surface. Narayana et al. [17] investigated the thermocapillary effect on laminar flow of a thin film of a power-law nanoliquid over an unsteady stretching surface. Mishra et al. [16] studied the analytical and numerical solution of the viscoelastic electrically conducting fluid flow over a porous surface with non-uniform heat source/sink. Seth et al. [24] studied the radiation effect on magnetohydrodynamic viscoelastic free convective flow and heat transfer over a stretching surface in presence of partial slip. Galerkin Finite element method is used to solve the nonlinear fluid flow and heat transfer equations. Sureshkumar Raju [25] studied the Viscoelastic Darcy-Forchheimer flow and heat transfer over moving neddle with viscous dissipation. Ramesh et al. [22] studied the effects of thermal radiation, chemical reaction on viscoelastic nanoparticles flow, heat and mass transfer over stretching surface with convective boundary condition.

It is worth mentioning that heat transfer in porous media which is induced by internal heat generation arises in various physical problems such as heat removal from nuclear fuel debris in nuclear reactors, the underground disposal of radioactive waste materials, fire and combustion modeling, the development of metal waste from spent nuclear fuel, and exothermic chemical reaction in packed-bed reactors. Exact modeling of internal heat source/sink is impossible and hence simple mathematical models considering average behavior in most physical situations. In the present work we worked on Newtonian liquids investigated to viscoelastic liquid flows. The main aim of the article is to analyze the effect of space dependent and temperature dependent heat generation absorption parameters, Prandtl number, magnetic parameter, viscoelastic parameter, and porosity parameter on a viscoelastic boundary layer flow and heat transfer over stretching sheet with suction-blowing effects.

2 Mathematical Formulation

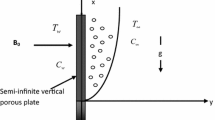
Two-dimensional flow of an incompressible electrically conducting viscoelastic fluid of the type Walter’s liquid B past a porous stretching sheet embedded in a porous medium is considered. The flow is generated due to stretching sheet along x-axis by application of two equal and opposite forces. This flow obeys the rheological equation of state derived by Beard and Walters [4], further this flow field is exposed under the influence of uniform transverse magnetic field. Hence, under the usual boundary layer assumptions, the equations of continuity, momentum and energy for the flow of MHD viscoelastic fluid of Walter’s B model are:

$$\begin{aligned}&\frac{\partial u}{\partial x}+\frac{\partial u}{\partial y}= 0. \end{aligned}$$

(36.1)

$$\begin{aligned}&\begin{array}{l} u\frac{\partial u}{\partial x}+\nu \frac{\partial u}{\partial y} =\nu \frac{\partial ^{2}u}{\partial y^{2}}-\frac{\sigma B^{2}_{0}}{\rho }u \\ - k_{0} \left[ u\frac{\partial ^{3}u}{\partial x \partial y^{2}}+\nu \frac{\partial ^{3}u}{\partial y^{3}}+\frac{\partial u}{\partial x} \frac{\partial ^{2} u}{\partial y^{2}} -\frac{\partial ^{2} u}{\partial x \partial y}\frac{\partial u}{\partial y} \right] -\frac{v}{k^{'}}u. \end{array} \end{aligned}$$

(36.2)

$$\begin{aligned}&\rho c_{p} \left\{ u\frac{\partial T}{\partial x}+\nu \frac{\partial T}{\partial y}\right\} =k \frac{\partial ^{2} T}{\partial y^{2}}+q'''. \end{aligned}$$

(36.3)

Here, $B_{0}$ is the applied magnetic field, $\sigma$ is the electrical conductivity of the fluid, $k_{0}$ is the first moment of the distribution function of relaxation times, $\nu$ is Kinematic viscosity and $k'$ is the permeability of the porous medium. The magnetic field $B_{0}$ is applied in the transverse direction of the sheet and induced magnetic field is assumed to be negligible.

where u, v and T are the fluid x-component of velocity, y-component of velocity and the temperature, respectively. $\rho , \nu , k$ and $c_{p}$ are the fluid density, Kinematic viscosity, thermal conductivity and specific heat at constant pressure of the fluid respectively, $q'''$ is the rate of internal heat source $( > 0 )$ or sink $(< 0 )$ coefficient. The internal heat source or sink term is modeled according to the following equation

$$\begin{aligned} q^{'''}=\left( \frac{ku_{w}(x)}{x\nu }\right) [A^*(T_{w}-T_{\infty })e^{-\alpha \eta }+B^*(T-T_{\infty })], \end{aligned}$$

(36.4)

In (36.4), the first term represents the dependence of the internal heat source or sink on the space coordinates while the latter represents its dependence on the temperature. Note that when both $A^{*} >0$ and $B^{*} >0$, this case corresponds to internal heat source while for both $A^{*} <0$ and $B^{*} <0$, this case corresponds to internal heat sink.

3 Boundary Conditions

The boundary conditions for the flow situation are

$$\begin{aligned} u_{w}(x)=cx,~~~v=-v_{0}~~~\textrm{at}~~~y=0,~~~~\textrm{and}~~~ u\rightarrow 0~~~u_{y}=0~~~\textrm{as}~~~y\rightarrow \infty . \end{aligned}$$

(36.5)

3.1 Prescribed Surface Temperature (PST)

For this case boundary conditions are:

$$\begin{aligned} T=T_{w}=T_{\infty }+Ax^{1}~~~\textrm{at}~~~y=0~~\textrm{and}~~T\rightarrow \infty ~~~\textrm{as}~~~y\rightarrow \infty , \end{aligned}$$

(36.6)

where l is the wall temperature parameter, $T_{w}$ is the temperature at the wall, and A is a constant. When $l=0$, the thermal boundary conditions become isothermal. We define non-dimensional temperature profile as

$$\begin{aligned} \theta (\eta )=\frac{T-T_{\infty }}{T_{w}-T_{\infty }}. \end{aligned}$$

(36.7)

3.2 Prescribed Wall Heat Flux (PHF)

The boundary conditions are

$$\begin{aligned} -k \frac{\partial T}{\partial y}= T_{w}=D x^ {m}, ~~~\textrm{at}~~~ y=0,~~\textrm{and}~~ T \rightarrow T_{\infty }~~~ \textrm{as}~~~ y\rightarrow \infty . \end{aligned}$$

(36.8)

Here, m is the wall heat flux parameter, for $m=0$, the stretching sheet is subjected to uniform heat flux. Defining

$$\begin{aligned} T-T_{\infty }=Ex^{m}(\nu c)^{\frac{1}{2}} g(\eta ), \end{aligned}$$

(36.9)

where E is another constant. Further change of dependent variable (36.9),

4 Dimensionless Quantities

Equations (36.1) and (36.2) admit self-similar solution of the form

$$\begin{aligned} u=cxf^{'}(\eta ),~~~~v=-(c\nu )^{\frac{1}{2}}f(\eta )~~~~{where}~~~\eta =\left( \frac{c}{\nu }\right) ^{\frac{1}{2}}y. \end{aligned}$$

(36.10)

Equations (36.1)–(36.3) with Eqs. (36.5)–(36.7) and (36.10), we obtain following equations.

5 Reduced Non-linear Ordinary Differential Equations

$$\begin{aligned} f'^{2}-ff''=f'''-Mnf'-k_{1}\left\{ 2f'f'''-f''^{2}-ff^{iv}\right\} -k_{2}f', \end{aligned}$$

(36.11)

$$\begin{aligned} \theta ^{''}+Prf\theta ^{'}+(B^{*}-Prlf^{'})\theta =-A^{*}f^{'}. \end{aligned}$$

(36.12)

$$\begin{aligned} g''+Prfg'+(B^{*}-Prlf')g=-A^{*}f', \end{aligned}$$

(36.13)

where $k_{1}=\frac{k_{0}c}{\nu }$ is the viscoelastic parameter, $Mn=\frac{\sigma B^{2}_{0}}{\rho }$ the magnetic parameter, $k_{2}=\frac{\nu }{k^{'}c}$ is the porosity parameter, $Pr=\frac{\mu c_{p}}{k}$ is the Prandtl number and $A^*$ and $B^*$ are space and temperature dependent internal heat generation/absorption.

Corresponding boundary condition.

6 Reduced Boundary Conditions

$$\begin{aligned} f'(0)=1,~~~f(0)=R~~~at~~~\eta =0~~~and~~~f' (\infty )=0,~~~f''(\infty )=0~~~as~~~\eta \rightarrow \infty , \end{aligned}$$

(36.14)

where $R=\frac{\nu _{0}}{\sqrt{cv}}$ is the suction parameter.

The flow behavior permits us to assume the solution of (36.11) in the form which satisfies the basic equation (36.1) and boundary conditions (36.14) with

$$\begin{aligned} f(\eta )=A+B~exp(-\alpha \eta ),~~~\alpha > 0, \end{aligned}$$

(36.15)

with $A=R+\frac{1}{\alpha }$, and $B=-\frac{1}{\alpha }$.

Here, $\alpha$ is the positive real root of the cubic equation

$$\begin{aligned} \alpha ^{3}+\frac{(k_{1}-1)}{Rk_{1}}\alpha ^{2}+\frac{1}{k_{1}}\alpha +\frac{(1+M_{n}+k_{2})}{Rk_{1}}=0. \end{aligned}$$

(36.16)

Hence, the resultant solutions of velocity components are

$$\begin{aligned} u=cxexp(-\alpha \eta ), \nonumber \\ \nu =-(vc)^{\frac{1}{2}}\left\{ A+B exp(-\alpha \eta )\right\} . \end{aligned}$$

(36.17)

6.1 Prescribed Surface Temperature (PST)

Similarly boundary conditions (36.6) take the form

$$\begin{aligned} \theta (0)=1~~at~~~\eta =0~~~,~~~~~~\theta (\infty )=0~~~as~~~\eta \rightarrow \infty , \end{aligned}$$

(36.18)

6.1.1 Introducing a New Independent Variable

$$\begin{aligned} \xi =\frac{Pr B exp(-\alpha \eta )}{\alpha }, \end{aligned}$$

(36.19)

substituting above equation in (36.12) and considering the value f, we obtain,

$$\begin{aligned} \xi \theta ^{''}+\left( 1-\frac{Pr A}{\alpha }-\xi \right) \theta ^{'}-lB^{*}\theta =\frac{A^{*}}{Pr}. \end{aligned}$$

(36.20)

The corresponding boundary conditions are

$$\begin{aligned} \theta \left( \frac{Pr B}{\alpha }\right) =1,~~~~~~\theta (0)=0. \end{aligned}$$

(36.21)

The solution of (36.20) subjected to the boundary conditions (36.21) is

$$\begin{aligned} \theta (\eta )=c_{1}(e^{-\alpha \eta })^{p_{1}} M \left[ {1}+l B^{*},p_{1}+ 1,(\frac{Pr Be^{-\alpha \eta }}{\alpha } \right] +c_{2}\left( \frac{Pr Be^{-\alpha \eta }}{\alpha } \right) ^{2}. \end{aligned}$$

(36.22)

Here M denotes the Kummer’s function with

$$\begin{aligned} c_{1}=\frac{\left( 1-c_{2}(\frac{PrB}{\alpha })^{2}\right) }{\left( \frac{Pr B}{\alpha } \right) ^{p_{1}} M [p_{1}+l B^{*},p_{1}+1,\frac{Pr B}{\alpha }]}, \end{aligned}$$

(36.23)

$$\begin{aligned} c_{1}=\frac{A^{*}}{Pr[4-2p_{1}-lB^{*}]}, \end{aligned}$$

(36.24)

$$\begin{aligned} p_{1}=\frac{PrA}{\alpha },~~~A=R+\frac{1}{\alpha },~~~B=-\frac{1}{\alpha }. \end{aligned}$$

(36.25)

The non-dimensional wall temperature gradient derived from (36.11), (36.14)–(36.15) is

$$\begin{aligned} \theta ^{'}(0)=c_{1} \left\{ -\alpha p_{1}M \left[ p_{1}+lB^{*},p_{1};\frac{PrB}{\alpha }\right] +\right. \nonumber \\ \left. +\frac{p_{1}lB^{*}PrB}{\alpha }M \left[ p_{1}+lB^{*}+1,p_{1}+2;\frac{PrB}{\alpha }\right] \right\} - \nonumber \\ -c_{2}\frac{Pr^{2}B^{2}}{\alpha }. \end{aligned}$$

(36.26)

6.2 Prescribed Heat Flux (PHF)

$$\begin{aligned} g'(0)=-1~~~~~~at~~~\eta =0~~~\textrm{and}~~~~~g(\infty )=0~~~as~~~\eta \rightarrow \infty . \end{aligned}$$

(36.27)

Here prime denotes derivative w.r.t $\eta$

Using transformation (36.19), Eqs. (36.13) and (36.27) take the following respective form

$$\begin{aligned} \xi g''+\left( 1-\frac{PrA}{\alpha }-\xi \right) g'-lB^{*}g=\frac{A^{*}}{Pr}, \end{aligned}$$

(36.28)

$$\begin{aligned} g'\left( \frac{PrB}{\alpha }\right) =\frac{1}{PrB}~~~\textrm{and}~~~g(0)=0, \end{aligned}$$

(36.29)

where prime denotes derivative w.r.t. $\xi$. The solution of (36.28), w.r.t the boundary conditions (36.29) is

$$\begin{aligned} g(\eta )=c_{3}(e^{-\alpha \eta })^{p_{1}} M\left[ p_{1}+mB^{*},p_{1}+1;\frac{PrB}{\alpha } e^{-\alpha \eta }\right] +c_{2}\left( \frac{PrB}{\alpha }e^{-\alpha \eta }\right) ^{2}, \end{aligned}$$

(36.30)

where:

• $c_{2}=\frac{A^{*}}{Pr[4-2p_{1}-lB^{*}]}$,

• $c_{3}=\frac{1-2c Pr B}{\alpha p_{1} M \left[ p_{1}+mB^{*},p_{1}+1;\frac{Pr B}{\alpha }\right] -\frac{PrB}{\alpha } \frac{p_{1}+mB^{*}}{p_{1}+1}M \left[ p_{1}+mB^{*}+1,p_{1}+2;\frac{Pr B}{\alpha } \right] }$, and

• $p_{1}=\frac{Pr A}{\alpha }$.

7 Results and Discussion

A boundary layer problem for momentum and heat transfer in MHD boundary layer viscoelastic fluid flow over a stretching surface in porous media with space and temperature dependent internal heat source/sink is examined in this paper. Linear stretching of the porous boundary, temperature dependent, space dependent, heat source/sink and porosity, magnetic parameter are taken into consideration in this study. The basic boundary layer partial differential equations, which are highly non-linear, have been converted into a set of non-linear ordinary differential equations by applying suitable similarity transformations and their analytical solutions are obtained in terms of confluent hyper geometric function (Kummer’s function). Different analytical expressions are obtained for non-dimensional temperature profile for two general cases of boundary conditions, namely (i) Prescribed power law surface temperature (PST) and (ii) Prescribed power law heat flux (PHF).

In order to have some insight of the flow and heat transfer characteristics, results are plotted graphically for typical choice of physical parameters. Figure 36.1a, b are graphical representation of horizontal velocity profiles $f'(\eta )$ for different values of viscoelastic parameter $k_{1}$ and porous parameter $k_{2}$. Figure 36.1a provides the information that the increase of viscoelastic parameter leads to the decrease of the horizontal velocity profile. This is because of the fact that introduction of tensile stress due to viscoelasticity causes transverse contraction of the boundary layer and hence velocity decreases. The effect of porosity parameter on the horizontal velocity profile in the boundary layer is shown in Fig. 36.1b, it is observed that the increase of permeability parameter $k_{2}$ leads to the decrease of the horizontal velocity profiles, which leads to the enhanced deceleration of the flow and hence, the velocity decreases.

Fig. 36.1

Velocity profiles for various values of parameters of interest

Figure 36.1c illustrates that the effect of magnetic parameter i.e., the introduction of transverse magnetic field normal to the direction, has a tendency to create a drag due to horizontal force which tends to resist the flow and, hence the horizontal velocity boundary layer decreases. This result is even true for the presence of porous parameter $k_{2}$.

The presence of magnetic field in an electrically conducting fluid tends to produce a body force against the flow. This type of resistive force tends to slow down the motion of the fluid in the boundary layer which, in turn reduces the rate of heat in the flow and appears in increasing the flow temperature.

Figure 36.1d, e depict the influence of suction/blowing parameter R on the velocity profiles in the boundary layer. It is known that imposition of the wall suction $(R >0)$ has the tendency to reduce the momentum boundary layer thickness, this causes reduction in the velocity profiles. However, the opposite behaviour is observed by imposition of the wall fluid blowing or injection $(R <0)$.

In Fig. 36.2a, b, $\theta (\eta )$ temperature distribution $\theta (\eta )$ in both PST and PHF case respectively for different values of viscoelastic parameters $k_{1}$ are plotted. Figure 36.2a, b reveals that increase of viscoelastic parameter $k_{1}$ leads to increase of temperature profile $\theta (\eta )$ in the boundary layer. This is consistent with the fact that thickening of thermal boundary layer occurs due to the increase of non-Newtonian viscoelastic normal stress.

Fig. 36.2

Temperature profiles for various values of k1

Fig. 36.3

Temperature profiles for various values of k2

The effect of porosity parameter $k_{2}$ on temperature profiles for PST and PHF case is shown in Fig. 36.3a and b, respectively. It is observed that the effect of porosity parameter $k_{2}$ is to decrease the temperature profile in the boundary layer.

The effect of magnetic parameter on temperature profile for PST and PHF case in presence of porosity parameter and heat source/sink parameter is shown in Fig. 36.4a and b, respectively. It is observed that the effect of magnetic parameter is to increase the temperature profile in the boundary layer. The Lorentz force has the tendency to increase the temperature profile, also the effect on the flow and thermal fields become more so as the strength of the magnetic field increases. The effect of magnetic parameter is to increase the wall temperature gradient in PST and PHF case.

Figure 36.5a, b depict the influence of suction/blowing parameter R on the temperature profile in the boundary layer. It is observed that imposition of the wall suction $(R>0)$ have the tendency to reduce the thermal boundary layer thickness. This causes reduction in the temperature profile. However, opposite behaviour is observed by imposition of the wall fluid blowing or injection $(R<0)$ as shown in Fig. 36.6a, b.

Fig. 36.4

Temperature profiles for various values of Mn

Fig. 36.5

Temperature profiles for various values of $R~(R > 0)$

The influence of the presence of space dependent internal heat source $(A^* > 0)$ or sink $(A^* < 0)$ in the boundary layer on the temperature field is presented in Fig. 36.7a and b in PST and PHF case respectively, it is clear from this graph that increasing the value of $A^*$ produces increase in temperature distributions of the fluid. This is expected since the presence of heat source $(A^* > 0 )$ in the boundary layer generates energy which causes the temperature of the fluid to increase. This increase in the temperature produces an increase in the flow field due to the buoyancy effect. However, as the heat source effect becomes large $(A^* =1, A^*=2 )$, a distinctive peak in the temperature profile occurs in the fluid adjacent to the wall. This means that the temperature of the fluid near the sheet is higher than the sheet temperature and consequently, heat is expected to transfer to the wall. On the contrary, heat sink $(A^* < 0 )$ has the opposite effect, namely cooling of the fluid.

Fig. 36.6

Temperature profiles for various values of $R~(R<0)$

Fig. 36.7

Temperature profiles for various values of $A^*$

When the internal heat source is absent or present, it is seen that the effect of the internal heat source is especially pronounced for high values of $A^*$. The fluid temperature is greater when internal heat source exists. This is logical because the increase of the heat transfer close to the plate and this will induce more flow along the plate.

The influence of the temperature-dependent internal heat source $( B^* > 0 )$ or sink $(B^* < 0 )$ in the boundary layer on the temperature field is the same as that of space-dependent internal heat source or sink. Namely, for $B^* > 0$ (heat source), the temperature of fluid increase while they decrease for $B^* < 0$ (heat sink). These behaviours are depicted in Fig. 36.8a and b in PST and PHF case respectively.

In Fig. 36.9a and b several temperature profiles are drawn in both PST and PHF cases respectively. The effect of Prandtl number on heat transfer may be analyzed from these figures. Both graphs implicate that the increase of Prandtl number results in the decrease of temperature distribution at a particular point. This is due to the fact that there would be a decrease of thermal boundary layer thickness with the increasing values of Prandtl number. Temperature distribution in both situations asymptotically approaches to zero in the free stream region.

Fig. 36.8

Temperature profiles for various values of $B^*$

Fig. 36.9

Temperature profiles for various values of Pr

8 Conclusion

A mathematical model study on the influence of heat transfer in MHD boundary layer viscoelastic fluid flow over stretching surface in porous media with space and temperature dependent internal heat source/sink, where flow is subject to suction/blowing through the porous boundary are taken in to consideration in this study. Analytical solutions of the governing boundary layer problem have been obtained in terms of confluent hyper geometric function (Kummer’s function) and its special form, different analytical expressions are obtained for non-dimensional temperature profile for two general cases of boundary conditions, namely (i) Prescribed surface temperature (PST) and (ii) Prescribed wall heat flux (PHF). Explicit analytical expressions are also obtained for dimensionless temperature gradient $\theta '(0)$ and heat flux $q_{w}$ for general cases as well as for special cases of different physical situations. The special conclusions derived from this study can be listed as follows.

• 1. Explicit expressions are obtained for various heat transfer characteristics in the form of confluent hyper geometric function (Kummer’s function), several expressions are also obtained in the form of some other elementary functions as the special cases of Kummer’s function.

• 2. The combined effect of increasing values of viscoelastic parameter $k_{1}$ and porosity parameter $k_{2}$ is to decrease velocity of the fluid significantly in the boundary layer region, this is because of the fact that introduction of tensile stress due to viscoelasticity causes transverse contraction of the boundary layer and hence velocity decreases, and increasing the values of porosity parameter which leads to enhanced deceleration of the flow and hence, velocity decreases.

• 3. The effect of increasing values of magnetic parameter Mn is to decrease velocity of the fluid, i.e., the introduction of transverse magnetic field normal to the direction have a tendency to create a drag due to horizontal force which tends to resist the flow and, hence the horizontal velocity boundary layer decreases.

• 4. The effect of increasing values of suction parameter $(R>0)$ is to decrease the velocity, where as it has opposite effect for $R<0$.

• 5. The combined effect of increasing values of magnetic parameter Mn and viscoelastic parameter $k_{1}$ is to increase temperature distribution in the flow region, as the increasing values of magnetic parameter is to increase the temperature, because Lorentz force has the tendency to increase the temperature profile, also the effect on the flow and thermal fields become more so as the strength of the magnetic field increases. An increasing values of viscoelastic parameter is to increase temperature, this is consistent with the fact that thickening of thermal boundary layer occurs due to the increase of non-Newtonian viscoelastic normal stress.

• 6. The effect of increasing the values of porosity parameter $k_{2}$ is to decrease the temperature distribution in the flow region.

• 7. The effect of increasing values of suction parameter R is to decrease the temperature distribution and that of blowing is to increase the same, it is known that imposition of the wall suction $(R >0)$ have the tendency to reduce the momentum boundary layer thickness. This causes reduction in the velocity profiles. However the opposite behavior is observed by imposition of the wall fluid blowing or injection $(R <0)$.

• 8. The combined effect of increasing values of space dependent and temperature dependent heat source/sink parameters $A^*$ and $B^*$ respectively is to increase the temperature distribution in the boundary layer flow region, as increase in the values of $A^*$ is to increase fluid temperature is greater when internal heat source exists. This is logical because the increase of the heat transfer close to the plate and this will induce more flow along the plate.

• 9. The effect of increasing values of Prandtl number Pr is to reduce the temperature largely in the boundary layer flow region. This is due to the fact that there would be a decrease of thermal boundary layer thickness with the increasing values of Prandtl number. Temperature distribution in both situations asymptotically approaches to zero in the free stream region.