Abstract
A protocol realizing a secure computation using a deck of physical cards is called a card-based cryptographic protocol. Since Niemi and Renvall first proposed a few protocols using a commercially available deck of playing cards in 1999, several protocols for the two-input AND and XOR functions have been proposed. By combining these existing protocols, one can construct a protocol for any Boolean function using a standard deck of playing cards. However, the minimal numbers of cards needed for Boolean functions having more than two inputs have not been revealed so much. Recently, Koyama et al. developed a card-minimal three-input AND protocol. In this study, by extending Koyama’s AND protocol, we construct a card-minimal protocol for the three-input majority function. Furthermore, carrying the idea behind these protocols further, we provide a generic card-minimal three-input protocol, which covers many important three-input Boolean functions.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Card-based cryptographic protocols realize a secure computation using a deck of physical cards (refer to [5, 25, 37] for surveys). Many researches on card-based cryptography typically use a two-colored deck of cards whose fronts are red
 or black
or black
 and whose backs are indistinguishable
and whose backs are indistinguishable
 . The Boolean values are encoded as follows:
. The Boolean values are encoded as follows:

When two face-down cards
 represent a bit \(x\in \{0,1\}\) according to Eq. (1), we call them a commitment to x and denote it as follows:
represent a bit \(x\in \{0,1\}\) according to Eq. (1), we call them a commitment to x and denote it as follows:

Given commitments as input, a committed-format protocol produces a commitment to the output value of some predetermined function. For example, the (two-input) AND protocol designed in [26] produces a commitment to \(a\wedge b\) via a series of actions, given two commitments to \(a,b\in \{0,1\}\) and two helping cards as input:

1.1 Card-Based Protocols with a Standard Deck of Cards
The protocols using a two-colored deck of cards cannot be implemented with a single standard deck of commercially available playing cards. The reason is that such playing cards contain numbers (such as \(\textrm{A},2,3,4,\ldots ,\textrm{J},\textrm{Q},\textrm{K}\)) in addition to suits (\(\clubsuit ,\heartsuit ,\spadesuit ,\diamondsuit \)), i.e., all the cards are distinct. Therefore, we need to prepare either multiple decks of playing cards or a tailor-made deck of cards to implement the protocols.
Fortunately, Niemi and Renvall [30] solved this problem by constructing a few protocols using a single standard deck of commercially available playing cards. They regarded a deck of playing cards as a total order on natural numbers from 1 to 52 because there are 52 combinations of numbers and suits in playing cards (excluding the joker); we denote these cards by
 . In their protocols, a bit \(x\in \{0,1\}\) is encoded using
. In their protocols, a bit \(x\in \{0,1\}\) is encoded using
 and
and
 satisfying \(1\le i < j\le 52\), as follows:
satisfying \(1\le i < j\le 52\), as follows:

That is, if the number on the left card is smaller, it represents 0, and if the number on the left card is larger, it represents 1. Thus, similar to the two-colored-deck case (as defined in Eq. (1)), using two cards
 and
and
 (of different numbers), we can create a commitment to \(x \in \{0,1\}\), denoted by
(of different numbers), we can create a commitment to \(x \in \{0,1\}\), denoted by

where the set \(\{i,j\}\) is called the base of the commitment. (We sometimes omit the description of the base.) For example,

is a commitment to x of base \(\{1,4\}\); if \(x=0\), the order of the sequence is
 , and if \(x=1\), it is
, and if \(x=1\), it is
 .
.
1.2 Existing Protocols
Including the Niemi–Renvall protocols mentioned above, there are several existing protocols (working on a standard deck) in the literature, as shown in Table 1. In this subsection, we briefly review these protocols one by one.
Throughout the paper, ‘2-AND,’ ‘2-XOR,’ and ‘3-AND’ mean the two-input AND, two-input XOR, and three-input AND functions, respectively; we also use similar notations for other functions. In addition, when simply writing ‘AND protocol’ or ‘XOR protocol,’ it means a two-input protocol, i.e., a 2-AND protocol or 2-XOR protocol.
Two-Input AND and XOR. As mentioned in Sect. 1.1, Niemi and Renvall [30] proposed the first protocols working on a standard deck. Specifically, they constructed a protocol for the two-input AND function (namely, 2-AND) using five cards:

Therefore, aside from the two input commitments to \(a,b\in \{0,1\}\), this AND protocol uses one helping card, namely
 . The protocol (with the slight modification by Koch et al. [6]) uses 7.5 shuffles in expectation; thus, it is a Las Vegas protocol (and it is not a finite-runtime protocol). See the first protocol listed in Table 1. We call this the Niemi–Renvall AND protocol, whose detailed explanation will be shown in Sect. 2.4.
. The protocol (with the slight modification by Koch et al. [6]) uses 7.5 shuffles in expectation; thus, it is a Las Vegas protocol (and it is not a finite-runtime protocol). See the first protocol listed in Table 1. We call this the Niemi–Renvall AND protocol, whose detailed explanation will be shown in Sect. 2.4.
Niemi and Renvall [30] also constructed a 2-XOR protocol with four cards:

Because the two input commitments need four cards as long as we follow the encoding rule in Eq. (2), this XOR protocol, which does not use any helping card, is card-minimalFootnote 1. As shown in Table 1, the protocol uses seven shuffles in expectation.
In 2016, Mizuki [22] proposed AND and XOR protocols with eight and four cards, respectively:

and

The AND and XOR protocols use four and one shuffles, respectively, and both the protocols are finite-runtime; see Table 1. While the XOR protocol is card-minimal, the AND protocol needs four helping cards.
As seen thus far, there had been card-minimal XOR protocols, whereas no card-minimal AND protocol had been found until 2019: Koch et al. [6] constructed a card-minimal AND protocol in 2019:

As seen in Table 1, this is a Las Vegas protocol, which uses six shuffles in expectation.
Three-Input AND. If we execute the above-mentioned card-minimal 2-AND protocol designed by Koch et al. [6] twice, we can securely compute 3-AND without any helping card, although it needs 12 shuffles in expectation.
In 2021, Koyama et al. [12] improved upon this by nicely making use of the Niemi–Renvall AND protocol. That is, they proposed a card-minimal 3-AND protocol with 8.5 shuffles (in expectation):

Hereinafter, we call this protocol Koyama’s AND protocol.
Thus, there have already been card-minimal protocols for 3-AND. In addition, one can easily construct a card-minimal 3-XOR protocol by executing one of the existing 2-XOR protocols twice. However, aside from 2-AND and 2-XOR, there are many other three-input Boolean functions, and it is open to determine whether all the three-input Boolean functions can be securely computed without any helping card.
For example, the three-input majority function \(\textsf{maj}:\{0,1\}^3\rightarrow \{0,1\}\) defined as
can be securely computed by combining the existing protocols (including the “copy” protocols, which will be mentioned in Sect. 1.4), because it suffices to apply AND, OR, and copy protocols by following a circuit such as
Note that a 2-OR protocol is obtained immediately by a 2-AND protocol with De Morgan’s laws, or we will directly display a 2-OR protocol in Sect. 3.1. When following the circuit for 3-majority above, we need to duplicate some input commitments, and hence, we need some helping cards, implying that such a construction is not card-minimal. Thus, designing card-minimal protocols for three-input Boolean functions (including 3-majority) is considered to be non-trivial.
1.3 Contribution
In this study, we focus on designing card-minimal protocols for three-input Boolean functions by extending the idea behind Koyama’s AND protocol [12] further. Specifically, the contribution of this paper is twofold:
-
For the three-input majority function, we construct a protocol using six cards, i.e., we design a card-minimal 3-majority protocol:

As will be explained, our protocol is based on Koyama’s AND protocol [12], and uses the same number of shuffles, namely 8.5 shuffles (in expectation). Note that the 3-majority is one of the most important three-input Boolean functions in terms of practical use.
-
We generalize the idea behind Koyama’s AND protocol so that we obtain a generic card-minimal three-input protocol, which accommodates many three-input Boolean functions (namely, 140 functions), including important functions such as 3-OR, 3-XOR, 3-NAND, 3-NOR, 3-XNOR, and the 3-minority.
1.4 Related Work
Aside from the existing AND and XOR protocols introduced in Sect. 1.2, there are “copy” protocols working on a standard deck [13, 22, 30]. A copy protocol duplicates a commitment without revealing any information about the value of the commitment. Using such a copy protocol as well as 2-AND, 2-XOR, and NOT protocolsFootnote 2, we can construct a protocol for any Boolean function. However, determining whether there exist card-minimal protocols for multi-input functions remains an open problem (except the n-AND and n-XOR functions).
There are also attractive applications using a standard deck of cards: zero-knowledge proof protocols for Sudoku [34] and millionaire protocols [18]. Moreover, under another computation model which accepts “private operations” such as revealing a card behind player’s back, card-minimal AND, XOR, and copy protocols were constructed [16].
As mentioned at the beginning of this section, many card-based protocols work on a two-color deck of cards; under several kinds of settings of decks (including the standard-deck and two-color-deck settings), the research area on card-based cryptography has grown rapidly recently from both theoretical and practical aspects. Examples are: constructing zero-knowledge proof protocols [15, 32, 33, 35], investigating computation models [3, 9, 23, 39] and shuffles [8, 21, 36], designing private-operation-model protocols [1, 17, 28, 29, 31], seeking practical and/or efficient protocols [2, 7, 14, 20, 40], and making use of other physical objects [4, 11, 19, 27, 38].
1.5 Outline
In Sect. 2, we introduce operations used in card-based cryptography and describe the existing protocol [30] and technique [12]. In Sect. 3, we show how to construct a three-input majority protocol by extending the ideas behind the Niemi–Renvall AND protocol and Koyama’s AND protocol. In Sect. 4, we construct a generic protocol which covers many three-input Boolean functions by generalizing the ideas further. Section 5 summarizes our study.
2 Preliminaries
In this section, we introduce the description of operations formalized in the computational model of card-based cryptography [24]. We also introduce the two practical shuffles called the “random cut” and “random bisection cut.” Finally, we describe the Niemi–Renvall AND protocol [30] and the useful technique [12] called the “swap operation by commitment value.”
2.1 Operations
We here introduce three operations, namely rearrangement, turn, and shuffle. We assume that we have a sequence of n face-down cards for some natural number \(n\,(\ge 2)\).
Rearrangement. This applies some permutation \(\pi \in S_n\) to the sequence, where \(S_n\) denotes the symmetric group of degree n. This is written as \((\textsf{perm},{\pi })\), and the sequence changes as follows:

Turn. This reveals the t-th card from the left in the sequence to check its number. This is written as \((\textsf{turn},{\{t\}})\), and the sequence changes as follows (for example):

Shuffle. This applies a permutation \(\pi \) drawn from a permutation set \(\varPi \subseteq S_n\) according to a probability distribution \(\mathcal {F}\) on \(\varPi \). This is written as \((\textsf{shuf},{\varPi ,\,\mathcal {F}})\), and the sequence changes as follows:

Note that no one learns which permutation in \(\varPi \) was applied. If \(\mathcal {F}\) is uniform, then we simply write it as \((\textsf{shuf},{\varPi })\).
2.2 Random Cut
A random cut, denoted by \(\langle \,\cdot \,\rangle \), is an operation that shuffles a sequence by cyclically shifting it. Applying a random cut to a sequence of n cards results in one of n possibilities, each occurring with a probability of 1/n:

Thus, this operation can be written as \((\textsf{shuf},{\langle \,\!(1 \ 2\cdots n)\!\,\rangle })\), where \(\langle \,\!(i_1 \ i_2\cdots i_\ell )\!\,\rangle \) denotes the cyclic group generated by a (cyclic) permutation \((i_1 \ i_2\cdots i_\ell )\).
2.3 Random Bisection Cut (RBC)
A random bisection cut (RBC) [26], denoted by \([\,\cdot \, |\,\cdot \,]\), is a shuffling operation, which bisects a sequence of cards and then randomly swaps the two halves. Thus, when an RBC is applied to a sequence of 2n cards, the sequence becomes either the original one, or the one in which the first n cards are swapped with the last n cards, as follows:

This operation can be written as \((\textsf{shuf},{\{\textsf{id},(1 \ n\!+\!1)(2 \ n\!+\!2)\cdots (n \ 2n)\}})\), where \(\textsf{id}\) denotes the identity permutation.
2.4 The Niemi–Renvall AND Protocol
The Niemi–Renvall AND protocol [30] takes as input two commitments to \(a,b\in \{0,1\}\) as well as an additional card and outputs a commitment to \(a\wedge b\). This protocol proceeds as follows.
-
1.
Place the two input commitments and the additional card
 as follows, and turn over the face-up card:
as follows, and turn over the face-up card: 
-
2.
Swap the third and fourth cards:

The initial and swapped sequences for each input are described in the third and fourth columns of Table 2. Observe that the order of
 ,
,
 , and
, and
 in the swapped sequence is
in the swapped sequence is
 if and only if \(a\wedge b=1\). Therefore, we try to remove the two cards
if and only if \(a\wedge b=1\). Therefore, we try to remove the two cards
 and
and
 in the next steps.
in the next steps. -
3.
Apply a random cut to the sequence:

-
4.
Turn over the first card. Remove the revealed card if it is either
 or
or
 ; otherwise, turn the card face down. Return to Step 3 unless both
; otherwise, turn the card face down. Return to Step 3 unless both
 and
and
 are already removed.
are already removed. -
5.
Now, the sequence is one of the three possibilities as described in the fifth column of Table 2. Apply a random cut to the sequence again and then turn over the first card. We can obtain a commitment to \(a\wedge b\) (as output), as follows:Footnote 3

If the first card is
 , then we obtain a commitment to the negation of \(a\wedge b\); we can obtain a commitment to \(a\wedge b\) by swapping the two cards comprising the commitment.
, then we obtain a commitment to the negation of \(a\wedge b\); we can obtain a commitment to \(a\wedge b\) by swapping the two cards comprising the commitment. Table 2. The sequence of five cards for each input during the Niemi–Renvall protocol
The correctness of this protocol is clear from Table 2. In addition, no information about the input and output is leaked when a card is turned over because we always apply a random cut before turning over a card.
2.5 Swapping by Commitment Value
Koyama et al. [12] proposed a sub-protocol called the swapping by commitment value based on the idea of behind the two-input XOR protocol [22] proposed by Mizuki. This led to the construction of the 3-AND protocol [12]. Given two target cards
 and a commitment to \(c\in \{0,1\}\) of base \(\{i,j\}\), the swapping by commitment value is to swap the two cards
and a commitment to \(c\in \{0,1\}\) of base \(\{i,j\}\), the swapping by commitment value is to swap the two cards
 if and only if \(c=1\), without leaking any information about the value of c as follows:
if and only if \(c=1\), without leaking any information about the value of c as follows:

The procedure is shown below.
-
1.
Place the two target cards and the commitment to c as follows:

-
2.
Swap the second and third cards, i.e., apply \((\textsf{perm},{(2\,3)})\).
-
3.
Apply \((\textsf{shuf},{\{\textsf{id},(1\,3)(2\,4)\}})\), i.e., apply an RBC as follows:

-
4.
Apply \((\textsf{perm},{(2\,3)})\) again. Then, the sequence becomes one of the following two possibilities depending on the value of c:

Observe that the order of the first and second cards are desirable if the order of
 and
and
 is
is
 .
. -
5.
Turn over the third and fourth cards to reveal the order of
 and
and
 .
.-
(a)
If
 appears, then output the first and second cards.
appears, then output the first and second cards. -
(b)
If
 appears, then swap the first and second cards and output them.
appears, then swap the first and second cards and output them.
-
(a)
Thus, the above sub-protocol achieves the desired functionality without leaking any information about c.
3 Three-Input Majority Protocol
In this section, we construct a card-minimal protocol for the three-input majority function \(\textsf{maj}(a,b,c)\) working on a standard deck. The idea behind our proposed protocol is based on the Niemi–Renvall AND protocol [30] and Koyama’s AND protocol [12].
To construct a 3-majority protocol, we utilize the following equation:
To compute \(\textsf{maj}(a,b,c)\), observe that, if \(c=0\), it suffices to compute \(a\wedge b\) using the Niemi–Renvall AND protocol introduced in Sect. 2.4; otherwise, we want to compute \(a\vee b\). Therefore, we first construct an OR protocol by modifying the Niemi–Renvall protocol and then construct a 3-majority protocol.
3.1 Two-Input or Protocol
We construct a two-input OR protocol by changing the rearrangement positions in the Niemi–Renvall AND protocol. The protocol takes as input two commitments to a, b as well as an additional card and outputs a commitment to \(a\vee b\), as follows.
-
1.
Place the two input commitments and the additional card
 and turn it over as follows:
and turn it over as follows: 
-
2.
Rearrange the sequence as follows, i.e., apply \((\textsf{perm},{(2 \ 3 \ 5 \ 4)})\):

The input and rearranged sequences for each input are described in the third and fourth columns of Table 3. Observe that the order of
 ,
,
 , and
, and
 in the rearranged sequence is
in the rearranged sequence is
 if and only if \(a\vee b=1\).
if and only if \(a\vee b=1\). -
3.
Apply Steps 3, 4, and 5 of the Niemi–Renvall AND protocol shown in Sect. 2.4 to obtain a commitment to \(a\vee b\).
Table 3. The sequence of five cards for each input during the 2-OR protocol
3.2 Idea
Remember that in Step 2 of the Niemi–Renvall AND protocol and our OR protocol, we rearrange the sequence of cards, i.e., the AND protocol uses \((\textsf{perm},{(3 \ 4)})\) and the OR protocol uses \((\textsf{perm},{(2 \ 3 \ 5 \ 4)})\).
Observe that if we apply \((\textsf{perm},{(3 \ 4)})\), namely

and apply \((\textsf{perm},{(2 \ 3)(4 \ 5)})\), namely

the resulting sequence becomes the same as the one after executing Step 2 of our OR protocol. In other words, \(((2 \ 3)(4 \ 5))(3 \ 4) = (2 \ 3 \ 5 \ 4)\).
Therefore, after applying \((\textsf{perm},{(3 \ 4)})\), if we do nothing, it results in the AND protocol. If we apply \((\textsf{perm},{(2 \ 3)(4 \ 5)})\) after applying \((\textsf{perm},{(3 \ 4)})\), it results in the OR protocol. Therefore, it suffices to perform the swap operation by commitment value [12] introduced in Sect. 2.5 to apply \((\textsf{perm},{(2 \ 3)(4 \ 5)})\) if and only if \(c=1\) (see Eq. (3) again).
3.3 Description of Protocol
We are ready to describe the procedure for our 3-majority protocol. The protocol takes three commitments to a, b, c as input and outputs a commitment to \(\textsf{maj}(a,b,c)\).
-
1.
Place three input commitments as follows:

-
2.
Swap the second and the third cards:

-
3.
Apply the swap operation by the commitment to c [12] to apply \((\textsf{perm},{(1 \ 2)(3 \ 4)})\) if and only if \(c=1\) as follows:
-
(a)
Rearrange the sequence as follows:

-
(b)
Apply \((\textsf{shuf},{\{\textsf{id},(1\,4)(2\,5)(3\,6)\}})\), i.e., apply an RBC as follows:

-
(c)
Rearrange the sequence as follows:

-
(d)
Turn over the fifth and sixth cards. If their order is
 , do nothing; if it is
, do nothing; if it is
 , swap the first and second cards as well as the third and fourth cards. The sequence for each input is described in Table 4 where the order of the revealed two cards
, swap the first and second cards as well as the third and fourth cards. The sequence for each input is described in Table 4 where the order of the revealed two cards
 does not matter.
does not matter.
-
(a)
-
4.
Execute Steps 3, 4, and 5 of the Niemi–Renvall AND protocol to obtain a commitment to \(\textsf{maj}(a,b,c)\), where we use the first through fourth cards as input, and the
 turned over in Step 3d as an additional card (i.e., place the
turned over in Step 3d as an additional card (i.e., place the
 in the first from the left).
in the first from the left).
 in Step 3d.
in Step 3d.3.4 Correctness and Security
The correctness of this protocol is clear from Table 4 because when the input (a, b, c) satisfies \(\textsf{maj}(a,b,c)=0\), the resulting sequence after Step 3 is
 (where
(where
 ,
,
 , and
, and
 are removed); otherwise, the sequence is
are removed); otherwise, the sequence is
 . As for the security, we execute the swap operation by commitment value [12] in Step 3 and then the part of the Niemi–Renvall AND protocol (and Steps 1 and 2 just place and swap the sequence, respectively), no information about the input and output is leaked.
. As for the security, we execute the swap operation by commitment value [12] in Step 3 and then the part of the Niemi–Renvall AND protocol (and Steps 1 and 2 just place and swap the sequence, respectively), no information about the input and output is leaked.
More formally, we use the KWH-tree [10] to prove the security (and correctness) of this protocol; we depict the KWH-tree of our three-input majority protocol in Fig. 1. In the diagram, states of a sequence of cards are expressed as nodes, and operations on the sequence of cards are expressed as edges. Because the sum of the probability distributions of the nodes is equal to the probability distribution of the input, the protocol is guaranteed to be secure.
4 Generic Protocol for Three-Input Functions
In this section, we generalize our 3-majority protocol described in Sect. 3 so as to obtain a generic card-minimal protocol for three-input Boolean functions.
After we describe the idea behind the generalization in Sect. 4.1, we generalize the Niemi–Renvall AND protocol and the swap operation by commitment value [12] in Sects 4.2 and 4.3, respectively.
Before going into the subsections, we define a notation; hereinafter, \(\pi _{ijk\ell }\) denotes a permutation in \(S_4\) such that
for four distinct integers \(i,j,k,\ell \in \{1,2,3,4\}\). For example, \(\pi _{1234}=\textsf{id}\) and \(\pi _{1324}=(2 \ 3)\).
4.1 Idea
Our idea is that, as \(\textsf{maj}(a,b,c)\) is represented with the two elementary functions of a and b depending on the value of c (as in Eq. (3)), every three-input Boolean function \(f:\{0,1\}^3\rightarrow \{0,1\}\) can be also written as follows:
where there exist two functions \(g,h:\{0,1\}^2\rightarrow \{0,1\}\).
Remember that in our 3-majority protocol proposed in Sect. 3, we first apply the permutation \(\pi _{1324}\) (to compute 2-AND) and then, if \(c=1\), apply the permutation \(\pi _{2143}\) by the swap operation (to compute 2-OR); \(\pi _{1324}\) leads to 2-AND, and \(\pi _{2143}\pi _{1324}\) leads to 2-OR. If we replace these two permutations with other ones, then we will obtain (possibly) another three-input protocol.
Bearing this in mind, we first investigate what two-input function (as a candidate for g or h in Eq. (4)) will be computed for every permutation \(\pi _{ijk\ell }\in S_4\) (in Sect. 4.2). Then, we enumerate all possible swap operations (in Sect. 4.3).
4.2 Generalizing the Niemi–Renvall and Protocol
In this subsection, we generalize the Niemi–Renvall AND protocol by considering all permutations for Step 2 of the protocol.
Assume that we apply a permutation \(\pi \in S_4\) (instead of the original permutation) in Step 2 of the Niemi–Renvall AND protocol. Then, at the end of the protocol, we should obtain a commitment to a certain two-input function; we denote this function by \(\textsf{NR}^\pi :\{0,1\}^2\rightarrow \{0,1\}\).
We examined all 4! possibilities for \(\pi \) and write \(\textsf{NR}^\pi (a,b)\) in Table 5. This table tells us that aside from 2-XOR and 2-XNOR, all two-input functions can be obtained.
4.3 Generalizing Swap Operation by Commitment Value
In this subsection, consider all possible swapping operations.
Assume that we have four cards along with a commitment to \(c\in \{0,1\}\) of base \(\{5,6\}\):

We want to apply a permutation in \(S_4\) to the first four cards if and only if \(c=1\). What are the possible permutations? We can consider two kind of swap operations.
\((i \ j)\)-swap. Remember that the swap operation introduced in Sect. 2.5 swaps two cards (or does not) depending on the value of c. As a natural extension, let us consider a swap operation such that the i-th and j-th cards (among the leftmost four cards) for \(1\le i<j\le 4\) are swapped or not; we call this the \((i \ j)\)-swap, which can be achieved as follows.
-
1.
Apply the permutation corresponding to \((i \ j)\) according to Table 6.
-
2.
Apply \((\textsf{shuf},{\{\textsf{id},(3\,5)(4\,6)\}})\) , i.e., apply an RBC as follows:

-
3.
Apply the inverse of the permutation applied in Step 1.
-
4.
Turn over the fifth and sixth cards (namely, apply \((\textsf{turn},{\{5,6\}})\)). If the order of the revealed cards are
 , swap the i-th and j-th cards (namely, \((\textsf{perm},{(i\ j)})\)); otherwise, do nothing.
, swap the i-th and j-th cards (namely, \((\textsf{perm},{(i\ j)})\)); otherwise, do nothing.
\((i \ j)(k \ \ell )\)-swap. Remember that our 3-majority protocol uses \((\textsf{perm},{(2 \ 3)(4 \ 5)})\) in the swap operation, and note that the permutations \((2 \ 3)\) and \((4 \ 5)\) are disjoint. Therefore, we can consider a swap operation such that the i-th and j-th cards as well as the k-th and \(\ell \)-th cards are swapped or not for \(1\le i< j\le 4\) and \(\{k,\ell \}=\{1,2,3,4\}-\{i,j\}\); we call this the \((i \ j)(k \ \ell )\)-swap, which can be achieved as follows.
-
1.
Apply the permutation corresponding to \((i \ j)(k \ \ell )\) according to Table 7.
-
2.
Apply \((\textsf{shuf},{\{\textsf{id},(1\,4)(2\,5)(3\,6)\}})\), i.e., apply an RBC as follows:
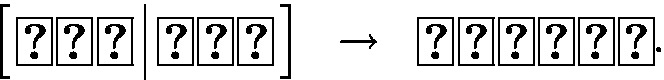
-
3.
Apply the inverse of the permutation applied in Step 1.
-
4.
Turn over the fifth and sixth cards (namely, apply \((\textsf{turn},{\{5,6\}})\)). If the order of the revealed cards are
 , swap the i-th and j-th cards as well as k-th and \(\ell \)-th cards (namely, \((\textsf{perm},{(i \ j)(k \ \ell )})\)); otherwise, do nothing.
, swap the i-th and j-th cards as well as k-th and \(\ell \)-th cards (namely, \((\textsf{perm},{(i \ j)(k \ \ell )})\)); otherwise, do nothing.
4.4 Description of Protocol
We are now ready to describe our generic protocol for three-input Boolean function.
Our protocol owns two permutations \(\pi ,\sigma \in S_4\) as parameter, where either \(\sigma = (i \ j)\) for \(1\le i<j\le 4\), or \(\sigma =(i \ j)(k \ \ell )\) for \(1\le i< j\le 4\) and \(\{k,\ell \}=\{1,2,3,4\}-\{i,j\}\); it proceeds as follows.
-
1.
Place three input commitments as:

-
2.
Apply \((\textsf{perm},{\pi })\).
-
3.
Apply \(\sigma \)-swap.
-
4.
Apply Steps 3, 4, and 5 of the Niemi–Renvall AND protocol.
4.5 Covered Functions
In this subsection, we comprehensively reveal what three-input functions our generic protocol computes.
Executing our generic protocol with parameter \(\pi ,\sigma \in S_4\) is equivalent to executing a protocol for the three-input Boolean function f such that
For example, if we take \(\pi ,\sigma \) as in the first and second columns of Table 8, we have \(\textsf{NR}^\pi \) and \(\textsf{NR}^{\sigma \pi }\) as in the fourth and fifth columns, and hence, the corresponding three-input Boolean functions are shown in the sixth column. This table tells us that major three-input Boolean functions are covered by our generic protocol.
From the user’s perspective, given a three-input function f, we want to find two permutations \(\pi ,\sigma \in S_4\) which lead to f. Table 9 helps us: We first find g, h such that
then, using Table 9, find the corresponding parameter \(\pi ,\sigma \).
Although not all three-input Boolean functions have a corresponding parameter \(\pi ,\sigma \), our generic protocol covers 140 three-input Boolean functions among the 256 ones.
5 Conclusion
In this study, we showed how to construct a card-minimal 3-majority protocol by extending the Niemi–Renvall AND protocol [30] and Koyama’s AND protocol [12]. Furthermore, we constructed a generic card-minimal protocol that covers many three-input Boolean functions as shown in Table 9.
Although the proposed protocol accommodates many major functions as seen in Table 8, not all the three-input Boolean functions can be computed by it. It is open to determine whether there exists a six-card protocol for every three-input Boolean function. While 3-XOR and 3-XNOR can be computed without any helping card by using the existing protocols, we conjecture that some functions, say
would need helping cards.
Notes
- 1.
This paper (and the literature) assume the encoding (2), i.e., a two-card-per-bit encoding, when discussing the card-minimality of protocols; thus, an n-input (Boolean function) protocol always needs 2n cards for input commitments, and such a protocol using only 2n cards is card-minimal.
- 2.
A NOT protocol can be simply constructed: swapping two cards comprising a commitment produces a commitment to the negation.
- 3.
This step was proposed by Koch et al. [6], reducing the number of shuffles.
References
Abe, Y., et al.: Efficient card-based majority voting protocols. New Gener. Comput. 40, 173–198 (2022). https://doi.org/10.1007/s00354-022-00161-7
Abe, Y., Hayashi, Y., Mizuki, T., Sone, H.: Five-card AND computations in committed format using only uniform cyclic shuffles. New Gener. Comput. 39(1), 97–114 (2021). https://doi.org/10.1007/s00354-020-00110-2
Dvořák, P., Koucký, M.: Barrington plays cards: the complexity of card-based protocols. In: Bläser, M., Monmege, B. (eds.) Theoretical Aspects of Computer Science. LIPIcs, vol. 187, pp. 26:1–26:17. Schloss Dagstuhl, Dagstuhl (2021). https://doi.org/10.4230/LIPIcs.STACS.2021.26
Isuzugawa, R., Miyahara, D., Mizuki, T.: Zero-knowledge proof protocol for cryptarithmetic using dihedral cards. In: Kostitsyna, I., Orponen, P. (eds.) UCNC 2021. LNCS, vol. 12984, pp. 51–67. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-87993-8_4
Koch, A.: Cryptographic protocols from physical assumptions. Ph.D. thesis, Karlsruhe Institute of Technology (2019). https://doi.org/10.5445/IR/1000097756
Koch, A., Schrempp, M., Kirsten, M.: Card-based cryptography meets formal verification. In: Galbraith, S.D., Moriai, S. (eds.) ASIACRYPT 2019. LNCS, vol. 11921, pp. 488–517. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-34578-5_18
Koch, A., Schrempp, M., Kirsten, M.: Card-based cryptography meets formal verification. New Gener. Comput. 39(1), 115–158 (2021). https://doi.org/10.1007/s00354-020-00120-0
Koch, A., Walzer, S.: Foundations for actively secure card-based cryptography. In: Farach-Colton, M., Prencipe, G., Uehara, R. (eds.) Fun with Algorithms. LIPIcs, vol. 157, pp. 17:1–17:23. Schloss Dagstuhl, Dagstuhl (2020). https://doi.org/10.4230/LIPIcs.FUN.2021.17
Koch, A., Walzer, S.: Private function evaluation with cards. New Gener. Comput. 1–33 (2022, in press). https://doi.org/10.1007/s00354-021-00149-9
Koch, A., Walzer, S., Härtel, K.: Card-based cryptographic protocols using a minimal number of cards. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9452, pp. 783–807. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48797-6_32
Komano, Y., Mizuki, T.: Coin-based secure computations. Int. J. Inf. Secur. 1–14 (2022, in press). https://doi.org/10.1007/s10207-022-00585-8
Koyama, H., Miyahara, D., Mizuki, T., Sone, H.: A secure three-input AND protocol with a standard deck of minimal cards. In: Santhanam, R., Musatov, D. (eds.) CSR 2021. LNCS, vol. 12730, pp. 242–256. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-79416-3_14
Koyama, H., Toyoda, K., Miyahara, D., Mizuki, T.: New card-based copy protocols using only random cuts. In: ASIA Public-Key Cryptography Workshop, pp. 13–22. ACM, New York (2021). https://doi.org/10.1145/3457338.3458297
Kuzuma, T., Toyoda, K., Miyahara, D., Mizuki, T.: Card-based single-shuffle protocols for secure multiple-input AND and XOR computations. In: ASIA Public-Key Cryptography, pp. 1–8. ACM, New York (2022, to appear). https://doi.org/10.1145/3494105.3526236
Lafourcade, P., Miyahara, D., Mizuki, T., Robert, L., Sasaki, T., Sone, H.: How to construct physical zero-knowledge proofs for puzzles with a “single loop’’ condition. Theor. Comput. Sci. 888, 41–55 (2021). https://doi.org/10.1016/j.tcs.2021.07.019
Manabe, Y., Ono, H.: Card-based cryptographic protocols with a standard deck of cards using private operations. In: Cerone, A., Ölveczky, P.C. (eds.) ICTAC 2021. LNCS, vol. 12819, pp. 256–274. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-85315-0_15
Manabe, Y., Ono, H.: Card-based cryptographic protocols with malicious players using private operations. New Gener. Comput. 40, 67–93 (2022). https://doi.org/10.1007/s00354-021-00148-w
Miyahara, D., Hayashi, Y., Mizuki, T., Sone, H.: Practical card-based implementations of Yao’s millionaire protocol. Theor. Comput. Sci. 803, 207–221 (2020). https://doi.org/10.1016/j.tcs.2019.11.005
Miyahara, D., Komano, Y., Mizuki, T., Sone, H.: Cooking cryptographers: secure multiparty computation based on balls and bags. In: Computer Security Foundations Symposium, pp. 1–16. IEEE, New York (2021). https://doi.org/10.1109/CSF51468.2021.00034
Miyahara, D., Ueda, I., Hayashi, Y., Mizuki, T., Sone, H.: Evaluating card-based protocols in terms of execution time. Int. J. Inf. Secur. 20(5), 729–740 (2020). https://doi.org/10.1007/s10207-020-00525-4
Miyamoto, K., Shinagawa, K.: Graph automorphism shuffles from pile-scramble shuffles. New Gener. Comput. 40, 199–223 (2022). https://doi.org/10.1007/s00354-022-00164-4
Mizuki, T.: Efficient and secure multiparty computations using a standard deck of playing cards. In: Foresti, S., Persiano, G. (eds.) CANS 2016. LNCS, vol. 10052, pp. 484–499. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-48965-0_29
Mizuki, T., Komano, Y.: Information leakage due to operative errors in card-based protocols. Inf. Comput. 1–15 (2022, in press). https://doi.org/10.1016/j.ic.2022.104910
Mizuki, T., Shizuya, H.: A formalization of card-based cryptographic protocols via abstract machine. Int. J. Inf. Secur. 13(1), 15–23 (2013). https://doi.org/10.1007/s10207-013-0219-4
Mizuki, T., Shizuya, H.: Computational model of card-based cryptographic protocols and its applications. IEICE Trans. Fundam. E100.A(1), 3–11 (2017). https://doi.org/10.1587/transfun.E100.A.3
Mizuki, T., Sone, H.: Six-card secure AND and four-card secure XOR. In: Deng, X., Hopcroft, J.E., Xue, J. (eds.) FAW 2009. LNCS, vol. 5598, pp. 358–369. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-02270-8_36
Murata, S., Miyahara, D., Mizuki, T., Sone, H.: Efficient generation of a card-based uniformly distributed random derangement. In: Uehara, R., Hong, S.-H., Nandy, S.C. (eds.) WALCOM 2021. LNCS, vol. 12635, pp. 78–89. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-68211-8_7
Nakai, T., Misawa, Y., Tokushige, Y., Iwamoto, M., Ohta, K.: Secure computation for threshold functions with physical cards: power of private permutations. New Gener. Comput. 1–19 (2022, in press). https://doi.org/10.1007/s00354-022-00153-7
Nakai, T., Misawa, Y., Tokushige, Y., Iwamoto, M., Ohta, K.: How to solve millionaires’ problem with two kinds of cards. New Gener. Comput. 39(1), 73–96 (2021). https://doi.org/10.1007/s00354-020-00118-8
Niemi, V., Renvall, A.: Solitaire zero-knowledge. Fundam. Inf. 38(1,2), 181–188 (1999). https://doi.org/10.3233/FI-1999-381214
Ono, H., Manabe, Y.: Card-based cryptographic logical computations using private operations. New Gener. Comput. 39(1), 19–40 (2020). https://doi.org/10.1007/s00354-020-00113-z
Robert, L., Miyahara, D., Lafourcade, P., Mizuki, T.: Card-based ZKP for connectivity: applications to Nurikabe, Hitori, and Heyawake. New Gener. Comput. 40, 149–171 (2022). https://doi.org/10.1007/s00354-022-00155-5
Robert, L., Miyahara, D., Lafourcade, P., Libralesso, L., Mizuki, T.: Physical zero-knowledge proof and NP-completeness proof of Suguru puzzle. Inf. Comput. 1–14 (2021, in press). https://doi.org/10.1016/j.ic.2021.104858
Ruangwises, S.: Two standard decks of playing cards are sufficient for a ZKP for Sudoku. New Gener. Comput. 1–17 (2022, in press). https://doi.org/10.1007/s00354-021-00146-y
Ruangwises, S., Itoh, T.: Physical zero-knowledge proof for ripple effect. Theor. Comput. Sci. 895, 115–123 (2021). https://doi.org/10.1016/j.tcs.2021.09.034
Saito, T., Miyahara, D., Abe, Y., Mizuki, T., Shizuya, H.: How to implement a non-uniform or non-closed shuffle. In: Martín-Vide, C., Vega-Rodríguez, M.A., Yang, M.-S. (eds.) TPNC 2020. LNCS, vol. 12494, pp. 107–118. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-63000-3_9
Shinagawa, K.: On the construction of easy to perform card-based protocols. Ph.D. thesis, Tokyo Institute of Technology (2020)
Shinagawa, K.: Card-based cryptography with dihedral symmetry. New Gener. Comput. 39(1), 41–71 (2021). https://doi.org/10.1007/s00354-020-00117-9
Takashima, K., Miyahara, D., Mizuki, T., Sone, H.: Actively revealing card attack on card-based protocols. Nat. Comput. 1–13 (2021, in press). https://doi.org/10.1007/s11047-020-09838-8
Toyoda, K., Miyahara, D., Mizuki, T.: Another use of the five-card trick: card-minimal secure three-input majority function evaluation. In: Adhikari, A., Küsters, R., Preneel, B. (eds.) INDOCRYPT 2021. LNCS, vol. 13143, pp. 536–555. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-92518-5_24
Acknowledgements
We thank the anonymous referees, whose comments have helped us improve the presentation of the paper. We also thank Hiroto Koyama for his cooperation in preparing a Japanese draft version of Sect. 3 at an earlier stage of this work. This work was supported in part by JSPS KAKENHI Grant Numbers JP21K11881 and JP19H01104.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Haga, R., Hayashi, Y., Miyahara, D., Mizuki, T. (2022). Card-Minimal Protocols for Three-Input Functions with Standard Playing Cards. In: Batina, L., Daemen, J. (eds) Progress in Cryptology - AFRICACRYPT 2022. AFRICACRYPT 2022. Lecture Notes in Computer Science, vol 13503. Springer, Cham. https://doi.org/10.1007/978-3-031-17433-9_19
Download citation
DOI: https://doi.org/10.1007/978-3-031-17433-9_19
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-17432-2
Online ISBN: 978-3-031-17433-9
eBook Packages: Computer ScienceComputer Science (R0)






 as follows, and turn over the face-up card:
as follows, and turn over the face-up card: 

 ,
,
 , and
, and
 in the swapped sequence is
in the swapped sequence is
 if and only if
if and only if  and
and
 in the next steps.
in the next steps.
 or
or
 ; otherwise, turn the card face down. Return to Step 3 unless both
; otherwise, turn the card face down. Return to Step 3 unless both
 and
and
 are already removed.
are already removed.
 , then we obtain a commitment to the negation of
, then we obtain a commitment to the negation of 


 and
and
 is
is
 .
. and
and
 .
. appears, then output the first and second cards.
appears, then output the first and second cards. appears, then swap the first and second cards and output them.
appears, then swap the first and second cards and output them. and turn it over as follows:
and turn it over as follows: 

 ,
,
 , and
, and
 in the rearranged sequence is
in the rearranged sequence is
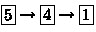 if and only if
if and only if 




 , do nothing; if it is
, do nothing; if it is
 , swap the first and second cards as well as the third and fourth cards. The sequence for each input is described in Table
, swap the first and second cards as well as the third and fourth cards. The sequence for each input is described in Table  does not matter.
does not matter. turned over in Step 3d as an additional card (i.e., place the
turned over in Step 3d as an additional card (i.e., place the
 in the first from the left).
in the first from the left).

 , swap the i-th and j-th cards (namely,
, swap the i-th and j-th cards (namely, 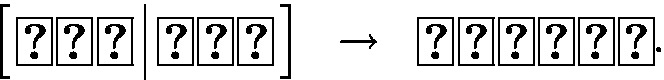
 , swap the i-th and j-th cards as well as k-th and
, swap the i-th and j-th cards as well as k-th and 