Adaptive Design Space Reconstruction Method in Surrogate Based Global Optimization

Abstract

Surrogate-based global optimization (SBO) has gained rapid dominance in engineering design. However, traditional SBO method over entire design space with large size interval would be considerably time-consuming. In order to improve the optimization efficiency in SBO, an adaptive design space reconstruction (ADS) method based on fuzzy clustering method and effective sample points is proposed in this paper. Fuzzy c mean clustering method is applied to divide the initial design space into several sub-regions from which we choose the sub-region which is most likely to contain the global optima. During the optimization process, effective sample points are collected to be the center of new space constructed by trust region method, instead of a single sample point, to keep optimization from getting trapped in local minimums. Then the optimization search will be managed in the reconstructed promising sub-region. We test and verify the proposed method with the airfoil drag minimization problems proposed by Aerodynamic Design Optimization Discussion Group (ADODG), which could demonstrate that better results can be obtained within the reconstructed design space with high efficiency.

1 Introduction

Due to the increasingly complexity of engineering design, surrogate-based global optimization (SBO) methods are widely used to reduce the computational cost [1,2,3]. However, the size interval of design space has large influence on accuracy of surrogate model, so as to the efficiency of optimization. Too small the design space is, it would bear the risks that the global optima could be outside the current design space; As the design space becomes larger, it will bring burden to the accuracy of surrogate, leading the failure on finding the global optima. To solve these problems, an effective branch of research is the design space reduction (DSR).

The basic idea of DSR is to gradually resize the design space during the optimization process. In general, the DSR could be classified into two categories: (1) reducing the number of design variables, which is also called dimensionality reduction. Satyajit et al. [4] presented an innovative proper orthogonal decomposition based reduced order design scheme method to reduce the number of design variable. Steven et al. [5] used principal component analysis to reduce space dimensionality based on the covariance matrix of the gradient. Trent et al. [6] employed the active subspace method to exploit the low dimensionality space with an evenly spread set of observed sample points. Asha et al. [7] transformed the high dimensionality data set into a low dimensional latent space by nonlinear latent variables model called generative topographic mapping. Nowadays, the nonlinear dimensionality reduction methods have become more and more popular for its ability on capturing the feature of latent space [8]; (2) reducing the size interval of the design variables. The widen of design space brings significant computational burden to the improve approximation level of surrogate model. To solve this problem, the designers usually tend to define conservative bound to design variables based on their prior knowledge, which would lack applicability for other design problems. To get rid of this situation, plenty of researches on design space reduction have been developed. Wang et al. [9] utilized the proposed fuzzy clustering based hierarchical metamodeling to intuitively capture promising regions and efficiently identify the near-global design optima. Tseng et al. [10] proposed a novel design space reduction method to shrink the space range rapidly before the simulation-based local search started, which could decrease computational costs without sacrificing accuracy. Yong Wang et al. [11] focused search effort onto specific area of feasible region by shrinking the constrained search space. Long et al. [12] developed a trust region sampling space method to reduce the space range gradually. The sequential sampling as well as adaptive surrogate method are used to improve the optimization efficiency and convergence. These methods could reduce large initial design space into a small near-optima region, while the new sub-region based on only one sample point could lead premature of optimization [9]. Besides, most of these methods treat all design variables uniformly when reducing the size interval, which is not sufficient for problems with high dimensionality.

To shake off the limitation of design space’s range, reduce the computational cost and improve the efficiency of design space exploration, this paper proposes an adaptive design space reconstruction based on the fuzzy c mean clustering and effective sample points, drawing the initial space into a relatively small near-optima space. The method can be roughly divided into four parts: (1) obtain the reduced the design space using the FCM; (2) add new sample point to sample library to update the kriging model; (3) collect the effective sample points to reconstruct the design space; (4) resize the range of the sensitive design variable if necessary.

The rest of this paper is as follows. Related information of fuzzy c mean clustering, and trust region method are presented in Sect. 2. In the Sect. 3, the proposed methodology is introduced. In Sect. 4, the proposed method is applied to two airfoil optimization problems. Finally, the concluding remarks and future work are given.

2 Background

2.1 Fuzzy C Mean Clustering

Fuzzy c mean (FCM) is a data clustering technique originally introduced by Bezdek [13]. The FCM algorithm is one of the most widely used clustering algorithms in engineering design [9].

The objective of FCM is to minimize the cost function formulated as Eq. (1),

$$J(U,V) = \sum\limits_{j = 1}^{c} {\sum\limits_{i = 1}^{N} {(\mu_{ij} )^{m} \left\| {x_{i} - v_{j} } \right\|^{2} } }$$

(1)

where $V{\text{ = \{ v}}_{1} {\text{,v}}_{2} {,}...{\text{v}}_{c} {\text{\} }}$ represents the cluster centers, $N$ is the number of sample points and $c$ is the number of clusters. The exponent $m \in [1,\infty ]$ (typically $m = 2$) is a weighting factor to measuring the fuzziness of each cluster. $U = (\mu_{ij} )_{N * c}$ is a fuzzy partition matrix, where the $\mu_{ij}$ reflects the degree of membership between the $x_{i}$ and the jth cluster:

$$\mu_{ij} = \frac{1}{{\sum\nolimits_{k = 1}^{c} {(\left\| {x_{i} - v_{j} } \right\|\;/\left\| {x_{i} - v_{k} } \right\|\;)^{{\frac{2}{m - 1}}} } }}$$

(2)

The value of matrix $U$ should satisfy the following conditions: $\sum\nolimits_{j = 1}^{c} {\mu_{ij} = 1} ,\;0 \le \mu_{ij} \le 1$. For a specified number of clusters, given the exponent $m$ and the termination criteria, $\max_{ij} \{ \left| {\mu_{ij}^{(T + 1)} - \mu_{ij}^{(T)} } \right|\} < \varepsilon ,\;\varepsilon \in [0,1]$ $[0,1]$. The optimal solution $U_{*}$ and $V_{*}$ is obtained on the following conditions:

$$Min\{ J_{cm} (U,V)\}$$

(3)

The global optima would be more possible to be nearby the cluster with better objective values. Even if the optima locate outside the initial design space, better sample points will be gained in fewer iterations and the possibility of finding the global optima will be greatly increased.

In this paper, the fuzzy c mean clustering is adopted for its simplicity, robustness and convenience. But the proposed method does not dictate the exclusive use of fuzzy c mean clustering while other clustering methods may be equally acceptable.

2.2 Trust Region Method

The trust region method (TRM) [14, 15] is a classical space reduction sequential sampling methods. It is used to construct the promising sampling space step by step based on current best point and fitting quality of the surrogate model. In TRM, the current best sample point is chosen as the center of new design space. And the trust factor $r_{k}$ and trust region radius $\delta_{k}$ are computed through Eq. (4) and Eq. (5):

$$r_{k} = \frac{{f(x_{k - 1} ) - f(x_{k} )}}{{f(x_{k - 1} ) - \mathop f\limits^{\sim } (x_{k} )}} = \frac{\Delta f}{{f_{k - 1} - \mathop f\limits^{\sim }_{k} }}$$

(4)

$$\delta_{k} = \left\{ \begin{gathered} c_{1} \left\| {x_{k} - x_{k - 1} } \right\|\;\;\;\;\;\;\;\;\;\;\;\;\;\;r_{k} < r_{1} \hfill \\ \min (c_{2} \left\| {x_{k} - x_{k - 1} } \right\|,\Delta )\;\;r_{k} > r_{2} \hfill \\ \left\| {x_{k} - x_{k - 1} } \right\|\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;r_{2} \ge r_{k} \ge r_{1} \hfill \\ \delta_{\min } \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;r_{k} < 0 \hfill \\ \end{gathered} \right.$$

(5)

In this paper, “~” means surrogate prediction. If $\Delta f > 0$, the current surrogate model is capable of searching better design result, and then the trust radius $\delta_{k}$ is updated according to Eq. (5), in which $c_{1} = 0.75,\;c_{2} = 1.25,\;r_{1} = 0.1,\;\;r_{2} = 0.75$ [12]. Otherwise, the current surrogate has bad performance and plenty of computational cost would be need to find the global optima. The TRM is then forced to exploit a small neighborhood around the current best point. Although the TRM has shown improvements in optimization efficiency, it may lead the optimization to get trapped in local minimums and be premature for it use only one point as the center at one time.

3 Proposed Method

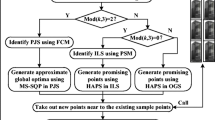
In the optimization process, the functions (both objective functions and constraint functions) usually guide the optimization from the initial broad design space into a small region nearby the global optima. With the increment of size interval, it would impose daunting computational cost. To efficiently reduce the size interval of design space, this paper proposes an adaptive design space reconstruction method to resize the design space. The flowchart of the method is illustrated in Fig. 1, and the following are the detailed steps of this method:

Step 1: generate initial sample points and construct Kriging model. At the beginning step, the initial sample points are generated by the Latin Hypercube sampling (LHS) [16] method, sampling the design space more uniformly and can achieve better approximation with fewer sample points.

Step 2: clustering and space determined. In this step, the FCM is utilized to cluster the found sample points. The number of clusters is usually set two as discussed in [9]. Usually there are some properties can be used to choose the ideal cluster such as mean, variance, maximum and minimum of sample points. In this paper we make the constraint (both geometry and aerodynamic constraints) one of the properties to be considered in choosing the cluster. The cluster outside the constraint boundary is got rid when constructing the design space. To decide how much each constraint function must be expanded in order to provide the sufficient number of sample points to construct the design space during clustering, we consider the concept of $\varepsilon$ tubes from the support vector regression [17], which could also be used on collecting effective sample points.

Step 3: identify the reconstruction moment. The moment to reconstruct the design space is hard to identify, as it is difficult to differentiate whether optimizer converging to optima or the optimizer traversing a complicated area of the design space [18]. In this paper, we define the moment that objective function value keeps unchanged for $N$ iterations during the exploration of current design space. The small value for $N$ would lead a more aggressive system. For complex optimization problem, this can cause premature when the objective function value only makes a small improvement through highly non-linear area. For this reason, $N$ can be increased for exploration and only trigger reconstruction when objective function value consistently stagnates.

Step 4: select the effective sample points. Sample points with good performance are defined as the effective sample points. The space based on effective sample points describes a landscape near the global optima, whose variation can reflect the trend of optimization. That’s to say, as effective sample points update, the reconstructed sub-region would approach the global optima step by step. During this process, the quantity of effective sample points directly influences the size of the sub-region. Too large the number is, it will bring burden to exploration in new sub-region because of the bad surrogate accuracy. Therefore, we retain the best 20% of sample points within the constraints boundary as the effective sample points [7]. At the beginning, the difference between the effective sample points would make sure the reconstructed sub-region contains global optima. After a few iterations, the difference of each effective sample point could grow smaller, the reconstructed sub-region shrinks significantly, resulting in high efficiency of optimization.

Step 5: reconstruct the sub-region. The sub-region is not only determined by the boundary of the collected effective sample points. To guarantee an adequate design space, here we make use of the trust region method (TRM), which resizes new design space in the light of the improvement of objective function value. The space is adaptively adjusted by the center and radius. In the proposed method, when the trigger moment comes, the effective sample points are selected as the center of new space. $L_{k}$ is the unit radius defined as the 10% of size interval on each dimensionality, where $VR\max$ and $VR\min$ are the upper and lower bound of the new design space. And radius factor $c$ is decided by surrogate accuracy threshold $Tr$ and rolling average of surrogate error $\mathop {fr}\limits^{\sim }$. The trust radius $r_{k}$ is updated according to Eq. (8) where the typical values of $c_{1}$, $c_{2}$ are used, namely, $c_{1} = 0.5,c_{2} = 2$. In Eq. (7), $c_{2} *L_{k}$ is the upper bound of the radius.

$$L_{k} = 0.1*(VR\max - VR\min )$$

(6)

$$c = \frac{Tr}{{\sum\limits_{i = k - N + 1}^{k} {\mathop {fr}\limits^{\sim }_{i} } }}$$

(7)

$$r_{k} = \left\{ \begin{gathered} c*L_{k} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;c_{1} \le c \le c_{2} \hfill \\ \min (c*L_{k} ,c_{2} *L_{k} )\;\;\;c_{2} < c \hfill \\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;c \le c_{1} \hfill \\ \end{gathered} \right.$$

(8)

It’s well known that for surrogate-based global optimization, surrogate accuracy is related to the sample density of design space. Sometimes, the reconstructed sub-region may far beyond the boundary of the initial design space leading the local sample points distribution extremely sparse. Ordinarily, there’re two ways to improve the local sample density, one is to generate sample points in the current design space which would lead to extra computational cost. The other one is to shrink the space size to guarantee the surrogate accuracy when surrogate has a bad performance. However, each dimensionality of design space has different impact on the objective function even if they vary in a same range. Dimensionalities making dramatic changes of objective function manipulate bigger design space from the view of parameterization, meaning more sensitive to objective function. Therefore, there’s no need to narrow all dimensionalities if we can figure out sensitive design variables. To distinguish these design variables, we adopt the elementary effect method. In this method, the large mean indicates a latent dimensionality with large influence on the objective function, whereas large variance indicates latent dimensionalities responsible for nonlinear effects. Let $\Psi (q)$ be defined as

$$\Psi (q) = \frac{{\sum\nolimits_{j \in J(q)} {v_{j} } }}{{\sum\nolimits_{j = 1}^{p} {v_{j} } }} \ge c$$

(9)

where $0 \le c \le 1$ is some fraction of the total sensitivity. For example, $J(q)$ might be selected such that $\Psi (q) \ge 0.8$ to capture 80% of the sensitivity, which are defined as main effect variables.

4 Test on Benchmark Problems

In this section, the proposed ADS method was tested on the airfoil optimization cases provided by ADODG. Moreover, it was compared to the multi-round optimization method with fixed design space, to test and verify its global convergence, efficiency and robustness.

4.1 Case I. Symmetric Transonic Airfoil Design

The first test case involves drag minimization for a symmetric airfoil, NACA 0012, under inviscid transonic condition. The design Mach number is 0.85, while the angle of attack is fixed at $\alpha = 0^{{^{o} }}$. Since the airfoil in this case should be symmetric, the upper half with a symmetry boundary condition is used. Under this circumstance, the constraints satisfied when $y \ge y_{baseline}$ everywhere on the upper surface. The problem can be summarized as

$$\begin{gathered} Min\;\;\;C_{d} \hfill \\ s.t.\;\;\;\;\;t \ge t_{baseline} \;\forall x \in [0,1] \hfill \\ \end{gathered}$$

(10)

From the reference [19,20,21] we can know there exists great shape difference between the optimized foil and traditional airfoils, which requires an unconventional design space to get to the optima. It will test the applicability of proposed method on transferring the design space to find the ideal design result.

The Bezier curve with 24 design variables is adopt to deform the airfoil and the initial design space is shown as Fig. 2, where 100 initial sample points are generated by LHS method. Table 1 and Fig. 3 demonstrate the set of the computational grid. Another 200 sample points would be infilled during optimization process.

Fig. 1.

Flowchart of method.

Table 1. Summary of grid’s properties.

The optimized airfoils and corresponding pressure distribution are presented in Fig. 4 and Fig. 5, respectively. It’s shown that all optimized airfoils share the similar shape deformation, which means the optimization tendency is efficient for the proposed method. These are strong shocks extending far into the flow field on the initial geometry. Due to the thickness constraints, the optimizer thickens the airfoil and create a surface that delays the pressure recovery, leading weaker shocks to occur near the trailing edge of the optimized airfoil. The later pressure recovers, the smaller drag coefficient it occurs.

Table 2. Computational results of optimized airfoils by different design space.

Figure 6 shows the cost effectiveness comparisons of adaptive design space method (ADS) and fixed design space (FDS), where FDS round 2 is based on the FDS round 1 as multi-round optimization. It turns out the ADS strongly outperforms FDS. Optimization in the fixed design space stalls quite early, indicating that space size interval is the limitation that keeps the optimizer from reaching the global optima in this case. Figure 7 shows the final space size interval of ADS, which has large difference with the initial design space, especially for the regions on the trailing edge. Besides, the size interval of final adaptive design space is really small which is beneficial to fitting quality of surrogate model, as well as the optimization efficiency. As for multi-round optimization method, making up the enough space for further exploration to obtain the ideal design results would take plenty of work for designers and computational cost, as shown in Table 2, leading to bad efficiency of optimization.

Fig. 2.

Initial design space of NACA0012 airfoil.

Fig. 3.

The computational grid of NACA0012.

Fig. 4.

Comparison of airfoil shape

Fig. 5.

Comparison of pressure distribution

Fig. 6.

Cost-effectiveness of different design space

Fig. 7.

Boundaries of different design space

4.2 Case II. Transonic Airfoil Design

The Case II revisits transonic airfoil design (Mach 0.734). The objective is to reduce the drag coefficient, while constraints are imposed on lift coefficient, pitching moment coefficient and the area, as shown in Eq. (11):

$$\begin{gathered} Min\;\;C_{d} \hfill \\ s.t.\;\;\;\;C_{l} = 0.824 \hfill \\ \;\;\;\;\;\;\;\;\left| {C_{m} } \right| \le 0.092 \hfill \\ \;\;\;\;\;\;\;\;Area \ge Area_{initial} \hfill \\ \end{gathered}$$

(11)

The baseline shape is the RAE 2822 airfoil. The design variables are the z-coordinates of the CST parameterization with 24 shape parameters in total. The initial design space is shown as Fig. 8. Similar to Case I, 100 sample points are generated in the initial design space with LHS method, and 200 sample points are to be infilled by EI method during optimization progress. The computational grid (Fig. 9) setting is shown as Table 3.

Fig. 8.

Initial design space

Fig. 9.

The computational grid of RAE 2822

Table 3. Parameters of RAE 2822 computational grid.

The comparisons of optimized airfoils and their pressure distribution are shown in Fig. 10 and Fig. 11, respectively. From Fig. 11 we can know that the suction peak of the optimized airfoil gets much stronger and the shock wave is nearly eliminated, compared to RAE 2822 airfoil. The leading edges of all optimized airfoils get sharper, and upper surfaces become more flat, which is good for pressure recovery and shock wave elimination. The comparisons of cost-effectiveness of different optimization methods are shown in Fig. 12, showing that the result of ADS and FDS round 2 are much better than that of FDS round 1. The optimizer in FDS round 1 stall so early as a result of the boundary limitation (Fig. 13). With larger design space, FDS round 2 acquires a better result eventually, which is similar to ADS referring to Table 4.

Table 4. Computational results of optimized airfoils by different design space.

5 Conclusion

In this paper, an adaptive design space reconstruction method (ADS) based on fuzzy c mean clustering and effective sample points is proposed. The proposed method improves the optimization efficiency and applicability by transferring the inefficient design space into a sub-region where the optimization can be more efficient. Fuzzy c mean clustering is adopted to determine the preliminary reduced space so that the computational cost could be reduced significantly. Effective sample points selection with constraints rules based on the trust region method are used to reconstruct the promising design space with the help of elementary effect method. The performance of the proposed method is tested on two airfoil optimization problems compared to the multi-round optimization method. The comparison results reveal that the proposed method gains better performance on global convergence, efficiency and robustness. Nowadays, with the development of aviation engineering demands, the aerodynamic shape of modern aircrafts will be largely distinct from the traditional ones. Under these circumstances, ADS exhibits a good prospect to efficiently solve modern unconventional aircraft design problems. However, the current work still has some limitations, as follows. Firstly, fuzzy c mean clustering is not good enough when the sample distribution is not the convex for it’s based on Euclidean distance. Secondly, ADS may be still trapped in local optima when solving some complex functions with massive and crowded local optima with the limitation of trust region method. Although effective sample points selection could ease that situation, the selection rules could still be consummate. Further enhancement of ADS is expected to upgrade the global exploration.

Fig. 10.

Comparison of airfoil shape.

Fig. 11.

Comparison of pressure distribution.

Fig. 12.

Cost-effectiveness of different design space.

Fig. 13.

Boundary of different design space.