Keywords

1 Introduction

The increasing capacity of human beings of collecting large amount of data gave rise to the need of developing models to study how variables interact with one another. Benefits of such discoveries are well known, for example in clinical and genetic applications it is useful to understand how risk factors are related so that patient-specific therapies may be planned. See [5, 9, 27] for cancer applications. The same reasoning applies to problems in economics, for example [25] studied the interconnectedness of credit risk.

Probabilistic graphical modeling is a possible approach to the task of studying the dependence structure among a set of variables. It relies on the concept of conditional independence between variables that is described through a map between a graph and a family of multivariate probability models. When such a family of probabilities is chosen to be Gaussian, those models are known as Gaussian graphical models [12]. This is the choice made throughout the paper, which is the most common in the literature.

Let \(\boldsymbol{X}\) be a p-random vector distributed as \(N_{p}(\boldsymbol{0},\boldsymbol{\Sigma })\). \(\boldsymbol{\Sigma }\) is the covariance matrix and we assume \(\boldsymbol{X}\) to be centered without loss of generality. Let \(G=(V,E)\) be an undirected graph, where \(V=\{1,\dots ,p\}\) is the set of nodes and E is the set of undirected edges. \(\boldsymbol{X}\) is said to be Markov with respect to G if, for any edge (i, j) that does not belong to E, the i-th and j-th variables are conditionally independent given all the others. Moreover, under the normality assumption, the conditional independence relationship between variables can be represented in terms of the null elements of the precision matrix \(\boldsymbol{K}=\boldsymbol{\Sigma }^{-1}\). Therefore the following equivalence provides an interpretation of the graph

$$\begin{aligned} X_{i} \perp \!\!\! \perp X_{j} ~|~\boldsymbol{X}_{-(ij)} \iff (i,j)\notin E \iff k_{ij} = 0, \end{aligned}$$
(1)

where \(\boldsymbol{X}_{-(ij)}\) is the random vector containing all elements in \(\boldsymbol{X}\) except the i-th and the j-th. Each node is associated to one of the variables of interest and its links describe the structure of the non-zero elements of the precision matrix. The absence of a link between two vertices means that the two corresponding variables are conditionally independent, given all the others. Usually, G is unknown and it is the goal of the statistical inference, along with \(\boldsymbol{K}\). Such a process is also known as structural learning. In a Bayesian framework, we set a \({\text {G-Wishart}}\) prior distribution for the precision matrix \(\boldsymbol{K}\) [1, 20] , which is attractive as it is conjugate to the likelihood. Since the graph G is considered to be a random variable having values in the space \(\mathcal {G}\) of all possible undirected graphs with p nodes, we need to specify a prior on it. A common practice is to choose an uniform distribution over \(\mathcal {G}\). This is appealing for its simplicity but it assigns most of its mass to graphs with a “medium” number of edges [9]. On the other hand, it is known that an undirected graph is uniquely identified by its set of edges \(\mathcal {E}\). Therefore it is simpler to define a prior on \(\mathcal {E}\), which then naturally induces a prior over \(\mathcal {G}\). In this setting, the most natural choice is to assign independent \({\text {Bernoulli}}\) priors to each link. The \({\text {Bernoulli}}\) parameters \(\theta \) could be different from edge to edge, but one usually assigns a common value. For example, [9] suggested to choose \(\theta = 2/(p-1)\) to induce more sparsity in the graph. Scott and Carvalho [21] placed instead a \({\text {Beta}}\) hyperprior on that parameter, a solution known as multiplicity correction prior. Similarly, [22] described a multivariate \({\text {Bernoulli}}\) distribution where edges are not necessarily independent. A common feature of previously described priors is that they are non-informative. The only type of prior information they can include in the model is the expected sparsity.

In this work we propose a prior for the graph that aims to be informative, according to the prior information available for the application at hand. Since the graph describes the conditional dependence structure of variables involved in complex and high-dimensional phenomena, it is unrealistic to assume that prior knowledge is available for one-to-one relationships between the observed quantities. It is instead more reasonable to assume that variables may be grouped in smaller subsets. This is common in biological application where the groups may be families of bacteria [17], or genomics where groups of genes are known to be part of a common process. Also in market basket analysis products and customers can easily be grouped; see, for instance [6].

We propose a class of priors, called block graph priors, that encodes such information and imposes a block structure in the adjacency matrix that describes the graph. We allow variables in different groups only to be fully connected or not connected at all. Therefore, the goal is no longer in looking for all possible relationships between nodes but on deriving the underlying pattern between groups.

We introduce a Reversible Jump sampler that leverages the structure induced by our new prior. In particular, we generalize the procedure by Lenkoski [13]. The resulting method is called Block Double Reversible Jump (BDRJ for short). Its main feature is that it modifies, at each step of the chain, an entire block of links to guarantee a block structure that is always compatible with our hypotheses.

The remainder of the paper is organized as follows. Section 2 introduces the block structured graph priors and Sect. 3 provides the sampling strategy. In Sect. 4 we present a simulation study along with a comparison against an existing approach. Finally, we conclude with a brief discussion in Sect. 5.

2 Block Structured Graph Priors

The starting point for our proposed model is that we assume the p observed variables to be grouped, a priori, in M mutually exclusive groups. Each group has cardinality \(n_{i}\) and \(\sum _{i = 1}^{M}n_{i} = p\). We admit the possibility of having some \(n_{i} = 1\), as long as \(M<p\). Groups whose cardinality is equal to one are called singletons.

We aim to study relationships between groups of variables. Therefore the usual graph representation \(G=(V,E)\), where V is the set of nodes and E is set of links, is redundant. Indeed we assume that groups are given and links have to satisfy a precise block structure. As a consequence, we synthesize those information by defining a new space of undirected graphs whose nodes represent the chosen groups of variables and links represent the structure of relationships between them. Namely, let \(V_{B}=\{B_{1},\dots ,B_{M}\}\) be a partition of V in M groups that are available a priori. Then we define \(G_{B}=(V_{B},E_{B})\) to be an undirected graph whose nodes are the sets \(B_{k}, k=1,\dots ,M\) and that allows for self-loops if \(n_{k}>1\). Namely,

$$\begin{aligned} E_{B}\subset \mathcal {E}_{B}= \Bigl \{ (l,m) |l,m \in V_{B}, \quad \wedge \; l<m, \quad (l,l) |l \in V_{B}, \quad \wedge \; n_{l}>1 \Bigr \}. \end{aligned}$$
(2)

In graph theory, graphs that have self-loops are called multigraphs. Finally, let \(\mathcal {G}_{B}\) be the set of all possible multigraphs \(G_{B}\) having \(V_{B}\) as set of nodes. In the following, we want to clarify the relationship between this space and \(\mathcal {G}\).

Consider \(G_{B}\in \mathcal {G}_{B}\) and \(G \in \mathcal {G}\). By definition, the set of nodes of the first multigraph is obtained by grouping together the nodes of the second graph. What about the set of edges? Is there any relation between the two sets? The following map defines a relationship between them. Let \(\rho : \mathcal {G}_{B} \rightarrow \mathcal {G}\), such that \(G_{B}=(V_{B},E_{B})\mapsto G=(V,E)\) by the following transformations

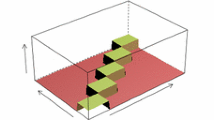
$$\begin{aligned}{} & {} V = \{B_{l,h}, l=1,\dots n_{h}, h = 1,\dots M\} = \{1,\dots ,p\} \nonumber \\{} & {} \text {if }(l,m)\in E_{B} \Rightarrow ~ (i,j)\in E ~\forall i \in B_{l}, \quad \forall j \in B_{m} \nonumber \\{} & {} \text {if }(l,m)\notin E_{B} \Rightarrow ~ (i,j)\notin E ~\forall i \in B_{l}, \quad \forall j \in B_{m} \end{aligned}$$
(3)

A visual representation of this mapping is given in Fig. 1. Once \(\rho \) is set we are able to associate each \(G_{B}\) in \(\mathcal {G}_{B}\) to one and only one G in \(\mathcal {G}\), since \(\rho \) is clearly injective. We refer to \(G_{B}\) as the multigraph form of G.

Fig. 1
figure 1

The map from multigraph \(G_{B}\in \mathcal {G}_{B}\) (left) to its block structured form \(G\in \mathcal {B}\) (right)

Full size image

Nevertheless, \(\rho \) is not surjective which implies that there are graphs that do not have a representative in \(\mathcal {G}_{B}\). Indeed, only those graphs with a particular block structure can be represented in a multigraph form. A non surjective map is the key ingredient to define a subset of \(\mathcal {G}\) of block structured graphs that satisfy our modelling assumptions. Let us consider the image of \(\rho \), denoted by \(\mathcal {B}\). It is the subset of \(\mathcal {G}\) containing all the graphs having p nodes and a block structure consistent with \(V_B\). Moreover, \(\rho : \mathcal {G}_{B} \rightarrow \mathcal {B}\) is a bijection, which means that every graph \(G \in \mathcal {B}\) is associated to its representative \(G_{B} \in \mathcal {G}_{B}\) via \(\rho ^{-1}\). We say that \(G \in \mathcal {B}\) is the block graph representation of the multigraph \(G_{B} \in \mathcal {G}_{B}\). This synthesised representation of block graphs allows us to work in a space where we can use standard tools of graphical analysis. In a different setting, [4] adopts a similar approach to model the conditional dependence across Markov processes.

In particular, such a representation allows us to introduce a class of priors that encodes the knowledge about the partition of the nodes. We place zero mass probability on all those graphs that belong to \(\mathcal {G}\backslash \mathcal {B}\), which is the set of all those graphs that do not satisfy our block structure constraint. Then, we place a standard prior, say \(\pi _B(\cdot )\), over \(\mathcal {G}_{B}\), which is possible as it is a space of undirected multigraphs where links can be considered to be independent with one another. Finally, we map the results in \(\mathcal {B}\) using \(\rho ^{-1}\). Namely

$$\begin{aligned} \pi (G) \propto {\left\{ \begin{array}{ll} ~\pi _B\left( \rho ^{-1}(G)\right) , &{} \text {if } G \in \mathcal {B} \\ ~0, &{}\text {if }G \in \mathcal {G} \backslash \mathcal {B}. \\ \end{array}\right. } \end{aligned}$$
(4)

We refer to those priors as block graph priors. In this work, we consider a block-Bernoulli prior, \(\pi (G)\), that is obtained by applying (4) to \(\pi _{B}(G_B)=\theta ^{|E_B|}(1 - \theta )^{\left( {\begin{array}{c}M\\ 2\end{array}}\right) - |E_B |}\), that is the \({\text {Bernoulli}}\) prior where each link has prior probability of inclusion \(\theta \), which is fixed a priori. The reasoning used to define block priors is similar to priors described in [7]. However, in this case we are not limiting the learning of the graph to the class of the decomposable ones but to block structured graphs. Moreover, this limitation is not due to computational limitations but because prior knowledge is available. In the next section we present a method to learn such a structure. In principle, one can still apply such prior to limit the analysis to the class of decomposable block graphs to exploit their properties. However, in this work we do not make such assumption and we present a method that is valid also for non-decomposable graphs.

3 Sampling Strategy

One of the difficulties in the development of efficient methods for structural learning is the presence of the \({\text {G-Wishart}}\) prior distribution. Given a random matrix \(\boldsymbol{K}\), we say that \(\boldsymbol{K}|G,b,D \sim {\text {G-Wishart}}\,(b,D)\) if its density is

$$\begin{aligned} P\left( \boldsymbol{K}~|~ G, b,D \right) = I_{G}\left( b, D\right) ^{-1} |\boldsymbol{K}|^{\frac{b - 2}{2}} \exp \left\{ - \frac{1}{2}tr\left( \boldsymbol{K}D\right) \right\} \mathbb {1}_{\mathbb {P}_{G}}\left( \boldsymbol{K}\right) , \end{aligned}$$
(5)

where b and D are fixed hyperparameters, \(\mathbb {P}_{G}\) is the space of all \(p\times p\) symmetric and positive definite matrices whose null elements are associated to links absent in graph G and

$$\begin{aligned} I_{G}(b,D) = \int \limits _{\mathbb {P}_{G}}|\boldsymbol{K}|^{\frac{b - 2}{2}} \exp \left\{ - \frac{1}{2}tr\left( \boldsymbol{K}D\right) \right\} d\boldsymbol{K}, \end{aligned}$$
(6)

is an intractable normalizing constant. Numerical methods to approximate such a constant [1] are unstable in high dimensional problems [9, 15]. Several techniques that avoid any calculation of \(I_{G}(b,D)\) are available in the literature, but an exhaustive review of them is beyond the goals of this work. In the following, we limit ourselves to present how our proposed method, called Block Double Reversible Jump (BDRJ for short). It generalizes the procedure by Lenkoski [13] to get a Reversible Jump chain defined over the joint space of graph and precision matrix that visits only the subspace \(\mathcal {B}\) of block structured graphs. Note that if one is interested only in decomposable graph models, the normalizing constant \(I_{G}(b,D)\) can be computed explicitly and it would be enough to use a standard Metropolis-Hastings algorithm without resorting to the usage of the Reversible Jump technique presented in the remaining part of this paper.

We denote the current state of the chain by \((\boldsymbol{K}^{[s]}, G^{[s]})\), with \(\boldsymbol{K}^{[s]}\in \mathbb {P}_{G^{[s]}}\). The proposed state \((\boldsymbol{K}', G')\) is constructed in two subsequent steps; in Sect. 3.1 we describe the proposal for the new graph \(G'\) and then in Sect. 3.2 we discuss how to get the proposed precision matrix \(\boldsymbol{K}'\in \mathbb {P}_{G'}\). Once that \((\boldsymbol{K}', G')\) has been drawn, we accept or reject the whole state with a Metropolis-Hastings step.

3.1 Construction of Proposed Graph G\(^{\prime }\)

A common factor in most of the existing MCMC methods for graphical models is to set up chains such that the proposed graph \(G'=(V,E')\) belongs to the one-edge-away neighbourhood of G. Namely, \(nbd_{p}(G) = nbd_{p}^{+}(G) \cup nbd_{p}^{-}(G)\) where \(nbd_{p}^{+}(G)\) and \(nbd_{p}^{-}(G)\) are the sets of undirected graphs having p nodes that can be obtained by adding, or removing, an edge to \(G\in \mathcal {G}\), respectively. A step in the Markov chain that selects \(G'\in nbd_{p}(G^{[s]})\) is said to be a local move.

The proposed BDRJ approach is innovative because we derive moves that modifies an entire block of links, not just a single one. In other words, our moves are local in \(\mathcal {G}_{B}\) but not in \(\mathcal {G}\). Suppose \(G^{[s]}\in \mathcal {B}\), we propose a new graph \(G'\in \mathcal {B}\) by first drawing its multigraph representation \(G'_B \in \mathcal {G}_B\) from

$$\begin{aligned} q(G'_B|G^{[s]}) = \frac{1}{2}\text {Unif}\left( nbd^{\mathcal {B},+}_{M}\left( \rho ^{-1}(G^{[s]})\right) \right) + \frac{1}{2}\text {Unif}\left( nbd^{\mathcal {B},-}_{M}\left( \rho ^{-1}(G^{[s]})\right) \right) , \end{aligned}$$
(7)

where \(nbd^{\mathcal {B}}_{M}(G^{[s]}_{B})\) is the one-edge-away neighbourhood of \(G_{B}^{[s]} = \rho ^{-1}(G^{[s]})\) with respect to the space of multigraphs \(\mathcal {G}_{B}\). Addition and removal moves are chosen with the same probability. Given this choice, \(q(G'_B|G^{[s]})\) chooses, with uniform probability, which link is to be added (or removed). Finally \(\rho \) is applied once again to map the resulting multigraph back in \(\mathcal {B}\) to obtain \(G'\), i.e. setting \(G' = \rho \left( G'_B\right) \). A closer look at (7) reveals how our multigraph representation allows us to use standard tools of structural learning in the space \(\mathcal {G}_{B}\) to get non-standard proposal in the usual space \(\mathcal {G}\).

3.2 Construction of Proposed Precision Matrix K\(^{\prime }\)

Once that the graph is selected, we need to specify a method to construct a proposed precision matrix \(\boldsymbol{K}'\) that satisfies the constraints imposed by the new graph. The method by Wang and Li [26] based on the partial analytical structure of the \({\text {G-Wishart}}\) appears to be an efficient choice. However, it strongly relies on the possibility of writing down an explicit formula for the full conditional of the elements of \(\boldsymbol{K}\). Such results, presented in [20], can be handled in practice only if at each step of the graph only one link of the graph is modified. Instead, the proposal distribution presented in Sect. 3.1 modifies an arbitrary number of links. Hence, it is complicated, if possible at all, to generalize the method by Wang and Li [26] to such framework. As a consequence, we rely on a generalization of the Reversible Jump mechanism by Lenkoski [13]. The idea is that is it possible to guarantee the positive definiteness of \(\boldsymbol{K}'\) and the zero constraints imposed by \(G'\) just by working on the Cholesky decomposition matrix \(\boldsymbol{\Phi }^{[s]}\) of \(\boldsymbol{K}^{[s]}\). Indeed, [20] and [1] showed that the zero constraints imposed by \(G^{[s]}\) on the off-diagonal elements of \(\boldsymbol{K}^{[s]}\) induce a precise structure and properties on \(\boldsymbol{\Phi }^{[s]}\). Let \(\nu (G^{[s]}) = \{(i,j)~|~i,j\in V, i=j \text { or } (i,j)\in E^{[s]}\}\) be the set of the diagonal elements and the links belonging to \(G^{[s]}\) and define the set of free elements of \(\boldsymbol{\Phi }^{[s]}\) as \(\boldsymbol{\Phi }^{\nu (G^{[s]})}=\{\phi _{ij} ~|~i,j \in \nu (G^{[s]})\}\). The remaining entries, that we simply refer to as non-free elements, are uniquely determined through the completion operation [1, Prop. 2] as a function of the free elements.

Suppose the proposed graph \(G'\) is obtained by adding edge (l, m) to the multigraph representation of \(G^{[s]}\). The set of links that are changing in \(\mathcal {G}\) is \(L=\{(i,j)~|~i,j\in V, i < j, (i,j)\in E', (i,j)\notin E^{[s]}\}\). Its cardinality \(l=|L |\) is arbitrary and, in general, different from one. We call \(V(L)=B_{l}\cup B_{m}\) the set of the vertices involved in the change. Note that \(\nu (G')=\nu (G^{[s]})\cup L\). Our solution to define the new free elements is to maintain the same value for all the ones that are not involved in the change and to set the new ones by perturbing the current, non free elements, independently and all with the same variance \(\sigma _{g}^{2}\). Namely, draw \(\eta _{h}\mathop \sim ^{ind}N(\phi _{h}^{[s]}, \sigma ^{2}_{g})\) and set \(\phi '_{h}=\eta _{h}\) for each \(h\in L\). Then, it is enough to derive all non free elements of \(\Phi '\) though completion operation and finally to set \(\boldsymbol{K}'= (\boldsymbol{\Phi }')^{T}\boldsymbol{\Phi }\). Note that, by doing so, we are generating a random variable \(\boldsymbol{\eta }\) of length l that matches the dimension gap between \(\boldsymbol{K}\) and \(\boldsymbol{K}'\). As usual, the dimension decreasing case is deterministically defined in terms of the dimension increasing one.

4 Simulation Study

We compare our performances to the Birth and Death approach (BDMCMC for short) proposed by Mohammadi and Wit [14] and available in the R package BDgraph [16].

All final estimates, both from BDRJ and BDMCMC outputs, were obtained by controlling the Bayesian False Discovery Rate, as presented in [18] and [3]. Performances are assessed in terms of the standardized Structural Hamming Distance (Std-SHD, [23]) and the \(\text {F}_{1}\text {-score}\) [2, 19]. The first one prefers lower values, the second one higher values. Following the same approach of [14, 24], precision matrix estimation is measured using one half of the Stein loss score (\(\text {SL}\)) [8] which is equal to the Kullback-Leibler divergence [10] between \(N_{p}(\boldsymbol{0},\boldsymbol{K}_{true}^{-1})\) and \(N_{p}(\boldsymbol{0},\widehat{\boldsymbol{K}}^{-1})\).

In the first experiment, we set \(p=40\), \(n = 500\) and \(M=p/2\) groups of equal size, which leads to off-diagonal blocks of size \(2\,\times \,2\). The true underlying graph is itself a block structured graph (see Fig. 2), while the true precision matrix was sampled by drawing from a \({\text {G-Wishart}}\left( 3,\boldsymbol{I}_{p}\right) \). \(\sigma ^{2}_{g}\) was set equal to 0.5 after a little tuning phase. 400,000 iterations were run plus 100,000 extra iterations as burn-in period that were discarded. A simple visual inspection of Fig. 2 suggests that BDRJ is more precise than BDMCMC. The number of misclassified edges is rather low, \(\text {Std-SHD}= 0.0243\), and it is well balanced between false positiveness (10) and negativeness (9). Many true discoveries are achieved and indeed it has \(\text {F}_{1}\text {-score} = 0.954\). BDMCMC does not recognize the block structure of the true graph, actually it does not even look for such a structure because the prior information can not be included in the model. It estimates the probability of inclusion of every possible link independently from the others. This entails more errors in the final estimate as well as a less informative structure of the graph. It would be hard to explain why there are missing edges within some structures that are clearly blocked ones. We repeated the same experiments for 18 different dataset: the true underlying graphs were randomly generated by sampling from (4) with different sparsity indices \(\theta \) uniformly distributed in \(\left[ 0.2,0.6\right] \). The mean values, along with the standard deviations, for the \(\text {F}_{1}\text {-scores}\) are 0.845(0.13) and 0.80(0.03) and for the \(\text {Std-SHD}\) we have 0.053(0.04) and 0.060(0.02), respectively for BDRJ and BDMCMC. We see that BDRJ is more unstable with respect to BDMCMC. This is probably due to the fact that we used the same \(\sigma ^{2}_{g}\) for all dataset, without tuning it every time. However both indices prefer BDRJ.

Fig. 2
figure 2

The adjacency matrices of true underlying graph (middle panel), the BDRJ one (leftmost panel) and the one obtained using BDgraph (rightmost panel). Squares represent the included links, crosses stand for edges that are wrongly classified

Full size image

The second experiment is inspired by a simulation study presented in [11] that aims to learn a graph and precision matrix under a noisy setting. The true underlying graph G is displayed in Fig. 3. We sample \(\boldsymbol{K}_{\text {true}}|G \sim {\text {G-Wishart}}(3,\boldsymbol{I}_{p})\) and set \(\boldsymbol{K}_{\text {noisy}}\) to be a random perturbation of \(\boldsymbol{K}_{\text {true}}\): every possible value is perturbed, with probability s, by adding a random noise 0.1u. Here \(u\sim \text {Unif}\left( -k^{*},k^{*}\right) \), where \(k^{*}=\textrm{max}_{i < j}|k^{\text {true}}_{ij} |\). Finally, data are generated from \(N_{p}\left( \boldsymbol{0},\boldsymbol{K}_{\text {noisy}}^{-1}\right) \). To investigate the behaviour under different volumes of noise, \(s = 0.10,0.20,0.25\), we repeat each experiment 15 times. Results are reported in Table 1.

Fig. 3
figure 3

The true underlying graph (leftmost panel) used to generate the true precision matrix \(\boldsymbol{K}_{\text {true}}\) (middle panel). The rightmost panel is \(\boldsymbol{K}_{\text {noisy}}\) (obtained with \(s = 0.25\)). For plotting purposes, we removed the diagonal in both precision matrices

Full size image
Table 1 \(\text {F}_{1}\text {-score}\), \(\text {Std-SHD}\) and Stein loss \(\text {SL}\) under different noise levels s
Full size table

BDRJ outperforms BDMCMC on every dataset and with respect to all indices we considered. Its robustness is due to the fact that to conclude that a whole block has to be inserted in the final graph a single, isolated link is not enough. Those isolated values are not compatible with the block structured graph that BDRJ is looking for, therefore they are rightly ignored. On the other hand, BDMCMC does not look for any particular structure, hence it does not recognize the perturbed values as noise.

5 Discussion

In the setting of graphical models, this work proposed a new class of priors, called block graph priors. They allow to include in the model the prior knowledge available about the partition of the nodes. We also introduced a new sampling strategy that leverage these priors to look only for a block structured graph, whose block, if included, have to be complete. In some applications, as the number of variables grows, the importance of each possible dependence loses of interest as it is more natural, and more interpretable, to understand the general structure of dependencies. This is the case of genomics applications as genes may be grouped in pathways, therefore a block structured graph is expected and more interpretable. Another example is market basket analysis which aims to find patterns of association between retailed items so that they can be bundled together to the end of delivering an appealing offer. Finally, we compared our model, on synthetic data, with BDMCMC. In both experiments, BDRJ estimates are better in terms of \(\text {Std-SHD}\), \(\text {F}_{1}\text {-score}\) and \(\text {SL}\).

As future developments, we aim to further develop the BDRJ technique, expand the simulation study by investigating the behaviour of BDRJ when the underlying graph has incomplete blocks and to assess its performances in real world applications. Moreover, experiments are performed using groups of only two nodes. Larger groups imply larger jumps of the chain in the state space and therefore they are less likely to be accepted. We aim to better investigate the behaviour of our methodology in such cases. We would also like to understand if the proposed methodology could be also extended to Gaussian structured chain graph models for modelling the DAG model induced by the chain components. Finally, we would like to add flexibility to the model by allowing for a random partition of the nodes.