Keywords

1 Introduction

The scientific research of ceramic materials has been an extensive field since centuries due to their outstanding combination of physical, mechanical and chemical properties. Nowadays, many technologies of the every-day life involve ceramics or ceramic matrix composites. In particular, alumina, Al\(_2\)O\(_3\), is one of the most researched ceramic materials and it is currently implemented on a wide variety of applications, such as mechanical, high temperature or biomaterials [1,2,3]. Therefore, there are still major fundamental and technological interests in the fabrication processes of alumina, which involves a high-temperature treatment for the sintering (also known as consolidation or densification) of the precursor compacted powders in order to obtain a fully dense bulk ceramic material.

Despite that the fabrication of ceramics has been known since centuries, the understanding of the sintering behavior and the evolution of the microstructure of the compacted powders are still subjects of research. Hence, a wide variety of procedures have been considered for the fabrication of ceramics, starting from different recipes of the synthesis of the precursor powders, to the employment of different densification methods, such as pressureless sintering, hot isostatic pressure sintering, spark plasma sintering, or reactive sintering [1, 4, 5]. Typically, the goal is to obtain the fully dense material and the finest grain size, but saving as much as energy and time as possible.

Sintering is a process that leads to the densification of the material thanks to viscous flow and/or diffusion to reduce porosity [6]. In addition, other processes could be involved such as surface dehydroxylation, crystallization and grain boundary formation, or phase transformations. In brief, the system tends to diminish its energy through the reduction of the interface solid-gas (or solid-vacuum) and grain boundaries. In the case of crystalline materials, the formation of the grains and boundaries are additional mechanisms consuming time and energy during densification, but, again, the driving mechanism is reducing the surface energy, which involves the grain boundaries in addition to the external interface solid-gas. It should be noted that these diffusion processes are energy-activated, being coarsening more relevant at low temperature. For example, viscous sintering is driven by the gained energy through interface surface reduction [6], and the viscosity, \(\eta \), depends on the temperature through an Arrhenius-like relation with a threshold temperature, \(T_{th}\), namely

$$\begin{aligned} \eta = \eta _0 e^{[Q/k(T-T_{th})]} \end{aligned}$$
(1)

In summary, the densification of the powders is a complex phenomenon that involves different concomitant and competing physical processes that govern the morphology of the powders, the crystal and grain sizes, and the disappearance of the porosity. The dependence of each phenomenon with time and temperature, the threshold temperatures of each process, and the influence of the microstructural and chemical composition of the precursor powders have been deeply studied, and they are still under research. In particular, several studies can be found in the literature assessing the sintering behavior, namely, the evolution of the microstructure of the precursor powders, and monitoring the gradual reduction of the porosity among the powders throughout the consolidation process. Moreover, the dependence of the residual porosity is typically analysed by the relative density, that is, the ratio of the actual sample density with regard to the theoretical bulk alumina density of 3.98 g/cm\(^3\). Hence, in all cases, a direct relation between decreasing porosity with time and temperature has been confirmed [1, 6, 7].

The use of simulation techniques in the field of materials science has a double interest. On the one hand, the improvement of the properties of the material for its industrial use and, secondly, the theoretical interest in the knowledge of the physical processes involved. Traditionally, Monte Carlo simulation methods have been considered but their sequential update of randomly selected points may not be able to capture the simultaneous evolution of grains and the realistic representation of the physical processes also it is very inefficient when applied to large sets of data [8]. On the contrary, in Cellular Automata models, the simultaneous update of every single cell in the lattice of the discretized system appear to reflect more realistically the underlying physical phenomena during nature process. Recently, numerous studies in the field are using models based on cellular automata [9,10,11,12]. Most of these models focus on the study of the dynamic recrystallization [13, 14] process and its kinetics [15]. However, there is a lack of studies on the structural patterns that originate during densification, for example, of the boehmite (\(\gamma \)-AlOOH) precursor powders on sapphire substrates, where vermicular structures are formed and studied by electron microscopy [16].

In this work, we present a probabilistic model of cellular automata, in which the evolution of the system is determined exclusively by the minimization of the energy at the interface boundaries. The patterns generated in the simulation qualitatively reproduce the vermicular structures found experimentally [16] for different temperatures. In addition, the decreasing trend of the porosity with the temperature is also well reproduced, allowing the correspondence between simulation and sintering temperatures.

Fig. 1.
figure 1

The neighborhood for the calculus of the surface energy of a given configuration, which is obtained as \(E=\sum _{ij}J_{ij}( 1-\delta _{ij})\). If \(i=j, \delta _{ij}=1\) otherwise, if \(i\ne j, \delta _{ij}=0\), and \(J_{ij}=1\) in all cases.

Full size image

2 The Cellular Automaton Model

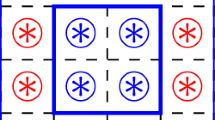
We take a two dimensional array of \(N=L \times L\) cells with periodic boundary conditions to avoid border effects. The set of possible states is \(\sigma =\{ 0,1 \}\), which correspond to a void lattice cell or cell filled with an elemental portion of alumina, respectively. To conserve the number of filled cells, the Margolus neighborhood is used, the lattice is split in non-overlapping sub-lattices and the updating is done simultaneously on each block of size \(2 \times 2\). In Fig. 1, one block and its neighborhood are sketched. Note that, in the current model, we have considered only one state for the alumina. But the proposed model is so versatile that different crystallographic orientations can be implemented simply by assigning different states to the alumina cells. This feature will allow the detailed study of crystallographic domains behavior. Nevertheless, different crystallographic orientations are left for elsewhere.

2.1 The Interface Energy

We assume that the energy E of a certain configuration only depends on the interfaces between neighboring cells. Figure 1 shows the elementary block of four cells (a,b,c,d) and the neighbors cells (e,f,g,h,k,l,m,n). The configuration energy is defined as:

$$\begin{aligned} E=\sum _{ij}J_{ij}( 1-\delta _{ij}) \end{aligned}$$
(2)

where \(\delta _{ij}\) is the Kronecker delta, and \(J_{ij}\) is the surface energy of one elemental interface, which in this work is considered to be the same for all the alumina-void interfaces (\(J=1\)). Thus, the total energy of the system is obtained summing up the energy of all the blocks. In other words, the configuration energy is obtained as the total number of sides of the lattice cells that are found between lattice cells with different states.

2.2 Transition Probabilities

The evolution rule assigns to each configuration at time t a different one at time \(t+1\), depending exclusively on the difference between both energies \(\varDelta E= E(t+1)-E(t)\). Table 1 shows the lookup table of the rule. All possible initial states of the elementary blocks, not including rotations, are shown along with all the possible outputs. Each of these possible outputs is assigned a function of Arrhenius type:

$$\begin{aligned} q_i= A\cdot e^{-\frac{\varDelta E_i}{kT}} \end{aligned}$$
(3)

the prefactor A is taken as 1. And finally the probability is obtained by normalizing between the set of possible corresponding final states.

$$\begin{aligned} p_i = \frac{q_j}{\sum _i q_j} \end{aligned}$$
(4)
Table 1. Lookup table rule of the cellular automata. All the 5 possible initial states of the blocks at time t and their possible states at instant \(t+1\) are shown. For each transition, the difference between the interface energies of the block is obtained and the Ahrrenius-type coefficient \(q_i=e^{-\frac{\varDelta E_i}{kT}}\) is calculated. The probability assigned to each of the outputs are normalized \(p_i= q_i/(\sum _j q_j)\)
Full size table

Therefore, in our probabilistic CA model, all states have a probability of being able to occur, contrary to what happens in other simulation methods in which, for example, transitions with \(\varDelta E>0\) are rejected while if \(\varDelta E \le 0\) are accepted with probability 1. These different methodologies (namely, the soft one and the hard one, respectively), involve different physical considerations and lead to different final states.

In the hard case, the system reaches the equilibrium state in a few time steps. However, in the final state, the system has a total energy higher than in the soft case. In other words, the system upon the typical hard transition probabilistic methodologies achieves faster some “local” equilibrium, while the soft probabilistic methodology allows a wider exploration of the energy pathway, which leads to a more stable equilibrium state.

Fig. 2.
figure 2

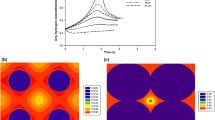
Simulation results of the CA model. Lattice size \(500 \times 500\), periodic boundary conditions. Starting from a random initial condition with a density of 0.6. Dependence of the relative decrease of the total energy versus the temperature. The “frozen” system (\(T=0\)) would not exhibit any change of the energy, as expected

Full size image

3 Results

The simulations are performed on lattices of \(N=500\times 500\) cells and start from a random initial state with a concentration \(\rho = \frac{1}{N} \sum _i^N \sigma _i \) = 0.6. The system evolves under the transition rules described above and the different data are recorded after \(10^4\) time steps. Since \(k=1\) and \(J=1\) the energy and temperature values are in arbitrary units.

3.1 The Total Interface Energy

Figure 2 shows the relative decrease of the total interface energy versus the temperature. It was found that the largest relative decreases of the energy, \(\varDelta E/E_0\) are observed in the range of lower temperatures, that is, for \(0.5<T<0.75\). It is below this value of \(T=0.75\) where it makes physical sense that the mechanism to reach equilibrium is the decrease of the total interface energy. On the other hand, when T increases, the thermal energy of the particles is the dominant factor against the minimization of energy.

The analysis of the evolution of the energy can be also made in terms of the distribution of the energy throughout the system. Figure 3 shows the spatial distribution of local energies for two different temperatures. For evaluating this local energy, the Von-Neumman neighborhood of each cell is taken into account. In the case of low temperature, the energy, which is only found in the interface between matter and the vacuum, clearly depicts the contour of the particulate, partially-sintered, system. On the contrary, at higher temperatures, the energy is distributed throughout the network, meaning that, even at the final equilibrium state, there are interfaces throughout the sample. We assume that, during the simulation of the sintering of the sample at high temperature, there are multiple remaining pores (void cells) located within the domains of alumina, due to the soft probabilistic transition methodology, which allows that some kind of thermal agitation of the cells prevails over the minimization of the interface energy. This could also explain the increase of the relative reduction of the energy above \(T=0.75\) observed in Fig. 2.

Fig. 3.
figure 3

Contour Plot of the local energy at \(t=10^4\) time steps for two temperatures: (a) \(T=0.5\), (b) \(T=1.5\). The minimum value of the energy are the pixels of black color, while the yellow color represents the maximum values. (Color figure online)

Full size image

3.2 Vermicular Structures

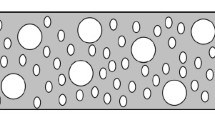
The spatial arrangements of the matter obtained at the final configurations can be discussed and compared with experimental images in Fig. 4, where the top file shows the patterns generated at various temperatures after \(10^4\) time steps, in which the equilibrium was reached in all cases. A blue pixel is a lattice with alumina.

In the case of \(T=1.5\), we have plotted the temporal average of \(\sigma \) for \(10^4\) time steps, so thermal fluctuations at high temperatures are neglected. In the plots, it can be seen how the particles are distributed minimizing the interface energy forming clusters, with vermicular shapes of different sizes that are directly related with the temperature. Surprisingly, this type of patterns has already been observed experimentally in the sintering of alumina on sapphire surfaces, as shown in the bottom file of Figure 4. Therefore, the ability of the proposed CA model for simulating partially sintered structures is clearly supported by the structural similarity of the simulated and experimental systems.

Fig. 4.
figure 4

Top line: Vermicular structures shown by the CA model at different temperatures. a) \(T=0.25\), b) \(T=0.50\), c) \(T=0.80\), d) \(T=1.5\). The initial concentration is 0.6. For d) each pixel is a temporal average of the cell state. A blue pixel if \(\langle \sigma \rangle >0.5\). Bottom line: Scanning electron microscopy images of vermicular structures of partially sintered alumina. Reproduced with permission from [16]. (Color figure online)

Full size image
Fig. 5.
figure 5

Evolution of the porosity of the sample vs. temperature. Simulation data (red circles) reproduced reasonably well the decreasing trend exhibited by the experimental data. The temperature of the samples of alumina were maintained during 600 min. (Exp1, green squares) and 300 min (Exp2, cyan triangles). Data from ref. [17]. (Color figure online)

Full size image
Fig. 6.
figure 6

Log-log plot of the number N(s) of void clusters versus the size s. The initial concentration was \(\rho _0=0.6\) and the simulation temperature \(T=1.5\). The slope of the straight line drawn is \(-1\).

Full size image

3.3 A Measure of the Porosity

During the preparation of ceramics such as alumina, voids among the precursor particles progressively disappear resulting in the densification of the sample. Nevertheless, partial or imperfect preparations lead to incomplete densifications and then the material exhibits some remaining porosity. In this simple CA model, we can measure the porosity by interpreting the existence of holes in the sample when the time average occupancy of a given cell is less than 0.5. Figure 5 shows the results obtained through the simulation where some experimental data have also been included. The porosity decreases as the temperature increases and above a certain critical value it practically reaches a null value, meaning that, above a given T, fully-dense samples are obtained, which makes an absolute realistic sense. Moreover, the correlation between the trends of both sets of results is remarkable. Finally, we have correlated the sintering temperature with the simulation temperature obtaining that \(T_{simulated}=1 \approx T_{real}=1450~K\). We have found also that the distribution of the holes within the sample follows a power law \(N(s) \approx s^{-1}\) as shown in the Fig. 6.

4 Conclusions

Among the simulation methods used in materials science, CA stand out for their ability to easily capture the complexity of material sintering processes. In this paper we have developed a probabilistic cellular automata in which the transition probability depends on the interface energies as an Arrhenius function. We point out the similarity between the patterns generated by the simulations and the vermicular patterns observed in sol-gel growth of alumina. The model also allows for a measurement of the porosity of the sample as a function of the temperature that qualitatively is in good agreement with experimental data. It is left for a future work the study of the influence of local crystallographic orientations and also the growth kinetics.