Keywords

1 Introduction

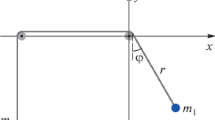
The swinging Atwood machine (SAM) is a well-known device that is obtained from a simple Atwood machine [1] when one body of mass \(m_1\) is allowed to oscillate in a plane while the other body of mass \(m_2 > m_1\) moves along a vertical (see [2] and Fig. 1). Owing to oscillations the system acquires two degrees of freedom and becomes essentially nonlinear; a general solution of its equations of motion cannot be written in symbolic form. As the system demonstrates very interesting dynamics, it has been a subject of many studies (see, for example, [3,4,5,6,7,8,9,10]). Detailed investigations have shown that only for the mass ratio \(m_2/m_1\) being equal to three the system is integrable (see [5, 7, 9,10,11]). Numerical analysis of the equations of motion has shown that, depending on the mass ratio and initial conditions, the SAM can demonstrate different types of motion, namely, periodic, quasi-periodic, and chaotic (see [3, 6, 8, 10]).

In [12] we studied numerically the equations of motion of the SAM and showed that a physical reason for such behaviour of the system is an increase of an averaged tension of the thread during oscillation. As this tension depends on the amplitude of oscillation one can choose initial conditions such that quasi-periodic motion of the system can take place. Although a simple Atwood’s machine with two bodies of different mass cannot be in a state of equilibrium (see [1]), owing to oscillations the system has a dynamic equilibrium state described by a periodic solution of the equations of motion (see [13]). If both bodies are allowed to oscillate in a plane the system acquires additional degree of freedom and demonstrates a quasi-periodic motion even in the case of equal masses \(m_2=m_1\) (see [14, 15]). Note that such unusual behaviour of the swinging Atwood machine is possible only due to oscillations of the bodies resulting in nonlinearity of the equations of motion.

In the present paper, we consider the SAM in case of small difference of masses of the bodies and planar oscillation of the mass \(m_1\). Our main purpose is to study the stability of periodic motion of the SAM. It should be noted that the constructing and investigation of periodic solutions of the equations of motion often imply rather cumbersome symbolic computations, which are convenient to carry out using computer algebra systems (see, for example, [16,17,18]). In this work, all symbolic calculations are performed with the aid of the computer algebra system Wolfram Mathematica (see [19]).

The paper is organized as follows. In Sect. 2 we describe the model and derive the equations of motion in the form that is convenient for applying the perturbation theory. Then in Sect. 3 we demonstrate shortly an algorithm for constructing the periodic solution in the form of power series in a small parameter. Section 4 is devoted to the investigation of stability of periodic solution in linear approximation. Integrating the linearized system of four differential equations with periodic coefficients which describes the perturbed motion, we compute the fundamental matrix in the form of power series in a small parameter and find the characteristic exponents for the system. At last, we summarize the obtained results in Sect. 5.

2 Model Description

The swinging Atwood machine under consideration consists of two small massless pulleys and two bodies of masses \(m_1 \le m_2\) attached to opposite ends of a massless inextensible thread (see Fig. 1). The body \(m_1\) is allowed to swing in vertical plane and it behaves like a pendulum of variable length while the body \(m_2\) is constrained to move only along a vertical. Note that in case of a pulley of finite radius used in the simple Atwood machine a length of the pendulum changes not only due to rotation of the pulley but due to the thread winding on the pulley during oscillation, as well. The last effect was investigated theoretically and experimentally in [10] and it does not modify qualitatively the system motion. Replacing one pulley of finite radius by the two pulleys of negligible radius, we obtain the swinging Atwood machine, where the pendulum length varies only due to rotation of the pulleys. Placing the pulleys at some distance between each other enables to avoid collisions of the bodies during oscillations but does not change the physical properties of the system.

Fig. 1.
figure 1

The SAM with two small pulleys

Full size image

The Lagrangian function of the system is (see [14])

$$\begin{aligned} \mathcal {L}=\frac{m_1+m_2}{2} \dot{r}^2+\frac{m_1}{2}r^2 \dot{\varphi }^2-m_2 g r+m_1 g r \cos \varphi , \end{aligned}$$
(1)

where the dot over a symbol denotes the total derivative of the corresponding function with respect to time, g is a gravity acceleration, r is the distance between the pulley and the mass \(m_1\), and the angle \(\varphi \) determines the deviation of the mass \(m_1\) from the vertical.

To simplify analysis of the system it is expedient to introduce dimensionless variables. As we expect the body \(m_1\) in the state of dynamic equilibrium behaves like a pendulum of a length \(R_0\), the distance r can be made dimensionless by using \(R_0\) as a characteristic distance, whereas the time t can be made dimensionless by using the inverse of the pendulum’s natural frequency \(\sqrt{g/R_0}\). Thus, making the substitutions \(r\rightarrow r R_0\), \(t \rightarrow t \sqrt{R_0/g}\), where r and t denote now the dimensionless variables, and dividing the Lagrangian by constant \(m_1 g R_0\), we rewrite (1) in the form

$$\begin{aligned} \mathcal {L}=\frac{2+\varepsilon }{2} \dot{r}^2+\frac{1}{2}r^2 \dot{\varphi }^2-(1+\varepsilon ) r+r \cos \varphi , \end{aligned}$$
(2)

where the parameter \(\varepsilon =(m_2-m_1)/m_1\) represents the ratio of the masses difference to the mass \(m_1\). Note that the Lagrangian (2) depends on a single dimensionless parameter \(\varepsilon \) which we shall assume to be small (\(0\le \varepsilon \ll 1\)).

Using (2), we obtain the equations of motion in the Lagrangian form (see [20])

$$\begin{aligned} (2+\varepsilon ) \ddot{r}= & {} -\varepsilon -(1-\cos \varphi )+r \dot{\varphi }^2, \nonumber \\ r \ddot{\varphi }= & {} -\sin \varphi -2\dot{r} \dot{\varphi }. \end{aligned}$$
(3)

One can easily check that system (3) has an equilibrium solution \(r=\text{ const }\), \(\varphi =0\) only in the case of equal masses (\(\varepsilon =0\)). This equilibrium state is unstable, and the system leaves it as soon as the mass \(m_1\) gets even very small initial velocity (see [12]). On the other hand, in the case of different masses, the constant term \(\varepsilon > 0\) in the right-hand side of the first Eq. (3) causes the uniformly accelerated motion of the Atwood machine in the absence of oscillations as it is in the classical Atwood’s machine (see [1]). However, if the masses difference is sufficiently small one can expect that an averaged value of the oscillating functions in the right-hand side of the first Eq. (3) compensates the constant \(\varepsilon \), and the smaller oscillating mass \(m_1\) can balance the larger mass \(m_2\). Our aim is to demonstrate that such a state of dynamical equilibrium of the system exists and it is described by the periodic solution of system (3).

3 Periodic Solution

To simplify the calculations we assume that the oscillations are small (\(|\varphi | \ll 1\)) and replace the sine and cosine functions by their expansions in power series accurate to the sixth order inclusive. As we will see later, such expansions are necessary to construct periodic solution accurate to the third order in \(\varepsilon \). Then the system (3) takes the form

$$\begin{aligned} (2+\varepsilon ) \ddot{r}= & {} -\varepsilon -\frac{1}{2} \varphi ^2+r \dot{\varphi }^2+\frac{1}{24} \varphi ^4-\frac{1}{720} \varphi ^6, \nonumber \\ r \ddot{\varphi }= & {} - \varphi -2\dot{r} \dot{\varphi }+\frac{1}{6} \varphi ^3-\frac{1}{120} \varphi ^5. \end{aligned}$$
(4)

It is obvious that constant term \(\varepsilon \) in the right-hand side of the first Eq. (4) can vanish only if the amplitude of \(\varphi \) is proportional to \(\sqrt{\varepsilon }\). In this case, the oscillating part of the distance r will be proportional to \(\varepsilon \). Doing the substitution

$$\begin{aligned} r(t) \rightarrow 1+\varepsilon r(t),\ \ \varphi (t) \rightarrow \sqrt{\varepsilon } \varphi (t), \end{aligned}$$
(5)

we reduce system (4) to the form

$$\begin{aligned}&2\ddot{r}=-1-\frac{1}{2} \varphi ^2+\dot{\varphi }^2+\varepsilon (-\ddot{r}+r \dot{\varphi }^2+\frac{1}{24} \varphi ^4)-\frac{1}{720}\varepsilon ^2 \varphi ^6, \end{aligned}$$
(6)
$$\begin{aligned}&\ddot{\varphi }+ \varphi = -\varepsilon (r \ddot{\varphi } +2 \dot{r} \dot{\varphi }-\frac{1}{6} \varphi ^3)-\frac{1}{120} \varepsilon ^2 \varphi ^5. \end{aligned}$$
(7)

One can readily check that a general solution to nonlinear system (6)–(7) cannot be found in symbolic form. As parameter \(\varepsilon \) is assumed to be small the Poincaré–Lindstedt perturbation technique for obtaining periodic solutions may be applied (see [21, 22]). Note that in the case of \(\varepsilon =0\), Eq. (7) becomes independent of (6) and determines harmonic oscillations of the angle \(\varphi \). Obviously, the amplitude of the corresponding function \(\varphi (t)\) may be chosen in such a way that the constant part of the function in the right-hand side of (6) vanishes. Therefore, the corresponding solution r(t) to (6) will be a bounded oscillating function. Taking into account the higher order terms in the right-hand sides of (6)–(7) for \(\varepsilon >0\) results in the appearance of corrections to zero-order solutions. Thus, we can look for an approximate solution to system (6)–(7) in the form of power series in \(\varepsilon \):

$$\begin{aligned}&r(t)=r_0(t)+\varepsilon r_1(t)+\varepsilon ^2 r_2(t)+\varepsilon ^3 r_3(t)+\ldots , \end{aligned}$$
(8)
$$\begin{aligned}&\varphi (t)=\varphi _0(t)+\varepsilon \varphi _1(t)+\varepsilon ^2 \varphi _2(t)+\varepsilon ^3 \varphi _3(t)+ \ldots . \end{aligned}$$
(9)

Computation of unknown functions \(r_j(t), \varphi _j(t)\) in (8)–(9) is done in rather standard way but requires quite tedious symbolic computations (see [22]), which in this paper are performed using Wolfram Mathematica. Substituting (8)–(9) into (6)–(7) and collecting coefficients of equal powers of \(\varepsilon \), we obtain the following system of linear differential equations:

$$\begin{aligned} \ddot{\varphi }_0+ \varphi _0= & {} 0, \end{aligned}$$
(10)
$$\begin{aligned} 2\ddot{r}_0= & {} -1-\frac{1}{2} \varphi _0^2+ \dot{\varphi }_0^2, \end{aligned}$$
(11)
$$\begin{aligned} \ddot{\varphi }_1+ \varphi _1= & {} r_0 \varphi _0-2\dot{r}_0 \dot{\varphi }_0+\frac{1}{6} \varphi _0^3, \end{aligned}$$
(12)
$$\begin{aligned} 2\ddot{r}_1= & {} -\ddot{r}_0+ 2 \dot{\varphi }_0 \dot{\varphi }_1+r_0 \dot{\varphi }_0^2-\varphi _0 \varphi _1+\frac{1}{24} \varphi _0^4, \end{aligned}$$
(13)
$$\begin{aligned} \ddot{\varphi }_2+ \varphi _2= & {} r_0 \varphi _1+r_1 \varphi _0-2\dot{r}_0 \dot{\varphi }_1-2\dot{r}_1 \dot{\varphi }_0+2r_0 \dot{r}_0 \dot{\varphi }_0 \nonumber \\&-\,r_0^2 \varphi _0+\frac{1}{2} \varphi _0^2 \varphi _1-\frac{1}{6} r_0 \varphi _0^3-\frac{1}{120} \varphi _0^5, \end{aligned}$$
(14)
$$\begin{aligned} 2\ddot{r}_2= & {} -\ddot{r}_1+ 2 \dot{\varphi }_0 \dot{\varphi }_2+\dot{\varphi }_1^2+2r_0 \dot{\varphi }_0 \dot{\varphi }_1+r_1 \dot{\varphi }_0^2 \nonumber \\&-\,\frac{1}{2} \varphi _1^2-\varphi _0 \varphi _2+\frac{1}{6} \varphi _0^3 \varphi _1-\frac{1}{720} \varphi _0^6, \ldots \end{aligned}$$
(15)

Obviously, Eqs. (10)–(15) may be solved in succession. Without loss of generality, we may assume that at the initial instant of time, the body \(m_1\) is on the vertical (\(\varphi (0)=0\)) and has some initial velocity \(w_0>0\). The corresponding solution of Eq. (10) is

$$\begin{aligned} \varphi _0(t)=w_0 \sin t. \end{aligned}$$
(16)

On substituting (16) into (11) we obtain

$$\begin{aligned} 2\ddot{r}_1= -1+\frac{w_0^2}{4}+\frac{3}{4} w_0^2 \cos 2t. \end{aligned}$$
(17)

As we are looking for an oscillating function \(r_1(t)\) the amplitude \(w_0\) is chosen from the condition that the constant term in the right-hand side of (17) vanishes. Due to this condition we set \(w_0=2\) and solve Eq. (17) with initial condition \(\dot{r}_1(0)=0\). Then we obtain

$$\begin{aligned} r_1(t)=r_{10}-\frac{3}{8} \cos 2t, \end{aligned}$$
(18)

where \(r_{10}\) is an arbitrary constant.

On substituting (16) and (18) with \(w_0=2\) into (12) and reducing the trigonometric functions, we obtain

$$\begin{aligned} \ddot{\varphi }_1+ \varphi _1= \left( 2 r_{10}-\frac{1}{8}\right) \sin t -\frac{53}{24} \sin 3t. \end{aligned}$$
(19)

Equation (19) describes the forced oscillations of a pendulum, and to avoid an increase of the amplitude we need to eliminate a resonance term in the right-hand side. So putting \(r_{10}=1/16\) and solving differential equation (19) with initial condition \(\varphi _1(0)=0\), we find

$$\begin{aligned} \varphi _1(t)=\left( w_{1}+\frac{53}{96}\right) \sin t+\frac{53}{192} \sin 3t, \end{aligned}$$
(20)

where \(w_1\) is an arbitrary constant.

On substituting (16), (18), and (20) into (13) and reducing the trigonometric functions, we derive the following differential equation

$$\begin{aligned} 2\ddot{r}_2= \frac{53}{96}+w_1+\left( 3 w_{1}+\frac{37}{64}\right) \cos 2t +\frac{105}{64} \cos 4t. \end{aligned}$$
(21)

Again the unknown \(w_1\) is chosen from the condition of vanishing constant terms in the right-hand side of (21), therefore, \(w_1=-53/96\). Then integrating (21) with the initial condition \(\dot{r}_2(0)=0\), we find

$$\begin{aligned} r_2(t)=r_{20}+\frac{69}{512} \cos 2t - \frac{105}{2048} \cos 4t, \end{aligned}$$
(22)

where \(r_{20}\) is another arbitrary constant.

In order to find the solution more accurately we have to repeat such calculations step by step, solving successively linear differential equations (14), (15), and so on for the functions \(\varphi _k(t)\) and \(r_k(t)\) under the initial conditions \(\varphi _k(0)=0\), \(\dot{r}_k(0)=0\), \(k=1,2,\ldots .\) Each of the solutions \(\varphi _k(t)\), \(r_k(t)\) will contain an arbitrary constant which appears during integration and should be found from the condition that constant terms in the equation for \(r_{k+1}(t)\) and resonance terms in the equation for \(\varphi _{k+1}(t)\) vanish. We have done the calculations up to the third order in \(\varepsilon \), and the corresponding periodic solutions are given by

$$\begin{aligned} r_p(t)=1+ \frac{\varepsilon }{16}\left( 1-6 \cos 2t \right) - \frac{\varepsilon ^2}{2048} \left( 261-276 \cos 2t +105 \cos 4t \right) \nonumber \\ +\,\frac{\varepsilon ^3}{131072} \left( 4275-8166 \cos 2t +5067 \cos 4t - 1510 \cos 6t \right) ,\ \ \ \end{aligned}$$
(23)
$$\begin{aligned} \varphi _p(t)=\sqrt{\varepsilon } \left( 2\sin t+\frac{53\varepsilon }{192} \sin 3t+ \frac{\varepsilon ^2}{16384}\left( 2959 \sin t \right. \right. \nonumber \\ -\,\left. \left. 1699 \sin 3t+ \frac{5813}{5} \sin 5t \right) \right) . \end{aligned}$$
(24)

It follows from (23)–(24) that the initial length of the thread

$$\begin{aligned} r_p(0)=1-\frac{5\varepsilon }{16}-\frac{45}{1024} \varepsilon ^2 - \frac{167}{65536} \varepsilon ^3, \end{aligned}$$
(25)

and the initial angular velocity

$$\begin{aligned} \dot{\varphi }_p(0)=\sqrt{\varepsilon }\left( 2+\frac{53\varepsilon }{64}+\frac{3675\varepsilon ^2}{16384} \right) , \end{aligned}$$
(26)

corresponding to the periodic solution depend on parameter \(\varepsilon \); for larger \(\varepsilon \) or larger masses difference, the initial velocity must increase to provide a larger amplitude of oscillations. Dependence of the initial length \(r_p(0)\) on \(\varepsilon \) means that the frequency of oscillation depends on the amplitude; such dependence is typical of nonlinear oscillations (see [20, 22]).

4 Stability Analysis

The existence of periodic solution to equations of motion (4) means that for given value of parameter \(\varepsilon \), one can choose initial conditions (25), (26), \(\dot{r}_p(0)=0\), and \(\varphi _p(0)=0\) such that the system is in the state of dynamical equilibrium when the bodies oscillate near some equilibrium positions. Note that for \(\varepsilon >0\), the system under consideration has no static equilibrium state when the coordinates r(t), \(\varphi (t)\) are some constants. So it is natural to investigate whether the system will remain in the neighborhood of the equilibrium if the initial conditions are perturbed or whether the periodic solution (23)–(24) is stable.

It should be noted that studying the stability of periodic solution is much more complicated in comparison to the case of equilibrium state stability and the relevant symbolic computations become much more cumbersome. First of all, we need to derive the equations of perturbed motion in the form of four first-order differential equations. Using (2) and doing the Legendre transformation (see [20]), we define the Hamiltonian in case of \(|\varphi |\ll 1\)

$$\begin{aligned} \mathcal {H}=\frac{p_r^2}{2(2+\varepsilon )} +\frac{p_{\varphi }^2}{2r^2} +\varepsilon r+\frac{r}{2} \left( \varphi ^2-\frac{1}{12}\varphi ^4+\frac{1}{360}\varphi ^6 \right) . \end{aligned}$$
(27)

The equations of motion written in the Hamiltonian form are

$$\begin{aligned} \dot{r}=\frac{\partial \mathcal {H}}{\partial p_r}=\frac{p_r}{2+\varepsilon },\ \ \dot{p}_r=-\frac{\partial \mathcal {H}}{\partial r}=-\varepsilon -\frac{1}{2} \varphi ^2 \left( 1-\frac{1}{12}\varphi ^2+\frac{1}{360}\varphi ^4 \right) +\frac{p_{\varphi }^2}{r^3}, \nonumber \\ \dot{\varphi }=\frac{\partial \mathcal {H}}{\partial p_{\varphi }}=\frac{p_{\varphi }}{r^2},\ \ \dot{p}_{\varphi }=-\frac{\partial \mathcal {H}}{\partial \varphi }=- r \varphi \left( 1-\frac{1}{6}\varphi ^2+\frac{1}{120}\varphi ^4 \right) ,\ \ \ \ \ \end{aligned}$$
(28)

where \(p_r, p_\varphi \) are the conjugate momenta to \(r, \varphi \), respectively.

One can readily check that periodic solution (23)–(24) satisfy Eqs. (28). To investigate its stability we define new canonical variables \(q_1, q_2, p_1, p_2\) according to the rule

$$\begin{aligned} r \rightarrow r_p+q_1,\ \varphi \rightarrow \varphi _p+q_2,\ p_r\rightarrow p_{r0}+p_1,\ p_{\varphi }\rightarrow p_{\varphi 0}+p_2, \end{aligned}$$
(29)

where the momenta \(p_{r0}=(2+\varepsilon ) \dot{r}_p, p_{\varphi 0}=r_p^2 \dot{\varphi }_p\) are obtained by substituting (23)–(24) into (28). Doing the canonical transformation (29) and expanding the Hamiltonian (27) into power series in terms of \(q_1, q_2, p_1, p_2\) up to second order inclusive, we represent it in the form

$$\begin{aligned} \tilde{\mathcal {H}}=\mathcal {H}_0+\mathcal {H}_1+\mathcal {H}_2+\ldots , \end{aligned}$$
(30)

where \(\mathcal {H}_k\) is the kth order homogeneous polynomial with respect to canonical variables \(q_1, q_2, p_1, p_2\) which are considered as small perturbations of periodic solution (23)–(24). Note that zero-order term \(\mathcal {H}_0\) in (30) can be omitted as a function of time which does not influence the equations of motion. The first-order term \(\mathcal {H}_1\) is equal to zero because periodic solution (23)–(24) satisfy the unperturbed equations of motion (28). Therefore, the first non-zero term in the expansion (30) is a quadratic one that is

$$\begin{aligned}&\mathcal {H}_2=\frac{p_1^2}{2(2+\varepsilon )} +\frac{3p_{\varphi 0}^2}{2r_p^4} q_1^2+\frac{p_2^2}{2r_p^2}+\frac{r_p}{2} q_2^2\left( 1-\frac{1}{2}\varphi _p^2+\frac{1}{24} \varphi _p^4 \right) - \nonumber \\&\qquad \quad \,\,\, -\frac{2p_{\varphi 0}}{r_p^3} q_1 p_2+q_1 q_2 \left( \varphi _p -\frac{1}{6} \varphi _p^3 +\frac{1}{120} \varphi _p^5 \right) . \end{aligned}$$
(31)

The quadratic part \(\mathcal {H}_2\) of the Hamiltonian determines the linearized equations of the perturbed motion which is convenient to write in the matrix form

$$\begin{aligned} \dot{x}=J\cdot H(t,\varepsilon ) x, \end{aligned}$$
(32)

where \(x^T=(q_1,q_2,p_1,p_2)\) is a 4-dimensional vector, \(J=\left( \begin{array}{cc} 0 &{} E_2 \\ -E_2 &{} 0 \end{array} \right) \), \(E_2\) is the second-order identity matrix, and the fourth-order matrix-function \(H(t,\varepsilon )\) is

$$\begin{aligned} H(t,\varepsilon )=\left( \begin{array}{cccc} \frac{3p_{\varphi 0}^2}{r_p^4} &{} \varphi _p &{} 0 &{} -\frac{2p_{\varphi 0}}{r_p^3} \\ \varphi _p &{} r_p &{} 0 &{} 0 \\ 0 &{} 0 &{} \frac{1}{2+\varepsilon } &{} 0 \\ -\frac{2p_{\varphi 0}}{r_p^3} &{} 0 &{} 0 &{} \frac{1}{r_p^2} \end{array} \right) . \end{aligned}$$
(33)

Note that the elements of matrix (33) are obtained by differentiation of \(\mathcal {H}_2\):

$$ H_{i,j}=\frac{\partial ^2 \mathcal {H}_2}{\partial x_i \partial x_j},\ \ i,j=1,2,3,4. $$

It is clear that matrix \(H(t,\varepsilon )\) is periodic function of time, and so the perturbed motion of the system is described by the linear system of four differential equations with periodic coefficients (32).

4.1 Computing the Monodromy Matrix

The systems of linear differential equations with periodic coefficients and their general properties have been studied quite well (see [23]). The behavior of solutions to system (32) is determined by its characteristic multipliers which are the eigenvalues of the monodromy matrix \(X(2\pi ,\varepsilon )\), where \(X(t,\varepsilon )\) is a fundamental matrix for system (32) satisfying the initial condition \(X(0)=E_4\). As periodic solution (23)–(24) is represented by power series in parameter \(\varepsilon \), the matrix \(H(t,\varepsilon )\) can also be represented in the form of power series

$$\begin{aligned} H(t,\varepsilon )=H_0(t)+\sqrt{\varepsilon } H_1(t)+\varepsilon H_2(t)+\varepsilon ^{3/2} H_3(t)+\ldots , \end{aligned}$$
(34)

where \(H_k(t), k=0,1,2,\ldots ,\) are continuous periodic fourth-order square matrices which are obtained by substitution of solution (23)–(24) into (33) and expanding each element of the matrix \(H(t,\varepsilon )\) into power series in \(\varepsilon \).

The fundamental matrix \(X(t,\varepsilon )\) can be sought in the form of power series

$$\begin{aligned} X(t,\varepsilon )=X_0(t)+\sqrt{\varepsilon } X_1(t)+\varepsilon X_2(t)+\varepsilon ^{3/2} X_3(t)+\ldots , \end{aligned}$$
(35)

where \(X_k(t), k=0,1,2,\ldots ,\) are continuous matrix functions. On substituting (34) and (35) into (32) and collecting coefficients of equal powers of \(\varepsilon \), we obtain the following sequence of differential equations:

$$\begin{aligned}&\dot{X}_0=J H_0 X_0(t), \end{aligned}$$
(36)
$$\begin{aligned}&\dot{X}_k-J H_0 X_k=\mathop {\sum }\limits _{j=1}^k J H_j(t) X_{k-j}(t),\ \ (k\ge 1). \end{aligned}$$
(37)

The functions \(X_k(t)\) must satisfy the following initial conditions:

$$\begin{aligned} X_0(0)=E_4,\ \ X_k(0)=0\ \ (k\ge 1). \end{aligned}$$
(38)

As \(H_0\) is a constant matrix, Eq. (36) has a solution

$$\begin{aligned} X_0(t)=\exp (J H_0 t). \end{aligned}$$
(39)

Making a substitution

$$\begin{aligned} X_k(t)=\exp (J H_0 t) Y_k(t), \end{aligned}$$
(40)

we transform Eq. (37) to the form

$$\begin{aligned} \dot{Y}_k=\sum _{j=1}^k \exp (-J H_0 t) J H_j(t) \exp (J H_0 t) Y_{k-j}(t),\ \ (k\ge 1), \end{aligned}$$
(41)

where initial conditions for the functions \(Y_k(t)\) are

$$\begin{aligned} Y_0(0)=E_4,\ \ Y_k(0)=0\ \ (k\ge 1). \end{aligned}$$
(42)

Now we can easily integrate Eq. (41) and its solution satisfying the initial conditions (42) is given by

$$\begin{aligned} Y_k(t)=\sum _{j=1}^k \int _0^t \exp (-J H_0 \tau ) J H_j(\tau ) \exp (J H_0 \tau ) Y_{k-j}(\tau ) d\tau ,\ \ (k\ge 1). \end{aligned}$$
(43)

As the right-hand side of Eq. (43) determining \(Y_k(t)\) depends only on \(Y_0, Y_1, \ldots , Y_{k-1}\) the functions \(Y_k(t)\) may be computed in succession. Such computations are performed with Wolfram Mathematica but the results are very bulky and we do not show them here. Finally, the monodromy matrix \(X(2\pi ,\varepsilon )\) of system (32) can be found in the form

$$\begin{aligned} X(2\pi ,\varepsilon )=\exp (2\pi J H_0) \sum _{j=1}^\infty Y_{k}(2\pi ) \varepsilon ^{k/2}. \end{aligned}$$
(44)

4.2 Characteristic Multipliers

Characteristic multipliers for system (32) are the eigenvalues of the monodromy matrix (44) and to find them we need to compute the monodromy matrix first. To find \(X_0(t)\) it is not necessary to compute the exponential function of the matrix \(J H_0 t\) according to (39). It is much easier to solve Eq. (36) with initial conditions (38) and

$$\begin{aligned} H_0=\left( \begin{array}{cccc} \ 0 \ \ \ {} &{} \ 0 \ \ {} &{} \ 0 \ \ {} &{} \ 0 \ \\ \ 0 \ \ \ {} &{} \ 1 \ \ &{} \ 0 \ \ {} &{} \ 0 \ \\ \ 0 \ \ \ {} &{} \ 0 \ \ {} &{} \ 1/2 \ \ {} &{} \ 0 \ \\ \ 0 \ \ \ {} &{} \ 0 \ \ {} &{} \ 0 \ \ &{} \ 1 \ \end{array} \right) , \end{aligned}$$

the corresponding solution is

$$\begin{aligned} X_0(t)=\left( \begin{array}{cccc} \ 1 \ {} &{} \ 0 \ {} &{} t/2 \ {} &{} \ 0 \ \\ \ 0 \ {} &{} \ \ \ \cos t &{} 0 \ {} &{} \ \sin t \ \\ \ 0 \ {} &{} \ 0 \ {} &{} 1 &{} 0 \ \\ \ 0 \ {} &{} \ -\sin t &{} 0 \ {} &{} \ \cos t \ \end{array} \right) . \end{aligned}$$

But the next steps require to multiply and integrate matrices as it follows from (43) and to do quite cumbersome symbolic calculations. So application of the computer algebra system Wolfram Mathematica turned out to be very helpful. We do not show here the intermediate results of calculations because they are quite bulky. Using the monodromy matrix which was computed up to the third order in parameter \(\epsilon \), we can write the characteristic equation determining the characteristic multipliers for system (32) in the form

$$\begin{aligned} \det (X(2\pi ,\varepsilon )-\rho E_4)=(\rho -1)^2 (\rho ^2+2B\rho +1)=0, \end{aligned}$$
(45)

where

$$ B=-2+3\pi ^2 \varepsilon -\frac{3\pi ^2}{16}(17+4\pi ^2) \varepsilon ^2+\frac{3\pi ^2}{5120}(4845+2720\pi ^2+128\pi ^4) \varepsilon ^3. $$

Solving (45), we obtain four characteristic multipliers

$$ \rho _{1,2}=1, $$
$$ \rho _{3,4}=1\pm i \pi \sqrt{3\varepsilon }-\frac{3\pi ^2}{2} \varepsilon \mp i \frac{\pi \sqrt{3}}{32} (17+16\pi ^2) \varepsilon ^{3/2}+\frac{3\pi ^2}{32}(17+4\pi ^2) \varepsilon ^2. $$

Note that two characteristic multipliers \(\rho _{1,2}=1\) determine two independent periodic solutions to system (32). One can readily check that the absolute value of the second couple of the characteristic multipliers \(\rho _{3,4}\) is equal to 1. They are complex conjugate and determine two purely imaginary characteristic exponents

$$ \lambda _{3,4}= \frac{1}{2\pi } \log \rho =\pm i \frac{\sqrt{3\varepsilon }}{2} \left( 1-\frac{17}{32} \varepsilon +\frac{85}{256} \varepsilon ^2 \right) . $$

According to Floquet–Lyapunov theory (see [23]), four linearly independent solutions to system (32) with \(2\pi \)-periodic matrix may be represented in the form

$$\begin{aligned} x_1(t)=f_1(t),\ x_2(t)=f_2(t),\ x_3(t)=\exp (\lambda _3 t) f_3(t), x_4(t)=\exp (\lambda _4 t) f_4(t), \end{aligned}$$
(46)

where \(f_k(t), (k=1,2,3,4)\) are \(2\pi \)-periodic functions. Therefore, in the case of \(\varepsilon > 0\) solutions (46) describe the perturbed motion of the system in the bounded domain in the neighborhood of the periodic solution (23)–(24). It means this solution is stable in linear approximation, and so the SAM is an example of mechanical system in which the equilibrium state is stabilized by oscillations.

5 Conclusion

In the present paper, we have considered a swinging Atwood machine in the case when one body of smaller mass is permitted to oscillate in a vertical plane. Such a system has a state of equilibrium only in the case of equal masses but this state is unstable. Doing necessary symbolic computations, we have demonstrated that owing to oscillations the system has a dynamic equilibrium state described by a periodic solution of the equations of motion. It is a very interesting peculiarity of the system which takes place only due to the nonlinearity of the equations of motion.

We have found the initial conditions under which the equations of motion have periodic solution and proved its linear stability. Simulation of the system shows that this periodic motion is stable but its stability in Lyapunov sense still should be proved; so the problem requires further investigation. Note that the stability analysis of periodic solutions is a very complicated problem which involves quite tedious symbolic computations; so the application of computer algebra systems for doing such calculations is very helpful. In this work, we realized all the symbolic computations with the aid of the computer algebra systems Wolfram Mathematica.