Abstract
For the given non-unary input alphabet \(\varSigma \), a maximal prefix code h mapping strings over \(\varSigma \) to binary strings, and an optimal deterministic finite automaton (DFA) \(\mathcal {A}\) with n states recognizing a language \(\mathcal {L}\) over \(\varSigma \), we consider the problem of how many states we need for an automaton \(\mathcal {A}'\) that decides membership in \(h(\mathcal {L})\), the binary coded version of \(\mathcal {L}\). Namely, \(\mathcal {A}'\) accepts binary inputs belonging to \(h(\mathcal {L})\) and rejects binary inputs belonging to \(h(\mathcal {L}^{\scriptscriptstyle \mathrm {C}})\), where \(\mathcal {L}^{\scriptscriptstyle \mathrm {C}}\) is the complement of \(\mathcal {L}\). The outcome on inputs that are not valid binary codes for any string in \(\varSigma ^{*}\) can be arbitrary: \(\mathcal {A}'\) may accept, reject, or halt in a “don’t care” state. We show that any optimal deterministic don’t care finite automaton (dcDFA) \(\mathcal {A}'\) solving this promise problem uses at most \((\Vert {\varSigma }\Vert -1){\cdot }n\) states but at least n states. We also show that, for each non-unary input alphabet \(\varSigma \), there exists a maximal binary prefix code h such that, for each \(n\ge 2\) and for each N in range from n to \((\Vert {\varSigma }\Vert -1){\cdot }n\), there exists a language \(\mathcal {L}\) over \(\varSigma \) such that the optimal DFA recognizing \(\mathcal {L}\) uses exactly n states and any optimal dcDFA for solving the above promise problem uses exactly N states. Thus, we have the complete state hierarchy for deciding membership in the binary coded version of \(\mathcal {L}\), with no magic numbers in between the lower and upper bounds.
Supported by the Slovak grant contract VEGA 1/0177/21.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
One of the earliest results in automata theory is the subset construction [16]: every n-state nondeterministic finite automaton (NFA) can be replaced by an equivalent deterministic finite automaton (DFA) using at most \(2^n\) states. This raised later the question of whether it is possible, for a given number n, to find some \(N\in \{n,\ldots ,2^n\}\) such that there is no optimal DFA with exactly N states, equivalent to some optimal NFA with exactly n states [10]; such numbers were named “magic”. The problem was solved in [11], showing that there are no magic numbers for ternary languages, contrary to the unary languages [5]. Since then, the magic numbers were studied for language operations, e.g., in [9], it was shown that, for the intersection of two languages, given by two DFAs with n and m states, we have no magic numbers in \(\{1,\ldots ,n{\cdot }m\}\). Such state hierarchies were studied for other operations as well [4, 7, 9, 11].
From a different starting point, we are going to land in yet another complete state hierarchy with no magic numbers. Our initial motivation was the fact that most present-day computers store data in a binary coded form. This raises the following natural question: given a standard DFA \(\mathcal {A}\) with n states for a regular language \(\mathcal {L}\) over an input alphabet \(\varSigma \), how many states we need to recognize \(h(\mathcal {L})\), the binary coded version of \(\mathcal {L}\)? Clearly, the answer depends also on \(h\,{:}\,\varSigma ^{*}{\rightarrow }\{0,1\}^{*}\), the binary code in use. In most cases, we can work with the assumption that the code is a homomorphism, such that \(h(\alpha _1)= h(\alpha _2)\) implies \(\alpha _1= \alpha _2\), so that each encoded string can be unambiguously decoded back. Since it is well known that regular languages are closed under any homomorphism (not necessarily a code—see e.g. [8, Sect. 4.2.3]), the situation seems clear at first glance:Footnote 1 construct an optimal DFA for \(h(\mathcal {L})\).
However, if the automaton for \(h(\mathcal {L})\) receives only inputs that are valid binary images of strings in \(\varSigma ^{*}\), the outcome on inputs that are not valid images can be quite arbitrary, which allows us to save some states. This brings us to a modified problem: given a code \(h\,{:}\,\varSigma ^{*}{\rightarrow }\{0,1\}^{*}\) and a standard DFA \(\mathcal {A}\) with n states for \(\mathcal {L}\subseteq \varSigma ^{*}\), how many states we need for an automaton \(\mathcal {A}'\) that accepts each \(\beta \in h(\mathcal {L})\) and rejects each \(\beta \in h(\mathcal {L}^{\scriptscriptstyle \mathrm {C}})\)? Here \(\mathcal {L}^{\scriptscriptstyle \mathrm {C}}\) denotes the complement of \(\mathcal {L}\).
This approach is not completely new: in general, we are given a pair of disjoint languages \(\langle {}\mathcal {L}^{{\scriptscriptstyle \oplus }},\mathcal {L}^{{\scriptscriptstyle \ominus }}{}\rangle \) over the same alphabet \(\varSigma \), called a promise problem, and we decide whether \(w\in \mathcal {L}^{{\scriptscriptstyle \oplus }}\) or \(w\in \mathcal {L}^{{\scriptscriptstyle \ominus }}\) by the use of a don’t care deterministic finite automaton (dcDFA) which, besides accepting and rejecting states, may also use neutral or “don’t care” states, otherwise it behaves like a standard DFA (see e.g. [6, 13]). In our settings, \(\mathcal {L}^{{\scriptscriptstyle \oplus }}= h(\mathcal {L})\) and \(\mathcal {L}^{{\scriptscriptstyle \ominus }}= h(\mathcal {L}^{\scriptscriptstyle \mathrm {C}})\), where \(h\,{:}\,\varSigma ^{*}{\rightarrow }\{0,1\}^{*}\) is a code. We shall concentrate on the most common binary codes used in practice, that allow decoding by one-way deterministic finite-state transducers in real time and minimize \(\sum _{a\in \varSigma }|{h(a)}|\), the sum of lengths of codewords. Such codes are called maximal prefix codes in literature [1, 3]. (See Definition 1.)
This paper shows that, for each maximal prefix code \(h\,{:}\,\varSigma ^{*}{\rightarrow }\{0,1\}^{*}\) and each optimal DFA \(\mathcal {A}\) with n states recognizing some \(\mathcal {L}\) over the alphabet \(\varSigma \), the binary promise problem \(\langle {}h(\mathcal {L}),h(\mathcal {L}^{\scriptscriptstyle \mathrm {C}}){}\rangle \) can be solved by a dcDFA \(\mathcal {A}'\) using at most \((\Vert {\varSigma }\Vert -1){\cdot }n\) states, but at least n states.Footnote 2 We also show that, for each non-unary input alphabet \(\varSigma \), there exists a maximal binary prefix code h such that, for each \(n\ge 2\) and each \(N\in \{n,\ldots ,(\Vert {\varSigma }\Vert -1){\cdot }n\}\), there exists a language \(\mathcal {L}\subseteq \varSigma ^{*}\) such that the optimal DFA recognizing \(\mathcal {L}\) uses exactly n states and any optimal dcDFA for solving \(\langle {}h(\mathcal {L}), h(\mathcal {L}^{\scriptscriptstyle \mathrm {C}}){}\rangle \) uses exactly N states.
2 Preliminaries
Here we shall fix some basic definitions, notation, and preliminary properties. For more details, we refer the reader to [6, 8], or any other standard textbooks.
Definition 1
A homomorphism between strings over two alphabets is a mapping \(h\,{:}\,\varSigma _1^{*}{\rightarrow }\varSigma _2^{*}\) preserving concatenation, i.e., \(h(\alpha _1{\cdot }\alpha _2)= h(\alpha _1){\cdot }h(\alpha _2)\), for each \(\alpha _1,\alpha _2\in \varSigma _1^{*}\). The image of a language \(L\subseteq \varSigma _1^{*}\) is \(h(L)= \{h(\alpha )\,{:}\,\alpha \in L\}\subseteq \varSigma _2^{*}\).
If \(h(\alpha _1)= h(\alpha _2)\) implies that \(\alpha _1= \alpha _2\), then h is called a code.
h is a prefix code, if no string in \(h(\varSigma _1)= \{h(a)\,{:}\,a\in \varSigma _1\}\) is a proper prefix of another one. The code h is maximal, if there is no other code \(h'\,{:}\,{\varSigma '_1}^{*}\,{\rightarrow }\,\varSigma _2^{*}\) (for some \(\varSigma '_1\supseteq \varSigma _1\)) such that \(h'(\varSigma '_1)\) is a proper superset of \(h(\varSigma _1)\).
Each homomorphism h is completely determined by the strings in \(h(\varSigma _1)\), since \(h(a_1{\cdots }a_{\ell })= h(a_1){\cdots }h(a_{\ell })\), for each \(a_1,\ldots ,a_{\ell }\in \varSigma _1\). In addition, if h is a code, each \(\beta \in h(\varSigma _1^{*})\) has a unique factorization into \(\beta =\beta _1{\cdots }\beta _{\ell }\), where \(\ell \ge 0\) and \(\beta _1,\ldots ,\beta _{\ell }\in h(\varSigma _1)\). For examples of codes, see Fig. 1.
Examples of homomorphisms establishing some binary prefix codes. Each homomorphism is displayed as a tree in which each leaf represents some \(a_i\), a letter of the original input alphabet; the edges are labeled so that the path from the root to \(a_i\) gives the corresponding string \(h(a_i)\). Internal nodes of the tree are related to prefixes of strings in \(\{h(a)\,{:}\,a\in \varSigma \}\). The code h (left), defined by \(h(a_0)=1\), \(h(a_1)=01\), \(h(a_2)=001\), \(h(a_3)=0001\), \(h(a_4)=00001\), and \(h(a_5)=00000\), is maximal, while the code \(\tilde{h}\) (right), with \(\tilde{h}(a_0)=1\), \(\tilde{h}(a_1)=00011\), and \(\tilde{h}(a_2)=00010\), is not—it can be extended, e.g., by defining \(\tilde{h}(a_3)=01\).
Prefix codes allow easy decoding by a one-way deterministic finite-state machine such that, for the given \(\beta \in h(\varSigma _1^{*})\), it computes the factorization of \(\beta \) into \(h(a_1){\cdots }h(a_{\ell })\) and prints \(a_1{\cdots }a_{\ell }\) on the output in real time [1, Prop. 5.1.6].
Maximal codes minimize \(\sum _{a\in \varSigma }|{h(a)}|\) and do not have “gaps” in images: each \(\beta \in \varSigma _2^{*}\) can be extended to an image of some \(\alpha \in \varSigma _1^{*}\), that is, to \(\beta {\cdot }\beta '= h(\alpha )\), for some \(\beta '\in \varSigma _2^{*}\) and some \(\alpha \in \varSigma _1^{*}\), not excluding \(\beta '= \varepsilon \).
Since we shall deal with binary codes only, we are going to simplify notation and write \(\varSigma \) instead of \(\varSigma _1\) and fix \(\varSigma _2= \{0,1\}\).
Definition 2
A don’t care deterministic finite automaton (dcDFA) is a 6-tuple \(\mathcal {A}=\langle {}Q,\varSigma , q_{\scriptscriptstyle \mathrm {I}}, f, F^{{\scriptscriptstyle \oplus }},F^{{\scriptscriptstyle \ominus }}{}\rangle \), in which Q is a finite set of states; \(\varSigma \) is a finite input alphabet; \(q_{\scriptscriptstyle \mathrm {I}}\in Q\) is the initial state; \(f:Q\times \varSigma \rightarrow Q\) is a transition function; \(F^{{\scriptscriptstyle \oplus }}\subseteq Q\) is the set of accepting states; and \(F^{{\scriptscriptstyle \ominus }}\subseteq Q\) the set of rejecting states, \(F^{{\scriptscriptstyle \oplus }}\cap F^{{\scriptscriptstyle \ominus }}=\) Ø. The remaining states are called neutral or “don’t care” states.
A (standard) deterministic finite automaton (DFA) is a 5-tuple \(\mathcal {A}=\langle {}Q,\varSigma , q_{\scriptscriptstyle \mathrm {I}}, f,F{}\rangle \), with \(F\subseteq Q\) denoting the set of accepting states and \(Q{\setminus }F\) the set of rejecting states; the remaining components have the same meaning as above.
The transition function f can be extended to \(f^{*}\,{:}\,Q\times \varSigma ^{*}\rightarrow Q\) in a natural way, taking by definition \(f^{*}(q,\varepsilon )=q\) and \(f^{*}(q,\alpha a)=f(f^{*}(q,\alpha ),a)\), for each \(q\in Q\), \(\alpha \in \varSigma ^{*}\), and \(a\in \varSigma \). To simplify notation, \(f^{*}(q,\alpha )= q'\) shall sometimes be displayed in a more compact form \(q\mathop {\longrightarrow }\limits ^{\alpha }q'\).
A promise problem (see e.g. [6]) is a pair of disjoint languages \(\langle {}\mathcal {L}^{{\scriptscriptstyle \oplus }},\mathcal {L}^{{\scriptscriptstyle \ominus }}{}\rangle \) over the same alphabet \(\varSigma \). The promise problem is solved by a dcDFA \(\mathcal {A}\), if \(\mathcal {A}\) accepts each \(w\in \mathcal {L}^{{\scriptscriptstyle \oplus }}\) (that is, \(f^{*}(q_{\scriptscriptstyle \mathrm {I}},w)\in F^{{\scriptscriptstyle \oplus }}\)) and rejects each \(w\in \mathcal {L}^{{\scriptscriptstyle \ominus }}\) (\(f^{*}(q_{\scriptscriptstyle \mathrm {I}},w)\in F^{{\scriptscriptstyle \ominus }}\)). We do not have to worry about the outcome on inputs belonging neither to \(\mathcal {L}^{{\scriptscriptstyle \oplus }}\) nor to \(\mathcal {L}^{{\scriptscriptstyle \ominus }}\): on such inputs, \(\mathcal {A}\) may accept, reject, or halt in a neutral state.
\(\mathcal {A}\) is optimal for \(\langle {}\mathcal {L}^{{\scriptscriptstyle \oplus }},\mathcal {L}^{{\scriptscriptstyle \ominus }}{}\rangle \), if it solves \(\langle {}\mathcal {L}^{{\scriptscriptstyle \oplus }},\mathcal {L}^{{\scriptscriptstyle \ominus }}{}\rangle \) and there is no dcDFA \(\mathcal {A}'\) that solves \(\langle {}\mathcal {L}^{{\scriptscriptstyle \oplus }},\mathcal {L}^{{\scriptscriptstyle \ominus }}{}\rangle \) with fewer states than does \(\mathcal {A}\).
If \(\mathcal {L}^{{\scriptscriptstyle \oplus }}\cup \mathcal {L}^{{\scriptscriptstyle \ominus }}= \varSigma ^{*}\), then \(\mathcal {A}\) has no neutral reachable states and can be viewed as a standard DFA; we have the standard language recognition and say that \(\mathcal {L}^{{\scriptscriptstyle \oplus }}\) is recognized by \(\mathcal {A}\). The language \(\mathcal {L}^{{\scriptscriptstyle \oplus }}\) is then usually denoted by \(\mathcal {L}(\mathcal {A})\) and its complement \(\mathcal {L}^{{\scriptscriptstyle \ominus }}\) by \(\mathcal {L}(\mathcal {A})^{\scriptscriptstyle \mathrm {C}}\). In this case, the concept of optimal dcDFA coincide with the concept of minimal DFA for \(\mathcal {L}^{{\scriptscriptstyle \oplus }}\).
Note that if a promise problem \(\langle {}\mathcal {L}^{{\scriptscriptstyle \oplus }},\mathcal {L}^{{\scriptscriptstyle \ominus }}{}\rangle \) can be solved by a dcDFA \(\mathcal {A}\) with n states, it can also be solved by a standard dcDFA \(\mathcal {A}'\) with n states, none of which is neutral: any neutral state could be set as accepting or rejecting, without affecting \(\langle {}\mathcal {L}^{{\scriptscriptstyle \oplus }},\mathcal {L}^{{\scriptscriptstyle \ominus }}{}\rangle \). This leaves us some degree of freedom, leading to different machines. Namely, if \(\mathcal {A}\) uses k neutral reachable states, we obtain \(2^k\) different automata solving the same promise problem, all of them of size at most n. These automata do not agree in acceptance/rejection on inputs not belonging to \(\mathcal {L}^{{\scriptscriptstyle \oplus }}\cup \mathcal {L}^{{\scriptscriptstyle \ominus }}\). Thus, the given dcDFA can also be viewed as a more concise template representing these \(2^k\) DFAs.
This is related to the following separation problem: given DFAs \(\mathcal {A}^{{\scriptscriptstyle \oplus }}\) and \(\mathcal {A}^{{\scriptscriptstyle \ominus }}\) for two disjoint languages \(\mathcal {L}^{{\scriptscriptstyle \oplus }}\) and \(\mathcal {L}^{{\scriptscriptstyle \ominus }}\), find a DFA \(\mathcal {A}'\) with minimal number of states, such that \(\mathcal {L}^{{\scriptscriptstyle \oplus }}\subseteq \mathcal {L}(\mathcal {A}')\) and \(\mathcal {L}^{{\scriptscriptstyle \ominus }}\subseteq \mathcal {L}(\mathcal {A}')^{\scriptscriptstyle \mathrm {C}}\). In general, this problem is NP-complete [13, Thm. 9]. This was shown by a simple application of NP-completeness for a slightly different computational model (in which some transitions f(q, a) may be undefined), presented in [14, 15].
The next theorem will play the same role for don’t care automata as the fooling set technique [2] for standard automata:
Theorem 1
Let \(\mathcal {L}^{{\scriptscriptstyle \oplus }}\), \(\mathcal {L}^{{\scriptscriptstyle \ominus }}\) be two disjoint languages over the same alphabet \(\varSigma \). Suppose there exist m-tuple \(X= \langle {}x_{e}{}\rangle _{e=1}^{m}\) and \({m\atopwithdelims ()2}\)-tuple \(Y= \langle {}y_{e,\tilde{e}}{}\rangle _{e,\tilde{e}=1,\,e<\tilde{e}}^{m}\) consisting of strings in \(\varSigma ^{*}\) such that, for each \(e,\tilde{e}\in \{1,\ldots ,m\}\), \(e<\tilde{e}\),
- (I):
-
both \(x_{e}{\cdot }y_{e,\tilde{e}}\) and \(x_{\tilde{e}}{\cdot }y_{e,\tilde{e}}\) are in \(\mathcal {L}^{{\scriptscriptstyle \oplus }}\cup \mathcal {L}^{{\scriptscriptstyle \ominus }}\),
- (II):
-
\(x_{e}{\cdot }y_{e,\tilde{e}}\in \mathcal {L}^{{\scriptscriptstyle \oplus }}\) if and only if \(x_{\tilde{e}}{\cdot }y_{e,\tilde{e}}\in \mathcal {L}^{{\scriptscriptstyle \ominus }}\).
Then any dcDFA solving the promise problem \(\langle {}\mathcal {L}^{{\scriptscriptstyle \oplus }},\mathcal {L}^{{\scriptscriptstyle \ominus }}{}\rangle \) uses at least m states.
Proof
Let \(\mathcal {A}=\langle {}Q,\varSigma , q_{\scriptscriptstyle \mathrm {I}}, f, F^{{\scriptscriptstyle \oplus }},F^{{\scriptscriptstyle \ominus }}{}\rangle \), satisfying \(F^{{\scriptscriptstyle \oplus }}\cap F^{{\scriptscriptstyle \ominus }}=\) Ø, be an arbitrary dcDFA for solving \(\langle {}\mathcal {L}^{{\scriptscriptstyle \oplus }},\mathcal {L}^{{\scriptscriptstyle \ominus }}{}\rangle \). Suppose that \(\mathcal {A}\) uses less than m states.
Now, for the given m-tuple \(X= \langle {}x_{1},x_{2},\ldots ,x_{m}{}\rangle \), let \(q_{1},q_{2},\ldots ,q_{m}\) denote the respective states reached by \(\mathcal {A}\) on these inputs, that is, \(q_{\scriptscriptstyle \mathrm {I}}\mathop {\longrightarrow }\limits ^{x_e}q_{e}\), for each \(e\in \{1,\ldots ,m\}\). But then, using a pigeonhole argument, some state must be repeated, i.e., we have \(q_{e}=q_{\tilde{e}}\), for some \(1\le e<\tilde{e}\le m\). This implies that the computations on inputs \(x_{e}{\cdot }y_{e,\tilde{e}}\) and \(x_{\tilde{e}}{\cdot }y_{e,\tilde{e}}\) must end in the same state, denoted here by r. That is, we have the following computations: \(q_{\scriptscriptstyle \mathrm {I}}\mathop {\longrightarrow }\limits ^{x_e}q_{e}\mathop {-\!\!\!-\!\!\!-\!\!\!\longrightarrow }\limits ^{y_{e,\tilde{e}}}r\) and \(q_{\scriptscriptstyle \mathrm {I}}\mathop {\longrightarrow }\limits ^{x_{\tilde{e}}}q_{\tilde{e}}=q_{e}\mathop {-\!\!\!-\!\!\!-\!\!\!\longrightarrow }\limits ^{y_{e,\tilde{e}}}r\). There are now two possibilities:
First, let \(x_{e}{\cdot }y_{e,\tilde{e}}\in \mathcal {L}^{{\scriptscriptstyle \oplus }}\). Then, using (II), we also have that \(x_{\tilde{e}}{\cdot }y_{e,\tilde{e}}\in \mathcal {L}^{{\scriptscriptstyle \ominus }}\). This implies that the computation on \(x_{e}{\cdot }y_{e,\tilde{e}}\) ends in \(r\in F^{{\scriptscriptstyle \oplus }}\) and, at the same time, the computation on \(x_{\tilde{e}}{\cdot }y_{e,\tilde{e}}\) in \(r\in F^{{\scriptscriptstyle \ominus }}\). But this is a contradiction: \(F^{{\scriptscriptstyle \oplus }}\cap F^{{\scriptscriptstyle \ominus }}=\) Ø.
Second, let \(x_{e}{\cdot }y_{e,\tilde{e}}\notin \mathcal {L}^{{\scriptscriptstyle \oplus }}\). Then, using (II), we have \(x_{\tilde{e}}{\cdot }y_{e,\tilde{e}}\notin \mathcal {L}^{{\scriptscriptstyle \ominus }}\). Now, by (I), we see that \(x_{e}{\cdot }y_{e,\tilde{e}}\in \mathcal {L}^{{\scriptscriptstyle \ominus }}\) and \(x_{\tilde{e}}{\cdot }y_{e,\tilde{e}}\in \mathcal {L}^{{\scriptscriptstyle \oplus }}\). This leads to the same kind of contradiction as above, swapping the roles of \(x_{e}{\cdot }y_{e,\tilde{e}}\) and \(x_{\tilde{e}}{\cdot }y_{e,\tilde{e}}\). \(\square \)
Note that, apart from providing the lower bound on the number of states, the statement of the above theorem does not deal with states in any dcDFA solving \(\langle {}\mathcal {L}^{{\scriptscriptstyle \oplus }},\mathcal {L}^{{\scriptscriptstyle \ominus }}{}\rangle \) but, rather, with strings in \(\varSigma ^{*}\). However, if there does exist a dcDFA \(\mathcal {A}\) with m states for \(\langle {}\mathcal {L}^{{\scriptscriptstyle \oplus }},\mathcal {L}^{{\scriptscriptstyle \ominus }}{}\rangle \), that is, if the lower bound provided by Theorem 1 matches the upper bound, then one can establish a one-to-one correspondence between states in \(\mathcal {A}\) and strings in \(X= \langle {}x_{1},x_{2},\ldots ,x_{m}{}\rangle \), with \(Y= \langle {}y_{e,\tilde{e}}{}\rangle _{e,\tilde{e}=1,\,e<\tilde{e}}^{m}\) giving the pairwise distinguishability of states in \(\mathcal {A}\). The standard fooling set technique (for DFAs) uses \(y_{e,{\tilde{e}_1}}= y_{e,{\tilde{e}_2}}= \ldots ,\) with the condition (I) satisfied automatically.
3 Upper and Lower Bounds
We are now going to show that \((\Vert {\varSigma }\Vert -1){\cdot }n\) states are sufficient but n states necessary for a dcDFA that decides whether the given binary input is in \(h(\mathcal {L})\) or in \(h(\mathcal {L}^{\scriptscriptstyle \mathrm {C}})\), that is, for a dcDFA solving \(\langle {}h(\mathcal {L}),h(\mathcal {L}^{\scriptscriptstyle \mathrm {C}}){}\rangle \), the binary promise-problem version of \(\mathcal {L}\). Here \(h\,{:}\,\varSigma ^{*}{\rightarrow }\{0,1\}^{*}\) is a maximal prefix code and \(\mathcal {A}\) is an optimal DFA with n states, recognizing a language \(\mathcal {L}\) over a non-unary alphabet \(\varSigma \).
For the given code h, let us begin by fixing some additional notation for the images of letters and proper prefixes:
Recall that h is a maximal prefix code. Thus, P includes the empty string \(\varepsilon \), but no string from H. Next, if \(\pi \in P\), then \(\pi {\cdot }0,\pi {\cdot }1\in P\cup H\) (see also Fig. 1). The next two theorems provide the upper and lower bounds.
Theorem 2
Let \(h\,{:}\,\varSigma ^{*}{\rightarrow }\{0,1\}^{*}\) be a maximal binary prefix code and let \(\mathcal {L}\) be a language over the non-unary alphabet \(\varSigma \). Then, if \(\mathcal {L}\) can be recognized by a DFA \(\mathcal {A}=\langle {}Q,\varSigma , q_{\scriptscriptstyle \mathrm {I}}, f,F{}\rangle \) with n states, the binary promise problem \(\langle {}h(\mathcal {L}),h(\mathcal {L}^{\scriptscriptstyle \mathrm {C}}){}\rangle \) can be solved by a dcDFA \(\mathcal {A}'\) with at most \(n'\le (\Vert {\varSigma }\Vert -1){\cdot }n\) states.
Proof
(a sketch). The idea of the construction is to remember \(q\in Q\), the current state of \(\mathcal {A}\) at the moment when \(\mathcal {A}\) has read \(a_1{\cdots }a_{\ell }\in \varSigma ^{*}\), and \(\pi \in P\), the prefix of a code for the next input symbol \(a_{\ell +1}\), not completed yet. This leads to \(Q'= Q{\times }P\), with \(q'_{\scriptscriptstyle \mathrm {I}}= \langle {}q_{\scriptscriptstyle \mathrm {I}},\varepsilon {}\rangle \), \(F^{{\scriptscriptstyle \oplus }}= F{\times }\{\varepsilon \}\), and \(F^{{\scriptscriptstyle \ominus }}= (Q{\setminus }F){\times }\{\varepsilon \}\). Transitions in \(\mathcal {A}'\) are defined as follows, for each \(q\in Q\), \(\pi \in P\), and \(b\in \{0,1\}\):
- (I):
-
\(f'(\langle {}q,\pi {}\rangle ,b)= \langle {}q,\pi b{}\rangle \), provided that \(\pi {\cdot }b\in P\),
- (II):
-
\(f'(\langle {}q,\pi {}\rangle ,b)= \langle {}f(q,a),\varepsilon {}\rangle \), provided that, for some \(a\in \varSigma \), \(\pi {\cdot }b= h(a)\in H\).
\(\square \)
The above construction can be updated so that it works for prefix codes that are not maximal. Then \(\pi \in P\) does not imply that \(\pi {\cdot }b\) is in \(P\cup H\). In such cases, we can define \(f'(\langle {}q,\pi {}\rangle ,b)= q'_{\scriptscriptstyle \mathrm {E}}\), where \(q'_{\scriptscriptstyle \mathrm {E}}\) is an additional trap state, in which we scan the rest of the input—the input can no longer be extended to a string in \(h(\varSigma _1^{*})= h(H^{*})\). However, for such codes, \(\Vert {P}\Vert \) is not bounded by \(\Vert {\varSigma }\Vert -1\).
Theorem 3
Let \(h\,{:}\,\varSigma ^{*}{\rightarrow }\{0,1\}^{*}\) be a binary prefix code (not necessarily maximal) and let \(\mathcal {L}\) be a language over the alphabet \(\varSigma \) (not necessarily non-unary). Then, if the binary promise problem \(\langle {}h(\mathcal {L}),h(\mathcal {L}^{\scriptscriptstyle \mathrm {C}}){}\rangle \) can be solved by a dcDFA \(\mathcal {A}'= \langle {}Q',\{0,1\}, q'_{\scriptscriptstyle \mathrm {I}}, f', F^{{\scriptscriptstyle \oplus }},F^{{\scriptscriptstyle \ominus }}{}\rangle \) with \(n'\) states, the language \(\mathcal {L}\) can be recognized by a standard DFA \(\mathcal {A}= \langle {}Q,\varSigma , q_{\scriptscriptstyle \mathrm {I}}, f,F{}\rangle \) with at most \(n\le n'\) states.
Proof
If, for some \(q,q'\in Q'\) and \(a\in \varSigma \), the original \(\mathcal {A}'\) has a path beginning in q, ending in \(q'\), and reading from the input the string \(h(a)\in H\) (introduced by (1)), we shall add the transition \(q\mathop {\longrightarrow }\limits ^{a}q'\) to \(\mathcal {A}\). Recall that \(\mathcal {A}'\) is deterministic and \(h(a)= b_1{\cdots }b_m\) is unique for each \(a\in \varSigma \). But then \(q'= {f'}^{*}(q,h(a))\) is also unique for each \(q\in Q'\) and each \(a\in \varSigma \), and hence \(\mathcal {A}\) will be deterministic.
In addition, we can restrict the set of finite control states in \(\mathcal {A}\) to states that can be reached from \(q'_{\scriptscriptstyle \mathrm {I}}\) by reading some \(\beta \in h(\varSigma ^{*})= H^{*}\), that is, to
Thus, \(Q= R\), \(q_{\scriptscriptstyle \mathrm {I}}= q'_{\scriptscriptstyle \mathrm {I}}\), and \(F= R\cap F^{{\scriptscriptstyle \oplus }}\). Clearly, \(R\subseteq F^{{\scriptscriptstyle \oplus }}\cup F^{{\scriptscriptstyle \ominus }}\), since no \(\mathcal {A}'\) solving \(\langle {}h(\mathcal {L}),h(\mathcal {L}^{\scriptscriptstyle \mathrm {C}}){}\rangle \) halts in a neutral state on any \(h(\alpha )\in h(\varSigma ^{*})\). Finally, let
-
\(f(q,a)= {f'}^{*}(q,h(a))\), for each \(q\in R\) and each \(a\in \varSigma \).
It is easy to see, for each \(q,q'\in R\) and each \(a\in \varSigma \), that \(\mathcal {A}\) has a transition from q to \(q'\) reading the symbol \(a\in \varSigma \) if and only if \(\mathcal {A}'\) has a path connecting the same states and reading the string \(h(a)\in H\). By a straightforward induction on the length of \(\alpha \in \varSigma ^{*}\), we have \(q\mathop {\longrightarrow }\limits ^{\alpha }q'\) in \(\mathcal {A}\) if and only if \(q\mathop {-\!\!\!-\!\!\!-\!\!\!\longrightarrow }\limits ^{h(\alpha )}q'\) in \(\mathcal {A}'\).
Thus, if \(\alpha \in \mathcal {L}\), then \(h(\alpha )\in h(\mathcal {L})\) must be accepted by dcDFA \(\mathcal {A}'\), which gives \(q'_{\scriptscriptstyle \mathrm {I}}\mathop {-\!\!\!-\!\!\!-\!\!\!\longrightarrow }\limits ^{h(\alpha )}q'\) for some \(q'\in F^{{\scriptscriptstyle \oplus }}\). Moreover, since \(h(\alpha )\in H^{*}\), \(q'\) must also belong to R. But then, for \(\mathcal {A}\), we have \(q_{\scriptscriptstyle \mathrm {I}}= q'_{\scriptscriptstyle \mathrm {I}}\mathop {\longrightarrow }\limits ^{\alpha }q'\) with \(q'\in R\cap F^{{\scriptscriptstyle \oplus }}= F\), and hence \(\alpha \) is accepted by \(\mathcal {A}\). Similarly, if \(\alpha \notin \mathcal {L}\), then \(\mathcal {A}'\) has a path \(q'_{\scriptscriptstyle \mathrm {I}}\mathop {-\!\!\!-\!\!\!-\!\!\!\longrightarrow }\limits ^{h(\alpha )}q'\) ending in \(q'\in R\cap F^{{\scriptscriptstyle \ominus }}\). For \(\mathcal {A}\), this gives \(q_{\scriptscriptstyle \mathrm {I}}= q'_{\scriptscriptstyle \mathrm {I}}\mathop {\longrightarrow }\limits ^{\alpha }q'\) ending in \(q'\in R{\setminus }F^{{\scriptscriptstyle \oplus }}= R{\setminus }(R\cap F^{{\scriptscriptstyle \oplus }})= Q{\setminus }F\), and hence \(\alpha \) is rejected by \(\mathcal {A}\).
Summing up, \(\mathcal {A}\) is a standard DFA recognizing \(\mathcal {L}\), with \(n\le n'\) states. \(\square \)
By combining Theorems 2 and 3, we get:
Theorem 4
Let \(h\,{:}\,\varSigma ^{*}{\rightarrow }\{0,1\}^{*}\) be a maximal binary prefix code and let \(\mathcal {L}\) be a language over the non-unary alphabet \(\varSigma \). Then, if the optimal DFA \(\mathcal {A}\) recognizing \(\mathcal {L}\) uses n states, any optimal dcDFA \(\mathcal {A}'\) solving the binary promise problem \(\langle {}h(\mathcal {L}),h(\mathcal {L}^{\scriptscriptstyle \mathrm {C}}){}\rangle \) uses at least n states and at most \((\Vert {\varSigma }\Vert -1){\cdot }n\) states.
Proof
The upper bound is a direct consequence of Theorem 2: this theorem does not necessarily produce a dcDFA that is optimal, however, it does guarantee \((\Vert {\varSigma }\Vert -1){\cdot }n\) states for \(\mathcal {A}'\). The lower bound follows from Theorem 3: suppose that \(\langle {}h(\mathcal {L}),h(\mathcal {L}^{\scriptscriptstyle \mathrm {C}}){}\rangle \) can be solved by \(\mathcal {A}'\) with \(n'<n\) states. But then, by this theorem, we could obtain a standard DFA recognizing \(\mathcal {L}\) with fewer states than n, which is a contradiction, since \(\mathcal {A}\) is optimal. \(\square \)
4 The Hierarchy
We are now ready to establish the complete state hierarchy and provide a witness language for each N between n and \((\Vert {\varSigma }\Vert -1){\cdot }n\). First, for the given
define a maximal binary prefix code \(h_{{\scriptscriptstyle \varSigma }}\,{:}\,\varSigma ^{*}{\rightarrow }\{0,1\}^{*}\) as follows:
Second, for the given \(\varSigma \) and any given
define a DFA \(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k}= \langle {}Q,\varSigma , q_{\scriptscriptstyle \mathrm {I}}, f,F{}\rangle \) with the state set \(Q= \{0,\ldots ,n-1\}\), \(q_{\scriptscriptstyle \mathrm {I}}=0\), \(F=\{0\}\), and the following transitions:
There are two special cases. The first one is \(g= n-1\), with no states \(i\in Q\) satisfying \(i>g\). Moreover, this case differs in one value, namely, in \(f(g,a_d)\):
The second special case is \(g= n\), with no states \(i\in Q\) satisfying \(i>g\) or \(i=g\). Thus, the condition \(i<g\) is satisfied automatically for each \(i\in Q\), which reduces (5)–(6) above to \(f(i,a)= (i+1){\,\bmod \,}n\) for each \(i\in Q\) and each \(a\in \varSigma \).
Examples of \(h_{{\scriptscriptstyle \varSigma }}\), \(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k}\), and subsequent \(\mathcal {A}'_{{\scriptscriptstyle \varSigma },n,g,k}\) are displayed in Fig. 1 (left), Fig. 2 (bottom), and Fig. 2 (top), respectively, for \(d=5\), \(n=7\), \(g=3\), and \(k=2\). The special case of \(g=n-1\) is illustrated by Fig. 3.
Examples of a DFA \(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k}\) (bottom) and the corresponding dcDFA \(\mathcal {A}'_{{\scriptscriptstyle \varSigma },n,g,k}\) (top), if \(\varSigma = \{a_0,\ldots ,a_5\}\), \(d=5\), \(n=7\), \(g=3\), and \(k=2\). Accepting states are tagged by “\(+\)”, rejecting states by “−”, and neutral don’t care states by no sign. To simplify notation for \(\mathcal {A}'_{{\scriptscriptstyle \varSigma },n,g,k}\), the ordered pairs “\(\langle {}i,j{}\rangle \)” are displayed here in the form “ij”.
Finally, for the given \(\varSigma ,n,g,k\) satisfying (4), consider a dcDFA \(\mathcal {A}'_{{\scriptscriptstyle \varSigma },n,g,k}= \langle {}Q',\{0,1\}, q'_{\scriptscriptstyle \mathrm {I}}, f', F^{{\scriptscriptstyle \oplus }},F^{{\scriptscriptstyle \ominus }}{}\rangle \), not constructed for \(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k}\) by the use of Theorem 2, but defined as follows. First, let \(Q'= Q_0 \cup \ldots \cup Q_{n-1}\), where
There are no sections \(Q_i\) with \(i>g\), if \(g= n-1\), and no section \(Q_g\), if \(g= n\), in accordance with the two special cases for \(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k}\).
Now, let \(q'_{\scriptscriptstyle \mathrm {I}}=\langle {}0,0{}\rangle \), \(F^{{\scriptscriptstyle \oplus }}= \{\langle {}0,0{}\rangle \}\), and \(F^{{\scriptscriptstyle \ominus }}= \{\langle {}1,0{}\rangle ,\langle {}2,0{}\rangle ,\ldots ,\langle {}n-1,0{}\rangle \}\). Transitions are defined as follows:
Note that also here the case of \(g=n-1\) is different. (See also Fig. 3).
Examples of \(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k}\) and \(\mathcal {A}'_{{\scriptscriptstyle \varSigma },n,g,k}\) for the special case of \(g= n-1\), namely, for \(\varSigma = \{a_0,\ldots ,a_5\}\), \(d=5\), \(n=7\), \(g= n-1= 6\), and \(k=2\) (graph rotated, so that the state \(g=n-1\) is not displayed at the right end).
Lemma 1
Let \(h_{{\scriptscriptstyle \varSigma }}\), \(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k}\), and \(\mathcal {A}'_{{\scriptscriptstyle \varSigma },n,g,k}\) be the binary code, DFA, and dcDFA defined above. Then \(\mathcal {A}'_{{\scriptscriptstyle \varSigma },n,g,k}\) solves the binary promise problem \(\langle {}h_{{\scriptscriptstyle \varSigma }}(\mathcal {L}(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k})), h_{{\scriptscriptstyle \varSigma }}(\mathcal {L}(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k})^{\scriptscriptstyle \mathrm {C}}){}\rangle \).
Proof
First, it is not too hard to see that if \(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k}\) has a transition \(i\mathop {\longrightarrow }\limits ^{a}i'\), then \(\mathcal {A}'_{{\scriptscriptstyle \varSigma },n,g,k}\) has the corresponding computation path \(\langle {}i,0{}\rangle \mathop {-\!\!\!-\!\!\!-\!\!\!\longrightarrow }\limits ^{h_{{\scriptscriptstyle \varSigma }}(a)}\langle {}i',0{}\rangle \). This can be shown by consulting (3) and by comparing all transitions presented by (5), (6), and (8), for each \(i\in Q\) and each \(a\in \varSigma \):
-
\(f(i,a)= (i+1){\,\bmod \,}n\), if \(i<g\) and \(a\in \varSigma \) (which covers the case of \(g=n\)):
-
\(\langle {}i,0{}\rangle \mathop {\longrightarrow }\limits ^{0^j} \langle {}i,j{}\rangle \mathop {\longrightarrow }\limits ^{1} \langle {}(i+1){\,\bmod \,}n,0{}\rangle \), for \(h_{{\scriptscriptstyle \varSigma }}(a)=0^j1\), \(j\in \{0,\ldots ,d-1\}\),
-
\(\langle {}i,0{}\rangle \mathop {-\!\!\!-\!\!\!-\!\!\!\longrightarrow }\limits ^{0^{d-1}} \langle {}i,d-1{}\rangle \mathop {\longrightarrow }\limits ^{0} \langle {}(i+1){\,\bmod \,}n,0{}\rangle \), for \(h_{{\scriptscriptstyle \varSigma }}(a)=0^d\).
-
-
\(f(g,a)= (g+1){\,\bmod \,}n\), if \(g\le n-2\) and \(a\in \{a_0,\ldots ,a_k\}\cup \{a_d\}\):
-
\(\langle {}g,0{}\rangle \mathop {\longrightarrow }\limits ^{0^j} \langle {}g,j{}\rangle \mathop {\longrightarrow }\limits ^{1} \langle {}(g+1){\,\bmod \,}n,0{}\rangle \), for \(h_{{\scriptscriptstyle \varSigma }}(a)=0^j1\), \(j\in \{0,\ldots ,k\}\),
-
\(\langle {}g,0{}\rangle \mathop {\longrightarrow }\limits ^{0^k} \langle {}g,k{}\rangle \mathop {\longrightarrow }\limits ^{0} \langle {}g+1,0{}\rangle \mathop {-\!\!\!-\!\!\!-\!\!\!\longrightarrow }\limits ^{0^{d-k-1}} \langle {}g+1,0{}\rangle = \langle {}(g+1){\,\bmod \,}n,0{}\rangle \), for \(h_{{\scriptscriptstyle \varSigma }}(a)=0^d\).
-
-
\(f(g,a)= (g+2){\,\bmod \,}n\), if \(g\le n-2\) and \(a\in \{a_{k+1},\ldots ,a_{d-1}\}\):
-
\(\langle {}g,0{}\rangle \mathop {\longrightarrow }\limits ^{0^k} \langle {}g,k{}\rangle \mathop {\longrightarrow }\limits ^{0} \langle {}g+1,0{}\rangle \mathop {-\!\!\!-\!\!\!-\!\!\!\longrightarrow }\limits ^{0^{j-k-1}} \langle {}g+1,0{}\rangle \mathop {\longrightarrow }\limits ^{1} \langle {}(g+2){\,\bmod \,}n,0{}\rangle \), for \(h_{{\scriptscriptstyle \varSigma }}(a)=0^j1\), \(j\in \{k+1,\ldots ,d-1\}\).
-
-
\(f(i,a)= (i+1){\,\bmod \,}n\), if \(i>g\) and \(a\in \varSigma {\setminus }\{a_d\}\):
-
\(\langle {}i,0{}\rangle \mathop {\longrightarrow }\limits ^{0^j} \langle {}i,0{}\rangle \mathop {\longrightarrow }\limits ^{1} \langle {}(i+1){\,\bmod \,}n,0{}\rangle \), for \(h_{{\scriptscriptstyle \varSigma }}(a)=0^j1\), \(j\in \{0,\ldots ,d-1\}\).
-
-
\(f(i,a)= i\), if \(i>g\) and \(a=a_d\):
-
\(\langle {}i,0{}\rangle \mathop {\longrightarrow }\limits ^{0^d} \langle {}i,0{}\rangle \), for \(h_{{\scriptscriptstyle \varSigma }}(a)=0^d\).
-
The same can be seen for different transitions in the case of \(g=n-1\):
-
\(f(g,a)= (g+1){\,\bmod \,}n = 0\), if \(g= n-1\) and \(a\in \{a_0,\ldots ,a_k\}\):
-
\(\langle {}g,0{}\rangle \mathop {\longrightarrow }\limits ^{0^j} \langle {}g,j{}\rangle \mathop {\longrightarrow }\limits ^{1} \langle {}(g+1){\,\bmod \,}n,0{}\rangle \), for \(h_{{\scriptscriptstyle \varSigma }}(a)=0^j1\), \(j\in \{0,\ldots ,k\}\).
-
-
\(f(g,a)= (g+2){\,\bmod \,}n = 1\), if \(g= n-1\) and \(a\in \{a_{k+1},\ldots ,a_d\}\):
-
\(\langle {}g,0{}\rangle \mathop {\longrightarrow }\limits ^{0^k} \langle {}g,k{}\rangle \mathop {\longrightarrow }\limits ^{0} \langle {}0,k+1{}\rangle \mathop {-\!\!\!-\!\!\!-\!\!\!\longrightarrow }\limits ^{0^{j-k-1}} \langle {}0,j{}\rangle \mathop {\longrightarrow }\limits ^{1} \langle {}1,0{}\rangle = \langle {}(g+2){\,\bmod \,}n,0{}\rangle \), for \(h_{{\scriptscriptstyle \varSigma }}(a)=0^j1\), \(j\in \{k+1,\ldots ,d-1\}\),
-
\(\langle {}g,0{}\rangle \mathop {\longrightarrow }\limits ^{0^k} \langle {}g,k{}\rangle \mathop {\longrightarrow }\limits ^{0} \langle {}0,k+1{}\rangle \mathop {-\!\!\!-\!\!\!-\!\!\!\longrightarrow }\limits ^{0^{d-k-2}} \langle {}0,d-1{}\rangle \mathop {\longrightarrow }\limits ^{0} \langle {}1,0{}\rangle = \) \(\langle {}(g+2){\,\bmod \,}n,0{}\rangle \), for \(h_{{\scriptscriptstyle \varSigma }}(a)=0^d\).
-
Now, by induction on the length of \(\alpha = a_{i_1}\!{\cdots }a_{i_{\ell }}\in \varSigma ^{*}\), we easily obtain that the computation path \(i\mathop {\longrightarrow }\limits ^{\alpha }i'\) in \(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k}\) implies the existence of the corresponding path \(\langle {}i,0{}\rangle \mathop {-\!\!\!-\!\!\!-\!\!\!\longrightarrow }\limits ^{h_{{\scriptscriptstyle \varSigma }}(\alpha )} \langle {}i',0{}\rangle \) for \(\mathcal {A}'_{{\scriptscriptstyle \varSigma },n,g,k}\), for each \(i,i'\in Q\) and each \(\alpha \in \varSigma \).
Thus, if \(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k}\) has a path \(q_{\scriptscriptstyle \mathrm {I}}= 0\mathop {\longrightarrow }\limits ^{\alpha }0\in F\), then \(\mathcal {A}'_{{\scriptscriptstyle \varSigma },n,g,k}\) has the corresponding path \(q'_{\scriptscriptstyle \mathrm {I}}= \langle {}0,0{}\rangle \mathop {-\!\!\!-\!\!\!-\!\!\!\longrightarrow }\limits ^{h_{{\scriptscriptstyle \varSigma }}(\alpha )} \langle {}0,0{}\rangle \in F^{{\scriptscriptstyle \oplus }}\), and hence \(h_{{\scriptscriptstyle \varSigma }}(\alpha )\) is accepted by \(\mathcal {A}'_{{\scriptscriptstyle \varSigma },n,g,k}\), if \(\alpha \in \mathcal {L}(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k})\). On the other hand, if this path in \(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k}\) halts in some \(i'\ne 0\), that is, in some \(i'\in Q{\setminus }F\), the corresponding path in \(\mathcal {A}'_{{\scriptscriptstyle \varSigma },n,g,k}\) will halt in \(\langle {}i',0{}\rangle \in F^{{\scriptscriptstyle \ominus }}\), and hence \(h_{{\scriptscriptstyle \varSigma }}(\alpha )\) is rejected by \(\mathcal {A}'_{{\scriptscriptstyle \varSigma },n,g,k}\), if \(\alpha \in \mathcal {L}(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k})^{\scriptscriptstyle \mathrm {C}}\).
Therefore, \(\mathcal {A}'_{{\scriptscriptstyle \varSigma },n,g,k}\) is a valid dcDFA for solving the binary promise problem \(\langle {}h_{{\scriptscriptstyle \varSigma }}(\mathcal {L}(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k})), \,h_{{\scriptscriptstyle \varSigma }}(\mathcal {L}(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k})^{\scriptscriptstyle \mathrm {C}}){}\rangle \). \(\square \)
\(\mathcal {A}'_{{\scriptscriptstyle \varSigma },n,g,k}\) uses fewer states than dcDFA obtained by the use of Theorem 2, but it may accept/reject some binary inputs that are not images of any \(\alpha \in \varSigma ^{*}\). That is, it does not necessarily halt in a neutral state on such inputs.
Lemma 2
Let \(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k}\) be the DFA defined above. Then \(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k}\) is optimal and uses exactly n states.
Proof
Using (5) and (6), we see that \(f(i,a_0)= (i+1){\,\bmod \,}n\), for each \(i\in Q= \{0,\ldots ,n-1\}\), not excluding the special cases of \(g= n-1\) or \(g= n\). Since \(q_{\scriptscriptstyle \mathrm {I}}=0\) and \(F=\{0\}\), \(a_0^e\in \mathcal {L}(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k})\) if and only if e is an integer multiple of n.
This implies that \(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k}\) cannot be replaced by an equivalent DFA using fewer states: such DFA would accept \(a_0^n\) by a computation path \(r_0\mathop {\longrightarrow }\limits ^{a_0}{} r_1\mathop {\longrightarrow }\limits ^{a_0}{} r_2\mathop {\longrightarrow }\limits ^{a_0}{} \cdots {} \mathop {\longrightarrow }\limits ^{a_0}{} r_n\) along which some state would be repeated, which gives a valid accepting computation path for some \(a_0^e\) with \(0<e<n\), a contradiction. \(\square \)
Lemma 3
Let \(h_{{\scriptscriptstyle \varSigma }}\), \(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k}\), and \(\mathcal {A}'_{{\scriptscriptstyle \varSigma },n,g,k}\) be the binary code, DFA, and dcDFA defined above. Then \(\mathcal {A}'_{{\scriptscriptstyle \varSigma },n,g,k}\) is optimal for solving the binary promise problem \(\langle {}h_{{\scriptscriptstyle \varSigma }}(\mathcal {L}(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k})), h_{{\scriptscriptstyle \varSigma }}(\mathcal {L}(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k})^{\scriptscriptstyle \mathrm {C}}){}\rangle \) and uses exactly \(m= (\Vert {\varSigma }\Vert -1){\cdot }g+ (k+1)+ (n-g-1)\) states, if \(g\le n-1\), but exactly \(m= (\Vert {\varSigma }\Vert -1){\cdot }n\) states, if \(g=n\).
Proof
By Lemma 1, \(\mathcal {A}'_{{\scriptscriptstyle \varSigma },n,g,k}\) solves the given promise problem and, by (7), it uses \(m= d{\cdot }g+ (k+1)+ (n-g-1)\) states, if \(g\le n-1\). For \(g=n\), all sections \(Q_i\) are of equal size d in (7), which gives \(m= d{\cdot }n\). Since \(d= \Vert {\varSigma }\Vert -1\), the upper bound for \(m= \Vert {Q'}\Vert \) follows.
We only have to show that this bound cannot be reduced. Let \(\langle {}i,j{}\rangle ,\langle {}\tilde{\imath },\tilde{\jmath }{}\rangle \) represent two arbitrary—but different—states in \(Q'\), that is, either \(i<\tilde{\imath }\), or \(i=\tilde{\imath }\) but \(j<\tilde{\jmath }\). For \(i=\tilde{\imath }\) we have two subcases, depending on whether \(i<g\) or \(i=g\). (There are no pairs of different states with \(i=\tilde{\imath }>g\); this condition implies \(j=\tilde{\jmath }=0\), by (7). We do not consider \(i>\tilde{\imath }\), or \(i=\tilde{\imath }\) with \(j>\tilde{\jmath }\) either—the roles of \(\langle {}i,j{}\rangle ,\langle {}\tilde{\imath },\tilde{\jmath }{}\rangle \) can be swapped). Let us now define the following binary strings:
It can be seen from (8) that each state \(\langle {}i,j{}\rangle \in Q'\) is reached by reading \(x_{\scriptscriptstyle \langle {}i,j{}\rangle }\) from the input: \(q'_{\scriptscriptstyle \mathrm {I}}= \langle {}0,0{}\rangle \mathop {\longrightarrow }\limits ^{1^i} \langle {}i{\,\bmod \,}n,0{}\rangle = \langle {}i,0{}\rangle \mathop {\longrightarrow }\limits ^{0^j} \langle {}i,j{}\rangle \).
If \(g=n-1\), we get \(y_{\scriptscriptstyle \langle {}g,j{}\rangle \langle {}g,\tilde{\jmath }{}\rangle }= 0^{k+1-\tilde{\jmath }}1\), if \(g=n\), we do not define \(y_{\scriptscriptstyle \langle {}g,j{}\rangle \langle {}g,\tilde{\jmath }{}\rangle }\).
We are now going to show that (i) both \(x_{\scriptscriptstyle \langle {}i,j{}\rangle }{\cdot } y_{\scriptscriptstyle \langle {}i,j{}\rangle \langle {}\tilde{\imath },\tilde{\jmath }{}\rangle }\) and \(x_{\scriptscriptstyle \langle {}\tilde{\imath },\tilde{\jmath }{}\rangle }{\cdot } y_{\scriptscriptstyle \langle {}i,j{}\rangle \langle {}\tilde{\imath },\tilde{\jmath }{}\rangle }\) are valid binary images of some strings in \(\varSigma ^{*}\), i.e., both of them are in \(h_{{\scriptscriptstyle \varSigma }}(\varSigma ^{*})\), and that (ii) the computation of \(\mathcal {A}'_{{\scriptscriptstyle \varSigma },n,g,k}\) on \(x_{\scriptscriptstyle \langle {}i,j{}\rangle }{\cdot }y_{\scriptscriptstyle \langle {}i,j{}\rangle \langle {}\tilde{\imath },\tilde{\jmath }{}\rangle }\) starts in \(q'_{\scriptscriptstyle \mathrm {I}}= \langle {}0,0{}\rangle \) and ends in \(\langle {}0,0{}\rangle \in F^{{\scriptscriptstyle \oplus }}\), while the computation on \(x_{\scriptscriptstyle \langle {}\tilde{\imath },\tilde{\jmath }{}\rangle }{\cdot }y_{\scriptscriptstyle \langle {}i,j{}\rangle \langle {}\tilde{\imath },\tilde{\jmath }{}\rangle }\) starts in \(q'_{\scriptscriptstyle \mathrm {I}}= \langle {}0,0{}\rangle \) and ends in some \(\langle {}i',0{}\rangle \in F^{{\scriptscriptstyle \ominus }}\), with \(i'\ne 0\). Taking into account (i), this gives that \(x_{\scriptscriptstyle \langle {}i,j{}\rangle }{\cdot }y_{\scriptscriptstyle \langle {}i,j{}\rangle \langle {}\tilde{\imath },\tilde{\jmath }{}\rangle }\in h_{{\scriptscriptstyle \varSigma }}(\mathcal {L}(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k}))\) and \(x_{\scriptscriptstyle \langle {}\tilde{\imath },\tilde{\jmath }{}\rangle }{\cdot }y_{\scriptscriptstyle \langle {}i,j{}\rangle \langle {}\tilde{\imath },\tilde{\jmath }{}\rangle }\in h_{{\scriptscriptstyle \varSigma }}(\mathcal {L}(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k})^{\scriptscriptstyle \mathrm {C}})\). These statements can be shown by analyzing all cases, using (9), (3), and (8) (see also Figs. 2 and 3):
-
If \(0\le i<\tilde{\imath }\le n-1\), and hence \(0<\tilde{\imath }-i\le n-1\), with \(j,\tilde{\jmath }\in \{0,\ldots ,d-1\}\):
-
\(x_{\scriptscriptstyle \langle {}i,j{}\rangle }{\cdot }y_{\scriptscriptstyle \langle {}i,j{}\rangle \langle {}\tilde{\imath },\tilde{\jmath }{}\rangle }= 1^i{\cdot }0^j{\cdot }1{\cdot }1^{n-i-1}= h_{{\scriptscriptstyle \varSigma }}(a_0^i{\cdot }a_j{\cdot }a_0^{n-i-1})\), \(\langle {}0,0{}\rangle \mathop {\longrightarrow }\limits ^{1^i0^j} \langle {}i,j{}\rangle \mathop {\longrightarrow }\limits ^{1} \langle {}(i+1){\,\bmod \,}n,0{}\rangle \mathop {-\!\!\!-\!\!\!-\!\!\!\longrightarrow }\limits ^{1^{n-i-1}} \langle {}0,0{}\rangle \),
-
\(x_{\scriptscriptstyle \langle {}\tilde{\imath },\tilde{\jmath }{}\rangle }{\cdot }y_{\scriptscriptstyle \langle {}i,j{}\rangle \langle {}\tilde{\imath },\tilde{\jmath }{}\rangle }= 1^{\tilde{\imath }}{\cdot }0^{\tilde{\jmath }}{\cdot }1{\cdot }1^{n-i-1}= h_{{\scriptscriptstyle \varSigma }}(a_0^{\tilde{\imath }}{\cdot }a_{\tilde{\jmath }}{\cdot }a_0^{n-i-1})\), \(\langle {}0,0{}\rangle \mathop {\longrightarrow }\limits ^{1^{\tilde{\imath }}0^{\tilde{\jmath }}} \langle {}\tilde{\imath },\tilde{\jmath }{}\rangle \mathop {\longrightarrow }\limits ^{1} \langle {}(\tilde{\imath }+1){\,\bmod \,}n,0{}\rangle \mathop {-\!\!\!-\!\!\!-\!\!\!\longrightarrow }\limits ^{1^{n-i-1}} \langle {}\tilde{\imath }-i,0{}\rangle \ne \langle {}0,0{}\rangle \).
-
-
If \(0\le i<g\) and \(0\le j<\tilde{\jmath }\le d-1\), and hence \(1\le j+d-\tilde{\jmath }\le d-1\):
-
\(x_{\scriptscriptstyle \langle {}i,j{}\rangle }{\cdot }y_{\scriptscriptstyle \langle {}i,j{}\rangle \langle {}i,\tilde{\jmath }{}\rangle }= 1^i{\cdot }0^j{\cdot }0^{d-\tilde{\jmath }}1{\cdot }1^{n-i-1}= h_{{\scriptscriptstyle \varSigma }}(a_0^i{\cdot }a_{j+d-\tilde{\jmath }}{\cdot }a_0^{n-i-1})\), \(\langle {}0,0{}\rangle \mathop {\longrightarrow }\limits ^{1^i0^j} \langle {}i,j{}\rangle \mathop {-\!\!\!-\!\!\!-\!\!\!\longrightarrow }\limits ^{0^{d-\tilde{\jmath }}} \langle {}i,j+d-\tilde{\jmath }{}\rangle \mathop {\longrightarrow }\limits ^{1} \langle {}(i+1){\,\bmod \,}n,0{}\rangle \mathop {-\!\!\!-\!\!\!-\!\!\!\longrightarrow }\limits ^{1^{n-i-1}} \langle {}0,0{}\rangle \),
-
\(x_{\scriptscriptstyle \langle {}i,\tilde{\jmath }{}\rangle }{\cdot }y_{\scriptscriptstyle \langle {}i,j{}\rangle \langle {}i,\tilde{\jmath }{}\rangle }= 1^i{\cdot }0^{\tilde{\jmath }}{\cdot }0^{d-\tilde{\jmath }}1{\cdot }1^{n-i-1}= h_{{\scriptscriptstyle \varSigma }}(a_0^i{\cdot }a_d{\cdot }a_0^{n-i})\), \(\langle {}0,0{}\rangle \mathop {\longrightarrow }\limits ^{1^i0^{\tilde{\jmath }}} \langle {}i,\tilde{\jmath }{}\rangle \mathop {-\!\!\!-\!\!\!-\!\!\!\longrightarrow }\limits ^{0^{d-1-\tilde{\jmath }}} \langle {}i,d-1{}\rangle \mathop {\longrightarrow }\limits ^{0} \langle {}(i+1){\,\bmod \,}n,0{}\rangle \mathop {-\!\!\!-\!\!\!-\!\!\!\longrightarrow }\limits ^{1^{n-i}} \langle {}1,0{}\rangle \).
-
-
If \(g\le n-1\) and \(0\le j<\tilde{\jmath }\le k\), and hence \(1\le j+k+1-\tilde{\jmath }\le k\):
-
\(x_{\scriptscriptstyle \langle {}g,j{}\rangle }{\cdot }y_{\scriptscriptstyle \langle {}g,j{}\rangle \langle {}g,\tilde{\jmath }{}\rangle }= 1^g{\cdot }0^j{\cdot }0^{k+1-\tilde{\jmath }}1{\cdot }1^{n-g-1}= h_{{\scriptscriptstyle \varSigma }}(a_0^g{\cdot }a_{j+k+1-\tilde{\jmath }}{\cdot }a_0^{n-g-1})\), \(\langle {}0,0{}\rangle \mathop {\longrightarrow }\limits ^{1^g0^j} \langle {}g,j{}\rangle \mathop {-\!\!\!-\!\!\!-\!\!\!\longrightarrow }\limits ^{0^{k+1-\tilde{\jmath }}} \langle {}g,j+k+1-\tilde{\jmath }{}\rangle \!\mathop {\longrightarrow }\limits ^{1} \langle {}(g+1){\,\bmod \,}n,0{}\rangle \mathop {-\!\!\!-\!\!\!-\!\!\!\longrightarrow }\limits ^{1^{n-g-1}} \langle {}0,0{}\rangle \),
-
\(x_{\scriptscriptstyle \langle {}g,\tilde{\jmath }{}\rangle }{\cdot }y_{\scriptscriptstyle \langle {}g,j{}\rangle \langle {}g,\tilde{\jmath }{}\rangle }= 1^g{\cdot }0^{\tilde{\jmath }}{\cdot }0^{k+1-\tilde{\jmath }}1{\cdot }1^{n-g-1}= h_{{\scriptscriptstyle \varSigma }}(a_0^g{\cdot }a_{k+1}{\cdot }a_0^{n-g-1})\), \(\langle {}0,0{}\rangle \mathop {\longrightarrow }\limits ^{1^g0^{\tilde{\jmath }}} \langle {}g,\tilde{\jmath }{}\rangle \mathop {-\!\!\!-\!\!\!-\!\!\!\longrightarrow }\limits ^{0^{k-\tilde{\jmath }}} \langle {}g,k{}\rangle \), with two different ways to continue: if \(g\le n-2\), then \(\langle {}g,k{}\rangle \mathop {\longrightarrow }\limits ^{0} \langle {}g+1,0{}\rangle \mathop {-\!\!\!-\!\!\!-\!\!\!\longrightarrow }\limits ^{1^{n-g}} \langle {}(n+1){\,\bmod \,}n,0{}\rangle = \langle {}1,0{}\rangle \), if \(g= n-1\), then \(\langle {}g,k{}\rangle \mathop {\longrightarrow }\limits ^{0} \langle {}0,k+1{}\rangle \mathop {-\!\!\!-\!\!\!-\!\!\!\longrightarrow }\limits ^{1^{n-g}} \langle {}(n-g){\,\bmod \,}n,0{}\rangle = \langle {}1,0{}\rangle \).
-
Summing up, we have constructed m-tuple \(X= \langle {}x_{\scriptscriptstyle \langle {}i,j{}\rangle }{}\rangle _{\langle {}i,j{}\rangle \in Q'}\) and \({m\atopwithdelims ()2}\)-tuple \(Y= \langle {}y_{\scriptscriptstyle \langle {}i,j{}\rangle \langle {}\tilde{\imath },\tilde{\jmath }{}\rangle }{}\rangle _ {\langle {}i,j{}\rangle {,}\langle {}\tilde{\imath },\tilde{\jmath }{}\rangle \in Q', \,\langle {}i,j{}\rangle \ne \langle {}\tilde{\imath },\tilde{\jmath }{}\rangle }\), where \(m= \Vert {Q'}\Vert \), consisting of binary strings such that, for each pair \(\langle {}i,j{}\rangle \ne \langle {}\tilde{\imath },\tilde{\jmath }{}\rangle \),
-
both \(x_{\scriptscriptstyle \langle {}i,j{}\rangle }{\cdot } y_{\scriptscriptstyle \langle {}i,j{}\rangle \langle {}\tilde{\imath },\tilde{\jmath }{}\rangle }\) and \(x_{\scriptscriptstyle \langle {}\tilde{\imath },\tilde{\jmath }{}\rangle }{\cdot } y_{\scriptscriptstyle \langle {}i,j{}\rangle \langle {}\tilde{\imath },\tilde{\jmath }{}\rangle }\) are in \(h_{{\scriptscriptstyle \varSigma }}(\varSigma ^{*})= h_{{\scriptscriptstyle \varSigma }}(\mathcal {L}(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k}))\cup h_{{\scriptscriptstyle \varSigma }}(\mathcal {L}(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k})^{\scriptscriptstyle \mathrm {C}})\),
-
\(x_{\scriptscriptstyle \langle {}i,j{}\rangle }{\cdot } y_{\scriptscriptstyle \langle {}i,j{}\rangle \langle {}\tilde{\imath },\tilde{\jmath }{}\rangle }\in h_{{\scriptscriptstyle \varSigma }}(\mathcal {L}(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k}))\) and \(x_{\scriptscriptstyle \langle {}\tilde{\imath },\tilde{\jmath }{}\rangle }{\cdot } y_{\scriptscriptstyle \langle {}i,j{}\rangle \langle {}\tilde{\imath },\tilde{\jmath }{}\rangle }\in h_{{\scriptscriptstyle \varSigma }}(\mathcal {L}(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k})^{\scriptscriptstyle \mathrm {C}})\).
But then, by Theorem 1, any dcDFA solving the binary promise problem \(\langle {}h_{{\scriptscriptstyle \varSigma }}(\mathcal {L}(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k})), h_{{\scriptscriptstyle \varSigma }}(\mathcal {L}(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k})^{\scriptscriptstyle \mathrm {C}}){}\rangle \) must use at least \(m= \Vert {Q'}\Vert \) states, which gives that \(\mathcal {A}'_{{\scriptscriptstyle \varSigma },n,g,k}\) is optimal. \(\square \)
Theorem 5
For each non-unary input alphabet \(\varSigma \), there exists a maximal binary prefix code \(h\,{:}\,\varSigma ^{*}{\rightarrow }\{0,1\}^{*}\) such that, for each \(n\ge 2\) and each value \(N\in \{n,\ldots ,(\Vert {\varSigma }\Vert -1){\cdot }n\}\), there exists a language \(\mathcal {L}\subseteq \varSigma ^{*}\) such that the optimal DFA recognizing \(\mathcal {L}\) uses exactly n states and any optimal dcDFA for solving \(\langle {}h(\mathcal {L}), h(\mathcal {L}^{\scriptscriptstyle \mathrm {C}}){}\rangle \), the binary promise-problem version of \(\mathcal {L}\), uses exactly N states.
Proof
Let us handle the pathological case of \(\varSigma = \{a_0,a_1\}\) first. There are only two maximal prefix codes in this case, both of them are bijections from \(\{a_0,a_1\}\) to \(\{0,1\}\), and none of them can change the state complexity of any language. This corresponds to the fact that here \(N\in \{n,\ldots ,(\Vert {\varSigma }\Vert -1){\cdot }n\}= \{n\}\).
Now, for the given \(\varSigma \), with \(\Vert {\varSigma }\Vert \ge 3\), let us fix \(h=h_{{\scriptscriptstyle \varSigma }}\), as introduced by (3). Next, the witness language \(\mathcal {L}\) depends on \(\varSigma \) and on the given values n and N:
First, if \(N\le (\Vert {\varSigma }\Vert -1){\cdot }n-1= d{\cdot }n -1\), we can take \(\mathcal {L}= \mathcal {L}(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k})\), using the following parameters:
Clearly, \(g\le \lfloor {(d{\cdot }n-1-n)/(d-1)}\rfloor = \lfloor {n-\frac{1}{d-1}}\rfloor = n-1\) and \(k\le d-2\). By Lemma 2, \(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k}\) is the optimal DFA for recognizing \(\mathcal {L}\), using exactly n states. Similarly, by Lemma 3, \(\mathcal {A}'_{{\scriptscriptstyle \varSigma },n,g,k}\) is optimal dcDFA for solving \(\langle {}h_{{\scriptscriptstyle \varSigma }}(\mathcal {L}), h_{{\scriptscriptstyle \varSigma }}(\mathcal {L}^{\scriptscriptstyle \mathrm {C}}){}\rangle \) and uses exactly \(m= d{\cdot }g\,+\,(k\,+\,1)\,+\,(n\,-\,g\,-\,1)\) states. This gives \(m= d{\cdot }g\,+\,(k\,+\,1)\,+\,(n\,-\,g\,-\,1) = (d\,-\,1){\cdot }g\,+\, k\,+\, n = (d-1){\cdot }\lfloor {(N\,-\,n)/(d\,-\,1)}\rfloor \,+\, (N\,-\,n){\,\bmod \,}(d\,-\,1)+ n = (N\,-\,n)+ n = N\) states, using the fact that \(a{\cdot }\lfloor {b/a}\rfloor + b{\,\bmod \,}a= b\).
Second, if \(N= (\Vert {\varSigma }\Vert -1){\cdot }n\), take \(\mathcal {L}= \mathcal {L}(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k})\) with \(g=n\) and \(k=0\). (Here \(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k}\) does not actually depend on k.) Again, by Lemma 2, \(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k}\) is optimal and uses exactly n states and, by Lemma 3, \(\mathcal {A}'_{{\scriptscriptstyle \varSigma },n,g,k}\) is optimal for solving \(\langle {}h_{{\scriptscriptstyle \varSigma }}(\mathcal {L}), h_{{\scriptscriptstyle \varSigma }}(\mathcal {L}^{\scriptscriptstyle \mathrm {C}}){}\rangle \), this time with exactly \(m= (\Vert {\varSigma }\Vert -1){\cdot }n= N\) states. \(\square \)
5 Concluding Remarks
By a more careful analysis of the construction in Theorem 3, we see that it does not increase the number of accepting or rejecting states. As a direct consequence, if the optimal DFA \(\mathcal {A}\) recognizing \(\mathcal {L}\) uses \(n^{{\scriptscriptstyle \oplus }}\) accepting and \(n^{{\scriptscriptstyle \ominus }}\) rejecting states (neither of these values can be reduced, since the optimal \(\mathcal {A}\) is unique), then any optimal dcDFA \(\mathcal {A}'\) solving the binary promise problem \(\langle {}h(\mathcal {L}),h(\mathcal {L}^{\scriptscriptstyle \mathrm {C}}){}\rangle \) must use at least \(n^{{\scriptscriptstyle \oplus }}\) accepting and at least \(n^{{\scriptscriptstyle \ominus }}\) rejecting states. But all states in \(\mathcal {A}'\) that cannot be reached from \(q'_{\scriptscriptstyle \mathrm {I}}\) by reading some \(\beta \in h(\varSigma ^{*})\) can be made neutral (see also (2) in the proof of Theorem 3). This will only change acceptance/rejection to “don’t care” answers on some inputs not belonging to \(h(\varSigma ^{*})\).
This allows to establish some kind of pseudo-isomorphism between \(\mathcal {A}\) and \(\mathcal {A}'\). (Proof omitted here due to space constraints, to appear in a journal version.) Namely, there exists a bijective function \(t\,{:}\,Q{\rightarrow }F^{{\scriptscriptstyle \oplus }}{\cup }F^{{\scriptscriptstyle \ominus }}\) that maps \(q_{\scriptscriptstyle \mathrm {I}}\) to \(q'_{\scriptscriptstyle \mathrm {I}}\), F to \(F^{{\scriptscriptstyle \oplus }}\), and \(Q{\setminus }F\) to \(F^{{\scriptscriptstyle \ominus }}\), preserving the machine’s transitions, i.e., \(t(f(q,a))= {f'}^{*}(t(q),h(a))\), for each \(q\in Q\) and \(a\in \varSigma \). However, such pseudo-isomorphism does not exclude, for some transition \(q\mathop {\longrightarrow }\limits ^{a}q'\) in \(\mathcal {A}\), passing through some state \(t(q'')\in F^{{\scriptscriptstyle \oplus }}{\cup }F^{{\scriptscriptstyle \ominus }}\) along the corresponding path \(t(q)\mathop {-\!\!\!-\!\!\!-\!\!\!\longrightarrow }\limits ^{h(a)}t(q')\) in \(\mathcal {A}'\)—even more than once in the meantime.Footnote 3
There are more open questions in the related area than the known answers. As an example, we do not know the cost of binary coded intersection; the same holds for other basic operations with regular languages. It can be expected that answers may depend also on the code h in use, and we expect some anomalies for prefix codes that are not maximal.
Notes
- 1.
State complexity of homomorphisms depends on the length of the images of symbols and is somewhat difficult to define in the general case. Perhaps the only existing related result is the state complexity of projections (that is, homomorphisms mapping each symbol either to itself or to \(\varepsilon \)), which was determined to be \(3/4{\cdot }2^n-1\) in [12].
- 2.
Throughout the paper, \(\Vert {X}\Vert \) denotes the cardinality of the set X.
- 3.
This phenomenon can be seen in Fig. 2, where we have “3”\(\mathop {\longrightarrow }\limits ^{a_4}\)“5” for \(\mathcal {A}_{{\scriptscriptstyle \varSigma },n,g,k}\). Since \(h(a_4)=\) “00001”, this corresponds to
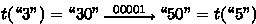 for \(\mathcal {A}'_{{\scriptscriptstyle \varSigma },n,g,k}\), passing twice through
for \(\mathcal {A}'_{{\scriptscriptstyle \varSigma },n,g,k}\), passing twice through
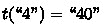 .
.
References
Berstel, J., Perrin, D., Reutenauer, C.: Codes and Automata. Cambridge University Press, Cambridge (2010)
Birget, J.-C.: Intersection and union of regular languages and state complexity. Inform. Process. Lett. 43, 185–190 (1992)
Bruyère, V.: Maximal codes with bounded deciphering delay. Theoret. Comput. Sci. 84, 53–76 (1991)
Čevorová, K.: Kleene star on unary regular languages. In: Jurgensen, H., Reis, R. (eds.) DCFS 2013. LNCS, vol. 8031, pp. 277–288. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39310-5_26
Geffert, V.: Magic numbers in the state hierarchy of finite automata. Inform. Comput. 205, 1652–1670 (2007)
Goldreich, O.: On promise problems: a survey. In: Goldreich, O., Rosenberg, A.L., Selman, A.L. (eds.) Theoretical Computer Science. LNCS, vol. 3895, pp. 254–290. Springer, Heidelberg (2006). https://doi.org/10.1007/11685654_12
Holzer, M., Rauch, C.: The range of state complexities of languages resulting from the cascade product—the unary case (extended abstract). In: Maneth, S. (ed.) CIAA 2021. LNCS, vol. 12803, pp. 90–101. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-79121-6_8
Hopcroft, J., Motwani, R., Ullman, J.: Introduction to Automata Theory, Languages, and Computation. Addison-Wesley, Boston (2001)
Hricko, M., Jirásková, G., Szabari, A.: Union and intersection of regular languages and descriptional complexity. In: Proceedings of Descriptional Complexity of Formal Systems, pp. 170–181. IFIP & University, Milano (2005)
Iwama, K., Kambayashi, Y., Takaki, K.: Tight bounds on the number of states of DFA’s that are equivalent to \(n\)-state NFA’s. Theoret. Comput. Sci. 237, 485–494 (2000)
Jirásková, G.: Magic numbers and ternary alphabet. Internat. J. Found. Comput. Sci. 22, 331–344 (2011)
Jirásková, G., Masopust, T.: On a structural property in the state complexity of projected regular languages. Theoret. Comput. Sci. 449, 93–105 (2012)
Moreira, N., Pighizzini, G., Reis, R.: Optimal state reductions of automata with partially specified behaviors. Theoret. Comput. Sci. 658, 235–245 (2017)
Paull, M.C., Unger, S.H.: Minimizing the number of states in incompletely specified sequential switching functions. IRE Trans. Electron. Comput. 3, 356–367 (1959)
Pfleeger, C.P.: State reduction in incompletely specified finite-state machines. IEEE Trans. Comput. C–22, 1099–1102 (1973)
Rabin, M., Scott, D.: Finite automata and their decision problems. IBM J. Res. Develop. 3, 114–125 (1959)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 IFIP International Federation for Information Processing
About this paper
Cite this paper
Geffert, V., Pališínová, D., Szabari, A. (2022). State Complexity of Binary Coded Regular Languages. In: Han, YS., Vaszil, G. (eds) Descriptional Complexity of Formal Systems. DCFS 2022. Lecture Notes in Computer Science, vol 13439. Springer, Cham. https://doi.org/10.1007/978-3-031-13257-5_6
Download citation
DOI: https://doi.org/10.1007/978-3-031-13257-5_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-13256-8
Online ISBN: 978-3-031-13257-5
eBook Packages: Computer ScienceComputer Science (R0)








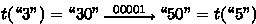 for
for 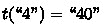 .
.