Oscillations in Biological Systems

Abstract

As it is well known, many physical, chemical and biological phenomena are modelled by parabolic equations, among these one of the most frequently examined type is the reaction-diffusion equation. One of the fascinating features of these equations is the variety of special types of solutions they exhibit.

1 Introduction

As it is well known, many physical, chemical and biological phenomena are modelled by parabolic equations, among these one of the most frequently examined type is the reaction-diffusion equation. One of the fascinating features of these equations is the variety of special types of solutions they exhibit. Certain systems of this type have, for example, travelling wave solutions or rotating waves (cf. [14]) or via bifurcation analysis one can find a new class of solutions (cf. [13]).

In this chapter we consider the autonomous systems of reaction-diffusion equations

$$\displaystyle \begin{aligned} {\mathbf{u}}_t=D\Delta_{\mathbf{r}} \mathbf{u}+\mathbf{f}\circ(\mathbf{u},\mu), \end{aligned} $$

(1)

on $\Omega \times \mathbb {R}^+_0\ni (\mathbf {r},t)$, with the usual zero flux boundary and non-negative initial condition

$$\displaystyle \begin{aligned} (\mathbf{n}\cdot\nabla_{\mathbf{r}})\mathbf{u}=\mathbf{0}\qquad \text{on}\qquad \partial\Omega\times\mathbb{R}^+_0, \end{aligned} $$

(2)

and

$$\displaystyle \begin{aligned} \mathbf{u}(\cdot,0)={\mathbf{u}}_0(\cdot)\qquad \text{on}\qquad \overline{\Omega}\times\{0\}, \end{aligned} $$

(3)

where D is a positive diagonal matrix:

$$\displaystyle \begin{aligned}D:=\operatorname{\mathrm{diag}}(d_1,\ldots,d_n),\end{aligned}$$

the kinetic function

$$\displaystyle \begin{aligned}\mathbf{f}=(f_1,\ldots,f_n):\mathbb{R}^n\times I\rightarrow\mathbb{R}^n\end{aligned}$$

belongs to $\mathfrak {C}^1$, μ is a parameter in an open interval $I\subset \mathbb {R}$, Ω is a bounded domain in $\mathbb {R}^n$ with piecewise smooth boundary, n is the outer unit normal to ∂ Ω and u ₀ is a bounded non-negative, resp. not identically vanishing smooth function.

Insomuch as system (1) is biologically motivated it is necessary to show that (1) is biologically well-posed. Usually, this means positivity, resp. dissipativeness, i.e.

• the solution

  $$\displaystyle \begin{aligned}{\boldsymbol{\Phi}}=(\Phi_1,\ldots,\Phi_n)\in\overline{\Omega}\times\mathbb{R}^+_0\rightarrow\mathbb{R}^n\end{aligned}$$

  of (1) with non-negative initial data

  $$\displaystyle \begin{aligned} {\mathbf{u}}_0=(u_0^1,\ldots,u_0^n)\qquad \text{with}\qquad u_0^i\not\equiv0\quad (i\in\{1,\ldots,n\}) \end{aligned}$$

  remains non-negative for all t ≥ 0 in their domain of existence, resp.

• all solutions of system (1) are bounded and therefore defined for all t ≥ 0.

The first requirement can be formulated as follows: the positive quadrant of the phase space

$$\displaystyle \begin{aligned} \left\{\mathbf{u}=(u_1,\ldots,u_n)\in\mathbb{R}^n:\;u_k\geq0\;(k\in\{1,\ldots,n\}\right\} \end{aligned} $$

(4)

is (positively) invariant. This motivates the following

Definition 1.1

A closed subset $\Sigma \subset \mathbb {R}^n$ (positively) invariant region for the local solution defined by (1), if for suitable T > 0 any solution Φ having all of its boundary and initial values in Σ satisfies

$$\displaystyle \begin{aligned} {\boldsymbol{\Phi}}(\mathbf{r}, t)\in\Sigma\qquad ((\mathbf{r}, t)\in\overline{\Omega}\times[0,T)). \end{aligned}$$

It is obvious that the set Σ in (4) is a closed subset.

In [5] one can find the following fundamental result about the existence of (positively) invariant region.

Theorem 1.1

Let $m\in \mathbb {N}$ and consider the region Σ of the form

$$\displaystyle \begin{aligned} \Sigma:=\bigcap\limits_{k=1}^m\left\{\mathbf{r}\in U:\;G_i(\mathbf{r})\leq0\right\}, \end{aligned}$$

where $U\subset \mathbb {R}^n$ is an open subset and $G_i:\mathbb {R}^n\rightarrow \mathbb {R}$ are smooth functions (i ∈{1, …, m}) whose gradient ∇G _i never vanishes. If at each point r ∈ ∂ Σ we have for all i ∈{1, …, m}:

• (i) ∇G _i(r) is a left eigenvector of the diffusion matrix D;

• (ii) the functions G _i are quasi-convex, i.e. for all r ∈ U, resp. for all $\mathbf {s}\in \mathbb {R}^n$ the equality 〈∇G _i(r), s〉 = 0 implies 〈s, ∇² G _i(r)s)〉≥ 0;

• (iii) 〈∇G _i(r), f(r, μ)〉 < 0 (μ ∈ I)

then Σ is positively invariant for system (1).

As an example we show that the region

$$\displaystyle \begin{aligned} \Sigma:=\left\{(n,T)\in\mathbb{R}^2:\;0\leq n\leq a,\;\alpha\leq T\right\} \end{aligned}$$

is an invariant region for the parabolic system

$$\displaystyle \begin{aligned} \partial_tn=k_1\Delta_{\mathbf{r}}n-n\exp\left(-E/RT\right),\qquad \partial_tT=k_2\Delta_{\mathbf{r}}T+Qn\exp\left(-E/RT\right) \end{aligned}$$

arising in the theory of combustion (cf. [10]) where the quantities T and n denote the temperature and concentration, respectively, of a combustible substance and k ₁, k ₂, N, E and Q are positive constants, 0 < n(r, 0) < a, 0 < α ≤ T(r, 0). Indeed, for

$$\displaystyle \begin{aligned} f_1(n,T,\mu):=-n\exp\left(-E/RT\right),\qquad f_2(n,T):=Qn\exp\left(-E/RT\right) \end{aligned}$$

and

$$\displaystyle \begin{aligned} G_1(n,T,\mu):=n-a,\quad G_2(n,T):=-n-\varepsilon\;\,(\varepsilon>0)\quad \text{resp.}\quad G_3(n,T):=\alpha-T \end{aligned}$$

where μ ∈{k ₁, k ₂, N, E, ε} we have

$$\displaystyle \begin{aligned} \langle\nabla G_1,(f_1,f_2)\rangle_{n=a}=-a\exp\left(-E/RT\right)<0, \end{aligned}$$

$$\displaystyle \begin{aligned} \langle\nabla G_2,(f_1,f_2)\rangle_{n=-\epsilon}=-\varepsilon\exp\left(-E/RT\right)<0, \end{aligned}$$

resp.

$$\displaystyle \begin{aligned} \langle\nabla G_3,(f_1,f_2)\rangle_{n>0,\,T=\alpha}=-Qn\exp\left(-E/R\alpha\right)<0. \end{aligned}$$

As a further example we deal with the reaction-diffusion system proposed by A. Lemarchand and B. Nowakowski (cf. [18]) which describes the macroscopic evolution of two variable concentrations A and B and is given by the two deterministic equation

$$\displaystyle \begin{aligned} \left. \begin{array}{lll} \partial_tA & = & d_A\Delta_{\mathbf{r}}A+f_1(A,B,\mu),\\ \partial_tB & = & d_B\Delta_{\mathbf{r}}B+f_2(A,B,\mu) \end{array} \right\} \end{aligned} $$

(5)

on $\overline {\Omega }\times \mathbb {R}_0^+$ where $\Omega \subset \mathbb {R}^2$ is a bounded, connected spatial domain with piecewise smooth boundary ∂ Ω, f := (f ₁, f ₂) with

$$\displaystyle \begin{aligned} f_1(A,B,\mu):=-\alpha A+\beta A^2B,\qquad f_2(A,B,\mu):=\gamma -\delta B-\beta A^2B \end{aligned} $$

(6)

belongs to $\mathfrak {C}^1$, where μ ∈{α, β, γ, δ}, d _A > 0, d _B > 0 represent the diffusion coefficients, A(r, t) and B(r, t) are the concentrations of the species at time t ∈ [0, +∞) and place $\mathbf {r}\in \overline {\Omega }$.

We show now that the interior of the first quadrant of the phase space of is an invariant region.

Lemma 1.1

All solutions ${\boldsymbol {\Phi }}=(\Phi _1,\Phi _2):\overline {\Omega }\times \mathbb {R}^+_0\rightarrow \mathbb {R}^2$ of (5) with positive initial values Φ ₁(0) > 0, Φ ₂(0) > 0 remain positive for all t ≥ 0 in their domain of existence.

Proof

We have to show that the region

$$\displaystyle \begin{aligned} \Sigma:=\left\{(A,B)\in\mathbb{R}^2:\;A\geq0,B\geq0\right\}. \end{aligned}$$

is positively invariant for (5). Let assume that ${\boldsymbol {\Phi }}=(\Phi _1,\Phi _2):\overline {\Omega }\times \mathbb {R}^+_0\rightarrow \mathbb {R}^2$ is a solution of (5) satisfying positive initial conditions. Clearly, Φ₁ ≡0 is a solution of the first equation. Thus, by uniqueness we can argue that no solution Φ₁(⋅, t) at any times t ≥ 0 can become zero in finite time. It is obvious furthermore that (0, −1) is a left eigenvector of the diffusion matrix

$$\displaystyle \begin{aligned} D:=\left[\begin{array}{cc} d_A & 0 \\ 0 & d_B \end{array} \right]. \end{aligned}$$

Thus, if we set

$$\displaystyle \begin{aligned} G(A,B):=-B\qquad ((A,B)\in\Sigma), \end{aligned}$$

then

$$\displaystyle \begin{aligned} \langle\nabla G,(f_1,f_2)\rangle_{B=0}=-\gamma<0\qquad \text{in}\qquad \Sigma. \end{aligned}$$

This proves that Σ is invariant for system (5). □

In what follows we shall consider system (5) restricted to $(\mathbb {R}^+_0)^2$ and show that all solutions stay bounded in $0\leq t\in \mathbb {R}$ which implies the existence of solutions for every t > 0.

Lemma 1.2

System (5) is dissipative.

Proof

Let ${\boldsymbol {\Phi }}=(\Phi _1,\Phi _2):\overline {\Omega }\times \mathbb {R}^+_0\rightarrow \mathbb {R}^2$ be a solution of (5). Thus, for the second component of Φ we have

$$\displaystyle \begin{aligned} \dot{\Phi}_2-d_B\Delta_{\mathbf{r}}\Phi_2\leq\gamma-\delta\Phi_2 \end{aligned}$$

in its domain of existence and from the comparison principle (cf. [19, Thm. 10.1., p. 94]) we obtain on this domain Φ₂ ≤ Ψ where Ψ is a function of time t satisfying

$$\displaystyle \begin{aligned} \Psi^{\prime}=\gamma-\delta\Psi,\qquad \Psi(0):=\max\limits_{\mathbf{r}\in\overline{\Omega}}\Phi_2(\mathbf{r},0). \end{aligned}$$

Clearly, $\lim \limits _{+\infty }\Psi =\gamma /\delta$ which implies that the function Φ₂(r, ⋅) $(\mathbf {r}\in \overline {\Omega })$ is defined on the whole positive half line and

$$\displaystyle \begin{aligned} \limsup\limits_{t\rightarrow+\infty}\max\limits_{\mathbf{r}\in\overline{\Omega}}\Phi_2(\mathbf{r},t)\leq\gamma/\delta. \end{aligned}$$

The boundedness of Φ₁ follows similarly. Thus, we have proved that all solutions of (5) stay bounded in $t\in \mathbb {R}^+_0$ which implies the existence of solutions of (5) for every t > 0. □

Clearly, a spatially constant solution Φ(⋅) = ( Φ₁(⋅), Φ₂(⋅)) of system (1) satisfies boundary conditions (2) and the kinetic system

$$\displaystyle \begin{aligned} \dot{\mathbf{u}}=\mathbf{f}\circ(\mathbf{u},\mu) \end{aligned} $$

(7)

The equilibria $\overline {\mathbf {u}}$ of system (7) for which

$$\displaystyle \begin{aligned} \mathbf{f}\circ(\overline{\mathbf{u}},\mu)=\mathbf{0}\qquad (\mu\in I) \end{aligned} $$

(8)

holds are constant solutions of (1), (2) at the same time. If e.g. the equality βγ ² = 2αδ in system (5) hold then we have a unique interior equilibrium

$$\displaystyle \begin{aligned} \left(\overline{A},\overline{B}\right):=\left(\frac{\gamma}{2\alpha},\frac{\gamma}{2\delta}\right). \end{aligned}$$

In order to investigate the local dynamical behavior of system (1) near the equilibrium $\overline {\mathbf {u}}$ of (7) we linearize (1) at these equilibria. The realisation of the linearization depends strongly on which type of solution is investigated.

The chapter is organised as follows. In the next section we show how to investigate the occurrence of rotating waves on two types of planar domains: on disk and annulus. In the section that follows we examine the possibility the occurrence of time periodic solution of (1) when the kinetic system (7) exhibits periodic solution, as well.

2 Bifurcation of Rotating Waves

In this section we are interested in the problem of finding rotating wave solution of (1)–(2). The kinetic function f in (1) is required to have the following properties

$$\displaystyle \begin{aligned} \mathbf{(F1)}\quad \mathbf{f}\in\mathfrak{C}^2(\mathbb{R}^n\times I)\qquad \text{and}\qquad \mathbf{(F2)}\quad \mathbf{f}(0,\mu)=0\;\,(\mu\in I). \end{aligned}$$

Assumption (F1) implies that the kinetic term in (1) depends only on the parameter μ and the variables u ₁, …, u _n, furthermore its second order derivative of its components are continuous. Assumption (F2) requires that Φ(r) ≡0 is a solution of (1)–(2) for all μ ∈ I.

Rotating waves are nonuniform periodic solutions to partial differential equations which rotate with a nonzero angular velocity. Thus, rotating waves can exist mathematically only in problems that have at least SO(2) symmetry (cf. [11]), i.e. there is a function $R_\vartheta \in Lin(\mathbb {R}^2)$ with

$$\displaystyle \begin{aligned} \begin{bmatrix}R_\vartheta\end{bmatrix}= \begin{bmatrix}\cos{}(\vartheta)&\sin{}(\vartheta)\\ -\sin{}(\vartheta)&\cos{}(\vartheta)\end{bmatrix} \quad \text{and} \quad R_\vartheta\left(\overline{\Omega}\right)=\overline{\Omega}\quad (\vartheta\in[0,2\pi)). \end{aligned}$$

The domains disk, resp. annulus

$$\displaystyle \begin{aligned} \Omega_d:=\left\{(x,y)\in\mathbb{R}^2\big\vert x^2+y^2<1\right\}, \end{aligned}$$

resp.

have this property (cf. Fig. 1).

Fig. 1

Ω = Ω_d and Ω = Ω_a

Definition 2.1

Let Ω be one of the radial symmetric domains Ω_d, Ω_a. A nontrivial non-negative solution ${\boldsymbol {\Phi }}:\overline {\Omega }\times \mathbb {R}^+_0\rightarrow \mathbb {R}^n$ of (1) is called rotating wave if there is a function $\mathbf {T}:\overline {\Omega }\rightarrow \mathbb {R}^n$ and a number $0\neq c\in \mathbb {R}$ (wave speed) such that

$$\displaystyle \begin{aligned} {\boldsymbol{\Phi}}(r,\vartheta;t)=\mathbf{T}(r,\vartheta-ct)\qquad ((r,\vartheta;t)\in\Omega\times(0,+\infty)) \end{aligned}$$

and

$$\displaystyle \begin{aligned} \mathbf{T}(r,\xi)=\mathbf{T}(r,\xi+2\pi)\qquad (r\in(0,1)\cup(1,\sigma),\,\xi\in[0,2\pi)) \end{aligned}$$

hold.

Because we are looking for solutions Φ of (1) for which

$$\displaystyle \begin{aligned} (\mathbf{n}\cdot\nabla_{\mathbf{r}}){\boldsymbol{\Phi}}=\mathbf{0}\qquad \text{on}\qquad \partial\Omega\times\mathbb{R}^+_0, \end{aligned}$$

resp.

$$\displaystyle \begin{aligned} {\boldsymbol{\Phi}}(\cdot,0)={\boldsymbol{\Phi}}_0(\cdot)\geq\mathbf{0}\qquad \text{on}\qquad \overline{\Omega}\times\{0\} \end{aligned}$$

hold, therefore using polar coordinates (r, 𝜗) on Ω and denoting ξ := 𝜗 − ct one can easily see that chain rule implies

$$\displaystyle \begin{aligned} \partial_t {\boldsymbol{\Phi}}=-c\partial_\xi\mathbf{T},\qquad (\mathbf{n}\cdot\nabla_{\mathbf{r}}){\boldsymbol{\Phi}}=\partial_r \mathbf{T}\qquad \text{and}\qquad \Delta_{\mathbf{r}}{\boldsymbol{\Phi}}=\Delta\mathbf{T}, \end{aligned}$$

where the Laplacian Δ is given by

$$\displaystyle \begin{aligned} \Delta:=\frac{1}{r}\partial_r(r\partial_r)+\frac{1}{r^2}\partial_{\xi\xi}. \end{aligned}$$

This means that T is a periodic function of period 2π in the second variable for which

$$\displaystyle \begin{aligned} D\Delta\mathbf{T}+c\partial_\xi\mathbf{T}+\mathbf{f}(\mathbf{T}, \mu)=\mathbf{0}\quad ((r,\xi)\in\Omega), {} \end{aligned} $$

(9)

$$\displaystyle \begin{aligned} \partial_r\mathbf{T}=\mathbf{0}\quad ((r,\xi)\in\partial\Omega) {} \end{aligned} $$

(10)

hold. Thus, we are interesting to seek those non-zero real numbers c for which system (9) and (10) has a non-trivial solution.

2.1 The Linearized Problem

Let $\overline {\mathbf {u}}$ denote one of the interior equilibria of the kinetic system (7). Moving the origin into $\overline {\mathbf {u}}$ by the coordinate transformation

$$\displaystyle \begin{aligned} z_1:=u_1-\overline{u}_1,\qquad z_2:=u_2-\overline{u}_2 \end{aligned}$$

and linearizing system (9) and (10) we get the linear boundary value problem

$$\displaystyle \begin{aligned} D\Delta\mathbf{z}+c\partial_\xi\mathbf{z}+Q(\mu)\mathbf{z}= \mathbf{0}\quad \text{in}\quad \Omega, \end{aligned} $$

(11)

$$\displaystyle \begin{aligned} \partial_r\mathbf{z}=\mathbf{0}\quad \text{on} \quad \partial\Omega \end{aligned} $$

(12)

where $Q(\mu ):=\partial _1\mathbf {f}(\overline {\mathbf {u}},\mu )$. The Eq. (12) has the form in case of the disc Ω = Ω_d:

$$\displaystyle \begin{aligned} \partial_r\mathbf{z}(1,\xi)=\mathbf{0}\qquad (\xi\in[0,2\pi)), \end{aligned}$$

and in case of the annulus Ω = Ω_a:

$$\displaystyle \begin{aligned} \partial_r\mathbf{z}(1,\xi)=\mathbf{0}=\partial_r\mathbf{z}(\sigma,\xi)\qquad (\xi\in[0,2\pi)). \end{aligned}$$

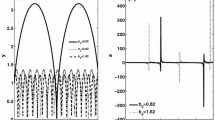
It is well know (cf. [4, 6, 9]) that if J _m, resp. Y _m denotes the Bessel function, resp. the Bessel function of second kind (c.f. Fig. 2) both of order m ($\in \mathbb {N}$) and

$$\displaystyle \begin{aligned} 0<\nu^d_{m,1}<\nu^d_{m,2}<\dots<\nu^d_{m,n}<\dots\qquad (n\in\mathbb{N}), \end{aligned}$$

resp.

$$\displaystyle \begin{aligned} 0<\nu^a_{m,1}<\nu^a_{m,2}< \dots<\nu^a_{m,n}<\dots\qquad (n\in\mathbb{N}) \end{aligned}$$

are the roots of

$$\displaystyle \begin{aligned} J_m^{\prime}(\cdot),\qquad \text{resp.}\qquad J_m^{\prime}(\cdot\sigma)Y_m^{\prime}(\cdot)-J_m^{\prime}(\cdot)Y_m(\cdot\sigma) \end{aligned}$$

then the eigenfunctions of the minus Laplacian on Ω_d, resp. Ω_a with homogeneous Neumann boundary conditions corresponding to the eigenvalues

$$\displaystyle \begin{aligned} \epsilon_{m,n}^k:=(\nu_{m,n}^k)^2\qquad (k\in\{d,a\}) \end{aligned}$$

are the functions

$$\displaystyle \begin{aligned} \Omega\ni(r,\xi)\mapsto A(r)\exp(\imath m\xi) \end{aligned}$$

where in case of the disc

$$\displaystyle \begin{aligned} A(r):\equiv J_m\left(\nu^d_{m,n}r\right), \end{aligned}$$

resp. in case of the annulus

$$\displaystyle \begin{aligned} A(r):\equiv J_m(\nu^a_{m,n}r)Y_m^{\prime}(\nu^a_{m,n})-J_m^{\prime}(\nu^a_{m,n})Y_m(\nu^a_{m,n}r). \end{aligned}$$

Then the non-trivial solution of the (11) and (12) linear boundary value problem has the form (cf. [3])

$$\displaystyle \begin{aligned} \mathbf{T}(r,\xi)=A(r)\exp(\imath m\xi)\mathbf{e}\qquad ((r,\xi)\in\Omega) {} \end{aligned} $$

(13)

where e is the eigenvector of the matrix

$$\displaystyle \begin{aligned} Q_{m,n}(\mu):=Q(\mu)-\epsilon_{m,n}^kD. \end{aligned}$$

corresponding to the eigenvalue ımc. From symmetry considerations rotating wave solutions of (1) may rotate either clockwise or anticlockwise around the domain $\overline {\Omega }$ (cf. [1]). Given a solution with c > 0, there is another solution in the opposite direction with c < 0 so we will restrict our attention to the case c positive (or anticklockwise waves).

Fig. 2

The graphs of J ₁ and of Y ₁

Thus, the linear boundary value problem (11)–(12) has non-trivial solution if and only if the matrix Q _m,n(μ) has purely imaginary eigenvalues. The eigenvalues z of Q _m,n(μ) are roots of the polynomial

$$\displaystyle \begin{aligned} z^2-Tr\left(Q_{m,n}(\mu)\right)z+\det\left(Q_{m,n}(\mu)\right)\qquad (z\in\mathbb{C}) \end{aligned}$$

where

$$\displaystyle \begin{aligned} Tr\left(Q_{m,n}(\mu)\right)=Tr(Q(\mu))-\epsilon^k_{m,n}Tr(D) \end{aligned} $$

(14)

and

$$\displaystyle \begin{aligned} \det\left(Q_{m,n}(\mu)\right)=\det(D)\cdot\left(\epsilon^k_{m,n}\right)^2- \Pi\cdot\epsilon^k_{m,n}+\det(Q(\mu)) \end{aligned} $$

(15)

with

$$\displaystyle \begin{aligned} \Pi:=-Tr\left(D\left(PQP\right)^T\right),\qquad \text{resp.}\qquad P:=\left[ \begin{array}{cc} 0 & 1 \\ -1 & 0 \\ \end{array} \right]. \end{aligned}$$

In [2] and in [3] it was shown that for a parameter value μ ₀ ∈ I the non-linear (9) and (10) has rotating wave solution only if the linear system (11) and (12) has non-trivial solution.

In case of system (5) the matrix Q(μ) has for μ = α and $\overline {\mathbf {u}}=(\overline {A},\overline {B})$ the form

$$\displaystyle \begin{aligned} Q(\alpha)=\left[\begin{array}{cc} \alpha & \delta \\ -2\alpha & -2\delta \end{array} \right], \end{aligned}$$

provided βγ ² = 4α ² δ holds. Therefore we can prove the following

Theorem 2.1

If the boundary value problem (9) and (10) with kinetic term f defined in (5) has a nontrivial solution, then

$$\displaystyle \begin{aligned} d_A>d_B \end{aligned} $$

(16)

must hold.

Proof

The matrix Q _m,n(α) has purely imaginary eigenvalues when

(17)

The first condition in (17) holds if and only if

$$\displaystyle \begin{aligned} \alpha=\alpha_0:=\alpha^k_{m,n}=2\delta+\epsilon^k_{m,n}(d_A+d_B). \end{aligned} $$

(18)

When $\alpha =\alpha ^k_{m,n}$, then

$$\displaystyle \begin{aligned} \det\left(Q_{m,n}(\alpha^k_{m,n})\right)=d_Ad_B(\epsilon^k_{m,n})^2+(2\delta d_A-\alpha^k_{m,n} d_B)\epsilon^k_{m,n}. \end{aligned}$$

An easy calculation shows that in this case the polynomial

$$\displaystyle \begin{aligned} p(z)\equiv-d_Bz^2+2\delta(d_A-d_B)z, \end{aligned} $$

(19)

must have a positive root, which is valid if (16) holds. □

There are only finite number of eigenvalues $\epsilon ^k_{m,n}$ of the minus Laplacian on Ω_k (k ∈{d, a}) for which $\det \left (Q_{m,n}(\alpha ^k_{m,n})\right )>0$ holds. Because condition (16) implies that there is a unique positive root of the polynomial p defined in (19), say $\widehat {\varepsilon }$, therefore rotating wave can bifurcate for system (5) with no-flux boundary conditions on Ω_k only from the eigenvalue $\epsilon ^k_{m,n}$ for which $0<\epsilon ^k_{m,n}<\widehat {\varepsilon }$ holds.

2.2 The Nonlinear Problem

Note that the theorem in the last subsection gives necessary but not sufficient condition for bifurcation of rotating wave. To actually prove that there is a bifurcation at a critical value α ₀ requires further analysis: certain transversality condition must be verified. In [2, 3, 13, 14] there was sketched a method, how the problem of finding rotating wave solution of (1) and (2) may be converted to one of finding non-trivial solution of operator equations in appropriate Banach spaces.

Clearly, introducing the new vector of variation $\mathbf {S}:=\mathbf {T}-\overline {\mathbf {u}}$ where $\overline {\mathbf {u}}$ is the equilibrium of the kinetic system (cf. (8)), (9) and (10) assumes the form

$$\displaystyle \begin{aligned} D\Delta\mathbf{S}+c\partial_{\xi}\mathbf{S}+\mathbf{F}(\mathbf{S},\mu)=\mathbf{0}\quad \text{in}\quad \Omega {} \end{aligned} $$

(20)

(21)

where F(0, μ) = 0 (μ ∈ I) with $\mathbf {F}\in \mathfrak {C}^2((\mathbb {R}^+_0)^2\times I,\mathbb {R}^2)$ holds for some open interval $I\subset \mathbb {R}$.

Using the implicit function theorem it can be shown (cf. e.g. [14] and [13]) that at the critical value α = α ₀ in (18) the trivial solution 0 of the non-linear problem (20) and (21) undergoes a bifurcation causing rotating waves and (20) and (21) has the solution in case of the disc

$$\displaystyle \begin{aligned} {\boldsymbol{\Xi}}(r,\xi;s)=s\left[\begin{array}{c} \cos{}(n\xi) \\ -e_{m,n}\cos{}(n\xi+\varphi_{m,n}) \end{array}\right] J_m(\nu^d_{m,n}r)+O(s) \end{aligned}$$

and in the case of the annulus

$$\displaystyle \begin{aligned} \begin{array}{ll} {\boldsymbol{\Xi}}(r,\xi;s) & =s\left[\begin{array}{c} \cos{}(n\xi) \\ -e_{m,n}\cos{}(n\xi+\varphi_{m,n}) \end{array}\right]\cdot \\ & \cdot\left(J_m(\nu^a_{m,n}r)Y_m^{\prime}(\nu^a_{m,n})-J_m^{\prime}(\nu^a_{m,n})Y_m(\nu^a_{m,n}r)\right)+O(s), \end{array} \end{aligned}$$

where

$$\displaystyle \begin{aligned} e_{m,n}:=\frac{\sqrt{(\epsilon^k_{m,n}d_A-\alpha)^2+\det \left(Q_{m,n}(\epsilon^k_{m,n})\right)}}{\delta} \end{aligned}$$

and

$$\displaystyle \begin{aligned} \varphi_{m,n}:=\tan^{-1}\left(\frac{\sqrt{\det \left(Q_{m,n}(\epsilon^k_{m,n})\right)}}{\alpha_0-\epsilon^k_{m,n}d_A}\right)\qquad \text{with}\qquad \varphi_{m,n}\in(0,\pi/2). \end{aligned}$$

Since s is considered to be small here, we this solution is called a small amplitude rotating wave.

3 Periodic Solutions of Reaction-Diffusion Systems

In this section we assume that n = 2, and the parameter dependence is not emphasized in the right hand side of (1), resp. (7), i.e. we deal with the kinetic system

$$\displaystyle \begin{aligned} \dot{\mathbf{u}}=\mathbf{f}\circ\mathbf{u} \end{aligned} $$

(22)

and the parabolic system

$$\displaystyle \begin{aligned} {\mathbf{u}}_t=D\Delta_{\mathbf{r}} \mathbf{u}+\mathbf{f}\circ\mathbf{u}, \end{aligned} $$

(23)

on a bounded spatial domain $\Omega \subset \mathbb {R}^2$ with piecewise smooth boundary with homogeneous Neumann boundary condition (2), resp. bounded non-negative initial condition (3), where D is a positive diagonal matrix: $D= \operatorname {\mathrm {diag}}\{d_1,d_2\}$.

We assume that (22) has a non-constant orbitally asymptotically stable T-periodic solution

$$\displaystyle \begin{aligned} \mathbf{p}:[0,+\infty)\rightarrow\mathbb{R}^2,\qquad \mathbf{p}(t+T)\equiv \mathbf{p}(t), \end{aligned}$$

and this solution is, at the beginning, a stable solution of the parabolic system (23), too. Varying one of the system parameters we consider the situation in which under certain conditions this spatially constant time periodic solution loses its stability and a spatially non-constant time periodic solution emerges.

Theorem 3.1

[ Andronov-Witt ] Let be $\Phi :[0,+\infty )\rightarrow \mathbb {R}^2$ a fundamental matrix of the variational system

$$\displaystyle \begin{aligned} \dot{\mathbf{v}}=({\mathbf{f}}^{\prime}\circ\mathbf{p})\mathbf{v} {} \end{aligned} $$

(24)

with Φ(0) = I and M the monodromy matrix, i.e. M =  Φ(T). The asymptotic orbital stability of p as a solution the kinetic system (22) depends on the modulus of the Floquet-multiplier of (24), i.e. on the modulus of the second eigenvalue μ ₂₀ of M /μ ₁₀ = 1/. p is an orbitally asymptotically stable, resp. unstable solution of (23) if and only if 0 < μ ₂₀ < 1, resp. μ ₂₀ ≥ 1, i.e. δ < 0, resp. δ > 0 holds, where

$$\displaystyle \begin{aligned} \delta:=\int_0^T\mathrm{div}(\mathbf{f}(\mathbf{p}(t))\,\mathrm{d}t. \end{aligned}$$

Example 3.1

The system corresponding to the Van der Pol’s differential equation

$$\displaystyle \begin{aligned} \ddot{u}+m(u^2-1)\dot{u}+u=0 {} \end{aligned} $$

(25)

has the form

$$\displaystyle \begin{aligned} \dot{u}_1=u_2,\qquad \dot{u}_2=m(1-u_1^2)u_2-u_1. {} \end{aligned} $$

(26)

If m > 0 then system (26) has a non-constant periodic solution u _m with period T _m, but not in the strip ∥u∥ < 1. The variational system of (26) is

$$\displaystyle \begin{aligned} \dot{v}_1=v_2,\quad \dot{v}_2=-(1+2mu_m\dot{u}_m)v_1+m(1-u_m^2)v_2. {} \end{aligned} $$

(27)

Thus, if

$$\displaystyle \begin{aligned} \delta=m\int_0^{T_m}(1-u_m^2(t))\,\mathrm{d}t=mT_m-m\int_0^{T_m}u_m^2(t)\,\mathrm{d}t<0 \end{aligned}$$

holds, the periodic solution u _m is orbitally asymptotically stable.

Example 3.2

If λ, ω > 0, then

$$\displaystyle \begin{aligned} \mathbf{p}(t):=(\sqrt{\lambda}\cos{}(\omega t),\sqrt{\lambda}\sin{}(\omega t))\quad (t\in[0,+\infty)) \end{aligned}$$

is a non-constant T-periodic solution of the autonomous system

$$\displaystyle \begin{aligned} \left.\begin{array}{l} \dot{u}_1=\lambda u_1-\omega u_2-u_1(u_1^2+u_2^2), \\ \dot{u}_2=\omega u_1+\lambda u_2-u_2(u_1^2+u_2^2) \end{array} \right\} {} \end{aligned} $$

(28)

where T := 2π∕ω. The variational system is

$$\displaystyle \begin{aligned} \dot{\mathbf{v}}(t)\equiv\left[\begin{array}{cc} -2\lambda\cos^2(\omega t) & -\omega-\lambda\sin{}(2\omega t) \\ \omega-\lambda\sin{}(2\omega t) & -2\lambda\sin^2(\omega t) \end{array} \right]\mathbf{v}(t). \end{aligned}$$

Because

$$\displaystyle \begin{aligned} \delta=\int_0^T\left\{-2\lambda\cos^2(\omega t)-2\lambda\sin^2(\omega t)\right\}\,\mathrm{d}t=-4\lambda\pi/\omega \end{aligned}$$

the non-constant periodic solution p of (28) is orbitally asymptotically stable.

Example 3.3

(cf. [7]) If

$$\displaystyle \begin{aligned} {\boldsymbol{\varphi}}(t):=((1/2)\sin{}(t)-t,t)\quad (t\in[0,+\infty)) \end{aligned}$$

is a derivo-periodic solution (cf. [8]) of the kinetic system (22) and the variational system (24) has the form

$$\displaystyle \begin{aligned} \dot{\mathbf{v}}=A\mathbf{v} {} \end{aligned} $$

(29)

with

$$\displaystyle \begin{aligned} A(t):\equiv\left[\begin{array}{cc} \sin{}(t)/(2-\cos{}(t))-2 & \cos{}(t)-2 \\ 2/(2-\cos{}(t)) & 1 \end{array}\right], \end{aligned}$$

then

$$\displaystyle \begin{aligned} \mathbf{p}(t):\equiv \dot{{\boldsymbol{\varphi}}}(t)\equiv((1/2)\cos{}(t)-1,1) \end{aligned}$$

is a 2π-periodic solution of (29). It follows that

$$\displaystyle \begin{aligned} \int_0^{2\pi}\left\{\frac{\sin{}(t)}{2-\cos{}(t)}-1\right\}\,\mathrm{d}t=-2\pi<0, \end{aligned}$$

thus p is orbitally asymptotically stable.

Example 3.4 (Biochemical Oscillator)

If ν, μ, η > 0 and the function g belongs to $\mathfrak {C}^1(\mathbb {R}^2,\mathbb {R})$ then certain biochemical systems can be modelled by

$$\displaystyle \begin{aligned} \left.\begin{array}{l} \dot{u}_1=\nu-g(u_1,u_2)=:f_1(u_1,u_2), \\ \dot{u}_2=\eta\nu-\mu u_2+g(u_1,u_2)=:f_2(u_1,u_2) \end{array} \right\} {} \end{aligned} $$

(30)

where

$$\displaystyle \begin{aligned} g(0,u_2)\leq0,\qquad g(u_1,0)\geq0\qquad (u_1,u_2\geq0) \end{aligned}$$

and

$$\displaystyle \begin{aligned} \partial_1g(u_1,u_2)>0,\qquad \partial_2g(u_1,u_2)>0\qquad (u_1,u_2>0) \end{aligned}$$

holds. If for all u ₂ > 0

$$\displaystyle \begin{aligned} \lim\limits_{u_1\rightarrow+\infty}g(u_1,u_2)>u_2 \end{aligned}$$

then (30) has a unique equilibrium (a, b) with b = (1 + η)ν∕μ in the positive quadrant of the phase space. If

$$\displaystyle \begin{aligned} \gamma:=\partial_2g(a,b)-\partial_1g(a,b)-\mu>0 \end{aligned}$$

then (a, b) is unstable and (30) has a T-periodic solution p which is orbitally asymptotically stable (Fig. 3).

Fig. 3

Phase portrait of the system (30) in case $g(u_1,u_2):\equiv u_1u_2^2$

Theorem 3.2 (cf. [12, 16])

If

• δ < 0 and d ₁ = d ₂ or the difference |d ₁ − d ₂| is sufficiently small then p is also an orbitally asymptotically stable periodic solution of (23)–(2).

• δ < 0,

  $$\displaystyle \begin{aligned} \displaystyle\int_0^T\partial_2f_2(\mathbf{p}(t))\,\mathrm{d}t>0, \end{aligned}$$

  for small 𝜖 > 0 d ₂ = 𝜖 and d ₁ = 𝜖 ⁻¹ , then p is an orbitally asymptotically stable solution of (22) but unstable solution of (23)–(2).

Clearly, the periodic solution in Example 3.2 remains orbitally asymptotically stable:

$$\displaystyle \begin{aligned} \int_0^{2\pi}-2\lambda\sin^2(\omega t)\,\mathrm{d}t=-2\lambda\pi<0, \end{aligned}$$

while the solution in Example 29 becomes unstable:

$$\displaystyle \begin{aligned} \int_0^{2\pi}\,\mathrm{d}t=2\pi>0. \end{aligned}$$

The condition for change of stability in case of Example 3.4 is

$$\displaystyle \begin{aligned} \displaystyle\int_0^T\partial_2g(\mathbf{p}(t))\,\mathrm{d}t>\mu T. \end{aligned}$$

3.1 Bifurcation of Time-Periodic Patterns

The linearized system of (23) at p is

$$\displaystyle \begin{aligned} {\mathbf{v}}_t=D\Delta_{\mathbf{r}} \mathbf{v}+({\mathbf{f}}^{\prime}\circ\mathbf{p})\mathbf{v} {} \end{aligned} $$

(31)

with boundary conditions

$$\displaystyle \begin{aligned} (\mathbf{n}\cdot\nabla_{\mathbf{r}})\mathbf{v}=0\qquad \text{on}\qquad \partial\Omega\times\mathbb{R}^+_0 {} \end{aligned} $$

(32)

and smooth initial conditions

$$\displaystyle \begin{aligned} \mathbf{v}(\mathbf{r},0)={\mathbf{v}}_0(\mathbf{r})\geq0\qquad \text{on}\qquad \overline{\Omega}\times\{0\}, {} \end{aligned} $$

(33)

Using the method of Fourier we obtain a sequence of solutions of (31) and (32):

$$\displaystyle \begin{aligned} {\boldsymbol{\Lambda}}_{kn}\left(\mathbf{r}, t\right)=\psi_n\left(\mathbf{r}\right) \cdot{\boldsymbol{\varphi}}_{nk}\left(t\right)\qquad \left((\mathbf{r}, t)\in\overline{\Omega}\times\mathbb{R}^+_0\right) \end{aligned}$$

$$\displaystyle \begin{aligned} (n\in\mathbb{N}_0,\;k\in\{1,2\}), \end{aligned}$$

where ψ _n is the (eigenfunction-)solution of the problem

$$\displaystyle \begin{aligned} \Delta_{\mathbf{r}}\psi=-\lambda_n\psi,\qquad \qquad \partial_{\mathbf{n}}\psi \big|{}_{\partial\Omega}=0 \end{aligned}$$

and

$$\displaystyle \begin{aligned} {\boldsymbol{\varphi}}_{nk}:[0,+\infty)\rightarrow\mathbb{R}^2\qquad (k\in\{1,2\}) \end{aligned}$$

are two linearly independent solutions satisfying

$$\displaystyle \begin{aligned} \dot{{\boldsymbol{\varphi}}} =\left({\mathbf{f}}^{\prime}\circ\mathbf{p}-\lambda_nD\right){\boldsymbol{\varphi}} {} \end{aligned} $$

(34)

for fixed n. In order to consider the initial condition (33) let us introduce the notation

$$\displaystyle \begin{aligned} {\boldsymbol{\Lambda}}_{{n}}:=\int_{\Omega}{\mathbf{v}}_{0}\left(\mathbf{r}\right) \psi_{n}\left(\mathbf{r}\right)\,\mathrm{d}\mathbf{r}. \end{aligned}$$

Thus the solution of (31) and (32) has the form

$$\displaystyle \begin{aligned} {\boldsymbol{\Lambda}}\left(\mathbf{r},t\right)=\sum_{n=0}^\infty\psi_{n}\left(\mathbf{r} \right)\exp\left(A_nt\right){\boldsymbol{\Lambda}}_{{n}}\quad \left((\mathbf{r}, t)\in\overline{\Omega}\times\mathbb{R}^+_0\right) \end{aligned}$$

where

$$\displaystyle \begin{aligned} A_n:={\mathbf{f}}^{\prime}\circ\mathbf{p}-\lambda_nD\qquad \text{and} \qquad \exp\left(A_n0\right)=I. \end{aligned}$$

Introducing the notation

$$\displaystyle \begin{aligned} \exp\left(A_nt\right){\boldsymbol{\Lambda}}_{{n}}\equiv:\alpha_{n1}{\boldsymbol{\omega}}_{{n1}}(t)+\alpha_{n2}{\boldsymbol{\omega}}_{{n2}}(t) \end{aligned}$$

and denoting the Floquet-multipliers of (34) by μ _nk $(n\in \mathbb {N}_0$, k ∈{1, 2}) one can assume that in the stable case μ ₁₀ = 1 holds and all other multipliers are in modulus less than one. If d ₂ increases then at a certain critical value d _∗ the multiplier μ ₁₁ = 1 while the rest of the multipliers stay in modulus less than 1. In this situation system (34) has one periodic solution ω ₁₁, while another (linearly independent) solution tends exponentially to zero. In this case

$$\displaystyle \begin{aligned} {\boldsymbol{\Lambda}}\left(\mathbf{r},t\right)-(\alpha_{n0}p(t)+\alpha_{11}{\boldsymbol{\omega}}_{{11}}(t) \psi_{1}\left(\mathbf{r}\right))\longrightarrow\mathbf{0}\qquad (t\rightarrow\infty) \end{aligned}$$

where

$$\displaystyle \begin{aligned}{}[0,+\infty)\ni t\mapsto\mathbf{P}(t):=\alpha_{n0}\mathbf{p}(t)+\alpha_{11}\psi_{1}\left(\mathbf{r}\right){\boldsymbol{\omega}}_{{11}}(t) \end{aligned}$$

is the time periodic spatially non-constant solution of (31) and (32), which is called time-periodic pattern (Fig. 4).

Fig. 4

Periodic pattern for system (30) in case $g(u_1,u_2):\equiv u_1u_2^2$

Finally, we note that this pattern P is only a solution of the linearized system (31) and (32). About the extension of this result to the nonlinear system (23)–(2) we refer the reader to [15].