A New Approach to the Supercomputer Simulation of Carbon Burning Sub-grid Physics in Ia Type Supernovae Explosion

Abstract

Supernovae are the major sources of elements in the periodic table, planets, and life. Type Ia supernovae (SNeIa) are not only sources of elements, but also “standard candles” to measure distances in the Universe. We propose a mechanism of carbon burning that causes non-standard Type Ia supernova explosions. The mechanism is based on intensity variations in the incomplete nuclear burning of carbon. In this case, the explosion energy can vary significantly due to the presence of different regimes of carbon burning during the development of turbulence in the burning zone. The energy released during burning, sufficient for the explosion of a white dwarf (as a type Ia supernova), can be achieved with a smaller Chandrasekhar mass. In addition, the explosion energy of a white dwarf with a Chandrasekhar mass can differ considerably. Such a conclusion can be made from modern observations of incomplete burning and chemistry of burning, which determine the explosion energy. In the present paper, a software tool is proposed to demonstrate a significant difference in the values of the explosion energy obtained with different parameterizations of subgrid carbon burning. For computational experiments, we use a code developed by the authors, which is extended using an adaptive nested grid approach to achieve a more accurate reproduction of turbulent burning.

1 Introduction

Supernovas are the major sources of “life” elements—from carbon to iron. Type Ia supernovas are very bright and, therefore, are used as “standard candles” to determine distances to galaxies and the expansion rate of the Universe. The mathematical simulation of supernova explosions is the major tool for studying their dynamics and formation. The formation of complex flows in supernova explosions imposes rigid requirements on the spatial resolution of the simulation. The major scenario [17] of supernova explosion is based on the merging of two degenerate white dwarfs with the subsequent collapse of a new star when it reaches the Chandrasekhar mass, ignition of the carbon burning process, and type Ia supernova explosion.

The realistic computer simulation of SNeIa remains an unsolved problem. However, there exist some approaches to solving this problem. These are the collision of white dwarfs [28, 37, 38], violent merger [34, 40], spiral instability [18, 19], and tidal heating [8], D6 [13, 34, 41]. In the present paper, no review of possible scenarios is made: it is also too early to compare our preliminary results with those of other authors; it is planned to do this in the forthcoming paper. Here the process of the noncentral ignition of a white dwarf in a merging close pair, first studied in [16], is considered. This model will be extended with modern computational tools enabling a more detailed description of the process of nuclear carbon burning. The model demonstrates that tidal heating shifts the maximum temperature point in a degenerate dwarf from the center to the mantle.

Noncentral explosions should be studied for the following reason: the observed “dipole” character of SNeIa explosions is typically explained by the presence of a close satellite of a degenerate dwarf [5], although it may be a result of a noncentral explosion. Both scenarios are considered in the present paper. Double detonation, which can cause a noncentral explosion, is due to other chemistry and other masses of the explosion point [12]. Tidal heating is also studied in [8]. It should be noted that the noncentral location of the explosion point can be caused by other reasons: helium layer detonation, magnetic field, jet formation, etc. Therefore, a comprehensive study of possible noncentral explosions is of great interest.

The goal of this paper is to determine the role of the ignition point in nuclear fuel burning and in the dynamics of the remnants of a degenerate dwarf explosion. For this, the nuclear burning of carbon in the development of supersonic turbulence will be simulated directly, not as a subgrid process. The computational model is implemented by using distributed computing: the hydrodynamic evolution of white dwarfs is simulated on nested meshes (basic calculation). As the temperature and density reach some critical values, a new task is started on a distributed memory architecture to simulate the development of hydrodynamic turbulence leading to supersonic nuclear carbon burning (satellite calculation).

The present paper is devoted to the study of the pattern of 3D gas dynamical explosions of carbon dwarfs. The main parameter of the problem is the intensity of the nuclear burning of carbon in the explosion zone. In this case, the explosion energy can vary considerably due to the variable carbon burning regime during the development of turbulence in the burning region. The goal of this study is to assess the impact of some so far undetermined parameters and factors on the observed manifestations of explosions and on the limits to what extent SNeIa can be considered “standard”.

In the second section, a numerical model of white dwarfs is formulated. The third section describes the parallel and distributed organization of calculations for a detailed description of turbulent carbon burning and explosion hydrodynamics. The fourth section is devoted to the results of computational experiments. In the fifth section, we will discuss some important issues. The sixth section provides conclusions to the paper.

2 Numerical Model

2.1 Hydrodynamic Equations

Consider an overdetermined conservative form of the equations of gravitational gas dynamics: the law of conservation of mass

$$\begin{aligned} \frac{\partial \rho }{\partial t} + \nabla \cdot (\rho \mathbf {u}) = 0, \end{aligned}$$

(1)

the law of conservation of momentum

$$\begin{aligned} \frac{\partial \rho \mathbf {u}}{\partial t} + \nabla \cdot (\rho \mathbf {u} \mathbf {u}) = - \nabla p - \rho \nabla \varPhi , \end{aligned}$$

(2)

the law of conservation of total mechanical energy

$$\begin{aligned} \frac{\partial }{\partial t} \left[ E + \rho \frac{\mathbf {u}^2}{2} \right] + \nabla \cdot \left( \left[ E + \rho \frac{\mathbf {u}^2}{2} \right] \mathbf {u} \right) = - \nabla \cdot \left( p \mathbf {u}\right) - \left( \rho \nabla \varPhi ,\mathbf {u} \right) + Q, \end{aligned}$$

(3)

and the equation for entropy S

$$\begin{aligned} \frac{\partial \rho S}{\partial t} + \nabla \cdot (\rho S \mathbf {u}) = \frac{2 Q}{3 \rho ^{2/3}}, \end{aligned}$$

(4)

supplemented by the Poisson equation for the gravitational potential

$$\begin{aligned} \varDelta \varPhi = 4 \pi G \rho , \end{aligned}$$

(5)

where $\rho$ is the density, $\mathbf {u}$ is the velocity, p is the pressure, $\varPhi$ is the gravitational potential, E is the internal energy of the gas, G is the gravitational constant, and Q is the energy source due to nuclear reactions.

2.2 Stellar Equation of State

The stellar equation of state consists of the pressure of a nondegenerate hot gas, the pressure due to radiation, and a degenerate gas [42]. In the case of a degenerate gas, relativistic and nonrelativistic regimes are considered. In the equation of state $p = \left( \rho , T \right)$, p will be sought for as the sum of four components:

$$\begin{aligned} p = p_{rad} + p_{ion} + p_{deg,nrel} + p_{deg,rel}, \end{aligned}$$

(6)

where T is the temperature, $p_{rad}$ is the radiation pressure, $p_{ion}$ is the pressure of a nondegenerate hot gas (ions), $p_{deg,nrel}$ is the pressure of a degenerate nonrelativistic gas, and $p_{deg,rel}$ is the pressure of a degenerate relativistic gas. Let us present formulas for each pressure type:

$$\begin{aligned} p_{rad} = \frac{4 \sigma T^4}{3 c}, \end{aligned}$$

(7)

where c is the speed of light, and $\sigma$ is the Stefan-Boltzmann constant. Let us write the pressure of a cold gas in terms of an entropy function:

$$\begin{aligned} p_{ion} = \frac{k}{\mu } T \rho = S \rho ^{5/3}, \end{aligned}$$

(8)

where k is the Boltzmann constant, and $\mu$ is the chemical potential,

$$\begin{aligned} p_{deg,nrel} = \left\{ \begin{array}{c} \rho _{0} K_{deg,nrel} \left( \frac{\rho }{\rho _{0} \mu _{e}} \right) ^{5/3}, \rho < \rho _{0}\\ 0, \rho > \rho _{0} \end{array} \right. , \end{aligned}$$

(9)

where $K_{deg,nrel} = 10^{13}$ Erg/g, $\mu _{e}$ is the number of nucleons per electron, and $\rho _{0} = 10^{6}$ g/cm$^{3}$,

$$\begin{aligned} p_{deg,rel} = \left\{ \begin{array}{c} \rho _{0} K_{deg,rel} \left( \frac{\rho }{\rho _{0} \mu _{e}} \right) ^{4/3}, \rho > \rho _{0}\\ 0, \rho < \rho _{0} \end{array} \right. , \end{aligned}$$

(10)

where $K_{deg,rel} = 10^{15}$ Erg/g. In this case, the internal energy is written as

$$\begin{aligned} E = E_{rad} + E_{ion} + E_{deg,nrel} + E_{deg,rel} \end{aligned}$$

(11)

$$ = 3 p_{rad} + \frac{3}{2} p_{ion} + \frac{3}{2} p_{deg,nrel} + 3 p_{deg,rel}. $$

The formulation of pressure and internal energy in terms of the entropy function makes it possible to calculate temperature variations without solving a nonlinear equation.

2.3 Initial Profile

To specify the equilibrium initial data, we fix the initial temperature T and the characteristic density. The latter is important for determining the adiabatic index of a degenerate gas. Assume that the adiabatic index $\gamma$ is determined as a constant K at the exponential function for the pressure of a degenerate gas (9) or (10). Let us present the balance of pressure and gravity forces in Eq. (2) and Poisson Eq. (5) in spherical one-dimensional coordinates using ordinary differential equations:

$$ -\frac{d p}{d r} = \rho \frac{d \varPhi }{d r}, \qquad \frac{d}{d r} \left( r^2 \frac{d \varPhi }{d r} \right) = 4 \pi G r^2 \rho , $$

where r is the spherical radius. With the fixed parameters, we obtain an equation of the Emden type:

$$ -\frac{d}{d r} \left( \frac{r^2}{\rho } \frac{d}{d r} \left[ \frac{4 \sigma }{3 c} T^4 + \frac{k}{\mu } T \rho + K \rho ^{\gamma } \right] \right) = 4 \pi G r^2 \rho . $$

It is evident that the radiation term $\frac{4 \sigma }{3 c} T^4$ does not depend on the radius r. Therefore, the equation for the equilibrium density profile can be written as

$$\begin{aligned} -\frac{d}{d r} \left( \frac{r^2}{\rho } \frac{d}{d r} \left[ \frac{k}{\mu } T \rho + K \rho ^{\gamma } \right] \right) = 4 \pi G r^2 \rho . \end{aligned}$$

(12)

Equation (12) can be solved numerically [43]. To speed up the iterative process, one can linearize the equation and use the solution to the linearized problem as an initial temperature approximation.

2.4 Carbon Burning

When burning carbon in white dwarfs, the main way to obtain heavy elements (such as nickel and iron) is to pass the $\alpha$-network [39]. Since we are primarily interested in the explosion energy, we will consider a chain of reactions of the form $14 \times ^{12}C \rightarrow 3 ^{56} Ni$. Let $X_C$ be the abundance of carbon. Carbon burning may be written as [11]

$$\begin{aligned} \frac{d X_c}{dt} = -\frac{7}{36} \times \rho \times N_A \times \lambda \times X_c^2, \end{aligned}$$

(13)

where $\rho$ is the density, $N_A$ is the Avogadro number, and $\lambda$ is the reaction rate, which can be written as

$$\begin{aligned} \lambda = \frac{1.26 \times 10^{27} \times T_{9a}^{\frac{5}{6}} \times T_{9}^{-\frac{3}{2}} \times exp \left( -84.165 \times T_{9a}^{-\frac{1}{3}} \right) }{ N_A \times \left( exp \left( -0.01 \times T_{9a}^{4} \right) + exp \left( 1.685 \times T_{9a}^{\frac{2}{3}} \right) \right) }, \end{aligned}$$

(14)

where $T_9$ is a temperature of 10$^9$ K, $T_{9a} = T_9 / \left( 1 + 0.067 \times T_9 \right)$. The energy release is determined as follows:

$$\begin{aligned} Q = - \rho \times \varepsilon \times \frac{d X_c}{dt} = \frac{7 \times \varepsilon }{36} \times \rho \times N_A \times \lambda \times X_c^2, \end{aligned}$$

(15)

where $\varepsilon = 7 \times 10^7$ Erg/g [20].

The burning rate in the above equation cannot be found with the IEEE 754 standard. Therefore, we use the following method:

$$ 10^{27} \times exp \left( -84.165 \times T_{9a}^{-\frac{1}{3}} \right) = exp \left( 27 \times ln 10 - 84.165 \times T_{9a}^{-\frac{1}{3}} \right) . $$

This expression can be represented in the IEEE 754 floating point standard and used in calculations.

Fig. 1.

Schematic diagram of Parallel & Distributed computing on nested grids (blue color) and regular grids (red color). (Color figure online)

3 Parallel & Distributed Code

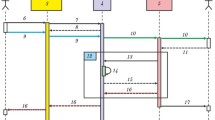
To simulate the evolution of white dwarfs, supernova explosions, and turbulent carbon burning, we will use a modification of our code published in [22, 23, 25]. Figure 1 shows a schematic diagram of the calculations. Nested grids are used to simulate the basic process of the evolution of white dwarfs. In the subgrid carbon burning process, the evolution of a cell where carbon burning takes place is simulated on regular grids. Note that the simulations on the nested and regular grids are performed with all MPI processes being used. The calculation algorithm is as follows:

• 1. Construct a workable nested grid configuration to simulate the hydrodynamics of a single dwarf or a system of white dwarfs. For this, a simulation corresponding to the simple analytics described in Sect. 2.4 can be performed on regular grids using subgrid carbon burning. This configuration is used to minimize the reconstruction of nested grids. The nested grid configuration turns out to be appropriate, and the Increase/Decrease operations with the nested grids do not require additional balancing of data loading.

• 2. Balance the loading of calculations on the nested grids between the MPI processes (see Sect. 3.2 for a detailed description of the balancing).

• 3. Determine a single time step $\tau _{WD}$ in solving the hydrodynamic equations to describe the evolution of white dwarfs on nested grids. For this, the maximum velocity $v_{max}$ and the sound speed $c_{max}$ are determined for all cells of the nested grids. For definiteness, let $h_{min}$ be the minimum cell size of the nested grids, and let CFL be the Courant number. In this case, the time step is calculated from the condition

  $$\begin{aligned} \frac{ \left( v_{max} + c_{max} \right) \tau _{WD}}{ h_{min} } = CFL. \end{aligned}$$

  (16)

  This method of determining the time step provides the uniqueness of the numerical solution on nested grids, since in this case the characteristics obtained from the Riemann problems on the nested grid cells do not intersect. Note that this calculation method allows using nested grids with any ratio of the neighboring cells (not only $1\!:\!2$, as described in [4]).

• 4. Calculate the hydrodynamics of the evolution of white dwarfs in time $\tau _{WD}$ on nested grids (see Sect. 3.2 for a detailed description of the calculation).

• 5. Define nested grid cells (i, j, k, l, m, n), where (i, j, k) is the number of a root grid cell, and (l, m, n) is the number of the nested grid cell (i, j, k); in these cells there is a carbon burning trigger $T = 10^9$ K, and a density $\rho = 10^7$ g cm$^{-3}$. Form a list of cells $R_n$, $n = 1, \ldots , K$, where K is the number of cells with the real trigger of carbon burning.

• 6. For all cells $R_n$, $n = 1, \ldots , K$, to implement subgrid turbulent carbon burning, perform an individual simulation of hydrodynamic turbulence. The size of the simulated domain is equal to that of the cell $h_n$, $\tau _{WD}$ is the turbulence simulation time, $\rho _0 = \rho _n$ is the initial density, $T_0 = T_n$ is the temperature, and $\sigma ^2_n$ is the velocity dispersion, which is determined from the neighboring cells (see Sect. 3.1 for a detailed deception of turbulent carbon burning). All problems of turbulent burning are simulated sequentially on a regular grid using all MPI processes. The percentage of burned carbon and the released energy are returned to the corresponding cell of the nested grids (i, j, k, l, m, n). The calculation of the hydrodynamic equations on regular grids is described in detail in [25].

Such an organization of calculations naturally requires great computational costs, since a single problem of hydrodynamic turbulence is calculated in a large number of cells. Note that the calculation time needed for turbulence problems is two orders of magnitude greater than that for the hydrodynamics of the evolution of white dwarfs. Therefore, the speedup and scalability of Parallel & Distributed computing are determined by the source code and coincide with those obtained in [25]. Section 3.3 presents the estimates of the efficiency of a code modification for the calculation on nested grids.

3.1 Turbulence Model of Carbon Burning

When the temperature in the cell reaches a critical value, $T = 10^9$ K, and the density $\rho = 10^7$ g cm$^{-3}$, distributed calculations of the hydrodynamic turbulence of carbon burning are launched on a regular mesh, and the results are returned to the main calculation of hydrodynamics. Carbon burning during the development of turbulence [7] and in the process of a collapse [27] are considered by many authors. We propose a method when turbulent carbon burning takes place “on the fly” when calculating the basic hydrodynamics of the process. In [26], we study in detail the development of hydrodynamic turbulence with and without self-gravity forces. In the present paper, gravitation is neglected, since the characteristic time of the process is much less than the free fall time. However, if necessary, we can take into account the collapse process (as in [27]) or self-gravity forces in the development of hydrodynamic turbulence [26].

The critical density $\rho = 10^7$ g cm$^{-3}$ of the transition from deflagration to detonation is taken as a characteristic density value, and the temperature $T = 10^9$ K. The initial velocity perturbation at a known turbulence energy, $\sigma ^2$, is taken from [1]. Let us describe this procedure in detail. Consider the energy spectrum $E(k) = A \times k^{-5/3}$ with the known turbulence energy, $\sigma ^2$. Then the coefficient A can be found from the equation

$$\begin{aligned} \int _{k_{min}}^{k_{max}} E(k) dk = \sigma ^2, \end{aligned}$$

(17)

where $k_{min}$ and $k_{max}$ are the minimum and maximum wave numbers, respectively. The turbulent pulsation field $\mathbf {u}(x)$, where x is a space point, is given by the equation

$$\begin{aligned} \mathbf {u}(x) = \frac{3 \sigma }{\sqrt{2N}} \sum _{n=1}^{N} \mathbf {u}_n (x), \end{aligned}$$

(18)

where N is the number of harmonics. Each of the harmonics is given by the equation

$$\begin{aligned} \mathbf {u}_n (x) = Q \left( w^n \right) \left[ \xi ^n sin \left( k_n \left( w^n , x \right) \right) + \eta ^n cos \left( k_n \left( w^n , x \right) \right) \right] , \end{aligned}$$

(19)

where $w^n = \left( w_1^n, w_2^n, w_3^n \right)$ is the unit vector uniformly distributed over the sphere to provide $\nabla \cdot \mathbf {u} = 0$, $Q \left( w^n \right)$ is a random matrix with elements $q_{ij}^n = \delta _{ij} - w_i^n \times w_j^n$, $\delta _{ij}$ is the Kronecker symbol, the coefficients $\xi ^n$ and $\eta ^n$ have the standard Gaussian distribution N(0, 1). The wave numbers $k_n$ are distributed with the density $\rho (k) = E(k) / \sigma ^2$.

The model of subgrid carbon burning based on turbulent burning being used exactly corresponds to the model described in [10]. The main difference is as follows: the process of subgrid turbulence starts when the critical temperature of carbon burning is reached. This is primarily due to computational aspects. In the present paper, the critical temperature is used to start the burning process, and the “turbulization” of the medium increases the efficiency of burning. In [10], a temperature starting from $T = 10^8$ K is considered, and the use of such an initial temperature is mainly motivated by the reproduction of the initial burning front. In our study, we use the energy component where the kinetic energy of turbulence transforms to the internal energy and becomes an additional trigger for carbon burning intensification and, hence, for obtaining more explosion energy with less fuel consumption. In this way we demonstrate a possible SNeIa explosion scenario at masses smaller than the Chandrasekhar mass.

3.2 Nested Grid

To discretize with nested grids, we introduce, in a three-dimensional solution domain, a uniform cubic root grid with the coordinates of the centers of cells $x_{i}=i \times h - h/2$, $i=1,..,I_{max}$, $y_{k}=k \times h - h/2$, $k=1,..,K_{max}$, $z_{l}=l \times h - h/2$, $l=1,..,L_{max}$, where h is the root grid spacing, $I_{max}$, $K_{max}$, $L_{max}$ is the number of cells in the x, y, z directions, respectively. In this implementation, for the convenience of organizing calculations and without loss of generality of the code, we use $I_{max} = K_{max} = L_{max} = N$. In a cell (i, k, l), we introduce a nested cubic grid with the coordinates of the centers of cells $x_{i,nested}=i \times h_{nested} - h_{nested}/2$, $i=1,..,M$, $y_{k,nested}=k \times h_{nested} - h_{nested}/2$, $k=1,..,M$, $z_{l,nested}=l \times h_{nested} - h_{nested}/2$, $l=1,..,M$, where $h_{nested}$ is the nested grid spacing, and M is the number of nested grid cells in the x, y, z directions. The hydrodynamic equations will be calculated for quantities in the cells of the root and nested grids. A detailed arrangement of the hydrodynamic quantities in the calculations is shown in Fig. 2. Solving the equations of hydrodynamics (finding solutions to the Riemann problems) consists of the following two steps:

• 1. solving the Riemann problems at all nested grid boundaries,

• 2. solving the Riemann problems at all internal nested grid interfaces.

Fig. 2.

Arrangement of hydrodynamic quantities on the root and nested grids: the hydrodynamic parameters on the root grid (blue asterisks), the hydrodynamic parameters on the nested grid (red circles), nested grid nodes (yellow rhombuses), the Riemann problem solution at the interfaces between the internal cells of the nested grid, the intraboundary cells of the nested grid, and the cells of the neighboring root cell (green rectangles). (Color figure online)

Fig. 3.

Three types of arrangement of the cells of neighboring nested grids: a cell for which the Riemann problem is solved (pink color), and a cell of the neighboring nested grid (blue color) (Color figure online)

Fig. 4.

Refinement (top) and coarsening (bottom) of the nested grid

Whereas the second step of finding solutions to the Riemann problems is trivial, the first step requires a specific method of calculations depending on the cell sizes of two neighboring nested grids. Only three types of arrangement of the cells of neighboring grids are possible (see Fig. 3). If the cell sizes are equal (Fig. 3 (middle)), the solution of the Riemann problem is similar to that of the Riemann problems at the internal interfaces of the nested grid, and is trivial. If the cell of the neighboring nested grid is larger than the one being considered (Fig. 3 (left)), it is assumed that the quantities in the blue cell have a uniform distribution, and the Riemann problem is solved at the interface between the decreased blue cell and the pink cell. If the pink cell borders on several cells of the neighboring nested grid (Fig. 3 (right)), a uniform distribution of the hydrodynamic quantities in the pink cell is assumed, the Riemann problems are solved at all interfaces, and then the fluxes are averaged. The grid is restructured according to the root cell mass. The size of the nested grid is calculated from the condition

$$\begin{aligned} M = 2^{\mathcal {C}_1 \lfloor log \left( \rho \right) \rfloor + \mathcal {C}_2}, \end{aligned}$$

(20)

where $\mathcal {C}_{1,2}$ are the scaling constants chosen according to the requirements of the characteristic density and the minimum resolution of the problem. We use $\mathcal {C}_{1} = 1$ and $\mathcal {C}_{2} = 5$ as characteristic parameters in this work, i.e., at the characteristic carbon combustion density $\rho = 10^7$ g cm$^{-3}$, a grid with an effective resolution of $4096^3$ is used. At each time step, it is checked whether the grid needs to be restructured. Therefore, the grid is changed not more than by a factor of two. The grid restructuring scheme is shown in Fig. 4. Figure 4 illustrates the projections of the conservative quantities (density, angular momentum, entropy density, and total energy). Once the grid is restructured, the nonconservative quantities (primitive in the case of relativistic hydrodynamics) are calculated from the conservative variables. A detailed description of the calculation for the hydrodynamic equations in nested grids can be found in [24]. To balance the load between the processes, we use the following algorithm performed by all MPI processes (P processes in total) located on individual nodes:

• 1. Calculate the number of nested grid cells in each slice (YZ plane) of the root grid $W_i$, where $i = 1,\ldots ,N$ and N is the number of root grid cells in the X-direction.

• 2. Determine the average number of cells in the slice for the entire root grid $M = \sum {W_i}/P$, and distribute this value as evenly as possible between the processes.

• 3. Set $k = 1$, where k is the number of the process for which the slice thickness is formed.

• 4. Set $i = 1$, where $1 \le i \le N$ is the number of the slice.

• 5. Set $N_k = 0$, where $N_k$ is the slice thickness of the kth process.

• 6. If $N_k + W_i > M$, $N_k$ is the final slice thickness for the processor k. Increase k by unity and go to step 5. Otherwise, go to step 7.

• 7. Increase the slice thickness $N_k$ by $W_i$, increase the number of the slice i by unity and go to step 6.

As a result, the slice thicknesses between the processes differ by no more than unity. To perform the boundary layer exchange between the overlapping nested grids, a plan of overlapping YZ planes for nested grids is formed.

3.3 Performance

To perform calculations and computational experiments, we use a hybrid supercomputer, NKS-1P of the Siberian Supercomputer Center at ICM & MG SB RAS (16 nodes, RSC Tornado Phi architecture: Intel Xeon Phi 7290 1.5 GHz, 72 cores, 16 GB MCDRAM; 96 GB DDR4 DRAM; Intel Omni Path 100 Gb/s interconnect). The performance of the solver on regular grids is estimated in [25]. In the parallel implementation on nested grids, we use a $128^3$ root grid and the following three configurations of nested grids:

• 1. Config 1: All nested grids have a size of 4$^3$ (a uniform grid with an effective resolution of $512^3$).

• 2. Config 2: 75% of nested grids have a size of 2$^3$, and 25% have a size of 8$^3$ (the effective resolution is 1024$^3$).

• 3. Config 3: 75% nested grids have a size of 2$^3$, 15% have a size of 8$^3$, and 10% have a size of 32$^3$ (the effective resolution is 4096$^3$).

The code speedup for some nested grid configurations is presented in Table 1. At a uniform distribution of calculations, we have a 38-fold code speedup; less uniform calculations drop the speedup to 34-fold, which is achieved with fewer threads. In a study of scalability when the grid configuration is doubled for a given number of processes, it is found that the scalability corresponds to the source code one and is about 96% with 16 Intel Xeon Phi 7290 accelerators.

Table 1. Speedup.

4 Numerical Simulation of SNeIa Explosion

Here we consider two components of the problem of type Ia supernova explosion: turbulent carbon burning and an experimental study of the energy released at various perturbations, and the hydrodynamics of SNeIa explosion.

4.1 Turbulence Carbon Burning

To study various regimes of turbulent carbon burning, we will consider a 100 km$^3$ domain with the density $\rho = 10^7$ g cm$^{-3}$ and the temperature $T = 10^9$ K with a normal velocity distribution and a Mach number of the root-mean-square deviation $\mathcal {M}_{RMS}$. The characteristic density corresponding to the density of the transition from deflagration to detonation in carbon burning is taken according to [14, 30, 45]. Figure 5 presents the results of simulation: the relative increase in the explosion energy versus the Mach number of the root-mean-square deviation $\mathcal {M}_{RMS}$. One can see in Fig. 5 that in considerable supersonic turbulence, the explosion energy can have a relative increase of more than three times. In the present paper, the question of whether such a turbulence regime can be achieved in the merging of white dwarfs is not considered. In what follows, we will study how the explosion energy affects the explosion hydrodynamics pattern. This issue has been actively studied recently, for instance, in [2, 29]. The simulation with all the resources of the Siberian Supercomputer Center (16 Intel Xeon Phi 7290 and 72 physical cores in an accelerator on a regular $256^3$ calculation grid) is about 10 min. When simulating an SNeIa explosion on the basis of the merging of white dwarfs and the asymmetric explosion of a single dwarf, the typical time step, $\tau _{WD}$, is 10 ms. Thus, the typical calculation time of the next two problems using the approach with the direct simulation of turbulent carbon burning is about one week. As mentioned earlier, the major computational load is the reproduction of turbulent carbon burning as an individual problem. In a series of experiments, we consider the turbulent combustion of carbon at various perturbation velocity dispersions. The kinetic energy obtained from the nonzero dispersion of perturbation velocities is converted into the internal energy and, as a result, into a more intense mode of carbon combustion, which gives a greater energy yield compared to static combustion used in classical methods for specifying subgrid processes. In further calculations, we use this problem as a component for describing the subgrid process of carbon combustion.

Fig. 5.

Relative increase in the explosion energy versus Mach number of the root-mean-square deviation $\mathcal {M}_{RMS}$. The basic explosion energy corresponds to an energy release of $10^{51}$ Erg.

4.2 Hydrodynamics of SNeIa Explosion

We identified 11 possible scenarios (see Fig. 6) of a supernova explosion, which differ in the hydrodynamics of the process:

• 1. The merger of white dwarfs [15] is the classical scenario of a merger of two white dwarfs with the achievement of a mass greater than the mass of Chandrasekhar and the subsequent explosion of a type Ia supernova (see Fig. 6I).

• 2. The off-center collision of white dwarfs [37] is a collision of two white dwarfs of arbitrary masses moving in parabolic orbits. The high kinetic energy and, therefore, the interaction energy lead to the launch of the nuclear combustion of the material of white dwarfs, followed by a type Ia supernova explosion (see Fig. 6II).

• 3. The central collision of white dwarfs [38] is a degenerate scenario of a high-velocity collision of two white dwarfs, followed by a type Ia supernova explosion (see Fig. 6III).

• 4. The close passage of white dwarfs [28] is a motion of white dwarfs along parabolic trajectories without collision. The high speed of movement prevents the dwarfs from entering the merge mode (see Fig. 6IV).

• 5. The forced fusion of white dwarfs of equal [34] and different masses [40] is a merger of white dwarfs forced out of equilibrium due to a mass difference of 20% or the slowing down of the dwarf’s velocity in a tight binary pair. Both scenarios result in dwarf fusion and Chandrasekhar mass excess, leading to a Type Ia supernova explosion (see Fig. 6V).

• 6. The supernova explosion based on the development of spiral instability [18, 19] is a type Ia supernova explosion based on the development of turbulence in spirals in merging white dwarfs. The development of turbulence in high-density islands that are in spirals is the main explosion mechanism [10]. A feature of such turbulent combustion can be the occurrence of any scenario of the nuclear combustion of the material: detonation model [3], deflagration model [32], delayed detonation model [21] (see Fig. 6VI).

• 7. Tidal heating [8] is a scenario of the explosion of a new super or new type Ia based on a combination of tidal heating, accretion heating and material nuclear burning. The location of ignition due to tidal heating is a feature of this scenario. In the case of a surface explosion, the white dwarf degenerates into a new star. When the detonation point is deep enough, an off-center explosion of a type Ia supernova occurs (see Fig. 6VII).

• 8. The dynamic double detonation of double degenerate dwarfs of a pre-Chan-drasekhar mass or D6 [13] is a scenario of a merging of two degenerate dwarfs, one of which receives a shear momentum of the base relative to the nucleus. As a result, an instability of the Kelvin-Helmholtz type develops at the boundary between the nucleus and the shell of one of the dwarfs. Primary detonation occurs in dense waves of an unstable flow. The shock waves from waves come on the shell surface. At this moment, a second detonation, sufficient for the formation of a type Ia supernova, occurs (see Fig. 6VIII).

• 9. The tidal detonation of a white dwarf during the close passage of a black hole [41] is a scenario of a shell detonation of a white dwarf of an arbitrary mass and an explosion in the form of a type Ia supernova due to tidal heating caused by the close passage of a black hole. A preliminary analysis of such scenarios shows that a medium-mass black hole is sufficient (see Fig. 6IX).

• 10. The merger of a white dwarf with a star of main sequence [44] is another classical scenario of the merging of a white dwarf with a star of main sequence with achieving a mass greater than the Chandrasekhar mass, followed by a type Ia supernova explosion (see Fig. 6X).

• 11. The collision of a white dwarf type with a terrestrial planet is a hypothetical scenario of a collision of a white dwarf with a planet from the terrestrial type to a gas giant. The achieved Chandrasekhar mass and, in addition, the kinetic impulse obtained from the planet lead to a type Ia supernova explosion (see Fig. 6XI).

The consideration of these possible scenarios from the point of view of the hydrodynamics of the process can be reduced to three fundamentally different scenarios:

• 1. “Merger” is a scenario of stars interaction, among which three variants can also be distinguished: evolutionary merging, central and off-center collisions of stars.

• 2. “Gravity Shock” is a scenario with an explosion of a static or moving point of detonation. The movement of the detonation point is associated with the direction of the influence of the gravitational impact.

• 3. “Bubbles” is a multiple detonation when the number of detonation points can reach hundreds [9].

Next, we will demonstrate computational experiments to study these scenarios.

Fig. 6.

SNeIa Explosion Scenarios

Fig. 7.

Relative density distribution in the equatorial plane during the merger of white dwarfs and the subsequent type Ia supernova explosion at 0 s (a), 40 s (b), 60 s (c), and 70 s (d).

SNeIa Explosion Scenario Based on White Dwarf Merger. We will simulate two white dwarfs with solar masses and the temperature $T = 10^9$ K. The angular velocity of white dwarfs, v, is obtained from an analytical solution based on the following equality of the centripetal force and the force of gravity:

$$ \frac{v^2}{r} = G \frac{M_{\odot }}{r^2}, $$

where v is the equilibrium angular velocity, $M_{\odot }$ is the mass of dwarfs, and r is the distance between the dwarfs. The rotation speed of one of the dwarfs is decreased by 20%. This results in the merger of the white dwarfs. Figure 7 presents the simulation results: the initial state of the dwarfs, the beginning of the merging of the dwarfs, the state of the merging at the time of the explosion, and an asymmetric supernova Ia explosion. To simulate nuclear carbon burning, we use the perturbation rate obtained by simulating the hydrodynamics of the merging of the dwarfs. The simulation results (7) show that critical densities for starting detonation carbon burning are reached in the merger. The explosion dynamics is subsequently determined by the results of the non-center white dwarf explosion.

SNeIa Explosion Scenario Based on White Dwarf Central Collision. We will simulate two white dwarfs with solar masses and the temperature $T = 10^9$ K. The velocity of the central collision is equal to 1000 km s$^{-1}$. Figure 8 presents the simulation results: the initial state of the dwarfs, the beginning of the collision of the dwarfs, the late state of the collision, and an supernova Ia explosion. To simulate nuclear carbon burning, we use the perturbation rate obtained by simulating the hydrodynamics of the merging of the dwarfs. It can be seen from the simulation results that after the explosion, two diverging shock fronts, similar to jets, are formed. The whole simulation in general repeats the previous scenario.

Fig. 8.

Relative density distribution in the equatorial plane during the central collision of white dwarfs and the subsequent type Ia supernova explosion at 0 s (a), 20 s (b), 40 s (c), and 45 s (d).

SNeIa Explosion Scenario Based on White Dwarf Non Central Collision. We will simulate two white dwarfs with solar masses and the temperature $T = 10^9$ K. The velocity of the non-central collision is equal to 1000 km s$^{-1}$. Figure 9 presents the simulation results: the initial state of the dwarfs, the beginning of the collision of the dwarfs, the late state of the collision, and an supernova Ia explosion. To simulate nuclear carbon burning, we use the perturbation rate obtained by simulating the hydrodynamics of the merging of the dwarfs. The whole simulation in general repeats the previous scenarios.

Fig. 9.

Relative density distribution in the equatorial plane during the non-central collision of white dwarfs and the subsequent type Ia supernova explosion at 0 s (a), 20 s (b), 40 s (c), and 45 s (d).

Fig. 10.

Relative density distribution in the equatorial plane at explosion energy values of $1/2 \times E_{0}$ (a), $E_{0}$ (b), $2 \times E_{0}$ (c), $4 \times E_{0}$ (d).

Asymmetric Explosions of White Dwarfs. Let us simulate a single white dwarf with two solar masses and the temperature $T = 10^9$ K. The explosion zone is specified at a distance of 20% of the radius from the center. The explosion energy is specified with the values obtained in the previous subsection. Figure 10 presents the simulation results: the density distribution at the time when the explosion takes place in most of the star at various explosion energies. The simulation results (10) show that when the explosion force is considerable, the star collapses, and a thin shock wave from the supernova is formed. As the explosion energy decreases, the wave dissipates over a sufficiently large distance. It is obvious that in this case, the brightness of the supernova changes considerably depending on the carbon burning mode and the subsequent explosion energy. Increasing the explosion energy produces a hydrodynamic instability due to the presence of a small perturbation in the white dwarf density (see Fig. 10 for relative densities at one second after the explosion).

Multiply Explosions of White Dwarfs. Finally, let us simulate a single white dwarf with two solar masses and the temperature $T = 10^9$ K. The explosion zones are specified at a distance of 20% of the radius from the center and in the center. The explosion energy is specified with the values obtained in the previous subsection. Figure 11 presents the simulation results. Thanks to the numerical simulation, we can see the result of the supernovae Ia explosion in the form of a “horseshoe” image.

Fig. 11.

Isolines (left) and isosurface (right) of the relative density distribution in 5 s.

5 Discussion

• 1. We do not deny the concept of “standard candles” for measuring distances in the Universe. Let us only pay attention to the fact that the energy behavior of the process of the explosion of white dwarfs in the form of supernovae with the incomplete combustion of the material is non-standard. We offer only one scenario that reveals the ambiguity of the burning process.

• 2. The computational model has a simple adiabatic form of the stellar equation of state. Although numerous studies of the stellar equation of state are available, we have not found any convincing arguments in favor of using more complicated coefficients of the adiabatic density function when considering the energy behavior. Maybe the model should be complicated considering the concentration distributions of the elements.

• 3. In our model of burning, we use the alpha process of carbon burning up to iron and nickel. The concentration distributions of the elements in supernova explosions are not considered. The major attention is given to the explosion energy with incomplete carbon burning and the non-standard character of this process.

• 4. To describe subgrid carbon burning, the model considered in detail in [39] is used. The advantage of this model is that it has an analytical solution for determining the energy released as a result of carbon burning. In the present paper, the chemical composition of the remnant is not considered. The chemical composition of the remnant is described in [6, 31, 33, 35, 36].

• 5. The main calculation time in our model of the evolution of white dwarfs and the explosion of type Ia supernovae is spent on modeling the subgrid process of carbon combustion in white dwarfs. We start such turbulent combustion at each time step in each computational cell of nested grids used to simulate the hydrodynamics of white dwarfs, provided that the required values of temperature and density in the cells are reached. In fact, at each time step, we run a fairly large number of full-fledged hydrodynamic calculations using a regular grid on the time step of white dwarf hydrodynamics. For the calculation, we use the already developed parallel code computing infrastructure from [25]. The calculations of the hydrodynamics of white dwarfs take negligible time and are reduced by the use of nested grids. In connection with this way of organizing calculations, we do not consider scalability studies on regular grids (they are described in detail in [25]), but we present scalability results only for nested grids.

• 6. It is known that the classical SNeIa supernova scenario is based on the merger of white dwarfs, reaching the mass of Chandrasekhar, the start of the thermonuclear combustion of carbon, and the subsequent supernova explosion with the almost complete combustion of the material. Professor A.V. Tutukov proposed a hypothesis about the possibility of an explosion of SNeIa during the combustion of a mass smaller than the mass of Chandrasekhar, which led to the formation of many scenarios described in this article. The key point, in our opinion, is related to the more intense combustion of the white dwarf material. To describe such combustion, we propose the subgrid carbon combustion apparatus in the form of an independent hydrodynamic problem of turbulence development.

6 Conclusions

In this paper, a non-standard mechanism of carbon burning in type Ia supernova explosions is proposed. The mechanism is based on intensity variations in the nuclear burning of carbon during its incomplete combustion. In this case, the explosion energy can vary significantly due to the presence of different regimes of carbon burning during the development of turbulence in the burning zone. The energy released during burning, sufficient for the explosion of a white dwarf (as a type Ia supernova), can be achieved with a mass smaller than the Chandrasekhar mass. In addition, the explosion energy of a white dwarf with a Chandrasekhar mass can differ considerably.