Data Processing Methods for Onboard Gravity Anomaly Measurements

Abstract

This Chapter gives an overview of data processing methods used in measuring gravity anomalies on a moving base. Data processing and software of Russian mobile relative gravimeters Chekan and GT-2 are described. Information is given on optimal and suboptimal filtering and smoothing algorithms for estimation of gravity anomalies, and the methods used to identify the models needed for the algorithm design. The method of designing suboptimal smoothing algorithms with a constant delay is considered as applied to marine gravity measurements. Fusion of airborne gravimetric data and the global EGF models by multiscale representation of an anomalous gravity field using wavelet expansion on the sphere is addressed.

FormalPara Introduction

This chapter gives a comprehensive overview of data processing methods used in measuring gravity anomalies (GA) on a moving base. The chapter contains five sections.

Sections 2.1 and 2.2 describe the features of data processing and software of Russian mobile relative gravimeters of the Chekan series (Sect. 2.1) and GT-2 series (Sect. 2.2) that are widely used for taking high-precision measurements of the Earth’s gravitational field from marine vessels and aircraft, including measurements in remote areas of the Arctic and the Antarctic.

Each section provides a description of the technology for acquisition, onboard quality control, postprocessing, and subsequent geophysical interpretation of marine and airborne gravity survey data. Algorithms and mathematical software used for acquisition and postprocessing of gravimetric data obtained using gravimeters of these series are discussed.

Section 2.3 focuses on the design of optimal and suboptimal filtering and smoothing algorithms for estimation of gravity anomalies, and the methods used to identify the models needed for the algorithm design.

The optimal filtering and smoothing problem is considered in general form within the Bayesian approach; an example is given to illustrate the design of optimal algorithms as applied to GA estimation. Within this approach, the potential estimation accuracy can be calculated with the specified models of the anomalies and the errors of the measuring instruments, which allows objective estimation of the efficiency of various suboptimal algorithms. Further, the practical stationary algorithms based on the Butterworth filter and the two-stage estimation procedure are discussed, and their efficiency is analyzed. The importance of structural and parametric identification of the models is emphasized, which provides the required information on the models when implementing optimal algorithms. An identification algorithm is proposed, which is based on nonlinear filtering methods and actually makes the GA estimation process and the algorithms adaptive. The results of real data processing using the proposed algorithm are given in Conclusions.

Section 2.4 describes the method of designing suboptimal smoothing algorithms with a constant delay applied to the problem of marine gravity measurements.

A theoretical justification of the proposed method is given, and a methodical example is used to compare the proposed suboptimal algorithm with optimal filtering and smoothing algorithms. The section describes the smoothing algorithm for marine gravity surveys which is designed using the method under consideration and implemented in the GT-2M gravimeter software. The results of survey data processing using the proposed algorithm are presented.

Section 2.5 discusses the problem of combining airborne gravimetric data and the data from the global models of the Earth’s gravitational field. The problem is solved by applying multiscale representation of an anomalous gravity field in the area of an airborne gravimetric survey using wavelet expansion on the sphere. The algorithm for data integration obtained by this method is described and the results of its work are discussed.

2.1 Chekan-Series Gravimeter Data Acquisition and Processing Software

High-precision gravity surveying from moving vehicles remains the most common and promising method for studying the Earth’s gravitational field. The development of gravimetric equipment involves intense research based on high technology and profound knowledge base. An important aspect on which the final quality of geophysical data depends is functionality and efficiency of mathematical software.

A distinctive feature of marine and airborne gravity surveys is that the data is processed in successive steps that include data acquisition, onboard quality control, postprocessing, and subsequent geophysical interpretation of measurement results. Inadequacy of software at any of these steps can result in a significant deterioration in the quality of the survey results or even complete loss of the material, which is unacceptable for hard-to-reach areas of the Earth.

Choosing an adequate mathematical model that takes into account the design features of the gravimeter used and its calibration parameters, the possibility of applying various corrections and changing the coefficients and structure of the digital filter is of vital importance in postprocessing of gravity data.

Section 2.1 considers algorithms and mathematical software used in the acquisition and postprocessing of the gravimetric data obtained using the Chekan gravimeters described in detail in Sect. 1.2. All processing steps are described, including calibration and diagnostics of the system equipment that are carried out before the survey starts, real-time data acquisition, processing of the marine and airborne gravimetric profiles and final postprocessing of the survey results (Krasnov and Sokolov 2015). The structure of the software for various stages and types of gravity surveys is shown in Table 2.1.

Table 2.1 Structure of the software for Chekan gravimeters

2.1.1 Calibration and Diagnostics of the Gravimeter Equipment

Periodic calibration of the sensing element is a mandatory procedure for any type of gravimeter. In addition, during marine and especially airborne gravity surveys, it is necessary to calibrate sensing elements of the gyro stabilization system. In order to automate the setup procedures for the gravity sensor (GS), gyro platform (GP), and UMT unit at the manufacturer’s plant and provide for their field diagnostics, a special software was developed that comprises 3 programs: TestGrav, TestGyro, and TestUMT.

The GS is adjusted with the TestGrav program, which provides for the following basic operations:

• adjustment of the optoelectronic converter, including its alignment, setup of the intensity and shape of autocollimation images (Fig. 2.1);

  Fig. 2.1

  

  Screen of the TestGrav program during the setup of intensity and shape of autocollimation images

• adjustment of the GS digital thermal stabilization system;

• determination of the gravimeter elastic system (GES) response time;

• in-depth diagnostics of the GS hardware.

The TestGyro program is intended to solve similar problems of GP setup; it has the following main functions:

• automatic adjustment of the gearless servo drive in all modes of the GP operation;

• calibration of zero drifts and scale factors of floated one-degree-of-freedom gyroscopes (Fig. 2.2);

  Fig. 2.2

  

  Screen of the TestGyro program during calibration of gyroscopes

• calibration of zero drifts and scale factors of horizontal accelerometers;

• calibration of zero drift and the scale factor of azimuthal FOG;

• in-depth diagnostics of all the GP hardware.

The results of the GP primary setup are stored in the ROMs of microcontrollers and can be refined during operation.

GS calibration is traditionally done by tilting, wherein the known gravity decrements are set by changing the position of the GS measuring axis relative to the local vertical (Zheleznyak and Elinson 1982). Setting and determining tilting angles should be made using high-precision tilt-rotary benches. A special technology for GS calibration was developed and implemented in Chekan-AM and Shelf-E, in which the gyro platform is used to set and determine the gravimeter tilting angles. This technology eliminates the need for high-precision and expensive bench test equipment; and GS calibration can be done in the field (Sokolov et al. 2015).

A special program Calibr was developed to calibrate the GS using a gyro platform. The program provides both for automatic tilting of the GS at specified angles and certain intervals and processing of measurement results (Dudevich et al. 2014).

During the entire measurement cycle, the current readings of the gravimeter and GP tilting angles are recorded in a file (Fig. 2.3). The measurement for each tilting angle of the platform lasts 30 min. The entire calibration period does not exceed 9 h.

Fig. 2.3

Screen of the Calibr program

The results of data processing are available as a program operation protocol including the values of the following parameters:

• quadratic coefficient a and linear coefficients b₁, b₂ of the calibration characteristic of each quartz gravimeter system;

• specified decrements of gravity acceleration ∆a_eti and the results of measuring ∆g_i for each GP tilting angle;

• deviations δg_i of the ∆g_i measurement results from the specified values of ∆a_eti;

• the fiducial error of the gravimeter calibration characteristic which is taken as the ratio of the absolute maximum of the obtained values of δg_i to the upper limit of the gravimeter measurement range;

• the margin for the gravimeter measurement range.

The protocol generated by the program is a requisite document sufficient to prepare verification certificates for Chekan-AM and Shelf-E gravimeters as measuring instruments.

2.1.2 Real-Time Algorithms and Software

The main purpose of the real-time software is synchronous recording of the original gravimetric and navigation data at a frequency of 10 Hz in the course of measurements on survey lines. Taking into account the fundamental differences in marine and airborne gravity surveys, real-time data acquisition software comprises two different programs, SeaGrav and AirGrav, both of which provide for the following operations (Demyanenkov et al. 2014; Dudevich et al. 2007):

• GS, GP, and UMT data acquisition;

• reception of navigation information from GNSS equipment and synchronization of the gravimeter data;

• recording of raw data on the hard disk at a frequency of 10 Hz;

• linearization of the GS scale in accordance with formula (1.2.7);

• introduction of the gravimeter drift correction in accordance with formula (1.2.9);

• calculation and filtering of the gravity increment with respect to the initial gravity reference station (GRS) (this data is used for display and can also be used for onboard quality control);

• graphic display of the recorded parameters and recording of output data on the hard disk at a frequency of 1 Hz.

Additionally, the AirGrav program provides for the correction of the carrier motion effect on the gravimeter gyro platform with the use of GNSS data and the generation of current heading values, the algorithm block diagrams of which are presented, respectively, in Figs. 1.15 and 1.16 of Chap. 1.

The SeaGrav and AirGrav programs are designed to work under the Windows operating systems. The exchange of information with the GS, GP, and UMT is carried out using the RS-232 serial interface. Any modern laptop with standard USB/COM interface adapters can be used to operate the gravimeter.

Signals received from the gravimeter equipment are displayed on the screen in graphic and digital form (Fig. 2.4). The interface of SeaGrav and AirGrav provides wide capabilities for zoom control and the choice of colors for the charts. The software is adapted for two languages: Russian and English.

Fig. 2.4

Screen of the real-time data acquisition software in the reference observation mode

An essential feature of real-time programs is the availability of built-in diagnostics for the basic systems of the gravimeter, which provides for an integral test of the gravimeter operation and reliability of its readings. These diagnostic capabilities greatly simplify the operator’s work, especially in airborne gravimetric surveys.

The output data of the real-time gravity data acquisition software is text files, the main content of which is presented in Table 2.2, as well as protocols of the software.

Table 2.2 Text files

Symbol “*” in the table indicates a unique file name generated automatically. The main output files of data acquisition software are G*.RAW files, in which the readings of the gravity sensor m₁, m₂ and time t are recorded with a frequency of 10 Hz. In the G*.RAW files generated by the SeaGrav program, additional signals are recorded that can be used to calculate dynamic corrections, such as the readings of the horizontal accelerometers of the gyro platform W_ψ, W_θ, the floated gyro pick-offs U_ψ, U_θ, pitch angles ψ and roll angles θ, temperature T (GS temperature for the Shelf-E gravimeter or the temperature inside the GP for the Chekan-AM gravimeter).

For the same purpose, the AirGrav program generates a separate T*.DAT output file which, in addition to the signals listed, contains the FOG readings Ω_z, the control signals of the gyroscope torquers ψ, ω_θ and also some calculated corrections and derivatives of the GNSS signals received: heading K, track over ground TOG, north and east speed components V_N, V_E, speed mismatch ΔV_N, ΔV_E, corrections for the horizontal components of Coriolis acceleration W_corψ, W_corθ, and the Earth rate horizontal component Ωcosφ.

Both programs record G*.NAV navigation data files containing the values of latitude φ and longitude λ received from GNSS. The values of height H are additionally recorded in the AirGrav program files. It should be noted that the AirGrav G*.NAV program files are used only for real-time control of survey data; however, satellite information refined during office processing is used for postprocessing of gravimetric data.

The SeaGrav and AirGrav programs work in two modes: reference observations and gravimetric surveys. The mode of reference observations is necessary to calculate the reference g_r0 of the gravimeter at the GRS; the time of reference observations T₀, and the drift rate of gravimeter C based on current measurements in accordance with the formulas obtained using the least squares method:

$$g_{r0} = \frac{{\sum_{i = 1}^n {g_{ri} } }}{n},$$

(2.1.1)

$$T_0 = \frac{{\sum_{i = 1}^n {t_i } }}{n},$$

(2.1.2)

$$C = \frac{{\sum_{i = 1}^n {g_{ri} } \cdot \sum_{i = 1}^n {t_i } - n \cdot \sum_{i = 1}^n {g_{ri} \cdot t_i } }}{{\left( {\sum_{i = 1}^n {t_i } } \right)^2 - n \cdot \sum_{i = 1}^n {t_i^2 } }},$$

(2.1.3)

where $g_{ri}$ are the current measurements of the gravimeter calculated in accordance with (1.2.7), t is the measurement time, and n is the number of measurements.

In the gravimetric survey mode, the current values of the gravity increment are calculated relative to the reference at the GRS, taking into account the gravimeter drift according to formula:

$$\updelta g = g_r - g_{r0} - C \cdot \left( {t - T_0 } \right).$$

(2.1.4)

Gravity increments smoothed by the low-pass filter (LPF) described below are stored in the G*.DAT or R*.DAT files, depending on the mode of operation. When conducting a marine survey, G*.DAT files can be used for quality control of gravity data. R*.DAT files are used to calculate the gravimeter readings at the GRS and refine the gravimeter drift.

2.1.3 Marine Gravity Measurement Processing

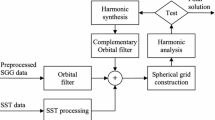
Figure 2.5 shows a block diagram of marine gravimetric line data processing. As described above, the data for the postprocessing of the line are formed from the following files: G*.RAW for gravimetric data, and G*.NAV for navigation data.

Fig. 2.5

Block diagram of marine gravity line data processing

Processing of the line data begins with the conversion of the GS readings into acceleration units using the coefficients of the gravimeter calibration characteristic in accordance with formula (1.2.7). The current values of the gravity increment are calculated and the gravimeter drift correction is accounted for in accordance with formula (2.1.4).

To calculate the values of gravity and its anomalies on a line, it is necessary to combine gravimetric and navigation data and calculate at least two corrections, namely, the Eotvos correction and the normal gravity correction.

For marine gravimetric surveys, the Eotvos correction, which eliminates the effect of the Coriolis and centripetal accelerations, is calculated using the following simplified formula:

$$\Delta g_E = 7.502\cos^2 \upvarphi \cdot {{d\uplambda } / {dt}} + 0.0041 \cdot V^2 ,$$

(2.1.5)

where V is the vessel speed, kn; ${{d\uplambda } / {dt}}$ is the longitude rate, arcmin/h; $\upvarphi$ is the latitude, rad.

Figure 2.6 gives an example how the Eotvos correction changes the systematic component of the gravimeter signal and compensates for the accelerations caused by minor changes in the heading and speed of the carrier on the survey line.

Fig. 2.6

Introducing the Eotvos correction $\Delta g_E$ to gravity readings

Normal gravity correction $\upgamma$ is usually calculated by the Helmert formula.

The value of gravity at a marine gravimetric station is calculated using the following formula:

$$g = g_0 + \updelta g + \Delta g_E ,$$

(2.1.6)

where $g_0$ is the value of gravity at the GRS relative to which the survey was conducted.

The GA value in free air $\Delta g$ is defined as the difference of gravity at the marine station and the normal value of gravity:

$$\Delta g = g - \upgamma .$$

(2.1.7)

If depth data is available, the gravity anomaly is calculated in the Bouguer reduction taking into account the gravity of the layer between the gravity station and the sea level in accordance with the following formula (Torge 1989):

$$\Delta g_B = g - \upgamma + g_B ,$$

(2.1.8)

where $g_B = 0.0419 \cdot H \cdot \left( {{\upsigma }_1 - {\upsigma }_2 } \right)$ is the Bouguer correction, H is the sea depth, m; σ₁ is the density of seabed rocks; σ₂ = 1.03 g/cm³ is the density of sea water.

The effect of vertical accelerations is eliminated from the measurement results using a low-pass filter, to which the value of the gravity increment is input after taking into account all the corrections. For marine surveys, the use of a low-pass filter is fully justified since the power spectral densities (PSDs) of the useful signal and the disturbing acceleration are separated in the frequency domain. For processing the data from Chekan gravimeters, it is recommended to use a combined digital filter which consists of the 1st order aperiodic filter with the time constant T_a and the 4th order Butterworth filter with the time constant T_b.

The data processing using the combined digital filter is conducted in two stages. During the first stage, the readings of the gravimeter are passed through the filter in the forward time mode. After that, the time is inverted, and the gravimeter readings are processed by the same filter in reversed time. As mentioned in Sect. 2.3, the data processing technology in the forward and reversed time modes agrees with the solution of the smoothing problem and allows, among other things, eliminating the phase distortions of signals introduced by the filtering procedure.

Figure 2.7 shows the amplitude-frequency characteristics of the low-pass filter described for various values of the time constants T_a and T_b. The advantage of data processing by survey lines is that it is possible to vary these parameters for various sea states in order to ensure maximum spatial resolution. Table 2.3 presents the recommended values of T_a and T_b, the cutoff frequency f_c of the LPF and their corresponding spatial resolution L/2 at a speed of 5 kn for various sea states obtained empirically so that the root-mean-square deviation (RMSD) of the residual error for the vertical acceleration is less than 0.1 mGal.

Fig. 2.7

Amplitude-frequency response of the filter

Table 2.3 Filter parameters

Additional corrections ∆g_Wz and ∆g_Wx may be introduced in the readings of Chekan gravimeters in order to improve the final accuracy of marine gravimetric surveys, as shown in Fig. 2.5. This is especially relevant for marine surveys with significant sea waves or even in stormy weather (Zheleznyak et al. 2010). As described in Chap. 1, under vertical accelerations above 50 Gal, the readings of Chekan-AM gravimeters may include a systematic error δW_z caused by the nonlaminar nature of the fluid damping of GES pendulums. The value of the error δW_z is quadratic in nature; it largely depends on the degree of the GES damping and is substantially lower in the Shelf-E gravimeter. Nevertheless, it is possible to introduce the ∆g_Wz correction into gravimeter readings in accordance with the algorithm shown in Fig. 2.8.

Fig. 2.8

Calculation of the vertical acceleration correction ∆g_Wz

The values of specific force W_z acting on the pendulums are determined from formula (2.1.4) and are input into the scheme for calculation of ∆g_Wz correction. In order to eliminate the gravitational component from the values of specific force, the scheme includes negative feedback on the current gravity increments $\updelta g$ generated by a filter of the 3rd order with the time constant T = 60 s. As it is, ∆g_Wz correction is determined using the following formula:

$$\Delta g_{Wz} = k_{Wz} \cdot \tilde{W}_z^2 ,$$

(2.1.9)

where k_Wz is a coefficient determined empirically during the gravimeter testing on a vertical displacement test bench. The ∆g_Wz correction is calculated in real time.

An example of improving the measurement accuracy in stormy weather owing to the ∆g_Wz correction is shown in Fig. 2.9. It is clear that not only the systematic component but also the high-frequency component of the δW_z error are compensated for, which makes it possible to increase the spatial resolution L/2 of the measurements by using an LPF with a higher cutoff frequency f_c. In addition, in the case of a significant change in sea state on the line, the error δW_z cannot be taken into account by the tie methods of the survey but, as can be seen from Fig. 2.9, can be compensated for by introducing the correction ∆g_Wz.

Fig. 2.9

Introduction of the correction for vertical accelerations on a marine line

Another correction shown in Fig. 2.10 is introduced to compensate for the effect of the joint action of horizontal accelerations and residual GP tilting, which is referred to as the Harrison effect. The Harrison effect correction can be represented as (Panteleev 1983):

$$\Delta g_{Wx} = W_X \upalpha + W_Y \upbeta ,$$

(2.1.10)

Fig. 2.10

Introduction of the Harrison correction

where W_X, W_Y are the longitudinal and transverse horizontal accelerations, respectively; α, β are the gyro vertical tilting angles about the respective stabilization axes.

The tilting angles of the gyro vertical due to the errors of the gearless gyro servo drive do not exceed 15 arcsec, that is, they do not affect the gravimeter accuracy. Therefore, while calculating the Harrison correction, it is necessary to take into account only the errors of the gyroscope accelerometric correction system, which was discussed in Sect. 1.2. Angles α, β are calculated by multiplying the horizontal accelerations obtained from the recordings of accelerometer signals by the transfer function of the gyro vertical which, according to the block diagram presented in Fig. 1.15, takes the form:

$$H_w^\alpha (p) = \frac{{\frac{1}{R}F(p)}}{{{p^2} + \frac{g}{R}F(p)}},$$

(2.1.11)

where F(p) is the transfer function of the filter (1.2.10), and R is the average radius of the Earth. 

Figure 2.11 shows the introduction of the Harrison correction on a gravimetric survey line at high sea. The Harrison correction is mainly systematic, and its value for Chekan gravimeters does not usually exceed 1–1.5 mGal.

Fig. 2.11

Screen of the Chekan_PP program during the processing of a marine survey line

All the above procedures for processing of gravimetric survey lines are implemented in the Chekan_PP program, which is designed for comprehensive office processing of marine gravimetric survey data (Zamakhov et al. 2013). The Chekan_PP program is designed to work under the Windows operating systems and can be used both for office processing of survey data and onboard data quality control. The program interface is quite convenient and clear; all intermediate and final results are presented to the operator in digital and graphical forms.

Logical data control in the *.DAT, *.RAW, *.NAV source files and elimination of minor data gaps are also automatically performed during survey line processing. In the case of low-quality gravimetric data on the survey line, the latter can be divided into several parts. At the user’s request, a filtering procedure can also be carried out, which is implemented not only by selecting the values of T_a and T_b but also by sequential repeated use of the LPF. In addition, the cutoff frequency f_c and the spatial resolution L/2 on the survey line are calculated automatically. The results of survey line processing are saved in text files of the *.XYZ type and the calculation and filtering parameters are recorded in the program operation protocols.

2.1.4 Airborne Gravity Measurement Processing

Measurements of gravity onboard aircraft are taken against the background of carrier-induced vertical accelerations which not only exceed the “useful” signal by several orders of magnitude but they also overlap in the frequency domain. Figure 2.12 shows a block diagram of processing of an airborne gravimetric survey line. Vertical accelerations in gravimeter readings are partially compensated for during postprocessing using altitude information from GNSS data. However, due to the significant background noise, the final detection of the “useful” signal is also performed using filtering and smoothing (Krasnov and Sokolov 2013).

Fig. 2.12

Block diagram of airborne gravimetric survey line data processing

For the processing of airborne gravimetric survey lines, gravimeter readings are converted into acceleration units (just like it was with marine gravimetric survey lines); GAs are calculated, and corrections are introduced for the gravimeter drift, the normal value of gravity, and the Eotvos effect.

Since the response time of a heavily damped Chekan gravimeter ranges from 40 to 100 s, it is necessary to determine the real value of specific force during the processing of airborne gravimetric measurements. To do this, the smoothed gravimeter signal is passed through a digital recovery filter, in which the aperiodic element of the first order is used as a model of fluid damping, and the transfer function of the recovery filter has the form of formula (1.2.8).

The vertical acceleration of the carrier has the predominant effect on the GS in airborne surveys. It is taken into account based on the results of flight altitude measured by GNSS equipment operating in the differential mode. In the absence of base stations, ephemerides corrections are used to refine the navigation data.

The offset of the GNSS receiver antenna relative to the GS location is calculated in accordance with the following formula:

$$H = H_{GNSS} - \left( {R_X \sin \uppsi + R_Y \sin \uptheta + R_Z \left( {\cos \uppsi - 1} \right) + R_Z \left( {\cos \uptheta - 1} \right)} \right),$$

(2.1.12)

where H_GNSS is the altitude value measured at the GNSS receiver antenna location; H is the altitude value at the GS location; R_X, R_Y, R_Z are the offsets of the GNSS receiver antenna relative to the GS measured by the operator in three planes; ψ, θ are the angles of pitch and roll according to the readings of the gravimeter GP angle sensors.

The Eotvos correction in the processing of airborne gravimetric measurements is calculated using the formula that takes into account the nonspherical nature of the Earth and flight altitude variations:

$$\begin{aligned} \Delta g_E & = 15V_E {\text{cos}}\upvarphi + \left( {\frac{V_N^2 }{R}\left( {1 + \frac{H}{R} - 0.5e^2 \left( {2 - 3{\text{sin}}^2 \upvarphi } \right)} \right)} \right. \\ & \quad + \left. {\frac{V_E^2 }{R}\left( {1 + \frac{H}{R} - 0.5e^2 {\text{sin}}^2 \upvarphi } \right)} \right) \cdot 10^5 , \\ \end{aligned}$$

(2.1.13)

where φ is the latitude; V_N, V_E are the north and east components of the linear speed; R, e are the parameters of the WGS84 common reference ellipsoid. Formula (2.1.13) shall be used in processing of extended survey lines when the nonspherical nature of the Earth cannot be neglected.

Another requisite operation is the reduction of measurement results to the surface of the reference ellipsoid, which is carried out in accordance with the formula that takes into account the normal vertical gradient of gravity:

$$\Delta g = \Delta g_h + 0.3086H,$$

(2.1.14)

where $\Delta g_h$ is the GA at altitude H; $\Delta g$ is the GA reduced to the surface of the ellipsoid.

Even in the case that all the known corrections are thoroughly taken into account, the gravimeter signal remains noisy. Filtering and smoothing are applied in order to identify the useful component. The software of Chekan gravimeters offers a two-stage procedure, which, at the first stage, uses a finite impulse response filter with a trapezoidal Tukey weight function in the time domain (Krasnov and Sokolov 2013). This filter has a finite impulse response, resulting in a constant shift of all the harmonics of the input signal, which is easy to take into account during processing. The amplitude-frequency response of the filter is shown in Fig. 2.13.

Fig. 2.13

Amplitude-frequency response of the filter at a cut-off frequency of 0.006 Hz

The result of processing is a signal, the noise level of which is a few mGal. Next, at the second stage, a smoothing operation is performed, wherein a fast Fourier transform is used to transform the signal into the frequency domain; high-frequency harmonics of the signal are truncated, after which a reverse transition into the time domain is performed. When choosing the required number of harmonics in the final signal, this procedure does not deteriorate the spatial resolution, nor does it cause negative edge effects, provided that the duration of the realization is not decreasing (Fig. 2.14).

Fig. 2.14

An example of gravimetric measurement smoothing

In the conditions of airborne gravimetric surveys, of extreme importance is not only postprocessing of the survey line but also onboard quality control of measurements to identify unreliable data. The Grav_PP_A program, operating under the Windows operating system, was developed to solve these two problems.

The purpose of onboard quality control is to detect survey lines or some parts of lines with poor data quality and identify the causes of quality deterioration. The primary analysis of the initial gravimetric and navigation information is aimed at detecting equipment failures. In addition, the program provides for comparison of the measured gravity profile with independent sources of gravimetric data; for example, the results of previous surveys made in this area, the global models of the Earth’s gravitational field, and gravity databases, such as the Arctic gravimetric project, ArcGP (Forsberg and Kenyon 2004).

Grav_PP_A program also provides for estimation of the functioning criteria of all gravimeter systems, as well as the conditions for measurements (Fig. 2.15). The presence of such criteria allows effective identification of possible causes of data quality deterioration. The following parameters are analyzed for this purpose:

Fig. 2.15

Screen of the Grav_PP_A program with data control

• gravity sensor: the difference between the readings of quartz systems;

• gyro stabilization system: stabilization errors and heading error;

• satellite receiver: no failures in data reception;

• flight conditions: stable altitude, vertical and horizontal accelerations, the constancy of pitch and roll angles, and constancy of the ground speed.

Similarly to the Chekan_PP program, the results of the airborne gravity line processing are stored in *.XYZ text files used for the subsequent office processing of the survey results.

2.1.5 Postprocessing of Gravimetric Survey Data

The final processing of the results of both marine and airborne gravimetric surveys carried out by Chekan gravimeters is performed with the use of the previously mentioned Chekan_PP program. The results of measurements on lines are loaded into the survey database. The program automatically calculates the statistical parameters of the survey, including the lengths of survey lines, the number of cross points, survey RMS errors and RMS deviations.

The survey RMS error is calculated using the formula:

$$\upsigma_{RMS} = \sqrt {\upsigma_{CP}^2 + \upsigma_{interp}^2 } .$$

(2.1.15)

The RMS error of a single GA determination at cross points σ_CP is calculated using the formula:

$$\upsigma_{CP} = \sqrt {\frac{\Sigma d^2 }{{2n}}} ,$$

(2.1.16)

where d is the difference in measuring gravity anomaly at cross points; n is the number of cross points.

An essential feature is that the survey RMS error also takes into account the interpolation error σ_interp in the measurement results between the survey lines:

$$\upsigma_{{\text{interp}}} = \sqrt {\frac{{\sum_{{\text{i}} = 1}^{\text{N}} {\left[ {\Delta {{g}}_\upkappa - \left( {{{g}}_{{\text{c}}1} + g_{c2} } \right)/2} \right]_i^2 } }}{N}} ,$$

(2.1.17)

where Δg_k is the value of the gravity anomaly on the tie line at point K located midway between the survey lines; g_c1 and g_c2 are the values of the gravity anomaly on the adjacent survey lines, between which point K is located, at the points of intersection with the tie lines; N is the number of points K in the survey.

The RMSD of the survey error does not take into account systematic difference in the measurement results at cross points; it has the following form:

$$\upsigma_{RMSD} = \sqrt {\frac{{\Sigma \left( {d - r} \right)^2 }}{{2\left( {n - 1} \right)}}} ,$$

(2.1.18)

where $r = \frac{\sum d }{n}$.

Since marine geophysical surveys are often conducted without final reference measurements, but initial reference measurements are not long enough to obtain a reliable estimate of the gravimeter drift C, a significant feature is the calculation and introduction of the correction ΔC using the difference between GA measurements at the cross points of the lines (Fig. 2.16).

Fig. 2.16

Screen of the Chekan_PP program during processing of survey results

In the case of multiple reference observations at the same airport, they can also be compiled into an appropriate database to refine the gravimeter drift using all the data obtained.

Another important procedure is tying of survey results, in which averages of discrepancies at cross points are calculated and added into each survey line.

The values of all corrections introduced during data processing are stored along with processing parameters in the program protocols generated automatically.

The results of the survey processing can be exported for further processing in the text format XYZ suitable for loading into most of the modern geophysical data processing packages.

2.1.6 Conclusion

Features of data acquisition and processing using gravimeters of the Chekan series have been described.

The design, structure, and functionality of the software used at each stage of acquisition, processing, and analysis of marine and airborne gravimetric data are presented.

Some examples are given to illustrate the improvement of measurement accuracy owing to the introduction of dynamic corrections.

2.2 Data Processing in GT-2 Airborne Gravimeters

In 2000, the Laboratory of Control and Navigation of Lomonosov Moscow State University started developing software for data postprocessing in the first-generation GT-1A airborne gravimeters designed by the Gravimetric Technologies (Russia) (the second-generation gravimeters are known as the GT-2 series). At the same time, preparations began for the first test of the prototype MAG-1 (the first commercial name of the GT-1A airborne gravimeter) aboard an AN-30 aircraft. The tests were carried out in 2001 (Berzhitsky et al. 2002). Earlier, the Laboratory created software for two other Russian airborne gravimeters (Bolotin et al. 2002):

• the airborne gravimeter Graviton-M developed by VNIIGeofizika, Moscow Institute of Electromechanics and Automation (MIEA), and Bauman Moscow State Technical University. The first flight tests (3 flights) of this system were conducted aboard an MI-8 helicopter in December 1995 and January 1996. In July and August 1999, for the first time in Russia, a full-scale areal surveying was carried out aboard an AN-26 aircraft not far from Kaluga. Later on, this system was used by GNPP Aerogeophysica;

• the airborne gravimetric system developed by MIEA. The project, which started in 1996, was financed by the World GeoScience Corporation (Australia). Three series of flight tests were conducted: (1) 3 flights in December 1997; (2) 2 flights in May 1998 aboard an AN-26 aircraft flying near Vologda; (3) a flight in July 1999 aboard an L-410 aircraft, Brno, the Czech Republic.

The flight tests of these gravimeters were attended by experts from The Schmidt Institute of Physics of the Earth of the Russian Academy of Sciences.

Thus, by the time the Laboratory of Control and Navigation started joint work with the Gravimetric Technologies, the Laboratory had already gained considerable experience in processing airborne gravimetric data from Graviton-M and the MIEA system so that it was easy to formulate the objectives of postprocessing and the design philosophy of the software.

The first stage of postprocessing software is quality control (QC) of experimental data. It is very important for a survey operator to be able to quickly answer the question about the quality of the recorded experimental data:

• (1) measurements of the gravimeter sensing element (GSE);

• (2) data of the GNSS receivers on the aircraft and at base stations;

• (3) data of the INS responsible for the GSE vertical orientation;

• (4) data from the recording and information-flow-synchronization systems of the gravimetric system.

The main document for the development of the express diagnostic software was The Information Exchange Protocol in the Airborne Gravimetric System which was developed jointly by the Gravimetric Technologies and the Laboratory of Control and Navigation of Moscow State University. The exchange protocol describes the formats of raw data files as well as the formats of output files. The latter contain all relevant information for quality control.

In general, the software for GT-2 airborne gravimeters consists of the two main parts: the GTNAV and GTGRAV modules. The first part includes algorithms for developing satellite navigation parameters and integration of INS and GNSS data; the second part presents the solution to the airborne gravimetry problem based on GSE measurements and navigation data prepared by the GTNAV module.

In addition, for the purposes of quality control, the GTNAV module provides for the analysis of the following parameters:

• correct synchronization of information flows from the INS and GNSS. INS data are recorded with a frequency of about 3 Hz, the GNSS data are recorded at 1, 2, 5, 10, and 20 Hz sampling rates. Synchronization of flows is carried out using the 1PPS (pulse per second) mechanism, recording of the INS and GNSS time scales and their relative biases;

• data integrity (gaps);

• occurrence of events indicative of the gravimeter malfunctioning. For example, such events as ‘GSE not normal’, ‘abnormal ARS drift’, etc. The list of possible events is described in the data exchange protocol;

• correctness of the base station coordinates, its immobility;

• the level of misalignment error estimates of the instrument (gyro platform), levels of DTG and FOG drift estimates.

It is very important that quality control software should be easy to use because operators conducting surveys may be well trained in gravimetry, less competent in satellite navigation, and totally incompetent in inertial navigation. All they need is to enter raw data filenames––INS, GNSS (aircraft and/or base station(s))––as initial information for the GTNAV module, and then run the program. The program can work separately with INS and GNSS data or with their various combinations. Many years of experience in using this software by various companies, both Russian and international, have shown its effectiveness for the purposes of quality control.

GTGRAV program is responsible for processing of the GSE measurements, GTNAV output data, as well as GA determination. Like GTNAV, this program (to be more exact, its auxiliary module GTQC) performs additional preliminary verification of GSE measurements integrity and synchronizes information flows. Unlike GTNAV, GTGRAV has an advanced graphical interface. The need for an interface is associated with the “creative” nature of the GA determination problem, where customizable processing parameters are often found by the trial-and-error method.

2.2.1 Airborne Gravimetry Software

Let us briefly describe the airborne gravimetry problem from the point of view of theoretical mechanics (a more detailed description can be found in Sect. 1.1) and write down the main gravimetric equation in the form convenient for further consideration. In Sects. 2.2.3, 2.2.4, this equation is specified for the case of the GT-2A gravimeter with a leveled platform.

The problem of gravimetry is the inverse problem of mechanics: to determine force from motion. It should be recalled that force, as a vector quantity, is characterized by magnitude and direction. However, in classical, “scalar” gravimetry, the direction of GA action is not usually specified. This is partly due to the fact that the difference between the magnitude of the gravity vector and the value of its vertical component was, until recently, an order of magnitude lower than the available measurement accuracy. At present, vector gravimetry methods are actively developing (see Sect. 5.2) so that they make it possible to determine three components of the gravity disturbance vector, and thereby, eliminate the above uncertainty.

It should also be noted that, from the mathematical point of view, the problem of GA determination belongs to the class of ill-posed problems since it is solved by differentiation (Tikhonov and Arsenin 1979).

The main equations of airborne scalar gravimetry are Newton’s equations that describe the vertical motion of a material point of a unit mass in the field of the Earth’s gravitational force under the action of an external force that is accessible for measurement (Torge 1989; Bolotin et al. 1999):

$$\ddot{h} = \dot{V}_3 = \Delta g_E - \upgamma_0 - \updelta \upgamma + f_3 + \Delta g,\;\Delta g_E = \left( {\frac{V_E^2 }{{R_E }} + \frac{V_N^2 }{{R_N }} + 2\Omega V_E \cos \upvarphi } \right).$$

(2.2.1)

The equation uses the following notation: $h$ is the flight altitude above the reference ellipsoid (Torge 1989); $V_3$ is the vertical velocity; $V_E ,\,V_N$ are the Eastern and Northern components of the relative velocity of the carrier; $R_E ,\,R_N$ are the radii of curvature of the longitudinal and latitudinal cross-sections; $\Omega$ is the modulus of the angular rate of the Earth rotation; $\upvarphi$ is the geographical latitude; $\upgamma_0$ is the magnitude of the normal gravity on the reference ellipsoid; $\updelta \upgamma$ is the correction of the normal gravity value for the flight altitude above the reference ellipsoid; $f_3$ is the projection of the specific force on the geographic vertical; $\Delta g$ is the GA to be found. The term $\Delta g_E$ is due to the motion of the aircraft; it is called the Eotvos correction.

The goal of the airborne scalar gravimetry problem is to determine (estimate) the values of GA $\Delta g$ based on model (2.2.1) from the other measured or calculated terms.

The equipment used for information support of the airborne gravimetry problem is directly determined from the main gravimetric Eq. (2.2.1), from which it follows that any airborne gravimetric system with a leveled platform should include:

• a GSE to measure the value of $f_3$ as a specific force acting on its sensitive mass;

• a navigation system to provide high-accuracy information about the altitude $h$, coordinates, and the vector of the linear velocity of the vehicle on which the gravimetric system is installed. Currently, such a system is a Global Satellite Navigation System operating in differential carrier phase mode;

• a navigation system providing the vertical orientation of the GSE sensitive axis. An example is a gimbaled INS which, using a gyrostabilized platform, physically simulates the geodetic reference frame, with the GSE sensitive axis rigidly attached to its vertical axis.

The basis for the solution of gravimetric Eq. (2.2.1) with respect to $\Delta g$ is GSE measurement $f^{\prime}_3$, measurements of the INS horizontal accelerometers $f_1^{\prime}$, $f_2^{\prime}$, and altitude measurements $h^{\prime}$ from the GNSS. In the linear approximation, the measurement equations can be written as follows:

$$h^{\prime} = h + \Delta h^{gps} ,$$

(2.2.2)

$$\begin{aligned} f^{\prime}_3 \left( {t \, - \, \uptau_3 } \right) & = f_{z3} + \upkappa_3 f_{z3} + \Delta f_3^0 + \Delta f_3^s + \upkappa_2 f_{z1} - \upkappa_1 f_{z2} , \\ f_{z3} & = f_3 + \upalpha_2 f_{z1} - \upalpha_1 f_{z2} , \\ \end{aligned}$$

(2.2.3)

$$f_1^{\prime} \left( t \right) = f_{z1} + \Delta f_1^s ,f_2^{\prime} \left( t \right) = f_{z2} + \Delta f_2^s .$$

(2.2.4)

The equations use the following notation: $f_{z3}$ is the projection of the specific force of the proof mass on the instrument axis; $\upkappa_3$ is the error of the GSE scale factor, $\Delta f_3^0$ is the GSE bias; $\Delta f_3^s$ is the noise component of the measurement error; $\upkappa_1 ,\,\upkappa_2$ are the angular errors of the installation of the GSE sensitive axis to the platform; $f_{z1} ,\,\,f_{z2}$ are the horizontal (in the platform axes) components of the specific force; $\upalpha_1 ,\,\upalpha_2$ are the misalignment errors of the instrument vertical; $t$ is the absolute time; $\uptau_3$ is the time constant of the GSE clock skew, $\Delta h^{GNSS}$ is the error in the GNSS altitude determination.

Parameters $\Delta f_{z3}^0$, ${\upkappa }_{1} {,}\,\upkappa_2 {,}\,{\upkappa }_3$, $\upalpha_1 ,\;\,\upalpha_2$, $\uptau_3$ are unknown and should be determined (estimated) during the solution of the airborne gravimetry problem. It should be noted that coefficients ${\upkappa }_{1} {,}\,\upkappa_2 {,}\,{\upkappa }_3$ are normally determined during laboratory and prestart calibrations and are used to adjust GSE readings. However, the experience of data processing has shown that it is advisable to determine and control these coefficients during postprocessing from airborne measurements. Parameter $\uptau_3$ is used to refine data synchronization.

The sources of information for determining coordinates and velocities are GNSS positional and velocity solutions obtained by processing the raw GNSS measurements: code pseudo-ranges, Doppler pseudo-range rates, and carrier phase measurements. The source of information for determining $\upalpha_1 ,\,\upalpha_2$ is solution of the INS/GNSS integration problem. This is what defines the scope of tasks for the postprocessing software.

2.2.2 Software for GNSS Solutions

The software for GNSS solutions implemented in the GTNAV module provides for different options of calculations depending on the following circumstances:

• the data used can be received from several (one, two, three) GNSS base stations. The software must be able to maintain solutions for different combinations of base stations;

• GNSS receivers may have different data sampling rates; for example, 1, 2, 5, 10, 20 Hz. The software must be able to maintain solutions at a common frequency;

• the carrier phase receivers used can be of multi-frequency type (at present, dual-frequency); accordingly, solutions should be provided both for the L1 frequency and for combinations of carrier phases free of ionospheric delays;

• the software must be able to maintain solutions when data are provided by single- and/or dual-frequency receivers;

• velocity solutions should be obtained not only by processing Doppler measurements but also based on carrier phases.

These features are implemented in the GTNAV software.

All of the above requires the solutions of numerous auxiliary problems such as the ephemeris problem to determine the coordinates and vector velocity of navigation satellites, estimation of the integer ambiguities of carrier phases, detection and elimination of satellite measurement failures. In reference (Vavilova et al. 2009), the authors show basic models of the problems of raw GNSS data processing for the standard (autonomous) mode of operation of GNSS receivers, on the basis of which the satellite navigation software was developed.

Described below in general terms is only one problem of velocity determination using raw carrier phases; its solution usually provides the highest accuracy.

The model of carrier phases $Z_\upphi$ looks as follows:

$$Z_\upphi = \uprho /\uplambda + f_\upphi \left( {\Delta \uptau - \Delta T} \right) + N + \updelta \upphi_{ion} + \updelta \upphi_{trop} + \updelta \upphi^s ,$$

(2.2.5)

where ρ is the range between the vehicle and the satellite; $f_\upphi$ is the frequency of the radio signal; $\uplambda$ is the wavelength of a frequency; N is an unknown number, an integer ambiguity of the carrier phase measurement; $\updelta \upphi_{ion}$, $\updelta \upphi_{trop}$ are the ionospheric and tropospheric delays, respectively; $\updelta \upphi^s$ is a random component of the carrier phase error.

The single $\nabla Z_{\upphi_i }$, $\Delta Z_{\upphi_i }$ and double $\nabla \Delta Z_{\upphi_i }$ differences of carrier phase are defined by the following formulas:

$$\nabla Z_{\upphi_i } = Z_{\upphi_i } - Z_{\upphi_z } ,\Delta Z_{\upphi_i } = Z_{\upphi_i }^b - Z_{\upphi_i }^M ,\nabla \Delta Z_{\upphi_i } = \left( {Z_{\upphi_i }^b - Z_{\upphi_i }^M } \right) - \left( {Z_{\upphi_z }^b - Z_{\upphi_z }^M } \right),$$

(2.2.6)

where $Z_{\upphi_i }^b$ is the carrier phase measurement of the base station; $Z_{\upphi_i }^M$ is the similar measurement of the aircraft receiver, hereinafter referred as to rover; indices i, z correspond to the measurements obtained from the satellites with the corresponding numbers; z is usually used for the number of the zenith satellite. Taking into account (2.2.6), measurement (2.2.5) takes the form:

$$\nabla \Delta Z_{\upphi_i } = \nabla \Delta \uprho_i /\uplambda + \nabla \Delta N_i + \nabla \Delta \upphi_{ion_i } + \nabla \Delta \upphi_{trop_i } + \nabla \Delta \upphi_i^s ,$$

where

$$\begin{aligned} \nabla \Delta \uprho_i & = \left( {\uprho_i^b - \uprho_i^M } \right) - \left( {\uprho_z^b - \uprho_z^M } \right); \\ \nabla \Delta N_i & = \left( {N_i^b - N_i^M } \right) - \left( {N_z^b - N_z^M } \right); \\ \nabla \Delta \upphi_{( \ast \ast \ast )_i } & = \left( {\updelta \upphi_{(***)_i }^b - \updelta \upphi_{(***)_i }^M } \right) - \left( {\updelta \upphi_{(***)_z }^b - \updelta \upphi_{(***)_z }^M } \right). \\ \end{aligned}$$

(2.2.7)

The useful signal in measurement (2.2.7) is the value $\nabla \Delta \uprho_i /\uplambda$. The residual errors in (2.2.7) are double differences $\nabla \Delta \upphi_{ion_i }$, $\nabla \Delta \upphi_{trop_i }$, $\nabla \Delta \upphi_i^s$ of the ionospheric, tropospheric, and random measurement errors (marked as (***) in the last Eq. (2.2.7)).

The main property of measurement (2.2.7) is the absence of instrumental errors of the receiver and satellites and the errors of their clocks in the model, as well as the decrease in the level of residual errors $\nabla \Delta \upphi_{ion_i }$, $\nabla \Delta \upphi_{trop_i }$ of the ionosphere and troposphere; note that the smaller are the distances between the bases and rover and the differences in their altitudes, the smaller is the level of the above residual errors.

The value $\nabla \Delta N_i$ is the integer ambiguity of the double differences of carrier phases, which is not fundamentally compensated in this method of phase measurement formation.

Consider the numerical derivative

$$\nabla \Delta Z_{V_{\uprho_i } }^* \left( {t_j } \right) = \uplambda \frac{{\nabla \Delta Z_{\upphi_i } \left( {t_{j + 1} } \right) - \nabla \Delta Z_{\upphi_i } \left( {t_{j - 1} } \right)}}{{t_{j + 1} - t_{j - 1} }}$$

(2.2.8)

of the differential carrier phases $\nabla \Delta Z_{\upphi_i } \left( {t_j } \right)$. The result of (2.2.8) is the estimate of the double differences $\nabla \Delta V_{\uprho_i } = \left( {V_{\uprho_i^b } - V_{\uprho_i^M } } \right) - \left( {V_{\uprho_z^b } - V_{\uprho_z^M } } \right)$ of the radial velocities of the receivers relative to the satellites at time t_j:

$$\nabla \Delta Z_{V_{\uprho_i } }^* \left( {t_j } \right) \cong \frac{{\nabla \Delta \uprho_i \left( {t_{j + 1} } \right) - \nabla \Delta \uprho_i \left( {t_{j - 1} } \right)}}{{t_{j + 1} - t_{j - 1} }} \cong \nabla \Delta V_{\uprho_i } .$$

On the other hand, the satellite radial velocity $V_{\uprho_i^b }$ relative to the base station (which is stationary) for each i-th satellite can be calculated according to Vavilova et al. (2009):

$$V_{\uprho_i^b } = \frac{{\left( {R_\upeta^{sat_i } - R_\upeta^b } \right)^T }}{\uprho_i^b }V_\upeta^{sat_i } ,$$

where $R_\upeta^{sat_i } = \left[ {\begin{array}{*{20}c} {R_{\upeta 1}^{sat_i } } & {R_{\upeta 2}^{sat_i } } & {R_{\upeta 3}^{sat_i } } \\ \end{array} } \right]^T$ is the vector of the Cartesian coordinates of the i-th satellite; $R_\upeta^b$ is the vector of the Cartesian coordinates of the base station; $V_\upeta^{sat_i }$ is the vector of the relative velocity of the i-th navigation satellite. Symbol $\upeta$ means that the corresponding vectors are defined in the geocentric coordinate system associated with the Earth (Greenwich, rotating), also referred to as ECEF (Earth Centered Earth Fixed). The radial speed of the satellite relative to the vehicle is defined by a similar formula which takes into account both the vector of the vehicle coordinates $R_\upeta^M$ and the vector of its own velocity $V_\upeta^M$:

$$V_{\uprho_i^M } = V_{\uprho_i^M }^{\left( 1 \right)} + V_{\uprho_i^M }^{\left( 2 \right)} ;\;V_{\uprho_i^M }^{\left( 1 \right)} = \frac{{\left( {R_\upeta^{sat_i } - R_\upeta^M } \right)^T }}{\uprho_i^M }V_\upeta^{sat_i } ;\;V_{\uprho_i^M }^{\left( 2 \right)} = \frac{{\left( {R_\upeta^{sat_i } - R_\upeta^M } \right)^T }}{\uprho_i^M }V_\upeta^M .$$

The component $V_{\uprho_i^M }^{\left( 1 \right)}$ is explicitly calculated from the known information on the coordinates and vector velocities of navigation satellites, the vehicle coordinates. The component $V_{\uprho_i^M }^{\left( 2 \right)}$ contains information on the vehicle’s vector velocity $V_\upeta^M$. Let us form measurement equations in linear approximation:

$$\nabla \Delta Z_{V_{\uprho_i } } = \nabla \Delta Z_{V_{\uprho_i } }^* \left( {t_j } \right) - \left[ {\left( {V_{\uprho_i^b } - V_{\uprho_i^M }^{\left( 1 \right)} } \right) - \left( {V_{\uprho_z^b } - V_{\uprho_z^M }^{\left( 1 \right)} } \right)} \right].$$

(2.2.9)

Thus,

$$\nabla \Delta Z_{V_{\uprho_i } } = - \left( {V_{\uprho_i^M }^{\left( 2 \right)} - V_{\uprho_z^M }^{\left( 2 \right)} } \right) + \nabla \Delta V_{ion_i } + \nabla \Delta V_{trop_i } + \nabla \Delta V_i^s = h_{(i)}^{\text{T}} V_\upeta^M + \nabla \Delta r_{\dot{\uprho }_i } .$$

(2.2.10)

The following notation is used here:

$$h_{(i)}^T = \left( {\frac{{R_\upeta^{sat_i } - R_\upeta^M }}{\uprho_i^M } - \frac{{R_\upeta^{sat_z } - R_\upeta^M }}{\uprho_z^M }} \right)^T ,\nabla \Delta r_{\dot{\uprho }_i } = \nabla \Delta V_{ion_i } + \nabla \Delta V_{trop_i } + \nabla \Delta V_i^s ,$$

where $\nabla \Delta r_{\dot{\uprho }_i }$ is the residual error of the triple differences of carrier phases. As a result, using the vector form of the equations, we can write:

$$\nabla \Delta {\bf{Z}}_{V_\uprho } = \left[ {\begin{array}{*{20}c} {\nabla \Delta z_{V_{\uprho_1 } } } \\ {\nabla \Delta z_{V_{\uprho_2 } } } \\ \vdots \\ {\nabla \Delta z_{V_{\uprho_{N - 1} } } } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {h_{\left( 1 \right)}^T } \\ {h_{\left( 2 \right)}^T } \\ \vdots \\ {h_{\left( {N - 1} \right)}^T } \\ \end{array} } \right]V_\upeta^M + \left[ {\begin{array}{*{20}c} {\nabla \Delta r_{\dot{\uprho }_1 } } \\ {\nabla \Delta r_{\dot{\uprho }_2 } } \\ \vdots \\ {\nabla \Delta r_{\dot{\uprho }_{N - 1} } } \\ \end{array} } \right] = {\bf{H}}_{(\upeta )} V_\upeta^M + \nabla \Delta {\bf{r}}_{\dot{\uprho }}$$

(2.2.11)

The solution to (2.2.11) by the least-squares method (with postulation of the corresponding hypotheses about error $\nabla \Delta r_{\dot{\uprho }_i }$) is as follows:

$$\tilde{V}_\upeta^M = \left( {{\bf{H}}_{(\upeta )}^T \Sigma^{ - 1} {\bf{H}}_{(\upeta )} } \right)^{ - 1} {\bf{H}}_{(\upeta )}^T \Sigma^{ - 1} \nabla \Delta {\bf{Z}}_{V_\uprho } .$$

(2.2.12)

Here, $\Sigma$ is the covariance matrix of errors $\nabla \Delta r_{\dot{\uprho }_i }$. The elevation angles of navigation satellites are usually used for parameterization of matrix $\Sigma$ (2.2.12) (Vavilova et al. 2009).

We need to make the following comments.

• (1) The described algorithm assumes that the velocities $V_\upeta^{sat_i }$ of the navigation satellites are known. In this case, GNSS users need to supplement the standard algorithm used to determine coordinates of navigation satellites with an algorithm to calculate their relative velocities.

• (2) When forming differential combinations of carrier phases, it is necessary to solve the problem of mutual synchronization of measurements since they are obtained from two receivers operating in their own time scales.

• (3) The central part of the algorithm is numerical differentiation of the double differences of phase measurements. Correct implementation of this procedure assumes the absence of cycle slips in carrier phases (changes in the values of uncertainties $\left\{ {\nabla \Delta N_i } \right\}$) in the differentiation interval. Therefore, the algorithms of detection and compensation for possible faults in carrier phases is a requisite element of the problem. The Doppler velocity solution is useful additional information in this case. In addition, the problem (2.2.12) can also be solved with the use of L1-optimization since it allows eliminating “bad” satellites (Mudrov and Kushko 1971; Akimov et al. 2012).

• (4) In the case of double-frequency receivers, in differentiation, it is possible to use combinations of carrier phases free from the ionospheric error.

For the quality control of satellite navigation solutions, the GTNAV software generates a number of parameters that allow the operator to decide on the normal or problematic functioning of GNSS receivers. Such parameters include data gaps, the number of visible satellites, PDOP values, baseline lengths, solution accuracies, statistical characteristics of solutions based on the analysis of residuals of raw measurements, etc.

The software was adjusted in terms of GNSS solutions based on the processing of a great amount of experimental data obtained during commercial gravimetric surveys in various regions of the Earth, using GNSS equipment produced by various manufacturers and with various characteristics, under various conditions of piloting the carrier of the gravimetric system, etc.

The software supports the following formats of raw data files: Javad’s *.jps format, Ashtech’s format (e-, b-files), which were used in the first version of the software, the format using the Waypoint GrafNav software (epp, gpb-files). Satellite data processing can be carried out both for a single file (aircraft receiver or base station) and for data from several receivers.

The source data for the software are the names of data files containing raw GNSS measurement records and ephemeris information, calculation time limits and the minimum set of control parameters such as coordinates of the base stations used, satellite mask angle, satellite number with a corresponding time interval which is forced out of processing.

In other words, the software is maximally focused both on the operator of the gravimetric survey, who conducts quality control of satellite data, and on obtaining satellite navigation solutions specific to the airborne gravimetry problem.

Below is the list of options of the GTNAV software.

• 1. Differential mode (different combinations of base stations):

  • determination of coordinates using carrier phase measurements;

  • determination of coordinates using code measurements;

  • determination of velocity using Doppler measurements;

  • determination of velocity using phase measurements;

  • determination of acceleration using carrier phase measurements.

• 2. Standard (autonomous) mode:

  • determination of coordinates using carrier phase measurements;

  • determination of coordinates using code measurements;

  • determination of velocity using Doppler measurements;

  • determination of velocity using carrier phase measurements;

  • determination of acceleration using carrier phase measurements.

2.2.3 Software for INS/GNSS Integration

First of all, it should be noted once again that the GTNAV module provides for the following functions: data integrity check, check for synchronization of inertial data recording with GNSS data, check for warning messages about any failure or malfunction of gravimeter sensors.

The GTNAV module also provides INS/GNSS integration solutions, which are used for quality control and solution of the GA estimation problem. The magnitudes of vertical misalignment errors, azimuth (heading) error, and constant components of the gyro drifts are important for quality control. Thus, if the magnitudes of the misalignment errors are within ±4 arcmin, the GT-2A leveling system operates normally. Otherwise, it may be indicative of the DTG and/or FOG malfunctioning.

For the GA estimation problem, the estimates of misalignment errors are input parameters (see (2.2.3)). Estimation of misalignment errors in the GT-1A, GT-2A airborne gravimeters was a nontrivial problem to solve. The key points of the above problem are given below:

• the GT-2A uses GNSS-derived position and velocity to damp Schuler oscillations in real time. Therefore, it was necessary to record real-time damping signals for postprocessing, which is reflected in the data exchange protocol;

• the damping algorithm is based on a simplified channel-by-channel model of the INS error equations;

• INS dead-reckoning algorithms use the model of the so-called compass heading, based on the GNSS-derived velocity;

• the model of the dead-reckoning algorithm uses relative and absolute angular rates of the geodetic reference frame, which caused certain difficulties in the integration problem given below.

Let us describe this problem. The mechanization equations of the two-component INS with the leveled platform (Golovan and Parusnikov 2012) of GT-series airborne gravimeters are as follows (Bolotin and Golovan 2013):

$$\begin{aligned} \dot{v^{\prime}}_1 & = \Omega^2 R_E \sin \upvarphi^{GNSS} \cos \upvarphi^{GNSS} \sin A^{\prime} + f_1^{\prime} - a_3 Z_{V_1 } - \tilde{\nu }_3^{(1)} , \\ \dot{v^{\prime}}_2 & = \Omega^2 R_E \sin \upvarphi^{GNSS} \cos \upvarphi^{GNSS} \cos A^{\prime} + f_2^{\prime} - a_3 Z_{V_2 } - \tilde{\nu }_3^{(2)} , \\ \dot{V^{\prime}}_1 & = \Omega \sin \upvarphi^{GNSS} V_{a2}^{GNSS} + f_1^{\prime} - a_0 Z_{V_1 } , \\ \dot{V^{\prime}}_2 & = - \Omega \sin \upvarphi^{GNSS} V_{a1}^{GNSS} + f_2^{\prime} - a_0 Z_{V_2 } , \\ \dot{\tilde{\nu }}_3^{\left( 1 \right)} & = a_2 Z_{V_1 } , \\ \dot{\tilde{\nu }}_3^{\left( 2 \right)} & = a_2 Z_{V_2 } , \\ \upomega^{\prime}_1 & = - \frac{{v^{\prime}_2 }}{R_E } - \frac{{V_N^{GNSS} }}{R_E }\left( {1 - \frac{R_N }{{R_E }}} \right)\cos A^{\prime} + a_1 \frac{{Z_{V_2 } }}{R_E }, \\ \upomega^{\prime}_2 & = - \frac{{v^{\prime}_1 }}{R_E } - \frac{{V_N^{GNSS} }}{R_E }\left( {1 - \frac{R_N }{{R_E }}} \right)\sin A^{\prime} - a_1 \frac{{Z_{V_1 } }}{R_E }. \\ \end{aligned}$$

(2.2.13)

Equations (2.2.13) use the following notation: $v_1^{\prime}$, $v_2^{\prime}$, $V_1^{\prime}$, $V_2^{\prime}$ are the horizontal components of the absolute and relative velocities of the vehicle motion; $\upomega^{\prime}_{1}$, $\upomega^{\prime}_{2}$ are the gyro platform leveling signals; $\Omega$ is the Earth angular rate; $R_E$ is the radius of curvature of prime vertical, $a$, $e^2$ are the semi-major axis and the square of the first eccentricity of the Earth’s model ellipsoid; $h^{GNSS}$, $\upvarphi^{GNSS}$, $V_E^{GNSS} ,\,\,V_N^{GNSS}$ are the altitude, geographic latitude, eastern and northern components of velocity; the superscript ‘GNSS’ hereinafter means that the values of such quantities are taken from the navigation satellite system during calculations; $A^{\prime}$ is the azimuth angle defined as:

$$A^{\prime} = arctg\left( { - \frac{{v^{\prime}_2 - V_2^{GNSS} }}{{v^{\prime}_1 - V_1^{GNSS} }}} \right);$$

$V_1^{GNSS} = V_E^{GNSS} \cos A^{\prime} + V_N^{GNSS} \sin A^{\prime},$ $V_2^{GNSS} = - V_E^{GNSS} \sin A^{\prime} + V_N^{GNSS} \cos A^{\prime}$ are the transformed components of the relative velocity $f_1^{\prime}$, $f_2^{\prime}$ are the readings of the horizontal accelerometers; $Z_{V_1 } = V^{\prime}_1 - V_1^{GNSS} ,$ $Z_{V_2 } = V^{\prime}_2 - V_2^{GNSS}$ are velocity aiding measurements; $a_1 ,\ \,a_2 ,\,\ a_3 ,\ \,a_4$ are the gain (damping) coefficients calculated as a function of parameter $T_{gg}$ (this refers to the characteristic time of the transition process).

The corresponding equations of the INS errors are the following:

$$\begin{aligned} \updelta \dot{v}_1 & = - \vartheta_3 v_2^{GNSS} - \upalpha_2 \left( {g + \Omega^2 R_E \cos^2 \upvarphi^{GNSS} } \right) + \Delta f_1 \\ & \quad - \left( {\frac{{\updelta v_1 \sin A^{\prime} + \updelta v_2 \cos A^{\prime} - \Delta V_N^{GNSS} }}{{v_E^{GNSS} }}} \right)\Omega^2 R_E \sin \upvarphi^{GNSS} \cos \upvarphi^{GNSS} \cos A^{\prime} \\ & \quad - a_3 Z_{V_1 } - \tilde{\nu }_3^{(1)} , \\ \updelta \dot{v}_2 & = \vartheta_3 v_1^{GNSS} + \upalpha_1 \left( {g + \Omega^2 R_E \cos^2 \upvarphi^{GNSS} } \right) + \Delta f_2 \\ & \quad + \left( {\frac{{\updelta v_1 \sin A^{\prime} + \updelta v_2 \cos A^{\prime} - \Delta V_N^{GNSS} }}{{v_E^{GNSS} }}} \right)\Omega^2 R_E \sin \upvarphi^{GNSS} \cos \upvarphi^{GNSS} \sin A^{\prime} \\ & \quad - a_3 Z_{V_2 } - \tilde{\nu }_3^{(2)} , \\ \end{aligned}$$

$$\begin{aligned} \dot{\upalpha }_1 & = - \frac{\updelta v_1 }{{R_E }} + \vartheta_{1} - \frac{{\Delta V_N^{GNSS} }}{R_E }\left( {1 - \frac{R_N }{{R_E }}} \right)\cos A^{\prime} \\ & \quad - \left( {\frac{{\updelta v_1 \sin A^{\prime} + \updelta v_2 \cos A^{\prime} - \Delta V_N^{GNSS} }}{{v_E^{GNSS} }}} \right)\frac{{V_N^{GNSS} }}{R_E }\left( {1 - \frac{R_N }{{R_E }}} \right)\sin A^{\prime} + a_1 \frac{{Z_{V_2 } }}{R_E }, \\ \dot{\upalpha }_2 & = \frac{\updelta v_2 }{{R_E }} + \vartheta_{2} + \frac{{\Delta V_N^{GNSS} }}{R_E }\left( {1 - \frac{R_N }{{R_E }}} \right)\sin A^{\prime} \\ & \quad - \left( {\frac{{\updelta v_1 \sin A^{\prime} + \updelta v_2 \cos A^{\prime} - \Delta V_N^{GNSS} }}{{v_E^{GNSS} }}} \right)\frac{{V_N^{GNSS} }}{R_E }\left( {1 - \frac{R_N }{{R_E }}} \right)\cos A^{\prime} - a_1 \frac{{Z_{V_1 } }}{R_E }, \\ \end{aligned}$$

$$\begin{aligned} \updelta \dot{V}_1 & = - \vartheta_3 V_2^{GNSS} - \upalpha_2 g + \Delta f_1 + \Delta V_2^{GNSS} \Omega \sin \upvarphi^{GNSS} \\ & \quad + \left( {\frac{{\updelta v_1 \sin A^{\prime} + \updelta v_2 \cos A^{\prime} - \Delta V_N^{GNSS} }}{{v_E^{GNSS} }}} \right)\Omega \sin \upvarphi^{GNSS} V_1^{GNSS} - a_0 Z_{V_1 } , \\ \updelta \dot{V}_2 & = \, \vartheta_3 V_1^{GNSS} + \upalpha_1 g + \Delta f_2 - \Delta V_2^{GNSS} \Omega \sin \upvarphi^{GNSS} \\ & \quad + \left( {\frac{{\updelta v_1 \sin A^{\prime} + \updelta v_2 \cos A^{\prime} - \Delta V_N^{GNSS} }}{{v_E^{GNSS} }}} \right)\Omega \sin \upvarphi^{GNSS} V_2^{GNSS} - a_0 Z_{V_2 } . \\ \end{aligned}$$

Here,

$$\begin{aligned} v_1^{GNSS} & = \left( {V_E^{GNSS} + \Omega R_E \cos \upvarphi^{GNSS} } \right)\cos A^{\prime} + V_N^{GNSS} \sin A^{\prime} , \\ v_2^{GNSS} & = - \left( {V_E^{GNSS} + \Omega R_E \cos \upvarphi^{GNSS} } \right)\sin A^{\prime} + V_N^{GNSS} \cos A^{\prime} , \\ \Delta V_1^{GNSS} & = \Delta V_E^{GNSS} \cos A^{\prime} + \Delta V_E^{GNSS} \sin A^{\prime}, \\ \Delta V_2^{GNSS} & = - \Delta V_E^{GNSS} \sin A^{\prime} + \Delta V_E^{GNSS} \cos A^{\prime}, \\ \end{aligned}$$

$\updelta v_1$, $\updelta v_2$, $\updelta V_1 ,\,\,\updelta V_2$ are the dynamic errors in the determination of the absolute and relative velocities; $\upalpha_1 ,\,\,\upalpha_2$ are the misalignment angular errors of the instrument vertical; $\Delta f_1 ,\,\,\Delta f_2$ are the accelerometer errors; $\vartheta = \left[ {\begin{array}{*{20}c} {\vartheta_1 ,} & {\vartheta_2 ,} & {\vartheta_3 } \\ \end{array} } \right]^T$ is the vector of the gyro platform drift, each component of which is described by the Wiener process; $g$ is the gravity assumed to be 9.81 m/s².

The aiding measurement model takes the form:

$$\begin{aligned} Z_{V_E } & = V_1^{\prime} \cos A^{\prime} - V_2^{\prime} \sin A^{\prime}V^{\prime}_E - V_E^{GNSS} = V_1 \cos A^{\prime} - \updelta V_2 \sin A^{\prime} \\ & \quad - \updelta A \cdot V_N^{GNSS} - \Delta V_E^{GNSS} , \\ Z_{V_N } & = V^{\prime}_1 \sin A^{\prime} + V^{\prime}_2 \cos A^{\prime} - V_N^{GNSS} = \updelta V_1 \sin A^{\prime} + \updelta V_2 \cos A^{\prime} \\ & \quad + \updelta A \cdot V_E^{GNSS} - \Delta V_N^{GNSS} , \\ Z_{v_E } & = v^{\prime}_1 \cos A^{\prime} - v^{\prime}_2 \sin A^{\prime} - \left( {V_E^{GNSS} + \Omega R_E \cos \upvarphi^{GNSS} } \right) \\ & = \updelta v_{a1} \cos A^{\prime} - \updelta v_{a2} \sin A^{\prime} - \updelta A \cdot V_N^{GNSS} - \Delta V_E^{GNSS} , \\ \updelta A & = - \frac{{\updelta v_1 \sin A^{\prime} + \updelta v_2 \cos A^{\prime} - \Delta V_N^{GNSS} }}{{v_E^{GNSS} }}. \\ \end{aligned}$$

(2.2.14)

Here, $\Delta V_E^{GNSS}$, $\Delta V_N^{GNSS}$ are the errors of GNSS velocity solutions.

Thus, the behavior of INS errors is described by a general model of the form $\dot{x} = Ax + Bu + w,$ where the state vector $x$ includes the inertial system errors and the errors of the inertial sensors; $w$ is a zero-mean white noise; $u$ is the vector of known control signals.

Further, to solve the estimation problem, i.e., to estimate the state vector $x$ using measurements $Z_{V_E }$, $Z_{V_N }$, $Z_{v_E }$, smoothing algorithms are used in the postprocessing mode (see Vavilova et al. (2009) and Sect. 2.3).

The GTNAV software provides the algorithms to solve the described problem. Note that calculations can be carried out using both differential GNSS solutions and GNSS solutions in autonomous mode. The latter is especially important for quality control because in this case it is possible to solve the integration problem without data from base stations, i.e., immediately after the aircraft has landed.

No additional external settings of the integration algorithm are required, which makes the operator’s work easier.

The INS/GNSS software makes the work of the gravimetric survey operator simpler from the viewpoint of quality control.

2.2.4 Software for the Solution of the Basic Gravimetry Equation

Based on the results of the GTNAV software operation, the so-called V-files, containing GNSS positional and velocity solutions, and I-files, containing the description of the gyro platform misalignment angles, are generated. Along with the S-files and G-files generated by the GT-2A gravimeter, these data are used during the final processing in the GTQC20 and GTGRAV modules to form a GA estimate on the trajectory recorded in the G3-file.

The GTQC20 module is responsible for monitoring the data quality in the binary files generated by the GT-2A gravimeter. It checks the synchronization of data with the GNSS clock pulse and gaps in processing cycles, makes a conclusion about the data quality and, if possible, restores the omissions and records the refined and synchronized data into text files. The GTGRAV module generates the GA estimate.

Let us briefly discuss the mathematical part of processing. Consider a “model” basic gravimetric equation that differs from (2.2.1) in the absence of GAs and the substitution of measurements instead of the true values of variables (Bolotin et al. 2002):

$$\begin{aligned} \ddot{h}^{\prime} & = \, \dot{V}_3^{\prime} , \\ \dot{V}_3^{\prime} & = \Delta f_E^{\prime} - \upgamma_0^{\prime} - \updelta \upgamma^{\prime} + f_3^{\prime} . \\ \end{aligned}$$

Subtracting this equation from (2.2.1), denoting $\Delta h = h - h^{\prime}$, $\Delta W = V_3 - V^{\prime}_3 - \uptau_3 \;f^{\prime}_3$, $q_f = \Delta f_3^s$ and taking into account the measurement Eqs. (2.2.2)–(2.2.4), we obtain the equations for the vertical channel errors:

$$\begin{aligned} \Delta \dot{h} & = \Delta W + \uptau_3 f^{\prime}_3 , \\ \Delta \dot{W} & = \upkappa_3 f^{\prime}_3 + q_f + (\upkappa_2 + \upalpha_2 )f^{\prime}_1 - (\upkappa_1 + \upalpha_1 )f^{\prime}_2 + \Delta g. \\ \end{aligned}$$

(2.2.15)

The zero drift of the GSE is not taken into account here since it is compensated for during the reference measurements.

Depending on the situation, GNSS measurements can be used in carrier phase (standard or differential) or Doppler modes (Wei et al. 1991; Stepanov et al. 2002). The GNSS altitude increment serves as positional measurements when using GNSS carrier phase measurements (Bolotin et al. 2002):

$$\Delta h^* = \int\limits_{t_0 }^t {V_3^{GNSS} dt - h^{\prime}} ,\;\Delta h^* = \Delta h + q_h^s + q_h^i .$$

(2.2.16)

Here, $q_h^s$ is the random error of the altitude increment caused by the noise of the GNSS and GSE raw data, and $q_h^i$ is an intermittent error caused by the cycle slip in the carrier phases.

When using GNSS Doppler measurements, we have (Bolotin et al. 2002):

$$\Delta V_3^* = V_3^{GNSS} - W^{\prime}_3 ,\;\Delta V_3^* = \Delta W_3 + q_v^s .$$

(2.2.17)

Here, $q_v^s$ is a random error of the altitude increment caused by the noises of the GNSS and GSE raw data.

Equation (2.2.15) are supplemented with the calibration parameters vs time model (Bolotin and Golovan 2013):

$$\dot{\uptau }_3 = q_\uptau ,\;\dot{\upkappa }_3 = q_{\upkappa 3} ,\;\dot{\upkappa }_1 = q_{\upkappa 1} ,\;\dot{\upkappa }_2 = \, q_{\upkappa 2} ,$$

(2.2.18)

By combining (2.2.15)–(2.2.18) and introducing the vector $q_p { = (}q_\uptau , \, q_{\upkappa 3} , \, q_{\upkappa 1} ,q_{\upkappa 2} {)}$ of parameters drifts, we obtain the model of the vertical channel in the matrix form:

$$\begin{aligned} \dot{x}_g & = \, A_g x_g + B_f q_f + B_p q_p + B_{\Delta g} \Delta g, \\ z & = C_g x_g + q_h^s + q_h^i . \\ \end{aligned}$$

(2.2.19)

A GA stochastic model is used for solution of (2.2.19) (Bolotin and Popelensky 2007). The GA is assumed to be a stationary (time-invariant) random process with a given PSD $S_{\Delta g} {(}\upomega {)}$ represented as an output of a finite-dimensional shaping filter with white noise at the input (in the GTGRAV software, the parameters of the first- or second-order model are selected by the user):

$$\begin{aligned} \dot{x}_a & = \, A_a x_a + B_a q_a , \\ \Delta g & = C_a x_a . \\ \end{aligned}$$

(2.2.20)

Equations (2.2.19), (2.2.20) are used to determine GA on the trajectory with the use of the smoothing filter. Here, it is worth pointing out the following features.

• The filter takes into account the nonstationary (time-varying) nature of the noise; in particular, possible cycle slips $q_h^i$, changes in the number of visible satellites and GSE saturation caused by abnormal vertical accelerations. Both phenomena are simulated by increasing the corresponding noise-variance matrices, which leads to a reduction in the weight of the corresponding measurement when the estimate is calculated. The filter may have several iterations, where noise variances increase with greater values of the residuals. It should be noted that this heuristic technique makes the filter nonlinear.

• The filter automatically takes into account the turns between the survey lines by increasing the value of noise covariance matrices on the turns. This makes it possible to significantly reduce the duration of transient processes at the ends of survey lines.

• The filter provides estimates of the gravimeter calibration parameters, which are used for additional control of data quality.

• The filter allows for the state vector expansion in order to take into account additional correlations caused by angular motions of the aircraft.

• The GA is usually determined in two stages. At the first stage, the model includes the maximum number of external factors to verify data quality. At the second stage, the factors whose values do not reach the reliability threshold are removed from the model.

• The software developed allows survey data to be processed in the drape flight mode. This mode requires very high accuracy of the GSE scale factor $\upkappa_3$ estimation, which makes it necessary to carry out the so-called calibration maneuver. After that, $\upkappa_3$ is determined using the algorithms described above.

• Adaptive modification of the filtering algorithm is possible, wherein GA is described by a nonstationary Markov process (Bolotin and Doroshin 2011).

A block diagram of the GTGRAV software data flows is shown in Fig. 2.17.

Fig. 2.17

Block diagram of data flows in the GTGRAV software modules

A general block diagram of the data flows in the GT-2A gravimeter and postprocessing software modules is shown in Fig. 2.18.

Fig. 2.18

General block diagram of the GT-2A gravimeter and postprocessing software data flows

2.2.5 Conclusion

The features and methods of GT-2 data postprocessing have been discussed. The stages of integrated data postprocessing provided by data acquisition system, GNSS receivers on the aircraft and those at the base stations, inertial navigation system, and the GSE have been considered. They include processing of GNSS raw data, estimation of the gyro platform misalignment errors, and solution of the basic gravimetric equation. The data flows in the postprocessing software have been described.

2.3 Optimal and Adaptive Filtering and Smoothing Methods for Onboard Gravity Anomaly Measurements

The previous sections of this Chapter describe the processing algorithms used in the Chekan and GT series gravimeters. When developing the algorithms, a question often arises if the accuracy of gravimetric surveys can be enhanced by improving the processing algorithms. This question is, generally speaking, still open. In our opinion, it can be answered by applying the Bayesian approach. It offers great advantages by helping not only to formalize the problem of designing the estimation algorithms, including optimal ones, but also to obtain their accuracy characteristics in the form of calculated (conditional) and unconditional covariance matrices. The ability to obtain an unconditional covariance matrix of optimal estimation errors, in turn, makes it possible to calculate the potential accuracy with the given models and thus to objectively estimate the performance of various suboptimal algorithms. However, a significant disadvantage of the Bayesian approach is the necessity for the stochastic description (modeling) of the sensor errors and estimated values. This need for the knowledge of consistent (adequate) models hinders the application of optimal estimation methods. Nevertheless, the progress in computer technology and identification methods used to build the required models provides a new potential for improving the processing methods applied to onboard gravity anomaly measurements.

The present section is devoted to the synthesis of optimal Bayesian algorithms and identification methods, which provide the required models.

2.3.1 General Formulation and Solution of Optimal Filtering and Smoothing Problems

First, let us formulate the problem of optimal Bayesian estimation of gravity anomaly onboard a vehicle, assuming that the models of errors of the measuring instruments and of GA to be estimated are known. For this purpose, let us first formulate the filtering and smoothing problems in the general form and briefly describe the algorithms used to solve them (Meditch 1969; Stepanov 2017b).

Suppose an n-dimensional Markov process is given,

$$\dot{x}\left( t \right) = F\left( t \right)x\left( t \right) + G\left( t \right)w\left( t \right),x\left( {t_0 } \right) = x_0$$

(2.3.1)

and m-dimensional measurements are taken

$$y\left( t \right) = H\left( t \right)x\left( t \right) + v\left( t \right),$$

(2.3.2)

where $F\left( t \right)$, $G\left( t \right)$, $H\left( t \right)$ are the generally known time-dependent $n \times n$, $n \times p$, $m \times n$ matrices; $x_0$ is the zero-mean vector of initial conditions with covariance matrix $P_0$; $w\left( t \right)$, $v\left( t \right)$ are p- and $m$-dimensional vectors of zero-mean white noises with a given PSD, which are noncorrelated with each other and have the initial conditions $x_0$, i.e.:

$$E\left\{ {x_0 w^T \left( t \right)} \right\} = 0;E\left\{ {w\left( t \right)v^T \left( t \right)} \right\} = 0;E\left\{ {x_0 v^T \left( t \right)} \right\} = 0;$$

(2.3.3)

$$E\left\{ {w\left( t \right)w^T \left( \uptau \right)} \right\} = Q\left( t \right)\updelta \left( {t - \uptau } \right),Q\left( t \right) \ge 0;$$

(2.3.4)

$$E\left\{ {v\left( t \right)v^T \left( \uptau \right)} \right\} = R\left( t \right)\updelta \left( {t - \uptau } \right),R\left( t \right) > 0.$$

(2.3.5)

The filtering problem is formulated as follows. Using the measurements (2.3.2) $Y\left( t \right) = \left\{ {y\left( \uptau \right):\uptau \in \left[ {0,t} \right]} \right\}$ accumulated over the interval $\left[ {0,t} \right]$, it is needed to obtain the linear mean-square optimal estimate $\hat{x}\left( t \right)$ of vector $x\left( t \right)$ at time t, which minimizes the criterion

$$r^B \left( t \right) = E\left\{ {\left( {x\left( t \right) - \hat{x}\left( t \right)} \right)^T \left( {x\left( t \right) - \hat{x}\left( t \right)} \right)} \right\}.$$

(2.3.6)

It is well known that the estimate $\hat{x}\left( t \right)$ and its error covariance matrix $P\left( t \right)$ are determined using the following formulas for the Kalman-Bucy filter (Kalman and Bucy 1961; Meditch 1969):

$$\dot{\hat{x}}\left( t \right) = F\left( t \right)\hat{x}\left( t \right) + K\left( t \right)\left( {y\left( t \right) - H\left( t \right)\hat{x}\left( t \right)} \right);$$

(2.3.7)

$$K\left( t \right) = P\left( t \right)H\left( t \right)^T R^{ - 1} \left( t \right);$$

(2.3.8)

$$\begin{aligned} \dot{P}\left( t \right) & = P\left( t \right)F\left( t \right)^T + F\left( t \right)P\left( t \right) - P\left( t \right)H\left( t \right)^T R^{ - 1} \left( t \right)H\left( t \right)P\left( t \right) \\ & \quad + G\left( t \right)Q\left( t \right)G^T \left( t \right). \\ \end{aligned}$$

(2.3.9)

In practice, the estimate is calculated using the discrete form of the filter (Kalman 1960; Meditch 1969):

$$\hat{x}_i = \hat{x}_{i/i - 1} + K_i \left( {y_i - H_i \hat{x}_{i/i - 1} } \right);$$

(2.3.10)

$$\hat{x}_{i/i - 1} = \Phi_i \hat{x}_{i - 1} ,P_{i/i - 1} = \Phi_i P_{i - 1} \Phi_i^T + \Gamma_i Q_i \Gamma_i^T ;$$

(2.3.11)

$$K_i = P_i H_i^T R_i^{ - 1} ,P_i = \left( {P_{i/i - 1}^{ - 1} + H_i^T R_i^{ - 1} H_i } \right)^{ - 1} ;$$

(2.3.12)

where $\Phi_i = \Phi \left( {t_i ;t_i - \Delta t} \right)$ is the transition matrix of the system (2.3.1) between times $t_i - \Delta t$ and $t_i$ ($\Delta t$ is the sample interval); $\Gamma_i$ and $Q_i$ are the matrices chosen so as to satisfy the formula

$$\Gamma_i Q_i \Gamma_i^T \approx G\left( {t_i } \right)Q\left( {t_i } \right)G^T \left( {t_i } \right)\Delta t,$$

corresponding to the condition of stochastic equivalence of the continuous process $x\left( t \right)$ and the discrete sequence $x_i$ (Stepanov 2017b), the matrix $R_i = R{(}t_i {)}/\Delta t$, and $H_i = H\left( {t_i } \right)$. Note that here Eq. (2.3.11) generate the optimal prediction $\hat{x}_{i/i - 1}$ and the corresponding covariance matrix $P_{i/i - 1}$ at time $t_i$.

The smoothing problem is formulated as follows. Using the measurements (2.3.2) $Y\left( {t_1 } \right) = \left\{ {y\left( \uptau \right):\uptau \in \left[ {t_0 ,t_1 } \right]} \right\}$ accumulated over the interval $\left[ {t_0 ,t_1 } \right]$ at time $t$, it is required to obtain a linear mean-square optimal estimate $\hat{x}^s \left( t \right)$ of the vector $x\left( t \right)$ at time $t < t_1$, which minimizes the criterion

$$r^B \left( t \right) = E\left\{ {\left( {x\left( t \right) - \hat{x}^s \left( t \right)} \right)^T \left( {x\left( t \right) - \hat{x}^s \left( t \right)} \right)} \right\}.$$

There are three types of smoothing problems: fixed-interval smoothing, constant delay smoothing, and fixed-point smoothing (Meditch 1969; Stepanov 2017b).

Focus on a possible algorithm for solving the problem over a fixed interval, which is used in this study. This algorithm is based on preliminary solution of the filtering problem over the entire time interval $\left[ {t_0 ,t_1 } \right]$, resulting in the generation of estimates and their covariance matrices. Further the filtering estimates are denoted by $\hat{x}^f \left( t \right)$, $P^f \left( t \right)$ and smoothing estimates, by $\hat{x}^s \left( t \right)$, $P^s \left( t \right)$. Assume that $P^f \left( t \right)$ is nonsingular and the inverse matrix $\left( {P^f \left( t \right)} \right)^{ - 1}$ exists. In this case, the smoothing solution in the form of the optimal estimate $\hat{x}^s \left( t \right)$ and the corresponding covariance matrix $P^s \left( t \right)$ can be defined by the following equations (Meditch 1969):

$$\dot{\hat{x}}^s \left( t \right) = F\left( t \right)\hat{x}^s \left( t \right) + K^s \left( t \right)\left( {\hat{x}^s \left( t \right) - \hat{x}^f \left( t \right)} \right);$$

(2.3.13)

$$K^s \left( t \right) = G\left( t \right)Q\left( t \right)G\left( t \right)^T \left( {P^f \left( t \right)} \right)^{ - 1} ;$$

(2.3.14)

$$\dot{P}^s \left( t \right) = \left[ {F\left( t \right) + K^s \left( t \right)} \right]P^s \left( t \right) + P^s \left( t \right)\left[ {F\left( t \right) + K^s \left( t \right)} \right]^T - G\left( t \right)Q\left( t \right)G^{\text{T}} \left( t \right).$$

(2.3.15)

These equations determine the solution of a continuous optimal smoothing problem over a fixed interval. It is clear that for time $t = t_1$, the formulation and, hence, the solution of the smoothing problem coincide with the formulation and solution of the filtering problem. It should be noted that the residual $\hat{x}^s \left( t \right) - \hat{x}^f \left( t \right)$ in (2.3.13) has dimension $n$ coinciding with the dimension of the state vector.

The algorithm (2.3.13)–(2.3.15) in the discrete form is referred to as the Rauch-Tung-Striebel (RTS) smoothing algorithm (Rauch et al. 1965) or simply as the optimal smoothing filter (OSF). At the first step, similarly to filtering problem, the conventional Kalman filter (KF) (2.3.10)–(2.3.12) is used to obtain the optimal estimates $\hat{x}_i^f$ and $P_i^f$. At the second step, a modified filter is used with account for the obtained values, where the filtering estimate is used instead of the predicted estimate, and the residual is the difference between the estimate smoothed at the previous step and the predicted estimate (Simon 2006; Stepanov 2017a):

$$\begin{aligned} \hat{x}_i^s & = x_i^f + K_i^s \left( {\hat{x}_{i + 1}^s - \hat{x}_{i + 1/i}^f } \right), \\ K_i^s & = P_i^f \Phi_i^T \left( {P_{i + 1/i}^f } \right)^{ - 1} , \\ P_i^s & = P_i^f + K_i^s \left( {P_{i + 1}^s - P_{i + 1/i}^f } \right)\left( {K_i^s } \right)^T . \\ \end{aligned}$$

(2.3.16)

It is important that the filter (2.3.16) runs in inverse time, since the smoothed estimate at time $t_i$ depends on the similar estimate at time $t_i + \Delta t.$ It also follows from the Eq. (2.3.16) that it is not needed to calculate the smoothing error covariance matrix $P^s$ to obtain the estimate. However, it can be used as a characteristic of estimation accuracy. The analysis of the above equations also shows that to obtain a smoothed estimate, it is necessary to save the estimates, the predicted estimates, and their error covariance matrices obtained during filtering. Obviously, this increases the requirements for the computer memory when solving the smoothing problem.

2.3.2 Optimal Filtering and Smoothing Algorithms for Onboard Gravity Anomaly Measurements

Let us specify the above problem formulations as applied to the gravity anomaly measurements. As a rule, by the filtering stage the most corrections such as the normal gravity correction, Eotvos correction, altitude correction, etc., have already been introduced in gravimeter measurements. Thus, the gravimeter measurements $g_{GR} {(}t{)}$ can be represented as follows:

$$g_{GR} (t) = \Delta g(t) + a_o (t) + w_{GR} (t),$$

(2.3.17)

where $\Delta g{(}t{)}$ is the GA in free air; $a_o {(}t{)}$ is the vertical acceleration of the vehicle; $w_{GR} {(}t{)}$ are the total random measurement errors of the gravimeter. Based on the measurements (2.3.17), to apply the optimal filtering and smoothing algorithms it is needed to determine the shaping filter of the form (2.3.1) for GA $\Delta g{(}t{)}$ and the vertical accelerations $a_o {(}t{)}$.

The gravity anomaly can be described with the Jordan model, the Schwarz model (Jordan 1972) and other models, along with their approximations as the integrals of white noise (Bolotin et al. 2002). Here, let us consider the Jordan model corresponding to the stationary third-order Markov process with the correlation function (Jordan 1972):

$$K_{\Delta g} \left( \uprho \right) = \upsigma_{\Delta g}^2 \left( {1 + \upalpha \uprho - \frac{{\left( {\upalpha \uprho } \right)^2 }}{2}} \right)e^{ - \upalpha \uprho } ,$$

(2.3.18)

where ${\upsigma }_{\Delta g}^2$ is the GA variance; ${\upalpha }$ is the inverse correlation interval; ${\uprho }$ is the length of a rectilinear trajectory. To transform (2.3.18) to the time domain, use the formula ${\uprho } = Vt$, where $V$ is the vehicle speed. Note that the process with the correlation function (2.3.18) is differentiable and the variance of its derivative can be defined as follows:

$$\upsigma_{\partial \Delta g/\partial \uprho }^2 = \left. { - \frac{d^2 }{{d\uprho^2 }}K_{\Delta g} \left( \uprho \right)} \right|_{\uprho = 0} = 2\upalpha^2 \upsigma_{\Delta g}^2 .$$

It should also be noted that $\upsigma_{\partial \Delta g/\partial \ \uprho }$ characterizes the spatial variability of GA. Further, for simplicity, we will call this quantity the gradient of the gravitational field. PSD of the function (2.3.18) is defined as follows:

$$S_{\Delta g} \left( \upomega \right) = 2\upalpha^3 \cdot \upsigma_{\Delta g}^2 \cdot \frac{5 \cdot \upomega^2 + \upalpha^2 }{{\left( {\upomega^2 + \upalpha^2 } \right)^3 }},$$

(2.3.19)

where $\upomega$ is the analogue of the circular frequency for the process depending on the length of the straight section. The PSD can be represented as

$$S_{\Delta g} \left( \upomega \right) = 2\upalpha^3 \cdot \upsigma_{\Delta g}^2 \cdot \frac{{\left( {\upalpha + \sqrt 5 j\upomega } \right)\left( {\upalpha - \sqrt 5 j\upomega } \right)}}{{\left( {\upalpha + j\upomega } \right)^3 \left( {\upalpha - j\upomega } \right)^3 }},$$

(2.3.20)

so it is easy to show that $\Delta g{(}t{)}$ samples corresponding to this PSD can be generated using the components of the third-order Markov process (Stepanov 2017b):

$$\left\{ {\begin{array}{*{20}l} {\dot{b}_1 = - \upbeta b_1 + b_2 ;} \hfill \\ {\dot{b}_2 = - \upbeta b_2 + b_3 ;} \hfill \\ {\dot{b}_3 = - \upbeta b_3 + w_{GA} ,} \hfill \\ \end{array} } \right.$$

(2.3.21)

where $\upbeta = V\upalpha$; $V$ is the vehicle speed; $w_{GA}$ is the generating white noise with the PSD $q_w = 10\upbeta^3 \upsigma_{\Delta g}^2$. In this case, GA $\Delta g$ is defined as

$$\Delta g = - \upbeta \vartheta b_1 + b_2 ,\;{\text{where}}\;\vartheta = \frac{\sqrt 5 - 1}{{\sqrt 5 }}.$$

(2.3.22)

The vehicle vertical acceleration $a_o {(}t{)}$ can also be generally described as a random process. Clearly, its frequency properties significantly depend on the vehicle type.

In marine gravimetry, the frequency properties of the processes $\Delta g{(}t{)}$ and $a_o {(}t{)}$ greatly differ, so the acceptable accuracy of $\Delta g{(}t{)}$ estimation can be achieved without using additional data on vertical accelerations $a_o {(}t{)}$. In practice, stationary filtering and smoothing algorithms described in Sect. 2.3.3 are often applied to such problems.

In airborne gravimetry, due to the high speed of the vehicle, the PSDs of $\Delta g{(}t{)}$ and $a_o {(}t{)}$ substantially overlap in the frequency domain. Therefore, vertical displacements $h_o {(}t{)}$ should be applied to achieve the required accuracy of $\Delta g{(}t{)}$ estimation. As follows from the previous sections, these data can be obtained using high-precision GNSS measurements of altitude $h_s {(}t{)}$ in the differential phase mode. By presenting them as

$$h_s (t) = h_o (t) + v_s (t),$$

(2.3.23)

where h_o(t) is the vehicle altitude; $v_s {(}t{)}$ are GNSS measurement errors, formulate the problem of GA optimal estimation as the problem of estimating the state vector $x = \left[ {h_o ,V_o ,a_o ,b_1 ,b_2 ,b_3 ,} \right]^T$ specified by the following equations:

$$\left\{ {\begin{array}{*{20}l} {\dot{h}_o = V_o ;} \hfill \\ {\dot{V}_o = a_o ;} \hfill \\ {\dot{b}_1 = - \upbeta b_1 + b_2 ;} \hfill \\ {\dot{b}_2 = - \upbeta b_2 + b_3 ;} \hfill \\ {\dot{b}_3 = - \upbeta b_3 + w_{GA} ;} \hfill \\ \end{array} } \right.$$

(2.3.24)

by measurements (2.3.17), (2.3.23). However, such a formulation requires the description of vehicle accelerations $a_o$ using a shaping filter in the state space. A common way to avoid this in practice is to proceed to the formulation not requiring the introduction of the model of vehicle vertical accelerations (Nesenyuk and Khodorkovsky 2010). By double integration of the gravimeter readings (2.3.17), we obtain

$$\left\{ {\begin{array}{*{20}l} {\dot{h}_{GR} = V_{GR} ;} \hfill \\ {\dot{V}_{GR} = \Delta g + a_o + w_{GR} ,} \hfill \\ \end{array} } \right.$$

(2.3.25)

where $h_{GR} = h_o + \Delta h_{GR}$, $V_{GR} = V_o + \Delta V_{GR}$ are the increments of altitude and speed obtained by integrating the gravimeter readings. Considering (2.3.24), (2.3.25) and the fact that $\Delta g = - \upbeta \vartheta b_1 + b_2$, we obtain the following formulas:

$$\left\{ {\begin{array}{*{20}l} {\Delta \dot{h}_{GR} = \Delta V_{GR} ;} \hfill \\ {\Delta \dot{V}_{GR} = - \, \upbeta \, \vartheta b_1 + b_2 + w_{GR} ;} \hfill \\ {\dot{b}_1 = - \upbeta b_1 + b_2 ;} \hfill \\ {\dot{b}_2 = - \upbeta b_2 + b_3 ;} \hfill \\ {\dot{b}_3 = - \upbeta b_3 + w_{GA} .} \hfill \\ \end{array} } \right.$$

(2.3.26)

Forming the differential measurements as

$$y = h_{GR} (t) - h_s (t) = \Delta h_{GR} (t) + v_s (t),$$

(2.3.27)

the problem of GA optimal estimation by GNSS and gravimeter data can be formulated as the problem of estimating the state vector $x = \left[ {\Delta h_{GR} ,\Delta V_{GR} ,b_1 ,b_2 ,b_3 } \right]^T$ described by Eq. (2.3.26) using measurements (2.3.27). Obviously, the above formulation of the problem is invariant to vertical accelerations due to the use of differential measurements (2.3.27). This technique is often applied to process redundant measurements, especially in navigation applications (Groves 2013; Stepanov 2016). However, it should be noted that the above formulation is not invariant to GA: its description is required and in this case specified using the Jordan model (2.3.21), (2.3.22). For more information on invariant and non-invariant algorithms, see Brown and Hwang (1977), Dmitriev and Stepanov (2000), Stepanov (2016).

For example, let us specify the problem formulation by introducing the random error models of gravimeter readings $w_{GR} {(}t{)}$ and measurements $v_s {(}t{)}$. Following (Stepanov et al. 2002), describe them for simplicity by white-noise random processes with the known PSD $R_{GR}$ and $Q_{SNS}$, respectively. In this case, the problem is a linear estimation problem, and its solution is reduced to the optimal KF or the smoothing filter described in the previous subsection, and the corresponding models (2.3.1), (2.3.2) with the following matrices included in them:

$$F = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & { - \upbeta \vartheta } & 1 & 0 \\ 0 & 0 & { - \upbeta } & 1 & 0 \\ 0 & 0 & 0 & { - \upbeta } & 0 \\ 0 & 0 & 0 & 0 & { - \upbeta } \\ \end{array} } \right],G = \left[ {\begin{array}{*{20}c} 0 & 0 \\ {\sqrt {R_{GR} } } & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & {q_w } \\ \end{array} } \right],H = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 & 0 \\ \end{array} } \right].$$

To implement the algorithms, the initial covariance matrix $P_0$ is required, which, as can be easily seen, has a block-diagonal form due to the structure of the system (2.3.26).

2.3.3 Stationary Estimation Algorithms and Their Performance Analysis

As follows from the previous sections, stationary filtering and smoothing algorithms, which, unlike the optimal algorithms, minimize the error variance only in the steady state, are applied to simplify the processing algorithms in GA estimation (Stepanov 2017b).

One of the methods to construct such filters is based on using the filtering and smoothing solution in the state space for a steady state. Discuss this method in more detail as applied to fixed-interval smoothing assuming that the matrices in (2.3.1), (2.3.2) do not depend on time. It is thought that there exists a steady-state solution for the filtering problem. To simplify the formula, let us put here that the PSD of the generating noise is an identity matrix. Present the solution of the steady-state smoothing problem by the algorithm (2.3.13)–(2.3.15) discussed in Sect. 2.3.2 using the transfer functions (TF). To do this, first obtain the filtering estimate using a conventional steady-state KF

$$\dot{\hat{x}}_\infty^f \left( t \right) = \left( {F - K_\infty^f H} \right)\hat{x}_\infty^f \left( t \right) + K_\infty^f y\left( t \right),$$

(2.3.28)

where

$$K_\infty^f = P_\infty^f H^T R^{ - 1} ,$$

(2.3.29)

and then find the smoothed estimate by processing $\hat{x}^f \left( t \right)$ with the filter

$$\dot{\hat{x}}_\infty^s \left( t \right) = F\hat{x}_\infty^s \left( t \right) + K_\infty^s \left( {\hat{x}_\infty^s \left( t \right) - \hat{x}_\infty^f \left( t \right)} \right)$$

(2.3.30)

with

$$K_\infty^s = Q\left( {P_\infty^f } \right)^{ - 1} ,$$

(2.3.31)

where

$$Q = GG^T .$$

(2.3.32)

The matrix $P_\infty^f$ included in these formulas corresponds to the solution of the covariance equation (2.3.9) for the steady state. The solution is sought for the steady state, so the TF matrix can be found for the optimal KF:

$$W_x^f \left( p \right) = \left( {pE - F + K_\infty^f H} \right)^{ - 1} K_\infty^f .$$

(2.3.33)

Considering that $\hat{x}_\infty^f \left( p \right) = W_x^f \left( p \right)y\left( p \right)$, we get the following to estimate smoothing:

$$\begin{aligned} \hat{x}_\infty^s \left( p \right) & = \left( { - pE + F + Q\left( {P_\infty^f } \right)^{ - 1} } \right)^{ - 1} Q\left( {P_\infty^f } \right)^{ - 1} \hat{x}_f^f \left( p \right) \\ & = \left( { - pE + F + Q\left( {P_\infty^f } \right)^{ - 1} } \right)^{ - 1} Q\left( {P_\infty^f } \right)^{ - 1} W_x^f \left( p \right)y\left( p \right), \\ \end{aligned}$$

where $W_x^f \left( p \right)$ is given by (2.3.33).

It follows that the TF matrix for a smoothing filter, providing the estimation of all state vector components, is defined as

$$W_x^s \left( p \right) = \left( { - pE + F + Q\left( {P_\infty^f } \right)^{ - 1} } \right)^{ - 1} Q\left( {P_\infty^f } \right)^{ - 1} W_x^f \left( p \right).$$

(2.3.34)

A number of methods have been developed to find the required filter TF $W_x^f \left( p \right)$, including approximate ones, such as the method of PSD local approximation (Loparev et al. 2012; Stepanov et al. 2014). It constructs the PSDs of the useful signal and noise and searches for their intersection point, where the PSDs are equal. To obtain this intersection point, the PSDs in its vicinity are approximated by linear functions. The found frequency is taken to be the cutoff frequency of the filter, and the TF order is determined by the steepness of the linear approximation slope. It follows from the above that with this method, the parameters of the TF significantly depend only on the properties of the PSDs in the vicinity of the found point. Thus, simpler models can be applied to describe the error and the value to be estimated: for example, the GA model can be specified as the second or third integral of white noise instead of the Jordan model. The studies (Stepanov et al. 2002; Koshaev and Stepanov 2010) show that with the GA model specified as the second integral of white noise, for the models described in 2.3.2 the TF of the stationary smoothing filter can be represented with a certain degree of approximation using the fourth-order Butterworth filter TF:

$$w_{B_4 } \left( p \right) = \frac{\upmu^4 }{{p^4 + \upgamma p^3 \upmu + \frac{\upgamma^2 }{2}p^2 \upmu^2 + \upgamma p\upmu^3 + \upmu^4 }},$$

(2.3.35)

where $\upmu = \left( {{{q_{\ddot{\tilde{g}}} } / {R_h }}} \right)\,\,^{1 / 8}$ is the filter cutoff frequency; $q_{\ddot{\tilde{g}}} = \upsigma_{\partial \tilde{g}/\partial \uprho }^2 3V^3 /\uprho$; $V$ is the vehicle speed; $R_h$ is the standard deviation of altitude error; $\uprho$ is the trajectory length; and $\upgamma = \sqrt {2\left( {2 + \sqrt 2 } \right)}$ is a dimensionless coefficient.

In the design of smoothing algorithms, various techniques are also applied to reduce their computational complexity. For example, it is known (Stepanov 2017b) that in a particular estimation of a scalar process with a fractional-rational PSD against the white noise background, the TF in the smoothing problem for the measured scalar component $z = Hx$ can be represented as follows:

$$W_z^s (p) = W_* ( - p)W_* (p) = \left| {W_* (p)} \right|^2 ,$$

(2.3.36)

where the function $W_* (p)$ is defined as $W_* (p) = rG^T (P_\infty^f )^{ - 1} W_x^f (p)$ with $r = \sqrt R$.

This implies that if the measured and estimated components coincide, a computationally inexpensive algorithm can be employed to obtain the optimal smoothing estimate. It includes the following steps (Stepanov 2017b):

• generation of the estimate vector $\hat{x}^f \left( t \right)$ using the KF, which generally estimates the n-dimensional state vector by the scalar measurement $y\left( t \right) = z\left( t \right) + v\left( t \right) = Hx\left( t \right) + v\left( t \right)$;

• generation and saving of the scalar sample $\hat{\tilde{z}}\left( t \right) = T\hat{x}^f \left( t \right)$ using the row matrix $T = rG^T \left( {P_\infty^f } \right)^{ - 1}$, where $r = \sqrt R$;

• generation of the n-dimensional estimate vector $\hat{x}^s \left( t \right)$ by processing the scalar $\hat{\tilde{z}}\left( t \right)$ in the inverse time in the same Kalman-type filter.

The idea of this modified smoothing algorithm is that it requires saving only the scalar estimates obtained in the filtering mode.

When using this algorithm, as applied to the considered example with the models described in Sect. 2.3.2 and the GA model specified as the second integral of white noise, it can be shown that processing is reduced to differentiating the measurements and applying the Butterworth filters in the forward and inverse time:

$$W_h^{\text{c}} \left( p \right) = w_{B_4 } \left( p \right)w_{B_4 } \left( { - p} \right)\left( \begin{gathered} 1 \hfill \\ p \hfill \\ p^2 \hfill \\ p^3 \hfill \\ \end{gathered} \right).$$

(2.3.37)

The study (Stepanov et al. 2002) shows that despite the simplified specification of the anomaly model in the local approximation method, the resulting algorithm is close to the optimal in the steady-state mode for the models described above, including the Jordan model for GA.

Another modification of a suboptimal smoothing algorithm is discussed in Sect. 2.4.

In practice, finite impulse response (FIR) filters are also applied to process airborne gravimetry data. For example, in the two-stage procedure of processing the Chekan gravimeter data described in Sect. 2.1.3, the first stage uses a FIR filter with a trapezoidal Tukey weight function. The use of such a filter with a fixed window width decreases the estimation interval by half the window width on both ends of the trajectory; besides, sometimes the filter fails to achieve the acceptable estimation accuracy. Therefore, a second stage is provided, where the received signal is transferred to the frequency domain, where high-frequency harmonics are reduced by Fourier transformation. This procedure smoothes the resulting estimate but does not reduce the spatial resolution of the survey. The transfer back to the time domain is performed at the final stage. A diagram of this procedure is shown in Fig. 2.19.

Fig. 2.19

Two-stage processing procedure

The processing algorithm is tuned by selecting the width of Tukey window and the number of harmonics in Fourier transformation. It should be noted that, due to the heuristic nature of this algorithm, there exists no formalized tuning sequence for it. In practice, its parameters are selected so that the resulting estimate is typical of GA. Spectral analysis of the resulting estimate can additionally be used. The estimate is verified by comparison with the known rough map of the gravitational field with the marked characteristic points (GA minima and maxima). The performance of the estimation algorithm is assessed based on the coincidence of the anomalies at these points. Thus, when processing real data using such a procedure, the accuracy of GA estimation largely depends on the experience of the engineer processing the measurements.

As noted in Introduction of this chapter, the Bayesian approach offers the advantage of calculating the potential accuracy of the specified models. This creates a good basis for objective estimation of the efficiency of various simplified algorithms in simulation studies. The results of such a study for the models described in 2.3.2 are presented in Figs. 2.20, 2.21 and 2.22 showing the actual RMS errors (RMSE) for the optimal smoothing algorithm, the stationary Butterworth filter (2.3.35), and the two-stage estimation procedure.

Fig. 2.20

GA estimation RMSE

Fig. 2.21

Steady RMSE of GA estimation

Fig. 2.22

Transient process for GA estimation RMSE

Stationary suboptimal algorithms do not generate the estimation accuracy characteristic during the operation, so the corresponding RMSEs are obtained by statistical testing as described, for example, in Stepanov (2017b). It is also important to note that the true GA was generated in accordance with the Jordan model in all cases.

The simulation results generally confirm that stationary suboptimal algorithms in steady-state mode are close to the optimal algorithm, but suffer from large errors (up to hundreds of mGal) at the boundaries of the intervals. In this case, the transient process recalculated to the trajectory length lasts for up to 25 km.

The transient process of a two-stage procedure generally features somewhat smaller RMSE and a longer time to reach the steady state compared with the stationary algorithm. However, due to the nature of the Fourier transformation, it is accompanied by significant fluctuations up to 50 km long. To prevent this effect, the authors of the algorithm proposed to increase the observation interval by extrapolating the measurements outside the trajectory with high-frequency harmonics (Krasnov and Sokolov 2013).

The advantages of stationary algorithms include low computational complexity and easy implementation. Such algorithms, in some cases, require no explicit models for GA anomalies and the errors of the measuring instruments. However, they suffer from the pronounced boundary effects at the trajectory ends and are able neither to assess the estimation accuracy during the transient process nor to account for the varying motion parameters of the aircraft.

It should also be emphasized that the smoothing mode provides a much better GA estimation accuracy as compared to the filtering mode. Figure 2.23 shows GA estimates and their RMSEs in various modes during the processing of airborne gravimetric data.

Fig. 2.23

GA estimation RMSE in filtering and smoothing modes (left); the obtained GA estimates (right)

It can be seen that the estimate obtained in the filtering mode has a non-typical high-frequency component, as well as the phase shift. The use of smoothing procedures eliminates these negative effects. As noted in Sect. 2.3.1, the RMSE of filtering and smoothing coincide at the end of the interval, thus, the minimum filtering RMSE corresponds to the maximum smoothing RMSE. In general, the use of all measurements in the smoothing process increases the accuracy 2–3 times in the steady state. It should be noted that the FIR filter described in the analysis of the two-stage estimation procedure, strictly speaking, also solves the smoothing problem, since it obtains an estimate for the middle of the window, i.e., uses the measurements obtained both before and after the estimation.

2.3.4 Model and Parametric Identification of Gravity Anomaly and Measurement Errors Using Onboard Gravity Measurements

As follows from the previous material, the design of optimal estimation algorithms requires stochastic models of the GA and errors of the measuring instruments. Note that attempts to process real data using optimal filtering and smoothing algorithms for the model (2.3.26), (2.3.27) have failed (Sokolov et al. 2016). It should also be said that the parameters of the GA model (2.3.21), (2.3.22) may vary depending on the survey area: the field gradient may be within 0.5–3 mGal/km in a flat terrain and reach 10 mGal/km and more in a mountainous terrain. Simulation has shown (Stepanov et al. 2015; Motorin and Nosov 2019) that inaccurate setting of this value can critically reduce the GA estimation RMSE. If the used models differ from the actual ones, the calculated accuracy characteristic in the form of diagonal elements of the covariance matrix does not match the actual estimation accuracy (Stepanov and Koshaev 2011). All this proves the importance of structural and parametric identification of models used in GA measurements. Next, let us discuss the algorithm proposed for identification.

Note that the model used to design the optimal algorithm within the Bayesian approach can generally be represented as a shaping filter:

$$\begin{aligned} x_i^k & = \Phi_i^k \left( {\uptheta^k } \right)x_{i - 1}^k + \Gamma_i^k \left( {\uptheta^k } \right)w_i^k , \\ \uptheta_i^k & = \uptheta_{i - 1}^k = \uptheta^k , \\ \end{aligned}$$

(2.3.38)

$$y_i = H_i^k \left( {\uptheta^k } \right)x_i^k + \Psi_i^k \left( {\uptheta^k } \right)v_i^k ,$$

(2.3.39)

where $x_i^k$ is the state vector; $\Phi_i^k \left( {{\uptheta }^k } \right)$, $\Gamma_i^k \left( {\uptheta^k } \right)$, $H_i^k \left( {{\uptheta }^k } \right)$, $\Psi_i^k \left( {{\uptheta }^k } \right)$ are the shaping filter matrices characterizing the error model, whose elements generally nonlinearly depend on the parameter vector ${\uptheta }^k$; $w_i^k$ and $v_i^k$ are the $p^k$- and $m^k$-dimensional white-noise Gaussian sequences with identity covariance matrices; k is the number of a candidate model used to describe the errors. The structure of the model described by the number $k$ and dimensions of the vectors ${\uptheta }^k$ and $x_i^k$(different for different $k$) included in Eqs. (2.3.38), (2.3.39) may be unknown.

Considering the above equations and introducing the hypotheses for the model number $k$, the problem of structural and parametric identification can be formulated (Dmitriev and Stepanov 2004; Motorin and Stepanov 2015; Toropov et al. 2016; Stepanov and Motorin 2019). It consists in determining the number of the hypothesis k, which best fits the vector of all measurements obtained by the time i $Y_i = \left[ {\begin{array}{*{20}c} {y_1 } & {...} & {y_i } \\ \end{array} } \right]^T$, and obtaining the estimates of the parameter vector ${\uptheta }^k$ and the state vector $x_i^k$ corresponding to this hypothesis.

Let us interpret the set of suggested hypotheses as a random variable H, which takes the values $h_k$, where $k = \overline{1 \ldots K}$, K is the total number of hypotheses. The probability density function (PDF) of H can be represented as follows (Dmitriev and Stepanov 2004):

$$f_{\text{H}} \left( {\text{H}} \right) = \sum_{k = 1}^K {\Pr \left( {{\text{H}} = h_k } \right)} \updelta \left( {{\text{H}} - h_k } \right),$$

(2.3.40)

where $\Pr \left( {{\text{H}} = h_k } \right)$ is the probability that the hypothesis for the model H = h_k is true, and $\sum_{k = 1}^K {\Pr \left( {{\text{H}} = h_k } \right)} = 1$. The value of $h_k$ is selected such that to maximize the conditional probability $\Pr \left( {{\text{H}} = h_k /Y_i } \right)$ or, which is the same, to maximize the a posteriori (conditional) PDF $f_{\text{H}} \left( {{\text{H}}/Y_i } \right)$:

$$h_k^* = \arg \mathop {\max }\limits_{h_k } f_{\text{H}} \left( {{\text{H}}/Y_i } \right).$$

(2.3.41)

With a fixed value of the hypothesis, the estimates of the vectors $\uptheta^k$ and $x_i^k$ are found as the Bayesian optimal estimates, i.e.:

$$\hat{\uptheta }_i^k \left( {Y_i } \right) = \int {\uptheta^k f_{\uptheta^k } \left( {\uptheta^k /Y_i ,{\text{H}} = h_k } \right)d\uptheta^k } ,\hat{x}_i^k \left( {Y_i } \right) = \int {x_i^k f_{x_i^k } \left( {x_i^k /Y_i ,{\text{H}} = h_k } \right)dx_i^k } ,$$

(2.3.42)

where $f_{\uptheta^k } \left( {\uptheta^k /Y_i ,{\text{H}} = h_k } \right)$ and $f_{x_i^k } \left( {x_i^k /Y_i ,{\text{H}} = h_k } \right)$ are a posteriori PDFs of vectors $\uptheta^k$ and $x_i^k$, respectively, with a fixed hypothesis about the error model ${\text{H}} = h_k$. Thus, the problem of identifying the model (2.3.28), (2.3.39) and estimating its parameters is reduced to finding the PDF $f_{\text{H}} \left( {{\text{H}}/Y_i } \right)$, $f_{\uptheta^k } \left( {\uptheta^k /Y_i ,{\text{H}} = h_k } \right)$, $f_{x_i^k } \left( {x_i^k /Y_i ,{\text{H}} = h_k } \right)$ and calculating the integrals (2.3.42). These integrals are normally calculated using numerical methods based on various techniques for approximating a posteriori density. In the general case, the dimension of these integrals is determined by the dimension of the vectors $\uptheta^k$ and $x_i^k$.

Using the Bayesian formulas, we get:

$$\Pr \left( {{\text{H}} = h_k /Y_i } \right) = \frac{{f\left( {y_i /Y_{i - 1} ,{\text{H}} = h_k } \right)f_{\text{H}} \left( {{\text{H}} = h_k /Y_{i - 1} } \right)}}{{\sum_{k = 1}^K {f\left( {y_i /Y_{i - 1} ,{\text{H}} = h_k } \right)f_{\text{H}} \left( {{\text{H}} = h_k /Y_{i - 1} } \right)} }},$$

(2.3.43)

where $f\left( {y_i /Y_{i - 1} ,{\text{H}} = h_k } \right)$ is the measurement likelihood function at step i for a fixed hypothesis; it can be represented as follows:

$$f\left( {y_i /Y_{i - 1} ,{\text{H}} = h_k } \right) = \int {f_{y_i } \left( {y_i /Y_{i - 1} ,{\text{H}} = h_k ,\uptheta^k } \right)f_{\uptheta^k } \left( {\uptheta^k /Y_{i - 1} ,{\text{H}} = h_k } \right)d\uptheta^k } .$$

(2.3.44)

In this formula, $f_{y_i } \left( {y_i /Y_{i - 1} ,{\text{H}} = h_k ,\uptheta^k } \right)$ is the measurement likelihood function at the step i for the fixed hypothesis and the parameter vector $\uptheta^k$, $f_{\uptheta^k } \left( {\uptheta^k /Y_{i - 1} ,{\text{H}} = h_k } \right)$ is a posteriori PDF at the step i – 1. For the PDF of the state vector $x_i^k$, the following is also true:

$$f_{x_i^k } \left( {x_i^k /Y_i ,{\text{H}} = h_k } \right) = \int {f_{x_i^k } \left( {x_i^k /Y_i ,{\text{H}} = h_k ,\uptheta^k } \right)} f_{\uptheta^k } \left( {\uptheta^k /Y_i ,{\text{H}} = h_k } \right)d\uptheta^k .$$

(2.3.45)

The peculiar feature of the problem is that the model (2.3.38), (2.3.39) describes the problem of linear Gaussian filtering for fixed values of the hypothesis and the parameter vector $\uptheta^k$. Let $\uptheta^{kj}$, $j = \overline{1 \ldots M_k }$ be the grid of the vectors $\uptheta^k$ for the fixed hypothesis $h_k$. Under these conditions, the likelihood functions $f_{y_i } \left( {y_i /Y_{i - 1} ,{\text{H}} = h_k ,\uptheta^k = \uptheta^{kj} } \right)$ and a posteriori PDF $f_{x_i^k } \left( {x_i^k /Y_i ,{\text{H}} = h_k ,\uptheta^k = \uptheta^{kj} } \right)$ are Gaussian, i.e.:

$$\begin{aligned} & f_{y_i } \left( {y_i /Y_{i - 1} ,H = h_k ,\uptheta^k = \uptheta^{kj} } \right) = N\left( {y_i ;H_i^{kj} \hat{x}_{i/i - 1}^{kj} ,\Lambda_i^{kj} } \right), \\ & f_{x_i^k } \left( {x_i^k /Y_i ,H = h_k ,\uptheta^k = \uptheta^{kj} } \right) = N\left( {x_i^k ;\hat{x}_i^{kj} ,P_i^{kj} } \right), \\ \end{aligned}$$

(2.3.46)

where $\Lambda_i^{kj} = H_i^{kj} P_{i/i - 1}^{kj} {(}H_i^{kj} {)}^T + \Psi_i^{kj} {(}\Psi_i^{kj} {)}^T$; and $\hat{x}_i^{kj}$, $P_i^{kj}$ and $\hat{x}_{i/i - 1}^{kj}$, $P_{i/i - 1}^{kj}$ are the optimal estimate with the covariance matrix and the optimal prediction for the step i, respectively, which can be obtained using the KF bank. Thus, to calculate the integrals (2.3.42), approximation should be introduced only for the PDF $f_{\uptheta^k } \left( {\uptheta^k /Y_{i - 1} ,{\text{H}} = h_k } \right)$, and the dimension of the integrals will be determined only by the dimension of the vector $\uptheta^k$. The technique reducing the dimension of the integrals to be found numerically is referred to as the partitioning method (Lainiotis 1976; Stepanov 1998; Beloglazov and Kazarin 1998), the method of analytical integration over a part of variables, or Rao-Blackwellization procedure (Doucet et al. 2001).

In order to calculate the estimates, approximate the PDF for vector $\uptheta^k$ as follows:

$$\begin{aligned} f_{\uptheta^k } \left( {\uptheta^k /Y_i ,{\text{H}} = h_k } \right) & = \sum_{j = 1}^{M_k } {\upmu_i^{kj} \updelta \left( {\uptheta^k - \uptheta^{kj} } \right)} ,f_{\uptheta^k } \left( {\uptheta^k /{\text{H}} = h_k } \right) \\ & = \sum_{j = 1}^{M_k } {\upmu_0^{kj} \updelta \left( {\uptheta^k - \uptheta^{kj} } \right)} , \\ \end{aligned}$$

(2.3.47)

According to Bayesian theorem, with this approximation, the recursive formula is valid for the coefficients $\upmu_i^{kj}$:

$$\upmu_i^{kj} = \frac{{\upmu_{i - 1}^{kj} \cdot f_{y_i } \left( {y_i /Y_{i - 1} ,{\text{H}} = h_k ,\uptheta^k = \uptheta^{kj} } \right)}}{{\sum_{j = 1}^L {\upmu_{i - 1}^{kj} } f_{y_i } \left( {y_i /Y_{i - 1} ,{\text{H}} = h_k ,\uptheta^k = \uptheta^{kj} } \right)}}.$$

(2.3.48)

Thus, the sought integrals (2.3.42) for the estimates of the parameter vector and the state vector, as well as the probability (2.3.43) can be calculated using the following formula:

$$\hat{\uptheta }_i^k \left( {Y_i } \right) \approx \sum_{j = 1}^{M_k } {\upmu_i^{kj} \uptheta^{kj} } ,\hat{x}_i^k \left( {Y_i } \right) \approx \sum_{j = 1}^{M_k } {\upmu_i^{kj} \hat{x}_i^{kj} } ,$$

(2.3.49)

$$\begin{aligned} & \Pr ({\text{H}} = h_k /Y_i ) \\ & \quad \approx \frac{{\left[ {\sum_{j = 1}^{M_k } {\upmu_{i - 1}^{kj} N\left( {y_i ;H_i^{kj} \hat{x}_{i/i - 1}^{kj} ;\Lambda_i^{kj} } \right)} } \right]\Pr ({\text{H}} = h_k /Y_{i - 1} )}}{{\sum_{k = 1}^K {\left[ {\left[ {\sum_{j = 1}^{M_k } {\upmu_{i - 1}^{kj} N\left( {y_i ;H_i^{kj} \hat{x}_{i/i - 1}^{kj} ;\Lambda_i^{kj} } \right)} } \right]\Pr ({\text{H}} = h_k /Y_{i - 1} )} \right]} }}. \\ \end{aligned}$$

(2.3.50)

An important advantage of the considered approach is that the accuracy characteristic can be obtained in the form of covariance matrices for the estimates (2.3.49):

$$\begin{aligned} & P_i^{\uptheta k} \left( {Y_i } \right) \approx \sum_{j = 1}^{M_k } {\upmu_i^{kj} \uptheta^{kj} \left( {\uptheta^{kj} } \right)^T - \hat{\uptheta }_i^k \left( {\hat{\uptheta }_i^k } \right)^T } , \\ & P_i^{xk} \left( {Y_i } \right) \approx \sum_{j = 1}^{M_k } {\left[ {\upmu_i^{kj} \left( {\hat{x}_i^{kj} \left( {\hat{x}_i^{kj} } \right)^T + P_i^{kj} } \right)} \right] - \hat{x}_i^k \left( {\hat{x}_i^k } \right)^T } . \\ \end{aligned}$$

(2.3.51)

Since the parameter vector $\uptheta^k$ does not change with time, its estimate obtained in the filtering mode over the entire set of measurements will coincide with the estimate in the smoothing mode. Considering this and the linearity of the filtering problem (2.3.28), (2.3.29) with the known models and the fixed parameter vector, the smoothed estimate of the state vector $x$ and, as a result, the smoothed GA can be obtained using the above optimal linear smoothing algorithms tuned for the identified model. It can be easily seen that the use of the described approach actually makes the estimation process and the filtering and smoothing algorithms adaptive.

2.3.5 The Results of Using Adaptive Filtering and Smoothing Algorithms in Airborne Gravity Anomaly Measurements

Let us illustrate the application of the above algorithms to processing the experimental airborne geophysical survey data. They were obtained onboard an L-410 aircraft on March 6, 2015, near the town of Stupino about 150 km south of Moscow, Russia. The Chekan-AM mobile gravimeter manufactured by Concern CSRI Elektropribor (Peshekhonov et al. 2015) was installed onboard an aircraft. A NovAtel SE-D-RT2-G-J-Z dual-frequency GLONASS/GPS onboard receiver with an IMU and a GPS-702 GG antenna was applied to obtain the velocity and coordinates. A NovAtel DL-V3-L1L2-G receiver with a GPS-702 GGL antenna was installed at the reference point to enable the differential correction mode. The maximum distance between the vehicle and the base station during the flight was about 150 km. During the flight, a return survey line about 170 km long was completed with general headings of 170° and 350°. The gravimeter and GNSS receiver data were recorded and processed in the offline mode.

To identify the errors of the measuring instruments and to refine the parameter ${\upsigma }_{\partial \Delta g/\partial {\uprho }}^2$ in the GA model, the general model (2.3.26), (2.3.27) was supplemented with the error component $z$ described by the first-order Markov process with unknown standard deviation ${\upsigma }_m$ and the correlation interval $\uptau_m = 1/\upalpha_m$. Two hypotheses were suggested: the first for an additional error in differential measurements, which can be caused, for example, by inaccurate synchronization of the GNSS receiver and the gravimeter; the second for an additional error component directly in the gravimeter measurements. The shaping filters and measurement equations for the models of these hypotheses can be written as follows:

$$\begin{aligned} & \left\{ \begin{gathered} \Delta \dot{h}_{GR} = \Delta V_{GR} ; \hfill \\ \Delta \dot{V}_{GR} = - \, \upbeta \, \vartheta b_1 + b_2 + w_{GR} ; \hfill \\ \dot{b}_1 = - \upbeta b_1 + b_2 ; \hfill \\ \dot{b}_2 = - \upbeta b_2 + b_3 ; \hfill \\ \dot{b}_3 = - \upbeta b_3 + w_{GA} ; \hfill \\ \dot{z} = - a_m z + \upsigma_m \sqrt {2\upalpha_m } w_m ; \hfill \\ \end{gathered} \right.\quad k = 1, \\ & y = \Delta h_{GR} + z + v_s . \\ \end{aligned}$$

(2.3.52)

$$\begin{aligned} & \left\{ \begin{gathered} \Delta \dot{h}_{GR} = \Delta V_{GR} ; \hfill \\ \Delta \dot{V}_{GR} = - \, \upbeta \, \vartheta b_1 + b_2 + z + w_{GR} ; \hfill \\ \dot{b}_1 = - \upbeta b_1 + b_2 ; \hfill \\ \dot{b}_2 = - \upbeta b_2 + b_3 ; \hfill \\ \dot{b}_3 = - \upbeta b_3 + w_{GA} ; \hfill \\ \dot{z} = - a_m z + \upsigma_m \sqrt {2\upalpha_m } w_m ; \hfill \\ \end{gathered} \right.\quad k = 2, \\ & y = \Delta h_{GR} + v_s . \\ \end{aligned}$$

(2.3.53)

Thus, the problem of structural identification of the error model (2.3.52), (2.3.53) with the vector of unknown parameters

$$\uptheta = \left[ {\begin{array}{*{20}c} {\uptau_m } & {\upsigma_m } & {\upsigma_{\partial \Delta g/\partial \uprho } } \\ \end{array} } \right]^T$$

and the estimated vector $x{(}t{)} = \left[ {\begin{array}{*{20}c} {\Delta h_{GR} } & {\Delta V_{GR} } & {b_1 } & {b_2 } & {b_3 } & z \\ \end{array} } \right]^T$ was solved. The GA estimate was generated using the ratio (2.3.22).

Application of the adaptive algorithm with the models introduced above to process the data of the experimental airborne geophysical survey has shown that the hypothesis (2.3.52) for the model with additional error in differential measurements proved to be most likely. The diagrams illustrating the dependence of parameter estimates on time are shown in Fig. 2.24. The estimates of the components of the parameter vector ${\uptheta }$ on the forward and inverse survey lines converge to approximately the same values.

Fig. 2.24

Estimates of model parameters on the forward and inverse survey lines

Figure 2.25 presents the smoothing estimates for GA obtained using the adaptive algorithm and the two-stage estimation procedure described in 2.3.3. The discrepancy between the GA estimates obtained on mutually inverse trajectories using the proposed algorithm complies with the desired accuracy characteristics (RMSE) calculated using the diagonal elements of the covariance matrix obtained by the algorithm (Fig. 2.26).

Fig. 2.25

GA estimates obtained using the adaptive algorithm and the two-stage procedure

Fig. 2.26

Difference between GA estimates on the forward and inverse survey lines for the adaptive algorithm and the two-stage procedure

Thus, it can be stated that the proposed adaptive algorithm provides the expected GA estimation accuracy. Its undoubted advantages include its rigorous approach to the estimation problem, higher accuracy in the transient mode and, most importantly, the ability to obtain consistent characteristics of the estimation accuracy.

The described algorithm was also tested on data obtained in the area of the Arctic Ocean. Ten intersecting survey lines shown in Fig. 2.27 were processed.

Fig. 2.27

Location of survey lines in the area of the Arctic Ocean

The estimates of the parameters determining the properties of the additional error $z$ for various survey lines are shown in Fig. 2.28: the correlation interval of the additional error during data processing was 1.5–2.5 min and the standard deviation was 6–12 cm.

Fig. 2.28

Estimation of the correlation interval and the additional error standard deviation for 10 survey lines

Examples of GA estimates for two survey lines are shown in Fig. 2.29. Figure 2.30 presents the RMSE of the obtained estimates and the difference of estimates at the line intersection points. As can be seen, the difference is 1–4 mGal at these points. This suggests that the RMSE of GA estimation is at the level of 1–2 mGal, which agrees with the calculations.

Fig. 2.29

Examples of GA estimates for two survey lines

Fig. 2.30

Difference of GA estimates at survey line intersection points (left); the calculated RMSE of GA estimates in the smoothing mode on various survey lines (right)

The results confirm the efficiency of the proposed algorithms for GA estimation. Their main advantages include (a) the ability to identify both the GA model and the error model, which reduces the survey time, since there is no need for empirical tuning of filter parameters and manual processing of each survey line; (b) the ability to estimate the accuracy during the calculation; and (c) the reduction of the transient estimation process.

2.3.6 Conclusion

An optimal estimation problem in general form has been formulated within the Bayesian approach, and an example of designing optimal nonstationary filtering and smoothing algorithms for GA estimation has been considered. The features of designing stationary filtering and smoothing algorithms have been analyzed.

It is noted that a significant advantage of the Bayesian approach lies in its ability to calculate the potential estimation accuracy for the given models of anomalies and the errors of the measuring instruments. This allows objective estimation of the efficiency of various suboptimal algorithms. The applied stationary algorithms based on the Butterworth filter and the two-stage estimation procedure have been compared, and their performance has been analyzed.

The section emphasizes the importance of the model structural and parametric identification, providing the required data on the models for implementing the optimal algorithms, and describes the proposed identification algorithm based on nonlinear filtering methods and actually making the estimation process and algorithms adaptive. The results of real data processing using the proposed algorithm in gravity anomaly estimation are provided, which confirm the algorithm efficiency.

2.4 Suboptimal Smoothing in Marine Gravimetric Surveys Using GT-2M Gravimeters

It was stated earlier that in airborne gravimetry, the PSDs of perturbing accelerations and the GA to be measured overlap because of high carrier speeds (Hein 1995; Koshaev and Stepanov 2010). In this regard, in order to extract gravity anomalies from the GSE readings, one needs precise external information about the flight altitude usually provided by the GNSS operating in the differential phase mode (Koshaev and Stepanov 2010; Bolotin et al. 2002). In marine gravimetry, due to low speeds of vessels, the PSDs of perturbing accelerations lie in a higher frequency range than those of the anomaly components being measured. Therefore, the problem of identifying GAs in GSE readings can be solved, at least in the case of surface vessels, using filtering without precise external information (Panteleev 1983; Krasnov et al. 2014). However, given the fact that the level of noise is five to six orders of magnitude higher than the level of the useful signal, rather stringent requirements may be imposed on the gravimetric filter in terms of its effectiveness when used in real time.

In postprocessing, it is possible to use optimal smoothing algorithms on a fixed interval. As noted in Sect. 2.3, they provide higher estimation accuracy compared with the KF but such algorithms are much more difficult to implement, one of the reasons being the necessity to store a significant amount of data. In this regard, the development of suboptimal smoothing algorithms is relevant.

Design of such algorithms with regard to marine vessels is what this section is devoted to.

2.4.1 Constant-Delay Optimal and Suboptimal Smoothers for Continuous-Time Systems

The search for an algorithm that combines the simplicity of the KF and the quality of the optimal smoothing on a fixed interval is of interest both for the problem of marine gravimetry and other applications. Constant-delay smoothing may be a compromise solution in this case, which, however, imposes an additional restriction: the algorithm should have a filter structure with an infinite impulse response of the same order as the original system.

The proposed algorithm of suboptimal smoothing is designed in relation to the problem (2.3.1), (2.3.2) under the assumption that the system noise is neglected at the smoothing stage, i.e., $Q = 0$. In this case, it is easy to show that the algorithm for generating a suboptimal smoothed estimate is reduced to the ‘inversed’ extrapolation of the last current optimal estimate of the KF using the transient state matrix, i.e., $\hat{x}_s \left( {t|t_1 } \right)\, = \Phi \left( {t,t_1 } \right)\hat{x}\left( {t_1 |t_1 } \right)$, where $\Phi \left( {t,t_1 } \right)$ is the transient matrix of the system. Thus, the suboptimal smoothing algorithm is simpler than the optimal algorithm and does not require repeated filtering of the estimates obtained at the first stage.

In this case, the equations for the suboptimal smoothing error covariance matrix $P_s$ can be written as follows (Meditch 1969):

$$\begin{aligned} & \dot{P}_s \left( {t|t_1 } \right) = FP_s \left( {t|t_1 } \right) + P_s \left( {t|t_1 } \right)F^T + \Phi \left( {t,t_1 } \right)\Phi_{F - KH} \left( {t_1 ,t} \right)GQG^T \\ & \quad + GQG^T \Phi_{F - KH}^T \left( {t_1 ,t} \right)\Phi^T \left( {t,t_1 } \right) - GQG^T , \\ \end{aligned}$$

(2.4.1)

where $\Phi_{F - KH} \left( {t_1 ,t} \right)$ is the linear system state transient matrix $\dot{x} = \left( {F - KH} \right)x$. Equation (2.4.1) is solved in the inverse time with the boundary condition $P_s \left( {t_1 |t_1 } \right) = P\left( {t_\infty } \right)$, where $P\left( {t_\infty } \right)$ is the steady-state value of the KF error covariance matrix. The algorithm for finding the suboptimal smoothing estimate with a constant delay $\uptau$ is determined by solving the following differential equation (Meditch 1969):

$$\frac{d}{dt}\hat{x}_s \left( {t|t + \uptau } \right) = F\hat{x}_s \left( {t|t + \uptau } \right) + L\left( t \right)\left[ {y\left( {t + \uptau } \right) - H\Phi \left( {t,t + \uptau } \right)\hat{x}_s \left( {t|t + \uptau } \right)} \right],$$

(2.4.2)

where $L\left( t \right) = \Phi \left( {t,t + \uptau } \right)^{ - 1} \,K\left( t \right)$ is the feedback coefficient of the smoothing filter, and $K\left( t \right) = P\left( {t + \uptau |t + \uptau } \right)H^T R^{ - 1}$ is the KF feedback ratio.

Obviously, the variance of the optimal smoothed estimate with a constant delay is a non-increasing function of interval $\uptau$. Due to the methodic error caused by the neglect of the generating noise of the system, the suboptimal smoothed estimate has an error variance greater than the optimal smoothing error variance and does not necessarily decrease with time. Thus, the effective use of suboptimal smoothing is only possible on a limited interval due to the increase in the above-mentioned methodic error with the increase in the interval length.

In order to discuss the effectiveness of the proposed suboptimal smoothing filter and to estimate the interval on which suboptimal smoothing is appropriate to implement, consider the following methodic example. Assume that it is required to estimate the state of a scalar system with a scalar measurement:

$$\begin{aligned} \dot{x}\left( t \right) & = w\left( t \right), \\ y\left( t \right) & = x\left( t \right) + v\left( t \right), \\ \end{aligned}$$

(2.4.3)

where $w\left( t \right)$ and $v\left( t \right)$ are stationary uncorrelated white noises with intensities $Q$ and $R$, respectively.

Assume that for some $t_0 > 0$, the KF, generating a current estimate of the system state (2.4.3), is in a steady state, and it is required to obtain a smoothed state estimate on a fixed interval $\left[ {t_0 ,t_1 } \right]$. To compare the accuracy of the optimal and suboptimal smoothing algorithms, let us solve the problem in the optimal and suboptimal problem statements. For (2.4.3), it is easy to obtain analytical solutions of the covariance equations for the KF, the optimal and suboptimal smoothing filters on a fixed interval. For this case, $F = 0,\,\;H = 1,\;\Phi {(}t_1 ,t{)} = 1$. The steady-state values of the variance of the optimal filtering error and the KF gain coefficient are determined by the following formulas: $P{(}t_\infty {)} = \sqrt {QR}$, $K = \sqrt {Q/R}$ (Meditch 1969; Stepanov 2017b). The formula for the error variance of the optimal smoothing filter on a fixed interval takes the form:

$$\dot{P}\left( {t|t_1 } \right) = - 2\sqrt{\frac{Q}{R}} P\left( {t|t_1 } \right) + Q.$$

By integrating the last equation in the inverse time with the initial condition $P{(}t_1 |t_1 {)} = P{(}t_\infty {)} = \sqrt {QR}$ and considering that $\uptau = t_1 - t$, we get:

$$P\left( {t|t + \uptau } \right) = \frac{{\sqrt {RQ} }}{2}\left( {1 + e^{ - 2\frac{\uptau }{T_0 }} } \right),$$

(2.4.4)

where $T_0 = 1/K = \sqrt {R/Q}$ is the KF time constant. It can be seen that for $\uptau \to \infty$, the variance $P\left( {t|t + \uptau } \right)$ tends to the fixed value $P({\uptau }_\infty ) = \sqrt {RQ} /2$.

Now, consider the suboptimal smoothing problem. Since in the case under consideration $\Phi \left( {t,t_1 } \right) = 1$, the equation of the suboptimal smoothing filter becomes the following relation: $\hat{x}_s \left( {t|t_1 } \right) = \hat{x}\left( {t_1 |t_1 } \right)$. Thus, for this example, suboptimal smoothing is reduced to a shift back on the time scale of the current KF estimate. In accordance with (2.4.1), we obtain the equation that determines the suboptimal smoothing error variance:

$$\dot{P}_s \left( {t|t_1 } \right) = - 2e^{ - K\uptau } Q + Q,$$

which should be solved in the inverse time with the boundary condition at the right end of the interval $P_s \left( {t_1 |t_1 } \right) = \sqrt {QR}$. After solving the equation, we obtain:

$$P_s \left( {t|t + \uptau } \right) = 2\sqrt {RQ} e^{ - \frac{\uptau }{T_0 }} + Q \cdot \uptau - \sqrt {RQ} .$$

(2.4.5)

In order to find the parameter $\uptau$ of the suboptimal smoother, for which the minimum of the estimate error variance is feasible, we differentiate (2.4.5) with respect to $\uptau$ and equate the derivative to zero:

$$\frac{{dP_s \left( {t|t + \uptau } \right)}}{d\uptau } = - 2Qe^{ - \frac{\uptau }{T}} + Q = 0.$$

Hence, the optimal value of the suboptimal smoothing interval length is determined by the formula $\uptau^\ast = T_0 \ln 2 \cong 0.7\;T_0 .$ Substituting the value $\uptau^\ast$ and $T_0$ into (2.4.5), we derive $P_s^* = 0.7\sqrt {RQ} > 0.5\sqrt {RQ} = P\left( {\uptau_\infty } \right)$.

The RMSD values of filtering errors, for the optimal and suboptimal smoothers, depending on the length of the smoothing interval, are presented in Fig. 2.31.

Fig. 2.31

RMSD versus delay time

Analyzing the curves, it is pertinent to note that the ratio of the RMSDs of the optimal and suboptimal smoothers for $\uptau \le 0.7\,T$ does not exceed the value of $\upsigma_s /\upsigma < 1.05$, and the ratio of the minimum RMSD of the suboptimal smoothing to the minimum attainable error of the optimal smoothing is $\upsigma_s^* /\upsigma^* < 1.18$. We can state that, in the example under consideration, the accuracy of the suboptimal smoothing algorithm on an optimally selected delay interval is only 5% lower than that of the optimal smoothing with a constant delay and 18% lower than the potential accuracy of the optimal smoothing on a fixed interval. Thus, it appears that the proposed method for the synthesis of suboptimal smoothing algorithms may be successfully applied in practice.

2.4.2 Suboptimal Gravimetric Filter

Let us solve the problem of suboptimal filter design for the problem of marine gravimetry. Consider a gravimeter with a non-damped (non-inertial) GSE with a vertical sensitive axis, installed on a gyro-stabilized platform. Denote the GSE measurement (vertical specific force) as $g_{GR}$. Now, subtract the normal gravity value $g_0$ from the GSE readings, take into account the Eotvos correction $\Delta g_E$ and the altitude correction $g_{ZZ}^0 h_o$, where $\upvarphi$ is the latitude, $V$ is the relative velocity vector, $g_{ZZ}^0$ is the normal value of the gravity gradient, $h_s$ is the external altitude information delivered by, for example, the GNSS. Let us integrate the result twice and compare it with the external altitude information (Fig. 2.32).

Fig. 2.32

Schematic of GSE data preprocessing

The mechanization equations corresponding to the structure shown in Fig. 2.32 are written as follows:

$$\begin{aligned} \dot{h}_{GR} & = V_{GR} , \\ \dot{V}_{GR} & = g_{GR} + {\Delta g}_E - g_0 - g_{ZZ}^0 h_o , \\ y & = h_s - h_{GR} . \\ \end{aligned}$$

(2.4.6)

Note that these equations are similar to (2.3.25), (2.3.27).

Earlier in Sect. 2.3, it was noted that when designing a stationary filter without significant loss in accuracy, the Jordan model can be approximated by models in the form of integrals of white noise. Other fractionally rational PSDs of the gravity anomaly, for example, the Schwartz model, are also well approximated by this model (Bolotin et al. 2002). Therefore, we will describe the gravity anomaly using the model in the form of the third integral of white noise $w{}_{GA}$. Considering errors $v_s$ in the altitude measurements $h_s = h_0 + v_s$ as white noise and neglecting the generating noise in the GA model, we will write the equations of the system state in the deviations $\Delta h = h_0 - h_{GR}$, $\Delta V = V_0 - V_{GR}$ similar to (2.3.26) in the following form:

$$\begin{aligned} & \Delta \dot{h} = \Delta V,\;\dot{b}_1 = b_2 , \\ & \Delta \dot{V} = \Delta g,\;\dot{b}_2 = w_{GA} , \\ & \Delta \dot{g} = b_1 ,\;y = \Delta h + v_s , \\ \end{aligned}$$

(2.4.7)

where $w_{GA}$ and $v_s$ are white noises with intensities $Q$ and $R$, respectively, and $\Delta g,b_1 ,b_2$ describe the GA model. By introducing the state vector $x = \left[ {\Delta h\;\;\Delta V\;\;\Delta g\;\;b_1 \;\;b_2 } \right]^T$, it is also possible to reduce (2.4.7) to the matrix form.

The KF equations for (2.4.7) become: 

$$\begin{aligned} \Delta \dot{\hat{h}} & = \Delta \hat{V} + k_{1} \left( {y - \Delta \hat{h}} \right), \\ \Delta \dot{\hat{V}} & = \Delta \hat{g} + k_{2} \left( {y - \Delta \hat{h}} \right), \\ \Delta \dot{\hat{g}} & = \hat{b}_{1} + k_{3} \left( {y - \Delta \hat{h}} \right), \\ \dot{\hat{b}}_{1} & = \hat{b}_{2} + k_{4} \left( {y - \Delta \hat{h}} \right), \\ \dot{\hat{b}}_{2} & = k_{5} \left( {y - \Delta \hat{h}} \right). \\ \end{aligned}$$

(2.4.8)

The values of the KF gain vector $k_1 \ldots k_5$ can be obtained through the analytical solution of the Riccati equation and are given by the following formulas:

$$\begin{aligned} k_1 & = \upmu \left( {Q/R} \right)^{1/10} ,\;k_2 = \left( {\upmu + 2} \right)\left( {Q/R} \right)^{2/10} \\ k_3 & = \left( {\upmu + 2} \right)\left( {Q/R} \right)^{3/10} ,\;k_4 = \left( {\upmu + 2} \right)\left( {Q/R} \right)^{4/10} , \\ k_5 & = \left( {Q/R} \right)^{5/10} ,\;\upmu = 1 + \sqrt 5 \cong 3.24. \\ \end{aligned}$$

Introduce parameter $T = \left( {R/Q} \right)^{1/10} ,$ characterizing the filter time constant. Thus,

$$\begin{aligned} k_1 & = \frac{\upmu }{T} \approx \frac{3.24}{T},k_2 = \frac{\upmu + 2}{{T^2 }} \approx \frac{5.24}{{T^2 }},k_3 = \frac{\upmu + 2}{{T^3 }} \approx \frac{5.24}{{T^3 }}, \\ k_4 & = \frac{\upmu }{T^4 } \approx \frac{3.24}{{T^4 }},k_5 = \frac{1}{T^5 }. \\ \end{aligned}$$

(2.4.9)

Write the equations of the suboptimal smoothing filter with the delay $\uptau$ for the system under consideration:

$$\begin{aligned} \Delta \dot{\hat{h}}_s & = \Delta \hat{V}_s + l_1 (y - \Delta \hat{h}),\;\dot{\hat{b}}_{1s} = \hat{b}_{2s} + l_4 (y - \Delta \hat{h}), \\ \Delta \dot{\hat{V}}_s & = \Delta \hat{g}_s + l_2 (y - \Delta \hat{h}),\;\dot{\hat{b}}_{2s} = l_5 (y - \Delta \hat{h}), \\ \Delta \dot{\hat{g}}_s & = \hat{b}_{1s} + l_3 (y - \Delta \hat{h}),\;\Delta \hat{h} = \Delta \hat{h}_s - \uptau \Delta \hat{V}_s - \frac{\uptau^2 }{2}\Delta \hat{g}_s - \frac{\uptau^3 }{6}\hat{b}_{1s} - \frac{\uptau^4 }{{24}}\hat{b}_{2s} . \\ \end{aligned}$$

(2.4.10)

Here, we use the following notation:

$$\begin{aligned} l_1 & = k_1 - \uptau k_2 + \frac{\uptau^2 }{2}k_3 - \frac{\uptau^3 }{6}k_4 + \frac{\uptau^4 }{{24}}k_5 , \\ l_2 & = k_2 - \uptau k_3 + \frac{\uptau^2 }{2}k_4 - \frac{\uptau^3 }{6}k_5 , \\ l_3 & = k_3 - \uptau k_4 + \frac{\uptau^2 }{2}k_5 , \\ l_4 & = k_4 - \uptau k_5 , \\ l_5 & = k_5 . \\ \end{aligned}$$

(2.4.11)

The estimate of the suboptimal smoothing filter with the constant delay $\uptau$ is associated with the KF estimate by the backward-in-time extrapolation formula $\hat{x}_c = {\Phi }\left( {t - \uptau ,t} \right)^{ - 1} \cdot \hat{x}$ or, which is the same, $\hat{x} = \Phi \left( {t - \uptau ,t} \right)\hat{x}_c$. Write down the latter equation in the scalar form:

$$\begin{aligned} \Delta \hat{h} & = \Delta \hat{h}_s + \uptau \Delta \hat{V}_s + \frac{\uptau^2 }{2}\Delta \hat{g}_s + \frac{\uptau^3 }{6}\hat{b}_{1s} + \frac{\uptau^4 }{{24}}\hat{b}_{2s} , \\ \Delta \hat{V} & = \Delta \hat{V}_s + \uptau \Delta \hat{g}_s + \frac{\uptau^2 }{2}\hat{b}_{1s} + \frac{\uptau^3 }{6}\hat{b}_{2s} , \\ \Delta \hat{g} & = \Delta \hat{g}_s + \uptau \hat{b}_{1s} + \frac{\uptau^2 }{2}\hat{b}_{2s} , \\ \hat{b}_1 & = \hat{b}_{1s} + \uptau \hat{b}_{2s} , \\ \hat{b}_2 & = \hat{b}_{2s} . \\ \end{aligned}$$

(2.4.12)

Taking into account the formulas for $\Delta \hat{h}$ from (2.4.7), as well as the fact that $\hat{h} = h_{GR} - \Delta \hat{h}$, Eq. (2.4.10) can be written as follows:

$$\begin{aligned} \Delta \dot{\hat{h}}_s & = \Delta \hat{V}_s + l_1 \left( {\hat{h} - h_o } \right), \\ \Delta \dot{\hat{V}}_s & = \Delta \hat{g}_s + l_2 \left( {\hat{h} - h_o } \right), \\ \Delta \dot{\hat{g}}_s & = \hat{b}_{1s} + l_3 \left( {\hat{h} - h_o } \right), \\ \dot{\hat{b}}_{1s} & = \hat{b}_{2s} + l_4 \left( {\hat{h} - h_o } \right), \\ \dot{\hat{b}}_{2s} & = l_5 \left( {\hat{h} - h_o } \right). \\ \end{aligned}$$

(2.4.13)

By multiplying the fifth equation in (2.4.13) by $\uptau^4 /24$, the fourth one by $\uptau^3 /6$, the third one by $\uptau^2 /2$, the second one by $\uptau$, and adding it to the first one, and also by multiplying the fifth equation by $\uptau^3 /6$, the fourth one by $\uptau^2 /2$, the third one by $\uptau$, and adding it to the second one, taking into account (2.4.11), we obtain:

$$\begin{aligned} \Delta \dot{\hat{h}} & = \Delta \hat{V}_s + k_1 \left( {\hat{h} - h_o } \right), \\ \Delta \dot{\hat{V}} & = \Delta \hat{g}_s + \uptau \hat{b}_{1s} + \frac{\uptau^2 }{2}\hat{b}_{2s} + k_2 \left( {\hat{h} - h_o } \right), \\ \Delta \dot{\hat{g}}_s & = \hat{b}_{1s} + \left( {k_3 - \uptau k_4 + \uptau k_5 } \right)\left( {\hat{h} - h_o } \right), \\ \dot{\hat{b}}_{1s} & = \hat{b}_{2s} + \left( {k_4 + \uptau k_5 } \right)\left( {\hat{h} - h_o } \right), \\ \dot{\hat{b}}_{2s} & = k_5 \left( {\hat{h} - h_o } \right). \\ \end{aligned}$$

(2.4.14)

By subtracting the first two equations of (2.4.14) from the first two equations of (2.4.6) and taking into account that $\hat{h}_{GR} = h_{GR} - \Delta \hat{h}$, $\hat{V}_{GR} = V_{GR} - \Delta \hat{V}$, we finally derive the vertical channel equations:

$$\begin{aligned} \dot{\hat{h}}_{GR} & = \hat{V}_{GR} - k_1 \left( {\hat{h} - h_o } \right), \\ \dot{\hat{V}}_{GR} & = g_{GR} - g_{zz}^\circ h^* - g_0 + \Delta g_E - \Delta \hat{g}_s - \uptau \hat{b}_{1s} - \frac{\uptau^2 }{2}\hat{b}_{2s} - k_2 \left( {\hat{h} - h_o } \right), \\ \Delta \dot{\hat{g}}_s & = \hat{b}_{1s} + l_3 \left( {\hat{h} - h_o } \right), \\ \dot{\hat{b}}_{1s} & = \hat{b}_{2s} + l_4 \left( {\hat{h} - h_o } \right), \\ \dot{\hat{b}}_{2s} & = k_5 \left( {\hat{h} - h_o } \right). \\ \end{aligned}$$

(2.4.15)

These are the equations of the suboptimal gravimetric smoothing filter (SGSF) which generates an optimal filtering estimate for the current time of the flight altitude $h_{GR}$, the vertical velocity $V_{GR}$ and the suboptimal smoothed estimate with the constant delay $\uptau$ of the gravity anomaly $\Delta \hat{g}_s$. It is easy to show that the current KF estimate can be calculated using the formula:

$$\Delta \hat{g} = \Delta \hat{g}_s + \uptau \hat{b}_{1s} + \frac{\uptau^2 }{2}\hat{b}_{2s} .$$

(2.4.16)

The SGSF block diagram for the vertical channel is shown in Fig. 2.33.

Fig. 2.33

SGSF block diagram for the vertical channel

To complete the design of the filter, it is necessary to choose the time delay $\uptau$. The studies conducted by numerical solution of the covariance equation for the estimate of the form (2.4.10) of the suboptimal fifth-order smoothing gravimetric filter show that the optimal time of the constant delay is very close to $\uptau^* = k_4 /k_5$. Taking into account (2.4.9), $\uptau^* = \upmu T \approx 3.24\,T$. As follows from (2.4.11), the coefficients $l_3 ,l_4$ in (2.4.15) become equal to zero.

Of great importance for practice is the filter resolution in time––the averaging time $T_a$. In space, it usually corresponds to half-wavelength $L_s$ passed through the filter. These parameters are related as $L_s = T_a V/2$, where $V$ is the horizontal speed of the vessel. For the given optimal delay time $\uptau^*$, we have:

$$T = \frac{\uptau^* }{{1 + \sqrt 5 }},\;T_a = 2\uppi T \approx 1.94\,\uptau^* ,\;L_s \approx 0.97\,\uptau^* V.$$

2.4.3 Frequency Properties of the Suboptimal Gravimetric Filter

In the frequency domain, the amplitude response of the SGSF anomaly estimate $\Delta \hat{g}_s \rm{(\upomega }{)}$ can be written as follows:

$$|\Delta \hat{g}_s (\upomega )| = \sqrt {|v(\upomega )|^2 \cdot \upomega^4 + |\Delta g(\upomega )|^2 } \frac{{\sqrt {\frac{1}{4}(\upmu T - \uptau )^4 \upomega^4 + 1} }}{{\sqrt {1 + T^{10} \upomega^{10} } }},$$

(2.4.17)

where $v\rm{(\upomega }{)}$ is the Fourier transform of the error in the external altitude information, $\Delta g\rm{(\upomega }{)}$ is the Fourier transform of GA as a function of time, $\rm{\upomega }$ is the angular frequency. When the delay time is zero, the output amplitude coincides with the KF output amplitude defined by the following formula:

$$|\Delta \hat{g}_s (\upomega )| = \sqrt {|v(\upomega )|^2 \cdot \upomega^4 + |\Delta g(\upomega )|^2 } \frac{{\sqrt {\frac{1}{4}(\upmu T)^4 \upomega^4 + 1} }}{{\sqrt {1 + T^{10} \upomega^{10} } }}.$$

(2.4.18)

With the optimal delay $\uptau^* = \upmu T \approx 3.24\,T$, the amplitude of the SGSF output is equal to the amplitude of the 5th order Butterworth filter output with the same inputs:

$$|\Delta \hat{g}_s (\upomega )| = \sqrt {|v(\upomega )|^2 \cdot \upomega^4 + |\Delta g(\upomega )|^2 } \frac{1}{{\sqrt {1 + T^{10} \upomega^{10} } }}.$$

(2.4.19)

The main difference between the Butterworth filter and the SGSF is the behavior of the phase characteristics.

The output amplitude of the optimal smoothing filter (OSF) is defined by the formula:

$$|\Delta \hat{g}_s (\upomega )| = \sqrt {|v(\upomega )|^2 \cdot \upomega^4 + |\Delta g(\upomega )|^2 } \frac{1}{{1 + T^{10} \upomega^{10} }}.$$

(2.4.20)

The relevant plots of the amplitude-frequency and phase-frequency characteristics of the anomaly estimates for different algorithms (2.4.18)–(2.4.20) are shown in Figs. 2.34 and 2.35. The delay interval for smoothing algorithms was 100 s.

Fig. 2.34

Amplitude-frequency characteristics (AFC) of the GA estimate for KF, OSF, and SGSF. The filter averaging time is 100 s

Fig. 2.35

Phase-frequency characteristics (PFC) of the GA estimate for KF, OSF, SGSF, and Butterworth filter

2.4.4 Results of the Experimental Data Processing

The GT-2M gravimeter has three parallel vertical channels operating in accordance with the algorithm described above with different operator-defined time constants. These channels generate three suboptimal smoothed GA estimates in real time, which allow the operator, in the process of the anomaly map generation, to choose the number of the vertical channel output, depending on the sea state. Typically, the averaging time $T_a$ varies from 300 to 800 s in order to provide the error RMSD within 0.2–0.3 mGal with the best filter resolution.

Figures 2.36 and 2.37 show GA estimation plots obtained using the GTGRAV software for processing the GT-2A gravimeter data and the GA estimation error as a function of time for OSF and SGSF for various averaging times. Figure 2.36 shows anomaly estimation plots; Fig. 2.37 shows anomaly estimation errors. The red curve in Fig. 2.36 corresponds to the averaging time of 800 s, which is taken to be a true anomaly during the analysis since there are no independent data to compare with sufficient resolution. Noisier plots correspond to an averaging time of 300 s. The smoothing error RMSD is estimated as 0.28 mGal for SGSF and 0.24 mGal for OSF. Note that the sea was rather rough (the blue dots in both figures indicate the moments of time when the vertical acceleration exceeded $0.5\,g$). This somewhat reduced the accuracy of the estimation. An important fact is that the OSF calculation took about a minute in the GTGRAV software, and the SGSF calculation took less than a second.

Fig. 2.36

GA estimation plots for OSF and SGSF at averaging times of 800 and 300 s

Fig. 2.37

GA estimation error plots for OSF and SGSF with an averaging time of 300 s. The estimate with an averaging of 800 s is used as a reference

2.4.5 Conclusion

The design of a constant-delay suboptimal smoothing filter has been described. Its feature is the neglect of the generating noise in the shaping filter equations for the state vector being estimated. For a linear stochastic system, the estimation equations and the covariance equation are given for the suboptimal smoothing filter in continuous time. A methodic example is used to compare such a filter with the optimal smoothing filter and the Kalman filter. For this example, it is shown that, as compared with the optimal smoothing filter, the suboptimal filter does not require any additional computation and memory. At the same time, it is close to the optimal filter in accuracy. Using the proposed method, we have synthesized a suboptimal smoothing gravimetric filter corresponding to the steady state under the assumption that GAs are described as the third integral of white noise and its parameters are defined. It is noted that such a gravimetric filter is integrated in the GT-2M marine gravimeter (Bolotin and Yurist 2011), mass-produced by Gravimetric Technologies. Using data from a real marine gravimetric survey, it is shown that the errors of the suboptimal smoothing gravimetric filter do not differ significantly from the errors of the optimal smoothing filter. At the same time, the designed gravimetric filter shows high accuracy, even at rough seas.

2.5 Using Spherical Wavelet Expansion to Combine Airborne Gravimetry Data and Global Gravity Field Model Data

In airborne gravimetry, the problem of gravity anomaly (GA) determination includes the stages of along-line anomaly estimation and construction of anomaly maps in the survey area. The latter often includes GA transformations (downward continuation, calculation of deflections of the vertical, etc.). Correct transformations require the use of nonlocal information about the gravity field, therefore, airborne gravimetry data are usually combined with gravity data provided by a global EGF model (EGM2008, EIGEN-6C2, etc.), given in terms of coefficients of the spherical harmonic expansion (Kern et al. 2003). The use of such an expansion in the problem under consideration is often technically difficult since working with a full set of coefficients is required. Another well-known approach, the collocation method (Kern et al. 2003), is based on a priori stochastic gravity models, the reliability of which, however, is often questionable. Relatively new approaches to the local GA determination are based on expansions of the gravity field using a system (complete system in a Hilbert space) of spherical radial basis functions that have the spatial localization property (Schmidt et al. 2007). One of such expansions is based on the use of spherical scaling and wavelet functions; it can be found in (Freeden and Michel 2004). In addition to localization in space, in the opinion of the authors of this section, an important feature of this approach is multiscale representation of gravity data, which is a framework for combining airborne gravimetry data and gravity data from a global gravitational field model. The combination is based on selecting a common spherical harmonic bandwidth in both gravity datasets.

Section 2.5 describes the method developed for GA determination in a local area of the airborne gravimetric survey based on joint processing of airborne gravity data and the global EGF model data using the multiscale analysis on the sphere. An algorithm for combining airborne gravity data and global gravity data was developed based on the least squares method.

Section 2.5 is organized as follows. First, the multiscale analysis based on the Abel–Poisson spherical wavelets is briefly described; next, the stages of the local anomaly determination technique developed by the authors of this section are described, one of which solves the problem of combining the wavelet coefficients obtained from airborne gravimetry data and the global EGF model. In the problem, the errors of the wavelet coefficients are assumed to be random values with the known statistical characteristics obtained from the airborne and global gravity data. The problem of gravity data combination (through wavelet coefficients) is formulated as a problem of determining a linear nonbiased estimate optimal under the criterion of the minimum mean square error and is solved by the least squares method (LSM) in the covariance form. The section concludes with the discussion of the results of the experimental data processing using the algorithms developed for the GA local determination.

2.5.1 Spherical Wavelet Expansion and Multiscale Representation of the Anomalous Gravity Field

Let us elucidate the basics of the multiscale analysis on the sphere (Freeden and Michel 2004). The gravity anomaly Δg is assumed to be a function defined in the outer space of the Bjerhammer sphere and square integrable on this sphere. Further, the GA is represented as a convolution of the radial derivative of the scaling function $\Phi_J \left( {x,y_s } \right)$ and the scaling coefficient (SC) $a_J \left( {y_s } \right)$ of a certain resolution level J (Freeden and Michel 2004; Bolotin and Vyazmin 2015):

$$\Delta g\left( x \right) = \sum_s {\upomega_s a_J \left( {y_s } \right)\frac{{\partial \Phi_J \left( {x,y_s } \right)}}{\partial |x|}} ,$$

(2.5.1)

where y_s are the nodes of an equiangular grid on the Bjerhammer sphere Ω_R of radius R, ω_s are the integration weights, $x \in {\text{R}}^3$, $|x| = \left( {x^T x} \right)^{1/2} \ge R$. Due to the normalization of the scaling functions, SCs have the dimension of the potential. The resolution level J (where J = 0, 1, 2…) is chosen according to the required spatial resolution of the GA map. The spherical scaling function of the resolution level J is defined by the following formula (Freeden and Michel 2004):

$$\Phi_J \left( {x,y} \right) = \sum_{n = 0}^\infty {\upphi_J \left( n \right)\left( {\frac{R}{|x|}} \right)^{n + 1} \frac{2n + 1}{{4\uppi R^2 }} \, P_n \left( {\upxi^T \upeta } \right)} ,$$

where φ_J(n) is the so-called scaling function symbol, $P_n \left( {{\upxi }^T {\upeta }} \right)$ is the Legendre polynomial of the degree n, ξ = x/|x|, η = y/|y|. The scaling function has the following properties:

• (1) axisymmetry, i.e., it depends only on the spherical distance between x, y with fixed values of |x|, |y|; it decreases as the spherical distance between x, y increases;

• (2) harmonic in the outer space of the sphere;

• (3) it tends to the Dirac delta function on the sphere as $J \to \infty$ in the norm of the Hilbert space $L^2 (\Omega_R )$ of the functions quadratically integrated on the sphere.

In this work, the Abel–Poisson scaling function with the symbol $\upphi_J \left( n \right) = \exp \left( { - 2^{ - J} n} \right)$ is chosen, which rapidly decreases in the spatial and spherical harmonic domain and can be represented as an elementary function (Fig. 2.38):

$$\Phi_J \left( {x,y} \right) = \frac{1}{4\pi R}\frac{|x|^2 - R^2 b_J^2 }{{\left( {|x|^2 + R^2 b_J^2 - 2b_J x^T y} \right)^{3/2} }},b_J = \exp \left( { - 2^{ - J} } \right).$$

(2.5.2)

Fig. 2.38

The Abel–Poisson scaling function $\Phi_J \left( {x,y} \right)$ (cross-section) on a sphere with a unit radius at J = 2, 3, depending on the angle (rad) between x, y (left), and its symbol φ_J(n) (right)

The expansion in the scaling functions (2.5.1) is performed at the finest resolution level. To solve the gravity data combination problem, however, it is convenient to make an expansion into the components of different resolution levels called the multiscale representation.

The multiscale representation of the GA includes the spherical wavelet decomposition and wavelet reconstruction procedures. GA wavelet decomposition is the calculation of the spherical wavelet coefficients (SWC) at various resolution levels j ≤ J. The SWC contains information about the anomaly within a certain spherical harmonic bandwidth and is determined using the following formulas (Freeden and Michel 2004):

$$c_J \left( {y_s } \right) = a_J \left( {y_s } \right) - \sum_m {\upomega_m \Phi_J \left( {y_s ,y_m } \right)a_J \left( {y_m } \right)} ,$$

(2.5.3)

$$c_j \left( {y_{sj} } \right) = \sum_m {\upomega_m \Psi_j \left( {y_{sj} ,y_m } \right)a_J \left( {y_m } \right)} ,\quad j = j_0 , \ldots ,J - 1,$$

(2.5.4)

where $c_j \left( {y_{sj} } \right)$ is the SWC at the node y_sj of the equiangular grid at the resolution level j, $\Psi_j \left( {y_{sj} ,y_m } \right)$ is the Abel–Poisson spherical wavelet function of the resolution level j defined by the formula:

$$\Psi_j \left( {y_{sj} ,y_m } \right) = \Phi_{j + 1} \left( {y_{sj} ,y_m } \right) - \Phi_j \left( {y_{sj} ,y_m } \right).$$

The Abel–Poisson wavelet function and its symbol ψ_j(n) = φ_j+1(n) – φ_j(n) are shown in Fig. 2.39.

Fig. 2.39

Abel–Poisson wavelet $\Psi_j \left( {x,y} \right)$ (cross-section) on a sphere of a unit radius when j = 1, 2, depending on the angle (rad) between x, y (left), and its symbol (right)

The reconstruction of the anomaly from the calculated SWC is defined by the formula (Freeden and Michel 2004):

$$\Delta \tilde{g}\left( x \right) = \sum_{j = j_0 }^J {\Delta g_j \left( x \right)} ,$$

(2.5.5)

where $\Delta g_j \left( x \right)$ is the detailing component of the anomaly at the resolution level j calculated using the convolution formulas (in the discrete form):

$$\Delta g_j \left( x \right) = \sum_s {\upomega_{sj} c_j \left( {y_{sj} } \right)\frac{{\partial \Psi_j^d \left( {x,y_{sj} } \right)}}{\partial |x|}} ,\quad j = j_0 , \ldots ,J - 1,$$

(2.5.6)

$$\Delta g_J \left( x \right) = \sum_s {\upomega_s c_J \left( {y_s } \right)\frac{{\partial \Phi_J \left( {x,y_s } \right)}}{\partial |x|}} .$$

(2.5.7)

Here, $\Delta \tilde{g}$ is the result of GA reconstruction, $\Psi_j^d \left( {x,y_s } \right)$ is the dual wavelet function defined by the following formula (Freeden and Michel 2004):

$$\Psi_j^d \left( {x,y_s } \right) = \Phi_{j + 1} \left( {x,y_s } \right) + \Phi_j \left( {x,y_s } \right).$$

The result of wavelet reconstruction (2.5.5) coincides with the representation of the anomaly in the form of (2.5.1) with an accuracy of the error of the quadrature formulas of the convolutions (2.5.3), (2.5.4).

Note that the Abel–Poisson wavelet functions at various resolution levels are not orthogonal in the space of functions square integrable on the sphere. Therefore, in the deterministic case, the detailing components of the anomalies Δg_j, Δg_m of various resolution levels j ≠ m cannot be calculated independently; and in the stochastic sense, i.e., if there are independent random errors in the SWC, these components are correlated, and the weighted LSM should be used for estimation. Also noteworthy as one of the advantages of the technique is that, similarly to (2.5.5), other functionals of the anomalous field, such as the geoid height, deflections of the vertical, etc., can be calculated from SWC. For this, instead of the wavelet function in (2.5.6)–(2.5.7), one should use the result of its convolution with the kernel of the corresponding transformation.

2.5.2 Technique of Local Gravity Anomaly Determination from Airborne Gravimetry Data and Global Gravity Field Model Data Using Multiscale Representation

Figure 2.40 describes the methodology for the local GA determination from airborne gravity data and the global EGF model data.

Fig. 2.40

Data flow diagram of airborne and global gravity data processing

The developed technique includes the following stages:

• (1) estimation of the GA SCs using the Abel–Poisson scaling functions at the finest resolution level $J$ corresponding to the desirable spatial resolution of the GA map based on the results of airborne measurements at survey lines. The recurrent LSM is used in the information form (the covariance form is not suitable since the covariance matrices may be ill-conditioned at initial iterations) with the survey line number as the recursion step; regularization of the information matrix of the SC estimates is used at the last recursion step due to the ill-conditioning of the problem;

• (2) SWC calculation at various resolution levels j ≤ J based on the SCs estimated at the first stage;

• (3) calculation of the anomaly SWC based on the global model of the Earth’s gravitational field at various resolution levels j ≤ J_glob, where the J_glob value is determined by the resolution of the global EGF model;

• (4) combination of the SWCs obtained from airborne measurements and the global model data at common resolution levels;

• (5) reconstruction of the anomaly estimate (and other functionals of the gravitational field) from the SWC combining results.

Let us describe these stages in more detail.

At the first stage of the technique, the input data in the problem being solved are GAs at survey lines obtained from airborne measurements and smoothed using the gravimetric filter (Stepanov et al. 2015; Bolotin and Yurist 2011) and recorded at the discrete moments of time $t_{ik}$, i = 1…M_k, where k, k = 1…K, is the survey line number, M_k is the number of measurements at the kth survey line. The filter, assumed here to be stationary for simplicity, is characterized in time by the impulse response function $h_f \left( {t_{ik} - t_{mk} } \right)$. The filter support, i.e., the number of moments $t_{mk}$, for which $h_f \left( {t_{ik} - t_{mk} } \right) \ne 0$, is assumed to be finite and equal to 2M + 1. The resolution of the filter in time is characterized by the cutoff frequency ${\upomega }_{cut}$. The resolution in space is defined as half-wavelength $L = 2\pi \, V/{\upomega }_{cut}$, where V is the speed of the aircraft. The model of the smoothed airborne GA data $\Delta g^{\prime}_k \left( {t_{ik} } \right)$ at the kth survey line at the moment of time $t_{ik}$ can be represented as follows:

$$\Delta g^{\prime}_k \left( {t_{ik} } \right) = \sum_{m = i - M}^{i + M} {h_f \left( {t_{ik} - t_{mk} } \right)\Delta g\left( {x\left( {t_{mk} } \right)} \right)} + \updelta g_k \left( {t_{ik} } \right),$$

(2.5.8)

where Δg is the true free air GA, $x\left( {t_{mk} } \right) \in {\text{R}}^3$ are the coordinates of the measurement point at the kth survey line in the geocentric coordinate system, ${\updelta }g_k \left( {t_{ik} } \right)$ is the measurement error. It is assumed that

• the coordinates of the measurement points are known exactly from GNSS data;

• the measurement error ${\updelta }g_k \left( t \right)$ is a random process with a zero mean and known correlation function defined by the measurement errors of the gravimeter sensing element, the GNSS and the properties of the gravimetric filter;

• measurement errors at different flight lines are uncorrelated.

By replacing Δg in (2.5.8) with representation (2.5.1), we obtain:

$$\Delta g^{\prime}_k \left( {t_{ik} } \right) = \sum_{m = i - M}^{i + M} {h_f \left( {t_{ik} - t_{mk} } \right)\sum_s {\upomega_s a_J \left( {y_s } \right)\frac{{\partial \Phi_J \left( {x\left( {t_{mk} } \right),y_s } \right)}}{\partial |x|}} } + \updelta g_k \left( {t_{ik} } \right),$$

(2.5.9)

where i = 1, …, M_k, k = 1, …, K. The resolution level J is determined based on the desired spatial resolution of the map as indicated above. The SC nodes $y_s$ in (2.5.9) are defined on the sphere $\Omega_R$, the radius R of which will be chosen equal to the minimum distance from the center of the Earth to the measurement points at the survey lines. Due to the fast attenuation property of the scaling function, in (2.5.9), it is sufficient to take into account only the nodes $y_s$ from a certain neighborhood of point x(t_mk). The size of the neighborhood is chosen based on the attenuation rate of the scaling function and the required accuracy of the map. An example of a set of SC nodes defined by the survey lines is shown in Fig. 2.41.

Fig. 2.41

A set of nodes of the scaling coefficients (dots) defined by survey lines (solid lines) on the longitude–spherical latitude plane (km × km)

Rewrite the model of the smoothed airborne measurements at the kth survey line (2.5.9) in the vector form:

$$\Delta g^{\prime}_k = H_k a_{kJ} + \updelta g_k ,\quad k = 1 \ldots K,$$

(2.5.10)

where $\Delta g^{\prime}_k = \left( {\Delta g^{\prime}_k \left( {t_{1k} } \right), \ldots ,\Delta g^{\prime}_k \left( {t_{ \, M_k k} } \right)} \right)^T$ and $\updelta g_k = \left( {\updelta g_k \left( {t_{1k} } \right), \ldots ,\updelta g_k \left( {t_{ \, M_k k} } \right)} \right)^T$ are M_k × 1 vectors of measurements and their errors, a_kJ is the N_k × 1 vector of unknown SCs $a_J \left( {y_s } \right)$ in the nodes y_s corresponding to the kth survey line. H_k denotes the M_k × N_k matrix consisting of the sum of the products of the filter impulse response function in (2.5.9), the weights ω_s and the values of the scaling function derivative at the nodes y_s:

$\begin{aligned} H_k & = \left( {\begin{array}{*{20}c} {w_1 \left( {t_{1k} } \right)} & \ldots & {w_{N_k } \left( {t_{1k} } \right)} \\ \vdots & \ddots & \vdots \\ {w_1 \left( {t_{M_k k} } \right)} & \ldots & {w_{N_k } \left( {t_{M_k k} } \right)} \\ \end{array} } \right) \\ w_s \left( {t_{ik} } \right) & = \upomega_s \sum_{m = i - M}^{i + M} {h_f \left( {t_{ik} - t_{mk} } \right)\Phi_J \left( {x\left( {t_{mk} } \right),y_s } \right)} . \\ \end{aligned}$,

Introduce the covariance matrix $R_k = E\left[ {{\updelta }g_k {\updelta }g_k^T } \right]$ which is determined from the assumed known correlation function of the airborne gravimetric measurement errors. It should be recalled that $E\left[ {\updelta g_k \updelta g_m^T } \right] = 0,\quad k \ne m.$ Let us solve the problem of estimating the scaling coefficients a_kJ based on measurements (2.5.9) using the generalized least squares method with the following criterion:

$$\begin{aligned} & \sum_{k = 1}^K {\left\| {\Delta g^{\prime}_k - H_k a_{kJ} } \right\|_{R_k^{ - 1} }^2 } \\ & \quad = \sum_{k = 1}^K {\left( {\Delta g^{\prime}_k - H_k a_{kJ} } \right)^T R_k^{ - 1} \left( {\Delta g^{\prime}_k - H_k a_{kJ} } \right)} \to \mathop {\min }\limits_{a_{kJ} \in R^{N_k } } \\ \end{aligned}$$

(2.5.11)

Problem (2.5.11) is essentially the problem of the downward continuation of the gravity field (Freeden and Michel 2004), since the nodes y_s of the SCs of interest are given on the underlying sphere $\Omega_R$. Thus, the problem belongs to the class of inverse ill-posed problems (Tikhonov and Arsenin 1979). Solution (2.5.11) is determined using the recurrent LSM in the information form with the survey line number k as a recursion step (Kailath et al. 2000):

$$Q_k = Q_{k - 1} + I_k^T H_k^T R_k^{ - 1} H_k I_k ,\quad k = 1 \ldots K,$$

(2.5.12)

$$b_k = b_{k - 1} + I_k^T H_k^T R_k^{ - 1} \Delta g_k^{\prime} ,$$

(2.5.13)

with the initial conditions Q₀ = 0, b₀ = 0, where Q_k is the information N × N matrix of the vector $a_J \in {\text{R}}^N$ consisting of the SCs defined by all the K survey lines; b_k is the information estimate of the vector a_J, I_k is the N_k × N matrix specifying the projection of the vector a_J onto a subset of the SCs correlated only with the kth survey line: ${\text{I}}_{\text{k}} a_J = a_{kJ}$.

Algorithm (2.5.12)–(2.5.13) is written in the form for a given set of K survey lines and, therefore, for the state vector of the known and constant dimension. However, the form of the algorithm, in which the dimension of the vector of the estimated SCs automatically increases when a new survey line is added to the processing, is practically more convenient. The algorithm in this form is as follows:

$$Q_{\left( k \right)} = \left( {\begin{array}{*{20}c} {Q_{\left( {k - 1} \right)} } & 0 \\ 0 & 0 \\ \end{array} } \right) + {\text{I}}_{\left( k \right)}^T H_k^T R_k^{ - 1} H_k {\text{I}}_{\left( k \right)} ,\quad k = 1,2 \ldots$$

(2.5.14)

$$b_{\left( k \right)} = \left( {\begin{array}{*{20}c} {b_{\left( {k - 1} \right)} } \\ 0 \\ \end{array} } \right) + {\text{I}}_{\left( k \right)}^T H_k^T R_k^{ - 1} \Delta g_k^{\prime} ,$$

(2.5.15)

with the initial conditions Q₍₀₎ = 0, b₍₀₎ = 0. Here, Q_(k) is the information N_(k) × N_(k) matrix of the SC vector defined by k survey lines; b_(k) is the informational estimate of the SC vector, I_(k) is the N_k × N_(k) matrix that specifies the projection of the vector of SCs defined by k survey lines onto a subset of the SCs correlated only with the kth survey line.

The estimate of the N_(K) × 1-SC vector a_J after the Kth recursion step is determined based on the solution of the equation: b_(K) = Q_(K)a_J. The estimate error covariance matrix is calculated using the information matrix Q_(K). The Q_(K) matrix may be ill-conditioned. Let us define the estimate of the covariance matrix of the SC estimate errors $\tilde{P}_{{\updelta }a_J }$ as the inverse of the regularized information matrix:

$$\tilde{P}_{\updelta a_J } = \left( {Q_{(K)} + \upmu^2 {\text{I}}} \right)^{ - 1} ,$$

(2.5.16)

where I is the unit N_(K) × N_(K) matrix, μ is a regularization parameter. The estimate of the SC vector is

$$\tilde{a}_J = \tilde{P}_{\updelta a_J } b_{(K)} .$$

(2.5.17)

The selection of the regularization parameter is discussed below.

The second stage of the technique is the wavelet decomposition (Freeden and Michel 2004) of airborne gravimetry data which includes the calculation of the wavelet coefficients at various resolution levels j ≤ J based on the SC estimates $\tilde{a}_J (y_s )$ found. The need for this stage is due to the fact that the data of airborne gravimetry and the global EGF model have different spatial resolutions (in terms of the multiscale analysis: different maximum resolution levels). Wavelet decomposition makes it possible to combine SWC estimates of airborne gravimetry data and global EGF model data at common resolution levels. Note that SWCs can be treated as the results of bandpass filtering of anomaly data.

Let us denote the SWCs calculated at various resolution levels j = j₀…J as $\tilde{c}_j \left( {y_{sj} } \right)$ from the SC estimates $\tilde{a}_J \left( {y_s } \right)$ according to formulas (2.5.3), (2.5.4). Denote the N_j × 1 vector of the SWCs as $\tilde{c}_j$ and represent (2.5.3), (2.5.4) in the vector form $\tilde{c}_j = U_j \tilde{a}_J$. U_j is an N_j × N_j matrix composed of products of the integration weights and the wavelet function values at the nodes of the grid. The covariance matrix for the SWC vector estimation error obtained from airborne gravimetry data is determined from the covariance matrix for the SC estimation error by the following formula:

$$\tilde{P}_j = U_j \tilde{P}_{\updelta a_J } U_j^T \quad j = j_0 \ldots J.$$

(2.5.18)

The third stage of the technique is the wavelet decomposition of the global model of the gravitational field, namely, the SWC $c_j^{glob}$ of anomalies and the covariance matrices of their errors $P_j^{glob}$ are calculated at various resolution levels j = j₀…J_glob using formulas (2.5.3), (2.5.4), where the SCs $a_{J_{glob} } \left( {y_s } \right)$ are calculated using the scaling expansion formula:

$$a_{J_{glob} } \left( {y_s } \right) = \sum_p {\upomega_p \Phi_{Jglob} \left( {y_s ,y_p } \right)\Delta g_{glob} \left( {y_p } \right)} ,$$

(2.5.19)

and y_s, y_p are the grid nodes from (2.5.1), J_glob is the maximum resolution level of the global model determined from the spatial resolution of the global data, Δg_glob(y_p) = g_glob(y_p) − g₀(y_p) is the GA for which the gravity g_glob is calculated from the spherical harmonic coefficients of the global model, and g₀ is calculated using the normal gravity formula used in the GA estimation on survey lines based on airborne gravimetric measurements. Note that the maximum resolution level of the global model is lower than the maximum level of the airborne gravimetry data.

The covariance matrices $P_j^{glob}$ are calculated from the covariance matrix of the global gravity data errors E[δg_globδg_glob^T] calculated from the estimates of RMS errors of the spherical harmonics coefficients provided by the developers of the global model.

The fourth stage of the technique is devoted to the combination of multiscale representations of airborne gravimetry data and the global EGF model at common resolution levels and is discussed in detail below.

At the final fifth stage of the technique, the reconstruction of the anomaly estimate (and other functionals of the gravitational field) is performed based on the combination results.

2.5.3 Multiscale Representation of Gravity Anomaly Based on Combination of Airborne Gravimetry Data and Global Gravity Field Model Data

The following is the algorithm for combining airborne gravimetry data and the global EGF model in a multiscale representation in the terms of SWCs based on the specific statistical assumptions mentioned below.

Consider the resolution level $j$, j = j₀…J. Let us pose the problem of refining the estimates of the N_j × 1 vectors of SWCs $\tilde{c}_j$ and the covariance matrices of their errors obtained from airborne gravimetric measurements by the global model data. Let us represent the obtained above estimate of the SWC vector as $\tilde{c}_j = c_j + {\updelta }c_j$, where $c_j$ is the vector of the true SWCs, ${\updelta }c_j$ is a random SWC error vector with zero mean and the covariance matrix $\tilde{P}_j = E\left[ {{\updelta }c_j {\updelta }c_j^T } \right]$ determined from airborne gravimetric data using formula (2.5.18).

Assume that $c_j^{glob}$ and $P_j^{glob}$ are the N_j × 1 SWC vector of the anomaly and the N_j × N_j matrix of the covariances of their errors calculated from the global model data at the resolution levels j = j₀…J_glob. Since the spatial resolution of airborne gravimetry data is usually higher than that of global data, the corresponding maximum resolution levels of the data satisfy the inequality J_glob ≤ J. Let us represent the SWC vector of global data in the form $c_j^{glob} = c_j + {\updelta }c_j^{glob}$ assuming that ${\updelta }c_j^{glob}$ is a random vector with zero mean and the covariance matrix $P_j^{glob} = E\left[ {\updelta c_j^{glob} (\updelta c_j^{glob} )^T } \right].$ Let us assume the positive definiteness of the matrix $\tilde{P}_j + P_j^{glob}$ and the lack of correlation of the SWC errors of both airborne gravity data and global data at various resolution levels. Let us specify the problem of refining the estimate $\tilde{c}_j$ of the vector $c_j$ by $c_j^{glob}$ at the common resolution levels j = j₀…J_glob as a problem of the SWC vector optimal estimation $c_j$ in the class of linear estimates of the form $F_{1j} \tilde{c}_j + F_{2j} c_j^{glob} \,$, where F_1j, F_2j are arbitrary N_j × N_j matrices. As a criterion, let us use the minimum for all F_1j, F_2j of the guaranteed value for the second moment of the estimation error:

$$\mathop {\sup }\limits_{c_j \in R^{N_j } } E\left[ {\left\| {c_j - F_{1j} \tilde{c}_j - F_{2j} c_j^{glob} } \right\|^2 } \right] \to \mathop {\min }\limits_{F_{1j} ,F_{2j} } ,\quad j = j_0 \ldots J_{glob} .$$

(2.5.20)

The unknown vector $c_j$ is assumed to be deterministic. By transforming the formula for the second moment of the estimation error, it is easy to show that (2.5.20) is reduced to a problem of the form:

$$tr\left( {F_{1j} \tilde{P}_j F_{1j}^T + F_{2j} P_j^{glob} F_{2j}^T } \right) \to \mathop {\min }\limits_{F_{1j} + F_{2j} = I_j } ,$$

(2.5.21)

where ${\text{tr}}$ is the trace of the matrix, I_j is a unit N_j × N_j matrix. Solution (2.5.21) and the optimal estimate of the vector c_j are determined by the LSM algorithm in the covariance form (Kailath et al. 2000):

$$\begin{aligned} \tilde{c}_j^+ & = \left( {I - \tilde{F}_{2j} } \right)\tilde{c}_j + \tilde{F}_{2j} c_j^{glob} , \\ \tilde{P}_j^+ & = \left( {I - \tilde{F}_{2j} } \right)\tilde{P}_j , \\ \tilde{F}_{2j} & = \tilde{P}_j \left( {\tilde{P}_j + P_j^{glob} } \right)^{ - 1} , \\ \end{aligned}$$

(2.5.22)

with j = j₀…J_glob, where $\tilde{c}_j^+$, $\tilde{P}_j^+$ denote the result of vector c_j estimation and the estimation error covariance matrix. It should be noted that problem (2.5.20) is actually the least squares collocation problem but it is posed in the space of wavelet coefficients and does not require a priori stochastic hypotheses about GA.

2.5.4 Results of the Real Data Processing

The developed local GA determination technique using the combination algorithm (2.5.22) was applied to the airborne gravimetric data from a survey in the Arctic (Smoller et al. 2013). The airborne measurements were collected using the GT-1A gravimeter. Note that at the same time, the Chekan-AM gravimeter was also used in this onboard survey (Krasnov et al. 2014; Peshekhonov et al. 2015). The spatial resolution of the gravimetric filter of GT-1A was 5 km. Its output data frequency was 18 Hz. The prefiltered measurement errors roughly correspond to the white noise model at the frequency of 1 Hz with the RMS of 50 mGal. The geographical latitude of the survey area varies from 73 to 77°. The average flight altitude is 3700 m. The Helmert formula for the normal gravity was used in calculations (Golovan and Parusnikov 2012). Airborne gravimetric measurements were used to estimate the SC a_J of the gravity anomaly based on algorithm (2.5.14)–(2.5.15) at the maximum resolution level J = 11 approximately corresponding to the filter resolution (the first stage of the developed technique). The airborne data at forty survey lines (north–south) with the line spacing of 1 km were processed. The scaling coefficients were estimated at nodes of 1.0 km × 1.4 km grid on the sphere with the radius R = 6358 km. The radius of the area of the SC computation (2.5.9) was chosen to be 20 km. The regularization parameter μ of the information matrix Q_(K) in (2.5.16) was selected according to the criterion of the proximity of the anomaly estimate reconstructed at survey lines from the SC estimates $\tilde{a}_J$ (2.5.17) using formula (2.5.1) to the original airborne gravimetric data with the RMS value for the discrepancy not greater than 0.5 mGal.

At the second stage of the technique for SC estimation $\tilde{a}_J$, SWC estimates $\tilde{c}_j$ and the covariance matrices of their errors were calculated using formulas (2.5.3)–(2.5.4) and (2.5.18) at the levels of j = 9, 10, 11. The value of the wavelet reconstruction RMS error (2.5.5) of the SWC anomaly $\tilde{c}_j$ on survey lines is 0.65 mGal.

For combining, the EGM2008 global EGF model was used up to the spherical harmonic degree and order of 1800 (the maximum spherical harmonic degree of the model is 2190, the nominal spatial resolution at the equator is 9.3 km × 9.3 km). Based on EGM2008 data, the SWCs $c_j^{glob}$ and the covariance matrices of their errors were calculated at the levels j = 9, 10 (the third stage of the technique). The RMS error values of the SWCs of the global EGM2008 model and SWCs of airborne gravimetric data are given in Table 2.4.

Table 2.4 RMS errors of global and airborne SWCs

The integration of SWCs $\tilde{c}_j$ and $c_j^{glob}$ (the fourth stage) is performed by the LSM algorithm (2.5.22).

At the final (fifth) stage of the technique, the SWC estimates were used to calculate the free air GA estimates at the 1.5 km × 1.5 km grid nodes on the reference ellipsoid surface in the survey area.

The GA maps (Fig. 2.42) and GA along a survey line are shown in Fig. 2.43. The GA based on SC estimates obtained from airborne gravimetric data and the GA resulting from the data combination are oversmoothed in the east–west direction as the distance between the survey lines is smaller than the spatial resolution of the gravimetric filter.

Fig. 2.42

Free air GA at 1.5 km × 1.5 km grid nodes on the surface of the reference ellipsoid in the survey area (mGal): a is the anomaly based on the SC estimates obtained from airborne gravity data, at the maximum level J = 11, and survey lines; b is the anomaly based on the combined SWCs; c is the anomaly based on the EGM2008 model

Fig. 2.43

Free air GAs along the survey line (mGal): solid line: anomaly from the original airborne gravimetric data; dash-dotted line: anomaly based on the SWCs resulting from data combination

The RMS value of the difference between the GAs obtained from the SCs $\tilde{a}_J$ estimated from airborne gravimetric data and the GAs obtained from data combination is 5.4 mGal.

2.5.5 Conclusion

The multiscale representation method based on spherical wavelet expansion was applied to the problem of local determination of the anomalous gravity field from the airborne gravimetric data and gravity data from a global model of the Earth’s gravitational field. A method for this problem solution was developed and applied to real airborne data and global gravity data (EGM2008). The LSM-based algorithm for combining airborne gravimetric and global data was developed and tested. The gravity anomaly estimate obtained from the data weighted combination is slightly oversmoothed in the east–west direction, which is due to the fact that the spatial resolution of the gravimetric filter (north–south direction) is coarser than the data spatial resolution in the east–west direction defined by the line spacing.

The proposed algorithms make it possible to deal with the inverse ill-posed problem of local gravity determination on the reference ellipsoid surface from airborne gravimetric measurements of GAs at the flight altitude. It is shown that the RMS error of the gravity anomaly reconstruction from the airborne wavelet coefficients did not exceed 0.7 mGal. The proposed algorithms have certain advantages as compared with the algorithms that are often used to combine different types of gravity data and based on the collocation method, since the presented algorithms do not require any statistical hypotheses about GA.