1 Introduction

Bayesian statistics often requires sampling from conditional, posterior distributions. For example, to estimate Bayesian models using Gibbs sampling (Geman & Geman 1984), we have to repeatedly sample from the full-conditional distributions of model parameters, and to produce plausible values (Mislevy 1991; Mislevy et al. 1993) for secondary analyses of educational surveys, we have to sample from pupils’ conditional, posterior ability distributions. This chapter is about two algorithms that were designed for this problem: A rejection algorithm that was mentioned by Rubin (1984) and was applied in the European Survey on Language Competences (ESLC; Maris 2012) and the Single-Variable Exchange (SVE) algorithm developed by Murray et al. (2012).

Both algorithms are based on the observation that a sample from a conditional distribution can be obtained from samples drawn from the joint distribution. The practical significance of this observation lies in the fact that sampling from the joint distribution is often easier because it can be done in two ways. Specifically, the joint density of X and Y can be factored in two ways:

$$\displaystyle \begin{aligned} f(x\mid y)f(y) = f(y\mid x)f(x), \end{aligned}$$

and to obtain a sample from the joint distribution, we can use the method of composition (Tanner 1993) and sample from f(y) and then from f(x∣y) or sample from f(x) and then from f(y∣x). Thus, if it is difficult to sample from f(x∣y), we can try to sample from f(y∣x), or vice versa. For instance, if we encounter a posterior distribution that is highly intractable, we can sample from it by generating data. Thus, the algorithms are extremely useful when it is difficult to sample from the posterior but easy to generate data as is the case for Item Response Theory (IRT) models. As both algorithms use composition to sample from the joint distribution, we refer to them as composition algorithms. The algorithms differ in the way they select observations from the joint distribution to obtain a sample from the conditional distribution of interest.

Marsman et al. (2017) recently showed that the two composition algorithms could be made more efficient when we need not one but many samples from similar posterior distributions. This occurs, for instance, in educational surveys, where we have to sample from the posterior distribution of each of N individuals to produce plausible values. In this chapter, we use the composition algorithms to sample from conditional distributions of the following form:

$$\displaystyle \begin{aligned} f_r(\theta\mid{\mathbf{x}}_r) \propto f({\mathbf{x}}_r\mid\theta) f_r(\theta) \end{aligned} $$
(12.1)

where Θ is a random effect that varies across replications r = 1, …, N. We follow Marsman et al. (2017) and demonstrate how the composition algorithms can be tailored for the situation where N is very large. Over the last decade, large values of N have become increasingly more common as more and more data are being produced. This implies that there is a growing need to analyze large data sets and our algorithms are specifically designed for this purpose, mainly because their efficiency increases with N. The algorithms are not developed for situations where N is small.

The algorithms are useful in many contexts. Marsman et al. (2017) discussed their use for models in the exponential family and illustrated them using the Rasch (1960) model. The main goal of this chapter is to illustrate how the algorithms can be used in educational measurement applications where X is a vector of discrete item responses,Footnote 1 Θ is a latent ability, P(X∣θ) is an IRT model with fixed item parameters, and we use the composition algorithms to sample from the posterior distribution of ability for each of N persons, either for its one right or as part of a Gibbs sampler. Compared to alternative approaches, the main advantage of the composition algorithms is that they become more efficient when the number of persons increases, as explained in Sect. 12.3.

The composition algorithms only require that we can generate data which is trivial for common IRT models. A nice feature is that we only need to know f(θ) and P(X∣θ) up to a constant. This opens the door to new applications which would be difficult to handle with existing algorithms. We will illustrate this with an example involving a random-effects gamma model for response times. The normalizing constant (i.e., the gamma function) is not available in closed form and sometimes difficult to approximate.

To set the stage, we will first introduce the two composition algorithms as they stand. After having introduced the composition algorithms, we explain how they can be made more efficient and illustrate their use with simulated and real-data applications. The chapter ends with a discussion.

2 Sampling from a Conditional Distribution

2.1 The Rejection Algorithm

The rejection algorithm (see Algorithm 1) works as follows. To sample from a conditional distribution f(θ∣x), we repeatedly sample {θ ∗, x ∗} from the joint distribution of θ and x until we produce a sample for which x ∗ = x. This generates an i.i.d. sample from the conditional distribution f(θ∣x). The algorithm requires two things: First, it must be possible to sample from f(θ) and P(x∣θ); that is, we should be able to generate data under the model. Second, the random variable X must be discrete with a finite range so that there is a non-zero probability to generate a value x ∗ equal to the observed value x.

Algorithm 1 A rejection algorithm for f(θ∣x)

1: repeat

2:   Generate θ ∗∼ f(θ)

3:   Generate x ∗∼ P(x∣θ ∗)

4: until x ∗ = x

5: Set θ = θ ∗

It will be clear that the number of trials needed increases with the number of values X can assume so that the rejection algorithm is only useful when this number is small. In the special case when P(x∣θ) belongs to the exponential family, the posterior depends on the data only via the sufficient statistic t(x) (Dawid 1979). Since X is a discrete random variable, t(X) is also a discrete random variable, and this means that we may replace x ∗ = x with t(x ∗) = t(x) in line 4 of Algorithm 1. This version of the rejection algorithm was developed for the ESLC, and it is the focus of the present chapter.

Note that the more realizations of X lead to the same value on the sufficient statistic, the more efficient the algorithm becomes. The ESLC shows that the algorithm is efficient enough to be used in large-scale educational surveys using the Partial Credit Model (PCM; Masters 1982). The same holds for other exponential family IRT models, such as the Rasch model (Rasch 1960), the One-Parameter Logistic Model (OPLM; Verhelst & Glas, 1995), and special cases of the Generalized Partial Credit Model (GPCM; Muraki 1992) and Nominal Response Model (NRM; Bock 1972) where the category parameters are integer.

2.2 The Single-Variable Exchange Algorithm

The rejection algorithm rejects all samples for which x ∗ does not exactly match x and thus requires the random variable X to be discrete, preferably assuming a small number of values. To allow X to be continuous, we adapt the rejection step such that we accept or reject samples with a probability other than 0 or 1. That is, we consider the generated θ ∗ as a sample from the proposal distribution f(θ∣x ∗) and accept this value as a realization from the target distribution f(θ∣x) with a probability f(θ ∗∣x)∕(M f(θ ∗∣x ∗)), where M > 0 is an appropriate bound on f(θ ∗∣x)∕f(θ ∗∣x ∗) for all possible values of x and x ∗. In general, however, it is difficult to find M, and we therefore consider a Metropolis algorithm. That is, we choose the probability to accept such that the accepted values are a sample from a Markov chain whose stationary distribution is f(θ∣x). The price to pay is that we now produce a dependent and identically distributed (d.i.d.) sample.

To ensure that the Markov chain generated by the Metropolis algorithm has the desired stationary distribution, the following detailed balance condition must hold (Tierney 1994):

$$\displaystyle \begin{aligned} &\pi(\theta^\prime \rightarrow \theta^\ast)\frac{P(\mathbf{x}\mid \theta^\prime)f(\theta^\prime)}{P(\mathbf{x})}\frac{P({\mathbf{x}}^\ast\mid \theta^\ast)f(\theta^\ast)}{P({\mathbf{x}}^\ast)}\\ &\qquad =\pi(\theta^\ast \rightarrow \theta^\prime)\frac{P(\mathbf{x}\mid \theta^\ast)f(\theta^\ast)}{P(\mathbf{x})}\frac{P({\mathbf{x}}^\ast\mid \theta^\prime)f(\theta^\prime)}{P({\mathbf{x}}^\ast)}, \end{aligned} $$

where θ ′ is the current parameter setting and π(θ ′→ θ ∗) the probability to make a transition of θ ′ to θ ∗. It is easily checked that the detailed balance condition holds when \(\pi (\theta ^\prime \rightarrow \theta ^\ast )=\min \{1,\omega (\theta ^\prime \rightarrow \theta ^\ast )\}\), with

$$\displaystyle \begin{aligned} \omega(\theta^\prime \rightarrow \theta^\ast)=\frac{P(\mathbf{x}\mid \theta^\ast)f(\theta^\ast)P({\mathbf{x}}^\ast\mid \theta^\prime)f(\theta^\prime)}{P(\mathbf{x}\mid \theta^\prime)f(\theta^\prime)P({\mathbf{x}}^\ast\mid \theta^\ast)f(\theta^\ast)}=\frac{P(\mathbf{x}\mid \theta^\ast)P({\mathbf{x}}^\ast\mid \theta^\prime)}{P(\mathbf{x}\mid \theta^\prime)P({\mathbf{x}}^\ast\mid \theta^\ast)}, \end{aligned} $$
(12.2)

and the probability to accept θ ∗ depends on the relative likelihood to observe x ∗ and x given the parameter settings θ ′ or θ ∗, respectively. Using this probability in the Metropolis algorithm, we arrive at the SVE; see Algorithm 2.

Algorithm 2 The Single-Variable Exchange algorithm

1: Draw θ ∗∼ f(θ)

2: Draw x ∗∼ P(x∣θ ∗)

3: Draw \(u \sim \mathcal {U}(0,1)\)

4: if (u < π(θ ′→ θ ∗)) then

5:   θ ′ = θ ∗

6: end if

To use the SVE algorithm, we must be able to compute ω(θ ′→ θ ∗), and the SVE algorithm was designed to make this task as simple as possible. To see this, we write

$$\displaystyle \begin{aligned} P(\mathbf{x}\mid \theta) = \frac{h(\mathbf{x}\text{; }\theta)}{Z(\theta)}, \end{aligned}$$

where Z(θ) =∑x h(x; θ) is a normalizing constant, or partition function, which is often difficult or even impossible to compute.Footnote 2 Since ω(θ ′→ θ ∗) in (12.2) is the product of likelihood ratios, it follows that

$$\displaystyle \begin{aligned} \omega(\theta^\prime \rightarrow \theta^\ast) = \frac{\frac{h(\mathbf{x}\text{; }\theta^\ast)}{Z(\theta^\ast)}\frac{h({\mathbf{x}}^\ast\text{; }\theta^\prime)}{Z(\theta^\prime)}}{\frac{h(\mathbf{x}\text{; }\theta^\prime)}{Z(\theta^\prime)}\frac{h({\mathbf{x}}^\ast\text{; }\theta^\ast)}{Z(\theta^\ast)}}=\frac{h(\mathbf{x}\text{; }\theta^\ast)h({\mathbf{x}}^\ast\text{; }\theta^\prime)}{h(\mathbf{x}\text{; }\theta^\prime)h({\mathbf{x}}^\ast\text{; }\theta^\ast)}. \end{aligned}$$

Thus, there is no need to compute Z(θ) (or P(x)).

As an illustration, Table 12.1 gives \(\ln (\omega (\theta ^\prime \rightarrow \theta ^\ast ))\) for a selection of IRT models. Note that for many of the models in Table 12.1, \(\ln (\omega (\theta ^\prime \rightarrow \theta ^\ast ))\) is of the form:

$$\displaystyle \begin{aligned} (\theta^\ast-\theta^\prime)(t(\mathbf{x}) - t({\mathbf{x}}^\ast)). \end{aligned}$$

That is, the acceptance probability depends on the product of the difference in parameter settings and the difference between the statistics of the generated and observed data. It also shows that, as the range of t(X) increases, ω(θ ′→ θ ∗) tends to become lower, on average.

Table 12.1 \(\ln (\omega (\theta ^\prime \rightarrow \theta ^\ast ))\) for a selection of IRT models
Full size table

2.3 Limitations

In educational measurement, we often have to sample from the posterior ability distribution of each of N persons, where N is large. In the Programme for International Student Assessment, a large-scale educational survey, plausible values have to be produced for more than half a million pupils. And below, we have to sample from the posterior distribution of ability when we analyze a hierarchical IRT model for the responses from over 150, 000 pupils on a Dutch educational test. To sample from N posterior distributions, the composition algorithms would require about N times the amount of work needed to sample from a single posterior; see below. Thus, the algorithms do not become more efficient when N increases and are inefficient when N is large. The algorithms are also inefficient for applications with many items. Suppose the number of possible response patterns (or sufficient statistics) increases. In that case, the rejection algorithm will need increasingly more trials, and the SVE algorithm will tend to have lower acceptance probabilities so that the correlation between successive draws will tend to be higher.

We illustrate this with a small simulation study, the results of which are shown in Fig. 12.1. We simulate data with N persons answering to each of J dichotomous items, with N varying between 100 and 10, 000, and J ∈{10, 20, 30}. We assume a standard normal distribution for ability Θ. For the rejection algorithm, the IRT model is the Rasch model. For the SVE algorithm, we use the Two-Parameter Logistic (2PL) model. The item parameters are fixed, with difficulty parameters sampled from a standard normal distribution and discrimination parameters sampled uniformly between 1 and 3. For each combination of N and J, we generated 100 data sets. With the item parameters fixed, our goal is to sample for each of the N persons an ability from the posterior distribution given his or her observed response pattern.

Fig. 12.1
figure 1

Simulation results. (a) Number of trials for rejection. (b) Acceptance probability for SVE

Full size image

Results for the rejection algorithm are in Fig. 12.1a, which shows the average number of trials that are required to sample from each of the N posteriors as a function of N and J. It is clear that the average number of trials required quickly stabilizes around the number of possible realizations of t(X), which is J + 1 in this simulation.Footnote 3 Thus, we need approximately (J + 1) × N iterations to produce a value from each of the N posteriors, and this number grows linear in both N and J. Results for the SVE algorithm are in Fig. 12.1b which shows the average proportion of values accepted in the 100th iteration of the algorithm as a function of N and J. The acceptance probabilities are seen to be low and decreasing with an increase of the number of items. Thus, for both algorithms, it follows that as N and J grow, we need more iterations to obtain a certain amount of independent replicates from each of the N posteriors. We conclude that the algorithms, as they stand, are unsuited for applications with large N (and J).

3 Large-Scale Composition Sampling

The rejection and SVE algorithm sample from one posterior at the time. Consequently, sampling from N posteriors requires N times the amount of work needed to sample from a single posterior. If the algorithms are to be prepared for applications with an increasing number of posteriors, the amount of work per posterior has to decrease with N. To see how, observe that both algorithms generate samples that are not used efficiently, i.e., samples that are either rejected or accepted with a low probability. Thus, to improve the efficiency of the algorithms for increasing N, we need to make more efficient use of the generated samples. To this aim, we consider the SVE algorithm as an instance of what Tierney (1994, 1998) refers to as a mixture of transition kernels. This way of looking at the SVE algorithm suggests two approaches to improve its efficiency. One of these will be seen to apply to the rejection algorithm as well.

3.1 A Mixture Representation of the SVE Algorithm

In every realization of the SVE algorithm, we sample one of the possible response patterns (denoted x ∗), together with a random value for ability (denoted θ ∗). The sampled ability value is a sample from the posterior distribution f(θ∣x ∗) which is the proposal distribution in the SVE algorithm. The probability that we use f(θ∣x ∗) as proposal distribution in the SVE algorithm is equal to P(x ∗), which follows from the factorization:

$$\displaystyle \begin{aligned} P({\mathbf{x}}^\ast\mid \theta^\ast) f(\theta^\ast) = f(\theta^\ast\mid {\mathbf{x}}^\ast) P({\mathbf{x}}^\ast). \end{aligned}$$

That is, every simulated response pattern corresponds to a unique proposal distribution and, hence, to an unique transition kernel f(θ ∗∣θ, x ∗). Each of these transition kernels has the target posterior distribution as its invariant distribution; that is,

$$\displaystyle \begin{aligned} f(\theta^\ast\mid \mathbf{x}) = \int_{\mathbb{R}} f(\theta^\ast\mid \theta\text{, }{\mathbf{x}}^\ast) f(\theta\mid \mathbf{x}) \,\text{d}\theta. \end{aligned}$$

As shown by Tierney (1994), the same is true for their mixture, that is,

$$\displaystyle \begin{aligned} f(\theta^\ast\mid \mathbf{x}) = \int_{\mathbb{R}} \sum_{{\mathbf{x}}^\ast} f(\theta^\ast\mid \theta\text{, }{\mathbf{x}}^\ast) P({\mathbf{x}}^\ast) f(\theta\mid \mathbf{x}) \,\text{d}\theta, \end{aligned}$$

where the sum is taken over all possible response patterns, and we now see that the P(x ∗) are the mixture weights.

To make matters concrete, consider the posterior distribution for a Rasch model with J items and a standard normal prior for ability θ. Because the Rasch model is an exponential family model with the test score t(x) as sufficient statistic for ability, we know that posteriors for the different ways to obtain the same test score are all the same (Dawid 1979). That is, the mixture weights are nothing but the distribution of test scores. Moreover, the posterior distributions f(θ∣t(x)) are stochastically ordered by the test score, which makes the acceptance probability lower, the larger the difference between the value of t(x) conditioned on in the target and t(x ∗) conditioned on in the proposal distribution; see Table 12.1. Figure 12.2 shows the mixture probabilities P(t(x)) for a test of 20 items. We see in Fig. 12.2 that the SVE algorithm will tend to generate many transition kernels for which the acceptance probability is not very high.

Fig. 12.2
figure 2

Empirical distribution over transition kernels for the SVE algorithm

Full size image

3.2 Oversampling

Since the SVE algorithm tends to frequently generate transition kernels for which the acceptance probability is low, we consider changing the mixture probabilities, in such a way that more probability mass is concentrated on transition kernels with high acceptance probability.

Suppose that instead of simulating a single proposal value θ ∗, with a corresponding single response pattern x ∗, we simulate a number of i.i.d. proposal values, each with its own response pattern. From those, we choose the one for which the test score is closest to the test score conditioned on in the target distribution, and hence the acceptance rate tends to be the highest.

In Fig. 12.3, we illustrate the effectiveness of this oversampling approach in sampling from a posterior f(θ∣t(x) = 9). Clearly, even with 5 samples, we already improve the probability to generate directly from the target from close to 0.1 to close to 0.4. With 20 samples, this probability even exceeds 0.8. Moreover, if the proposal is not identical to the target, it is increasingly more likely to be close to the target as the number of samples increases.

Fig. 12.3
figure 3

Probability distribution over transition kernels after modulating the mixture probabilities. (a) 5 samples. (b) 20 samples

Full size image

Since oversampling can easily be implemented in a parallel implementation, this approach need not lead to a large increase in computer time. This makes the approach computationally attractive.

3.3 Matching

Consider the situation where there are many proposal distributions (i.e., N large) and hence many target posterior distributions, each one independent from the others. The SVE algorithm can once again be considered as a mixture of transition kernels for the whole collection of N posteriors:

$$\displaystyle \begin{aligned} f(\boldsymbol{\theta}^\ast\mid \underline{\mathbf{x}})= \int_{\mathbb{R}^N}\prod_i f(\theta_i^\ast\mid \theta_i\text{, }{\mathbf{x}}^\ast_i) P(\underline{\mathbf{x}}^\ast) f(\boldsymbol{\theta}\mid \underline{\mathbf{x}}) \,\text{d}\boldsymbol{\theta}, \end{aligned}$$

where \( \underline {\mathbf {x}}\) denotes the matrix IMAGE. Observe that the transition kernel for person i only depends on \( \underline {\mathbf {x}}^\ast \) via the i-th response pattern. Suppose that for a matrix \( \underline {\mathbf {x}}^\ast \), we permute the person indices i, in some fixed way (denoted perm(i)). Then, the transition kernel for person i depends on \( \underline {\mathbf {x}}^\ast \) via one of the response patterns in \( \underline {\mathbf {x}}^\ast \), and every response pattern is used exactly once:

$$\displaystyle \begin{aligned} f(\boldsymbol{\theta}^\ast\mid \underline{\mathbf{x}})= \int_{\mathbb{R}^N}\prod_i f(\theta_{\text{perm}(i)}^\ast\mid \theta_i\text{, }{\mathbf{x}}^\ast_{\text{perm}(i)}) P(\underline{\mathbf{x}}^\ast) f(\boldsymbol{\theta}\mid \underline{\mathbf{x}}) \,\text{d}\boldsymbol{\theta}. \end{aligned}$$

Clearly, not all proposal distributions lead to the same acceptance probability, and thus, not all permutations lead to the same overall acceptance rate. Hence, some permutations work better than others. Notice that all permutations lead to a valid transition kernel with the posterior distribution as its invariant distribution, as long as our permutation strategy does not depend on Θ ′ or Θ ∗. Finding, for every matrix \( \underline {\mathbf {x}}^\ast \) and every observed matrix \( \underline {\mathbf {x}}\), the best permutation will in general be an NP-complete problem. However, the better the permutation, the more efficient the algorithm.

In Algorithm 3, we consider the general situation where each person may receive its own prior distribution, and we denote the prior of a person i with f i(θ). We generate a proposal using the prior v = 1, …, N (v now indexes the proposals), and we reorder the index vector V = [v i] of the proposals by using a permutation function perm(). When we use \(\theta ^\ast _v\sim f_v(\theta \mid {\mathbf {x}}^\ast _v)\) as a proposal for a posterior f i(θ∣x i) (i need not equal v), then we accept \(\theta ^\ast _v\) with probability \(\pi (\theta _i^\prime \rightarrow \theta _v^\ast )=\min \{1,\omega (\theta _i^\prime \rightarrow \theta _v^\ast )\}\), and

$$\displaystyle \begin{aligned} \omega(\theta_i^\prime \rightarrow \theta_v^\ast) &= \frac{f_i(\theta^\ast\mid {\mathbf{x}}_i)f_v(\theta^\prime\mid {\mathbf{x}}^\ast)}{f_{i}(\theta^\prime\mid {\mathbf{x}}_i)f_v(\theta^\ast\mid {\mathbf{x}}^\ast)} =\frac{h({\mathbf{x}}_i\text{; }\theta^\ast)h({\mathbf{x}}^\ast\text{; }\theta^\prime)}{h({\mathbf{x}}_i\text{; }\theta^\prime) h({\mathbf{x}}^\ast\text{; }\theta^\ast)}\times\frac{f_{i}(\theta^\ast)f_v(\theta^\prime)}{f_{i}(\theta^\prime)f_v(\theta^\ast)}, \end{aligned} $$

a product of likelihood ratios times a product of prior ratios, where the normalizing constants P(x) and Z(θ) cancel as before (as do the normalizing constants of the prior distributions).

Algorithm 3 Single-Variable Exchange algorithm with matching

Require: Index vector V = [v i] = i, for i = 1, 2, …, N

Require: A permutation function perm()

1: for v = 1 to N do

2:   Generate \(\theta ^\ast _v \sim f_v(\theta )\)

3:   Generate \({\mathbf {x}}^\ast _v \sim P(\mathbf {X}\mid \theta ^\ast _v)\)

4: end for

5: Match proposals to targets by rearranging V based on perm().

6: for i = 1 to N do

7:   Set v = v i

8:   Draw \(u \sim \mathcal {U}(0,1)\)

9:   if (\(u < \pi (\theta ^\prime _i \rightarrow \theta ^\ast _v)\)) then

10:      Set \(\theta _i^\prime = \theta ^\ast _v\)

11:   end if

12: end for

Simple permutation functions are often readily available. For instance, the test score is usually correlated with Θ and gives a simple procedure to permute the indices of proposals and targets. When the IRT model is a member of the exponential family, the sufficient statistic t(x) contains all information about Θ from the data and gives another simple procedure for permutation. More general solutions would be the use of maximum likelihood or Bayes’ modal estimates, when they are not too expensive to compute. We give some examples of permutation strategies in our applications below.

3.4 Recycling in the Rejection Algorithm

The main idea underlying matching is that a proposal need not be associated to one particular posterior. We can use the same idea for the rejection algorithm for the situation with N posteriors using a common prior f(θ). The idea behind recycling is that if we sample {θ ∗, x ∗}, θ ∗ can be assigned to any observation i where t(x i) = t(x ∗) (or x i = x ∗). In general, we need to sample from \(N = \sum _{u = 1}^U n_u\) posteriors f(θ∣t(x) = t u), where t u is one of the U unique values the statistic t(X) can take, N u is the number of observations of response patterns x i for which t(x i) = t u, and it is arbitrary how the values of t(X) are indexed. As seen in Algorithm 4, we sample from the joint distribution of Θ and X until we have n u values for each u. In Algorithm 4, we store generated values in a vector R and the index corresponding to the generated statistic in a vector S. If necessary, we can use S to assign the drawn parameters to observations. Note that this version of the rejection algorithm has been implemented in the R-package dexter (Maris et al. n.d.).

Algorithm 4 A rejection algorithm with recycling

Require: n u for u = 1, 2, …, U.

Require: A counter c and vectors R = [r i] and S = [s i], i = 1, 2, …, N.

1: c = 0.

2: repeat

3:   Generate θ ∗∼ f(θ)

4:   Generate x ∗∼ P(X∣θ ∗)

5:   Determine u, such that t(x ∗) = t u

6:   if n u ≥ 1 then

7:      n u = n u − 1

8:      c = c + 1

9:      [r c] = θ ∗

10:      [s c] = u

11:   end if

12: until n u = 0 for u = 1, …, U

In the context of IRT, the situation with N posteriors using a common prior describes the situation of N persons sampled from the same population. In practice, however, we often encounter situations where the persons are sampled from different groups, e.g., boys and girls. In this situation, posteriors are of the form

$$\displaystyle \begin{aligned} f(\theta\mid {\mathbf{x}}_i) \propto P({\mathbf{x}}_i\mid \theta)f_m(\theta), \end{aligned}$$

i.e., persons are grouped into marginals m, where f m(θ) denotes the prior distribution in marginal m, and recycling applies to each marginal separately. It will be clear that in this situation, the algorithm becomes efficient only when there are many persons in each marginal. When the prior distributions are person specific, and each person has its own marginal distribution, recycling reduces to the standard rejection algorithm.

3.5 Has the Efficiency of the Algorithms Improved?

We considered recycling and matching as ways to improve the rejection and SVE algorithm when samples are required from many posteriors. To illustrate that this works, we compare the efficiency of the rejection algorithm with and without recycling and the SVE algorithm with and without matching under the conditions of our previous simulation.

Results for the rejection algorithm with recycling are in Fig. 12.4a, which shows the average number of trials required to sample from the N posteriors as a function of N and J. If we compare the results in Fig. 12.4a with the results in Fig. 12.1a, we see that recycling requires relatively few iterations per posterior. Note that the required number of iterations decreases as N increases and increases when J increases. It is clear from Fig. 12.4a that as both N and J increase, recycling makes the rejection algorithm more efficient when N increases faster than J. For fixed J, Fig. 12.4a confirms that as N becomes large, the number of iterations per posterior tends to 1.

Fig. 12.4
figure 4

Simulation results. (a) Number of trials with recycling. (b) Proportion accepted with matching

Full size image

To illustrate that the matching procedure improves the efficiency of the SVE algorithm, we consider the following simple strategy. We order target distributions using the statistic \(t({\mathbf {x}}_i\text{, }\boldsymbol {\alpha }) = \sum _{j=1}^Jx_{ij}\alpha _j\) (see Table 12.1), such that the values of the statistic are ordered from small to large, and we do the same for the proposal distributions using the t(x ∗, α). This simple permutation strategy ensures that if the Markov chain is stationary, the first proposal is likely to be a good proposal for the first target (since the difference between t(x, α) and t(x ∗, α) is likely to be small), and the same holds for the second, the third, and so on. Results for the SVE algorithm using this procedure are given in Fig. 12.4b, which shows the average acceptance rate in the 100th iteration of the algorithm as a function of N and J. If we compare the results in Fig. 12.4b with the results in Fig. 12.1b, we see that matching results in much higher acceptance rates. Note that, similar to the results for the recycling, the proportion of accepted values increase as N increases and decrease as J increases and matching makes the SVE algorithm more efficient when N increases faster than J. For fixed J, Fig. 12.4b confirms that as N becomes large, the average acceptance rate tends to 1.

We conclude that recycling and matching make sampling from a large number of posteriors entirely feasible. Most appealing is that the efficiency improves as a function of N. As N tends to infinity, this means that we need to generate the data only once to obtain a draw from each of N posteriors and both algorithms generate i.i.d. from each of the N posteriors. For moderate N, we can already see that the number of trials needed for the rejection algorithm approaches 1 and that the acceptance rate of the SVE algorithm approaches 1. This shows that, even for moderate N, both algorithms require little more than one generated data set and that the SVE algorithm is close to sampling i.i.d.

To illustrate that matching makes the autocorrelation in the SVE algorithm a decreasing function of N, we perform a small simulation. We run 5000 Markov chains for 500 iterations each. We use the 5000 Markov chains to estimate the autocorrelation by correlating the 5000 draws in some iteration i and iteration i + 1, i + 2, …. Figure 12.5 shows the autocorrelation spectra for the SVE algorithm with matching. In Fig. 12.5, we see that the autocorrelations are a decreasing function of N, meaning that as N becomes sufficiently large, we sample approximately i.i.d.

Fig. 12.5
figure 5

Estimated autocorrelation spectra using J = 30 items. (a) N = 100 persons, θ = 0. (b) N = 100 persons, θ = 0.5. (c) N = 1000 persons, θ = 0. (d) N = 1000 persons, θ = 0.5. (e) N = 10, 000 persons, θ = 0. (f) N = 10, 000 persons, θ = 0.5

Full size image

3.6 How Do Our Algorithms Compare to Existing Algorithms?

When it is difficult to sample from f(θ∣x) directly, it is sometimes easier to sample from a more complex (augmented) posterior distribution f(θ, y∣x) using the Gibbs sampler. In the context of educational measurement, this approach has been advocated by Albert (1992) for Normal Ogive models and by Jiang and Templin (2018, 2019) for logistic IRT models. Due to the use of conditioning in the Gibbs sampler, the data augmentation procedure of Albert (1992) introduces a constant amount of autocorrelation to the Markov chain (Liu et al. 1994). As a result, the number of iterations that are required to obtain a fixed amount of independent replicates from each of the N posteriors is linear in N. In this sense, our algorithms scale better, since the amount of autocorrelation reduces as a function of N.

A more general approach to sampling from f(θ∣x) is to sample a proposal value θ ∗ from a conditional distribution f(θ ∗∣θ ′) and use the Metropolis-Hastings algorithm to either move to the proposed value θ ∗ or stay at the current state θ ′. This approach has been advocated by Patz and Junker (1999), who suggest to use \(f(\theta ^\ast \mid \theta ^\prime ) = \mathcal {N}(\theta ^\prime \text{, }\sigma ^2)\) as proposal distribution (i.e., a random walk). Setting the value of σ 2 in the proposal distribution requires some effort from the user (Rosenthal 2011): when σ 2 is too large, most samples are rejected, but when σ 2 is too small, only small steps are taken, and the chain does not mix properly. To overcome this problem altogether, one could use an unconditional proposal distribution g(θ) (i.e., an independence chain). This is the approach we took in this chapter. Whenever the proposal distribution g(θ) closely resembles the target distribution, the Metropolis-Hastings algorithm is very efficient. In general, it can be difficult to find good proposal distributions, but the matching procedure automatically finds proposal distributions g(θ∣x ∗) that closely resemble the target f(θ∣x), and as N increases, this procedure becomes more likely to generate good proposal distributions.

4 Simulated and Real-Data Examples

In this section, we discuss three examples illustrating the practical use of the SVE algorithm for Bayesian estimation using the Gibbs sampler. The Gibbs sampler is an abstract divide-and-conquer algorithm that generates a dependent sample from a multivariate posterior distribution. In each iteration, the algorithm generates a sample from the distribution of each variable in turn, conditional on the current values of the other variables. These are called the full-conditional distributions. It can be shown that the sequence of samples constitutes a Markov chain and the stationary distribution of that Markov chain is the joint posterior distribution of interest.

In each of our examples, there will be one or more full-conditional distributions that are not easily sampled from, and we use the SVE algorithms developed in this chapter to sample from these full-conditional distributions. All analyses have been performed using a Dell OptiPlex 980 PC with an Intel Core 5 CPU and clock speed 3.20 Ghz and 4Gb of memory running on Windows 7 Enterprise(32 bit) with a single core.

4.1 Gamma Regression

The random-effects gamma model is a model for responses times proposed by Fox (2013) as an alternative to the log-normal model that is commonly used (van der Linden 2007; Klein Entink et al. 2009). The model is difficult to estimate, because the normalizing constant of the gamma distribution (i.e., the gamma function Γ(⋅)) is not available in closed form and can produce overflow errors in its computation. We develop a Gibbs sampler for this model to illustrate how the SVE algorithm can be used to avoid the calculation of the gamma function.

Let X ij denote the time needed by person i to respond to item j; i = 1, …, N, and j = 1, …, J. The X ij are assumed to be independent, gamma distributed random variables with

$$\displaystyle \begin{aligned} f(\underline{\mathbf{x}}\mid \boldsymbol{\lambda}\text{, }\boldsymbol{\eta}) = \prod_{i=1}^N\prod_{j=1}^J \frac{\lambda_{ij}^{\eta_{ij}}}{\Gamma(\eta_{ij})} x_{ij}^{\eta_{ij}-1}\exp\left\lbrace-x_{ij}\lambda_{ij}\right\rbrace. \end{aligned} $$
(12.3)

In the model of Fox (2013), a relatively simple regression structure was used, namely, λ ij = ν∕(2 θ i) and η ij = ν∕2. We will use a slight alteration in this simulation, with λ ij = ν∕(θ i δ j) and η ij = ν, such that \(\mathbb {E}[X_{ij}]=\theta _i \,\delta _j\), and \(\text{Var}(X_{ij})= \mathbb {E}[X_{ij}]^2/\nu \). The person parameter θ i > 0 represents the speed of person j, the item parameter δ j > 0 the time intensity of item j, and ν a common rate parameter. We further assume that \(\theta _i \sim \ln \mathcal {N}(\mu _\theta \text{, }\sigma ^2_\theta )\), and \(\delta _j \sim \ln \mathcal {N}(\mu _\delta \text{, }\sigma _\delta ^2)\), where \(\ln \mathcal {N}(\mu \text{, }\sigma ^2)\) denotes the log-normal distribution with mean μ and variance σ 2. The location and scale parameters of the person and item parameters are unknown and are to be estimated. To complete the specification of the model, we use the following priors: ν ∼ Γ(a, b), \(f(\mu _\theta \text{, }\sigma _\theta ^2) \propto \sigma _\theta ^{-2}\), and \(f(\mu _\delta \text{, }\sigma _\delta ^2) \propto \sigma _\delta ^{-2}\).

Given the person and item parameters, the location and scale parameters are easily sampled from their full-conditional distributions (Gelman et al. 2004):

$$\displaystyle \begin{aligned} f(\mu_\theta\mid \boldsymbol{\theta}\text{, }\sigma^2_\theta) &\propto \mathcal{N}\left(\frac{1}{N}\sum_{i=1}^N\ln(\theta_i)\text{, } \sigma^2_\theta/N\right)\\ f(\sigma^2_\theta\mid \boldsymbol{\theta}) &\propto \text{Inv-}\chi^2\left(N-1\text{, }\frac{1}{N-1}\sum_{i=1}^N\left(\ln(\theta_i) - \frac{1}{N}\sum_{i=1}^N\ln(\theta_i) \right)^2\right)\\ f(\mu_\delta\mid \boldsymbol{\delta}\text{, }\sigma_\delta^2) &\propto \mathcal{N}\left(\frac{1}{J}\sum_{j=1}^J\ln(\delta_j)\text{, } \sigma^2_\delta/J\right)\\ f(\sigma^2_\delta\mid \boldsymbol{\delta}) &\propto \text{Inv-}\chi^2\left(J-1,\frac{1}{J-1}\sum_{j=1}^J\left(\ln(\delta_j) - \frac{1}{J}\sum_{j=1}^J\ln(\delta_j) \right)^2\right). \end{aligned} $$

The full-conditional distribution of ν, the person, and the item parameters, however, are not easily sampled from, and for these, we will use the SVE algorithms developed in this chapter.

To sample from the full-conditional distribution of ν, we generate ν ∗ from the prior f(ν∣a, b) and generate a data matrix \( \underline {\mathbf {x}}^\ast \) from \(f( \underline {\mathbf {x}}\mid \boldsymbol {\theta }\text{, }\boldsymbol {\delta }\text{, }\nu ^\ast )\). The probability π(ν ′→ ν ∗) to make a transition from ν ∗ to ν ′ using this set-up is then equal to \(\min \left \lbrace 1\text{, }\omega (\nu ^\prime \rightarrow \nu ^\ast ) \right \rbrace \), with

$$\displaystyle \begin{aligned} \ln\omega(\nu^\prime \rightarrow \nu^\ast) = (\nu^\ast - \nu^\prime)(t(\underline{\mathbf{x}}\text{, }\boldsymbol{\theta}\text{, }\boldsymbol{\delta}) - t(\underline{\mathbf{x}}^\ast\text{, }\boldsymbol{\theta}\text{, }\boldsymbol{\delta})), \end{aligned}$$

where

$$\displaystyle \begin{aligned} t(\underline{\mathbf{x}}\text{, }\boldsymbol{\theta}\text{, }\boldsymbol{\delta}) = \sum_{i=1}^N\sum_{j=1}^J\left(\ln(x_{ij}) - \frac{x_{ij}}{\theta_i\delta_j}\right). \end{aligned}$$

Note that we do not need to evaluate the Γ() function at ν ′ or ν ∗, making \(\ln \omega \) a relatively simple function to compute.

We have seen earlier that in this set-up, the SVE algorithm is likely to generate transition kernels for which the acceptance probability is low. We therefore use the oversampling procedure. That is, we generate a number of i.i.d. proposal values ν ∗, each with its own data matrix \( \underline {\mathbf {x}}^\ast \). From these, we choose the one for which the statistic \(t( \underline {\mathbf {x}}^\ast \text{, }\boldsymbol {\theta }\text{, }\boldsymbol {\delta })\) is closest to \(t( \underline {\mathbf {x}}\text{, }\boldsymbol {\theta }\text{, }\boldsymbol {\delta })\). We use 100 proposals in this example. The R-code that we used for this full-conditional is given in Appendix A.

To sample from the full-conditional distributions of the person and the item parameters, we use the matching procedure. Since we use the same matching procedure for the person and the item parameters, we only describe the procedure for the person parameters. We generate \(\theta _v^\ast \), v = 1, …, N, from \(f(\theta \mid \mu _\theta \text{, }\sigma _\theta ^2)\) and use it to generate a vector of response times \({\mathbf {x}}_v^\ast \) from \(f(\mathbf {x}\mid \theta _v^\ast \text{, }\boldsymbol {\delta }\text{, }\nu )\). Say that we use \(f(\theta \mid {\mathbf {x}}^\ast _v\text{, }\nu \text{, }\mu _\theta \text{, }\sigma _\theta )\) as proposal for a target i (i need not equal v), the probability \(\pi (\theta _i^\prime \rightarrow \theta _v^\ast )\) to make a transition from \(\theta _i^\prime \) to \(\theta _v^\ast \) is then equal to \(\min \left \lbrace 1\text{, }\omega (\theta _i^\prime \rightarrow \theta _v^\ast )\right \rbrace \), with

$$\displaystyle \begin{aligned} \ln\omega(\theta_i^\prime \rightarrow \theta_v^\ast) = \nu\left(\frac{1}{\theta_v^\ast} - \frac{1}{\theta_i^\prime}\right)\left(t({\mathbf{x}}^\ast_v,\boldsymbol{\delta})-t({\mathbf{x}}_i,\boldsymbol{\delta})\right), \end{aligned} $$
(12.4)

where

$$\displaystyle \begin{aligned} t({\mathbf{x}}_i\text{, }\boldsymbol{\delta}) = \sum_{j=1}^J \frac{x_{ij}}{\delta_j}. \end{aligned}$$

Note again that we do not need the evaluate the Γ() function in \(\ln \omega \) and the acceptance probabilities are simple to compute.

From (12.4), we see that it is opportune to use t(x i, δ) to permute proposals and targets. To this aim, we compute t(x, δ) for each person in the sample and for each proposal. Then, we order the targets using the t(x i, δ), such that the corresponding statistics are ordered from small to large, and do the same for the proposals using the \(t({\mathbf {x}}_v^\ast \text{, }\boldsymbol {\delta })\). This simple permutation strategy ensures that if the Markov chain is stationary, the first proposal is likely to be a good proposal for the first target (since the difference between t(x, δ) and t(x ∗, δ) is likely to be small) and the same holds for the second, the third, and so on. The R-code that we used for this full-conditional is given in Appendix B.

To see how it works, we simulated data for N = 10, 000 persons on a test consisting of J = 40 items. We set the mean and variance of the person and the item parameters equal to 10 and 1, respectively, from which we can solve for the location and scale parameters in the log-normal model. Using these location and scale parameters, we sample the person and item parameters from the log-normal model. The parameter ν was set equal to 40.

Note that the gamma model that we use is not identified, since multiplying the person parameters with a constant and dividing the item parameters with the same constant give the same model. Since we know the true values of the parameters in this simulation, we simply set the estimated parameter of the first item equal to its true value.

We ran the Gibbs sampler for 2000 iterations, which took approximately 2.5 h (about 4.7 s per iteration). The main computational cost of this Gibbs sampler resides in sampling the entire N × J data matrix m + 2 times in each iteration, of which m = 100 times for sampling from the full-conditional of ν. Since the cost per iteration is the same in each iteration, we see that we need approximately 0.1 s to sample the person and the item parameters in each iteration and approximately 4.6 s to sample ν. This means that we can reduce the computational time by reducing m. Note, however, that this would also reduce the acceptance rate in sampling ν.

The results are in Figs. 12.6 and 12.7. As expected, our use of the SVE algorithm does not lead to high acceptance rates for the item parameters; the average acceptance rate was 0.05. The main reason is that we only generate 40 proposals to assign to 40 targets, with a large variation on the conditioning statistic t(x, θ) due to the large number of observations. In the next example, we show that the oversampling procedure can be used to remedy this. We did obtain high efficiency for the person parameters, with an average acceptance rate of 0.96. In Fig. 12.6, we show the trace plot for a person and an item parameter. It is clear that both converge quickly to the stationary distribution. In Fig. 12.7, we show scatterplots of the true person and item parameters against the parameter states in iteration 2000, which illustrates that we are able to recover the parameters of the generating model. Finally, the proportion of accepted values for the ν parameter equalled 0.30, which is certainly reasonable for such a complex full-conditional distribution. In Fig. 12.6c, we show the trace plot of ν, from which we see that once the person and item parameters converge, ν also quickly converges to its stationary distribution.

Fig. 12.6
figure 6

Trace plot of ν, a person, and an item parameter in the gamma mixture example. (a) Trace plot of a person parameter. (b) Trace plot of an item parameter. (c) Trace plot of ν

Full size image
Fig. 12.7
figure 7

Scatterplot of the true person (item) parameters at the states of the person (item) parameters in iteration 2000 of the Gibbs sampler for the gamma mixture example. (a) Scatterplot of the person parameters. (b) Scatterplot of the item parameters

Full size image

4.2 The Amsterdam Chess Test Data

The Signed Residual Time (SRT) model is an exponential family IRT model for item response accuracy and response times and is derived by Maris and van der Maas (2012) from the following scoring rule:

$$\displaystyle \begin{aligned} (2X_{ij}-1)(\text{d} - S_{ij}), \end{aligned}$$

for an item response X ij, which equals 1 if the response is correct and 0 if incorrect, after S ij time units when the time limit for responding is d. This scoring rule assigns the residual time as the score for a correct response and minus the residual time for an incorrect response. Thus, subjects need to be both fast and accurate to obtain a high score and, thereby, a high estimated ability. The SRT model is

$$\displaystyle \begin{aligned} f(X_{ij}=x_{ij}\text{, }S_{ij}=s_{ij}\mid \theta_i\text{, }\delta_j\text{, }\text{d}) {=} (\theta_i-\delta_j)\frac{\exp\left[(2x_{ij}-1)(\text{d}-s_{ij})(\theta_i-\delta_j)\right]}{\exp\left[\text{d}(\theta_i-\delta_j)\right] - \exp\left[-\text{d}(\theta_i-\delta_j)\right]}, \end{aligned}$$

for 0 ≤ s ≤d. The statistics

$$\displaystyle \begin{aligned} t({\mathbf{x}}_i\text{, }{\mathbf{s}}_i) &= \sum_{j=1}^J(2x_{ij}-1)(\text{d}-s_{ij})\\ t({\mathbf{x}}_j\text{, }{\mathbf{s}}_j) &= -\sum_{i=1}^N(2x_{ij}-1)(\text{d}-s_{ij}) \end{aligned} $$
(12.5)

are sufficient for the ability θ i of a person i and the difficulty δ j of an item j, respectively. We assume that \(\theta _i \sim \mathcal {N}(\mu _\theta \text{, }\sigma _\theta ^2)\) and \(\delta _j \sim \mathcal {N}(\mu _\delta \text{, }\sigma _\delta ^2)\), and to complete specification of the model used the following priors: \(f(\mu _\theta \text{, }\sigma _\theta ^2) \propto \sigma _\theta ^{-2}\) and \(f(\mu _\delta \text{, }\sigma _\delta ^2) \propto \sigma _\delta ^{-2}\).

Given the person and item parameters, the location and scale parameters are easily sampled from their full-conditional distributions (Gelman et al. 2004):

$$\displaystyle \begin{aligned} f(\mu_\theta\mid \boldsymbol{\theta}\text{, }\sigma^2_\theta) &\propto \mathcal{N}\left(\frac{1}{N}\sum_{i=1}^N\theta_i\text{, } \sigma^2_\theta/N\right)\\ f(\sigma^2_\theta\mid \boldsymbol{\theta}) &\propto \text{Inv-}\chi^2\left(N-1\text{, }\frac{1}{N-1}\sum_{i=1}^N\left(\theta_i - \frac{1}{N}\sum_{i=1}^N\theta_i \right)^2\right)\\ f(\mu_\delta\mid \boldsymbol{\delta}\text{, }\sigma_\delta^2) &\propto \mathcal{N}\left(\frac{1}{J}\sum_{j=1}^J\delta_j\text{, } \sigma^2_\delta/J\right)\\ f(\sigma^2_\delta\mid \boldsymbol{\delta}) &\propto \text{Inv-}\chi^2\left(J-1\text{, }\frac{1}{J-1}\sum_{j=1}^J\left(\delta_j - \frac{1}{J}\sum_{j=1}^J\delta_j \right)^2\right). \end{aligned} $$

The full-conditional distributions of the person and item parameters are not easily sampled from, and we will use an SVE algorithm to sample from these full-conditional distributions. To save space, we will only describe the procedure for the person parameters.

We generate \(\theta _v^\ast \), v = 1, …, N, from \(f(\theta \mid \mu _\theta \text{, }\sigma _\theta ^2)\) and use it to generate a vector of item responses \({\mathbf {x}}_v^\ast \) and response times s v from \(f(\mathbf {x}\text{, }\mathbf {s}\mid \theta _v^\ast \text{, }\boldsymbol {\delta })\) (see Appendix C). Say that we use \(f(\theta \mid {\mathbf {x}}^\ast _v\text{, }{\mathbf {s}}^\ast _v\text{, }\mu _\theta ,\sigma _\theta )\) as proposal for a target i (i need not equal v), the probability \(\pi (\theta _i^\prime \rightarrow \theta _v^\ast )\) to make a transition from \(\theta _i^\prime \) to \(\theta _v^\ast \) is then equal to \(\min \left \lbrace 1\text{, }\omega (\theta _i^\prime \rightarrow \theta _v^\ast )\right \rbrace \), with

$$\displaystyle \begin{aligned} \ln\omega(\theta_i^\prime \rightarrow \theta_v^\ast) = \left(\theta_v^\ast - \theta_i^\prime\right)\left(t({\mathbf{x}}^\ast_v\text{, }{\mathbf{s}}^\ast_v)-t({\mathbf{x}}_i\text{, }{\mathbf{s}}_i)\right), \end{aligned}$$

with t(x i, s i) defined in (12.5).

Although the sufficient statistics (12.5) can be used to permute the indices of targets and proposals, we only have a few person and item parameters in this example. To obtain some efficiency of the SVE algorithm in this application, we use a variant of the oversampling strategy. In each iteration, we generate a number of i.i.d. proposals and for each target distribution choose the proposal for which the statistic t(x ∗, s ∗) is closest to the observed statistic t(x, s) while ensuring that each proposal is used only once.

Van der Maas and Wagenmakers (2005) describe data from the Amsterdam Chess Test (ACT), collected during the 1998 open Dutch championship in Dieren, the Netherlands. The data we consider consists of the accuracy and response times of N = 259 subjects on J = 80 choose-a-move items administered with a time limit of 30 s. We started the mean and variance of the person and item parameters at 0 and 1, respectively. Using these values, we sampled the person and item parameters from the prior. In each iteration, we generated 2 × N = 498 proposals for the persons and 5 × J = 400 proposals for the items. We ran the Gibbs sampler for 10,000 iterations, which took approximately 12 min (about 0.07 s per iteration). The average acceptance rate was 0.98 for the persons and 0.93 for the items.

An important advantage of this illustrative application is that for chess expertise, an established external criterion is available in the form of the Elo ratings of chess players, which has high predictive power for game results. For those 225 participants for whom a reliable Elo rating was available, we correlated the expected a posteriori (EAP) estimates with their Elo ratings. The results are given in Fig. 12.8. The correlation between EAP estimates and Elo ratings is equal to 0.822.

Fig. 12.8
figure 8

Scatterplot of EAP versus Elo rating in the ACT example

Full size image

4.3 The 2012 Eindtoets Data

In educational measurement, population models are commonly used to describe structure in the distribution of the latent abilities. For example, in equating two exams, one can characterize the two exam groups by using a normal distribution with a group-specific mean and variance; in the analyses of tests consisting of different scales, a multivariate normal distribution can be used to characterize the latent correlations; and in educational surveys, a normal regression model can be used to study the effects of covariates on the ability distribution. Whenever the abilities are observed, inference is relatively straightforward in each of these situations. Our focus in this section is to show how the SVE algorithm can be used to sample from the full-conditional distribution of the latent abilities, allowing the analyses of structural IRT models using the Gibbs sampler, even for large data sets.

We use response data of N = 158, 637 Dutch end of primary school pupils on the 2012 Cito Eindtoets to illustrate our approach using a multidimensional IRT model. In specific, we used data from the non-verb spelling (10 items), verb spelling (10 items), reading comprehension (30 items), basic arithmetic (14 items), fractions (20 items), and geometry (15 items) scales. That is, we have six unidimensional IRT models (a between multidimensional IRT model) and use a multivariate normal distribution to infer about the latent correlations between the six scales. To keep our focus on sampling the latent abilities, we assume that an IRT model is given (i.e., the parameters characterizing the items in the IRT model are known). For simplicity, we use the Rasch model for each of the scales in our example and fix the item parameters at the conditional maximum likelihood (CML) estimates.

We use a multivariate normal distribution with an unknown Q × 1 vector of means μ and Q × Q covariance matrix Σ to describe the latent correlations between the Q = 6 dimensions. To complete the model, we use the multivariate Jeffreys prior for the mean vector and the covariance matrix:

$$\displaystyle \begin{aligned} f(\boldsymbol{\mu}\text{, }\boldsymbol{\Sigma}) \propto \mid \boldsymbol{\Sigma}\mid ^{-\frac{Q + 1}{2}}. \end{aligned}$$

The Gibbs sampler is used to sample from the joint posterior distribution \(f(\boldsymbol {\theta }\text{, }\boldsymbol {\mu }\text{, }\boldsymbol {\Sigma }\mid \underline {\mathbf {x}})\). For this model, the full-conditional distributions of μ and Σ are easily sampled from (Gelman et al. 2004):

$$\displaystyle \begin{aligned} f( \boldsymbol{\mu}\mid \boldsymbol{\theta}\text{, }\boldsymbol{\Sigma} ) &\propto \mathcal{N}_Q(\bar{\boldsymbol{\theta}}\text{, }\boldsymbol{\Sigma}/N)\\ f(\boldsymbol{\Sigma}\mid \boldsymbol{\theta}) &\propto \text{Inverse-Wishart}_{N-1}({\mathbf{S}}^{-1}) \end{aligned} $$

where \(\bar {\boldsymbol {\theta }} = \frac {1}{N}\sum _{i=1}^N\boldsymbol {\theta }_i\) is the mean ability vector and \(\mathbf {S} = \sum _{i=1}^N (\boldsymbol {\theta }_i - \bar {\boldsymbol {\theta }} )(\boldsymbol {\theta }_i - \bar {\boldsymbol {\theta }} )^T\) the sums of squares matrix around the mean ability vector. The full-conditional distributions \(f(\boldsymbol {\theta }_i\mid \underline {\mathbf {x}}_i\text{, } \boldsymbol {\mu }\text{, }\boldsymbol {\Sigma })\) are intractable, however, and for this, we use the SVE algorithm.

Instead of sampling from f(θ i∣x i, μ, Σ) directly, we sample pupil abilities in a dimension q given the Q − 1 other dimensions, for q = 1, …, Q. The full-conditional distribution for the ability of a pupil i in a dimension q is proportional to

$$\displaystyle \begin{aligned} f(\theta_{iq}\mid {\mathbf{x}}_{iq}\text{, }\boldsymbol{\theta}^{(q)}\text{, }\boldsymbol{\mu}\text{, }\boldsymbol{\Sigma}) \propto \prod_{i=1}^{J_q} \frac{\exp\left\lbrace x_{ijq}(\theta_{iq} - \delta_{jq})\right\rbrace}{1 + \exp\left\lbrace \theta_{iq} - \delta_{jq}\right\rbrace} \exp\left\lbrace -\frac{(\theta_{iq} - \lambda_{iq})^2}{2\eta^2_q} \right\rbrace, \end{aligned}$$

where δ jq is the difficulty of the j-th out of J q items in dimension q, \(\boldsymbol {\theta }_i^{(q)}\) is the ability vector of pupil i excluding entry q, and λ iq and \(\eta ^2_q\) are the conditional mean and variance of θ iq given \(\boldsymbol {\theta }_i^{(q)}\) in the population model, respectively, given by

$$\displaystyle \begin{aligned} \lambda_{iq} &= \mu_q + \boldsymbol{\sigma}_q^{(q)}\left(\boldsymbol{\Sigma}^{(q\text{, }q)}\right)^{-1}\left(\boldsymbol{\theta}^{(q)}_i - \boldsymbol{\mu}^{(q)}\right)\\ \eta^2_q &= \sigma_{qq} - \boldsymbol{\sigma}_q^{(q)}\left(\boldsymbol{\Sigma}^{(q\text{, }q)}\right)^{-1}(\boldsymbol{\sigma}_q^{(q)})^T, \end{aligned} $$

where \(\boldsymbol {\sigma }_q^{(q)}\) contains the off-diagonal elements of the q-th row in Σ, i.e., \(\boldsymbol {\sigma }_2^{(2)} = [\sigma _{21}\text{, }\sigma _{23}\text{, }\dots \text{, }\sigma _{26}]\).

We sample from the full-conditionals f(θ iq∣x iq, θ (q), μ, Σ), as follows. First, we compute λ iq for i = 1, …, N (note that these depend on the abilities from the remaining Q − 1 dimensions). Then, we sample \(\theta ^\ast _{vq}\) from \(\mathcal {N}(\lambda _{vq}\text{, }\eta _q^2)\) and use these to generate an item response vector \({\mathbf {x}}^\ast _{vq}\) from \(P({\mathbf {X}}_q\mid \theta _{vq}^\ast \text{, }\boldsymbol {\delta }_q)\), for v = 1, …, N. Say that we use \(f(\theta _{vq}\mid {\mathbf {x}}^\ast _{vq}\text{, }\boldsymbol {\theta }_v^{(q)}\text{, }\boldsymbol {\mu }\text{, }\boldsymbol {\Sigma })\) as proposal for a target i (i need not equal v), then the probability \(\pi (\theta ^\prime _{iq} \rightarrow \theta ^\ast _{vq})\) to make a transition of \(\theta ^\prime _{iq}\) to \(\theta ^\ast _{vq}\) is equal to \(\min \{1\text{, }\omega (\theta ^\prime _{iq} \rightarrow \theta ^\ast _{vq})\}\), with

$$\displaystyle \begin{aligned} \ln\omega(\theta^\prime_{iq} \rightarrow \theta^\ast_{vq}) = (\theta^\prime_{iq} - \theta^\ast_{vq})(t({\mathbf{x}}_{vq}^\ast\text{, }\lambda_{vq}\text{, }\eta_q)- t({\mathbf{x}}_{iq}\text{, }\lambda_{iq}\text{, }\eta_q)), \end{aligned}$$

where

$$\displaystyle \begin{aligned} t({\mathbf{x}}_{iq}\text{, }\lambda_{iq}\text{, }\eta_q) = \sum_{i=1}^{J_q}x_{ijq} + \lambda_{iq}/\eta_q^2. \end{aligned}$$

Note that t(x iq, λ iq, η q) combines information from the likelihood with information from the population model.

To match proposals to targets (full-conditionals), it is opportune to use t(x iq, λ iq, η q), since if \(t({\mathbf {x}}_{vq}^\ast \text{, }\lambda _{vq}\text{, }\eta _q)\) is close to t(x iq, λ iq, η q), the acceptance probability tends to be high. In matching the N proposals to the N targets, we start with computing t(x iq, λ iq, η q) for each target and computing \(t({\mathbf {x}}_{vq}^\ast \text{, }\lambda _{vq}\text{, }\eta _q)\) for each proposal. Then, we order the targets using the t(x iq, λ iq, η q), such that the corresponding statistics are ordered from small to large and do the same for the proposals using the \(t({\mathbf {x}}_{vq}^\ast \text{, }\lambda _{vq}\text{, }\eta _q)\). If the Markov chain is stationary, the first proposal is likely to be a good proposal for the first target (since the difference between t(x, λ, η) and t(x ∗, λ, η) will be small), and the same holds for the second, the third, and so on.

We start our analyses by setting μ equal to 0 and Σ equal to the Q × Q identity matrix. To get reasonable starting values for the latent ability vectors, we performed a single run of the SVE algorithm where we accepted all proposals. We ran the Gibbs sampler for 2000 iterations, which took approximately 80 min (about 2.5 s per iteration). The acceptance rates of the SVE algorithm were high in this example, averaging to 0.98, 1.00, 0.97, 0.99, 0.99, and 1.00 for dimensions 1 to 6, respectively. This means that we sample approximately i.i.d. from the full-conditional distributions of the abilities, and thus, using the SVE algorithm in this example does not introduce additional autocorrelation to the Markov chain.

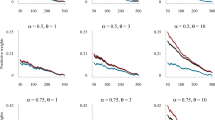
Despite the observation that we sample the abilities approximately i.i.d. in this example, the amount of autocorrelation in the chain is high. To illustrate, we show the trace plot for three parameters: an ability, a mean, and a variance. Note the wave-like patterns that emerge, which indicate a strong relation between subsequent states in the Markov chain (i.e., high amount of autocorrelation). The reason for this high amount of autocorrelation is due to the high correlations that we obtain between some of the dimensions (see Table 12.2) and the fact that we sampled from each dimension conditional upon the others. The high correlations between dimensions then provide a strong relation between draws in subsequent iterations, inducing a high amount of autocorrelation (Fig. 12.9).

Fig. 12.9
figure 9

Trace plots of an ability, a mean, and a variance in the Eindtoets example. (a) The ability of person i=59, 137 in dimension 1. (b) The mean of dimension 6. (c) The variance of dimension 3

Full size image
Table 12.2 Estimated correlations between scales in the 2012 Cito Eindtoets
Full size table

The estimated correlation matrix is shown in Table 12.2. From Table 12.2, it is seen that the two spelling scales are closely related, as are the three mathematics scales. The remaining correlations are only moderately large, yet they are all positively correlated. The correlations in Table 12.2 suggest that there are three distinct dimensions in this problem: spelling, reading comprehension, and mathematics.

5 Discussion

In this chapter, we have described two composition algorithms that can be used to sample from conditional distributions and discussed how their efficiency can be improved to handle large data sets where one needs to sample from many similar distributions.

We have illustrated how the algorithms can be used in a variety of educational measurement applications. We used the composition algorithms for a simulated latent regression example using the random-effects gamma model proposed by Fox (2013), analyzed Amsterdam Chess Test data using the signed residual time model (Maris & van der Maas 2012; Deonovic et al. 2020), and analyzed one big-data example—the Cito Eindtoets—using a multidimensional 2PL model (Reckase 2009). These examples allowed us to illustrate the feasibility of using composition algorithms for simulating from random-effects distributions assessed by complex measurement models. It also allowed us to illustrate that while their efficiency is guaranteed if the algorithms are used in high-dimensional settings (i.e., when there are many instances of a random effect), they are less efficient in low-dimensional settings (e.g., to simulate from the posteriors of the item parameters).

Finally, we note that we used GNU-R to perform the analyses, which was entirely feasible, even for the large applications. Computational time can be decreased by implementing (parts of) the code in a compiled language (e.g., Fortran, C, Delphi). Furthermore, most computer systems run on multiple cores, and computational time could be decreased further by making use of the additional cores in implementations. For instance, proposals can be generated in batches, with each batch running on a single core.