Task Bundle Delegation for Reducing the Flowtime

Abstract

In this paper, we study the problem of task reallocation for load-balancing in distributed data processing models that tackle vast amount of data. We propose a strategy based on cooperative agents used to optimize the rescheduling of tasks in multiple jobs which must be executed as soon as possible. It allows agents to determine locally the next tasks to process, to delegate, possibly to swap according to their knowledge, their own belief base and their peer modelling. The novelty lies in the ability of agents to identify opportunities and bottleneck agents, and afterwards to reassign some bundles of tasks thanks to concurrent bilateral negotiations. The strategy adopted by the agents allows to warrant a continuous improvement of the flowtime. Our experimentation reveals that our strategy reaches a flowtime which is better than the one reached by a DCOP resolution, close to the one reached by the classical heuristic approach, and significantly reduces the rescheduling time.

1 Introduction

The problem of efficient task assignment among executing entities is common to many real-world applications for logistics [13, 15], collective robotics [7, 22], distributed systems [12, 20], or more recently Big Data [1]. In particular, Data Science, which involves the processing of large volumes of data which requires distributed file systems and parallel programming, challenges distributed computing with regard to task allocation and load-balancing. This paper is concerned with a class of practical applications where (a) some concurrent jobs (sets of tasks) must be performed as soon as possible, (b) the resources (e.g. data) required to successfully execute a task are distributed among nodes. Here we consider the most prominent distributed data processing model for tackling vast amount of data on commodity clusters, i.e. the MapReduce design pattern [24]. Jobs are composed of tasks executed by the different nodes where the resources are distributed. Since several resources are necessary to perform a task, its execution requires fetching some of these resources from other nodes, thus incurring an extra time cost for its execution.

Many works adopt the multi-agent paradigm to address the problem of task reallocation and load-balancing in distributed systems [12]. The individual-based approach allows the decentralization of heuristics to scale-up the resolution of scheduling problem despite of the combinatory explosion. Furthermore, due to their inherent reactive nature, the multi-agent methods for task reallocation are adaptive to the inaccurate estimation of task execution time and some disruptive phenomena (task consumption, job release, slowing down nodes, etc.). Most of these works adopt the market-oriented approach which models problems as non-cooperative games [7, 23], eventually with machine learning techniques which assume past experiences [20, 22]. By contrast, we suppose as [1] that: (a) the agents are cooperative, i.e. they have a partial and local perception of the task allocation but they share the same goal, and (b) neither generalizable predictive patterns nor prior model of the data/environment are available since it is not the case for the class of practical applications we are concerned with. We go further here by considering several concurrent jobs composed of tasks. Each task can be executed by a single agent, all of them are competent. Agents want to minimize the mean flowtime of jobs. The main difficulty lies in the formulation of complex systems for the reassignment of tasks-workers which are decentralized and adaptive, i.e. the design of individual and asynchronous behaviours that lead to the emergence of feasible allocations combining the objectives of the task requesters.

We propose a strategy that decides which bilateral reallocation is suggested or accepted. Based on peer modelling, the strategy determines the agent behaviour in the negotiation protocol. The offer strategy selects a potential delegation, i.e. an offer bundle and a respondant. The acceptability rule determines whether the agent accepts or rejects all or part of this delegation. Specifically, our contributions are as follows:

• 1. We formalize the multi-agent task allocation problem where concurrent jobs are composed of situated tasks with different costs depending on the location of the resources.

• 2. We propose a strategy that continuously identifies bottleneck agents and opportunities within unbalanced allocations to trigger concurrent and bilateral negotiations in order to delegate or swap tasks.

• 3. We conduct extensive experiments that show that our method reaches a flowtime close to the one reached by the classical heuristic and significantly reduces the rescheduling time.

This paper is a extended version of [2].

• 1. We generalize the notion of delegation to consider any bilateral reallocation (delegation or swap of several tasks).

• 2. We redefine the acceptability criterion of the bilateral reallocations in order to reduce the rescheduling time and the mean flowtime reached by our strategy.

• 3. We quantitatively compare the performance of our strategy with the performance of a DCOP resolution method.

After an overview of related works in Sect. 2, we formalize the multi-agent situated task allocation problem in Sect. 3. Section 4 describes the consumption/delegation operations and the negotiation process. Section 5 specifies how agents choose which tasks to negotiate and with whom. Our empirical evaluation is described in Sect. 6. Section 7 summarizes our contribution and future work.

2 Related Work

Table 1. Analysis grid of methods for task assignment (at top) or reassignment (at bottom).

Table 1 summarizes all the works discussed here according to our analysis grid. The left-hand side of the table shows the problems which are addressed, i.e. their ingredients (resources, tasks, workers and objectives). The right-hand side reveals the features of these methods and the techniques used. While the upper part of the table contains some classical task assignment methods, the lower part presents some dynamic and decentralized reassignment methods.

Scheduling theory [6] includes off-line methods for solving various problems of task assignment among workers. For instance, the Kuhn-Munkres algorithm, also called the Hungarian method, minimizes the total cost (denoted $\text {W}(\overrightarrow{\text {A}})$) for n tasks and n workers [13]. Shortest processing time first (SPT) is a very simple method that minimizes the flowtime of n single-worker tasks with one multi-task worker [8]. This result generalizes to the problem with m multi-task workers if the cost of tasks is identical from one worker to another (denoted $P_m$). The scheduling problem, which consists in minimizing the total delay (denoted $\text {C}(\overrightarrow{\text {A}})$) with m multi-task workers and n single-worker tasks whose costs depend on the worker (denoted $R_m$), can be formalized by a linear-program (LP). This problem reduces to a weighted matching problem in a bipartite graph with n tasks and $n \times m$ positions. This problem is polynomial [11]. Based on the Ford-Fulkerson algorithm, the complexity of the algorithm described by [5] is $\mathcal {O}(max(mn^2,n^3))$. These approaches are not suitable for task reassignment in distributed systems where decentralization and adaptability are required. Indeed, global control is a performance bottleneck, since it must constantly collect information about the state of the system. By contrast, our agents make local decisions on an existing allocation with the aim to improve the load-balancing. Moreover, classical scheduling problems are static. The inaccurate estimation of the task execution time and some disruptive phenomena (task consumption, job release, slowing down nodes, etc.) may require major modifications in the existing allocation to stay optimal. Furthermore, agents can operate in dynamic environments that change over time.

The multi-agent paradigm is particularly suitable for the design and implementation of distributed and adaptive mechanisms for the reassignment of tasks-workers [12]. The existing models differ due to the nature of the tasks and the agents, whether they represent workers or task requesters. Coalition formation is justified if a task requires more than one worker or if its cost decreases with the number of assigned workers. For instance, Shehory and Kraus propose decentralized, greedy and anytime algorithms for assigning multi-worker tasks with precedence constraints to some workers with heterogeneous capabilities/efficiencies [21]. Similarly to a coalition, a team aims at maximizing an overall objective function rather than the individual welfares. However, a team performs single-worker tasks. For instance, Lesser et al. propose a domain-independent coordination framework with a hierarchical task network representation for resource allocation and task assignment/scheduling [14]. The main objective of Generalized Partial Global Planning (GPGP) is the maximization of the combined utility accrued by the group of agents as a result of successful completion of its high-level goals. GPGP adopts a planning-oriented approach of coordination which assumes that the effort required for coordination (reasoning and communication) is negligible compared to the tasks execution time. Inspired by economic theories, the market-oriented approach models distributed planning problems as the search of an equilibrium for a non-cooperative game [23]. The agents delegate/swap tasks. Contrary to a team, a marketplace assumes that the constraints and objectives are fully distributed. Among the market-oriented methods, we distinguish three families.

DCOP. The reassignment problems can be formalized as Distributed Constraint Optimization Problems (DCOP). Many resolution methods have been developed for finding an optimal solution to a DCOP which is an NP-hard problem (see a recent survey [9]). The main difficulty in applying these methods for task reassignment lies in the representation of a real-world problem as a DCOP, or even several COP sub-problems, since it requires expertise in the resolution method (e.g. [15]).

CBBA. Consensus Based Bundle Algorithm [7] is a multi-agent assignment method that consists of: (a) selecting the negotiated tasks; (b) determining the winner of these negotiations. In the same line, Turner et al. study the continuous task assignment for a multi-robot team in order to maximise the throughput before running out of fuel [22]. Thanks to machine learning (ML), they propose a prediction mechanism that uses past experience to select which task allocation strategy yields the optimal global task allocation.

MARL. The reassignment problems can also be formalized as Markov decision processes [4], in particular Decentralized Partially Observed Markov Decision Process (Dec-POMDP). The optimization of a Dec-POMDP with a finite horizon is a NEXPTIME problem. Approximate resolution methods can only be applied to small problem instances, they do not scale up. Beyond these off-line planning methods, Multi-Agent Reinforcement Learning (MARL) requires a perfect knowledge of the environment and a learning phase [20].

Conversely, we consider neither generalizable predictive patterns nor prior model of the data/environment are available since it is not the case for the class of practical applications we are concerned with. For instance, Baert et al. have in [1] an egalitarian objective which is the minimization of the makespan (denoted $\text {C}_{max}(\overrightarrow{\text {A}})$). We consider here the problem of coordinating decisions between agents to find a globally optimal solution for a multi-objective function. Agents want to minimize the mean flowtime of several concurrent jobs, each consisting of several tasks.

This paper is a extended version of [2].

• 1. While our previous work only considers delegations of single task, we here generalize our formal framework to consider any bilateral reallocation (delegation or swap of several tasks) in order to reduce not only the mean flowtime but also the rescheduling time.

• 2. We here redefine the acceptability criterion of the bilateral reallocations by the agents. Previously, this criterion was based on the local flowtime, i.e. the flowtime restricted to the two contractors. Since this criterion does not guarantee the termination of the multi-agent reallocation algorithm, it was combined with the makespan, the maximum completion of all the jobs. In this paper, a bilateral reallocation is acceptable for an agent if, according to its beliefs, it reduces the global flowtime. This acceptability criterion is sufficient to guarantee the convergence of the reallocation process. Moreover, it allows to reduce the rescheduling time and the mean flowtime reached by our strategy.

• 3. We quantitatively compare the performance of our strategy with the performance of a DCOP resolution method.

3 Multi-agent Situated Task Allocation

In this section, we formalize the multi-agent situated task allocation problem with concurrent jobs.

We consider distributed jobs, each job being a set of independent, non divisible tasks without precedence order. Tasks are non preemptive, and the execution of each task requires resources which are distributed across different nodes. These resources are transferable and non consumable.

Definition 1 (Distributed System)

A system is a triple $\mathscr {D}= \langle \mathscr {N}, \mathscr {E}, \mathscr {R}\rangle$ where:

• $\mathscr {N}= \{ \nu _{1}, \ldots , \nu _{m} \}$ is a set of m nodes;

• $\mathscr {E}$ is an acquaintance relation, i.e. a binary and symmetric relation over $\mathscr {N}$;

• $\mathscr {R}= \{ \rho _{1}, \ldots , \rho _{k}\}$ is a set of k resources, each resource $\rho _{i}$ having a size $|\rho _{i}|$. The locations of the resources, which are possibly replicated, are determined by the function:

  $$\begin{aligned} l : \mathscr {R}\rightarrow 2^{\mathscr {N}} \end{aligned}$$

  (1)

For simplicity, we assume exactly one agent per node (the set of agents is $\mathscr {N}$), and any agent can access any resource.

Running a job (without a deadline) consists in a set of independent tasks which require resources to produce an outcome.

Definition 2 (Job/Task)

Let $\mathscr {D}$ be a distributed system and $\text {Res}$ be the space of outcomes. We consider the set of $\ell$ jobs $\mathscr {J}= \{ \text {J}_{1}, \ldots , \text {J}_{\ell } \}$. Each job $\text {J}_{i}$ is a set of $k_i$ tasks $\text {J}_{i} = \{ \tau _{1}, \ldots , \tau _{k_i} \}$ where each task $\tau _{}$ is a function which links a set of resources to an outcome: $\tau _{}: 2^{\mathscr {R}} \mapsto \text {Res}$.

It is worth noticing that we consider in this paper a set of jobs having the same release date. $\mathscr {T}= \bigcup _{1 \le i \le \ell } \text {J}_{i}$ denotes the set of the n tasks of $\mathscr {J}$ and $\mathscr {R}_{\tau _{}} \subseteq \mathscr {R}$ is the set of the resources required for the task $\tau _{}$. The job containing the task $\tau _{}$ is written $\text {job}(\tau _{})$.

Each task has a cost for a node, which is its estimated execution time by this node. As the fetching time of resources is supposed to be significant, the cost function must verify that the task $\tau _{}$ is cheaper for $\nu _{i}$ than for $\nu _{j}$ if the required resources are “more local” to $\nu _{i}$ than to $\nu _{j}$:

Property 1 (Cost)

Let $\mathscr {D}$ a distributed system and $\mathscr {T}$ a set of tasks. The cost function $c: \mathscr {T}\times \mathscr {N}\mapsto \mathbb {R}^*_+$ is such that:

$$\begin{aligned}&\text {c}(\tau _{},\nu _{i}) \le \text {c}(\tau _{},\nu _{j}) \Leftrightarrow \\&\Sigma _{\rho _{} \in \mathscr {R}_{\tau _{}}, \nu _{i} \in l(\rho _{})} | \rho _{} | > \Sigma _{\rho _{} \in \mathscr {R}_{\tau _{}}, \nu _{j} \in l(\rho _{})} | \rho _{} | \nonumber \end{aligned}$$

(2)

The cost function can be extended to a set of tasks:

$$\begin{aligned} \forall \mathrm {T}\subseteq \mathscr {T},~ \text {c}(\mathrm {T},\nu _{i}) = \Sigma _{\tau _{} \in \mathrm {T}} \text {c}(\tau _{},\nu _{i}) \end{aligned}$$

(3)

Note that in practice, it is difficult to design this function with a good estimation of the runtime. However the adaptability of our multi-agent system compensates for a poor estimation of the cost function. It is one of the benefits of our approach.

A multi-agent situated task allocation problem with concurrent jobs consists in assigning several jobs to some nodes according to their costs.

Definition 3 (MASTA+)

A multi-agent situated task allocation problem with concurrent jobs is a quadruple $\text {MASTA+}= \langle \mathscr {D}, \mathscr {T}, \mathscr {J}, c \rangle$ where:

• $\mathscr {D}$ is a distributed system with m nodes;

• $\mathscr {T}= \{ \tau _{1}, \ldots , \tau _{n} \}$ is a set of n tasks;

• $\mathscr {J}= \{ \text {J}_{1}, \ldots , \text {J}_{\ell } \}$ is a partition of $\mathscr {T}$ into $\ell$ jobs;

• $c: \mathscr {T}\times \mathscr {N}\mapsto \mathbb {R}^*_+$ is the cost function.

A task allocation is an assignation of sorted bundles to different nodes.

Definition 4 (Allocation)

Let $\text {MASTA+}$ be a task allocation problem. An allocation $\overrightarrow{\text {A}}$ is a vector of m sorted task bundles $((\text {B}_{1}, \prec _{1}), \ldots , (\text {B}_{m},\prec _{m}))$. Each bundle $(\text {B}_{i},\prec _{i})$ is the set of tasks ($\text {B}_{i} \subseteq \mathscr {T}$) assigned to the node $\nu _{i}$ associated with a scheduling order, i.e. a strict and total order ($\prec _{i} \subseteq \mathscr {T}\times \mathscr {T}$) such that $\tau _{j} \prec _{i} \tau _{k}$ means that if $\tau _{j}, \tau _{k} \in \text {B}_{i}$ then $\tau _{j}$ is performed before $\tau _{k}$ by $\nu _{i}$.

The allocation $\overrightarrow{\text {A}}$ is such that:

$$\begin{aligned} \forall \tau _{} \in \mathscr {T},~ \exists \nu _{i} \in \mathscr {N},~ \tau _{} \in \text {B}_{i}\end{aligned}$$

(4)

$$\begin{aligned} \forall \nu _{i} \in \mathscr {N}, \forall \nu _{j} \in \mathscr {N}\setminus \{ \nu _{i} \},~ \text {B}_{i} \cap \text {B}_{j} = \varnothing \end{aligned}$$

(5)

The set $\mathscr {T}$ is partitioned by an allocation: all the tasks are assigned (Eq. 4) and each task is assigned to a single node (Eq. 5). To simplify, we use the following notations:

• $\overrightarrow{\text {B}}_{i} = (\text {B}_{i}, \prec _{i})$, the sorted bundle of $\nu _{i}$;

• $\min _{\prec _{i}} \text {B}_{i}$, the next task to perform by $\nu _{i}$:

• $\text {jobs}({\text {B}_{i}})$, the set of jobs assigned to $\nu _{i}$, i.e. such that at least one task is in $\text {B}_{i}$;

• $\text {node}({\tau _{}},{\overrightarrow{\text {A}}})$, the node whose bundle contains $\tau _{}$ in $\overrightarrow{\text {A}}$;

• $\text {w}_{i}(\overrightarrow{\text {A}}) = \text {c}(\text {B}_{i},\nu _{i}) = \Sigma _{\tau _{} \in \text {B}_{i}} \text {c}(\tau _{},\nu _{i})$, the workload of $\nu _{i}$ for $\overrightarrow{\text {A}}$.

We assume that nodes are never idle, so the completion time of a task is its delay before the task is started, plus its estimated execution time:

$$\begin{aligned} \text {C}_{\tau _{}}(\overrightarrow{\text {A}})= \text {t}(\tau _{},\text {node}({\tau _{}},{\overrightarrow{\text {A}}})) + \text {c}(\tau _{},\text {node}({\tau _{}},{\overrightarrow{\text {A}}}))\\ \text {with } \text {t}(\tau _{},\nu _{i})= \Sigma _{ \tau _{}' \in \text {B}_{i} \mid \tau _{}' \prec _{i} \tau _{}} \text {c}(\tau _{}',\nu _{i})\nonumber \end{aligned}$$

(6)

Unlike the cost, the delay (so the completion time) depends on the scheduling order over the bundle.

The quality of an allocation is measured by the mean flowtime for all the jobs, where the flowtime of one job is its completion time. The makespan is the time necessary to perform all the jobs. Then, the makespan is the maximum completion time of the jobs and also the maximum workload of the nodes.

Definition 5 (Flowtime/Makespan)

Let $\text {MASTA+}$ a task allocation problem and $\overrightarrow{\text {A}}$ an allocation. We define:

• the completion time of $\text {J}_{} \in \mathscr {J}$ for $\overrightarrow{\text {A}}$,

  $$\begin{aligned} \text {C}_{\text {J}_{}}(\overrightarrow{\text {A}})= \max _{\tau _{} \in \text {J}_{}} \{ \text {C}_{\tau _{}}(\overrightarrow{\text {A}})\} \end{aligned}$$

  (7)

• the (mean) flowtime of $\mathscr {J}$ for $\overrightarrow{\text {A}}$,

  $$\begin{aligned} \text {C}_{mean}(\overrightarrow{\text {A}}) = \frac{1}{\ell } \text {C}(\overrightarrow{\text {A}}) \text { with } \text {C}(\overrightarrow{\text {A}}) = \Sigma _{\text {J}_{} \in \mathscr {J}} \text {C}_{\text {J}_{}}(\overrightarrow{\text {A}})\end{aligned}$$

  (8)

• the makespan of $\mathscr {J}$ for $\overrightarrow{\text {A}}$,

  $$\begin{aligned} \text {C}_{max}(\overrightarrow{\text {A}}) = \max _{\nu _{i} \in \mathscr {N}} \{ \text {w}_{i}(\overrightarrow{\text {A}}) \} \end{aligned}$$

  (9)

• the local availability ratio of $\overrightarrow{\text {A}}$,

  $$\begin{aligned} \text {L}(\overrightarrow{\text {A}}) = \Sigma _{\tau _{} \in \mathscr {T}} \frac{\Sigma _{\rho _{} \in \mathscr {R}_{\tau _{}},~\text {node}({\tau _{}},{\overrightarrow{\text {A}}}) \in l(\rho _{})} | \rho _{}|}{\Sigma _{\rho _{} \in \mathscr {R}_{\tau _{}}} | \rho _{}|} \end{aligned}$$

  (10)

Unlike the makespan, the flowtime depends on the scheduling order. The local availability ratio of $\overrightarrow{\text {A}}$ measures the proportion of locally processed resources (Eq. 10).

Table 2. Cost function.

Fig. 1.

Resource distribution and task allocation for Example 1.

Example 1

($\text {MASTA+}$). From the distributed system $\mathscr {D}= \langle \mathscr {N}, \mathscr {E}, \mathscr {R}\rangle$ with $\mathscr {N}=\{\nu _{1},\nu _{2},\nu _{3}\}$, $\mathscr {E}= \{ (\nu _{1}, \nu _{2}), (\nu _{1}, \nu _{3}), (\nu _{2}, \nu _{3}) \}$ and $\mathscr {R}= \{ \rho _{1}, \ldots , \rho _{9}\}$ where resources are replicated on 2 nodes (cf. Fig. 1a), we consider $\text {MASTA+}= \langle \mathscr {D}, \mathscr {T}, \mathscr {J},c \rangle$ with $\mathscr {T}= \{ \tau _{1}, \ldots , \tau _{9} \}$ where each task $\tau _{i}$ needs resource $\rho _{i}$, $\mathscr {J}= \{ \text {J}_{1}, \text {J}_{2}, \text {J}_{3}\}$ such that $\text {J}_{1} = \{ \tau _{1}, \tau _{2}, \tau _{3}\}$, $\text {J}_{2} = \{ \tau _{4}, \tau _{5}, \tau _{6}\}$ and $\text {J}_{3} = \{ \tau _{7}, \tau _{8}, \tau _{9}\}$ and c is the cost function given in Table 2. We assume the cost of a task is proportional to the resources size, and two times greater if the resource is distant. We consider here the allocation $\overrightarrow{\text {A}}$ (see Fig. 1b) with $\overrightarrow{\text {B}}_{1} = (\tau _{5}, \tau _{8}, \tau _{3}, \tau _{2})$, $\overrightarrow{\text {B}}_{2} = (\tau _{4}, \tau _{9})$ and $\overrightarrow{\text {B}}_{3} = (\tau _{7}, \tau _{1}, \tau _{6})$. The makespan and the flowtime are $\text {C}_{max}(\overrightarrow{\text {A}})=12$ and $\text {C}(\overrightarrow{\text {A}})=8+12+12 = 32$.

To conclude this section, due to the locality of resources, a task has not the same cost for every nodes. In this paper, our objective is to minimize the mean flowtime, for a set of concurrent jobs composed of many tasks.

4 Consumption and Reallocation

We describe in this section the operations of consumption and reallocation as well as the negotiation protocol.

A task consumption is the removal by a node of a task from its bundle in order to process it. This operation modifies not only the current allocation but also the underlying $\text {MASTA+}$ problem since the consumed task is no longer present. The consumption strategy adopted by an agent specifies the tasks scheduling for the node it is in charge of. Since we aim at minimizing the mean flowtime of the jobs, we consider here a job-oriented strategy which sorts first jobs and then the tasks inside the same job (the tasks of a same job are consecutive in the bundle). More precisely, the less expensive jobs are prior on the most expensive ones in order to minimize locally the completion time of the jobs. Thereafter, means that the tasks in $\text {J}_{1}$ are prior to the tasks in $\text {J}_{2}$. $\tau _{1} \lhd _{i} \tau _{2}$ means that the task $\tau _{1}$ is prior to the task $\tau _{2}$. Formally,

(11)

The addition/removal of a list of tasks $\mathrm {T}$ in the bundle $\overrightarrow{\text {B}}_{i}$ of the node $\nu _{i}$ may modify the tasks execution order since these operations imply a rescheduling of the bundle:

• $\overrightarrow{\text {B}_{i} \oplus \mathrm {T}}$ denotes the bundle containing the set of tasks $\text {B}_{i} \cup \mathrm {T}$ sorted with $\prec _{i}$;

• $\overrightarrow{\text {B}_{i} \ominus \mathrm {T}}$ denotes the bundle containing $\text {B}_{i} \setminus \mathrm {T}$ sorted with $\prec _{i}$.

• $\overrightarrow{\text {B}_{i} \ominus \mathrm {T}_1 \oplus \mathrm {T}_2}$ denotes the bundle containing $\text {B}_{i} \setminus \mathrm {T}_1 \cup \mathrm {T}_2$ sorted with $\prec _{i}$.

A bilateral reallocation is an operation which modifies the current allocation by exchanging one or several tasks between two agents.

Definition 6 (Bilateral Reallocation)

Let $\text {MASTA+}= \langle \mathscr {D}, \mathscr {T}, \mathscr {J}, c \rangle$ be an allocation problem and $\overrightarrow{\text {A}}= (\overrightarrow{\text {B}}_{1}, \ldots ,\overrightarrow{\text {B}}_{m})$ an allocation. The bilateral reallocation of the non-empty list of tasks $\mathrm {T}_{1}$ assigned to the proposer $\nu _{i}$ in exchange for the list of tasks $\mathrm {T}_{2}$ assigned to the responder $\nu _{j}$ in $\overrightarrow{\text {A}}$ ($\mathrm {T}_1 \subseteq \text {B}_{i}$ and $\mathrm {T}_2 \subseteq \text {B}_{j}$) leads to the allocation $\gamma (\mathrm {T}_1, \mathrm {T}_2, \nu _{i}, \nu _{j}, \overrightarrow{\text {A}})$ with m bundles $\gamma (\mathrm {T}_1, \mathrm {T}_2, \nu _{i}, \nu _{j}, \overrightarrow{\text {B}}_{k})$ such that:

$$\begin{aligned} \gamma (\mathrm {T}_{1}, \mathrm {T}_{2}, \nu _{i}, \nu _{j}, \overrightarrow{\text {B}}_{k}) =&{\left\{ \begin{array}{ll} \overrightarrow{\text {B}_{i} \ominus \mathrm {T}_{1} \oplus \mathrm {T}_{2}} &{} \text { if } k = i, \\ \overrightarrow{\text {B}_{j} \ominus \mathrm {T}_{2} \oplus \mathrm {T}_{1}} &{} \text { if } k = j, \\ \overrightarrow{\text {B}}_{k} &{} \text {otherwise} \\ \end{array}\right. } \end{aligned}$$

(12)

We distinguish two cases:

• a swap where the two lists of tasks are non-empty ($\mathrm {T}_{1} \ne \varnothing \wedge \mathrm {T}_{2} \ne \varnothing$), denoted $\sigma (\mathrm {T}_{1}, \mathrm {T}_{2}, \nu _{i}, \nu _{j}, \overrightarrow{\text {A}})$;

• a delegation where an agent gives a part of its tasks to one of its peers without counterpart ($\mathrm {T}_{2}= \varnothing$), denoted $\delta (\mathrm {T}_1, \nu _{i}, \nu _{j}, \overrightarrow{\text {A}})$. If $|\mathrm {T}_1|=1$, this is an unary delegation. Otherwise, this is an n -ary delegation.

We will see later that the bilateral reallocation of lists of tasks rather than sets allows to specify the order in which the tasks should be evaluated to validate the interest of all or part of the transaction.

In order to improve an allocation, we introduce the notion of socially rational bilateral reallocation which verifies if a reallocation reduces the global flowtime, i.e. the completion time of the jobs for all nodes.

Definition 7 (Socially Rational Bilateral Reallocation)

Let $\text {MASTA+}= \langle \mathscr {D}, \mathscr {T}, \mathscr {J}, c \rangle$ be an allocation problem, $\overrightarrow{\text {A}}$ an allocation. The bilateral reallocation $\gamma (\mathrm {T}_{1}, \mathrm {T}_{2}, \nu _{i}, \nu _{j}, \overrightarrow{\text {A}})$ is socially rational with respect to the flowtime if and only if the global flowtime decreases,

$$\begin{aligned}&\text {C}(\gamma (\mathrm {T}_1, \mathrm {T}_2, \nu _{i}, \nu _{j}, \overrightarrow{\text {A}})) < \text {C}(\overrightarrow{\text {A}}) \end{aligned}$$

(13)

An allocation is stable if there is no socially rational bilateral delegation.

Contrary to [2], we do not consider as socially rational the reallocations reducing the local flowtime (the completion time of jobs restricted to the nodes implied in the reallocation) which does not guarantee the convergence of the reallocation process, nor even the reallocations reducing the local flowtime and the makespan (the maximum workload of the agents). The reduction of the global flowtime guarantees the termination of the process. Hereafter, when it comes to flowtime, it will be, unless specified, the global flowtime (denoted $\text {C}(\overrightarrow{\text {A}})$ defined in Eq. 8).

Property 2 (Termination)

Let $\text {MASTA+}= \langle \mathscr {D}, \mathscr {T}, \mathscr {J}, c \rangle$ be an allocation problem and $\overrightarrow{\text {A}}$ a non-stable allocation with respect to the flowtime. There exists a finite path of socially rational bilateral reallocations with respect to the flowtime which leads to a stable allocation for this criterion.

Proof

Let $\text {MASTA+}= \langle \mathscr {D}, \mathscr {T}, \mathscr {J}, c \rangle$ be an allocation problem and $\overrightarrow{\text {A}}$ a non-stable allocation with respect to the flowtime. Let $\gamma$ be a socially rational reallocation which leads to the allocation $\overrightarrow{\text {A}}'$ from $\overrightarrow{\text {A}}$. Since $\gamma$ is socially rational with respect to the flowtime, the flowtime strictly decreases. Formally, . Since there is a finite number of allocations and $\Sigma _{\text {J}_{\in }\mathscr {J}} \text {C}_{\text {J}_{}}(\overrightarrow{\text {A}})$ strictly decreases at each step, there can only be a finite number of such allocations.

For tasks reallocation, the agents are involved in multiple bilateral single-round negotiation. Each negotiation is based on the alternating offers protocol [18] and includes three decision steps: (a) the offer strategy of the proposer which selects a delegation, i.e. a list of tasks in its bundle and a responder, (b) the counter-offer strategy which allows the responder to determine whether it declines, accepts or makes a counter-offer to the delegation, and (c) the eventual reallocation is confirmed or withdrawn by the proposer according to the consumptions that happen concurrently (cf. Fig. 2).

Fig. 2.

Bilateral negotiation protocol between a proposer and a responder.

Fig. 3.

Allocations of the first example resulting from bilateral reallocations.

Example 2 (Consumption and Reallocation)

Let us consider the problem $\text {MASTA+}$ from the Example 1 and the allocation $\overrightarrow{\text {A}}$ in Fig. 1b. According to the consumption strategy adopted by the agents, each bundle is sorted. The less expensive jobs are prior (e.g. ). In case of a tie, the natural order over the identifiers ensures a strict and total order (e.g. ). The tasks among a same job are sorted by increasing cost ($\tau _{3} \lhd _{1} \tau _{2}$). The delegation of the task $\tau _{9}$ by the node $\nu _{2}$ to the node $\nu _{1}$ leads to the allocation $\overrightarrow{\text {A}}' =\delta ([\tau _{9}], \nu _{2}, \nu _{1}, \overrightarrow{\text {A}})$. This delegation (cf. Fig. 3a) is socially rational since it decreases the flowtime from 32 to 31. The swap of $\tau _{9} \in \text {B}_{2}$ and $\tau _{5} \in \text {B}_{1}$ between the nodes $\nu _{2}$ and $\nu _{1}$ leads to the allocation $\overrightarrow{\text {A}}''= \sigma ([\tau _{9}], [\tau _{5}], \nu _{2}, \nu _{1}, \overrightarrow{\text {A}})$. This swap (cf. Fig. 3b) decreases the flowtime from 32 to 29.

5 Negotiation Strategy

We describe in this section the different parts of the negotiation strategy and we sketch the agent behaviour in the negotiation process.

5.1 Peer Modelling

The peer modelling is built upon exchanged information through messages between the agents. Before the negotiation process and between each bilateral reallocation it is implied in, the agent $\nu _{i}$ informs its peers about the cost of each job $\text {J}_{}$ for it ($\text {c}(\text {J}_{,}\nu _{i})$). Since the number of jobs is negligible compared to the number of tasks, the messages size is insignificant compared to the bundle descriptions. The modelling for the target $\nu _{k}$ by the subject $\nu _{i}$ is based on:

• 1. the belief base of the subject, possibly partial or obsolete, which contains the beliefs about the costs of the jobs for $\nu _{k}$ ($\text {c}^{i}(\text {J}_{},\nu _{k}),~\forall \text {J}_{} \in \mathscr {J}$) and so the beliefs about the workload of $\nu _{k}$ ($\text {w}^{i}_{k}(\overrightarrow{\text {A}}) = \Sigma _{\text {J}_{} \in \mathscr {J}} \text {c}^{i}(\text {J}_{},\nu _{k})$);

• 2. the consumption strategy of the target assumed by the subject, written .

The subject can then deduce:

• the completion time ($\text {C}^{~i}_{\text {J}_{}}(\overrightarrow{\text {B}}_{k})$) of the job $\text {J}_{}$ for a target k, possibly itself ($\nu _{k}=\nu _{i}$), after the addition ($\text {C}^{~i}_{\text {J}_{}}( \overrightarrow{\text {B}_{k} \oplus \mathrm {T}} )$), the removal ($\text {C}^{~i}_{\text {J}_{}}(\overrightarrow{\text {B}_{k} \ominus \mathrm {T}})$) and the replacing of tasks ($\text {C}^{~i}_{\text {J}_{}}(\overrightarrow{\text {B}_{k} \ominus \mathrm {T}_{1} \oplus \mathrm {T}_{2}})$);

• the completion time of a job $\text {J}_{}$ for the allocation,

  

  (14)

• the bottleneck node for each job $\text {J}_{}$, denoted $\nu _{\text {max}}^{i}(\overrightarrow{\text {A}}, \text {J}_{})$, i.e. the node $\nu _{k}$ for which the completion time of this job is the maximum completion time in the allocation,

  $$\begin{aligned} \text {C}^{~i}_{\text {J}_{}}(\overrightarrow{\text {B}}_{k})=\text {C}^{~i}_{\text {J}_{}}(\overrightarrow{\text {A}}) \end{aligned}$$

  (15)

• the flowtime of the allocation $\overrightarrow{\text {A}}$

  $$\begin{aligned} \text {C}^{~i}(\overrightarrow{\text {A}}) = \Sigma _{\text {J}_{} \in \mathscr {J}} \text {C}^{~i}_{\text {J}_{}}(\overrightarrow{\text {A}}) \end{aligned}$$

  (16)

5.2 Acceptability Rule

The acceptability rule is a local decision made by an agent which is implied in a bilateral reallocation. This rule, which is based on the agent knowledge and the peer modelling, decides to accept or decline a reallocation.

Definition 8 (Acceptability)

Let $\text {MASTA+}= \langle \mathscr {D}, \mathscr {T}, \mathscr {J}, c \rangle$ be a problem and $\overrightarrow{\text {A}}$ an allocation. The bilateral reallocation $\gamma (\mathrm {T}_{1}, \mathrm {T}_{2}, \nu _{i}, \nu _{j}, \overrightarrow{\text {A}})$ is acceptable by the agent $\nu _{k} \in \mathscr {N}$ with respect to the flowtime if an only if the agent believes that the flowtime decreases,

$$\begin{aligned} {\begin{matrix} \Sigma _{\text {J}_{} \in \mathscr {J}} \max _{\forall \nu _{o} \in \mathscr {N}\setminus \{\nu _{i}, \nu _{j} \}} ( \text {C}^{~k}_{\text {J}_{}}(\overrightarrow{\text {B}_{i} \ominus \mathrm {T}_1 \oplus \mathrm {T}_2}), \text {C}^{~k}_{\text {J}_{}}(\overrightarrow{\text {B}_{j} \ominus \mathrm {T}_2 \oplus \mathrm {T}_1}), \text {C}^{~k}_{\text {J}_{}}(\text {B}_{o}) )< \text {C}^{~k}(\overrightarrow{\text {A}}) \end{matrix}} \end{aligned}$$

(17)

The acceptability with respect to the flowtime is based on the beliefs about the completion time of the jobs for all the nodes before and after the reallocation (Eq. 17).

We propose in this paper a process where the agents trigger concurrent bilateral negotiations leading to socially rational reallocations.

5.3 Offer Strategy

The offer strategy of an agent, which is based on its knowledge, its beliefs and its peer modelling, identifies a delegation in three steps. An agent $\nu _{i}$ selects an offer bundle, i.e. a list of tasks to delegate to a responder in a set $\mathscr {N}'$ in order to reduce the completion time of a job in a set $\mathscr {J}'$ for which it is a bottleneck. Initially, $\mathscr {J}'=\mathscr {J}$, $\mathscr {N}'=\mathscr {N}$.

1. Job Selection. In order to reduce not only the completion time of a job but also the completion time of the next jobs in its bundle, our heuristic selects the most prior job $\text {J}_{*}$ for which it is a bottleneck,

(18)

2. Responder Selection. The jobs of a responder that are impacted by the delegation are those after $\text {J}_{*}$ according to . Not to increase the completion time of these jobs, our heuristic selects a responder $\nu _{*}$ for whom the sum of the differences between the completion time for the allocation and the completion time for the agent is the greatest one,

(19)

where random is a random choice function which selects a node from any set of nodes.

3. Offer Bundle Selection. To determine the offer bundle, we distinguish a strategy which selects a single task as in [2] and a strategy which selects several tasks.

3.a. Unary Delegation Selection. In order to reduce the completion time of $\text {J}_{*}$, the proposer selects a distant task, i.e. a task whose delegation will reduce its cost. Our heuristic selects the task in the job $\text {J}_{*}$ or in the prior jobs in $\overrightarrow{\text {B}}_{i}$ with the best payoff in terms of cost. In case of a tie, the prior task is chosen,

The delegation $\delta ([\tau _{*}], \nu _{i}, \nu _{*}, \overrightarrow{\text {A}})$ is triggered if it is acceptable for the proposer (cf Definition 8).

3.b. N -ary Delegation Selection. The proposer iteratively builds an offer bundle $\mathrm {T}_*$. This bundle is a stack of tasks that will be evaluated by the acceptability strategy of the responder in order to accept all or part of this bundle by unstacking it (cf. Sect. 5.4). As illustrated in Algorithm 1, our heuristic considers the tasks in $\text {J}_{*}$ or in the prior jobs in $\overrightarrow{\text {B}}_{i}$ (line 2). The proposer $\nu _{i}$ selects in priority the distant tasks, i.e. the tasks whose delegation will reduce at most the processing time (lines 3 and 6). According to this ratchet algorithm, the flowtime strictly decreases during the building of the offer bundle (line 8). Moreover, the algorithm stops as soon as a task does not improve the flowtime. If the offer bundle $\mathrm {T}_*$ is non-empty, the delegation $\delta (\mathrm {T}_{*}, \nu _{i}, \nu _{*}, \overrightarrow{\text {A}})$, which is acceptable for the initiator, is triggered.

Whatever the offer bundle selection strategy is (3.a or 3.b), if no delegation is triggered, the offer strategy returns to step #2 to choose another responder ($\mathscr {N}' \leftarrow \mathscr {N}' \setminus \{ \nu _{*} \}$). Otherwise, the offer strategy returns to step #1 to choose another job ($\mathscr {J}' \leftarrow \mathscr {J}' \setminus \{ \text {J}_{*} \}$). In case of failure, no delegation is proposed and the agent goes into pause state until its belief base is updated and a new opportunity (i.e. a delegation) is found.

5.4 Acceptation Strategy

According to the acceptation strategy, the responder accepts a delegation which is acceptable for it. Otherwise, it unstacks one by one the tasks in the offer bundle $\mathrm {T}_*$ (cf. Algorithm 2) for possibly accepting a part of it. When the sub-bundle $\mathrm {T}_{acc}$ is empty, the responder declines the offer.

5.5 Agent Behaviour

In our approach, a reallocation is the outcome of the negotiation process between agents adopting the same behaviour. The agent behaviour is specified in [3] by a deterministic finite state automaton¹. An agent executes its behaviour according to its knowledge and its beliefs. In order to avoid deadlock, the proposals are associated with deadlines. The agent’s belief base is updated by the reception of messages. None proposal is sent if the agent believes that the allocation is stable.

Example 3 (Negotiation Strategy)

Let us consider the $\text {MASTA+}$ problem from Example 1 and the initial allocation $\overrightarrow{\text {A}}$ (cf. Fig. 4a) such that $\overrightarrow{\text {B}}_{1} = (\tau _{5}, \tau _{1})$, $\overrightarrow{\text {B}}_{2} = (\tau _{3}, \tau _{2}, \tau _{7}, \tau _{8}, \tau _{9})$ and $\overrightarrow{\text {B}}_{3} = (\tau _{4}, \tau _{6})$. The flowtime is $\text {C}(\overrightarrow{\text {A}})=7+9+17 = 33$. We consider that the belief bases are up-to-date. The offer strategy of the agent $\nu _{2}$ selects a delegation as follows:

• 1. it selects the most prior job for which it is a bottleneck (cf. Eq. 18), $\text {J}_{*} = \text {J}_{3}$;

• 2. it selects an agent which is the least bottleneck for the job $\text {J}_{3}$ (cf. Eq. 19). As neither $\nu _{1}$ nor $\nu _{3}$ have tasks from $\text {J}_{3}$, the agent $\nu _{2}$ randomly chooses, $\nu _{*} = \nu _{1}$;

• 3. The Algorithm 1 allows the agent $\nu _{2}$ to select its offer bundle:

  • 1. the candidate tasks, i.e. the tasks in $\text {J}_{3}$ or the previous ones in its bundle, are sorted by decreasing payoff, $\mathrm {T}' = [\tau _{9}, \tau _{3}, \tau _{2}, \tau _{8}, \tau _{7}]$;

  • 2. the delegation of the task $\tau _{9}$ improves the flowtime (cf. Fig. 4b),

    $$\begin{aligned} \text {C}^{~2}(\delta ([\tau _{9}], \nu _{2}, \nu _{1}, \overrightarrow{\text {A}})) = 11 + 9 + 9 = 29 < 33 \end{aligned}$$

    (20)

    The task $\tau _{9}$ is added to the offer bundle, $\mathrm {T}_* = [\tau _{9}]$,

  • 3. the delegation of the tasks $\tau _{3}$ and $\tau _{9}$ improves the flowtime (cf. Fig. 4c),

    $$\begin{aligned} \text {C}^{~2}(\delta ([\tau _{9},\tau _{3}], \nu _{2}, \nu _{1}, \overrightarrow{\text {A}})) = 12 + 9 + 7 = 28 < 29 \end{aligned}$$

    (21)

    The task $\tau _{3}$ is added to the offer bundle, $\mathrm {T}_* = [\tau _{9}, \tau _{3}]$,

  • 4. The delegation of the tasks $\tau _{2}$, $\tau _{3}$ and $\tau _{9}$ does not improve the flowtime (cf. Fig. 4c),

    $$\begin{aligned} \text {C}^{~2}(\delta ([\tau _{9}, \tau _{3}, \tau _{2}], \nu _{2}, \nu _{1}, \overrightarrow{\text {A}})) = 15 + 9 + 6 = 30 > 28 \end{aligned}$$

    (22)

    The selected offer bundle is $\mathrm {T}_* = [\tau _{9}, \tau _{3}]$.

In summary, the agent $\nu _{2}$ proposes the delegation $\delta ([\tau _{9},\tau _{3}], \nu _{2}, \nu _{1}, \overrightarrow{\text {A}})$ to the agent $\nu _{1}$.

Fig. 4.

Allocations from Example 3.

6 Results and Discussion

After having presented the experimental context, we empirically compare our approach with a classic heuristic and with a distributed constraint optimization (DCOP) resolution method. Moreover, we consider our new acceptability criterion and n-ary delegation.

6.1 Context of Experiments

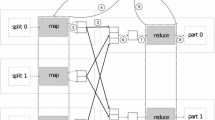
The practical application we consider is the distributed deployment of the MapReduce design pattern in order to process large datasets on a cluster, as with Spark [24]. We focus here on the Reduce stage of MapReduce jobs. This can be formalized by a $\text {MASTA+}$ problem where several jobs are concurrently submitted and the cost function is s.t.:

$$\begin{aligned} {\begin{matrix} c_i(\tau _{}, \nu _{j})=\sum \limits _{\rho _{j} \in \mathscr {R}_{\tau _{}}} c_i(\rho _{j},\nu _{j})\\ \text {with}\ c_i(\rho _{j},\nu _{i})={\left\{ \begin{array}{ll} |\rho _{j}| \text { if } \nu _{i} \in l(\rho _{j}) \\ \kappa \times |\rho _{j}| \text { else} \end{array}\right. } \end{matrix}} \end{aligned}$$

(23)

where we empirically calibrate $\kappa =2$ as a realistic value to capture the overhead due to remote resource fetching.

Our prototype [3] is implemented with the programming language Scala and Akka [16] for highly concurrent, distributed, and resilient message-driven applications. We assume that: (a) the message transmission delay is arbitrary but not negligible, (b) the message order per sender-receiver pair is preserved, and (c) the delivery of messages is guaranteed. Experiments have been conducted on a blade with 20 CPUs and 512Go RAM.

This work is a first step for evaluating our strategies. Indeed we compare the reallocation process, i.e. a $\text {MASTA+}$ problem solving, without considering the iterations induced by task consumptions, even if the task consumption strategy is required to sort the agent’s task bundle. We consider $\text {MASTA+}$ problem instance such that $m \in [2; 16]$ nodes/agents, $\ell = 4$ jobs, $n = 3 \times \ell \times m$ tasks, with one resource per task. Each resource $\rho _{i}$ is replicated 3 times and $|\rho _{i}| \in [0;100]$. We generate 10 $\text {MASTA+}$ problem instances, and for each we randomly generate 10 initial allocations. We assess the medians and the standard deviations of three metrics: (1) the mean flowtime (Eq. 8), (2) the local availability ratio (Eq. 10), and (3) the rescheduling time.

6.2 Classical Heuristic and Acceptability Criterion

The hypothesis we want to test are: (1) the flowtime reached by our strategy is close to the one reached by the classical approach and (2) the decentralization significantly reduces the scheduling time. Moreover, unlike our previous work [2] where we used the local flowtime and the makespan in our acceptability criterion, here, we only consider the global flowtime which is sufficient to ensure the negotiation process convergence. We also want to verify that the acceptability criterion allows to significantly improve the quality of the outcome.

Fig. 5.

The flowtime and the rescheduling time of our strategy, the strategy in [2] and an hill climbing algorithm.

Figures 5a and 5b respectively compare the flowtime and rescheduling time of our unary delegation strategy with the strategy presented in [2] and an hill climbing algorithm. These three algorithms start with the same random initial allocation. At each step, the hill climbing algorithm selects among all the possible delegations, the one which minimizes the flowtime.

In Fig. 5a, we observe that, while the quality of the solution reached by the strategy proposed in [2] is slightly lower than the one reached with the hill climbing algorithm, our strategy now reaches similar solutions. This is due to the fact that a socially rational reallocation according to the global flowtime can only decrease the flowtime, while it is not the case when the local flowtime is used. Moreover, since the acceptability criterion is no more based on the makespan, the number of possible delegations, which can improve the flowtime, increases.

Figure 5b shows that the rescheduling time of our new strategy remains approximately the same as the former one. Then, it is much better than the rescheduling time of the hill climbing algorithm which exponentially grows with the number of nodes. Thus, the acceptability criterion we proposed in this article significantly improves the flowtime with a similar rescheduling time. It is worth noticing that the hill climbing algorithm has been used with small $\text {MASTA+}$ instances due to its prohibitive scheduling time. One can expect to obtain a greater rescheduling time with a local search method, such as simulated annealing, with no guarantee to have a more qualitative outcome. As a result, even if the number of agents is small, the gain realized on the flowtime by the hill climbing algorithm will be penalized and cancelled by the overhead of its scheduling time. This overhead penalized the time-extented assignment in a distributed system which should be adaptive to disruptive phenomena (task consumption, job release, slowing down nodes).

Fig. 6.

Local availability ratio of the initial allocation, the allocations reached by our strategy, by the strategy proposed in [2], and by the hill climbing algorithm.

Fig. 7.

Rescheduling time of our strategy with one or more threads compared with the rescheduling time of the hill climbing algorithm

Figure 6 compares the local availability ratio of the initial allocation, the allocations reached by our strategy, by the strategy proposed in [2] and by the hill climbing algorithm. We observe that the availability ratios obtained with our strategies or with the hill climbing algorithm are close. Even if, unlike the latter, our strategy does not consider all the possible unary delegations, it turns out to be efficient by selecting the remote tasks whose delegation decreases the cost.

Figure 7 compares the rescheduling time of our strategy with one or more threads and the rescheduling time of the hill climbing algorithm. Since our multi-thread strategy run on several cores, we observe that the speedup increases with the number of agents. By example, with a similar flowtime (if the observable non determinism of the executions is neglected), the multi-thread version is 10 times faster than the mono-thread version for 16 agents.

6.3 N-Ary Delegation

Here, we want to verify that the n-ary delegations allow to reduce the flowtime.

Fig. 8.

Flowtime and rescheduling time for our unary strategy and our n-ary strategy.

Figures 8a and 8b respectively compare the flowtime and rescheduling time for our unary strategy with our n-ary strategy. We observe that, if the flowtime of our n-ary delegation is slightly not as good as than the one of the unary delegation strategy, the gain in terms of rescheduling time gain is much more beneficial.

Fig. 9.

Flowtime of the unary (left) and n-ary (right) delegation strategies by number of delegations (top) and by time (bottom).

Figure 9 shows the evolution of the flowtime for both offer strategies for a particular reallocation problem. We observe that the n-ary strategy reduces the number of delegations (40 versus 66) required to reach a stable allocation with similar flowtime. Therefore, the n-ary strategy reduces the rescheduling time (0, 35 s versus 1, 8 s).

6.4 Distributed Constraint Optimization Problem (DCOP)

We want to compare our strategy with a DCOP resolution method to show that: (a) our rescheduling time is much lower, (b) our flowtime is better.

Finding the optimal allocation for a $\text {MASTA+}$ problem with n tasks, m nodes and $\ell$ jobs (cf. Sect. 3) can be formalized with:

• 1. n decision variables $x_{i}$ such that,

  $$\begin{aligned} x_{i} = (o - 1) \times n + k \text { if } \tau _{i} \text { is the } k^{th} \text { task starting from the end on } \nu _{o} \end{aligned}$$

  (24)

• 2. $n^2$ constraints ensuring that each task is assigned to a single position

  $$\begin{aligned} \forall i \in [1,n] \forall j \in [1,n] \setminus \{ i \}~ x_{i} \ne x_{j}; \end{aligned}$$

  (25)

• 3. the objective function to minimize is $\text {C}(\overrightarrow{\text {A}})$.

We consider here the MGM2 algorithm [17] – Maximum Gain Message – as the most suitable DCOP resolution method, since it is a distributed local search algorithm which is approximate and asynchronous. We used the pyDCOP library [19]. We consider 100 $\text {MASTA+}$ problems with $m = 2$ nodes, $\ell = 4$ jobs and $n = \ell \times m = 8$ tasks.

Fig. 10.

Box plot of flowtimes reached by our strategy in 55 ms (mean value) and by the MGM2 algorithm with a timeout of 2, 5 and 10 s, respectively.

Figure 10 compares the flowtimes reached by our strategy in 55 ms (mean value) and by the MGM2 algorithm with a timeout of 2, 5 and 10 s, respectively. It is worth noticing that MGM2 never returns a solution when the timeout is 2 s. In this case, we consider that the random initial allocation is returned. Beyond the fact that the rescheduling time can be explained because MGM2 is implemented in Python whereas our strategy runs on a Java Virtual Machine [10], our experiments show that even if the timeout is set to 5 s, MGM2 provides an allocation whose flowtime is greater than the one reached by our strategy. Increasing the timeout does not allow to improve the flowtime of the allocation returned by MGM2. We can notice that MGM2 never returns an allocation with $m = 3$ nodes, $\ell = 5$ jobs and $n = 3 \times \ell \times m = 45$ tasks even with a timeout of 15 minutes. This algorithm does not scale for this kind of problems.

7 Conclusion

In this paper, we have proposed a multi-agent strategy for the reassignment of tasks-nodes based on the location of the required resources in order to minimize the mean flowtime of concurrent jobs. We generalized the notion of delegation to consider any bilateral reallocation (delegation or swap of several tasks) and we defined an acceptability criterion of the bilateral reallocations in order to reduce the rescheduling time and the mean flowtime reached by our strategy.

Since our negotiation process continuously adapts the allocation by reducing the completion time of the jobs for the bottleneck agents in order to improve the load-balancing, the flowtime reached by our strategy is similar to the one reached by a classical heuristic approach while significantly reducing the rescheduling time. On the one hand, the consumption strategy performs the cheapest jobs before the most expensive ones. On the other hand, the offer strategy selects a job which can reduce the completion times of the proposer by choosing a receiver which is not a bottleneck for the impacted jobs and by choosing a task whose delegation reduces its cost since it is locally executed. This task selection strategy is repeated by the proposer to build an offer bundle as long as it improves the flowtime. Our experiments show that such n-ary delegations improve the rescheduling time. We have compared our approach with a DCOP resolution method, i.e. the MGM2 algorithm for which the rescheduling time and flowtime are significantly higher.

Beyond the scope of this work, the influence of the replication factor could be investigated in a sensitivity analysis. Since no negotiation is triggered when the agents believe that the allocation is stable, the effort required for negotiation (reasoning and communication) is negligible compared to the benefit of the load-balancing. Due to the local decisions of agents about the next task to delegate/execute, our multi-agent strategy can tackle a large number of tasks, so it is scalable.

Since our negotiation framework allows it, we are considering to add a counter-offer strategy that selects a counterpart for suggesting swaps in order to improve the flowtime. More generally, future works should extend the task reallocation process toward an iterated, dynamic and on-going process, which takes place concurrently with the task execution, allowing the distributed system to be adaptive to disruptive phenomena (task consumption, job release, slowing down nodes).