MRVAE: Variational Autoencoder with Multiple Relationships for Collaborative Filtering

Abstract

Variational Autoencoder (VAE)-based collaborative filtering (VAE-based CF) methods have shown their effectiveness in top-N recommendation. Mult-VAE is one of them that achieves state-of-the-art performance. Multinomial likelihood and additional hyperparameter $\beta$ on the KL divergence term controlling the strength of regularization make Mult-VAE a strong baseline. However, Mult-VAE uses non-linear MLPs as its encoder and decoder, which will boost the performance on the dense datasets but degrade the performance on the sparse datasets in our experiments. While recent studies shed light on the non-linearity for modeling the relationships between users and items, they ignore the importance of linearity between users and items, especially on the sparse datasets. To bridge the gap and consider both the linearity and non-linearity user-item relationships, we design a hybrid encoder that incorporates both linearity and non-linearity, and use a linear decoder for VAE-based CF, which can achieve competitive performance on both sparse and dense datasets. Moreover, most VAE-based CF methods only consider the relationships between users and items but ignore the relationships between items for improving the performance in collaborative filtering. To overcome this limitation, we try to incorporate item-item relationships into VAE-based CF with the help of cosine similarity between items. Unifying these relationships into VAE-based CF forms our proposed method, Variational Autoencoder with Multiple Relationships (MRVAE) for collaborative filtering. Extensive experiments on several dense and sparse datasets show the effectiveness of MRVAE.

This work is supported by the National Natural Science Foundation of China (U1911203, 61902439, 61902438, U1811264, U1811262), Guangdong Basic and Applied Basic Research Foundation (2021A1515011902, 2019A1515011159, 2019A1515011704), National Science Foundation for Post-Doctoral Scientists of China underGrant (2019M663237), Macao Young Scholars Program (UMMTP2020-MYSP-016), the Key-Area Research and Development Program of Guangdong Province (2020B0101100001).

1 Introduction

Recommender Systems (RSs) are widely used in many platforms, such as e-commerce, music apps, short videos platform and so on. RSs can help recommend items to users according to their personalized preferences. Collaborative filtering (CF) is an effective recommendation method for mining users’ personalized preferences [15], given the implicit feedback data of user, e.g., click and purchase. CF methods mainly use the similarity pattern (relationships) across users and items for recommendations [10]. Recently, top-N recommendation with CF has become prevalent in current researches [5, 19].

Among the top-N recommendation CF methods, Variational Autoencoder (VAE)-based methods, such as Mult-VAE [10], have achieved state-of-the-art performance. Mult-VAE resembles the structure of common VAE but with some changes: (1) additional hyperparameter $\beta$ is introduced to the Kullback-Leibler (KL) divergence term for controlling the regularization; (2) multinomial likelihood is used for model training. While these changes are helpful in boosting the recommendation performance in dense datasets, where each user has multiple interactions on average, Mult-VAE achieves a poor performance in relatively sparse datasets [4]. We attribute the performance degradation in sparse datasets to the improper design of model structure: non-linear encoder and decoder with neural networks. The non-linear structure makes Mult-VAE capture only the non-linearity relationships between users and items, but ignore the linearity relationships between users and items, which are important when the data is sparse [11]. Recent study [13] shows that it is not wise to adopt non-linear MLPs as the interaction function between users and items, compared with the dot product, which indicates that the non-linear decoder used in Mult-VAE may be burdensome and unnecessary and a linear decoder is desired.

While Mult-VAE considers only the relationships between users and items, other relationships are lack of mining, e.g., item-item relationships. Item-item relationships are proved significant for performance improvement in some neighbor-based CF methods [1, 15, 16]. For instance, item-based CF is effective in early rating prediction task [16]. They use the cosine similarity, the Pearson correlation coefficient, or the ajusted cosine similarity to compute the similarity between items. The calculated item-item similarity is used to select the most similar items for rating prediction of the target item. We argue that such item-item similarity can also be used in VAE-based CF to boost the recommendation performance.

To combine the linearity and non-linearity user-item relationships, and item-item relationships into a unified VAE-based framework, we propose a VAE-based CF model called Variational Autoencoder with Multiple Relationships (MRVAE) for CF. Firstly, we design a hybrid encoder that combines linear structure and non-linear structure in parallel with self-attention. Then we simplify the non-linear MLPs of the decoder in Mult-VAE into a linear single-layer neural network that contains merely the weight and bias. Finally, we use the cosine similarity to calculate the item-item similarity and select the top-M most similar items of each interacted item for model training. To the best of our knowledge, MRVAE is the first VAE-based CF that considers these three relationships at a unified model.

To sum up, the main contributions of this paper are summarized as follows:

• We propose a model termed MRVAE to incorporate the linearity and non-linearity user-item relationships, and item-item relationships in a unified model.

• We design an asymmetric model structure, including a hybrid encoder and a linear decoder.

• We try to incorporate item-item relationships into MRVAE through calculating the item-item similarity with the cosine similarity, and selecting the top-M most similar items of each interacted item for model training.

• We perform extensive experiments to show the effectiveness of MRVAE, compared to other variants of VAE-based CF methods and other state-of-the-art recommendation methods.

2 Preliminary

In this section, we will first introduce the notations used in this paper. Then, the problem definition is presented. Finally, the basics of Mult-VAE will be introduced.

2.1 Notations

Notations used in this paper are summarized in Table 1. We will use bold lower-case letter to denote the vector, and bold upper-case letter to denote the matrix by default. Further notations will be introduced when necessary in the later section.

2.2 Problem Definition

We consider the implicit feedback setting as in many other literatures for top-N recommendation. Our problem of top-N recommendation can be formulated as follows: given a user $u \in \mathcal {U}$ and u’s interacted items, denoted by $N_u$, the goal is to design a personalized recommendation method that can recommend the top-N items user u most probably prefers among items user u has not interacted with, i.e., $\mathcal {I}\backslash N_u$. For the binary matrix $\boldsymbol{X} \in \mathbb {R}^{|\mathcal {U}| \times |\mathcal {I}|}$, a positive value (i.e., 1) of its entry indicates that there is an interaction between the user and the item, while a value 0 indicates the opposite.

2.3 Basics of Mult-VAE

Model Description. Mult-VAE is originally a generative model, which models the generative process of user’s interaction data. As a latent factor model, Mult-VAE assumes that the user’s interaction data is generated from a latent variable. Figure 1 shows the graphical model of Mult-VAE. Taking user u as an example, the generative process of u’s interaction data can be described as follows:

Table 1. Notations.

• (1) The model samples a latent representation of user u, ${\textbf {z}}_u$, from a Gaussian prior;

• (2) A non-linear function $f_{\boldsymbol{\theta }}(\cdot )$ (usually MLPs), with ${\textbf {z}}_u$ as input, is used to produce a probability $\boldsymbol{\pi }_u$ over $|\mathcal {I}|$ items;

• (3) The user u’s interaction vector, ${\textbf {x}}_u$, is drawn from the multinomial distribution parameterized by $\boldsymbol{\pi }_u$.

Specifically, the generative process ${\textbf {x}}_u$ can be formulated as follows:

$$\begin{aligned} {\textbf {z}}_u \sim \mathcal {N}(\boldsymbol{0}, \boldsymbol{I}), \quad \boldsymbol{\pi }_u = \mathrm{softmax}(f_{\boldsymbol{\theta }}({\textbf {z}}_u)), \quad {\textbf {x}}_u \sim \mathrm{Mult}(n_u, \boldsymbol{\pi }_u). \end{aligned}$$

(1)

$n_u$ denotes the number of interacted items of user u. $\mathrm{Mult}(n_u, \boldsymbol{\pi }_u)$ represents the multinomial distribution parameterized by $n_u$ and $\boldsymbol{\pi }_u$. The multinomial likelihood for user u is:

$$\begin{aligned} \log p_{\boldsymbol{\theta }}({\textbf {x}}_u \mid {\textbf {z}}_u)\overset{c}{=} \sum _i {\textbf {x}}_{ui} \log \boldsymbol{\pi }_{ui}. \end{aligned}$$

(2)

${\textbf {x}}_{ui}$ and $\boldsymbol{\pi }_{ui}$ are the i’s element in ${\textbf {x}}_u$ and $\boldsymbol{\pi }_u$, respectively.

Fig. 1.

Graphical model of Mult-VAE [10]. The shaded nodes are observed variables while the transparent nodes are latent.

Variational Inference. According to the Variational Inference [6], Mult-VAE introduces a variational distribution $q_{\boldsymbol{\phi }}({\textbf {z}}_u\mid {\textbf {x}}_u)$ with parameter $\boldsymbol{\phi }$ to help learn the model parameters $\boldsymbol{\theta }$ in Eq. (1). Specifically, $q_{\boldsymbol{\phi }}({\textbf {z}}_u\mid {\textbf {x}}_u)$ is used to approximate the intractable posterior distribution $p_{\boldsymbol{\theta }}({\textbf {z}}_u\mid {\textbf {x}}_u)$, and the Evidence Lower BOund (ELBO) can be derived as follows:

$$\begin{aligned} \mathcal {L}(\boldsymbol{\theta }, \boldsymbol{\phi };{\textbf {x}}_u)=\mathbb {E}_{q_{\boldsymbol{\phi }}({\textbf {z}}_u\mid {\textbf {x}}_u)}[\log p_{\boldsymbol{\theta }}({\textbf {x}}_u\mid {\textbf {z}}_u)]-\beta \cdot D_{KL}(q_{\boldsymbol{\phi }}({\textbf {z}}_u\mid {\textbf {x}}_u)\Vert p_{\boldsymbol{\theta }}({\textbf {z}}_u)), \end{aligned}$$

(3)

where $\log p_{\boldsymbol{\theta }}({\textbf {x}}_u\mid {\textbf {z}}_u)$ refers to the negative reconstruction error, $D_{KL}(\cdot \Vert \cdot )$ refers to the KL divergence between two distributions, $p_{\boldsymbol{\theta }}({\textbf {z}}_u)$ refers to the prior distribution, and $\beta$ is introduced to control the strength of the regularization, i.e., the KL divergence term $D_{KL}(q_{\boldsymbol{\phi }}({\textbf {z}}_u\mid {\textbf {x}}_u)\Vert p_{\boldsymbol{\theta }}({\textbf {z}}_u))$. To calculate Eq. (3) analytically, we need to calculate $D_{KL}(q_{\boldsymbol{\phi }}({\textbf {z}}_u\mid {\textbf {x}}_u)\Vert p_{\boldsymbol{\theta }}({\textbf {z}}_u))$ and $\mathbb {E}_{q_{\boldsymbol{\phi }}({\textbf {z}}_u\mid {\textbf {x}}_u)}[\log p_{\boldsymbol{\theta }}({\textbf {x}}_u\mid {\textbf {z}}_u)]$, respectively. When the prior $p_{\boldsymbol{\theta }}({\textbf {z}}_u)$ is a standard Gaussian distribution, the KL divergence term $D_{KL}(q_{\boldsymbol{\phi }}({\textbf {z}}_u\mid {\textbf {x}}_u)\Vert p_{\boldsymbol{\theta }}({\textbf {z}}_u))$ can be calculated analytically. $\mathbb {E}_{q_{\boldsymbol{\phi }}({\textbf {z}}_u\mid {\textbf {x}}_u)}[\log p_{\boldsymbol{\theta }}({\textbf {x}}_u\mid {\textbf {z}}_u)]$ can be calculated with Eq. (2). However, ${\textbf {z}}_u$ needs to be sampled from the variational distribution $q_{\boldsymbol{\phi }}({\textbf {z}}_u\mid {\textbf {x}}_u)$ and the sampling process is non-differentiable, which blocks the backpropagation with gradient descent. To solve the problem, the reparameterization trick [9, 14] is introduced: ${\textbf {z}}_u = \mu _{\boldsymbol{\phi }}({\textbf {x}}_u)+\boldsymbol{\epsilon } \odot \varSigma _{\boldsymbol{\phi }}({\textbf {x}}_u)$. $\mu _{\boldsymbol{\phi }}({\textbf {x}}_u)$ and $\varSigma _{\boldsymbol{\phi }}({\textbf {x}}_u)$ together are the encoder of VAE, implemented by non-linear MLPs. They produce the mean vector and variance vector (diagonal elements of the covariance matrix) of $q_{\boldsymbol{\phi }}({\textbf {z}}_u\mid {\textbf {x}}_u)$. $\boldsymbol{\epsilon }$ is sampled from standard Gaussian $\boldsymbol{\mathcal {N}}(\boldsymbol{0}\mid \boldsymbol{I})$. The reparameterization trick samples ${\textbf {z}}_u$ in a novel way and the gradient with respect to $\boldsymbol{\phi }$ can be taken since $\boldsymbol{\epsilon }$ is not required to be optimized. So far, stochastic gradient descent can be applied to Eq. (3) to learn model parameters $\boldsymbol{\phi }$ and $\boldsymbol{\theta }$. After the parameters $\boldsymbol{\phi }$ and $\boldsymbol{\theta }$ are learned, given a user interaction vector ${\textbf {x}}_u$, we can reconstruct it with Mult-VAE, and items in $\mathcal {I}\backslash N_u$ with the top-N highest scores are recommended to the user.

3 MRVAE

In this section, we will firstly introduce the hybrid encoder and linear decoder. We then detail how to incorporate item-item relationships into our model.

3.1 Hybrid Encoder and Linear Decoder

While Mult-VAE uses a non-linear encoder and a non-linear decoder that consider the non-linearity between users and items, we instead design a model structure that considers both the linearity and non-linearity relationships between users and items, so that our model can adapt to both sparse and dense datasets.

As mentioned in Sect. 2.3, the encoder of Mult-VAE consists of a mean network and a variance network that output the mean and the diagonal elements of the covariance matrix of the variational distribution, respectively. In MRVAE, we use a single-layer neural network to serve as the variance network:

$$\begin{aligned} \log \varSigma _{\boldsymbol{\phi }}({\textbf {x}}_u) = \mathrm{{\textbf {W}}}_\varSigma ^T {\textbf {x}}_u + \mathrm{{\textbf {b}}}_\varSigma . \end{aligned}$$

(4)

$\mathrm{{\textbf {W}}}_\varSigma \in \mathbb {R}^{|\mathcal {I}| \times K}$ and $\mathrm{{\textbf {b}}}_\varSigma \in \mathbb {R}^K$ are weight and bias of the variance network, where K is the latent dimension.

Fig. 2.

The model structure of MRVAE. Inside the dotted rectangle is the backbone of MRVAE that incorporates the linearity and non-linearity user-item relationships. The ‘item-item’ module introduces item-item relationships.

The mean network consists of two parallel networks, i.e., the linear network and the non-linear network. The linear network has the same structure as the variance network, described as follows:

$$\begin{aligned} \mu _{\boldsymbol{\phi }}^{l}({\textbf {x}}_u) = {\mathrm{{\textbf {W}}}_\mu ^l}^T {\textbf {x}}_u + \mathrm{{\textbf {b}}}_\mu ^l. \end{aligned}$$

(5)

$\mathrm{{\textbf {W}}}_\mu ^l \in \mathbb {R}^{|\mathcal {I}| \times K}$ and $\mathrm{{\textbf {b}}}_\mu ^l \in \mathbb {R}^K$ are weight and bias of the linear network. The non-linear network is a two-layer MLPs with one hidden layer and the network structure is: $|\mathcal {I}| \rightarrow K_h \rightarrow K$, where $K_h$ denotes the hidden dimension of the hidden layer, described as follows:

$$\begin{aligned} \mu _{\boldsymbol{\phi }}^n ({\textbf {x}}_u) = {\mathrm {{\textbf {W}}}_\mu ^{n_2}}^T (\sigma ({\mathrm {{\textbf {W}}}_\mu ^{n_1}}^T {\textbf {x}}_u + \mathrm {{\textbf {b}}}_\mu ^{n_1})) + \mathrm {{\textbf {b}}}_\mu ^{n_2}. \end{aligned}$$

(6)

$\mathrm {{\textbf {W}}}_\mu ^{n_2} \in \mathbb {R}^{K_h \times K}$ and $\mathrm {{\textbf {W}}}_\mu ^{n_1} \in \mathbb {R}^{|\mathcal {I}| \times K_h}$ refer to the weights of the non-linear network, $\mathrm {{\textbf {b}}}_\mu ^{n_2} \in \mathbb {R}^{K}$ and $\mathrm {{\textbf {b}}}_\mu ^{n_1} \in \mathbb {R}^{K_h}$ are the biases. $\sigma$ refers to the non-linear activation function, e.g., $\tanh$. To combine the linear network and the non-linear network into a unified mean network, we resort to the self-attention mechanism. Specifically, the final mean vector of user u is obtained by the weighted sum of $\mu _{\boldsymbol{\phi }}^{l}({\textbf {x}}_u) \in \mathbb {R}^K$ and $\mu _{\boldsymbol{\phi }}^n ({\textbf {x}}_u) \in \mathbb {R}^K$:

$$\begin{aligned} \boldsymbol{\mu }_u = \alpha _l \cdot \mu _{\boldsymbol{\phi }}^{l}({\textbf {x}}_u) + \alpha _n \cdot \mu _{\boldsymbol{\phi }}^n ({\textbf {x}}_u), \end{aligned}$$

(7)

where $\alpha _l$ and $\alpha _n$ can be calculated as follows:

$$\begin{aligned} \begin{aligned} \alpha _l = \frac{\exp (\gamma _l)}{\exp (\gamma _l) + \exp (\gamma _n)}, \\ \alpha _n = \frac{\exp (\gamma _n)}{\exp (\gamma _l) + \exp (\gamma _n)}. \end{aligned} \end{aligned}$$

(8)

According to the self-attention mechanism, $\gamma _l$ and $\gamma _n$ are expressed as follows:

$$\begin{aligned} \begin{aligned} \gamma _l = q^T \tanh (\mathrm {{\textbf {W}}}_{att} \mu _{\boldsymbol{\phi }}^l ({\textbf {x}}_u) + \mathrm {{\textbf {b}}}_{att}), \\ \gamma _n = q^T \tanh (\mathrm {{\textbf {W}}}_{att} \mu _{\boldsymbol{\phi }}^n ({\textbf {x}}_u) + \mathrm {{\textbf {b}}}_{att}). \end{aligned} \end{aligned}$$

(9)

$q^T \in \mathbb {R}^{K \times 1}$ is a learnable global query vector for self-attention. $\mathrm {{\textbf {W}}}_{att} \in \mathbb {R}^{K \times K}$ and $\mathrm {{\textbf {b}}}_{att} \in \mathbb {R}^{K}$ are weight and bias of the self-attention network, respectively.

After obtaining the mean vector and the variance vector, we can adopt reparameterization trick to calculate ${\textbf {z}}_u$. Then ${\textbf {z}}_u$ is fed into a linear decoder, which can be expressed as follows:

$$\begin{aligned} f_{\boldsymbol{\theta }}({\textbf {z}}_u) = \mathrm{{\textbf {W}}}_{\boldsymbol{\theta }}^T {\textbf {z}}_u + \mathrm{{\textbf {b}}}_{\boldsymbol{\theta }}. \end{aligned}$$

(10)

$\mathrm{{\textbf {W}}}_{\boldsymbol{\theta }} \in \mathbb {R}^{K \times |\mathcal {I}|}$ and ${\textbf {b}}_{\boldsymbol{\theta }} \in \mathbb {R}^{|\mathcal {I}|}$ are the weight and bias of the decoder, respectively. The decoder is a simple single-layer MLP and is equivalent to dot product with an additional bias.

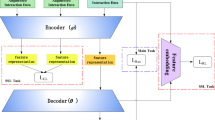
The model structure of MRVAE is not a symmetric one as in Mult-VAE. Instead, we incorporate linearity user-item relationships in both the encoder and the decoder, and incorporate non-linearity user-item relationships in the encoder only. In the experiments, we show that such a model structure can achieve superior performance. Figure 2 shows the model structure of MRVAE.

3.2 Incorporating Item-Item Relationships

In this subsection, we detail the process of incorporating the item-item relationships into our model.

Some early works [16] use cosine similarity to calculate the item-item similarity between the target item and the rated items by the user for rating prediction. To predict the rating of a target item of the user, the ratings of the rated items of the user and their similarities are combined through weighted sum. However, in MRVAE, which is a latent factor model for top-N recommendation, we take a different strategy: we select the top-M most similar items to each interacted item of the user to help model training. During training, for each interacted item of the user, the selected top-M most similar items together with their similarities to the interacted item are used to more accurately reconstruct the preference score of each interacted item. To clearly show our strategy, we adapt Eq. (2) to our strategy as follows:

$$\begin{aligned} \log p_{\boldsymbol{\theta }}({\textbf {x}}_u \mid {\textbf {z}}_u)\overset{c}{=} \sum _i {\textbf {x}}_{ui} \left( \log \boldsymbol{\pi }_{ui} + \eta \sum _{j \in \mathcal {N}_i} s_{ij} \log \boldsymbol{\pi }_{uj} \right) . \end{aligned}$$

(11)

$\eta$ is a hyperparameter used to control the strength of item-item relationships and $s_{ij}$ denotes the cosine similarity between item i and item j. Specifically, $s_{ij}$ is expressed as follows:

$$\begin{aligned} s_{ij} = \frac{{\textbf {X}}_{*,i} \cdot {\textbf {X}}_{*,j}}{|{\textbf {X}}_{*,i}| \cdot |{\textbf {X}}_{*,j}|}, \end{aligned}$$

(12)

where ${\textbf {X}}_{*,i}$ and ${\textbf {X}}_{*,j}$ denote the interaction vectors of item i and item j, respectively.

3.3 Discussion

Firstly, the linearity user-item relationships are reflected by both the encoder and the decoder, especially by the decoder since the decoder directly reconstructs the user’s interaction vector. If we regard the weights $\mathrm {{\textbf {W}}}_{\boldsymbol{\theta }}$ as the item embeddings with each column representing an item’s embedding, the decoder is equivalent to the dot product between the user embedding and item embedding, with an additional bias term. This is in line with the finding in [13] that dot product is a better approximation of the interaction function. As for the encoder, we integrate the linear structure and the non-linear structure to let the model itself learn when to focus on the linearity relationships more and when to concentrate more on the non-linearity relationships, between users and items.

Secondly, while the design of encoder and decoder considers the linearity and non-linearity user-item relationships, we incorporate item-item relationships by means of the multinomial likelihood. The top-M most similar items measured by cosine similarity of each interacted item of the user can provide more information about the preferences of the user, thus can filter out the less preferred items and give more attention to the preferred items. In the experiments, we empirically choose a small value for M because a larger M will introduce some ‘negative’ items that the user dislikes.

4 Experiments

In this section, we empirically evaluate our method on four datasets in Top-N recommendation task. We firstly show the experimental settings, followed by the performance comparison of MRVAE with other competing methods. Ablation study and hyperparameter analysis are also conducted.

4.1 Experimental Settings

Datasets and Evaluation Metrics. We use four public datasets that are commonly used in the CF methods for implicit feedback: ML-1M [2], Yelp2018¹, Amazon-Book and Video-Games. ML-1M, which contains one million explicit ratings, is one of the version of MovieLens datasets². We binarize the explicit ratings by regarding ratings of four or higher as implicit feedback. Yelp2018 is adopted from the 2018 edition of the Yelp challenge, where the local businesses are viewed as items [19]. Amazon-Book and Video-Games are collected from the Amazon-review datasets [3]. Yelp2018 and Video-Games are sparse datasets since they have a small average number of user’s interactions, while Amazon-Book and Ml-1M are relatively dense datasets. Table 2 shows the statistics of the datasets. For each user, 80% of the interactions are used for training and the remaining 20% of interactions are used for testing. From the training set, we can select 10% of interactions as validation set to tune hyperparameters. We use recall@20 and ndcg@20 computed by the all-rank protocol, i.e., all items that are not interacted by a user are candidates, as the evaluation metrics.

Table 2. Statistics of the experimented datasets.

Baseline Methods. Since MRVAE is a VAE-based CF method, we compare MRVAE with several VAE-based CF variants. Moreover, we also compare MRVAE with matrix factorization and graph-based CF methods. We choose the MF-BPR [12] as the representative of matrix factorization method and LightGCN [4] as the representative of the graph-based CF method. We also additionally include a popularity-based, non-personalized method ItemPop. They are introduced as follows:

• ItemPop This is a non-personalized recommendation method that recommends items based on how many users have interacted with the item.

• MF-BPR [12] This is a matrix factorization method that resorts to the Bayesian personalized ranking loss for model learning.

• LightGCN [4] This is a state-of-the-art graph convolutional network (GCN)-based CF method. It is the lighter version of NGCF [19]. By propagating the embeddings of users and items on the user-item bipartite graph through graph convolution, multiple relationships are implicitly captured in LightGCN.

• Mult-VAE [10] This is the base model of our proposed method. It uses non-linear encoder and decoder. Only user-item relationships are considered in Mult-VAE.

• EVCF [7] This is an enhancing VAE model for CF. It adopts flexible prior and gating mechanism, to enhance the Gaussian prior and encoder in the original Mult-VAE, respectively.

• RecVAE [17] This is an improved model of Mult-VAE. It adds multiple novelties to Mult-VAE and improves the recommendation performance significantly compared with Mult-VAE.

• BiVAE [18] This is a VAE-based CF method that uses two encoders to encode user and item interaction vectors, respectively, and uses a simple decoder to reconstruct the user interaction vectors for recommendations.

Hyperparameter Settings. For fair comparison, the embedding size or latent dimension of MRVAE and all the latent factor models of the competing methods are set to 64. For the VAE-based variants, we set the hidden dimension to 128 if a hidden layer exists. We tune the number of hidden layers among [0, 1, 2], except for RecVAE that has a complicated encoder. For example, we adopt the model architecture: $128 \rightarrow 64 \rightarrow 128$, for Mult-VAE. All the models are trained with Adam [8]. The learning rates of all the methods are tuned among [1e-3, 5e-4, 1e-4]. The number of graph convolution layers of LightGCN is tuned among [2, 3, 4]. For MRVAE, we use MLPs with structure $64 \rightarrow 64$ for the non-linear mean network to make MRVAE be in the same magnitude of parameters as Mult-VAE. For simplicity, we set $\beta$ to 0.8 without KL annealing for MRVAE. The hyperparameter $\eta$ is tuned among 0–100 and M is tuned among 5–100.

4.2 Performance Comparison

The experiment results of MRVAE and all other competing methods are shown in Table 3. The results show that MRVAE surpasses all the competing methods in terms of the two evaluation metrics, on sparse and relatively dense datasets. Firstly, MRVAE outperforms the traditional methods ItemPop and MF-BPR. Secondly, MRVAE outperforms VAE-based variants, in particular, by a large margin over Mult-VAE on four datasets (31.98% on recall@20 and 35.01% on ndcg@20, on average). EVCF, RecVAE and BiVAE achieve a better performance than Mult-VAE, but by a relatively smaller margin, compared with MRVAE’s performance, which indicates the significance of mining more relationships among different entities in CF. Thirdly, MRVAE outperforms the strong baseline LightGCN on four datasets, which shows that MRVAE can capture more important relationships for recommendations.

Table 3. The comparison of over performance of MRVAE and competing methods. The best results are highlighted in bold. The second best ones are underlined. “%Improve” denotes the performance improvement of MRVAE over Mult-VAE.

Table 4. Experiment results of ablation study. Variant (i) denotes MRVAE with non-linear encoder and linear decoder; Variant (ii) denotes MRVAE with linear encoder and linear decoder; Variant (iii) denotes MRVAE with non-linear encoder and non-linear decoder; Variant (iv) denotes MRVAE without incorporating item-item relationships. Variant (v) denotes MRVAE with self-attention in the hybrid encoder replaced by average pooling. See the text for more details.

4.3 Ablation Study

We conduct some experiments on the experimented datasets to justify the effectiveness of the components of MRVAE, which include the hybrid encoder, the integration of the linearity and non-linearity user-item relationships, the incorporation of item-item relationships. Five variants of MRVAE are considered, specifically, variant (i) is generated by removing the linear mean network; variant (ii) is generated by removing the non-linear mean network; variant (iii) is generated by removing the linear mean network and transforming the linear decoder into a non-linear decoder with network structure: $64 \rightarrow 128 \rightarrow |\mathcal {I}|$; variant (iv) is generated by removing the item-item relationships; variant (v) is generated by replacing self-attention in the hybrid encoder with average pooling. Variant (i) verifies the hybrid encoder of MRVAE, variant (ii) and variant (iii) verify the importance of integrating the linearity and non-linearity user-item relationships. Variant (iv) verifies the effectiveness of item-item relationships. Variant (v) verifies the effectiveness of self-attention in the hybrid encoder. Experiment results are shown in Table 4.

We have the following observations: (1) MRVAE outperforms all the variants on four datasets, which indicates the necessity of fusing the linearity and non-linearity user-item relationships, and item-item relationships; (2) the outperformance of MRVAE over variant (i) and variant (v) verifies the effectiveness of the proposed hybrid encoder and the self-attention used in it; (3) in most cases, variant (i) achieves better performance than variant (ii) and (iii), verifying our idea of integrating the linearity and non-linearity user-item relationships; (4) the importances of item-item relationships on different datasets vary, specifically, item-item relationships play an important role in Amazon-Book dataset but contribute less to the performance improvement on other three datasets, by comparing MRVAE with variant (iv); (5) comparing variant (ii) and variant (iii) shows that linearity user-item relationships contribute more to the superiority of MRVAE on Yelp2018 and Video-Games (sparse user interactions), but non-linearity user-item relationships play a more important role on ML-1M and Amazon-Books (relatively dense user interactions), which corresponds to the average number of interactions of users in Table 2, i.e., dataset with relatively dense user interactions favors non-linearity and dataset with sparse user interactions favors linearity. We argue that dense dataset with more ID features needs more powerful non-linear networks to learn while the sparse dataset is the opposite.

Fig. 3.

The impact of M on the performance on Yelp2018 (left) and Video-Games (right).

Fig. 4.

The impact of $\eta$ on the performance on four datasets. From left to right and from top to bottom: ML-1M, Yelp2018, Amazon-Book and Video-Games.

4.4 Hyperparameter Analysis

In this subsection, we conduct experiments to explore the impact of the hyperparameters M and $\eta$ on the recommendation performance in terms of recall@20 and ndcg@20.

Impact of $\boldsymbol{M}$ . Figure 3 shows the experiment results of MRVAE with different M on Yelp2018 and Video-Games. We set M among [5, 10, 20, 40, 80, 100]. Usually, a small M can achieve the best performance, since a larger M will introduce some irrelevant item-item relationships which will hurt the performance instead, e.g., we set M to 10 for Yelp2018 and Video-Games. Similar observations can be found on ML-1M and Amazon-Book. Specifically, we set M to 5 for ML-1M and Amazon-Book and omit their illustrations due to the page limit.

Impact of $\boldsymbol{\eta }$ . Figure 4 shows the experiment results on four datasets. The scales of $\eta$ on different datasets vary. On ML-1M, Yelp2018 and Video-Games, a small value of $\eta$ can achieve the best performance and a large $\eta$ will degrade the performance, especially on the ML-1M dataset. On the contrary, a relatively larger value of $\eta$ is favored on Amazon-Book. Specifically, the best $\eta$ on ML-1M, Yelp2018, Amazon-Book and Video-Games are 0.02, 0.08, 60 and 0.1, respectively. These show that the contributions of item-item relationships to the performance on different datasets vary. We conjecture that the linearity and non-linearity user-item relationships are more important than item-item relationships in ML-1M, Yelp2018 and Video-Games, for boosting the performance. Increasing the influence of item-item relationships will instead make the linearity and non-linearity user-item relationships fade away on these three datasets. While we get the opposite conclusion on Amazon-Book, in which item-item relationships dominate.

5 Related Works

5.1 VAE-Based CF Methods

In this subsection, we present some relevant VAE-based CF methods that make top-N recommendation under the implicit feedback setting [7, 10, 17, 18]. Mult-VAE is the pioneer work that extends VAE to CF for implicit feedback. The multinomial likelihood and hyperparameter $\beta$ on the KL divergence term are two novel contributions of Mult-VAE, which are adopted by later VAE-based CF methods [17], including our proposed MRVAE. The work proposed by [7] uses a more flexible prior to replace the original standard Gaussian distribution, and uses gated linear units to deepen the neural networks of encoder and decoder. RecVAE [17] proposes several novelties for improving Mult-VAE, including a sophisticated encoder, a novel composite prior distribution, a new approach to setting the hyperparameter $\beta$ and a novel approach for training the model. Note that RecVAE also proposes to use a linear encoder, but it does not consider the linearity in the encoder and does not incorporate item-item relationships into the model, compared with MRVAE. In [18], the authors propose to use two encoders, user- and item-based, parameterized by neural networks and the decoder can take any differentiable function, e.g., inner product. While two encoders are used, they do not consider the combination of the linearity and non-linearity user-item relationships as MRVAE. Our proposed MRVAE differs from these VAE-based CF methods in that we focus on mining more relationships across users and items, to further improve the recommendation performance.

5.2 Other CF Methods

Latent factor models still dominate the CF methods family [4, 11, 12, 19]. They can roughly divided into the matrix factorization (MF) models [11, 12] and models with more powerful encoder, e.g., graph-based CF methods [4, 19]. MF models project the user/item IDs into embeddings, then use dot product to calculate the preference score on item for user. Point-wise loss [11] or pair-wise loss [12] are widely used in these methods. While MF models only consider the pattern between users and items, graph-based CF methods implicitly incorporate the user-user, item-item and user-item relationships into the model, by conducting multi-layer graph convolution on the user-item bipartite graph [4, 19]. Though multiple types of relationships are considered in the graph-based CF methods, some relationships between entities may be harmful for model learning since these relationships are incorporated in an implicit manner, without carefully distinguishing the helpful ones from all the relationships. Instead, our proposed MRVAE explicitly incorporates the linearity and non-linearity user-item relationships, and item-item relationships. Especially for item-item relationships, we use cosine similarity to measure the relative importance of item-item relationships and selectively incorporate them to the model.

6 Conclusion

In this paper, we propose a model called MRVAE, aiming at incorporating more relationships between entities (i.e., users or items), to boost the top-N recommendation performance. Firstly, we carefully design a hybrid encoder and a linear decoder as a backbone of our model, in which the linearity and non-linearity user-item relationships are considered. Secondly, we selectively incorporate item-item relationships into the models further through adding additional term to the multinomial likelihood. We use cosine similarity to calculate the similarity between items. Extensive experiments demonstrate the effectiveness of MRVAE, compared to other SOTAs. Future work could be exploring other similarity measures between items and attempting to incorporate user-user relationships into the VAE-based CF methods. Mining more accurate relationships by incorporating side information into MRVAE can also be a possible direction in the future.