Abstract
We introduce a component model for graph rewriting that allows to model a system as a network of components with interfaces representing shared views of internal states and transformations. Their composition assembles a global view whose behaviour is equivalent to the synchronised distributed execution of local components in the network. Formally, components are arrows in a category with interfaces as objects that, with suitable component connectors, forms a Frobenius algebra. This allows the use of string diagrams to model the architecture of basic components and connectors, such that their assembly is freely generated by the algebraic structure. The compositionality of the proposed model is reflected by Structural Operational Semantic rules.
Research partly supported by MIUR PRIN project 2017FTXR7S “IT-MaTTerS”.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Software development relies on encapsulation, modularity, and reuse to manage complexity. At the level of software architecture, these principles are supported by components that provide the basic blocks from which larger systems are built. While languages, technologies, and architectural styles change over time and differ between domains, the main feature that separates components from lower-level (e.g., object-oriented) concepts is the use of interfaces describing not only the services provided by components but also their requirements towards their runtime context. This enables reuse of components across contexts that satisfy the stated requirements.
With the confluence of concepts from semantic web, graph databases, and model-based engineering, knowledge graphs [15] are emerging as key technology in enterprise and e-commerce applications, medical data management, cognitive digital twins, and social networks [16] to support data integration, sharing and mapping, graph-based analytics and machine learning [17]. In current applications, knowledge graphs lack the basic modularity, encapsulation and flexibility of deployment offered by most component models. But global centralised data models make applications hard to evolve and maintain, hinder reuse, distributed development, analysis, and verification [8]. We need a discipline of graph-based software engineering using dedicated abstractions and language constructs to develop modular graph-based applications.
This paper addresses the theoretical foundations of components in graph-based applications, where graphs are central runtime artefacts to be shared, queried, mapped and synchronised, updated, transformed and analysed. Such operations can commonly be described by graph rewriting. The novel challenge for components of graph rewriting-based applications is that, while traditionally the internal state is fully encapsulated, graph data must be shared between organisations along with rights to query, change or analyse graphs locally and coordinate changes globally. Access to and operations on graphs should be offered as services ensuring data integrity. While maintaining local ownership, a virtual global graph should emerge as the central artefact for data integration and analytics [19].
We propose the architectural abstraction of Graph Rewriting Components (GReCos) as building blocks for graph-based systems, encapsulating graphs and their operations and offering these to other components and applications. This is realised by defining GReCos as graph transformation systems with interfaces for composition with other systems.
Formally, GReCos are cospans of morphisms between graph transformation systems with state, called runtime systems, where the central system represents the partially hidden implementation, the left interface describes the types, rules and graph provided and the right interface those required by the component. In particular, we are interested in strict components, where the interface graphs are projections of the internal state graph.
Morphisms between runtime systems that are strict in that sense reflect transformations, so interfaces provide a partial view of the behaviour of the implementation. We can compose components via pushouts of such morphisms, and if the given components are strict and satisfy a compatibility condition ensuring that their composition is strict, too, the resulting component represents a global view of the synchronised execution of its constituents. Vice versa, the global behaviour can be decomposed into matching local behaviours, allowing us to move freely between the two levels. This supports the need for a virtual global graph that can be used centrally without giving up localised representation.
To support flexible connections between components we establish the category of graph rewriting components as a symmetric monoidal category, specifically a Frobenius algebra [3], and use the associated syntax of string diagrams to represent the interconnection of components and interfaces. This view of the software architecture is analogous to component diagrams in UML. Given realisations of the basic components in terms of GReCos, architecture-level string diagrams are mapped freely to (basic and composite) GReCos, compiling the system from its architecture description and its basic components.
The approach thus represents a convergence of distributed graph transformation [18], service-oriented and modular graph transformation [7], and string diagrams [3]. We prove compositionality results relating local and composite behaviours. In particular, the behaviour of (disjoint) parallel compositions and (interface-based) functional compositions of components can be fully inferred from the behaviours of their constituents and basic architectural connectors. This supports the reuse of components in different contexts, guaranteeing that behavioural equivalence of components is maintained by composition.
2 Example
We model a simple architecture to motivate, illustrate and evaluate our concepts and results. The model consists of three components: a Client C, a Service S and a Database D. The component diagram below gives a high-level view of the architecture. The components are connected via three interfaces. The Service Interface SI describes the operations provided by S and used by C. Conversely, the Client Interface CI is implemented by C and used by S. The idea is that C sends a requests through SI to be executed by S which, in turn, replies via the callback interface CI. While executing the request, S calls on D to verify and update the data.

Components and interfaces are typed graph transformation systems with states related by morphisms. For our architecture. they are shown in Fig. 1. For each system we have the type graph in the left, followed by the rules, and the state graph made up of a single customer and its contract as a minimal test case.
The morphisms mapping type, state graphs and rules between interfaces and components are indicated by vertical arrows on the left. They describe how internal type and state graphs are partially visible through the interfaces. Rules in the interfaces are subrules of projections of the rules in components to the interface types. If the projection results in a rule without effect, this rule can be dropped, e.g. the process rule is in S but not SI, unless we want to use it to synchronise actions between components, e.g. between S and D via DI. Rules that are vertically aligned are related by morphisms. We use the integrated rule notation where left and right-hand sides are shown in the same graph, with deleted and created elements distinguished by colours blue and green and labelled \(\{ delete \}\) and \(\{ new \}\) respectively. In the bottom we show the global system view Sys obtained by composing components over their shared interfaces.
The model describes a claims process where C represents an insurance company’s customer interface used to issue a request for payment. S is the service processing the request by checking the data D of the contract and, if successful, marking the customer as OK. Then a decision is made to either accept or reject the request, where acceptance requires a successful check and results in removing the link between customer and contract, indicating that after a payout the contract needs to be renewed. Either decision results in deleting the request’s link to the customer to avoid making a decision repeatedly.
Apart from the rules modelling operations that can be invoked through an interface, we distinguish change event rules, such as new-req and del-custlink, representing change events whose purpose is to notify a component that is sharing part of its state with another one that this other component has changed the shared state. This is conceptually different from an operation call, although it can be implemented as one, and is essential for keeping states synchronised between components.
3 Basic Notions
Assume an adhesive base category \({\mathbf {C}}\) with a strict initial object \(\emptyset \) and arbitrary pushouts, where pushouts are stable under pullbacks; for example, let \({\mathbf {C}}\) be \({\mathbf {Graph}}\), the category of directed multigraphs. Then, for any object T of \({\mathbf {C}}\) the slice category \({\mathbf {C}}_T\) represents instances over T and their morphisms. Formally, an object of \({\mathbf {C}}_T\) is an arrow \(g: G \rightarrow T\) in \({\mathbf {C}}\) where T represents the type, G an instance object with g providing the typing. A morphism \(h: g \rightarrow g'\) for \(g': G' \rightarrow T\) is a morphism f in \({\mathbf {C}}\) such that \(g' \circ h = g\).
The types in T represent domain or application concepts that may vary between different systems. When we relate states or rules between systems we should be able to do so across different types. Given a morphism of types \(f: T \rightarrow T'\), we can define an operations of retyping by pullback of instances from target to source types. This defines retyping functors \(f^<: {\mathbf {C}}_{T'} \rightarrow {\mathbf {C}}_{T}\) for all \(f: T \rightarrow T'\). From the local categories \({\mathbf {C}}_T\) and the retyping functors we can define a global category \({\mathbf {TC}}\) whose objects are morphisms \(g: G \rightarrow T\). Morphisms are pairs \(f = \langle f_\tau , f_G\rangle : g \rightarrow g'\) with \(f_\tau : T \rightarrow T'\) in \({\mathbf {C}}\) and \(f_G: G \rightarrow f_\tau ^<(G') \in {\mathbf {C}}_T\). It can be shown that \({\mathbf {TC}}\) is equivalent to the arrow category \({\mathbf {C}}^{\rightarrow }\), and thus it inherits limits and colimits from \({\mathbf {C}}\), computed componentwise.Footnote 1 A morphism \(\langle f_\tau , f_G\rangle \) is strict if \(f_G\) is an iso. For the pushout of two strict morphisms the injections are not strict in general: a sufficient condition, by adhesivity of \({\mathbf {C}}\), is that one of the type morphism is mono.
Rules and transformations in a system are represented by spans of monomorphisms \(s = L {\mathop {\longleftarrow }\limits ^{{l}}} K {\mathop {\longrightarrow }\limits ^{{r}}} R\) in \({\mathbf {C}}_T\), i.e. they are defined over the local type T of the system. Morphisms between spans are DPO diagrams, i.e., triples of morphisms \(h = \langle h_L, h_K, h_R\rangle : s \rightarrow s'\) with \(h_L: L \rightarrow L', h_K: K \rightarrow K', h_R: R \rightarrow R'\) and such that the resulting squares are pushouts. This defines the local categories \(\mathbf {MSpan}_T\). A morphism in \(\mathbf {MSpan}_T\) represents a relation between rules where the target rule of the morphism creates and deletes the same structures as the source, but may have additional context.
To relate rules across different types we let \(\mathbf {MSpan}\) be the category that has as objects monic spans s in \({\mathbf {C}}_T\) for some T in \({\mathbf {C}}\) and as morphisms pairs \(f = \langle f_\tau , f_\pi \rangle : s \rightarrow s'\) with \(f_\tau : T \rightarrow T'\) in \({\mathbf {C}}\) and \(f_\pi : s \rightarrow f_\tau ^<(s') \in \mathbf {MSpan}_T\). Composition of such morphisms is well-defined: in fact the pullback functor preserves pushouts because they are stable under pullbacks in \({\mathbf {C}}\). This category has pullbacks and is finitely co-complete thanks to the properties of \({\mathbf {C}}\). In particular, the initial object is span \(\langle \emptyset \leftarrow \emptyset \rightarrow \emptyset \rangle \), called the empty rule, typed over \(\emptyset \).
Another interpretation of morphisms in \(\mathbf {MSpan}_T\) is as DPO transformations, with the source representing the rule applied and the target the state transformation. Sometimes we want to relate such transformations, and for this purpose we introduce \(\mathbf {DPO}_T\), the arrow category \(\mathbf {MSpan}^\rightarrow _T\), which has local \(\mathbf {MSpan}_T\) morphisms (i.e., DPO diagrams over T) \(d: s_1 \rightarrow s_2\) as objects and pairs of such morphisms \(\langle f_{top}, f_{bot}\rangle : d \rightarrow d'\) as arrows where \(f_{top}: s_1 \rightarrow s_1'\) and \(f_{bot}: s_2 \rightarrow s_2'\) such that the resulting square in \(\mathbf {MSpan}_T\) commutes.
We relate DPO diagrams across different types in a global category \(\mathbf {DPO}\) that has as objects DPO diagrams d in \({\mathbf {C}}_T\) for some T in \({\mathbf {C}}\) and as morphisms pairs \(f = \langle f_\tau , f_{d}\rangle : d \rightarrow d'\) with \(f_\tau : T \rightarrow T'\) in \({\mathbf {C}}\) and \(f_{d}: d \rightarrow f_\tau ^<(d') \in \mathbf {DPO}_T\). That means, objects in \(\mathbf {DPO}\) represent DPO transformations in different systems, and morphisms are mappings between them allowed to extend types and rules. Composition, limits and colimits are defined component-wise in \(\mathbf {MSpan}\).
Categories \({\mathbf {TC}}\), \(\mathbf {MSpan}\), and \(\mathbf {DPO}\) are equipped with a functor to \({\mathbf {C}}\) mapping objects and morphisms to their type objects and morphisms, respectively, which we denote by \(\__\tau : {\mathbf {X}} \rightarrow {\mathbf {C}}\) for \({\mathbf {X}} \in \{{\mathbf {TC}}, \mathbf {MSpan}, \mathbf {DPO}\}\).
4 Transformation and Runtime Systems
We want to use the empty rule to model steps at an interface due to unobservable steps in the body of a component, but also to model idle steps in the body itself. To this aim we introduce the rule name \(\phi \) that maps to the empty rule. Apart from this feature, the following definition is standard.
Definition 1 (transformation systems)
A transformation systems is a triple \(R = \langle T, P, \pi \rangle \) where
-
\(T \in |{\mathbf {C}}|\) is a type object;
-
P is a set of rule names, including the special rule name \(\phi \);
-
\(\pi : P \rightarrow | \mathbf {MSpan}_T |\) assigns a monic span over T to each rule name, such that \(\pi (\phi ) = \emptyset \leftarrow \emptyset \rightarrow \emptyset \).
Assuming a second system \(R' = \langle T', P', \pi '\rangle \), a morphism of transformation systems is a triple \(f = \langle f_\tau , f_p, f_\pi \rangle : R \rightarrow R'\) of
-
a morphism of types \(f_\tau : T \rightarrow T'\)
-
a mapping from target to source rule names \(f_P: P' \rightarrow P\)
-
a \(P'\)-indexed family of \(\mathbf {MSpan}\) morphisms \(f_\pi (p'): \pi (f_P(p')) \rightarrow \pi '(p')\)
such that \(f_\tau = (f_\pi (p'))_\tau \) for all \(p' \in P'\). This defines the category \(\mathbf {Sys}\).
Morphisms are defined to reflect behaviour, as discussed later. Observe that each rule name \(p'\in P'\) of the target system \(S'\) is mapped to a rule name \(f_P(p') \in P\) of the source system S, and there is an \(\mathbf {MSpan}\) morphism \(f_\pi (p')\) from the latter rule to the first one. Spelling out the definiton of \(\mathbf {MSpan}\) morphism, there is a DPO morphism from \(\pi (f_P(p'))\) to the retyped rule \(f^<_\tau (\pi '(p'))\). In particular, this implies that if \(f_P(p') = \phi \), then the retyped rule must be a span of isomorphisms, i.e. it has no effect when applied to any graph.
To model a system at runtime, we include its current state.
Definition 2 (runtime systems)
A runtime system \(S = \langle R, G\rangle \) consists of a transformation system \(R = \langle T, P, \pi \rangle \) and a state object G in \({\mathbf {C}}_T\). A morphism of runtime systems \(f = \langle f_R, f_G\rangle : S \rightarrow S'\) with \(S' = \langle \langle T', P', \pi '\rangle , G'\rangle \) is a morphism of transformation systems \(f_R = \langle f_\tau , f_p, f_\pi \rangle \) augmented by a \({\mathbf {TC}}\) morphism \(f_G=\langle f_\tau ,f'_G\rangle : G \rightarrow G'\). Morphism \(f: S \rightarrow S'\) is strict if so is \(f_G\), i.e. if \(f'_G: G \rightarrow f_\tau ^<(G')\) is an isomorphism. This defines the category \(\mathbf {RSys}\) of runtime systems.
Coming back to the example, in Fig. 1 we show seven runtime systems (three components, three interfaces and one global system), each with their type graph, rule names and associated rule spans (in integrated notation), and runtime state. The morphisms indicated in the left margin are all strict, representing inclusions of type graphs, state graphs, and sets of rule names, except for change event rules where request in S and C both map to new-req in CI, and accept and reject in S and C all map to del-custlink in SI. Implicitly, component rules that do not have a corresponding rule in an interface map to the empty rule \(\phi \), i.e., process in S maps to \(\phi \) in both SI and CI and request in S maps to \(\phi \) in DI. As observed above, this is allowed because after retyping these rules along the injections of type graphs, the resulting rules are spans of isomorphisms.
Given a transformation system R with type T, a transformation via p in R, denoted \(G {\mathop {\Longrightarrow }\limits ^{{p,m}}}_R H\), is a DPO diagram seen as an \(\mathbf {MSpan}_T\) morphism \(t = \langle t_L, t_K, t_R\rangle : \pi (p) \rightarrow s\) that relates the rule span \(\pi (p)= L \leftarrow K \rightarrow R\) and the bottom span \(s = (G \leftarrow D \rightarrow H)\), with match \(t_L = m\). We also write \(p/t: G \Rightarrow _R H\) or just \(\Rightarrow _R\) for the set of transformations.
A transformation sequence \(s = G_0 {\mathop {\Longrightarrow }\limits ^{{p_1, m_1}}} \dots {\mathop {\Longrightarrow }\limits ^{{p_n, m_n}}} G_n\) in R is a sequence of transformations.Footnote 2 We write \(\Rightarrow ^*_R\) for the set of transformation sequences in R.
Transformations in \(R'\) are reflected by \(\mathbf {Sys}\) morphisms. That means, if \(p'/t'\) is a transformation in \(R'\) then \(f^<(p'/t') = f_P(p')/f_\tau ^<(t') \circ f_\pi (p')\) is a transformation in R because \(f_\tau ^<\) preserves DPO diagrams and DPOs compose vertically (as \({\mathbf {MSpan}}\) morphisms). This yields a function \(f^<: (\Rightarrow _{R'}) \rightarrow (\Rightarrow _{R})\) extending to sequences as \(f^<: (\Rightarrow _{R'})^* \rightarrow (\Rightarrow _{R})^*\).
Transformation sequences in a runtime system \(S = \langle R,G\rangle \) are sequences in R that start from state G. The projection of sequences against morphisms extends to runtime systems as \(f^<: (\Rightarrow _{S'})^* \rightarrow (\Rightarrow _{S})^*\), provided that \(f: S \rightarrow S'\) is strict. Strict morphisms are preserved by transformations, that is, if \(f = \langle f_R,f_G\rangle : \langle R,G\rangle \rightarrow \langle R',G'\rangle \) is strict, \(p' / t': G' \Rightarrow H'\) in \(R'\) and \(f^<(p'/t') : G \Rightarrow H\) in R, then \(\langle f_R,id_H\rangle : \langle R,H\rangle \rightarrow \langle R',H'\rangle \) is strict, as \(H = f_{\tau }^<(H')\).
\(\mathbf {Sys}\) is finitely co-complete because it has an initial object \(R_\varnothing = \langle \emptyset , \{\phi \}, \pi \rangle \), where \(\pi (\phi ) = \emptyset \leftarrow \emptyset \rightarrow \emptyset \), and pushouts are built component-wise as pushouts on types, pullbacks on sets of rule names, and using amalgamation (pushouts in \(\mathbf {MSpan}\)) on rule spans.
Definition 3 (pushouts of systems)
Given a span of transformation systems \(R_1 {\mathop {\longleftarrow }\limits ^{{f_1}}} R_0 {\mathop {\longrightarrow }\limits ^{{f_2}}} R_2\) in \(\mathbf {Sys}\) with \(R_i = \langle T_i, P_i, \pi _i\rangle \), their pushout \(R_1 {\mathop {\longrightarrow }\limits ^{{f_2^*}}} R {\mathop {\longleftarrow }\limits ^{{f_1^*}}} R_2\) with \(R = \langle T, P, \pi \rangle \), is defined as follows.
-
\(T_1 {\mathop {\longrightarrow }\limits ^{{{f_2}_\tau ^*}}} T {\mathop {\longleftarrow }\limits ^{{{f_1}_\tau ^*}}} T_2\) is a pushout of \(T_1 {\mathop {\longleftarrow }\limits ^{{{f_1}_\tau }}} T_0 {\mathop {\longrightarrow }\limits ^{{{f_2}_\tau }}} T_2\) in \({\mathbf {C}}\)
-
\(P_1 {\mathop {\longleftarrow }\limits ^{{{f_2}_P^*}}} P {\mathop {\longrightarrow }\limits ^{{{f_1}_P^*}}} P_2\) is a pullback of \(P_1 {\mathop {\longrightarrow }\limits ^{{{f_1}_P}}} P_0 {\mathop {\longleftarrow }\limits ^{{{f_2}_P}}} P_2\) in \({\mathbf {Set}}^\bullet \)
-
for \(p \in P\) with \({f_2}_P^*(p) = p_1\), \({f_1}_P^*(p) = p_2\), and \({f_1}_P(p_1) = p_0 = {f_2}_P(p_2)\), let \({f_2}^*_\pi (p), {f_1}^*_\pi (p)\) and \(\pi (p)\) be defined by the pushout \(\pi _1(p_1) {\mathop {\longrightarrow }\limits ^{{{f_2}^*_\pi (p)}}} \pi (p) {\mathop {\longleftarrow }\limits ^{{{f_1}^*_\pi (p)}}} \pi _2(p_2)\) of \(\pi _1(p_1) {\mathop {\longleftarrow }\limits ^{{{f_1}_\pi (p_1)}}} \pi _0(p_0) {\mathop {\longrightarrow }\limits ^{{{f_2}_\pi (p_2)}}} \pi _2(p_2)\) in \(\mathbf {MSpan}\).
For a similar span in \(\mathbf {RSys}\) with local state graphs \(G_1 {\mathop {\longleftarrow }\limits ^{{{f_1}_G}}} G_0 {\mathop {\longrightarrow }\limits ^{{{f_2}_G}}} G_2\), the pushout in \(\mathbf {Sys}\) of the underlying transformation systems is lifted to \(\mathbf {RSys}\) by the pushout \(G_1 {\mathop {\longrightarrow }\limits ^{{{f_2}_G^*}}} G {\mathop {\longleftarrow }\limits ^{{{f_1}_G^*}}} G_2\) over the span of state graphs.
\({\mathbf {Set}}^\bullet \) is the category of pointed sets, i.e., sets with a distinguished element that is preserved by mappings. In our case these are the sets of rule names with the distinguished name \(\phi \) bound to the empty rule. It is easy to see that pushouts injections thus constructed are indeed \(\mathbf {Sys}\) or \(\mathbf {RSys}\) morphisms because their components are pushouts in \({\mathbf {C}}, {\mathbf {Set}}^\bullet \) and \(\mathbf {MSpan}\). The universal property follows directly from the component-wise construction.
Applying this to our example in Fig. 1, the pushout of S and D via DI results in a union of their type and state graphs and an amalgamation of rules over shared interface rules in DI. This leads to a disjoint parallel composition of rules where this interface rule is empty.
A coproduct of two systems \(R_1\) and \(R_2\) is a pushout over the empty system \(R_\varnothing \), which is initial in \(\mathbf {Sys}\). By contravariance of mapping types and rule names, this results in a coproduct of types and a product of rule names, such that each pair of rule names in the product is assigned a coproduct of the associated rules.
We can compose and decompose transformations over pushouts of systems if the morphisms relating them are strict.
Theorem 1 (compositionality of transformations)
Assume
-
a pushout \(S_1 {\mathop {\longrightarrow }\limits ^{{f_2^*}}} S {\mathop {\longleftarrow }\limits ^{{f_1^*}}} S_2\) of runtime systems \(S_1 {\mathop {\longleftarrow }\limits ^{{f_1}}} S_0 {\mathop {\longrightarrow }\limits ^{{f_2}}} S_2\), where all morphisms are strict, \(S_i = \langle R_i, G_i\rangle \) for \(i \in \{0,1,2\}\) and \(S = \langle R, G\rangle \);
-
a triple of transformations \(p_i/t_i: G_i \Rightarrow H_i\) in \(R_i\), whose DPO diagrams \(t_i\) are related by \(\mathbf {DPO}\) morphisms \(t_1 {\mathop {\longleftarrow }\limits ^{{{f_1}_\pi (p_1)}}} t_0 {\mathop {\longrightarrow }\limits ^{{{f_2}_\pi (p_2)}}} t_2\) and where \({f_1}_P(p_1) = p_0 = {f_2}_P(p_2)\).
Then, the transformations can be composed by a pushout in \(\mathbf {DPO}\) to yield a transformation \(p/t: G \Rightarrow H\) in S with \({f_1^*}_P(p) = p_2\) and \({f_2^*}_P(p) = p_1\).
Vice versa, a transformation \(p/t: G \Rightarrow H\) in \(\langle R,G\rangle \) decomposes into a pushout of transformations over \(S_1 {\mathop {\longleftarrow }\limits ^{{f_1}}} S_0 {\mathop {\longrightarrow }\limits ^{{f_2}}} S_2\) as \(p_1/t_1 = {f_2^*}^<(p/t)\) in \(S_1\), \(p_2/t_2 = {f_1^*}^<(p/t)\) in \(S_2\) and \({f_1}^<(p_1/t_1) = p_0/t_0 = {f_2}^<(p_2/t_2)\) in \(S_0\).
Proof (sketch)
Both directions require that pushouts are stable under pullbacks, which is true in \({\mathbf {C}}\) by assumption.
Applying a sequence of accept, process, accept to the state graph in S, the result is a graph that looks like the right-hand side (preserved black and new green parts) of accept. In D the first step is an application of the empty rule \(\phi \), the second step has no effect on the graph but extends the match of process in S to check for a contract linked to the customer, and the third step deletes that link and adds the accept node and its edge, leaving a graph that looks like the right-hand side accept in D.
Since the state graph of S in Fig. 1 is a subgraph of that of D, when the pushout of runtime systems S and D via DI merges their state graphs, the resulting graph is isomorphic to that of D. The result above ensures that we can either transform this graph in the pushout system of S and D over DI, or do so in S and D with shared transformations in DI and then merge the resulting graphs, i.e. synchronised local transformations exist if and only if there is a global transformation, and they have the same effect.
Theorem 1 ensures the compositionality of the operational semantics of components in Sect. 7, where transformations compose along composition of components and transformations in a composite component can be decomposed into synchronised transformations in its constituents.
5 Components
A component has runtime systems as body, left and right interfaces. Both interfaces are equipped with a morphism to the body. Formally, components are defined as abstract cospans in \(\mathbf {RSys}\). Components with matching left-right interfaces can be composed using pushouts in \(\mathbf {RSys}\). Note that, in our running example, the left and right interfaces are conceptually the provided and required interfaces of components. However, we stick to the typical left/right terminology of cospans, instead of using the provide/require terminology of software components, because in our operational semantic introduced later both interfaces behave identically, allowing to synchronize the transformations of the components they are connected to. The provided/required terminology suggests instead an invocation-based semantics, where a component can trigger through the required interface the execution of another component connected to the matching provided interface. This kind of semantics is topic of future work.
Components can also be composed in parallel using coproducts. The resulting structure is a symmetric monoidal category \(\mathbf {Com}\) having the same objects of \(\mathbf {RSys}\) and components as arrows (from the left to the right interface). This category is shown to be also a Frobenius algebra, implying that one can define arbitrary topologies of components.
Here we focus on the static interconnections of components, while in Sect. 7 we discuss their operational semantics based on transformations. We anticipate that the rich structure of the category of components cannot be fully exploited for the operational semantics, because only strict morphisms reflect transformations. We introduce strict components, where morphism to the body are strict, and discuss conditions ensuring that strictness is preserved by composition.
Cospans \(c = (A {\mathop {\longrightarrow }\limits ^{{a}}} C {\mathop {\longleftarrow }\limits ^{{b}}} B)\) and \(c' = (A {\mathop {\longrightarrow }\limits ^{{a'}}} C' {\mathop {\longleftarrow }\limits ^{{b'}}} B)\) are isomorphic if there is an isomorphism \(i: C \rightarrow C'\) commuting the resulting triangles. We denote by \(A [{\mathop {\longrightarrow }\limits ^{{a}}} C {\mathop {\longleftarrow }\limits ^{{b}}}] B\) the isomorphism class of c, called an abstract cospan.
Definition 4 (components)
A component is an abstract cospan \(c = \langle Li [{\mathop {\longrightarrow }\limits ^{{li}}} Bd {\mathop {\longleftarrow }\limits ^{{ri}}}] Ri\rangle \) in \(\mathbf {RSys}\). Morphisms \(li: Li \rightarrow Bd\) and \(ri: Ri \rightarrow Bd\) map the left and right interfaces to the body. Component c is strict if both li and ri are strict.
The category \(\mathbf {Com}\) of components has runtime systems as objects and components as arrows. The composition of components \(c_2 \circ c_1\), for \(c_i = \langle Li_i [{\mathop {\longrightarrow }\limits ^{{li_i}}} Bd_i {\mathop {\longleftarrow }\limits ^{{ri_i}}}] Ri_i\rangle \) and \(i = 1,2\), is defined if \(Li_2 = Ri_1\). Then
is the isomorphism class of the cospan obtained by a pushout \(Bd_1 {\mathop {\longrightarrow }\limits ^{{li_2^*}}} Bd {\mathop {\longleftarrow }\limits ^{{ri_1^*}}} Bd_2\) of \(ri_1\) and \(li_2\) with \(li = li_2^* \circ li_1\) and \(ri = ri_1^* \circ ri_2\). If \(c_1\) and \(c_2\) are both strict, then they are compatible if the pushout injections \(li^*_2\) and \(ri^*_1\) are strict. In this case also \(c_2 \circ c_1\) is strict because strict morphisms compose. If \(c_1\) and \(c_2\) are strict and compatible we will denote their strict composition also by \(c_2 \circ _{\!s}c_1\).
For a runtime system S in \(|\mathbf {RSys}|\) its identity component is given by \(id_{S} = \langle S [{\mathop {\longrightarrow }\limits ^{{id_{S}}}} S {\mathop {\longleftarrow }\limits ^{{id_{S}}}}] S\rangle \), and it is strict.
Composition over shared interfaces allows to connect strict components by synchronising their transformations. In \(\mathbf {Com}\) our example’s components are represented as arrows \(C: CI \rightarrow SI\), \(S: SI \rightarrow CI + DI\) and \(D: DI \rightarrow R_\varnothing \), their composition realised by the composition in \(\mathbf {Com}\), e.g., \(S \circ C: CI \rightarrow CI + DI\) is the composition of C and D over SI. In order to link interface CI from the right of S to the left of C (as required for its use as a callback interface) we need the additional structure of parallel composition and component connectors.
Definition 5
(parallel composition in Com). The parallel composition \(c_1+ c_2\) of components \(c_i = \langle Li_i [{\mathop {\longrightarrow }\limits ^{{li_i}}} Bd_i {\mathop {\longleftarrow }\limits ^{{ri_i}}}] Ri_i\rangle \) for \(i = 1,2\) is defined as the isomorphism class of the cospans obtained by a coproduct of the interface and body systems in \(\mathbf {RSys}\)
This defines a monoidal functor \(+: \mathbf {Com}\times \mathbf {Com}\rightarrow \mathbf {Com}\). Furthermore, for each S, \(S'\), let \(\sigma _{S, S'}: \langle S + S' [{\mathop {\longrightarrow }\limits ^{{ [inr_{S}, inl_{S'}] }}} S' + S {\mathop {\longleftarrow }\limits ^{{id_{S'+S}}}}] S' + S\rangle \) be their symmetry component.
The parallel composition of two strict components can be shown to be strict, and so are the symmetries. We can represent a component c, the composition \(c_2\circ c_1\) and the parallel composition \(c_1+ c_2\) in an intuitive graphical way as:

Identity and symmetry components are seen as connectors passing actions from one interface to the other. Other such connectors can be defined, for every systems S and \(S'\), by exploiting suitable morphisms in \(\mathbf {RSys}\).
-
The duplicator is component
 ;
; -
The co-duplicator is component \(\varDelta _{S} = \langle S + S [{\mathop {\longrightarrow }\limits ^{{ [id_{S}, id_{S}] }}} S {\mathop {\longleftarrow }\limits ^{{id_{S}}}}] S\rangle \);
-
The discharger is component \(!_{S} = \langle S [{\mathop {\longrightarrow }\limits ^{{id_{S}}}} S {\mathop {\longleftarrow }\limits ^{{\emptyset }}}] R_\varnothing \rangle \);
-
The co-discharger is component \(?_{S} = \langle R_\varnothing [ {\mathop {\longrightarrow }\limits ^{{\emptyset }}} S {\mathop {\longleftarrow }\limits ^{{id_{S}}}} ] S\rangle \).
Graphically, we show such connector components, which are all strict, as:

Theorem 2
(Com as Frobenius algebra). Category \(\mathbf {Com}\) with the monoidal functor \(+\) and the family \(\sigma \) of symmetries of Definition 5 is a symmetric monoidal category. Furthermore, equipped with the families of connector components  , \(\varDelta \), ! and ? as defined above \(\mathbf {Com}\) is a Frobenius algebra.
, \(\varDelta \), ! and ? as defined above \(\mathbf {Com}\) is a Frobenius algebra.
Proof
The category of abstract cospans built from a category with coproducts inherits a monoidal structure, induced by coproducts, which satisfies the laws for Frobenius algebras: see e.g. [3, Section 2.2].
6 Architectural Models
Due to Theorem 2 we can depict networks of components as string diagrams [3], a graphical syntax for structures whose basic elements take multiple inputs and outputs. The axioms of Frobenius algebras are sound and complete for string diagrams, in the sense that the diagrams representing two terms of the algebra can be topologically deformed into each other without cutting or joining wires if and only if the two terms are provably equal by the axioms.
Thanks to the axioms of symmetric monoidal categories (which we omit for brevity) the axioms of Frobenius algebras can be depicted as follows.
-
for each object, \(\varDelta \) and ? form a commutative monoid, i.e., they satisfy associativity, commutativity, and ? is the unit:

-
for each object,
 and ! form a cocommutative comonoid, i.e., they satisfy associativity, commutativity, and ! is the counit:
and ! form a cocommutative comonoid, i.e., they satisfy associativity, commutativity, and ! is the counit: 
-
the monoid and comonoid structures satisfy the Frobenius and special laws:
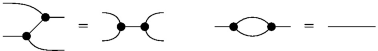
Since \(\mathbf {Com}\) satisfies the axioms of Frobenius algebras, we can specify a complex component in \(\mathbf {Com}\) by connecting the interfaces of its basic components. Any such drawings representing the same connections between interfaces are equivalent, such as two the string diagrams on the left below, both representing the component diagram of Sect. 2 with basic components C, S, and D.

On the right we show how the left string diagram arises as sequential composition  of expressions in the algebra of components and connectors, with vertical dashed lines in the figure representing “;”. Based on the interpretation of basic components and connectors in \(\mathbf {Com}\), the constituent expressions represent the following cospans.
of expressions in the algebra of components and connectors, with vertical dashed lines in the figure representing “;”. Based on the interpretation of basic components and connectors in \(\mathbf {Com}\), the constituent expressions represent the following cospans.
-
1.
\(?_{CI} = \langle R_\varnothing [{\mathop {\longrightarrow }\limits ^{{\emptyset }}} CI {\mathop {\longleftarrow }\limits ^{{id_{CI}}}}] CI\rangle \);
-
2.
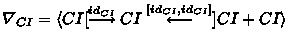 ;
; -
3.
\(id_{CI} + C = \langle CI + CI [{\mathop {\longrightarrow }\limits ^{{id_{CI} + ci_C}}} CI + C {\mathop {\longleftarrow }\limits ^{{id_{CI} + si_C}}} ] CI + SI\rangle \);
-
4.
\(id_{CI} + S = \langle CI+SI [{\mathop {\longrightarrow }\limits ^{{id_{CI} + si_S}}} CI+S {\mathop {\longleftarrow }\limits ^{{id_{CI} + [ci_S, di_S]}}} ] CI+CI+DI\rangle \);
-
5.
\(\varDelta _{CI} + id_{DI} = \langle CI+CI+DI [{\mathop {\longrightarrow }\limits ^{{[id_{CI}, id_{CI}] + id_{DI}}}} CI+DI {\mathop {\longleftarrow }\limits ^{{id_{CI}+id_{DI}}}} ] CI+DI\rangle \);
-
6.
\(!_{CI} + D = \langle CI+DI [{\mathop {\longrightarrow }\limits ^{{id_{CI}+di_D}}} CI+D {\mathop {\longleftarrow }\limits ^{{[\emptyset , \emptyset ]}}} ]R_\varnothing \rangle \).
Thus string diagrams serve as a bridge between the network-level description of an architecture in a component diagram and its “implementation” in graph rewriting components. The result of composing cospans 1–6 is the global system Sys in Fig. 1 with global rules emerging as amalgamation of component over interfaces rules and global state as pushout of component over interface states.
String diagrams providing a syntax for component networks are generated freely from an architectural signature of basic components and interfaces, just as term syntax for algebras is generated freely from an algebraic signature.
Definition 6 (architectural signature)
An architectural signature \(AS = \langle I, C, dom, cod\rangle \) consists of sets of interface names I and component names C with functions \(dom, cod: C \rightarrow I^*\) assigning each component name their sequences of names of left and right interfaces.
The free Frobenius algebra \(\text{ frob }(AS)\) over AS is a category that has sequences \(I^*\) as objects. Morphisms are directed hypergraphs with sorted interface nodes, called network graphs. They play the role of terms in algebraic signatures. Named components are represented by hyberedges distinguishing attachments of left and right interfaces. An architectural model assigns interpretations to interface and component names.
Definition 7 (interpretation, model)
An interpretation for a signature AS is a hypergraph morphism \(f = \langle f_I, f_C\rangle : AS \rightarrow \mathbf {Com}\), i.e. a pair of mappings compatible with the domains and codomains of component names in AS and components in \(\mathbf {Com}\). That means, each \(c: Li_1 \dots Li_n \rightarrow Ri_1 \dots Ri_m\) in AS is mapped to an arrow \(f_C(c): f_I(Li_1) + \cdots + f_I(Li_n) \rightarrow f_I(Ri_1) + \cdots + f_I(Ri_m)\).
The architectural model for interpretation f is given by the functor \(F: \text{ frob }(AS) \rightarrow \mathbf {Com}\) that freely extends the given interpretation, i.e., such that \(F \circ \eta _{AS} = f\) for the embedding \(\eta _{AS}: AS \rightarrow \text{ frob }(AS)\).
Theorem 2 ensures that F is well defined, i.e., for \(g, h: S \rightarrow T\) in \(\text{ frob }(AS)\), \(g = h\) implies \(F(g) = F(h)\), because \(\mathbf {Com}\) satisfies the Frobenius algebra axioms.
Category \(\text{ frob }(AS)\) and model functor F represent the space of all component networks over a given collection of basic components with their interpretations. Since \(\text{ frob }(AS)\) is free over AS, the extension F is unique and can be represented finitely by the hypergraph morphism \(f: AS \rightarrow \mathbf {Com}\). If we consider the states of components only, this is similar to distributed graphs where a network graph forms the shape of a diagram in a category of local graphs, except that in our case graphs with interfaces are (part of) the arrows rather than the objects of the categories involved. However, in addition to states, we distribute entire runtime systems with interfaces along a network graph given by a morphism g in \(\text{ frob }(AS)\). For a model F, a configuration consists of g and its interpretation F(g) mapping the components named in g to their implementation in \(\mathbf {Com}\).
In our example, interface names are \(I = \{si, ci, di\}\) and component names are \(C = \{c, s, d\}\) with dom and cod given by \(c: c i\rightarrow si, s: si \rightarrow ci\,di\) and \(d: di \rightarrow \epsilon \) (the empty sequence). Interpretation f is defined by replacing lower with upper case characters, e.g., \(f(s: si \rightarrow ci\,di) = S: SI \rightarrow CI + DI\).
7 Structural Operational Semantics
We exploit the compositionality of runtime system transformations for defining a structural operational semantics that derives the behaviour of complex components from that of basic ones and Frobenius algebra connectors. Since only morphims that are strict reflect transformations between runtime systems, we will focus on strict components only.
When presenting an architecture model, a basic component with n left interfaces and m right interfaces is shown as a diagram in \(\mathbf {RSys}\) of shape \(D = \langle Li_i {\mathop {\longrightarrow }\limits ^{{li_i}}} Bd {\mathop {\longleftarrow }\limits ^{{ri_j}}} Ri_j\rangle \) with \(1 \le i \le n\) and \(1 \le j \le m\). In \(\mathbf {Com}\) this basic component is an abstract cospan constructed by the coproducts of their left and right interfaces as
where \(li = [li_1, \dots , li_n]\) and \(ri = [ri_1, \dots , ri_m]\) are the co-pairings of the interface morphisms, induced by the universality of the respective coproducts. It is sufficient to require that all the interface morphisms are strict: the strictness of the co-pairing morphisms can be shown easily.
Since strict components are based on strict \(\mathbf {RSys}\) morphisms, they have an internal state in the body projected to corresponding states of the interfaces. Let \(c = \langle Li [{\mathop {\longrightarrow }\limits ^{{li}}} Bd {\mathop {\longleftarrow }\limits ^{{ri}}}] Ri\rangle \) be a strict component. When the state changes through an internal transformation \(s: G_{Bd} \Rightarrow _c G_{Bd'}\) of the body, s is only partly hidden because it is reflected by the strict morphisms li and ri to interface transformation \(a= li^<(s)\) in Li and \(b = ri^<(s)\) in Ri, that we call (left and right) observations. This defines a strict component transformation that we denote as
where \(c'\) is the resulting component that shares types and rules with c, and may only differ for the states. Note that this notation only makes sense if c is strict, thus its use establishes an assumption or a proof obligation, depending on the context. The strictness of \(c'\) follows by that of c and because strict morphisms are preserved by transformations.
If strict components \(c_i = \langle Li_i [{\mathop {\longrightarrow }\limits ^{{li_i}}} Bd_i {\mathop {\longleftarrow }\limits ^{{ri_i}}}] Ri_i\rangle \) for \(i = 1,2\) are connected through \(Li_2 = Ri_1\), internal transformations of \(c_1\) and \(c_2\) need to synchronize by projecting the same observation to the shared interface, that is if
then we must have \(b_1 = a_2\). If \(c_1\) and \(c_2\) are compatible (and thus \(c_2 \circ c_1\) is strict, see Definition 4) then also \(c'_1\) and \(c'_2\) can be shown to be compatible, and this results in a composed transformation of \(c_2 \circ _{\!s}c_1\), projecting to interfaces \(Li_1\) and \(Ri_2\) the same observation projected by the transformations of \(c_1\) and \(c_2\), respectively.
For the parallel composition of strict components, which is strict, recall that the set of rule names of a coproduct of systems \(R_1 + R_2\) is a product \(P_1 \times P_2\). Therefore, a transformation \(a = p/t\) in \(R_1 + R_2\) is an application of a rule pair \(p = \langle p_1, p_2\rangle \in P_1 \times P_2\) with \(p_i \in P_i\). The rule span \(\pi (\langle p_1, p_2\rangle ) = \pi _1(p_1) + \pi _2(p_2)\) is a coproduct in \(\mathbf {MSpan}\) and the DPO diagram \(t = t_1 + t_2\) a coproduct in \(\mathbf {DPO}\). Hence, a represents the disjoint parallel occurrence of transformations \(a_i = p_i/t_i\) in \(R_i\) for \(i = 1,2\), which we write using juxtaposition as \(a_1\, a_2\).
Summarizing, for strict and parallel composition we have the rules
For all connector components, we can easily infer from the definitions that their transformations are triggered by a transformation in the left or right interface. For interface transformations \(a: S \Rightarrow S', a_i: S_i \Rightarrow S'_i\), we have the following connector component transformations:
-
\(id_{S} \mathrel {\mathop {\Longrightarrow }\limits ^{a}_{a}} id_{S'}\) synchronises transformations between the two interfaces;
-
\(\sigma _{S_1, S_2} \mathrel {\mathop {\Longrightarrow }\limits ^{a_1 a_2}_{a_2 a_1}} \sigma _{S_2', S_1'}\) crosses the wires between \(S_1+ S_2\) and \(S_2 + S_1\);
-
 synchronises transformations of its left and two right interfaces;
synchronises transformations of its left and two right interfaces; -
\(\varDelta _{S} \mathrel {\mathop {\Longrightarrow }\limits ^{a a}_{a}} \varDelta _{S'}\) synchronises transformations of its right and two left interfaces;
-
\(!_{S} \mathrel {\mathop {\Longrightarrow }\limits ^{a}_{\emptyset }} !_{S'}\) allows arbitrary transformations on its left interface;
-
\(?_{S} \mathrel {\mathop {\Longrightarrow }\limits ^{\emptyset }_{a}} ?_{S'}\) allows arbitrary transformations on its right interface.
Component transformations can be composed and decomposed along both strict and parallel composition of components.
Theorem 3 (composition and decomposition of transformations)
Assume strict components \(c_i = \langle Li_i [{\mathop {\longrightarrow }\limits ^{{li_i}}} Bd_i {\mathop {\longleftarrow }\limits ^{{ri_i}}}] Ri_i\rangle \) for \(i = 1,2\). Then,
For \(c_1, c_2\) as above such that \(Li_2 = Ri_1\) and \(c_1, c_2\) compatible,
Proof
The parallel composition \(c_1 + c_2\) is based on a component-wise coproduct of the body and interface runtime systems of \(c_1\) and \(c_2\). Viewing the coproduct as a pushout over the initial system \(R_\varnothing \), we can use Theorem 1 to derive s as composition of \(s_1\) and \(s_2\), and \(s_1, s_2\) as decomposition of s.
This means that rule and DPO diagram of s are coproducts of rules and DPO diagrams of \(s_1\) and \(s_2\), respectively. Since \(a_1, a_2, b_1, b_2\) are defined by projections via pullbacks which, in an adhesive category with strict initial object, preserve coproducts, the same relation holds for the rules and transformations of interfaces. Hence \(a_1, a_2\) and \(b_1, b_2\) composes into \(a_1\, a_2\) and \(b_1\, b_2\) respectively, and vice versa. For strict composition we can apply Theorem 1 directly: The body of \(c_2 \circ _{\!s}c_2\) is a pushout of those of \(c_1\) and \(c_2\) over the shared interface, and interface states and transformations are projections of those in the bodies, so s is the composition of \(s_1\) and \(s_2\) and vice versa.
With bisimilarity \(\equiv \) of strict components as the largest relation satisfying \(f \equiv g\) iff for all a, b \(f \mathrel {\mathop {\Longrightarrow }\limits ^{a}_{b}} h \text{ iff } g \mathrel {\mathop {\Longrightarrow }\limits ^{a}_{b}} k \text{ and } h \equiv k\), we have the following result.
Theorem 4 (bisimilarity as congruence)
Bisimilarity \(\equiv \) on strict components is a congruence for parallel composition \(+\) and strict composition \(\circ _{\!s}\).
Proof
Assume \(f \equiv f', g \equiv g'\). If \(g \circ _{\!s}f \mathrel {\mathop {\Longrightarrow }\limits ^{a}_{b}} k \circ _{\!s}h\) then \(f \mathrel {\mathop {\Longrightarrow }\limits ^{a}_{c}} h\) and \(g \mathrel {\mathop {\Longrightarrow }\limits ^{c}_{b}} k\) by Theorem 3 (decomposition). This implies \(f' \mathrel {\mathop {\Longrightarrow }\limits ^{a}_{c}} h'\) and \(g' \mathrel {\mathop {\Longrightarrow }\limits ^{c}_{b}} k'\) since \(f \equiv f'\) and \(g \equiv g'\), and then \(g' \circ _{\!s}f' \mathrel {\mathop {\Longrightarrow }\limits ^{a}_{b}} k' \circ _{\!s}h'\) by Theorem 3 (composition). Reversing the roles of f, g and \(f', g'\) we can show the inverse implication. Then, by coinduction, \(h \circ _{\!s}k \equiv h' \circ _{\!s}k'\) implies \(g \circ _{\!s}f \equiv g' \circ _{\!s}f'\). The proof for \(+\) is analogous.
Concretely this means that, if a component works in a given context, e.g. C in the context of S and D as defined in our example architecture, and we replace that context by a behaviourally equivalent one, e.g., adding a second instance of D for redundancy, the resulting system will have an equivalent overall behaviour.
8 Conclusion and Related Work
We introduced a component model for graph rewriting systems that allows to represent a global system as a network of components with interfaces representing shared views of internal states and transformations, and such that their composition reconstructs the global system.
Formally and conceptually our model represents the convergence of three main ingredients: Distributed graph transformations [18] formalise synchronised transformations of distributed graphs. Various notions of morphisms between graph transformation systems, discussed in [7] with their semantic properties, support the modularisation of types and rules. Algebraic representations of (network) graphs as arrows in a symmetric monoidal category and their visualisation by string diagrams [3] provide a syntax for component architectures.
Early steps towards modularity of formal specifications have been made in algebraic specifications [5] where the body of a module is related by morphisms with its import and export interfaces defining, respectively, required and provided services. In graph rewriting, work on modularity was inspired by algebraic specifications, programming and software engineering concepts [5], resulting in a number of proposals surveyed in [13]. More recently, [11] also proposes a compositional approach to graph transformations where local graphs with shared interfaces are composed via colimits into a global graph, and rules acting on local graphs are composed into a global rule acting on the global graph. Differently from our approch, however, compositionality is addressed at the instance level, not at the type level. Several other contributions address compositionality in graph transformation at instance level, including among others synchronized hyperedge replacement [9, 14], rule amalgamation [2], distributed graph transformation [18] and borrowed contexts [1, 6]. An interesting topic for future work is to compare the expressive power of compositionality modeled at instance or at type level.
Modules of typed graph transformation systems [12] follow the structure of algebraic specification modules while [7] combines modularity and service-oriented concepts. None of the above include a notion of state, i.e. they structure the specification but not the runtime of a system. We consider this the main difference between modules and components. Conversely, distributed graph transformations capture the distribution of graphs, rules and transformations in a category of diagrams over graphs [18] but without modularity at specification level.
We provide for the first time a component model integrating these two features. In this more general setting we achieve compositionality like in distributed graph transformations, relating global and synchronised local transformations, and describe the network architecture using Frobenius algebras to provide a constructive “compilation” assembling complex components from basic constituents.
In the future we would like to make explicit the invocation-based intuition of components, using a type system and refined operational semantics to distinguish provided and required interfaces and caller/callee roles in the synchronised applications of rules. We will exploit and extend the Frobenius structure to (1) support architectural equations defining, e.g., derived components as expressions over basic ones or behavioural equalities between configurations; (2) allow architectural reconfiguration as string diagram rewriting; and (3) consider a bigraph-like network level with hierarchical components.
Our notion of bisimilarity over doubly-labelled transformations as a congruence is analogous to functoriality of tile bisimilarity, and we can indeed phrase our operational semantics as an instance of the tile model [10]. In [4] tile bisimilarity is extended to remain compositional under dynamic reconfiguration.
Notes
- 1.
\({\mathbf {TC}}\) is obtained by applying the Grothendieck construction to the indexed category \({\mathbf {C}}^{op} \rightarrow {\mathbf {Cat}}\), mapping each object T to category \({\mathbf {C}}_T\) and each arrow to the corresponding retyping functor.
- 2.
We may drop the reference to the system if this is clear from context.
References
Baldan, P., Ehrig, H., König, B.: Composition and decomposition of DPO transformations with borrowed context. In: Corradini, A., Ehrig, H., Montanari, U., Ribeiro, L., Rozenberg, G. (eds.) ICGT 2006. LNCS, vol. 4178, pp. 153–167. Springer, Heidelberg (2006). https://doi.org/10.1007/11841883_12
Boehm, P., Fonio, H., Habel, A.: Amalgamation of graph transformations: a synchronization mechanism. J. Comput. Syst. Sci. 34(2/3), 377–408 (1987). https://doi.org/10.1016/0022-0000(87)90030-4
Bonchi, F., Gadducci, F., Kissinger, A., Sobocinski, P., Zanasi, F.: String diagram rewrite theory I: rewriting with Frobenius structure. J. ACM 69(2), 14:1–14:58 (2022)
Bruni, R., Montanari, U., Sassone, V.: Observational congruences for dynamically reconfigurable tile systems. Theoret. Comput. Sci. 335(2–3), 331–372 (2005). https://eprints.soton.ac.uk/261844/
Ehrig, H., Mahr, B.: Fundamentals of Algebraic Specification 2: Module Specifications and Constraints. EATCS Monographs on Theoretical Computer Science, vol. 21. Springer Verlag, Berlin (1990). https://doi.org/10.1007/978-3-642-61284-8
Ehrig, H., König, B.: Deriving bisimulation congruences in the DPO approach to graph rewriting with borrowed contexts. Math. Struct. Comput. Sci. 16(6), 1133–1163 (2006). https://doi.org/10.1017/S096012950600569X
Engels, G., Heckel, R., Cherchago, A.: Flexible interconnection of graph transformation modules. In: Kreowski, H.-J., Montanari, U., Orejas, F., Rozenberg, G., Taentzer, G. (eds.) Formal Methods in Software and Systems Modeling. LNCS, vol. 3393, pp. 38–63. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-31847-7_3
Evans, E.: Domain-Driven Design: Tackling Complexity in the Heart of Software. Addison-Wesley, Boston (2004)
Ferrari, G.L., Hirsch, D., Lanese, I., Montanari, U., Tuosto, E.: Synchronised hyperedge replacement as a model for service oriented computing. In: de Boer, F.S., Bonsangue, M.M., Graf, S., de Roever, W.-P. (eds.) FMCO 2005. LNCS, vol. 4111, pp. 22–43. Springer, Heidelberg (2006). https://doi.org/10.1007/11804192_2
Gadducci, F., Montanari, U.: The tile model. In: Plotkin, G.D., Stirling, C., Tofte, M. (eds.) Proof, Language, and Interaction, Essays in Honour of Robin Milner, pp. 133–166. The MIT Press, Cambridge (2000)
Ghamarian, A.H., Rensink, A.: Generalised compositionality in graph transformation. In: Ehrig, H., Engels, G., Kreowski, H.-J., Rozenberg, G. (eds.) ICGT 2012. LNCS, vol. 7562, pp. 234–248. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-33654-6_16
Groe-Rhode, M., Presicce, F.P., Simeoni, M.: Refinements and modules for typed graph transformation systems. In: Fiadeiro, J.L. (ed.) WADT 1998. LNCS, vol. 1589, pp. 138–151. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48483-3_10
Heckel, R., Engels, G., Ehrig, H., Taentzer, G.: Classification and comparison of modularity concepts for graph transformation systems. In: Engels, G., Kreowski, H.J., Rozenberg, G. (eds.) Handbook of Graph Grammars and Computing by Graph Transformation, vol. 2, pp. 669–690. World Scientific (1999)
Dan, H., Ugo, M.: Synchronized hyperedge replacement with name mobility. In: Larsen, K.G., Nielsen, M. (eds.) CONCUR 2001. LNCS, vol. 2154, pp. 121–136. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44685-0_9
Hogan, A., et al.: Knowledge Graphs. No. 22 in Synthesis Lectures on Data, Semantics, and Knowledge, Morgan & Claypool (2021). https://kgbook.org/
Lassila, O.: Graph abstractions matter, December 2021. https://2021.connected-data.world
Schad, J.: Graph powered machine learning: Part 1. ML Conference Berlin, October 2021. https://mlconference.ai/ml-summit/
Taentzer, G.: Distributed graphs and graph transformation. Appl. Categorical Struct. 7(4), 431–462 (1999)
Xiao, G., Ding, L., Cogrel, B., Calvanese, D.: Virtual knowledge graphs: an overview of systems and use cases. Data Intell. 1(3), 201–223 (2019). https://doi.org/10.1162/dint_a_00011
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Heckel, R., Corradini, A., Gadducci, F. (2022). Graph Rewriting Components. In: Behr, N., Strüber, D. (eds) Graph Transformation. ICGT 2022. Lecture Notes in Computer Science, vol 13349. Springer, Cham. https://doi.org/10.1007/978-3-031-09843-7_2
Download citation
DOI: https://doi.org/10.1007/978-3-031-09843-7_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-09842-0
Online ISBN: 978-3-031-09843-7
eBook Packages: Computer ScienceComputer Science (R0)






 ;
;
 and ! form a cocommutative comonoid, i.e., they satisfy associativity, commutativity, and ! is the counit:
and ! form a cocommutative comonoid, i.e., they satisfy associativity, commutativity, and ! is the counit: 
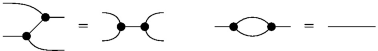
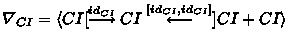 ;
;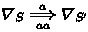 synchronises transformations of its left and two right interfaces;
synchronises transformations of its left and two right interfaces;