Active Channel Sparsification: Realizing Frequency-Division Duplexing Massive MIMO with Minimal Overhead

Abstract

Multiuser multiple-input multiple-output (MIMO) consists of exploiting multiple antennas at the base station (BS) side, in order to multiplex over the spatial-domain several data streams to a number of users sharing the same time–frequency transmission resource (channel bandwidth and time slots).

11.1 Introduction

Multiuser multiple-input multiple-output (MIMO) consists of exploiting multiple antennas at the base station (BS) side, in order to multiplex over the spatial-domain several data streams to a number of users sharing the same time–frequency transmission resource (channel bandwidth and time slots). For a block-fading channel with spatially independent fading and a coherence block of T symbols,¹ the high-SNR sum capacity behaves as $C(\text{SNR}) = M^* (1 - M^*/T) \log \text{SNR} + O(1)$, where $M^* = \min \{M,K,T/2\}$, M denotes the number of BS antennas, and K denotes the number of single-antenna users [1, 39, 61]. When M and the number of users are potentially very large, the system pre-log factor ² is maximized by serving K = T∕2 data streams (users). While any number M ≥ K of BS antennas yields the same (optimal) pre-log factor, a key observation made in [40] is that, when training a very large number of antennas comes at no additional overhead cost, it is indeed convenient to use M ≫ K antennas at the BS. In this way, at the cost of some additional hardware complexity, very significant benefits at the system level can be achieved. These include: (i) energy efficiency (due to the large beamforming gain); (ii) inter-cell interference reduction; (iii) a dramatic simplification of user scheduling and rate adaptation, due to the inherent large-dimensional channel hardening [34]. Systems for which the number of BS antennas M is much larger than the number of DL data streams K are generally referred to as massive MIMO (see [34, 40, 41] and references therein). Massive MIMO has been the subject of intense research investigation and development and is expected to be a cornerstone of the 5th generation of wireless/cellular systems [5].

In order to achieve the benefits of massive MIMO, the BS must learn the downlink (DL) channel coefficients for K users and M ≫ K BS antennas. For time-division duplexing (TDD) systems, due to the inherent UL–DL channel reciprocity [39], this can be obtained from K mutually orthogonal UL pilots transmitted by the users. Unfortunately, the UL–DL channel reciprocity does not hold for frequency-division duplexing (FDD) systems, since the UL and DL channels are separated in frequency by much more than the channel coherence bandwidth [56]. Hence, unlike TDD systems, in FDD, the BS must actively probe the DL channel by sending a common DL pilot signal and request the users to feed their channel state back.

In order to obtain a “fresh” channel estimate for each coherence block, T _dl out of T symbols per coherence block must be dedicated to the DL common pilot. Assuming (for simplicity of exposition) a delay-free channel-state feedback, the resulting DL pre-log factor is given by $K \times \max \{0, 1 - T_{\text{ dl}}/T\}$, where K is the number of served users, and $\max \{0, 1 - T_{\text{ dl}}/T\}$ is the penalty factor incurred by DL channel training. Conventional DL training consists of sending orthogonal pilot signals from each BS antenna. Thus, in order to train M antennas, the minimum required training dimension is T _dl = M. Hence, with such scheme, the number of BS antennas M cannot be made arbitrarily large. For example, consider a typical case taken from the LTE system [53], where groups of users are scheduled over resource blocks spanning 14 OFDM symbols × 12 subcarriers, for a total dimension of T = 168 symbols in the time–frequency plane. Consider a typical massive MIMO configuration serving K ∼ 20 users with M ≥ 200 antennas (e.g., see [37]). In this case, the entire resource block dimension would be consumed by the DL pilot, leaving no room for data communication. Furthermore, feeding back the M-dimensional measurements (or estimated/quantized channel vectors) also burdens the system with a significant UL feedback overhead [7, 27, 32, 35, 60].

While the argument above is kept informal on purpose, it can be made information-theoretically rigorous. The central issue is that, if one insists to estimate the K × M channel matrix in an “agnostic” way, i.e., without exploiting the channel fine structure, a hard dimensionality bottleneck kicks in and fundamentally limits the number of data streams that can be supported in the DL by FDD systems. It follows that gathering “massive MIMO gains” in FDD systems is a challenging problem. On the other hand, current wireless networks are mostly based on FDD. Such systems are easier to operate and more effective than TDD systems in situations with symmetric traffic and delay-sensitive applications [9, 26, 47]. In addition, converting current FDD systems into TDD would represent a non-trivial cost for wireless operators. With these motivations in mind, a significant effort is recently dedicated to reduce the common DL training dimension and feedback overhead in order to materialize the numerous benefits of massive MIMO also for FDD systems.

The focus of this chapter is to put forth an efficient scheme for massive MIMO in FDD systems. Our goal is to be able to serve as many users as possible even with a very small number of DL pilots, compared to the inherent channel dimension. Similar to previous works [11, 15, 47], we consider a scheme where each user sends back its T _dl noisy pilot observations per slot, using non-quantized analog feedback (see [7, 32]). Hence, achieving a small T _dl yields both a reduction of DL training and UL feedback overhead. It turns out that we have to artificially reduce each user channel dimension in a clever way, such that a single common DL pilot of assigned dimension T _dl is sufficient to estimate a large number of user channels. In the CS-based works mentioned above, the pilot dimension depends on the channel sparsity level s (the number of non-zero components in the angle/beam domain). In fact, standard CS theory states that stable sparse signal reconstruction is possible using $T_{\text{ dl}} = O(s \log M)$ measurements.³ In a rich scattering environment, s is large or may in fact vary from user to user or in different cell locations. Even if the channel support is known, one needs at least s measurements for a stable channel estimation. Hence, these CS-based methods (including the ones having access to support information) may or may not work well, depending on the propagation environment. In order to allow channel estimation with a given pilot dimension T _dl, we use the DL covariance information in order to design an optimal sparsifying precoder. This is a linear transformation that depends only on the (estimated) channel covariances that impose that the effective channel matrix (including the precoder) has large rank and yet each of its columns has sparsity not larger than T _dl. In this way, our method is not at the mercy of nature, i.e., it is flexible with respect to various types of environments and channel sparsity orders. We cast the optimization of the sparsifying precoder as a mixed-integer linear program (MILP), which can be efficiently solved using standard off-the-shelf software.

We note that the material of this chapter is based on a number of publications by the authors [22, 29, 30].

Notation

We denote scalars, vectors, matrices, and sets by lower case letters, lower case bold letters, upper case bold letters, and calligraphic letters, i.e., x, x, X, $\mathcal {X}$, respectively. We refer to the i-th element of a vector x by [x]_i, and to the (i, j)-th element of a matrix X by [X]_i,j. For a non-negative integer M, we define the set [M] = {0, 1, …, M − 1}. Superscripts (⋅)^∗, (⋅)^T, (⋅)^H, (⋅)⁻¹, and (⋅)^† represent the complex conjugate, transpose, conjugate transpose, inverse, and Moore–Penrose pseudoinverse, respectively. For a vector x, the symbol diag(x) denotes a matrix with x as its main diagonal. The ℓ _p-norm of a vector x is referred to as ∥x∥_p, where for simplicity we drop the subscript for the case of p = 2. The Frobenius norm of a matrix X is denoted by ∥X∥_F. We denote a bipartite graph as, for example, $\mathcal {G} = (\mathcal {V}_1,\mathcal {V}_2,\mathcal {E})$, where $\mathcal {V}_1$ and $\mathcal {V}_2$ are the two color classes and $\mathcal {E}$ is the edge set. For a vertex x, the degree of x refers to the number of edges in $\mathcal {E}$ incident on x and is denoted by $\text{deg}_{\mathcal {G}}(x)$. The neighbors of x, $\mathcal {N}_{\mathcal {G}}(x)$, are those vertices that are connected to x.

11.2 System Model

Consider a BS equipped with a uniform linear array (ULA) with M antennas, operating in FDD mode: UL transmission from a user to the BS takes place over a frequency band

$$\displaystyle \begin{aligned}\mathcal{F}_{\text{ul}}=[f_{\text{ ul}}-\frac{\text{BW}_{\text{ul}}}{2},f_{\text{ ul}}+\frac{\text{BW}_{\text{ul}}}{2}]\end{aligned}$$

with carrier frequency f _ul and a bandwidth BW_ul, and downlink (DL) transmission from the BS to the user takes place over a band

$$\displaystyle \begin{aligned}\mathcal{F}_{\text{dl}}=[f_{\text{ dl}}-\frac{\text{BW}_{\text{dl}}}{2},f_{\text{ dl}}+\frac{\text{BW}_{\text{dl}}}{2}]\end{aligned}$$

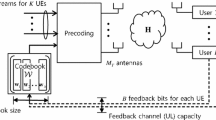
with carrier frequency f _dl and a bandwidth BW_dl. For example, one mode of operation in the 3GPP standard uses the $\mathcal {F}_{\text{ ul}}=[1920,1980]$ MHz band for UL and the $\mathcal {F}_{\text{ dl}} = [2110,2170]$ MHz band for DL transmission, so that f _ul = 1950 MHz, f _dl = 2140 MHz, and BW_ul = BW_dl = 60 MHz [53]. The gap between UL and DL bands is larger than the channel coherence bandwidth. For example, the gap between UL and DL bands in the example above is equal to 190 MHz, while the coherence bandwidth in a macrocell is in the order of 1 MHz [48]. Therefore, for an FDD system, channel reciprocity does not hold, which means that UL and DL instantaneous channels are not the same. As a result, to transmit data, the BS has to first obtain the DL CSI. This is done by sending a number of T _dl pilot symbols to the user and receiving measurement feedback from the user, which enables the BS to estimate the DL CSI and design the beamformer. If there exist multiple users, this is done simultaneously for each one of them, and the beamformer is designed depending on all estimated channels, using one of the various methods such as zero-forcing beamforming [59].

In a massive MIMO system, this proves to be a challenge, due to the high channel dimension (M ≫ 1). In order to train M antennas, a conventional scheme requires a minimum pilot dimension of T _dl = M. Hence, with such a scheme, the number of BS antennas cannot be made arbitrarily large, since the pilot dimension is limited to the dimension of the time–frequency coherence block. For example, consider a typical scenario in LTE, where groups of users are scheduled over resource blocks spanning 14 OFDM symbols × 12 subcarriers, for a total dimension of T = 168 symbols in the time–frequency plane [53], and a typical massive MIMO configuration serving K ∼ 20 users with M ≥ 200 antennas (see, e.g., [37]). In this case, since M ≥ T, the entire resource block dimension would be consumed by the DL pilot, leaving no room for data communication. Designing a massive MIMO system that operates in FDD mode requires developing methods that overcome these dimensionality issues.

11.2.1 Related Work

Several works have proposed to reduce both the DL training and UL feedback overheads by exploiting the sparse structure of the massive MIMO channel. In particular, these works assume that propagation between the BS array and the user antenna occurs through a limited number of scattering clusters, with limited support in the angle-of-arrival/angle-of-departure (AoA–AoD) domain.⁴ A common model is to represent the channel as a superposition of the array response to the electromagnetic wave incoming from a small number of AoAs (p ≪ M), i.e.,

$$\displaystyle \begin{aligned} \mathbf{h} = \sum_{i=1}^{p} c_p \mathbf{a} (\theta_p)\in {\mathbb C}^M, \end{aligned}$$

where c _p are complex coefficients and $\mathbf {a} (\theta _p) \in {\mathbb C}^M$ is the vector containing array element responses to a wave coming from the AoA θ _p. Hence, by decomposing the angle domain into discrete “virtual beam” directions, the M-dimensional channel h admits a sparse representation in the beam domain [3, 52]. Building on this idea, a large number of works (see, e.g., [11, 15, 19, 47, 54, 57]) have proposed to use “compressed pilots,” i.e., a reduced DL pilot dimension T _dl < M, in order to estimate the channel vectors using compressed sensing (CS) techniques [8, 16]. For example, in [3], the sparse representation of channel multipath components in angle, delay, and Doppler domains was exploited to propose CS methods for channel estimation using far fewer measurements than required by conventional least-square (LS) methods. In [19], the authors note that the angles of the multipath channel components are common among all the subcarriers in the OFDM signaling. Then they propose to exploit the common sparsity pattern of the channel coefficients to further reduce the number of required pilot measurements. This gives rise to a so-called multiple measurement vector (MMV) setup, which is typically applied when multiple snapshots of a random vector with common sparse support can be acquired and jointly processed [10, 17]. This was adapted to FDD in the massive MIMO regime, where the frequent idea is to probe the channel using compressed DL pilots, receiving the measurements at the BS via feedback and performing channel estimation there. A recent work based on this approach was presented in [47], starting with the observation that, as shown in many experimental studies [18, 24, 28, 33], the propagation between the BS antenna array and the users occurs along scattering clusters that may be common to multiple users, since they all belong to the same scattering environment. In turn, this yields that the channel sparse representations (in the angle/beam domain) share a common part of their support. Then, [47] considers a scheme where the users feed back their noisy DL pilot measurements to the BS, and the latter runs a joint recovery algorithm, coined as joint orthogonal matching pursuit (J-OMP), able to take advantage of the common sparsity. It follows that in the presence of common sparsity, J-OMP improves upon the basic CS schemes that estimate each user channel separately.

More recent CS-based methods, in addition, make use of the angular reciprocity between the UL and DL channels in FDD systems to improve channel estimation. Namely, this refers to the fact that the directions (angles) of propagation for the UL and DL channel are invariant over the frequency range spanning the UL and DL bands, which is generally very small with respect to the carrier frequency (e.g., UL/DL separation of the order of 100 MHz, for carrier frequencies ranging between 2 and 6 GHz) [2, 25, 58]. In [57], the sparse set of AoAs is estimated from a preamble transmission phase in the UL, and this information is used for user grouping and channel estimation in the DL according to the well-known joint spatial division and multiplexing (JSDM) paradigm [1, 44]. In [15], the authors proposed a dictionary learning-based approach for training DL channels. First, in a preliminary learning phase, the BS “learns” a pair of UL–DL dictionaries that are able to sparsely represent the channel. Then, these dictionaries are used for a joint sparse estimation of instantaneous UL–DL channels. An issue with this method is that the dictionary learning phase requires off-line training and must be re-run if the propagation environment around the BS changes (e.g., due to large moving objects such as truck and buses, or a new building). In addition, the computation involved in the instantaneous channel estimation is prohibitively demanding for real-time operations with a large number of antennas (M > 100). In [11], the authors propose estimating the DL channel using a sparse Bayesian learning framework, aiming at joint-maximum a posteriori (MAP) estimation of the off-grid AoAs and multipath power coefficients by observing instantaneous UL channel measurements. This method has the drawback that it fundamentally assumes discrete and separable (in the AoA domain) multipath components and that the number of signal paths (the number of channel AoAs) is known a priori. Hence, the method simply cannot be applied in scenarios with diffuse (continuous) scattering, where the scattering power is distributed over an interval of the angular domain with non-negligible width. Such scattering is observed and modeled for various types of communication channels, and they do not necessarily admit a sparse angular representation [45, 49, 50, 55].

11.2.2 Contribution

The main problem shared among all the methods above is that they are not robust with respect to the channel sparsity assumption and, as we will show in our simulation results, can lead to poor channel estimates when this assumption is violated. Throughout this chapter, we develop the idea of active channel sparsification (ACS), which aims at DL data multiplexing with any pilot dimension that is available at the BS for channel training. This is done by designing a joint precoder that projects the user channels onto a lower-dimensional subspace such that the sparsity order (the ℓ ₀ pseudo-norm) of each projected channel is less than the pilot dimension. We argue that such a projection comprises a necessary step for interference-free DL data transmission. Among all precoders satisfying this condition, we select one that, in a certain probabilistic sense, maximizes the projected channel matrix rank. As is well-known, the channel matrix rank is equivalent to the channel multiplexing gain, i.e., the number of independent data streams that can be simultaneously multiplexed on the communication link [56]. Then the BS estimates the projected channel matrix (and not the full-dimensional channel matrix), and it communicates with the users through it. Figure 11.1 graphically sketches the idea. The projection enables stable estimation of the “effective channels,” and its rank maximization capability results in maximization of the multiplexing gain and (implicitly) the DL sum rate. We emphasize that our scheme does not rely on channel sparsity and in fact is specifically designed to induce it in a clever way despite the channels being of arbitrary sparsity orders. In this sense, it is a solution to the FDD massive MIMO problem in its generality.

Fig. 11.1

Schematic of the idea of active channel sparsification. The dotted shape in the middle represents the beam-domain channel matrix, in which the columns associate with user channels and rows with (virtual) beams, and filled dots represent non-zero channel coefficients. The precoder is designed to select a set of beams (and users) over which the BS transmits data in the DL

11.3 Channel Model

Consider a BS equipped with a uniform linear array (ULA) of M antennas, serving K users in a cell.⁵ The channel of user k is assumed to be a zero-mean, complex Gaussian vector ${\mathbf {h}}_k \in {\mathbb C}^M$ with covariance $\boldsymbol {\Sigma }_k = \mathbb {E} \left [ {\mathbf {h}}_k {\mathbf {h}}_k^{\mathsf {H}} \right ]$. There are a number of ways to obtain the DL channel covariance of a user in MIMO FDD systems [11, 13, 43, 51], including one proposed by some of the authors of this chapter [22]. For example, the BS can first estimate the UL covariance from UL pilots that are naturally received from the users. Then it can estimate the DL covariance by “transforming” the UL covariance. We do not discuss the details of DL covariance estimation, and in order to isolate the problem of channel training from the effects of an covariance estimation, here we assume that the covariances are known to the BS.

Denoting the channel of a generic user with $\mathbf {h} \in {\mathbb C}^M$, it can be expressed as

$$\displaystyle \begin{aligned} \mathbf{h} = \int_{-\theta_{\max}}^{\theta_{\max}} dW (\theta) \mathbf{a} (\theta), \end{aligned} $$

(11.1)

where $\theta \in [-\theta _{\max },\theta _{\max }]$ stands for the AoA, $\theta _{\max }$ is the maximum array angular aperture (e.g., $\theta _{\max }=\pi /3$), W is a zero-mean, complex Gaussian stochastic process that represents the random angular gains, and thereby the right-hand side (RHS) of (11.1) is understood as an stochastic integral [31]. In addition, $\mathbf {a} (\theta ) \in {\mathbb C}^{M}$ is the far-field array response to a wave impinging from the AoA θ, whose m-th element is given as

$$\displaystyle \begin{aligned}{}[\mathbf{a} (\theta)]_m = \exp\left( j\frac{2\pi d}{\lambda} m \sin \theta\right), \end{aligned} $$

(11.2)

where λ is the carrier wavelength and d denotes the antenna spacing. We consider the latter to be taking the standard value $d=\frac {\lambda }{2\sin \theta _{\max }}$. To simplify notation, we can introduce the normalized AoA ξ by making the change of variables $\xi =\sin \theta / \sin \theta _{\max }$. This results in the element response (11.2) to turn into $[\mathbf {a} (\xi )]_m = \exp \left ( j\pi m \xi \right )$ for m ∈ [M], and the channel vector in (11.1) to be expressed as

$$\displaystyle \begin{aligned} \mathbf{h} = \int_{-1}^1 dW(\xi) \mathbf{a} (\xi). \end{aligned} $$

(11.3)

Assuming uncorrelated scattering, the autocorrelation of W is given as

$$\displaystyle \begin{aligned} \mathbb{E} [ dW(\xi)dW(\xi') ] = \delta (\xi - \xi') \gamma (\xi) d\xi, \end{aligned} $$

(11.4)

in which γ is non-negative and known as the angular scattering function (ASF). The channel covariance is then given as

$$\displaystyle \begin{aligned} \boldsymbol{\Sigma} = \mathbb{E} [\mathbf{h}{\mathbf{h}}^{\mathsf{H}} ] = \int_{-1}^1 \gamma (\xi) \mathbf{a} (\xi) \mathbf{a} (\xi)^{\mathsf{H}} d\xi. \end{aligned} $$

(11.5)

It is easy to show that for a ULA, the channel covariance is Toeplitz Hermitian. This results in a nice property that will be outlined below.

Approximate Common Eigenspace of ULA Channels

Let γ be a function over [−1, 1] bounded to $[\gamma _{\min },\gamma _{\max }]$ with $0\le \gamma _{\min }\le \gamma _{\max }$, whose Fourier transform samples over the integer set [M] are equal to the sequence [σ]_m = [ Σ]_n,n−m, i.e.,

$$\displaystyle \begin{aligned}{}[\boldsymbol{\sigma}]_m = \int_{-1}^1 \gamma (\xi) e^{j\pi m \xi } d\xi. \end{aligned} $$

(11.6)

According to the Szegö theorem, the Toeplitz covariance Σ can be approximated by a circulant matrix $\text{IMAGE}$ whose first column is given as [20]

(11.7)

where for a negative index i < 0, we define $[\boldsymbol {\sigma }]_i = [\boldsymbol {\sigma }]_{-i}^\ast$. The approximation of the Toeplitz matrix with the circulant matrix is understood in the following senses [1]:

• 1. The set of eigenvalues of Σ and $\text{IMAGE}$ denoted as {λ _m} and $\text{IMAGE}$ are asymptotically equally distributed. This means that for any continuous function f defined over $[\gamma _{\min },\gamma _{\max }]$, we have

  

  (11.8)

• 2. The eigenvectors of Σ are approximated by those of $\text{IMAGE}$ in the following sense. Define the asymptotic cumulative distribution function (CDF) of the eigenvalues of Σ as $F(\lambda )= \int _{-1}^1 {\mathbf {1}}_{\{\gamma (\xi )\le \lambda \}} d\xi$. Define U = [u ₀, …, u _M−1] and $\text{IMAGE}$ as the eigenvector matrices of Σ and $\text{IMAGE}$ corresponding to the descendingly ordered eigenvalues {λ _m} and $\text{IMAGE}$, respectively. For any interval $[a,b]\subseteq [\gamma _{\min },\gamma _{\max }]$ such that F is continuous on [a, b], define two sets of indices as $\mathcal {I}_{[a,b]} =\{ m : \lambda _m \in [a,b] \}$ and $\text{IMAGE}$, corresponding to those eigenvalues that lie in [a, b]. Also define the column-wise submatrices of U and $\text{IMAGE}$ associated with these indices as ${\mathbf {U}}_{[a,b]} = \left ( {\mathbf {u}}_m:m \in \mathcal {I}_{[a,b]} \right )$ and $\text{IMAGE}$. Then

  

  (11.9)

Besides the points above, we know that the eigenvectors of a circulant matrix are given by the DFT basis $\mathbf {F}\in {\mathbb C}^{M\times M}$ of the same dimension, whose (m, n)-th entry is given by $[\mathbf {F}]_{m,n}=\frac {1}{\sqrt {M}} e^{-j2\pi \frac {mn}{M}},~m,n\in [M]$. This highly simplifies the precoder design, since now the user channels can all be (asymptotically) expressed in a shared eigenspace that is given by the DFT columns.

For a user k, let $\boldsymbol {\Sigma }_k = {\mathbf {U}}_k \boldsymbol {\Lambda }_k {\mathbf {U}}_k^{\mathsf {H}}$ be its channel covariance eigendecomposition and Λ _k = diag(λ _k) its diagonal matrix of ordered eigenvalues and U _k its unitary matrix of eigenvectors. The Karhunen–Loéve (KL) expansion of a random channel realization is given by Grimmett et al. [21]

$$\displaystyle \begin{aligned} {\mathbf{h}}_k = {\mathbf{U}}_k{\mathbf{g}}_k^{\prime}, \end{aligned} $$

(11.10)

where ${\mathbf {g}}_k^{\prime } \sim \mathcal {C}\mathcal {N} (\mathbf {0},\boldsymbol {\Lambda }_k)$ is a complex Gaussian-distributed vector. As a consequence of Szegö’s theorem, we have that asymptotically as M →∞, this channel realization is equal to

$$\displaystyle \begin{aligned} {\mathbf{h}}_k = \mathbf{F}\, {\mathbf{g}}_k, \end{aligned} $$

(11.11)

where ${\mathbf {g}}_k \sim \mathcal {C}\mathcal {N} (\mathbf {0}, \widetilde {\boldsymbol {\Lambda }}_k)$ and where $\widetilde {\boldsymbol {\Lambda }}_k = \text{diag}(\boldsymbol {\Pi }_k \boldsymbol {\lambda }_k)$ for some permutation matrix $\boldsymbol {\Pi }_k \in {\mathbb C}^{M\times M}$. In this decomposition, the columns of F give the eigenvectors (KL basis vectors), and unlike the eigenvectors matrix U _k in (11.10), they do not depend on the user index. The product Π _k λ _k simply reorders the eigenvalues in λ _k so that they match with their eigenvectors ordered as in F. For any user k, the exact eigenvectors converge to the DFT columns f ₀, …, f _M−1, that is to say in the sense of Point 2 above, we have

$$\displaystyle \begin{aligned} \{ {\mathbf{u}}_{0}^{(k)},\ldots,{\mathbf{u}}_{M-1}^{(k)} \} \to \{ {\mathbf{f}}_0,\ldots,{\mathbf{f}}_{M-1} \}, \end{aligned}$$

for all k ∈ [K]. Later we exploit this property in designing the sparsifying precoder.

Furthermore, note that the columns of F are similar to array response vectors, and in fact, each column with index m ∈ [M] of the DFT matrix can be seen as the array response to an angular direction $\theta = \sin ^{-1}(\frac {m}{M}\sin \theta _{\max })$, where [λ _k]_m can be seen as the power of the channel vector associated with user k along that direction. Due to the presumably limited number of local scatterers as seen at the BS and the large number of antennas of the array, one can hypothesize that only a few entries of λ _k are significantly large, implying that the DL channel vector h _k is sparse in the Fourier basis. This sparsity in the beam-space domain is precisely what has been exploited in the CS-based works discussed in Sect. 11.2.1, in order to reduce the DL pilot dimension T _dl. As seen in the next section, our proposed approach does not rely on any intrinsic channel sparsity assumption but adopts a novel artificial sparsification technique that smartly reduces the effective channel dimension to enable channel estimation regardless of its sparsity.

11.4 Active Channel Sparsification and DL Channel Training

In order to perform multiuser communication, the BS needs to train instantaneous DL channels of the users. This is done by transmitting a pilot matrix $\boldsymbol {\Phi } \in {\mathbb C}^{T_{\text{ dl}} \times M}$, where T _dl represents the pilot dimension. To obtain a good configuration for Φ, we first decompose it as the product

$$\displaystyle \begin{aligned} \boldsymbol{\Phi} = \boldsymbol{\Psi} \mathbf{B}, \end{aligned} $$

(11.12)

where $\mathbf {B} \in {\mathbb C}^{M'\times M}$ is the to-be-designed sparsifying precoder with M′≤ M being an intermediate dimension that will be determined within the precoder design, and $\boldsymbol {\Psi } \in {\mathbb C}^{T_{\text{ dl}} \times M'}$ is a matrix that can be chosen from a random ensemble, e.g., i.i.d. Gaussian or random unitary. Note that the design of B and Ψ does not depend on instantaneous channel realizations, which in fact must be estimated via the closed-loop DL probing and channel-state feedback mechanism.

The precoded DL training length (in time–frequency symbols) spans T _dl dimensions, and the DL training phase is repeated at each fading block of dimension T. Collecting the T _dl training symbols in a column vector, the corresponding observation at user k receiver is given by

$$\displaystyle \begin{aligned} {\mathbf{y}}_k&= \boldsymbol{\Phi} {\mathbf{h}}_k + {\mathbf{z}}_k \\ &=\boldsymbol{\Psi} \mathbf{B} {\mathbf{h}}_k + {\mathbf{z}}_k = \boldsymbol{\Psi} \widetilde{\mathbf{h}}_k + {\mathbf{z}}_k, \end{aligned} $$

(11.13)

where B is the precoding matrix, h _k is the channel vector of user k, and we have defined $\widetilde {\mathbf {h}}_k := \mathbf {B} {\mathbf {h}}_k$ as the effective channel vector, formed by the concatenation of the actual DL channel (antenna-to-antenna) with the precoder B. We consider additive white Gaussian noise (AWGN) with distribution ${\mathbf {z}}_k\sim \mathcal {C}\mathcal {N}(\mathbf {0},N_0 {\mathbf {I}}_{T_{\text{ dl}}})$. The training and precoding matrices are normalized such that

$$\displaystyle \begin{aligned} \mathrm{tr} ( \boldsymbol{\Psi} \mathbf{B} {\mathbf{B}}^{\mathsf{H}} \boldsymbol{\Psi}^{\mathsf{H}} ) = T_{\text{ dl}} P_{\text{dl}}, \end{aligned} $$

(11.14)

where P _dl denotes the total BS transmit power, and we define the DL signal-to-noise ratio as SNR= P _dl∕N ₀.

Most works on channel estimation focus on the estimation of the actual channels {h _k}. This is recovered in our setting by letting B = I _M. However, our goal here is to design the sparsifying precoder such that each effective channel $\widetilde {\mathbf {h}}_k$ becomes sparse enough to be “stably” estimated from the measurements taken Ψ, and yet the collection of all effective channels forms a matrix $\widetilde {\mathbf {H}}=[\widetilde {\mathbf {h}}_0,\ldots ,\widetilde {\mathbf {h}}_{K-1}]$ that has a high rank. In this way, each user’s channel can be partly estimated using a small pilot overhead T _dl, but the BS is still able to serve many data streams using spatial multiplexing in the DL (in fact, as many as the rank of the effective channel matrix).

11.4.1 Necessity and Implication of Stable Channel Estimation

Suppose that the channel representation (11.11) holds exactly and that the eigenvalue vectors λ _k, k ∈ [K] have support $\mathcal {S}_k = \{ m : [\boldsymbol {\lambda }_k]_m \neq 0 \}$ with sparsity order $s_k = |\mathcal {S}_k|$. We hasten to point out that the above are convenient design assumptions, made in order to obtain a tractable problem, and that the eventual precoder is applied to the actual physical channels.

Definition 11.1 (Stable Estimation)

Consider the noisy, linear measurement model y =  Φh + z as introduced in (11.13), where $\mathbf {z} \sim \mathcal {C}\mathcal {N} (\mathbf {0},N_0 \mathbf {I})$. We say that an estimator $\widehat {\mathbf {h}}$ of h given y is stable if $\lim _{N_0 \downarrow 0} \, \mathbb {E} \left [ \Vert \mathbf {h} - \widehat {\mathbf {h}} \Vert ^2 \right ]=0$.⁶

The following lemma yields necessary and sufficient conditions for stable estimation of the channel vectors h _k.

Lemma 11.1

Consider the Gaussian vector h _k described via (11.11) and with support set $\mathcal {S}_k$ . Let $\widehat {\mathbf {h}}_k$ denote any estimator of h _k given the observation ⁷ y _k =  Ψ h _k + z _k . If T _dl ≥ s _k , there exist pilot matrices $\boldsymbol {\Psi } \in {\mathbb C}^{T_{\mathit{\text{ dl}}} \times M}$ for which $\lim _{N_0 \downarrow 0} \mathbb {E} \left [ \Vert \mathbf {h} - \widehat {\mathbf {h}} \Vert ^2 \right ]= 0$ for all support sets $\mathcal {S}_k$ with $|\mathcal {S}_k| = s_k$ . Conversely, for any support set $\mathcal {S}_k : |\mathcal {S}_k| = s_k$ , any pilot matrix $\boldsymbol {\Psi } \in {\mathbb C}^{T_{\mathit{\text{ dl}}} \times M}$ with T _dl < s _k yields $\lim _{N_0 \downarrow 0} \mathbb {E} \left [ \Vert \mathbf {h} - \widehat {\mathbf {h}} \Vert ^2 \right ] > 0$.

Proof

The proof follows by using the KL representation ${\mathbf {h}}_k= \sum _{m \in \mathcal {S}_k} g_{k,m}\sqrt {[\boldsymbol {\lambda }_k]_m} {\mathbf {f}}_m$, which holds exactly by assumption. Estimating h _k is equivalent to estimating the vector of KL Gaussian i.i.d. coefficients ${\mathbf {g}}_k = (g_{k,m}: m \in \mathcal {S}_k) \in {\mathbb C}^{s_k \times 1}$. Define the M × s _k DFT submatrix ${\mathbf {F}}_{\mathcal {S}_k} = ({\mathbf {f}}_m : m \in \mathcal {S}_k)$, and the corresponding diagonal s _k × s _k matrix of the non-zero eigenvalues $[\boldsymbol {\Lambda }_k]_{\mathcal {S}_k,\mathcal {S}_k}$. After some simple standard algebra, the MMSE estimation error covariance of g _k from y _k in (11.13) with B = I _M can be written in the form

$$\displaystyle \begin{aligned} \widetilde{\mathbf{R}}_e & = {\mathbf{I}}_{s_k} - \left ( [\boldsymbol{\Lambda}_k]_{\mathcal{S}_k,\mathcal{S}_k} \right )^{1/2} {\mathbf{F}}_{\mathcal{S}_k}^{\mathsf{ H}} \boldsymbol{\Psi}^{\mathsf{H}} \\ & \times \left ( \boldsymbol{\Psi} {\mathbf{F}}_{\mathcal{S}_k} [\boldsymbol{\Lambda}_k]_{\mathcal{S}_k,\mathcal{S}_k} {\mathbf{F}}_{\mathcal{S}_k}^{\mathsf{H}} \boldsymbol{\Psi}^{\mathsf{H}} + N_0 {\mathbf{I}}_{T_{\text{ dl}}} \right )^{-1} \boldsymbol{\Psi} {\mathbf{F}}_{\mathcal{S}_k} \left ( [\boldsymbol{\Lambda}_k]_{\mathcal{S}_k,\mathcal{S}_k} \right )^{1/2}. \end{aligned} $$

(11.15)

Using the fact that ${\mathbf {R}}_e = {\mathbf {F}}_{\mathcal {S}_k} ( [\boldsymbol {\Lambda }_k]_{\mathcal {S}_k,\mathcal {S}_k})^{1/2} \widetilde {\mathbf {R}}_e ( [\boldsymbol {\Lambda }_k]_{\mathcal {S}_k,\mathcal {S}_k})^{1/2} {\mathbf {F}}_{\mathcal {S}_k}^{\mathsf {H}}$, such that $\mathrm {tr} ({\mathbf {R}}_e) = \mathrm {tr} ([\boldsymbol {\Lambda }_k]_{\mathcal {S}_k,\mathcal {S}_k} \widetilde {\mathbf {R}}_e)$, we have that tr(R _e) and $\mathrm {tr} (\widetilde {\mathbf {R}}_e)$ have the same vanishing order with respect to N ₀. In particular, it is sufficient to consider the behavior of $\mathrm {tr} (\widetilde {\mathbf {R}}_e)$ as a function of N ₀. Now, using the Sherman–Morrison–Woodbury matrix inversion lemma [23], after some algebra omitted for the sake of brevity, we arrive at

$$\displaystyle \begin{aligned} \mathrm{tr} (\widetilde{\mathbf{R}}_e) = s_k - \sum_{i=1}^{s_k} \frac{\mu_i}{N_0+ \mu_i}, {} \end{aligned} $$

(11.16)

where μ _i is the i-th eigenvalue of the s _k × s _k matrix

$$\displaystyle \begin{aligned}\mathbf{A} = ( [\boldsymbol{\Lambda}_k]_{\mathcal{S}_k,\mathcal{S}_k})^{1/2} {\mathbf{F}}^{\mathsf{H}}_{\mathcal{S}_k} \boldsymbol{\Psi}^{\mathsf{H}} \boldsymbol{\Psi} {\mathbf{F}}_{\mathcal{S}_k} ( [\boldsymbol{\Lambda}_k]_{\mathcal{S}_k,\mathcal{S}_k})^{1/2}.\end{aligned}$$

Next, notice that

$$\displaystyle \begin{aligned} \mathrm{rank}(\mathbf{A}) = \mathrm{rank} ({\mathbf{F}}^{\mathsf{H}}_{\mathcal{S}_k} \boldsymbol{\Psi}^{\mathsf{H}} \boldsymbol{\Psi} {\mathbf{F}}_{\mathcal{S}_k} ) = \mathrm{rank} ({\mathbf{F}}_{\mathcal{S}_k} {\mathbf{F}}^{\mathsf{H}}_{\mathcal{S}_k} \boldsymbol{\Psi}^{\mathsf{H}}) \leq \min\{ s_k , T_{\text{ dl}}\}. \end{aligned} $$

(11.17)

In fact, $[\boldsymbol {\Lambda }_k]_{\mathcal {S}_k,\mathcal {S}_k}$ is diagonal with strictly positive diagonal elements, such that left and right multiplication by $( [\boldsymbol {\Lambda }_k]_{\mathcal {S}_k,\mathcal {S}_k})^{1/2}$ yields rank-preserving row and column scalings, the matrix ${\mathbf {F}}_{\mathcal {S}_k} {\mathbf {F}}^{\mathsf {H}}_{\mathcal {S}_k}$ is the orthogonal projector onto the s _k-dimensional column space of ${\mathbf {F}}_{\mathcal {S}_k}$ and has rank s _k, while the matrix $\boldsymbol {\Psi }^{\mathsf {H}} \in {\mathbb C}^{M \times T_{\text{ dl}}}$ has the same rank of Ψ ^H Ψ, that is at most T _dl.

For T _dl ≥ s _k, the existence of matrices Ψ such that the rank upper bound (11.17) holds with equality (i.e., for which rank(A) = s _k for any support set $\mathcal {S}_k$ of size s _k) is shown as follows. Generate a random Ψ with i.i.d. elements $\sim \mathcal {C}\mathcal {N}(0,1)$. Then, the columns of ${\mathbf {F}}^{\mathsf {H}}_{\mathcal {S}_k} \boldsymbol {\Psi }^{\mathsf {H}}$ form a collection of T _dl ≥ s _k mutually independent s _k-dimensional Gaussian vectors with i.i.d. $\sim \mathcal {C}\mathcal {N}(0,1)$ components. The event that these vectors span a space of dimension less than s _k is a null event (zero probability). Hence, such randomly generated matrix satisfies the rank equality in (11.17) with probability 1. As a consequence, for T _dl ≥ s _k, we have that μ _i > 0 for all i ∈ [s _k], and (11.16) vanishes as O(N ₀) as N ₀ ↓ 0. In contrast, if T _dl < s _k, by (11.17) for any matrix Ψ at most T _dl, eigenvalues μ _i in (11.16) are non-zero and $\lim _{N_0\downarrow 0} s_k - \sum _{i=1}^{s_k} \frac {\mu _i}{N_0 + \mu _i} \geq s_k - T_{\text{ dl}} > 0$. □

As a direct consequence of Lemma 11.1, we have that any scheme relying on intrinsic channel sparsity cannot yield stable estimation if T _dl < s _k for some user k ∈ [K]. Furthermore, we need to impose that the sparsity order of the projected channels Bh _k, k ∈ [K] is less than or equal to the desired pilot dimension T _dl.

It is important to note that the requirement of estimation stability is essential in order to achieve high spectral efficiency in high SNR conditions, irrespective of the DL precoding scheme. In fact, if the estimation mean squared error (MSE) of the user channels does not vanish as N ₀ ↓ 0, the system self-interference due to the imperfect channel knowledge grows proportionally to the signal power, yielding a signal-to-interference plus noise ratio (SINR) that saturates to a constant when SNR becomes large. Hence, for sufficiently high SNR, the best strategy would consist of transmitting just a single data stream, since any form of multiuser precoding would inevitably lead to an interference-limited regime, where the sum rate remains bounded, while SNR →∞ [12]. Conversely, it is also well-known that when the channel estimation error vanishes as O(N ₀) for N ₀ ↓ 0, the high-SNR sum rate behaves as if the channel was perfectly known and can be achieved by very simple linear precoding [7]. A possible solution to this problem consists of serving only the users whose channel support s _k is not larger than T _dl. This is assumed implicitly in all CS-based schemes and represents a major intrinsic limitation of the CS-based approaches. In contrast, by artificially sparsifying the user channels, we manage to serve all users given a fixed DL pilot dimension T _dl.

11.4.2 Sparsifying Precoder Design

We now introduce a graphical model that encodes the power profile of each user along the common virtual beams, namely along the DFT columns. Define $\mathcal {G} = (\mathcal {V},\mathcal {K},\mathcal {E})$ as a bipartite graph with two color classes $\mathcal {V}$ and $\mathcal {K}$, where $\mathcal {V}$ is a node set of cardinality M, representing the set of virtual beams and $\mathcal {K}$ is a node set of cardinality K, representing the users. Also $(k,v)\in \mathcal {E}$ if and only if [λ _k]_v > δ ₀, where δ ₀ > 0 is a small threshold that ensures that when the link is very weak, it does not appear in the graph. Therefore, the biadjacency matrix of this graph is given by an M × K binary matrix A for which [A]_v,k = 1 if and only if $(v,k)\in \mathcal {E}$. The weighted biadjacency matrix is defined as the M × K matrix W in which $[\mathbf {W}]_{m,k} = [\boldsymbol {\lambda }_k]_m^{1/2}$.

From (11.11), the DL channel matrix $\mathbf {H} = [{\mathbf {h}}_0,\ldots ,{\mathbf {h}}_{K-1}]\in {\mathbb C}^{M\times K}$ is related to the matrix of angular channel gains $\mathbf {G} = [{\mathbf {g}}_0,\ldots ,{\mathbf {g}}_{K-1}]\in {\mathbb C}^{M\times K}$ as H = FG. Particularly interesting is the relation between H and the bipartite graph $\mathcal {G}$, specifically the rank of H and the size of the largest subgraph in $\mathcal {G}$ that contains a perfect matching. The rigorous statement is given in Theorem 11.1, but before that, we provide the following lemma as a requirement for proving this theorem.

Definition 11.2 (Matching)

A matching is a set of edges in a graph that do not share any endpoints. A perfect matching is a matching that connects all nodes of the graph.

Lemma 11.2 (Rank and Perfect Matchings)

Let Q be an r × r matrix with some elements identically zero and the non-identically zero elements independently drawn from a continuous distribution. Consider a bipartite graph $\mathcal {Q}$ with biadjacency matrix A such that [A]_i,j = 1 if [Q]_i,j is not identically zero, and [A]_i,j = 0 otherwise. Then, Q has rank r with probability 1 if and only if $\mathcal {Q}$ contains a perfect matching.

Proof

The determinant of Q is given by the expansion

$$\displaystyle \begin{aligned}\text{det}(\mathbf{Q})=\sum_{\iota\in \boldsymbol{\pi}_r} \text{sgn}(\iota) \prod_{i} [\mathbf{Q}]_{i,\iota (i)},\end{aligned}$$

where ι is a permutation of the set {1, 2, …, r}, π _r is the set of all such permutations, and sgn(ι) is either 1 or -1. From the construction of $\mathcal {Q}$, it is clear that the product ∏_i[Q]_i,ι(i) is non-zero only if the edge subset {(i, ι(i)), i = 1, …, r)} is a perfect matching. Hence, if $\mathcal {Q}$ contains a perfect matching, then det(Q) ≠ 0 with probability 1 (and rank(Q) = r), since the non-identically zero entries of Q are drawn from a continuous distribution, such that all elements involved in the product ∏_i[Q]_i,ι(i) are independent. If it does not contain a perfect matching, then det(Q) = 0 and therefore rank(Q) < r. □

Theorem 11.1

For a submatrix ${\mathbf {G}}_{\mathcal {V}',\mathcal {K}'}$ consisting of rows and columns with indices in $\mathcal {V}'$ and $\mathcal {K}'$ , respectively, define its associated subgraph as the subgraph $\mathcal {G}' = (\mathcal {V}', \mathcal {K}', \mathcal {E}')\subseteq \mathcal {G}$ . The rank of H is given, with probability 1, by the side length of the largest square intersection submatrix of G whose associated subgraph in $\mathcal {G}$ contains a perfect matching.

Proof

Note that since H = FG and F is unitary, the rank of H is equal to that of G. In addition, the rank of G is equivalent to the largest order of any non-zero minor in G,⁸ i.e., the side length of the largest non-singular square submatrix of G. The elements of G are either identically zero or drawn from a Gaussian distribution with zero mean and a variance [λ _k]_m for some (k, m) ∈ [K] × [M]. Now, according to Lemma 11.2, any such submatrix Q is non-singular (has rank equal to its side length) if and only if its associated subgraph $\mathcal {Q} \subseteq \mathcal {G}$ contains a perfect matching. This concludes the proof. □

Theorem 11.1 implies that the rank of the channel matrix is given, with probability 1, by the size of a certain matching in the user-virtual beam bipartite graph $\mathcal {G}$. This matching is contained in a subgraph of $\mathcal {G}' = (\mathcal {V}',\mathcal {K}',\mathcal {E}')\subseteq \mathcal {G}$ that specifies the selected users and virtual beams that must satisfy certain criteria. In particular, given a pilot dimension T _dl, we want to select $\mathcal {G}'$ such that which node on either color class $\mathcal {K}'$ or $\mathcal {V}'$ has a degree of at least one, and such that:

Stability constraint: :

For all $k \in \mathcal {K}'$, we should have $\text{deg}_{\mathcal {G}'}(k) \le T_{\text{ dl}}$, where $\text{deg}_{\mathcal {G}'}$ denotes the degree of a node in the selected subgraph.

Power constraint: :

The sum of weights of the edges incident to any node $k \in \mathcal {K}'$ in the subgraph $\mathcal {G}'$ is greater than a threshold, i.e., $\sum _{m\in \mathcal {N}_{\mathcal {G}'} (k)} w_{m,k} \ge P_{\text{th}},$ for some P _th and for all k.

Rank objective: :

The channel matrix ${\mathbf {G}}_{\mathcal {V}',\mathcal {K}'}$ obtained from G by selecting $a \in \mathcal {V}'$ (“selected beam directions”) and $k\in \mathcal {K}'$ (“selected users”) has large rank.

The first constraint enables stable estimation of the effective channel of any selected user with only T _dl common pilot dimensions and T _dl complex symbols of feedback per selected user. The second constraint makes sure that the effective channel strength of any selected user is greater than a desired threshold, since we do not want to spend resources on probing and serving users with weak effective channels (where “weak” is quantitatively determined by the value of P _th). Therefore, P _th is a parameter that serves to obtain a trade-off between the rank of the effective matrix (which ultimately determines the number of spatially multiplexed DL data streams) and the beamforming gain (i.e., the power effectively conveyed along each selected user effective channel). The objective is motivated by the equivalence between the channel matrix rank and the system multiplexing gain. In fact, one can show that the pre-log factor in the total sum rate is given by $\mathrm {rank} ( {\mathbf {G}}_{\mathcal {V}',\mathcal {K}'} ) \times \max \{ 0 , 1 - T_{\text{ dl}}/T\}$, and it is obtained by serving a number of users equal to the rank of the effective channel matrix. We can summarize these in the form of the following problem.

Problem 11.1

Let T _dl denote the available DL pilot dimension, and let $\mathcal {M} (\mathcal {V}',\mathcal {K}')$ denote a matching of the subgraph $\mathcal {G}' (\mathcal {V}',\mathcal {K}',\mathcal {E}')$ of the bipartite graph $\mathcal {G} (\mathcal {V},\mathcal {K},\mathcal {E})$. Find the solution of the following optimization problem:

(11.18a)

$$\displaystyle \begin{aligned} & \text{subject to} && \text{deg}_{\mathcal{G}'} (k) \le T_{\text{ dl}}~ \forall k\in \mathcal{K}', {} \end{aligned} $$

(11.18b)

(11.18c)

$\lozenge$

The theorem below shows that this problem can be cast as a mixed-integer linear program (MILP). We refer the interested reader to [29] for the proof.

Theorem 11.2

The optimization problem in (11.18) is equivalent to the MILP below:

(11.19a)

$$\displaystyle \begin{aligned} & \mathit{\text{subject to}} && z_{m,k} \le [\mathbf{A}]_{m,k} ~~\forall m\in\mathcal{V},k\in \mathcal{K}, {} \end{aligned} $$

(11.19b)

$$\displaystyle \begin{aligned} &~ && \sum_{k\in \mathcal{K}}z_{m,k} \le x_m ~~ \forall m\in \mathcal{V}, \end{aligned} $$

(11.19c)

$$\displaystyle \begin{aligned} &~ && \sum_{m\in \mathcal{V}}z_{m,k} \le y_k ~~ \forall k\in \mathcal{K}, \end{aligned} $$

(11.19d)

(11.19e)

$$\displaystyle \begin{aligned} &~ &&P_{\mathit{\text{th}}} \, y_k \le \sum_{m \in \mathcal{V}} [\mathbf{W}]_{m,k} x_m ~~\forall k \in \mathcal{K}, \end{aligned} $$

(11.19f)

$$\displaystyle \begin{aligned} &~&& x_m \le \sum_{k\in \mathcal{K}} [\mathbf{A}]_{m,k} y_k ~~ \forall m\in \mathcal{V}, \end{aligned} $$

(11.19g)

$$\displaystyle \begin{aligned} &~&& x_m, y_k \in \{0,1\} ~~\forall a\in \mathcal{V},k\in \mathcal{K}, \end{aligned} $$

(11.19h)

$$\displaystyle \begin{aligned} &~&& z_{m,k} \in [0,1] ~~\forall m\in \mathcal{V},k\in \mathcal{K}. {} \end{aligned} $$

(11.19i)

The solution subgraph is given by the set of nodes $\mathcal {V}' = \{m:x_m^\star = 1\}$ and $\mathcal {K}' = \{k:y_k^\star =1\}$ , with $\{x_m^\star \}_{m=0}^{M-1}$ and $\{y_k^\star \}_{k=0}^{K-1}$ being a solution of (11.19).

The solution to this optimization, however, is not necessarily unique, i.e., there may exist several subgraphs with the same (maximum) matching size. For example, consider the miniature beam–user bipartite graph of Fig. 11.2 and suppose that we have a pilot dimension T _dl = 2. Here the matching $\mathcal {M} = \{ (0,0), (1,1) \}$ is a matching of maximum size that is contained in two subgraphs, the first one defined by beams $\mathcal {V}_1 = \{ 0,1 \}$ and users $\mathcal {K}_1 = \{ 0,1\}$, and the second one defined by the beams $\mathcal {V}_2 = \{ 0,1,2\}$ and users $\mathcal {K}_2 = \{ 0,1\}$ (both satisfy the constraints). In such cases, we want to select the subgraph that includes the larger number of beams. In this example, this is the second subgraph. The reason is that as long as adding beams does not violate the stability constraint, we want to probe (and eventually transmit along) more beams, since this naturally increases the beamforming gain due to channel hardening. In fact, a prominent advantage of a massive MIMO system is its high beamforming gain, and in this way, the algorithm encourages solutions that result in larger beamforming gains.

Fig. 11.2

A toy example of the bipartite graph with M = 3 beams and K = 2 users

In order to incorporate the preference for more selected beams in sparsification, we introduce a regularization term to the objective of (11.19) to favor solutions containing more active beams. The regularized form of (11.19) is given as

(PMILP)

where the feasibility set $\mathcal {S}_{\text{feasible}}$ encodes the constraints (11.19a)–(11.19i). Here, the regularization factor 𝜖 is chosen to be a small positive value such that it does not affect the matching size of the solution subgraph. In fact choosing $\epsilon <\frac {1}{M}$ ensures this, since then $\epsilon \sum _{m \in \mathcal {V}} x_m < 1$ and a solution to P_MILP must have the same matching size as a solution to (11.19); otherwise, the objective of P_MILP can be improved by choosing a solution with a larger matching size. The introduced MILP can be efficiently solved using an off-the-shelf optimization toolbox. In the simulation results of this chapter, we have used the MATLAB i n t l i n p r o g, which adopts a branch-and-bound method to find the solution to an MILP [42]. Figure 11.3 illustrates an example of the beam–user bipartite graph and how ACS acts on it with a pilot dimension of T _dl = 2. The algorithm selects a subgraph containing a matching of maximum size while not violating the estimation stability constraint (assuming for simplicity that the power constraint is satisfied). The selected beams in this graph, i.e., the nodes $\{1,2,3,5,6 \}\subset \mathcal {V}$, are additionally represented by the highlighted rows of the channel matrix in Fig. 11.1.

Fig. 11.3

An example of the beam–user bipartite graph, its weighted biadjacency matrix, and the sparsification process with M = 7, K = 3 and the assumed pilot dimension T _dl = 2. The faded nodes represent the “eliminated” beams ($\{m\,:\, x_m^\star = 0\}$), schematically crossed out in the weighted biadjacency matrix. The non-faded edges (in blue and black) represent the user–beam connections that exist in the selected subgraph. The blue edges further highlight the matching of maximum size

11.4.3 Channel Estimation and Multiuser Precoding

For a given set of user covariance matrices, let $\left \{x_m^\star \right \}$ and $\left \{y_k^\star \right \}$ denote the MILP solutions, and denote by $\mathcal {B}=\{m:x_m^\star =1\} = \{m_1,m_2,\ldots , m_{M'}\}$ the set of selected beam directions of cardinality $|\mathcal {B}| = M'$ and by $\mathcal {K} = \{k: y^\star _k = 1\}$ the set of selected users of cardinality $|\mathcal {K}| = K'$. The resulting sparsifying precoding matrix B in (11.13) is simply obtained as

$$\displaystyle \begin{aligned} \mathbf{B} = {\mathbf{F}}_{\mathcal{B}}^{\mathsf{H}}, \end{aligned} $$

(11.20)

where ${\mathbf {F}}_{\mathcal {B}} = [{\mathbf {f}}_{m_1}, \ldots , {\mathbf {f}}_{m_{M'}}]$ and f _m denotes the m-th column of the M × M unitary DFT matrix F. For a DFT column f _m, we have

$$\displaystyle \begin{aligned} \mathbf{B} {\mathbf{f}}_m = \left \{ \begin{array}{ll} \mathbf{0} & \mbox{if} \;\; m \notin \mathcal{B} \\ {\mathbf{u}}_i & \mbox{if} \;\; m = m_i \in \mathcal{B}, \end{array} \right . \end{aligned}$$

where u _i denotes a M′× 1 vector with all zero components but a single “1” in the i-th position. Using the above property and (11.11), the effective DL channel vectors take on the form

(11.21)

In words, the effective channel of user k is a vector with non-identically zero elements only at the positions corresponding to the intersection of the beam directions in $\mathcal {S}_k$, along which the physical channel of user k carries positive energy, and in $\mathcal {B}$, selected by the sparsifying precoder. The non-identically zero elements are independent Gaussian coefficients $\sim \mathcal {C}\mathcal {N}(0, [\boldsymbol {\lambda }_k]_{m_i})$. Notice also that, by construction, the number of non-identically zero coefficients are $|\mathcal {B} \cap \mathcal {S}_k| \leq T_{\text{ dl}}$ and their positions (encoded in the vectors u _i in (11.21)), plus an estimate of their variances $[\boldsymbol {\lambda }_k]_{m_i}$, are known to the BS. Hence, the effective channel vectors can be estimated from the T _dl-dimensional DL pilot observation (11.13) with an estimation MSE that vanishes as 1/SNR. The pilot observation in the form (11.13) is obtained at the user k receiver. In this chapter, we assume that each user sends its pilot observations using T _dl channel uses in the UL, using analog unquantized feedback, as analyzed for example in [7, 32]. At the BS receiver, after estimating the UL channel from the UL pilots, the BS can apply linear MMSE estimation and recovers the channel-state feedback that takes on the same form as (11.13) with some additional noise due to the noisy UL transmission.

Remark 11.1

As an alternative, one can consider quantized feedback using T _dl channel uses in the UL. Digital quantized feedback yields generally a better end-to-end estimation MSE in the absence of feedback errors. However, the effect of decoding errors on the channel-state feedback is difficult to characterize in a simple manner since it depends on the specific joint source-channel coding scheme employed. Hence, in this chapter, we restrict to the simple analog feedback.

With the above precoding, we have $\mathbf {B} {\mathbf {B}}^{\mathsf {H}} = {\mathbf {I}}_{M'}$. There are several options for selecting the matrix Ψ, among which we take Ψ to be proportional to an arbitrary unitary matrix of dimension T _dl × M′, such that $\boldsymbol {\Psi } \boldsymbol {\Psi }^{\mathsf {H}} = P_{\text{dl}} {\mathbf {I}}_{T_{\text{ dl}}}$. In this way, the DL pilot phase power constraint (11.14) is automatically satisfied. The estimation of $\widetilde {\mathbf {h}}_k$ from the DL pilot observations (11.13) (with suitably increased AWGN variance due to the noisy UL feedback) is completely straightforward and shall not be treated here in detail.

For the sake of completeness, we conclude this section with the DL precoded data phase and the corresponding sum-rate performance metric that we shall later use for numerical analysis and comparison with other schemes. Let $\widetilde {\mathbf {H}}^\star = [ \widetilde {\mathbf {h}}_0^\star , \ldots , \widetilde {\mathbf {h}}_{K'-1}^\star ]$ be the matrix of the estimated effective channels for the selected users, where we have assumed without loss of generality the order {0, 1, …, K′− 1} for the selected users. We consider the ZF beamforming matrix V given by the column-normalized version of the Moore–Penrose pseudoinverse of the estimated channel matrix, i.e.,

$$\displaystyle \begin{aligned}\mathbf{V} = \left(\widetilde{\mathbf{H}}^\star\right)^\dagger {\mathbf{J}}^{1/2},\end{aligned}$$

where $\left (\widetilde {\mathbf {H}}^\star \right )^\dagger = \widetilde {\mathbf {H}}^\star \left ( \widetilde {\mathbf {H}}^{\star \mathsf {H}} \widetilde {\mathbf {H}}^\star \right )^{-1}$ and J is a diagonal matrix that makes the columns of V to have unit norm. A channel use of the DL precoded data transmission phase at the k-th user receiver takes on the form $r_k= \left ( {\mathbf {h}}_k \right )^{\mathsf {H}} {\mathbf {B}}^{\mathsf {H}} \mathbf {V} {\mathbf {P}}^{1/2} \mathbf {d} + n_k,$, where $\mathbf {d} \in {\mathbb C}^{K' \times 1}$ is a vector of unit-energy user data symbols and P is a diagonal matrix defining the power allocation to the DL data streams. The transmit power constraint is given by tr(B ^H VPV ^H B) = tr(V ^H VP) = tr(P) = P _dl, where we used $\mathbf {B} {\mathbf {B}}^{\mathsf {H}} = {\mathbf {I}}_{M'}$ and the fact that V ^H V has unit diagonal elements by construction. In particular, in the simulation results section, we use the simple uniform power allocation P _k = P _dl∕K′ to each k-th user data stream. In the case of perfect ZF beamforming, i.e., for $\widetilde {\mathbf {H}}^\star = \widetilde {\mathbf {H}}$, we have $r_k= \sqrt {J_k P_k} d_k + n_k$, where J _k is the k-th diagonal element of the norm normalizing matrix J, P _k is the k-th diagonal element of the power allocation matrix P, and d _k is the k-th user data symbol. Since in general $\widetilde {\mathbf {H}}^\star \neq \widetilde {\mathbf {H}}$, due to non-zero estimation error, the received symbol at user k receiver is given by $r_k= b_{k,k} d_k + \sum _{k' \neq k} b_{k,k'} d_{k'} + n_k,$, where the coefficients $(b_{k,1}, \ldots , b_{k,K'})$ are given by the elements of the 1 × K′ row vector $\left ( {\mathbf {h}}_k \right )^{\mathsf {H}} {\mathbf {B}}^{\mathsf {H}} \mathbf {V} {\mathbf {P}}^{1/2}$. Of course, in the presence of an accurate channel estimation, we expect that $b_{k,k} \approx \sqrt {J_k P_k}$ and $b_{k,k'} \approx 0$ for k′≠ k. For simplicity, in this chapter, we compare the performance of the proposed scheme with that of the state-of-the-art CS-based scheme in terms of ergodic sum rate, assuming that all coefficients $(b_{k,1}, \ldots , b_{k,K'})$ are known to the corresponding receiver k. Including the DL training overhead, this yields the rate expression (see [6])

$$\displaystyle \begin{aligned} R_{\mathrm{sum}} = \left (1 - \frac{T_{\text{ dl}}}{T} \right ) \sum_{k \in \mathcal{K}} \mathbb{E} \left [ \log \left ( 1 + \frac{\left|b_{k,k}\right|{}^2}{1 + \sum_{k' \neq k} \left|b_{k,k'} \right|{}^2} \right ) \right ]. \end{aligned} $$

(11.22)

11.5 Simulation Results

In this section, we provide simulation results to see the empirical evidence for the performance of ACS. We also compare ACS to two of the most recent CS-based methods proposed in [47] and [15] in terms of channel estimation error and sum rate. In [47], the authors proposed a method based on common probing of the DL channel with random Gaussian pilots. The DL pilot measurements y _k at users k = 1, …, K (similar to (11.13), but with a different pilot matrix) are fed back and collected by the BS, which recovers the channel vectors using a joint orthogonal matching pursuit (J-OMP) technique able to exploit the possible common sparsity between the user channels. In [15], a method based on dictionary learning for sparse channel estimation was proposed. In this scheme, the BS jointly learns sparsifying dictionaries for the UL and DL channels by collecting channel measurements at different cell locations (e.g., via an offline learning phase). The actual user channel estimation is posed as a norm-minimization convex program using the trained dictionaries and with the constraint that UL and DL channels share the same support over their corresponding dictionaries. Following [15], we refer to this method as JDLCM.

11.5.1 Channel Estimation Error and Sum Rate vs. Pilot Dimension

In order to have a fair comparison, we involve the UL pilot transmission step in the simulation. The JDLCM method requires UL and DL instantaneous channel samples to train its sparse-representation dictionaries. Our method (ACS) uses the UL channel samples to estimate the UL covariance and then uses that to obtain the DL covariance via a transformation (see [22] for details). Then it uses the estimated (and not the true) DL covariance to perform sparsification. The J-OMP method does not make any use of either the UL or DL covariance, and it is not clear how one can incorporate the covariance information in this algorithm.

For this comparison, we considered M = 128 antennas at the BS, K = 13 users, and resource blocks of size T = 128 symbols. For JDLCM, the sparse-representation dictionary is jointly trained for N = 1000 instantaneous UL and DL channels as proposed in [15]. For ACS, the BS computes the users’ sample UL covariance matrices by taking N = 1000 UL pilot observations and then runs a non-negative least-square optimization to estimate a parametric form of the angular scattering function γ in (11.6). This estimate is then used to transform the UL covariance to the DL covariance. Given the obtained DL channel covariance matrix estimates, we first perform the circulant approximation and extract the vector of approximate eigenvalues λ _k, k ∈ [K]. Then, we compute the sparsifying precoder B via the MILP solution. In the results presented here, we set the parameter P _th in the MILP to a small value in order to favor a high rank of the resulting effective channel matrix over the beamforming gain.⁹ After probing the effective channel of the selected users along these active beam directions via a random unitary pilot matrix Ψ, we calculate their MMSE estimate using the estimated DL covariance matrices.

Eventually, for all the three methods, we compute the ZF beamforming matrix based on the obtained channel estimates. In addition, instead of considering all selected users, in both cases, we apply the Greedy ZF user selection approach of [14], which yields a significant benefit when the number of users is close to the rank of the effective channel matrix. As said before, the DL SNR is given by SNR = P _dl∕N ₀, and during the simulations, we consider ideal noiseless feedback for simplicity, i.e., we assume that the BS receives the measurements in (11.13) without extra feedback noise to the system.¹⁰ The sparsity order of each channel vector is given as an input to the J-OMP method, but not to the other two methods. This represents a genie-aided advantage for J-OMP that we introduce here for simplicity. As the simulation geometry, we consider three MPC clusters with random locations within the angular range (parametrized by ξ rather than θ) [−1, 1). We denote by Ξ the i-th interval and set each interval size to be | Ξ_i| = 0.2, i = 1, 2, 3. The ASF for each user is obtained by selecting at random two out of three such clusters, such that the overlap of the angular components among users is large. The ASF is non-zero over the angular intervals corresponding to the chosen MPCs and zero elsewhere, i.e., $\gamma _k(\xi ) = \beta {\mathbf {1}}_{\Xi _{i_1} \cup \Xi _{i_2}},$, where $\beta = 1/\int _{-1}^{1} \gamma _k(\xi )d\xi$ and i ₁, i ₂ ∈{1, 2, 3}.

The described arrangement results in each generated channel vector being roughly s _k = 0.2 × M ≈ 26-sparse. To measure channel estimation error, we use the normalized Euclidean distance as follows. Let $\mathbf {H} \in {\mathbb C}^{M\times K'}$ define the matrix whose columns correspond to the channel vectors of the K′ served users, and let $\widehat {\mathbf {H}}$ denote the estimation of H. Then the normalized Euclidean error is defined as

$$\displaystyle \begin{aligned}E_{\text{euc}} = \mathbb{E}\left[\frac{\Vert \mathbf{H} - \widehat{\mathbf{H}}\Vert_{\mathsf{F}}^2}{\Vert \mathbf{H} \Vert_{\mathsf{F}}^2}\right]. \end{aligned}$$

Figure 11.4a shows the normalized channel estimation error for the J-OMP, JDLCM, and our proposed active channel sparsification (ACS) method as a function of the DL pilot dimension T _dl with SNR = 20 dB. Our ACS method outperforms the other two by a large margin, especially for low DL pilot dimensions. When the pilot dimension is below channel sparsity order, CS-based methods perform very poorly, since the number of channel measurements is less than the inherent channel dimension. Figure 11.4b compares the achievable sum rate for the three methods. Again our ACS method shows a much better performance compared to J-OMP and JDLCM. This figure also shows that there is an optimal DL pilot dimension that maximizes the sum rate. This optimal value is T _dl ≈ 40 for our proposed method, T _dl ≈ 60 for JDLCM, and T _dl ≈ 70 for J-OMP.

Fig. 11.4

(a) Normalized channel estimation error, and (b) achievable sum rate as a function of DL pilot dimension with SNR = 20 dB, M = 128, and K = 13.

11.5.2 The Effect of Channel Sparsity

The channels can have various sparsity levels in the angular domain. While the CS-based method is in this sense at the mercy of environmental features, our active sparsification method is able to deal with different scenarios by inducing more sparsity in the channel. This section examines the effect of channel sparsity order on sum rate when the ACS method is employed. We take user ASFs to consist of two clusters, chosen at random, out of three pre-defined clusters. To have different sparsity orders, we vary the size of the angular interval, each of the clusters occupies (| Ξ_i| = 0.2, 0.4, 0.6, 0.8), and we see how it affects the error and sum-rate metrics. The sparsifying precoder, DL training, feedback, and data precoding are performed as before. We take M = 128, and as the ASF consists of two clusters, the channel sparsity order takes on the values s _k = 26, 51, 77, 102 for all users k ∈ [K′]. Then the system sum rate is calculated empirically for each pilot dimension via Monte Carlo simulations. Notice that in these results we fix the channel coefficient power along each scattering component, such that richer (less sparse) channels convey more signal energy. This corresponds to the physical fact that the more scattered signal energy is collected at the receiving antennas the higher the received signal energy is. Figure 11.5 illustrates the results. As we can see, for a fixed T _dl, when the number of non-zero channel coefficients increases, i.e., when the channel is less sparse, we generally have a larger sum rate. This is due to the fact that, with less sparse channels, the beamforming gain is larger, since more scattering components contribute to the channel. Therefore, we can generally say that with our method, for a fixed pilot dimension, less sparse channels are, in a sense, better. Of course, this is not the case for techniques based on the sparsity assumption of a small number of discrete angular components, which tend to collapse and yield poor results when such sparsity assumptions are not satisfied.

Fig. 11.5

Sum rate vs. T _dl for various channel sparsity orders. Here SNR = 20 dB, M = 128, and K = 13.

11.6 Beam-Space Design for Arbitrary Array Geometries

The ACS can be applied to design precoders for cases with array geometries other than the ULA. As explained in Sect. 11.3, a necessary step before performing sparsification in a tractable way is that all channels share the same (approximate) eigenspace. Earlier in this chapter, we observed that, for a massive ULA, this common eigenspace is asymptotically given by the span of the DFT basis due to an application of Szegö’s theorem for large Hermitian Toeplitz matrices (see Sect. 11.3). For an arbitrary array geometry, the covariance is not necessarily Toeplitz, and we are not aware of any work suggesting the existence of a (approximate) common eigenspace for MIMO channels of generic array geometries. Then, what is a suitable strategy to obtain an approximate common eigenbasis? In order to extend ACS to arrays with arbitrary design, here we propose a method for obtaining an approximate common eigenspace for channels of a multiuser system with an arbitrary array geometry. Once a common eigenbasis is obtained, sparsification can be done simply by performing the MILP on a bipartite graph that encodes the link between the users and the set of obtained virtual beams.

Consider a BS equipped with an array of arbitrary geometry consisting of M antennas, communicating with K users. The user channels are all assumed zero-mean, complex Gaussian with covariances $\boldsymbol {\Sigma }_k = \mathbb {E} \left [ {\mathbf {h}}_k {\mathbf {h}}_k^{\mathsf {H}} \right ],\, k\in [K]$. Define the eigendecomposition of Σ _k as $\boldsymbol {\Sigma }_k = {\mathbf {U}}_k \boldsymbol {\Lambda }_k {\mathbf {U}}_k^{\mathsf {H}}$, where U _k is the unitary matrix of eigenvectors (${\mathbf {U}}_k^{\mathsf {H}} {\mathbf {U}}_k={\mathbf {I}}_M$) and Λ _k is the diagonal matrix of non-negative eigenvalues. We note that the eigenbasis of distinct covariances is generally different. This makes the joint processing of the channels and the precoding design difficult. Hence, we are interested in obtaining an approximate common eigenbasis U among all covariances { Σ _k}. An ideal choice for U is one that “approximately” diagonalizes all the members of { Σ _k}, such that the diagonal elements of U ^H ΣU “closely” follow the true eigenvalues of Σ _k for all k. If the covariances are in fact jointly diagonalizable, i.e., if there exists a unitary matrix U ^c such that U ₁ = U ₂ = … = U _K = U ^c, then it is desirable to obtain U ^c as the common eigenbasis. If the covariances are not jointly diagonalizable, then we want to obtain a unitary matrix U ^⋆ that “best” diagonalizes the covariances.

Some of the present authors have studied this problem in a slightly different context in [30], where the goal was to obtain the approximate common eigenbasis U given a number of N samples of the instantaneous channels of the K users. There, they assumed a parametric form of the covariances as $\{\boldsymbol {\Sigma }_k = \mathbf {U} \boldsymbol {\Lambda }_k^{\prime } {\mathbf {U}}^{\mathsf {H}}\}$ and performed a maximum likelihood (ML) estimation of U and $\{ \boldsymbol {\Lambda }_k^{\prime } \}$ given the samples. It turns out that the emergent ML problem can be cast as the following optimization:

(11.23)

where $\widehat { \boldsymbol {\Sigma }}_k = \frac {1}{N}\sum _{n=0}^{N-1} {\mathbf {h}}_k [i]{\mathbf {h}}_k [i]^{\mathsf {H}}$ is the sample covariance of the instantaneous channels for k ∈ [K]. However, in this chapter, we have assumed that the channel covariances (or estimates thereof) are readily given. Then it seems natural to apply the same formulation by substituting the sample covariance with the available (true or estimated) covariances. This results in the following problem:

(P1 )

which presents an optimization over the manifold of unitary matrices $\mathcal {U} = \{ \mathbf {U} \in {\mathbb C}^{M\times M}:\, {\mathbf {U}}^{\mathsf {H}} \mathbf {U} ={\mathbf {I}}_M \}$. To solve the ML problem P₁ , we propose a gradient projection method and show that it converges to a stationary point of the cost function f. But first, let us study the problem when applied to a special class of user covariances.

11.6.1 Jointly Diagonalizable Covariances

One can show that, if the true channel covariances are jointly diagonalizable, then the global optimum of P₁ is given by the common eigenbasis. To see this, first note that the channel covariance of user k can be decomposed as Σ _k = U ^c Λ _k U ^cH, for k ∈ [K], where ${\mathbf {U}}^c \in {\mathbb C}^{M\times M}, \, {\mathbf {U}}^{c\, \mathsf {H}}{\mathbf {U}}^c = {\mathbf {I}}_M$ denotes the common eigenbasis.

Definition 11.3 (Majorization)

For $\mathbf {x} \in {\mathbb R}^{M}$, define x ^↓ as the vector containing the elements of x in descending order. Let $\mathbf {y} \in {\mathbb R}^M$ be another vector such that $\sum _{i=0}^{M-1}[\mathbf {x}]_i =\sum _{i=0}^{M-1}[\mathbf {y}]_i$. We say x majorizes y (x ≻y) iff $\sum _{i=0}^{m}{\mathbf {x}}^{\downarrow }_i \ge \sum _{i=0}^{m}{\mathbf {y}}^{\downarrow }_i,$ for all m ∈ [M].

The following theorem shows that U ^c is a global optimum of P₁ .

Theorem 11.3

Let Σ _k, k = 0, …, K − 1, be a set of jointly diagonalizable covariance matrices. Then U ^⋆ = U ^c is a global optimum of P₁ .

Proof

Given a unitary matrix U, let $\boldsymbol {\sigma }_k (\mathbf {U}) \in {\mathbb R}^M$ be a vector such that $[\boldsymbol {\sigma }_k (\mathbf {U})]_{m} = {\mathbf {u}}_m^{\mathsf {H}} \boldsymbol {\Sigma }_k {\mathbf {u}}_m$. Particularly, we can check that σ _k(U ^c) is the vector of eigenvalues of Σ _k. From the properties of eigenvalue decomposition, it follows that σ _k(U ^c) ≻σ _k(U) for all $\mathbf {U} \in \mathcal {U}$ and all k ∈ [K]. Besides, the function $h(\mathbf {x}) = \sum _i \log ([\mathbf {x}]_i)$ is Schur-concave [46], and hence, $\sum _m \log ([\boldsymbol {\sigma }_k ({\mathbf {U}}^c)]_m) \le \sum _m \log ([\boldsymbol {\sigma }_k (\mathbf {U})]_m)$ for all k. Therefore, we have f(U ^c) ≤ f(U) for all $\mathbf {U} \in \mathcal {U}$, proving U ^c to be the global minimizer of f over $\mathcal {U}$. □

This theorem shows that $\mathcal {P}_1$ satisfies a minimum requirement for finding a set of approximate common eigenvectors: at least when the channel covariances do share a common eigenbasis, the ML optimum coincides with it.

11.6.2 ML via Projected Gradient Descent

Now we turn to solving the ML problem P₁ . We use a projected gradient descent (PGD) method to minimize the objective cost function f. The PGD is a well-known iterative optimization algorithm [4], which starts from an initial point U ⁽⁰⁾ and consists of the following two steps per iteration:

$$\displaystyle \begin{aligned} \widetilde{\mathbf{U}}^{(t)} = {\mathbf{U}}^{(t)} - \alpha_t \nabla f({\mathbf{U}}^{(t)}) \end{aligned} $$

(Gradient Step)

$$\displaystyle \begin{aligned} {\mathbf{U}}^{(t+1)} = \mathcal{P}_{\mathcal{U}} (\widetilde{\mathbf{U}}^{(t)}) , \end{aligned} $$

(Projection Step)

where $\nabla f({\mathbf {U}}^{(t)})\in {\mathbb C}^{M\times M}$ is the gradient of f at U ^(t), $\mathcal {P}_{\mathcal {U}}:{\mathbb C}^{M\times M}\to \mathcal {U}$ is the orthogonal projection operator onto the set of unitary matrices, and α _t > 0 is a step size. The following lemma, proved in [38], shows how one can compute the orthogonal projection.

Lemma 11.3

Let $\mathbf {V} \in {\mathbb C}^{M\times M}$ be a matrix with singular value decomposition V = SDT ^H , where S and T are unitary matrices of left and right eigenvectors and D = diag(d) is non-negative diagonal. Then, the orthogonal projection of V onto the set of unitary matrices is given by $\mathcal {P}_{\mathcal {U}}(\mathbf {V}) =\mathbf {S} {\mathbf {T}}^{\mathsf {H}}$.

The following theorem presents a guarantee for the convergence of PGD when applied to solve P₁ (see [30] for the proof).

Theorem 11.4

Let ${\mathbf {U}}^{(0)}\in \mathcal {U}$ be an initial point and consider the gradient projection update rule

$$\displaystyle \begin{aligned} {\mathbf{U}}^{(t+1)} = \mathcal{P}_{\mathcal{U}} \left( {\mathbf{U}}^{(t)} - \alpha_t \nabla f ({\mathbf{U}}^{(t)}) \right),\,\, t=0,1,\ldots, \end{aligned} $$

(11.24)

with $\alpha _t \in (0,\frac {1}{L})$ for all t, where L is the Lipschitz constant of ∇f(U). Then the sequence {U ^(t), t = 0, 1, …} converges to a stationary point of f(U).

Theorem 11.4 guarantees that the sequence generated by PGD converges to a stationary point of the likelihood function. This gives a suitable common eigenbasis that, in a sense, approximately diagonalizes all the user covariance matrices. This basis can serve as the beam-space representation of the channel.

11.6.3 Extension of ACS to Arbitrary Array Geometries

We can directly extend the ACS technique for FDD massive MIMO channels with non-ULA geometries. In Sect. 11.6, we proposed a method of designing a common eigenbasis. Given user channel covariances { Σ _k}, or their estimates, this method yields a common eigenbasis U ^⋆, and the user-dependent “approximate eigenvalue” matrices $\boldsymbol {\Lambda }^\star _k = \text{diag}(\boldsymbol {\lambda }^\star _k),\, k\in [K]$, where $[\boldsymbol {\lambda }^\star _k]_m = {\mathbf {u}}_m^{\star \mathsf {H}} \boldsymbol {\Sigma }_k {\mathbf {u}}_m$. Eventually, the covariance of user k can be approximated as

$$\displaystyle \begin{aligned} \boldsymbol{\Sigma}_k \approx {\mathbf{U}}^\star \boldsymbol{\Lambda}^\star_k {\mathbf{U}}^{\star\,\mathsf{H}}. \end{aligned} $$

(11.25)

The eigenbasis U ^⋆ consists of the array virtual beams. Since this beam space is shared among all users, we can define the bipartite user–beam graph introduced in Sect. 11.4.2. In this case, the edge weight between a user k and a beam m is given by $w_{m,k}=[\boldsymbol {\lambda }^\star _k]_m$. Then we can solve the same matching-size maximization problem in (11.18) through the MILP. Let $\{ x_m^\star \}$ denote the MILP solution for the binary variables representing beam nodes and $\{ y_k^\star \}$ its solution for binary variables representing user nodes. Also let $\mathcal {B} =\{m\,:\, x_m^\star =1\}$ define the set of active beams and $\mathcal {K} = \{ k\,: \, y_k^\star = 1 \}$ the set of active users. The sparsifying precoder in this case is given as

$$\displaystyle \begin{aligned} \mathbf{B} = {\mathbf{U}}_{\mathcal{B}}^{\star\, \mathsf{H}}. \end{aligned} $$

(11.26)

The rest of the channel training and precoding procedure is performed just like the ULA case.

Remark 11.2

Note that since U ^⋆ is only an approximate eigenbasis of Σ _k, we cannot guarantee the coefficients of the linear expansion of a random channel vector h _k in terms of the columns of U ^⋆ to be independent random variables with a continuous distribution. Hence, we cannot prove that maximizing the matching size in the beam–user bipartite graph is equivalent to maximizing the channel matrix rank. The reason is that the conditions of Lemma 11.2 are violated, since we cannot assume a distribution on the coefficients. Nevertheless, we assume that the error of approximating the covariances as in (11.25) is not large, such that U ^⋆ is close to U _k for all k. This would lead the coefficients of the expansion in terms of the columns of U ^⋆ to be close to the Gaussian coefficients of the Karhunen–Loéve expansion. Then maximizing the matching size will maximize the channel matrix rank.