Lagrangian Modelling of Transport Phenomena Using Stochastic Differential Equations

Abstract

When modelling transport processes in marine waters one might have to solve the advection-diffusion equation or one can simulate the stochastic behaviour of individual particles of the constituent under study. By using the well-established theory of stochastic differential equations (SDEs) it is possible to derive for any advection-diffusion model an underlying SDE governing the behaviour of one particle of the constituent. Using a numerical scheme for approximating this SDE a particle model can then be obtained. In the present Chapter we first briefly describe the results of the theory of SDEs that are relevant for marine transport modelling. Then we derive a number of particle models for solving different types of transport problems and formulate these particle models as SDEs. Finally we discuss the numerical treatment of SDEs and propose a number of numerical schemes for the particle models. The performance of the methods is illustrated by a number of idealized test cases of turbulent dispersion. The test cases considered are inspired by shallow-sea dynamics and large-scale ocean transport processes.

9.1 Introduction

There are two different approaches to model transport processes in oceanic or coastal waters. One might adopt the Eulerian point of view and, hence, solve numerically the associated advection-diffusion equations. Another option consists in having recourse to Lagrangian models where the behaviour of individual particles of the constituent is considered. By simulating the position of many particles using a random generator the transport processes can be described (Dimou and Adams 1993; Hunter et al. 1993; Visser 1997, 2008).

In most textbooks the relation between the Eulerian and Lagrangian approaches is examined for the very simple case of a diffusion process with constant diffusivity. More general problems are seldom addressed. However, by using the well-established theory of SDEs it is possible to derive for any advection-diffusion model an underlying SDE governing the behaviour of one particle of the constituent. Using a numerical scheme for approximating the solution to this SDE a particle model can then be obtained. The latter is consistent with the advection-diffusion equation under consideration in the following sense: as the number of particles is increased and as the time step is decreased, the results of the particle model converge to the exact solution of the advection-diffusion equation.

The theory of SDEs and the numerical approximation thereof are not straightforward extensions of the deterministic case and, in many respects, seem to be counterintuitive. Most of the mathematical literature on these topics is difficult to comprehend for non-mathematicians. However, we do believe that a sufficient command of SDE theory would be very useful for those dealing with marine transport models. Eulerian and Lagrangian models are respectively based on two different views of the same transport processes. Knowledge on the relation between these two models increases the insight into both types of models and into the question as to which approach is optimal for a given problem. Moreover, if a Lagrangian model is formulated as an SDE then the higher order numerical schemes developed for SDEs can be used to obtain an accurate implementation of the particle model. As was clearly demonstrated by Stijnen et al. (2006), Shah et al. (2011), Shah (2015), Gräwe et al. (2012), just using the very simple Euler scheme is suboptimal in most cases. Therefore in this chapter we would like to bridge the gap between the mathematical theory and applications in oceanography. We do not present any new scientific results, but concentrate our efforts on explaining stochastic calculus and illustrating the theory with practical applications. We do not strive for mathematical rigor or completeness, but focus on the aspects that are relevant for marine transport problems. For a very good introduction on the theory of SDEs the reader is referred to the classical work of Jazwinski (1970) or, the more recent textbook of Oksendal (2003). Regarding the numerical treatment of SDEs, a comprehensive presentation may be found in the excellent book of Kloeden and Platen (1992).

In this chapter we first describe briefly the results of the theory of SDEs that are relevant for ocean transport modelling. We derive a number of particle models for solving different types of transport problems and formulate these particle models as SDEs. Then we discuss the numerical treatment of SDEs and propose a number of numerical schemes for the particle models. We finally describe a number of relevant transport test cases to illustrate the performance of the Lagrangian approach.

9.2 Stochastic Differential Equations

9.2.1 Introduction

The time varying behaviour of particles moving in a fluid in the absence of diffusive effects can be described by deterministic ordinary differential equations. If we define the state of the physical system as the particle position $\textbf{x}(t)=(x(t),y(t),z(t))$ we have the following model:

$$\begin{aligned} \frac{d \textbf{x}}{d t}=\textbf{f}(\textbf{x}, t), \quad \textbf{x}\left( t_{0}\right) =\textbf{x}_{0}. \end{aligned}$$

(9.1)

In case diffusive effects become important, the particle behaviour can only be described in terms of probability implying that a stochastic component needs to be added. Therefore in this chapter we discuss a SDE as a model for a stochastic process $\textbf{X}_t$. Here we first consider models of the following type:

$$\begin{aligned} \frac{d \textbf{X}_{t}}{d t}=\textbf{f}\left( \textbf{X}_{t}, t\right) +\mathbf {\sigma }\left( \textbf{X}_{t}, t\right) \textbf{N}_{t}, \quad \textbf{X}_{t_{0}}=\textbf{X}_{0}, \end{aligned}$$

(9.2)

where we have introduced a stochastic process $\textbf{N}_t$ to model uncertainties in the underlying deterministic differential equation. The initial particle position $\textbf{X}_0$ may also be a random variable. The notations $\textbf{f}$ and $\mathbf {\sigma }$ refer to deterministic functions while the capital representations $\textbf{X}_t$ and $\textbf{N}_t$ are associated with stochastic processes.

Let us first consider the scalar case, $X_t$, of the stochastic model (9.2):

$$\begin{aligned} \frac{d X_{t}}{d t}=f\left( X_{t}, t\right) +\sigma \left( X_{t}, t\right) N_{t}, \quad X_{t_{0}}=X_{0}. \end{aligned}$$

(9.3)

An essential property of this model is that it should be Markovian. This implies that information on the probability density of the state $x_t$ at time t is sufficient for computing the future model state (times $>t$). If the model is not Markovian, then the information on the system state for times $<t$ would also be required. This would make the model very impractical. The SDE (9.3) can be shown to be Markovian if $N_t$ is a continuous Gaussian white noise process with statistics:

$$\begin{aligned} E\left\{ N_{t}\right\} =0, \quad E\left\{ N_{t}. N_{s}\right\} =\delta (t-s). \end{aligned}$$

(9.4)

Here $E\{\cdot \}$ represents the expectation operator and $\delta (x)$ is the Dirac function. This is one of the very few processes that guarantee the model (9.3) to be Markovian. The importance of the white noise process lies in the fact that it has a very simple correlation structure. Therefore it is a good candidate for generating another process $X_t$ with a certain probabilistic structure by means of the SDE (9.3). By generating this process $X_t$ using a white noise forcing, the correlation structure of $X_t$ is completely created by the SDE and not partly by the structure of the input $N_t$. Since we need to be careful when working with delta functions we will rewrite the SDE (9.3) in terms of a Wiener process.

A standard Wiener process $W_t$, $t\ge 0$ is a process with $W_0=0$ and with stationary independent increments such that for any $0< s< t$ the increment $W_t-W_s$ is a Gaussian random variable with mean zero and variance equal to $t-s$. The formal derivative of the Wiener process can be shown to be the Gaussian continuous white noise process:

$$\begin{aligned} \frac{d W_t}{d t}=N_t, \end{aligned}$$

(9.5)

or:

$$\begin{aligned} dW_t=N_tdt. \end{aligned}$$

(9.6)

It is now convenient to rewrite the SDE (9.3) in term of the Wiener process:

$$\begin{aligned} \frac{d X_{t}}{d t}=f\left( X_{t}, t\right) +\sigma \left( X_{t}, t\right) \frac{d W_{t}}{d t}. \end{aligned}$$

(9.7)

This equation is usually rewritten as follows:

$$\begin{aligned} d X_{t}=f\left( X_{t}, t\right) d t+\sigma \left( X_{t}, t\right) d W_{t}, \end{aligned}$$

(9.8)

and can also be written as:

$$\begin{aligned} X_{t}=X_{t_{0}}+\int \limits _{t_{0}}^{t} f\left( X_{s}, s\right) d s+\int \limits _{t_{0}}^{t} \sigma \left( X_{s}, s\right) d W_{s}. \end{aligned}$$

(9.9)

The second integral in (9.9) is a stochastic integral and in order to solve (9.9) the stochastic integral needs to be defined precisely. Using the Wiener process as a random driving force introduces some mathematical difficulties in defining and evaluating the stochastic integral in (9.9).

As pointed out above the Wiener process is a very attractive driving noise process in the stochastic model (9.9). There are only a very few alternatives that also guarantee that $X_t$ is Markovian. Among them the Poisson jump process and the Lévy process are the most popular ones (Gardiner 1985). The Wiener process is often used for modelling physical processes, while the other two processes are very popular in finance. More recently the Lévy process (Hanert 2012; Vallaeys et al. 2017) has also been introduced for transport modelling.

9.2.2 Îto Stochastic Integrals

Dealing with stochastic model (9.9) requires the evaluation of a stochastic integral of the following type:

$$\begin{aligned} \int \limits _{t_0}^t \sigma _s dW_s, \end{aligned}$$

(9.10)

where $\sigma _s$ is a general stochastic process and $W_s$ is a Wiener process. To illustrate the mathematical difficulties associated with stochastic integrals, let us first consider for example the deterministic integral:

$$\begin{aligned} \int \limits _{t_0}^t sds. \end{aligned}$$

(9.11)

The classical Riemann-Stieltjes definition for this integral is:

$$\begin{aligned} \int \limits _{t_{0}}^{t} s d s=\lim _{\varDelta t \rightarrow 0} \sum t_{i}^{*}\left( t_{i+1}-t_{i}\right) =\frac{t^{2}}{2}-\frac{t_{0}^{2}}{2}, \end{aligned}$$

(9.12)

where the interval $[t_0,t]$ is divided into many small sub intervals $[t_i,t_{i+1}]$ of length $\varDelta t$ and the point $t_i^*$ is chosen somewhere in this interval. Let us now consider the stochastic integral:

$$\begin{aligned} \int \limits _{t_0}^t W_sdW_s, \end{aligned}$$

(9.13)

where $W_s$ is a Wiener process. Inspired by the deterministic case (9.12) an obvious definition for this stochastic integral would be:

$$\begin{aligned} \int \limits _{t_{0}}^{t} W_{s} d W_{s}={\text {l.i.m.}}_{\varDelta t \rightarrow 0} \sum W_{t_{i}^{*}}\left( W_{t_{i+1}}-W_{t_{i}}\right) , \end{aligned}$$

(9.14)

where again the interval $[t_0,t]$ is divided into many small sub intervals $[t_i,t_{i+1}]$ of length $\varDelta t$ and choose the point $t_i^*$ somewhere in this interval. The “l.i.m.” (limit in mean square sense) refers to a stochastic extension of a limit, i.e. a series of stochastic variables $X_n$ is said to converge in the mean square sense to a limit X if

$$\begin{aligned} \lim _{n\rightarrow \infty }E\left\{ \left( X_n-X\right) ^2\right\} =0, \end{aligned}$$

(9.15)

which is denoted by:

$$\begin{aligned} {\text {l.i.m.}}_{n\rightarrow \infty } X_n=X. \end{aligned}$$

(9.16)

This definition states that the variance of the stochastic variable defined as the difference between $X_n$ and X will approach zero for large values of n. This implies that the probability that $X_n$ will be significantly different from X will become very small in the limit $n\rightarrow \infty$.

Using the definition of the limit in mean square sense and the properties of the Wiener process it is possible to derive (after some clever algebra, Jazwinski (1970)) the stochastic limit of (9.14):

$$\begin{aligned} \int \limits _{t_{0}}^{t} W_{s} d W_{s}=\frac{W_{t}^{2}}{2}-\frac{W_{t_{0}}^{2}}{2}-\frac{\left( t-t_{0}\right) }{2}+\sum _{i}\left( t_{i}^{*}-t_{i}\right) . \end{aligned}$$

(9.17)

From this result we see that unlike in the deterministic case shown in (9.12) this stochastic limit is not uniquely defined. The choice of $t_i^*$ is important for the final result of the integral. Therefore we need another definition for a stochastic integral.

The Japanese mathematician Îto proposed the first and the most well-known definition of a stochastic integral. The Îto integral is defined as:

$$\begin{aligned} \int \limits _{t_{0}}^{t} \sigma _{s} d W_{s}={\text {l.i.m.}}_{\varDelta t \rightarrow 0} \sum _{\varDelta t \rightarrow 0} \sigma _{t_{i}}\left( W_{t_{i+1}}-W_{t_{i}}\right) . \end{aligned}$$

(9.18)

Using the Îto definition the evaluation point is always chosen at the beginning of the interval. Interpreting the integral (9.17) in Îto sense results in:

$$\begin{aligned} \int \limits _{t_{0}}^{t} W_{s} d W_{s}=\frac{W_{t}^{2}}{2}-\frac{W_{t_{0}}^{2}}{2}-\frac{\left( t-t_{0}\right) }{2}. \end{aligned}$$

(9.19)

This answer is not what we intuitively would expect. Compared to the corresponding deterministic result an additional term $\frac{(t-t_0)}{2}$ is obtained.

9.2.3 Îto Stochastic Differential Equations

Having defined the Îto stochastic integral we are now able to define the SDE (9.8)–(9.9) as an Îto SDE:

$$\begin{aligned} d X_{t}=f\left( X_{t}, t\right) d t+\sigma \left( X_{t}, t\right) d W_{t}, \end{aligned}$$

(9.20)

or:

$$\begin{aligned} X_{t}=X_{t_{0}}+\int \limits _{t_{0}}^{t} f\left( X_{s}, s\right) d s+\int \limits _{t_{0}}^{t} \sigma \left( X_{s}, s\right) d W_{s}, \end{aligned}$$

(9.21)

where the stochastic integral has to be interpreted in the Îto sense. Using the definition of the Îto stochastic integral it is possible to derive a simple numerical scheme for solving an Îto SDE (9.20)–(9.21). For a small time step we have:

$$\begin{aligned} \begin{aligned} X_{t+\varDelta t}&=X_{t}+\int \limits _{t}^{t+\varDelta t} f\left( X_{s}, s\right) d s+\int \limits _{t}^{t+\varDelta t} \sigma \left( X_{s}, s\right) d W_{s} \\&\approx X_{t}+\int \limits _{t}^{t+\varDelta t} f\left( X_{t}, t\right) d s+\int \limits _{t}^{t+\varDelta t} \sigma \left( X_{t}, t\right) d W_{s} \\&=X_{t}+f\left( X_{t}, t\right) \varDelta t+\sigma \left( X_{t}, t\right) \left( W_{t+\varDelta t}-W_{t}\right) \\&=X_{t}+f\left( X_{t}, t\right) \varDelta t+\sigma \left( X_{t}, t\right) \varDelta W, \end{aligned} \end{aligned}$$

(9.22)

where the Wiener increment $\varDelta W$ is a random variable with mean zero and variance $\varDelta t$. This approximation is called the Euler-Maruyama scheme. This scheme is consistent with the Îto definition of the stochastic integral and can only be used for an Îto SDE. By using a random number generator realizations of the Wiener increments can easily be obtained.

From the Euler approximation we can also see that $X_t$ is a Markov process. Additional information about $X_s$ for $s<t$ will not help us to obtain more accurate predictions at $t+\varDelta t$. The terms in the right hand side of (9.22) are exactly known given the value of $X_t$. The remaining Wiener increment is independent of previous increments and thus of $X_s$ for all times $s<t$. As a result, information on $X_s$ will not be useful to determine predictions of $\varDelta W$. Note that if the Wiener process would not have independent increments the process $X_t$ would not be Markovian.

9.2.4 Îto’s Differentiation Rule

Having defined the Îto integral we can now discuss Îto’s differentiation rule. Consider the process $X_t$ described by the Îto SDE:

$$\begin{aligned} d X_{t}=f\left( X_{t}, t\right) d t+\sigma \left( X_{t}, t\right) d W_{t}. \end{aligned}$$

(9.23)

Let g(x, t) be a sufficiently smooth deterministic function. Then the SDE for $g_t$ is:

$$\begin{aligned} d g_{t}=\frac{\partial g}{\partial t} d t+\frac{\partial g}{\partial x} d X_{t}+\frac{1}{2} \sigma ^{2} \frac{\partial ^{2} g}{\partial x^{2}} d t. \end{aligned}$$

(9.24)

Clearly, from this equation we can see that this result is not what one would expect from classical analysis.

To illustrate the use of Îto’s rule let us first consider a deterministic function $g(t)=e^{bt}$, where b is a constant. It is easy to see by differentiation that g(t) is the solution of the deterministic differential equation:

$$\begin{aligned} \frac{d g}{d t}=b g, \quad g(0)=1. \end{aligned}$$

(9.25)

Now suppose we have a Wiener process $W_t$ and let us derive the SDE for the process $g\left( W_t,t\right) =e^{bW_t}$. The application of the Îto differential rule for $x=w$, $\sigma =1$ and for $g(w,t)=e^{bw}$ results in:

$$\begin{aligned} \frac{\partial g}{\partial t}=0, \quad \frac{\partial g}{\partial x}=b g, \quad \frac{\partial ^{2} g}{\partial x^{2}}=b^{2} g. \end{aligned}$$

(9.26)

Substituting these results in (9.24) provides the SDE for $g_t$:

$$\begin{aligned} d g_{t}=\frac{b^{2}}{2} g_{t} d t+b g_{t} d W_{t}. \end{aligned}$$

(9.27)

Note that this Îto SDE for $g_t$ has an extra dt term compared to the deterministic result.

9.2.5 Stratonovich Stochastic Differential Equations

The Îto definition is not the only way to define stochastic integral (9.10). Stratonovich has introduced another definition:

$$\begin{aligned} \int \limits _{t_{0}}^{t} \sigma _{s} d W_{s}={\text {l.i.m}}_{\varDelta t \rightarrow 0} \sum \frac{\sigma _{t_{i+1}+t_{i}}}{2}\left( W_{t_{i+1}}-W_{t_{i}}\right) . \end{aligned}$$

(9.28)

In the Stratonovich definition the evaluation point is chosen in the middle of the interval. Interpreting the integral (9.17) in Stratonovich sense results in:

$$\begin{aligned} \int \limits _{t_{0}}^{t} W_{s} d W_{s}=\frac{W_{t}^{2}}{2}-\frac{W_{t_{0}}^{2}}{2}. \end{aligned}$$

(9.29)

This shows that the Stratonovich calculus is in agreement with the corresponding deterministic results. A SDE can also be defined in Stratonovich sense using the Stratonovich integral definition. The relation between the Îto and Stratonovich SDE is given below without proof. If a physical process $X_t$ can be described by the Îto equation:

$$\begin{aligned} d X_{t}=f\left( X_{t}, t\right) d t+\sigma \left( X_{t}, t\right) d W_{t}, \end{aligned}$$

(9.30)

then the same process can also be described by the Stratonovich equation:

$$\begin{aligned} d X_{t}=f\left( X_{t}, t\right) d t-\frac{1}{2} \sigma \left( X_{t}, t\right) \frac{\partial \sigma }{\partial x}\left( X_{t}, t\right) d t+\sigma \left( X_{t}, t\right) d W_{t}. \end{aligned}$$

(9.31)

On the other hand if a physical process $X_t$ can be described by the Stratonovich equation:

$$\begin{aligned} d X_{t}=f\left( X_{t}, t\right) d t+\sigma \left( X_{t}, t\right) d W_{t}, \end{aligned}$$

(9.32)

then the same process can also be described by the Îto SDE:

$$\begin{aligned} d X_{t}=f\left( X_{t}, t\right) d t+\frac{1}{2} \sigma \left( X_{t}, t\right) \frac{\partial \sigma }{\partial x}\left( X_{t}, t\right) d t+\sigma \left( X_{t}, t\right) d W_{t}. \end{aligned}$$

(9.33)

If $\sigma$ does not depend on $X_t$ the Îto and Stratonovich interpretations will both produce the same results.

For example, let $g_t$ be again the solution of Îto (9.27):

$$\begin{aligned} d g_{t}=\frac{b^{2}}{2} g_{t} d t+b g_{t} d W_{t}. \end{aligned}$$

(9.34)

Now from relation (9.31) we can establish that the same process is also the solution of the Stratonovich equation:

$$\begin{aligned} d g_{t}=b g_{t} d W_{t}. \end{aligned}$$

(9.35)

From this example we see that the same process can be modelled by an Îto equation or by a Stratonovich equation. The equations are different but their solutions are similar since Îto and Stratonovich equations have to be solved using different rules. Physically, there is no difference between the Îto approach and the Stratonovich one. We can choose the definition we prefer as long as we use the calculation rules that are consistent with this definition. This includes the use of the correct numerical scheme for approximating the SDE.

Both Îto and Stratonovich calculus have their advantages and disadvantages. Îto is more convenient for the analysis of an SDE, while the Stratonovich results are more in agreement with our physical intuition. The Stratonovich SDE is also very important for the development of numerical approximations, since many popular schemes for solving deterministic differential equations can only be used for approximating a Stratonovich SDE.

More recently, another interpretation of the stochastic integral (9.10) called the Îto-backward was introduced:

$$\begin{aligned} \int \limits _{t_{0}}^{t} \sigma _{s} d W_{s}={\text {l.i.m.}}_{\varDelta t \rightarrow 0} \sum \sigma _{t_{i+1}}\left( W_{t_{i+1}}-W_{t_{i}}\right) . \end{aligned}$$

(9.36)

Using this definition the evaluation point is chosen at the end of the interval. This stochastic integral is rarely used, but it has been shown by LaBolle et al. (2000) and Spivakovskaya et al. (2007b) that it is attractive for transport problems with diffusivity that strongly varies in space. If a physical process $X_t$ can be described by the Îto SDE (9.30) it is also possible to transform this SDE into an Îto-backward SDE:

$$\begin{aligned} d X_{t}=f\left( X_{t}, t\right) d t-\sigma \left( X_{t}, t\right) \frac{\partial \sigma }{\partial x}\left( X_{t}, t\right) d t+\sigma \left( X_{t}, t\right) d W_{t}. \end{aligned}$$

(9.37)

The process $X_t$ can also be described by this backward Îto equation.

9.2.6 Fokker-Planck Equation

Consider now the vector case of the Îto SDE (9.23). To gain insight into the probability density of the particle position $X_t$ which is related to the particle concentration we need to know the probability density function of $X_t$. Without proof we state that this function can be obtained by solving the Fokker-Planck equation also known as the Kolmogorov forward equation:

$$\begin{aligned} \frac{\partial p}{\partial t}=-\sum _{i=1}^{d} \frac{\partial \left( f_{i} p\right) }{\partial x_{i}}+\sum _{i=1}^{d} \sum _{j=1}^{d} \frac{\partial ^{2}\left( k_{i j} p\right) }{\partial x_{i} \partial x_{j}}. \end{aligned}$$

(9.38)

The initial condition for (9.38) could be:

$$\begin{aligned} p(\textbf{x}, t)=\delta \left( \textbf{x}-\textbf{x}_{0}\right) , \end{aligned}$$

(9.39)

implying that all particles were released at one point. The differential operator in (9.38) consists of the drift vector $\textbf{f}=f_i$ as well as diffusion term given by a matrix $K=k_{ij}$. This diffusivity matrix K is symmetric and semi-positive definite and is related to the matrix $\sigma$ in the following way:

$$\begin{aligned} k_{ij}=\frac{1}{2}\left( \sigma \sigma ^{\top }\right) _{ij}. \end{aligned}$$

(9.40)

Notice that the matrix $\sigma$ is not uniquely determined by the symmetric matrix $K=k_{ij}.$ Two possible choices of $\sigma$ are the symmetric square root of $k_{ij}$ and the lower triangular matrix given by the Cholesky decomposition of $K=k_{ij}$. All the choices of $\sigma$ that are consistent with (9.40) give statistically identical diffusion processes.

The probability distribution p(x, t) of the Fokker-Planck equation can be approximated by applying a numerical method to solve deterministic partial differential equation, but on the other hand the distribution p(x, t) can also be approximated by generating the trajectories of the following Îto SDE:

$$\begin{aligned} d \textbf{X}_{t}=f\left( \textbf{X}_{t}, t\right) d t+\sigma \left( \textbf{X}_{t}, t\right) d \textbf{W}_{t}, \quad \textbf{X}_{t_{0}}=\textbf{X}_{0}. \end{aligned}$$

(9.41)

The probability distribution of the Îto stochastic process (9.41) will satisfy the Fokker-Planck (9.38).

9.3 Particle Models for Marine Transport Problems

The Fokker-Planck equation describes the evolution in time of the particle concentration for a given SDE. But we can also use the theory the other way round. Although the Fokker-Planck equation models the distribution resulting from advection diffusion processes, it is not exactly equivalent to the classical advection diffusion equation. Therefore it is also possible to start from an advection diffusion equation that is often used for solving transport problems in oceans or coastal waters. By interpreting this transport model as a Fokker-Planck equation it is possible to derive the underlying SDE for the behaviour of the individual particles. In this way the particle model obtained can be considered as a Lagrangian solver for the original transport model.

Let us consider the following 3D advection diffusion equation written:

$$\begin{aligned} \frac{\partial C}{\partial t}=-\frac{\partial \left( u_{i} C\right) }{\partial x_{i}}+\frac{\partial }{\partial x_{i}}\left( k_{i j} \frac{\partial C}{\partial x_{j}}\right) , \quad t_{0} \le t \le T, \end{aligned}$$

(9.42)

with positive-definite diffusivity tensor K with elements $k_{ij}$ and the velocity field $\textbf{u}=u_i$. The above equation (9.42) can be rewritten in the form

$$\begin{aligned} \begin{aligned}&\frac{\partial C}{\partial t}=-\frac{\partial }{\partial x_{i}}\left( u_{i} C\right) -\frac{\partial }{\partial x_{i}}\left( C \frac{\partial k_{i j}}{\partial x_{j}}\right) +\frac{\partial }{\partial x_{i}}\left( k_{i j} \frac{\partial C}{\partial x_{j}}+C \frac{\partial k_{i j}}{\partial x_{j}}\right) \\ \Rightarrow&\frac{\partial C}{\partial t}=-\frac{\partial }{\partial x_{i}}\left[ \left( u_{i}+\frac{\partial k_{i j}}{\partial x_{j}}\right) C\right] +\frac{\partial ^{2}\left( k_{i j} C\right) }{\partial x_{i} \partial x_{j}}. \end{aligned} \end{aligned}$$

If we set $f_i=u_i+\frac{\partial k_{ij}}{\partial x_j}$ and $C=p$, the above equation will take the form of the Fokker-Planck equation (9.38). Thus the Îto stochastic model corresponding to (9.42) is obtained with this choice of $\textbf{f}$ and with matrix $\sigma$ as defined by (9.40) (Spivakovskaya et al. 2007a; Shah et al. 2011):

$$\begin{aligned} d \textbf{X}_{\textrm{t}}=f\left( \textbf{X}_{t}, t\right) d t+\sigma \left( \textbf{X}_{t}, t\right) d \textbf{W}_{t}, \quad \textbf{X}_{t_{0}}=\textbf{X}_{0}. \end{aligned}$$

(9.43)

It is also possible to include additional properties of the particle as an additional variable. Consider for example the particle model (9.43) with as additional parameter the age $A_t$ of this particle, i.e. the time elapsed since this particle enters a specified domain:

$$\begin{aligned} dA_t=dt. \end{aligned}$$

(9.44)

As long as the particle is in the specified domain $A_t$ increases with time. The corresponding Eulerian model can be derived in this case again from the Fokker-Planck (9.38) for the probability p(x, y, z, a, t)to find a particle at location (x, y, z) with age a:

$$\begin{aligned} \frac{\partial p}{\partial t}=-\frac{\partial p}{\partial a}+\nabla \cdot (K \cdot \nabla p). \end{aligned}$$

(9.45)

This equation is equivalent to the one derived by Delhez et al. (1999).

9.4 Numerical Approximation of Stochastic Differential Equations

Consider first the scalar deterministic equation:

$$\begin{aligned} \frac{d x}{d t}=f(x, t), x\left( t_{0}\right) =x_{0}. \end{aligned}$$

(9.46)

We can approximate this equation numerically with the Euler scheme:

$$\begin{aligned} x_{n+1}=x_{n}+f\left( x_{n}, t_{n}\right) \varDelta t, \end{aligned}$$

(9.47)

where $\varDelta t$ is the time step. Recall that the order of convergence of a numerical scheme for a deterministic differential equation is defined as follows: The order of convergence is $\gamma$ if there exists a positive constant c and a timestep $\varDelta$ such that for fixed $T=N\varDelta t$:

$$\begin{aligned} \left| x(T)-x_{N}\right| \le c(\varDelta t)^{\gamma }, \end{aligned}$$

(9.48)

for all $0<\varDelta t<\varDelta$.

Now consider the Îto SDE:

$$\begin{aligned} d X_{t}=f\left( X_{t}, t\right) d t+\sigma \left( X_{t}, t\right) d W_{t}, \end{aligned}$$

(9.49)

with the Euler scheme introduced in Sect. 9.2.3:

$$\begin{aligned} x_{t+\varDelta t}=x_{t}+f\left( x_{t}, t\right) \varDelta t+\sigma \left( x_{t}, t\right) \left( W_{t+\varDelta t}-W_{t}\right) , \end{aligned}$$

(9.50)

or with $t_{n}=n\varDelta t$:

$$\begin{aligned} x_{n+1}=x_{n}+f\left( x_{n}, t_{n}\right) \varDelta t+\sigma \left( x_{n}, t_{n}\right) \varDelta W_{n}. \end{aligned}$$

(9.51)

First we have to generalize the definition of the order of convergence to the stochastic case: The strong order of convergence is $\gamma$ if there exists a positive constant c and a $\varDelta$ such that for fixed $T=N\varDelta t$:

$$\begin{aligned} E\left\{ \left| X_{T}-X_{N}\right| \right\} \le c(\varDelta t)^{\gamma }, \end{aligned}$$

(9.52)

for $0<\varDelta t<\varDelta$.

Convergence in the strong sense is a track wise approach. The exact particle track $X_t$ is approximated as accurately as possible by a numerical track $X_n$. However for many practical particle simulation problems we are not interested in very accurate individual tracks. This is for instance the case if we want to compute the particle concentration or only the position variance of a particle. For these problems we can use a weaker form of convergence: The weak order of convergence is $\alpha$ if there exists a positive constant c and a $\varDelta$ such that for fixed $T=N\varDelta t$:

$$\begin{aligned} \left| E\left\{ h\left( X_{T}, T\right) \right\} -E\left\{ h\left( X_{N}, N \varDelta t\right) \right\} \right| \le c(\varDelta t)^{\alpha }, \end{aligned}$$

(9.53)

for all $0<\varDelta t<\varDelta$ and for all functions h(x, t) with polynomial growth.

If we take $h(x,t)=x$ the definition of weak order convergence reduces to:

$$\begin{aligned} \left| E\left\{ X_{T}\right\} -E\left\{ X_{N}\right\} \right| \le c(\varDelta t)^{\alpha }. \end{aligned}$$

(9.54)

In this case we use the realizations of $X_t$ only to determine the mean at time T, and we evaluate the accuracy of the numerical scheme by computing this quantity. We do not evaluate the accuracy of the underlying tracks. If $h(x,t)=x^2$ we have:

$$\begin{aligned} \left| E\left\{ \left( X_{T}\right) ^{2}\right\} -E\left\{ \left( X_{N}\right) ^{2}\right\} \right| \le c(\varDelta t)^{\alpha }, \end{aligned}$$

(9.55)

and we evaluate the accuracy of the numerical scheme only by computing the second moment.

For deterministic differential equations the Taylor series expansion is an important method to evaluate the order of accuracy, however, for the stochastic case we can use the stochastic version of the Taylor expansion (for more details the reader is referred to Kloeden and Platen (1992)). By analysing the error terms in the stochastic Taylor expansion the strong order of convergence of the Euler scheme can be determined: $\mathcal {O}(\varDelta t^{\frac{1}{2}})$. For weak order convergence many realizations are generated and averaged to determine an approximation of the particle concentration. Because of the averaging procedure certain random error terms cancel out and vanish for increasing number of realizations. This results in a weak order of convergence of the Euler scheme of $\mathcal {O}(\varDelta t)$. This implies that if we use the Euler scheme and generate many tracks then the individual tracks are only half order accurate (strong convergence) while for example the results on the mean and variance of the tracks are first order accurate (weak convergence). Certain stochastic errors in the track wise computations cancel out when computing ensemble mean quantities like the mean or variance.

From the stochastic Taylor expansion, more accurate schemes can been obtained, such as the following one:

$$\begin{aligned} x_{n+1}=x_{n}+\varDelta t f\left( x_{n}, t_{n}\right) +\sigma \left( x_{n}, t_{n}\right) \varDelta W_{n}+\frac{1}{2} \sigma \left( x_{n}, t_{n}\right) \frac{\partial \sigma }{\partial x}\left( x_{n}, t_{n}\right) \left( \varDelta W_{n}^{2}-\varDelta t\right) . \end{aligned}$$

(9.56)

This scheme is called the Milstein scheme and is $\mathcal {O}(\varDelta t)$ in the strong sense for scalar equations. For vector systems it is generally of order $\mathcal {O}(\varDelta t^{\frac{1}{2}})$ (except for very special differential equations when its accuracy is as in the scalar case). In the weak sense the Milstein scheme has the same order of convergence as the Euler scheme.

By including further terms of the stochastic Taylor expansion, the next higher order scheme is of 1.5 order accuracy in the strong sense and 2.0 order in the weak sense. The 1.5 order strong Taylor scheme is given as:

$$\begin{aligned} \begin{aligned} x_{n+1}=&\; x_{n}+\varDelta t f \varDelta t+\sigma \varDelta W_{n}+\frac{1}{2} \sigma \frac{\partial \sigma }{\partial x}\left( \varDelta W_{n}^{2}-\varDelta t\right) +\frac{\partial f}{\partial x} \sigma \varDelta Z_{n}+\\&\frac{1}{2}\left( f \frac{\partial f}{\partial x}+\frac{1}{2} \sigma ^{2} \frac{\partial ^{2} f}{\partial x^{2}}\right) (\varDelta t)^{2}+\left( f \frac{\partial \sigma }{\partial x}+\frac{1}{2} \sigma ^{2} \frac{\partial ^{2} \sigma }{\partial x^{2}}\right) \left( \varDelta W_{n} \varDelta t+\varDelta Z_{n}\right) \\&\frac{1}{2} \sigma \left( \sigma \frac{\partial ^{2} \sigma }{\partial x^{2}}+\left( \frac{\partial \sigma }{\partial x}\right) ^{3}\right) \left( \frac{1}{3} \varDelta W_{n}^{2}-\varDelta t\right) \varDelta W_{n}, \end{aligned} \end{aligned}$$

(9.57)

where all the functions are evaluated at $x=x_n$ and $t=t_n$. In addition to the noise increment $\varDelta W$ a second random variable $\varDelta Z$ is needed. $\varDelta Z$ is also a Gaussian random variable with the following properties: Mean 0, variance $\frac{\varDelta t}{3}$ and covariance $E\{\varDelta W\varDelta Z\}=\frac{\varDelta t^2}{2}$.

Weak approximation schemes can be simplified without losing accuracy. Instead of the generation of Gaussian random numbers, numbers can be generated from any probability distribution as long as the mean and variance are the same. The order 2.0 Milstein scheme is a one-step weak simplification of the previous scheme. Because only a weak approximation is needed, some terms of the Taylor 1.5 scheme can be skipped and there is no need for a second random variable. This scheme was proposed by Milstein (1979) and is of 2.0 order accuracy in the weak sense:

$$\begin{aligned} \begin{aligned} x_{n+1}=&\; x_{n}+\varDelta t f \varDelta t+\sigma \varDelta W_{n}+\frac{1}{2} \sigma \frac{\partial \sigma }{\partial x}\left( \varDelta W_{n}^{2}-\varDelta t\right) +\frac{\partial f}{\partial x} \sigma \varDelta Z_{n}+\\&\frac{1}{2}\left( f \frac{\partial f}{\partial x}+\frac{1}{2} \sigma ^{2} \frac{\partial ^{2} f}{\partial x^{2}}\right) (\varDelta t)^{2}+\frac{1}{2}\left( \frac{\partial f \sigma }{\partial x}+\frac{1}{2} \sigma ^{2} \frac{\partial ^{2} \sigma }{\partial x^{2}}\right) \varDelta W_{n} \varDelta t. \end{aligned} \end{aligned}$$

(9.58)

Similar to predictor-corrector schemes for ODEs, there exist equivalent methods for SDEs. This class is often used due to their numerical stability, which they inherit from the implicit counterparts of their corrector scheme. In addition, the difference between the predicted and the corrected values at each time step provides an indication of the local error. Thus, they can be beneficial in (time) adaptive schemes (Charles et al. 2009).

The lowest order predictor-corrector scheme is as follows:

$$\begin{aligned} \begin{aligned} x^{p}_{n+1}&=x_{n}+f\left( x_{n}, t_{n}\right) \varDelta t+\sigma \left( x_{n}, t_{n}\right) \varDelta W_{n} \\ x_{n+1}&=x_{n}+\frac{1}{2}\left( f\left( x_{n+1}^{p}, t_{n+1}\right) +f\left( x_{n}, t_{n}\right) \right) \varDelta t+\sigma \left( x_{n}, t_{n}\right) \varDelta W_{n}. \end{aligned} \end{aligned}$$

(9.59)

This is a stochastic version of the trapezoidal method also known as Heun scheme. Note that the predictor step is only applied to the deterministic part, the stochastic part cannot be corrected to keep the numerical approximation consistent with the original Îto SDE (Kloeden and Platen 1992). This Heun scheme is of order $\mathcal {O}(\varDelta t)$ in the weak sense and of order $\mathcal {O}(\varDelta t^{\frac{1}{2}})$ in the strong sense. At this stage, the question arises as to why another first order scheme is presented. In the limit of vanishing diffusivity, the Euler scheme is equivalent to its deterministic counterpart and is first order accurate. This is not the case for the Heun scheme. Due to the predictor-corrector step, the scheme converges to a second order approximation of the ordinary differential equation.

In case the stochastic term is also evaluated using the prediction step we obtain the Heun scheme that can be used for approximating a Stratonovich SDEs:

$$\begin{aligned} \begin{aligned} x^{p}_{n+1}=&x_{n}+f\left( x_{n}, t_{n}\right) \varDelta t+\sigma \left( x_{n}, t_{n}\right) \varDelta W_{n} \\ x_{n+1}=&x_{n}+\frac{1}{2}\left( f\left( x_{n+1}^{p}, t_{n+1}\right) +f\left( x_{n}, t_{n}\right) \right) \varDelta t \\&+\frac{1}{2}\left( \sigma \left( x^{p}_{n+1}, t_{n+1}\right) +\sigma \left( x_{n}, t_{n}\right) \right) \varDelta W_{n}. \end{aligned} \end{aligned}$$

(9.60)

For approximating a Stratonovich SDE this Heun scheme is first order accurate in the strong sense and also first order accurate in the weak sense.

There are two complications in deriving strong higher order schemes. First the number of error terms grows very rapidly, resulting in rather complicated numerical schemes involving many terms. Secondly, most Wiener integrals appearing in the expansion cannot be solved analytically like in the case of the Milstein scheme. As a result special numerical schemes have to be implemented to approximate these integrals too. For details the reader is referred to Kloeden and Platen (1992).

9.5 Test Cases for Marine Transport Problems

9.5.1 Simple Vertical Diffusion

Firstly, the numerical algorithms are applied to a simple diffusion problem in a domain limited by two boundaries. This can be visualised as a one dimensional water column that is bounded by the sea surface and the pycnocline. The model is discussed in detail in Deleersnijder et al. (2006) and Spivakovskaya et al. (2007a). The governing partial differential equation for this test case is given by simple diffusion equation:

$$\begin{aligned} \frac{\partial C}{\partial t}=\frac{\partial }{\partial z}\left( k(z) \frac{\partial C(z, t)}{\partial z}\right) , \quad t \ge 0 \text{ and } 0 \le z \le H, \end{aligned}$$

(9.61)

with a “no flux” boundary condition imposed at the boundaries domain and the initial condition is a delta like concentration peak at $z=z_0$:

$$\begin{aligned} \left. k(z) \frac{\partial C}{\partial z}\right| _{z=0, H}=0, \end{aligned}$$

(9.62)

$$\begin{aligned} C(z, 0)=\delta \left( z-z_{0}\right) . \end{aligned}$$

(9.63)

For the sake of generality, the above problem is normalized by introducing the dimensionless variables:

$$\begin{aligned} t^{\star }=\frac{t}{H^{2} / k}, \quad z^{\star }=\frac{z}{H}, \quad k^{\star }=\frac{k}{\bar{k}}, \end{aligned}$$

(9.64)

where $\bar{k}$ denotes the depth averaged diffusivity i.e.

$$\begin{aligned} \bar{k}=\frac{1}{H} \int \limits _{0}^{H} k(z) \textrm{d} z. \end{aligned}$$

(9.65)

The parabolic profile is a good approximation of the diffusivity profile in the mixed layer, but it is also a good description for a shallow, well-mixed, coastal region (Burchard et al. 1998; Warner et al. 2005). Moreover, the parabolic profile is until now the only realistic profile, for which analytical solutions exist (beside constant diffusivity). Therefore, the dimensionless diffusivity $k(z)=6z(1-z)$ is chosen to be a parabolic function.

The Îto SDE for the particle position $Z_t$ is the 1D version of the case described in Sect. 9.3 and takes the following form:

$$\begin{aligned} d Z_{t}=\frac{\partial k}{\partial z} d t+\sqrt{2 k(z)} d W_{t}, \quad Z_{t_{0}}=Z_{0}. \end{aligned}$$

(9.66)

Using this setup, an analytical solution for the dispersion of the initial concentration $C(z,0)=\delta (z-z_0)$ is known (Spivakovskaya et al. 2007a):

$$\begin{aligned} C(z, t)=1+\sum _{n=1}^{\infty }(2 n+1) P_{n}(2 z-1) P_{n}\left( 2 z_{0}-1\right) e^{(-6 n(n+1) t)}, \end{aligned}$$

(9.67)

where $P_n(z)$ denotes the nth order Legendre polynomial. Figure 9.1 presents the analytical solution for $z_0=0.5$ and for various times t.

We will now use various numerical schemes for the Îto SDEs introduced in Sect. 9.4 to compute the particle concentration and will compare the results with the analytical solution. Table 9.1 summarises the numerical schemes used for this test case.

The results for $z_0=0.5$ are shown in Fig. 9.2. The results clearly indicate that all schemes converge to the true solution according to the designed order of accuracy. Hence, by decreasing the time step, all schemes behave as expected and scale according to their designed convergence order.

Fig. 9.1

Analytical solution of the 1D diffusion equation at different times

By increasing the number of particles N, see Fig. 9.2b, the error also becomes smaller. Nevertheless, no differences in the scaling are visible, except from deviations in the offset. This is due to the intrinsic nature of random processes. The results include statistical errors proportional to $N^{\frac{1}{2}}$. Therefore, to increase the accuracy, the “brute-force-method” (using an excessively large number of particles) is an option, but due to the slow convergence, having recourse to a more accurate numerical scheme is much more rewarding. It is important to note that both the chosen numerical schemes and the use of a finite number of particles introduce errors. Preferably both type of errors should be of the same order of magnitude. Therefore, it makes no sense to use the fastest and most simple numerical scheme and a huge amount of particles. But it also makes no sense to use a very accurate scheme and only a limited amount of particles.

Comparing the efficiency, see Fig. 9.2c, it is visible, that the E1 scheme is the fastest, but the M1 and M2 schemes show a better overall scaling. Thus, with moderate time steps, these two schemes provide a higher accuracy at the same runtime. Therefore, these schemes should be preferred. From the efficiency plot, one can also see the additional overhead of the predictor-corrector scheme PC1. Since a predictor steps is needed, the efficiency is clearly lower than for the M1 scheme. Although the S1.5 scheme offers the highest accuracy, it is less efficient due to the high computational demand.

Fig. 9.2

Error of the dispersion test for a variation of the time step $\varDelta t$, b variation of the number of particles N, and c comparison of the efficiency (accuracy vs. runtime)

Table 9.1 Summary of the numerical schemes used

9.5.2 One Dimensional Water Column Including a Pycnocline

The starting point is the test case of Stijnen et al. (2006). The authors performed Lagrangian simulations in the shallow the coastal zone of the Netherlands. They were faced with the challenge of representing inhibition of mixing due to stratification associated with salinity contrasts, caused by river runoff. The stratification, which is associated with a rather thin pycnocline, is a quasi-impermeable barrier to vertical diffusive or turbulent motions. In Stijnen et al. (2006) it is showed that this is easily taken into account by Eulerian models, while obtaining a similar result in Lagrangian simulations is far from trivial. They could show that the pycnocline was no significant barrier to diffusion when the Euler scheme was used. However, when using a higher-order particle tracking scheme, the pycnocline remained almost impermeable to diffusive fluxes—as it is supposed to be.

To construct a possible test case we use the diffusivity profile of Stijnen et al. (2006) as a blueprint. We assume without any loss of generality that the pycnocline is located in the middle of the water column. Accordingly, it is suggested that the idealised vertical eddy diffusivity can be approximated by:

$$\begin{aligned} \begin{aligned} k(z)=&\frac{2(1+a)(1+2 a)}{a^{2} H^{1+\frac{1}{a}}} z(H-2 z)^{\frac{1}{a}}, \quad 0 \le z \le \frac{H}{2} \\ =&\bar{k} \frac{2(1+a)(1+2 a)}{a^{2} H^{1+\frac{1}{a}}}(H-z)(2 z-1)^{\frac{1}{a}}, \quad \frac{H}{2} \le z \le H, \end{aligned} \end{aligned}$$

(9.68)

where a is a constant that is larger than or equal to unity, z is the distance to the seabed, which is located at $z=0$, while the sea surface is at $z=H$. For more details the interested reader is referred to Gräwe (2011).

The important tuning parameter that controls the sharpness of the pycnocline is a. The dependence of the sharpness of the pycnocline on a is shown in Fig. 9.3. The important feature of this analytical eddy diffusivity is that it vanishes at the pycnocline and is small in the vicinity of the latter. The parameter a controls the steepness of the diffusivity profile. The larger the value of a, the larger the vertical diffusivity gradient near the pycnocline. Note, that setting $a=1$ will produce a double parabolic diffusivity profile.

Fig. 9.3

Diffusivity profile $K=\frac{k}{\bar{k}}$ for different values of the parameter a

For this test case, we have considered a pure diffusion problem so the SDE for the particle position $Z_t$ is again described by (9.61). The boundaries are treated again as “no flux” boundaries and the initial release is also in this test case a Dirac function. For an analytical solution of the posed problem in the special case of $a=1$, the interested reader is referred to Gräwe (2011). The intention of this test case is however not to reproduce the analytical solution. Our aim is to assess the ability of different numerical schemes to treat the pycnocline as the requested impermeable barrier. Thus, if we release particles in the upper half of the water column, a “perfect” scheme is characterised by zero concentration in the lower half of the water column at any instant of time. This is easily done in Eulerian-type numerical model. Lagrangian simulations, however, do show some crossings of the particles through pycnocline, thereby causing simulation errors that have to be assessed. To quantify to what extent the pycnocline is actually a barrier to vertical diffusion, we released N particles in the upper half of the water column. Since the number of particles has to remain constant, we constructed an error measure in such a way that $\epsilon = 0$, if no particles have crossed the pycnocline, and $\epsilon =1$ if the particles are uniformly distributed in the whole water column. Clearly, the lower $\epsilon$ the better the scheme under consideration.

An important point to mention is that although we are looking for the time evolution of a particle distribution and thus weak convergence (9.53), the crossing of the pycnocline tests for strong convergence (9.52). This is related to the fact that the individual particle path in the vicinity of the pycnocline is important and therefore a strong error measure is appropriate.

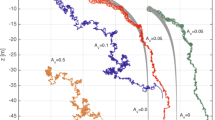
In Fig. 9.4 we show the time evolution of a point release of particles at $z_0=0.75$. We have used again all the schemes presented in Table 9.1. The results clearly indicate that for the E1 scheme the pycnocline is not at all a barrier. This is even true for small values of a. The M2 scheme shows for $a=1$ no crossing of particles of the pycnocline. For $a=4$ (Fig. 9.4d) there is a leakage of particles into the lower half of the water column. Hence, by simple visual inspection, it is obvious that the results obtained with the Euler scheme are completely wrong. Furthermore, variations of the time step would not reveal this failure as we are already using a very small time step for this problem (see Visser (1997)).

Fig. 9.4

Dispersion of a particle cloud initially located at $z_0=0.75$ for two different schemes and for two values of a. Color coded is the particle concentration for a E1 scheme with $a=1$, b E1 scheme with $a=4$, c M2 scheme with $a=1$, d M2 scheme with $a=4$. The time step is $10^{-6}$

To visualise the impact for different values of a, we show in Fig. 9.5 the convergence of the error for variations of the pycnocline sharpness. For moderate time steps and small values of a the M1, M2 and S1.5 schemes can treat the pycnocline as a barrier (Fig. 9.5a). However, for values of a larger then 7 all schemes fail this test. Only by decreasing the time step the M1, M2 and S1.5 schemes show a scaling of the error over the whole range of variations of a (Fig. 9.5b). Clearly, the S1.5 scheme shows the best performance. Again the E1 scheme and PC1 scheme do not treat the pycnocline correctly for all values of a.

Fig. 9.5

Variation of the error $\epsilon$ for the different numerical schemes and a a time step of $7\cdot 10^{-6}$ b a time step of $10^{-6}$. On the x-axis we show the pycnocline sharpness parameter a and on the y-axis the error $\epsilon$

9.5.3 Multidimensional Diffusion in an Unbounded Domain

Large-scale diffusion processes in the oceans occur mostly along isopycnal surfaces, i.e. surfaces of equal density. Diapycnal diffusion associated with a diffusion flux orthogonal to isopycnal surfaces is usually very small. The diapycnal and isopycnal diffusion fluxes are commonly parameterised á la Fourier-Fick (Redi 1982).

The natural coordinates for representing diffusive processes in oceans are diapycnal and isopycnal. The slope of the isopycnal surfaces, though generally small, contains significant information about the dynamics of the ocean and its interaction with the atmosphere. Most ocean models do not use iso and diapycnal coordinates. Instead they rely on the horizontal-vertical coordinates, in which the Redi diffusivity tensor is resorted to in order to model diapycnal and isopycnal diffusion. This diffusivity tensor contains off-diagonal terms.

The Eulerian discretisations of isopycnal diffusion terms yield discrete operators that are not monotonic (Beckers et al. 1998, 2000), occasionally producing spurious oscillations and over- or under-shootings in tracer concentration fields, which obviously are unrealistic (Mathieu and Deleersnijder 1998; Mathieu et al. 1999). To overcome these shortcomings Lagrangian numerical schemes can be used. In this Section, idealized test cases are constructed to assess Lagrangian methods for the iso- and diapycnal diffusion problems. For more details see Spivakovskaya et al. (2007a), Shah et al. (2011), Shah (2015).

9.5.3.1 Iso and Diapycnal Diffusion Along Flat Isopycnal Surfaces

If only large scales of motions are actually resolved, the unresolved motions comprise much more that those giving rise to the molecular diffusion. The unresolved phenomena are usually parameterised as non-isotropic diffusion. Such a formulation resorts to two diffusivity coefficients, $K^{I}$ and $K^{d}$, which are the isopycnal diffusivity and the diapycnal diffusivity, respectively. In the principal axes, the associated diffusivity tensor reads:

$$\begin{aligned} K=\left( \begin{array}{ccc} K^{I} &{} 0 &{} 0 \\ 0 &{} K^{I} &{} 0 \\ 0 &{} 0 &{} K^{d} \end{array}\right) . \end{aligned}$$

(9.69)

The z-principal axes is perpendicular to the isopycnal plane. To rotate the coordinate system associated with the isopycnal surface into the geodesic coordinate system we need two angles $\theta$ and $\gamma$ (Redi 1982) and the diffusivity tensor takes the form:

$$\begin{aligned} \begin{aligned} K&= \left( \begin{matrix} K^{I} \cos ^{2} \theta +\sin ^{2} \theta \left( K^{l} \sin ^{2} \gamma +K^{d} \cos ^{2} \gamma \right) \\ -\cos \gamma \sin \gamma \sin ^{2} \theta \left( K^{I}-K^{d}\right) \\ \cos \gamma \sin \theta \cos \theta \left( K^{l}-K^{d}\right) \end{matrix}\right. \\&\qquad \qquad \left. \begin{matrix} {}-\cos \gamma \sin \gamma \sin ^{2} \theta \left( K^{I}-K^{d}\right) &{} \cos \gamma \sin \theta \cos \theta \left( K^{I}-K^{d}\right) \\ {}K^{I} \cos ^{2} \theta +\sin ^{2} \theta \left( K^{l} \cos ^{2} \gamma +K^{d} \sin ^{2} \gamma \right) &{} \sin \gamma \sin \theta \cos \theta \left( K^{I}-K^{d}\right) \\ {}\sin \gamma \sin \theta \cos \theta \left( K^{I}-K^{d}\right) &{} K^{l} \sin ^{2} \theta +K^{d} \cos ^{2} \theta \end{matrix}\right) . \end{aligned} \end{aligned}$$

(9.70)

As a test case, it is assumed that the isopycnal surfaces are flat and equally spaced. Furthermore, we assume that the velocity field is zero and that the iso and diapycnal diffusivity are constant. As in Sect. 9.3 we consider the following partial differential problem in an infinite domain:

$$\begin{aligned} \frac{\partial C}{\partial t}=\nabla \cdot (K \cdot \nabla C), \quad -\infty<x<\infty , \quad C\left( x, t_{0}\right) =\delta (x-0), \end{aligned}$$

(9.71)

where $\delta$ denotes a Dirac function. The exact solution of problem (9.71) can be shown to be:

$$\begin{aligned} C(x, t)=\frac{\exp \left( -\frac{x^{\top } \cdot K^{-1} \cdot x}{4 t}\right) }{(4 \pi t)^{\frac{n}{2}} \sqrt{{\text {det}}(K)}}. \end{aligned}$$

(9.72)

Here $\text {det}(K)$ is the determinant of the constant diffusion matrix K while n is the number of space dimensions considered. Introducing the dimensionless quantities for space and time:

$$\begin{aligned} t^{*}=\frac{t}{T}, x^{*}=\frac{x}{L_{h}}, y^{*}=\frac{y}{L_{h}} \text{ and } z^{*}=\frac{z}{L_{v}}, \end{aligned}$$

(9.73)

where T, $L_h$ and $L_v$ represent the appropriate timescale, horizontal and vertical length scale, respectively. It is also convenient to define:

$$\begin{aligned} T=\frac{L_{h}^{2}}{K^{I}}=\frac{L_{h}^{2}}{K^{I}}, \quad \alpha =\frac{L_{h}}{L_{v}} \text{ and } C^{*}=\frac{C}{1 / L_{h}^{2} L_{v}}. \end{aligned}$$

(9.74)

The ratio to the vertical to horizontal length is given by $\alpha$ and the scaled concentration is represented by $C^*$. Using these quantities (9.73) and (9.74) into (9.70) and dropping the asterisk notation the diffusion tensor takes the following form:

$$\begin{aligned} \begin{aligned} K&= \left( \begin{matrix} \cos ^{2} \theta +\sin ^{2} \theta \left( \sin ^{2} \gamma +\alpha ^{2} \cos ^{2} \gamma \right) \\ -\cos \gamma \sin \gamma \sin ^{2} \theta \left( 1-\alpha ^{2}\right) \\ \cos \gamma \sin \theta \cos \theta \left( \alpha ^{-1}-\alpha \right) \end{matrix}\right. \\&\qquad \qquad \left. \begin{matrix} {}-\cos \gamma \sin \gamma \sin ^{2} \theta \left( 1-\alpha ^{2}\right) &{} \cos \gamma \sin \theta \cos \theta \left( \alpha ^{-1}-\alpha \right) \\ {}\cos ^{2} \theta +\sin ^{2} \theta \left( \cos ^{2} \gamma +\alpha ^{2} \sin ^{2} \gamma \right) &{} \sin \gamma \sin \theta \cos \theta \left( \alpha ^{-1}-\alpha \right) \\ {}\sin \gamma \sin \theta \cos \theta \left( \alpha ^{-1}-\alpha \right) &{} \sin ^{2} \theta +\alpha ^{-2} \cos ^{2} \theta \end{matrix}\right) , \end{aligned} \end{aligned}$$

(9.75)

and the exact solution (9.68) can be rewritten in the form:

$$\begin{aligned} \begin{array}{l} C(x, y, z, t)=\frac{1}{(4 \pi t)^{3 / 2}} \exp \left[ -\frac{1}{4 t}\left( z \cos \theta -\alpha ^{-1}(y \sin \theta \sin \gamma +x \sin \theta \cos \gamma )\right) ^{2}\right] \times \\ \exp \left[ -\frac{1}{4 \textrm{t}}(z \alpha \cos \theta +x \cos \alpha \cos \gamma +y \cos \theta \sin \gamma )^{2}\right] \times \exp \left[ -\frac{1}{4 t}(x \sin \gamma -y \cos \gamma )^{2}\right] . \end{array} \end{aligned}$$

(9.76)

The values of the parameters $\theta \approx \alpha \approx 10^{-3}$ are reasonable. The corresponding Îto SDE for the particle position whose probability distribution satisfies the diffusion problem (9.71) reads (see also Sect. 9.3):

$$\begin{aligned} d \boldsymbol{X}_{t}=\sigma \left( \textbf{X}_{t}, t\right) d \textbf{W}(t), \quad \boldsymbol{X}_{t_{0}}=\boldsymbol{X}_{0}. \end{aligned}$$

(9.77)

Since, the matrix K is symmetric and positive definite it may be decomposed using Cholesky decomposition in following form of $\sigma$:

$$\begin{aligned} \sigma =\left( \begin{array}{lll} \sigma _{x x} &{} 0 &{} 0 \\ \sigma _{y x} &{} \sigma _{y y} &{} 0 \\ \sigma _{z x} &{} \sigma _{z y} &{} \sigma _{z z} \end{array}\right) , \end{aligned}$$

(9.78)

with

$$\begin{aligned} \begin{array}{l} \sigma _{x x}=\sqrt{2 k_{x x}}, \sigma _{y x}=\frac{\sqrt{2} k_{y x}}{\sqrt{k_{x x}}}, \sigma _{z x}=\frac{\sqrt{2} k_{z x}}{\sqrt{k_{x x}}}, \sigma _{y y}=\sqrt{\frac{2\left( k_{x x} k_{y y}-k_{x y}^{2}\right) }{k_{x x}}} \\ \sigma _{z y}=\frac{\sqrt{2}\left( k_{x x} k_{y z}-k_{x y} k_{z x}\right) }{\sqrt{k_{x x}\left( k_{x x} k_{y y}-k_{x y}^{2}\right) }}, \sigma _{z z}=\sqrt{\frac{2\left( k_{x x} k_{y y} k_{z z}+2 k_{x y} k_{x z} k_{y z}-k_{x z}^{2} k_{y y}-k_{y z}^{2} k_{x x}-k_{x y}^{2} k_{z z}\right) }{k_{x x} k_{y y}-k_{x y}^{2}}}. \end{array} \end{aligned}$$

(9.79)

The main idea of the Lagrangian model is to simulate the trajectory of many different particles using an appropriate numerical scheme of the SDEs and then construct the probability distribution function which is in this case equal to the particle concentration using non-parametric statistical methods. In our experiment the trajectories of the SDE (9.77) are simulated using the Euler scheme described in Sect. 9.4. In order to obtain the concentration from the particle trajectories a kernel estimator (Silverman 1986; Spivakovskaya et al. 2007a) is used. Here we used the Gaussian kernel and the comparison between the Eulerian and Lagrangian is depicted in Fig. 9.6.

Fig. 9.6

Comparison between the particle model and the exact solution of the diffusion (9.69). This implies the Lagrangian model is indeed consistent with the concentration field of the diffusion equation. a–c shows the exact solution along the xy-, xz- and yz- plane and, d–f shows the probability distribution of $10^5$ Lagrangian particle initially released at origin

9.5.3.2 Isopycnal Diffusion Along Non-flat Isopycnal Surfaces

In case the isopycnal surfaces are flat, the Lagrangian simulation reveals that a first order Euler scheme is accurate enough to attain the desired accuracy. If the diapycnal diffusion is zero, the particles should remain on the isopycnal surface they are released on, even if a simple time stepping is used. By contrast, if the isopycnal surfaces are assumed to be not flat, particles tend to leave the isopycnal surface they are released on. In such cases, the first order Lagrangian schemes might fail due to numerical errors and higher order Lagrangian schemes might reduce these errors. This is why assessing different numerical schemes for isopycnal diffusion on a non-flat isopycnal surfaces is important.

The objective here is to simulate diffusion processes along non-flat isopycnal surfaces in the absence of diapycnal diffusion (Shah et al. 2011; Shah 2015; van Sebille et al. 2018). Here, it is more important to accurately reproduce the individual trajectories of the particles rather than the time evolution of a distribution. For approximating particle tracks, higher order strong, in lieu of weak, schemes should be used. A three dimensional idealised test case is constructed for purely isopycnal diffusion along non-flat isopycnal surfaces. Moreover, to validate, numerically, the equivalence between the Îto, Stratonovich and Îto-backward models the Îto, Stratonovich and Îto-backward Lagrangian models for transport along non-flat isopycnal are all considered.

Let x and y denote the horizontal coordinates, while z denotes the vertical coordinate (increasing upward). If $\rho$ is the density, then the isopycnal tensor (Redi 1982) reads:

$$\begin{aligned} K=\frac{K^{I}}{\rho _{x}^{2}+\rho _{y}^{2}+\rho _{z}^{2}}\left( \begin{array}{ccc} \rho _{y}^{2}+\rho _{z}^{2} &{} -\rho _{x} \rho _{y} &{} -\rho _{x} \rho _{z} \\ -\rho _{x} \rho _{y} &{} \rho _{x}^{2}+\rho _{z}^{2} &{} -\rho _{z} \rho _{y} \\ -\rho _{x} \rho _{z} &{} -\rho _{z} \rho _{y} &{} \rho _{x}^{2}+\rho _{y}^{2} \end{array}\right) . \end{aligned}$$

(9.80)

Density decreases as z increases, so lighter water lies on the top of heavier water. We consider the following three dimensional density field:

$$\begin{aligned} \rho (x, y, z)=\rho _{0}\left[ 1-\frac{N^{2} z}{g}+\alpha _{x} \sin \left( \kappa _{x} x\right) +\alpha _{x} \sin \left( \kappa _{y} y\right) \right] , \end{aligned}$$

(9.81)

where $\alpha _x$, $\alpha _y$, $\kappa _x$ and $\kappa _y$ are constants. The following values of these parameters seem to be a reasonable choice:

$$\begin{aligned} \alpha _{\xi }=10^{-3} \text{ and } \kappa _{\xi }=10^{-6}, \quad \xi =x, y. \end{aligned}$$

Note that the vertical density gradient is assumed to be constant, but the horizontal one is not, so that the isopycnal surfaces are not flat. The horizontal and vertical density gradients are

$$\begin{aligned} \rho _{x}=\rho _{0} \alpha _{x} \kappa _{x} \cos \left( \kappa _{x} x\right) , \rho _{x}=\rho _{0} \alpha _{y} \kappa _{y} \cos \left( \kappa _{y} y\right) \text{ and } \rho _{z}=-\frac{\rho _{0} N^{2}}{g}, \end{aligned}$$

(9.82)

and the corresponding isopycnal surface may be represented as follows:

$$\begin{aligned} z=\frac{g}{N^{2}}\left( 1-\frac{\rho ^{*}}{\rho _{0}}\right) +\frac{g \alpha _{x}}{N^{2}} \sin \left( \kappa _{x} x\right) +\frac{g \alpha _{y}}{N^{2}} \sin \left( \kappa _{y} y\right) . \end{aligned}$$

(9.83)

Substituting the density gradients (9.82) into (9.80) yields the actual expressions of the components of the diffusion tensor and substituting the resulting components (9.78) of $\sigma$ into (9.43), lead to the following system of Îto SDEs for non-flat isopycnal diffusion:

$$\begin{aligned} d \textbf{X}_{t}=f\left( \textbf{X}_{t}, t\right) d t+\sigma \left( \textbf{X}_{t}, t\right) d \textbf{W}_{t} \quad \textbf{X}_{t_{0}}=\textbf{X}_{0}. \end{aligned}$$

(9.84)

Here the components of the drift vector a are given by:

$$\begin{aligned} f_{x}=\frac{\partial k_{x x}}{\partial x}+\frac{\partial k_{x y}}{\partial y}, f_{y}=\frac{\partial k_{y x}}{\partial x}+\frac{\partial k_{y y}}{\partial y} \text{ and } f_{z}=\frac{\partial k_{z x}}{\partial x}+\frac{\partial k_{z y}}{\partial y}. \end{aligned}$$

(9.85)

The components of $\sigma$ are given in (9.78)-(9.79). This system of SDEs is again consistent with diffusion equation:

$$\begin{aligned} \frac{\partial C}{\partial t}=\nabla \cdot (K \cdot \nabla C), \quad -\infty<x<\infty , \quad C\left( x, t_{0}\right) =\delta \left( x-x_{0}\right) . \end{aligned}$$

(9.86)

For the numerical simulations the particles are all released at the origin $(x,y,z)=(0,0,0)$. This point belongs to the isopycnal surface whose equation reads:

$$\begin{aligned} z=\frac{g \alpha _{x}}{N^{2}} \sin \left( \kappa _{x} x\right) +\frac{g \alpha _{y}}{N^{2}} \sin \left( \kappa _{y} y\right) . \end{aligned}$$

(9.87)

The position $\left( x_i(t),y_i(t),z_i(t)\right)$, $j=1,2,\dots ,J$ of the particles is updated by means of Lagrangian schemes. Since the diapycnal diffusion is zero the particles should not leave the isopycnal surface (9.83), but numerical errors are unavoidable. Their magnitude may be estimated by means of the following error measure:

$$\begin{aligned} \mu (t)=\sqrt{\frac{1}{J} \sum _{j=1}^{J}\left[ z_{j}(t)-z=\frac{g \alpha _{x}}{N^{2}} \sin \left( \kappa _{x} x_{j}(t)\right) +\frac{g \alpha _{y}}{N^{2}} \sin \left( \kappa _{y} y_{j}(t)\right) \right] ^{2}}. \end{aligned}$$

(9.88)

This expression is approximately equal to the standard deviation of the distance of the particles to the isopycnal surface on which they should remain. Clearly, the better a Lagrangian scheme is, the slower the rate of increase of standard deviation $\mu (t)$ will be.

In order to depict the equivalence between the Îto, Stratonovich and Îto-backward stochastic models. The Îto SDEs (9.80)(80) is transformed into Stratonovich and Îto-backward SDEs. The drift coefficients in (9.80) is modified by using the transformations described in Sect. 9.3. The resulting Stratonovich and Îto-backward SDEs are then used to simulate the trajectories of the particles on the non-flat isopycnal surface. Note that careful attention is required to implement Lagrangian schemes for Îto, Stratonovich and Îto-backward models (Kloeden and Platen 1992). It is important to recall here that, assessing the pathwise strong approximations for Lagrangian model interpreted in Îto, Stratonovich and Ito-backward sense is a main goal here, that is why attention is not paid to the probability distribution.

Fig. 9.7

Comparison of the performance of the numerical schemes for different time steps

The comparison between the accuracy and efficiency of the Lagrangian schemes is shown in Fig. 9.7a, b. The standard deviation $\mu$ against the different time steps $\varDelta t$ is shown in Fig. 9.7a, while Fig. 9.7b depicts the CPU time of the Lagrangian schemes. The results reveals that Îto Euler and Îto-backward Euler converges with order 0.5 and Îto and Stratonovich Milstein schemes converges with the order 1.0. It is quite clear from these experiments that the higher order schemes produce better pathwise approximations. Another way of assessing the numerical schemes under consideration consists in estimating the spurious diapycnal diffusion $\left( K^D\right)$ they are associated with. The related spurious diapycnal diffusivity is of the order $\frac{\mu ^2(t)}{2t}$. The spurious diapycnal diffusivity of each Lagrangian scheme is determined and the results are displayed in Fig. 9.7c. The spurious diapycnal diffusivity of the Euler and Milstein schemes differs approximately by a factor of $10^{-4}$. This shows the spurious diffusivity in the Milstein scheme is negligible compared with the Euler scheme.

Moreover, it is can also be observed in Fig. 9.7 that the Îto-backward Euler solution converges to the Îto Euler and the Stratonovich Milstein solution converges to the Îto Milstein solution. This implies that if the SDE is interpreted in Îto sense then one can switch to Stratonovich and Îto-backward models by using the transformations described in Sect. 9.3 and one will reach to the same solution. The idealised test case for purely isopycnal diffusion on non-flat isopycnal surfaces was considered to evaluate the performance of the Lagrangian schemes. The idealised test case shows that the Euler approximation is not an appropriate option to simulate the movement of the particle on non-flat isopycnals. The implementation of the Milstein scheme shows that a relatively limited additional computational effort (Fig. 9.7) is required to obtain a good accuracy. The assessment of Lagrangian schemes suggests that one may not obtain satisfactory results with the Euler scheme, while the Milstein scheme is a more accurate and more reliable approximation for simulating the particle paths. Turning to the higher order strong Lagrangian schemes leads to a very significant improvement.

9.6 Conclusion

The Lagrangian random walk model which is dictated by the desired representation of the turbulent diffusion is broadly discussed in this chapter. This chapter provides the foundation to the useful concept to theory of SDEs and it numerical aspects that are used to model diffusive transport processes in marine modelling problems. Implementation of different Lagrangian schemes on various test cases has clearly shown that the order of convergence of the Euler scheme is not sufficient to achieve the desired result. However, the Milstein scheme shows that a relatively limited additional computational effort is required to obtain a good accuracy. The results obtained for the various higher order schemes has shown more accurate results than that of the Milstein scheme. But such schemes are not computationally attractive. Therefore, it is suggested that turning to the higher order strong Lagrangian schemes leads to a very significant improvement.