An Explicit Solution for an Inventory Model with Positive Lead Time and Server Interruptions

Abstract

A single server queuing system with inventory is considered. Customers arrive according to a Poisson process and service times follow exponential distribution. Inventory is replenished according to (s, S) policy with positive lead time which follows exponential distribution. Interruption to service process and repair of interrupted service are considered, times between two interruptions and repairs both follow exponential distributions. We assume that during interruption, the customer being served waits there until his service is completed, no inventory is lost due to interruption, no arrivals are allowed and order placed if any is cancelled. We also assume that no arrival is entertained when inventory level is zero. Stability of the above system is analyzed and the steady state vector is calculated explicitly. Expressions for several system performance measures such as expected number of customers in the system, expected inventory level, expected interruption rate etc. are obtained. Even though explicit expressions are obtained several other performance measures are calculated numerically as well.

1 Introduction

The pioneers in the study of queueing inventory models are Melikov and Molchanov [12] and Sigman and Simchi- Levi [16]. In Sigman and Simchi- Levi customers are allowed to join even when there is no inventory in the system. They also discuss the case of non exponential lead time distribution. Later Berman and et al. [2] considered an inventory system where a processing time is required for serving the inventory. Here they considered deterministic service time and the model was discussed as a dynamic programming model. Berman and Kim [3] and Berman and Sapna [4] later discussed inventory queueing systems with exponential service time distribution and with arbitrary distribution.

There are several papers on inventory queueing models by Krishnamoorthy and his co-authors [1, 5,6,7,8,9,10,11, 13]. They mainly used Matrix Analytic Methods to study these models. In most of the models service time for providing the inventoried item is assumed. Schwarz et al. [15] considered a queueing inventory model with Poisson arrivals and exponentially distributed service and lead times. They could obtain a product form solution for the system steady state. But they assumed that no customers join the system when the inventory level is zero.

2 Mathematical Model

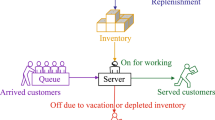
The system under consideration is described as below. There is a single server counter where inventory is served to which customers arrive for service. The number of arrivals by time t follows a Poisson process with parameter $\lambda t$. The service times are independently and identically distributed exponential random variables with parameter $\mu$. Inventory is replenished according to (s, S) policy, in the sense that whenever inventory level drops to s an order is placed, order quantity being fixed as $Q=S-s$. The replenishment times follow exponential distribution with parameter $\eta$. While a customer is being served by the server, the service may be interrupted, the interruption rate being exponential with rate $\delta _1$. Following a service interruption the service restarts at an exponential rate $\delta _2$.

We make the following assumptions for the model under consideration.

• i) There is no loss of inventory due to a service interruption.

• ii) The customer being served when interruption occurs waits there until his service is completed.

• iii) No arrival is entertained when the inventory level is zero.

• iv) An order placed if any is cancelled while the server is on interruption.

• v) We also assume that there are no arrivals while the server is on interruption.

We denote by N(t) the number of the customers in the system including the one being served (if any), L(t) the inventory level and S(t) the server status at time t.

$$\text {Let }S(t)= {\left\{ \begin{array}{ll} 0 &{} \text {if the server is idle}\\ 1 &{} \text {if the server is busy}\\ 2 &{} \text {if the server is on interruption} \end{array}\right. }$$

Then $\varOmega =X(t)=((N(t),S(t),L(t))$ will be a Markov chain. The state space of this Markov chain can be described as $E=\{(0,0,k): 0\le k\le S\}\cup \{(i,0,0): i\ge 1\}\cup \{(i,j,k): i\ge 1, j=1,2; 1\le k\le S\}.$ The above state space can be partitioned into levels L(i) where $L(0)= \left( (0,0,0),(0,0,1),\ldots ,(0,0,S)\right)$ and $L(i)=\left( (i,0,0),(i,1,1),(i,1,2),\ldots ,(i,1,S),(i,2,1),(i,2,2),\ldots ,(i,2,S)\right) ; i\ge 1.$ The Markov chain $\varOmega$ described above is a level independent quasi birth death process whose infinitesimal generator matrix is given by

$$T= \begin{bmatrix} B_0 &{} B_1&{} 0&{} 0&{}.&{}.&{}.\\ B_2&{} A_1&{} A_0&{} 0&{} 0&{}. &{} .\\ 0&{} A_2&{} A_1&{} A_0&{} 0&{} .&{} 0\\ 0&{} 0&{} A_2&{} A_1&{} A_0&{} 0&{} .\\ &{}&{}&{}.&{}.&{} .&{}\\ &{}&{}&{}&{}.&{} .&{}. \end{bmatrix}$$

Here $B_0,B_1,B_2$ are matrices of orders $(S+1)\times (S+1), (S+1)\times (2S+1)$ and $(2S+1)\times (S+1)$ respectively. All other matrices are square matrices of order $2S+1$. The different transitions in the Markov chain $\varOmega =X(t)=((N(t),S(t),L(t))$ are given below.

• i) Transitions due to arrival of customers

  $$(i,j,k)\xrightarrow {\lambda } (i+1,j,k); i\ge 0, 0< k\le S, j=0,1$$

• ii) Transitions due to service completion of customers

  $$(i,j,k)\xrightarrow {\mu } (i-1,j,k-1); i> 0, 0< k\le S, j=1$$

• iii) Transitions due to replenishment of inventory

  $$(i,j,k)\xrightarrow {\eta } (i,j,k+Q); i\ge 0, 0\le k\le S, j=0,1$$

• iv) Transitions due to server interruption

  $$(i,1,k)\xrightarrow {\delta _1} (i,2,k); i\ge 1, 0< k\le S$$

• v) Transitions due to restart of service after a service interruption

  $$(i,2,k)\xrightarrow {\delta _2} (i,1,k); i\ge 1, 0< k\le S$$

The matrix $B_0$ contains the transition rates within level L(0), $B_1$ records the transition rates from L(0) level to L(1) and $B_2$ that from L(1) to L(0). Similarly the matrices $A_0. A_1, A_2$ contains the transitions from levels L(i) to $L(i+1)$, L(i) to itself and $L(i+1)$ to L(i) for $i\ge 1$.

3 Analysis of the Model

Stability condition

Define $A=A_0+A_1+A_2$ and

$$\pi =\left( \pi (0,0),\pi (1,1),\pi (1,2),\ldots , \pi (1,S),\pi (2,1),\pi (2,2),\ldots ,\pi (2,S) \right) $$

be the steady state vector of A. We know the QBD process with generator matrix T is stable if and only if $\pi A_0e< \pi A_2e$ [14]. That is if and only if $\lambda \left[ \pi (1,1)+\pi (1,2)+\ldots +\pi (1,S)\right] < \mu \left[ \pi (1,1)+\pi (1,2)+\ldots +\pi (1,S)\right]$, that is if and only if $\lambda <\mu$.

Thus we have the following theorem for the stability of the system under study.

Theorem 1

The Markov chain is stable if and only if $\lambda <\mu$.

4 Computation of Steady State Vector

We first consider a system identical to the above system except for service time is negligible. For this system $\tilde{\varOmega }=\tilde{X}(t)=(S(t),L(t))$ will be a Markov chain where S(t) and L(t) are as defined for the original system. The state space of this Markov chain can be described as

$$\tilde{E}=\{(0,0),(1,1),(1,2)\ldots ,(1,S),(2,1),(2,2),\ldots ,(2,S)\}.$$

The infinitesimal generator matrix of the process is given by $\tilde{T}= \begin{bmatrix} \tilde{B_0}&{} \tilde{B_1}\\ \tilde{B_2} &{} \tilde{B_3} \end{bmatrix}$, where $\tilde{B_1}= \begin{bmatrix} 0\\ \delta _{1}I_{s} \end{bmatrix}_{(S+1)\times S}$, $\tilde{B_2}= \begin{bmatrix} 0&\delta _2I_s \end{bmatrix}_{S\times (S+1)}$, $\tilde{B_3}=-\delta _2I_s$, $\tilde{B_0}= \begin{bmatrix} C_1 &{} C_2\\ C_3 &{} C_4 \end{bmatrix}$ Here $C_1= \begin{bmatrix} -\eta &{} 0\\ 0&{} -(\lambda +\eta +\delta _1)I_{s-1} \end{bmatrix}_{(s+1)\times (s+1)}+\begin{bmatrix} 0&{} 0\\ \lambda I_{s-1}&{} 0 \end{bmatrix}_{(s+1)\times (s+1)}$, $C_4=-(\lambda +\delta _1)I_Q+ \begin{bmatrix} 0&{} 0\\ \lambda I_{Q-1}&{} 0 \end{bmatrix}_{Q\times Q}$, $C_3=\begin{bmatrix} 0&{} \lambda \\ 0&{} 0 \end{bmatrix}_{Q\times (s+1)}$, $C_2=\begin{bmatrix} 0&\eta I_{s+1} \end{bmatrix}_{(s+1)\times Q}$ Let $x=\left( x(0,0),x(1,1),\ldots ,x(1,S),x(2,1),\ldots ,x(2,S)\right)$ be the steady state probability vector of the process $\tilde{\varOmega }$. Then $x\tilde{T}=0$ and $xe=1$ gives

$$\begin{aligned} x(1,i)&=\dfrac{\eta }{\lambda }\left( \dfrac{\eta +\lambda }{\lambda }\right) ^{i-1}x(0,0)\,;\; 1\le i\le s+1\\ x(1,s+1)&=x(1,s+2)=\ldots =x(1,Q)\\ x(1,Q+i)&=x(1,Q)-x(1,i)\,; \; 1\le i\le s\\ x(2,i)&=\dfrac{\delta _1}{\delta _2}x(1,i)\,; \; 1\le i\le S \end{aligned}$$

where $x(0,0)=\left[ 1+Q\dfrac{\eta }{\lambda }\left( \dfrac{\eta +\lambda }{\lambda }\right) ^s\left( \dfrac{\delta _1+\delta _2}{\delta _2}\right) \right] ^{-1}$.

Let $\pi =(\pi _0,\pi _1,\pi _2,\ldots )$ be the steady state probability vector of the process $\varOmega$, where $\pi _0= (\pi (0,0,0),\pi (0,0,1),\ldots ,\pi (0,0,S)$ and $\pi _i=(\pi (i,0,0),\pi (i,1,1),\pi (i,1,2),\ldots ,\pi (i,1,S),\pi (i,2,1),\pi (i,2,2),\ldots ,\pi (i,2,S)) ;$ $i\ge 1$. Then $\pi$ satisfies $\pi T=0$ and $\pi e=1$. We have the equations

$$\begin{aligned} \pi _0B_0+\pi _1B_2&=0\\ \pi _0B_1+\pi _1A_1+\pi _2A_2&=0\\ \pi _i A_0+\pi _{i+1}A_1+\pi _{i+2}A_2&=0;\; i\ge 1 \end{aligned}$$

All the above equations are satisfied by taking

$$\begin{aligned} \pi _0&=\zeta (x(0,0),x(1,1),x(1,2),\ldots ,x(1,S)) \\ \pi _i&=\zeta \left( \dfrac{\lambda }{\mu }\right) ^i\bigg ( x(0,0),x(1,1),x(1,2),\ldots ,\\&\qquad x(1,S),\dfrac{\delta _1}{\delta _2}x(1,1),\dfrac{\delta _1}{\delta _2}x(1,2),\ldots ,\dfrac{\delta _1}{\delta _2}x(1,S)\bigg );\;i\ge 1 \end{aligned}$$

The value of $\zeta$ is obtained from $\pi e=1$ as $\zeta =\dfrac{(\mu -\lambda )\delta _2}{\delta _2\mu +\delta _1\lambda [1-x(0,0)]}$

5 System Performance Measures

5.1 Expected Waiting Time of a Customer in the Queue

First we compute the expected waiting time of a customer who joins the queue as the $r^{th}$ person. For that consider a Markov process $\psi =(\hat{N}(t),S(t),L(t))$, where $\hat{N}(t)$ represent the rank of the customer in the queue, S(t) the server status and L(t) the inventory level. The state space of the above Markov chain is $\hat{E}=\{(i,0,0),1\le i\le r-1\}\cup \{(i,j,k), 1\le i\le r; j=1,2;\, 1\le k\le S\}\cup \Delta$, where $\Delta$ correspond to the state, the $r^{th}$ customer is taken for service. The generator matrix of the Markov chain is given by $\hat{Q}= \begin{bmatrix} T &{} T^0\\ 0 &{} 0 \end{bmatrix}$, where $T^0$ is an $(r(2S+1)-1)\times 1$ matrix with $T^0(i,1)=\mu ; \, 2\le i\le S+1$ and

$$T=\begin{bmatrix} B&{} 0&{} 0 &{}\_ &{} \_ &{} \_ &{}0\\ A_2&{} B&{} 0&{}\_ &{} \_ &{} \_ &{}0\\ 0&{} A_2&{} B&{} 0&{} \_&{}\_&{}0\\ 0&{}0&{} A_2&{} B&{} &{}&{}\\ &{}&{}&{}\_&{}\_&{}\_&{}\_\\ &{}&{}&{}&{}\_&{}\_&{}\_\\ &{}&{}&{}&{}&{}\_&{}\_\\ 0&{}0&{}\_&{}\_&{}\_&{}\hat{A_2}&{}\hat{B} \end{bmatrix}$$

The different transitions in T are as follows.

• i) $(i,0,k)\xrightarrow {\eta } (i,1,k+Q); 1\le i\le r;\;0\le k\le s$

• ii) $(i,j,k)\xrightarrow {\eta } (i,j,k+Q); 1\le i\le r;\;j=1;\;0\le k\le s$

• iii) $(i,1,k)\xrightarrow {\delta _1} (i,2,k); 1\le i\le r;\;1\le k\le S$

• iv) $(i,2,k)\xrightarrow {\delta _2} (i,1,k); 1\le i\le r;\;1\le k\le S$

• v) $\hat{B}(i,j)=B(i+1,j+1);\; \hat{A}(i,j)=A_2(i+1,j)$

Now the waiting time of the customer who joins as the $r^{th}$ customer is given by $W^r=\hat{I}_{2S}(-T^{-1}e)$, where $\hat{I}_{2S}=\begin{bmatrix} 0&I_{2S} \end{bmatrix}_{(2S)\times (r(2S+1)-1)}$.

So the expected waiting time of a general customer is given by $E(W_L)=\sum \limits _{r=1}^\infty \hat{\pi }_rW^r$, where $\hat{\pi }_r(i)=\pi _r(i+1).$ Similarly the variance of waiting time of a general customer is also calculated numerically.

5.2 Other Performance Measures

• 1. The expected number of customers in the system,

  $$\begin{aligned} L_s&=\sum \limits _{i=1}^{\infty }\sum \limits _{j=1}^Si\left\{ \pi (i,1,j)+\pi (i,2,j)\right\} +\sum \limits _{i=1}^{\infty }i\pi (i,0,0) \\&= \zeta \dfrac{\lambda }{\mu }\left( \dfrac{\mu }{\mu -\lambda }\right) ^2\left[ 1+\dfrac{\delta _1}{\delta _2}(1-x(0,0))\right] . \end{aligned}$$

• 2. The expected inventory level in the system,

  $$\begin{aligned} INV_{mean}&=\sum \limits _{i=1}^{\infty }\sum \limits _{j=1}^S j\{\pi (i,1,j)+\pi (i,2,j)\}+\sum \limits _{j=1}^S j\pi (0,0,j)\\&=\zeta \dfrac{\lambda }{\mu }Q\left\{ 1+\dfrac{\delta _1}{\delta _2}\dfrac{\lambda }{\mu }\right\} \Bigg (\dfrac{(S+s+1)}{2}\dfrac{\eta }{\lambda }\left( \dfrac{\eta +\lambda }{\lambda }\right) ^s+\\&\qquad \qquad \left[ 1-\left( \dfrac{\eta +\lambda }{\lambda }\right) ^s\right] \Bigg )x(0,0). \end{aligned}$$

• 3. The expected rate of ordering, $E_{or}=\sum \limits _{i=1}^{\infty }\mu \pi (i,1,s+1)$.

• 4. The expected replenishment rate,

  $$REP_{mean}=\sum \limits _{i=0}^{\infty }\sum \limits _{j=0}^s\eta \left\{ \pi (i,0,j)+\pi (i,1,j)\right\} .$$

• 5. The expected interruption rate, $INT_{mean}=\sum \limits _{i=1}^{\infty }\sum \limits _{j=1}^S\delta _1\pi (i,1,j)=\delta _1P(busy)$.

• 6. The loss rate of customers,

  $LOSS_{mean}=\sum \limits _{i=0}^{\infty }\lambda \pi (i,0,0)+\sum \limits _{i=1}^{\infty }\sum \limits _{j=1}^S\lambda \pi (i,2,j)=\lambda \xi \dfrac{\mu }{\mu -\lambda }x(0,0)+\lambda P(int)$.

• 7. The probability that the server is busy,

  $P_{busy}=\sum \limits _{i=1}^{\infty }\sum \limits _{j=1}^S\pi (i,1,j)=\dfrac{\delta _2}{\delta _2\mu +\delta _1(1-x(0,0))}\dfrac{\lambda }{\mu -\lambda }Q\dfrac{\eta }{\lambda }\left( \dfrac{\eta +\lambda }{\lambda }\right) ^s$.

• 8. The probability that the server is on interruption,

  $P_{int}=\sum \limits _{i=1}^{\infty }\sum \limits _{j=1}^S\pi (i,2,j)=\dfrac{\delta _1}{\delta _2}P(busy)$.

5.3 Cost Analysis

We considered the following

Cost function $Cost=CI\times INV_{mean}+CN\times L_s+ CR\times E_{INTR}+(K+(S-s)K_1)\times E_{OR}+ CL\times Loss_{mean}$, where

CI :  Cost of holding Inventory

CN :  Cost of holding customers

CR :  Cost incurred due to interruption of service

K :  Fixed cost of ordering

$K_1 :$ Cost of a single inventory

CL :  Cost incurred due to loss of customers when inventory level drops to zero.

The effect of various parameters on the cost were studied.

6 Numerical Illustration

Eventhough we have explicit expressions for most of the system performance measures we provide numerical illustration of the effect of different parameters on the system performance measures in this section.

6.1 Effect of Arrival Rate $\lambda$

In Table 1 we see that as arrival rate increases, there is an increase in both P(busy), P(int) and $L_s$. The increase in server busy probability is as expected since when arrival rate increases the mean number of customers in the system obviously increases and so the probability that server is busy increases. P(int) is also seen to increase which may be due to the fact that an interruption to service occurs only when the server is busy. Also the decrease in $INV_{mean}$ is due to the fact that the more customers get service when P(busy) increases. Also notice the increase in mean waiting of a customer in the system due to increase in mean number of customers in the system.

6.2 Effect of Service Rate $\mu$

In Table 2 we see that as service rate increases, P(busy), P(int), $L_s$ and $WAIT_{mean}$ all decrease. As the service rate increases, customers leave the system after getting service at a faster rate. Hence the mean waiting time in the system clearly decreases. Also the probability that the server is idle increases with increase in service rate and so P(busy), P(int) and $L_s$ all decrease. It is seen from the tables that $\mu$ has no effect on $INV_{mean}$.

6.3 Effect of Interruption Rate $\delta _1$

In Table 3 we see that as interruption rate increases, P(busy) increases whereas P(int), $WAIT_{mean}$ and $L_s$ decrease. The reason for decrease in the mean number of customers in the system is due to our assumption that when the server is on interruption no arrivals are entertained. The decrease in mean waiting time of a customer in the system is due to the increase in P(busy). Also as mean number of customers in the system decreases, probability that server is idle increases and so P(int) decreases. The interruption rate seems to have no effect on average inventory level in the system.

6.4 Effect of Reorder Level S

In Table 4 we see that s has no considerable effect on the system performance measures P(busy), P(int) and $L_S$. The expected inventory level in the system increases with increase in re order level is as expected since orders are placed early with increase in s (Table 5, 6, 7, 8, 9 and Figs. 1, 2, 3, 4, 5).

Table 1. Effect of arrival rate on various performance measures $\mu =10\ \eta =2\ \delta _1=6 \delta _2=7\ s=5\ S=12$

Table 2. Effect of service rate on various performance measures $\lambda =3\ \eta =2\ \delta _1=6 \delta _2=7\ s=5\ S=12$

Table 3. Effect of interruption rate on various performance measures $\lambda =3\ \mu =9\ \eta =2 \delta _2=7\ s=5\ S=12$

Table 4. Effect of reorder level on various performance measures $\lambda =3\ \mu =9\ \eta =2 \delta _1=6\ \delta _2=7\ S=21$

Table 5. Effect of arrival rate on Cost

Table 6. Effect of service rate on Cost

Table 7. Effect of interruption rate on Cost

Table 8. Effect of repair rate on Cost

Table 9. Effect of reorder level on Cost

Fig. 1.

Arrival rate versus Cost

Fig. 2.

Service rate versus Cost

Fig. 3.

Interruption rate versus Cost

Fig. 4.

Repair rate versus Cost

Fig. 5.

Reorder level versus Cost

7 Conclusion

We studied a single server queueing model with positive service time, positive lead time and service interruptions. We could arrive at an explicit expression for the steady state probability vector. We wish to extend this model by considering retrials as well.