Elliptic Problems

Abstract

Sections 8.1 and 8.2 are devoted to the Laplacian, one of the basic operators of mathematical physics. In Sect. 8.3, using Schwarz’s symmetrization, we prove the isoperimetric inequality and the Faber–Krahn inequality on the first eigenvalue of the Laplacian. Section 8.4 is an introduction to distribution theory, with applications including elementary solutions of the Laplacian.

8.1 The Laplacian

The Laplacian, defined by

$$\displaystyle \begin{aligned} \varDelta u={\mathrm{div}~}\nabla u=\frac{\partial^2u}{\partial x_1^2}+\ldots + \frac{\partial^2u}{\partial x_{N}^2}, \end{aligned}$$

is related to the mean of functions.

Definition 8.1.1

Let Ω be an open subset of ${\mathbb {R}}^N$ and $u\in L^1_{{\mathrm {loc}}}(\varOmega )$. The mean of u is defined on

$$\displaystyle \begin{aligned} D=\{(x,r):x\in\varOmega,0<r<d(x,\partial\varOmega)\} \end{aligned}$$

by

$$\displaystyle \begin{aligned} M(x,r)=V_N^{-1}\int_{B_N}u(x+ry)dy. \end{aligned}$$

Lemma 8.1.2

Let $u\in {\mathcal {C}}^2(\varOmega )$ . The mean of u satisfies on D the relation

$$\displaystyle \begin{aligned} \lim_{r\downarrow 0}2\frac{N+2}{r^2}[M(x,r)-u(x)]=\varDelta u(x). \end{aligned}$$

Proof

Since we have uniformly for |y| < 1,

$$\displaystyle \begin{aligned} u(x+ry) =u(x)+r\nabla u(x) \cdot y + \frac{r^2}{2} D^2 u (x) (y,y) + o (r^2), \end{aligned}$$

we obtain by symmetry

□

Lemma 8.1.3

Let $u\in {\mathcal {C}}^2(\varOmega )$ . The following properties are equivalent:

• (a) Δu ≤ 0;

• (b) for all (x, r) ∈ D, M(x, r) ≤ u(x).

Proof

By the preceding lemma, (a) follows from (b).

Assume that (a) is satisfied. Differentiating under the integral sign and using the divergence theorem, we obtain

$$\displaystyle \begin{aligned} \frac{\partial M}{\partial r} (x,r) = V_N^{-1} \int_{B_N} \nabla u (x+ry) \cdot y dy = r V^{-1}_N \int_{B_N} \varDelta u (x+ry) \frac{1-|y|{}^2}{2} dy \leq 0. \end{aligned}$$

We conclude that

$$\displaystyle \begin{aligned} M(x,r) \leq \lim_{r\downarrow 0} M(x,r) = u(x). \end{aligned}$$

□

Definition 8.1.4

Let $u\in L^1_{{\mathrm {loc}}}(\varOmega )$. The function u is superharmonic if for every $v\in {\mathcal {D}}(\varOmega )$ such that v ≥ 0, ∫_Ω uΔvdx ≤ 0.

The function u is subharmonic if − u is superharmonic.

The function u is harmonic if for every $v\in {\mathcal {D}}(\varOmega )$, ∫_Ω uΔvdx = 0.

We extend Lemma 8.1.3 to locally integrable functions.

Theorem 8.1.5 (Mean-Value Inequality)

Let $u\in L^1_{{\mathrm {loc}}}(\varOmega )$ . The following properties are equivalent:

• (a) u is superharmonic;

• (b) for almost all x ∈ Ω and for all 0 < r < d(x, ∂Ω), M(x, r) ≤ u(x).

Proof

Let u _n = ρ _n ∗ u. Property (a) is equivalent to

• (c) for every n, Δu _n ≤ 0 on Ω _n.

Property (b) is equivalent to

• (d) for all x ∈ Ω _n and for all 0 < r < d(x, ∂Ω _n), $V_N^{-1}\displaystyle {\int _{B_N}}u_n(x+ry)dy\leq u_n(x)$.

We conclude the proof using Lemma 8.1.3.

• (a)⇒(c). By Proposition 4.3.6, we have on Ω _n that

  $$\displaystyle \begin{aligned} \varDelta u_n(x)=\varDelta\rho_n\ast u(x)=\int_{\varOmega} \bigl(\varDelta\rho_n(x-y)\bigr)u(y)dy\leq 0. \end{aligned}$$

• (c)⇒(a). It follows from the regularization theorem that for every $v\in {\mathcal {D}}(\varOmega )$, v ≥ 0,

  $$\displaystyle \begin{aligned} \int_{\varOmega} u\varDelta vdx=\lim_{n\rightarrow\infty}\int_{\varOmega} u_n\varDelta vdx=\lim_{n\rightarrow\infty}\int_{\varOmega}(\varDelta u_n)vdx\leq 0. \end{aligned}$$

• (b)⇒(d). We have on Ω _n that

  $$\displaystyle \begin{aligned} \begin{array}{ll} V_N^{-1}\displaystyle{\int_{B_N}u_n(x+ry)dy}&=V_N^{-1}\displaystyle{\int_{B(0,1/n)}dz\int_{B_N} \rho_n(z)u(x+ry-z)dy}\\ \\ &\leq\displaystyle{\int_{B(0,1/n)}\rho_n (z)u(x-z)dz=u_n(x).} \end{array} \end{aligned}$$

• (d)⇒(b). For j ≥ 1, we define

  $$\displaystyle \begin{aligned} \omega_j=\{x\in\varOmega :d(x,\partial\varOmega)> 1/j\mbox{ and }|x|<j\}. \end{aligned}$$

Proposition 4.2.10 and the regularization theorem imply the existence of a subsequence $(u_{n_k})$ converging to u in L ¹(ω _j) and almost everywhere on ω _j. Hence for almost all x ∈ ω _j and for all 0 < r < d(x, ∂ω _j), M(x, r) ≤ u(x). Since $\varOmega =\displaystyle {\bigcup ^{\infty }_{j=1}}\omega _j$, property (b) is satisfied. □

Theorem 8.1.6 (Maximum Principle)

Let Ω be an open connected subset of ${\mathbb {R}}^N$ and $u\in L^1_{{\mathrm {loc}}}(\varOmega )$ a superharmonic function such that u ≥ 0 almost everywhere on Ω and u = 0 on a subset of Ω with positive measure. Then u = 0 almost everywhere on Ω.

Proof

Define

$$\displaystyle \begin{aligned} \begin{array}{rcl} U_1& =&\displaystyle \{x\in\varOmega:\mbox{there exists }0<r<d(x,\partial\varOmega)\mbox{ such that }M(x,r)=0\}.\\ U_2& =&\displaystyle \{x\in\varOmega:\mbox{there exists }0<r<d(x,\partial\varOmega)\mbox{ such that }M(x,r)>0\}. \end{array} \end{aligned} $$

It is clear that U ₁ and U ₂ are open subsets of Ω such that Ω = U ₁ ∪ U ₂. By the preceding theorem, we obtain

$$\displaystyle \begin{aligned} U_2=\{x\in\varOmega:\mbox{for all }0<r<d(x,\partial\varOmega),M(x,r)>0\}, \end{aligned}$$

so that U ₁ and U ₂ are disjoint. If Ω = U ₂, then u > 0 almost everywhere on Ω by the preceding theorem. We conclude that Ω = U ₁ and u = 0 almost everywhere on Ω. □

8.2 Eigenfunctions

En nous servant de quelques conceptions de l’analyse fonctionnelle nous représentons notre problème dans une forme nouvelle et démontrons que dans cette forme le problème admet toujours une solution unique.

Si la solution cherchée existe dans le sens classique, alors notre solution se confond avec celle-ci.

S.L. Sobolev

Let Ω be a smooth bounded open subset of ${\mathbb {R}}^N$ with frontier Γ. An eigenfunction corresponding to the eigenvalue λ is a nonzero solution of the problem

$$\displaystyle \begin{aligned} \left\{\begin{array}{ll} -\varDelta u=\lambda u&\quad \mbox{in }\varOmega,\\ u=0&\quad \mbox{on }\varGamma. \end{array} \right. \end{aligned}$$

(P)

We will use the following weak formulation of problem $({\mathcal {P}})$: find $u\in H^1_{0}(\varOmega )$ such that for all $v\in H^1_{0}(\varOmega )$,

$$\displaystyle \begin{aligned} \int_{\varOmega}\nabla u\cdot\nabla v~dx=\lambda\int_{\varOmega} uv~dx. \end{aligned}$$

Theorem 8.2.1

There exist an unbounded sequence of eigenvalues of $({\mathcal {P}})$

$$\displaystyle \begin{aligned} 0<\lambda_1\leq\lambda_2\leq \cdots, \end{aligned}$$

and a sequence of corresponding eigenfunctions that is a Hilbert basis of $H_0^1(\varOmega )$.

Proof

On the space $H_0^1(\varOmega )$, we define the inner product

$$\displaystyle \begin{aligned} a(u,v)=\int_{\varOmega} \nabla u\cdot\nabla v~dx \end{aligned}$$

and the corresponding norm $\vert \vert u\vert \vert _a=\sqrt {a(u,u)}$.

For every $u\in H_0^1(\varOmega )$, there exists one and only one $Au\in H_0^1(\varOmega )$ such that for all $v\in H_0^1(\varOmega )$,

$$\displaystyle \begin{aligned} a(Au,v)=\int_{\varOmega} uv~dx. \end{aligned}$$

Hence problem $({\mathcal {P}})$ is equivalent to

$$\displaystyle \begin{aligned} \lambda^{-1}u=Au. \end{aligned}$$

Since a(Au, u) = ∫_Ω u ² dx, the eigenvalues of A are strictly positive. The operator A is symmetric, since

$$\displaystyle \begin{aligned} a(Au,v)=\int_{\varOmega} uv~dx=a(u,Av). \end{aligned}$$

It follows from the Cauchy–Schwarz and Poincaré inequalities that

$$\displaystyle \begin{aligned} \vert\vert Au\vert\vert_a^2=\int_{\varOmega} u~Au~dx\leq \vert\vert u\vert\vert_{L^2(\varOmega)}\vert\vert Au\vert\vert_{L^2(\varOmega)}\leq c\vert\vert u\vert\vert_{L^2(\varOmega)} \vert\vert Au\vert\vert_a. \end{aligned}$$

Hence

$$\displaystyle \begin{aligned} \vert\vert Au\vert\vert_a\leq c\vert\vert u\vert\vert_{L^2(\varOmega)}. \end{aligned}$$

By the Rellich–Kondrachov theorem, the embedding $H_0^1(\varOmega )\rightarrow L^2(\varOmega )$ is compact, so that the operator A is compact. We conclude using Theorem 3.4.8. □

Proposition 8.2.2 (Poincaré’s Principle)

For every n ≥ 1,

$$\displaystyle \begin{aligned} \lambda_n=\min\left\{\!\int_{\varOmega} |\nabla u|{}^2dx:u\in\! H_0^1(\varOmega),\!\!\int_{\varOmega} u^2dx=1,\!\!\int_{\varOmega} ue_1dx=\ldots=\int_{\varOmega} ue_{n-1}dx=0\right\}\!. \end{aligned}$$

Proof

We deduce from Theorem 3.4.7 that

$$\displaystyle \begin{aligned} \lambda_n^{-1}=\max\left\{\frac{a(Au,u)}{a(u,u)} :u\in H_0^1(\varOmega),u\neq 0,a(u,e_1)=\ldots= a(u,e_{n-1})=0\right\}. \end{aligned}$$

Since e _k is an eigenfunction,

$$\displaystyle \begin{aligned} a(u,e_k)=0\Longleftrightarrow\int_{\varOmega} ue_kdx=0. \end{aligned}$$

Hence we obtain

$$\displaystyle \begin{aligned} \lambda_n^{-1}=\max\left\{\frac{\int_{\varOmega} u^2dx}{\int_{\varOmega} |\nabla u|{}^2dx} :u\in H_0^1(\varOmega),u\neq 0,\int_{\varOmega} ue_1dx=\ldots=\int_{\varOmega} ue_{n-1}dx=0\right\}, \end{aligned}$$

or

$$\displaystyle \begin{aligned} \lambda_n=\min\left\{\frac{\int_{\varOmega} |\nabla u|{}^2dx}{\int_{\varOmega} u^2dx}:u\in H_0^1(\varOmega),u\neq 0,\int_{\varOmega} ue_1dx=\ldots=\int_{\varOmega} ue_{n-1}dx=0\right\}. \end{aligned}$$

□

Proposition 8.2.3

Let $u\in H_0^1(\varOmega )$ be such that ||u||₂ = 1 and $\vert \vert \nabla u\vert \vert ^2_2=\lambda _1$ . Then u is an eigenfunction corresponding to the eigenvalue λ ₁.

Proof

Let $v\in H_0^1(\varOmega )$. The function

$$\displaystyle \begin{aligned} g(\varepsilon)=\vert\vert\nabla (u+\varepsilon v)\vert\vert_2^2-\lambda_1\vert\vert u+\varepsilon v\vert\vert_2^2 \end{aligned}$$

reaches its minimum at ε = 0. Hence g′(0) = 0 and

$$\displaystyle \begin{aligned} \int_{\varOmega}\nabla u\cdot\nabla v~dx-\lambda_1\int_{\varOmega} uv~dx=0. \end{aligned}$$

□

Proposition 8.2.4

Let Ω be a smooth bounded open connected subset of ${\mathbb {R}}^N$ . Then the eigenvalue λ ₁ of $({\mathcal {P}})$ is simple, and e ₁ is almost everywhere strictly positive on Ω.

Proof

Let u be an eigenfunction corresponding to λ ₁ and such that ||u||₂ = 1. By Corollary 6.1.14, $v=|u|\in H_0^1(\varOmega )$ and $\vert \vert \nabla v\vert \vert _2^2=\vert \vert \nabla u\vert \vert _2^2=\lambda _1$. Since ||v||₂ = ||u||₂ = 1, the preceding proposition implies that v is an eigenfunction corresponding to λ ₁. Assume that u ⁺ ≠ 0. Then u ⁺ is an eigenfunction corresponding to λ ₁, and by the maximum principle, u ⁺ > 0 almost everywhere on Ω. Hence u = u ⁺. Similarly, if u ⁻≠ 0, then − u = u ⁻ > 0 almost everywhere on Ω. We can assume that e ₁ > 0 almost everywhere on Ω. If e ₂ corresponds to λ ₁, then e ₂ is either positive or negative, and ∫_Ω e ₁ e ₂ dx = 0. This is a contradiction. □

Example

Let Ω =  ]0, π[. Then $({\mathcal {P}})$ becomes

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} -u''=\lambda u\quad \mbox{in }]0,\pi[,\\ u(0)=u(\pi)=0. \end{array} \right. \end{aligned}$$

Sobolev’s embedding theorem and the du Bois–Reymond lemma imply that $u\in {\mathcal {C}}^2(]0,\pi [)\cap {\mathcal {C}}([0,\pi ])$. Hence λ _n = n ² and $e_n=\sqrt {\frac {2}{\pi }}\frac {\sin nx}{n}$. The sequence (e _n) is a Hilbert basis on $H_0^1(]0,\pi [)$ with scalar product $\displaystyle {\int _0^{\pi }}u'v'\,dx$, and the sequence (ne _n) is a Hilbert basis of L ²(]0, π[) with scalar product $\displaystyle {\int _0^{\pi }}uv\,dx$.

Definition 8.2.5

Let G be a subgroup of the orthogonal group O(N). The open subset Ω of ${\mathbb {R}}^N$ is G-invariant if for every g ∈ G and every x ∈ Ω, g ⁻¹ x ∈ Ω. Let Ω be G-invariant. The action of G on $H_0^1(\varOmega )$ is defined by gu(x) = u(g ⁻¹ x). The space of fixed points of G is defined by

$$\displaystyle \begin{aligned} {\mathrm{Fix}}(G)=\{u\in H_0^1(\varOmega):\mbox{for every }g\in G,gu=u\}. \end{aligned}$$

A function $J:H_0^1(\varOmega )\rightarrow {\mathbb {R}}$ is G-invariant if for every g ∈ G, J ∘ g = J.

Proposition 8.2.6

Let Ω be a G-invariant open subset of ${\mathbb {R}}^N$ satisfying the assumptions of Proposition 8.2.4 . Then e ₁ ∈Fix(G).

Proof

By a direct computation, we obtain, for all g ∈ G,

$$\displaystyle \begin{aligned} \vert\vert ge_1\vert\vert_2=\vert\vert e_1\vert\vert_2=1,\vert\vert\nabla ge_1\vert\vert^2_2=\vert\vert\nabla e_1\vert\vert^2_2=\lambda_1. \end{aligned}$$

Propositions 8.2.3 and 8.2.4 imply the existence of a scalar λ(g) such that

$$\displaystyle \begin{aligned} e_1(g^{-1}x)=\lambda(g)e_1(x). \end{aligned}$$

Integrating on Ω, we obtain λ(g) = 1. But then ge ₁ = e ₁. Since g ∈ G is arbitrary, e ₁ ∈ Fix(G). □

Example (Symmetry of the First Eigenfunction)

For a ball or an annulus

$$\displaystyle \begin{aligned} \varOmega=\{x\in{\mathbb{R}}^N:r<|x|<R\}, \end{aligned}$$

we choose G = O(N). Hence e ₁ is a radial function.

We define v(|x|) = u(x). By a simple computation, we have

$$\displaystyle \begin{aligned} \frac{\partial^2}{\partial x^2_k}u(x)=v''(\vert x\vert )\frac{x^2_k}{|x|{}^2}+v'(|x|)\left(\frac{1}{|x|}-\frac{x^2_k}{|x|{}^3}\right). \end{aligned}$$

Hence we obtain

$$\displaystyle \begin{aligned} \varDelta u=v'' +(N-1)v'/|x|. \end{aligned}$$

Let $\varOmega =B(0,1)\subset {\mathbb {R}}^3$. The first eigenfunction, u(x) = v(|x|), is a solution of

$$\displaystyle \begin{aligned} -v''-2v'/r=\lambda v. \end{aligned}$$

The function w = rv satisfies

$$\displaystyle \begin{aligned} -w''=\lambda w, \end{aligned}$$

so that

$$\displaystyle \begin{aligned} w(r)=a\sin{}(\sqrt{\lambda}r-b) \end{aligned}$$

and

$$\displaystyle \begin{aligned} v(r)=a\frac{\sin{}(\sqrt{\lambda}r-b)}{r}. \end{aligned}$$

Since $u\in H_0^1(\varOmega )\subset L^6(\varOmega )$, b = 0 and λ = π ². Finally, we obtain

$$\displaystyle \begin{aligned} u(x)=a\frac{\sin{}(\pi |x|)}{|x|}. \end{aligned}$$

It follows from Poincaré’s principle that

$$\displaystyle \begin{aligned} \pi^2=\min\left\{\vert\vert\nabla u\vert\vert^2 _{L^2(\varOmega)}/\vert\vert u\vert\vert^2_{L^2(\varOmega)}:u\in H^1_0(\varOmega)\setminus\{0\}\right\}. \end{aligned}$$

Let us characterize the eigenvalues without using the eigenfunctions.

Theorem 8.2.7 (Max-inf Principle)

For every n ≥ 1,

where ${\mathcal {V}}_{n-1}$ denotes the family of all (n − 1)-dimensional subspaces of $H^1_0(\varOmega )$.

Proof

Let us denote by Λ _n the second member of the preceding equality. It follows from Poincaré’s principle that λ _n ≤ Λ _n.

Let $V\in {\mathcal {V}}_{n-1}$. Since the codimension of V ^⊥ is equal to n − 1, there exists $x\in {\mathbb {R}}^N\setminus \{0\}$ such that $u=\displaystyle {\sum _{j=1}^n}x_je_j\in V^{\bot }$. Since

$$\displaystyle \begin{aligned} \int_{\varOmega} |\nabla u|{}^2dx=\sum^n_{j=1}\lambda_jx_j^2\int_{\varOmega} e^2_jdx\leq\lambda_n\int_{\varOmega} u^2dx, \end{aligned}$$

we obtain

Since $V\in {\mathcal {V}}_{n-1}$ is arbitrary, we conclude that Λ _n ≤ λ _n. □

8.3 Symmetrization

La considération systématique des ensembles E[a ≤ f < b] m’a été pratiquement utile parce qu’elle m’a toujours forcé à grouper les conditions donnant des effets voisins.

Henri Lebesgue

Fig. 8.1

Isodiametric inequality

According to the isodiametric inequality in ${\mathbb {R}}^2$, among all domains with a fixed diameter, the disk has the largest area. A simple proof was given by J.E. Littlewood in 1953 in A Mathematician’s Miscellany. We can assume that the domain Ω is convex and that the horizontal axis is tangent to Ω at the origin. We obtain

$$\displaystyle \begin{aligned} A=\frac{1}{2}\int_0^{\frac{\pi}{2}}\rho^2(\theta) +\rho^2\left(\theta +\frac{\pi}{2}\right)d\theta\leq\pi(d/2)^2. \end{aligned}$$

We will prove the isoperimetric inequality in ${\mathbb {R}}^N$ using Schwarz’s symmetrization.

In this section, we consider Lebesgue’s measure on ${\mathbb {R}}^N$. We define

$$\displaystyle \begin{aligned} \begin{array}{rl} {\mathcal{K}}_+({\mathbb{R}}^N)&=\{u\in{\mathcal{K}}({\mathbb{R}}^N):\mbox{for all }x\in{\mathbb{R}}^N, u(x)\geq 0\},\\ L^p_+({\mathbb{R}}^N)&=\{u\in L^p({\mathbb{R}}^N):\mbox{for almost all }u(x)\geq 0\},\\ W_+^{1,p}({\mathbb{R}}^N)&=W^{1,p}({\mathbb{R}}^N)\cap L^p_+({\mathbb{R}}^N),\\ BV_+({\mathbb{R}}^N)&=BV({\mathbb{R}}^N)\cap L_+^{1}({\mathbb{R}}^N). \end{array} \end{aligned}$$

Definition 8.3.1

Schwarz’s symmetrization of a measurable subset A of ${\mathbb {R}}^N$ is defined by $A^*=\{x\in {\mathbb {R}}^N:|x|{ }^NV_N <m(A)\}$. An admissible function $u:{\mathbb {R}}^N\rightarrow [0,+\infty ]$ is a measurable function such that for all t > 0, m _u(t) = m({u > t}) < ∞. Schwarz’s symmetrization of an admissible function u is defined on ${\mathbb {R}}^N$ by

$$\displaystyle \begin{aligned} u^*(x)=\sup\{t\in{\mathbb{R}} :x\in\{u>t\}^*\}. \end{aligned}$$

The following properties are clear:

• (a) $\chi _{A^*}=\chi _{A}^*$;

• (b) m(A ^∗∖ B ^∗) ≤ m(A ∖ B);

• (c) u ^∗ is radially decreasing, |x|≤|y|⇒ u ^∗(x) ≥ u ^∗(y);

• (d) u ≤ v ⇒ u ^∗≤ v ^∗.

Lemma 8.3.2

Let (A _n) be an increasing sequence of measurable sets. Then

$$\displaystyle \begin{aligned} \bigcup^{\infty}_{n=1}A^*_n =\left(\bigcup^{\infty}_{n=1}A_n\right)^* . \end{aligned}$$

Proof

By definition, $A^*_n=B(0,r_n)$, $\displaystyle {\left (\bigcup ^{\infty }_{n=1}A_n\right )^*}=B(0,r)$, where $r_n^NV_N=m(A_n)$, $r^NV_N=m\displaystyle {\left (\bigcup ^{\infty }_{n=1}A_n\right )}$. It suffices to observe that by Proposition 2.2.26,

$$\displaystyle \begin{aligned} m\left(\bigcup^{\infty}_{n=1}A_n\right)=\lim_{n\rightarrow\infty} m(A_n). \end{aligned}$$

□

Theorem 8.3.3

Let u be an admissible function. Then u ^∗ is lower semicontinuous, and for all t > 0, {u > t}^∗ = {u ^∗ > t} and $m_u(t)=m_{u^*}(t)$.

Proof

Let t > 0. Using the preceding lemma, we obtain

$$\displaystyle \begin{aligned} \{u>t\}^*=\left(\bigcup_{s>t}\{u> s\}\right)^*=\bigcup_{s>t}\{u>s\}^*\subset\{u^*>t\}\subset\{u>t\}^*. \end{aligned}$$

In particular, {u ^∗ > t} is open and m{u > t} = m{u ^∗ > t}. □

Proposition 8.3.4

Let 1 ≤ p < ∞ and $u,v\in L^p_+({\mathbb {R}}^N)$ . Then $u^*,v^*\in L^p_+({\mathbb {R}}^N)$ and

$$\displaystyle \begin{aligned} \vert\vert u^*\vert\vert_p =\vert\vert u\vert\vert_p,\vert\vert u^*-v^*\vert\vert_p\leq\vert\vert u-v\vert\vert_p. \end{aligned}$$

Proof

Using Cavalieri’s principle and the preceding theorem, we obtain

$$\displaystyle \begin{aligned} \vert\vert u^*\vert\vert_p^p=\int_0^{\infty}m_{(u^*)^p} (t)dt=\int^{\infty}_0 m_{u^p} (t)dt=\vert\vert u\vert\vert_p^p. \end{aligned}$$

Assume that p ≥ 2, and define g(t) = |t|^p, so that g is convex, even, of class ${\mathcal {C}}^2$, and g(0) = g′(0) = 0. For a < b, the fundamental theorem of calculus implies that

$$\displaystyle \begin{aligned} g(b-a)=\int^b_ads\int^b_sg''(t-s)dt. \end{aligned}$$

Hence we have that

$$\displaystyle \begin{aligned} g(u-v)=\int^{\infty}_0ds\int^{\infty}_s g''(t-s)\left[\chi_{\{u>t\}}(1- \chi_{\{v>s\}})+\chi_{\{v>t\}}(1- \chi_{\{u>s\}})\right]dt. \end{aligned}$$

Integrating on ${\mathbb {R}}^N$ and using Fubini’s theorem, we find that

$$\displaystyle \begin{aligned} \int_{{\mathbb{R}}^N}g(u-v)dx=\int_0^{\infty}ds\int_s^{\infty}g''(t-s) [m(\{u>t\}\setminus\{v > s\})+m(\{v>t\} \setminus\{u>s\})]dt. \end{aligned}$$

Finally, we obtain

$$\displaystyle \begin{aligned} \int_{{\mathbb{R}}^N}g(u^*-v^*)dx\leq\int_{{\mathbb{R}}^N}g(u-v)dx. \end{aligned}$$

If 1 ≤ p < 2, it suffices to approximate |t|^p by g _ε(t) = (t ² + ε ²)^p∕2 − ε ^p, ε > 0. □

Approximating Schwarz’s symmetrizations by polarizations, we will prove that if $u\in W_{+}^{1,p}({\mathbb {R}}^N)$, then $u^*\in W_+^{1,p}({\mathbb {R}}^N)$ and ||∇u ^∗||_p ≤||∇u||_p.

Definition 8.3.5

Let σ _H be the reflection with respect to the frontier of a closed affine half-space H of ${\mathbb {R}}^N$. The polarization (with respect to H) of a function $u:{\mathbb {R}}^N\rightarrow {\mathbb {R}}$ is defined by

$$\displaystyle \begin{aligned} \begin{array}{lll} u^H(x)&=\max\{u(x),u(\sigma_H(x))\},&\quad x\in H,\\ &=\min\{u(x),u(\sigma_H(x))\},&\quad x\in{\mathbb{R}}^N\setminus H. \end{array} \end{aligned}$$

The polarization A ^H of $A\subset {\mathbb {R}}^N$ is defined by $\chi _{A^H}= \chi _{A}^H$. We denote by ${\mathcal {H}}$ the family of all closed affine half-spaces of ${\mathbb {R}}^N$ containing 0.

Let us recall that a closed affine half-space of ${\mathbb {R}}^N$ is defined by

$$\displaystyle \begin{aligned} H=\{x\in{\mathbb{R}}^N:a\cdot x\leq b\}, \end{aligned}$$

where $a\in {\mathbb {S}}^{N-1}$ and $b\in {\mathbb {R}}$. It is clear that

$$\displaystyle \begin{aligned} \sigma_H(x)=x+2(b-a\cdot x)a. \end{aligned}$$

The following properties are easy to prove:

• (a) if A is a measurable subset of ${\mathbb {R}}^N$, then m(A ^H) = m(A);

• (b) {u ^H > t} = {u > t}^H;

• (c) if u is admissible, (u ^H)^∗ = u ^∗;

• (d) if moreover, $H\in {\mathcal {H}}$, (u ^∗)^H = u ^∗.

Lemma 8.3.6

Let $f:{\mathbb {R}}\rightarrow {\mathbb {R}}$ be convex and a ≤ b, c ≤ d. Then

$$\displaystyle \begin{aligned} f(b-d)+f(a-c)\leq f(a-d)+f(b-c). \end{aligned}$$

Proof

Define x = b − d, y = b − a, and z = d − c. By convexity, we have

$$\displaystyle \begin{aligned} f(x)-f(x-y)\leq f(x+z)-f(x+z-y). \end{aligned}$$

□

Proposition 8.3.7

Let 1 ≤ p < ∞ and $u,v\in L^p({\mathbb {R}}^N)$ . Then $u^H,v^H\in L^p({\mathbb {R}}^N)$ , and

$$\displaystyle \begin{aligned} \vert\vert u^H\vert\vert_p=\vert\vert u\vert\vert_p,\,\,\, \vert\vert u^H-v^H\vert\vert_p\leq\vert\vert u-v\vert\vert_p. \end{aligned}$$

Proof

Observe that

$$\displaystyle \begin{aligned} \begin{array}{ll} \displaystyle{\int_{{\mathbb{R}}^N} |u(x)|{}^pdx}&=\displaystyle{\int_H |u(x)|{}^p+|u(\sigma_H(x))|{}^pdx}\\ \\ &=\displaystyle{\int_H|u^H(x)|{}^p+|u^H(\sigma_H(x))|{}^pdx=\int_{{\mathbb{R}}^N} |u^H(x)|{}^pdx.} \end{array} \end{aligned}$$

Using the preceding lemma, it is easy to verify that for all x ∈ H,

$$\displaystyle \begin{aligned} \begin{array}{ll} &|u^H(x)-v^H(x)|{}^p+|u^H(\sigma_H(x))-v^H(\sigma_H(x))|{}^p \\ &~\leq |u(x)-v(x)|{}^p+|u(\sigma_H(x))-v(\sigma_H(x))|{}^p. \end{array} \end{aligned}$$

It suffices then to integrate over H. □

Lemma 8.3.8

Let $u:{\mathbb {R}}^N\rightarrow {\mathbb {R}}$ be a uniformly continuous function. Then the function $u^H:{\mathbb {R}}^N\rightarrow {\mathbb {R}}$ is uniformly continuous, and for all δ > 0, $\omega _{u^H}(\delta )\leq \omega _u(\delta )$.

Proof

Let δ > 0 and $x,y\in {\mathbb {R}}^N$ be such that |x − y|≤ δ. If x, y ∈ H or if $x,y\in {\mathbb {R}}^N\setminus H$, we have

$$\displaystyle \begin{aligned} |\sigma_H(x)-\sigma_H(y)|=|x-y|\leq\delta \end{aligned}$$

and

$$\displaystyle \begin{aligned} |u^H(x)-u^H(y)|\leq\max(|u(x)-u(y)|,|u(\sigma_H(x))-u(\sigma_H(y))|)\leq\omega_u(\delta). \end{aligned}$$

If x ∈ H and $y\in {\mathbb {R}}^N\setminus H$, we have

$$\displaystyle \begin{aligned} |x-\sigma_H(y)|=|\sigma_H(x)-y|\leq |\sigma_H(x)-\sigma_H(y)| =|x-y|\leq\delta \end{aligned}$$

and

$$\displaystyle \begin{aligned} \begin{array}{ll} |u^H(x)-u^H(y)|&\leq\max (|u(x)-u(\sigma_H(y))|,|u(\sigma_H(x))-u(y)|,\\ & |u(\sigma_H(x))-u(\sigma_H(y))|,|u(x)-u(y)|)\leq\omega_u(\delta). \end{array} \end{aligned}$$

We conclude that

$$\displaystyle \begin{aligned} \omega_{u^H}(\delta)=\sup_{|x-y|\leq\delta}|u^H(x)-u^H(y)|\leq\omega_u(\delta). \end{aligned}$$

□

Lemma 8.3.9

Let 1 ≤ p < ∞, $u\in L^p( {\mathbb {R}}^N)$ , and $H\in {\mathcal {H}}$ . Define $g(x)=e^{-|x|{ }^2}$ . Then

$$\displaystyle \begin{aligned} \int_{{\mathbb{R}}^N} ug~dx\leq\int_{{\mathbb{R}}^N} u^Hg~dx.\qquad \qquad {(*)} \end{aligned}$$

If, moreover, $0\in \stackrel {o}{H}$ and

$$\displaystyle \begin{aligned} \int_{{\mathbb{R}}^N} ug~dx=\int_{{\mathbb{R}}^N} u^Hg~dx,\qquad \qquad {(**)} \end{aligned}$$

then u ^H = u.

Proof

For all x ∈ H, we have

$$\displaystyle \begin{aligned} u(x)g(x)+u(\sigma_H(x))g(\sigma_H(x))\leq u^H(x)g(x)+u^H(\sigma_H(x))g(\sigma_H(x)). \end{aligned}$$

It suffices then to integrate over H to prove (∗).

If (∗∗) holds, we obtain, almost everywhere on H,

$$\displaystyle \begin{aligned} u(x)g(x)+u(\sigma_H(x))g(\sigma_H(x))=u^H(x)g(x)+u^H(\sigma_H(x))g(\sigma_H(x)). \end{aligned}$$

If $0\in \stackrel {o}{H}$, then g(σ _H(x)) < g(x) for all $x\in \stackrel {o}{H}$, so that

$$\displaystyle \begin{aligned} u(x)=u^H(x),u(\sigma_H(x))=u^H(\sigma_H(x)). \end{aligned}$$

□

Lemma 8.3.10

Let $u \in L^p(\mathbb {R}^N)\bigcap C(\mathbb {R}^N)(1 \leq p < \infty )$ be such that, for all $H \in \mathcal {H}, u^H= u$ . Then u ≥ 0 and u = u ^∗.

Proof

Let $x, y \in \mathbb {R}^N$ be such that x ≠ y and |x|≤|y|. There exists $H \in \mathcal {H}$ such that x ∈ H and y = σ _H(x). By assumption, we have

$$\displaystyle \begin{aligned} u(y) = u^H(y) \leq u^H(x) = u(x). \end{aligned}$$

Hence

$$\displaystyle \begin{aligned} |x| \leq |y| \Rightarrow u(y) \leq u(x). \end{aligned}$$

We conclude that there exists a (continuous) decreasing function $v : [0,+\infty [ \rightarrow \mathbb {R}$ such that u(x) = v(|x|). Since $u\in L^p(\mathbb {R}^N)$, it is clear that

$$\displaystyle \begin{aligned} \lim_{r\to+\infty} v(r) = 0. \end{aligned}$$

Hence u ≥ 0 and for all t > 0, {u > t} = {u ^∗ > t}, so that u = u ^∗. □

Consider a sequence of closed affine half-spaces

$$\displaystyle \begin{aligned} H_n=\{x\in{\mathbb{R}}^N:a_n\cdot x\leq b_n\} \end{aligned}$$

such that ((a _n, b _n)) is dense in ${\mathbb {S}}^{N-1}\times \,\,]0,+\infty [$.

The following result is due to J. Van Schaftingen.

Theorem 8.3.11

Let 1 ≤ p < ∞ and $u\in L^p_+( {\mathbb {R}}^N)$ . Define

$$\displaystyle \begin{aligned} \begin{array}{l} u_0=u,\\ u_{n+1}=u_n^{H_1 \ldots H_{n+1}}. \end{array} \end{aligned}$$

Then the sequence (u _n) converges to u ^∗ in $L^p({\mathbb {R}}^N)$.

Proof

Assume that $u\in {\mathcal {K}}_+({\mathbb {R}}^N)$. There exists r > 0 such that spt u ⊂ B[0, r]. Hence for all n,

$$\displaystyle \begin{aligned} {\mathrm{spt}~} u_n\subset B[0,r]. \end{aligned}$$

The sequence (u _n) is precompact in ${\mathcal {C}}(B[0,r])$ by Ascoli’s theorem, since

• (a) for every n, ||u _n||_∞ = ||u||_∞;

• (b) for every ε > 0, there exists δ > 0, such that for every n, $\omega _{u_n}(\delta )\leq \omega _u(\delta )\leq \varepsilon$.

Assume that $(u_{n_k})$ converges uniformly to v. Observe that

$$\displaystyle \begin{aligned} {\mathrm{spt}~}v\subset B[0,r]. \end{aligned}$$

We shall prove that v = u ^∗. Since by Proposition 8.3.4,

$$\displaystyle \begin{aligned} \vert\vert u^*-v^*\vert\vert_1=\vert\vert u^*_{n_k}-v^*\vert\vert_1\leq\vert\vert u_{n_k}-v\vert\vert_1\rightarrow 0, \quad k\rightarrow\infty, \end{aligned}$$

it suffices to prove that v = v ^∗.

Let m ≥ 1. For every n _k ≥ m, we have

$$\displaystyle \begin{aligned} u_{n_{k+1}}=u_{n_k}^{H_1 \ldots H_m \ldots H_{n_{k+1}}}. \end{aligned}$$

Lemma 8.3.9 implies that

$$\displaystyle \begin{aligned} \int_{{\mathbb{R}}^N} u_{n_k}^{H_1 \ldots H_m}g~dx\leq\int_{{\mathbb{R}}^N} u_{n_{k+1}}g~dx. \end{aligned}$$

It follows from Proposition 8.3.7 that

$$\displaystyle \begin{aligned} \int_{{\mathbb{R}}^N} v^{H_1\ldots H_m}g~dx\leq\int_{{\mathbb{R}}^N} vg~dx. \end{aligned}$$

By Lemma 8.3.9, $v^{H_1}=v$, and by induction, $v^{H_m}=v$.

Let $a\in {\mathbb {S}}^{N-1}$, b ≥ 0, and $H=\{x\in {\mathbb {R}}^N:a\cdot x\leq b\}$. There exists a sequence (n _k) such that $(a_{n_k},b_{n_k})\rightarrow (a,b)$. We deduce from Lebesgue’s dominated convergence theorem that

$$\displaystyle \begin{aligned} \vert\vert v^H-v\vert\vert_1=\vert\vert v^H-v^{H_{n_k}}\vert\vert_1\rightarrow 0,\quad k\rightarrow\infty. \end{aligned}$$

Hence for all $H\in {\mathcal {H}}$, v = v ^H. Lemma 8.3.10 ensures that v = v ^∗.

Let $u\in L^p_+({\mathbb {R}}^N)$ and ε > 0. The density theorem implies the existence of $w\in {\mathcal {K}}_+({\mathbb {R}}^N)$ such that ||u − w||_p ≤ ε. By the preceding step, the sequence

$$\displaystyle \begin{aligned} \begin{array}{rl} w_0&=w,\\ w_{n+1}&=w_n^{H_1\ldots H_{n+1}}, \end{array} \end{aligned}$$

converges to w ^∗ in $L^p({\mathbb {R}}^N)$. Hence there exists m such that for n ≥ m, ||w _n − w ^∗||_p ≤ ε. It follows from Propositions 8.3.4 and 8.3.7 that for n ≥ m,

$$\displaystyle \begin{aligned} \vert\vert u_n-u^*\vert\vert_p\leq\vert\vert u_n-w_n\vert\vert_p+\vert\vert w_n-w^*\vert\vert_p+\vert\vert w^*-u^*\vert\vert_p\leq 2\vert\vert u-w\vert\vert_p+\varepsilon\leq 3\varepsilon. \end{aligned}$$

Since ε > 0 is arbitrary, the proof is complete. □

Proposition 8.3.12

Let 1 ≤ p < ∞ and $u \in W^{1,p}({\mathbb {R}}^N)$ . Then $u^H \in W^{1,p} ({\mathbb {R}}^N)$ and ||∇u ^H||_p = ||∇u||_p.

Proof

Define v = u ∘ σ _H. Observe that

$$\displaystyle \begin{aligned} \begin{array}{lll} u^H&=\displaystyle{\frac{1}{2}(u+v)+\frac{1}{2}|u-v|}, &\quad \mbox{on }H,\\ \\ &= \displaystyle{ \frac{1}{2}(u+v)-\frac{1}{2}|u-v|},&\quad \mbox{on }{\mathbb{R}}^N\setminus H. \end{array} \end{aligned}$$

Since the trace of |u − v| is equal to 0 on ∂H, $u^H\in W^{1,p}({\mathbb {R}}^N)$. Let x ∈ H. Corollary 6.1.14 implies that for u(x) ≥ v(x),

$$\displaystyle \begin{aligned} \nabla u^H(x)=\nabla u(x),\nabla u^H(\sigma_H(x))=\nabla u(\sigma_H(x)), \end{aligned}$$

and for u(x) < v(x),

$$\displaystyle \begin{aligned} \nabla u^H(x)=\nabla v(x),\nabla u^H(\sigma_H(x))=\nabla v(\sigma_H(x)). \end{aligned}$$

We conclude that on H,

$$\displaystyle \begin{aligned} |\nabla u^H(x)|{}^p+|\nabla u^H(\sigma_H(x))|{}^p=|\nabla u(x)|{}^p+|\nabla u(\sigma_H(x))|{}^p. \end{aligned}$$

□

Proposition 8.3.13

Let $u \in BV({\mathbb {R}}^N)$ . Then $u^H \in BV({\mathbb {R}}^N)$ and ||Du ^H||≤||Du||.

Proof

Let u _n = ρ _n ∗ u. Propositions 4.3.14 and 8.3.7 imply that u _n → u and $u^H_n\rightarrow u^H$ in $L^1({\mathbb {R}}^N)$. Theorem 7.3.3 and Proposition 8.3.12 ensure that

$$\displaystyle \begin{aligned} \vert\vert Du_n^H\vert\vert =\vert\vert\nabla u^H_n\vert\vert_1=\vert\vert\nabla u_n\vert\vert_1. \end{aligned}$$

We conclude by Theorem 7.3.2 and Lemma 7.3.6 that

$$\displaystyle \begin{aligned} \vert\vert Du^H\vert\vert\leq\lim\vert\vert Du_n^H\vert\vert =\lim \vert\vert\nabla u_n\vert\vert_1=\vert\vert Du\vert\vert. \end{aligned}$$

□

Theorem 8.3.14 (Pólya–Szegő Inequality)

Let 1 < p < ∞ and $u\in W^{1,p}_+({\mathbb {R}}^N)$ . Then $u^*\in W^{1,p}_+({\mathbb {R}}^N)$ and ||∇u ^∗||_p ≤||∇u||_p.

Proof

The sequence (u _n) given by Theorem 8.3.11 converges to u ^∗ in $L^p({\mathbb {R}}^N)$. By Proposition 8.3.12, for every n, ||∇u _n||_p = ||∇u||_p. It follows from Theorem 6.1.7 that

$$\displaystyle \begin{aligned} \vert\vert\nabla u^*\vert\vert_p\leq\lim\vert\vert\nabla u_n\vert\vert_p=\vert\vert\nabla u\vert\vert_p. \end{aligned}$$

□

Theorem 8.3.15 (Hilden’s Inequality, 1976)

Let $u\in BV_+({\mathbb {R}}^N)$ . Then $u^*\in BV_+({\mathbb {R}}^N)$ and ||Du ^∗||≤||Du||.

Proof

The sequence (u _n) given by Theorem 8.3.11 converges to u ^∗ in $L^{1^*}({\mathbb {R}}^N)$. By Proposition 8.3.13, for every n,

$$\displaystyle \begin{aligned} \vert\vert Du_{n+1}\vert\vert\leq\vert\vert Du_n\vert\vert\leq\vert\vert Du\vert\vert. \end{aligned}$$

It follows from Theorem 7.3.2 that

$$\displaystyle \begin{aligned} \vert\vert Du^*\vert\vert\leq\lim\vert\vert Du_n\vert\vert\leq\vert\vert Du\vert\vert. \end{aligned}$$

□

Theorem 8.3.16 (De Giorgi’s Isoperimetric Inequality)

Let N ≥ 2, and let A be a measurable subset of ${\mathbb {R}}^N$ with finite measure. Then

$$\displaystyle \begin{aligned} NV_N^{1/N}(m(A))^{1-1/N}\leq p(A). \end{aligned}$$

Proof

If p(A) = +∞, the inequality is clear. If this is not the case, then $\chi _A\in BV_+({\mathbb {R}}^N)$. By definition of Schwarz’s symmetrization,

$$\displaystyle \begin{aligned} A^*=B(0,r),V_Nr^N=m(A). \end{aligned}$$

Theorems 7.4.1 and 8.3.15 imply that

$$\displaystyle \begin{aligned} NV_Nr^{N-1}=p(A^*)=\vert\vert D\chi_{A^*}\vert\vert_{{\mathbb{R}}^N}= \vert\vert D\chi^*_{A}\vert\vert_{{\mathbb{R}}^N}\leq\vert\vert D\chi_{A}\vert\vert_{{\mathbb{R}}^N}=p(A). \end{aligned}$$

It is easy to conclude the proof. □

Using scaling invariance, we obtain the following version of the isoperimetric inequality.

Corollary 8.3.17

Let A be a measurable subset of ${\mathbb {R}}^N$ with finite measure, and let B be an open ball of ${\mathbb {R}}^N$ . Then

$$\displaystyle \begin{aligned} p(B)/m(B)^{1-1/N}\leq p(A)/m(A)^{1-1/N}. \end{aligned}$$

The constant $NV_N^{1/N}$, corresponding to the characteristic function of a ball, is the optimal constant for the Gagliardo–Nirenberg inequality.

Theorem 8.3.18

Let N ≥ 2 and u ∈ L ^N∕(N−1) such that ||Du|| < +∞. Then

$$\displaystyle \begin{aligned} NV^{1/N}_N \vert\vert u\vert\vert_{N/(N-1)} \leq \vert\vert Du\vert\vert. \end{aligned}$$

Proof

• (a) Let $p=N/(N-1), v \in L^p (\mathbb {R}^N),v\geq 0$, and $g\in L^{p'} (\mathbb {R}^N)$. If $\vert \vert g\vert \vert _{p'}=1$, we deduce from Fubini’s theorem and Hölder’s inequality that

  $$\displaystyle \begin{aligned} \int_{\mathbb{R}^N} gvdx &= \int_{\mathbb{R}^N} dx \int^\infty_0 g \chi_{v>t} dt &= \int^\infty_0 dt \int_{\mathbb{R}^N} g \chi_{v>t} dx &\leq \int^\infty_0 m (\{v > t\})^{1/p} dt. \end{aligned}$$

  Hence we obtain

  $$\displaystyle \begin{aligned} \vert\vert v\vert\vert_p = \max_{\vert\vert g\vert\vert_{p'}=1} \int_{\mathbb{R}^N} gvdx \leq \int^\infty_0 m (\{v>t\})^{1/p} dt. \qquad (\ast) \end{aligned}$$

• (b) Let $u\in \mathcal {D}(\varOmega )$. Using inequality (∗), the Morse–Sard theorem (Theorem 9.3.1), the coarea formula (Theorem 9.3.3), and the isoperimetric inequality, we obtain

  $$\displaystyle \begin{aligned} NV^{1/N}_N \vert\vert u\vert\vert_p &\leq NV^{1/N}_N [\vert\vert u^+\vert\vert_p + \vert\vert u^- \vert\vert_p] \\[0.2cm] &\leq NV^{1/N}_N \left[\int^\infty_0 m (\{u>t\})^{1/p} dt + \int^0 _{-\infty} m (\{u<t\})^{1/p}dt\right] \\[0.2cm] &\leq \int^\infty_0 dt \int_{u=t} d\gamma + \int^0_{-\infty} dt \int_{u=t} d\gamma = \int_{\mathbb{R}^N} |\nabla u| dx. \end{aligned}$$

• (c) By density, we obtain, for every $u\in \mathcal {D}^{1,1} (\mathbb {R}^N)$,

  $$\displaystyle \begin{aligned} NV^{1/N}_N \vert\vert u\vert\vert_p \leq \vert\vert \nabla u\vert\vert_1. \end{aligned}$$

  We conclude using Proposition 4.3.14 and Lemma 7.3.6.

□

Definition 8.3.19

Let Ω be an open subset of ${\mathbb {R}}^N$. We define

$$\displaystyle \begin{aligned} \lambda_1(\varOmega)=\inf\left\{\vert\vert\nabla u\vert\vert^2_2/\vert\vert u\vert\vert^2_2:u\in W^{1,2}_0(\varOmega)\setminus\{0\}\right\}. \end{aligned}$$

Theorem 8.3.20 (Faber–Krahn Inequality)

Let Ω be an open subset of ${\mathbb {R}}^N$ with finite measure. Then λ ₁(Ω ^∗) ≤ λ ₁(Ω).

Proof

Define $Q(u)=\vert \vert \nabla u\vert \vert ^2_2/\vert \vert u\vert \vert ^2_2$. Let $u\in W^{1,2}_0(\varOmega )\setminus \{0\}$ and v = |u|. By Corollary 6.1.14, Q(v) = Q(u). Proposition 8.3.4 and the Pólya–Szegő inequality imply that Q(v ^∗) ≤ Q(v). It is easy to verify that $v^*\in W_0^{1,2}(\varOmega ^*)\setminus \{0\}$. Hence we obtain

$$\displaystyle \begin{aligned} \lambda_1(\varOmega^*)\leq Q(v^*)\leq Q(v)=Q(u). \end{aligned}$$

Since $u\in W_0^{1,2}(\varOmega )\setminus \{0\}$ is arbitrary, it is easy to conclude the proof. □

Using scaling invariance, we obtain the following version of the Faber–Krahn inequality.

Corollary 8.3.21

Let Ω be an open subset of ${\mathbb {R}}^N$ , and let B be an open ball of ${\mathbb {R}}^N$ . Then

$$\displaystyle \begin{aligned} \lambda_1(B)m(B)^{2/N} \leq \lambda_1(\varOmega)m(\varOmega)^{2/N}. \end{aligned}$$

Remark

Equality in the isoperimetric inequality or in the Faber–Krahn inequality is achieved only when the corresponding domain is a ball.

8.4 Elementary Solutions

There exists no locally integrable function corresponding to the Dirac measure.

Definition 8.4.1

The Dirac measure is defined on $\mathcal {K}(\mathbb {R}^N)$ by

$$\displaystyle \begin{aligned} \langle \delta,u \rangle = u(0). \end{aligned}$$

Definition 8.4.2

The elementary solutions of the Laplacian are defined on $\mathbb {R}^N \backslash \{0\}$ by

$$\displaystyle \begin{aligned} & E_N(x) = \frac{1}{2\pi} \log \frac{1}{|x|}, \qquad \qquad N=2, \\ & E_N(x) = \frac{1}{(N-2)NV_N} \ \frac{1}{|x|{}^{N-2}}, \quad N \geq 3. \end{aligned}$$

Theorem 8.4.3

Let N ≥ 2. In $\mathcal {D}^\ast (\mathbb {R}^N)$ , we have

$$\displaystyle \begin{aligned} -\varDelta E_N = \delta. \end{aligned}$$

Proof

Define v(x) = w(|x|). Since

$$\displaystyle \begin{aligned} \varDelta v = w'' + (N-1) w'/|x|, \end{aligned}$$

it is easy to verify that on $\mathbb {R}^N \backslash \{0\}, \varDelta E_N = 0$. It is clear that $E_N \in L^1_{\mathrm {loc}} (\mathbb {R}^N)$.

Let $u\in \mathcal {D} (\mathbb {R}^N)$ and R > 0 be such that spt u ⊂ B(0, R). We have to verify that

$$\displaystyle \begin{aligned} -u(0) = \int_{\mathbb{R}^N} E_N \varDelta u \ dx = \lim_{\varepsilon \to 0} \int_{\varepsilon < |x| < R} E_N \varDelta u \ dx. \end{aligned}$$

We obtain using the divergence theorem that

$$\displaystyle \begin{aligned} f(\varepsilon) = \int_{\varepsilon < |x| < R} (E_N \varDelta u - u\varDelta E_N) \ dx = \int_{\partial B(0,\varepsilon)} \left( u \nabla E_N \cdot \frac{\gamma}{|\gamma|} - E_N \nabla u \cdot \frac{\gamma}{|\gamma}| \right) \ d\gamma. \end{aligned}$$

By a simple computation,

$$\displaystyle \begin{aligned} \int_{\partial B(0,\varepsilon)} \nabla E_N \cdot \frac{\gamma}{|\gamma|} =-1, \quad \lim_{\varepsilon \to 0} \int_{\partial B(0,\varepsilon)} E_N d\gamma = 0, \end{aligned}$$

so that lim_ε→0 f(ε) = −u(0). □

Definition 8.4.4

Let $f,g\in \mathcal {D}^\ast (\varOmega )$. By definition, f ≤ g if for every $u\in \mathcal {D}(\varOmega )$ such that u ≥ 0, 〈f, u〉≤〈g, u〉.

Theorem 8.4.5 (Kato’s Inequality)

Let $g \in L^1_{\mathrm {loc}} (\varOmega )$ be such that $\varDelta g \in L^1_{\mathrm {loc}} (\varOmega )$ . Then

$$\displaystyle \begin{aligned} (\mathrm{sgn} \ g) \ \varDelta g \leq \varDelta |g|. \end{aligned}$$

Proof

Let $u\in \mathcal {D}(\varOmega )$ and ω ⊂⊂ Ω be such that u ≥ 0 and spt u ⊂ ω. Define g _n = ρ _n ∗ g, and for ε > 0, f _ε(t) = (t ² + ε ²)^1∕2. Since g _n → g in L ¹(ω), we can assume, passing if necessary to a subsequence, that g _n → g almost everywhere on ω.

For all ε > 0 and for n large enough, we have

$$\displaystyle \begin{aligned} \int_\varOmega f^{\prime}_\varepsilon (g_n) (\varDelta g_n) u \ dx \leq \int_\varOmega (\varDelta f_\varepsilon (g_n))u \ dx = \int_\varOmega f_\varepsilon (g_n) \varDelta u \ dx. \end{aligned}$$

When n →∞, we find that

$$\displaystyle \begin{aligned} \int_\varOmega f^{\prime}_\varepsilon (g) (\varDelta g) u \ dx \leq \int_\varOmega f_\varepsilon (g) \varDelta u \ dx. \end{aligned}$$

When ε ↓ 0, we obtain

$$\displaystyle \begin{aligned} \qquad \qquad \qquad \int_\varOmega (\mathrm{sgn} \ g) (\varDelta g) u \ dx \leq \int_\varOmega |g| \ \varDelta u \ dx. \end{aligned}$$

□

8.5 Comments

The notion of polarization of sets appeared in 1952, in a paper by Wolontis [87]. Polarizations of functions were first used by Baernstein and Taylor to approximate symmetrization of functions on the sphere in the remarkable paper [3]. The explicit approximation of Schwarz’s symmetrization by polarizations is due to Van Schaftingen [84]. See [73, 85] for other aspects of polarizations. The proof of Proposition 8.3.4 uses a device of Alberti [2]. The notion of symmetrization, and more generally, the use of reflections to prove symmetry, goes back to Jakob Steiner [79].

The elegant proof of Theorem 8.3.18 is due to O.S. Rothaus, J. Funct. Anal. 64 (1985) 296–313.

8.6 Exercises for Chap. 8

• 1. Let $u\in {\mathcal {C}}(\varOmega )$. The spherical means of u are defined on D by

  $$\displaystyle \begin{aligned} S(x,r)=(NV_{N})^{-1}\int_{{\mathbb{S}}^{N-1}}u(x+r\sigma)d\sigma. \end{aligned}$$

  Verify that when $u\in {\mathcal {C}}^2(\varOmega )$,

  $$\displaystyle \begin{aligned} \lim_{r\downarrow 0}\frac{2N}{r^2}[S(x,r)-u(x)]=\varDelta u(x). \end{aligned}$$

• 2. Let $u\in {\mathcal {C}}(\varOmega )$ be such that for every (x, r) ∈ D, u(x) = M(x, r). Then for every x ∈ Ω _n, ρ _n ∗ u = u.

  The argument is due to A. Ponce:

  $$\displaystyle \begin{aligned} \rho_n \ast u(x) &= \int_{{\mathbb{R}}^N} \rho_n (x-y) u(y) dy = \int^{\infty}_0 dt \int_{\rho (x-y)>t} u(y) dy\\ & = u(x) \int^{\infty}_0 dt\int_{\rho (x-y)>t} dy = u(x). \end{aligned} $$

• 3. (Weyl’s theorem.) Let $u\in L^1_{{\mathrm {loc}}}(\varOmega )$. The following properties are equivalent:

  • (a) u is harmonic;

  • (b) for almost all x ∈ Ω and for all 0 < r < d(x, ∂Ω), u(x) = M(x, r);

  • (c) there exists $v\in {\mathcal {C}}^{\infty }(\varOmega )$, almost everywhere equal to u, such that Δv = 0.

• 4. Let $u\in {\mathcal {C}}^2(\varOmega )$ be a harmonic function. Assume that u ≥ 0 on B[0, R] ⊂ Ω. Then for every 0 < r < R and |y| < R − r, we have

  $$\displaystyle \begin{aligned} \begin{array}{ll} |u(y)-u(0)|&\leq\displaystyle{\frac{1}{r^{N}V_N}\int_{r-|y|<|x|<r+|y|}u(x)dx}\\ \\ &=\displaystyle{\frac{(r+|y|)^N-(r-|y|)^N}{r^N}u(0).} \end{array} \end{aligned}$$

  Hint: Use the mean-value property.

• 5. (Liouville’s theorem.) Let $u\in {\mathcal {C}}^{\infty }({\mathbb {R}}^N)$ be a harmonic function, bounded from below on ${\mathbb {R}}^N$. Then u is constant.

• 6. Let Ω be an open connected subset of ${\mathbb {R}}^N$, and let $u\in {\mathcal {C}}^{\infty }(\varOmega )$ be a harmonic function such that for some x ∈ Ω, u(x) = inf_Ω u. Then u is constant.

• 7. If $u\in {\mathcal {D}}(]0,\pi [)$, then

  $$\displaystyle \begin{aligned} \int_0^{\pi}\Big|\frac{du}{dx}\Big|{}^2-u^2dx=\int^{\pi}_0\Big|\frac{du}{dx}-\frac{\cos x}{\sin x}u\Big|{}^2 dx. \end{aligned}$$

  Hence

  

• 8. (Min–max principle.) For every n ≥ 1,

  

  where ${\mathcal {V}}_n$ denotes the family of all n-dimensional subspaces of $H^1_0(\varOmega )$.

• 9. Let us recall that

  $$\displaystyle \begin{aligned} \lambda_1(G)=\inf\left\{\vert\vert\nabla u\vert\vert^2_2/\vert\vert u\vert\vert^2_2:u\in W_0^{1,2}(G)\setminus \{0\}\right\}. \end{aligned}$$

  Let Ω be an open subset of ${\mathbb {R}}^M$, and ω an open subset of ${\mathbb {R}}^N$. Then:

  • (a) λ ₁(Ω × ω) = λ ₁(Ω) + λ ₁(ω);

  • (b) $\lambda _1({\mathbb {R}}^N)=0$;

  • (c) $\lambda _1(\varOmega \times {\mathbb {R}}^N)=\lambda _1(\varOmega )$.

• 10. Define $u\in {\mathcal {D}}_+({\mathbb {R}}^N)$ such that for every $y\in {\mathbb {R}}^N$, τ _y u ≠ u ^∗, and for 1 ≤ p < ∞, ||∇u||_p = ||∇u ^∗||_p. Hint: Consider two functions v and w such that v = v ^∗, w = w ^∗, v ≡ 1 on B(0, 1), and spt w ⊂ B[0, 1∕2], and define u = v + τ _y w.

• 11. (Hardy–Littlewood inequality.) Let 1 < p < ∞, $u\in L_+^p({\mathbb {R}}^N)$, and $v\in L_+^{p'}({\mathbb {R}}^N)$. Then

  $$\displaystyle \begin{aligned} \int_{{\mathbb{R}}^N} u~v~dx\leq\int_{{\mathbb{R}}^N} u^*v^*dx. \end{aligned}$$

• 12. Let 1 ≤ p < ∞ and $u,v\in L^p_+({\mathbb {R}}^N)$. Then

  $$\displaystyle \begin{aligned} \vert\vert u+v\vert\vert_p\leq\vert\vert u^*+v^*\vert\vert_p. \end{aligned}$$

  Hint: Assume first that p > 1. Observe that

  

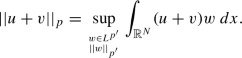
• 13. Let Ω be a domain in ${\mathbb {R}}^N$ invariant under rotations. A function $u:\varOmega \rightarrow {\mathbb {R}}$ is foliated Schwarz’s symmetric with respect to $e\in {\mathbb {S}}^{N-1}$ if u(x) depends only on $(r,\theta )=(|x|,\cos ^{-1}(\frac {x}{|x|}\cdot e))$ and is decreasing in θ.

  Let $e\in {\mathbb {S}}^{N-1}$. We denote by ${\mathcal {H}}_e$ the family of closed half-spaces H in ${\mathbb {R}}^N$ such that 0 ∈ ∂H and e ∈ H.

  Prove that a function $u:\varOmega \rightarrow {\mathbb {R}}$ is foliated Schwarz’s symmetric with respect to e if and only if for every $H\in {\mathcal {H}}_e$, u ^H = u.

• 14. Let $u\in L^p(\mathbb {R}^N)(1\leq p < \infty )$, and let the closed affine half-space $H \subset \mathbb {R}^N$ be such that u ^H = u. Then, for every n ≥ 1, (ρ _n ∗ u)^H = ρ _n ∗ u.

  Hint. For every x, y ∈ H, we have

  $$\displaystyle \begin{aligned} |x-y|=\big|\sigma_H (x) - \sigma_H(y)\big| \ \leq \ \big|x-\sigma_H(y)\big| = \big|\sigma_H(x)-y\big|. \end{aligned}$$

  Hence we obtain, for every x ∈ H,

  $$\displaystyle \begin{aligned} \begin{array}{rcl} & &\displaystyle \rho_n \ast u(x) - \rho_n \ast u \bigl(\sigma_H(x)\bigr)\\ & &\displaystyle \quad =\int_H \biggl[u(y)-u \bigl(\sigma_H(y)\bigr)\biggr] \ \bigl[\rho_n(x-y)-\rho_n \bigl(\sigma_H(x)-y\bigr)\bigr]dy\geq 0. \end{array} \end{aligned} $$

• 15. Let $u\in L^p(\mathbb {R}^N)(1\leq p < \infty )$ be such that, for all $H \in \mathcal {H}, u^H=u$. Then u ≥ 0 and u = u ^∗.