Abstract
A locally integrable function has a weak derivative of order α when its derivative of order α in the sense of distributions is represented by a locally integrable function. Sobolev spaces are spaces of differentiable functions with integral norms. In order to define complete spaces, we use weak derivatives. The Sobolev embedding theorem is the most important result of this chapter.
Access provided by Autonomous University of Puebla. Download chapter PDF
Keywords
6.1 Weak Derivatives
Throughout this chapter, we denote by Ω an open subset of \(\mathbb {R}^N\). We begin with an elementary computation.
Lemma 6.1.1
Let 1 ≤|α|≤ m and let \(f \in \mathcal {C}^m (\varOmega )\) . Then for every \(u\in \mathcal {C}^m(\varOmega ) \cap \mathcal {K}(\varOmega )\),
Proof
We assume that α = (0, …, 0, 1). Let \(u\in \mathcal {C}^1(\varOmega )\cap \mathcal {K}(\varOmega )\), and define
The fundamental theorem of calculus implies that for every \(x'\in \mathbb {R}^{N-1}\),

Fubini’s theorem ensures that

When |α| = 1, the proof is similar. It is easy to conclude the proof by induction. □
Weak derivatives were defined by S.L. Sobolev in 1938.
Definition 6.1.2
Let \(\alpha \in \mathbb {N}^N\) and \(f\in L^1_{\mathrm {loc}} (\varOmega )\). By definition, the weak derivative of order α of f exists if there is \(g\in L^1_{\mathrm {loc}} (\varOmega )\) such that for every \(u\in \mathcal {D} (\varOmega )\),
The function g, if it exists, will be denoted by ∂ α f.
By the annulation theorem, the weak derivatives are well defined.
Proposition 6.1.3
Assume that ∂ α f exists. On
we have that
Proof
We deduce from Proposition 4.3.6 and from the preceding definition that for every x ∈ Ω n,
□
Theorem 6.1.4 (du Bois–Reymond Lemma)
Let |α| = 1 and let \(f\in \mathcal {C}(\varOmega )\) be such that \(\partial ^{\alpha }f \in \mathcal {C}(\varOmega )\) . Then D α f exists and D α f = ∂ α f.
Proof
By the preceding proposition, we have
The fundamental theorem of calculus implies then that
By the regularization theorem,
uniformly on every compact subset of Ω. Hence we obtain
so that ∂ α f = D α f by the fundamental theorem of calculus. □
Notation
From now on, the derivatives of a continuously differentiable function will also be denoted by ∂ α.
Let us prove the closing lemma. The graph of the weak derivative is closed in \(L^1_{\mathrm {loc}}\times L^1_{\mathrm {loc}}\).
Lemma 6.1.5
Let \((f_n)\subset L^1_{\mathrm {loc}}(\varOmega )\) and let \(\alpha \in \mathbb {N}^N\) be such that in \(L^1_{\mathrm {loc}}(\varOmega )\),
Then g = ∂ α f.
Proof
For every \(u\in \mathcal {D}(\varOmega )\), we have by definition that
Since by assumption,
and
we obtain
□
Example (Weak Derivative)
If − N < λ ≤ 1, the function f(x) = |x|λ is locally integrable on \(\mathbb {R}^N\). We approximate f by
Then \(f_{\varepsilon }\in \mathcal {C}^{\infty }(\mathbb {R}^N)\) and
If λ > 1 − N, we obtain in \(L^1_{\mathrm {loc}}(\mathbb {R}^N)\) that
Hence ∂ k f(x) = λ |x|λ−2 x k.
Definition 6.1.6
The gradient of the (weakly) differentiable function u is defined by

The divergence of the (weakly) differentiable vector field  is defined by
is defined by

Let 1 ≤ p < ∞ and \(u\in L^1_{\mathrm {loc}} (\varOmega )\) be such that ∂ j u ∈ L p(Ω), j = 1, …, N. We define
Theorem 6.1.7
Let 1 < p < ∞ and let \((u_n)\subset L^1_{\mathrm {loc}}(\varOmega )\) be such that
-
(a)
u n → u in \(L^1_{\mathrm {loc}}(\varOmega )\);
-
(b)
for every n, \(\nabla u_n\in L^p(\varOmega ;\mathbb {R}^N)\);
-
(c)
c = supn||∇u n||p < ∞.
Then \(\nabla u\in L^p(\varOmega ;\mathbb {R}^N)\) and
Proof
We define f on \(\mathcal {D}(\varOmega ;\mathbb {R}^N)\) by
We have that
Since \(\mathcal {D}(\varOmega )\) is dense in \(L^{p'}(\varOmega )\), Proposition 3.2.3 implies the existence of a continuous extension of f to \(L^{p'}(\varOmega ;\mathbb {R}^N)\). By Riesz’s representation theorem, there exists \(g\in L^p(\varOmega ;\mathbb {R}^N)\) such that for every \(v\in \mathcal {D}(\varOmega ;\mathbb {R}^N)\),
Hence \(\nabla u=-g\in L^p(\varOmega ;\mathbb {R}^N)\). Choosing v = |∇u|p−2∇u, we find that
□
Sobolev spaces are spaces of differentiable functions with integral norms. In order to define complete spaces, we use weak derivatives.
Definition 6.1.8
Let k ≥ 1 and 1 ≤ p < ∞. On the Sobolev space
we define the norm
On the space H k(Ω) = W k, 2(Ω), we define the scalar product
The Sobolev space \(W^{k,p}_{\mathrm {loc}}(\varOmega )\) is defined by
A sequence (u n) converges to u in \(W_{\mathrm {loc}}^{k,p}(\varOmega )\) if for every ω ⊂⊂ Ω,
The space \(W_0^{k,p}(\varOmega )\) is the closure of \(\mathcal {D}(\varOmega )\) in W k, p(Ω). We denote by \(H_0^k(\varOmega )\) the space \(W_0^{k,2}(\varOmega )\).
Theorem 6.1.9
Let k ≥ 1 and 1 ≤ p < ∞. Then the spaces W k, p(Ω) and \(W_0^{k,p}(\varOmega )\) are complete and separable.
Proof
Let M = ∑ |α|≤k1. The space \(L^p(\varOmega ;\mathbb {R}^M)\) with the norm
is complete and separable. The map
is a linear isometry: ||Φ(u)||p = ||u||k,p. By the closing lemma, Φ(W k, p(Ω)) is a closed subspace of \(L^p(\varOmega ;\mathbb {R}^M)\). It follows that W k, p(Ω) is complete and separable. Since \(W_0^{k,p}(\varOmega )\) is a closed subspace of W k, p(Ω), it is also complete and separable. □
Theorem 6.1.10
Let 1 ≤ p < ∞. Then \(W_0^{1,p}(\mathbb {R}^N)=W^{1,p}(\mathbb {R}^N)\).
Proof
It suffices to prove that \(\mathcal {D}(\mathbb {R}^N)\) is dense in \(W^{1,p}(\mathbb {R}^N)\). We use regularization and truncation.
Regularization Let \(u\in W^{1,p}(\mathbb {R}^N)\) and define u n = ρ n ∗ u. By Proposition 4.3.6, \(u_n\in \mathcal {C}^{\infty }(\mathbb {R}^N)\). Proposition 4.3.14 implies that in \(L^p(\mathbb {R}^N)\),
We conclude that \(W^{1,p}(\mathbb {R}^N)\cap \mathcal {C}^{\infty }(\mathbb {R}^N)\) is dense in \(W^{1,p}(\mathbb {R}^N)\).
Truncation Let \(\theta \in \mathcal {C}^{\infty }(\mathbb {R})\) be such that 0 ≤ θ ≤ 1 and
We define the sequence
Let \(u\in W^{1,p}(\mathbb {R}^N)\cap \mathcal {C}^{\infty }(\mathbb {R}^N)\). It is clear that \(u_n=\theta _n u\in \mathcal {D}(\mathbb {R}^N)\). It follows easily from Lebesgue’s dominated convergence theorem that u n → u in \(W^{1,p}(\mathbb {R}^N)\). □
We extend some rules of differential calculus to weak derivatives.
Proposition 6.1.11 (Change of Variables)
Let Ω and ω be open subsets of \(\mathbb {R}^N\) , G : ω → Ω a diffeomorphism, and \(u\in W^{1,1}_{\mathrm {loc}}(\varOmega )\) . Then \(u\circ G\in W_{\mathrm {loc}}^{1,1}(\omega )\) and
Proof
Let \(v\in \mathcal {D}(\omega )\) and u n = ρ n ∗ u. By Lemma 6.1.1, for n large enough, we have
It follows from Theorem 2.4.5 with H = G −1 that
The regularization theorem implies that in \(L^1_{\mathrm {loc}}(\varOmega )\),
Taking the limit, it is permitted to replace u n by u in (∗∗). But then it is also permitted to replace u n by u in (∗), and the proof is complete. □
Proposition 6.1.12 (Derivative of a Product)
Let \(u\in W_{\mathrm {loc}}^{1,1}(\varOmega )\) and \(f\in \mathcal {C}^{1}(\varOmega )\) . Then \(fu\in W^{1,1}_{\mathrm {loc}}(\varOmega )\) and
Proof
Let u n = ρ n ∗ u, so that by the classical rule of derivative of a product,
It follows from the regularization theorem that
in \(L_{\mathrm {loc}}^1(\varOmega )\). We conclude by invoking the closing lemma. □
Proposition 6.1.13 (Derivative of the Composition of Functions)
Let \(u\in W^{1,1}_{\mathrm {loc}}(\varOmega )\) , and let \(f\in \mathcal {C}^1(\mathbb {R})\) be such that \(c=\displaystyle {\sup _{\mathbb {R}}}\vert f'\vert <\infty \) . Then \(f\circ u\in W^{1,1}_{\mathrm {loc}}(\varOmega )\) and
Proof
We define u n = ρ n ∗ u, so that by the classical rule,
We choose ω ⊂⊂ Ω. By the regularization theorem, we have in L 1(ω),
By Proposition 4.2.10, taking if necessary a subsequence, we can assume that u n → u almost everywhere on ω. We obtain
Hence in L 1(ω),
Since ω ⊂⊂ Ω is arbitrary, we conclude the proof by invoking the closing lemma. □
On \(\mathbb {R}\), we define
Corollary 6.1.14
Let \(g : \mathbb {R} \to \mathbb {R}\) be such that \(c=\sup _{\mathbb {R}} |g| < \infty \) and, for some sequence \((g_n) \subset \mathcal {C}(\mathbb {R})\) , g(t) =limn→∞ g n(t) everywhere on \(\mathbb {R}\) . Define
Then, for every \(u\in W^{1,1}_{\mathit {loc}} (\varOmega ), f \circ u \in W^{1,1}_{\mathit {loc}} (\varOmega )\) and
In particular \(u^+,u^-,|u|\in W^{1,1}_{\mathit {loc}} (\varOmega )\) and

Proof
We can assume that \(\displaystyle \sup _n \sup _{\mathbb {R}} |g_n| \leq c\). We define \(f_n(t) = \displaystyle \int ^t_0 g_n (s) ds\). The preceding proposition implies that
Since, in \(L^1_{\mathrm {loc}}(\varOmega )\), by Lebesgue’s dominated convergence theorem,
the closing lemma implies that
□
Corollary 6.1.15
Let 1 ≤ p < ∞ and let \(u\in W^{1,p}(\varOmega )\cap \mathcal {C}(\overline {\varOmega })\) be such that u = 0 on ∂Ω. Then \(u\in W_0^{1,p}(\varOmega )\).
Proof
It is easy to prove by regularization that \(W^{1,p}(\varOmega )\cap \mathcal {K}(\varOmega )\subset W_0^{1,p}(\varOmega )\).
Assume that spt u is bounded. Let \(f\in \mathcal {C}^1(\mathbb {R})\) be such that |f(t)|≤|t| on \(\mathbb {R}\),
Define u n = f(n u)∕n. Then \(u_n\in \mathcal {K}(\varOmega )\), and by the preceding proposition, u n ∈ W 1, p(Ω). By Lebesgue’s dominated convergence theorem, u n → u in W 1, p(Ω), so that \(u\in W_0^{1,p}(\varOmega )\).
If spt u is unbounded, we define u n = θ n u where (θ n) is defined in the proof of Theorem 6.1.10. Then spt u n is bounded. By Lebesgue’s dominated convergence theorem, u n → u in W 1, p(Ω), so that \(u\in W^{1,p}_0(\varOmega )\). □
Proposition 6.1.16
Let Ω be an open subset of \(\mathbb {R}^N\) . Then there exist a sequence (U n) of open subsets of Ω and a sequence of functions \(\psi _n\in \mathcal {D}(U_n)\) such that
-
(a)
for every n, U n ⊂⊂ Ω and ψ n ≥ 0;
-
(b)
\(\displaystyle {\sum ^{\infty }_{n=1}}\psi _n=1\) on Ω;
-
(c)
for every ω ⊂⊂ Ω there exists m ω such that for n > m ω we have U n ∩ ω = ϕ.
Proof
Let us define ω −1 = ω 0 = ϕ, and for n ≥ 1,
The theorem of partitions of unity implies the existence of \(\varphi _n\in \mathcal {D}(U_n)\) such that 0 ≤ φ n ≤ 1 and φ n = 1 on K n. It suffices then to define
□
Theorem 6.1.17 (Hajłasz)
Let \(1\!\leq \!p\!<\!\infty \), \(u\in W^{1,p}_{\mathrm {loc}}(\varOmega )\) , and ε > 0. Then there exists \(v\in \mathcal {C}^{\infty }(\varOmega )\) such that
-
(a)
\(v-u\in W_0^{1,p}(\varOmega )\);
-
(b)
\(\vert \vert v-u\vert \vert _{W^{1,p}(\varOmega )}<\varepsilon \).
Proof
Let (U n) and (ψ n) be given by the preceding proposition. For every n ≥ 1, there exists k n such that
and
By Proposition 3.1.6, \(\displaystyle {\sum ^{\infty }_{n=1}}(v_n-\psi _nu)\) converges to w in \(W_0^{1,p}(\varOmega )\). On the other hand, we have on ω ⊂⊂ Ω that
Setting \(v=\displaystyle {\sum ^{\infty }_{n=1}}v_n\), we conclude that
□
Corollary 6.1.18 (Deny–Lions)
Let 1 ≤ p < ∞. Then \(\mathcal {C}^{\infty }(\varOmega )\cap W^{1,p}(\varOmega )\) is dense in W 1, p(Ω).
6.2 Cylindrical Domains
Let U be an open subset of \(\mathbb {R}^{N-1}\) and 0 < r ≤∞. Define
The extension by reflection of a function in W 1, p(Ω +) is a function in W 1, p(Ω).
For every \(u:\varOmega _+\rightarrow \mathbb {R}\), we define on Ω:

Lemma 6.2.1 (Extension by Reflection)
Let 1 ≤ p < ∞ and u ∈ W
1, p(Ω
+). Then ρu ∈ W
1, p(Ω), ∂
k(ρu) = ρ(∂
k
u), 1 ≤ k ≤ N − 1, and  , so that
, so that
Proof
Let \(v\in \mathcal {D}(\varOmega )\). Then by a change of variables,

where

A truncation argument will be used. Let \(\eta \in \mathcal {C}^{\infty }(\mathbb {R})\) be such that
and define η n on Ω + by

The definition of weak derivative ensures that

where

Since w(x′, 0) = 0,  , where
, where

Lebesgue’s dominated convergence theorem implies that

Taking the limit in (∗∗), we obtain

It follows from (∗) that

Since \(v\in \mathcal {D}(\varOmega )\) is arbitrary,  . By a similar but simpler argument, ∂
k(ρu) = ρ(∂
k
u), 1 ≤ k ≤ N − 1. □
. By a similar but simpler argument, ∂
k(ρu) = ρ(∂
k
u), 1 ≤ k ≤ N − 1. □
It makes no sense to define an L p function on a set of measure zero. We will define the trace of a W 1, p function on the boundary of a smooth domain. We first consider the case of \(\mathbb {R}^N_+\).
Notation
We define

Lemma 6.2.2 (Trace Inequality)
Let 1 ≤ p < ∞. Then for every \(u\in \mathcal {D}(\overline {\mathbb {R}^N_+})\),

Proof
The fundamental theorem of calculus implies that for all \(x'\in \mathbb {R}^{N-1}\),

When 1 < p < ∞, using Fubini’s theorem and Hölder’s inequality, we obtain

The case p = 1 is similar. □
Proposition 6.2.3
Let 1 ≤ p < ∞. Then there exists one and only one continuous linear mapping \(\gamma _0:W^{1,p}(\mathbb {R}^N_+)\rightarrow L^p(\mathbb {R}^{N-1})\) such that for every \(u\in \mathcal {D}(\mathbb {R}_+^N)\) , γ 0 u = u(., 0).
Proof
Let \(u\in \mathcal {D}(\overline {\mathbb {R}^N_+})\) and define γ 0 u = u(., 0). The preceding lemma implies that
The space \(\mathcal {D}(\overline {\mathbb {R}^N_+})\) is dense in \(W^{1,p}(\mathbb {R}_+^N)\) by Theorem 6.1.10 and Lemma 6.2.1. By Proposition 3.2.3, γ 0 has a unique continuous linear extension to \(W^{1,p}(\mathbb {R}^N_{+})\). □
Proposition 6.2.4 (Integration by Parts)
Let 1 ≤ p < ∞, \(u\in W^{1,p}(\mathbb {R}_+^N)\) , and \(v\in \mathcal {D}(\overline {\mathbb {R}^N_+})\) . Then

and
Proof
Assume, moreover, that \(u\in \mathcal {D}(\overline {\mathbb {R}_+^N})\). Integrating by parts, we obtain for all \(x'\in \mathbb {R}^{N-1}\),

Fubini’s theorem implies that

Let \(u\in W^{1,p}(\mathbb {R}^N_+)\). Since \(\mathcal {D}(\overline {\mathbb {R}_+^N})\) is dense in \(W^{1,p}(\mathbb {R}^N_+)\), there exists a sequence \((u_n)\subset \mathcal {D}(\overline {\mathbb {R}_+^N})\) such that u n → u in \(W^{1,p}(\mathbb {R}_+^N)\). By the preceding lemma, γ 0 u n → γ 0 u in \(L^p(\mathbb {R}^{N-1})\). It is easy to finish the proof.
The proof of the last formulas is similar. □
Notation
For every \(u:\mathbb {R}^N_+\rightarrow \mathbb {R}\), we define \(\overline {u}\) on \(\mathbb {R}^N\) by

Proposition 6.2.5
Let 1 ≤ p < ∞ and \(u\in W^{1,p}(\mathbb {R}_+^N)\) . The following properties are equivalent:
-
(a)
\(u\in W_0^{1,p}(\mathbb {R}_+^N)\);
-
(b)
γ 0 u = 0;
-
(c)
\(\overline {u}\in W^{1,p}(\mathbb {R}^N)\) and \( \partial _k\overline {u} = \overline {\partial _k u}\), 1 ≤ k ≤ N.
Proof
If \(u\in W^{1,p}_0(\mathbb {R}_+^N)\), there exists \((u_n)\subset \mathcal {D}(\mathbb {R}_+^N)\) such that u n → u in \(W^{1,p}(\mathbb {R}_+^N)\). Hence γ 0 u n = 0 and γ 0 u n → γ 0 u in \(L^p(\mathbb {R}^{N-1})\), so that γ 0 u = 0.
If γ 0 u = 0, it follows from the preceding proposition that for every \(v\in \mathcal {D}(\mathbb {R}^N)\),
We conclude that (c) is satisfied.
Assume that (c) is satisfied. We define \(u_n=\theta _n\overline {u}\), where (θ n) is defined in the proof of Theorem 6.1.10. It is clear that \(u_n\rightarrow \overline {u}\) in \(W^{1,p}(\mathbb {R}^N)\) and spt \(u_n\subset B[0,2n]\cap \overline {\mathbb {R}_+^N}\).
We can assume that spt u n is a compact subset of \(\overline {\mathbb {R}_+^N}\). We define y n = (0, …, 0, 1∕n) and \(v_n=\tau _{y_n}\overline {u}\). Since \(\partial _kv_n =\tau _{y_n} \partial _k\overline {u}\), the lemma of continuity of translations implies that u n → u in \(W^{1,p}(\mathbb {R}^N_+)\).
We can assume that spt u is a compact subset of \(\mathbb {R}^N_+\). For n large enough, \(\rho _n\ast u\in \mathcal {D}(\mathbb {R}_+^N)\). Since ρ n ∗ u → u is in \(W^{1,p}(\mathbb {R}^N)\), we conclude that \(u\in W_0^{1,p}(\mathbb {R}^N)\). □
6.3 Smooth Domains
In this section we consider an open subset Ω = {φ < 0} of \(\mathbb {R}^N\) of class \(\mathcal {C}^1\) with a bounded boundary Γ. We use the notations of Definition 9.4.1.
Let γ ∈ Γ. Since ∇φ(γ) ≠ 0, we can assume that, after a permutation of variables, ∂ N φ(γ) ≠ 0. By Theorem 9.1.1 there exist r > 0, R > 0, and
such that, for |x′− γ′| < R and |t| < r, we have
and the set
is an open neighborhood of γ. Moreover
and
The Borel–Lebesgue theorem implies the existence of a finite covering U 1, …, U k of Γ by open subsets satisfying the above properties. There exists a partition of unity ψ 1, …, ψ k subordinate to this covering.
Theorem 6.3.1 (Extension Theorem)
Let 1 ≤ p < ∞ and let Ω be an open subset of \(\mathbb {R}^N\) of class \(\mathcal {C}^1\) with a bounded boundary or the product of N open intervals. Then there exists a continuous linear mapping
such that Pu| Ω = u.
Proof
Let Ω be an open subset of \(\mathbb {R}^N\) of class \(\mathcal {C}^1\) with a bounded boundary, and let u ∈ W 1, p(Ω). Proposition 6.1.11 and Lemma 6.2.1 imply that

Moreover,
We define \(\displaystyle {\psi _0=1-\sum ^k_{j=1}\psi _j}\),
and for 1 ≤ j ≤ k,
Formula (∗) and Proposition 6.1.12 ensure that for 0 ≤ j ≤ k,
(The support of ∇ψ 0 is compact!) Hence
and for all x ∈ Ω,
If Ω is the product of N open intervals, it suffices to use a finite number of extensions by reflections and a truncation. □
Theorem 6.3.2 (Density Theorem in Sobolev Spaces)
Let 1 ≤ p < ∞ and let Ω be an open subset of \(\mathbb {R}^N\) of class \(\mathcal {C}^1\) with a bounded boundary or the product of N open intervals. Then the space \(\mathcal {D}(\overline {\varOmega })\) is dense in W 1, p(Ω).
Proof
Let u ∈ W 1, p(Ω). Theorem 6.1.10 implies the existence of a sequence \((v_n)\subset \mathcal {D}(\mathbb {R}^N)\) converging to Pu in \(W^{1,p}(\mathbb {R}^N)\). Hence u n = v n|Ω converges to u in W 1, p(Ω). □
Theorem 6.3.3 (Trace Inequality)
Let Ω be an open subset of \(\mathbb {R}^N\) of class \(\mathcal {C}^1\) with a bounded boundary Γ. Then there exist a > 0 and b > 0 such that, for 1 ≤ p < ∞ and for every \(u\in \mathcal {D} (\bar \varOmega )\),
Proof
Let 1 < p < ∞, \(u\in \mathcal {D} (\bar \varOmega )\), and \(\nu \in \mathcal {C}^\infty (\mathbb {R}^N;\mathbb {R}^N)\).
Since
the divergence theorem implies that
Assume that 1 ≤ ν ⋅ n on Γ. Using Hölder’s inequality, we obtain that, for 1 < p < ∞,
where a = ∥divν∥∞ and b = ∥ν∥∞.
When p ↓ 1, it follows from Lebesgue’s dominated convergence theorem that
Let us construct an admissible vector field ν. Let \(U=\{x \in \mathbb {R}^N : \nabla \varphi (x) \neq 0\}\). The theorem of partition of unity implies the existence of \(\psi \in \mathcal {D}(U)\) such that ψ = 1 on Γ. We define the vector field w by
For n large enough, the \(\mathcal {C}^\infty \) vector field ν = 2ρ n ∗ w is such that 1 ≤ ν ⋅ n on Γ. □
Theorem 6.3.4
Under the assumptions of Theorem 6.3.3 , there exists one and only one continuous linear mapping
such that for all \(u\in \mathcal {D} (\bar \varOmega )\) , γ 0 u = u| Γ.
Proof
It suffices to use the trace inequality, Proposition 3.2.3, and the density theorem in Sobolev spaces. □
Theorem 6.3.5 (Divergence Theorem)
Let Ω be an open subset of \(\mathbb {R}^N\) of class \(\mathcal {C}^1\) with a bounded boundary Γ and \(\nu \in W^{1,1} (\varOmega ; \mathbb {R}^N)\) . Then
Proof
When \(\nu \in \mathcal {D} (\bar \varOmega ; \mathbb {R}^N)\), the proof is given in Section 9.4. In the general case, it suffices to use the density theorem in Sobolev spaces and the trace theorem. □
6.4 Embeddings
Let 1 ≤ p, q < ∞. If there exists c > 0 such that for every \(u\in \mathcal {D}(\mathbb {R}^N)\),
then necessarily
Indeed, replacing u(x) by u λ(x) = u(λx), λ > 0, we find that
so that q = p ∗.
We define for 1 ≤ j ≤ N and \(x\in \mathbb {R}^N\),

Lemma 6.4.1 (Gagliardo’s Inequality)
Let N ≥ 2 and  . Then \(f(x)=\displaystyle {\prod ^N_{j=1}}f_j(\widehat {x_j})\in L^1(\mathbb {R}^N)\) and
. Then \(f(x)=\displaystyle {\prod ^N_{j=1}}f_j(\widehat {x_j})\in L^1(\mathbb {R}^N)\) and
Proof
We use induction. When N = 2, the inequality is clear. Assume that the inequality holds for N ≥ 2. Let \(f_1,\ldots ,f_{N+1}\in L^N(\mathbb {R}^N)\) and
It follows from Hölder’s inequality that for almost every \(x_{N+1}\in \mathbb {R}\),
The generalized Hölder inequality implies that
□
Lemma 6.4.2 (Sobolev’s Inequalities)
Let 1 ≤ p < N. Then there exists a constant c = c(p, N) such that for every \(u\in \mathcal {D}(\mathbb {R}^N)\),
Proof
Let \(u\in \mathcal {C}^1(\mathbb {R}^N)\) be such that spt u is compact. It follows from the fundamental theorem of calculus that for 1 ≤ j ≤ N and \(x\in \mathbb {R}^N\),
By the preceding lemma,
Hence we obtain

For p > 1, we define q = (N − 1)p ∗∕N > 1. Let \(u\in \mathcal {D}(\mathbb {R}^N)\). The preceding inequality applied to |u|q and Hölder’s inequality imply that

It is easy to conclude the proof. □
Lemma 6.4.3 (Morrey’s Inequalities)
Let N < p < ∞ and λ = 1 − N∕p. Then there exists a constant c = c(p, N) such that for every \(u\in \mathcal {D}(\mathbb {R}^N)\) and every \(x,y\in \mathbb {R}^N\),
Proof
Let \(u\in \mathcal {D}(\mathbb {R}^N)\), and let us define \(B=B(a,r), a\in \mathbb {R}^N,r>0\), and

We assume that \(0\in \bar B\). It follows from the fundamental theorem of calculus and Fubini’s theorem that

Hölder’s inequality implies that

After a translation, we obtain that, for every x ∈ B[a, r],

Let \(x\in \mathbb {R}^N\). Choosing a = x and r = 1, we find

Let \(x,y \in \mathbb {R}^N\). Choosing a = (x + y)∕2 and r = |x − y|∕2, we obtain
□
Notation
We define
Theorem 6.4.4 (Sobolev’s Embedding Theorem, 1936–1938)
Let Ω be an open subset of \(\mathbb {R}^N\) of class \(\mathcal {C}^1\) with a bounded boundary or the product of N open intervals.
-
(a)
If 1 ≤ p < N and if p ≤ q ≤ p ∗ , then W 1, p(Ω) ⊂ L q(Ω), and the canonical injection is continuous.
-
(b)
If N < p < ∞ and λ = 1 − N∕p, then \(W^{1,p}(\varOmega )\subset \mathcal {C}_0(\overline {\varOmega })\) , the canonical injection is continuous, and there exists c = c(p, Ω) such that for every u ∈ W 1, p(Ω) and all x, y ∈ Ω,
$$\displaystyle \begin{aligned} \big|u(x)-u(y)\big|\leq c\vert\vert u\vert\vert_{W^{1,p}(\varOmega)}|x-y|{}^{\lambda}. \end{aligned}$$
Proof
Let 1 ≤ p < N and \(u\in W^{1,p}(\mathbb {R}^N)\). By Theorem 6.1.10, there exists a sequence \((u_n)\subset \mathcal {D}(\mathbb {R}^N)\) such that u n → u in \(W^{1,p}(\mathbb {R}^N)\).
We can assume that u n → u almost everywhere on \(\mathbb {R}^N\). It follows from Fatou’s lemma and Sobolev’s inequality that
Let P be the extension operator corresponding to Ω and v ∈ W 1, p(Ω). We have
If p ≤ q ≤ p ∗, we define 0 ≤ λ ≤ 1 by
and we infer from the interpolation inequality that
The case p > N follows from Morrey’s inequalities. □
Lemma 6.4.5
Let Ω be an open subset of \(\mathbb {R}^N\) such that m(Ω) < +∞, and let 1 ≤ p ≤ r < +∞. Assume that X is a closed subspace of W 1, p(Ω) such that X ⊂ L r(Ω). Then, for every 1 ≤ q < r, X ⊂ L q(Ω) and the canonical injection is compact.
Proof
The closed graph theorem implies the existence of c > 0 such that, for every u ∈ X,
Our goal is to prove that
is precompact in L q(Ω) for 1 ≤ q < r. Let 1∕q = 1 − λ + λ∕r. By the interpolation inequality, for every u ∈ S,
Hence it suffices to prove that S is precompact in L 1(Ω).
Let us verify that S satisfies the assumptions of M. Riesz’s theorem in L 1(Ω):
-
(a)
It follows from Hölder’s inequality that, for every u ∈ S,
$$\displaystyle \begin{aligned} \|u\|{}_{L^1 (\varOmega)} \leq {\|u\|}_{L^r (\varOmega)} m(\varOmega)^{1-1/r} \leq cm (\varOmega)^{1-1/r}. \end{aligned}$$ -
(b)
Similarly, we have that, for every u ∈ S,
$$\displaystyle \begin{aligned} \int_{\varOmega\backslash \omega_k} |u| dx \leq \|u\|{}_{L^r (\varOmega)} m (\varOmega\backslash \omega_k)^{1-1/r} \leq cm (\varOmega\backslash \omega_k)^{1-1/r} \end{aligned}$$where
$$\displaystyle \begin{aligned} \omega_k = \{x\in \varOmega\colon d (x, \partial\varOmega) > 1/k\}. \end{aligned}$$Lebesgue’s dominated convergence theorem implies that
$$\displaystyle \begin{aligned} \lim_{k\to \infty} m(\varOmega\backslash \omega_k) = 0. \end{aligned}$$ -
(c)
Let ω ⊂⊂ Ω. Assume that |y| < d(ω, ∂Ω) and \(u \in \mathcal {C}^\infty (\varOmega ) \cap W^{1,p}(\varOmega )\).
Since, by the fundamental theorem of calculus,
we obtain
Using Corollary 6.1.18, we conclude by density that, for every u ∈ S,
□
Theorem 6.4.6 (Rellich–Kondrachov Embedding Theorem)
Let Ω be a bounded open subset of \(\mathbb {R}^N\) of class \(\mathcal {C}^1\) or the product of N bounded open intervals:
-
(a)
If 1 ≤ p < N and 1 ≤ q < p ∗ , then W 1, p(Ω) ⊂ L q(Ω), and the canonical injection is compact.
-
(b)
If N < p < ∞, then \(W^{1,p} \subset \mathcal {C}_0 (\bar \varOmega )\) , and the canonical injection is compact.
Proof
Let 1 ≤ p < N, 1 ≤ q < p ∗. It suffices to use Sobolev’s embedding theorem and the preceding lemma.
The case p > N follows from Ascoli’s theorem and Sobolev’s embedding theorem. □
We prove three fundamental inequalities.
Theorem 6.4.7 (Poincaré’s Inequality in \(W^{1,p}_{0}\))
Let 1 ≤ p < ∞, and let Ω be an open subset of \(\mathbb {R}^N\) such that \(\varOmega \subset \mathbb {R}^{N-1}\times ]0,a[\) . Then for every \(u\in W_0^{1,p}(\varOmega )\),
Proof
Let \(1\!<\!p\!<\!\infty \) and \(v\in \mathcal {D}(]0,a[)\). The fundamental theorem of calculus and Hölder’s inequality imply that for 0 < x < a,
Hence we obtain
If \(u\in \mathcal {D}(\varOmega )\), we infer from the preceding inequality and from Fubini’s theorem that

It is easy to conclude by density. The case p = 1 is similar. □
Definition 6.4.8
A metric space is connected if the only open and closed subsets of X are ϕ and X.
Theorem 6.4.9 (Poincaré’s Inequality in W 1, p)
Let 1 ≤ p < ∞, and let Ω be a bounded open connected subset of \(\mathbb {R}^N\) . Assume that Ω is of class \(\mathcal {C}^1\) . Then there exists c = c(p, Ω), such that, for every u ∈ W 1, p(Ω),

where

Assume that Ω is convex. Then, for every u ∈ W 1, p(Ω),

where d =supx,y ∈ Ω|x − y|.
Proof
Assume that Ω is of class \(\mathcal {C}^1\). It suffices to prove that

Let (u n) ⊂ W 1, p(Ω) be a minimizing sequence :

By the Rellich–Kondrachov theorem, we can assume that u
n → u in L
p(Ω). Hence ∥u∥p = 1 and  . If λ = 0, then, by the closing lemma, ∇u = 0. Since Ω is connected,
. If λ = 0, then, by the closing lemma, ∇u = 0. Since Ω is connected,  . This is a contradiction.
. This is a contradiction.
Assume now that Ω is convex and that \(u\in \mathcal {C}^\infty (\varOmega ) \bigcap W^{1,p} (\varOmega )\). Hölder’s inequality implies that

It follows from the fundamental theorem of calculus and Hölder’s inequality that
We obtain that

We conclude by density, using Corollary 6.1.18. □
Theorem 6.4.10 (Hardy’s Inequality)
Let 1 < p < N. Then for every \(u\in W^{1,p}(\mathbb {R}^N)\), \(u/|x|\in L^p(\mathbb {R}^N)\) and
Proof
Let \(u\in \mathcal {D}(\mathbb {R}^N)\) and \(v\in \mathcal {D}(\mathbb {R}^N;\mathbb {R}^N)\). We infer from Lemma 6.1.1 that
Approximating v(x) = x∕|x|p by v ε(x) = x∕(|x|2 + ε)p∕2, we obtain
Hölder’s inequality implies that
We have thus proved Hardy’s inequality in \(\mathcal {D}(\mathbb {R}^N)\). Let \(u\in W^{1,p}(\mathbb {R}^N)\). Theorem 6.1.10 ensures the existence of a sequence \((u_n)\subset \mathcal {D}(\mathbb {R}^N)\) such that u n → u in \(W^{1,p}(\mathbb {R}^N)\). We can assume that u n → u almost everywhere on \(\mathbb {R}^N\). We conclude using Fatou’s lemma that
□
Fractional Sobolev spaces are interpolation spaces between L p(Ω) and W 1, p(Ω).
Definition 6.4.11
Let 1 ≤ p < ∞, 0 < s < 1, and u ∈ L p(Ω). We define
On the fractional Sobolev space
we define the norm
We give, without proof, the characterization of traces due to Gagliardo [26].
Theorem 6.4.12
Let 1 < p < ∞.
-
(a)
For every \(u\in W^{1,p}(\mathbb {R}^N)\), \(\gamma _0u\in W^{1-1/p,p}(\mathbb {R}^{N-1})\).
-
(b)
The mapping \(\gamma _0:W^{1,p}(\mathbb {R}^N)\rightarrow W^{1-1/p,p}(\mathbb {R}^{N-1})\) is continuous and surjective.
-
(c)
The mapping \(\gamma _0:W^{1,1}(\mathbb {R}^N)\rightarrow L^1(\mathbb {R}^{N-1})\) is continuous and surjective.
6.5 Comments
The main references on Sobolev spaces are the books:
-
R. Adams and J. Fournier, Sobolev spaces [1]
-
H. Brezis, Analyse fonctionnelle, théorie et applications [8]
-
V. Maz’ya, Sobolev spaces with applications to elliptic partial differential equations [51]
Our proof of the trace inequality follows closely:
-
A.C. Ponce, Elliptic PDEs, measures, and capacities, European Mathematical Society, 2016
The theory of partial differential equations was at the origin of Sobolev spaces. We recommend [9] on the history of partial differential equations and [55] on the prehistory of Sobolev spaces.
Because of Poincaré’s inequalities, for every smooth, bounded open connected set Ω, we have that
Hence the first eigenvalue λ 1(Ω) of Dirichlet’s problem
and the second eigenvalue μ 2(Ω) of the Neumann problem
are strictly positive. Let us denote by B an open ball such that m(B) = m(Ω). Then
Moreover, if Ω is convex with diameter d, then
We prove in Theorem 6.4.9 the weaker estimate
There exists a bounded, connected open set \(\varOmega \subset \mathbb {R}^2\) such that μ 2(Ω) = 0. Consider on two sides of a square Q, two infinite sequences of small squares connected to Q by very thin pipes.
6.6 Exercises for Chap. 6
-
1.
Let \(\varOmega =B(0,1)\subset \mathbb {R}^N\). Then for λ ≠ 0,
$$\displaystyle \begin{aligned} \begin{array}{rl} (\lambda -1)p+N>0&\Longleftrightarrow\vert x\vert^{\lambda}\in W^{1,p}(\varOmega),\\ \\ \lambda p+N<0&\Longleftrightarrow\vert x\vert^{\lambda}\in W^{1,p}(\mathbb{R}^N\setminus\overline{\varOmega}),\\ \\ p<N&\Longleftrightarrow\displaystyle{\frac{x}{\vert x\vert}}\in W^{1,p}(\varOmega;\mathbb{R}^N). \end{array} \end{aligned}$$ -
2.
Let 1 < p < ∞ and u ∈ L p(Ω). The following properties are equivalent:
-
(a)
u ∈ W 1, p(Ω);
-
(b)
\(\sup \displaystyle {\left \{\int _{\varOmega } u~\mathrm {div}~v~dx:v\in \mathcal {D}(\varOmega ,\mathbb {R}^N),\vert \vert v\vert \vert _{L^{p'}(\varOmega )} =1\right \}}<\infty \);
-
(c)
there exists c > 0 such that for every ω ⊂⊂ Ω and for every \(y\in \mathbb {R}^N\) such that |y| < d(ω, ∂Ω),
$$\displaystyle \begin{aligned} \vert\vert\tau_y u-u\vert\vert_{L^p(\omega)}\leq c\vert y\vert . \end{aligned}$$
-
(a)
-
3.
Let 1 ≤ p < N and let Ω be an open subset of \(\mathbb {R}^N\). Define

Then \(S(\varOmega )=S(\mathbb {R}^N)\).
-
4.
Let 1 ≤ p < N. Then
$$\displaystyle \begin{aligned} \frac{1}{2^N}S(\mathbb{R}^N)=\inf\left\{ \vert\vert \nabla u\vert\vert_{L^p(\mathbb{R}^N_+)}/\vert\vert u\vert\vert_{L^{p^*}(\mathbb{R}^N_+)}:u\in H^1(\mathbb{R}^N_+)\setminus\{0\}\right\}. \end{aligned}$$ -
5.
Poincaré–Sobolev inequality.
-
(a)
Let 1 < p < N, and let Ω be an open bounded connected subset of \(\mathbb {R}^N\) of class \(\mathcal {C}^1\). Then there exists c > 0 such that for every u ∈ W 1, p(Ω),
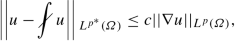
where
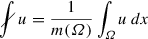 . Hint: Apply Theorem 6.4.4 to
. Hint: Apply Theorem 6.4.4 to  .
. -
(b)
Let A = {u = 0} and assume that m(A) > 0. Then
$$\displaystyle \begin{aligned} \|u\|{}_{L^{p^*}(\varOmega)} \leq c \left(1+\Big[\frac{m(\varOmega)}{m(A)}\Big]^{1/p^*}\right) \|\nabla u\|{}_{L^p(\varOmega)}. \end{aligned}$$Hint:
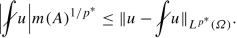
-
(a)
-
6.
Nash’s inequality. Let N ≥ 3. Then for every \(u\in \mathcal {D}(\mathbb {R}^N)\),
$$\displaystyle \begin{aligned} \vert\vert u\vert\vert_2^{2+4/N}\leq c\vert\vert u\vert\vert_1^{4/N}\vert\vert\nabla u\vert\vert_2^2. \end{aligned}$$Hint: Use the interpolation inequality.
-
7.
Let 1 ≤ p < N and q = p(N − 1)∕(N − p). Then for every \(u\in \mathcal {D}(\overline {\mathbb {R}^N_+})\),

-
8.
Verify that Hardy’s inequality is optimal using the family
$$\displaystyle \begin{aligned} \begin{array}{llll} u_{\varepsilon}(x)&=1,& &|x|\leq 1,\\ &=|x|{}^{\frac{p-N}{p}-\varepsilon},& &|x|>1. \end{array} \end{aligned}$$ -
9.
Let 1 ≤ p < N. Then \(\mathcal {D}(\mathbb {R}^N\setminus \{0\})\) is dense in \(W^{ 1,p}(\mathbb {R}^N)\).
-
10.
Let 2 ≤ N < p < ∞. Then for every \(u\in W^{1,p}_{0}(\mathbb {R}^N\setminus \{0\})\), \(u/|x|\in L^p(\mathbb {R}^N)\) and
$$\displaystyle \begin{aligned} \vert\vert u/|x|\vert\vert_{L^p(\mathbb{R}^N)}\leq\frac{p}{p-N}\vert\vert\nabla u\vert\vert_{L^p(\mathbb{R}^N)}. \end{aligned}$$ -
11.
Let 1 ≤ p < ∞. Verify that the embedding \(W^{1,p}(\mathbb {R}^N) \subset L^p(\mathbb {R}^N)\) is not compact. Let 1 ≤ p < N. Verify that the embedding \(W^{1,p}_0(B(0,1))\!\subset \!L^{p^*}(B(0,1))\) is not compact.
-
12.
Let us denote by \(\mathcal {D}_r(\mathbb {R}^N)\) the space of radial functions in \(\mathcal {D}(\mathbb {R}^N)\). Let N ≥ 2 and 1 ≤ p < ∞. Then there exists c(N, p) > 0 such that for every \(u\in \mathcal {D}_r(\mathbb {R}^N)\),
$$\displaystyle \begin{aligned} \big|u(x)\big|\leq c(N,p)\vert\vert u\vert\vert_p^{1/p'}\vert\vert\nabla u\vert\vert_p^{1/p}|x|{}^{(1-N)/p}. \end{aligned}$$Let 1 ≤ p < N. Then there exists d(N, p) > 0 such that for every \(u\in \mathcal {D}_r(\mathbb {R}^N)\),
$$\displaystyle \begin{aligned} \big|u(x)\big|\leq d(N,p)\vert\vert\nabla u\vert\vert_p|x|{}^{(p-N)/p}. \end{aligned}$$Hint: Let us write u(x) = u(r), r = |x|, so that
$$\displaystyle \begin{aligned} \begin{array}{rl} r^{N-1}\big|u(r)\big|{}^p&\leq p\displaystyle{\int^{\infty}_r \big|u(s)\big|{}^{p-1}\big|\frac{du}{dr}(s)\big|s^{N-1}}ds,\\ \\ \big|u(r)\big|&\leq \displaystyle{\int^{\infty}_r\Big|\frac{du}{dr}(s)\Big| }ds. \end{array} \end{aligned}$$ -
13.
Let us denote by \(W^{1,p}_r(\mathbb {R}^N)\) the space of radial functions in \(W^{1,p}(\mathbb {R}^N)\). Verify that the space \(\mathcal {D}_r(\mathbb {R}^N)\) is dense in \(W_r^{1,p}(\mathbb {R}^N)\).
-
14.
Let 1 ≤ p < N and p < q < p ∗. Verify that the embedding \(W_r^{1,p}(\mathbb {R}^N)\subset L^q(\mathbb {R}^N)\) is compact. Verify also that the embedding \(W^{1,p}_r(\mathbb {R}^N)\subset L^p(\mathbb {R}^N)\) is not compact.
-
15.
Let 1 ≤ p < ∞ and let Ω be an open subset of \(\mathbb {R}^N\). Prove that the map
$$\displaystyle \begin{aligned} W^{1,p}(\varOmega)\rightarrow W^{1,p}(\varOmega):u\mapsto u^+ \end{aligned}$$is continuous. Hint: ∇u + = H(u)∇u, where
$$\displaystyle \begin{aligned} \begin{array}{lll} H(t)&=1,&\quad t>0,\\ &=0,&\quad t\leq 0. \end{array} \end{aligned}$$ -
16.
Sobolev implies Poincaré. Let Ω be an open subset of \(\mathbb {R}^N\) (N ≥ 2) such that m(Ω) < +∞, and let 1 ≤ p < +∞. Then there exists c = c(p, N) such that, for every \(u\in W^{1,p}_0 (\varOmega )\),
$$\displaystyle \begin{aligned} \|u\|{}_p \leq c \ m (\varOmega)^{1/N} \|\nabla u\|{}_p. \end{aligned}$$Hint. (a) If 1 ≤ p < N, then
$$\displaystyle \begin{aligned} \|u\|{}_p \leq m (\varOmega)^{1/N} \| u\|{}_{p^\ast} \leq c \ m(\varOmega)^{1/N} \|\nabla u\|{}_p. \end{aligned}$$(b) If p ≥ N, then
$$\displaystyle \begin{aligned} \| u\|{}_{p} = \| u\|{}_{q^\ast} \leq c \| \nabla u \|{}_{q} \leq c\ m(\varOmega)^{1/N} \| \nabla u \|{}_{p}. \end{aligned}$$ -
17.
Let Ω be an open bounded convex subset of \(\mathbb {R}^N, N\geq 2\), and \(u\in \mathcal {C}^1 (\varOmega ) \bigcap W^{1,1} (\varOmega )\). Then, for every x ∈ Ω,

where
 and d =supx,y ∈ Ω |y − x|.
and d =supx,y ∈ Ω |y − x|.Hint. Define
$$\displaystyle \begin{aligned} v(y) &= |\nabla u (y)|&, y \in \varOmega, \qquad \\ &=0 & ,y\in \mathbb{R}^N\backslash \varOmega. \end{aligned}$$-
(a)
\(u(x)-u(y) = \displaystyle \int _0^{|y-x|} \nabla u (x+r\sigma ) \cdot \sigma dr, \ \sigma = {y-x \over |y-x|}\).
-
(b)

-
(a)
-
18.
Let us define, for every bounded connected open subset Ω of \(\mathbb {R}^N\), and for 1 ≤ p < ∞,

For every 1 ≤ p < ∞, there exists a bounded connected open subset Ω of \(\mathbb {R}^2\) such that λ(p, Ω) = 0.
Hint. Consider on two sides of a square Q two infinite sequences of small squares connected to Q by very thin pipes.
-
19.
Prove that, for every 1 ≤ p < ∞,
$$\displaystyle \begin{aligned} \inf \Big\{\lambda (p,\varOmega)\colon \varOmega \ \ \mbox{is a smooth bounded connected open subset of} \ \ \mathbb{R}^2, m(\varOmega)=1\Big \}=0.\end{aligned} $$Hint. Consider a sequence of pairs of disks smoothly connected by very thin pipes.
-
20.
Generalized Poincaré’s inequality. Let 1 ≤ p < ∞, let Ω be a smooth bounded connected open subset of \(\mathbb {R}^N\), and let f ∈ [W 1, p(Ω)]∗ be such that
$$\displaystyle \begin{aligned} <f,1>=1.\end{aligned} $$Then there exists c > 0 such that, for every u ∈ W 1, p(Ω),
$$\displaystyle \begin{aligned} \|u-<f,u>\|{}_p \leq c \|\nabla u\|{}_p. \end{aligned}$$
References
Adams, R., Fournier, J.: Sobolev Spaces, 2nd edn. Elsevier, Oxford (2003)
Brezis, H.: Analyse fonctionnelle, théorie et applications. Masson, Paris (1983)
Brezis, H., Browder, F.: Partial differential equations in the 20th century. Adv. Math. 135, 76–144 (1998)
Gagliardo, E.: Caratterizzazioni delle tracce sulla frontiera relative ad alcune classi di funzioni in n variabili. Rend. Sem. Mat. Univ. Padova 27, 284–305 (1957)
Maz’ya, V.: Sobolev Spaces with Applications to Elliptic Partial Differential Equations. Springer, Berlin (2011)
Naumann, J.: Remarks on the Prehistory of Sobolev Spaces, prépublication (2002)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2022 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Willem, M. (2022). Sobolev Spaces. In: Functional Analysis. Cornerstones. Birkhäuser, Cham. https://doi.org/10.1007/978-3-031-09149-0_6
Download citation
DOI: https://doi.org/10.1007/978-3-031-09149-0_6
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-031-09148-3
Online ISBN: 978-3-031-09149-0
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)



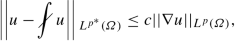
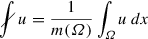 . Hint: Apply Theorem
. Hint: Apply Theorem  .
.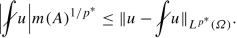


 and d =supx,y ∈ Ω |y − x|.
and d =supx,y ∈ Ω |y − x|.
