Controlling the BMO Semi-Norm of the Unit Normal

Abstract

Earlier we have estimated a certain brand of singular integral operators in terms of the geometry of the underlying “surface” in terms of the BMO semi-norm of the unit normal to the surface; hence, the flatter said surface, the smaller the norm of the singular integral operators. Here we proceed in the opposite direction, and control geometry through analysis. We quantify flatness of a given “surface” by estimating the BMO semi-norm of its unit normal via analytic entities, such as the operator norms of the harmonic double layer and commutators of Riesz transforms with pointwise multiplication by the unit normal, or various natural algebraic combinations of Riesz transforms. In this endeavor, the catalyst is the language of Clifford algebras allowing us to glue together singular integral operators of the sort described above into a single, Cauchy-like, singular integral which exhibits excellent non-degeneracy properties. We therefore begin with a brief tutorial about Clifford algebras, which are a highly non-commutative higher-dimensional version of the field of complex numbers, where some of the magic cancellations and algebraic miracles typically associated with the complex plane still occur. In this chapter we also characterize Muckenhoupt weights in terms of the boundedness Riesz transforms.

In the previous chapter we have succeeded in estimating the size of a certain brand of singular integrals operators (which includes the harmonic double layer operator; cf. Theorem 4.7) in terms of the geometry of the underlying “surface.” A key characteristic of these estimates (originating with Theorem 4.2) is the presence of the BMO semi-norm of the unit normal to the surface as a factor in the right side. In particular, the flatter said surface, the smaller the norm of the singular integral operators in question. Similar results are also valid for a specific type of commutators, of the sort described in Theorem 4.3.

By way of contrast, the principal goal in this chapter is to proceed in the opposite direction, and control geometry in terms of analysis. More specifically, we seek to quantify flatness of a given “surface” (by estimating the BMO semi-norm of its unit normal) in terms of analytic entities, such as the operator norms of the harmonic double layer and the commutators of Riesz transforms with the operator of pointwise multiplication by the (scalar components of the) unit normals, or various natural algebraic combinations of Riesz transforms (where all singular integral operators just mentioned are intrinsically defined on the given “surface”).

In this endeavor, the catalyst is the language of Clifford algebras which allows us to glue together singular integral operators of the sort described above into a single, Cauchy-like, singular integral which exhibits excellent non-degeneracy properties (i.e., up to normalization, such a Cauchy-Clifford operator is its own inverse; cf. (5.20)). We therefore begin with a brief tutorial about Clifford algebras, which are a highly non-commutative higher-dimensional version of the field of complex numbers, where some of the magic cancellations and algebraic miracles typically associated with the complex plane still occur. This chapter ends with Sect. 5.4 which contains results characterizing Muckenhoupt weights in terms of the boundedness Riesz transforms. The Clifford algebra formalism turns out to be useful in this regard, both as tool and as a mean to bring into play other types of operators, like the Cauchy–Clifford singular integral operator alluded to above.

5.1 Clifford Algebras and Cauchy–Clifford Operators

The Clifford algebra with n imaginary units is the minimal enlargement of ${\mathbb {R}}^n$ to a unitary real algebra $(\mathcal {C}\ell _n,+,\odot )$, which is not generated as an algebra by any proper subspace of ${\mathbb {R}}^n$ and such that

$$\displaystyle \begin{aligned} x\odot x=-|x|{}^2\,\,\text{ for every }\,\,x\in{\mathbb{R}}^n\hookrightarrow{\mathcal{C}}\ell_n. \end{aligned} $$

(5.1)

In particular, with {e_j}_1≤j≤n denoting the standard orthonormal basis in ${\mathbb {R}}^n$, we have

$$\displaystyle \begin{aligned} \begin{array}{c} {\mathbf{e}}_j\odot{\mathbf{e}}_j=-1\,\,\text{ for all }\,\,j\in\{1,\dots,n\}\,\,\text{ and} \\ {} {\mathbf{e}}_j\odot{\mathbf{e}}_k=-{\mathbf{e}}_k\odot{\mathbf{e}}_j \,\,\text{ for each distinct }\,\,j,k\in\{1,\dots,n\}. \end{array} \end{aligned} $$

(5.2)

This allows us to define an embedding ${\mathbb {R}}^n\hookrightarrow {\mathcal {C}}\ell _n$ by identifying

$$\displaystyle \begin{aligned} {\mathbb{R}}^n\ni x=(x_1,\dots,x_n)\equiv\sum_{j=1}^n x_j{\mathbf{e}}_j\in{\mathcal{C}}\ell_n. \end{aligned} $$

(5.3)

In particular, {e_j}_1≤j≤n become n imaginary units in ${\mathcal {C}}\ell _n$, and (5.2) implies

$$\displaystyle \begin{aligned} a\odot b+b\odot a=-2\langle a,b\rangle\,\,\text{ for all }\,\,a,b\in{\mathbb{R}}^n\hookrightarrow{\mathcal{C}}\ell_n. \end{aligned} $$

(5.4)

Moving on, any element $u\in {\mathcal {C}}\ell _n$ has a unique representation of the form

$$\displaystyle \begin{aligned} u=\sum_{\ell=0}^n\sideset{}{'}\sum_{|I|=\ell}u_I{\mathbf{e}}_I,\quad u_I\in{\mathbb{R}}, \end{aligned} $$

(5.5)

where $\sum '$ indicates that the sum is performed only over strictly increasing multi-indices I, i.e., I = (i₁, i₂, …, i_ℓ) with 1 ≤ i₁ < i₂ < ⋯ < i_ℓ ≤ n, and e_I denotes the Clifford algebra product ${\mathbf {e}}_I:={\mathbf {e}}_{i_1}\odot {\mathbf {e}}_{i_2}\odot \cdots \odot {\mathbf {e}}_{i_\ell }$. Write ${\mathbf {e}}_0:={\mathbf {e}}_{\varnothing }:=1$ for the multiplicative unit in ${\mathcal {C}}\ell _n$. For each $u\in {\mathcal {C}}\ell _n$ represented as in (5.5) define the vector part of u as

$$\displaystyle \begin{aligned} u_{\mathrm{vect}}:=\sum_{j=1}^n u_j{\mathbf{e}}_j\in{\mathbb{R}}^n, \end{aligned} $$

(5.6)

and denote by

$$\displaystyle \begin{aligned} u_{\mathrm{scal}}:=u_\varnothing{\mathbf{e}}_\varnothing=u_\varnothing\in{\mathbb{R}}, \,\text{ the scalar part of }\,\,u. \end{aligned} $$

(5.7)

We endow ${\mathcal {C}}\ell _n$ with the natural Euclidean metric, hence

$$\displaystyle \begin{aligned} |u|:=\left(\sum_{\ell=0}^n\sideset{}{'}\sum_{|I|=\ell}|u_I|{}^2\right)^{1/2} \,\,\text{ for each }\,\,u=\sum_{\ell=0}^n\sideset{}{'}\sum_{|I|=\ell}u_I{\mathbf{e}}_I\in{\mathcal{C}}\ell_n. \end{aligned} $$

(5.8)

Next, define the conjugate of each e_I as the unique element $\overline {{\mathbf {e}}_I}\in {\mathcal {C}}\ell _n$ such that ${\mathbf {e}}_I\odot \overline {{\mathbf {e}}_I}=\overline {{\mathbf {e}}_I}\odot {\mathbf {e}}_I=1$. Thus, if I = (i₁, …, i_ℓ) with 1 ≤ i₁ < i₂ < ⋯ < i_ℓ ≤ n, then the conjugate of e_I is given by $\overline {{\mathbf {e}}_I}=(-1)^{\ell }{\mathbf {e}}_{i_\ell }\odot \cdots \odot {\mathbf {e}}_2\odot {\mathbf {e}}_1$. More generally, for an arbitrary element $u\in {\mathcal {C}}\ell _n$ represented as in (5.5) we define

$$\displaystyle \begin{aligned} \overline{u}:=\sum_{\ell=0}^n\sideset{}{'}\sum_{|I|=\ell}u_I\overline{{\mathbf{e}}_I}. \end{aligned} $$

(5.9)

Note that $\overline {x}=-x$ for every $x\in {\mathbb {R}}^n\hookrightarrow {\mathcal {C}}\ell _n$, and $|u|=|\overline {u}|$ for every $u\in {\mathcal {C}}\ell _n$. One may also check that for any $u,v\in {\mathcal {C}}\ell _n$ we have

$$\displaystyle \begin{aligned} |u\odot v|\leq 2^{n/2}|u||v|,\qquad \overline{u\odot v}=\overline{v}\odot\overline{u}, \end{aligned} $$

(5.10)

and, in fact,

$$\displaystyle \begin{aligned} \begin{array}{c} |u\odot v|=|u||v|\,\,\text{ if either} \\ {} u\in{\mathbb{R}}^n\hookrightarrow{\mathcal{C}}\ell_n\,\,\text{ or }\,\, v\in{\mathbb{R}}^n\hookrightarrow{\mathcal{C}}\ell_n. \end{array} \end{aligned} $$

(5.11)

For further details on Clifford algebras, the reader is referred to [101].

Consider an arbitrary UR domain $\Omega \subseteq {\mathbb {R}}^n$. Abbreviate $\sigma :={\mathcal {H}}^{n-1}\lfloor \partial \Omega$ and denote by ν = (ν₁, …, ν_n) its geometric measure theoretic outward unit normal. For the goals we have in mind, it is natural to identify ν with the Clifford algebra-valued function ν = ν₁e₁ + ⋯ + ν_ne_n. Bearing this identification in mind, we then proceed to define the action of the boundary-to-boundary Cauchy–Clifford operator of any given $\mathcal {C}\ell _n$-valued function $f\in L^1\big (\partial \Omega ,\frac {\sigma (x)}{1+|x|{ }^{n-1}}\big )\otimes {\mathcal {C}}\ell _n$ as

(5.12)

for σ-a.e. point x ∈ ∂ Ω. In particular, with Riesz transforms {R_j}_1≤j≤n on ∂ Ω defined as in (4.297), for each function $f\in L^1\big (\partial \Omega ,\frac {\sigma (x)}{1+|x|{ }^{n-1}}\big )\otimes {\mathcal {C}}\ell _n$ we have

$$\displaystyle \begin{aligned} {\mathbf{C}}f=\frac{1}{2}\sum_{1\leq j,k\leq n}{\mathbf{e}}_j\odot{\mathbf{e}}_k\odot R_j(\nu_kf) \,\,\text{ at}\ \sigma\text{-a.e. point on }\,\,\partial\Omega. \end{aligned} $$

(5.13)

Another closely related integral operator which is of interest to us acts on each given function $f\in L^1\big (\partial \Omega ,\frac {\sigma (x)}{1+|x|{ }^{n-1}}\big )\otimes {\mathcal {C}}\ell _n$ according to

(5.14)

for σ-a.e. x ∈ ∂ Ω. Analogously to (5.13), for each $f\in L^1\big (\partial \Omega ,\frac {\sigma (x)}{1+|x|{ }^{n-1}}\big )\otimes {\mathcal {C}}\ell _n$ we have

$$\displaystyle \begin{aligned} {\mathbf{C}}^{\#}f=-\frac{1}{2}\sum_{1\leq j,k\leq n}{\mathbf{e}}_k\odot{\mathbf{e}}_j\odot\nu_kR_jf \,\,\text{ at}\ \sigma\text{-a.e. point on }\,\,\partial\Omega. \end{aligned} $$

(5.15)

As is apparent from (5.13), (5.15), both C and C^# are amenable to Proposition 3.4. Hence, whenever p ∈ (1, ∞) and w ∈ A_p(∂ Ω, σ),

$$\displaystyle \begin{aligned} {\mathbf{C}}:L^p(\partial\Omega,w)\otimes{\mathcal{C}}\ell_n\longrightarrow L^p(\partial\Omega,w)\otimes{\mathcal{C}}\ell_n \end{aligned} $$

(5.16)

and

$$\displaystyle \begin{aligned} {\mathbf{C}}^{\#}:L^p(\partial\Omega,w)\otimes{\mathcal{C}}\ell_n\longrightarrow L^p(\partial\Omega,w)\otimes{\mathcal{C}}\ell_n \end{aligned} $$

(5.17)

are well-defined, linear, and bounded operators, with

$$\displaystyle \begin{aligned} \begin{array}{c} \|{\mathbf{C}}\|{}_{L^p(\partial\Omega,w)\otimes{\mathcal{C}}\ell_n\to L^p(\partial\Omega,w)\otimes{\mathcal{C}}\ell_n},\,\, \|{\mathbf{C}}^{\#}\|{}_{L^p(\partial\Omega,w)\otimes{\mathcal{C}}\ell_n\to L^p(\partial\Omega,w)\otimes{\mathcal{C}}\ell_n} \\ {} \text{controlled in terms of}\ n, p, [w]_{A_p},\ \text{and the UR constants of}\ \partial\partial\Omega. \end{array} \end{aligned} $$

(5.18)

In fact (see [61, Sections 4.6-4.7] and [114, §1.6]),

(5.19)

For this reason, it is natural to refer to C^# as the “transpose” Cauchy–Clifford operator. Moreover, with I denoting the identity operator, we have

$$\displaystyle \begin{aligned} {\mathbf{C}}^2=\tfrac{1}{4}I\,\,\text{ and }\,\,\big({\mathbf{C}}^{\#}\big)^2=\tfrac{1}{4}I, \end{aligned} $$

(5.20)

on $L^p(\partial \Omega ,\sigma )\otimes {\mathcal {C}}\ell _n$ with p ∈ (1, ∞) (cf. [61, Sections 4.6-4.7]). In view of (5.16)–(5.18), a standard density argument then shows that these formulas remain valid on $L^p(\partial \Omega ,w)\otimes {\mathcal {C}}\ell _n$ whenever p ∈ (1, ∞) and w ∈ A_p(∂ Ω, σ).

Here we are interested in the difference C −C^# which, up to multiplication by 2⁻¹, may be thought of as the antisymmetric part of the Cauchy–Clifford operator C. The following lemma elaborates on the relationship between the antisymmetric part of the Cauchy–Clifford operator, i.e., C −C^#, and the harmonic boundary double layer potential (cf. (3.29)) together with commutators between Riesz transforms (cf. (4.297)) and operators of pointwise multiplication by scalar components of the unit vector. For a proof see [61, Lemma 4.45].

Lemma 5.1

Let $\Omega \subseteq {\mathbb {R}}^n$ be a UR domain. Abbreviate $\sigma :={\mathcal {H}}^{n-1}\lfloor \partial \Omega$ and denote by ν = (ν₁, …, ν_n) the geometric measure theoretic outward unit normal to Ω. For each index j ∈{1, …, n}, denote by $M_{\nu _j}$ the operator of pointwise multiplication by ν_j. Also, recall the boundary-to-boundary harmonic double layer potential operator K_Δ from (3.29) and the family of Riesz transforms {R_j}_1≤j≤n from (4.297). Then

$$\displaystyle \begin{aligned} (\mathbf{C}-{\mathbf{C}}^{\#})f &=2\sum_{\ell=0}^{n}\sideset{}{'}\sum_{|I|=\ell}(K_\Delta f_I){\mathbf{e}}_I \\ {} &\quad +\sum_{\ell=0}^{n}\sideset{}{'}\sum_{|I|=\ell} \sum_{j,k=1}^{n}\left([M_{\nu_j},R_k]f_I\right){\mathbf{e}}_j\odot{\mathbf{e}}_k\odot{\mathbf{e}}_I \end{aligned} $$

(5.21)

for each $\mathcal {C}\ell _n$-valued function $f=\sum _{\ell =0}^{n}\sum _{|I|=\ell }^{\prime }f_I\odot {\mathbf {e}}_I$ belonging to the weighted Lebesgue space $L^1\big (\partial \Omega ,\frac {\sigma (x)}{1+|x|{ }^{n-1}}\big )\otimes {\mathcal {C}}\ell _n$.

In turn, the structural result from Lemma 5.1 is a basic ingredient in the proof of the following corollary.

Corollary 5.1

Let $\Omega \subseteq {\mathbb {R}}^{n}$ be a UR domain. Abbreviate $\sigma :={\mathcal {H}}^{n-1}\lfloor \partial \Omega$ and denote by ν the geometric measure theoretic outward unit normal to Ω. Also, fix an integrability exponent p ∈ (1, ∞) and a Muckenhoupt weight w ∈ A_p(∂ Ω, σ). Then for each $m\in {\mathbb {N}}$ there exists some constant C_m ∈ (0, ∞) which depends only on m, n, p, $[w]_{A_p}$, and the UR constants of ∂ Ω such that, with the piece of notation introduced in (4.93), one has

$$\displaystyle \begin{aligned} \left\lVert{\mathbf{C}-{\mathbf{C}}^{\#}}\right\rVert_{L^p(\partial\Omega,w)\otimes\mathcal{C}\ell_n\to L^p(\partial\Omega,w)\otimes\mathcal{C}\ell_n}\leq C_m\|\nu\|{}^{\langle m\rangle}_{[\mathrm{BMO}(\partial\Omega,\sigma)]^n}. \end{aligned} $$

(5.22)

Moreover, if $\left \lVert {\nu }\right \rVert _{[\mathrm {BMO}(\partial \Omega ,\sigma )]^n}$ is sufficiently small relative to n, p, $[w]_{A_p}$, and the Ahlfors regularity constant of ∂ Ω one may take C_m ∈ (0, ∞) appearing in (5.22) to depend only on said entities ( i.e., n, p, $[w]_{A_p}$, the Ahlfors regularity constant of ∂ Ω) , and m.

Proof

This is a consequence of Lemmas 5.1, 2.15, (3.29), Corollary 4.2, (4.297), Proposition 3.4, Theorems 4.3, and 2.3. □

5.2 Estimating the BMO Semi-Norm of the Unit Normal

The next goal is to establish a bound from below for the operator norm of C −C^# on Muckenhoupt weighted Lebesgue spaces on the boundary of a UR domain in terms of the BMO semi-norm of the geometric measure theoretic outward unit normal vector to said domain.

Theorem 5.1

Let $\Omega \subseteq {\mathbb {R}}^n$ be a UR domain such that ∂ Ω is unbounded. Abbreviate $\sigma :={\mathcal {H}}^{n-1}\lfloor \partial \Omega$ and denote by ν the geometric measure theoretic outward unit normal to Ω. Also, fix an integrability exponent p ∈ (1, ∞) along with a Muckenhoupt weight w ∈ A_p(∂ Ω, σ). Then there exists some C ∈ (0, ∞) which depends only on n, p, $[w]_{A_p}$, and the Ahlfors regularity constant of ∂ Ω with the property that

$$\displaystyle \begin{aligned} \left\lVert{\nu}\right\rVert_{[\mathrm{BMO}(\partial\Omega,\sigma)]^n} \leq C\left\lVert{\mathbf{C}-{\mathbf{C}}^{\#}}\right\rVert_{L^p(\partial\Omega,w)\otimes\mathcal{C}\ell_n\to L^p(\partial\Omega,w)\otimes\mathcal{C}\ell_n}. \end{aligned} $$

(5.23)

A couple of comments are in order. First, as a consequence of (5.23), definitions, and a result from [111, §5.10] (based on work in [59]) to the effect that an Ahlfors regular domain is a half-space if and only if its geometric measure theoretic outward unit normal is a constant vector, we see that

(5.24)

Second, estimate (5.23) may fail without the assumption that ∂ Ω is unbounded. Indeed, from (5.12)–(5.14) one may easily check that C = C^# if Ω is an open ball, or the complement of a closed ball, in ${\mathbb {R}}^n$ and yet $\left \lVert {\nu }\right \rVert _{[\mathrm {BMO}(\partial \Omega ,\sigma )]^n}>0$ in either case. In fact, open balls, complements of closed balls, and half-spaces in ${\mathbb {R}}^n$ are the only UR domains for which C = C^# (see [60] for more on this).

We now turn to the task of presenting the proof of Theorem 5.1.

Proof of Theorem 5.1

Fix a location x₀ ∈ ∂ Ω along with a scale R > 0. Also, pick a sufficiently large number Λ ∈ (10, ∞), which ultimately will depend only on n and the Ahlfors regularity constant of ∂ Ω, in a manner to be specified later. Let C ∈ [1, ∞) be the Ahlfors regularity constant of ∂ Ω (cf. (2.32)) and choose

$$\displaystyle \begin{aligned} \lambda:=(2C)^{2/(n-1)}. \end{aligned} $$

(5.25)

We may then write (making use of the fact that no smallness condition on the scale is necessary since ∂ Ω is unbounded)

$$\displaystyle \begin{aligned} \sigma\big(\Delta(x_0,\lambda(\Lambda R))\setminus\Delta(x_0,\Lambda R)\big) &=\sigma\big(\Delta(x_0,\lambda(\Lambda R))\big)-\sigma\big(\Delta(x_0,\Lambda R)\big) \\ {} &\geq\Big(\frac{1}{C}\lambda^{n-1}-C \Big)(\Lambda R)^{n-1}>0. \end{aligned} $$

(5.26)

In turn, this guarantees that $\Delta (x_0,\lambda (\Lambda R))\setminus \Delta (x_0,\Lambda R)\neq \varnothing$, hence we may choose some point

$$\displaystyle \begin{aligned} y_0\in\Delta(x_0,\lambda(\Lambda R))\setminus\Delta(x_0,\Lambda R). \end{aligned} $$

(5.27)

As a consequence,

$$\displaystyle \begin{aligned} \Lambda R\leq|x_0-y_0|<\lambda(\Lambda R). \end{aligned} $$

(5.28)

Next, fix a point x ∈ Δ(x₀, R) and note that this entails |x₀ − y|≥ ( Λ − 1)R > 0 for all y ∈ Δ(y₀, R). As such, we may write

$$\displaystyle \begin{aligned} \int_{\Delta(y_0,R)} &\left\{\frac{x_0-y}{|x_0-y|{}^n}\odot\nu(y) +\nu(x)\odot\frac{x_0-y}{|x_0-y|{}^n}\right\}\,\mathrm{d}\sigma(y) \\ {} &=\int_{\Delta(y_0,R)}\left\{\frac{x_0-y}{|x_0-y|{}^n}\odot\nu(y) -\frac{x-y}{|x-y|{}^n}\odot\nu(y)\right\}\,\mathrm{d}\sigma(y) \\ {} &\qquad +\int_{\Delta(y_0,R)}\left\{\frac{x-y}{|x-y|{}^n}\odot\nu(y)+\nu(x)\odot\frac{x-y}{|x-y|{}^n}\right\}\,\mathrm{d}\sigma(y) \\ {} &\qquad +\int_{\Delta(y_0,R)}\left\{\nu(x)\odot\frac{x_0-y}{|x_0-y|{}^n} -\nu(x)\odot\frac{x-y}{|x-y|{}^n}\right\}\,\mathrm{d}\sigma(y) \\ {} &=:\mathrm{I}+\mathrm{II}+\mathrm{III}. \end{aligned} $$

(5.29)

Note that for each y ∈ Δ(y₀, R) we have

$$\displaystyle \begin{aligned} \Lambda R\leq|x_0-y_0|\leq|x_0-x|+|x-y|+|y-y_0|<|x-y|+2R. \end{aligned} $$

(5.30)

Based on definitions (cf. (5.12) and (5.14)), and the fact that, as seen from (5.30), we have |x − y| > ( Λ − 2)R for each y ∈ Δ(y₀, R), the second term in (5.29) is identified as

$$\displaystyle \begin{aligned} \mathrm{II}=\omega_{n-1}\,(\mathbf{C}-{\mathbf{C}}^{\#}){\mathbf{1}}_{\Delta(y_0,R)}(x). \end{aligned} $$

(5.31)

If for each $u,w,z\in {\mathbb {R}}^n$ with z∉{u, w} we now abbreviate

$$\displaystyle \begin{aligned} E(u,w;z):=\frac{u-z}{|u-z|{}^n}-\frac{w-z}{|w-z|{}^n}, \end{aligned} $$

(5.32)

and if we set

(5.33)

then, on account of (5.4),

$$\displaystyle \begin{aligned} \mathrm{I}+\mathrm{III} &=\int_{\Delta(y_0,R)}\big\{E(x_0,x;y)\odot\nu(y)+\nu(x)\odot E(x_0,x;y)\big\}\,\mathrm{d}\sigma(y) \\ {} &=-2\int_{\Delta(y_0,R)}\big\langle E(x_0,x;y),\nu_{\Delta(x_0,R)}\big\rangle\,\mathrm{d}\sigma(y) \\ {} &\quad +\int_{\Delta(y_0,R)}E(x_0,x;y)\odot\big(\nu(y)-\nu_{\Delta(x_0,R)}\big)\,\mathrm{d}\sigma(y) \\ {} &\quad +\int_{\Delta(y_0,R)}\big(\nu(x)-\nu_{\Delta(x_0,R)}\big)\odot E(x_0,x;y)\,\mathrm{d}\sigma(y) \\ {} &=:\mathrm{IV}+\mathrm{V}+\mathrm{VI}. \end{aligned} $$

(5.34)

Since

$$\displaystyle \begin{aligned} E(x_0,x;y) &=\frac{x_0-y}{|x_0-y|{}^n}-\frac{(x-x_0)-(y-x_0)}{|x-y|{}^n} \\ {} &=-\frac{x-x_0}{|x-y|{}^n}+(x_0-y)\Big(\frac{1}{|x_0-y|{}^n}-\frac{1}{|x-y|{}^n}\Big) \end{aligned} $$

(5.35)

for each y ∈ Δ(y₀, R), it follows that

$$\displaystyle \begin{aligned} \mathrm{IV} &=2\int_{\Delta(y_0,R)}\frac{\big\langle x-x_0,\nu_{\Delta(x_0,R)}\big\rangle}{|x-y|{}^n}\,\mathrm{d}\sigma(y) \\ {} &\quad +2\int_{\Delta(y_0,R)}\big\langle y-x_0,\nu_{\Delta(x_0,R)}\big\rangle\Big(\frac{1}{|x_0-y|{}^n}-\frac{1}{|x-y|{}^n}\Big)\,\mathrm{ d}\sigma(y) \\ {} &=:\mathrm{IV}_a+\mathrm{IV}_b. \end{aligned} $$

(5.36)

In view of (5.30) for each y ∈ Δ(y₀, R) we have ( Λ∕2)R < ( Λ − 2)R < |x − y| which, together with Proposition 2.15, permits us to estimate

$$\displaystyle \begin{aligned} |\mathrm{IV}_a| &=2\big|\big\langle x-x_0,\nu_{\Delta(x_0,R)}\big\rangle\big|\int_{\Delta(y_0,R)}\frac{1}{|x-y|{}^n}\,\mathrm{d}\sigma(y) \\ {} &\leq C\Lambda^{-n}\|\nu\|{}_{[\mathrm{BMO}(\partial\Omega,\sigma)]^n}, \end{aligned} $$

(5.37)

where C ∈ (0, ∞) depends only on n and the Ahlfors regularity constant of ∂ Ω. Also, since the Mean Value Theorem gives that for each point y ∈ Δ(y₀, R) we have, for some purely dimensional constant C ∈ (0, ∞),

$$\displaystyle \begin{aligned} \Big|\frac{1}{|x_0-y|{}^n}-\frac{1}{|x-y|{}^n}\Big| \leq\frac{CR}{(\Lambda R)^{n+1}}=C\Lambda^{-n-1}R^{-n}, \end{aligned} $$

(5.38)

we may use Proposition 2.15 and the fact that y ∈ Δ(y₀, R) ⊆ Δ(x₀, (1 + λ Λ)R) to conclude that

$$\displaystyle \begin{aligned} \big|\mathrm{IV}_b\big| &\leq C(\Lambda R\ln\Lambda)\|\nu\|{}_{[\mathrm{BMO}(\partial\Omega,\sigma)]^n} \Lambda^{-n-1}R^{-n}\sigma\big(\Delta(x_0,R)\big) \\ {} &\leq C(\Lambda^{-n}\ln\Lambda)\|\nu\|{}_{[\mathrm{BMO}(\partial\Omega,\sigma)]^n}, \end{aligned} $$

(5.39)

where C ∈ (0, ∞) depends only on n and the Ahlfors regularity constant of ∂ Ω. Next, the Mean Value Theorem shows that for each y ∈ Δ(y₀, R) we have

$$\displaystyle \begin{aligned} |E(x_0,x;y)|=\Big|\frac{x_0-y}{|x_0-y|{}^n}-\frac{x-y}{|x-y|{}^n}\Big| \leq\frac{CR}{(\Lambda R)^{n}}=C\Lambda^{-n}R^{1-n}, \end{aligned} $$

(5.40)

for some purely dimensional constant C ∈ (0, ∞). In addition, (2.104), (2.105), and (2.106) permit us to write

$$\displaystyle \begin{aligned} \big|\nu_{\Delta(x_0,R)}-\nu_{\Delta(y_0,R)}\big| &\leq \big|\nu_{\Delta(x_0,R)}-\nu_{\Delta(x_0,\lambda\Lambda R)}\big| +\big|\nu_{\Delta(x_0,\lambda\Lambda R)}-\nu_{\Delta(y_0,\lambda\Lambda R)}\big| \\ {} &\quad +\big|\nu_{\Delta(y_0,\lambda\Lambda R)}-\nu_{\Delta(y_0,R)}\big| \\ {} &\leq C(\ln\Lambda)\|\nu\|{}_{[\mathrm{BMO}(\partial\Omega,\sigma)]^n} \end{aligned} $$

(5.41)

for some C ∈ (0, ∞) which depends only on n and the Ahlfors regularity constant of ∂ Ω. Based on (5.40) and (5.41) we may then estimate

(5.42)

where C ∈ (0, ∞) depends only on n and the Ahlfors regularity constant of ∂ Ω. Finally, (5.40) implies that for some purely dimensional constant C ∈ (0, ∞) we have

$$\displaystyle \begin{aligned} \big|\mathrm{VI}\big| &\leq\int_{\Delta(y_0,R)}|E(x_0,x;y)|\big|\nu(x)-\nu_{\Delta(x_0,R)}\big|\,\mathrm{d}\sigma(y) \\ {} &\leq C\Lambda^{-n}\big|\nu(x)-\nu_{\Delta(x_0,R)}\big|. \end{aligned} $$

(5.43)

For further use, let us note here that (2.538) plus the John-Nirenberg inequality (cf. (2.102)) allow to estimate (for some exponent q′∈ (1, ∞) which depends only on p, $[w]_{A_p}$, n, and the Ahlfors regularity constant of ∂ Ω)

(5.44)

for some constant C ∈ (0, ∞) of the same nature as before. It is also useful to note that we may use (2.535) to estimate

(5.45)

where C ∈ (0, ∞) depends only on n, p, $[w]_{A_p}$, and the Ahlfors regularity constant of ∂ Ω.

Altogether, from (5.29), (5.31), (5.34), (5.36), (5.37), (5.39), (5.42), (5.43), (5.44), and (5.45) we conclude that

(5.46)

where C ∈ (0, ∞) depends only on n, p, $[w]_{A_p}$, and the Ahlfors regularity constant of ∂ Ω.

Going further, define

(5.47)

and

(5.48)

Note that

(5.49)

and observe that the Mean Value Theorem gives, for some purely dimensional constant C ∈ (0, ∞),

$$\displaystyle \begin{aligned} \Big|\frac{x_0-y}{|x_0-y|{}^n}-\frac{x_0-y_0}{|x_0-y_0|{}^n}\Big| \leq\frac{CR}{(\Lambda R)^{n}}=C\Lambda^{-n}R^{1-n}, \end{aligned} $$

(5.50)

for each y ∈ Δ(y₀, R). As a consequence of this and (5.28),

(5.51)

if Λ > 2C. Hence, if we also introduce

$$\displaystyle \begin{aligned} A:=b\odot\Big(\frac{a}{|a|{}^2}\Big)\in\mathcal{C}\ell_n, \end{aligned} $$

(5.52)

we may now estimate, using (5.6), (5.52), (5.51), (5.11), (5.1), (5.47), (5.48), and (5.46),

(5.53)

for some C ∈ (0, ∞) which depends only on n, p, $[w]_{A_p}$, and the Ahlfors regularity constant of ∂ Ω. From this, (2.109), and Lemma 2.14 we then deduce that

$$\displaystyle \begin{aligned} \|\nu\|{}_{[\mathrm{BMO}(\partial\Omega,\sigma)]^n} &\leq C(\Lambda^{-1}\ln\Lambda)\|\nu\|{}_{[\mathrm{BMO}(\partial\Omega,\sigma)]^n} \\ {} &\quad +C\Lambda^{2(n-1)}\big\|\mathbf{C}-{\mathbf{C}}^{\#}\big\|{}_{L^p(\partial\Omega,w)\otimes\mathcal{C}\ell_n\to L^p(\partial\Omega,w)\otimes\mathcal{C}\ell_n}, \end{aligned} $$

(5.54)

where C ∈ (0, ∞) depends only on n, p, $[w]_{A_p}$, and the Ahlfors regularity constant of ∂ Ω. By eventually further increasing the value of Λ as to ensure that we also have $\Lambda ^{-1}\ln \Lambda <1/(2C)$, we finally conclude from (5.54) that

$$\displaystyle \begin{aligned} \|\nu\|{}_{[\mathrm{BMO}(\partial\Omega,\sigma)]^n} \leq C\big\|\mathbf{C}-{\mathbf{C}}^{\#}\big\|{}_{L^p(\partial\Omega,w)\otimes\mathcal{C}\ell_n\to L^p(\partial\Omega,w)\otimes\mathcal{C}\ell_n}, \end{aligned} $$

(5.55)

where C ∈ (0, ∞) depends only on n, p, $[w]_{A_p}$, and the Ahlfors regularity constant of ∂ Ω. □

Our next result contains estimates in the opposite direction to those given in Theorem 4.6.

Theorem 5.2

Let $\Omega \subseteq {\mathbb {R}}^n$ be a UR domain. Abbreviate $\sigma :={\mathcal {H}}^{n-1}\lfloor \partial \Omega$ and denote by ν = (ν_k)_1≤k≤n the geometric measure theoretic outward unit normal to Ω. Also, fix an integrability exponent p ∈ (1, ∞) along with a Muckenhoupt weight w ∈ A_p(∂ Ω, σ). Finally, recall the boundary-to-boundary harmonic double layer potential operator K_Δ from (3.29), the Riesz transforms {R_j}_1≤j≤n on ∂ Ω from (4.297), and for each index k ∈{1, …, n} denote by $M_{\nu _k}$ the operator of pointwise multiplication by the k-th scalar component of ν.

Then there exists some C ∈ (0, ∞) which depends only on n, p, $[w]_{A_p}$, and the Ahlfors regularity constant of ∂ Ω with the property that

$$\displaystyle \begin{aligned} \left\lVert{\nu}\right\rVert_{[\mathrm{BMO}(\partial\Omega,\sigma)]^n} \leq C\Big\{&\left\lVert{K_\Delta}\right\rVert_{L^p(\partial\Omega,w)\to L^p(\partial\Omega,w)} \\ {} &\qquad +\max_{1\leq j,k\leq n}\left\lVert{[M_{\nu_k},R_j]}\right\rVert_{L^p(\partial\Omega,w)\to L^p(\partial\Omega,w)}\Big\}. \end{aligned} $$

(5.56)

Proof

If ∂ Ω is unbounded, then the estimate claimed in (5.56) is a direct consequence of Theorem 5.1 and Lemma 5.1 (also bearing in mind Lemma 2.15). In the case when ∂ Ω is bounded, we have $K_\Delta 1=\pm \tfrac {1}{2}$ (cf. [114, §1.5]) with the sign plus if Ω is bounded, and the sign minus if Ω is unbounded, hence $\left \lVert {K_\Delta }\right \rVert _{L^p(\partial \Omega ,w)\to L^p(\partial \Omega ,w)}\geq \tfrac {1}{2}$ in such a scenario. Since from (2.118) we know that we always have $\left \lVert {\nu }\right \rVert _{[\mathrm {BMO}(\partial \Omega ,\sigma )]^n}\leq 1$, the estimate claimed in (5.56) holds in this case if we take C ≥ 2. □

We conclude this section by presenting a characterization of δ-flat Ahlfors regular domains in terms of the size of the operator norms of the classical harmonic double layer and commutators of Riesz transforms with pointwise multiplication by the scalar components of the unit normal.

Corollary 5.2

Let $\Omega \subseteq {\mathbb {R}}^n$ be a UR domain. Abbreviate $\sigma :={\mathcal {H}}^{n-1}\lfloor \partial \Omega$ and denote by ν = (ν_k)_1≤k≤n the geometric measure theoretic outward unit normal to Ω. Also, fix an integrability exponent p ∈ (1, ∞) along with a Muckenhoupt weight w ∈ A_p(∂ Ω, σ). Finally, recall the boundary-to-boundary harmonic double layer potential operator K_Δ on ∂ Ω from (3.29), the Riesz transforms {R_j}_1≤j≤n on ∂ Ω from (4.297), and for each k ∈{1, …, n} denote by $M_{\nu _k}$ the operator of pointwise multiplication by the k-th scalar component of ν.

Then there exists some C ∈ (0, ∞) which depends only on n, p, $[w]_{A_p}$, and the Ahlfors regularity constant of ∂ Ω with the property that if

$$\displaystyle \begin{aligned} \left\lVert{K_\Delta}\right\rVert_{L^p(\partial\Omega,w)\to L^p(\partial\Omega,w)} +\max_{1\leq j,k\leq n}\big\|[M_{\nu_k},R_j]\big\|{}_{L^p(\partial\Omega,w)\to L^p(\partial\Omega,w)}<\delta \end{aligned} $$

(5.57)

then Ω is a (Cδ)–flat Ahlfors regular domain.

Proof

All desired conclusions follow from Theorem 5.2 and Definition 2.15. □

5.3 Using Riesz Transforms to Quantify Flatness

Recall from (1.16) that for each j ∈{1, …, n} the j-th Riesz transform R_j associated with a UR domain $\Omega \subseteq {\mathbb {R}}^n$ is the formal convolution operator on ∂ Ω with the kernel $k_j(x):=\frac {2}{\omega _{n-1}}\frac {x_j}{|x|{ }^n}$ for $x\in {\mathbb {R}}^n\setminus \{0\}$. From Proposition 3.4 we know that these are bounded operators on L^p(∂ Ω, w) for each p ∈ (1, ∞) and w ∈ A_p(∂ Ω, σ). The most familiar setting is when $\Omega ={\mathbb {R}}^n_{+}$, in which case it is well known that

$$\displaystyle \begin{aligned} \sum_{j=1}^n R_j^2=-I\,\,\text{ and }\,\,R_jR_k=R_kR_j\,\,\text{ for all }\,\,j,k\in\{1,\dots,n\}, \end{aligned} $$

(5.58)

when all operators are considered on Muckenhoupt weighted Lebesgue spaces. Indeed, in such a setting, for the integrability exponent p = 2 and the weight w = 1 these are immediate consequences of the fact that each R_j is a Fourier multiplier in $\partial \Omega \equiv {\mathbb {R}}^{n-1}$ corresponding to the symbol iξ_j∕|ξ|, then said identities extend to L^p(∂ Ω, w) via a density argument. For ease of reference, we shall refer to the formulas in (5.58) as being URTI, i.e., the usual Riesz transform identities.

Remarkably, Theorem 5.3 below provides a stability result to the effect that if $\Omega \subseteq {\mathbb {R}}^n$ is a UR domain with an unbounded boundary for which the URTI are “almost” true in the context of a Muckenhoupt weighted Lebesgue space, then ∂ Ω is “almost” flat, in that the BMO semi-norm of the outward unit normal to Ω is small.

Theorem 5.3

Let $\Omega \subseteq {\mathbb {R}}^n$ be a UR domain with an unbounded boundary. Abbreviate $\sigma :={\mathcal {H}}^{n-1}\lfloor \partial \Omega$ and denote by ν the geometric measure theoretic outward unit normal to Ω. Also, fix an integrability exponent p ∈ (1, ∞) along with a Muckenhoupt weight w ∈ A_p(∂ Ω, σ), and recall the Riesz transforms {R_j}_1≤j≤n on ∂ Ω from (4.297). Then there exists some C ∈ (0, ∞) which depends only on n, p, $[w]_{A_p}$, and the UR constants of ∂ Ω with the property that

$$\displaystyle \begin{aligned} \left\lVert{\nu}\right\rVert_{[\mathrm{BMO}(\partial\Omega,\sigma)]^n} \leq C\Big\{&\Big\|I+\sum_{j=1}^{n}R_j^2\Big\|{}_{L^p(\partial\Omega,w)\to L^p(\partial\Omega,w)} \\ {} &\qquad +\max_{1\leq j,k\leq n}\big\|[R_j,R_k]\big\|{}_{L^p(\partial\Omega,w)\to L^p(\partial\Omega,w)}\Big\}. \end{aligned} $$

(5.59)

It is perhaps surprising (but nonetheless true; cf. [60]) that URTI are also valid in the context of Muckenhoupt weighted Lebesgue spaces when Ω is an open ball, or the complement of a closed ball in ${\mathbb {R}}^n$. This shows that, in the context of Theorem 5.3, our assumption that ∂ Ω is unbounded is warranted, since otherwise (5.59) may fail.

Proof of Theorem 5.3

Formula [61, (4.6.46), p. 2752] (which is valid in any UR domain, irrespective of whether its boundary is compact or not) tells us that for each $f\in L^p(\partial \Omega ,\sigma )\otimes {\mathcal {C}}\ell _n$ we have

$$\displaystyle \begin{aligned} ({\mathbf{C}}-{\mathbf{C}}^{\#})f &={\mathbf{C}}\Big(I+\sum_{j=1}^{n}R_j^2\Big)f +\sum_{1\leq j<k\leq n}{\mathbf{C}}\big([R_j,R_k]({\mathbf{e}}_j\odot{\mathbf{e}}_k\odot f)\big). \end{aligned} $$

(5.60)

Since $\big (L^p(\partial \Omega ,\sigma )\cap L^p(\partial \Omega ,w)\big )\otimes {\mathcal {C}}\ell _n$ is a dense subspace of $L^p(\partial \Omega ,w)\otimes {\mathcal {C}}\ell _n$ and since all operators involved are continuous on $L^p(\partial \Omega ,w)\otimes {\mathcal {C}}\ell _n$, we conclude that formula (5.60) continues to hold for each $f\in L^p(\partial \Omega ,w)\otimes {\mathcal {C}}\ell _n$. From this version of (5.60) we then see that

$$\displaystyle \begin{aligned} ({\mathbf{C}}-{\mathbf{C}}^{\#})f={\mathbf{C}}\Big(I+\sum_{j=1}^{n}R_j^2\Big)f +\sum_{1\leq j<k\leq n}{\mathbf{C}}\big([R_j,R_k]({\mathbf{e}}_j\odot{\mathbf{e}}_k\odot f)\big) \end{aligned} $$

(5.61)

for each $f\in L^p(\partial \Omega ,w)\otimes {\mathcal {C}}\ell _n$. In concert with (5.18), this implies

$$\displaystyle \begin{aligned} &\|{\mathbf{C}}-{\mathbf{C}}^{\#}\|{}_{L^p(\partial\Omega,w)\otimes{\mathcal{C}}\ell_n\to L^p(\partial\Omega,w)\otimes{\mathcal{C}}\ell_n} \\ {} &\hskip 1.00in \leq C\Big\|I+\sum_{j=1}^{n}R_j^2\Big\|{}_{L^p(\partial\Omega,w)\to L^p(\partial\Omega,w)} \\ {} &\hskip 1.00in \quad +C\sum_{1\leq j<k\leq n}\big\|[R_j,R_k]\big\|{}_{L^p(\partial\Omega,w)\to L^p(\partial\Omega,w)} \end{aligned} $$

(5.62)

Then (5.59) becomes a consequence of (5.62) and Theorem 5.1. □

Our next result contains estimates in the opposite direction to those from Theorem 5.3. Collectively, Theorems 5.4 and 5.3 amount to saying that, under natural background geometric assumptions on the set Ω, the URTI are “almost” true in the context of a Muckenhoupt weighted Lebesgue space if and only if ∂ Ω is “almost” flat (in that the BMO semi-norm of the outward unit normal to Ω is small).

Theorem 5.4

Let $\Omega \subseteq {\mathbb {R}}^{n}$ be a UR domain. Abbreviate $\sigma :={\mathcal {H}}^{n-1}\lfloor \partial \Omega$ and denote by ν the geometric measure theoretic outward unit normal to Ω. Also, fix an exponent p ∈ (1, ∞) along with a Muckenhoupt weight w ∈ A_p(∂ Ω, σ), and recall the Riesz transforms {R_j}_1≤j≤n on ∂ Ω from (4.297).

Then for each $m\in {\mathbb {N}}$ there exists some constant C_m ∈ (0, ∞) which depends only on m, n, p, $[w]_{A_p}$, and the Ahlfors regularity constant of ∂ Ω such that, with the piece of notation introduced in (4.93), one has

$$\displaystyle \begin{aligned} \Big\|I+\sum_{j=1}^{n}R_j^2\Big\|{}_{L^p(\partial\Omega,w)\to L^p(\partial\Omega,w)} \leq C_m\|\nu\|{}^{\langle m\rangle}_{[\mathrm{BMO}(\partial\Omega,\sigma)]^n}, \end{aligned} $$

(5.63)

and

$$\displaystyle \begin{aligned} \max_{1\leq j<k\leq n}\big\|[R_j,R_k]\big\|{}_{L^p(\partial\Omega,w)\to L^p(\partial\Omega,w)} \leq C_m\|\nu\|{}^{\langle m\rangle}_{[\mathrm{BMO}(\partial\Omega,\sigma)]^n}. \end{aligned} $$

(5.64)

Furthermore, if $\left \lVert {\nu }\right \rVert _{[\mathrm {BMO}(\partial \Omega ,\sigma )]^n}$ is sufficiently small relative to n, p, $[w]_{A_p}$, and the Ahlfors regularity constant of ∂ Ω one may take C_m ∈ (0, ∞) appearing in (5.63)–(5.64) to depend only on said entities ( i.e., n, p, $[w]_{A_p}$, the Ahlfors regularity constant of ∂ Ω) and m.

Proof

From the Muckenhoupt version of (5.20) and (5.61) we see that for each function $f\in L^p(\partial \Omega ,\sigma )\otimes {\mathcal {C}}\ell _n$ we have

$$\displaystyle \begin{aligned} {\mathbf{C}}({\mathbf{C}}^{\#}-{\mathbf{C}})f=-\tfrac{1}{4}\Big(I+\sum_{j=1}^{n}R_j^2\Big)f -\tfrac{1}{4}\sum_{1\leq j<k\leq n}[R_j,R_k]({\mathbf{e}}_j\odot{\mathbf{e}}_k\odot f). \end{aligned} $$

(5.65)

Fix a scalar function f ∈ L^p(∂ Ω, w) normalized so that $\|f\|{ }_{L^p(\partial \Omega ,w)}=1$. In particular, this shows that the function f belongs to the space $L^p(\partial \Omega ,w)\otimes {\mathcal {C}}\ell _n$ and $\|f\|{ }_{L^p(\partial \Omega ,w)\otimes {\mathcal {C}}\ell _n}=1$. Bearing this in mind, for each $m\in {\mathbb {N}}$ we may then write

$$\displaystyle \begin{aligned} &\max\Bigg\{\Big\|\tfrac{1}{4}\Big(I+\sum_{j=1}^{n}R_j^2\Big)f\Big\|{}_{L^p(\partial\Omega,w)}\,,\, \max_{1\leq j<k\leq n}\Big\|\tfrac{1}{4}[R_j,R_k]f\Big\|{}_{L^p(\partial\Omega,w)}\Bigg\} \\ {} &\qquad \leq\Bigg\|\left\{\Big|\tfrac{1}{4}\Big(I+\sum_{j=1}^{n}R_j^2\Big)f\Big|{}^2 +\sum_{1\leq j<k\leq n}\Big|\tfrac{1}{4}[R_j,R_k]f\Big|{}^2\right\}^{1/2}\Bigg\|{}_{L^p(\partial\Omega,w)} \\ {} &\qquad =\Big\|\tfrac{1}{4}\Big(I+\sum_{j=1}^{n}R_j^2\Big)f+\tfrac{1}{4} \sum_{1\leq j<k\leq n}([R_j,R_k]f){\mathbf{e}}_j\odot{\mathbf{e}}_k\Big\|{}_{L^p(\partial\Omega,w)\otimes{\mathcal{C}}\ell_n} \\ {} &\qquad =\|{\mathbf{C}}({\mathbf{C}}^{\#}-{\mathbf{C}})f\|{}_{L^p(\partial\Omega,w)\otimes{\mathcal{C}}\ell_n} \\ {} &\qquad \leq\left\lVert{\mathbf{C}}\right\rVert_{L^p(\partial\Omega,w)\otimes\mathcal{C}\ell_n\to L^p(\partial\Omega,w)\otimes\mathcal{C}\ell_n} \left\lVert{\mathbf{C}-{\mathbf{C}}^{\#}}\right\rVert_{L^p(\partial\Omega,w)\otimes\mathcal{C}\ell_n\to L^p(\partial\Omega,w)\otimes\mathcal{C}\ell_n} \\ {} &\qquad \leq C_m\|\nu\|{}^{\langle m\rangle}_{[\mathrm{BMO}(\partial\Omega,\sigma)]^n}, \end{aligned} $$

(5.66)

where the first inequality is trivial, the subsequent equality is implied by (5.8), the second equality is seen from formula (5.65) (since f is scalar-valued), the penultimate estimate uses the normalization of f, while the last inequality is provided by (5.18) and (5.22). With estimate (5.66) in hand, the claims in (5.63)–(5.64) readily follow (in view of the arbitrariness of the scalar-valued function f ∈ L^p(∂ Ω, w) with $\|f\|{ }_{L^p(\partial \Omega ,w)}=1$). The final claim in the statement is a direct consequence of Theorem 2.3. □

5.4 Using Riesz Transforms to Characterize Muckenhoupt Weights

Assume $\Sigma \subseteq {\mathbb {R}}^{n}$, where $n\in {\mathbb {N}}$ with n ≥ 2, is a closed UR set and abbreviate $\sigma :={\mathcal {H}}^{n-1}\lfloor \Sigma$. For j ∈{1, …, n}, the j-th Riesz transform R_j on Σ is defined as the operator acting on each $f\in L^1\big (\Sigma ,\frac {\sigma (x)}{1+|x|{ }^{n-1}}\big )$ according to

(5.67)

From Proposition 3.4 we know that these Riesz transforms are well defined in this context, and that for each integrability exponent p ∈ (1, ∞) and Muckenhoupt weight w ∈ A_p( Σ, σ) they induce linear and bounded mappings on L^p( Σ, w). The goal in this section is to show that the class of Muckenhoupt weights is the largest class of weights for which the latter boundedness properties hold.

As a preamble, we note that for a variety of purposes it is convenient to glue together all Riesz transforms {R_j}_1≤j≤n from (5.67) into a unique operator now acting on Clifford algebra-valued functions $f\in L^1\big (\Sigma ,\frac {\sigma (x)}{1+|x|{ }^{n-1}}\big )\otimes {\mathcal {C}}\ell _n$ according to

(5.68)

Theorem 5.5

Suppose $\Sigma \subseteq {\mathbb {R}}^{n}$ is a closed UR set and abbreviate $\sigma :={\mathcal {H}}^{n-1}\lfloor \Sigma$. Fix p ∈ (1, ∞) and consider a weight w on Σ which belongs to $L^1_{\mathrm {loc}}(\Sigma ,\sigma )$ and has the property that, for each j ∈{1, …, n}, the j-th Riesz transform R_j on Σ originally defined as in (5.67) extends to a linear and bounded operator on L^p( Σ, w). Then necessarily w ∈ A_p( Σ, σ) and there exists C ∈ (0, ∞) which depends only on the Ahlfors regularity constant of Σ, n, and p with the property that

$$\displaystyle \begin{aligned}{}[w]_{A_p}\leq C\left\{ \begin{array}{ll} \max_{1\leq j\leq n}\|R_j\|{}_{L^p(\Sigma,w)\to L^p(\Sigma,w)}^{2p} & \mathit{\text{ if}}\ \Sigma\ \mathit{\text{unbounded}}, \\ {} \max_{1\leq j\leq n}\|R_j\|{}_{L^p(\Sigma,w)\to L^p(\Sigma,w)}^{5p} & \mathit{\text{ if}}\ \Sigma\ \mathit{\text{bounded}}. \end{array} \right. \end{aligned} $$

(5.69)

From assumptions and (2.508) we know that σ is a complete, locally finite (hence also sigma-finite), separable, Borel-regular measure on Σ. Since the weight w belongs to $L^1_{\mathrm {loc}}(\Sigma ,\sigma )$, it follows that

(5.70)

Granted this, results in [7], [111, §3.7] then guarantee that the natural inclusion

$$\displaystyle \begin{aligned} {\mathscr{X}}:=\big\{\phi\big|{}_{\Sigma}:\,\phi\in{\mathscr{C}}^{\infty}_0({\mathbb{R}}^n)\big\} \hookrightarrow L^p(\Sigma,w)\,\,\text{ has dense range}. \end{aligned} $$

(5.71)

From the preamble to Theorem 5.5 we know that the Riesz transforms (5.67) act in a meaningful fashion on ${\mathscr {X}}$, and this is the manner in which the R_j’s are originally considered in the context of Theorem 5.5. The point of the latter theorem is that if the R_j’s originally defined on ${\mathscr {X}}$ extend via density (cf. (5.71)) to linear and bounded operators on L^p( Σ, w) then necessarily w ∈ A_p( Σ, σ).

Let us now present the proof of Theorem 5.5.

Proof of Theorem 5.5

The fact that all Riesz transforms on Σ originally defined as in (5.67) on functions $f\in {\mathscr {X}}:=\big \{\phi \big |{ }_{\Sigma }:\,\phi \in {\mathscr {C}}^{\infty }_0({\mathbb {R}}^n)\big \}$ induce (via density; cf. (5.71)) linear and bounded mappings on L^p( Σ, w), implies that the operator R from (5.68), originally defined on functions $f\in {\mathscr {X}}\otimes {\mathcal {C}}\ell _n$ induces (via density) a linear and bounded mapping on $L^p(\Sigma ,w)\otimes {\mathcal {C}}\ell _n$. Henceforth abbreviate

$$\displaystyle \begin{aligned} C_0:=\|R\|{}_{L^p(\Sigma,w)\otimes{\mathcal{C}}\ell_n\to L^p(\Sigma,w)\otimes{\mathcal{C}}\ell_n} \end{aligned} $$

(5.72)

and note that there exists a dimensional constant C_n ∈ (0, ∞) with the property that

$$\displaystyle \begin{aligned} C_0\leq C_n\cdot\max_{1\leq j\leq n}\|R_j\|{}_{L^p(\Sigma,w)\to L^p(\Sigma,w)}. \end{aligned} $$

(5.73)

To proceed in earnest, denote by $C_{{ }_{\mathrm {AR}}}\in [1,\infty )$ the Ahlfors regularity constant of Σ and fix a number λ ∈ (1, ∞) which is sufficiently large relative to the Ahlfors regularity constant of Σ as to ensure that

$$\displaystyle \begin{aligned} \Delta(x,\lambda\rho)\setminus\Delta(x,\rho)\neq \varnothing\,\,\text{ for each }\,\,x\in\Sigma \,\,\text{ and }\,\,\rho\in\big(0,\mathrm{diam}(\Sigma)\big/\lambda\big). \end{aligned} $$

(5.74)

For example, any $\lambda >C_{{ }_{\mathrm {AR}}}^{2/(n-1)}$ will do. Fix r ∈(0, diam( Σ)/(10λ)) and suppose x₁, x₂ ∈ Σ are such that

$$\displaystyle \begin{aligned} 10\,r\le |x_1-x_2|\le 200\lambda r. \end{aligned} $$

(5.75)

Abbreviate

$$\displaystyle \begin{aligned} \Delta_1:=\Delta(x_1,r)\,\,\text{ and }\,\,\Delta_2:=\Delta(x_2,r). \end{aligned} $$

(5.76)

Next, select a real-valued function $f\in {\mathscr {X}}$ and set $f_{\pm }:=\max \{\pm f,0\}$. We then have 0 ≤ f_±≤|f| = f₊ + f₋ on Σ, and f_±∈ L^p( Σ, w) since ${\mathscr {X}}\subseteq L^p(\Sigma ,w)$. For each y ∈ Σ define

$$\displaystyle \begin{aligned} g_{\pm}(y):=\left\{ \begin{array}{ll} \displaystyle -\frac{x_2-y}{|x_2-y|}f_{\pm}(y) &\text{ if }\,\,y\in\Delta_1, \\ {} \qquad 0 &\text{ if }\,\,y\in\Sigma\setminus\Delta_1, \end{array} \right. \end{aligned} $$

(5.77)

so g_± belong to $L^p(\Sigma ,w)\otimes {\mathcal {C}}\ell _n$ and are supported in Δ₁. Consequently,

$$\displaystyle \begin{aligned} Rg_{\pm}(x)=\frac{2}{\omega_{n-1}}\int_{\Delta_1}\frac{x-y}{|x-y|{}^n}\odot\frac{-(x_2-y)}{|x_2-y|}f_{\pm}(y)\,\mathrm{d}\sigma(y) \,\text{ for each }\,x\in\Delta_2. \end{aligned} $$

(5.78)

Recall that the scalar component u_scal of a Clifford algebra element $u\in {\mathcal {C}}\ell _n$ is defined as in (5.7). For each x ∈ Δ₂ and y ∈ Δ₁ we may use (5.1), (5.8), (5.11), as well as (5.75) to compute

$$\displaystyle \begin{aligned} \Big(\frac{x-y}{|x-y|{}^n}\odot\frac{-(x_2-y)}{|x_2-y|}\Big)_{\mathrm{scal}} &=\Big(\frac{x-y}{|x-y|{}^n}\odot\frac{-(x-y)}{|x_2-y|}\Big)_{\mathrm{scal}} \\ {} &\quad +\Big(\frac{x-y}{|x-y|{}^n}\odot\frac{x-x_2}{|x_2-y|}\Big)_{\mathrm{scal}} \\ {} &=\frac{1}{|x-y|{}^{n-2}\cdot|x_2-y|}+\Big(\frac{x-y}{|x-y|{}^n}\odot\frac{x-x_2}{|x_2-y|}\Big)_{\mathrm{scal}} \\ {} &\geq\frac{1}{|x-y|{}^{n-2}\cdot|x_2-y|}-\frac{|x-x_2|}{|x-y|{}^{n-1}\cdot|x_2-y|} \\ {} &=\frac{|x-y|-|x-x_2|}{|x-y|{}^{n-1}\cdot|x_2-y|} \\ {} &\geq \frac{7r}{(200\lambda r+2r)^{n-1}(200\lambda r+r)}=c_{n,\lambda}\cdot r^{1-n}, \end{aligned} $$

(5.79)

where the last equality defines c_n,λ. Based on (5.78) and (5.79) we then conclude that we have the pointwise lower bound

(5.80)

In concert with the boundedness of R on $L^p(\Sigma ,w)\otimes {\mathcal {C}}\ell _n$ (mentioned in the first part of the proof) and the piece of notation introduced in (5.72), this permits us to estimate

(5.81)

Combining the two versions of (5.81), corresponding to f₊ and f₋, yields

(5.82)

Specializing (5.82) to the case when the real-valued function $f\in {\mathscr {X}}$ is chosen such that f ≡ 1 on Δ₁ then yields

$$\displaystyle \begin{aligned} c_{n,\lambda}^p\cdot C_{{}_{\mathrm{AR}}}^{-p}\leq 2^{p-1}\cdot C_0^p\frac{w(\Delta_1)}{w(\Delta_2)}. \end{aligned} $$

(5.83)

Running the same type of argument as above but with the roles of x₁ and x₂ (which are interchangeable) reversed then produces, in place of (5.83),

$$\displaystyle \begin{aligned} c_{n,\lambda}^p\cdot C_{{}_{\mathrm{AR}}}^{-p}\leq 2^{p-1}\cdot C_0^p\frac{w(\Delta_2)}{w(\Delta_1)}. \end{aligned} $$

(5.84)

From (5.84) and (5.82) we then conclude that for each real-valued function $f\in {\mathscr {X}}$ we have

(5.85)

with

$$\displaystyle \begin{aligned} C_1:=\big(2^{1-1/p}\cdot C_0\cdot c_{n,\lambda}^{-1}\cdot C_{{}_{\mathrm{AR}}}\big)^2. \end{aligned} $$

(5.86)

Consider now an arbitrary function $h\in L^p_{\mathrm {loc}}(\Sigma ,w)$. In particular, the extension of $h\big |{ }_{\Delta _1}$ by zero to the rest of Σ belongs to L^p( Σ, w). Granted this, (5.71) guarantees the existence of a sequence of functions $\{f_j\}_{j\in {\mathbb {N}}}\subseteq {\mathscr {X}}$ such that

$$\displaystyle \begin{aligned} f_j\big|{}_{\Delta_1}\to h\big|{}_{\Delta_1}\,\,\text{ in }\,\,L^p(\Delta_1,w)\,\,\text{ as }\,\,j\to\infty. \end{aligned} $$

(5.87)

By eventually passing to sub-sequences there is no loss of generality in also assuming that $\lim \limits _{j\to \infty }f_j(x)=h(x)$ for σ-a.e. x ∈ Δ₁. Based on this, Fatou’s lemma, and (5.85) we may then write

(5.88)

Ultimately, this goes to show that for each $h\in L^p_{\mathrm {loc}}(\Sigma ,w)$ we have

(5.89)

with C₁ ∈ (0, ∞) as in (5.86) (hence, in particular, independent of h, x₁, and r).

Start now with an arbitrary point x ∈ Σ, and continue to assume that the scale r belongs to (0, diam( Σ)/(10λ)). We may then employ (5.74) with ρ := 10 r to conclude that there exists some $\widetilde {x}\in \Delta (x,10\lambda r)\setminus \Delta (x,10\,r)$. For such a choice we then have $10\,r\leq |x-\widetilde {x}|<10\lambda r$ which, in light of (5.75), shows that we may run the argument so far with x₁ := x and $x_2:=\widetilde {x}$. In place of (5.89) we then arrive at the conclusion that, with C₁ ∈ (0, ∞) as in (5.86),

(5.90)

In the case when Σ is unbounded, from (5.90) (which now holds with no restriction on the size of the scale r since diam( Σ) = ∞) and the second part of Lemma 2.12 we conclude that

$$\displaystyle \begin{aligned} w\in A_p(\Sigma,\sigma)\,\,\text{ and }\,\,[w]_{A_p}\leq C_1^p. \end{aligned} $$

(5.91)

There remains to treat the scenario in which Σ is bounded. When this is the case, starting with (5.90), the argument in the proof of Lemma 2.12 that has led to (2.529) presently gives (with p′ denoting the Hölder conjugate exponent of p)

(5.92)

To obtain a similar inequality in the regime

$$\displaystyle \begin{aligned} \mathrm{diam}(\Sigma)\big/(10\lambda)\leq r\leq\mathrm{diam}(\Sigma), \end{aligned} $$

(5.93)

observe that for each x ∈ Σ we may estimate, using the Ahlfors regularity of Σ and the fact that r is comparable with diam( Σ),

(5.94)

At this stage, there remains to bound the right-hand side of (5.94) by a suitable finite constant which is independent of w. To this end, introduce the following threshold r₀ := diam( Σ)/(20λ). We claim that there exist an integer

$$\displaystyle \begin{aligned} N\in{\mathbb{N}}\,\,\text{ with }\,\,N\leq C_{{}_{\mathrm{AR}}}^{2}\cdot(40\lambda)^{n-1} \end{aligned} $$

(5.95)

along with a family of points $\{x_j\}_{j=1}^N\subseteq \Sigma$ satisfying

$$\displaystyle \begin{aligned} \begin{array}{c} |x_j-x_k|\geq r_0\ \text{for every}\ j,k\in\{1,\dots,N\}\ \text{with}\ j\neq k \\ {} \displaystyle \text{and }\,\,\Sigma\subseteq\bigcup\limits_{j=1}^N\Delta(x_j,r_0). \end{array} \end{aligned} $$

(5.96)

To justify this claim, observe that

$$\displaystyle \begin{aligned} {\mathcal{A}}:=\Big\{A\subseteq\Sigma:\,|x-x'|\geq r_0\,\,\text{ for all}\ x,x'\in A\ \text{with}\ x\neq x'\Big\} \end{aligned} $$

(5.97)

is a partially ordered set with respect to the canonical inclusion of sets. It is also clear that any totally ordered subset ${\mathcal {B}}$ of ${\mathcal {A}}$ has an upper bound in ${\mathcal {A}}$, namely $\bigcup _{B\in {\mathcal {B}}}B$. By Zorn’s lemma, there exists a maximal element A_max in ${\mathcal {A}}$. By maximality we necessarily have

$$\displaystyle \begin{aligned} \Sigma\subseteq\bigcup\limits_{x\in A_{\mathrm{max}}}\Delta(x,r_0). \end{aligned} $$

(5.98)

Since $\Sigma \subseteq {\mathbb {R}}^{n}$ is currently assumed to be compact, there exist $\{x_j\}_{j=1}^N\subseteq A_{\mathrm {max}}$ such that $\Sigma \subseteq \bigcup \limits _{j=1}^N\Delta (x_j,r_0)$. This takes care of (5.96). To estimate N as in (5.95), start by observing that the balls $\big \{B(x_j,r_0/2)\big \}_{j=1}^N$ are, thanks to the first line in (5.96), mutually disjoint. Bearing this in mind, we may use the Ahlfors regularity of Σ to write

$$\displaystyle \begin{aligned} C_{{}_{\mathrm{AR}}}\cdot(\mathrm{diam}(\Sigma)\big)^{n-1} &\geq\sigma(\Sigma) \geq\sum_{j=1}^N\sigma\big(B(x_j,r_0/2)\cap\Sigma\big) \\ {} &\geq N\cdot C_{{}_{\mathrm{AR}}}^{-1}\cdot(r_0/2)^{n-1}= N\cdot C_{{}_{\mathrm{AR}}}^{-1}\cdot\big(\mathrm{ diam}(\Sigma)\big/(40\lambda)\big)^{n-1} \end{aligned} $$

(5.99)

from which (5.95) readily follows.

Moving on, note that for every j, k ∈{1, …, N} with j ≠ k one has

$$\displaystyle \begin{aligned} r_0\leq|x_j-x_k|\leq\mathrm{diam}(\Sigma)=20\lambda r_0. \end{aligned} $$

(5.100)

Thus, (5.75) holds with r := r₀∕10 = diam( Σ)∕(200λ), and x_j, x_k playing the role of x₁ and x₂. As such, (5.76) and (5.83) yield

$$\displaystyle \begin{aligned} \frac{w\big(\Delta(x_k,r_0/10)\big)}{w\big(\Delta(x_j,r_0/10)\big)} \leq 2^{p-1}\cdot C_0^p\cdot c_{n,\lambda}^{-p}\cdot C_{{}_{\mathrm{AR}}}^p. \end{aligned} $$

(5.101)

On the other hand, Ahlfors regularity and (5.90) applied to Δ(x_k, r₀) and the function $h={\mathbf {1}}_{\Delta (x_k,r_0/10)}$ readily gives

$$\displaystyle \begin{aligned} C_{{}_{\mathrm{AR}}}^{-2p}\cdot 10^{-(n-1)p} \leq\left(\frac{\sigma\big(\Delta(x_k,r_0/10)\big)}{\sigma\big(\Delta(x_k,r_0)\big)}\right)^p \leq C_1^p\cdot\frac{w\big(\Delta(x_k,r_0/10)\big)}{w\big(\Delta(x_k,r_0)\big)}. \end{aligned} $$

(5.102)

Collecting then (5.101) and (5.102) we conclude that

$$\displaystyle \begin{aligned} \frac{w\big(\Delta(x_k,r_0)\big)}{w\big(\Delta(x_j,r_0)\big)}\leq C_{{}_{\mathrm{AR}}}^{2p}\cdot 10^{(n-1)p}\cdot C_1^p\cdot \frac{w\big(\Delta(x_k,r_0/10)\big)}{w\big(\Delta(x_j,r_0/10)\big)}\leq C_2, \end{aligned} $$

(5.103)

with

$$\displaystyle \begin{aligned} C_2:=2^{3p-3}\cdot 10^{(n-1)p}\cdot C_{{}_{\mathrm{AR}}}^{5p}\cdot C_0^{3p}\cdot c_{n,\lambda}^{-3p}. \end{aligned} $$

(5.104)

Since the latter estimate holds for every j, k ∈{1, …, N} with j ≠ k we obtain that for every j ∈{1, …, N}

$$\displaystyle \begin{aligned} w(\Sigma)\leq\sum_{j=1}^N w\big(\Delta(x_k,r_0)\big)\leq N\cdot C_2\cdot\,w\big(\Delta(x_j,r_0)\big) \leq C_3\cdot w\big(\Delta(x_j,r_0)\big), \end{aligned} $$

(5.105)

where

$$\displaystyle \begin{aligned} C_3:=2^{3p-3}\cdot 10^{(n-1)p}\cdot(40\lambda)^{n-1}\cdot C_{{}_{\mathrm{AR}}}^{5p+2}\cdot C_0^{3p}\cdot c_{n,\lambda}^{-3p}. \end{aligned} $$

(5.106)

From (5.105) and (5.90) used with r := r₀ ∈(0, diam( Σ)/(10λ)) we then obtain that for each h ∈ L^p( Σ, w) we have

(5.107)

Summing up in j further yields

(5.108)

Having established (5.108), the argument in the proof of Lemma 2.12 that has produced (2.529) (used with Δ :=  Σ) then currently gives

(5.109)

Together with (5.94) this finally proves that w ∈ A_p( Σ, σ) and that

$$\displaystyle \begin{aligned}{}[w]_{A_p}\leq C\|R\|{}_{L^p(\Sigma,w)\otimes{\mathcal{C}}\ell_n\to L^p(\Sigma,w)\otimes{\mathcal{C}}\ell_n}^{5p} \end{aligned} $$

(5.110)

for C ∈ (0, ∞) depending only on the Ahlfors regularity constant of Σ, n, and p.

Finally, from (5.91), (5.86), (5.110), and (5.73) we conclude that (5.69) holds. □

In concert with earlier results, Theorem 5.5 yields the following remarkable characterization of Muckenhoupt weights.

Theorem 5.6

Let $\Omega \subseteq {\mathbb {R}}^{n}$ be a UR domain and abbreviate $\sigma :={\mathcal {H}}^{n-1}\lfloor \partial \Omega$. Fix a function $w\in L^1_{\mathrm {loc}}(\partial \Omega ,\sigma )$ which is strictly positive σ-a.e. on ∂ Ω, along with an integrability exponent p ∈ (1, ∞). Then the following statements are equivalent.

• (1) The weight w belongs to the Muckenhoupt class A_p(∂ Ω, σ).

• (2) For each j ∈{1, …, n}, the j-th Riesz transform R_j on ∂ Ω ( cf. (4.297)) induces a linear and bounded operator on L^p(∂ Ω, w).

• (3) The Cauchy–Clifford operator C from (5.12) induces a linear and bounded mapping on $L^p(\partial \Omega ,w)\otimes {\mathcal {C}}\ell _n$.

• (4) The “transpose” Cauchy–Clifford operator C^# from (5.14) induces a linear and bounded mapping on $L^p(\partial \Omega ,w)\otimes {\mathcal {C}}\ell _n$.

• (5) For each complex-valued function $k\in {\mathscr {C}}^\infty \big (\mathbb {R}^{n}\setminus \{0\}\big )$ which is odd and positive homogeneous of degree 1 − n, the integral operator originally defined for each function $f\in L^1\big (\partial \Omega ,\frac {\sigma (x)}{1+|x|{ }^{n-1}}\big )$ as

  

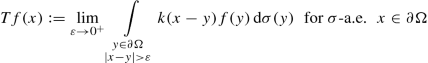  (5.111)

  induces a linear and bounded mapping on L^p(∂ Ω, w).

Proof

The implications (1)⇒(2) and (1)⇒(5) are direct consequences of Proposition 3.4 and (4.297). From (4.297) it is also clear that (5)⇒(2). To proceed, let ν = (ν₁, …, ν_n) denote the geometric measure theoretic outward unit normal to Ω. Then (5.13) and (5.15) imply that the Cauchy–Clifford operator C from (5.12) as well as the “transpose” Cauchy–Clifford operator C^# from (5.14) induce linear and bounded mappings on $L^p(\partial \Omega ,w)\otimes {\mathcal {C}}\ell _n$ whenever all Riesz transforms on ∂ Ω, i.e., R_j as in (4.297) with 1 ≤ j ≤ n, induce linear and bounded operators on L^p(∂ Ω, w). This takes care of the implications (2)⇒(3) and (2)⇒(4).

Going further, bring in the integral operator R defined as in (5.68) for Σ := ∂ Ω, i.e., Rf = e₁ ⊙ R₁f + ⋯ + e_n ⊙ R_nf for each $f\in L^1\big (\partial \Omega ,\frac {\sigma (x)}{1+|x|{ }^{n-1}}\big )\otimes {\mathcal {C}}\ell _n$, where {R_j}_1≤j≤n are Riesz transforms on ∂ Ω defined in (4.297). From definitions and the fact that ν ⊙ ν = −1 at σ-a.e. point of ∂ Ω (cf. (5.1)) we then see that for each $f\in L^1\big (\partial \Omega ,\frac {\sigma (x)}{1+|x|{ }^{n-1}}\big )\otimes {\mathcal {C}}\ell _n$ we have

$$\displaystyle \begin{aligned} \begin{array}{c} \nu\odot{\mathbf{C}}^{\#}f=\tfrac{1}{2}Rf,\quad -{\mathbf{C}}(\nu\odot f)=\tfrac{1}{2}Rf,\quad {\mathbf{C}}f=\nu\odot{\mathbf{C}}^{\#}(\nu\odot f), \\ {} {\mathbf{C}}^{\#}f=-\tfrac{1}{2}\nu\odot Rf,\quad {\mathbf{C}}f=\tfrac{1}{2}R(\nu\odot f),\quad {\mathbf{C}}^{\#}f=\nu\odot{\mathbf{C}}(\nu\odot f). \end{array} \end{aligned} $$

(5.112)

It is also clear that the statement in item (2) is equivalent to the demand that R induces a linear and bounded operator on $L^p(\partial \Omega ,w)\otimes {\mathcal {C}}\ell _n$. On account of this and (5.112) we then conclude that the implications (3)⇒(2) and (4)⇒(2) are valid. Finally, Theorem 5.5 gives the implication (2)⇒(1). The proof of Theorem 5.6 is therefore complete. □