Abstract
We construct the first non-interactive zero-knowledge (NIZK) proof systems in the fine-grained setting where adversaries’ resources are bounded and honest users have no more resources than an adversary. More concretely, our setting is the \(\mathsf {NC^1}\)-fine-grained setting, namely, all parties (including adversaries and honest participants) are in \(\mathsf {NC^1}\).
Our NIZK systems are for circuit satisfiability (SAT) under the worst-case assumption, \(\mathsf {NC^1}\subsetneq \mathsf{\oplus L/poly}\) . As technical contributions, we propose two approaches to construct NIZKs in the \(\mathsf {NC^1}\)-fine-grained setting. In stark contrast to the classical Fiat-Shamir transformation, both our approaches start with a simple \(\varSigma \)-protocol and transform it into NIZKs for circuit SAT without random oracles. Additionally, our second approach firstly proposes a fully homomorphic encryption (FHE) scheme in the fine-grained setting, which was not known before, as a building block. Compared with the first approach, the resulting NIZK only supports circuits with constant multiplicative depth, while its proof size is independent of the statement circuit size.
Extending our approaches, we obtain two NIZK systems in the uniform reference string model and two non-interactive zaps (namely, non-interactive witness-indistinguishability proof systems in the plain model). While the previous constructions from Ball, Dachman-Soled, and Kulkarni (CRYPTO 2020) require provers to run in polynomial-time, our constructions are the first one with provers in \(\mathsf {NC^1}\).
Y. Wang—Supported by the National Natural Science Foundation for Young Scientists of China under Grant Number 62002049 and the Fundamental Research Funds for the Central Universities under Grant Number ZYGX2020J017.
J. Pan—Supported by the Research Council of Norway under Project No. 324235.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Non-interactive zero-knowledge (NIZK) proof systems [11] are a central topic in complexity theory and theoretical cryptography. In the recent years, it also provides numerous novel applications in cryptography. An important line of research is to construct NIZKs based on different assumptions. An earlier work has shown that NIZKs require a trusted setup, such as a common reference string (CRS) [4]. Moreover, Pass and shelat [16] showed that (non-uniform) one-way functions are sufficient for NIZK for \(\mathsf {AM}\). Recently, it is possible to construct efficient NIZKs such as Diffie-Hellman-based constructions [12, 13]. In this paper, we are interested in NIZKs based on much mild assumptions.
\(\mathsf {NC^1}\) -fine-grained cryptography. Fine-grained cryptography [7] designs cryptographic schemes in a setting where adversaries have only bounded resources and honest users have no more resources than adversaries. In this setting, it is possible to have more efficient schemes and base their security on weaker, or extremely mild assumptions. Although this notion of cryptography was firstly proposed by Degwekar, Vaikuntanathan, and Vasudevan [7], it has long history starting from the Merkle key exchange protocol [15].
In this paper, we consider \(\mathsf {NC^1}\)-fine-grained cryptography where adversaries are in \(\mathsf {NC^1}\). Cryptography in this setting is often based on the worst-case assumption on complexity classes, \(\mathsf {NC^1}\subsetneq \mathsf{\oplus L/poly}\). Here \(\mathsf{\oplus L/poly}\) is the class of languages with polynomial-size branching programs, and all languages in \(\mathsf {NC^1}\) have polynomial-size branching programs of constant width by the Barrington theorem [3]. The \(\mathsf {NC^1}\subsetneq \mathsf{\oplus L/poly}\) assumption states that there exists at least one language having only polynomial-size branching programs with non-constant width.
We suppose that it is interesting to study \(\mathsf {NC^1}\)-fine-grained cryptography. First, it is a fundamental question to consider which kind of cryptographic schemes can be constructed in such a setting by assuming \(\mathsf {NC^1}\subsetneq \mathsf{\oplus L/poly}\). Currently, we know that one-way functions [7], (somewhat homomorphic) public-key encryption [5, 7], hash proof systems (HPS) [9], and attribute-based encryption [20] are possible in this setting. We want to explore whether it is possible to push the boundary further. Second, as pointed out in [7], these primitives in \(\mathsf {NC^1}\) can be combined with other constructions against polynomial-time adversaries under stronger assumptions. Although the resulting scheme relies on stronger assumptions (e.g., factoring, Diffie-Hellman, and learning with errors) for polynomial-time adversaries, it is secure for \(\mathsf {NC^1}\) adversaries as long as \(\mathsf {NC^1}\subsetneq \mathsf{\oplus L/poly}\).
Current NIZKs in \(\mathsf {NC^1}\) . We aim at constructing NIZKs in the \(\mathsf {NC^1}\)-fine-grained setting. To the best of our knowledge, there are three proof systems under the assumption \(\mathsf {NC^1}\subsetneq \mathsf{\oplus L/poly}\) [2, 9, 20], but none of them achieves our goal, and, in particular, it is inherently difficult to transform them in achieving our goal.
A fine-grained NIZK proof system has previously been constructed by Ball, Dachman-Soled, and Kulkarni [2] assuming \(\mathsf {NC^1}\subsetneq \mathsf{\oplus L/poly}\), but in a stronger setting, where the prover is polynomial-time and more powerful than \(\mathsf {NC^1}\) circuits and the verifier, simulator, and adversaries are in \(\mathsf {NC^1}\). To be a bit more technical, we suppose their requirement on polynomial-time provers is inherent, since their provers need to compute the determinant of some matrix, which cannot be done in \(\mathsf {NC^1}\). Another example is the hash proof system (HPS) by Egashira, Wang, and Tanaka [9]. Although in their scheme adversaries and all honest parties are in \(\mathsf {NC^1}\), an HPS is a weaker form of NIZK, namely, the designated verifier needs to hold the secret hash key to verify the proof. Recently, Wang, Pan, and Chen [20] proposed a quasi-adaptive NIZK in \(\mathsf {NC^1}\) with public verification. However, their scheme can only support languages that can be expressed as linear subspaces, which is rather restricted, and their scheme is in the weaker quasi-adaptive model, namely, their CRSs have to be dependent on the language parameter.
1.1 Our Contributions
We construct the first NIZK proof systems in the fully \(\mathsf {NC^1}\) setting, where adversaries, honest provers, and verifiers are all in \(\mathsf {NC^1}\). We note that this is in contrast to schemes in [2] which requires the provers to be polynomial and more powerful than \(\mathsf {NC^1}\) circuits. Similar to previous \(\mathsf {NC^1}\)-fine-grained primitives [5, 7, 9, 20], the security of our scheme is based on the \(\mathsf {NC^1}\subsetneq \mathsf{\oplus L/poly}\) assumption.
Our approach first constructs a simple \(\varSigma \)-protocol that runs in \(\mathsf {AC^0[2]}\) which is a subset of \(\mathsf {NC^1}\), and then compiles it to NIZKs for circuit satisfiability (SAT) in the CRS model. Our transformation does not require random oracles as in the classical Fiat-Shamir transformation [10], or pairings as in the recent work of Couteau and Hartmann [6].
Our transformation contains several intermediate steps, as described figuratively in Fig. 1. We first transform our \(\varSigma \)-protocol to a NIZK for linear languages, namely, a NIZK for proving whether a vector belongs to
where \(\mathbf {{M}}\in \{0, 1\}^{n\times t}\). Based on this, we construct an OR-proof system for disjunction.
Starting from our OR-proof, we have two methods to construct NIZKs for circuit SAT. Our first method uses the additive homomorphic encryption from Degwekar, Vaikuntanathan, and Vasudevan (DVV) [7] (in a non-black-box way) to transform our OR-proof to a NIZK for circuit SAT. Its proof size grows linearly with the size of the statement circuit. The resulting NIZK can prove statements that can be represented as \(\mathsf {NC^1}\) circuits, since our provers are \(\mathsf {NC^1}\) circuits.
We stress that in the (fully) \(\mathsf {NC^1}\)-fine-grained setting a statement circuit cannot go beyond \(\mathsf {NC^1}\). This is because if the statement circuit is outside \(\mathsf {NC^1}\), then even the honest prover in \(\mathsf {NC^1}\) cannot decide with the witness if the statement is true or not. However, if we allow the honest prover to run in polynomial-time as in [2], our construction works for any statement circuits with polynomial-size.
Our second method first constructs a fully homomorphic encryption (FHE) scheme in the \(\mathsf {NC^1}\) setting, and then uses it to construct a NIZK for circuit SAT. On the one hand, different to our first method, this NIZK’s proof size is independent of the statement size. On the other hand, our NIZK from the second method supports statements in \(\mathsf {AC^0_{CM}[2]}\), since our FHE supports homomorphic evaluation of \(\mathsf {AC^0_{CM}[2]}\) circuits. Here \(\mathsf {AC^0_{CM}[2]}\) circuits are \(\mathsf {AC^0[2]}\) circuits with constant multiplicative depth, where multiplicative depth can be thought of as the degree of the lowest-degree polynomial in GF(2) evaluating to a circuit [5] (See Definition 4).
Interlude: fine-grained FHE. We highlight that our FHE scheme is of independent interest. To the best of our knowledge, the scheme of Campanelli and Gennaro [5] is the only known somewhat homomorphic encryption (SHE) in the \(\mathsf {NC^1}\)-fine-grained setting, where SHE is a weaker notion of FHE. Thus, our scheme is the first FHE in the \(\mathsf {NC^1}\)-fine-grained setting. Moreover, our FHE is conceptually simpler and compatible with our OR-proof in constructing NIZK for circuit SAT. In terms of efficiency, our scheme is comparable to the SHE scheme in [5]: our public key has \(\lambda ^2\) bits, while theirs has \(O(\lambda ^3)\) bits. Also, our scheme uses less parallel running-time, in the sense that it only computes the parity of \(\lambda \) bits in parallel for homomorphic multiplication, while theirs has to compute the parity of \(\lambda ^2\) bits. Here \(\lambda \) is the security parameter.
We leave improving the power of homomorphic computation of our scheme as an open problem. We are also optimistic that all FHE-based applications can be realized in the \(\mathsf {NC^1}\)-fine-grained setting using our FHE, and we leave a detailed treatment of it as a future work.
Extensions. We extend our NIZKs to construct non-interactive zaps [8] (i.e., non-interactive witness-indistinguishability proof systems in the plain model) by improving the techniques in [12]. The key enabler for this is that all our NIZKs have verifiable correlated key generation which is a property used in [12] and formally defined by us. Roughly speaking, this property states that a perfectly sound CRS (i.e., a binding CRS) is correlated to a perfectly zero-knowledge one (i.e., a hiding CRS), and in some particular case this can even be verified.
All the aforementioned NIZKs are in the CRS model. We further extend them to the uniform random string (URS) model, where a trust setup only samples public coins.
1.2 Technical Details
In this section, we give more details about our techniques with a particular focus on constructing NIZKs for circuit SAT in the CRS model. A figurative overview for this is given in Fig. 1.
Starting point: a
\(\varSigma \)
-protocol in
\(\mathsf {AC^0[2]}\)
. Rather than directly constructing a NIZK under the worst-case assumption \(\mathsf {NC^1}\subsetneq \mathsf{\oplus L/poly}\), we first construct a \(\varSigma \)-protocol with unconditionally special soundness and special honest-verifier zero-knowledge. Our protocol does not require any cryptographic group structure where the discrete logarithm or factoring assumption holds. For the aforementioned linear language \(\mathsf {L}_{\mathbf {{M}}}\), the prover sends the commitment \(\mathbf {{C}}=\mathbf {{M}}\mathbf {{R}}\), where  , to the verifier and receives a challenge
, to the verifier and receives a challenge  back. The response to the challenge is \(\mathbf {{D}}=(\mathbf {{R}}||\mathbf {w})\mathbf {{A}}\), where \(\mathbf {{A}}=(\widehat{\mathbf {{R}}}||\widehat{\mathbf {{R}}} \widetilde{\mathbf {r}})^\top \) and \(\widehat{\mathbf {{R}}}=\begin{pmatrix}\mathbf {0}\\ \mathbf {{I}}_{\lambda -1}\end{pmatrix}\in \{0, 1\}^{\lambda \times (\lambda -1)}\). \(\mathbf {{I}}_{\lambda -1}\) is an identity matrix in \(\{0, 1\}^{(\lambda -1)\times (\lambda -1)}\). The verifier checks whether \((\mathbf {{C}}||\mathbf {x})\mathbf {{A}}=\mathbf {{M}}\mathbf {{D}}\). In our \(\varSigma \)-protocol, all computations are in GF(2), and all parties can run in \(\mathsf {AC^0[2]}\). We refer the reader to Sect. 3 for the detailed proof, which reflects our main technical contribution in this part.
back. The response to the challenge is \(\mathbf {{D}}=(\mathbf {{R}}||\mathbf {w})\mathbf {{A}}\), where \(\mathbf {{A}}=(\widehat{\mathbf {{R}}}||\widehat{\mathbf {{R}}} \widetilde{\mathbf {r}})^\top \) and \(\widehat{\mathbf {{R}}}=\begin{pmatrix}\mathbf {0}\\ \mathbf {{I}}_{\lambda -1}\end{pmatrix}\in \{0, 1\}^{\lambda \times (\lambda -1)}\). \(\mathbf {{I}}_{\lambda -1}\) is an identity matrix in \(\{0, 1\}^{(\lambda -1)\times (\lambda -1)}\). The verifier checks whether \((\mathbf {{C}}||\mathbf {x})\mathbf {{A}}=\mathbf {{M}}\mathbf {{D}}\). In our \(\varSigma \)-protocol, all computations are in GF(2), and all parties can run in \(\mathsf {AC^0[2]}\). We refer the reader to Sect. 3 for the detailed proof, which reflects our main technical contribution in this part.
Compiling \(\varSigma \) -protocol to NIZK. Couteau and Hartmann [6] showed how to convert a \(\varSigma \)-protocol into a NIZK for \(\mathsf {L}_{(g^{\mathbf {{M}}})}\), where \(\mathsf {L}_{(g^{\mathbf {{M}}})}\) is the language including all the group vectors with exponents in the span of \(\mathbf {{M}}\). Their main idea is to put the challenge originally in \(\mathbb {Z}_p\) into the group and set it as the common reference string. Verification can be executed by using bilinear map, and finding a valid proof can be reduced to breaking the (extended) kernel matrix Diffie-Hellman assumption. Although this assumption is falsifiable and has analysis in the generic group model and algebraic group model, we want a NIZK based on assumptions weaker than that. Moreover, in the fine-grained cryptographic landscape, we are not aware of the existence of any bilinear map.
Our work exploits the indistinguishability of the following two distributions against \(\mathsf {NC^1}\) adversaries used in [2, 5, 7, 9, 20]:

Here, \(\lambda \) is the security parameter, and the randomized sampling algorithms \({\mathsf {ZeroSamp}}\) and \({\mathsf {OneSamp}}\) output matrices with rank \(\lambda -1\) and full rank, respectively. Concrete definitions of these algorithms are given in Sect. 2.2. Note that this indistinguishability holds under the assumption \(\mathsf {NC^1}\subsetneq \mathsf{\oplus L/poly}\) [1, 14]. Based on the indistinguishability between \(D_0\) and \(D_1\), we develop a new compiler from a \(\varSigma \)-protocol to a NIZK in \(\mathsf {NC^1}\)-fine-grained cryptography.
The main idea is to generate \(\widehat{\mathbf {{R}}}\) in our \(\varSigma \)-protocol as  instead of \(\begin{pmatrix}\mathbf {0}\\ \mathbf {{I}}_{\lambda -1}\end{pmatrix}\), where \(\mathbf {e}_1^\lambda =(1,0,\cdots ,0)^\top \) and \({\mathsf {LSamp}}\) is an intermediate algorithm in \({\mathsf {ZeroSamp}}\). This makes the distribution of \(\mathbf {{A}}=(\widehat{\mathbf {{R}}} || \widehat{\mathbf {{R}}}\widetilde{\mathbf {r}})^\top \) in the \(\varSigma \)-protocol identical to \(D_0\) (see Sect. 2.2 for details). The hiding CRS of the resulting NIZK is \(\mathbf {{A}}\) with \(\widetilde{\mathbf {r}}\) being the simulation trapdoor, and a proof consists of \((\mathbf {{C}},\mathbf {{D}})\) (i.e., the first and third round messages of the \(\varSigma \)-protocol). Perfect zero knowledge follows from the honest-verifier zero-knowledge of the aforementioned \(\varSigma \)-protocol. To prove soundness, we switch the distribution of \(\mathbf {{A}}\) from \(D_0\) to \(D_1\), which corresponds to switching a hiding CRS to a binding one. In this case, the kernel of \(\mathbf {{A}}^\top \) becomes empty and there exists no invalid statements passing the verification.
instead of \(\begin{pmatrix}\mathbf {0}\\ \mathbf {{I}}_{\lambda -1}\end{pmatrix}\), where \(\mathbf {e}_1^\lambda =(1,0,\cdots ,0)^\top \) and \({\mathsf {LSamp}}\) is an intermediate algorithm in \({\mathsf {ZeroSamp}}\). This makes the distribution of \(\mathbf {{A}}=(\widehat{\mathbf {{R}}} || \widehat{\mathbf {{R}}}\widetilde{\mathbf {r}})^\top \) in the \(\varSigma \)-protocol identical to \(D_0\) (see Sect. 2.2 for details). The hiding CRS of the resulting NIZK is \(\mathbf {{A}}\) with \(\widetilde{\mathbf {r}}\) being the simulation trapdoor, and a proof consists of \((\mathbf {{C}},\mathbf {{D}})\) (i.e., the first and third round messages of the \(\varSigma \)-protocol). Perfect zero knowledge follows from the honest-verifier zero-knowledge of the aforementioned \(\varSigma \)-protocol. To prove soundness, we switch the distribution of \(\mathbf {{A}}\) from \(D_0\) to \(D_1\), which corresponds to switching a hiding CRS to a binding one. In this case, the kernel of \(\mathbf {{A}}^\top \) becomes empty and there exists no invalid statements passing the verification.
Extension to OR-proof. Let \(\mathbf {{A}}\) be a binding CRS in \(D_1\). From \(\mathbf {{A}}\), we show that a prover can derive a hiding CRS \(\mathbf {{A}}_{1-j}\) with a trapdoor \(\widetilde{\mathbf {r}}_{1-j}\) and a binding CRS \(\mathbf {{A}}_{j}\). Moreover, switching the distribution of \(\mathbf {{A}}\) to \(D_0\) leads both \(\mathbf {{A}}_j\) and \(\mathbf {{A}}_{1-j}\) to become hiding CRSs. Based on this crucial step, we develop a fine-grained version of the “OR-proof techniques” [12, 17] to achieve the target OR-proof system. Roughly, the prover generates proofs with respect to both \(\mathbf {{A}}_j\) and \(\mathbf {{A}}_{1-j}\). Soundness is guaranteed when one of them is binding, and perfect zero-knowledge is guaranteed when both are hiding.
NIZK for circuit SAT using DVV. We now give an overview on how we construct a NIZK for circuit SAT in \(\mathsf {NC^1}\) by using our OR-proof and improving the GOS framework by Groth, Ostrovsky, and Sahai [12].
In the GOS NIZK, for each input/output pair \(((\mathsf {w}_{i},\mathsf {w}_{j}),\mathsf {w}_{k})\) of a NAND gate, the prover encrypts the bits of wires with an additive homomorphic commitment scheme, and proves that the plaintexts satisfy the relation \(\mathsf {w}_{i}+\mathsf {w}_{j}+2\mathsf {w}_{k}-2\in \{0, 1\}\).Footnote 1 However, since all the computations are performed in GF(2) in \(\mathsf {NC^1}\)-fine-grained cryptography, \(\mathsf {w}_{i}+\mathsf {w}_{j}+2\mathsf {w}_{k}-2\in \{0, 1\}\) always holds, and thus proving this relation becomes meaningless.
To address the above problem, we adopt another OR-relation:
One can check that each valid input/output pair of a NAND gate should satisfy it.Footnote 2 Then we use the DVV encryption scheme by Degwekar, Vaikuntanathan, and Vasudevan [7] to encrypt \(\mathsf {w}_{i}\), \(\mathsf {w}_{j}\), and \(\mathsf {w}_{k}\) respectively and prove that the plaintexts satisfy this new relation with our OR-proof. There are two nice properties of the DVV encryption useful in our case: (1) additive homomorphism and (2) a ciphertext of 0 (respectively, 1) is in (respectively, outside) the linear subspace of the public key, which make it compatible with our OR-proof.
NIZK for circuit SAT using FHE. In our NIZK for circuit SAT mentioned above, we generate a ciphertext for each wire of a statement circuit and a proof of compliance for each gate. Thus, the final proof size grows linearly with the circuit size.
Our second construction circumvents this by constructing a fine-grained FHE scheme. In this way, we only have to encrypt the input bits (i.e., witness) and execute the fully homomorphic evaluation of a statement circuit on these ciphertexts to obtain an output ciphertext. Afterwards, we exploit our OR-proof to prove that all the input ciphertexts are valid and the output ciphertext corresponds to 1. The final NIZK proof does not include intermediate ciphertexts generated during the homomorphic evaluation. Thus, the proof size is independent of the circuit size. To verify the final proof, one can just evaluate the ciphertext homomorphically and check the proofs for the input/output ciphertexts. Due to the correctness of the FHE and the soundness of the OR-proof, a valid witness can be extracted from any valid proof with the secret key of the FHE.
Similar to the fine-grained SHE proposed by Campanelli and Gennaro [5], our FHE scheme supports the homomorphic evaluation of circuits in \(\mathsf {AC^0_{CM}[2]}\), which makes the supporting statement of the resulting NIZK somewhat limited. Using the generic technique in [5, Section 3.3], we can extend our FHE to support homomorphic evaluation of circuits in \(\mathsf {AC^0[2]}\) with constant number of non-constant fan-in gates. Also, our FHE enjoys short public key size and parallel running-time, and compatibility with our OR-proof.
“Extensions to non-interactive zap and NIZK in the URS Model. For the conversion from NIZKs to non-interactive zaps, the bulk of our technical contribution is to prove that all our NIZKs have verifiable correlated key generation. At the core of our proof we show that if \(\mathbf {{N}}_\lambda =\mathbf {{A}}_0+\mathbf {{A}}_1\) for any \((\mathbf {e}^\lambda _1||\overline{\mathbf {{A}}}_0^\top )\in {\mathsf {LSamp}}(\lambda )\) and any matrix, where \(\mathbf {{N}}_\lambda \) is some constant matrix (See Sect. 2), either \(\mathbf {{A}}_0\) or \(\mathbf {{A}}_1\) must be a binding CRS with perfect soundness. This allows us to improve the GOS technique to generically convert our NIZKs into non-interactive zaps.
Moreover, we show the existence of an algorithm that can sample matrices with only public coins, while its output distribution is identical to \(D_0\) and \(D_1\) with “half-half” probability. Since the CRSs of our NIZKs consist only of matrices in \(D_0\) and \(D_1\), we can sample CRSs by using this new algorithms for multiple times, and generate proofs for a same statement in parallel. Zero-knowledge follows from that of the underlying NIZK and the indistinguishability between \(D_0\) and \(D_1\). Statistical soundness holds since with high probability, at least one of the CRSs is binding. Since the sampling procedure for CRSs only uses public coins, the resulting NIZK is in the URS model.
2 Preliminaries
Notations. We note that all arithmetic computations are over GF(2) in this work. Namely, all arithmetic computations are performed with a modulus of 2. We write  (respectively, \(a=\mathcal {A}(b)\)) to denote the random variable outputted by a probabilistic (respectively, deterministic) algorithm (or circuit) \(\mathcal {A}\) on input b. By
(respectively, \(a=\mathcal {A}(b)\)) to denote the random variable outputted by a probabilistic (respectively, deterministic) algorithm (or circuit) \(\mathcal {A}\) on input b. By  we denote the process of sampling an element x from a set or distribution \(\mathcal {S}\) uniformly at random. Let \(\mathcal R\) be the randomness space of \(\mathcal {A}\),
we denote the process of sampling an element x from a set or distribution \(\mathcal {S}\) uniformly at random. Let \(\mathcal R\) be the randomness space of \(\mathcal {A}\),  is equivalent to \(a=\mathcal {A}(b;r)\) for
is equivalent to \(a=\mathcal {A}(b;r)\) for  . By \(\mathbf {x}\in \{0, 1\}^n\) we denote a column vector with size n and by, say, \(\mathbf {x}\in \{1\}\times \{0, 1\}^{n-1}\) we mean that the first element of \(\mathbf {x}\) is 1. By \(x_i\) (respectively, \(\mathsf x_i\)) we denote the ith element of a vector \(\mathbf {x}\) (respectively, \(\mathsf x\)). By [n] we denote the set \(\{1, \cdots , n\}\). By \(\mathsf {negl}\) we denote an unspecified negligible function.
. By \(\mathbf {x}\in \{0, 1\}^n\) we denote a column vector with size n and by, say, \(\mathbf {x}\in \{1\}\times \{0, 1\}^{n-1}\) we mean that the first element of \(\mathbf {x}\) is 1. By \(x_i\) (respectively, \(\mathsf x_i\)) we denote the ith element of a vector \(\mathbf {x}\) (respectively, \(\mathsf x\)). By [n] we denote the set \(\{1, \cdots , n\}\). By \(\mathsf {negl}\) we denote an unspecified negligible function.
For a matrix \(\mathbf {{A}}\in \{0, 1\}^{n\times t}\) with rank \(t'\le n\), we denote the sets \(\{\mathbf {y} \, | \, \exists \mathbf {x} \;\; \text{ s.t. } \;\; \mathbf {y} = \mathbf {{A}}\mathbf {x} \}\) and \(\{\mathbf {x} \, | \, \mathbf {{A}}\mathbf {x} = \mathbf {0} \}\) by \({{\,\mathrm{Im}\,}}(\mathbf {{A}})\) (i.e., the span of \(\mathbf {{A}}\)) and \({{\,\mathrm{Ker}\,}}(\mathbf {{A}})\) respectively. By \(\mathbf {{A}}^\bot \in \{0, 1\}^{n\times (n-t')}\) we denote a matrix consisting of \(n-t'\) linear independent column vectors in the kernel of \(\mathbf {{A}}^\top \). Note that for any \(\mathbf {y}\notin {{\,\mathrm{Im}\,}}(\mathbf {{A}})\), we have \(\mathbf {y}^\top \mathbf {{A}}^\bot \ne \mathbf {0}\). For a matrix \(\mathbf {{A}}\in \{0, 1\}^{\lambda \times \lambda }\), by \(\overline{\mathbf {{A}}}\) (respectively, \(\underline{\mathbf {{A}}}\)) we denote the upper \((\lambda -1)\times \lambda \) matrix (respectively, lower \(1\times \lambda \) vector) of \(\mathbf {{A}}\). Let \(b\in \{0, 1\}\), by \(b\mathbf {{A}}\) we denote a zero matrix \(\mathbf {{0}}\in \{0, 1\}^{n\times t}\) if \(b=0\) or \(\mathbf {{A}}\) if \(b=1\).
By \(\mathbf {e}^\lambda _i\) we denote the column vector in \(\{0, 1\}^\lambda \) with the ith element being 1 and the other elements being 0. By \(\mathbf {{0}}\) we denote a zero vector or matrix. By \(\mathbf {{I}}_n\) we denote an identity matrix in \(\{0, 1\}^{n\times n}\). By \(\mathbf {{M}}^n_0\), \(\mathbf {{M}}^n_1\), and \(\mathbf {{N}}_n\), we denote the following \(n \times n\) matrices: \(\mathbf {{M}}^n_0 = \begin{pmatrix}\mathbf {0} &{}0\\ \mathbf {{I}}_{n-1} &{} \mathbf {0}\end{pmatrix}\), \(\mathbf {{M}}^n_1 = \begin{pmatrix}&{}\mathbf {0} &{}1\\ &{}\mathbf {{I}}_{n-1} &{} \mathbf {0}\end{pmatrix}\), \(\mathbf {{N}}_n=\begin{pmatrix}\mathbf {0}&{} \mathbf {{0}}\\ 1&{}\mathbf {0} \end{pmatrix}\).
2.1 Function Families
In this section, we recall the definitions of function family, \(\mathsf {NC^1}\) circuits, \(\mathsf {AC^0[2]}\) circuits, \(\mathsf {AC^0_{CM}[2]}\) circuits, and \(\mathsf{\oplus L/poly}\) circuits. Note that \(\mathsf {AC^0[2]}\subsetneq \mathsf {NC^1}\) [18, 19].
Definition 1
(Function family). A function family is a family of (possibly randomized) functions \(\mathcal {F}=\{f_{\lambda }\}_{\lambda \in \mathbb {N}}\), where for each \(\lambda \), \(f_{\lambda }\) has a domain \(D^f_{\lambda }\) and a range \(R^f_{\lambda }\).
Definition 2
( \(\mathsf {NC^1}\) ). The class of (non-uniform) \(\mathsf {NC^1}\) function families is the set of all function families \(\mathcal {F} = \{f_{\lambda }\}_{\lambda \in \mathbb {N}}\) for which there is a polynomial \(p(\cdot )\) and constant c such that for each \(\lambda \), \(f_{\lambda }\) can be computed by a (randomized) circuit of size \(p(\lambda )\), depth \(c\log (\lambda )\), and fan-in 2 using AND, OR, and NOT gates.
Definition 3
( \(\mathsf {AC^0[2]}\) ). The class of (non-uniform) \(\mathsf {AC^0[2]}\) function families is the set of all function families \(\mathcal {F} = \{f_{\lambda }\}_{\lambda \in \mathbb {N}}\) for which there is a polynomial \(p(\cdot )\) and constant c such that for each \(\lambda \), \(f_{\lambda }\) can be computed by a (randomized) circuit of size \(p(\lambda )\), depth c, and unbounded fan-in using AND, OR, NOT, and PARITY gates.
One can see that multiplication of a constant number of matrices can be performed in \(\mathsf {AC^0[2]}\), since it can be done in constant-depth with PARITY gates.
Next we recall the definitions of multiplicative depth in [5], which can be thought of as the degree of the lowest-degree polynomial in GF(2) evaluating to a circuit.
Definition 4
(Multiplicative depth [5]). Let C be a circuit, \(\mathsf {type}_C(g)\) be the type of a gate g in C, and \(\mathsf {parents}_C(g)\) be the list of gates of C whose output is an input to C. The multipicative depth of C is \(\mathsf {md}(g_\mathsf {out})\), where \(g_\mathsf {out}\) is the output gate and the function \(\mathsf {md}\) is defined as
\(\mathsf {md}(g)={\left\{ \begin{array}{ll} 1 &{} \text {if}\,\ \mathsf {type}_C(g)=\mathsf{input} \\ \max \{\mathsf {md}(g'):g'\in \mathsf {parents}_C(g)\} &{} \text {if}\,\ \mathsf {type}_C(g)=\mathsf{XOR} \\ \sum _{g'\in \mathsf {parents}_C(g)}\mathsf {md}(g') &{} \text {if}\,\ \mathsf {type}_C(g)\in \{\mathsf{AND},\mathsf{OR}\} \end{array}\right. },\) where the sum in the last case is over the integers.
Definition 5
( \(\mathsf {AC^0_{CM}[2]}\) [5]). \(\mathsf {AC^0_{CM}[2]}\) is the class of circuits in \(\mathsf {AC^0[2]}\) with constant multiplicative depth (as defined in Definition 4).
Note that an AND gate of fan-in \(\lambda \) (i.e., the security parameter) cannot be performed in \(\mathsf {AC^0_{CM}[2]}\).
Definition 6
( \(\mathsf{\oplus L/poly}\) ). \(\mathsf{\oplus L/poly}\) is the set of all boolean function families \(\mathcal {F} = \{f_{\lambda }\}_{\lambda \in \mathbb {N}}\) for which there is a constant c such that for each \(\lambda \), there is a non-deterministic Turing machine \(\mathcal M_{\lambda }\) such that for each input x with length \(\lambda \), \(\mathcal M_{\lambda }(x)\) uses at most \(c\log (\lambda )\) space, and \(f_{\lambda }(x)\) is equal to the parity of the number of accepting paths of \(\mathcal M_{\lambda }(x)\).
2.2 Sampling Procedure
We now recall the definitions of four sampling procedures \({\mathsf {LSamp}}\), \({\mathsf {RSamp}}\), \({\mathsf {ZeroSamp}}\), and \({\mathsf {OneSamp}}\) in Fig. 2. Note that the output of \({\mathsf {ZeroSamp}}(n)\) is always a matrix of rank \(n-1\) and the output of \({\mathsf {OneSamp}}(n)\) is always a matrix of full rank [7]. Additionally, in Fig. 3, we define an algorithm \(\widetilde{{\mathsf {ZeroSamp}}}\) which runs in exactly the same way as \({\mathsf {ZeroSamp}}\) except that it additionally outputs a vector \(\widetilde{\mathbf {r}}=(r_i)_{i=1}^{n-1}\) consisting of the random bits used in generating \(\mathbf {{R}}_1\). We have \(\begin{pmatrix}\widetilde{\mathbf {r}}\\ 1\end{pmatrix}\in {{\,\mathrm{Ker}\,}}(\mathbf {{R}}_0\mathbf {{M}}^n_0\mathbf {{R}}_1)\), since \(\mathbf {{R}}_0\mathbf {{M}}^n_0\mathbf {{R}}_1 \begin{pmatrix}\widetilde{\mathbf {r}}\\ 1\end{pmatrix}=\mathbf {{R}}_0\begin{pmatrix}\mathbf {0} &{} 0\\ \mathbf {{I}}_{\lambda -1} &{} \mathbf {0}\end{pmatrix}\begin{pmatrix} \mathbf {{I}}_{\lambda -1}&{} \widetilde{\mathbf {r}} \\ \mathbf {0}&{} 1 \end{pmatrix}\begin{pmatrix}\widetilde{\mathbf {r}}\\ 1\end{pmatrix}=\mathbf {{0}}\). This implies the following lemma.
Lemma 1
(Lemma 3 in [9]). For all \(\lambda \in \mathbb {N}\) and all \(\mathbf {{M}} \in {\mathsf {ZeroSamp}}(\lambda )\), it holds that \({{\,\mathrm{Ker}\,}}(\mathbf {{M}}) = \{\mathbf {0}, \mathbf {k} \}\) where \(\mathbf {k}\) is a vector such that \(\mathbf {k} \in \{0, 1\}^{\lambda -1}\times \{1\}\).
We now recall an assumption and a lemma on \({\mathsf {ZeroSamp}}\) and \({\mathsf {OneSamp}}\) given in [7].
Definition 7
(Fine-grained matrix linear assumption [7]). There exists a polynomial \(n=n(\lambda )\) in the security parameter \(\lambda \) such that for any family \(\mathcal {A}= \{a_{\lambda }\}_{\lambda \in \mathbb {N}}\) in \(\mathsf {NC^1}\) and any \(\lambda \in \mathbb {N}\), we have

Lemma 2
(Lemma 4.3 in [7]). If \(\mathsf {NC^1}\subsetneq \mathsf{\oplus L/poly}\), then the fine-grained matrix linear assumption holds.
Remark. Notice that for any polynomial \(n=n(\lambda )\), we have \(\{f_{n}\}_{\lambda \in N} \in \mathsf {NC^1}\) iff \(\{f_\lambda \}_{\lambda \in N} \in \mathsf {NC^1}\) since \(O(\log (n(\lambda )))=O(\log (\lambda ))\). Hence, in the above lemma, we can also set \(n(\cdot )\) as an identity function, i.e., \(n=\lambda \). For simplicity, in the rest of the paper, we always let \({\mathsf {ZeroSamp}}(\cdot )\) and \({\mathsf {OneSamp}}(\cdot )\) take as input \(\lambda \).
The following lemma indicates a simple relation between the distributions of the outputs of \({\mathsf {ZeroSamp}}(\lambda )\) and \({\mathsf {OneSamp}}(\lambda )\).
Lemma 3
(Lemma 7 in [9]). For all \(\lambda \in \mathbb {N}\), the distributions of \(\mathbf {{M}} + \mathbf {{N}}_\lambda \) and \(\mathbf {{M}}'\) are identical, where  and
and  .
.
2.3 Proof Systems
In this section, we give the definitions of \(\varSigma \)-protocol, NIZK, and non-interactive zap. Below, for a language description \(\rho \) with the associated language \(\mathsf {L}_\rho \) and relation \({\mathsf {R}}_\rho \), by \(\mathsf {x}\in \mathsf {L}_\rho \) we mean that there exists \(\mathsf w\) such that \({\mathsf {R}}_\rho (\mathsf {x},\mathsf w)=1\).
\(\varSigma \) -protocol. The definition of \(\varSigma \)-protocol is as follows.
Definition 8
( \(\varSigma \) -protocol). A \(\mathcal C_1\)-\(\varSigma \)-protocol for a language distribution \(\{\mathcal {D}_\lambda \}_{\lambda \in \mathbb {N}}\) is a function family \(\{{\mathsf {Prover}}^1_\lambda ,\, {\mathsf {ChSet}}_\lambda ,\, {\mathsf {Prover}}^2_\lambda ,\, {\mathsf {SVer}}_\lambda ,\,{\mathsf {SExt}}_\lambda ,{\mathsf {SSim}}_\lambda \}_{\lambda \in \mathbb {N}}\in \mathcal C_1\) with the following properties.
-
\({\mathsf {Prover}}^1_\lambda (\rho \in \mathcal {D}_\lambda ,\mathsf {x},\mathsf w)\) returns a commitment \(\mathsf {com}\) and a state \(\mathsf {st}\).
-
\({\mathsf {ChSet}}_\lambda \) returns a uniformly random string \(\mathsf {ch}\).
-
\({\mathsf {Prover}}^2_\lambda (\mathsf {ch},\mathsf {st})\) returns a response \(\mathsf {resp}\).
-
\({\mathsf {SVer}}_\lambda (\rho ,\mathsf {x},\mathsf {com},\mathsf {ch},\mathsf {resp})\) deterministically returns 1 (accept) or 0 (reject).
-
\({\mathsf {SExt}}_\lambda (\mathsf {x},\mathsf {com},(\mathsf {ch},\mathsf {resp}),(\mathsf {ch}',\mathsf {resp}'))\) returns a witness \(\mathsf w\).
-
\({\mathsf {SSim}}_\lambda (\rho ,\mathsf {x},\mathsf {ch})\) returns a commitment \(\mathsf {com}\) and a response \(\mathsf {resp}\).
Completeness is satisfied if for all \(\lambda \in \mathbb {N}\), all \(\rho \in \mathcal {D}_\lambda \) with the associated relation \({\mathsf {R}}_\rho \), all \((\mathsf {x},\mathsf w)\) such that \({\mathsf {R}}_\rho (\mathsf {x},\mathsf w)=1\), all \((\mathsf {com},\mathsf {st}) \in {\mathsf {Prover}}^1_\lambda (\rho ,\mathsf {x},\mathsf w)\), all \(\mathsf {ch}\in {\mathsf {ChSet}}_\lambda \), and all \(\mathsf {resp}\in {\mathsf {Prover}}^2_\lambda (\mathsf {ch}, \mathsf {st})\), we have \({\mathsf {SVer}}_\lambda (\rho ,\mathsf {x},\mathsf {com},\mathsf {ch},\mathsf {resp})=1\).
Special Soundness is satisfied if for all \(\lambda \in \mathbb {N}\), all \(\rho \in \mathcal {D}_\lambda \), and all \((\mathsf {x}, \mathsf {com},(\mathsf {ch},\mathsf {resp}),(\mathsf {ch}',\mathsf {resp}'))\) such that \(\mathsf {ch}\ne \mathsf {ch}'\) satisfying
we have \({\mathsf {R}}_\rho (\mathsf {x},\mathsf w)=1\) for \(\mathsf w={\mathsf {SExt}}_\lambda (\mathsf {x},\mathsf {com},(\mathsf {ch},\mathsf {resp}),(\mathsf {ch}',\mathsf {resp}'))\).
Special honest-verifier zero-knowledge is satisfied if for all \(\lambda \in \mathbb {N}\), all \(\rho \in \mathcal {D}_\lambda \), all \((\mathsf {x},\mathsf w)\) such that \({\mathsf {R}}_\rho (\mathsf {x},\mathsf w)=1\), and all \(\mathsf {ch}\in {\mathsf {ChSet}}_\lambda \), the distributions of \((\mathsf {com},\mathsf {resp})\) and \((\mathsf {com}',\mathsf {resp}')\) are identical, where  ,
,  , and
, and  .
.
NIZK. We now give the definition of fine-grained NIZK with composable zero-knowledge and statistical/perfect soundness.
Definition 9
(Non-interactive zero-knowledge (NIZK) proof). A \(\mathcal C_1\) -NIZK for a set of language distributions \(\{\mathcal {D}_\lambda \}_{\lambda \in \mathbb {N}}\) is a function family \({\mathsf {NIZK}}=\{{\mathsf {Gen}}_\lambda ,{\mathsf {TGen}}_\lambda ,{\mathsf {Prove}}_\lambda ,{\mathsf {Ver}}_\lambda ,{\mathsf {Sim}}_\lambda \}_{\lambda \in \mathbb {N}}\in \mathcal C_1\) with the following properties.
-
\({\mathsf {Gen}}_\lambda \) returns a binding CRS \(\mathsf {crs}\).
-
\({\mathsf {TGen}}_\lambda \) returns a hiding CRS \(\mathsf {crs}\) and a simulation trapdoor \(\mathsf {td}\).
-
\({\mathsf {Prove}}_\lambda (\mathsf {crs}, \rho \in \mathcal {D}_\lambda , \mathsf {x},\mathsf w)\) returns a proof \(\pi \).
-
\({{\mathsf {Ver}}}_\lambda (\mathsf {crs},\rho ,\mathsf {x},\pi )\) deterministically returns 1 (accept) or 0 (reject).
-
\({\mathsf {Sim}}_\lambda (\mathsf {crs},\mathsf {td},\rho ,\mathsf {x})\) returns a simulated proof \(\pi \).
Completeness is satisfied if for all \(\lambda \in \mathbb {N}\), all \(\rho \in \mathcal {D}_\lambda \) with the associated relation \({\mathsf {R}}_\rho \), all \((\mathsf {x},\mathsf w)\) such that \({\mathsf {R}}_\rho (\mathsf {x},\mathsf w)=1\), all \(\mathsf {crs}\in {\mathsf {Gen}}_\lambda \), and all \(\pi \in {\mathsf {Prove}}_\lambda (\mathsf {crs}, \rho , \mathsf {x},\mathsf w)\), we have \({\mathsf {Ver}}_\lambda (\mathsf {crs},\rho , \mathsf {x},\pi )=1\).
\(\mathcal C_2\) -composable zero-knowledge is satisfied if for any adversary \(\mathcal {A}=\{a_\lambda \}_{\lambda \in \mathbb {N}}\in \mathcal C_2\), we have

and for all \(\lambda \in \mathbb {N}\), all \(\rho \in \mathcal {D}_\lambda \), and all \((\mathsf {x},\mathsf w)\) such that \({\mathsf {R}}_\rho (\mathsf {x},\mathsf w)=1\), the following distributions are identical.

where  .
.
Statistical soundness is satisfied if for all \(\lambda \in \mathbb {N}\) and all \(\rho \in \mathcal {D}_\lambda \), we have

where \(\mathsf {x}\in \mathsf {L}_\rho \) iff there exists \(\mathsf w\) such that \({\mathsf {R}}_\rho (\mathsf {x},\mathsf w)=1\).
Perfect soundness is satisfied if the above probability is 0.
Definition 10
(NIZK in the uniform random string (URS) model.). A NIZK \({\mathsf {NIZK}}=\{{\mathsf {Gen}}_\lambda ,{\mathsf {TGen}}_\lambda ,{\mathsf {Prove}}_\lambda ,{\mathsf {Ver}}_\lambda ,{\mathsf {Sim}}_\lambda \}_{\lambda \in \mathbb {N}}\) is in the URS model if \({\mathsf {Gen}}_\lambda \) only samples a public coin  at random for some polynomial p and returns \(\mathsf {urs}\).
at random for some polynomial p and returns \(\mathsf {urs}\).
Non-interactive Zap. A non-interactive zap is a witness-indistinguishable non-interactive proof system in the plain model, where there is no trusted setup. The definition is as follows.
Definition 11
(Non-interactive zap). A \(\mathcal C_1\) -non-interactive zap for a set of language distributions \(\{\mathcal {D}_\lambda \}_{\lambda \in \mathbb {N}}\) is a function family \({\mathsf {ZAP}}=\{{\mathsf {ZProve}}_\lambda ,{\mathsf {ZVer}}_\lambda \}_{\lambda \in \mathbb {N}}\) with the following properties.
-
\({\mathsf {ZProve}}_\lambda (\rho \in \mathcal {D}_\lambda , \mathsf {x},\mathsf w)\) returns a proof \(\pi \).
-
\({\mathsf {ZVer}}_\lambda (\rho ,\mathsf {x},\pi )\) deterministically returns 1 (accept) or 0 (reject).
Completeness is satisfied if for all \(\lambda \in \mathbb {N}\), all \(\rho \in \mathcal {D}_\lambda \), all \((\mathsf {x},\mathsf w)\) such that \({\mathsf {R}}_\rho (\mathsf {x},\mathsf w)=1\), and all \(\pi \in {\mathsf {ZProve}}_\lambda (\rho , \mathsf {x},\mathsf w)\), we have \({\mathsf {ZVer}}_\lambda (\rho , \mathsf {x},\pi )=1\).
\(\mathcal C_2\) -witness indistinguishability is satisfied if for all \(\lambda \in \mathbb {N}\), all \(\rho \in \mathcal {D}_\lambda \) with the associated relation \({\mathsf {R}}_\rho \), all \((\mathsf {x},\mathsf w_0,\mathsf w_1)\) such that \({\mathsf {R}}_\rho (\mathsf {x},\mathsf w_0)={\mathsf {R}}_\rho (\mathsf {x},\mathsf w_1)=1\), and any adversary \(\mathcal {A}=\{a_\lambda \}_{\lambda \in \mathbb {N}}\in \mathcal C_2\), we have

Perfect soundness is satisfied if for all \(\lambda \in \mathbb {N}\), all \(\rho \in \mathcal {D}_\lambda \), all \(\mathsf {x}\notin \mathsf {L}_\rho \), and all \(\pi \), we have \({\mathsf {ZVer}}_\lambda (\rho ,\mathsf {x},\pi )=0\).
3 \(\mathsf {AC^0[2]}\)-\(\varSigma \)-Protocol for Linear Languages
Let \(\mathcal {D}_{\lambda }\) be a probability distribution outputting language descriptions \(\mathbf {{M}}\in \{0, 1\}^{n\times t}\), where \(n(\cdot )\) and \(t(\cdot )\) are functions in \(\lambda \). We define the associated language as \(\mathsf {L}_{\mathbf {{M}}}=\{ {\mathbf {t}}:\exists \mathbf {w} \in \{0, 1\}^t, \text { s.t. } \mathbf {t}= \mathbf {{M}} \mathbf {w}\}\). For the associated relation \({\mathsf {R}}_{\mathbf {{M}}}\), we have \({\mathsf {R}}_{\mathbf {{M}}}(\mathbf {x},\mathbf {w})=1\) iff \(\mathbf {x}=\mathbf {{M}}\mathbf {w}\). Let \(\widehat{\mathbf {{R}}}=\begin{pmatrix}\mathbf {0}\\ \mathbf {{I}}_{\lambda -1}\end{pmatrix}\). We give a \(\varSigma \)-protocol \({\mathsf {\varSigma }}\) for \(\{\mathcal {D}_\lambda \}\) in Fig. 4.
Definition of \({\mathsf {\varSigma }}=\{{\mathsf {Prover}}^1_\lambda ,{\mathsf {ChSet}}_\lambda ,{\mathsf {Prover}}^2_\lambda ,{\mathsf {SVer}}_\lambda ,{\mathsf {SExt}}_\lambda ,{\mathsf {SSim}}_\lambda \}_{\lambda \in \mathbb {N}}\). Note that \(\widehat{\mathbf {{R}}}^\top =(\mathbf {0}|| \mathbf {{I}}_{\lambda -1})\) where \(\mathbf {{I}}_{\lambda -1}\) is an identity matrix in \(\{0, 1\}^{(\lambda -1)\times (\lambda -1)}\).
Theorem 1
\({\mathsf {\varSigma }}\) is an \(\mathsf {AC^0[2]}\)-\(\varSigma \)-protocol with special soundness and special honest-verifier zero-knowledge.
Proof
First, we note that \(\{{\mathsf {Prover}}^1_\lambda ,{\mathsf {ChSet}}_\lambda ,{\mathsf {Prover}}^2_\lambda ,{\mathsf {SVer}}_\lambda ,{\mathsf {SExt}}_\lambda ,{\mathsf {SSim}}_\lambda \}_{\lambda \in \mathbb {N}}\) are computable in \(\mathsf {AC^0[2]}\), since they only involve operations including multiplication of a constant number of matrices and sampling random bits.
Completeness. Perfect completeness follows from the fact that for \(\mathbf {{C}}=\mathbf {{M}}\mathbf {{R}}\) and \(\mathbf {{D}}=(\mathbf {{R}}||\mathbf {w})\mathbf {{A}}\), we have \( (\mathbf {{C}}||\mathbf {x})\mathbf {{A}}=(\mathbf {{M}}\mathbf {{R}}||\mathbf {{M}}\mathbf {w})\mathbf {{A}}=\mathbf {{M}}(\mathbf {{R}}||\mathbf {w})\mathbf {{A}}=\mathbf {{M}}\mathbf {{D}}\).
Special Soundness. For a statement \(\mathbf {x}\), a commitment \((\mathbf {{C}},\widehat{\mathbf {{R}}})\), and two valid challenge/response pairs \(((\widetilde{\mathbf {r}},\mathbf {{D}}),(\widetilde{\mathbf {r}}',\mathbf {{D}}'))\) such that \(\widetilde{\mathbf {r}}\ne \widetilde{\mathbf {r}}'\), we have
Combining the above two equations yields \( \mathbf {x} ((\widetilde{\mathbf {r}}^{\top }-\widetilde{\mathbf {r}}'^{\top }) \widehat{\mathbf {{R}}}^\top )=\mathbf {{M}}(\mathbf {{D}}-\mathbf {{D}}'). \) Since the rank of \(\widehat{\mathbf {{R}}}\) is \(\lambda -1\), we have \(\widetilde{\mathbf {r}}^{\top }\widehat{\mathbf {{R}}}^\top \ne \widetilde{\mathbf {r}}'^{\top }\widehat{\mathbf {{R}}}^\top \) if \(\widetilde{\mathbf {r}}^{\top }\ne \widetilde{\mathbf {r}}'^{\top }\). Let the ith bit of \((\widetilde{\mathbf {r}}^{\top }-\widetilde{\mathbf {r}}'^{\top }) \widehat{\mathbf {{R}}}^\top \) be 1 and the ith column vector of \(\mathbf {{D}}-\mathbf {{D}}'\) be \(\mathbf {d}_i\), we have \(\mathbf {x}=\mathbf {{M}}\mathbf {d}_i\). Therefore, the extractor can successfully extract a witness for \(\mathbf {x}\). This completes the proof of special soundness.
Special Honest-Verifier Zero-Knowledge. For \(\mathbf {x}=\mathbf {{M}}\mathbf {w}\), since \(\mathbf {{M}}\mathbf {{R}}=\mathbf {{M}}(\mathbf {{R}}+\mathbf {w}\cdot \widetilde{\mathbf {r}}^\top )-\mathbf {x}\cdot \widetilde{\mathbf {r}}^\top \) and
and the distribution of \(\mathbf {{R}}+\mathbf {w}\cdot \widetilde{\mathbf {r}}^\top \) is uniform for  , the simulator perfect simulates honest proofs, completing the proof of special honest-verifier zero-knowledge.
, the simulator perfect simulates honest proofs, completing the proof of special honest-verifier zero-knowledge.
Putting all the above together, Theorem 1 immediately follows. \(\square \)
4 Fine-Grained NIZK for Linear Languages
In this section, we show how to compile the \(\varSigma \)-protocol in Sect. 3 to a fine-grained NIZK for linear languages.
Let \(\mathcal {D}_{\lambda }\) be a probability distribution outputting language descriptions \(\mathbf {{M}}\) of rank \(t'< n\) from \(\{0, 1\}^{n\times t}\), where \(n(\cdot )\), \(t(\cdot )\), and \(t'(\cdot )\) are functions in \(\lambda \) and there exists \(\mathbf {{M}}^\bot \in \{0, 1\}^{n\times (n-t')}\) such that \(\mathbf {{M}}^\top \mathbf {{M}}^\bot =\mathbf {{0}}\). We define the language as
For the associated relation \({\mathsf {R}}_{\mathbf {{M}}}\), we have \({\mathsf {R}}_{\mathbf {{M}}}(\mathbf {x},\mathbf {w})=1\) iff \(\mathbf {x}=\mathbf {{M}}\mathbf {w}\). We give the construction of NIZK in Fig. 5. Note that each proof of our NIZK consists of a commitment/response pair in our \(\varSigma \)-protocol, and \(\mathbf {{A}}\) used by \({\mathsf {Prover}}^2_\lambda \) and \({\mathsf {SVer}}_\lambda \) is generated by using \({\mathsf {OneSamp}}(\lambda )\) and plays a binding CRS now. A hiding CRS is generated by \(\widetilde{{\mathsf {ZeroSamp}}}(\lambda )\), and its trapdoor \(\widetilde{\mathbf {r}}\) essentially corresponds to the challenge in the \(\varSigma \)-protocol. Roughly, soundness follows from the fact that when \(\mathbf {{A}}\) is of full rank, the kernel of \(\mathbf {{A}}^\top \) is empty and no invalid proof can pass the verification. Zero-knowledge follows immediately from that of our \(\varSigma \)-protocol when switching \(\mathbf {{A}}\) to a non-full rank matrix.
Theorem 2
If \(\mathsf {NC^1}\subsetneq \mathsf{\oplus L/poly}\), then \({\mathsf {LNIZK}}\) in Fig. 5 is an \(\mathsf {AC^0[2]}\)-NIZK with perfect soundness and \(\mathsf {NC^1}\)-composable zero-knowledge.
Proof
First, we note that \(\{{\mathsf {Gen}}_\lambda ,{\mathsf {TGen}}_\lambda ,{\mathsf {Prove}}_\lambda ,{\mathsf {Ver}}_\lambda ,{\mathsf {Sim}}_\lambda \}_{\lambda \in \mathbb {N}}\) are computable in \(\mathsf {AC^0[2]}\), since they only involve operations including multiplications of a constant number of matrices and sampling random bits.
Completeness. Completeness follows from the fact that for \(\mathbf {x}=\mathbf {{M}}\mathbf {w}\), \(\mathbf {{C}}=\mathbf {{M}}\mathbf {{R}}\), and \(\mathbf {{D}}=(\mathbf {{R}}||\mathbf {w})\mathbf {{A}}\), we have \( (\mathbf {{C}}||\mathbf {x})\mathbf {{A}}=(\mathbf {{M}}\mathbf {{R}}||\mathbf {{M}}\mathbf {w})\mathbf {{A}}=\mathbf {{M}}(\mathbf {{R}}||\mathbf {w})\mathbf {{A}}=\mathbf {{M}}\mathbf {{D}}. \)
\(\mathsf {NC^1}\)
-composable Zero-Knowledge. For any adversary \(\mathcal {A}=\{a_\lambda \}_{\lambda \in \mathbb {N}}\in \mathsf {NC^1}\), the advantage of \(a_\lambda \) in distinguishing  from
from  is the same as its advantage in breaking the fine-grained matrix linear assumption, which is negligible if \(\mathsf {NC^1}\subsetneq \mathsf{\oplus L/poly}\), due to Lemma 2.
is the same as its advantage in breaking the fine-grained matrix linear assumption, which is negligible if \(\mathsf {NC^1}\subsetneq \mathsf{\oplus L/poly}\), due to Lemma 2.
According to the definition of \(\widetilde{{\mathsf {ZeroSamp}}}\) (see Sect. 2.2), we can give the running procedure of \({\mathsf {TGen}}_\lambda \) in an explicit way, namely, randomly sampling  and
and  , and setting \(\mathbf {{A}}^\top =\mathbf {{R}}_0\mathbf {{M}}_0^\lambda \mathbf {{R}}_1\). In this case, \(\mathbf {{A}}^\top =(\mathbf {e}^\lambda _1||\widehat{\mathbf {{R}}})\begin{pmatrix}\mathbf {0} &{} 0\\ \mathbf {{I}}_{\lambda -1} &{} \mathbf {0}\end{pmatrix}\begin{pmatrix} \mathbf {{I}}_{\lambda -1}&{} \widetilde{\mathbf {r}} \\ \mathbf {0}&{} 1 \end{pmatrix}=(\widehat{\mathbf {{R}}}||\widehat{\mathbf {{R}}}\widetilde{\mathbf {r}})\). Then for \(\mathbf {x}=\mathbf {{M}}\mathbf {w}\), we have \(\mathbf {{M}}\mathbf {{R}}=\mathbf {{M}}(\mathbf {{R}}+\mathbf {w}\cdot \widetilde{\mathbf {r}}^\top )-\mathbf {x}\cdot \widetilde{\mathbf {r}}^\top \) and
, and setting \(\mathbf {{A}}^\top =\mathbf {{R}}_0\mathbf {{M}}_0^\lambda \mathbf {{R}}_1\). In this case, \(\mathbf {{A}}^\top =(\mathbf {e}^\lambda _1||\widehat{\mathbf {{R}}})\begin{pmatrix}\mathbf {0} &{} 0\\ \mathbf {{I}}_{\lambda -1} &{} \mathbf {0}\end{pmatrix}\begin{pmatrix} \mathbf {{I}}_{\lambda -1}&{} \widetilde{\mathbf {r}} \\ \mathbf {0}&{} 1 \end{pmatrix}=(\widehat{\mathbf {{R}}}||\widehat{\mathbf {{R}}}\widetilde{\mathbf {r}})\). Then for \(\mathbf {x}=\mathbf {{M}}\mathbf {w}\), we have \(\mathbf {{M}}\mathbf {{R}}=\mathbf {{M}}(\mathbf {{R}}+\mathbf {w}\cdot \widetilde{\mathbf {r}}^\top )-\mathbf {x}\cdot \widetilde{\mathbf {r}}^\top \) and
Moreover, for  , the distribution of \(\mathbf {{R}}+\mathbf {w}\cdot \widetilde{\mathbf {r}}^\top \) is uniformly random in \(\{0, 1\}^{t\times (\lambda -1)}\). Thus, for any statement, the simulator perfect simulates honest proofs, completing the proof of composable zero-knowledge.
, the distribution of \(\mathbf {{R}}+\mathbf {w}\cdot \widetilde{\mathbf {r}}^\top \) is uniformly random in \(\{0, 1\}^{t\times (\lambda -1)}\). Thus, for any statement, the simulator perfect simulates honest proofs, completing the proof of composable zero-knowledge.
Perfect Soundness. For any valid statement/proof pair \((\mathbf {x},(\mathbf {{C}},\mathbf {{D}}))\) such that \( (\mathbf {{C}}||\mathbf {x})\mathbf {{A}}=\mathbf {{M}}\mathbf {{D}} \) for \(\mathbf {{M}}\in \mathcal {D}_\lambda \), we have \((\mathbf {{M}}^\bot )^\top (\mathbf {{C}}||\mathbf {x})\mathbf {{A}}=\mathbf {0}\). Since \(\mathbf {{A}}^\top \in {\mathsf {OneSamp}}\) is of full rank, we must have \((\mathbf {{M}}^\bot )^\top \mathbf {x}=\mathbf {0}\), i.e., \(\mathbf {x} \in \mathsf {L}_{\mathbf {{M}}}\), completing the proof of perfect soundness. Notice that \(\mathbf {{M}}^\bot \) is not necessarily efficiently computable here.
Putting all the above together, Theorem 2 immediately follows. \(\square \)
Remark. By replacing \({\mathsf {OneSamp}}\) with \({\mathsf {ZeroSamp}}\) in \({\mathsf {Gen}}_\lambda \), we immediately achieve a fine-grained NIZK with perfect zero-knowledge and computational soundness. The proof is almost identical to that of Theorem 2 except that we exploit the fine-grained matrix linear assumption in the proof of soundness this time. Similar arguments can also be made for our OR-proof and NIZKs for circuit SAT given in the following sections.
5 Fine-Grained OR-Proof
In this section, we extend \({\mathsf {LNIZK}}\) in Sect. 4 to an OR-proof system.
Let \(\mathcal {D}_{\lambda }^{\mathsf {or}}\) be a probability distribution outputting matrices of rank \(t'< n\) from (\(\mathbf {{M}}_0,\mathbf {{M}}_1)\in \{0, 1\}^{n\times t}\times \{0, 1\}^{n\times t}\), where \(n(\cdot )\), \(t(\cdot )\), and \(t'(\cdot )\) are functions in \(\lambda \) and there exists \(\mathbf {{M}}_i^\bot \in \{0, 1\}^{n\times (n-t')}\) such that \(\mathbf {{M}}_i^\top \mathbf {{M}}_i^\bot =\mathbf {{0}}\) for \(i\in \{0, 1\}\). We define the following language
For the associated relation \(\mathsf {R}^{\mathsf {or}}_{\mathbf {{M}}_0,\mathbf {{M}}_1}\), we have \(\mathsf {R}^{\mathsf {or}}_{\mathbf {{M}}_0,\mathbf {{M}}_1}((\mathbf {x}_0,\mathbf {x}_1),\mathbf {w})=1\) iff \(\mathbf {x}_0=\mathbf {{M}}_0\mathbf {w}\) or \(\mathbf {x}_1=\mathbf {{M}}_1\mathbf {w}\). The OR-proof is given in Fig. 6.
Definition of \({\mathsf {ORNIZK}}=\{{\mathsf {ORGen}}_\lambda ,{\mathsf {ORTGen}}_\lambda ,{\mathsf {ORProve_\lambda }},{\mathsf {ORVer_\lambda }},{\mathsf {ORSim_\lambda }}\}_{\lambda \in \mathbb {N}}\) for \(\{\mathcal {D}_\lambda ^{\mathsf or}\}_{\lambda \in \mathbb {N}}\) to \(\{\mathcal {D}_\lambda ^{\mathsf {or}}\}_{\lambda \in \mathbb {N}}\). Recall that \(\overline{\mathbf {{A}}}\) (respectively, \(\underline{\mathbf {{A}}}\)) denotes the upper \((\lambda -1)\times \lambda \) matrix (respectively, lower \(1\times \lambda \) vector) of \(\mathbf {{A}}\).
Theorem 3
If \(\mathsf {NC^1}\subsetneq \mathsf{\oplus L/poly}\), then \({\mathsf {ORNIZK}}\) in Fig. 6 is an \(\mathsf {AC^0[2]}\)-NIZK with perfect soundness and \(\mathsf {NC^1}\)-composable zero-knowledge.
Proof
First, we note that \(\{{\mathsf {ORGen}}_\lambda ,{\mathsf {ORTGen}}_\lambda ,{\mathsf {ORProve_\lambda }},{\mathsf {ORVer_\lambda }},{\mathsf {ORSim_\lambda }}\}_{\lambda \in \mathbb {N}}\) are computable in \(\mathsf {AC^0[2]}\), since they only involve operations including multiplications of a constant number of matrices and sampling random bits.
Completeness. Completeness follows from the fact that for \(\mathbf {x}_j=\mathbf {{M}}_j\mathbf {w}\), \(\mathbf {{C}}_j=\mathbf {{M}}_j\mathbf {{R}}_j\), and \(\mathbf {{D}}_j=(\mathbf {{R}}_j||\mathbf {w})\mathbf {{A}}_j\), we have
and for \(\mathbf {{A}}_{1-j}=\begin{pmatrix}\overline{\mathbf {{A}}}\\ \widetilde{\mathbf {r}}_{1-j}^\top \overline{\mathbf {{A}}}\end{pmatrix}\), \(\mathbf {{C}}_{1-j}=\mathbf {{M}}_{1-j}\mathbf {{R}}'_{1-j}-\mathbf {x}_{1-j}\cdot \widetilde{\mathbf {r}}_{1-j}^\top \), and \(\mathbf {{D}}_{1-j}=(\mathbf {{R}}'_{1-j}||\mathbf {0}) \mathbf {{A}}_{1-j}\), we have
\(\mathsf {NC^1}\)
-composable Zero-Knowledge. For any adversary \(\mathcal {A}=\{a_\lambda \}_{\lambda \in \mathbb {N}}\in \mathsf {NC^1}\), the advantage of \(a_\lambda \) in distinguishing  from
from  is negligible if the fine-grained matrix linear assumption holds.
is negligible if the fine-grained matrix linear assumption holds.
According to the definition of \(\widetilde{{\mathsf {ZeroSamp}}}\) (see Sect. 2.2), we can give the running procedure of \({\mathsf {ORTGen}}_\lambda \) in an explicit way by randomly sampling  and
and  and setting \(\mathbf {{A}}^\top =(\mathbf {e}^\lambda _1||\widehat{\mathbf {{R}}})\begin{pmatrix}\mathbf {0} &{} 0\\ \mathbf {{I}}_{\lambda -1} &{} \mathbf {0}\end{pmatrix}\begin{pmatrix} \mathbf {{I}}_{\lambda -1}&{} \widetilde{\mathbf {r}} \\ \mathbf {0}&{} 1 \end{pmatrix}=(\widehat{\mathbf {{R}}}||\widehat{\mathbf {{R}}}\widetilde{\mathbf {r}})\), where the distribution of \(\widetilde{\mathbf {r}}\) is uniform in \(\{0, 1\}^{\lambda -1}\). Thus we have \(\underline{\mathbf {{A}}}=\widetilde{\mathbf {r}}^\top \overline{\mathbf {{A}}}\). Therefore, the distributions of \((\mathbf {{A}}_0,\mathbf {{A}}_1)\) generated by \({\mathsf {ORProve_\lambda }}\) and \({\mathsf {ORSim_\lambda }}\) on input a CRS generated by \({\mathsf {TGen}}_\lambda \) are identical. Moreover, we have \(\mathbf {{M}}_j\mathbf {{R}}_j=\mathbf {{M}}_j(\mathbf {{R}}_j+\mathbf {w}\cdot \widetilde{\mathbf {r}}^\top )-\mathbf {x}_j\cdot \widetilde{\mathbf {r}}^\top \) and
and setting \(\mathbf {{A}}^\top =(\mathbf {e}^\lambda _1||\widehat{\mathbf {{R}}})\begin{pmatrix}\mathbf {0} &{} 0\\ \mathbf {{I}}_{\lambda -1} &{} \mathbf {0}\end{pmatrix}\begin{pmatrix} \mathbf {{I}}_{\lambda -1}&{} \widetilde{\mathbf {r}} \\ \mathbf {0}&{} 1 \end{pmatrix}=(\widehat{\mathbf {{R}}}||\widehat{\mathbf {{R}}}\widetilde{\mathbf {r}})\), where the distribution of \(\widetilde{\mathbf {r}}\) is uniform in \(\{0, 1\}^{\lambda -1}\). Thus we have \(\underline{\mathbf {{A}}}=\widetilde{\mathbf {r}}^\top \overline{\mathbf {{A}}}\). Therefore, the distributions of \((\mathbf {{A}}_0,\mathbf {{A}}_1)\) generated by \({\mathsf {ORProve_\lambda }}\) and \({\mathsf {ORSim_\lambda }}\) on input a CRS generated by \({\mathsf {TGen}}_\lambda \) are identical. Moreover, we have \(\mathbf {{M}}_j\mathbf {{R}}_j=\mathbf {{M}}_j(\mathbf {{R}}_j+\mathbf {w}\cdot \widetilde{\mathbf {r}}^\top )-\mathbf {x}_j\cdot \widetilde{\mathbf {r}}^\top \) and
for \(\mathbf {x}_j=\mathbf {{M}}_j\mathbf {w}\). Since the distribution of \(\mathbf {{R}}_j+\mathbf {w}\cdot \widetilde{\mathbf {r}}_j^\top \) for  is uniform in \(\{0, 1\}^{t\times (\lambda -1)}\), the simulator perfectly simulate transcripts generated by honest protocol executions, completing the proof of composable zero-knowledge.
is uniform in \(\{0, 1\}^{t\times (\lambda -1)}\), the simulator perfectly simulate transcripts generated by honest protocol executions, completing the proof of composable zero-knowledge.
Perfect Soundness. For a valid statement/proof pair \((\mathsf {x},\pi )\) where \(\mathsf {x}=(\mathbf {x}_0,\mathbf {x}_1)\) and \(\pi =((\mathbf {{C}}_i,\mathbf {{D}}_i)_{i=0,1},\underline{\mathbf {{A}}_0})\), we set \(\mathbf {{A}}_0=\begin{pmatrix}\overline{\mathbf {{A}}}\\ \underline{\mathbf {{A}}_0} \end{pmatrix}\) and \(\mathbf {{A}}_1=\begin{pmatrix}\overline{\mathbf {{A}}}\\ \underline{\mathbf {{A}}}-\underline{\mathbf {{A}}_0} \end{pmatrix}\). Since \(\mathbf {{A}}^\top \in {\mathsf {OneSamp}}(\lambda )\) is of full rank, at least one of \(\mathbf {{A}}_0\) and \(\mathbf {{A}}_1\) is of full rank.
For \(i=0,1\) and \( (\mathbf {{C}}_i||\mathbf {x}_i)\mathbf {{A}}_i=\mathbf {{M}}_i\mathbf {{D}}_i, \) we have \((\mathbf {{M}}_i^\bot )^\top (\mathbf {{C}}_i||\mathbf {x}_i)\mathbf {{A}}_i=\mathbf {0}\). Let \(\mathbf {{A}}_j^\top \) be of full rank for \(j=0\) or \(j=1\). We must have \((\mathbf {{M}}_j^\bot )^\top \mathbf {x}_j=\mathbf {0}\). This means that \(\mathsf {x}\in \mathsf {L}^{\mathsf {or}}_{\mathbf {{M}}_0,\mathbf {{M}}_1}\) must hold, completing the proof of perfect soundness. Notice that \(\mathbf {{M}}_j^\bot \) is not necessarily efficiently computable here.
Putting all the above together, Theorem 3 immediately follows. \(\square \)
6 Fine-Grained NIZK Proof for Circuit SAT
In this section, we propose a fine-grained NIZK for circuit SAT running in \(\mathsf {NC^1}\) and secure against adversaries in \(\mathsf {NC^1}\).
Let \(\{\mathcal{ND}\mathcal{}_\lambda \}_{\lambda \in \mathbb {N}}\) be any family of language distributions such that for all \(\rho \in \mathcal{ND}\mathcal{}_\lambda \) and all \(\mathsf {x}\in \mathsf {L}_\rho \), we have \(\{{\mathsf {R}}_\rho (\mathsf {x},\cdot )\}_{\lambda \in \mathbb {N}}\in \mathsf {NC^1}\), where \(\mathsf {L}_\rho \) and \({\mathsf {R}}_\rho \) are the associated language and relation respectively. Without loss of generality, we assume that each \({\mathsf {R}}_\rho (\mathsf {x},\cdot )\) only consists of \(\mathsf{NAND}\) gates, since an \(\mathsf {NC^1}\) circuit can be transformed to an \(\mathsf {NC^1}\) circuits consisting only of NAND gates, and the transformation can also be performed in \(\mathsf {NC^1}\) by changing the gates in parallel. Let \({\mathsf {ORNIZK}}=\{{\mathsf {ORGen}}_\lambda ,{\mathsf {ORTGen}}_\lambda ,{\mathsf {ORProve_\lambda }},{\mathsf {ORVer_\lambda }},{\mathsf {ORSim_\lambda }}\}_{\lambda \in \mathbb {N}}\) be a NIZK for distributions \(\{\mathcal {D}_\lambda ^{\mathsf {or}}\}_{\lambda \in \mathbb {N}}\) defining the language
where \(\mathbf {{M}}'=\begin{pmatrix}\mathbf {{M}} &{} \mathbf {{0}}\\ \mathbf {{0}}&{} \mathbf {{M}}\end{pmatrix}\) for \(\mathbf {{M}}\in {\mathsf {ZeroSamp}}(\lambda )\). We give our NIZK for \(\{\mathcal{ND}\mathcal{}_\lambda \}_{\lambda \in \mathbb {N}}\) in Fig. 7.
Definition of \({\mathsf {NCNIZK}}=\{{\mathsf {NCGen}}_\lambda ,{\mathsf {NCTGen}}_\lambda ,{\mathsf {NCProve}}_\lambda ,{\mathsf {NCVer}}_\lambda ,{\mathsf {NCSim}}_\lambda \}_{\lambda \in \mathbb {N}}\) for \(\{\mathcal {D}_\lambda \}_{\lambda \in \mathbb {N}}\). Recall that \(\mathbf {e}_\lambda ^\lambda =(0 \cdots 0 1)^\top \in \{0, 1\}^\lambda \).
Theorem 4
If \(\mathsf {NC^1}\subsetneq \mathsf{\oplus L/poly}\) and \({\mathsf {ORNIZK}}\) is an \(\mathsf {AC^0[2]}\)-NIZK with perfect soundness and \(\mathsf {NC^1}\)-composable zero-knowledge, then \({\mathsf {NCNIZK}}\) is an \(\mathsf {NC^1}\)-NIZK with perfect soundness and \(\mathsf {NC^1}\)-composable zero-knowledge.
Proof
First, we note that \(\{{\mathsf {NCGen}}_\lambda ,{\mathsf {NCTGen}}_\lambda ,{\mathsf {NCProve}}_\lambda ,{\mathsf {NCVer}}_\lambda ,{\mathsf {NCSim}}_\lambda \}_{\lambda \in \mathbb {N}}\) are computable in \(\mathsf {NC^1}\), since they only involve operations including multiplications of a constant number of matrices, sampling random bits, running \({\mathsf {ORNIZK}}\), and computing \({\mathsf {R}}_\rho (\mathsf {x},\mathsf w)\in \mathsf {NC^1}\). Notice that after computing the values of all wires, the prover can generate ciphertexts and run \({\mathsf {ORNIZK}}\) for each wire and gate in parallel and the verifier can check the proofs in parallel.
Completeness. Let \(\mathsf {w}_{i}\) and \(\mathsf {w}_{j}\) be the input bits of a NAND gate, and \(\mathsf {w}_{k}\) be the true output. We must have \(1+\mathsf {w}_{i}+\mathsf {w}_{k}=0\wedge 1+\mathsf {w}_{j}=0 \ \text {or}\ 1+\mathsf {w}_{k}=0\wedge \mathsf {w}_{j}=0\). Let \(\mathsf {ct}_{i}=\mathbf {{M}}\mathbf {r}_{i}+\mathbf {e}_\lambda ^\lambda \mathsf {w}_{i}\) and \(\mathsf {ct}_{j}=\mathbf {{M}}\mathbf {r}_{j}+\mathbf {e}_\lambda ^\lambda \mathsf {w}_{j}\) be the input ciphertexts and \(\mathsf {ct}_{k}=\mathbf {{M}}\mathbf {r}_{k}+\mathbf {e}_\lambda ^\lambda \mathsf {w}_{k}\) be the output ciphertext. We have
or
Therefore, we have \(\mathsf {x}_{i}\in {{\,\mathrm{Im}\,}}(\mathbf {{M}}')\) if \(\mathsf {w}_{j}=1\) and \(\mathsf {x}_{j}\in {{\,\mathrm{Im}\,}}(\mathbf {{M}}')\) otherwise. Then the completeness of \({\mathsf {NCNIZK}}\) follows from the completeness of \({\mathsf {ORNIZK}}\).
\(\mathsf {NC^1}\) -composable Zero-Knowledge. The indistinguishability of CRSs generated by \({\mathsf {NCGen}}_\lambda \) and \({\mathsf {NCTGen}}_\lambda \) follows immediately from Lemma 2 and the composable zero-knowledge of \({\mathsf {ORNIZK}}\).
Next we define a modified prover \({\mathsf {NCProve}}_\lambda '\), which is exactly the same as \({\mathsf {NCProve}}_\lambda \) except that for each NAND gate, \(\pi _{ij}\) is generated as  . The following distributions are identical due to the composable zero-knowledge of \({\mathsf {ORNIZK}}\).
. The following distributions are identical due to the composable zero-knowledge of \({\mathsf {ORNIZK}}\).

for  and any \((\mathsf {x},\mathsf w)\) such that \({\mathsf {R}}_\rho (\mathsf {x},\mathsf w)=1\).
and any \((\mathsf {x},\mathsf w)\) such that \({\mathsf {R}}_\rho (\mathsf {x},\mathsf w)=1\).
Moreover, since the distribution of \(\mathsf {ct}_i=\mathbf {{M}}\mathbf {r}_i\) is identical to that of \(\mathsf {ct}_i=\mathbf {{M}}\mathbf {r}_i+\mathbf {e}_\lambda ^\lambda \mathsf w_i\) for  when \(\mathbf {{M}}\in {\mathsf {OneSamp}}(\lambda )\) is of full rank, the distributions of
when \(\mathbf {{M}}\in {\mathsf {OneSamp}}(\lambda )\) is of full rank, the distributions of

where  and \({\mathsf {R}}_\rho (\mathsf {x},\mathsf w)=1\), are identical as well, completing the proof of composable zero-knowledge.
and \({\mathsf {R}}_\rho (\mathsf {x},\mathsf w)=1\), are identical as well, completing the proof of composable zero-knowledge.
Perfect Soundness. Due to the perfect soundness of \({\mathsf {ORNIZK}}\), for each NAND gate with input ciphertexts \((\mathsf {ct}_{i},\mathsf {ct}_{j})\) and an output ciphertext \(\mathsf {ct}_{k}\) in a valid proof, we have
Let \(\mathbf {k}=(\widetilde{\mathbf {r}}^\top ,1)^\top \) be the vector in the kernel of \(\mathbf {{M}}^\top \), which must exist according to Lemma 1. We have
or
i.e., we can extract a true input/output pair \(((\mathbf {k}^\top \mathsf {ct}_{i},\mathbf {k}^\top \mathsf {ct}_{j}),\mathbf {k}^\top \mathsf {ct}_{k})\) for each NAND gate. For the output wire, we have \(\mathbf {k}^\top \mathsf {ct_{\mathsf {out}}}=\mathbf {k}^\top \mathbf {e}_\lambda ^\lambda =1\). As a result, we can extract the bits of all the wires leading to a final output 1, completing the proof of perfect soundness.
Putting all the above together, Theorem 4 immediately follows. \(\square \)
Remark. If we relax the restriction on the computational resources of the prover and allow it to run in, say, polynomial-time, our NIZK can also prove statements in \(\mathsf {NP}\). The same argument can also be made for our non-interactive zap and NIZK in the URS model (based on this NIZK) given later in Sects. 8.2 and 9. Notice that for the security proof of the non-interactive zap with a polynomial-time prover, we have to ensure that the reduction can simulate proofs in \(\mathsf {NC^1}\). This is possible by hard-wiring the extended witness in the reduction beforehand. We refer the reader to the full paper for details.
7 Fine-Grained NIZK for \(\mathsf {AC^0_{CM}[2]}\) with Short Proofs
In this section, we propose another fine-grained NIZK generically constructed from fine-grained NIZKs (instantiated as in Sects. 4 and 5) and a new fine-grained strongly FHE (sFHE) scheme that we give later. Different from the NIZK in Sect. 6, we only consider statement circuits in \(\mathsf {AC^0_{CM}[2]}\) here, while the proof size is independent with the statement circuit size and only dependent on the length of witness. Specifically, while the proof size of the NIZK in Sect. 6 is \(l\cdot O(\lambda ^2)\), that of the NIZK in this section is \(n\cdot O(\lambda ^2)\), where l and n are the circuit and witness sizes respectively.
7.1 Definition of Fine-Grained sFHE
For an sFHE scheme, additionally to the properties of a standard FHE, we require that the homomorphic evaluation do not change the form of ciphertexts, and there exist an algorithm \({\mathsf {RandEval}}_\lambda \) outputting the corresponding randomness of a homomorphically evaluated ciphertext on input the messages and randomness of the originally ciphertexts. Moreover, we define a composable version of indistinguishability against chosen plaintext attacks (CPA), which requires that the adversary cannot distinguish an honest public key with an “invalid” public key, and a ciphertext generated by an invalid public key reveals no information on the message.
Definition 12
(Strongly fully homomorphic encryption (sFHE)). A \(\mathcal C_1\)-sFHE scheme for \(\mathcal C_3\) circuits is a function family \({\mathsf {sFHE}}=\{{\mathsf {FHEGen}}_\lambda ,{\mathsf {FHEGen}}_\lambda ',\mathsf {Enc}_\lambda , \mathsf {Dec}_\lambda ,{\mathsf {Eval}}_\lambda ,{\mathsf {RandEval}}_\lambda \}_{\lambda \in \mathbb {N}}\in \mathcal C_1\) with the following properties.
-
\({\mathsf {FHEGen}}_\lambda \) returns a public/secret key pair \((\mathsf {pk},\mathsf {sk})\).
-
\({\mathsf {FHEGen}}_\lambda '\) returns a public key \(\mathsf {pk}\).
-
\(\mathsf {Enc}_\lambda (\mathsf {pk},\mathsf m\in \{0, 1\};\mathsf {r}\in \mathcal R)\) returns a ciphertext \(\mathsf {ct}\).
-
\(\mathsf {Dec}_\lambda (\mathsf {sk},\mathsf {ct})\) (deterministically) returns a message \(\mathsf m\in \{0, 1\}\).
-
\({\mathsf {Eval}}_\lambda (\mathsf {pk},{\mathsf {f}}\in \mathcal C_3,(\mathsf {ct}_1,\cdots ,\mathsf {ct}_n))\) (deterministically) return a ciphertext \(\mathsf {ct}\). Without loss of generality, we require that \({\mathsf {f}}\) is represented as an arithmetic circuit in GF(2) with XOR gates of unbounded fan-in and AND gates with fan-in 2.
-
\({\mathsf {RandEval}}_\lambda (\mathsf {pk},{\mathsf {f}}\in \mathcal C_3,(\mathsf m_1,\cdots ,\mathsf m_n),(\mathsf {r}_1,\cdots ,\mathsf {r}_n))\) (deterministically) return a randomness \(\mathsf {r}\in \mathcal R\). We require that \({\mathsf {f}}\) is represented in the same way as above.
Correctness is satisfied if we have \(\mathsf m=\mathsf {Dec}_\lambda (\mathsf {sk},\mathsf {Enc}_\lambda (\mathsf {pk},\mathsf m;\mathsf {r}))\) for all \(\lambda \in \mathbb {N}\), all \(\mathsf m\in \{0, 1\}\), all \((\mathsf {pk},\mathsf {sk})\in {\mathsf {FHEGen}}_\lambda \), and all \(\mathsf {r}\in \mathcal R\).
\(\mathcal C_2\) -composable CPA security is satisfied if for any adversary \(\mathcal {A}=\{a_\lambda \}_{\lambda \in \mathbb {N}}\in \mathcal C_2\), we have

and for all \(\lambda \in \mathbb {N}\) and all \(\mathsf {pk}\in {\mathsf {FHEGen}}_\lambda '\), the distributions of  and
and  are identical.
are identical.
Strong homomorphism is satisfied if for every function family \(\{{\mathsf {f}}_\lambda \}_{\lambda \in \mathbb {N}}\in \mathcal C_3\), all \(\lambda \in \mathbb {N}\), all \((\mathsf {pk},\mathsf {sk})\in {\mathsf {FHEGen}}_\lambda \), all \(\mathsf m_1,\cdots ,\mathsf m_n\in \{0, 1\}\), and all \(\mathsf {r}_1,\cdots ,\mathsf {r}_n\in \mathcal R\), we have
One can easily see that composable CPA security implies standard CPA security. Also, strong homomorphism implies standard homomorphism, since a homomorphically evaluated ciphertext can be decrypted to the right value due to correctness.
7.2 Construction of Fine-Grained sFHE
We now give our construction of sFHE \({\mathsf {sFHE}}=\{{\mathsf {FHEGen}}_\lambda ,{\mathsf {FHEGen}}_\lambda ',\mathsf {Enc}_\lambda ,\mathsf {Dec}_\lambda ,{\mathsf {Eval}}_\lambda ,{\mathsf {RandEval}}_\lambda \}_{\lambda \in \mathbb {N}}\) in Fig. 8. \({\mathsf {Eval}}_\lambda \) is defined by evaluation algorithms of AND and XOR gates, i.e., \({\mathsf {Eval}}^\mathsf {and}_\lambda \) and \(\mathsf {Eval}^\mathsf {xor}_\lambda \). Similarly, \({\mathsf {RandEval}}_\lambda \) is defined by \(\mathsf {RandEval}^\mathsf {and}_\lambda \) and \(\mathsf {RandEval}^\mathsf {xor}_\lambda \).
Definition of \({\mathsf {sFHE}}=\{{\mathsf {FHEGen}}_\lambda ,{\mathsf {FHEGen}}_\lambda ',\mathsf {Enc}_\lambda ,\mathsf {Dec}_\lambda ,{\mathsf {Eval}}_\lambda ,{\mathsf {RandEval}}_\lambda \}_{\lambda \in \mathbb {N}}\) where \({\mathsf {Eval}}_\lambda \) (respectively, \({\mathsf {RandEval}}_\lambda \)) is defined by \({\mathsf {Eval}}^\mathsf {and}_\lambda \) and \(\mathsf {Eval}^\mathsf {xor}_\lambda \) (respectively, \(\mathsf {RandEval}^\mathsf {and}_\lambda \) and \(\mathsf {RandEval}^\mathsf {xor}_\lambda \)). Recall that \(\mathbf {{I}}_\lambda \) is an identity matrix in \(\{0, 1\}^{\lambda \times \lambda }\).
Theorem 5
If \(\mathsf {NC^1}\subsetneq \mathsf{\oplus L/poly}\), then \({\mathsf {sFHE}}\) is an \(\mathsf {AC^0[2]}\)-sFHE scheme for \(\mathsf {AC^0_{CM}[2]}\) circuits that is \(\mathsf {NC^1}\)-composable CPA secure.
Proof
First, we note that \({\mathsf {sFHE}}\) is computable in \(\mathsf {AC^0[2]}\), since the key generation algorithms, the encryption algorithm, and the decryption algorithm only involve operations including multiplications of a constant number of matrices, sampling random bits, and computing parity, and we only consider homomorphic evaluation of circuits in \(\mathsf {AC^0_{CM}[2]}\) (i.e., with constant multiplicative depth), which only involve multiplications of a constant number of matrices as well.
Correctness. Correctness follows from the fact that the \(\lambda \)th column vector of a ciphertext for \(\mathsf m\) is in the form of \( \mathbf {{M}}\mathbf {r}_\lambda +\mathbf {e}_\lambda ^\lambda \mathsf m\in \{0, 1\}^\lambda \) (where \(\mathbf {e}_\lambda ^\lambda =(0,\cdots ,0,1)^\top \)) and we have \((\widetilde{\mathbf {r}}^\top ||1)(\mathbf {{M}}\mathbf {r}_\lambda +\mathbf {e}_\lambda ^\lambda \mathsf m)=\mathbf {{0}}+(\widetilde{\mathbf {r}}^\top ||1)\mathbf {e}_\lambda ^\lambda \mathsf m=\mathsf m\).
Strong Homomorphism. To prove strong homomorphism, we just have to show the correctness of the homomorphic evaluation for XOR and AND gates.
For homomorphic addition, we have
For homomorphic multiplication, we have
Hence, \(\sum _{i=1}^n\mathsf {ct}_i\) and \(\mathsf {ct}_0\mathsf {ct}_1\) are ciphertexts for \(\sum _{i=1}^n\mathsf m_i\) and \(\mathsf m_0\mathsf m_1\) with randomness \(\sum _{i=1}^n\mathbf {{R}}_n\) and \(\mathbf {{R}}_0\mathsf {ct}_1+ \mathsf m_0\mathbf {{R}}_1\) respectively, i.e., strong homomorphism holds.
Composable CPA Security. The security follows immediately from Lemma 2 and the fact that when \(\mathbf {{M}}\in {\mathsf {OneSamp}}(\lambda )\), \(\mathbf {{M}}\) is of full rank, and thus the distributions of \(\mathbf {{M}}\mathbf {{R}}+ \mathbf {{I}}_\lambda \) and \(\mathbf {{M}}\mathbf {{R}}\) are identical for  .
.
Putting all the above together, Theorem 5 immediately follows. \(\square \)
We now give some remarks on our scheme.
Remark on \(\mathsf {AC^0_{CM}[2]}\) . We follow Campanelli and Gennaro [5] to define \(\mathsf {AC^0_{CM}[2]}\) circuits with constant multiplicative depth. The reason that we only consider this class is that the main overhead for homomorphic evaluation is given by the multiplication gates. Each homomorphic multiplication in our case involves multiplication of two \(\lambda \times \lambda \) matrices, which can be performed in an \(\mathsf {AC^0[2]}\) circuit with depth 2 (the first layer consists of fan-in 2 multiplication gates and the second layer consists of fan-in \(\lambda \) addition gates). But it requires \(\Omega (\log (\lambda ))\) depth with fan-in two gates. Hence, a circuit with non-constant multiplicative depth would require an evaluation of \(\omega (log(\lambda ))\) depth, which cannot be performed in \(\mathsf {NC^1}\), while addition of polynomial numbers of matrices and multiplication of a constant depth of matrices can be performed in \(\mathsf {AC^0[2]}\).
Remark on Efficiency. In our scheme, the public key size is only \(\lambda ^2\) and the depth of an \(\mathsf {NC^1}\) circuit required for homomorphic multiplication is small since it only computes the parity of \(\lambda \) bits (in parallel). In contrast, the somewhat homomorphic encryption in [5] has public keys of length \((L\cdot \lambda ^3+\lambda ^2)\), where L is an a-prior fixed upper bound for the multiplicative depth of evaluation circuits, and computes the parity of \(\lambda ^2\) bits in parallel for homomorphic multiplication.
Remark on Proofs for Ciphertexts. We note that our NIZK for linear languages in Sect. 4 and our OR-proof in Sect. 5 support the following two languages respectively including ciphertexts of 1 and all valid ciphertexts.
and
Here, \(\mathsf {pk}=\mathbf {{M}}\in \{0, 1\}^{\lambda \times \lambda }\). The reason is that, say, \(\mathsf {x}=\mathbf {{M}}\mathbf {{R}}\) is equivalent to \(\mathsf {x}'=\mathbf {{M}}'\mathbf {r}'\), where \(\mathsf {x}'\) and \(\mathbf {r}'\) are concatenations of column vectors in \(\mathsf {x}\) and \(\mathbf {{R}}\) respectively, and \(\mathbf {{M}}'\in \{0, 1\}^{\lambda ^2\times \lambda ^2}\) is a large matrix with the diagonal being matrices \(\mathbf {{M}}\) and other positions being \(\mathbf {{0}}\).
7.3 Generic Construction of NIZK
Let \(\{\mathcal{AD}\mathcal{}_\lambda \}_{\lambda \in \mathbb {N}}\) be any family of language distributions such that for all \(\rho \in \mathcal{AD}\mathcal{}_\lambda \) and all \(\mathsf {x}\in \mathsf {L}_\rho \), we have \(\{{\mathsf {R}}_\rho (\mathsf {x},\cdot )\}_{\lambda \in \mathbb {N}}\in \mathsf {AC^0_{CM}[2]}\), where \(\mathsf {L}_\rho \) and \({\mathsf {R}}_\rho \) are the associated language and relation respectively.
Let \({\mathsf {sFHE}}=\{{\mathsf {FHEGen}}_\lambda ,{\mathsf {FHEGen}}_\lambda ',\mathsf {Enc}_\lambda ,\mathsf {Dec}_\lambda ,{\mathsf {Eval}}_\lambda ,{\mathsf {RandEval}}_\lambda \}_{\lambda \in \mathbb {N}}\) be an sFHE scheme with the randomness space \(\mathcal R\) satisfying \(\mathsf {NC^1}\)-composable CPA security and \(\mathsf {AC^0_{CM}[2]}\)-randomness homomorphism. Let \({\mathsf {ORNIZK}}=\{{\mathsf {ORGen}}_\lambda ,{\mathsf {ORTGen}}_\lambda ,{\mathsf {ORProve_\lambda }},{\mathsf {ORVer_\lambda }},{\mathsf {ORSim_\lambda }}\}_{\lambda \in \mathbb {N}}\) be a NIZK for distributions \(\{\mathcal {D}_\lambda ^{\mathsf {or}}\}_{\lambda \in \mathbb {N}}\) defining the language \(\mathsf {L}^{\mathsf {valid}}_{\mathbf {{M}}}\) and \({\mathsf {LNIZK}}=\{{\mathsf {Gen}}_\lambda ,{\mathsf {TGen}}_\lambda ,{\mathsf {Prove}}_\lambda ,{\mathsf {Ver}}_\lambda ,{\mathsf {Sim}}_\lambda \}_{\lambda \in \mathbb {N}}\) be a NIZK for a distribution \(\{\mathcal {D}_\lambda \}_{\lambda \in \mathbb {N}}\) defining \(\mathsf {L}^{\mathsf {1}}_{\mathbf {{M}}}\) (see the remark in Sect. 7.2 for \(\mathsf {L}^{\mathsf {valid}}_{\mathbf {{M}}}\) and \(\mathsf {L}^{\mathsf {1}}_{\mathbf {{M}}}\)). We give our NIZK for \(\{\mathcal{AD}\mathcal{}_\lambda \}_{\lambda \in \mathbb {N}}\) in Fig. 9.
Theorem 6
If \(\mathsf {NC^1}\subsetneq \mathsf{\oplus L/poly}\), \({\mathsf {LNIZK}}\) and \({\mathsf {ORNIZK}}\) are \(\mathsf {AC^0[2]}\)-NIZKs with perfect soundness and \(\mathsf {NC^1}\)-composable zero-knowledge, and \({\mathsf {sFHE}}\) is an \(\mathsf {AC^0[2]}\)-sFHE for \(\mathsf {AC^0_{CM}[2]}\) circuits with \(\mathsf {NC^1}\)-composable CPA security and strong homomorphism, then \({\mathsf {NCNIZK}}^*\) is an \(\mathsf {AC^0[2]}\)-NIZK with perfect soundness and \(\mathsf {NC^1}\)-composable zero-knowledge.
Proof
First, we note that \(\{{\mathsf {NCGen}}_\lambda ,{\mathsf {NCTGen}}_\lambda ,{\mathsf {NCProve}}_\lambda ,{\mathsf {NCVer}}_\lambda ,{\mathsf {NCSim}}_\lambda \}_{\lambda \in \mathbb {N}}\) are computable in \(\mathsf {AC^0[2]}\), since they only involve operations including multiplications of a constant number of matrices, sampling random bits, and running \({\mathsf {LNIZK}},{\mathsf {ORNIZK}}\), and homomorphic evaluation for \({\mathsf {R}}_\rho (\mathsf {x},\cdot )\in \mathsf {AC^0_{CM}[2]}\) is computable in \(\mathsf {AC^0[2]}\). Notice that the prover can generate ciphertexts and run \({\mathsf {ORNIZK}}\) for each input wire in parallel, and the verifier can check the proofs in parallel.
Completeness. Due to the strong homomorphism of \({\mathsf {sFHE}}\), we must have \(\mathsf {ct_{\mathsf {out}}}=\mathsf {Enc}_\lambda (\mathsf {pk},1;\mathsf {r}_\mathsf {out})\in \mathsf {L}^{\mathsf {1}}_{\mathbf {{M}}}\) when \(\mathsf w\) is a valid witness and \(\mathsf {ct_{\mathsf {out}}}\) and \(\mathsf {r}_\mathsf {out}\) are honestly generated. Then the completeness of \({\mathsf {NCNIZK}}^*\) follows immediately from the completeness of \({\mathsf {LNIZK}}\) and \({\mathsf {ORNIZK}}\).
\(\mathsf {NC^1}\) -composable Zero-Knowledge. The indistinguishability of CRSs generated by \({\mathsf {NCGen}}_\lambda \) and \({\mathsf {NCTGen}}_\lambda \) follows immediately from Lemma 2, the composable zero-knowledge of \({\mathsf {LNIZK}}\) and \({\mathsf {ORNIZK}}\), and the composable CPA security of \({\mathsf {sFHE}}\).
Next we define a modified prover \({\mathsf {NCProve}}_\lambda '\), which is exactly the same as \({\mathsf {NCProve}}_\lambda \) except that for each \(i\in [n]\), \(\pi ^{\mathsf {valid}}_i\) is generated as  and \(\pi _{\mathsf {out}}\) is generated as
and \(\pi _{\mathsf {out}}\) is generated as  Then the following distributions are identical due to the composable zero-knowledge of \({\mathsf {ORNIZK}}\) and \({\mathsf {LNIZK}}\).
Then the following distributions are identical due to the composable zero-knowledge of \({\mathsf {ORNIZK}}\) and \({\mathsf {LNIZK}}\).

for  and any \((\mathsf {x},\mathsf w)\) such that \({\mathsf {R}}_\rho (\mathsf {x},\mathsf w)=1\).
and any \((\mathsf {x},\mathsf w)\) such that \({\mathsf {R}}_\rho (\mathsf {x},\mathsf w)=1\).
Moreover, since the distribution of \(\mathsf {ct}_i\leftarrow \mathsf {Enc}_\lambda (\mathsf {pk},0)\) is identical to that of  for
for  , the distributions of
, the distributions of

where  and \({\mathsf {R}}_\rho (\mathsf {x},\mathsf w)=1\), are identical as well, completing the proof of composable zero-knowledge.
and \({\mathsf {R}}_\rho (\mathsf {x},\mathsf w)=1\), are identical as well, completing the proof of composable zero-knowledge.
Perfect Soundness. Let \(\varPi =((\mathsf {ct}_i)_{i=1}^n,(\pi ^{\mathsf {valid}}_i)_{i=1}^n,\pi _{\mathsf {out}})\) be a valid proof for \(\mathsf {x}\). Due to the perfect soundness of \({\mathsf {ORNIZK}}\) and \({\mathsf {LNIZK}}\), there must exist \(\mathsf w_i\) and \(\mathsf {r}_i\) such that \(\mathsf {ct}_i=\mathsf {Enc}_\lambda (\mathsf {pk},\mathsf w_i;\mathsf {r}_i)\) for all i. Then we must have \(\mathsf {Dec}_\lambda (\mathsf {sk},\mathsf {ct}_\mathsf {out})={\mathsf {R}}_\rho (\mathsf {x},(\mathsf w_i)_{i=1}^n)\) for \(\mathsf {ct_{\mathsf {out}}}={\mathsf {Eval}}_\lambda (\mathsf {pk},{\mathsf {R}}_\rho (\mathsf {x},\cdot ),(\mathsf {ct}_1,\cdots ,\mathsf {ct}_n))\), due to the homomorphism of \({\mathsf {sFHE}}\). Moreover, due to the completeness of \({\mathsf {LNIZK}}\), we have \(\mathsf {ct_{\mathsf {out}}}\in \mathsf {L}^{\mathsf {1}}\), i.e., \(\mathsf {Dec}_\lambda (\mathsf {sk},\mathsf {ct}_\mathsf {out})=1\). Therefore, we have \({\mathsf {R}}_\rho (\mathsf {x},(\mathsf w_i)_{i=1}^n)=1\), completing the proof of perfect soundness.
Putting all the above together, Theorem 4 immediately follows. \(\square \)
Remark on the CRS. The size of \(\mathsf {CRS}\) in \({\mathsf {NCNIZK}}^*\) can be further reduced, since we can let \({\mathsf {LNIZK}}\) and \({\mathsf {ORNIZK}}\) share a single matrix \(\mathbf {{A}}\) such that  as their CRS, and use \(\mathbf {{A}}+\mathbf {{N}}^\lambda \) as the public-key of the FHE since the distribution of \(\mathbf {{A}}+\mathbf {{N}}^\lambda \) is identical to \({\mathsf {ZeroSamp}}(\lambda )\) according to Lemma 3.
as their CRS, and use \(\mathbf {{A}}+\mathbf {{N}}^\lambda \) as the public-key of the FHE since the distribution of \(\mathbf {{A}}+\mathbf {{N}}^\lambda \) is identical to \({\mathsf {ZeroSamp}}(\lambda )\) according to Lemma 3.
8 Fine-Grained Non-Interactive Zap
In this section, we formally define verifiable correlated key generation, and show that all our fine-grained NIZKs have such type of key generation. Then we improve the framework in [12] to transform our NIZKs into zaps in the fine-grained setting.
8.1 Verifiable Correlated Key Generation
Definition 13
(Verifiable correlated key generation). A \(\mathcal C_1\)-NIZK \({\mathsf {NIZK}}=\{{\mathsf {Gen}}_\lambda ,{\mathsf {TGen}}_\lambda ,{\mathsf {Prove}}_\lambda ,{\mathsf {Ver}}_\lambda ,{\mathsf {Sim}}_\lambda \}_{\lambda \in \mathbb {N}}\) has verifiable correlated key generation if there exists a function family \(\{{\mathsf {Convert}}_\lambda ,{\mathsf {Check}}_\lambda \}_{\lambda \in \mathbb {N}}\in \mathcal C_1\) such that
-
1.
the distribution of \({\mathsf {Convert}}_\lambda (\mathsf {crs}_0)\) is identical to that of \(\mathsf {crs}_1\), where
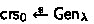 and
and  ,
, -
2.
\({\mathsf {Check}}_\lambda (\mathsf {crs}_0,{\mathsf {Convert}}_\lambda (\mathsf {crs}_0))=1\) for all \(\mathsf {crs}_0\in {\mathsf {Gen}}_\lambda \), and
-
3.
for any \(\mathsf {crs}_0,\mathsf {crs}_1\) (not necessarily in the support of \({\mathsf {Gen}}_\lambda \) or \({\mathsf {TGen}}_\lambda \)) such that \({\mathsf {Check}}_\lambda (\mathsf {crs}_0,\mathsf {crs}_1)=1\), we have \(\mathsf {crs}_0\in {\mathsf {Gen}}_\lambda \) or \( \mathsf {crs}_1\in {\mathsf {Gen}}_\lambda \).
Lemma 4
\({\mathsf {LNIZK}}\) in Sect. 4 (see Fig. 5) and \({\mathsf {ORNIZK}}\) in Sect. 5 (see Fig. 6) have verifiable correlated key generation.
Proof
For \({\mathsf {LNIZK}}\) and \({\mathsf {ORNIZK}}\), where a binding (respectively, hiding) CRS consists only of a matrix sampled by \({\mathsf {OneSamp}}(\lambda )\) (respectively, \({\mathsf {ZeroSamp}}(\lambda )\)), we define \(\{{\mathsf {Check}}_\lambda \}_{\lambda \in \mathbb {N}}\) and \(\{{\mathsf {Convert}}_\lambda \}_{\lambda \in \mathbb {N}}\) as in Fig. 10.
Definitions of \(\{{\mathsf {Check}}_\lambda \}_{\lambda \in \mathbb {N}}\) and \(\{{\mathsf {Convert}}_\lambda \}_{\lambda \in \mathbb {N}}\) for \({\mathsf {LNIZK}}\) and \({\mathsf {ORNIZK}}\). See Sect. 2 for the definitions of \(\mathbf {e}_i^\lambda \), \(\mathbf {{N}}_\lambda \), and \({\mathsf {LSamp}}\).
First we note that \(\{{\mathsf {Convert}}_\lambda \}_{\lambda \in \mathbb {N}}\in \mathsf {AC^0[2]}\) and \(\{{\mathsf {Check}}_\lambda \}_{\lambda \in \mathbb {N}}\in \mathsf {AC^0[2]}\) since they only involve addition of matrices and it is straightforward that checking whether \((\mathbf {e}^\lambda _1||\overline{\mathbf {{A}}_0}^\top )\in {\mathsf {LSamp}}(\lambda )\) is in \(\mathsf {AC^0[2]}\).
For  and
and  , the distributions of \(\mathbf {{A}}_0+\mathbf {{N}}_\lambda \) and \(\mathbf {{A}}_1\) are identical due to Lemma 3. Thus, the first condition in Definition 13 is satisfied.
, the distributions of \(\mathbf {{A}}_0+\mathbf {{N}}_\lambda \) and \(\mathbf {{A}}_1\) are identical due to Lemma 3. Thus, the first condition in Definition 13 is satisfied.
We now generate \(\mathbf {{A}}_0^\top \) explicitly by sampling  and
and  and computing \(\mathbf {{A}}_0^\top =\mathbf {{R}}_0\mathbf {{M}}_1^\lambda \mathbf {{R}}_1\). In this case,
and computing \(\mathbf {{A}}_0^\top =\mathbf {{R}}_0\mathbf {{M}}_1^\lambda \mathbf {{R}}_1\). In this case,
i.e., \(\overline{\mathbf {{A}}_0}=\widehat{\mathbf {{R}}}^\top \). Hence, we must have \((\mathbf {e}^\lambda _1||\overline{\mathbf {{A}}_0}^\top )\in {\mathsf {LSamp}}(\lambda )\) for \(\mathbf {{A}}_0^\top \in {\mathsf {OneSamp}}(\lambda )\). Moreover, for \(\mathbf {{A}}_1=\mathbf {{A}}_0+\mathbf {{N}}_\lambda \) we have \(\mathbf {{N}}_\lambda =\mathbf {{A}}_0+\mathbf {{A}}_1\). Hence, the second condition in Definition 13 is satisfied.
According to the above arguments, for \(\mathbf {{A}}_0\) such that \((\mathbf {e}^\lambda _1||\overline{\mathbf {{A}}_0}^\top )\in {\mathsf {LSamp}}(\lambda )\), if \(\underline{\mathbf {{A}}_0}^\top \in {{\,\mathrm{Im}\,}}(\overline{\mathbf {{A}}_0}^\top )\), i.e., there exists \(\widetilde{\mathbf {r}}\in \{0, 1\}^{\lambda -1}\) such that \(\underline{\mathbf {{A}}_0}^\top =\overline{\mathbf {{A}}_0}^\top \widetilde{\mathbf {r}}\), then \(\mathbf {{A}}_0^\top +\mathbf {{N}}_\lambda ^\top \in {\mathsf {OneSamp}}(\lambda )\). If \(\underline{\mathbf {{A}}_0}^\top \notin {{\,\mathrm{Im}\,}}(\overline{\mathbf {{A}}_0}^\top )\), we must have \((\overline{\mathbf {{A}}_0}^\top ||\mathbf {e}^\lambda _1)\begin{pmatrix}\widetilde{\mathbf {r}}\\ 1\end{pmatrix}=\underline{\mathbf {{A}}_0}^\top \) for some \(\widetilde{\mathbf {r}}\in \{0, 1\}^{\lambda -1}\), since \((\overline{\mathbf {{A}}_0}^\top ||\mathbf {e}^\lambda _1)\) is of full rank and \((\overline{\mathbf {{A}}_0}^\top ||\mathbf {e}^\lambda _1)\begin{pmatrix}\widetilde{\mathbf {r}}\\ 0\end{pmatrix}\ne \underline{\mathbf {{A}}_0}^\top \) for any \(\widetilde{\mathbf {r}}\). Since \((\overline{\mathbf {{A}}_0}^\top ||\mathbf {e}^\lambda _1)\begin{pmatrix}\widetilde{\mathbf {r}}\\ 1\end{pmatrix}=\underline{\mathbf {{A}}_0}^\top \) (equivalently, \(\underline{\mathbf {{A}}_0}=\widetilde{\mathbf {r}}^\top \overline{\mathbf {{A}}_0}+{\mathbf {e}_1^\lambda }^\top \)) implies \(\mathbf {{A}}_0=\begin{pmatrix}\overline{\mathbf {{A}}_0}\\ \widetilde{\mathbf {r}}^\top \overline{\mathbf {{A}}_0} \end{pmatrix}+\mathbf {{N}}_\lambda \), we have \(\mathbf {{A}}_0^\top \in {\mathsf {OneSamp}}(\lambda )\). As a result, either \(\mathbf {{A}}_0^\top \) or \(\mathbf {{A}}_1^\top \) must be in the support of \({\mathsf {OneSamp}}(\lambda )\) when \(\mathbf {{A}}_0+\mathbf {{A}}_1=\mathbf {{N}}_\lambda \) and \((\mathbf {e}^\lambda _1||\overline{\mathbf {{A}}_0}^\top )\in {\mathsf {LSamp}}(\lambda )\), i.e., the third condition is satisfied.
Putting all the above together, the proof of Lemma 4 immediately follows. \(\square \)
Lemma 5
\({\mathsf {NCNIZK}}\) and \({\mathsf {NCNIZK}}^*\) in Sects. 6 and 7 (see Figs. 7 and 9) have verifiable correlated key generation if the underlying NIZKs \({\mathsf {ORNIZK}}\) have verifiable correlated key generation.Footnote 3
Let \(\{{\mathsf {Check}}_\lambda \}_{\lambda \in \mathbb {N}}\in \mathsf {AC^0[2]}\) and \(\{{\mathsf {Convert}}_\lambda \}_{\lambda \in \mathbb {N}}\in \mathsf {AC^0[2]}\) be the checking and converting algorithms for \({\mathsf {ORNIZK}}\). For \({\mathsf {NCNIZK}}\) and \({\mathsf {NCNIZK}}^*\), we define \(\{{\mathsf {Check'}}_\lambda \}_{\lambda \in \mathbb {N}}\) and \(\{{\mathsf {Convert'}}_\lambda \}_{\lambda \in \mathbb {N}}\) as in Fig. 11.
The proof of Lemma 5 follows immediately from the verifiable correlated key generation of \({\mathsf {ORNIZK}}\) and the proof of Lemma 4. Notice that \(\mathbf {{M}}\) is sampled from \({\mathsf {ZeroSamp}}(\lambda )\) rather than \({\mathsf {OneSamp}}(\lambda )\) in the CRS of \({\mathsf {NCNIZK}}\). However, one can see that this does not make any essential difference and some minor changes on the proof of Lemma 4 is sufficient.
8.2 Construction of Fine-Grained Non-Interactive Zap
In this section, we give the transformation from NIZKs with verifiable correlated key generation to non-interactive zaps by using the technique in [12].
Let \(\{\mathcal {D}_\lambda \}_{\lambda \in \mathbb {N}}\) be any family of language distributions such that for all \(\rho \in \mathcal{ND}\mathcal{}_\lambda \) and all \(\mathsf {x}\in \mathsf {L}_\rho \), we can run \(\{{\mathsf {R}}_\rho (\mathsf {x},\cdot )\}_{\lambda \in \mathbb {N}}\) in \(\mathsf {NC^1}\), where \(\mathsf {L}_\rho \) and \({\mathsf {R}}_\rho \) are the associated language and relation of \(\rho \) respectively. Let \({\mathsf {NIZK}}=\{{\mathsf {Gen}}_\lambda ,{\mathsf {TGen}}_\lambda ,{\mathsf {Prove}}_\lambda ,{\mathsf {Ver}}_\lambda ,{\mathsf {Sim}}_\lambda ,{\mathsf {Check}}_\lambda ,{\mathsf {Convert}}_\lambda \}_{\lambda \in \mathbb {N}}\) be a NIZK with verifiable correlated key generation for \(\{\mathcal {D}_\lambda \}_{\lambda \in \mathbb {N}}\). We give a non-interactive zap \({\mathsf {ZAP}}=\{{\mathsf {ZProve}}_\lambda ,{\mathsf {ZVer}}_\lambda \}_{\lambda \in \mathbb {N}}\) for \(\{\mathcal {D}_\lambda \}_{\lambda \in \mathbb {N}}\) in Fig. 12.
Theorem 7
If \({\mathsf {NIZK}}\) is an \(\mathsf {NC^1}\)-NIZK with \(\mathsf {NC^1}\)-composable zero-knowledge, perfect soundness, and verifiable correlated key generation, then \({\mathsf {ZAP}}\) is an \(\mathsf {NC^1}\)-non-interactive zap with perfect soundness and \(\mathsf {NC^1}\)-witness indistinguishability.
We refer the reader to the full paper for the security proof.
By instantiating the underlying NIZK with our NIZK in Sect. 6, we obtain an \(\mathsf {NC^1}\)-non-interactive zap with \(\mathsf {NC^1}\)-witness indistinguishability. Also, by using our NIZK for \(\mathsf {AC^0_{CM}[2]}\) in Sect. 7, we immediately achieve an \(\mathsf {AC^0[2]}\)-non-interactive zap for \(\mathsf {AC^0_{CM}[2]}\), while the proof is almost identical to that of Theorem 7. Similar argument can also be made for our NIZKs in the URS model in Sect. 9.
9 Fine-Grained NIZK in the URS Model
In this section, we extend our fine-grained NIZKs in the CRS model to ones in the URS model. We first show the existence of a public coin distribution that is identical to the output distributions of \({\mathsf {ZeroSamp}}(\lambda )\) and \({\mathsf {OneSamp}}(\lambda )\) with “half-half” probability, and then show how to convert our fine-grained NIZKs into ones in the URS model by exploiting this distribution.
Matrices Represented by Random Coins. Let \(\mathbf {r}=(r_{1,2}, \cdots , r_{1,\lambda }, r_{2,3}, \cdots , r_{2,\lambda },\cdots , r_{\lambda -1,\lambda })\in \{0, 1\}^{\lambda (\lambda -1)/2}.\) We define the a function family \(\{{\mathsf {F}}_\lambda \}_{\lambda \in \mathbb {N}}\) such that
One can see that for uniform random  , the distribution of \(\mathbf {e}^\lambda _\lambda ||{\mathsf {F}}_\lambda (\mathbf {r})\) is exactly the output distribution of \({\mathsf {LSamp}}(\lambda )\) in Fig. 2.
, the distribution of \(\mathbf {e}^\lambda _\lambda ||{\mathsf {F}}_\lambda (\mathbf {r})\) is exactly the output distribution of \({\mathsf {LSamp}}(\lambda )\) in Fig. 2.
Lemma 6
If \(\mathsf {NC^1}\subsetneq \mathsf{\oplus L/poly}\), for any \(\{a_\lambda \}_{\lambda \in \mathbb {N}}\in \mathsf {NC^1}\), we have

Proof
Let  ,
,  ,
,  , and
, and  . Since \(\mathbf {e}^\lambda _\lambda ||{\mathsf {F}}_\lambda (\mathbf {r})\) is of full rank, the distribution of \({\mathsf {F}}_\lambda (\mathbf {r})\widetilde{\mathbf {r}}+\mathbf {e}^\lambda _1\cdot b\), where
. Since \(\mathbf {e}^\lambda _\lambda ||{\mathsf {F}}_\lambda (\mathbf {r})\) is of full rank, the distribution of \({\mathsf {F}}_\lambda (\mathbf {r})\widetilde{\mathbf {r}}+\mathbf {e}^\lambda _1\cdot b\), where  and
and  , is uniform over \(\{0, 1\}^\lambda \). Moreover, since the distributions of
, is uniform over \(\{0, 1\}^\lambda \). Moreover, since the distributions of
and
are exactly the same as the output distributions of \({\mathsf {ZeroSamp}}(\lambda )\) and \({\mathsf {OneSamp}}(\lambda )\) respectively, the distribution of \({\mathsf {F}}_\lambda (\mathbf {r})||\mathbf {s}\) is identical to \({\mathsf {ZeroSamp}}(\lambda )\) and \({\mathsf {OneSamp}}(\lambda )\) with probability 1/2 (over the choice of b) respectively. Then Lemma 6 immediately follows from the fine-grained matrix linear assumption (see Lemma 2). \(\square \)
One can see that the proof of Lemma 6 also implies the following lemma.
Lemma 7
If \(\mathsf {NC^1}\subsetneq \mathsf{\oplus L/poly}\), for \(\mathbf {r}\in \{0, 1\}^{\lambda (\lambda -1)/2}\) and  , we have
, we have
Moreover, combining Lemmata 6 and 2 immediately yields the following corollary.
Corollary 1
For any \(\{a_\lambda \}_{\lambda \in \mathbb {N}}\in \mathsf {NC^1}\), we have

Constructions in the URS Model. Let n be some constant and \({\mathsf {NIZK}}=\{{\mathsf {Gen}}_\lambda ,{\mathsf {TGen}}_\lambda ,{\mathsf {Prove}}_\lambda ,{\mathsf {Ver}}_\lambda ,{\mathsf {Sim}}_\lambda \}_{\lambda \in \mathbb {N}}\) be a NIZK with perfect soundness and composable zero-knowledge, where each CRS consists of n matrices outputted by \({\mathsf {ZeroSamp}}(\lambda )\) or \({\mathsf {OneSamp}}(\lambda )\). We construct a statistical NIZK \({\mathsf {URSNIZK}}\) in the URS model as follows (Fig. 13).
Definition of \({\mathsf {URSNIZK}}=\{{\mathsf {UGen}}_\lambda ,{\mathsf {UTGen}}_\lambda ,{\mathsf {UProve}}_\lambda ,{\mathsf {UVer}}_\lambda ,{\mathsf {USim}}_\lambda \}_{\lambda \in \mathbb {N}}\) for \(\{\mathcal {D}_\lambda \}_{\lambda \in \mathbb {N}}\). \(\ell \) denotes some polynomial in \(\lambda \) and n is some constant.
Theorem 8
If \(\mathsf {NC^1}\subsetneq \mathsf{\oplus L/poly}\) and \({\mathsf {NIZK}}\) is an \(\mathsf {NC^1}\)-NIZK for a set of language distributions \(\{\mathcal {D}_\lambda \}_{\lambda \in \mathbb {N}}\) with perfect soundness and \(\mathsf {NC^1}\)-composable zero-knowledge, then \({\mathsf {URSNIZK}}\) is an \(\mathsf {NC^1}\)-NIZK for \(\{\mathcal {D}_\lambda \}_{\lambda \in \mathbb {N}}\) in the URS model with statistical soundness and \(\mathsf {NC^1}\)-composable zero-knowledge.
The composable zero-knowledge of \({\mathsf {URSNIZK}}\) follows from that of \({\mathsf {NIZK}}\) and Lemma 6 and Corollary 1. Statistical soundness follows from the fact that among a sufficiently large number of CRSs, at least one of them should be binding with overwhelming probability according to Lemma 7. We refer the reader to the full paper for the formal proof.
Change history
25 May 2022
In an older version of this paper, there was an erroneous insertion of an equation on page 315. This has been removed.
Notes
- 1.
Recall that any circuit can be converted to one consisting only of NAND gates, and \(1-\mathsf {w}_{i}\mathsf {w}_{j}=0\) is equivalent to \(\mathsf {w}_{i}+\mathsf {w}_{j}+2\mathsf {w}_{k}-2\in \{0, 1\}\) in \(\mathbb {Z}_p\) for a large number p.
- 2.
Notice that all the computations are performed in GF(2) and thus addition and subtraction are equivalent.
- 3.
As remarked in Sect. 7.3, we can make the CRS of \({\mathsf {NCNIZK}}^*\) a single matrix in \({\mathsf {OneSamp}}(\lambda )\).
References
Applebaum, B., Ishai, Y., Kushilevitz, E.: Cryptography in NC\(^0\). In: 45th FOCS, pp. 166–175. IEEE Computer Society Press, October 2004
Ball, M., Dachman-Soled, D., Kulkarni, M.: New techniques for zero-knowledge: leveraging inefficient provers to reduce assumptions, interaction, and trust. In: Micciancio, D., Ristenpart, T. (eds.) CRYPTO 2020, Part III. LNCS, vol. 12172, pp. 674–703. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-56877-1_24
Barrington, D.A.M.: Bounded-width polynomial-size branching programs recognize exactly those languages in \(\text{NC}^1\). In: 18th ACM STOC, pp. 1–5. ACM Press, May 1986
Blum, M., Feldman, P., Micali, S.: Non-interactive zero-knowledge and its applications (extended abstract). In: 20th ACM STOC, pp. 103–112. ACM Press, May 1988
Campanelli, M., Gennaro, R.: Fine-grained secure computation. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018, Part II. LNCS, vol. 11240, pp. 66–97. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03810-6_3
Couteau, G., Hartmann, D.: Shorter non-interactive zero-knowledge arguments and ZAPs for algebraic languages. In: Micciancio, D., Ristenpart, T. (eds.) CRYPTO 2020, Part III. LNCS, vol. 12172, pp. 768–798. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-56877-1_27
Degwekar, A., Vaikuntanathan, V., Vasudevan, P.N.: Fine-grained cryptography. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016, Part III. LNCS, vol. 9816, pp. 533–562. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53015-3_19
Dwork, C., Naor, M.: Zaps and their applications. In: 41st FOCS, pp. 283–293. IEEE Computer Society Press, November 2000
Egashira, S., Wang, Y., Tanaka, K.: Fine-grained cryptography revisited. J. Cryptol. 34(3), 23 (2021)
Fiat, A., Shamir, A.: How to prove yourself: practical solutions to identification and signature problems. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 186–194. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-47721-7_12
Goldwasser, S., Micali, S., Rackoff, C.: The knowledge complexity of interactive proof systems. SIAM J. Comput. 18(1), 186–208 (1989)
Groth, J., Ostrovsky, R., Sahai, A.: New techniques for noninteractive zero-knowledge. J. ACM 59(3), 11:1–11:35 (2012)
Groth, J., Sahai, A.: Efficient non-interactive proof systems for bilinear groups. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 415–432. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_24
Ishai, Y., Kushilevitz, E.: Randomizing polynomials: a new representation with applications to round-efficient secure computation. In: 41st FOCS, pp. 294–304. IEEE Computer Society Press, November 2000
Merkle, R.C.: Secure communications over insecure channels. Commun. ACM 21(4), 294–299 (1978)
Pass, Rafael, shelat, abhi: Unconditional characterizations of non-interactive zero-knowledge. In: Shoup, Victor (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 118–134. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_8
Ràfols, C.: Stretching Groth-Sahai: NIZK proofs of partial satisfiability. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part II. LNCS, vol. 9015, pp. 247–276. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_10
Razborov, A.A.: Lower bounds on the size of bounded depth circuits over a complete basis with logical addition. Math. Notes Acad. Sci. USSR 41(4), 333–338 (1987)
Smolensky, R.: Algebraic methods in the theory of lower bounds for Boolean circuit complexity. In: Aho, A. (ed.) 19th ACM STOC, pp. 77–82. ACM Press, May 1987
Wang, Y., Pan, J., Chen, Y.: Fine-grained secure attribute-based encryption. In: Malkin, T., Peikert, C. (eds.) CRYPTO 2021, Part IV. LNCS, vol. 12828, pp. 179–207. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-84259-8_7
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 International Association for Cryptologic Research
About this paper
Cite this paper
Wang, Y., Pan, J. (2022). Non-Interactive Zero-Knowledge Proofs with Fine-Grained Security. In: Dunkelman, O., Dziembowski, S. (eds) Advances in Cryptology – EUROCRYPT 2022. EUROCRYPT 2022. Lecture Notes in Computer Science, vol 13276. Springer, Cham. https://doi.org/10.1007/978-3-031-07085-3_11
Download citation
DOI: https://doi.org/10.1007/978-3-031-07085-3_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-07084-6
Online ISBN: 978-3-031-07085-3
eBook Packages: Computer ScienceComputer Science (R0)














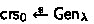 and
and  ,
,



