Abstract
The supercontinuum light generated in an appropriate dielectric such as a highly nonlinear dispersive fiber is described quantum mechanically. A Lagrangian is introduced to describe the propagation of light in an inhomogeneous, dispersive, and anisotropic dielectric. Proper creation and annihilation operators are introduced to define the linear part of the Hamiltonian, while the nonlinear term(s) of the Hamiltonian are defined in terms of these operators. As an example, the devised quantum theory is applied to the pulse propagation through an optical fiber. A coupled stochastic nonlinear Schrödinger equation (NLSE) type is obtained via the coherent positive-P representation in order to describe pulse propagation through the optical fiber. This approach is finally applied to the pulse propagation along a photonic crystal fiber when the response function of the medium is taken into account. The coupled stochastic generalized NLSE provided the quantum treatment of the supercontinuum light source. In addition to the coupling form of the equations and the stochastic terms, the main difference between the coupled stochastic equations and its classical form (i.e., GNLSE) is an additional term which has no counterpart in classical form. This additional term is brought about by commutation relations, which holds for creation and annihilation operators. This coupled quantum stochastic equation predicts squeezing in the region of anomalous dispersion, and the fluctuation can be reduced in the vicinity of the formed solitons in the supercontinuum generation process. Also, these equations can be used to study the soliton self-frequency shift quantum mechanically. Here, the coupled equation is simulated in the mean case. The quantum treatment of supercontinuum generation is essential for the high-intensity short-width pulses which are best described as photons.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
- Supercontinuum generation
- Third-order dispersion
- Ostrogradsky’s theorem
- Generalized nonlinear Schrödinger equation (GNLSE)
- Stochastic GNLSE
- Quantum soliton
- Soliton fission
- Fluctuation
- Stochastic field
- Stochastic variable
14.1 Introduction
Supercontinuum light sources have influenced the advancement of science and technology due to their widespread applications (Agrawal, 2012; Alfano, 2016; Alfano & Shapiro, 1970; Cumberland et al., 2008; Dudley & Genty, 2013; Dudley & Taylor, 2010; Fujimoto, 2003; Li et al., 2021; Venck et al., 2020, Vengris et al., 2019). However, a supercontinuum source exhibits unstable spectrum which affects their common use. The supercontinuum sources exhibit up to 50% fluctuation in their time-dependent profile depending on the initial photon intensity (Corwin et al., 2003; Dudley & Genty, 2013; Gonzalo et al., 2018; Wetzel et al., 2012). This fluctuation is partially dependent on the imperfect structure of fiber or dielectric media. Nonetheless, the fluctuation in the supercontinuum generation, SCG, has quantum origin as well (Corwin et al., 2003; Dudley & Genty, 2013; Gonzalo et al., 2018; Wetzel et al., 2012; Safaei Bezgabadi & Bolorizadeh, 2022). The quantum fluctuation in supercontinuum was studied semi-classically by Corwin et al. (2003), who introduced methodologically an additional term to the classical nonlinear Schrödinger equation. Controlling the supercontinuum source fluctuation is an important issue, yet. However, many researchers are working on different aspects of this fluctuation.
The main goal of this chapter is to describe the supercontinuum generation in a dielectric, such as an optical fiber, quantum mechanically. Here, initially, a Lagrangian is defined for the nonlinear propagation of light in an inhomogeneous, dispersive, and anisotropic dielectric, specifically an optical fiber. Then, the propagating fields are quantized by imposing the standard commutation relations. In the next step, the Hamiltonian is written in terms of creation and annihilation operators. As an example, the present theory is applied for pulse propagation through a simple optical fiber. Making use of the obtained Hamiltonian and the positive-P representation (Drummond & Gardiner, 1980; Drummond et al., 1981), the coupled stochastic nonlinear Schrödinger equation (NLSE) is obtained to describe the pulse propagation along the fiber. In addition, the quantum noise present in this process could be treated by these coupled equations (Drummond & Hillery, 2014). Also, by using these coupled equations, the equations for noise in the vicinity of the input soliton are obtained which they describe soliton squeezing. Finally, this approach is used for pulse propagation along a photonic crystal fiber when the retarded response function of the medium is considered, and a coupled stochastic generalized NLSE is presented for quantum treatment of the SCG process. The obtained results for the quantum model are simulated in the mean case. The simulation results for quantum model are compared with the simulation results of the classical model. As a methodological standpoint in order to verify the presented quantum model, the simulation results for quantum model are compared with the experimental ones.
14.2 Quantum Theory for Pulse Propagation in a Dielectric
The quantum treatment of field propagation inside a dielectric becomes more important when the electromagnetic field should be described as photons, specifically for quantum photonics technologies (Dechoum et al., 2016; Drummond, 1990; Drummond & Corney, 2001; Drummond & Hillery, 2014; Drummond & Opanchuk, 2020; Drummond et al., 1993; Carter, 1995; Corona et al., 2011; Grangier et al., 1998; Sun et al., 2019; Yao, 1997). In this section, a detailed study of quantum field propagation through a dielectric is presented when dispersion is included up to the third order. The third-order dispersion coefficient was neglected in earlier quantum treatments of the pulse propagation through a dielectric in the literature. Due to the critical role of the third-order dispersion coefficient (Alfano, 2016) on optical phenomena, especially when the second-order dispersion coefficient is zero or infinitesimal, it is essential to include the third-order dispersion coefficient.
Firstly, a proper canonical Lagrangian is introduced which results in Maxwell’s equations and the classical energy. Secondly, a constrained quantization approach (Faddeev & Jackiw, 1988; Gitman & Tyutin, 1990) is applied by using Ostrogradsky’s theorem (Woodard, 2007) for higher-order field derivatives in the Lagrangian. Finally, a Hamiltonian is derived in terms of properly defined annihilation and creation operators. The resulted annihilation and creation operators are used to obtain the quantum fields that describe electromagnetic waves propagation inside a chosen dielectric in this work. The number operator defines the number of photon-polariton pairs in the dielectric. Additionally, the creation and annihilation operators were used to describe the nonlinearity of pulse propagation in a medium by adding the proper perturbation terms. In the next section, the present quantum theory will be applied to a simple optical fiber when a light signal is propagating along it. This theory has the ability to add the higher-order dispersions and higher nonlinear terms into the governing equations, e.g., to describe supercontinuum generation process.
14.2.1 Classical Energy and the Equation of Motion
It is necessary to define an appropriate canonical Lagrangian to establish a theory for quantization of the pulse propagation along a dielectric. The resulted Hamiltonian and the equations of motion should, respectively, be equal to the classical energy and Maxwell’s equations for the propagation of light in a dielectric when the dispersion terms up to the third-order dispersion are included. The usual definitions that have also been implemented by Drummond and Hillery (Drummond, 1990; Drummond & Hillery, 2014; Hillery, 2009) are used here. One can write the energy density for electromagnetic radiation as:
where He and Hm are, respectively, the energy density due to the electric and the magnetic fields. The Fourier transform of the fields (e.g., electric field):
could be replaced in Eq. (14.1). The conditions:
and
hold as the fields are real. One can rewrite E(t, x) ⋅ ∂ D(t, x)/∂t in terms of the product of two Fourier integrals as:
A similar argument can be applied to the magnetic part of the energy, which results in:
Note that the difference between the electric filed energy, Eq. (14.4), and the corresponding relation for the magnetic field, Eq. (14.5), is that the magnetic permeability is assumed to be independent of frequency, while the electric permeability is frequency dependent. The frequency integral of Eq. (14.4) is split into two equal terms, and −ω is substituted for ω in one of the terms. Then, Eq. (14.4) and Eq.(14.5) are substituted into Eq. (14.1). Finally, by integrating the resulting Eq. (14.1) over time and assuming all the local fields and stored energies are initially zero at t = − ∞, one finds the energy density as:
Assuming a narrowband field at frequency, ω 0, there are significant contributions to the integral, Eq. (14.6), at ω = ω′ + δω ≈ ± ω 0. Note that for small values of δω, the relation:
holds. If ∂(ω ε(ω, x))/∂ω varies slowly over the field bandwidth, the time-averaged “linear energy” for the monochromatic pulse propagation at frequency ω through a dielectric is obtained as:
which can be written in terms of displacement fields as:
for:
Detailed derivation of Equation (14.9) from (14.8) is given in the Appendix.
For a charge free media, one can make use of a dual potential function (Drummond & Hillery, 2014; Drummond, 1990; Hillery, 2009), Λ, to define the electric displacement and magnetic fields, respectively, as:
and:
for:
where 2N + 1 narrowband field numbers (mode numbers), ν, are included in the field. The gauge used, here, is different from the usual Coulomb gauge as the dual potential, Λ(t, x) or Λν(t, x), is different from the vector potential. Note that the condition [Λν(t, x)]∗ = Λ−ν(t, x) should hold to have real dual function. Expansion of η(ω, x) up to the third order in the Taylor series near the narrow-field frequency, ων, leads to:
where:
Rewriting Eq. (14.14) as:
where η ν(x), \( {\boldsymbol{\upeta}}_{\nu}^{\prime}\left(\mathbf{x}\right) \), \( {\boldsymbol{\upeta}}_{\nu}^{{\prime\prime}}\left(\mathbf{x}\right) \) and \( {\boldsymbol{\upeta}}_{\nu}^{{\prime\prime\prime}}\left(\mathbf{x}\right) \) are, respectively, defined as:
and:
Note that the quantities η ν(x), \( {\boldsymbol{\upeta}}_{\nu}^{\prime}\left(\mathbf{x}\right) \), \( {\boldsymbol{\upeta}}_{\nu}^{{\prime\prime}}\left(\mathbf{x}\right) \), and \( {\boldsymbol{\upeta}}_{\nu}^{{\prime\prime\prime}}\left(\mathbf{x}\right) \) are not derivatives of one another. Substituting η(ω, x) from Eq. (14.16) into Eq. (14.9), the time averaged “linear energy” takes the form of:
The higher-order terms of expansion (14.14) are neglected with respect to the second-order (if nonzero) and the third-order terms in many applications of optical fibers. Hence, expansion (14.18) is valid for nearly all applications which is free from term \( {\boldsymbol{\upeta}}_{\nu}^{\prime}\left(\mathbf{x}\right) \).
Inserting definitions 14.11, 14.12, and 14.13 into Eq. (14.18), one arrives at:
Then, taking Fourier transform of Eq. (14.19) and assuming a narrow pulse of frequencies ων, one has:
where the frequency and the position vector dependence of the dual potential function are omitted to shorten Eq. (14.20). Applying the superposition principle and the slowly varying envelope approximation (Drummond, 1990; Drummond & Hillery, 2014; Hillery, 2009) over narrowband field numbers -N to N, the average linear energy for a wideband field could be expressed in terms of the local fields and their time derivatives at the frequency ων. Substituting \( \pm i{\dot{\boldsymbol{\Lambda}}}^{\pm \nu } \) for ων Λ±ν, keeping the symmetry in terms of the field vector derivatives and orthogonality of modes, the inverse Fourier transform of Eq. (14.20) will result in:
The nonlinear features of pulse propagation in dielectrics are included in the nonlinear part of the energy as perturbations (Drummond, 1990; Drummond & Hillery, 2014). In practice, the medium’s response functions are frequency dependent (Alfano, 2016; Boyd, 2008). However, when the response time is relatively fast, the frequency dependence of the medium’s nonlinear response function is neglected. In the supercontinuum generation process, the medium’s response function is retarded (Agrawal, 2012; Dudley & Taylor, 2010).
Here, Maxwell’s equations are the equations of motion for the pulse propagation through a dielectric. ∇ ⋅ D = 0 and ∇ × H = ∂ D/∂t are satisfied by definitions (14.11) and (14.12), respectively. Also, it is understood that the dual potential must be a transverse field as ∇ ⋅ B = 0. So the main equation of motion is:
where E could be generally given by (Alfano, 2016; Boyd, 2008; Drummond & Hillery, 2014):
and η n is the nth-order nonlinear response of the medium. It should be noted that η in Eq. (14.14) is the linear response of the medium, and, therefore, it is equal to η 1. However, the quantities η n are assumed to be independent of frequency when n > 1.
By implementing Hillery’s method (2009) and using the nonlinear polarization term in Maxwell’s equations (Alfano, 2016; Boyd, 2008), the nonlinear part of energy is obtained as:
where in terms of the dual functions, it is written as:
Finally, the total energy can be written as:
The equation of motion (14.22a) for the present system is written in terms of dual potential for a mode number, ν, as:
by applying the slowly varying envelope approximation which is demonstrated in the Appendix. Here, the slowly varying envelope approximation requires that \( {e}^{-i{\omega}^{\nu}\tau }{\boldsymbol{\Lambda}}^{\nu}\left(t-\tau, \mathbf{x}\right) \) is treated as a slowly varying envelope function of τ, and it can be expanded in a Taylor series near τ = 0. Generally, a term proportional to \( {\boldsymbol{\upeta}}_{\nu}^{\prime}\left(\mathbf{x}\right) \) does not appear in the linear dispersive energy, i.e., Eq. (14.18). However, a term proportional to \( {\boldsymbol{\upeta}}_{\nu}^{\prime}\left(\mathbf{x}\right) \) appears in the wave equation as a result of changes in phase velocity due to dispersion. Note that when the terms proportional to \( {\boldsymbol{\upeta}}_{\nu}^{{\prime\prime\prime}}\left(\mathbf{x}\right) \) are neglected, Eqs. (14.18, 14.19, 14.20, 14.21, 14.22a, 14.22b, 14.23, 14.24, 14.25, and 14.26) are similar to the corresponding equations in reference (Drummond, 1990).
14.2.2 Canonical Lagrangian and Hamiltonian Functions
To establish a quantum theory for the pulse propagation through a nonlinear dispersive dielectric in the presence of third-order dispersion (Drummond, 1990; Drummond & Hillery, 2014), a canonical Lagrangian leading to the equation of motion (14.26) and the classical energy (14.25) should be defined based on Ostrogradsky’s theorem (Woodard, 2007). Due to the presence of third-order dispersion, the defined Lagrangian contains higher-order time derivatives. For the pulse propagation through a dielectric when the third-order dispersion is included, the Euler-Lagrange equation for the jth component of the dual potential, Λν, is written as:
where \( {L} \) is Lagrangian density and k represents the space coordinates x, y, or z. Note that the summation rule is applied to k. For the present system, a proper form for the linear and nonlinear parts of the Lagrangian density will be:
and:
where the total Lagrangian can be written as:
Detailed derivation of the resulted equation of motion and the Hamiltonian, which are, respectively, equal to Equation (14.26) and Equation (14.25), are described in the Appendix. The linear part of the Lagrangian density, Eq. (14.28), is implemented to quantize the propagation of electromagnetic field through a nonlinear dispersive dielectric. As the Lagrangian density (14.28) is a function of higher-order time derivatives of the field, one should implement Ostrogradsky’s theorem (Woodard, 2007) for higher-order scalar fields. Here, according to Ostrogradsky’s theorem, there are two canonical coordinates qν and Qν corresponding to Λν and \( {\dot{\boldsymbol{\Lambda}}}^{\nu } \). These canonical coordinates and their canonical momenta construct a canonical space. The canonical momenta:
and:
correspond respectively to canonical coordinates qν and Qν or Λν and \( {\dot{\boldsymbol{\Lambda}}}^{\nu } \). By neglecting the third-order dispersion term, \( {\boldsymbol{\upeta}}_{\nu}^{{\prime\prime\prime}}\left(\mathbf{x}\right) \), the linear Lagrangian agrees with Eq. (3.117) in reference (Drummond & Hillery, 2014).
In summary, the results obtained by implementing the total Lagrangian agree in both dynamics and energy with the results obtained from Maxwell’s equations and Poynting’s theorem for slowly varying envelope functions. So, the total Lagrangian, describing the field propagation through a medium with a combination of dispersion, nonlinearity, and inhomogeneity, is unique as one can derive the correct equation of motion and the Hamiltonian. Additionally, the linear Lagrangian density (14.28) describes the system in the framework of a local field theory of a linear dispersive medium. The first and the last terms of the linear Lagrangian density and the linear Hamiltonian resemble a massless boson, while the remaining terms indicate dispersive correction.
14.2.3 Field Quantization
For the present system, Dirac’s commutation relations for the components of vector operators Λνand Πν are:
Similar commutation relations hold between \( {\dot{\boldsymbol{\Lambda}}}^{\nu } \) and Σν. Since the dual potentials and their canonical momenta are transverse, the commutation relations (14.33) are transverse. Equation (14.33) expresses that the present system is a constrained system (Faddeev & Jackiw, 1988; Gitman & Tyutin, 1990) because no standard commutation relation holds. To extend the common approach of quantization to this constrained quantization, it is necessary to construct the appropriate form of the Dirac commutation relations for new coordinates. Thus, the dual potential functions are expanded in terms of spatial modes as:
to rephrase the constraint, where the expansion coefficients are the new coordinates, \( {\lambda}_{\mathbf{k},\alpha}^{\nu } \). By inserting expansion (14.34) into Eq. (14.28), the linear part of Lagrangian is obtained as:
where:
and:
See the detailed derivation of Equation (14.35) and the coming results, Equation 14.37, in the Appendix. It is important to note that when the medium exhibits losses due to scattering or absorption, they appear as complex values in elements of η ν(x). In turn, these losses appear in matrices M. The M matrices will be diagonal when the response tensor of the medium is isotropic and homogeneous. The linear Lagrangian (14.35) is re-written as:
by omitting the summations over (k, α, k’, α’) and the corresponding indices for simplicity. In order to rephrase the constraint and obtain standard commutation relations, the new canonical momenta corresponding to the new set of coordinates are derived as:
and:
Here, Ostrogradsky’s theorem is applied again in order to obtain canonical momenta (14.38) from the Lagrangian density (14.28) where the Ostrogradsky choices for canonical coordinates are λν ≡ qν and \( {\dot{\lambda}}^{\nu}\equiv {Q}^{\nu } \). One must impose the standard commutation relations between the canonical coordinates and momenta, to quantize the fields for the current problem. These relations no longer have transversality restrictions as compared with the operators Λν and Πν (or \( {\dot{\boldsymbol{\Lambda}}}^{\nu } \) and Σν). The commutation relations between coordinates and momenta can be simply written as:
and:
It is straightforward to find the linear part of the Hamiltonian in terms of the new canonical coordinates and momenta as:
New canonical coordinate:
and momentum:
are defined to write the Hamiltonian (14.40) in a simpler form, where Aν to Kν (i.e.; Aν, Bν, Cν, Dν, Eν, Fν, Gν and Kν) are arbitrary invertible complex matrices. The coordinate and momentum, (14.41), obey the standard commutation relation. Thus, the conditions:
and:
hold for the coefficients defined by Eqs. (14.41). Nonetheless, the Hamiltonian (14.40) is written in terms of the defined coordinate and momentum operators as:
where Θν, ϒν, and Δν are the frequency matrices. Equating the two forms of the Hamiltonian, (14.40) and (14.43), six equations in addition to equations (14.42) relating the frequency matrices and the arbitrary invertible complex matrices Aν to Kν are derived. Therefore, the unknown matrices (the frequency matrices and the matrices Aν to Kν) can be determined. The reader is referred to Appendix for the details of derivation of relations for the matrices Aν to Kν.
Using boson creation and annihilation operators, the linear part of the Hamiltonian is re-expanded. The operators aν and bν are defined as annihilation operators, while (aν)† and (bν)† are creation operators. These operators are defined as column vectors:
and:
where the transformation matrix Wν is an invertible complex matrix to be defined. Commutation relations for elements of these operators are:
and:
Now, the Hamiltonian (14.43) is written in terms of the creation and the annihilation operators as:
where Ω±ν is defined as frequency matrices and the relations:
and:
hold by equating the two forms of the Hamiltonians (14.43) and (14.48) while neglecting zero-point energy. The relation:
holds for the matrices Wν by eliminating Ω±ν in Eqs. (14.49). It could be shown that Eq. (14.48) holds when Wν is the solution to the matrix Eq. (14.50). The corresponding frequency matrices are found as:
In general, the resultant Hamiltonian is not diagonal as the M(1)ν to M(4)ν matrices are not diagonal. The matrices Ω±ν are diagonalized to obtain the frequency bands as:
The final form of the Hamiltonian is:
where:
and:
The Hamiltonian (14.53) is diagonal operator leading to normal and anomalous modes corresponding to operators \( {\tilde{\mathbf{a}}}^{\nu } \) and \( {\tilde{\mathbf{b}}}^{\nu } \). The operators in Eq. (14.53) indicate the number of photon-polariton pairs of the system. Note that the quantities M(1)ν to M(3)ν, defined by Eqs. (14.36), change when the third-order dispersion is absent and M(4)ν is zero.
The nonlinear term in the total Hamiltonian is:
when only the third-order nonlinear term of Eq. (14.24) is taken into account. This nonlinear part of the Hamiltonian is found in terms of annihilation and creation operators where displacement field is written in terms of these two operators. The theory developed here could properly quantize the electromagnetic radiation in a three-dimensional dielectric, where the third-order nonlinear term is effective. When an optical soliton propagates along a dielectric waveguide, there are fluctuations in the vicinity of the soliton (Drummond & Hillery, 2014; Safaei Bezgabadi et al., 2019, 2020a and 2020b) depending on the intensity of the soliton.
The present quantization scheme is a fundamental basis for squeezing the soliton fluctuations. Drummond applied a model to squeeze the fluctuations for soliton propagation along an optical fiber when the dispersion is expanded up to the second order. In a more realistic view, the third-order dispersion has a vital role for pulse propagation along optical fibers. Therefore, this section provides a basic theory for pulse propagation when the third-order dispersion is included. The method devised here is capable of being extended to higher-order dispersions and also enables one to study quantum aspects of noise in dielectrics, especially fibers (Drummond & Hillery; 2014; Safaei Bezgabadi et al., 2018, 2020a). Generally, quantum treatment of pulse propagation through dielectric waveguides is essential for light propagation along photonic chips used in quantum simulations, quantum sensing, and quantum communications experiments.
14.3 Application of the Present Quantum Theory to an Optical Fiber
In this section, the field propagation along an optical fiber, i.e., a cylindrical optical waveguide, is presented making use of the theory established in the previous section. This field is assumed to be a polarized single-frequency plane wave, i.e. a single transverse mode ν, while the longitudinal mode components have discrete wave numbers k ranging from –k min to k max. For an optical fiber, it is assumed a cylindrical waveguide whose axis lies along the z-axis. Making use of the dual potential as described by Eq. (14.13) and the Maxwell’s equation (14.22a) for the usual case of η(ω, x) ≡ η(ω), one could derive the wave equation. The wave equation for the dual potential is:
where \( \tilde{\varepsilon} \) is the permittivity of the medium and the relation:
holds. It is also assumed that the three εs are equal. The polarized dual potential is defined as:
where:
One can show that the functions fν(ρ) and gν(ρ) are Bessel functions satisfying the differential equation:
where \( {\kappa}^2={k}_{\rho}^2+{k}^2 \). The boundary conditions lead to the quantized values for k ρ, \( {k}_{\rho}^{(m)} \). Each transverse mode, ν, stands for n and m, and mode -ν corresponds to -n and m.
The displacement vector and the magnetic fields, respectively, are:
and:
where:
One could assume the solution to gν(ρ) to be:

where  is a normalization factor.
is a normalization factor.
The gauge condition, ∇ ⋅ Λ(t, x) = 0, for the dual potential, leads to:
where the final form for fν(ρ) is:

In order to find  , the condition:
, the condition:
should be satisfied.
It is assumed that the response tensor for the medium is homogeneous and isotropic (η ν(x) = η ν) and that the first nonzero nonlinear term corresponds to η 3 (centro-symmetric media). The linear part of the Lagrangian density (Eq. (14.28)) and the Hamiltonian (Eq. (14.21)) can be, respectively, simplified to:
and:
where:
Similar to the definition (14.34), the scalar field Λν(t, z) is defined in terms of the canonical coordinates \( {\lambda}_k^{\nu }(t) \vspace*{-3pt} \) as:
where L is the length of the optical fiber. Therefore, the linear part of the Lagrangian for the field propagation along the optical fiber can be written as:
where  and
and  , making use of Equation (14.28). The Lagrangian (14.73a) will be:
, making use of Equation (14.28). The Lagrangian (14.73a) will be:
where \( {\lambda}_{-k}^{-\nu}\equiv {\left({\lambda}_k^{\nu}\right)}^{\dagger } \), \( {\dot{\lambda}}_{-k}^{-\nu}\equiv {\left({\dot{\lambda}}_k^{\nu}\right)}^{\dagger } \) and \( {\ddot{\lambda}}_{-k}^{-\nu}\equiv {\left({\ddot{\lambda}}_k^{\nu}\right)}^{\dagger } \). It is assumed earlier that a single transverse mode ν for mode numbers n and m are considered, so the summation over ν in Eq. (14.73b) is dropped for the rest of this section.
The canonical momenta associated with \( {\lambda}_k\equiv {\lambda}_k^{\nu } \), \( {\lambda}_k^{\dagger}\equiv {\left({\lambda}_k^{\nu}\right)}^{\dagger } \), \( {\dot{\lambda}}_k\equiv {\dot{\lambda}}_k^{\nu } \) and \( {\dot{\lambda}}_k^{\dagger}\equiv {\left({\dot{\lambda}}_k^{\nu}\right)}^{\dagger } \) are:
and:
respectively, when Ostrogradsky’s theorem (Woodard, 2007) is implemented. The canonical coordinates are q k, \( {q}_k^{\dagger } \), Q k, and \( {Q}_k^{\dagger } \) which are equal to λ k, \( {\lambda}_k^{\dagger } \), \( {\dot{\lambda}}_k \), and \( {\dot{\lambda}}_k^{\dagger } \), respectively. Similarly, the linear part of the Hamiltonian, HL, for field propagation along optical fibers is written as Eq. (14.40). Here, the M matrices defined by Equations (14.36) are diagonal, and they are obtained as:
and:
Note should be added that a careful comparison between the dual potential defined by Eq. (14.34) and the dual potential of a system with discrete modes, similar to our example, is needed to find the correct M matrices.
In order to use the Hamiltonian (14.43), the frequency matrices (Θν, ϒν, and Δν) and the arbitrary invertible complex matrices Aν to Kν must be determined. For the present simple example, these matrices are reduced to complex numbers. By using the six obtained relations and conditions (14.42), these complex numbers can be obtained.
Similar to operators given by Eqs. (14.41), new canonical coordinates, \( {\tilde{q}}_k^{\nu } \), and momenta, \( {\tilde{p}}_k^{\nu } \), are defined as:
and:
In this one-dimensional example, the field is quantized when operators \( {\tilde{q}}_k^{\nu } \) and \( {\tilde{p}}_k^{\nu } \) obey the commutation relation:
Operators defined by Eqs. (14.44) and (14.45) are, respectively, given as:
and:
where \( {W}_k^{\nu } \) is generally a complex number. The creation operator \( {\left({a}_k^{\nu}\right)}^{\dagger } \) and the annihilation operator \( {b}_k^{\nu } \) are likewise defined. Therefore, the linear part of Hamiltonian is:
while ω(k) is the solution to equations:
where \( {W}_k^{\nu } \) is given as:
In order to calculate the nonlinear parts of the Hamiltonian, Eq. (14.56), it is essential to obtain \( {\Lambda}_k^{\nu } \) (or equivalently \( {\lambda}_k^{\nu } \)). It is straightforward to find the equation of motion as:
where:
and:
Note that the Ostrogradsky’s choices for canonical coordinates are qν ≡ λν and \( {Q}^{\nu}\equiv {\dot{\lambda}}^{\nu } \).
According to the Heisenberg equation of motion, the operators \( {a}_k^{\nu }(t) \) and \( {\left({b}_k^{\nu }(t)\right)}^{\dagger } \) evolve as \( {a}_k^{\nu }(t)={a}_k^{\nu }(0){e}^{-i\;{\omega}^{+\nu }(k)t} \) and \( {\left({b}_k^{\nu }(t)\right)}^{\dagger }={\left({b}_k^{\nu }(0)\right)}^{\dagger }{e}^{i\;{\omega}^{-\nu }(k)t} \), respectively. The solution to Eq. (14.87) can be straightforwardly given as:
where:
and:
In most optical waveguides, especially those used for SCG, C1 is a relatively large positive number as \( {C}_1\propto \left|{\eta}_{\nu}^{{\prime\prime} }/{\eta}_{\nu}^{{\prime\prime\prime}}\right| \), so that the first term in the right side of Eq. (14.92) can be neglected compared with other terms. In addition, the third term should be dropped as it corresponds to the anomalous modes (non-physical modes) defined by the operators \( {b}_k^{\nu } \) and \( {\left({b}_k^{\nu}\right)}^{\dagger } \). The reader is referred to (Drummond, 1990) for detailed discussion on the anomalous modes. Therefore, Eq. (14.92) will be:
Making use of the scalar field, Λν(t, z), defined by Eq. (14.72), one can rewrite it for the mode ν in terms of the annihilation operator \( {a}_k^{\nu } \):
where:

It is assumed a single transverse mode ν; thus, the displacement vector is:
Making use of Eqs. (14.97a) and (14.62), one has:
where:
The formalism introduced in this section can describe the propagation of quantum fields in nonlinear dispersive optical fibers. Assuming the field wavenumber and frequency to be near k 0 and ω = ω(k 0), respectively, the slowly varying quantum photon-polariton field is defined as (Drummond & Hillery, 2014; Safaei et al., 2018):
to describe the field propagation along an optical fiber with nonlinearity η3.
Ignoring the smearing effect for all practical purposes, the commutation relation for these fields can be expressed as:
which is applicable for temporally ultrashort fields. Inverting the relation between a k and ψ(z, t) yields:
One can insert Eq. (14.103) into Eq. (14.84) to express the Hamiltonian in terms of ψ(z, t). Here, the first term of Eq. (14.84), i.e., normal solution, is taken into account. Thus, the linear part of Hamiltonian can be written as:
Expanding ω(k) near k 0 as:
where \( {\omega}^{\prime}\left({\left.= d\omega /d{k}\right|}_{k=k_0}\right) \), \( {\omega}^{{\prime\prime}}\left({={d}^2\omega /d{k}^2|}_{k=k_0}\right) \), and \( {\omega}^{{\prime\prime\prime}}\left({={d}^3\omega /d{k}^3|}_{k=k_0}\right) \) are the group velocity and the first and second derivatives of group velocity, respectively. The expression in the parenthesis in Eq. (14.104) becomes:
where the operator form is written as:
The linear part of Hamiltonian is, therefore, given by:
where the argument of the photon-polariton field has been eliminated for simplicity. The nonlinear part of the Hamiltonian is given by:
for:
Therefore, the nonlinear part of the Hamiltonian can be approximated as:
Hence, keeping the slowly varying terms, one obtains:
where:
There are terms proportional to ψ† ψ, ψ†, and/or ψ in the nonlinear part of the Hamiltonian (Eq. (14.112)), which is usually called simple terms as they could be interpreted similar to the term of the linear Hamiltonian (Eq. (14.108)). Therefore, they do not show any nonlinear effect.
The total Hamiltonian and field operator is expressed in the interaction picture as:
and:
where h is defined as:
A new frame is defined that moves at the group velocity (Z = z − ω′ t). One obtains the following equation of motion in this frame from the interaction Hamiltonian:
where . Equation (14.117) is an operator form of the nonlinear Schrödinger equation taking the third-order dispersion term into account. There is another operator equation, the equation of motion for \( {\psi}_I^{\dagger } \), which is coupled to Eq. (14.117) by transforming \( {\psi}_I\to {\psi}_I^{\dagger } \) and i → − i.
Depending on the optical fiber characteristics, the signs of g (nonlinear parameter) and ω″ (group velocity dispersion) can be positive or negative. Taking into account their signs, one can form the quantum solitons and study their interactions in the presence of the third-order dispersion term. Note that the terms proportional to (ψ†)2 ψ2 in Eq. (14.111) lead to the last term in Eq. (14.117). The terms of the order ψ† ψ in Eq. (14.111), which have been omitted, would lead to a linear term and have no nonlinear effect on the operator form of the nonlinear Schrödinger equation, Eq. (14.117) or equivalently Eq. (14.118). These terms just change ω(k 0) in the first term of Eq. (14.108), so the nonlinear term of Equations (14.117) and (14.118) is not affected by them.
To solve the coupled operator equation, Eq. (14.117) is written as common partial differential equations. The positive-P representation method is followed here (Drummond & Gardiner, 1980; Drummond & Hillery, 2014). The Glauber-Sudarshan P representation (Glauber, 1963; Sudarshan, 1963) is not used here, as it leads to a Fokker-Planck equation with non-positive definite diffusion coefficients. By using the positive-P representation in the master equation, one can arrive at the coupled stochastic partial differential equation (Carter, 1995; Drummond & Gardiner, 1980; Drummond & Hillery, 2014; Drummond & Corney, 2001; Drummond & Carter, 1987):
and:
for the functions ΨI(T, z) and ΨI +(T, z), respectively, which are related to the creation and annihilation operators. The fields ζ(T, z) and ζ+(T, z) are Gaussian stochastic fields with correlation relations:
and:
The origin of stochastic partial differential equations (14.118) for the functions ΨI(T, z) and \( {\Psi}_I^{+}\left(T,z\right) \) comes from the positive-P representation. Making use of the positive-P representation, the Fokker-Planck equation with positive semi-definite diffusion coefficients amounts to an equivalent Ito stochastic differential equation, Equations (14.118) (Carter, 1995; Drummond & Corney, 2001; Drummond & Carter, 1987, Koleden & Platen, 1992; Sauer, 2013). ΨI(T, z) and \( {\Psi}_I^{+}\left(T,z\right) \) are not complex conjugates of one another except in the mean case (Koleden & Platen, 1992; Sauer, 2013).
Equations (14.118) govern the quantum treatment of pulse propagation in an optical fiber in the presence of the third-order dispersion term (β 3 = ω‴/ω′4). To increase the bit rate in optical communication systems, a light source (a laser) is usually employed close to the zero dispersion wavelength (ZDW) of optical fibers, \( \left({\beta}_2={\left.{\omega}^{{\prime\prime} }/{\omega^{\prime}}^3\right|}_{\omega_0}=0\,\, \mathrm{i.e.}\,\, {\omega}^{{\prime\prime} } = 0\right) \), where β 3 plays an important role (Agrawal, 2012). Thus, Equations (14.118) provide the quantum treatment of pulse propagation in this situation.
The quantum noise near the propagating solitons is simulated using the linearized fluctuation equation (Drummond & Carter, 1987) for the propagating soliton as:
where Ψ(T, z) = ψ 0(T, z) + δΨ(T, z) and ψ 0(T, z) = 〈Ψ(T, z)〉. Recall that Eq. (14.122) together with the equation obtained by using the transformation Ψ → Ψ+, i → − i, and ζ → ζ+ forms a set of coupled equations.
Here, ψ 0 is the classical solution to the generalized first-order approximation of the nonlinear Schrödinger equation. The function ψ 0 corresponds to a classical coherent input state at z = 0, which has a form of \( {\psi}_0\left(T,z=0\right)=\sqrt{P_0}\operatorname{sech}\left(T/{T}_0\right) \), where P 0 and T 0 are, respectively, the peak power and width of the input pulse launched into an optical fiber.
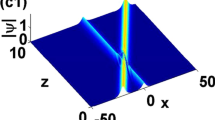
To find the solutions to Eqs. 14.118 and 14.122, numerical algorithms can be applied to solve these stochastic partial differential equations (Sauer, 2013; Dennis et al., 2013). One could assume that the input solitonic pulse ψ 0(T, 0) is launched into an optical fiber in which the dispersion length \( \left({L}_D={T}_0^2/\left|{\beta}_2\right|\right) \), third-order dispersion length (\( {L}_D^{\prime }={T}_0^3/\left|{\beta}_3\right| \)), and nonlinear length (L NL = ω′/gP 0) are approximately equal, \( {L}_D\approx {L}_D^{\prime}\approx {L}_{NL} \). Figure 14.1 shows the evolution of the intensity of the travelling solitonic pulse along the optical fiber. The soliton intensity evolution and the soliton amplitude fluctuations at the center are shown in Figs. 14.2 and 14.3, respectively. The central intensity evolution of the propagated soliton has been obtained from Eq. 14.118, while the soliton’s amplitude fluctuation at its central peak is deduced from Eq. 14.122. Due to the present simulation results, it is understood that the propagated soliton suffers from quantum noise, and there are fluctuations in the vicinity of the soliton. These fluctuations should be taken into consideration in the future quantum technologies (Vinh et al., 2021).
14.4 Quantum Model for Supercontinuum Generation Process
In Sect. 14.2, the propagation of electromagnetic field was quantized when the third-order dispersion term was present. The method discussed in Sect. 14.2 was applied to an optical fiber, when the electromagnetic field was travelling along it in Sect. 14.3. The method introduced could be applied to higher dispersive terms if needed. The process by which a high-intensity light pulse is launched into a dispersive dielectric; the extreme frequency broadening is observed due to dispersive and nonlinear effects, known as supercontinuum generation. Both experimental and theoretical studies performed by several groups indicate the formation of the supercontinuum light in a dielectric, e.g., optical fiber. A comprehensive study of this process was published by Dudley et al. (2006) based on classical models. In this section, the quantum treatment of SCG by pulse propagation in the presence of the higher-order dispersion terms, retarded response of the medium, and the third-order susceptibility is focused (Safaei Bezgabadi & Bolorizadeh, 2022).
Generation of noise in a dielectric used to generate supercontinuum light source is the main cause of instability in it and, therefore, reducing its applicability in industry. Depending on the parameters of the input pulse, the generated supercontinuum noise could cause up to 50% fluctuation in the temporal intensity profile of output pulse (Corwin et al., 2003; Dudley & Genty, 2013; Gonzalo et al., 2018; Wetzel et al., 2012). The fundamental part of this noise has its root in quantum noise, which is inherent in the nonlinear process leading to the generated continuum light. Corwin and coworkers measured the noise and provided a model describing it (Corwin et al., 2003). Their model, which is called a semi-classical model, adds a noise term into the generalized nonlinear Schrödinger equation (GNLSE). The term added to GNLSE, by Corwin and coworkers (2003), is a quantum noise, which has been phenomenologically a sound term to be added to the classical GNLSE. Real-time measurements of optical noise showed long-tailed statistics in the spectral intensity of a generated supercontinuum light (Wetzel et al., 2012; Närhi et al., 2016). Gonzalo and coworkers (2018) were able to reduce noise fluctuation in all-normal dispersion supercontinuum sources. However, the instability of the supercontinuum light due to the noise is still an open question.
It is intended to devise a quantum mechanical model to treat the SCG in a dielectric using the positive-P representation (Safaei Bezgabadi & Bolorizadeh, 2022). This model describes the soliton self-frequency shift, nonetheless, and the noise associated with solitons in a dielectric. The quantum treatment of supercontinuum is essential for the development of quantum communication, quantum computers, and spectroscopy. The higher-order solitons split into lower order and fundamental ones due to the soliton interactions, the third order dispersion effect, the Raman effect, and the self-steepening phenomenon. A powerful quantum theory is needed to explain all these effects.
The usual model for a centrosymmetric fiber (photonic crystal fiber (PCF)) is chosen where the first nonlinear term to be included is the third-order nonlinear susceptibility, which is not instantaneous in all practical applications (for details, see Ref. (Alfano, 2016; Agrawal, 2012)). The proper canonical Lagrangian leading to the correct Hamiltonian and to the Maxwell’s equations as the Hamilton’s equation of motion was devised earlier. The Hamiltonian is:
where R(t), a k, D, and η 3 are, respectively, the response function of the medium, the mode operators, the electric displacement operator, and the third-order nonlinear response of the medium. The first term in Eq. (14.123) was derived earlier, by the approach presented in the previous sections, which included the higher-order dispersion terms. The interaction picture is assumed, Eq. (14.114), and the spatial dependence is discretized making use of the expansion (14.105) near k 0.
Due to the discrete nature of the longitudinal mode spacing (Δk = 2π/L ) in an optical fiber of length L, the local operators are defined as (Drummond & Carter, 1987):
where spatial z-dependence, (z ≡ ℓΔz), is discrete and the steps of Δz = L/(2N' + 1) are arranged along the optical fiber from ℓ = − N' to +N’. The local operators satisfy the harmonic oscillator commutation relations (Drummond & Carter, 1987). As discussed earlier, the quantum mechanical treatment of the SCG process is done making use of the positive-P representation, the method developed by Drummond (Drummond & Hillery, 2014; Drummond & Carter, 1987). The definition (Drummond & Hillery, 2014; Drummond & Carter, 1987):
is the starting point where |α〉 and α ℓ are the coherent state of total field and the eigenvalue for the local operator α ℓ, respectively. In addition, ∣θ(t)〉 is the total wave function for the interaction Hamiltonian, while P(t; α, α+) develops in time according to a Fokker-Planck equation with positive semi-definite diffusion coefficient. The Fokker-Planck equation amounts to an equivalent equation of motion for appropriate stochastic variables α(t) and α+(t):
and:
where:
and:
Here, ξ ℓ(t) and \( {\xi}_{\mathrm{\ell}}^{+}(t) \) are real Gaussian stochastic functions. The correlation relations \( \left\langle {\xi}_{\mathrm{\ell}}\left({t}_1\right){\xi}_{\mathrm{\ell}^{\prime} }^{+}\left({t}_2\right)\right\rangle =0 \) and \( \left\langle {\xi}_{\mathrm{\ell}}\left({t}_1\right){\xi}_{\mathrm{\ell}^{\prime} }\left({t}_2\right)\right\rangle =\left\langle {\xi}_{\mathrm{\ell}}^{+}\left({t}_1\right){\xi}_{\mathrm{\ell}^{\prime} }^{+}\left({t}_2\right)\right\rangle ={\delta}_{\mathrm{\ell \ell}^{\prime} }\delta \left({t}_1-{t}_2\right) \) are valid for the functions ξ ℓ(t) and \( {\xi}_{\mathrm{\ell}}^{+}(t) \). Note, firstly that the rotating wave approximation is used to calculate the integral term of the Hamiltonian (14.123) and secondly α ℓ and \( {\alpha}_{\mathrm{\ell}}^{+} \) are not exactly complex conjugate to each other as the positive-P representation is used. The stochastic field, Φ, is defined as (Drummond & Carter, 1987):
in the limit Δz → 0, at the location z = ℓΔz. As the continuum representation is now used, the discrete stochastic terms are replaced by Gaussian stochastic fields ξ(T, z) and ξ+(T, z), with correlation relations similar to Eq. (14.119) to Eq. (14.121).
In addition to the quantum noise, one may include additional fluctuations due to variations in the refractive index, which would result in a set of correlation relation different from those of Eq. (14.119) to Eq. (14.121). However, these fluctuations are ignored for the ideal photonic system or the photonic crystal fibers. Making use of the transformation (T = t − z/ω′), the problem is solved in a new frame moving at a velocity equal to the group velocity. Now, a wavenumber dependent nonlinear parameter, χ Φ, is defined which is similar to χ α. For all practical cases, it can be expanded as:
where \( \chi {^{\prime} }_{\Phi}={\left.d{\chi}_{\Phi}/ dk\right|}_{k={k}_0} \).
Finally, the full stochastic equation governing the SCG for the field Φ(T,z) is obtained as:
where:
There is also a coupled equation to Eq. (14.131) by transforming Φ → Φ+, i → − i and \( \overline{\xi}\to {\overline{\xi}}^{+} \), which in the mean case it is the complex conjugate of Eq. (14.131). Equation (14.131) can be regarded as the fundamental result of the present work. Equation (14.131) and its coupled equation for Φ+(T, z) form a set of coupled generalized nonlinear Schrödinger equations for the quantum treatment of the SCG in fibers (e.g., PCF). Here, the stochastic terms introduce fluctuations originated from quantum noise. In addition to the coupling form of the two equations, the main difference between the coupled quantum-stochastic equations and its classical form is the term proportional to \( {\int}_{-\infty}^TR\left({T}^{\prime}\right)\Phi \left(T-{T}^{\prime },z\right)d{T}^{\prime } \) in Eq. (14.131) which has no counterpart in classical form. This additional term is brought about by commutation relations, which holds for creation and annihilation operators. Indeed, this term appears when one obtains the Fokker-Planck equation (from master equation) by using Hamiltonian (14.123). Also, note that the quantity χ Φ introduced here for the quantum case is half its value for the classical form.
In the instantaneous medium response limit, R(T) is replaced by delta function where the quantity defined by Eq. (14.132) takes the form:
Therefore, the coupled quantum-stochastic equation leads to the well-known coupled stochastic nonlinear Schrödinger equation (Drummond & Hillery, 2014; Drummond & Carter, 1987) which resulted from the Fokker-Planck equation (Drummond & Hillery, 2014) or the results of the previous section (Eq. 14.118). Hence, Eq. (14.131) gives a rigorous basis for earlier results (Drummond & Carter, 1987) for instantaneous medium response. Also, if one does not apply the nature of the commutation relation, the resulted equation of motion (master equation) from Hamiltonian (14.123) leads to the classical generalized nonlinear Schrödinger equation (Alfano, 2016; Dudley et al., 2006; Dudley & Taylor, 2010). There are self-phase modulation and cross-phase modulation, which are the side effect of Kerr effect and four wave mixing due to nonzero value for the χ Φ. Also, the stimulated Raman scattering and self-steepening are discussed assuming the retarded response function, R(T), and the dispersive nature ofχ Φ.
The coupled quantum-stochastic equations will have soliton solutions, called quantum solitons. There are many works in the literature to study quantum solitons (Drummond & Hillery, 2014; Drummond et al., 1993; Yao, 1997; Vinh et al., 2021), but these solitons have not studied in SCG process, and in these works, the higher-order dispersion coefficients were not included. If these solitons are not a fundamental one, they split into the lower order and fundamental ones after propagating inside the optical fiber, which is known as soliton fission. In some applications of the supercontinuum generation (e.g., quantitative experiments), it is necessary to squeeze the quantum noise in the vicinity of these solitons. The linearized fluctuation equation to study quantum noise will be:
where ϕ 0(T, z) = 〈Φ(T, z)〉 and Φ(T, z) = ϕ 0(T, z) + δΦ(T, z). Equation (14.134) together with the equation obtained by transforming Φ → Φ+, i → − i, and \( \overline{\xi}\to {\overline{\xi}}^{+} \) forms a new set of coupled equations to be called the coupled quantum-stochastic noise equations.
Here, ϕ0 can be considered as a mean case solution to the coupled generalized nonlinear Schrödinger equations for the quantum treatment of SCG (Eq. 14.131). The function ϕ 0 at z = 0 corresponds to a classical coherent input state, which, in resemblance to the classical case, can be treated as \( {\phi}_0\left(T,z=0\right)=\sqrt{P_0}\operatorname{sech}\left(T/{T}_0\right) \), where P 0 and T 0 are, respectively, peak power and width of the input pulse which is launched into the photonic crystal fiber.
In summary, a quantum description of SCG of highly nonlinear pulse propagation in an optical fiber is established. This theory leads to a coupled quantum-stochastic generalized nonlinear Schrödinger equation. In addition to the coupling term, the second term in Eq. (14.132) is not present in the classical generalized nonlinear Schrödinger equation for the description of SCG. The reason behind this difference is the commutation relation that holds for the stochastic fields of the master equation, leading to the Fokker-Planck equation.
Making use of a stochastic field, the quantum noise source was included in the governing equation. Subsequently, the coupled linearized fluctuation equation is obtained by implementing the proper definition for squeezed quantum solitons (Drummond & Carter, 1987). One argues that the resultant squeezing for the normal dispersion regime is different from the resultant squeezing for the anomalous dispersion regime. In order to arrive at this prediction, it is necessary to solve the coupled linearized fluctuation equation numerically. The equations, obtained here, could be used to study non-optical systems involving the retarded response, when the Hamiltonian (14.123) holds.
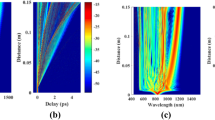
Applying the fourth-order Runge-Kutta algorithm and employing the quantum formalism, Eq. (14.131), the supercontinuum generation in photonic crystal fibers under the mean case can be studied where Φ and Φ+ are complex conjugates to each other. Note that the expectation value of the last term in Eq. (14.131) is zero under mean case (Drummond & Hillery, 2014; Drummond & Carter, 1987). A PCF and incoming light parameters assumed by Dudley et al. (2006) were used in the experimental results of Corwin and coworkers (2003) which is compared with the results of the present quantum mechanical model as shown in Fig. 14.4. A pulse of a 0.9 nJ energy at ultrashort width was used to measure the supercontinuum spectrum between 400 and 1400 nm as shown in Fig. 14.4 (Corwin et al., 2003). The present quantum model for the generation of SCG is plotted in Fig. 14.4 for comparison with the experimental results, where the two agree. The peak of solitons in the experimental results agrees with the quantum mechanical model. The results of the quantum and classical models for the retarded nonlinear response condition are shown in Fig. 14.5. The input pulse of 10 kW peak power and 28.4 fs width at 835 nm was chosen in this work. Due to the additional term in Eq. (14.131), which is absent in the classical GNLSE, there are differences between the two results for the SCG. Note that the higher dispersion terms and retarded response of the medium were not included in the work reported in 2016 (Safaei Bezgabadi & Bolorizadeh, 2016), and therefore the results do not show the soliton self-frequency shift and soliton fission present in this work as shown in Fig. 14.5. The resulting simulation of the SCG is shown by Fig. 14.5a, b for the quantum model, while similar data is provided in Fig. 14.5c, d for the classical model. The difference between the two results, classical and quantum treatments, arises due to the presence of the additional term. One can compare the spectral broadening of a pulse inside the optical fiber by the two methods as shown in Fig. 14.6. Comparing the results of the classical treatment of the SCG in a specific PCF shown by Figs. 14.5c, d and 14.6b and the quantum results presented in Figs. 14.5a, b and 14.6a show that not only the spectral broadening increases in the quantum treatment but also that the generated frequency combs are closer and richer. In Fig. 14.5b, the quantum mechanical model predicts longer delay for the formed soliton as compared with the classical result of Fig. 14.5d. However, the two models predict the soliton fission to occur at about the same travel distance of the pulse along the optical fiber. Figure 14.6a indicates that the peak intensity of soliton pulse calculated by the present quantum model is at 1300 nm which fits well with the experimental results of Corwin and coworkers (2003) shown in Fig. 14.4, while the classical result, Fig. 14.6b, shows that the peak of soliton pulse is at 1220 nm. As shown in Fig. 14.6b, the simulation of the supercontinuum spectrum in the classical model reaches the background level at wavelengths 1400 nm, while both experimental data and quantum results extend beyond this wavelength.
A comparison between the present simulation of SCG (the blue line) in the fiber and the experimental results of Corwin et al. (2003) (the red line)
Simulation results for the quantum mechanical (a and b) and classical treatment (c and d) of SCG along the first 15 cm of a PCF fiber. Photons generated at wavelengths from 400 nm (a) to 1450 nm in a quantum treatment and (c) to 1350 nm in a classical treatment of SCG. Time development of the input pulse is shown in (b) and (d) with respect to the delayed pulse in a quantum and classical models, respectively
As described earlier, the additional term in Eq. (14.132) originated from the non-commutative nature of the creation and the annihilation operators defined in obtaining the Fokker-Planck equation. This term changes the evolution of the optical pulse inside an optical fiber, which causes the difference in the simulation results between the two treatments. In reality, this term alters how the nonlinear part would affect the broadening of the pulse and generation of new frequencies. As an example, the soliton evolves according to the interplay between the third-order dispersion term, the Raman scattering term, and the self-steepening term. Thus, the evolution of solitons is predicted differently in the quantum treatment as compared with the classical model.
In an experimental work, the resolution of the spectrometer should be less than 1 nm, in order to be able to show deeper details of the SCG. We therefore suggest a more detailed and precise experimental work needed in this field to be able to understand the deeper physics behind the nonlinear effects in dielectrics and, especially, fibers. This is essential in order to understand and to reduce the noise and, most important, the quantum noise.
In the following, the quantum mechanical treatment results are compared with the classical ones for different peak powers and pulse widths. Figure 14.7 indicates that when the peak power is low, such as 1 kW, and the pulse width is large, 10 ps, the two models lead, approximately, to similar results. Note that the quantum mechanical description of wave and particles is the same and leads to the wave packet descriptions of both. When the width of a light pulse is small, it represents a small particle which makes the quantum treatment essential. It is interesting that the two results, classical and quantum models, deviate as the width of input pulse changes from 10 ps to 1 ps. The classical results are closer to the quantum mechanical model at the pulse width of 10 ps as compared with the 1 ps ones. This study shows how important is the quantum nature of pulse for short width. In practice, the nonlinear terms do not have significant contributions on the generation of pulses of new wavelengths at such peak powers and pulse widths. However, the quantum mechanical treatment of the pulse propagation along dielectrics or optical fibers is still indispensable, because this approach is applicable to study quantum solitons and to reduce the fluctuations in the vicinity of these solitons. From a quantum mechanical point of view, a soliton is considered as a collection of particles traveling together in a medium.
14.5 Conclusion
In summary, a higher-order Lagrangian has been introduced for the field propagation in an inhomogeneous, dispersive, and anisotropic dielectric in Sect. 14.2, specifically an optical fiber. By establishing a quantum theory, the propagating fields are quantized by imposing the Dirac commutation relations. The Hamiltonian is then written in terms of proper creation and annihilation operators. In Sect. 14.3, the quantum theory is applied to study pulse propagation inside a conventional optical fiber where the coupled stochastic NLSE is resulted as the governing equation. By using this coupled stochastic NLSE, propagation of quantum soliton in the presence of higher-order dispersion can be described, and the quantum noise in the vicinity of the soliton can be reduced.
As it is essential to study SCG quantum mechanically, this approach is applied for ultrashort pulse propagation along a nonlinear media when the retarded response function of the medium should be taken into account. Here, the quantum theory for the SCG process is presented, and it has included the terms with the significant contributions involved in the supercontinuum generation a nonlinear media, specifically the PCFs. Besides the obtained coupled stochastic equation for the quantum treatment of the SCG, the source of significant difference is the additional term which has no classical resemblance and roots in the non-commutative nature of the creation and the annihilation operators defined in obtaining the Fokker-Planck equation. The result of the quantum treatment, as compared with the experimental results, indicates conformity between theory and experiment (Corwin et al., 2003). The generated supercontinuum spectrums for the quantum mechanical and the classical treatments are studied for different peak powers and widths of the input pulse. It is concluded that the pulses of fs width behave as particles and described best by quantum models. In conclusion, the quantum theoretical treatments of light pulses passing through a nonlinear media describes the supercontinuum generation process closer to the experimental data as compared with classical models.
There are different types of noise involved in supercontinuum light, or generally in the propagation of electromagnetic waves in a nonlinear media, which are related to absorption, gain, Raman effects, and the quantum mechanical noise that could be described by stochastic equations. The noise involved in Raman effects has quantum origin, and it is present in a vacuum state (Corwin et al., 2003) due to spontaneous Raman effects. A semi-classical model of noise, due to the propagation of light pulses in fibers devised by Corwin and coworkers (2003), is based on adding this kind of noise to the GNLSE. However, the second-order nonlinear term was not included which is the source of the Raman noise. Nonetheless, this noise exists and should be included in the quantum theory of the field propagation in dielectric media (Corwin et al., 2003). In the present work, in order to reduce the fluctuations near solitons, one has to make use of Eq. (14.134) instead of Eq. (14.131), a process that is referred to as linearization (Safaei et al., 2018). However, it should be noted that the linearization is handled for squeezed photons, and, therefore, Eq. (14.134) is not valid for long-distance travel of light pulses even for an instantaneous nonlinear response. It is important to add the quantum noise involved in Raman effects to Eq. (14.131), to correctly reduce the quantum noises in the vicinity of the solitons, which were formed during the SCG process. New experimental work based on real-time measurement, similar to those of Närhi and coworkers (2016) and Wetzel and coworkers (2012) at 1550 nm pulses, is needed to study the SCG and all noises involved. Detailed understanding of the physics of ultrashort light pulses needs more experimental works and their comparison with the present quantum theory of pulse propagation, specifically in fiber applications. Nonetheless, the medium response function and/or the parameters involved in it (such as Raman parameters and Raman delayed factor) could be different when a light pulse should be modeled quantum mechanically.
References
Agrawal, G. P. (2012). Nonlinear fiber optics. 5th Ed. Academic Press.
Alfano, R. R. (2016). The supercontinuum laser source: The ultimate white light. Springer.
Alfano, R. R., & Shapiro, S. L. (1970). Emission in the region 4000–7000 A via four-photon coupling in glass; Observation of self-phase modulation and small scale filaments in crystals and glasses; Direct distortion of electronic clouds of rare-gas atoms in intense electric fields. Physical Review Letters, 24, 584, 592, 1217.
Boyd, R. W. (2008). Nonlinear optics. Academic.
Carter, S. J. (1995). Quantum theory of nonlinear fiber optics phase-space representations. Physical Review A, 51, 3274.
Corona, M., Palmett, K. G., & U’Ren, A. B. (2011). Third order spontaneous parametric down conversion in thin optical fiber as a photon triplet sources. Physical Review A, 84, 033823.
Corwin, K., Newbury, N., Dudley, J. M., Coen, S., Diddams, S. A., Weber, K., & Windeler, R. (2003). Fundamental noise limitations to supercontinuum generation in microstructure fiber. Physical Review Letters, 90, 113904.
Cumberland, B. A., Travers, J. C., Popov, S. V., & Taylor, J. R. (2008). 29 W High power CW supercontinuum source. Optics Express, 16, 5954.
Dechoum, K., Rosales-Zárate, L., & Drummond, P. D. (2016). Critical fluctuations in an optical parametric oscillator: When light behaves like magnetism. Journal of the Optical Society of America B: Optical Physics, 33, 871.
Dennis, G. R., Hope, J. J., & Johnson, M. T. (2013). XMDS2: Fast, scalable simulation of coupled stochastic partial differential equations. Computer Physics Communications, 184, 201.
Drummond, P. D. (1990). Electromagnetic quantization in dispersive inhomogeneous nonlinear dielectrics. Physical Review A, 42, 6845.
Drummond, P. D., & Carter, S. J. (1987). Quantum field theory of squeezing in solitons. Journal of the Optical Society of America B: Optical Physics, 4, 1565.
Drummond, P. D., & Corney, J. F. (2001). Quantum noise in optical fibers: I. Stochastic equations. Journal of the Optical Society of America B: Optical Physics, 18, 139.
Drummond, P. D., & Gardiner, C. W. (1980). Generalized P-representations in quantum optics. Journal of Physics A, 13, 2353.
Drummond, P. D., & Hillery, M. (2014). The quantum theory of nonlinear optics. Cambridge University Press.
Drummond, P. D., & Opanchuk, B. (2020). Initial states for quantum field simulations in phase space. Physical Review Research, 2, 033304.
Drummond, P. D., Gardiner, C. W., & Walls, D. F. (1981). Quasiprobability methods for nonlinear chemical and optical systems. Physical Review A, 24, 914.
Drummond, P. D., Shelby, R. M., Friberg, S. R., & Yamamoto, Y. (1993). Quantum solitons in optical fibres. Nature, 365, 307.
Dudley, J. M., & Genty, G. (2013). Supercontinuum light. Physics Today, 66, 29.
Dudley, J. M., & Taylor, J. R. (2010). Supercontinuum generation in optical fibers. Cambridge University Press.
Dudley, J. M., Genty, G., & Coen, S. (2006). Supercontinuum generation is photonic crystal fiber. Reviews of Modern Physics 78, 1135–1184.
Faddeev, L., & Jackiw, R. (1988). Hamiltonian reduction of unconstrained and constrained systems. Physical Review Letters, 60, 1692.
Fujimoto, J. G. (2003). Optical coherence tomography for ultrahigh resolution in vivo imaging. Nature Biotechnology, 21, 1361.
Gitman, F. D. M., & Tyutin, I. V. (1990). Quantization of fields with constraints. Springer.
Glauber, R. J. (1963). Coherent and incoherent states of the radiation field. Physics Review, 131, 2766.
Gonzalo, I. B., Engelsholm, R. D., & Bang, O. (2018). Noise study of all-normal dispersion supercontinuum sources for potential application in optical coherence tomography. Proceedings of SPIE, 10591, 105910C.
Grangier, P., Levenson, J. A., & Poizat, J. P. (1998). Quantum nondemolition measurements in optics. Nature, 396, 537.
Hillery, M. (2009). An introduction to the quantum theory of nonlinear optics. Acta Physica Slovaca, 59, 1.
Koleden, P. E., & Platen, E. (1992). Numerical solution of stochastic differential equations. Springer.
Li, J., Tan, W., Si, J., Kang, Z., & Hou, X. (2021). Generation of ultrabroad and intense supercontinuum in mixed multiple thin plates. Photonics, 8, 311.
Närhi, M., Turunen, J., Friberg, A. T., & Genty, G. (2016). Experimental Measurement of the Second-Order Coherence of Supercontinuum. Physical Review Letters, 116, 243901.
Safaei Bezgabadi, A., & Bolorizadeh, M. A. (2016). Quantum mechanical treatment of the third order nonlinear term in NLS equation and the supercontinuum generation. Proceedings of SPIE, 9958, 995803.
Safaei Bezgabadi, A., Borhani Zarandi, M., Bolorizadeh, M., & Bolorizadeh, M. A. (2019). Quantum noise for the propagating solitons in an optical fiber in presence of the third order dispersion coefficient. Proceedings of SPIE, 11123, 111230S.
Safaei Bezgabadi, A., Borhani Zarandi, M., & Bolorizadeh, M. A. (2020a). A quantum approach to electromagnetic wave propagation inside a dielectric. European Physical Journal Plus, 135, 650.
Safaei Bezgabadi, A., Borhani Zarandi, M., & Bolorizadeh, M. A. (2020b). Quantizing the propagated field through a dielectric including general class of permutation symmetries for nonlinear susceptibility tensors. Results in Physics, 19, 103622.
Safaei Bezgabadi, A., & Bolorizadeh, M. A. (2022). Quantum model for supercontinuum generation process. Scientific Reports, 12, 9666.
Safaei, A., Bassi, A., & Bolorizadeh, M. A. (2018). Quantum treatment of field propagation in a fiber near the zero dispersion wavelength. Journal of Optics, 20, 055402.
Sauer, T. (2013). Computational solution of stochastic differential equations WIREs. Computational Statistics, 5, 362.
Sudarshan E. C. G. (1963). Equivalence of semiclassical and quantum mechanical descriptions of statistical light beams. Physical Review Letters, 10, 277.
Sun, F.-X., He, Q., Gong, Q., Teh, R. Y., Reid, M. D., & Drummond, P. D. (2019). Schrödinger cat states and steady states in subharmonic generation with Kerr nonlinearities. Physical Review A, 100, 033827.
Venck, S., et al. (2020). 2–10 μm mid-infrared fiber- based supercontinuum laser source: Experiment and simulation. Laser & Photonics Reviews, 14, 2000011.
Vengris, M., et al. (2019). Supercontinuum generation by co-filamentation of two color femtosecond laser pulses. Scientific Reports, 9, 9011.
Vinh, N. T., Tsarev, D. V., & Alodjants, A. P. (2021). Coupled solitons for quantum communication and metrology in the presence of particle dissipation. Journal of Russian Laser Research, 42, 523.
Wetzel, B., et al. (2012). Real-time full bandwidth measurement of spectral noise in supercontinuum generation. Scientific Reports, 2, 882.
Woodard, R. (2007). Avoiding dark energy with 1/R modifications of gravity. In L. Papantonopoulos (Ed.), The invisible universe: Dark matter and dark energy (Lecture Notes in Physics, vol 720). Springer.
Yao, D. (1997). Schrödinger-cat-like states for quantum fundamental solitons in optical fibers. Physical Review A, 55, 3184.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix
Appendix
Derivation of Eqs. (14.9) from (14.8) in this Chapter
Starting with the definition of displacement vector and its relation with the electric field as:
one can rewrite it as:
where η−1(ω, x) = ε(ω, x). Therefore, Eq. (14.8) is rewritten as:
One can simplify the frequency dependent factor of the first term in the integrand of equation (A.3) as:
which results in Eq. (14.9) in the chapter.
Derivation of Eq. 14.26, Starting from Maxwell’s Equations
Let’s start with the Maxwell equation (14.22a) from the manuscript. Substituting the dual potential for magnetic field from Equation (14.12), one arrives at:
Rewriting Equation (14.22b) for the electric field as:
and substituting into (A.5), one concludes:
for the equation of motion. Making use of the dual potential for displacement vector, Eq. (14.12) in the chapter, Eq. (A.7) could be written as:
where it is assumed that η n(x) for n > 1 to be independent of frequency. Substituting expansion (14.13) for the dual potential into Eq. (A.8), one arrives at:
where the equation of motion for mode ν is:
Note the parameters of summation \( \sum \limits_{\nu; {\nu}_1,{\nu}_2,\cdots, {\nu}_n} \) stands for summation over all frequency modes other than mode ν. Additionally, the quantity η 1(τ, x) will be written as η ν(τ, x). Inserting \( {e}^{i{\omega}^{\nu}\tau }{e}^{-i{\omega}^{\nu}\tau }=1 \) into the integrand of Eq. (A.9b), one has:
The quantity \( {e}^{-i{\omega}^{\nu}\tau }{\boldsymbol{\Lambda}}^{\nu}\left(\mathbf{x},t-\tau \right) \) is expanded into a Taylor series in terms of τ up to the third order as:
where slowly varying envelope approximation is applied. Equation (A.11) is rewritten as:
Now, Eq. (A.12) is replaced into the first term in the relation (A.10), and integrated over τ, the result will be:
Similar arguments could be used for other terms of Eq. (A.11b), where one gets:
and:
Therefore, by substituting results (A.13) into Eq. (A.10), the equation of motion will be:
Lagrangian Method to Derive Eqs. 14.25 and 14.26
Here, the equation of motion and the Hamiltonian will be derived making use of the Lagrangian density (14.28), which will, respectively, be equal to Equation (14.26) and Equation (14.25). When the Lagrangian density \( \mathcal{L} \) is a function of Λν, \( {\dot{\boldsymbol{\Lambda}}}^{\nu } \), and \( {\ddot{\boldsymbol{\Lambda}}}^{\nu } \), the Euler-Lagrange equation is:
where k represents the space coordinates x, y, and z and double k means summation over it. For an arbitrary vector w, the transverse derivatives with respect to the components of vector Λ have the property:
It is assumed that in Eq. (A.16), the vector Λ stands for either Λν or Λ−ν or their time derivative. For the present system, a general form of the Lagrangian density is defined as:
where coefficients a to g are to be determined by comparing the equation of motion and the Hamiltonian resulting from the Lagrangian density, Equation (A.17), with Equations 14.26 and 14.25 forming the chapter, respectively. Making use of Equation (A.16), the terms in Equation (A.15) are written as:
and:
Substituting the results (A.18, A.19, A.20, A.21, and A.22) into Euler-Lagrange equation, Eq. (A.15), each component of the equation of motion will be:
where the equation of motion will be:
Comparing (A.24) with Eq. (14.26) in the chapter, the relations:
are found for the parameters a to g in Eq. (A.17).
According to Ostrogradsky’s theorem, when the Lagrangian density is a function of Λν, \( {\dot{\boldsymbol{\Lambda}}}^{\nu } \), \( {\ddot{\boldsymbol{\Lambda}}}^{\nu } \), Λ−ν, \( {\dot{\boldsymbol{\Lambda}}}^{-\nu } \), and \( {\ddot{\boldsymbol{\Lambda}}}^{-\nu } \), there are four canonical coordinates and momenta. Therefore, the canonical momenta are obtained by the definitions:
and:
Substituting relations (A.19), (A.21), and (A.22) into definitions (A.26) and (A.27), the components of canonical momenta for the canonical coordinates Λ−ν and \( {\dot{\boldsymbol{\Lambda}}}^{-\nu } \) are found as:
and:
Therefore, the canonical momenta associated with the canonical coordinatesΛ−ν, \( {\dot{\boldsymbol{\Lambda}}}^{-\nu } \), Λν, and \( {\dot{\boldsymbol{\Lambda}}}^{\nu } \)are:
and:
respectively.
Making use of the definition for Hamiltonian as:
in the Euler-Lagrange formalism, integrating some of the terms by parts as:
with the fact that the fields vanish at infinity, one finds the Hamiltonian to be:
Again, comparing the parameters in (A.36) with the Hamiltonian (14.25) in the chapter which are similar to the parameters (A.25) and assuming the symmetry in the Lagrangian density, the final parameters will be:
In summary, the results obtained implementing the Lagrangian density A.17 agree both in dynamics and energy with the results obtained from Maxwell equations and Poynting’s theorem for slowly varying envelope functions. Thus, the Lagrangian density (A.17) describes the system in the framework of a local field theory of a nonlinear dispersive medium. By using the scaler coefficients, A.37, and separating the Lagrangian density A.17 into the linear and nonlinear parts, Eqs. 14.28 and 14.29 of the chapter are yielded. In addition, Eqs. 14.25, 14.26, 14.31, and 14.32 are also obtained by implementing the coefficients A.37 into A.36, A.24, A.32, and A.33, respectively.
Derivation of Eqs. 14.35, 14.36, and 14.37
Starting with Equation 14.34 from the manuscript and the fact that (Λν(t, x))∗ = Λ−ν(t, x), it is concluded that:
Thus:
and:
By simple algebra, it can be shown that:
and:
Substituting (A.40) and (A.41) into the linear part of Lagrangian density (14.28) in the chapter, one arrives at the linear part of the Lagrangian as:
Defining the quantities:
and:
the Lagrangian (A.42) will be simplified as:
It is necessary to discuss the quantities M, specifically for definitions (A.47) and (A.48). Starting with Eq. (A.48), one arrives at:
where k and k’ are changed into −k and −k’, respectively. Now making use of the relation (A.39), one concludes that:
Another change into Eq. (A.51), i.e., interchanging k with k’, leads to:
A similar argument holds for definition (A.44), which results in:
Therefore, the Lagrangian will be simplified as:
which is the same as Eq. 14.35 in the chapter. Eq. 14.37 in the chapter is resulted by removing the indices k, k', α, and α' for simplicity. Additionally, the limits of ν have changed from –N to N to 0 to N. It should be noted that the negative values of ν are taken into account by removing the factor ½ into 1/(1 + δ ν, 0). However, the factor 1/(1 + δ ν, 0) has been neglected for the simplicity of the equations as it affects only the first term.
Derivation of Relations Between the Parameters in Equations (14.41)
In order to find the Hamiltonian (14.40) for the optical fiber, new set of canonical coordinates and momenta are defined by Equations (14.41) in the chapter. In order to quantize the system, standard Dirac’s commutation relations:
and:
should hold between the new canonical coordinates \( {\tilde{q}}^{\nu } \) and \( {\tilde{p}}^{\nu } \) to arrive at the relations (14.42a), (14.42b), and (14.42c), respectively. Note that the commutation relations for quantities X and Y are related to the Poisson’s bracket as:
where q i and p i are also coordinates qν, Qν, qν†, and Qν† and their corresponding momenta.
Substituting Equations (14.41) for the canonical coordinates and momenta in Equation 14.43 and comparing it with the Hamiltonian 14.40, following six equations:
and:
will be resulted. These six relations in addition to the relations (14.42) are used to find the frequency matrices and the matrix parameters Aν to Kν, which are needed to define coordinates \( {\tilde{q}}^{\nu } \) and \( {\tilde{p}}^{\nu } \).
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Bolorizadeh, M.A., Safaei Bezgabadi, A. (2022). Quantum Mechanical Theory and Treatment of NLS Equations for Supercontinuum Generation. In: Alfano, R.R. (eds) The Supercontinuum Laser Source. Springer, Cham. https://doi.org/10.1007/978-3-031-06197-4_14
Download citation
DOI: https://doi.org/10.1007/978-3-031-06197-4_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-06196-7
Online ISBN: 978-3-031-06197-4
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)