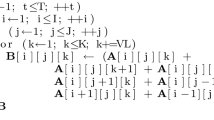Accelerating FFT Using NEC SX-Aurora Vector Engine

Abstract

Novel architectures leveraging long and variable vector lengths like the NEC SX-Aurora or the vector extension of RISCV are appearing as promising solutions on the supercomputing market. These architectures often require re-coding of scientific kernels. For example, traditional implementations of algorithms for computing the fast Fourier transform (FFT) cannot take full advantage of vector architectures. In this paper, we present the implementation of FFT algorithms able to leverage these novel architectures. We evaluate these codes on NEC SX-Aurora, comparing them with the optimized NEC libraries. We present the benefits and limitations of two approaches of RADIX-2 FFT vector implementations. We show that our approach makes better use of the vector unit, reaching higher performance than the optimized NEC library for FFT sizes under 64k elements. More generally, we prove the importance of maximizing the vector length usage of the algorithm and that adapting the algorithm to replace memory instructions with register shuffling operations can boost the performance of FFT-like computational kernels.

1 Introduction

Accelerated computing is becoming more and more relevant in High-Performance Computing (HPC). The limitation to the performance improvements imposed by the slow-down of Moore’s law applied to general purpose CPUs has made HPC architects looking for solutions that can complement the computational power delivered by standard CPUs (i.e., accelerators). The most visible example of this are GP-GPU based systems, that populate 3 places within the first 5 most powerful supercomputers in the world (Top500).

GP-GPUs, however are not the only approach to acceleration: the use of vector or SIMD extensions is becoming more and more relevant in HPC systems. Beside the AVX-512 SIMD extension by Intel, we detect appearing on the market the first CPU implementing the Arm SVE extension (Fujitsu A64FX, ranked first in the Top500) and the NEC SX-Aurora vector engine, a discrete accelerator leveraging vector CPUs able to operate with registers of up to 256 double precision elements. On top of this market movements, we can not ignore the RISC-V architecture which recently ratified v1.0 of the V-extension, boosting vector computation from the academic world and the open-source community.

The efficient use of vector accelerators often require to adapt or rewrite classical algorithms to exploit their full computing power. In most cases, vendor specific libraries coupled with optimized compilers allow to port large HPC codes to vector accelerators in a relatively smooth way. For portability reasons however, scientists often look for open-source libraries including kernels already optimized for specific architectures. The computation of the Fourier transformation using the FFT algorithms is an example of a relevant HPC kernel extremely used by the HPC community. For this reason we focused this paper on the design and the evaluation of non-parallel vectorized FFT implementations.

The main contributions of this paper are: i) we developed four implementations of the FFT algorithms targeting large vector architectures; ii) we evaluate our FFT codes on the NEC SX-Aurora accelerator, analyzing benefits and limitations of its architecture with an in depth study of hardware counters; iii) we compare our performance results with the vendor library distributed by NEC.

The remaining part of the paper is structured as follows: Sect. 2 compiles the related work in the field of FFT implementations for HPC systems; Sect. 3 briefly presents the NEC SX-Aurora accelerator; Sect. 4 analyzes the optimizations targeting large vector architectures; Sect. 5 includes the measurements gathered on NEC SX-Aurora; Sect. 6 closes the paper with general remarks and conclusions.

2 Related Work

FFT is a kernel of paramount importance in several algorithms of scientific computing. Therefore, a large body of research about FFT optimization on many architectures has been published in the last decades. The key reference publications used as background for our implementations are the book of E. Chu et al. [4], the paper of M. C. Pease [10] and the paper of P. N. Swarztrauber [11].

More recently, the research community is focusing on developing efficient FFT implementations targeting emerging architectures with different degrees of parallelism, e.g., high number of cores and long SIMD or vector units. Chow et al. [3] report their effort in taking advantage of the IBM Cell BE for the computation of large FFTs; Anderson et al. [1] make use of FPGAs for accelerating 3D FFTs; Wang et al. [13] present an FFT optimization for Armv8 architectures; Malkovsky et al. [9] evaluate FFTs on heterogeneous HPC compute nodes including GP-GPUs. Most of those studies are limited to up to 8-elements SIMD units in CPUs or high thread-level parallelism in GPUs while the implementations proposed in our paper are targeting wider vector units.

D. Bailey [2] and Paul N. Swarztrauber [11] studied various FFT algorithms, including Pease’s and Stockham’s, for the firsts vector computers which were limited by their inefficiency accessing non continuous data. The algorithms they propose have a minimum vector length of $\sqrt{N}$ at best, which is lower than our algorithm’s $\frac{N}{8}$. Moreover, our implementations propose an exploitation of the data locality in the many vector registers that the SX-Aurora has, reducing the accesses to the main memory.

Furthermore, our method extends the approach of Franchetti et al. [5] since we explore larger FFT sizes as well as double precision data types.

Promising results for acceleration with the NEC SX-Aurora accelerator have been shown for SpMV in [6] and for spectral element method for fluid dynamics in [7]. We extend those evaluation efforts of NEC’ accelerator with FFT. This paper continues the work done in the thesis from Pablo Vizcaino Serrano [12].

3 Hardware Platform: The NEC SX-Aurora

We implemented and evaluated our FFT codes targeting the NEC SX-Aurora VE (VE), the latest NEC’s long vector architecture which combines SIMD and pipelining. Vector units and vector registers use a $32\times 64$-bit wide SIMD front in an 8-cycles deep pipeline resulting in a maximum vector length of $256\times 64$-bit elements or $512\times 32$-bit elements. The VE10B processor used for this publication was presented at the IEEE HotChips 2018 [14], and the first performance evaluation was described in the same year [8].

Each of the 8 VE cores consists of a scalar processing unit (SPU) and a vector processing unit (VPU) and is connected to a shared last level cache (LLC) of 16 MB. Three fused multiply-add vector units deliver a peak performance of 269 GLFOPS (double precision) per core at 1.4 GHz. The peak performance of the used VE variant is 2.15 TFLOPS delivering a byte/FLOP ratio of 0.56.

Vector Engines are integrated as PCIe cards into their host machines. Programmers can use languages like C, C++, Fortran, and parallelize with MPI as well as OpenMP, while accelerator code can still use almost any Linux system call transparently. The proprietary compilers from NEC support automatic vectorization aided by directives. They are capable of using most features of the extensive vector engine ISA¹ from high-level languages loop constructs. For the work presented in this paper, we employed the open-source LLVM-VE project², which supports intrinsics allowing tight control over VE features to operate with complex numbers, control vector registers, and LLC cache affinity.

4 Implementation

There exist multiple algorithms for the computation of the FFT, each with its benefits and disadvantages from the computational point of view. In this paper, we focus on a subset of algorithms, those that are denominated RADIX-2. Considering an FFT with N being the number of transformed elements, a RADIX-2 FFT requires N to be a power of two and divides the required computation in $\log _2(N)$ phases. FFT algorithms are also split into in-place and out-of-place, with the latest requiring an additional buffer alongside the input and output arrays. All implementations proposed in this paper are out-of-place since our objective is an efficient vectorization and not a reduced memory footprint. Moreover, some FFT algorithms require a permutation of the resulting elements and others are self-sorting. In this paper we study both approaches.

All implementations in this paper are designed for complex double-precision data. The visual representations of the algorithms shown in this paper are simplified, presenting only the real component because the computation of the imaginary component is conceptually equivalent to its real counterpart.

For the FFT calculation, we often refer to twiddle factors. W is the set of the twiddle factors, which are complex exponents computed as $\text{ tf }(k,N)$ = ${e^{\frac{-2\pi i k}{N}}}$, with $k \in \{0, N-1\}$.

4.1 Pease FFT

The first implementation with the potential to be efficiently vectorized is the FFT algorithm developed by Marshall C. Pease [10]. In terms of arithmetic operations, each phase of a naive Pease’s FFT implementation requires N/2 additions, N/2 subtractions, and N/2 multiplications. One important downside of Pease’s algorithm is the permutation requirement at the end of the last phase. Modern vector ISA offer instructions to load and store scattered data, but they are typically less efficient than those that operate on contiguous or constant-strided data.

Pease’s algorithms is characterized by a constant geometry, that means that the same elements are operated in each of the $\log _2(N)$ phases. More specifically, the first half of the N elements operate with the second half of each phase. This leads to a potential N/2 elements that can be operated at the same time (i.e., vector length of N/2). Once a phase has been calculated, the vector registers no longer hold the first and second half of the N elements, so they must be shuffled. Due to the lack of instructions to perform this rearrangement on vector registers, this operation could be done storing all the elements in memory and loading them again in the correct order.

To mitigate the slowdown introduced by the need of accessing the memory in each phase, we propose an implementation of the Pease algorithm that distributes the N elements in eight registers instead of two. Sacrificing some potential vector length and using a precise distribution, this allows us for the computation of three phases before having to reorder the elements in memory.

A visualization of this technique is shown in the right of Fig. 1. This implementation is named 8-Pease in the rest of the paper. It uses a potential vector length of N/8 and only accesses memory every three phases while still needing the data permutation at the final stage of the algorithm. The downside of having an upper limit on the vector length of N/8 instead of N/2 is supressed for large FFT sizes where N/8 is larger than the maximum vector length (256).

Fig. 1.

8-Pease vectorization for N = 16. (Color figure online)

In Fig. 1 we also show that the twiddle factors are different in each phase; therefore, our first approach is to pre-compute them for each phase and to load them as the algorithm advances. The reason to not compute the twiddle factors during the execution is that they require the cosine operation, which is not present in the vector instruction set. Therefore, one needs to scalar compute them, store them in memory and load them in vector registers.

The pseudocode of the 8-Pease implementation is given in Algorithm 1.

Note that unlike Fig. 1, the pseudocode shows the operation of the real and imaginary parts. The vector loads, the PairOperations and the stores have been grouped for simplicity. The dark red elements from Fig. 1 are loaded in reg1, the light reds in reg2, etc. The function 3x4_PairOperation is equivalent to executing the function in Algorithm 2 for 3 phases with 4 PairOperations each. All vector instructions operate on N/8 vector elements. In reality, NEC limits the vector length to 256 elements, requiring our code to compute the phases in various iterations.

The function PairOperation() in Algorithm 2 takes advantage of fused operations to calculate the complex multiplication. Remember that the multiplication of two complex numbers, $(a + b \cdot i)\cdot (c + d \cdot i)=(e + f \cdot i)$ normally requires 7 operations: $e = a \cdot c - b \cdot d$, and $f = a\cdot d + b \cdot c$. We can group operations to have 2 multiplications and 2 fused operations (operations calculated with a single instruction are encapsulated using parenthesis): $t_1 = (a \cdot c)$, and $t_2= (a \cdot d)$, so that $e = (t_1 - b\cdot d)$ and $f = (t_2 + b \cdot c)$.

Looking at Fig. 1, it can be noted that there are only N/2 different twiddle factors ($W_0$,$W_1$,...$W_{N/2-1}$). More precisely, the number of different twiddle factors to be used in each phase is half compared to the previous one.

The repetition of the twiddle factors across the FFT brings three important observations: i) we are wasting memory since we were storing all of them for each phase; ii) we are missing potential cache locality; iii) for advanced phases, we could access a single twiddle factor per register and then replicate it. In each batch of three phases in 8-Pease, the twiddle factor of the second phase are identical for half the registers, and in the third one they are identical for all registers. This means that for the three phases, we only load 7 twiddle factor registers instead of 12.

Finally, another implementation of the Pease algorithm is proposed. Even with the twiddle factor access optimization, it still represents a slowdown.

To implement this optimization, we use gather vector instructions to load the twiddle factors. In reality, gather instructions offer a more general functionality than what we require since they are meant to load sparse data, while we need strided chunks of data. However, since no ad hoc instructions exist for our case, we decided to implement this version using gather instructions. In NEC architecture, gather operations require a vector with absolute addresses to index the memory. We use two registers, one holding the constant relative indexes that are reused and another temporarily holding the absolute indexes after adding the offset. A graphical representation of the use of gather operation is provided in Fig. 2, with its code equivalent in Algorithm 3. This implementation is named 8-Pease-gt in the rest of the paper.

Fig. 2.

Example of the proposed accesses to twiddle factors using gather operations

4.2 Stockham FFT

The other algorithm that has been studied for vectorization is Stockham’s algorithm [11]. While the algorithm is still RADIX-2 and out-of-place, it has two main differences with Pease’s algorithm. The first one is that it is a self-sorting algorithm, so it does not require a permutation at the last phase. The second difference is that Stockham’s algorithm does not have constant geometry like Pease’s. This complicates the algorithm and its vectorization, limiting the maximum vector length depending on the phase.

Using the same approach as with 8-Pease, we can divide the N elements of each phase into eight vector registers to compute three phases before rearranging the elements in memory.

Due to the self-sorting nature of the algorithm, the process of storing and loading the elements changes for every three phases. With p being the phase where the loads occurs, the stores on $p+3$ consist of $\frac{vector\_length}{2^{p}}$ groups of $2^{p}$ consecutive elements. Since an instruction that writes several consecutive elements before jumping a fixed stride does not exist in NEC’s architecture, we have two options in the implementation. We can limit the vector length of the problematic phases to be equal to the size of the groups, $2^{p}$. Since inside a group all the twiddle factors have the same value, we could use a broadcast operation to load them. The downside of this option is that for phases 3–5 and 6–8 this means limiting the vector length to 8 and 64. With SX-Aurora ’s maximum vector length of 256, this limit implies not taking full advantage of the vectorization potential.

If we do not want to limit the vector length, we can store values with a scatter operation and load twiddle factors with a gather. The initial interest in using the Stockham algorithm was removing this type of memory operations, so adding them again may seem counterproductive, even though the pattern of Stockham’s scatter operations contain consecutive elements while Pease’s is sparser. This difference is represented in a simplified example diagram in Fig. 3.

Regardless, using these long-latency instructions at the end of these special phases outperforms having up to 32 times more instructions during three phases when limiting the vector length to 8, so the final implementation uses scatters.

In terms of twiddle factors, we use the gather instruction that is also present in 8-Pease-gt and we name this new implementation 8-Stockham-gt.

Fig. 3.

Simplified example of the scatter operations used in Pease and Stockham’s algorithms, with a vector length of 8 elements.

A simplified pseudocode of this alternative is shown in Algorithm 4.

5 Evaluation

In this section we study the performance of our implementations in the vector accelerator from NEC, the SX-Aurora. We measure the real time used to compute the FFT, including the communication to the accelerator and other system interferences. The pre-computation is disregarded because it can be used for multiple FFT of the same size.

NEC has optimized math libraries called NEC Library Collection (NLC)³. Our usage of NLC is limited to aslfftw, a vectorized FFT whose interface is compatible with fftw. We have compared the performance of the proposed implementations in Sect. 4 with aslfftw, computing it as a speedup to a scalar (i.e., without vector instructions) fftw, compiled with NEC’s compiler ncc.

Fig. 4.

Speedup in NEC of the proposed vectorized FFT implementations and aslfftw.

We see in Fig. 4 how our implementations outperform aslfftw until an FFT size of 65536 elements. From that point on, aslfftw doubles the performance of our Pease’s implementations, while 8-Stockham-gt only underperforms aslffw by less than 10%. In our best case, we reach 17% of the peak performance of one VE node. It is also notable that while 8-Pease-gt was designed to improve 8-Pease, it obtained a lower performance.

In Fig. 5 we show the number of total instructions and vector instructions with respect to aslfftw. NEC’s implementation executes many more instructions than our implementations, with sizes up to 65536. From that point, we execute more instructions than aslfftw, except for the total instructions of 8-Stockham-gt.

Fig. 5.

Total (left) and vector (right) instructions with respect to aslfftw.

Figure 5 also shows us that 8-Pease-gt executes approximately 10% more instructions than 8-Pease. This is due to the gather instruction using absolute addresses in NEC, requiring additional operations to modify the indexes before the gathers.

To better understand the difference in instructions, we have to consider the number of elements being operated with each vector instruction. In Table 1 we display the average vector length used by the implementations, with greener colors indicating a higher vector length.

Table 1. Average vector length in elements for different FFT sizes and implementations.

We show that our proposed implementations are able to use the maximum vector length, 256 64-bit elements, with smaller problem sizes than aslfftw. This implies a better usage of the vector unit and a reduction in instructions since each is doing more operations.

A pair of relevant counters to understand the performance of the implementations is vec_arith_cyc and vec_load_cyc, which count the cycles spent in arithmetic vector instructions and load vector instructions respectively.

Fig. 6.

Vec arith (left) and load (right) cycles of our implementations wrto. aslfftw.

In Fig. 6 we see the number of cycles used by arithmetic and load vector instructions with respect to aslfftw. There is a difference of 25%–70% in arithmetic cycles for larger FFT sizes. The finer grain of using a small vector length of aslfftw can allow it to be more precise with arithmetic optimizations, but the significant disparity in large sizes suggests a core difference in the FFT algorithm. In FFT computation, the number of floating-point operations is related to the used RADIX. These results suggest that aslfftw is using a different RADIX for bigger transforms.

A much larger difference is present in load vector cycles. We find a notable spike in the cycles spent by our Pease’s algorithm in size 65536, taking 4 times more cycles loading vector elements. This is the exact size where alsfftw starts to outperform our implementations. We would also like to study the vector cycles spent in store operations, but these cycles are not mapped in any hardware counter present in the architecture.

To study if the increment in vector load cycles of our Pease’s implementations is due to loading more elements or due to slower loads, in Fig. 7 we show how many vector elements are being loaded per each cycle spent in vector load instructions, as a metric of “efficiency” of the vector loads. We also show the vector load cache hit ratio of the implementations, since it can be related with slower loads.

Fig. 7.

Vec. load elements per vec. load cycle (left) and hit ratio (right)

We see that from size 65536 onwards aslfftw has greater vector load efficiency than our Pease’s implementations, loading three times more elements per load cycle.

8-Pease-gt and 8-Stockham-gt present a nearly identical hit ratio, and they load the same number of elements from memory. Considering that the vector load efficiency is not lowered for 8-Stockham-gt, we can suggest that the difference in the efficiencies between implementations is caused by an unfavorable memory access pattern inherent to Pease’s algorithm, presumably related to the scatter operations executed at the last phase of the implementation. We also note in the left plot of Fig. 7 that the usage of the gather instruction in 8-Pease-gt does not accomplish its intended results since it lowers the efficiency of vector load instructions with respect to 8-Pease instead of improving it. The theoretically better memory access of 8-Pease-gt is reflected in the cache hit-ratio, when comparing it to 8-Pease.

6 Conclusions

Our implementations of the FFT for the NEC SX-Aurora show an efficient usage of the vector engine, overtaking the highly optimized proprietary vendor implementation found in NEC Libary Collection for FFT sizes up to 65536 elements. We achieve $20\times$ speedup for sizes under 1024 compared to NEC’s FFT, and $2\times$ speedup up to 65536 elements. We also discussed the performance of vector memory gather operations in our implementations, finding that optimizing memory accesses do not pay of because of their long latency.

We compared two algorithms for the FFT computation, Pease’s and Stockham’s. We found that for vectorized codes, the complex permutations needed by Pease’s impact negatively the performance, notably with large FFT sizes. We argue in favour of more specific register shuffling and memory accessing vector instructions. We evinced the importance of avoiding memory instructions that FFT computation often requires, even if this implies more vector registers or reducing the vector length.

We also highlight two main weaknesses of our proposed implementations for larger FFT sizes when comparing them with NEC’s implementation: i) both Pease and Stockham implementations spend ${\sim }25$% more cycles executing floating-point operations, suggesting the need to explore different RADIX FFT algorithms. ii) Pease’s implementation has a lower vector load efficiency.

We leave for future work the parallelization of our implementations, the exploration of different RADIX FFT algorithms and the evaluation on other vector architectures.