Effect of Porosity Distribution on Vibration and Stability Characteristics of FGM Plates Subjected to Nonlinearly Varying Edge Loads

ABSTRACT

In this article, the consequences of porosity type of imperfection on vibration and stability characteristics of Functionally Graded Material (FGM) plate members are examined. Since it is challenging to predict the type of porosity distribution in the plate, four diverse varieties of porosity distributions varying through the thickness are considered during the modelling of FGM plates. The porosity effect is included in material modelling by means of modified rule of mixture. The in-plane edge loads acting on plates are seldom uniform in nature during the operational condition. And hence, vibration and stability characteristics of the FGM plates comprising porosity is analyzed considering nonlinearly varying in-plane edge load incorporating Finite element (FE) method. The numerical outcomes obtained are compared to those reported in the literature to help decide the formulation's correctness. The effect of geometric configuration, volume fraction exponent, porosity and loading on vibration and stability characteristics of FGM plate member with porosity is investigated.

1 Introduction

With rapid advancement of technology and to meet the adverse demand arising in the engineering applications, several types of composites are analyzed and manufactured. Likewise, FGMs were developed by team of scientists in 1980s as a material for heat barrier. FGMs are advanced type of composite materials that is created in such way that the material change from one surface to other gradually. The mechanical properties affecting the strength characteristics of the FGM can be varied by altering the respective material gradation pattern. Thus, properties can be tailored according to the required applications. Advantages of FGM are high fracture toughness, high thermal resistance and improved energy absorption. The applications of FGM are widely found in aerospace, defense, automobile, civil, marine, biomedical and optoelectronics fields. Ample number of literatures are available that deals with structural responses like vibration and stability behaviour of FGM plate. Birman (1995) was the foremost person to provide result for stability problem of functionally graded hybrid composites exposed to uniformly distributed in plane edge loads. (Zenkour 2005; Swaminathan and Naveenkumar 2014; Reddy et al. 2013) obtained closed from solutions for buckling behaviour of FGM plates exposed to uniformly applied in-plane loadings along the edge. Most of the studies stated in research articles are on stability examination of plates exposed to uniformly applied in-plane compressive edge loadings. During the operation of the aerospace vehicles, structural members will have both tensile and compressive stress resulting from eccentric load transfer from the adjacent members. This type of load transfer results in nonlinear type of variation of the loads on the adjacent members. Hence it becomes essential to analyze the vibration and stability behaviour of the member considering several kinds of nonlinearly varying in-plane edge loads for safe and reliable design of structural member.

Few researches have investigated vibration and stability characteristics of plates exposed to nonlinearly varying type of loads. Soni et al. (2013) examined the stability problem of fibre reinforced laminated composites comprising of circular as well as square cutout/opening exposed to nonuniform in-plane loads by means of ABAQUS FE software package. Rajanna et al. (2016) performed vibrational and stability studies of laminated type of composite plates with and plates free of cutouts/geometric discontinuity subjected compressive and tensile edge loads (in-plane) varying linearly along the edge. The authors have incorporated FE method using nine nodded heterosis element to carry out the analysis. Zhong and Gu (2007) presented analytical type of solutions for buckling of symmetrical [0/90] (cross-ply) laminates under the in-plane loading linearly varying across the edge of the plate. Plane elasticity solutions for buckling loads using Galerkin’s method is adopted by Jana and Bhaskar (2006) to provide solution for stability of plates exposed to in-plane varying load.

During manufacturing process of FGMs, imperfection in the form of porosities occurs owing to large variance in the solidification temperature of the constituents. The porosities might also be introduced purposefully to reduce the weight of the structural member. Therefore, during the formulation and analysis stage it becomes essential to incorporate the porosity effect for the purpose of understanding the behavior of FGM plate/shell. Bansal et al. (2020) explored the vibration characteristics FGM plates comprising porosity imperfection with cutouts resting on partial supports with the aid of FE technique. Kiran et al. (2018) investigated the impact of porosity imperfection on free vibration and static/bending behaviour of functionally graded magneto-electro-elastic plates considering various skew angles. Further, Singh and Harsha (2020) worked on the consequence of porosity defect on stability and vibration behaviour of sandwich FGM plates. A new uneven and unsymmetrical porosity distribution model is presented. In this study closed form solution is introduced using Galerkin Vlasov’s method. Gupta and Talha (2018) analyzed the impact of porosity defect and thermal exposure on vibration behaviour of FGM plates implementing non-polynomial higher order shear and normal deformation theory. Ebrahimi and Jafari (2018) arrived at analytical type of solutions to the thermomechanical vibrational response of the FGM in the form of beams with porosity exposed to many types of thermal loading. The authors have proposed displacement field plate theory based containing four variables for the investigation.

In light of the aforementioned works in the literature, it is noticed that number of works have been accomplished on vibration and stability studies of isotropic, laminated and FGM plate exposed to uniformly distributed in-plane edge compressive loads. Further, studies are carried on buckling analysis pertaining to FGM plates disregard the consequence related to porosity and nonlinearly varying in-plane edge loads. Therefore, in the existing investigation the impact of porosity type of imperfection on vibrational and stability characteristics of plates member made of FGM exposed to nonlinearly varying loads has been investigated using FE technique. The novelty of the present work is consideration of FGM plate with different types of porosity distribution and nonlinearly varying in-plane edge loads to study vibration and buckling response. The current investigation is very significant, as porosity type of imperfections leads to prominent reduction of stiffness of the FGM structural member. Also, the nonlinearly varying edge loads causes stress concentration. Thus, the current investigation can help in better understanding and prediction of the behaviour of the plate member with porosity imperfection leading to improved and confident design. A broad parametric study has been performed considering porosity indices, porosity distribution and geometric parameters.

2 Theoretical Formulation

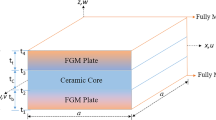
2.1 FGM Plate Geometry

The geometry of plate consists of dimensions a (length), b (width) and h (thickness) with respect to positive set of co-ordinate system along x, y, z axes are as illustrated in Fig. 1. The terms ${u}_{0},{v}_{0},{w}_{0}$ are the displacements components along the x-, y- and z-directions correspondingly of the points on the mid-plane surface. The rotational variation of the plane perpendicular to the middle plane about the axis y and x is termed as ${\theta }_{x}$ and ${\theta }_{y}$.

Fig. 1.

Schematics of FGM plate.

2.2 Displacement Field

FSDT theory is incorporated in this analysis to investigate the kinematics of the plate made of FGM member. The model for displacement is specified as below Eq. (1):

$$ \begin{aligned} & u\left( {x,y,z} \right) = u_{0} \left( {x,y} \right) + z\theta_{x} \left( {x,y} \right) \hfill \\ & v\left( {x,y,z} \right) = v_{0} \left( {x,y} \right) + z\theta_{y} \left( {x,y} \right) \hfill \\ & w\left( {x,y,z} \right) = w_{0} \left( {x,y} \right) \hfill \\ \end{aligned} $$

(1)

The terms $u\left(x,y,z\right), v\left(x,y,z\right)$ and $w(x,y,z)$ represent displacement components of a point in the plate member space. The other terms in the Eq. (1) are conversed in Sect. 2.1.

2.3 Constitutive Relationship and Material Properties

The FGM plate linear constitutive relation is represented using Eq. (2)

$$ \left\{ {\begin{array}{*{20}l} {\upsigma _{x} } \\ {\upsigma _{y} } \\ {\upsigma _{z} } \\ {\uptau _{xy} } \\ {\uptau _{yz} } \\ {\uptau _{xz} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & {0_{{}} } & 0 & 0 & 0 \\ {Q_{12} } & {Q_{22} } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {Q_{44} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {Q_{55} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {Q_{66} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\upvarepsilon _{x} } \\ {\upvarepsilon _{y} } \\ {\upvarepsilon _{z} } \\ {\upgamma _{xy} } \\ {\upgamma _{yz} } \\ {\upgamma _{xz} } \\ \end{array} } \right\} $$

(2)

where terms $\left\{{\sigma }_{x}, {\sigma }_{y},{\tau }_{xy}, {\tau }_{yz}, {\tau }_{xz}\right\}$ are the stresses and $\left\{{\varepsilon }_{x}, {\varepsilon }_{y},{\gamma }_{xy}{\gamma }_{yz}, {\gamma }_{xz}\right\}$ denote strains in the plate in relation to the plate axes. Further, ${Q}_{ij}$ are the elemental components of the plate stiffness matrix which are expressed as,

$$ Q_{11} = \frac{E(z)}{{(1 - \nu^{2} )}} = Q_{22} ; \, Q_{12} = \frac{\nu E(z)}{{(1 - \nu^{2} )}} = Q_{21} ; \, \frac{E(z)}{{2(1 + \nu )}} = Q_{33} = Q_{44} = Q_{55} $$

2.4 Material Properties of FGM with Porosity Plate Based on Homogenization

The effective properties of the material for FGM plate member with porosity imperfections can be evaluated with the help of modified rule of mixture, using Eq. (3).

$$ P(z) = P_{m} + (P_{c} - P_{m} )\left( {\frac{z}{h} + \frac{1}{2}} \right)^{n} - \frac{\beta }{2}(P_{c} + P_{m} )V_{P} $$

(3)

where P(z) is generalized function to denote the properties of the material such as E(z) and ρ(z). Ceramic and metal material properties are designated by the subscripts c and m. The term n refers to the volume fraction index and β is porosity indices. The term ${V}_{P}$ is the generalized function to denote various type of porosity and ${V}_{P}$ can be either on of {${V}_{UD}$/${V}_{CD}$/${V}_{XD}$/${V}_{VD}$}. The different porosity types are as depicted in the Fig. 2 and are presented Eqs. (3a)–(3d).

• a) Even/Uniform porosity:

  The porosities are evenly dispersed through depth (thickness)of the plate as depicted in Fig. 2(a) and ${V}_{P}$ is given by:

  $$ V_{UD} = 1 $$

  (3a)

• b) Central porosity:

  The porosities are in maximum concentration at the mid height parallel to the plate's thickness as depicted in Fig. 2(b) and ${V}_{P}$ is given by:

  $$ V_{CD} = \left( {1 - \frac{2\left| z \right|}{h}} \right) $$

  (3b)

• c) The top portion and bottom portion of plate consists of high concentration of porosity whereas low concentration at average height parallel to the plate's thickness (Fig. 2(c)) and ${V}_{P}$ is given by:

  $$ V_{XD} = \left( {\frac{2\left| z \right|}{h}} \right) $$

  (3c)

• d) Maximum concentration of porosities at the upper portion and minimal concentration at the lower portion (Fig. 2(d)) and ${V}_{P}$ is given by:

  $$ V_{VD} = \left( {1 + \frac{2\left| z \right|}{h}} \right) $$

  (3d)

Fig. 2.

Cross section showing porosity Distribution.

2.5 Finite Element Formulation

The plate element in the existing FE formulation is discretized by means of an isoparametric element having 8-nodes with 5 DOF’s per each node is chosen. In terms of shape functions, the generalized displacement vectors at every point and geometrical coordinates in the element can be stated as shown below (Eq. (4)):

$$ \begin{array}{*{20}l} {u = \sum\limits_{i = 1}^{8} {N_{i} u_{i} } } \hfill & {v = \sum\limits_{i = 1}^{8} {N_{i} v_{i} } } \hfill & {w = \sum\limits_{i = 1}^{8} {N_{i} w_{i} } } \hfill \\ {\theta_{x} = \sum\limits_{i = 1}^{8} {N_{i} \theta_{xi} } } \hfill & {\theta_{y} = \sum\limits_{i = 1}^{8} {N_{i} \theta_{yi} } } \hfill & {} \hfill \\ {x = \sum\limits_{i = 1}^{8} {N_{i} x_{i} } } \hfill & {y = \sum\limits_{i = 1}^{8} {N_{i} y_{i} } } \hfill & {} \hfill \\ \end{array} $$

(4)

The term x_i, y_i denote the i^th node's coordinates and u_i, v_i, and w_i are the node's displacement functions.

2.6 Governing Equations

By means of the extended Hamilton principle, the generalized governing differential equation of motion is given by Eq. (5).

$$ \left[ M \right]\left\{ {\ddot{q}} \right\} + \left( {\left[ {K_{e} } \right] \pm P_{{}} \left[ {K_{G} } \right]} \right)\left\{ q \right\} \, = \, \left\{ 0 \right\} $$

(5)

Further the governing equation to obtain frequencies and buckling loads are as follows Eq. (6):

$$ \left[ {K_{e} } \right]\left\{ q \right\} \pm P_{0} \left[ {K_{G} } \right]\left\{ q \right\}{ - }\omega^{2} \left[ M \right]\left\{ q \right\} = \, \left\{ 0 \right\} $$

(6)

If ${P}_{0}$ = 0, in the aforementioned Eq. (6), the corresponding mathematical relation describes a free vibration type of behaviour in absence of load along edge acting along the plane of the plate. If the load is present, the square of the frequency (ω²) takes the value of zero for a given value of ${P}_{0}$, and the associated applied load reflects the critical buckling load. Here, [${K}_{e}$] is the global elastic stiffness, [${K}_{G}$] represents geometric stiffness, and [M] denote consistent mass matrix that are attained by assembling the respective elemental matrices ([${k}_{e}$], [${k}_{G}$], and [m]) as follows Eqs. (7)–(9):

$$ \left[ {k_{e} } \right] = \int\limits_{ - 1}^{ + 1} { \, \int\limits_{ - 1}^{ + 1} {\left[ B \right]^{T} } } \left[ D \right]\left[ B \right]\left| J \right|d\xi d\eta $$

(7)

$$ \left[ {k_{G} } \right] = \int\limits_{ - 1}^{ + 1} { \, \int\limits_{ - 1}^{ + 1} {\left[ {B_{G} } \right]^{T} } } \left[ S \right]\left[ {B_{G} } \right]\left| J \right|d\xi d\eta $$

(8)

$$ \left[ m \right] = \int\limits_{ - 1}^{ + 1} { \, \int\limits_{ - 1}^{ + 1} {\left[ {\overline{N}} \right]^{T} } } \left[ I \right]\left[ {\overline{N}} \right]\left| J \right|d\xi d\eta $$

(9)

3 Results and Discussion

3.1 Convergence and Validation

Several example problems regarding free vibration and stability investigation of FGM plates are unraveled to substantiate the correctness and precision of the suggested formulation. The results found are verified through comparison with those found in the published research article.

Example 1:

In this example, FGM (Al/Al2O3) square thin plate under the application of Type-II load is considered, and the numerical results are tabulated in Table 1. Here UD type of the porosity distribution with β = 0.1 is chosen. It is observed from Table 2 that the buckling load parameters as well as non-dimensional frequencies results are well converged at 10 × 10 mesh size. Therefore, analysis in the successive problems is carried outsusing this mesh size.

Table 1. Convergences of buckling load parameters (λ_cr) and non-dimensional frequency values (ϖ) of thin square FGM plate subjected to load Type-II

Example 2:

A simply supported square FGM plate member (Al/Al₂O₃) exposed to uniform in-plane compressive force along single direction is examined in the 2^nd example. The non-dimensional critical buckling loads results are obtained and verified with the those given by Thai and Choi. (2013). The mechanical constituent properties of material is FGM E_m = 70 GPa, ρ_m = 2707 kg/m³ for Aluminium (Al) and E_c = 380 GPa, ${\rho }_{c}$ = 3800 kg/m³ for Alumina (Al₂O₃). As shown in Table 2, the outcomes derived from the current formulation are in accordance with those found in the literature.

Table 2. Comparison studies of non-dimensional critical buckling load (${N}_{cr}=N\frac{{a}^{2}}{{E}_{m}{h}^{3}}$) of FGM (simply support plate member exposed to uniaxial uniformly distributed compressive coplanar edge loadings along the x-axis

Example 3:

In third example, the non-dimensional frequency of a FGM plate made of Al/ZrO₂ is evaluated and compared with the results given by Jha et al. (2013) as in Table 3. The material properties of the constituent material are E_m = 68.9 GPa, ρ_m = 2700.0 kg/m³ for Aluminium (Al) and E_c = 211.0 GPa, ${\rho }_{c}$ = 4500.0 kg/m³ for Zirconia (ZrO₂). The results obtained from current formulation is in good agreement with the results in literature.

Table 3. Non-dimensional frequency comparison ( $\varpi =\omega \sqrt{{\rho }_{C}/G}$) of square simply supported FGM (Al/ZrO₂) plate

3.2 Parametric Studies

From the previous section, the present formulation is observed to be accurate. Therefore, in the current section, the impact of porosity on vibration and stability behaviour of plate made of are inspected by choosing various parametric variable such as porosity index (β), porosity distribution, volume fraction index (n), plate thickness ratio (b/h) and plate aspect ratio (a/b). The FGM plate is considered to be subjected to nonlinearly changing load along the plate edge as displayed in Fig. 3. All equation of the loads is tabulated in Table 4.

Table 4. Loading equations

Fig. 3.

Types of nonlinearly varying loads.

The mechanical Young’s modulus (E) and material density ($\rho$) of Al₂O₃ are ${E}_{c}$ = 380.0 GPa, ${\rho }_{c}$ = 3800.0 kg/m³ and those of SUS304 are ${E}_{m}$ = 207.0 GPa, ${\rho }_{m}$ = 8166 kg/m³. For both materials, the Poisson's ratio property (ʋ) is considered as 0.3. Here, the plate frequency and the critical buckling loads are expressed in non-dimensionals forms as mentioned below:

Non-dimensional frequency (ϖ): ω b²$\sqrt{\frac{{\rho }_{c}}{{E}_{c}{h}^{2}}}$; non-dimensional buckling load parameter (λ_cr):$\frac{{{P}_{cr}b}^{2}}{D}$, D = E_ch³/12(1-ʋ²).

3.2.1 Influence of Porosity on Vibration of FGM Plate Exposed to Nonlinearly Varying In-Plane Edge Loads

Fig. 4.

Variation of non-dimensional frequencies with non-dimensional loads for porous FGM plate having different (a) porosity distributions and (b) Load Types.

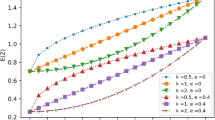
Figure 4 depicts fluctuations of non-dimensional frequency of porous FGM plate with several types of porosity distribution and in-plane edge loads. Here (Fig. 4(a)) U-D, C-D, X-D & V-D type of porosity distribution is considered. It is observed that, with increase in the in-plane edge loads, non-dimensional frequency decreases and approaches zero, thus that particular non-dimensional load which results in zero frequency gives the critical buckling load of the FGM plate member. It is possible to witness that for plate member made of FGM without porosity (perfect FGM) exhibits highest natural frequency. And amongst plate with porosity, C-D and V-D type of porosity distribution gives maximum and minimum non-dimensional frequency respectively. Further the fluctuation of non-dimensional frequency of FGM plate member with porosity subjected to different type of nonlinearly varying loads are plotted in Fig. 4(b). Here U-D type of porosity distribution with β = 0.2 is chosen. It can be observed that Type-IV loads exhibits maximum non-dimensional frequency due to the tensile part of the load, which increases the plate stiffness similar to stretching effect.

The behaviour of non-dimensional frequency of FGM plate member with UD type of porosity distribution exposed to Type-I load is presented in Fig. 5(a). Here β = 0.2 is chosen. It has been clearly perceived that with rise in the volume fraction index, the non-dimensional frequency drops for a particular non-dimensional load. Further, the effect of porosity indices on frequency response is evaluated and the outcomes are plotted in Fig. 5(b). It can be deduced that the variation in non-dimensional frequency between different porosity indices keeps on increasing as the non-dimensional load increases. Also, at a particular non-dimensional load the non-dimensional frequency falls with increase in porosity indices.

Fig. 5.

Variation of non-dimensional frequencies with non-dimensional load for porous FGM plate with several (a) Volume fraction index and (b) Porosity indices.

3.2.2 Influence of Porosity on Buckling Characteristics of FGM Plate Exposed to Nonlinearly Varying In-Plane Edge Loads

Table 5 presents buckling load parameter for simply supported SUS304/Al₂O₃ porous FGM plate for different volume fraction index and porosity indices. The buckling load parameters are obtained for plates subjected to Type-I and Type-II edge loads. The porosity coefficient is chosen as β = 0.1, 0.2, 0.3 and 0.4. Here, the volume fraction index is considered as n = 0.5, 1, 2 and 5. It is observed that the buckling load parameter decreases with increase in porosity indices for all types of porosity distribution, volume fraction index and loading type considered. Further, there is significant reduction of buckling load parameter with increase in porosity index for V-D type of porosity distribution, while C-D shows least reduction. Subsequently, it can also be witnessed from Table 5 that C-D type of porosity distribution possess maximum buckling load parameter amongst other types of porosity distribution in the order of C-D > X-D > U-D > V-D.

Table 5. Effect of volume fraction exponent and porosity indices on buckling loads parameter (λ_cr) of porous FGM plate subjected to Type-I and Type-II loads

Further, the buckling load parameters have been tabulated in Table 6 for simply supported porous FGM plate exposed to Type-III and Type-IV loads. In accordance with the explanation in the preceding discussion section on variations of the buckling load parameter, behaviour are alike for several volume fraction index and types of porosity distribution. It is detected from Table 5 and Table 6 that FGM plates subjected to Type-IV loading exhibits maximum buckling load parameter in the order of Type-IV > Type-I > Type-II > Type-III loading irrespective of porosity distribution type and volume fraction index. The maximum buckling load parameter for Type-IV loading is due to tensile loads which tries to reduces compressive stresses which causes the plate to buckle.

Table 6. Effect of volume fraction exponent and porosity indices on buckling loads parameter (λ_cr) of porous FGM plate subjected to Type-III and Type-IV edge loads

The consequence of thickness ratios (b/h) and aspect ratios (a/b) on the buckling load factor (λ_cr) of FGM plate with several boundary condition and types of porosity distribution is presented in Fig. 6. For this study UD type of porosity distribution is chosen with volume fraction index n = 2.0. It is detected that buckling load factor of CCCC plates are higher than SSSS plate. Further, it can be witnessed that buckling load parameter decrease with rise in the porosity index irrespective of the thickness ratio and aspect ratio due the reduction in the plate stiffness.

Fig. 6.

Variation of buckling load parameter of porous FGM plate subjected to Type-I load with different (a) Thickness ratio and (b) Aspect ratio.

From Fig. 6(a) it is clearly perceived that the plate buckling load parameter (λ_cr) rises in proportion to the rise in the thickness ratio. This unusual behaviour occurs due the non-dimensional parameter considered, where the thickness of the plate member is inversely proportional to the buckling load parameter and therefore buckling load parameter rises with decrease in the thickness of the plate. Furthermore, it is possible to perceive from Fig. 6 (b) that the plate buckling load parameter decrease abruptly till a particular aspect ratio between a/b = 1 and 2 and increases for plates with the aspect ratio a/b = 2 and then decreases and so on. This buckling load parameter behaviour with variation of aspect ratio is due to buckling mode shift from single half wave to double half wave with increase in the aspect ratio of the plate.

4 Conclusion

The impact of imperfection in the form of porosity on free vibration and stability characteristics of FGM plate member exposed to nonlinearly varying in-plane loads along the edge of plates are explored with the aid of FE method. The resultant material properties of the FGM plate having various porosity distributions are found using modified rule of mixture. The accurateness and credibility of the current mathematical modelling is substantiated by considering several examples. The key findings from the investigations are listed below:

• 1. The non-dimensional frequency and buckling load parameter decrease as the volume fraction index (n) increases.

• 2. The impact of porosity distribution type on non-dimensional frequency and buckling load parameter follows the trend C-D > X-D > U-D > V-D.

• 3. The buckling load parameter is more sensitive to V-D type of porosity distribution, while C-D shows least influence.

• 4. The buckling load parameter increases as the thickness ratio rises, while the buckling load parameter decrease with increase in the aspect ratio irrespective of the porosity indices.