Keywords

1 Introduction

Granular matter in nature is generally surrounded by an interstitial fluid, like water or air. Although in many situations the effect of the surrounding fluid on the dynamic properties of grains can be neglected, there are also other situations (for instance, when the stress exerted by the fluid phase on grains is significant) where the influence of the interstitial fluid must necessarily be taken into account. A typical example of it refers to the species segregation in granular mixtures [1]. Since a granular suspension is a multiphase process, in the context of kinetic theory, one could start from a set of coupled kinetic equations for each one of the velocity distribution functions of the phases. However, this approach involves many technical intricacies, especially in the case of granular mixtures. Thus, to avoid this problem, the effect of the interstitial fluid on grains is usually taken into account by means of an effective external force [2]. This fluid–solid force is composed of two terms: (i) a viscous drag force (Stokes’ law) proportional to the particles velocity and (ii) a stochastic force modeled as a Gaussian white noise. While the first term mimics the friction of grains with the surrounding gas, the second term accounts for the energy gained by grains due to their interaction with the particles of the gas phase (thermal reservoir).

An interesting and challenging problem is to assess the impact of gas phase on the Navier–Stokes transport coefficients of a binary granular mixture modeled as an ensemble of smooth inelastic hard spheres. This problem is not only relevant from a fundamental point of view but also from a realistic point of view since granular suspensions are present in nature formed by grains of different masses, sizes, densities, and coefficients of restitution. However, the determination of the transport coefficients of bidisperse gas–solid flows is a quite ambitious target due essentially to the large number of integro-differential equations involved as well as the wide parameter space of the system. For this reason and in order to offer a complete description, we consider here binary granular suspensions at low-density where the Boltzmann kinetic equation turns out to be a reliable starting point [3, 4].

As in previous papers [6,7,8], the Boltzmann equation (BE) is solved by means of the Chapman–Enskog (CE) method [9] adapted to dissipative dynamics. A subtle and important point of the expansion method is the choice of the reference distribution in the perturbation scheme. Although we are interested here in obtaining the transport coefficients under steady conditions, the presence of the surrounding fluid gives rise to a local energy unbalance in such a way the zeroth-order distributions \(f_i^{(0)}\) of each species (reference states) are not in general stationary distributions. Thus, in order to determine the Navier–Stokes transport coefficients, one has to obtain first the unsteady integral equations defining the above transport coefficients and solve (approximately) then these equations in steady-state conditions. An important consequence of this procedure is that the transport properties depend not only on the steady temperature but also on quantities such as the derivatives of the temperature ratio on the temperature.

The plan of the paper is as follows. The granular suspension model as well as the balance equations for the densities of mass, momentum, and energy are derived in Sect. 2. Then, the steady homogeneous state is studied in Sect. 3 where the temperature ratio \(T_1/T_2\) of both species is calculated and compared against the Monte Carlo simulations. Section 4 addresses the application of the CE method up to first order in the spatial gradients. As expected, transport coefficients are given in terms of the solutions of a set of coupled linear integral equations. These integral equations are approximately solved by considering the leading Sonine approximation; this procedure is explicitly displayed here for the diffusion transport coefficients in the special limit case where one of the components of the mixture is present in tracer concentration. As an application of the previous results, thermal diffusion segregation of an intruder or tracer particle is analyzed in Sect. 5. The paper is closed in Sect. 6 with a brief discussion of the results obtained in this work.

2 Granular Suspension Model

We consider a granular binary mixture of inelastic hard disks (\(d=2\)) or spheres (\(d=3\)) of masses \(m_i\) and diameters \(\sigma _i\) (\(i=1,2\)). The spheres are assumed to be completely smooth and so, the inelasticity of collisions is characterized by three constant (positive) coefficients of normal restitution \(\alpha _{ij}\le 1\). The solid particles are surrounded by a molecular gas of viscosity \(\eta _\textrm{g}\) and temperature \(T_{\textrm{ex}}\). As said before, the influence of the interstitial gas on grains is modeled via a fluid–solid force constituted by two terms: a deterministic drag force plus a stochastic force. In the low-density limit and taking into account the above terms, the one-particle velocity distribution function of each species verifies the Boltzmann kinetic equation [8]

$$\begin{aligned} \frac{\partial f_i}{\partial t}+\textbf{v}\cdot \nabla f_i-\gamma _i \Delta \textbf{U}\cdot \frac{\partial f_i}{\partial \textbf{v}}-\gamma _i\frac{\partial }{\partial \textbf{v}}\cdot \textbf{V}f_i-\frac{\gamma _i T_{\textrm{ex}}}{m_i}\frac{\partial ^2 f_i}{\partial v^2}=\sum _{j=1}^2\; J_{ij}[f_i,f_j], \end{aligned}$$
(1)

where \(J_{ij}[f_i,f_j]\) is the Boltzmann collision operator [4]. In addition, \(\Delta \textbf{U}=\textbf{U}-\textbf{U}_g\), \(\textbf{V}=\textbf{v}-\textbf{U}\) is the peculiar velocity,

$$\begin{aligned} \textbf{U}=\rho ^{-1}\sum _{i=1}^2\; \int d\textbf{v}\; m_i \textbf{v} f_i(\textbf{v}) \end{aligned}$$
(2)

is the mean flow velocity of the solid particles, and \(\textbf{U}_g\) is the known mean flow velocity of the interstitial gas. The friction coefficients \(\gamma _i\) are proportional to the gas viscosity \(\eta _{\textrm{g}}\) and are functions of the partial volume fractions \(\phi _i=(\pi ^{d/2}/(2^{d-1}d \Gamma \left( d/2\right) )n_i \sigma _i^d\), where

$$\begin{aligned} n_i=\int d\textbf{v}\; f_i(\textbf{v}) \end{aligned}$$
(3)

is the number density of species i. In the dilute limit, every particle is only subjected to its respective Stokes’ drag [10] so that for hard spheres (\(d=3\)) \(\gamma _i\) is

$$\begin{aligned} \gamma _i=\gamma _0 R_i, \quad \gamma _0= \frac{18\eta _\textrm{g}}{\rho \sigma _{12}^2}, \quad R_i=\frac{\rho \sigma _{12}^2}{\rho _i\sigma _i^2}\phi _i. \end{aligned}$$
(4)

Here, \(\rho _i=m_in_i\), \(\rho =\rho _1+\rho _2\) is the total mass density, and \(\sigma _{12}=(\sigma _1+\sigma _2)/2\). Apart from the partial densities \(n_i\) and the mean flow velocity \(\textbf{U}\), the other relevant hydrodynamic field is the granular temperature T, defined as

$$\begin{aligned} T=\frac{1}{n}\sum _{i=1}^2\int d\textbf{v}\frac{m_{i}}{d}V^{2}f_{i}(\textbf{v}), \end{aligned}$$
(5)

where \(n=n_{1}+n_{2}\) is the total number density.

The Boltzmann collision operators \(J_{ij}[f_i,f_j]\) conserve the number densities of each species and the total momentum but the total energy is not conserved:

$$\begin{aligned} \int d\textbf{v}\Big \{1, \sum _{i,j} m_i \textbf{v}, \sum _{i,j} m_i V^2 \Big \}J_{ij}[\textbf{v}|f_i,f_j]=\Big \{0,\textbf{0},-d n T \zeta \Big \}, \end{aligned}$$
(6)

where \(\zeta \) is the total cooling rate due to inelastic collisions among all species. The macroscopic balance equations for the densities of mass, momentum, and energy can be easily obtained by multiplying both sides of the BE (1) by 1, \(m_i\textbf{v}\), and \(m_i V^2\); integrating over \(\textbf{v}\); and taking into account the properties (6). After some algebra, one gets

$$\begin{aligned} D_t n_i+n_i\nabla \cdot \textbf{U}+\frac{\nabla \cdot \textbf{j}_i}{m_i}=0, \end{aligned}$$
(7)
$$\begin{aligned} D_t\textbf{U}+\rho ^{-1}\nabla \cdot \textsf{P}=-\rho ^{-1}\Delta \textbf{U}\sum _{i=1}^2\rho _i \gamma _i -\rho ^{-1}\left( \gamma _1-\gamma _2\right) \textbf{j}_1, \end{aligned}$$
(8)
$$\begin{aligned} D_tT-\frac{T}{n}\sum _{i=1}^2\frac{\nabla \cdot \textbf{j}_i}{m_i}+ & {} \frac{2}{dn} \left( \nabla \cdot \textbf{q}+\textsf{P}:\nabla \textbf{U}\right) =-\frac{2}{d n}\Delta \textbf{U}\cdot \sum _{i=1}^2 \gamma _i \; \textbf{j}_i\nonumber \\{} & {} + 2\sum _{i=1}^2 x_i \gamma _i\left( T_{\textrm{ex}}-T_i\right) -\zeta T. \end{aligned}$$
(9)

In the above equations, \(D_t=\partial _t+\textbf{U}\cdot \nabla \) is the material derivative,

$$\begin{aligned} \textbf{j}_i=m_i\int \;d\textbf{v}\; \textbf{V}f_i(\textbf{v}) \quad (\textbf{j}_1=-\textbf{j}_2) \end{aligned}$$
(10)

is the mass flux for the component i relative to the local flow \(\textbf{U}\),

$$\begin{aligned} \textsf{P}=\sum _{i=1}^2\int \; d\textbf{v}\; m_i\textbf{V}\textbf{V}f_i(\textbf{v}) \end{aligned}$$
(11)

is the pressure tensor, and

$$\begin{aligned} \textbf{q}=\sum _{i=1}^2\int d\textbf{v}\; \frac{m_i}{2}V^2\textbf{V}f_i(\textbf{v}) \end{aligned}$$
(12)

is the heat flux. In addition, the partial kinetic temperature \(T_i\) is

$$\begin{aligned} T_i=\frac{m_{i}}{d n_i}\int \; d\textbf{v}\;V^{2}f_{i}(\textbf{ v}). \end{aligned}$$
(13)

The partial temperature \(T_i\) measures the mean kinetic energy of particles of species i. The relationship between the granular temperature T and the partial temperatures \(T_i\) is simply given by \(T=\sum _i x_i T_i\), where \(x_i=n_i/n\) is the concentration of species i. The breakdown of energy equipartition in granular systems (\(T_i\ne T\)) predicted by kinetic theory [4] has been confirmed in computer simulations [11] as well as in real experiments [12].

It is quite apparent that the balance equations (7)–(9) become a closed set of differential equations for \(n_1\), \(n_2\), \(\textbf{U}\), and T when the fluxes, the cooling rate, and the partial temperatures are expressed in terms of the hydrodynamic fields and their gradients. These constitutive equations for \(\textbf{j}_i\), \(\textsf{P}\), \(\textbf{q}\), \(\zeta \), and \(T_i\) may be derived by solving the BE (1) by the CE expansion up to first order in spatial gradients. This will be analyzed in Sect. 4.

3 Homogeneous Steady States

As a first step and before studying inhomogeneous situations, we consider homogeneous states. In this case, \(n_i\) and T are spatially uniform, and with a convenient choice of the reference frame, the mean velocities vanish (\(\textbf{U}=\textbf{U}_g=\textbf{0}\)). For times longer than the mean free time, it is expected that the suspension achieves a steady state (\(\partial _t f_i=0\)) where the BE (1) reads

$$\begin{aligned} -\gamma _i\frac{\partial }{\partial \textbf{v}}\cdot \textbf{v}f_i-\frac{\gamma _i T_{\textrm{ex}}}{m_i}\frac{\partial ^2 f_i}{\partial v^2}=\sum _{j=1}^2\;J_{ij}[f_i,f_j]. \end{aligned}$$
(14)

The balance equation for the partial temperature \(T_i\) can be easily derived by multiplying both sides of Eq. (14) by \(m_i v^2\) and integrating over velocity:

$$\begin{aligned} 2\gamma _i\left( T_{\textrm{ex}}-T_i\right) =\zeta _i T_i, \end{aligned}$$
(15)

where the partial cooling rates \(\zeta _i\) for the partial temperatures \(T_i\) are defined as

$$\begin{aligned} \zeta _i=- \frac{m_i}{dn_iT_i}\sum _{j=1}^2\int d\textbf{v}\; v^{2}J_{ij}[f_{i},f_{j}], \quad (i=1,2). \end{aligned}$$
(16)

The relationship between \(\zeta \) and \(\zeta _i\) is

$$\begin{aligned} \zeta =\sum _{i=1}^2\; x_i \tau _i \zeta _i, \end{aligned}$$
(17)

where \(\tau _i=T_i/T\) is the temperature ratio of the species i. Upon deriving Eq. (17), use has been made of the relation \(T=\sum _i x_i T_i\) and Eq. (6).

For elastic collisions (\(\alpha _{ij}=1\)), \(\zeta =\zeta _i=0\), Eq. (15) yields \(T_i=T_\textrm{ex}=T\) so that the Maxwellian distribution with a common temperature is a solution of the BE (14). On the other hand, for inelastic collisions (\(\alpha _{ij}\ne 1\)), \(\zeta _i\) and \(\zeta \) are different from zero and to date the solution to Eq. (14) is unknown. Thus, one has to consider an approximate form for the distributions \(f_i\) to estimate \(\zeta _i\). Here, we take the simplest approximation for both distributions, namely the Maxwellian distributions \(f_{i,\textrm{M}}\) defined with the partial temperatures \(T_i\):

$$\begin{aligned} f_i(\textbf{v})\rightarrow f_{i,\textrm{M}}(\textbf{v})=n_i \Bigg (\frac{m_i}{2\pi T_i}\Bigg )^{d/2}\exp \Big (-\frac{m_iv^2}{2T_i}\Big ). \end{aligned}$$
(18)

The partial cooling rates can be computed from Eq. (16) by replacing \(f_i\) by \(f_{i,\textrm{M}}\). The result is [4]

$$\begin{aligned} \zeta _1= & {} \frac{\sqrt{2}\pi ^{\left( d-1\right) /2}}{d\Gamma \left( \frac{d}{2}\right) }n_1 \sigma _{1}^{d-1}\left( \frac{2T_1}{m_1}\right) ^{1/2}\left( 1-\alpha _{11}^2\right) +\frac{4\pi ^{\left( d-1\right) /2}}{d\Gamma \left( \frac{d}{2}\right) }n_2 \sigma _{12}^{d-1}\mu _{21}\nonumber \\{} & {} \times \left( \frac{2T_1}{m_1}+\frac{2T_2}{m_2}\right) ^{1/2}(1+\alpha _{12})\Bigg [1-\frac{\mu _{21}}{2}\left( 1+\alpha _{12}\right) \Bigg (1+\frac{m_1T_2}{m_2T_1}\Bigg )\Bigg ], \end{aligned}$$
(19)

where \(\mu _{ij}=m_i/(m_i+m_j)\). The expression for \(\zeta _2\) can be easily obtained from Eq. (19) by making the change \(1\leftrightarrow 2\).

Fig. 1
figure 1

Temperature ratio \(T_1/T_2\) versus the (common) coefficient of restitution \(\alpha \) for \(d=3\), \(x_1=0.5\), \(\sigma _1/\sigma _2=1\), \(T_\textrm{ex}^*=1\), and three different values of the mass ratio: \(m_1/m_2=0.5\) (a), \(m_1/m_2=4\) (b), and \(m_1/m_2=10\) (c). Lines are the theoretical results while symbols refer to the Monte Carlo simulations

Full size image

The partial temperatures \(T_i\) can be obtained from Eq. (15) (for \(i=1,2\)) when the expressions (19) for \(\zeta _1\) and \(\zeta _2\) are considered. Figure 1 plots the temperature ratio \(T_1/T_2\) as a function of the (common) coefficient of restitution \(\alpha \equiv \alpha _{ij}\) for \(x_1=0.5\), \(\sigma _1=\sigma _2\), \(T_\textrm{ex}^*=1\), and three different values of the mass ratio. Here, \(T_\textrm{ex}^*=T_\textrm{ex}/(\overline{m}\sigma _{12}^2\gamma _0^2)\) and \(\overline{m}=(m_1+m_2)/2\). Theory is compared against the Monte Carlo simulations [13]. As expected, energy equipartition is broken for inelastic collisions; the extent of the energy violation is greater when the mass disparity is large. The excellent agreement found between theory and computer simulations is also quite apparent, except for quite small values of \(\alpha \) (extreme inelasticity) where small discrepancies appear.

4 Chapman–Enskog Method. First-Order Solution

We assume now that the homogeneous steady state is perturbed by small spatial gradients. The existence of these gradients gives rise to nonzero contributions to the fluxes of mass, momentum, and energy. To first order in spatial gradients, the knowledge of the above fluxes allows one to identify the relevant Navier–Stokes transport coefficients of the granular suspension. As usual in the CE scheme [9], for times longer than the mean free time and distances larger than the mean free path, we suppose that the system achieves a hydrodynamic regime. This means that (i) the system has completely “forgotten” its initial preparation (initial conditions) and (ii) only the bulk domain of the system (namely, far away from the boundaries) is considered. Under these conditions, the BE (1) admits an special solution: the so-called normal or hydrodynamic solution where all space and time dependence of the distributions \(f_i(\textbf{r}, \textbf{v};t)\) is through a functional dependence on the hydrodynamic fields. This means that in the hydrodynamic regime, \(f_i(\textbf{r}, \textbf{v};t)\) adopts the normal form

$$\begin{aligned} f_i(\textbf{r}, \textbf{v}; t)=f_i\big [\textbf{v}|n_1(t), n_2(t), T(t), \textbf{U}(t)\big ]. \end{aligned}$$
(20)

The notation on the right-hand side of Eq. (20) indicates a functional dependence on the partial densities, temperature, and flow velocity. For small Knudsen numbers, the functional dependence (20) can be made local in space by expanding \(f_i\) in powers of the spatial gradients

$$\begin{aligned} f_i=f_i^{(0)}+\epsilon f_i^{(1)}+\epsilon ^2 f_i^{(2)}+\cdots , \end{aligned}$$
(21)

where \(\epsilon \) is a bookkeeping parameter that denotes an implicit spatial gradient (for instance, a term of order \(\epsilon \) is of first order in gradients). This parameter is taken to be equal to 1 at the end of the calculations.

An important point in the CE expansion is to characterize the magnitude of the friction coefficients \(\gamma _i\) and the term \(\Delta \textbf{U}\) with respect to the spatial gradients. On the one hand, since \(\gamma _i\) does not create any flux, then it is assumed to be to zeroth order in \(\epsilon \). On the other hand, because \(\Delta \textbf{U}=\textbf{0}\) in the absence of gradients, it should be considered to be at least of first order in spatial gradients (first order in \(\epsilon \)).

The implementation of the CE method to solve the BE (1) to first order in spatial gradients is very large and beyond the scope of the present contribution. We refer the interested reader to Ref. [8] for specific details. Since we want here to analyze thermal diffusion segregation in a granular suspension, in order to show more clearly the different competing mechanisms appearing in this phenomenon, we consider a binary mixture where the concentration of one of the species (let’s say species 1) is much smaller than that of the other species 2 (tracer limit, \(x_1\rightarrow 0\)). The consideration of this simple situation allows us to offer a simplified theory where a segregation criterion can be explicitly obtained.

In the tracer limit, the pressure tensor \(P_{ij}\), the heat flux \(\textbf{q}\), and the cooling rate \(\zeta \) of the binary mixture are the same as that of the excess species. While the fluxes \(P_{ij}\) and \(\textbf{q}\) are of first order in the spatial gradients in the Navier–Stokes description, the expression of \(\zeta \) must retain terms up to second order in gradients. Part of these second-order contributions to \(\zeta \) have been computed by Brey et al. [5] for dry (dilute) granular gases, while the complete set of these contributions has been determined by Brilliantov and Pöschel [14] for granular gases of viscoelastic particles. Nevertheless, it has been shown [5] that these second-order contributions to \(\zeta \) are negligible as compared with its zeroth-order counterparts. We expect that the same occurs for the case of binary granular suspensions and hence, they can be ignored.

4.1 Tracer Limit. Diffusion Transport Coefficients

In the tracer limit, the first-order contribution \(\textbf{j}_1^{(1)}\) to the mass flux is [8]

$$\begin{aligned} \textbf{j}_1^{(1)}=-\frac{m_1^2}{\rho }D_{11} \nabla n_1-\frac{m_1m_2}{\rho }D_{12} \nabla n_2-\frac{\rho }{T}D_1^T \nabla T-D_1^{U}\Delta \textbf{U}, \end{aligned}$$
(22)

where the diffusion transport coefficients are defined as

$$\begin{aligned} D_{11}=-\frac{\rho }{\rho _1d}\int d\textbf{v}\textbf{V}\cdot \boldsymbol{\mathcal {B}}_{11}\left( \textbf{V}\right) , \quad D_{12}=-\frac{1}{d}\int d\textbf{v}\textbf{V}\cdot \boldsymbol{\mathcal {B}}_{12}\left( \textbf{V}\right) , \end{aligned}$$
(23)
$$\begin{aligned} D_1^{T}=-\frac{m_1}{\rho d}\int d\textbf{v}\textbf{V}\cdot \boldsymbol{\mathcal {A}}_{1}\left( \textbf{V}\right) , \quad D_1^U=-\frac{m_1}{d}\int d\textbf{v}\textbf{V}\cdot \boldsymbol{\mathcal {E}}_{1}\left( \textbf{V}\right) . \end{aligned}$$
(24)

The unknowns \(\boldsymbol{\mathcal {A}}_{1}(\textbf{V})\), \(\boldsymbol{\mathcal {B}}_{11}\left( \textbf{V}\right) \), \(\boldsymbol{\mathcal {B}}_{12}\left( \textbf{V}\right) \), and \(\boldsymbol{\mathcal {E}}_{1}(\textbf{V})\) are the solutions of a set of coupled linear integral equations [8]. In the tracer limit, this set reads

$$\begin{aligned} -\Bigg (2\gamma _2 \theta ^{-1}+\frac{1}{2}\zeta ^{(0)}\Bigg )\boldsymbol{\mathcal {A}}_{1} -\gamma _1\frac{\partial }{\partial \textbf{V}}\cdot \left( \textbf{V}\boldsymbol{\mathcal {A}}_{1}\right){} & {} -\gamma _1 \frac{T_{\text {ex}}}{m_1}\frac{\partial ^2 \boldsymbol{\mathcal {A}}_{1}}{\partial v^2}-J_{12}[\boldsymbol{\mathcal {A}}_{1},f_2^{(0)}]\nonumber \\{} & {} =\textbf{A}_{1}+J_{12}[f_1^{(0)},\boldsymbol{\mathcal {A}}_2], \end{aligned}$$
(25)
$$\begin{aligned} -\gamma _1\frac{\partial }{\partial \textbf{V}}\cdot \left( \textbf{V}\boldsymbol{\mathcal {B}}_{11}\right) -\gamma _1 \frac{T_{\text {ex}}}{m_1}\frac{\partial ^2 \boldsymbol{\mathcal {B}}_{11}}{\partial v^2}-J_{12}[\boldsymbol{\mathcal {B}}_{11},f_1^{(0)}]=\textbf{B}_{11}, \end{aligned}$$
(26)
$$\begin{aligned} -\gamma _1\frac{\partial }{\partial \textbf{V}}\cdot \left( \textbf{V}\boldsymbol{\mathcal {B}}_{12}\right){} & {} -\gamma _1 \frac{T_{\text {ex}}}{m_1}\frac{\partial ^2 \boldsymbol{\mathcal {B}}_{12}}{\partial v^2} -J_{12}[\boldsymbol{\mathcal {B}}_{12},f_2^{(0)}]= \textbf{B}_{12}+J_{12}[f_1^{(0)},\boldsymbol{\mathcal {B}}_{21}]\nonumber \\{} & {} +\Bigg [\zeta ^{(0)}-2 \gamma _2\left( \theta ^{-1}-1\right) +2\lambda _1 \frac{\partial \tau _1}{\partial \lambda _1}\Bigg ]\boldsymbol{\mathcal {A}}_{1}, \end{aligned}$$
(27)
$$\begin{aligned} -\gamma _1\frac{\partial }{\partial \textbf{V}}\cdot \left( \textbf{V}\boldsymbol{\mathcal {E}}_{1}\right) -\gamma _1 \frac{T_{\text {ex}}}{m_1}\frac{\partial ^2 \boldsymbol{\mathcal {E}}_{1}}{\partial v^2}-J_{12}[{\mathcal {E}}_{1},f_2^{(0)}] =\textbf{E}_1. \end{aligned}$$
(28)

In the integral equations (25)–(28), \(\zeta ^{(0)}\) is the zeroth-order approximation to the cooling rate, \(\theta =T/T_\text {ex}\), \(\lambda _1=(2 T_\text {ex}^*)^{-1/2}(R_1/n\sigma _{12}^d)\), and \(\boldsymbol{\mathcal {A}}_{2}\) and \(\boldsymbol{\mathcal {B}}_{21}\) refer to quantities of the excess species 2. These quantities obey certain integral equations; their explicit forms are not needed for evaluating the diffusion transport coefficients in the so-called first Sonine approximation. In addition, the expression of the derivative \(\partial _{\lambda _1}\tau _1\) can be found in Appendix A of Ref. [8] while the inhomogeneous terms \(\textbf{A}_1\), \(\textbf{B}_{11}\), \(\textbf{B}_{12}\), and \(\textbf{E}_{1}\) are given, respectively, by

$$\begin{aligned} \textbf{A}_{1}\left( \textbf{V}\right) =-\textbf{V}\frac{\partial f_{1}^{(0)}}{\partial T}-\frac{p}{\rho }\frac{\partial f_{1}^{(0)}}{\partial \textbf{V}}, \quad \textbf{B}_{11}\left( \textbf{V}\right) = -\textbf{V} n_1 \frac{\partial f_{1}^{(0)}}{\partial n_1}, \end{aligned}$$
(29)
$$\begin{aligned} \textbf{B}_{12}\left( \textbf{V}\right) =-\textbf{V} n_2 \frac{\partial f_{1}^{(0)}}{\partial n_2}-\frac{T}{m_2}\frac{\partial f_{1}^{(0)}}{\partial \textbf{V}}, \quad \textbf{E}_1(\textbf{V})=\left( \gamma _1-\gamma _2\right) \frac{\partial f_{1}^{(0)}}{\partial \textbf{V}}. \end{aligned}$$
(30)

Note that Eqs. (25)–(28) have been obtained under steady-state conditions, namely when the conditions (15) apply. Furthermore, in order to obtain the above set of coupled integral equations, we have taken into account that while in the tracer limit \(D_{11}\) is independent of \(x_1\), the coefficients \(D_{12}\), \(D_1^T\), and \(D_1^U\) are proportional to \(x_1\). This dependence on \(x_1\) will be then self-consistently confirmed. Accordingly, \(\boldsymbol{\mathcal {A}}_{1}\propto x_1\), \(\boldsymbol{\mathcal {B}}_{12}\propto x_1\), and \(\boldsymbol{\mathcal {E}}_{1}\propto x_1\).

Although the exact form of the zeroth-order distributions \(f_i^{(0)}\) is not known, dimensional analysis requires that they have the scaled form \(f_i^{(0)}(\textbf{V})=n_i v_\textrm{th}^{-d} \varphi _i(\textbf{c}, \gamma _i^*,\theta )\). Here, \(\textbf{c}=\textbf{V}/v_\textrm{th}\) and \(\gamma _i^*=\gamma _i/\nu _0\), where \(\nu _0=n\sigma _{12}^{d-1}v_\textrm{th}\) is an effective collision frequency, and \(v_\textrm{th}=\sqrt{2T/\overline{m}}\) is the thermal velocity. Thus, one has the property

$$\begin{aligned} T \frac{\partial f_i^{(0)}}{\partial T}=-\frac{1}{2}\frac{\partial }{\partial \textbf{V}}\cdot \textbf{V}f_i^{(0)}+n_i v_\textrm{th}^{-d}\theta \frac{\partial \varphi _i}{\partial \theta }. \end{aligned}$$
(31)

4.2 Leading Sonine Approximation

Equations (25)–(28) are still exact. However, the determination of the diffusion transport coefficients requires to solve the above integral equations as well as to know the zeroth-order distributions \(f_i^{(0)}\). The results derived for driven granular mixtures [15] have shown that non-Gaussian corrections to \(f_i^{(0)}\) (which are measured through the fourth cumulants \(c_i\)) are in general very small. Thus, \(f_i^{(0)}\) is well represented by its Maxwellian form (18) and so, a theory incorporating the cumulants \(c_i\) seems to be unnecessary in practice for computing the diffusion transport coefficients. Regarding the functions \(\boldsymbol{\mathcal {A}}_{i}\), \(\boldsymbol{\mathcal {B}}_{ij}\), and \(\boldsymbol{\mathcal {E}}_{i}\), as usual we consider the leading terms in a series expansion of these quantities in Sonine polynomials. In this case, \(\boldsymbol{\mathcal {A}}_{2}\rightarrow 0\), \(\boldsymbol{\mathcal {B}}_{21}\rightarrow 0\), and the quantities \(\boldsymbol{\mathcal {A}}_{1}\), \(\boldsymbol{\mathcal {B}}_{11}\), \(\boldsymbol{\mathcal {B}}_{12}\), and \(\boldsymbol{\mathcal {E}}_{1}\) corresponding to the tracer species are approximated by

$$\begin{aligned} \boldsymbol{\mathcal {A}}_{1}(\textbf{V})\rightarrow -f_{1,\textrm{M}} \textbf{V} \frac{\rho }{n_1 T_1} D_1^T, \quad \boldsymbol{\mathcal {B}}_{11}(\textbf{V})\rightarrow -f_{1,\textrm{M}} \textbf{V} \frac{m_1^2}{\rho T_1} D_{11}, \end{aligned}$$
(32)
$$\begin{aligned} \boldsymbol{\mathcal {B}}_{12}(\textbf{V})\rightarrow -f_{1,\textrm{M}} \textbf{V} \frac{m_1}{n_1 T_1} D_{12}, \quad \boldsymbol{\mathcal {E}}_{1}(\textbf{V})\rightarrow -f_{1,\textrm{M}} \textbf{V} \frac{1}{n_1 T_1} D_{1}^U. \end{aligned}$$
(33)

Now, we substitute first Eqs. (32) and (33) into the integral equations (25)–(28), multiply them by \(m_1\textbf{V}\), and integrate over \(\textbf{v}\). After some algebra, \(D_{11}\), \(D_1^T\), \(D_{12}\), and \(D_1^U\) can be written, respectively, as

$$\begin{aligned} D_{11}=\frac{\rho T}{m_1^2\nu _0}\frac{\tau _1}{\nu _D^*+\gamma _1^*}, \quad D_1^{T}=\frac{nT}{\rho \nu _0} x_1\frac{\theta \frac{\partial \tau _1}{\partial \theta }-\left( \mu -\tau _1\right) }{\nu _D^*+\gamma _1^*-2\gamma _2^* \theta ^{-1}-\frac{1}{2}\zeta _0^*}, \end{aligned}$$
(34)
$$\begin{aligned} D_{12}=\frac{x_1 \rho T}{m_1 m_2\nu _0}\frac{\Big [\zeta _0^*-2\gamma _2^*\left( \theta ^{-1}-1\right) \Big ]x_1^{-1}D_1^{T*}-\mu -2\lambda _1\frac{\partial \tau _1}{\partial \lambda _1}}{\nu _D^*+\gamma _1^*}, \end{aligned}$$
(35)
$$\begin{aligned} D_1^{U}=\rho _1\frac{\gamma _1^*-\gamma _2^*}{\gamma _1^*-\nu _D^*}. \end{aligned}$$
(36)

Here, \(\mu =m_1/m_2\) is the mass ratio, the derivative \(\partial _\theta \tau _1\) is given in Appendix A of Ref. [8],

$$\begin{aligned} \zeta _0^*=\frac{\pi ^{\left( d-1\right) /2}}{d\Gamma \left( \frac{d}{2}\right) }\Big (\frac{\sigma _2}{\sigma _{12}}\Big )^{d-1}\mu _{21}^{-1/2} \left( 1-\alpha _{22}^2\right) , \end{aligned}$$
(37)

and the reduced collision frequency \(\nu _D^*\) is

$$\begin{aligned} \nu _D^*=\frac{2\sqrt{2}\pi ^{(d-1)/2}}{d\Gamma \left( \frac{d}{2}\right) } \mu _{21}^{3/2}\Big (\frac{1+\beta }{\beta }\Big )^{1/2}(1+\alpha _{12}), \end{aligned}$$
(38)

where \(\beta =\beta _1/\beta _2=\mu /\tau _1\).

Fig. 2
figure 2

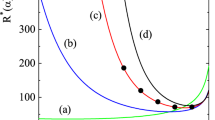
Plot of the (reduced) transport coefficients \(D_{11}(\alpha )/D_{11}(1)\) (a), \(D_{12}(\alpha )/D_{12}(1)\) (b), \(D_{1}^T(\alpha )/D_{1}^T(1)\) (c), and \(D_{1}^U(\alpha )/D_{1}^U(1)\) (d) as a function of the common coefficient of restitution for a binary mixture of hard spheres (\(d=3\)) in the tracer limit (\(x_1\rightarrow 0\)) with \(\sigma _1/\sigma _2=1\), \(m_1/m_2=10\), and \(T_\textrm{ex}^*=0.1\)

Full size image

Figure 2 shows the dependence of the reduced diffusion transport coefficients \(D_{ij}(\alpha )/D_{ij}(1)\), \(D_1^T(\alpha )/D_1^T(1)\), and \(D_1^U(\alpha )/D_1^U(1)\) for \(\sigma _1/\sigma _2=1\), \(m_1/m_2=10\), and \(T_\textrm{ex}^*=0.1\). Here, \(D_{ij}(1)\), \(D_1^T(1)\), and \(D_1^U(1)\) are the values of these coefficients for elastic collisions. We observe that the impact of inelasticity on those coefficients is in general quite important since they differ clearly from their elastic forms, especially in the case of the thermal diffusion coefficient \(D_1^T\). Moreover, a comparison with the results obtained in the dry granular limit (no gas phase) shows important qualitative differences between both theories (see, for instance, Fig. 6.3 of Ref. [4] for the diffusion coefficient \(D_{11}\)).

5 Thermal Diffusion Segregation of an Intruder in a Granular Suspension

A nice application of the previous results is the study of thermal diffusion segregation of an intruder or tracer particle in a granular suspension. Needless to say, segregation and mixing of dissimilar grains are one of the most interesting problems in granular mixtures, not only from a fundamental point of view but also from a more practical perspective. This problem has been widely studied in the past few years for dry granular mixtures. The objective here is to assess the influence of the interstitial gas phase on the segregation criterion.

Thermal diffusion is originated by the relative motion of the components of a mixture due to the presence of a temperature gradient. Due to this motion, concentration gradients appear in the mixture producing ordinary diffusion. A steady state is finally achieved in which the separating effect emerging from thermal diffusion is offset by the remixing effect arising from ordinary diffusion [16]. The partial separation between both components of the mixture is then observed; this effect is usually referred to as the Soret effect.

The amount of segregation parallel to the thermal gradient may be characterized by the so-called thermal diffusion factor \(\Lambda \). This quantity is defined in an inhomogeneous non-convecting (\(\textbf{U}=\textbf{U}_g=\textbf{0}\)) steady state with zero mass flux (\(\textbf{j}_1^{(1)}=\textbf{0}\)) as

$$\begin{aligned} -\Lambda \frac{\partial \ln T}{\partial z}=\frac{\partial }{\partial z}\ln \Big (\frac{n_1}{n_2}\Big ), \end{aligned}$$
(39)

where only gradients along the z-axis have been assumed for simplicity. Let us assume that the bottom plate is hotter than the top plate (\(\partial _z \ln T <0\)). If \(\Lambda \) is supposed to be constant over the relevant ranges of composition and temperature of the system, according to Eq. (39), when \(\Lambda >0\), the tracer particle tends to rise with respect to the gas particles 2, i.e., \(\partial _z \ln (n_1/n_2)>0\) (tracer particles accumulate near the cold plate). On the other hand, when \(\Lambda <0\), the tracer particle tends to fall with respect to the gas particles 2, i.e., \(\partial _z \ln (n_1/n_2)<0\) (tracer particles accumulate near the hot plate).

Let us determine the thermal diffusion factor. The mass flux \(j_{1,z}^{(1)}\) is given by Eq. (22) with \(\Delta \textbf{U}=\textbf{0}\). Since \(j_{1,z}^{(1)}=0\) in the steady state and \(\textbf{U}=\textbf{U}_g=\textbf{0}\), then Eq. (8) yields \(\partial _z (nT)=0\) and so,

$$\begin{aligned} \partial _z \ln T=-\partial _z \ln n_2. \end{aligned}$$
(40)

Here, we have taken into account that \(n\simeq n_2\) in the tracer limit. The factor \(\Lambda \) can be written in terms of the diffusion coefficients when one takes into account Eq. (40) and that \(j_{1,z}^{(1)}=0\). Its expression is finally given by

$$\begin{aligned} \Lambda =\frac{x_1^{-1}D_1^{T^*}-D_{11}^*-x_1^{-1}D_{12}^*}{D_{11}^*}, \end{aligned}$$
(41)

where we have introduced the dimensionless transport coefficients

$$\begin{aligned} D_{11}^*=\frac{m_1^2 \nu _0}{\rho T} D_{11}, \quad D_{12}^*=\frac{m_1 m_2 \nu _0}{\rho T} D_{11}, \quad D_1^{T*}=\frac{\rho \nu _0}{nT}D_1^T. \end{aligned}$$
(42)

The explicit dependence of \(\Lambda \) on the parameters of the granular suspension (mass and size ratios, the coefficients of restitution \(\alpha _{12}\) and \(\alpha _{22}\), and the dimensionless external temperature \(T_\textrm{ex}^*\)) can be obtained when one substitutes Eqs. (34) and (35) of \(D_{11}\), \(D_1^T\), and \(D_{12}\), respectively, into Eq. (41). Since \(D_{11}^*>0\), the condition \(\Lambda =0\) is

$$\begin{aligned} x_1^{-1}D_1^{T^*}=D_{11}^*+x_1^{-1}D_{12}^*. \end{aligned}$$
(43)

Equation (43) gives the marginal segregation curve separating intruder segregation toward the cold wall (\(\Lambda >0\)) from intruder segregation toward the hot wall (\(\Lambda <0\)). On the other hand, since the number of parameters involved in the segregation problem is still large, it is not easy to disentangle the influence of each mechanism (mass and size ratios, inelasticity in collisions, external temperature, \(\ldots \)) on the intruder segregation problem. Thus, it is convenient first to consider some simple situations.

Fig. 3
figure 3

Plot of the marginal segregation curve (\(\Lambda =0\)) for \(d=3\), \(\alpha _{22}=\alpha _{12}=1\), and \(T_\textrm{ex}^*=1\). Points below (above) the curve correspond to \(\Lambda >0\) (\(\Lambda <0\))

Full size image

5.1 Mechanically Equivalent Particles

This is quite trivial case since the system is in fact monodisperse (\(m_1=m_2\), \(\sigma _1=\sigma _2\), \(\alpha _{11}=\alpha _{22}\equiv \alpha \), \(\gamma _2=\gamma _1\equiv \gamma \)). In this limit case, \(\tau _1=1\) and according to Eqs. (34) and (35), \(x_1^{-1}D_1^{T*}=0\) and \(D_{11}^*=-x_1^{-1}D_{12}^*=(\nu _D^*+\gamma ^*)^{-1}\). Therefore, Eq. (41) yields \(\Lambda =0\) for any value of the coefficients of restitution \(\alpha _{12}\) and \(\alpha _{22}\) and the bath temperature \(T_\textrm{ex}^*\). This implies that no segregation is possible, as expected.

5.2 Elastic Collisions

For elastic collisions (\(\alpha _{22}=\alpha _{12}=1\)), \(\zeta _0^*=0\), \(\tau _1=\theta =1\), \(\beta =\mu \), and Eq. (43) leads to the condition

$$\begin{aligned} \left( \nu _D^*+\gamma _1^*\right) \frac{\partial \tau _1}{\partial \theta }=2\gamma _2^*\left( \mu -1\right) . \end{aligned}$$
(44)

Upon deriving Eq. (44), we have considered the region of parameter space where \(\nu _D^*+\gamma _1^*-2\gamma _2^*\ne 0\). It is quite apparent that even for elastic collisions, the segregation criterion (\(\Lambda =0\)) is not simple and differs from the simple segregation criterion obtained in the dry case (\(\mu =1\)). Figure 3 shows a phase diagram in the \(\left\{ m_2/m_1, \sigma _2/\sigma _1\right\} \)-plane at \(T_\textrm{ex}^*=1\). For a given value of the mass ratio \(m_2/m_1\), it is quite apparent that the region \(\Lambda >0\) (tracer particle falls with respect to excess granular gas) is dominant when the size of gas particles is much larger than that of the tracer particle. This tendency increases with increasing the mass ratio \(m_2/m_1\).

5.3 Inelastic Collisions

We consider now the general case where \(\alpha _{22}\) and \(\alpha _{12}\) are different from 1. In this case, considering the region of parameter space where \(\nu _D^*+\gamma _1^*-2\gamma _2^*\theta ^{-1}-\frac{1}{2}\zeta _0^*\ne 0\), Eq. (43) yields

$$\begin{aligned} \Big [\nu _D^*+\gamma _1^*-\zeta _0^*+2\gamma _2^*\left( \theta ^{-1}-1\right) \Big ]{} & {} \Big (\theta \frac{\partial \tau _1}{\partial \theta }-\mu +\tau _1\Big )=\Big (\tau _1-\mu -2\lambda _1\frac{\partial \tau _1}{\partial \lambda _1}\Big )\nonumber \\{} & {} \times \Big (\nu _D^*+\gamma _1^*-2\gamma _2^*\theta ^{-1}-\frac{1}{2}\zeta _0^*\Big ). \end{aligned}$$
(45)

This is quite a complex segregation criterion in comparison with the one derived in the dry granular case (no gas phase) where \(\Lambda =0\) if \(\mu =\tau _1\) [17, 18]. To illustrate more clearly the differences between both (with and without gas phase) segregation criteria, Fig. 4 shows the marginal segregation curve (\(\Lambda =0\)) for the (common) coefficient of restitution 0.9. Figure highlights that the impact of gas phase on tracer segregation is quite significant since, at a given value of the size ratio, the value of the mass ratio \(m_2/m_1\) at which \(\Lambda =0\) is greater in the granular suspension than in the dry granular system. In addition, we also observe that the main effect of gas phase on tracer segregation is to increase the size of the region \(\Lambda >0\) as \(\sigma _2/\sigma _1\) increases. This means that the tracer particle attempts to move toward the cold regions as its size decreases with respect to that of the excess granular gas.

Fig. 4
figure 4

The same as in Fig. 3 but for \(\alpha _{22}=\alpha _{12}=0.9\). The solid line corresponds to the segregation criterion for granular suspensions while the dashed line refers to the one derived for dry granular mixtures. Points below (above) each curve correspond to \(\Lambda >0\) (\(\Lambda <0\))

Full size image

6 Concluding Remarks

The primary objective of this short review has been to derive the Navier–Stokes hydrodynamic equations of a binary granular suspension within the context of the inelastic version of the Boltzmann kinetic equation. As usual, the effect of the interstitial surrounding gas on grains has been modeled through an effective external force constituted by a deterministic drag force plus an stochastic Langevin-like force. This way of modeling gas–solid flows is essentially based on the following assumptions and/or simplifications. First, assuming that the granular mixture is rarefied, one supposes that the state of the surrounding gas is not perturbed by the presence of grains and so, it can be treated as a thermostat. Second, the impact of gas phase on collision dynamics is very weak, and consequently, the Boltzmann collision operator is not affected by the presence of the interstitial gas. As a third simplification, one considers the friction coefficients appearing in the thermal-drag forces to be scalar quantities. Finally, as a fourth simplification, one assumes low Reynolds numbers so that only laminar flows are considered.

The road map for obtaining the Navier–Stokes hydrodynamic equations needs to characterize first the homogeneous state. This is important because the Navier–Stokes transport coefficients are obtained from the CE expansion around the above state. Given that the transport coefficients are given in terms of the solutions to a set of coupled linear integral equations, these equations are approximately solved by considering the leading terms in a series expansion of Sonine polynomials. This road map is large and involves many technical steps. Here, for the sake of simplicity, we have obtained the mass flux of a binary granular suspension where the concentration of one of the species is negligible (tracer limit). The tracer limit allows us to provide expressions that are easy to handle for potential applications. In particular, we have briefly analyzed here the thermal diffusion segregation of an intruder or tracer particle in a granular suspension. The segregation criterion obtained here shows significant discrepancies with respect to the one previously derived for dry granular mixtures [17, 18]. These differences between both situations (with and without interstitial gas) are clearly illustrated in Figs. 3 and 4 for elastic and inelastic collisions, respectively.

Multicomponent granular suspensions exhibit a wide range of interesting phenomena for which kinetic theory and hydrodynamics (in the broader sense) may be considered as useful tools for understanding the behavior of such complex materials. However, due to their complexity, many of their features are not still completely understood. For this reason, from the theoretical side, one has to introduce new ingredients in the model for approaching more realistic situations. In this context, the extension of the results presented in this review to inertial suspensions of inelastic rough hard spheres could be an interesting and challenging problem in the near future.