Keywords

12.1 Introduction

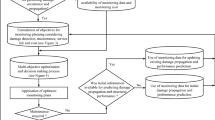
This paper briefly describes a sensor optimization framework with a target of maximizing the net savings as a consequence of using an SHM system over the life cycle of the structure. Conventionally, the cost-benefit analysis of an SHM system is carried out through pre-posterior decision analysis using the expected value of information (EVoI) metric (a differential metric). We use expected value of information (EVoI) (a differential metric) and risk-adjusted reward (a normalized metric) as an optimality criterion. Finally, the goal of this research is to obtain the optimal sensor network design that maximizes the value of information over the life cycle of the structure.

12.2 Value of Information Metric

Consider an SHM-based decision-making problem. Let the state of the structure at time t ∈ ΩT be defined by an uncertain state-parameter vector denoted by Θ(t) with a realization θ(t) ∈ ΩΘ(t). The data acquired by the SHM system z ∈ ΩZ at time t is defined by a random variable X z(t), where \( {x}_z(t)\in {\Omega}_{X_z(t)} \) denote an observed realization. The goal of an SHM system is to recommend a maintenance strategy selected from a set of predefined choices ΩD = {d 0, d 1, …, d n}. For a risk profile of the decision-maker parameterized by (γ, ξ), let L(d i, θ true; γ, ξ) denote the consequence cost/regret/loss function that defines the total perceived loss as a consequence of making the decision d i when the true state of the structure is θ true(t) at time t (see [1, 2]). To obtain the benefit of an SHM system in the design phase, we require the following:

  1. 1.

    We need a probabilistic state-parameter evolution model (see [2]). Let Θ(t) denote a random variable representing the state parameter at a time instance t ∈ ΩT. The prior state-parameter evolution model is then quantified by f Θ(t)(θ(t)).

  2. 2.

    We need an inflation-adjusted cost function. The factor (r(t) + 1)t adjusts for the future inflation, where r(t) is the assumed future monthly rate of inflation at time t in months. We consider four types of costs:

    • Cost A: The inflation-adjusted consequence-cost of decision making at time t, denoted by \( \overset{\sim }{L}\left({d}_j,{\theta}_{\mathrm{true}}(t),t;\gamma, \xi \right)=L\left({d}_j,{\theta}_{\mathrm{true}}(t);\gamma, \xi \right).{\left(r(t)+1\right)}^t \). The inspection and maintenance decisions are usually carried out at discrete time steps.

    • Cost B and Cost C: The maintenance (cost B) and operation (cost C) cost of the SHM system, denoted by C M(t) = C M. (r(t) + 1)t and C O(t) = C O. (r(t) + 1)t, respectively. Here, C M denotes the current estimated cost for one instance of maintenance of the system, and C O denotes the currently estimated operation cost per month. We assume that the maintenance is done periodically.

    • Cost D: The cost of design and initial installation of an information gathering system C(z). We assume this to be an initial cost and hence time-independent.

When new data/measurement \( {x}_z(t)\in {\Omega}_{X_z(t)} \)is obtained, the state of the structure is updated by obtaining the posterior distribution of the state parameter, denoted by \( {f}_{\Theta \mid {\mathrm{X}}_{\mathrm{z}}}\left(\theta |{x}_z\right) \), using Bayesian inference (see [3]). The updated posterior state-parameter evolution model, denoted by \( {f}_{\Theta \left(\mathrm{t}\right)\mid {\mathrm{X}}_{\mathrm{z}}(t)}\left(\theta (t)|{x}_z(t)\right) \), is obtained by using Bayesian inference utilizing the measurement data simulated by a finite element model that is assumed to be the ground truth.

The EVoI of the design z for a risk profile (γ, ξ) at a given time instance is defined as:

$$ \mathrm{EVoI}\left(z,t;\gamma, \xi \right)={C}_{\mathrm{save}}\left(z;\gamma, \xi \right)-C(z)\vspace*{-15pt} $$
(12.1a)
$$ {C}_{\mathrm{save}}\left(z,t;\gamma, \xi \right)={E}_{X_z(t)}\left[\underset{d_i}{\min }\ \overset{\sim }{L}\left({d}_j,{\theta}_{\mathrm{true}}(t),t;\gamma, \xi \right)\right]-\underset{d_i}{\min }{E}_{\Theta \left(\mathrm{t}\right)}\left[\overset{\sim }{L}\left({d}_j,{\theta}_{\mathrm{true}}(t),t;\gamma, \xi \right)\right] $$
(12.1b)

Here, C save(z, t; γ, ξ) gives the expected cost saved by making a better decision based on newly acquired measurements through the mechanism z at time t for the risk profile (γ, ξ). The EVoI over the life cycle for an SHM system z for the risk profile (γ, ξ), denoted by EVoILC(z; γ, ξ), and the risk-adjusted reward, denoted by λ LC(z; γ, ξ) is then defined as (derived in Chadha et al. [3]):

$$ \mathrm{EVo}{\mathrm{I}}_{\mathrm{LC}}\left(z;\gamma, \xi \right)={C}_{\mathrm{saveLC}}\left(z;\gamma, \xi \right)-\left(C(z)+{C}_{M\&O}(z)\right)\vspace*{-15pt} $$
(12.2a)
$$ {\lambda}_{\mathrm{LC}}\left(z;\gamma, \xi \right)=\frac{C_{\mathrm{saveLC}}\left(z;\gamma, \xi \right)}{\left(C(z)+{C}_{M\&O}(z)\right)} $$
(12.2b)

The quantity C saveLC(z; γ, ξ) denotes the expected savings over the life cycle of the structure as a consequence of making data-informed decision-making for the risk profile (γ, ξ), such that:

$$ {\displaystyle \begin{array}{c}{C}_{\mathrm{saveLC}}\left(z;\gamma, \xi \right)=\sum \limits_{n=1}^{N_A}\left(\underset{d_i}{\min }{E}_{\Theta \left({t}_{A_n}\right)}\left[\tilde{L}\left({d}_j,{\theta}_{\mathrm{true}}\left({t}_{A_n}\right),{t}_{A_n};\gamma, \xi \right)\right]\right)\\ {}-\sum \limits_{n=1}^{N_A}\left({E}_{X_z\left({t}_{A_n}\right)}\left[\underset{d_i}{\min }{E}_{\Theta \left({t}_{A_n}\right)\mid {X}_z\left({t}_{A_n}\right)}\left[\tilde{L}\left({d}_j,{\theta}_{\mathrm{true}}\left({t}_{A_n}\right),{t}_{A_n};\gamma, \xi \right)\right]\right]\right)\end{array}} $$
(12.3)

An SHM system is feasible if it satisfies either of these equivalent conditions:

$$ \mathrm{EVo}{\mathrm{I}}_{\mathrm{LC}}(z)\ge 0,\mathrm{or}\ {\lambda}_{\mathrm{LC}}(z)\ge 1. $$
(12.4)

Among many SHM system designs, optimal designs \( {\mathcal{z}}_{\mathrm{EVoI}} \) and \( {\mathcal{z}}_{\uplambda} \) are obtained as:

$$ {\mathcal{z}}_{\mathrm{EVoI}}=\arg \underset{z\in {\Omega}_Z}{\max}\mathrm{EVo}{\mathrm{I}}_{\mathrm{LC}}(z),\mathrm{and}\kern0.5em {\mathcal{z}}_{\lambda }=\arg \underset{z\in {\Omega}_Z}{\max }{\lambda}_{\mathrm{LC}}(z) $$
(12.5)

We obtain the optimal sensor design using EVoILC(z) and λ LC(z) as the objective functional by deploying the Bayesian optimization algorithm described in Yang et al. [3].

12.3 Application to Miter Gates

Let the state of the miter gate be completely defined by the loss of boundary contact (or a “gap”) between the gate and the concrete wall at the bottom of the gate, such that θ ∈ ΩΘ = [θ min = 0, θ max = 180 in]. Consider a binary decision-space ΩD = {d 0, d 1}, such that d0 is a decision to not do specified maintenance and d1 is a decision to perform some specified maintenance. Figure 12.1a below shows the optimal sensor network design \( {\mathcal{z}}_{\mathrm{EVoI}} \) obtained using Eq. (12.5) and the optimization algorithm delineated in Yang et al. [3]. It was observed that the Bayesian algorithm picked two sensors close to the gap (encircled with red) leading to maximum \( \mathrm{EVo}{\mathrm{I}}_{\mathrm{LC}}\left({\mathcal{z}}_{\mathrm{EVoI}}\right) \). However, for comparison purposes, we consider the optimal design \( {\mathcal{z}}_{\mathrm{EVoI}} \) and the random design z random to have five sensors. This shows that effectively, the optimal design would consist of a smaller number of sensors.

Fig. 12.1
figure 1

Miter gate and the sensor network design considering conservative decision profile. (a) Optimal sensor design \( {\mathcal{z}}_{\mathrm{EVoI}} \). (b) Random design z random

Full size image

We observe that the optimal sensor design leads to a higher expected value of information at an intermediate time period (5–30 months). Beyond this time period, the structural damage is high enough that a conservative decision-maker (the considered profile for the simulation) would recommend maintenance be carried out irrespective of the SHM design used to obtain the measurements. Therefore, for higher damage levels, decisions obtained using optimal design and random design are the same. The EVoI(z, t; γ, ξ) is not smooth in Fig. 12.2 because lower particle numbers were used for Bayesian inference using the particle filter technique. This was done to reduce computational costs.

Fig. 12.2
figure 2

Comparison of EVoI(z, t; γ, ξ) for optimal and random design at various time instances

Full size image

12.4 Conclusions

This paper briefly details the mathematical formulation behind a sensor optimization framework that aims at maximizing the net cost saving over the life cycle of the structure. The idea targets the core of an SHM system and attempts to come up with the most optimal data acquisition system design. This is currently ongoing research.