1 Introduction

Structural health monitoring (SHM) has been treated as an effective diagnostic tool to detect damage promptly and prevent unexpected structural failure of civil infrastructure systems [5]. The SHM is generally applied for the purposes of accurate and reliable system identification, condition assessment, structural performance prediction, and service life management. Over the last few decades, significant advances have been accomplished in developing SHM including non-destructive inspection techniques [7, 11, 57]. Along with the demands to improve the accuracy and efficiency in SHM, there have been significant developments of the next-generation SHM techniques using cameras, drones, robotic sensors, and smartphones [55]. These developments in the SHM techniques should lead to development of more accurate and reliable approaches to predict structural performance and manage the service life of deteriorating structures using SHM data.

The life-cycle cost analysis of deteriorating structures is based on the structural performance prediction considering maintenance interventions. For this reason, the uncertainties associated with structural performance assessment and prediction affect the uncertainties in the life-cycle cost analysis [18]. The reduction of the uncertainties associated with structural performance assessment and prediction can lead to timely and appropriate maintenance actions and, as a result, the life-cycle cost of a deteriorating structure can be reduced [3, 19]. These uncertainties can be significantly reduced by using the monitoring data in a rational way. The reduction in the life-cycle cost corresponds to the benefit of SHM application [15]. The benefit produced from SHM applications can be maximized through the optimum monitoring planning [22,23,24,27, 52].

The monitoring planning should consider the effects of SHM on damage propagation and structural performance prediction, maintenance actions and life-cycle cost. These effects have been investigated extensively during the last decade [16]. For instance, Liu et al. [38, 39], Kwon and Frangopol [33, 34], Kwon et al. [35] and Soliman et al. [54] presented the probabilistic approaches to predict the fatigue damage and structural performance based on monitoring data. The integration of SHM in life-cycle management of deteriorating structures can be found in Okasha et al. [46], Orcesi et al. [49], Orcesi and Frangopol [50], and Okasha and Frangopol [45]. Based on these investigations, several probabilistic approaches to establish the optimum monitoring plans have been developed in Kim and Frangopol [24, 26, 27, 31], and Sabatino and Frangopol [52]. However, these developed approaches may be limited to specific conditions for external loads (e.g., traffic loads and sea loads), deterioration mechanisms (e.g., corrosion in a reinforced concrete and fatigue in a steel structure) and target structures (bridges and marine structures). Therefore, it is necessary to integrate the recently developed approaches in a computational platform for a general application to civil infrastructure.

This paper presents such an integrated computational platform for optimum monitoring planning considering use of SHM for damage propagation and structural performance prediction, maintenance actions and life-cycle cost. The main components of the overall platform are described with the detailed computational flowchart and the associated theoretical background. In addition, a summary of approaches and applications associated with the computational platform for optimum monitoring planning is presented. The techniques used in the computational approach are based on probabilistic concepts and methods to rationally deal with the uncertainties associated with the monitoring data, damage occurrence and propagation prediction, and structural performance assessment and prediction. The presented computational platform can be applied to any deteriorating civil infrastructure such as bridges, buildings and nuclear power plants.

2 Computational platform for optimum monitoring planning

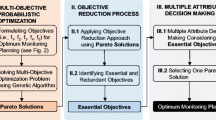
The presented computational platform for optimum monitoring planning consists of the three main components: (a) formulation of objectives for monitoring planning, (b) multi-objective optimization (MOPT) and decision making and (c) use of monitoring data for updating the damage occurrence/propagation and structural performance, as shown in Fig. 1. The optimum monitoring planning resulting from this computational platform is associated with the optimum number of monitorings, monitoring starting times and monitoring durations. The formulations of objectives for optimum monitoring planning are based on availability of monitoring data, monitoring cost, damage detection delay, maintenance delay, reliability (i.e., probability of survival) or reliability index, service life extension and life-cycle cost. The formulated objectives are used for the MOPT, which results in the multiple Pareto optimal solutions. Through the decision-making process, the best solution is selected from the Pareto optimal solutions. The optimum number of monitorings, monitoring starting times and monitoring durations are represented by the best Pareto solution. The information collected during monitoring can be used to predict the damage propagation and structural performance under uncertainty and update the existing information. The next monitoring plan can be established from the MOPT and decision making with the updated information. The details of the computational platform of Fig. 1 are described in the following sections of this paper.

Fig. 1
figure 1

Schematic of computational platform for optimum monitoring planning

Full size image

3 Formulation of objectives for optimum monitoring planning

The monitoring plans can be established with and without enough initial information on damage occurrence and propagation prediction. When the initial information is not enough to predict the damage occurrence and propagation reliably, the optimum monitoring planning can be based on the availability of monitoring data and cost. The associated MOPT considers two objectives: maximizing the expected average availability of monitoring data and minimizing the expected monitoring cost. If the damage occurrence and propagation can be predicted with enough initial information, the monitoring planning can be performed with multiple objectives including minimizing the expected damage detection delay, minimizing the expected maintenance delay, maximizing the reliability index, maximizing the expected service life extension and minimizing the expected life-cycle cost.

3.1 Objectives based on availability of monitoring data

The availability of monitoring data is defined as the probability that the structural performance prediction based on monitoring data will be effective during a non-monitoring time interval [24, 26, 52]. Considering the residual between the values from monitoring and performance prediction model, the availability of monitoring data is formulated. The expected average availability of monitoring data during the non-monitoring tnd days \( E\left( {\bar{A}} \right) \) is expressed as [26]

$$ E\left( {\bar{A}} \right) = \frac{{t_{\text{md}} }}{{t_{\text{nd}} }}\left[ {1 - \exp \left( {\frac{{t_{\text{nd}} }}{{t_{\text{md}} }}} \right)} \right], $$
(1)

where tmd is the monitoring duration. \( E\left( {\bar{A}} \right) \) ranges from zero to one. An increase in the monitoring duration tmd and/or reduction of the non-monitoring duration tnd results in an increase in \( E\left( {\bar{A}} \right) \) as indicated in Eq. (1).

The total monitoring cost Cmon can be estimated as [24]

$$ C_{\text{mon}} = \left( {\frac{{t_{\text{md}} }}{{t_{{{\text{md,}}o}} }} \cdot C_{\text{mon,o}} } \right) \cdot \sum\limits_{i = 1}^{{N_{\text{mon}} }} {\left( {\frac{1}{{\left( {1 + r} \right)^{{\left( {i - 1} \right)\left( {t_{\text{md}} + t_{\text{nd}} } \right)}} }}} \right)} , $$
(2)

where Cmon,o is the monitoring cost during the given monitoring period tmd,o; Nmon is the number of monitorings over a prescribed time; r is the discount rate of money. Larger \( E\left( {\bar{A}} \right) \), which is associated with more reliable prediction of structural performance, can be achieved by longer monitorings. However, it requires additional monitoring cost Cmon. Accordingly, the monitoring plan can be formulated as a bi-objective optimization based on the two conflicting objectives: maximizing \( E\left( {\bar{A}} \right) \) and minimizing Cmon.

The expected average availability \( E\left( {\bar{A}} \right) \) and the total monitoring cost Cmon can be integrated into the expected monetary loss (EML), which is formulated as [26]:

$$ {\text{EML}}\left( {a_{i} } \right) = C_{{{\text{mon}},i}} + C_{\text{loss}} \cdot \left( {1 - E_{i} \left( {\bar{A}} \right)} \right), $$
(3)

where ai is the alternative representing the ith monitoring plan, Closs is the monetary loss when the monitoring data is not effective for future structural performance prediction, and Cmon,i and \( E_{i} \left( {\bar{A}} \right) \) are the total monitoring cost and the expected average availability of monitoring data associated with the alternative ai, respectively. The alternative a* leading to the minimum EML of Eq. (3) corresponds to the optimum monitoring plan. Since the formulations of Eqs. (1), (2) and (3) consist of monitoring and non-monitoring durations, and monitoring cost, the monitoring planning based on the availability of monitoring data can be useful when the initial information to predict the damage occurrence and propagation is not enough.

3.2 Objectives with damage occurrence and propagation prediction

The damage occurrence and propagation prediction is the first phase of the formulations of objective functions considering damage detection, maintenance, service life and cost. Figure 2 shows the detailed computational procedure for prediction of damage propagation. To predict the structural performance of a deteriorating structure, the critical deterioration mechanisms (e.g., fatigue and corrosion) and locations affecting the structural performance need to be identified. The appropriate prediction models representing the critical deterioration mechanisms should be established. For a given time, the degree of damage under uncertainty can be expressed by the probability density function (PDF). The uncertainty associated with the time when the damage reaches a specific threshold of damage can be also represented by the PDF. For example, the fatigue crack size at can be estimated at time t as [28, 40]

$$ a_{t} = \left[ {a_{0}^{ (2 - m )/2} + \left( {\frac{2 - m}{2}} \right) \cdot C \cdot S_{\text{re}}^{m} \cdot Y^{m} \cdot \pi^{m/2} \cdot \left( {N_{\text{an}} \cdot t} \right)} \right]^{{\left( {\frac{2}{2 - m}} \right)}} \quad {\text{for}}\;m \ne 2, $$
(4)

where a0 is the initial crack size, Sre is the stress range, Y is the geometry constant, and Nan is the annual number of cycles. C and m are the material crack propagation parameters. Furthermore, the time t to reach at is predicted as [21, 22]

$$ t = \frac{{a_{N}^{ (2 - m )/2} - a_{o}^{ (2 - m )/2} }}{{\left( {\frac{2 - m}{2}} \right) \cdot C \cdot S_{\text{re}}^{m} \cdot Y^{m} \cdot \pi^{m/2} \cdot N_{\text{an}} }}\quad {\text{for}}\;m \ne 2. $$
(5)

By treating the parameters in Eqs. (4) and (5) as random variables, the PDF of the crack size for a given time and PDF of the time for a given crack size can be obtained as shown in Fig. 2. These PDFs are used to formulate the objective functions for optimum monitoring planning.

Fig. 2
figure 2

Detailed computational procedure for damage propagation prediction under uncertainty

Full size image

Figure 3 shows the computational procedure to formulate the objective functions: the expected damage detection delay E(tdel_d), expected maintenance delay E(tdel_m), reliability Ps (i.e., probability of survival) or reliability index β, expected service life extension E(texlife) and expected life-cycle cost Clife. The damage detection delay is formulated using the event tree considering the uncertainties associated with the damage occurrence and propagation, and damage detection. The expected damage detection delay E(tdel_d) for Nmon monitorings is expressed as [18, 29, 30]

$$ E\left( {t_{{{\text{del}}\_d}} } \right) = \sum\limits_{i = 1}^{{N_{\text{mon}} + 1}} {\left\{ {\int_{{t_{{{\text{ms}},i - 1}} + t_{\text{md}} }}^{{t_{{{\text{ms}},i}} }} {\left[ {\left( {t_{{{\text{ms,}}i}} - t} \right) \cdot f_{T} \left( t \right)} \right]} {\text{d}}t} \right\}} , $$
(6)

where tms,i is the ith monitoring starting time; tmd is the monitoring duration; and fT(t) is the PDF of the damage occurrence time t. The time tms,i−1 + tmd for i = 1 and tms,i for i = Nmon + 1 are zero and service life tlife, respectively.

Fig. 3
figure 3

Detailed computational procedure to formulate objective functions

Full size image

The maintenance delay is the time interval between the damage occurrence and the maintenance application. The expected maintenance delay is formulated based on the probabilistic relation among the degree of damage and type of maintenance. For example, when one-time monitoring is applied for a deteriorating structure subjected to fatigue, the expected maintenance delay E(tdel_m) can be expressed as [31]

$$ \begin{aligned} E\left( {t_{{{\text{del}}\_m}} } \right) & = \int_{0}^{{t_{{{\text{ms}},1}} }} {\left[ {P\left( {a_{1} \ge a_{\text{ma}} } \right) \cdot \left( {t_{\text{ms,1}} - t} \right)f_{T} \left( t \right)} \right]}_{{}} \\ & \quad + \int_{0}^{{t_{\text{ms,1}} + t_{\text{md}} }} {\left[ {P\left( {a_{1} < a_{\text{ma}} } \right) \cdot \left( {t_{\text{life}} - t} \right)f_{T} \left( t \right)} \right]}_{{}} + \int_{{t_{\text{ms,1}} + t_{\text{md}} }}^{{t_{\text{life}} }} {\left[ {\left( {t_{\text{life}} - t} \right)f_{T} \left( t \right)} \right]} , \\ \end{aligned} $$
(7)

where a1 is the monitored crack size at time tms,1 + tmd, and ama is the critical crack size requiring maintenance. The monitoring plan can be optimized by minimizing the expected maintenance delay E(tdel_m) [18, 31].

The reliability can be estimated based on the relation between the damage detection delay tdel_d and time-based safety margin tmar. The time-based safety margin tmar is the time interval between damage occurrence time and time to reach the critical crack size resulting in the structural failure. The associated state function g(t) is defined as [18, 27]

$$ g\left( {\mathbf{t}} \right) = t_{\text{mar}} - t_{{{\text{del}}\_{\text{d}}}} . $$
(8)

By treating tdel_d and tmar as random variables, the reliability Ps is estimated as

$$ P_{s} = P\left( {g\left( {\mathbf{t}} \right) \ge 0} \right). $$
(9)

The reliability index β associated with Ps is

$$ \beta = \varPhi^{ - 1} \left( {P_{s} } \right), $$
(10)

where Φ−1(·) is the inverse of the standard normal cumulative distribution function.

The service life can be extended by applying maintenance actions. According to the degree of damage detected by monitoring, the appropriate maintenance type can be determined. The service life extension is affected by the maintenance type applied to the damaged details. Therefore, the total service life extension texlife for fatigue-sensitive structures can be formulated as [18, 31]

$$ t_{\text{exlife}} = \sum\limits_{i = 1}^{{N_{\text{mon}} }} {\left[ {P\left( {t_{{{\text{ms}},i}} + t_{\text{md}} \le t_{{{\text{life}},i - 1}} } \right) \cdot \left( {\sum\limits_{j = 1}^{{N_{\text{ma}} }} {P\left( {a_{{{\text{ma}},j}} \le a_{i} < a_{{{\text{ma}},j + 1}} } \right) \cdot t_{{{\text{ex}},j}} } } \right)} \right]} , $$
(11)

where tlife,i−1 is the service life before the ith monitoring, ai is the crack size detected by the ith monitoring, ama,j is the jth maintenance type among Nma types and tex,j is the service life extension caused by the jth maintenance. Considering the uncertainties associated with the service life tlife,i−1 and service life extension tex,j in Eq. (11), the expected total service life extension E(texlife) can be used as an objective function for optimum monitoring planning.

The expected life-cycle cost Clife for monitoring planning can be formulated including the effects of monitorings, maintenance and structural failure on the life-cycle cost (see Fig. 3). The formulation of the expected life-cycle cost considering monitoring is [15]

$$ C_{\text{life}} = C_{\text{ma}} + C_{\text{fail}} + C_{\text{mon}} , $$
(12)

where Cfail is the failure cost. The maintenance cost Cma in Eq. (12) is estimated as [31]

$$ C_{\text{ma}} = \sum\limits_{i = 1}^{{N_{\text{mon}} }} {\left[ {P\left( {t_{{{\text{ms}},i}} + t_{\text{md}} \le t_{{{\text{life}},i - 1}} } \right) \cdot \left( {\sum\limits_{j = 1}^{{N_{\text{ma}} }} {P\left( {a_{{{\text{ma}},j}} \le a_{i} < a_{{{\text{ma,}}j + 1}} } \right) \cdot C_{{{\text{ma,}}j}} } } \right)} \right]} . $$
(13)

Furthermore, the monitoring cost Cmon in Eq. (12) is computed as [50]

$$ C_{\text{mon}} = \sum\limits_{i = 1}^{{N_{\text{mon}} }} {\left( {C_{{{\text{mon}}\_i}} + C_{{{\text{mon}}\_t}} \cdot t_{\text{md}} } \right)} , $$
(14)

where Cmon_i is the initial monitoring cost to install the monitoring system and Cmon_t is the monitoring cost to operate and maintain the monitoring system.

4 Multi-objective optimization and decision making

The computational procedure for the MOPT and decision-making process is illustrated in Fig. 4. When the two objectives (i.e., OA1 = maximizing the expected average availability of monitoring data \( E\left( {\bar{A}} \right) \), and OA2 = minimizing the expected monitoring cost Cmon) are used for the MOPT, the design variables are the monitoring and non-monitoring durations, tmd and tnd, respectively. The time period for monitoring planning and the monitoring cost for the prescribed time period are given. For example, the Pareto optimal solutions of the MOPT based on two objectives, OA1 and OA2, are illustrated in Fig. 5a. The solutions A1, A2, A3 and A4 in Fig. 5a are associated with \( E\left( {\bar{A}} \right) \) = 0.2, 0.4, 0.6 and 0.8, respectively. The solutions A1, A2, A3 and A4 represent the monitoring and prediction durations for a given time period, as shown in Fig. 5b. Detailed information can be found in Kim and Frangopol [22,23,26]. For MOPT formulated with the objectives considering damage occurrence and propagation prediction (i.e., OD1 = minimizing E(tdel_d), OD2 = minimizing E(tdel_m), OD3 = maximizing β, OD4 = maximizing E(texlife), and OD5 = minimizing Clife), the design variables are the monitoring starting time and monitoring duration. The number of monitorings, maintenance types and costs related to monitoring, maintenance and failure are given for the MOPT as shown in Fig. 4.

Fig. 4
figure 4

Detailed computational procedure for multi-objective optimization and decision making process

Full size image
Fig. 5
figure 5

(adapted from [25])

Pareto optimal solution set based on availability of monitoring data: a Pareto optimal solution set, b monitoring plans associated with the representative solutions A1, A2, A3 and A4

Full size image

When the MOPT is applied, there are two decision alternatives to determine the best optimal solution for monitoring planning: decision making before and after solving MOPT as shown in Fig. 4. The decision making before MOPT provides the weights of objectives, which are computed using the subjective weight determination methods such as rating and paired comparison methods. These methods depend on the subjective preference of the decision maker without information on the Pareto optimal solution set [41]. With the weights of the objectives, the multiple-objective functions are converted into a single-objective function as

$$ f_{\text{con}} = \sum\limits_{i = 1}^{{N_{\text{obj}} }} {w_{i} \cdot f_{i}^{\text{norm}} } , $$
(15)

where fcon is the converted single-objective function; Nobj is the number of objective functions; wi is the weight factor of the ith objective function; and fnormi is the ith normalized objective function. Finally, the best optimal solution for monitoring planning can be obtained by solving a single-objective optimization problem associated with the converted objective function fcon.

In the decision making after MOPT, the Pareto optimal solution set is obtained without converting the multiple objectives into a single objective. Using the dominance relation-based objective reduction approach [4], the essential objectives are identified. The essential objective set ΩES is the set with the smallest number of objectives that can result in the same Pareto optimal solutions of MOPT with the initial objective set ΩIN. Figure 6 compares the Pareto optimal sets of ΩIN = {OD1, OD2, OD3, OD4, OD5} and ΩES = {OD2, OD3, OD4}, when the number of monitorings Nmon is equal to one, and the design variable is the first monitoring starting time tms,1. The Pareto solutions of ΩIN associated with five dimensions (equal to the number of objectives for MOPT) are projected on the 3D Cartesian coordinate system consisting of E(tdel_m), β and E(texlife). As shown in Fig. 6, the Pareto optimal set of ΩIN is identical to the one of ΩES. As a result, the objectives OD2, OD3 and OD4 are the essential objectives, and OD1 and OD5 are redundant. Since there is no effect of the redundant objectives OD1 and OD5 on the Pareto optimal solutions, the weights of OD1 and OD5 are zero.

Fig. 6
figure 6

(adapted from [31])

Comparison between Pareto optimal solutions of initial and essential objective sets

Full size image

The weights of the essential objectives are computed using the objective weight determination methods (e.g., the standard deviation (SD), criteria importance through the inter-criteria correlation (CRITIC), and correlation coefficient and standard deviation (CCSD) methods). The multiple attribute decision-making approaches (e.g., the simple additive weighting (SAW), the technique for order preference by similarity to ideal solution (TOPSIS), and the elimination and choice expressing the reality (ELECTRE) methods) estimate the overall assessment values of the Pareto optimal solutions with the computed weights of the essential objectives. The best monitoring plan has the largest overall assessment values. Figure 7 shows the Pareto solutions and the three best solutions ASD, ACR and ACS, which use SD, CRITIC and CCSD methods, respectively, to determine the weights of objectives. For the formulation of the MOPT associated with Fig. 7, the design variables are monitoring starting time and duration for the given number of monitoring Nmon = 2. The overall assessment values of the three solutions ASD, ACR and ACS are estimated using the SAW method. The selected best Pareto optimal solution corresponds to the optimum monitoring plan. The details associated with Figs. 6 and 7 are described in Kim and Frangopol [31].

Fig. 7
figure 7

(adapted from [31])

Multi-attribute decision alternatives of the Pareto optimal solutions in the parallel coordinate system

Full size image

5 Use of monitoring data for damage propagation and performance prediction

Figure 1 includes the use of monitoring data for (a) initial damage propagation and structural performance prediction, and (b) updating the existing information on damage propagation and structural performance prediction after each monitoring. By using the information from monitoring (e.g., acceleration, strain, stress range and number of cycles under operational loadings) in an appropriate way, the accuracy of damage propagation and structural performance prediction can be improved effectively and, as a result, the monitoring planning computed from the presented computation platform becomes more reliable [19].

5.1 Use of monitoring data for initial damage propagation and structural performance prediction

When the initial information on damage propagation and structural performance prediction is not available, the monitoring plan can be optimized by maximizing the expected average availability of monitoring data and minimizing total monitoring cost as mentioned previously. The information obtained during the monitoring duration can be used to establish reliable damage propagation and structural performance prediction models. Accordingly, during the last two decades, various approaches to integrate the monitoring data for initial damage propagation and structural performance prediction have been developed [5, 13, 14, 14,15,18, 43,44,45,48, 56, 58].

The monitoring system can provide direct and indirect information for structural managers to predict the critical damage propagation. Through the efficient statistical and probabilistic procedures with the monitored data, the probabilistic parameters to establish the damage propagation model can be determined. For example, the embedded corrosion rate sensor provides the instantaneous rate of corrosion of the steel, which can be used to predict the corrosion damage occurrence and propagation [42, 43]. Furthermore, when the strain gauges and load cells are installed on the fatigue critical locations of a steel structure, the monitoring data over long-term period (i.e., time-history strain and stress) can be converted into the stress range and associated number of cycles. Finally, the probabilistic parameters to predict the fatigue crack initiation and propagation can be obtained [7,8,10].

The reliability, one of the representative structural performance indicators, is computed based on the state function. The general expression of the time-dependent state function is

$$ g\left( t \right) \, = R\left( t \right) \, {-}L\left( t \right), $$
(16)

where R and L are the random variables representing time-dependent resistance and load effect, respectively. Considering the types of monitored data, loading conditions and deterioration mechanisms, the state function g(t) can be modified. In terms of the monitored stress induced by live load, the state function of Eq. (16) can be expressed as [36, 37]

$$ g\left( t \right) \, = \sigma_{0} \left( t \right) \, {-} \, \left( {1 \, + e} \right) \times \sigma \left( t \right), $$
(17)

where σ0(t) is the predefined stress limit at time t; e is the measurement error in the monitored data; σ (t) is the monitored stress at time t. σ0(t) is estimated as the maximum allowable stress under live loads. The measurement error e can be assumed to be normally distributed with mean and standard deviation of zero and σe, respectively. An increase in σe can lead to an increase in the probability of failure based on Eq. (17). Kwon and Frangopol [33, 34] and Kwon et al. [35] investigated the fatigue reliability assessment based on monitoring data for bridge and ship structures, where the state function is defined as

$$ g\left( t \right) = \Delta - \left( {1 + e} \right) \cdot \frac{N}{A} \cdot S_{\text{re}}^{m} . $$
(18)

In Eq. (18), Δ is the Miner’s critical damage accumulation index, N is the number of cycles, A is the fatigue detail coefficient, Sre is the effective stress range and m is the constant. The monitoring data can provide the probabilistic information on the number of cycles N and the effective stress range Sre. Okasha et al. [46] estimated the reliability associated with the wave-induced bending moments of ship structures, where the state function is defined as

$$ g\left( t \right) = \varepsilon_{\text{R}} \cdot M\left( t \right) - \varepsilon_{\text{SW}} \cdot M_{\text{SW}} - \varepsilon_{\text{W}} \cdot \left( {M_{\text{W}} + k_{\text{d}} M_{\text{d}} } \right), $$
(19)

where M(t) is the resisting bending moment; Msw is the still water bending moment; Mw is the wave-induced bending moment; Md is the dynamic bending moment; kd is the correlation factor between Mw and Md. εR, εSW and εW are the model uncertainty factors related to the resistance determination, still water bending moment prediction and wave-induced bending moment prediction, respectively. According to Eqs. (9) and (10), the reliability Ps and reliability index β can be computed.

Through the approach provided in Kwon et al. [35], the average daily number of cycles Navg and the effective stress range Sre for a fatigue-sensitive structure can be estimated. Finally, the time-dependent reliability index for fatigue is predicted as shown in Fig. 8, where multiple locations (i.e., stations 4, 7, 10 and 13) and operation rate of 50% (i.e., α = 50%) are considered. The computational process for the fatigue reliability evaluation is illustrated in Fig. 9. Additional investigations on the fatigue reliability prediction considering various sea states and fatigue critical locations are provided in Kwon et al. [35].

Fig. 8
figure 8

(adapted from [35])

Monitoring-based fatigue reliability analysis for ship structures

Full size image
Fig. 9
figure 9

Detailed computational procedure for fatigue reliability evaluation based on monitoring data of ship structures

Full size image

5.2 Use of monitoring data to update existing damage propagation and structural performance prediction

The monitoring data can be used to update the existing probabilistic parameters associated with the damage propagation and structural performance prediction models. To incorporate the existing information with monitored data, the Bayesian theorem-based approaches have been developed. When the underlying random variable X is represented by the PDF fX(x), and the parameter θ involved in the PDF fX(x) is treated as a random variable, the parameter θ can be updated using the Bayesian theorem with the monitored data as follows [1]:

$$ f_{\varTheta }^{\prime \prime } (\theta ) = k \cdot L(\theta ) \cdot f_{\varTheta }^{\prime } (\theta ), $$
(20)

where \( f_{\varTheta }^{{\prime \prime }} (\theta ) \) is the updated PDF of the parameter θ, k is a normalizing constant, L(θ) is the likelihood function formulated with the monitored data and \( f_{\varTheta }^{{\prime }} (\theta ) \) is the initial PDF of the parameter θ. The likelihood function L(θ) with a set of the monitored data {x1, x2,…, xn} associated with X is expressed as

$$ L(\theta ) = \prod\limits_{i = 1}^{n} {f_{X} \left( {x_{i} \left| \theta \right.} \right)} . $$
(21)

With the updated PDF \( f_{\varTheta }^{{\prime \prime }} (\theta ) \) of the parameter θ, the updated PDF \( f_{X}^{{\prime \prime }} \left( x \right) \) of the underlying random variable X can be obtained as [6]

$$ f_{X}^{{\prime \prime }} \left( x \right) = \int_{ - \infty }^{\infty } {f_{X}^{{}} \left( {x\left| \theta \right.} \right) \cdot f_{\varTheta }^{{\prime \prime }} \left( \theta \right){\text{d}}\theta } . $$
(22)

When the two probabilistic parameters θ1 and θ2 for the PDF fX(x) are updated simultaneously, the updated joint PDF \( f_{\varTheta }^{{\prime \prime }} (\theta_{1} ,\theta_{2} ) \) of the parameters θ1 and θ2 can be computed as

$$ f_{\varTheta }^{{\prime \prime }} \left( {\theta_{1} ,\theta_{2} } \right) = k \cdot L\left( {\theta_{1} ,\theta_{2} } \right) \cdot f_{\varTheta }^{{\prime }} \left( {\theta_{1} ,\theta_{2} } \right). $$
(23)

The likelihood function L(θ1, θ2) in Eq. (23) is expressed as

$$ L(\theta_{1} ,\theta_{2} ) = \prod\limits_{i = 1}^{n} {f_{X} \left( {x_{i} \left| {\theta_{1} ,\theta_{2} } \right.} \right)} . $$
(24)

The updated PDF \( f_{X}^{{\prime \prime }} \left( x \right) \) of the underlying random variable X is [59]

$$ f_{X}^{{\prime \prime }} \left( x \right) = \int_{ - \infty }^{\infty } {\int_{ - \infty }^{\infty } {f_{X} \left( {x\left| {\theta_{1} ,\theta_{2} } \right.} \right) \cdot f_{\varTheta }^{{\prime \prime }} \left( {\theta_{1} ,\theta_{2} } \right){\text{d}}\theta_{1} \cdot {\text{d}}\theta_{2} } } . $$
(25)

The investigations by Okasha et al. [46, 48], Okasha and Frangopol [45] and Zhu and Frangopol [59] show the applications of monitored data for updating single or multiple parameters involved in the PDFs related to the resistance and load effect, and the effect of updating with monitored data on reliability prediction.

Furthermore, the parameters related to damage propagation model can be updated by using the Markov chain Monte Carlo (MCMC) sampling techniques. It may be difficult to compute the updated distributions of random variables by using the Bayesian theorem, because the high dimensional distribution of a model parameter requires complex integration. The MCMC techniques can generate the samples associated with the posterior distributions of the model parameters efficiently [20]. To generate the Markov chain, the cascaded Metropolis–Hastings sampling [23] and slice sampling methods [44] can be applied. The general description of the cascaded Metropolis–Hastings sampling algorithm in Hasting [23] and Rastogi et al. [51] is illustrated in Fig. 10. The required number of the samples for the cascaded Metropolis–Hastings sampling algorithm can be determined by the convergence analysis. The slice sampling can be used to verify the convergence of the samples generated from the cascaded Metropolis–Hastings method [48]. In the investigations by Soliman and Frangopol [53], Rastogi et al. [51] and Kim et al. [32], the parameters for fatigue crack propagation prediction [e.g., initial crack size a0, crack growth coefficient C and stress range Sre in Eqs. (4) and (5)] are updated with detected fatigue cracks using the cascaded Metropolis–Hastings sampling and slice sampling methods. As a result, the fatigue crack prediction is updated for service life management of fatigue-sensitive structures. Figure 11 compares the updated and prior PDFs of the material parameter C and stress range Sre, where the cascaded Metropolis–Hastings sampling algorithm is used with three detected fatigue crack sizes (i.e., adet = 1.5 mm, 2.3 mm and 3.0 mm). Based on the updated PDFs in Fig. 11, the PDFs of the time to reach the critical crack size after updating are obtained as shown in Fig. 12. The detailed information about Figs. 11 and 12 is available in Kim et al. [32].

Fig. 10
figure 10

Flowchart of Cascaded Metropolis–Hastings sampling algorithm

Full size image
Fig. 11
figure 11

(adapted from [32])

Updated PDFs of the parameters involved in fatigue crack propagation prediction: a material parameter C, b stress range Sre

Full size image
Fig. 12
figure 12

(adapted from [32])

Updated PDFs of the time to reach the critical crack size

Full size image

6 Conclusions

This paper presented a computational platform for optimum monitoring planning, which includes three main processes: (a) formulation of objectives for optimum monitoring planning; (b) MOPT and decision making; and (c) updating the damage propagation and structural performance prediction. The overall structure of the presented platform and the detailed interaction among these main processes were described with the associated theoretical backgrounds and several representative applications. Table 1 provides the summary of the approaches involved in the presented computational platform. Additional applications related to each approach are available in the associated references shown in Table 1. The following conclusions can be drawn:

  • The presented computational platform is developed to establish the optimum monitoring plan for any type of civil infrastructure (e.g., bridges, buildings and nuclear power plants) under various loading effects and deterioration mechanisms.

  • To treat the uncertainties associated with loading effects and deterioration mechanisms, the damage occurrence and propagation and structural performance are predicted probabilistically. Accordingly, the optimization for monitoring planning was formulated based on the probabilistic concepts and approaches.

  • Enhancement of the effectiveness of the presented computational platform can be achieved through (a) application of rational approaches to predict the damage occurrence and propagation, and structural performance deterioration; (b) accurate estimation of the interaction among the structural components and the structural system; (c) appropriate installation and operation of SHM systems; and (d) accurate interpretation of monitoring data.

  • The objectives used in the MOPT and decision making are formulated considering structural performance deterioration process under normal loading effects and environmental conditions. However, the presented computational platform can be extended to include the risk-based optimum monitoring planning considering abnormal loadings induced by extreme events such as earthquakes and hurricanes [2], and sensitivity analyses in a probabilistic context [12].

  • The presented computational platform may be effective for optimum monitoring planning associated with a single type of SHM system. Recently, the advanced SHM technologies (e.g., optical fiber-based SHM systems, wireless sensing and networking techniques, camera‐based SHM applications, global positioning system (GPS) techniques) have been developed and applied to various engineering structures. Considering monitoring data from multiple types of advanced SHM systems, optimum monitoring planning needs to be further investigated.

Table 1 Summary of approaches and applications associated with the presented computational platform for optimum monitoring planning
Full size table