Detecting Quantum Phase Transitions in Spin Chains

Abstract

Quantum entanglement is a unique physical property that distinguishes quantum systems from classical systems. Entanglement in spin chain models has potential application in quantum information processing. Studying quantum phase transitions of such models from the quantum information point of view is the foundation of quantum physics and an effective means in understanding and applying quantumness. This method achieves extensive research and rapid development because no a priori knowledge of symmetry of the system is needed. However, some key issues have not been effectively addressed, such as the determination of order parameters and the effectiveness and universality of each detector. Therefore, we focus on the performance of entanglement and its related quantum correlations in the characterization of quantum phase transitions under different conditions. The natural connection between quantum correlation and quantum phase transitions is mainly discussed, and a general context and the possible direction of its development are sorted out to provide help for the deep understanding of quantumness and the improvement of research methods of quantum phase transition.

1 Introduction to Quantum Entanglement

1.1 Quantum Entanglement and Quantum Phase Transitions

An essential feature that discriminates quantum mechanics from classical mechanics is quantum entanglement. Entanglement is a pure quantum phenomenon that has no classical counterpart. It describes a state of a system with multiple particles or multiple degrees of freedom that may not be written as a product of the states of its component systems [1]. In such an entangled state, the change of one particle is immediately reflected on other entangled particles, no matter how far away they are. Understanding this nonlocality that seems not limited by the speed of light has puzzled the scientific community [2,3,4]. However, the majority of experiments that have been done thus far are in favor of the nonlocality of quantum entanglement [5]. On the contrary, the fundamentally related property described by entanglement is considered an important resource in quantum information processing [6, 7]. Well-entangled states are the carriers of information; thus, the preparation of these states has always been an important issue in quantum computation and communication [8, 9]. Entanglement is the key to understanding quantum systems and future technological breakthroughs.

However, the essence of quantum entanglement still lacks a thorough understanding. Researchers are looking for the hidden variable behind entanglement and quantum theory [10,11,12,13]. Moreover, as the core of an information carrier, the stability of an entanglement state is crucial. However, decoherence in such a state remains a key to the unsolved problem in quantum information processing. The understanding of a quantum state and the control of its stability are related to quantum phase transitions’ research. Therefore, we study quantum phase transition from the perspective of quantum informatics instead of the traditional order parameter method by starting from quantum entanglement that is a representative physical quantity of quantum information theory. Quantum phase transition is also a pure quantum effect. The divergence of the correlation length is controlled by quantum correlation, which cannot be described by classical statistical mechanics. On the one hand, we can fully explore the quantum phases and phase transitions of different systems from the quantum correlation itself by studying the relationship between entanglement and quantum phase transition. On the other hand, we can deeply understand quantum entanglement and explore the origin of quantumness.

In the field of quantum information, spin chain system has always been considered the best candidate in solid state systems that carry quantum entanglement information because of its integrability and scalability in quantum communication. Any logic gate of quantum computing can be realized in such models as long as it is properly encoded [14, 15]. Many physical systems, such as nuclear spin, electron spin, molecular spin, quantum dot, and quantum optical lattice, can be modulated by spin chain models [16, 17]. Spin chain system is a natural quantum system in quantum information processing and exhibits potential application value in quantum information science. A spin chain can also be mapped to a fermion chain through Jordan-Wigner transformation [18]. Therefore, without loss of generality, we take the quasi one-dimensional system based on spin chain as the platform and quantum entanglement as the tool and object in the research of quantum phase transition and quantum cognition.

Phase transitions are widely used in our daily lives. Examples include the preparation of glass and ceramic materials and the production of austenitic and martensitic stainless steel with different flexibility and strength requirements. At present, many technological developments use phase transitions, for instance, the application of phase change materials in solar energy storage, waste heat recovery, engineering insulation, and corrosion-resistant metallic glass and the preparation of artificial superhard materials [19].

Quantum phase transitions belong to one kind of phase transition. In contrary to a thermal phase transition [20], which is driven by thermal fluctuations, a quantum phase transition occurs at absolute zero temperature. At such a temperature, thermal fluctuations are absent, and quantum effect dominates. According to Heisenberg uncertainty principle arising from the wave-particle duality in quantum mechanics, the momentum and the position of quantum particles cannot be determined precisely at the same time. These particles still possess zero-point energy even at absolute zero temperature, thereby leading to quantum fluctuations in the ground state of the system. Let us take a simple spin-1/2 system as an example. The principle of superposition indicates that any state of the system can be written as a linear combination of the spin up |↑〉 and the spin down |↓〉, i.e.,

$$\displaystyle \begin{aligned} \left\vert\psi\right\rangle=\alpha\left\vert\uparrow\right\rangle+\beta\left\vert\downarrow\right\rangle, \end{aligned} $$

(1)

where α and β are complex numbers, and they satisfy the normalization condition |α|² + |β|² = 1. The above equation shows that the arbitrary quantum state $\left \vert \psi \right \rangle$ can be regarded as a fluctuation between |↑〉 and |↓〉. A quantum phase transition is caused by such kind quantum fluctuations and a purely quantum mechanical process. In a general system, the energy spectrum of the system suffers an abrupt change when a slight change of a parameter λ near a so-called quantum critical point is added to the Hamiltonian. This scenario leads to a macroscopic change in the system’s properties, resulting in a quantum phase transition. In this work, λ is usually called the driving term. It can be a coupling constant or an external parameter, such as external magnetic or pressure.

The study of quantum phase transitions plays an important role in understanding quantum many-body systems. It not only reveals the relationship of microscopic energy spectrum and electronic structure with the macroscopic properties of materials from the viewpoint of condensed matter physics [21] but also helps us to understand quantumness deeply from the viewpoint of quantum information. A typical example of quantum phase transition is the superfluid-Mott insulator transition. It is observed experimentally in the trapped cold atoms in optical lattices by tracking the velocity distribution of runaway molecules [22]. When the potential barrier of the optical lattice is small, the cold atoms can shuttle freely in each potential well, and the system is in superfluid phase. The cold atoms are confined in the wells and cannot hop between different lattice sites when the barrier is raised above a certain threshold. The system becomes an insulator in this case [23]. In addition to the superfluid-Mott insulator transition, other examples of quantum phase transitions include the magnetic phase transitions in spin systems [24,25,26], charge density wave–superconducting phase transition in fermion systems [27, 28], and superconducting-insulator phase transition [29].

In recent decades, quantum computing and quantum communication based on quantumness have become an important research field in the frontier of science and technology with the improvement of the stability of quantum bit control and the continuous development of quantum algorithm. The discoveries of new phases of matter promoted by quantum phase transitions, such as unconventional superconductivity in a heavy-fermion system [30], and the close relationship between criticality and decoherence in the quantum computation and quantum communication [31] have greatly aroused scientists’ enthusiasm of studying quantum phase transitions.

As an analogy to thermal phase transitions, quantum phase transitions can also be understood as a result of the reconstruction in Hamiltonian’s energy spectrum [32]. In particular, the ground state or the low-lying energy spectra determines the quantum state of the system. From this point of view, the structure of the low-energy spectra changes when the driving parameter crosses the critical point, leading to a different quantum phase with quite different macroscopic properties. According to the reconstruction mechanisms, quantum phase transitions can be divided into different types and are incarnated in the nonanalytic behavior of the derivative of the ground-state properties at the transition point. The first type is the first-order phase transition corresponding to a level crossing in the ground state, in which the first derivative of the ground-state energy with respect to the driving parameter is usually discontinuous. The second one is the continuous phase transition, including the second-order and higher-order types, in which the energy levels of the ground state and the first excited state become infinitely close to one another with the increase of the system size. However, the occurrence of interlacing is always avoided. This type of phase transition usually corresponds to a low-lying excited state reconstruction and possesses discontinuity in an order higher than one in the derivative of the ground-state energy [33]. Figure 1 shows the illustration of the two cases [21].

Fig. 1

(a) When the energy levels of the ground state and the excited state intersect at a certain point in the parameter space, the properties of the ground state of the system change; (b) the situation in which the energy levels of the ground state and the excited state avoid the intersection

1.2 Methodologies from the Viewpoint of Quantum Information Theory

The traditional method for studying quantum phase transitions belongs to the category of Landau–Ginzburg–Wilson spontaneous symmetry-breaking theory. Researchers use local order parameters to characterize different quantum phases. However, quantum phase transitions, such as the topological phase transitions [34, 35] and Berezinskii-Kosterlitz-Thouless phase transitions [36], occur between phases that are not characterized by any local order parameter or symmetry-breaking description. Moreover, conducting a complete phase diagram analysis for a multistate system is usually difficult because each quantum state needs a specific characteristic order. Obtaining all possible orders of the system is a challenge, particularly for systems with unknown symmetry. Therefore, the traditional research on the quantum phase of multibody system has made slow progress for a long time.

The new method to study quantum phase transitions from the perspectives of quantum information begins from Ref. [31], where the entanglement concept from quantum information theory is originally borrowed to study quantum phase transitions in condensed matter physics. The authors determined the close relationship between quantum phase transition and entanglement through the scale analysis of entanglement near the critical point of the system. In this approach, no a priori knowledge of the symmetry of a system is needed, and the phase diagram of the system is obtained by studying this single quantity. The simplicity and effectiveness of this method have attracted a wide range of research enthusiasm. Along this direction, the research of quantum phase transition has made rapid and long-term development. Subsequently, many new concepts borrowed from quantum information theory have been successfully used to characterize quantum phase transition.

These concepts mainly include quantum entanglement [31], quantum fidelity (QF) [37], quantum discord (QD) [38], and quantum coherence (QC) based on Wigner and Yanase skewed information [39]. Quantum entanglement approach including the use of various measures, such as concurrence, von Neumann entropy, and negativity [40, 41], has been successfully applied to various systems, including interacting spin models [42], fermion models [38], and Bose Hubbard model [43]. This approach has been recently used to calibrate the superconducting phase and metal phase of one-dimensional fermion wire [44]. The connection between geometric Berry phase and quantum phase transitions for the case of a spin-XY  model has also been studied [45]. Quan et al. showed a remarkable relationship between Loschmidt echo and quantum phase transitions [37, 46]. Based on this finding, a simple quantity QF and its related fidelity susceptibility [26, 47] have been successfully applied to different types of quantum phase transitions, such as topological type [48, 49], and verified experimentally by a nuclear magnetic resonance quantum simulator [50]. Time correlations, Leggett-Garg inequalities, and Loschmidt echo have also been recently introduced into the study of static quantum phase transition and time domain dynamic quantum phase transition in multibody quantum systems [51, 52].

1.3 Open Questions

Although each of the above-mentioned quantum phase transition detectors has its successful examples, it also has limitations. The effectiveness and universality of these examples are not fully analyzed. Although fidelity reflects the quantum phase transition of Bose Hubbard model more clearly than quantum entanglement [43], it is ineffective in detecting Berezinskii-Kosterlitz-Thouless (BKT) quantum phase transition, such as the XXZ model [25], and QD can effectively describe this phase transition [38]. Our recent research determined that QC cannot only effectively detect such a BKT type quantum phase transition but also avoid the singularity of QD in nonquantum-critical points [53]. Determining whether QC is a more generic indicator for quantum phase transition than QD needs further exploration.

Moreover, absolute zero cannot be achieved in reality. Thus, the study of quantum phase transition at finite temperature has a high experimental value. However, research in this field is still insufficient. We showed that quantum entanglement and its temperature scaling behavior can be used to detect the quantum critical point of a spin system [42]. Similar works have also been done in Refs. [54, 55]. However, temperature has a great influence on the entanglement detection of quantum phase transition, and the influence degree can vary different for different detectors. For example, QD is more robust to thermal fluctuations than quantum entanglement [38]. Recent finding has indicated that QC spectrum is more robust to thermal fluctuations than QD and QC, and it is expected to be a powerful tool to detect quantum phase transitions [53]. The response to thermal fluctuations or the expression intensity of the quantum properties of the detected quantum states directly affects the ability of each detector to characterize the phase transition at finite temperature. The research in this area is still immature and lacks comprehensive and systematic analysis.

Although quantum information measures can clearly demarcate the quantum phase boundary, they cannot directly reveal the information of the order parameter for each of the quantum phases of the system. This scenario hinders us from understanding further the specific properties of quantum states. Therefore, developing a method to derive the order parameters from the same perspective of quantum information is urgently needed. The order parameters for some simple spin and fermion systems were constructed starting from the mutual information involved in entanglement and correlation through the spectral analysis of the reduced density matrix [56,57,58]. Magnifico et al. have further applied recently the order parameter we obtained to characterize the quantum phase transition in the topological Schwinger model [59]. This method is still in its infancy. Further investigations on its applicability to characterize different types of quantum phase transitions, such as those that involve low-lying excited energy levels or different topological phases, are required.

Quantum phase transitions and quantum entanglement have a close connection. Although open questions exist, quantum entanglement is an effective and promising method to reveal quantum phase transitions from the perspective of quantum correlations. Therefore, we try to establish a possible connection among various correlation detectors and quantum phase transition. We hope that this work will help to find an effective and universal quantum phase transition detector and improve and perfect the research method of quantum phase transition. Furthermore, we also hope that it will enlighten the understanding of the nature of quantumness and contribute in bridging condensed matter physics and quantum information science.

2 Concurrence and Quantum Phase Transitions in Spin Chains

Entanglement, which is absent in classical systems, is regarded as a purely quantum correlation. It serves as the resource to enable quantum computation and quantum communication and thus plays a core role in quantum informatics [8]. It can also be a good detector for quantum phase transitions in multibody system. The main idea is that the quantum phase transition changes the quantum correlation of the system, and the degree of entanglement inside the system is also changed, resulting in the extreme value of the quantum entanglement or its derivative near the phase transition point.

In 2002, Osterloh et al. studied the entanglement behavior near the critical point of XY  spin chain by using concurrence measure. The Hamiltonian of the XY  model reads

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} H& =&\displaystyle -\sum_{j=1}^N\left(\frac{1+\gamma}{2}\sigma_j^x\sigma_{j+1}^x+\frac{1-\gamma}{2}\sigma_j^y\sigma_{j+1}^y+ \lambda\sigma_j^z\right), \end{array} \end{aligned} $$

(2)

where the parameter N is the number of spins in the chain, γ describes the anisotropy of the system arising from the spin–spin interaction, λ is external magnetic field, σ^α (α = x, y, z) are the Pauli matrices. When γ = 1, the Hamiltonian corresponds to the transverse-field Ising model.

For a given local reduced density matrix $\rho _{ab}=Tr_{ab}\left \vert \psi \right \rangle \left \langle \psi \right \vert$, where Tr_ab stands for tracing the overall sites except the two arbitrary sites a and b in the chain, the quantum concurrence is defined as $C_{\rho _{ab}}=\max \{0,\lambda _1-\lambda _2-\lambda _3-\lambda _4\}$, where λ₁, λ₂, λ₃, and λ₄ are the square roots of the eigenvalues of $\rho _{ab}\tilde {\rho }_{ab}$ in descending order. Here, $\tilde {\rho }_{ab}=(\sigma _a^y\otimes \sigma _b^y)\rho _{ab}^\ast (\sigma _a^y\otimes \sigma _b^y)$ is the time-reversed matrix of ρ_ab. $\rho _{ab}^\ast$ is the complex conjugation of ρ_ab.

The authors found by analyzing the behaviors of the concurrence in the vicinity of the transition that the first derivative of concurrence with respect to λ shows a minimum at λ_m near the critical point. The minimum becomes increasingly considerable, and its position gradually approaches the true critical value λ_c = 1 as N increases. Although the concurrence itself does not show a singular behavior at the critical point, its first-order derivative is divergent in the thermodynamic limit. Similar phenomena were also observed for other critical points in the system. These results supplied direct evidences for the validity of concurrence in quantum phase transition detection.

The relationship between concurrence and quantum phase transitions is further studied in Refs. [60, 61]. At the quantum phase transition point Δ = 1 of the spin XXZ chain model, the ground-state concurrence shows a maximum behavior instead of the singularity behavior for the XY  model in Ref. [31]. This conclusion is also suitable for the dimensionality d ≥ 2 cases [61]. Different behaviors of quantum phase transition for different systems seem to indicate a certain nontrivial relationship between quantum concurrence behavior and phase transition types. Further study evidently is needed.

The types of the quantum phase transitions in several well-known spin systems were clarified by comparing the analyses of low-lying excited state spectra and quantum entanglement behaviors [33]. The different behaviors of the corresponding quantum concurrence were explained, and the relationship between quantum entanglement and phase transition types was tried to be established. According to the continuity and extremum of quantum concurrence, quantum phase transitions can be divided into three categories: The first one is the first-order quantum phase transition, which is caused by the level crossing of the ground state. The concurrence as a measure of ground-state entanglement information shows discontinuous behavior because of the change of ground state at the phase transition point. The second type is the case in which both sides of the corresponding phase transition point are in order or disorder usually because of the level crossing in low excited states, leading to a maximum behavior of the concurrence. The third kind of quantum phase transition corresponds to the transition from order to disorder with an energy gap opening, where the concurrence is continuous, but its high-order derivative shows extremum at the phase transition point. This work reveals that quantum entanglement and quantum phase transition are not only related to the ground state of the system but also affected by the excited states. Their relationship can be reflected by the behaviors of concurrence.

Concurrence can reflect the quantum phase transition of a system by measuring the entanglement between the two spins embedded in the system. However, some quantum information related to multiparticles is not reflected completely by concurrence because of the limitation of the definition itself. In particular, the quantum information in the two local spins may be too limited to reflect the quantum information of the whole system. For example, compared with physical quantities, such as the von Newman entropy and QD, the concurrence as a measure of entanglement eventually loses the ability to detect quantum phase transition with temperature disturbance [38, 62].

3 von Neumann Entropy and Quantum Phase Transitions

3.1 Single-Site Entanglement

Gu et al. introduced a different entanglement measure, namely von Neumann entropy, to study the quantum phase transition of the one-dimensional extended Hubbard model [40]. The corresponding Hamiltonian of the model reads

$$\displaystyle \begin{aligned} \begin{array}{rcl} H=& &\displaystyle \sum_{i,\sigma}\left(c^{\dag}_{i,\sigma}c_{i+1,\sigma}+c^{\dag}_{i+1,\sigma}c_{i,\sigma}\right)+ U\sum_in_{i\uparrow}n_{i\downarrow}+V\sum_in_in_{i+1},{} \end{array} \end{aligned} $$

(3)

where i = 1, …, N; $\sigma =\uparrow ,\downarrow ; c^{\dag }_{i,\sigma }$ and n_i are the creation and number operators at site i, respectively; U and V  define the on-site and the nearest-neighbor Coulomb interactions. The von Neumann entropy for a single site is then defined by the ground-state $\left \vert \psi \right \rangle$ of the system as

$$\displaystyle \begin{aligned} \begin{array}{rcl} E_{v}(\rho_{j}) =-Tr{\rho_{j}}{\mathrm{ln}}{\rho_{j},}{} \end{array} \end{aligned} $$

(4)

where ρ_j is the reduced density matrix of the ground state for the jth site. The authors calculated the one-site entropy E_v as functions of U and V . They determined that the extreme point of the von Neumann entropy corresponds to the phase transition point of the system, and the ground-state phase diagram of the system can be easily captured by the single quantity.

3.2 Multisite Entanglement

The success of the entanglement method has attracted researchers’ attention. Legeza et al. found that the one-site von Neumann entropy is not suitable for some quantum phase transitions, such as the phase transitions between the dimerized state, Haldane state, quantum spin-nematic state in spin-1 spin chain, the Ising-like phase transition, and BKT phase transition in the ionic Hubbard model. Therefore, they proposed to use two-site entropy, namely the reduced density matrix in Eq. (4) is taken for two neighboring sites instead of for one single site, to study the quantum phase transition. They found that compared with the single-site entanglement, the two-site entanglement entropy better reflects many phase transitions that cannot be recognized by the single-site entanglement entropy [41]. The phase information of the one-dimensional isotropic spin-1 chain presented by the two-site entropy is better than that presented by one-site entropy.

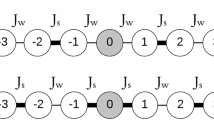
The block–block entanglement measured by the von Neumann entropy was also studied based on the above findings; its structure is richer than that of the local site entanglement for the one-dimensional extended Hubbard model because the nonlocal correlation is included [63]. Multisite entropy was also used to analyze quantum phase transitions in the frustrated spin ladder with next-nearest-neighbor (NNN) interactions [64]. The system is sketched in Fig. 2. Its Hamiltonian reads

$$\displaystyle \begin{aligned} H=\sum^{N}_{\alpha=1,2,i}\left[\left(J_1{\mathbf{S}}_{\alpha,i}\cdot{\mathbf{S}}_{\alpha,i+1}+J_2 {\mathbf{S}}_{\alpha,i}\cdot{\mathbf{S}}_{\alpha,i+2}\right)+ J_\perp{\mathbf{S}}_{1,i}\cdot{\mathbf{S}}_{2,i}+ J_\times\left({\mathbf{S}}_{1,i}\cdot{\mathbf{S}}_{2,i+1}+{\mathbf{S}}_{1,i+1}\cdot{\mathbf{S}}_{2,i}\right)\right], {} \end{aligned} $$

(5)

where S_α,i denotes spin-1/2 operators at site i of the α^th leg of the ladder, and N is the number of rungs; the other parameters J₁, J₂, J_⊥, and J_× correspond to the interactions between different spins, as indicated in Fig. 2.

Fig. 2

(Color online) Schematic diagram of the two-leg spin-1/2 ladder with diagonal and in-chain NNN interactions. Circles denote spin-1/2 sites coupled by exchange constants J₁ (black solid lines), J₂ (blue dashed lines), J_⊥ (red solid lines), and J_× (green dashed lines). The wine-pane L represents the four spins at the middle of the chain, and the dashed-pane R circles the four spins at its right side, where α = 1, …, 6 denotes the number of spins on L and R

Given the spin alignment frustration, materials with the spin-ladder structure exhibit rich quantum states, and many of them are still not fully understood. A good example is the highly controversial intermediated columnar dimer (CD) state in the frustrated antiferromagnetic state. The introduction of the in-chain NNN interaction further increases frustration among spins and may induce new quantum phases of great interest. Such in-chain NNN interaction does exist in real materials, e.g., BiCu₂PO₆ [65]. Therefore, studying the quantum phase diagram of the spin ladder with the in-chain NNN interaction is necessary and insightful. In such a system, the four-site entropy E₄_L (the subscript represents the four spins in the middle of the chain, as circled by the wine square marked L in Fig. 2) contains richer quantum information than the two-site entropy E₁₃ does because of the symmetry of the system. As shown in Fig. 3, E₄_L presents a clearer indication than E₁₃ does at the phase boundary of II and III. The controversial CD phase was confirmed by analyzing the four-site entropy combined with the correlation function, and an exotic tetramer phase was found. Finally, the quantum phase diagram of the system was obtained [64].

Fig. 3

E₄_L and E₁₃ as a function of J_× at J₂ = 0.4, J₁ = −1.0, and J_⊥ = −0.5 for rung number N=320. Dramatic changes in E₄_L show a clearer indicator than those in E₁₃ do in delimiting the three phases I, II, and III

In addition, two difficult issues related to quantum phase transition were solved using quantum entanglement: (I) the BKT type critical point at J₂∕J₁ ≈ 0.241 in the J₁ − J₂ model, which corresponds to a transition from spin fluid to dimerized phase and is difficult to be detected because of the problem of logarithmic correction [24, 66]; (II) the controversy—whether the bond-order-wave (BOW) state at a narrow strip along the U ≃ 2V  line exists in the half-filled one-dimensional extended Hubbard model [67].The BKT phase transition in the J₁ − J₂ model [68] and the intermediated BOW and superconducting states in the half-filled one-dimensional extended Hubbard model were successfully detected with the help of the two-site and block-site entanglement measured by von Neumann entropy and density matrix renormalization group (DMRG) numerical technique [63, 69].

Given that the local entanglement can be conveniently obtained by the exact diagonalization or density matrix renormalization group algorithms, the method can be applied to much complex systems that cannot be exactly solved. Many related studies on entanglement and phase transition of different quantum systems under different conditions can be performed [9].

Furthermore, the entanglement spectrum can also be used to study quantum phase transitions. Compared with the entanglement entropy, which is just a single number, entanglement spectrum can reveal much more information on quantum phase transition [70]. Some related works on different types of quantum phases can be found in Refs. [71,72,73].

The concurrence and the von Neumann entropy are the two main entanglement measures used in detecting quantum phase transitions. Although both of them can measure the degree of entanglement, they possess different physical natures. The concurrence describes the entanglement between the two sites constructing the reduced density matrix, whereas von Neumann entropy measures the entanglement of states on the selected sites with that on the remaining sites in the chain. The concurrence and the von Neumann entropy actually reflect different entanglement information in the system. Different abilities can detect quantum phase transitions for different detectors [62]. The main reason might be that the detectors actually contain different degrees of correlation. Further discussion about this topic is provided in Sects. 3.4 and 4.

3.3 Entanglement and Quantum Phase Transitions at Finite Temperatures

When the temperature is not too high to destroy the quantum order, the system is still dominated by quantumness, and quantum phase transitions still exist. The study on quantum phase transition at finite temperature has a high experimental value because absolute zero cannot be achieved in an actual experiment. However, related research in this field is sparse. The transfer matrix renormalization group (TMRG) technique [74], which is based on the Trotter-Suzuki decomposition of the partition function of a system and can directly handle infinite chains, is used in calculating the two-site thermal entanglement of the S = 1∕2 distorted diamond chain model to avoid the finite-size effect [42]. The model is sketched in Fig. 4. Its Hamiltonian is written as follows:

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \ H& =&\displaystyle \sum^{N}_{i=1}(J_1(\boldsymbol{S}_{2i-1}\cdot\boldsymbol{S}_{2i,a}+ \boldsymbol{S}_{2i,b}\cdot\boldsymbol{S}_{2i+1})\\ & &\displaystyle +J_2(\boldsymbol{S}_{2i-1}\cdot\boldsymbol{S}_{2i,b}+\ \boldsymbol{S}_{2i,a}\cdot\boldsymbol{S}_{2i+1})+ \ J_3\boldsymbol{S}_{2i,a}\cdot\boldsymbol{S}_{2i,b}, {} \end{array} \end{aligned} $$

(6)

where S_i are spin-1/2 operators at site i , and J_i with i = 1, 2, 3 denote exchange integrals along different directions.

Fig. 4

(Color online) Schematic diagram of the spin-half distorted diamond chain model, where the black circle represents the spin. J₁ (black solid lines), J₂ (green dashed lines), and J₃ (red dashed lines) indicate the exchange constants between spins

The definition of the thermal entanglement E_t is the same as that in Eq. (4), but the reduced density matrix is obtained from the thermodynamical average values of some correlation functions (see Ref. [42]). The results are shown in Fig. 5 for J₂ = J₁ antiferromagnetic spin frustrated case. As temperature T decreases, two dramatic changes appear near the two critical points J₃ = 1.0 and J₃ = 2.0 for T = 0.67, as shown in Fig. 5a. The derivative of E_t peaks near the two critical points, and the peak is pronounced as T decreases, as shown in Fig. 5b. The scaling behavior for the peak illustrates that it diverges at zero temperature [42]. The peak behavior of E_t reflects the quantum phase transition of the system at finite temperature. Therefore, we conclude that detecting quantum phase transitions at finite temperature by entanglement is possible and provides theoretical guidance for the experimental study of quantum phase transition.

Fig. 5

(Color online) (a) The thermal entanglement E_t for the antiferromagnetic case as a function of J₃ at J₁ = J₂ = 1.0 and T = 0.067. (b) The derivative of E_t with respect to J₃ under different values of M, where M is the Trotter number in the TMRG calculation, and T = 1∕(Mε) with ε = 0.1

3.4 Entanglement and Quantum Correlations

The essence of entanglement is a kind of quantum correlation, which plays a role in detecting quantum phase transition. However, it does not include all types of quantum correlations, and some quantum states have quantum correlations without quantum entanglement. For example, the authors pointed out that quantum correlations still exist in separable mixed states where the entanglement is absent [75]. Entanglement may fail to detect the quantum phase transitions in such a system [25, 38]. Correlation among different parts of a system is the main information to obtain in many-body physics and is believed to play a key role in quantum phase transitions detection. From this point of view, a quantity that can measure a larger amount of quantum correlation of a state may present an excellent performance.

An alternative measure of quantum correlations is the QD. The existing results showed that QD can detect the quantum correlations present in certain separable mixed states [76, 77] and may be responsible for the speeding up of a mix-state-based quantum computation [78, 79]. The related researches confirmed its advantage in detecting quantum phase transitions: QD can be more robust against temperature and shows more detailed information than entanglement does [38, 80]. The main reason could be that QD reflects the changes of quantum correlation in which entanglement is absent in such quantum phase transitions. In Refs. [83], the authors established the hierarchical relationship of different manifestations of quantum correlations on the basis of quantum relative entropy. Three kinds of quantum correlations measured by quantum entanglement, QD, and QC are mainly considered. The authors confirmed the above viewpoint and further determined that the amount of information contained in QC, QD, and entanglement decreases in turn. Given that QC contains the most correlation information, it can seem to be the best in detecting quantum phase transitions. Therefore, compared with the potential advantages of quantum entanglement, the potential advantages of QD and QC on quantum phase transition detections are focused in the later parts.

4 Quantum Discord, Quantum Coherence, and Quantum Phase Transitions

4.1 Quantum Discord

Introduced by Ollivier and Zurek [76], QD presents an alternative measure of quantum correlations. Given its application prospect in mixed state quantum computing, much attention has been focused on the properties of QD [81]. The relation between QD and quantum phase transition is an important aspect. One important finding is that QD is more robust against thermal fluctuations than entanglement is, and it can detect quantum phase transitions at finite temperatures [38].

The quantum discord is related to mutual information. Two equivalent mutual information expressions, I(ρ_ab) and ${\mathcal {C}(\rho _{ab})}$, exist in classical information theory to describe the correlation between two arbitrary parts, a and b. However, they become unequal when the quantum nature dominates, and the minimum of their difference is called QD [76]:

$$\displaystyle \begin{aligned} \begin{array}{rcl} D(\rho_{ab})=I(\rho_{ab})-\mathcal{C}(\rho_{ab}){} \end{array} \end{aligned} $$

(7)

with

$$\displaystyle \begin{aligned} \begin{array}{rcl} I(\rho_{ab})& =S(\rho_{a})+S(\rho_b)-S(\rho_{ab}),{} \end{array} \end{aligned} $$

(8)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathcal{C}(\rho_{ab}) & =S(\rho_{a})-\min_{\{b_k\}}\widetilde{S}(\rho_{ab}\vert\{b_k\}),{} \end{array} \end{aligned} $$

(9)

where S(ρ) is von Neumann entropy and ${\widetilde {S}(\rho _{ab}\vert \{b_k\})}$ is the conditional entropy and can be written as

$$\displaystyle \begin{aligned} \begin{array}{rcl} \widetilde{S}(\rho_{ab}\vert\{b_k\})=\sum_kp_kS(\rho_{ab}^k),{} \end{array} \end{aligned} $$

(10)

with ${\rho _{ab}^k=\frac {1}{p_k}\left (I\otimes b_k\right )\rho _{ab}\left (I\otimes b_k\right )}$ and p_k = Tr $\left [\left (I\otimes b_k\right )\rho _{ab}\left (I\otimes b_k\right )\right ]$. The minimum in Eq. (9) is achieved from a complete set of projective measures $\left \{b_k\right \}$ on site b. With the spin system as an example, the projectors in Eq. (10) can be written as

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} b_k=V\left\vert k\right\rangle\left\langle k\right\vert V^\dagger, \end{array} \end{aligned} $$

(11)

where $\{\left \vert k\right \rangle \}$ is the standard basis $\{\left \vert \uparrow \right \rangle ,\left \vert \downarrow \right \rangle \}$ of any two selected spins, and the transform matrix V  is parameterized as [81]

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} V=\left( \begin{array}{cccc} \cos\theta & \sin\theta e^{-i\varphi} \\ \sin\theta e^{i\varphi} & -\cos\theta \\ \end{array} \right). \end{array} \end{aligned} $$

(12)

Then, the minimum of condition entropy $\widetilde {S}(\rho _{r})$ only depends on θ and φ (traversing from 0 to π). We can determine from the definition that I(ρ_ab) should be the total correlation, and ${\mathcal {C}(\rho _{ab})}$ corresponds to the classical correlation. The QD reflects the quantum part included in the mutual information [38, 81].

The entanglement of formation (EOF) is a monotonically increasing function of the concurrence $C_{\rho _{ab}}$ defined in Sect. 2. It can be written as follows [38]:

$$\displaystyle \begin{aligned} EOF(\rho_{ab})=-f(C_{\rho_{ab}})\mathrm{log}_2f(C_{\rho_{ab}}) -\left[1-f(C_{\rho_{ab}})\right]\mathrm{log}_2\left[1-f(C_{\rho_{ab}})\right],\end{aligned} $$

(13)

where $f\left (C_{\rho _{ab}}\right )=(1+\sqrt {1-C_{\rho _{ab}}^2})/2$. It satisfies the criteria for entanglement monotone. Thus, we use it as a measure of entanglement instead of the concurrence itself.

In Ref. [38], one-dimensional spin XXZ model is used as an example model to demonstrate well the advantages of QD in quantum phase transition detection. The Hamiltonian of the model reads as

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} H_{XXZ}=\sum_j^N\sigma _{j}^{x}\sigma _{j+1}^{x}+\sigma _{j}^{y}\sigma _{j+1}^{y}+\Delta \sigma _{j}^{z}\sigma _{j+1}^{z}\,, \end{array} \end{aligned} $$

(14)

where N is the number of spins in the chain, Δ describes the anisotropy of the system arising from the spin–spin interactions, and $\sigma ^x_j$, $\sigma ^y_j$, and $\sigma ^z_j$ are the usual Pauli matrices of the j-th spin. This model has two critical points at zero temperature: an infinite-order phase transition at Δ = 1 and a first-order transition caused by the level crossing of ground state at Δ = −1 [82]. The continuous critical point at Δ = 1 is hardly detected by most detectors, such as the fidelity and the entanglement entropy [25, 53]. However, QD presents a clear signature for this critical point.

The advantages of QD in detecting quantum critical phenomena, particularly at finite temperatures, were further explored in the XY  spin chain model in a transverse field with three-spin interaction (XYT) [80]. The Hamiltonian is given by

$$\displaystyle \begin{aligned} H=&-\sum_{j=1}^N\left(\frac{1+\gamma}{2}\sigma_j^x\sigma_{j+1}^x+\frac{1-\gamma}{2}\sigma_j^y\sigma_{j+1}^y+ \lambda\sigma_j^z\right) &-\sum_{j=1}^N\alpha\left(\sigma_{j-1}^x\sigma_j^z\sigma_{j+1}^x+\sigma_{j-1}^y\sigma_j^z\sigma_{j+1}^y\right), \end{aligned} $$

(15)

where N is the number of spins in the chain, γ describes the anisotropy of the system arising from the spin-spin interaction, λ is the external magnetic field, and α denotes the three-spin interaction.

This system can be diagonalized in momentum space by introducing Jordan-Wigner transformation. Thus, it is a good experimental model. The capabilities of QD and entanglement in detecting quantum phase transitions at both zero and finite temperatures were analyzed. The pairwise QD of two neighboring spins is more reliable than entanglement in identifying quantum phase transitions. We obtained the quantum phase diagram of the system by the derivative of QD and further confirmed the robustness of QD against thermal fluctuations compared with entanglement (see Fig. 6). At T = 0, the vanishing EOF clearly detects the critical points at α = ±0.5. However, the EOF deviates from the critical points as T increases and tends to zero in the whole parameter region when T is larger than 1.0, as shown in Fig. 6a. Entanglement cannot detect the quantum phase transition when thermal fluctuation is added. On the contrary, even when T is as high as 2.0, QD is not zero (see Fig. 6b), and the peak structure of its derivative still points to the position of the phase transition point. Therefore, QD is more robust than quantum entanglement in resisting thermal disturbance and can be used to detect quantum phase transition at finite temperature. The advantage of QD in quantum phase transition detection fits the conclusion in Refs. [83] that QD contains more quantum correlation than entanglement.

Fig. 6

(Color online) (Left) EOF and (Right) QD as functions of λ and T for γ = 0.5 and λ = 0.0 at N = 2001

4.2 Quantum Coherence and Quantum Coherence Spectrum

Based on Wigner and Yanase skew information (WYSI), the simplified alternative version of K-coherence of a quantum state can be written as [84, 85]

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} I^L(\rho,K)=-\frac{1}{4}Tr\left[[{\rho},K]^2 \right], \end{array} \end{aligned} $$

(16)

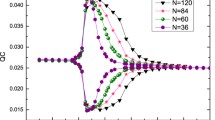
where ρ is the density matrix of a quantum state, K is an observable, and […] denotes the commutator. This definition satisfies all the criteria for coherence monotones and can be used as an efficient measure to quantify QC [84]. For a subsystem with two sites, A and B, if we choose A as the observable, then K is written as $K_A\bigotimes I_B$. Thus, I^L(ρ, K) is written as $I^L_{AB}(\rho _{AB},K_A\bigotimes I_B)$, which quantifies the QC between A and B. The effectiveness of the WYSI-based QC and its derivatives in detecting different types of quantum phase transitions is carefully analyzed based on the one-dimensional Hubbard model, XY spin model, and Su-Schrieffer-Heeger (SSH) model. QC is more robust than quantum entanglement in resisting thermal fluctuation. It can effectively characterize quantum phase transitions of the system at a relatively high temperature, where entanglement is not competent anymore. The main results are as follows. First, QC clearly shows the existence of the BOW state of the one-dimensional extended Hubbard model (see Eq. (3) for the Hamiltonian), which is not detected easily by entanglement [40] and fidelity [62]. QC results as a function of V  at U = 2.0 under different system sizes N, plotted in Fig. 7. For a given N, an obvious difference exists between the two neighboring two-site QDs, namely $I^L_{i,i+1}$ for i = N∕2 and i = N∕2 + 1. The difference becomes clear as N increases and does not disappear in the thermodynamic limit. This scenario corresponds to the BOW state that possesses the dimerized property (details see Ref. [62]). Second, QC shows the same effectiveness as QD in detecting quantum phase transition at finite temperatures, where the entanglement becomes incapable (see Fig. 8). The thermal fluctuation weakens the EOF when the temperature is added. For example, when T = 0.5, the turning point from zero to nonzero shifts away from the critical point at α = 0.5. EOF becomes zero in the whole parameter range when the temperature T increases to 1.0. EOF cannot reflect the continuous quantum phase transition at α = 0.5 of the XY  spin model in a transverse field with three-spin interaction (see Eq. 14 for its Hamiltonian). However, QC shows similar effectiveness as QD under such condition: the increment with α for them shows a turning point at the critical point α = 0.5 (see Fig. 8b,c for T = 0.5), and their derivative can still reflect the quantum phase transition even at a relative high temperature T = 1.2, as shown in Fig. 8d,e.

Fig. 7

(Color online) QC for neighboring two sites i = N∕2 and i = N∕2 + 1 of the extended Hubbard model at U = 2.0 under different system sizes N

Fig. 8

(Color online) (a) The EOF, (b) QD, and (c) QC as a function of α under specific temperatures at λ = 0.0 and γ = 0.5 with N = 1001 for the XYT model. (d) and (e) show the derivative of QD and QC, respectively, with respect to α at T = 1.2. The dashed line on the left panel indicates the turning point at α = 0.4 for EOF under T = 0.5

QC is indeed more prominent than entanglement in detecting quantum phase transitions. However, its performance is not better than QD. Moreover, it cannot detect the BKT type critical point of the XXZ model. Given the correlation information theory proposed in Ref. [83] and as mentioned in Sect. 3.4 that QC contains the most amount of correlation information compared to quantum discord and entanglement, we attempt to reveal further its internal relationship with quantum phase transitions. We showed its advantages in characterizing quantum phase transitions by analyzing the spectrum of QC [53].

The definition of QC in Eq. (16) is a single number. Some information may be covered up by neutralization in the process of summation. Therefore, we turned to the basic source of information, that is, its construction spectrum. We defined two quantities to determine the change of information in each coherence energy level and reflect the distribution property of the spectrum. The two quantities, namely coherence entropy S_QC and logarithm of the spectrum L_QC, are as follows:

$$\displaystyle \begin{aligned} \begin{array}{rcl} & S_{QC}=-\sum_{n=1}^4\alpha_n {\mathrm{ln}} \alpha_n,{} \end{array} \end{aligned} $$

(17)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & L_{QC}=-\sum_{n=1}^4 {\mathrm{ln}} \alpha_n,{} \end{array} \end{aligned} $$

(18)

where α_n with n = 1, 2, 3, and 4 is the four eigenvalues of I in Eq. (16), which consists of the four components in its spectrum.

Using the TMRG technique, we calculated the QD for the infinite XXZ spin chain, and the analytical method was used to deal with the XY and Ising models. The results for the XXZ model are shown in Fig. 9. The BKT type critical point at Δ = 1 is clearly detected by the sharp peaks of L_QC at different temperatures, whereas QD (considered the only effective detector for this critical point at present) tends to zero at a relatively high temperature. The two critical points are also characterized by the minimum point in S_QC (see Ref. [53]). Compared with QC, which is a single number, coherent spectrum contains complete coherent information. L_QC here acquires the disappearance of coherence information in some specific coherence energy levels by analyzing the spectrum. S_QC possesses the form of information entropy. It reflects the distribution property of the coherence spectrum and presents more considerable correlation information than QC itself. The conclusion is also suitable for the quantum phase transitions in the XY  and the topological-type quantum phase transition in the spin Kitaev models [53].

Fig. 9

(Color online) (a) QD and (b) L_QC as functions of Δ under different temperature T. QD tends to zero, and its cusp signature of CP disappears at a relative high T. (Reproduced from Ref. [53])

However, S_QC for the one-dimensional spin Kitaev model does not seem to be as robust against temperature as that for the other quantum phase transitions. The Hamiltonian of this model is as follows:

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} H=& \sum_{j}^N\left(J_1\sigma^x_{2j-1}\sigma^x_{2j}+J_{2}\sigma^y_{2j}\sigma^y_{2j+1}\right), \end{array} \end{aligned} $$

(19)

where J₁ and J₂ describe the spin–spin interactions alternatively along the chain. A topological critical point occurs at J₂∕J₁ = 1.0 in this model [86]. The peak moves away from the critical point at a low temperature T = 0.25. The weak robustness may come from the detector or the detected quantum state itself. The phase transition at J₂ = 1.0 here belongs to the topological type. No symmetry-breaking behaviors occur for such phase transition; thus, it cannot be characterized by a local order parameter [21, 34, 86]. Therefore, we considered that the weak robustness probably comes from the weak ability against thermal fluctuations of the state itself. This conclusion was verified by the specific heat result. The thermal excitation peak in the specific heat for Kitaev model is considerably lower than that in XXZ model, representing an easily destroyed quantum order by thermal fluctuation in Kitaev model. Therefore, the relatively weak robustness against the temperature behavior of S_QC for the Kitaev model should not be attributed to S_QC. Moreover, S_QC is more accurate in detecting the critical point than other detectors in this case (details see Ref. [53]).

In summary, for a detector, the more information about the quantum correlation it contains, the more effective it is in resisting thermal fluctuations. Qc is considered the most important physical quantity in quantifying the quantum correlation contained in the system thus far. Therefore, it possesses natural advantages in signaling the quantum phase transitions. The above-mentioned results further proved this claim.

5 Deducing Order Parameters from Entanglement Based Method

The quantum information methods introduced in the previous sections have succeeded in detecting the quantum phase transition points. However, a challenge still remains: they can only detect the phase boundaries and give us little information about the corresponding phase property, which is a core issue in understanding the phase diagram of a system. Therefore, deducing the potential order parameters for various phases, particularly the topological phases, from the quantum information point of view can help us to learn about the phases’ properties in unknown systems.

Several independent proposals to derive the order parameter exist. Furukawa et al. proposed a method by investigating a set of low-energy “quasi-degenerate” states that lead to the symmetry breaking in the thermodynamic limit [87]. Cheong and Henley [88] suggested to study the singular-value decomposition of the correlation density matrix to obtain the order parameter. Gu et al. [56] proposed a nonvariational and relatively more intuitive approach than the above-mentioned methods. Moreover, this approach may help establish the connection between the quantum phase transition detectors and the order parameters.

The main idea of Gu et al.’s approach is as follows. The order parameter is usually described by an operator. If an operator has a nonzero long-range expectation value, then a symmetry-breaking phase exists in the system. This operator can be used as an order parameter to describe the characteristic order of the quantum phase. The order parameter is usually expressed by the correlation function. For example, one can analyze the magnetic order of the system through the spin correlation to study the magnetic characteristics of a system. For one-dimensional case, the zero mode represents ferromagnetism, whereas the π mode predicts the antiferromagnetic order. The reduced density matrix, which is the core in the definition of each quantum phase transition detector, can be expressed by correlation function. Therefore, one can analyze the structure of the reduced density matrix to deduce the order parameter for a given unknown state. Along this direction, Gu et al. [56] proposed that if and only if the mutual information is nonvanishing at a long distance, then a long-range order exists in the system. One only needs to find the minimum block with the nonzero mutual information. Then, obtaining diagonal and off-diagonal long-range orders is possible depending on the reduced density matrix of the block (see Ref. [56] for detail). The method was applied analytically on several imaginary simple examples in Ref. [56]. We applied the method using DMRG and exactly diagonalization numerical techniques to a practical and relative complex model, namely the SSH model with interactions, to verify and develop the method further.

This model is given by the Hamiltonian

$$\displaystyle \begin{aligned} \begin{array}{rcl} H = & -&\displaystyle t\sum_j \left[ (1+\eta) c_{j,B}^{\dagger} c_{j,A} + (1+\eta) c_{j,A}^{\dagger} c_{j,B} \right. \\ & +&\displaystyle \left. (1-\eta) c_{j+1,A}^{\dagger} c_{j,B} +(1-\eta) c_{j,B}^{\dagger} c_{j+1,A} \right] \\ & +&\displaystyle U \sum_j n_{j,A} n_{j,B} + V \sum_j n_{j,B} n_{j+1,A}. {} \end{array} \end{aligned} $$

(20)

The operator c_j,α destroys a spinless fermion at the unit cell j of type α = A, B. The amplitude t is the hopping strength, η describes the dimerization, and U and V  are local Hubbard-like term coupling fermions from the same unit cell and from the adjacent unit cells, respectively. This model initially describes a dimerized chain of spinless fermions hopping in a tight-binding band. Given the dimerization, the unit cell indexed by j contains two atoms of types A and B. We add the interaction terms. For the noninteracting case, a phase transition exists between the topological and topological-trivial phases at η = 0.

The mutual information or correlation entropy defined in Eq. (8) should be calculated to implement the method. The subsystem is taken as a single unit cell consisting of two atoms of type A and B. The mutual information and the reduced density matrix spectrum are calculated. The results showed that, for η〈0, nonzero long-range mutual information exists, indicating that we can use Gu et al.’s method to deduce the order parameter. On the basis of $\left \vert n_{j,A},n_{j,B} \right \rangle =\{\left \vert 00 \right \rangle ,\left \vert 01 \right \rangle ,\left \vert 10 \right \rangle ,\left \vert 11 \right \rangle \}$, the eigenstates denoted by $\left \vert A \right \rangle , \left \vert B \right \rangle , \left \vert C \right \rangle ,$ and $\left \vert D \right \rangle$ are equally weighted. According to the scheme, the order parameter can be defined as

$$\displaystyle \begin{aligned} \begin{array}{rcl} O_- = w_A \vert A \rangle \langle A \vert +w_B \vert B \rangle \langle B\vert + w_C \vert C \rangle \langle C\vert+w_D \vert D \rangle \langle D\vert. \end{array} \end{aligned} $$

(21)

However, all four unknown coefficients must be fixed. This scenario is too much to deal with, because only the traceless and cut-off conditions exist. Therefore, we transformed the basis to the diagonal expression with the Majorana fermion operators to decrease the number of dominated states. In the transformed basis, the Hamiltonian is diagonalized, and the ground state is given by the vacuum state of the number operators n_f and n_d. The reduced density matrix is solely contributed by the state $\left \vert n_f=0,n_d=0 \right \rangle$. Thus, the order parameter can be defined by O₋ = |00〉〈00| in the diagonal basis. Then, we transformed the diagonal operators back to the original spinless fermion operators and obtained a quasi-local order parameter that characterizes the topological phase in the model [57].

For the topological-trivial phase for η > 0, we took the block consisting of a B atom at site j and an atom A at site j + 1 instead of the single-site block with atoms A and B at the same site. The mutual information is also nonzero in this case, and only one dominating eigenstate of the reduced density matrix exists. The order parameter O₊ for the topological-trivial phase can be deduced directly without a basis transformation [57].

The order parameters were deduced for all the phases when U and V  in Eq. (20) were added. Together with the entanglement entropy results and electronic configuration analysis, the order parameters results were verified, and the ground-state phase diagram of the system was obtained. Figure 10 shows the entanglement results where the confirmed phases are marked on its contour map. The deduced order parameter O − that characterizes the topological state in the interacting SSH model was further used to study the quantum phases in the Schwinger model (the model introduces gauge bosons to regulate the interaction between fermions) and successfully characterize the topological quantum phases in that model [59].

Fig. 10

(Color online) Single-site entanglement entropy and its contour map for η = 0.6 as a function of U and V . In each region, the dominant order parameters are shown (Reproduced from Ref. [57])

The SSH model described in Eq. (20) (without U and V  terms) becomes the SSH-Kiteav model by adding triplet TS pairing. A new Kitaev order topological phase is present in this system. The Hamiltonian is written as follows:

$$\displaystyle \begin{aligned} \begin{array}{rcl} H=& -t\sum_j \left[ (1+\eta) c_{j,B}^{\dagger} c_{j,A} + (1+\eta) c_{j,A}^{\dagger} c_{j,B} +(1-\eta) c_{j+1,A}^{\dagger} c_{j,B} +(1-\eta) c_{j,B}^{\dagger} c_{j+1,A} \right] \\ & + \Delta\sum_j\left[ (1+\eta) c_{j,B}^{\dagger} c_{j,A}^{\dagger} + (1+\eta) c_{j,A} c_{j,B} +(1-\eta)c_{j+1,A}^{\dagger} c_{j,B}^{\dagger} +(1-\eta) c_{j,B} c_{j+1,A} \right].\\{} \end{array} \end{aligned} $$

(22)

The phase diagram needs four order parameters to be described. We further deduced the order parameters $O_+^K$ and $O_-^K$ of the Kiteav-type topological states by using the operator basis transformation similar to the Majorana fermion operators, as mentioned above (see Ref. [89]). Under the transformed basis, the Hamiltonian of the system is diagonalized at the parameter value that is taken deep inside each phase, and its ground state is the vacuum state of the corresponding operator. Thus, the order parameter can be simply written as the expectation value of the projection operator on a subset of the system’s ground state. For example, at η = 0, the order parameters can be written as follows:

$$\displaystyle \begin{aligned} \begin{array}{rcl} O_{j,+}^K & =&\displaystyle \vert0 \rangle \langle 0\vert= 1 - n_{d} \\ & =&\displaystyle \frac{1}{2}-\frac{1}{2}H_j(t=\Delta=1)\end{array} \end{aligned} $$

(23)

and

$$\displaystyle \begin{aligned} \begin{array}{rcl} O_{j,-}^K & =&\displaystyle \frac{1}{2}-\frac{1}{2}H_j(t=-\Delta=1),\end{array} \end{aligned} $$

(24)

where H_j is the contribution from site j to the Hamiltonian. This observation indicates that the local Hamiltonian H_j itself may be used as the order parameter. The Hamiltonian of the system is expressed as H =∑_jH_j. Thus, H_j from deep inside each of the four phases can serve as the corresponding quantum state order parameters of the system. We verified the conclusion by comparing the results of local H_j for different phases with the deduced order parameters from the reduced density matrix approach. This method is simple and expected to be useful in deducing the order parameters for complex quantum states.

6 Summary and Outlook

Entanglement and its related quantum correlations are the cornerstones of quantum mechanics. The quantum effects encoded in entanglement are the essence of high-performance quantum computing and high-efficiency quantum communication in the future. Studying quantum phase transition in spin chain systems from the perspective of quantum correlation not only paves a way to detect the entire critical regions of a system without empirical knowledge but also contributes to the understanding of quantum property and its application in spin chain-based quantum processing.

In this chapter, we present a brief but comprehensive introduction about the gradual development of the related research methods. We focus on the success of each relevant work, while the possible problems are also collected. From the correlation point of view, the more quantum correlation that the detector can capture, the more useful it is in detecting the quantum phase transition. Therefore, among the three concepts, QC seems to be the best potential detector for quantum phase transitions because of its capability in detecting multiple types of phase transitions and its resistance to thermal fluctuations. Nevertheless, the research on QC are still far from complete. Its universality still needs further studies.

Another issue focuses on the systematic construction of the potential order parameters. We briefly introduce an approach to derive the order parameters starting from the reduced density matrix closely related to entanglement and quantum correlation. On this basis, we extend the approach to deal with the system with the relatively complex reduced density matrix spectrum by transforming the basis to the diagonalized basis of the Hamiltonian at specific values of the driving parameter. The connection between the order parameter and the reduced density matrix spectrum is established preliminarily, but the direct connection between the order parameter and the quantum phase transition detectors needs further analysis. A comprehensive method for the derivation of order parameters is constructive not only for the understanding of the properties of quantum states and quantum phase diagram construction but also for understanding of the performance of quantumness in quantum information science.

In addition, quantum simulators can successfully study the real-time dynamics of quantum many-body systems with the development of quantum level control technology. In recent years, the studies on dynamical quantum phase transitions have increased. Dynamical quantum phase transition studies have been developed to try to understand the dynamical behavior of quantum many-body systems by introducing the concept of phase transition in the time domain. At present, the research has two approaches: one is the order parameter method [90, 91], and the other is the nonresolution of the physical quantity, which mainly includes the Loschmidt echo and its correlation [52, 92] and the out-time-ordered correlation [93]. Dynamical quantum phase transitions in the case of quantum quench have been experimentally realized recently [92, 94]. For a detailed introduction, one can see the review article in Ref. [95]. In addition, the quantum phase transition of an equilibrium system is also studied from the dynamical correlation point of view [51]. The study of dynamic quantum phase transition is just at its beginning. The related work, such as definition understanding, phase transition classification, detection methods, and dynamical behaviors, must be further developed. In addition, the previous study of order parameter derivation has just been applied to equilibrium systems, whether it can be extended to such non-equilibrium systems is also an important issue.

Finally, finding efficient and universal quantum phase transition detectors and developing the methods for constructing the potential order parameters exhibit a lot of hope and challenge from the perspective of quantum information. Moreover, the essential relationship between entanglement and quantum phase transition still needs to be further explored. Further research on this topic is not only constructive to the improvement of the method itself but also expected to promote the development and utilization of quantumness in this process. We take this introductory text to sort out the relevant research and provide insights for future research. We hope that this work can stimulate advance ideas in building a real bridge between condensed matter physics and quantum informatics.