Quantum Map Approach to Entanglement Transfer and Generation in Spin Chains

Abstract

Quantum information processing protocols are efficiently implemented on spin-$\frac {1}{2}$ networks. A quantum communication protocol generally involves a certain number of parties having local access to a subset of a larger system, whose intrinsic dynamics are exploited in order to perform a specific task. In this chapter, we address such a scenario with the quantum dynamical map formalism, where the intended protocol is cast into the form of a map acting on the local subset of spins. We reformulate widely investigated protocols, such as one-qubit quantum state transfer and two-qubit entanglement distribution, with the quantum map formalism and demonstrate its usefulness in exploring less investigated protocols such as multi-qubit entanglement generation.

1 Introduction

Due to their formal analogy to quantum registers, quantum spin-$\frac {1}{2}$ networks have become the ideal testbed for many quantum information processing (QIP) protocols, ranging from quantum key distribution to quantum computation [1]. The availability of accurate theoretical models governing their dynamics, being amenable to solutions through either analytical techniques (especially for one-dimensional systems [2]) or powerful numerical techniques, such as those based on tensor network algorithms [3], allows for the investigation of various and distinct protocols. These include, on the one hand, standard QIP protocols such as one-qubit quantum state transfer or bipartite Bell-type entanglement generation, taking place in a Hilbert space having dimensionality higher than that generally accessible via exact diagonalisation techniques. On the other hand, new QIP protocols are being introduced, aimed at exploring the complexity of the geometry of high-dimensional Hilbert spaces [4], such as in particular quantum state transfer [5]. At the same time, remarkable progress has been made in order to experimentally verify these QIP protocols and communication processes on a variety of experimental platforms, with which the simulation of some quantum spin networks has been successfully achieved, using: cold atoms [6,7,8], Rydberg atoms [9,10,11], integrated photonic chips [12], trapped ions [13,14,15], atom–cavity systems [16, 17], and superconducting circuits [18, 19], among others.

In the realm of the QIP tasks implementable with spin systems, a series of basic operations have been identified falling into the class of quantum communication protocols [20], which includes both the distribution and the generation of quantum resources at different space-time locations. A common communication scenario, depicted in Fig. 1, is represented by the circumstance in which a certain number of parties P_i, i = 1, …n, each one having access to only a relatively small subset S_i of a larger physical system S (e.g., to a limited number of sites of a spin network), are required to receive/transfer quantum information from/to the others. Each party is then allowed to perform only local quantum operations; that is, P_i is able to act on S_i only, with the complementary system, S̄_i : S ∖ S_i, being inaccessible to any quantum operation it can carry out. Additionally, one can also allow for classical communication, i.e., the exchange of classical information among the parties. This combination is referred to as LOCC (local operations and classical communication), and the properties of LOCC operations determine to a large extent the fundamental limits for the performance of QIP protocols [21].

Fig. 1

Sketch of a generic quantum spin-$\frac {1}{2}$ network S, where each party P_i has access to the subset S_i (i = 1, 2, 3), on which local quantum operations are allowed. In addition, the parties can exchange classical communication among them. The shaded area encloses the subsets S_i, the dashed lines indicate quantum correlations between the spins entering the QIP protocol, and the black continuous lines are the interactions among the spins in the network

In this chapter, we will employ the quantum dynamical map formalism, typically used in the theory of open quantum systems [22], to illustrate QIP protocols for quantum state transfer, entanglement distribution, and generation on a homogeneous system, made up of a spin-$\frac {1}{2}$ network. We will assume that each party i has access to a subset of n_i spins of the network and has control over the interactions of the spins of this subset with the complementary system. Our aim is to derive the form of the dynamical map and, whenever possible, its analytical expression, in order to determine which LOCC operations maximise the efficiency of the investigated QIP protocols. We will focus, in particular, on the case of quantum dynamical maps obtained from spin Hamiltonians exhibiting U(1) symmetry and, in order to obtain analytical results, investigate specific instances where the spin Hamiltonian is integrable.

The chapter is organised as follows: in Sect. 2, we review the quantum dynamical map formalism and apply it to U(1)-symmetric Hamiltonians in Sect. 3. In Sect. 4, we illustrate the use of the formalism for case of single-qubit quantum state transfer and Bell-state distribution; in Sect. 5, we derive the two-qubit map for entanglement generation and distribution; in Sect. 7, we explore the use of a 4-qubit dynamical map for investigating multipartite entanglement; and, finally, in Sect. 8, we draw our conclusions and provide some outlooks.

2 Quantum Dynamical Maps

A quantum dynamical map between two systems associated to the Hilbert spaces $\mathcal {H}_1$, $\mathcal {H}_2$ can be identified with a linear homomorphism $\Phi :\mathcal {D}(\mathcal {H}_1){\rightarrow }\mathcal {D}(\mathcal {H}_2)$ mapping the space of density matrices acting on the input Hilbert space, into the space of density matrices acting on the output Hilbert space. Therefore, any Φ preserves the basic properties of the quantum states:

• Self-adjointness: Φ(ρ^†)^† =  Φ(ρ)

• Complete positivity: Φ(ρ) > 0

• Normalisation condition: Tr(ρ) = 1

• Linearity: Φ(aρ_A + bρ_B) = a Φ(ρ_A) + b Φ(ρ_B)

For the purpose of our investigation, we consider, from now on, finite-dimensional Hilbert spaces. For such finite-dimensional case, the space of linear maps $\mathcal {L}(\mathbb {C}^n)$ can be identified with the algebra of n × n complex matrices, M_n. Any orthonormal basis $\left \vert i\right \rangle :i{=}1,\ldots ,n$ in $\mathbb {C}^n$ allows to define the orthonormal basis of elementary matrices in M_n:

$$\displaystyle \begin{aligned} \begin{array}{rcl} e_\alpha=e_{ij}=\left\vert i\rangle\!\langle j\right\vert \,, \end{array} \end{aligned} $$

(1)

and any map can be expressed as

$$\displaystyle \begin{aligned} \begin{array}{rcl} \Phi(\rho)=\sum_{\alpha,\beta}A_\alpha^\beta \text{Tr}\{e_\beta\rho\} e_\alpha \,. \end{array} \end{aligned} $$

(2)

In this basis, the matrix A satisfies the following properties:

$$\displaystyle \begin{aligned} \begin{array}{rcl} A_\alpha^\beta\equiv A_{ij}^{nm} \,, \qquad \qquad \begin{cases}\left ( {A}_{ij}^{nm} \right)^*=A_{ji}^{mn} \,, \\ A_{ii}^{nm}=\delta_{mn} \,, \\ A_{ij}^{nm}\rho_{nm}>0 \,. \end{cases} \end{array} \end{aligned} $$

(3)

The map Φ is completely positive if there exists a family of N operators K_i : i=1, …, N in M_n, which satisfy the condition , and such that Φ can be decomposed as [23,24,25]

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \Phi\left(\rho\right)=\sum_{k=1}^N E_k\rho E_k^\dagger \,. \end{array} \end{aligned} $$

(4)

By explicitly writing the matrix elements, we immediately find the relationship between map and Kraus operators:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \left(\Phi\left(\rho\right)\right)_{ij}=\sum_{k=1}^N \sum_{nm}\left(E_k\right)_{in}\left(\rho\right)_{nm}\left(E_k^\dagger\right)_{mj}=\sum_{nm}A_{ij}^{nm}\left(\rho\right)_{nm}{}. \end{array} \end{aligned} $$

(5)

Note that, from Eq. (4), it is evident that for N = 1 the map Φ represents a unitary map $\mathcal {U}=U\rho U^\dagger$.

In this chapter, we are interested in entanglement generation and transfer between two sub-parties that we dub sender and receiver, each of them taking care, controlling and possibly making measurements on a subset of the system’s spins. We denote the states of the subsystems pertaining to sender and receiver as $\rho _{{ }_S}$ and $\rho _{{ }_R}$, respectively, and assume that these are the marginals obtained from the state of a larger system σ, whose time evolution is dictated by a Hamiltonian generating a unitary map, i.e., $\sigma (t) = \mathcal {U}(t)\left (\sigma (0)\right )$. We assume that the initial state of this larger system, σ(0), is a product state between $\rho _{{ }_S}$ and a reference pure state $\left \vert \Psi \right \rangle _{{ }_{\overline {S}}}$. In other words, we are concerned with maps of the following form:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \rho_{{}_R}=\Phi(\rho_{{}_S})=\text{Tr}_{{{}_{\overline{R}}}}\{\mathcal{U}(\rho_{{}_S}\otimes\left\vert \Psi\right\rangle_{{}_{\overline{S}}}\!\left\langle \Psi\right\vert)\}, \end{array} \end{aligned} $$

(6)

where we indicate with $\text{Tr}_{{ }_{\overline {R}}}$ the partial trace over all but R degrees of freedom. Denoting with $\left \vert r\right \rangle _{{ }_{\overline {R}}}$ an orthonormal basis of $\mathcal {H}_{{ }_{\overline {R}}}$, we have

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \rho_{{}_R}=\Phi(\rho_{{}_S})=\sum_{r}\left({}_{{}_{\overline{R}}}\!\left\langle r\right\vert U\left\vert \Psi\right\rangle_{{}_{\overline{S}}}\right)\rho_{{}_S}\left({}_{{}_{\overline{S}}}\!\left\langle \Psi\right\vert U^\dagger\left\vert r\right\rangle_{{}_{\overline{R}}}\right)=\sum_{r}E_r\rho_{{}_S} E_r^\dagger \,. \end{array} \end{aligned} $$

(7)

It is important to remember that the Kraus operators E_r are time-dependent and that they depend on the choice of the basis in ${\mathcal {H}_{\overline {R}}}$ and, more generally, on the choice of sender and receiver subsets themselves. The matrix representation of the corresponding map can be found according to Eq. (5).

3 U(1)-Symmetric Hamiltonians

In this section, we will derive the general form of the quantum dynamical map in Eq. (5) when the unitary evolution operator entering Eq. (6) exhibits U(1) symmetry. Without loss of generality, we focus on spin-$\frac {1}{2}$ Hamiltonians with isotropic Heisenberg-type interactions in the XY  plane:

$$\displaystyle \begin{aligned} \hat{H}=\sum_{i,j}\left(J_{ij}\left(\hat{\sigma}_i^x\hat{\sigma}_j^x+\hat{\sigma}_i^y\hat{\sigma}_j^y\right)+\Delta_{ij}\hat{\sigma}_i^z\hat{\sigma}_j^z\right)+\sum_i h_i \hat{\sigma}_j^z~, \end{aligned} $$

(8)

where $\hat {\sigma }_i^{\alpha }$ (α = x, y, z) are the usual Pauli matrices, i denotes the index of the site, J_ij and Δ_ij are, respectively, the two-qubit interaction terms in the XY  plane and along the Z-axis, and h_i is the magnetic field along the Z-axis. In fact, the class of Hamiltonians exhibiting the U(1) symmetry is larger than that described by Eq. (8) and encompasses Hamiltonians with Dzyaloshinskii–Moriya [26] and XY  isotropic cluster interaction terms [27], among others.

In terms of spin operators, the U(1) symmetry implies that the total magnetisation along the Z-axis, $\big \langle \hat {M}\big \rangle =\sum _{i=1}^N\left \langle \hat {\sigma }^z_i\right \rangle$, is a conserved quantity and the operator $\hat {M}$ commutes with U. Hence, it is possible to divide the whole Hilbert space into invariant subspaces, labelled by the eigenvalues of $\hat {M}$, with each subspace having the dimension determined by the degeneracy of the eigenvalue, $\binom {N}{i}$, where i denotes the number of flipped spins. Indeed, by writing the spectral decomposition of $\hat {M}$ as

$$\displaystyle \begin{aligned} \begin{array}{rcl} \hat{M}= \sum_k\sum_d \lambda_k \left\vert \phi_k^d\right\rangle\left\langle \phi_k^d\right\vert \,, \end{array} \end{aligned} $$

(9)

we know that $U\left \vert \phi _k^d\right \rangle$ is an eigenstate of $\hat {M}$ with eigenvalue λ_k, i.e.,

$$\displaystyle \begin{aligned} \begin{array}{rcl} \left\langle \phi_{k'}^{d'}\right\vert U\left\vert \phi_k^d\right\rangle=\left\langle \phi_{k'}^{d'}\right\vert U\left\vert \phi_k^d\right\rangle\delta_{kk'}=(f_k)^{d'}_{d}\delta_{kk'} \,. \end{array} \end{aligned} $$

(10)

Thus, we can then write U as a direct sum of unitary operators acting in each subspace

$$\displaystyle \begin{aligned} \begin{array}{rcl} U=U_0 \oplus U_1 \oplus U_2 \oplus \ldots \end{array} \end{aligned} $$

(11)

If we now observe the elements of the Kraus operators entering in Eq. (7), they take the form

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} (E_r)_{in}=\;_{{}_R}\!\left\langle i\right\vert E_r\left\vert n\right\rangle_{{}_S}=\;_{{}_R}\!\left\langle i\right\vert\;\!_{{}_{\overline{R}}}\!\left\langle r\right\vert U\left\vert \Psi\right\rangle_{{}_{\overline{S}}}\left\vert n\right\rangle_{{}_S} \,. \end{array} \end{aligned} $$

(12)

This inherently places some constraints on the elements of the Kraus operators and consequently on the map elements. Indeed, if the state $\left \vert \Psi \right \rangle _{{ }_{\overline {S}}}\left \vert n\right \rangle _{{ }_S}$ belongs in a given subspace, then $_{{ }_R}\!\left \langle i\right \vert { }_{{ }_{\overline {R}}}\!\left \langle r\right \vert$ must belong to that subspace as well in order for the above equation to be non-zero. Without loss of generality, we take $\left \vert \Psi \right \rangle _{{ }_{\overline {S}}}\left \vert n\right \rangle _{{ }_S}$ as living in the n-th supspace, implying that i + r = n. In the following, we will assume $\left \vert \Psi \right \rangle _{{ }_{\overline {S}}}=\left \vert \mathbf {0}\right \rangle$, i.e., a fully polarised state.

4 One-Qubit Map

To begin our analysis, let us consider the simplest case: a map from qubit i (the sender) to qubit j (the receiver): $\hat {\rho }_j(t)=\Phi (t)\hat {\rho }_i(0)$, where i and j are (possibly identical) positions in a spin network. In this case, we have two possible values of r = 0, 1 and, consequently, two Kraus operators:

$$\displaystyle \begin{aligned} \begin{array}{rcl} E_0=\begin{pmatrix} 1 & 0\\ 0& f_i^j \end{pmatrix} \,, \qquad E_1^k=\begin{pmatrix} 0 &\displaystyle 0\\ f_i^k& 0 \end{pmatrix} \; \text{with }k\neq j\,. \end{array} \end{aligned} $$

(13)

By using Eq. (5), we can write the map as

$$\displaystyle \begin{aligned} \begin{pmatrix} \rho_{00}\\ \rho_{01}\\ \rho_{10}\\ \rho_{11}\\ \end{pmatrix}_j= \begin{pmatrix} 1 &0&0&1-\left|f_i^j\right|{}^2\\ 0&f_i^j&0&0\\ 0&0&\left(f_i^j\right)^*&0\\ 0&0&0&\left|f_i^j\right|{}^2 \end{pmatrix} \begin{pmatrix} \rho_{00}\\ \rho_{01}\\ \rho_{10}\\ \rho_{11}\\ \end{pmatrix}_i \,, \end{aligned} $$

(14)

where we use the completeness relation $\sum _n \left |f_i^n\right |{ }^2=1$.

In this simple case, perfect state transfer, i.e., $\hat {\rho }^{j}_{nm}=\hat {\rho }^{i}_{nm}$, entails $f_i^j=\left (f_i^j\right )^*=1$. A considerable amount of research has been performed in order to investigate the conditions that allow to maximise the transition amplitude [28].

In Bose’s original protocol [29], this is achieved by a local magnetic field acting on the spins. The map in Eq. (14) is also informative about remote state preparation protocols: the coherence (in the computational basis) of spin j cannot increase with respect to that of spin i under the action of this map as the off-diagonal elements of the output density matrix can only be suppressed, or, at most, maintain their initial amplitude.

Apart from quantum state transfer protocols, the map in Eq. (14) can be used to analyse entanglement distribution protocols, like the one reported in Refs. [29, 30] and sketched in Fig. 2. Explicitly, the map is given by

(15)

where is the 4-dimensional identity map acting on qubit 0 and Φ_i(t) is given by the map in Eq. (14) acting on qubit i. The map reads

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \hspace{-9pt}\left( \begin{array}{c} \rho_{00}\\ \rho_{01}\\ \rho_{02}\\ \rho_{03}\\ \rho_{10}\\ \rho_{11}\\ \rho_{12}\\ \rho_{13}\\ \rho_{20}\\ \rho_{21}\\ \rho_{22}\\ \rho_{23}\\ \rho_{30}\\ \rho_{31}\\ \rho_{32}\\ \rho_{33}\\ \end{array}\right)_{0,j}= \left( \begin{array}{cccccccccccccccc} 1 & 0 & 0 & 0 & 0 & 1{-}| f|{}^2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & f & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 1{-}| f|{}^2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & f & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & f^* & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & | f|{}^2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & f^* & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & | f|{}^2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 1{-}| f|{}^2 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & f & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 1{-}| f|{}^2 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & f & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & f^* & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & | f|{}^2 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & f^* & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & | f|{}^2 \\ \end{array} \right) \left(\begin{array}{c} \rho_{00}\\ \rho_{01}\\ \rho_{02}\\ \rho_{03}\\ \rho_{10}\\ \rho_{11}\\ \rho_{12}\\ \rho_{13}\\ \rho_{20}\\ \rho_{21}\\ \rho_{22}\\ \rho_{23}\\ \rho_{30}\\ \rho_{31}\\ \rho_{32}\\ \rho_{33}\\ \end{array}\right)_{0,i}\hspace{-3pt}. \end{array} \end{aligned} $$

(16)

Fig. 2

A schematic picture of an entanglement distribution protocol. Initially, the external qubit 0 is entangled with qubit i, and the aim is to exploit the map in Eq. (16) to entangle the former with qubit j

In the original entanglement distribution protocol given in Ref. [29], the entanglement encoded in a singlet state on sites 0 and i is distributed to sites 0 and j resulting in a concurrence $C=\left |f_i^j(t)\right |$. From the map in Eq. (16), it is evident that the same holds true for any Bell state. On the other hand, for X-type density matrices [31], the distributed entanglement does not increase linearly with the (modulus of the) transition amplitude f but instead reads

$$\displaystyle \begin{aligned} C=2\max\left[0, C_1,C_2\right]~, \end{aligned} $$

(17)

where

$$\displaystyle \begin{aligned} C_1=\left|f\right|\left(\left|\rho_{12}\right|-\sqrt{\rho_{33}\left(\rho_{00}+\rho_{11}\left(1-\left|f\right|{}^2\right)\right)}\right) \,, \end{aligned} $$

(18)

$$\displaystyle \begin{aligned} C_2=\left|f\right|\left(\left|\rho_{03}\right|-\sqrt{\rho_{11}\left(\rho_{22}+\rho_{33}\left(1-\left|f\right|{}^2\right)\right)}\right) \, \end{aligned} $$

(19)

denote the so-called anti-parallel and parallel concurrences, respectively [32]. Looking carefully at the map, one can see that the ratio of transferred entanglement over initial entanglement depends only on the transition amplitude and not on the fact that entanglement is of the parallel or anti-parallel type. The dependence on $\left |f \right |$ is not linear, as in the pure Bell-state scenario, and in Fig. 3, we show the ratio of the transferred concurrence vs. the initial concurrence ($C = \frac {3p-1}{2}$) for an initial Werner state

(20)

where $\left \vert \Psi _B\right \rangle$ is any Bell state.

Fig. 3

Ratio of transferred entanglement vs. $\left |f \right |$ for a Werner state for different values of p in Eq. (20). The curves, from bottom to top, are drawn for p = 0.4, 0.5, 0.7, 0.9, 1

Now we consider the case where the entanglement distribution protocol is designed in order to send to sites $\left (n,\mu \right )$ (the receiver sites), and the entanglement initially shared between sites $\left (i,\nu \right )$ (sending sites) using two independent spin networks. A particular instance of this setup is given in Fig. 4, and both there and in the setting of the problem above, Latin (Greek) letters are used to denote the sites on the first (second) chain. This protocol is reminiscent of the dual-rail encoding protocol for sending a single-qubit state [33].

Fig. 4

A schematic picture of an entanglement distribution protocol. Initially, qubit i is entangled with qubit ν, and the aim is to exploit the map in Eq. (16) to entangle qubit j with qubit μ

The map is given by

$$\displaystyle \begin{aligned} \hat{\rho}(t)_{j\mu}=\left(\Phi_i(t)\otimes \Phi_{\nu}(t)\right)\hat{\rho}(0)_{i\nu}~ \end{aligned} $$

(21)

and reads

$$\displaystyle \begin{aligned} \left( \begin{array}{cccccccccccccccc} 1 & 0 & 0 & 0 & 0 & 1{-}| g|{}^2 & 0 & 0 & 0 & 0 & 1{-}| f|{}^2 & 0 & 0 & 0 & 0 & \left(1{-}| f|{}^2\right) \left(1{-}| g|{}^2\right) \\ 0 & g & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & g \left(1{-}| f|{}^2\right) & 0 & 0 & 0 & 0 \\ 0 & 0 & f & 0 & 0 & 0 & 0 & f \left(1{-}| g|{}^2\right) & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & f g & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & g^* & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \left(1{-}| f|{}^2\right) g^* & 0 \\ 0 & 0 & 0 & 0 & 0 & | g|{}^2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \left(1{-}| f|{}^2\right) | g|{}^2 \\ 0 & 0 & 0 & 0 & 0 & 0 & f g^* & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & f | g|{}^2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & f^* & 0 & 0 & 0 & 0 & \left(1{-}| g|{}^2\right) f^* & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & g f^* & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & | f|{}^2 & 0 & 0 & 0 & 0 & | f|{}^2 \left(1{-}| g|{}^2\right) \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & g | f|{}^2 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & f^* g^* & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & | g|{}^2 f^* & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & | f|{}^2 g^* & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & | f|{}^2 | g|{}^2 \\ \end{array} \right), \end{aligned} $$

(22)

where we have used the short-hand notation $f=f_i^j$ and $g=f_{\nu }^{\mu }$. If we assume that the two spin networks are identical and that the locations of the initially correlated sites and of the receiving ones are also the same on the two networks, the matrix above simplifies as f = g. Again, this is the same settings adopted in the dual-rail protocol [34] to attain perfect state transfer. In such a case, with $\hat {\rho }_{i\nu }$ being an X-type state, the anti-parallel and parallel concurrences reported in Eq. (17) are given by

$$\displaystyle \begin{aligned} &C_1=\left|f\right|{}^2\left(\left|\rho_{12}\right|-\sqrt{\rho_{33}\left(\rho_{00}+\left(1- \left|f\right|{}^2\right)\left(\rho_{11}+\rho_{22}+\left(1- \left|f\right|{}^2\right)\rho_{33} \right)\right)}\right) \end{aligned} $$

(23)

$$\displaystyle \begin{aligned} &C_2=\left|f\right|{}^2\left(\left|\rho_{03}\right|-\sqrt{\left(\rho_{11}+\left(1-\left|f\right|{}^2\right)\rho_{33}\right)\left(\rho_{22}+\left(1-\left|f\right|{}^2\right)\rho_{33}\right)}\right)~. \end{aligned} $$

(24)

Due to the use of two channels, as depicted in Fig. 4, the ratio of transferred over initial entanglement depends, this time, not only on the transition amplitude, but also on the type of entanglement (whether parallel or anti-parallel). This is also the case when investigating the effect of the spin environment on the entanglement, which has been carried out in Ref. [35], by analysing the properties of the map $\hat {\rho }(t)_{j\mu }=\left (\Phi _i(t)\otimes \Phi _{\nu }(t)\right )\hat {\rho }(0)_{j\mu }$.

As one can expect, the anti-parallel entanglement C₁ attains larger values with respect to C₂ at fixed transition amplitude $\left |f\right |$. Intuitively, this is due to the fact that in the former case, only one excitation is present in the system, whereas, in the latter, two excitations enter the dynamics. This leads to an increase in the effects of decoherence due to the dispersion of the extra excitation all over the network. A figure of merit describing the amount of transferred entanglement is reported in Fig. 5, in the case of initial Werner states (Eq. 20).

Fig. 5

Ratio of transferred over initial entanglement vs. $\left |f \right |$ for a Werner state for different values of p in Eq. (20). The curves, from bottom to top, are drawn for p = 0.4, 0.5, 0.7, 0.9, 1. The left plot corresponds to a Werner state with maximally entangled component given by $\left \vert \Psi _B \right \rangle = \left \vert \Phi ^+ \right \rangle$, whereas for the right plot we have chosen $\left \vert \Psi _B \right \rangle = \left \vert \Psi ^+ \right \rangle$

5 Two-Qubit Map

In this section, we derive the expression of Φ for the case of two sender qubits located at arbitrary positions i and j in a spin network. For a generic two-qubit receiver at sites n, m, it is instructive to write the map in matrix form.

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \left( \begin{array}{c} \rho_{00}\\ \rho_{01}\\ \rho_{02}\\ \rho_{03}\\ \rho_{10}\\ \rho_{11}\\ \rho_{12}\\ \rho_{13}\\ \rho_{20}\\ \rho_{21}\\ \rho_{22}\\ \rho_{23}\\ \rho_{30}\\ \rho_{31}\\ \rho_{32}\\ \rho_{33} \end{array}\right)_{i,j} = \left(\begin{array}{cccccccccccccccc} A_{00}^{00}&0&0&0&0&A_{00}^{11}&A_{00}^{12}&0&0&A_{00}^{21}&A_{00}^{22}&0&0&0&0&A_{00}^{33}\\ 0& A_{01}^{01} & A_{01}^{02} & 0 & 0 & 0 & 0 & A_{01}^{13} & 0 & 0 & 0 & A_{01}^{23} & 0 & 0 & 0 & 0 \\ 0 & A_{02}^{01} & A_{02}^{02} & 0 & 0 & 0 & 0 & A_{02}^{13} & 0 & 0 & 0 & A_{02}^{23} & 0 & 0 & 0 & 0 \\ 0& 0 & 0 & A_{03}^{03} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0& 0 & 0 & 0 & A_{10}^{10} & 0 & 0 & 0 & A_{10}^{20} & 0 & 0 & 0 &0 & A_{10}^{31} & A_{10}^{32} & 0 \\ 0& 0 & 0 & 0 & 0 & A_{11}^{11} & A_{11}^{12} & 0 & 0 & A_{11}^{21} & A_{11}^{22} & 0 & 0 & 0 & 0 & A_{11}^{33} \\ 0& 0 & 0 & 0 & 0 & A_{12}^{11} & A_{12}^{12} & 0 & 0 & A_{12}^{21} & A_{12}^{22} & 0 & 0 & 0 & 0 & A_{12}^{33} \\ 0& 0 & 0 & 0 & 0 & 0 & 0 & A_{13}^{13} & 0 & 0 & 0 & A_{13}^{23} & 0 & 0 & 0 & 0 \\ 0& 0 & 0 & 0 & A_{20}^{10} & 0 & 0 & 0 & A_{20}^{20} & 0 & 0 & 0 & 0 & A_{20}^{31} & A_{20}^{32} & 0 \\ 0& 0 & 0 & 0 & 0 & A_{21}^{11} & A_{21}^{12} & 0 & 0 & A_{21}^{21} & A_{21}^{22} & 0 & 0 & 0 & 0 & A_{21}^{33} \\ 0& 0 & 0 & 0 & 0 & A_{22}^{11} & A_{22}^{12} & 0 & 0 & A_{22}^{21} & A_{22}^{22} & 0 & 0 & 0 & 0 & A_{22}^{33} \\ 0& 0 & 0 & 0 & 0 & 0 & 0 & A_{23}^{13} & 0 & 0 & 0 & A_{23}^{23} & 0 & 0 & 0 & 0\\ 0& 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & A_{30}^{30} & 0 & 0 & 0\\ 0& 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & A_{31}^{31} & A_{31}^{32} &0 \\ 0& 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & A_{32}^{31} & A_{32}^{32} & 0 \\ 0& 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & A_{33}^{33} \end{array}\right) \left(\begin{array}{c} \rho_{00}\\ \rho_{01}\\ \rho_{02}\\ \rho_{03}\\ \rho_{10}\\ \rho_{11}\\ \rho_{12}\\ \rho_{13}\\ \rho_{20}\\ \rho_{21}\\ \rho_{22}\\ \rho_{23}\\ \rho_{30}\\ \rho_{31}\\ \rho_{32}\\ \rho_{33} \end{array}\right)_{n,m} \end{array} \end{aligned} $$

(25)

The map in Eq. (25) can be written in a more compact form defining the Kraus operators in all of magnetisation sectors, as illustrated in Sect. 3, where Eq. (12) has elements

$$\displaystyle \begin{aligned} \begin{array}{rcl} A=E_0\otimes E_0^*+E_1\otimes E_1^*+E_2\otimes E_2^* \,, \end{array} \end{aligned} $$

(26)

and

$$\displaystyle \begin{aligned} E_0=\left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & f_{j}^{m} & f_{i}^{m} & 0 \\ 0 & f_{j}^{n} & f_{i}^{n} & 0 \\ 0 & 0 & 0 & f_{ij}^{nm} \end{array} \right) \,, \, E_1^{k\neq i,j}=\left( \begin{array}{cccc} 0 & f_{j}^{k} & f_{i}^{k} & 0 \\ 0 & 0 & 0 & f_{ij}^{km} \\ 0 & 0 & 0 & f_{ij}^{nk} \\ 0 & 0 & 0 & 0 \end{array}\right) \,, \, E_2^{k,l \neq i,j}=\left( \begin{array}{cccc} 0 & 0 & 0 & f_{ij}^{kl} \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right) \,. \end{aligned} $$

(27)

This explicit form of the map shows, for example, that $\rho _{03}(t) = A_{03}^{03}\rho _{03}(0)$. As a consequence (and analogously to the impossibility of amplifying coherence in the single-qubit case), the Bell states $\left \vert \Phi ^{\pm }\right \rangle$ cannot be generated by this map, irrespective of the initial state of the qubits. On the other hand, the Bell states $\left \vert \Psi ^{\pm }\right \rangle$ can be generated by LOCC as the coherences ρ₁₂ can be build up starting from ρ₁₁, ρ₂₂, and/or ρ₃₃, i.e., by locally flipping the spins on the sender and/or receiver sites.

From Ref. [36], we can borrow the following two-qubit map’s elements for the case in which the receiver coincides with the sender (so that, in fact, we are evaluating how good is information storage at sites i, j), $\hat {\rho }_{ij}(t)=\Phi _t\hat {\rho }_{ij}(0)$

$$\displaystyle \begin{aligned} &A_{00}^{00}=1~,~A_{00}^{11}=1-\left|f_i^{i}\right|{}^2-\left|f_i^{j}\right|{}^2~,~A_{00}^{22}=1-\left|f_j^{i}\right|{}^2-\left|f_j^{j}\right|{}^2 \,, \\ &A_{00}^{33}=1-\left|f_{ij}^{mi}\right|{}^2-\left|f_{ij}^{mj}\right|{}^2-\left|f_{ij}^{ij}\right|{}^2~,~A_{00}^{12}=-f_i^{i}\left(f_j^{i}\right)^*-f_i^{i}\left(f_j^{i}\right)^* \,, \\ &A_{00}^{21}=-f_j^{i}\left(f_i^{i}\right)^*-f_j^{j}\left(f_i^{j}\right)^* \,, \\ &A_{01}^{01}=\left(f_i^j\right)^*~,~A_{01}^{02}=\left(f_j^j\right)^*~,~A_{01}^{13}=f_i^m\left(f_{ij}^{mj}\right)^*~,~A_{01}^{23}=f_j^m\left(f_{ij}^{mj}\right)^* \,, \\ &A_{02}^{01}=\left(f_{i}^{i}\right)^*~,~A_{02}^{02}=\left(f_{j}^{i}\right)^*~,~A_{02}^{13}=f_i^m\left(f_{ij}^{mi}\right)^*~,~A_{02}^{23}=f_j^m\left(f_{ij}^{mi}\right)^* \,, \\ &A_{03}^{03}=\left(f_{ij}^{ij}\right)^* \,, \\ &A_{11}^{11}=\left|f_i^j\right|{}^2~,~A_{11}^{12}=f_i^j\left(f_j^i\right)^*~,~A_{11}^{21}=f_j^j\left(f_i^j\right)^*~,~A_{11}^{22}=\left|f_j^j\right|{}^2~,~A_{11}^{33}=\left|f_{ij}^{mj}\right|{}^2 \,, \\ &A_{12}^{11}=f_i^j\left(f_i^i\right)^*~,~A_{12}^{12}=f_i^j\left(f_j^i\right)^*~,~ A_{12}^{21}=f_j^j\left(f_i^i\right)^*~,~A_{12}^{22}=f_j^j\left(f_j^i\right)^*~,~ A_{12}^{33}=f_{ij}^{mj}\left(f_{ij}^{mi}\right)^* \,, \\ &A_{13}^{13}=f_i^j\left(f_{ij}^{ij}\right)^*~,~A_{13}^{23}=f_j^j\left(f_{i}^{ij}\right)^* \,, \\ &A_{22}^{33}=\left|f_{ij}^{mi}\right|{}^2~,~A_{22}^{11}=\left|f_{i}^{i}\right|{}^2~,~A_{22}^{22}=\left|f_{j}^{i}\right|{}^2~,~A_{22}^{12}=f_{i}^{i}\left(f_{j}^{i}\right)^*~,~A_{22}^{21}=f_{j}^{i}\left(f_{i}^{i}\right)^* \,, \\ &A_{23}^{13}=f_{i}^{i}\left(f_{ij}^{ij}\right)^*~,~A_{23}^{23}=f_{j}^{i}\left(f_{ij}^{ij}\right)^*~,~A_{33}^{33}=\left|f_{ij}^{ij}\right|{}^2 \,, \end{aligned} $$

(28)

where, whenever the index m appears, a summation over all m ≠ S, R is intended.

For the general case describing the transfer of a given two-qubit state from the sending pair i, j to the receiving pair n, m, $\hat {\rho }_{nm}(t)=\Phi _t\hat {\rho }_{ij}(0)$, the matrix elements read

$$\displaystyle \begin{aligned} \begin{array}{rcl} A_{00}^{00}& =&\displaystyle 1 \, , \, A_{00}^{11}=f_{j}^{k} \left(f_{j}^{k}\right){}^* \, , \, A_{00}^{12}=f_{j}^{k} \left(f_{i}^{k}\right){}^*,\notag\\ A_{00}^{21}& =&\displaystyle f_{i}^{k} \left(f_{j}^{k}\right){}^* \, , \, A_{00}^{22}=f_{i}^{k} \left(f_{i}^{k}\right){}^* \, , \, A_{00}^{33}=f_{ij}^{{kl}} \left(f_{ij}^{{kl}}\right){}^* \,, \\ A_{01}^{01}& =&\displaystyle \left(f_{j}^{m}\right){}^* \, , \, A_{01}^{02}=\left(f_{i}^{m}\right){}^* \, , \, A_{01}^{13}=f_{j}^{k} \left(f_{ij}^{km}\right){}^* \, , \, A_{01}^{23}=f_{i}^{k} \left(f_{ij}^{km}\right){}^* \,, \\ A_{02}^{01}& =&\displaystyle \left(f_{j}^{n}\right){}^* A_{02}^{02}=\left(f_{i}^{n}\right){}^* \, , \, A_{02}^{13}=f_{j}^{k} \left(f_{ij}^{nk}\right){}^* \, , \, A_{02}^{23}= f_{i}^{k} \left(f_{ij}^{nk}\right){}^* \,, \\ A_{03}^{03}& =&\displaystyle \left(f_{ij}^{nm}\right){}^* \,, \\ A_{10}^{10}& =&\displaystyle f_{j}^{m} \, , \, A_{10}^{20}=f_{i}^{m} \, , \, A_{10}^{31}=f_{ij}^{km} \left(f_{j}^{k}\right){}^* \, , \, A_{10}^{32}=f_{ij}^{km} \left(f_{i}^{k}\right){}^* \,, \\ A_{11}^{11}& =&\displaystyle f_{j}^{m} \left(f_{j}^{m}\right){}^* \, , \, A_{11}^{12}=f_{j}^{m} \left(f_{i}^{m}\right){}^* \, , \, A_{11}^{21}=f_{i}^{m} \left(f_{j}^{m}\right){}^*,\notag\\ A_{11}^{22}& =&\displaystyle f_{i}^{m} \left(f_{i}^{m}\right){}^* \, , \, A_{11}^{33}=f_{ij}^{km} \left(f_{ij}^{km}\right){}^* \,, \\ A_{12}^{11}& =&\displaystyle f_{j}^{m} \left(f_{j}^{n}\right){}^* \, , \, A_{12}^{12}=f_{j}^{m} \left(f_{i}^{n}\right){}^* \, , \, A_{12}^{21}=f_{i}^{m} \left(f_{j}^{n}\right){}^* A_{12}^{22}=f_{i}^{m} \left(f_{i}^{n}\right){}^* ,\notag\\ A_{12}^{33}& =&\displaystyle f_{ij}^{km} \left(f_{ij}^{nk}\right){}^* \,, \\ A_{13}^{13}& =&\displaystyle f_{j}^{m} \left(f_{ij}^{nm}\right){}^* \, , \, A_{13}^{23}=f_{i}^{m} \left(f_{ij}^{nm}\right){}^* \,, \\ A_{20}^{10}& =&\displaystyle f_{j}^{n} \, , \, A_{20}^{20}=f_{i}^{n} \, , \, A_{20}^{31}=f_{ij}^{nk} \left(f_{j}^{k}\right){}^* \, , \, A_{20}^{32}=f_{ij}^{nk} \left(f_{i}^{k}\right){}^* \,, \\ A_{21}^{11}& =&\displaystyle f_{j}^{n} \left(f_{j}^{m}\right){}^* \, , \, A_{21}^{12}=f_{j}^{n} \left(f_{i}^{m}\right){}^* \, , \, A_{21}^{21}=f_{i}^{n} \left(f_{j}^{m}\right){}^* A_{21}^{22}=f_{i}^{n} \left(f_{i}^{m}\right){}^* ,\notag\\ A_{21}^{33}& =&\displaystyle f_{ij}^{nk} \left(f_{ij}^{km}\right){}^* \,, \\ A_{22}^{11}& =&\displaystyle f_{j}^{n} \left(f_{j}^{n}\right){}^* \, , \, A_{22}^{12}=f_{j}^{n} \left(f_{i}^{n}\right){}^* \, , \, A_{22}^{21}=f_{i}^{n} \left(f_{j}^{n}\right){}^* A_{22}^{22}=f_{i}^{n} \left(f_{i}^{n}\right){}^* \, ,\notag\\ A_{22}^{33}& =&\displaystyle f_{ij}^{nk} \left(f_{ij}^{nk}\right){}^* \,, \\ A_{23}^{13}& =&\displaystyle f_{j}^{n} \left(f_{ij}^{nm}\right){}^* \, , \, A_{23}^{23}=f_{i}^{n} \left(f_{ij}^{nm}\right){}^* \,, \\ A_{30}^{30}& =&\displaystyle f_{ij}^{nm} \,, \\ A_{31}^{31}& =&\displaystyle f_{ij}^{nm} \left(f_{j}^{m}\right){}^* \, , \, A_{31}^{32}=f_{ij}^{nm} \left(f_{i}^{m}\right){}^* \,, \\ A_{32}^{31}& =&\displaystyle f_{ij}^{nm} \left(f_{j}^{n}\right){}^* \, , \, A_{32}^{32}=f_{ij}^{nm} \left(f_{i}^{n}\right){}^* \,, \\ A_{33}^{33}& =&\displaystyle f_{ij}^{nm} \left(f_{ij}^{nm}\right){}^* \,. \end{array} \end{aligned} $$

(29)

6 Two-Qubit Entanglement Generation

In the simplest setting, Alice and Bob aim at generating entanglement between the qubits in their possession, respectively, A and B, located at some positions in the spin network, by performing local operations on their qubits and exchanging classical communication between them. By definition, LOCC by itself does not allow for neither the increase nor the generation of entanglement between qubits A and B; but the presence of the spin network can give rise to an effective interaction between these qubits, resulting in the possible generation of quantum correlation. In Fig. 6, an instance of such an entanglement generation protocol is depicted, where Alice and Bob have access to one spin at each end of a 1D spin chain. In Ref. [37], it has been shown that, by weakly coupling the end qubits to the wire, their state evolves into a Bell state at half of the transfer time of the excitation between the edges. This result has been extended in Ref. [38] to the generation of a Bell state between two users coupled at arbitrary positions in a spin network, provided control over the local magnetic field is allowed on the sites chosen to be entangled. Results similar to the weak-coupling scheme can be obtained by strong local magnetic fields on neighbouring spins both for one- and two-qubit quantum state transfer [39, 40].

Fig. 6

Alice and Bob have access, respectively, to qubits A and B, located at the two ends of a spin chain (wire). Entanglement between the two qubits can be generated by exploiting the dynamics of the quantum wire, whose Hamiltonian includes a nearest-neighbour interaction term

In Ref. [41], the authors showed that initialising the system in $\left \vert \Psi \right \rangle _{AB}=\left \vert +\right \rangle _A\left \vert +\right \rangle _B\left \vert \psi \right \rangle _W$, where $\left \vert +\right \rangle =\frac {1}{\sqrt {2}}\left (\left \vert 0\right \rangle +\left \vert 1\right \rangle \right )$ and $\left \vert \psi \right \rangle _W$ is an arbitrary state with fixed parity of the wire, and a maximally entangled state between qubits A and B can be achieved in a ballistic time, provided Alice and Bob can tune the strength of the couplings of their qubits to the wire to an optimal value [42].

7 Four-Qubit Entanglement Generation

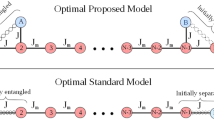
In Sect. 5, we have analysed the case where Alice and Bob each have access to one qubit in the spin network. Here, instead, we consider the case where they each have access to two qubits. An instance where each pair of qubits is located at an edge of a spin chain is depicted in Fig. 7. A general analysis of the entanglement generated in an arbitrary four-qubit state has not yet been performed, except for pure states [43, 44], due to the complexity of defining entanglement quantifiers for an arbitrary four-qubit mixed state (as a result of the mixed state being in the presence of infinitely many SLOCC classes [45]).

Fig. 7

Alice and Bob have access to qubits A₁, A₂ and B₁, B₂, respectively, located at the two ends of a spin chain (wire), which is capable of generating an entangled state by exploiting its intrinsic dynamics

Restricting only to the A|B partition, in Ref. [46], it is shown that starting from $\left \vert \Psi \right \rangle _{AB}=\left \vert 1100\right \rangle$ and $\left \vert \Psi \right \rangle _{AB}=\left \vert 1010\right \rangle$ (or their mirror-symmetric states $\left \vert \Psi \right \rangle _{AB}=\left \vert 0011\right \rangle$ and $\left \vert \Psi \right \rangle _{AB}=\left \vert 0101\right \rangle$), a product of two Bell states, i.e., $\left \vert \Psi \right \rangle _{AB}=\left \vert \Phi \right \rangle _{A_1B_2} \otimes \left \vert \Phi \right \rangle _{A_2B_1}$ or $\left \vert \Psi \right \rangle _{AB}=\left \vert \Phi \right \rangle _{A_1B_1} \otimes \left \vert \Phi \right \rangle _{A_2B_2}$, is attained at specific times during the evolution for g ≪ J. On the other hand, the initial state $\left \vert 1001\right \rangle$ (and its mirror-symmetric state $\left \vert 0110\right \rangle$) does not generate any entanglement in the A|B partition at any time.

Let us now characterise the type of entanglement these initial states achieve during the evolution of the dynamical map. Starting from the state $\left \vert \Psi \right \rangle _{AB}=\left \vert 1100\right \rangle$ results in the evolution

$$\displaystyle \begin{aligned} \left\vert \Psi(t)\right\rangle_{AB} = \frac{1}{2}\left[ \left(1-\cos\frac{g^2t}{J} \right)\left\vert 0011\right\rangle + i\sin\frac{g^2t}{J}\left\vert 0101\right\rangle \right. \,, \\ \left. -i\sin\frac{g^2t}{J}\left\vert 1010\right\rangle + \left(1+\cos\frac{g^2t}{J} \right)\left\vert 1100\right\rangle\right] \,, \end{aligned} $$

(30)

which can be written in a biseparable form

$$\displaystyle \begin{aligned} \left\vert \Psi(t)\right\rangle_{AB} = \left|\sin\frac{g^2t}{2J}\right|\left[\left(\left\vert 01\right\rangle + -i\cot\frac{g^2t}{2J}\left\vert 10\right\rangle \right)_{A_1B_2} \right. \,, \\ \otimes \left. \left( \left\vert 01\right\rangle + i\cot\frac{g^2t}{2J}\left\vert 10\right\rangle \right)_{A_2B_1} \right] \,, \end{aligned} $$

(31)

implying that the concurrence in each two-qubit state is equal to $C_{A_1B_2} = C_{A_2B_1} = \left | \sin \frac {g^2t}{J} \right |$. This means that a product of two Bell states is created after a time $t = \frac {\pi J}{2g^2}$. It is also noteworthy to consider the four-tangle [47], a measure of multipartite entanglement, which is defined for pure states as

$$\displaystyle \begin{aligned} \tau_{4}(\left\vert \psi\right\rangle) = \left| \left\langle \psi\right\vert \sigma_y \otimes \sigma_y \otimes \sigma_y \otimes \sigma_y \left\vert \psi^*\right\rangle \right|{}^2 \,. \end{aligned} $$

(32)

In this case, the calculation can be carried out explicitly, and we get that $\tau _4(\left \vert \Psi (t)\right \rangle _{AB}) \equiv \tau _{A_1A_2B_1B_2} = \left | \sin \frac {g^2t}{J} \right |{ }^4$. This means that even though the state (31) is biseparable, the four-tangle is non-zero when the two-qubit concurrences are non-zero, implying that the four-tangle is not a measure of exclusive four-way entanglement per se. One can also consider the three-tangle [48] of the three-qubit partitions, which contrary to the four-tangle, is exclusively a measure of three-way entanglement. The caveat of this measure is that it is only defined for pure states, while the generalisation to mixed states is described via the convex roof extension. Thus, the three-tangle of a mixed state ρ is given as the average pure state three-tangle minimised over all possible pure state decompositions:

$$\displaystyle \begin{aligned} \tau_{3}(\rho) = \min_{\left\{p_i, \left\vert \psi_i\right\rangle\right\}} \sum_{i} p_i \tau_{3}\left(\left\vert \psi_i\right\rangle\right) \,, \end{aligned} $$

(33)

which for a pure state

$$\displaystyle \begin{aligned} \tau_{3}(\left\vert \psi\right\rangle) = C_{A(BC)}^2 - C_{AB}^2 - C_{AC}^2 \,, \end{aligned} $$

(34)

and $C_{A(BC)} = \sqrt {2\left (1-\text{Tr}\left (\rho _A^2\right )\right )}$. If we now consider taking the Eigendecompositions of the partial trace of state (31) with respect to every qubit, we find that the three-tangle of each decomposed pure state for each traced out qubit is equal to zero. This means that we have found a minimal pure state decomposition so that the three-tangle of state (31), with respect to any partition involving three qubits, is equal to zero, implying there is no three-way entanglement generation between the senders and receivers at any time t. This is a consequence of the fact that the initial state does not exhibit any coherence between states having support in the magnetisation sectors with zero and three excitations, and the dynamics are not able to generate any. Clearly, multipartite entanglement distribution protocols are feasible whenever the initial state contains some amount of entanglement, as shown in Ref. [49] for the case of the three-tangle when the sender’s state is GHZ-like.

Let us now move to analyse the evolution of the state generated from $\left \vert \Psi \right \rangle _{AB}=\left \vert 1010\right \rangle$. We get that the evolution results in

$$\displaystyle \begin{aligned} \left\vert \Psi(t)\right\rangle_{AB} = \frac{1}{2}\left[ \left(\cos2Jt + \cos\frac{g^2t}{J} \right)\left\vert 1010\right\rangle + \left(\cos2Jt - \cos\frac{g^2t}{J} \right)\left\vert 0101\right\rangle \right. \,, \\ \left. -i\sin2Jt\left(\left\vert 1001\right\rangle + \left\vert 0110\right\rangle \right) -i\sin\frac{g^2t}{J}\left(\left\vert 1100\right\rangle - \left\vert 0011\right\rangle \right)\right] \,. \end{aligned} $$

(35)

To characterise the different types of entanglement in Eq. (35), we need to look towards a new entanglement measure further to the two-qubit concurrence and three- and four-tangles. We will specifically use the four-qubit concurrence given in Ref. [50], which is defined for a pure state as

$$\displaystyle \begin{aligned} C_{1234} = \left (C_{1(234)}C_{2(134)}C_{3(124)}C_{4(123)}C_{(12)(34)}C_{(13)(24)}C_{(14)(23)} \right)^{\frac{1}{7}} \,, \end{aligned} $$

(36)

where $C_{A(BCD)} = \sqrt {2\left (1-\text{Tr}\left (\rho _A^2\right )\right )}$ and $C_{(AB)(CD)} = \sqrt {\frac {4}{3}\left (1-\text{Tr}\left (\rho _{AB}^2\right )\right )}$. The n-partite concurrence is essentially the geometric mean of the concurrence over the set of all possible bipartitions, which is similar to the GME concurrence [51], although the latter is defined as the minimum value of the concurrence over all bipartitions. This inherently implies that the four-qubit concurrence is zero if and only if the four-qubit pure state is separable to some degree. Plotting the four-qubit concurrence $C_{A_1A_2B_1B_2}$ along with the two-qubit concurrences $C_{A_1B_2} (= C_{A_2B_1})$ and $C_{A_1A_2} (= C_{B_1B_2})$, and the four-tangle $\tau _{A_1A_2B_1B_2}$, for $\frac {J^2}{g^2} = 10^4$, we obtain Fig. 8.

Fig. 8

Plot of the two- and the four-qubit concurrences and of the four-tangle for the state (35) with t in units of J∕g². The three panels are at $t= \left [0, \pi \right ]$ (left), $t= \left [ \frac {\pi }{4g^2}, \frac {\pi }{4g^2}+\pi \right ]$ (centre), and $t= \left [ \frac {\pi }{2g^2}, \frac {\pi }{2g^2}+\pi \right ]$ (right), corresponding, respectively, to the beginning, a quarter and an half of the period of the longest time-scale dictated by g⁻²

The two-qubit concurrences $C_{A_1B_1}$ and $C_{A_2B_2}$ are equal to zero at all times t. We make a note that at time $t = \frac {\pi J}{2g^2}$ we acquire a product of two Bell states similar to when we use state (31). Once again, by taking the Eigendecompositions of the partial trace of state (35) with respect to every qubit, we find that the three-tangle is zero at all times t for every partition consisting of three qubits. Combining this with the fact that at certain times t, we have that the only non-zero two-qubit concurrences are $C_{A_1A_2}$ and $C_{B_1B_2}$ and that the four-qubit concurrence $C_{A_1A_2B_1B_2}$ is also non-zero, meaning that the state is fully inseparable, implies that there must be some non-zero value of exclusive four-way entanglement shared between the senders and the receivers.

8 Conclusion

In this chapter, we have adopted the general framework of quantum dynamical maps in order to investigate some instances of controlled quantum information dynamics on spin networks. Specifically, we considered those maps emerging from the dynamics of a subset of spin-$\frac {1}{2}$ particles embedded in a larger network that we divided into sender and receiver parts for convenience. Focusing on the case of a U(1)-symmetric Hamiltonian governing the dynamics of the network, we have derived the explicit form of the dynamical map in terms of the excitation transfer amplitude and applied it to review both single-qubit quantum state transfer and two-qubit transfer and corresponding entanglement generation. Finally, we have considered a specific topology of the network where analytical solutions are available for the transfer amplitude and have shown that the quantum map formalism allows the analysis of more complex scenarios such as multi-qubit entanglement generation. It is interesting to note that Ref. [52] provides another means of investigating entanglement generation in quantum state transfer protocols that has not been investigated in this chapter.

The range of applicability of the illustrated approach goes well beyond the cases investigated in this chapter, as it can be easily extended to include classical communication feedback, constraints on the achievable quantum information protocols stemming from the symmetries of the Hamiltonian reflected in the quantum map, and spin networks exposed to external noise.