Entanglement Dynamics in Spin Chains with Structured Long-Range Interactions

Abstract

The systems we encounter most often in condensed matter physics generally exhibit effective local interactions in regular 3D, 2D, or 1D structures. In these systems, correlations tend to spread, and entanglement builds up in a way constrained by a so-called Lieb–Robinson bound—where the development of correlations in time is strong within a lightcone (often determined away from criticality by the maximum group velocity for quasiparticles in a system), and correlations tend to decay exponentially outside that lightcone. This constrains (or delays) the development of entanglement, especially between distant regions in such systems.

1 Introduction

The systems we encounter most often in condensed matter physics generally exhibit effective local interactions in regular 3D, 2D, or 1D structures. In these systems, correlations tend to spread and entanglement builds up in a way constrained by a so-called Lieb–Robinson bound—where the development of correlations in time is strong within a lightcone (often determined away from criticality by the maximum group velocity for quasiparticles in a system), and correlations tend to decay exponentially outside that lightcone. This constrains (or delays) the development of entanglement, especially between distant regions in such systems.

With quantum simulators in atomic, molecular, and optical physics, we now have opportunities to go beyond this paradigm. In non-relativistic settings, we can obtain effective long-range interactions, ranging from direct dipole–dipole interactions in polar molecules, to genuine long-range interactions for experimental setups such as chains of trapped ions (mediated by the collective motional modes of the trapped ions) or atoms in optical cavities (mediated by light in the cavity). Experiments with neutral atoms in tweezer arrays (where interactions are mediated by exciting atoms to a Rydberg level with high principal quantum number) typically give us short-ranged Van der Waals interactions, but we can generate effective long-range interaction graphs by moving atoms in the traps. This gives us the opportunity to ask how the build-up of entanglement changes in these unusual systems with long-range interactions.

In this chapter, we give an introduction to these concepts, beginning in Sect. 2 by describing techniques that can be used to analyze these systems (including Lieb–Robinson bounds, quasiparticle techniques, and numerical methods), before discussing examples of spin chains with interactions decaying with distance R as R^−α for some α ≥ 0 in Sect. 3, and then sparse coupling graphs in Sect. 4. Such sparse graphs could be used to realize fast scrambling of information, in which we build up entanglement on timescales growing as t_∗∝log(N) with the system size, N. In Sect. 5, we then briefly discuss the implementations of each of the classes of models that we treat in the chapter, across trapped ions, neutral atoms in optical cavities, and tweezer arrays for neutral atoms with Rydberg excitations.

2 Quantifying Entanglement and Information Spreading

2.1 Measures of Entanglement Entropy

Let us consider a quantum system Q defined on a Hilbert space $\mathcal {H}$, which we split into two sub-Hilbert spaces A and B, $\mathcal {H} = \mathcal {H}_A \otimes \mathcal {H}_B$ with dimensions $D_{A,B} = \mathrm {dim}(\mathcal {H}_{A,B})$. By definition, entanglement between A and B implies that a state cannot be written in a product state form, i.e.,

(1)

where the states are defined on the sub-Hilbert spaces $\mathcal {H}_{A,B}$, respectively. The amount of entanglement can now be analyzed by constructing the reduced density matrix of either the sub-system A or B; w.l.o.g., focusing on sub-system A, it is defined as

(2)

where the trace is taken over sub-system B. In case of a product state , the reduced density matrix trivially becomes and is thus pure quantum states. This implies that all information about the state of sub-system A is contained in ρ_A and thus readily available through experimental probes of this sub-system. For a general entangled state that fulfills inequality (1), however, this is not true. The presence of entanglement implies that ρ_A will be a mixed density matrix. Now, information on the quantum state is encoded also in quantum correlations between A and B. Therefore, the entropy of ρ_A, i.e., the lack of information in ρ_A, provides a way to directly quantify the amount of such correlations.

Arguably, the most prominent definition for entropy is the von Neumann entropy,

$$\displaystyle \begin{aligned} S_A = S_{\mathrm{VN}}(\rho_A) = -\mathrm{tr}(\rho_A \mathrm{log}_2 \rho_A) = -\sum_\alpha^{D_A} \lambda_\alpha \mathrm{log}_2 \lambda_\alpha, {} \end{aligned} $$

(3)

where in the last step we have introduced the positive eigenvalues of ρ_A, λ_α ≥ 0 that must fulfill ∑_αλ_α = 1. Note that the base of the logarithm in the definition varies throughout the literature, however for spin-1/2 models or qubits log₂ is a convenient choice. For product states, it is easy to see that $S_{\mathrm {VN}}(\rho _A^{\mathrm {ps}})=0$ since the reduced density matrix only has one eigenvalue λ₁ = 1. The largest possible entropy occurs for maximally mixed states, for which all eigenvalues are λ_α = 1∕D_A, and thus for a bipartition of dimension D_A, the von Neumann entropy ranges between 0 ≤ S_VN(ρ_A) ≤log₂(D_A).

For example, considering a maximally entangled Bell state between two spin-1/2 particles, , the reduced density matrix for the first spin becomes corresponding to the largest possible von Neumann entropy of S_VN(ρ_A) = −log₂(1∕2) = 1.

Unfortunately, computing von Neumann entropies typically requires the knowledge of all eigenvalues of the reduced density matrix, i.e., knowledge of the full density matrix. Experimentally measuring full density matrices in experiments can be extremely cumbersome and becomes very difficult with increasing D_A. A quantity for measuring the “mixed-ness” of a reduced density matrix that can be experimentally more easily accessible is the purity $\mathrm {tr}(\rho _A^2)$, or more generally, non-linear functionals of the form $\mathrm {tr}(\rho _A^n)$ with integer n > 1 [1, 2]. Those are directly connected to the Rényi entropy of order n, which is defined as

$$\displaystyle \begin{aligned} S_A^{(n)} = S_n(\rho_A) = \frac{1}{1-n} \mathrm{log}_2 \mathrm{tr}(\rho_A^n). {} \end{aligned} $$

(4)

Formally, taking n as an arbitrary real-valued number, the Rényi entropy becomes equivalent to the von Neumann entropy in the limit S_VN(ρ_A) =lim_n→1S_n(ρ_A). Furthermore, the second-order Rényi entropy provides a lower bound to the von Neumann entropy, S_VN(ρ_A) ≥ S₂(ρ_A), and combinations of different Rényi entropies can be constructed to yield stronger bounds such as S_VN(ρ_A) ≥ 2S₂(ρ_A) − S₃(ρ_A) ≥ S₂(ρ_A), see Fig. 1.

Fig. 1

Entanglement entropy, operator growth, and Lieb–Robinson Bounds. (a) The time-dependent growth of various entanglement entropies in a soft- and hard-core Bose–Hubbard model (hopping rate J). The hard-core model is equivalent to an XY spin chain. The Rényi entropies S_n can be experimentally more easily accessible than the von Neumann entropy S_VN. The Rényi entropies S_n for n > 2 constitute lower bounds to the von Neumann entropies S_VN and can be used in combination to construct tight bounds (dashed black line: 2S₂ − S₃). Here, all entropies exhibit a growth behavior linear in time. Reprinted from [2]. (b) Growth of the operator $\mathcal {O}_i(t)$ (purple) in the Heisenberg picture on a sparse nonlocal graph G. (c) Lieb–Robinson bounds for 2-local Hamiltonians. Top: The bound is obtained by summing over contributions from connected chains linking vertices i, j. Each new “link” in the chain need not be added at the end of the chain; it may be added anywhere along the chain as illustrated by the “dead end” link marked a. Bottom: Linear lightcone for a one-dimensional, nearest-neighbor spin chain (reproduced from [3])

In practical settings, entanglement entropies can be used to analyze the time-dependent growth of entanglement in spin chains after a quench both in experiments and theory. To avoid boundary effects and to accommodate as much entanglement as possible, it is common to split a chain of N spins into two halves of N∕2 spins and to compute S_VN or S_n for the reduced density matrix of half of the chain. The time-dependent growth behavior of the entropy can then give important insight into the entanglement spreading and the correlation build-up in the chain. For example, a linear growth of S_VN or S_n can be a consequence of entangled quasiparticles with a linear dispersion relation (see below). Furthermore, linear entanglement growth can be connected to a computational complexity increasing exponentially in time (see Sect. 2.4) and is therefore of general interest for validating analog quantum simulation applications.

Note that in any realistic experiment, there will remain small but finite couplings to an environment. Then, the definition of entanglement as entropy in a bipartition becomes more delicate since a bipartition of the chain into two blocks is effectively a tripartition with the environment acting as third party. Then, entropy in sub-system A can originate from entanglement with the other chosen block B, or from entanglement with the environment. In such cases, statements about true entanglement in the chain can still be made in scenarios where the entropy of the full chain density matrix ρ remains sufficiently small, i.e., smaller than the sub-system entropies S_VN(ρ) < S_VN(ρ_A) [or S_n(ρ) < S_n(ρ_A)].

Finally, what is the maximum amount of entanglement that a system of N degrees of freedom can support? Quantum states in which every particle is maximally entangled are referred to as volume-law or scrambled states and feature a von Neumann entropy $S_{\mathrm {VN}} \propto \left |A\right |$ that grows like the number of degrees of freedom in region A for any bipartition Q = A ∪ B of the system (with $\left |A\right | < N/2$). Although such a high degree of entanglement is difficult to engineer in practice due to the destructive effects of decoherence, these volume-law states are actually quite generic, in the sense that a pure quantum state chosen uniformly at random from the many-body Hilbert space will have, on average, volume-law entanglement entropy

$$\displaystyle \begin{aligned} S_{\mathrm{VN}}(\rho_A) = - \frac{m-1}{2n} + \sum_{k = n+1}^{mn} \frac{1}{k} \approx {\mathrm{ln}} m - \frac{m}{2n} \end{aligned} $$

(5)

so long as 1 ≪ m ≤ n, where |A| = log₂m and |B| = log₂n [4].

2.2 Lieb–Robinson Bounds and OTOCs

In the previous section, we quantified entanglement growth by looking at the entropy of a local region A, quantified by the von Neumann entropy of the reduced density matrix ρ_A. Complementary to this state-centric notion of entanglement based on the Schrödinger picture, one can alternatively formulate an operator-centric notion of entanglement growth based on the Heisenberg picture. In many cases, this operator growth picture provides a more intuitive description for the growth of correlations in the system. It also naturally leads to discussion of fundamental Lieb–Robinson (LR) bounds and out-of-time-order correlators (OTOCs) that diagnose the spread of quantum information in the system.

Suppose we consider a system of N qubits, and we store information in a localized region A using an operator $\mathcal {O}_{A}$. In particular, one can imagine starting from a particular reference state ρ and perturbing it by some local operator $\mathcal {O}_{A}$ that encodes some information in the perturbed state. The subsequent growth of correlations in the system can be completely captured by the evolution of the operator O_A in the Heisenberg picture:

$$\displaystyle \begin{aligned} \mathcal{O}_{A}(t) = U_t \mathcal{O}_{A} U^{\dagger}_t = \sum_{{\mathbf{r}}} a_{{\mathbf{r}}}(t) \sigma^{{\mathbf{r}}}. \end{aligned} $$

(6)

In the last expression, we have expanded the operator in the orthonormal basis of many-body Pauli strings $\sigma ^{{\mathbf {r}}} = \sigma _1^{r_1} \sigma _2^{r_2} \ldots \sigma _N^{r_N}$, where $\sigma _i^{0,1,2,3}$ are the Pauli matrices on site i (with $\sigma _i^0 = \mathbb {I}_i$) and r = r₁r₂…r_N is a N-component string encoding which Pauli operators are present on each site. The time-dependent coefficients a^r(t) can be viewed as the “wavefunction” of the operator $\mathcal {O}_{A}(t)$ when expanded in the Pauli string basis and can be obtained by taking an operator inner product

$$\displaystyle \begin{aligned} a_{{\mathbf{r}}}(t) = \mathrm{Tr}\left[ \mathcal{O}_{A}(t) \sigma^{{\mathbf{r}}} \right]. \end{aligned} $$

(7)

These coefficients are real and normalized $\sum a_{{\mathbf {r}}}(t)^2 = 1$ when $\mathcal {O}_{A}$ is Hermitian and normalized.

Under generic scrambling dynamics, the initially localized operator $\mathcal {O}_{A}(0)$ rapidly grows into a complicated operator $\mathcal {O}_{A}(t)$, where the operator wavefunction a_r(t) acquires significant weight on large many-body Pauli strings. We can characterize this growth and simultaneously characterize the coefficients a_r(t), by considering commutators $[\mathcal {O}_{A},\sigma _j^{\alpha }]$ between the growing operator $\mathcal {O}_{A}$ and localized Pauli operators $\sigma _j^{\alpha }$, which we refer to as “probe” operators. A judicious choice of probe operators allows one to quantitatively map out the growth of the operator $\mathcal {O}_{A}(t)$. In particular, at t = 0, probe operators $\sigma _j^{\alpha }$ localized on sites outside of the region A must necessarily commute with $\mathcal {O}_{A}$: $[\mathcal {O}_{A}(0),\sigma _j^{\alpha }] = 0$. As the operator $\mathcal {O}_{A}(t)$ grows in time, however, it builds up nonzero weight on operators outside of A, causing the probe operators to fail to commute with $\mathcal {O}_{A}(t)$: $C(t) = [\mathcal {O}_{A}(t),\sigma _j^{\alpha }] > 0$. The size of this commutator, as measured by the operator norm $||C(t)|| = \sqrt {\mathrm {Tr}\left [ C^{\dagger } C \right ]}$, tells us “how much” of the operator $\mathcal {O}_{A}$ is present on site j (i.e., what fraction of $\mathcal {O}_{A}$ acts nontrivially on site j) (see Fig. 1b). These commutators provide direct evidence of entanglement growth in the system via a nonstandard correlation function called the out-of-time-order correlator (OTOC) [5,6,7].

Analysis of these commutators can be used to place fundamental bounds on the spread of information in the quantum system.

Historically, Lieb–Robinson bounds have been used to show the existence of an emergent “lightcone” in lattice systems that limits the speed of information propagation, similar to the speed of light in special relativity. Various forms of Lieb–Robinson bounds have been established for systems featuring both short-range [8, 9] and long-range [10,11,12,13] interactions. Here, we present generalized Lieb–Robinson bounds that apply to arbitrary 2-local Hamiltonians defined on any graph G, regardless of its connectivity or locality. In doing so, we demonstrate how the growth of operators $\mathcal {O}_{i}(t)$ is intimately tied to the structure of the interaction graph. The beauty of this approach is that it expresses the spread of quantum information in terms of standard results from graph theory, a well-developed branch of mathematics for which many powerful techniques and results are readily available [14,15,16]. We therefore begin by introducing the requisite graph theory terminology.

For simplicity, we will consider here only 2-local Hamiltonians. Similar results for the more general k-local case are derived in Appendix B of Ref. [17]. To any 2-local Hamiltonian

$$\displaystyle \begin{aligned} H = \sum_{(i, j)\in E} H_{ij}, {} \end{aligned} $$

(8)

we may associate a discrete, undirected graph G = (V, E), where degrees of freedom live on the vertices i ∈ V  and interact pairwise via couplings H_ij if and only if the pair i, j is connected by an edge e = (i, j) ∈ E. The connectivity of the graph G is described by the adjacency matrix

$$\displaystyle \begin{aligned} \mathcal{A}_{ij} = \left\lbrace \begin{array}{ll} 1 &\ (i,j) \in E \\ 0 &\ (i,j)\notin E\end{array}\right. \end{aligned} $$

(9)

and the degree matrix $\mathcal {D}_{ij} = k_i \delta _{ij}$, where the degree $k_i = \sum _j \mathcal {A}_{ij}$ of a given vertex i counts the number of vertices it is connected to. To be concrete, a familiar model of this form is the 2-dimensional Heisenberg spin model

$$\displaystyle \begin{aligned} H = J \sum_{\langle i,j \rangle} {\mathbf{S}}_i \cdot {\mathbf{S}}_j, \end{aligned} $$

(10)

with interaction graph G given by a regular D-dimensional square lattice where the sum is over nearest neighbors 〈i, j〉. The spin-1/2 degrees of freedom S_i reside on the vertices i of the lattice and interact via nearest-neighbor SU(2)-symmetric 2-body terms H_ij = JS_i ⋅S_j represented by the edges e of the graph, such that all vertices have degree k_i = 4 (assuming an infinite lattice).

We derive Lieb–Robinson bounds for 2-local models of the form (8) by expanding the commutator C(t) in powers of t and bounding each term in the sum. For probe operators $\mathcal {O}_{i},\mathcal {O}_{j}$ on vertices i ≠ j, we have

$$\displaystyle \begin{aligned} \left\|[\mathcal{O}_{j},\mathcal{O}_{i}(t)]\right\| \leq \left\|[\mathcal{O}_{j},\mathcal{O}_{i}]\right\| + t \left\|[\mathcal{O}_{j},[H,\mathcal{O}_{i}]]\right\| + \frac{t^2}{2!} \left\|[\mathcal{O}_{j},[H,[H,\mathcal{O}_{i}]]]\right\| + \cdots, \end{aligned} $$

(11)

where we have used the Baker–Campbell–Hausdorff formula to expand the exponentials in terms of nested commutators, and the triangle inequality to bound the commutator norm. The nested commutators on the right-hand side simplify considerably when we observe that commutators on disjoint sets vanish so that, for instance, $[\mathcal {O}_{j},[H,\mathcal {O}_{i}]] = [\mathcal {O}_{j},[H_{ij},\mathcal {O}_{i}]]$. As a result, the only nested commutators that survive are those corresponding to connected chains of 2-body terms (H_jx, H_xy, …, H_zi) on the interaction graph G that begin on vertex j and end on vertex i, as illustrated in Fig. 1c. Note that the consecutive links of these chains need not connect end-to-end: new links are allowed to be connected anywhere along the existing chain. For simplicity, we have also ignored all onsite terms (which can always be absorbed into the two-site terms in (8)). The fact that the bound can be written in terms of connected chains on the graph clearly illustrates that the structure of the interaction graph G plays a central role in our bounds on OTOC growth. We further simplify the right-hand side by applying the inequality $\left \|[A,B]\right \| \leq 2\left \|A\right \|\left \|B\right \|$ recursively to the nested commutators to obtain

$$\displaystyle \begin{aligned} \frac{\left\|[\mathcal{O}_{j},\mathcal{O}_{i}(t)]\right\|}{2 \left\|\mathcal{O}_{j}\right\|\left\|\mathcal{O}_{i}\right\|} \leq 1 + 2t \left\|H_{ij}\right\| + \frac{(2t)^2}{2!} \sum_x \left\|H_{jx}\right\| \left\|H_{xi}\right\| + \cdots {} \end{aligned} $$

(12)

Finally, we choose a constant c that bounds all 2-body terms in the Hamiltonian

$$\displaystyle \begin{aligned} \frac{c}{K} \geq \left\|H_{ij}\right\|, \end{aligned} $$

(13)

where $K = \frac {1}{N} \sum _i k_i$ is the mean degree of the graph G and c is a constant independent of N such that the Hamiltonian is extensive [10, 17]. Substituting the constant c∕K into Eq. (12) and resuming the right-hand side, we obtain the normalized out-of-time-ordered correlator (OTOC):

$$\displaystyle \begin{aligned} C_{ij}(t) \equiv \frac{\left\|[\mathcal{O}_{j},\mathcal{O}_{i}(t)]\right\|}{2 \left\|\mathcal{O}_{j}\right\|\left\|\mathcal{O}_{i}\right\|} \leq \mathrm{exp} \left[\frac{2 c \left|t\right|}{K} (\mathcal{D}+\mathcal{A}) \right]_{ij}, {} \end{aligned} $$

(14)

which depends only on the graph-theoretic quantities $\mathcal {A}_{ij},\mathcal {D}_{ij}$ and time t in units of the constant c∕K [17].

As a simple example, we can consider a one-dimensional chain with closed boundary conditions. In this case, the matrix $\mathcal {A}+\mathcal {D}$ is simply a circulant matrix:

$$\displaystyle \begin{aligned} \mathcal{A}+\mathcal{D} = \begin{bmatrix} 2 & 1 & 0 & 0 & \dots & 1 \\ 1 & 2 & 1 & 0 & & 0 \\ 0 & 1 & 2 & 1 & & 0 \\ \vdots & & & & \ddots & \\ 1 & 0 & 0 & 0 & & 2 \end{bmatrix} \end{aligned} $$

(15)

that can be easily diagonalized. From this result, we recover a linear lightcone, plotted in Fig. 1c, as originally predicted by Lieb and Robinson [8]. The generalized Lieb–Robinson bound in Eq. (14), however, is more powerful than the original result of Lieb and Robinson because it applies not only to regular lattice systems but also to quantum systems defined on arbitrary interaction graphs G. Moreover, the generalized bound contains detailed information about the graph structure, encoded in the matrices $\mathcal {A},\mathcal {D}$.

Because the result in Eq. (14) bounds the operator norm $\left \|\cdot \right \|$, the bound characterizes operator growth at infinite temperature since $\left \|\mathcal {O}_{}\right \|{ }^2 = \mathrm {Tr}\left [ \rho ^{\infty } \mathcal {O}_{ }^{\dagger } \mathcal {O}_{} \right ]$, where ρ^∞ is the infinite-temperature ensemble. At finite temperature, operators necessarily grow more slowly; obtaining tighter bounds at finite temperature is still an open problem [17,18,19,20]. We generally expect the spreading of information to slow down at finite temperature since the system has a much smaller probability of exciting high-energy modes. Roughly speaking, another way to say this is that at finite temperature the effective Hilbert space is reduced to a subspace consisting of eigenvectors whose energies are comparable to or less than the temperature. Because of this reduced Hilbert space, there are fewer accessible states and therefore fewer ways for information to propagate.

2.3 Quasiparticle Approaches

The spreading of correlations through a system and its limitations in terms of Lieb–Robinson bounds is connected to the growth of entanglement entropies after quenches. This connection can be made by means of quasiparticle excitations in situations where a quadratic Hamiltonian can be brought to a diagonal form in second quantization. To illustrate the concept, let us take a long-range transverse Ising spin chain with interactions decaying as a power law. The Hamiltonian can be written as

$$\displaystyle \begin{aligned} H_{\mathrm{LRTI}} = \sum_{i<j} \frac{\bar{J}}{|i-j|{}^\alpha} \sigma^x_i \sigma_j^x + B \sum_i \sigma_i^z. {} \end{aligned} $$

(16)

Here, $\bar {J}$ is the nearest-neighbor interaction strength, α is the power-law decay exponent, B is the transverse field strength, and $\sigma _i^{x,z}$ are the usual Pauli matrices. In one dimension, the Pauli matrices can be mapped to fermionic field operators c_i by a Jordan–Wigner transformation. Then, in the nearest-neighbor limit α →∞ after a transformation to quasimomentum space, the fermionic model is quadratic and can be diagonalized with a Bogoliubov transformation [21] giving rise to a Hamiltonian of the form (up to constants)

$$\displaystyle \begin{aligned} H_{\mathrm{LRTI}}^{\alpha \to \infty} = \sum_q \epsilon_q \gamma_q^\dag \gamma_q. \end{aligned} $$

(17)

Here, $\gamma _q^\dag$ are creation operators for fermionic quasiparticle excitations with quasimomentum q. They are superpositions of the fermionic field operators c_q with opposite quasimomenta $\gamma _q^\dag = u c_q^\dag - v c_{-q}$, where u and v are the Bogoliubov expansion coefficients, which depend on $\bar J$ and B. The dispersion relation for the quasiparticles is given by $\epsilon _q=2\sqrt {(\bar {J}-B)^2 + 4 \bar {J}B \sin ^2(q/2)}$. In a quench setup, the initial state is a highly excited state, which is not an eigenstate of the diagonal quasiparticle Hamiltonian. This gives rise to the following picture for entanglement build-up in the dynamics after the quench [22] (see illustration in Fig. 2a): The initially highly excited state serves as reservoir for producing quasiparticle excitations. Those quasiparticles are entangled superpositions of excitations with opposite momentum and spread through the system. The speed of their propagation is given by the group velocity v_g = d𝜖_q∕dq. For example, in the case of the nearest-neighbor transverse Ising model, their speed is limited by the maximum group velocity $\max |v_g| = 2J$. The propagating entangled pairs lead to a build-up of entanglement between blocks of the chain. A constant arrival rate of quasiparticles in the right half of the chain (R) that originated in the left half (L) therefore leads to a linear growth of entanglement entropies between L and R with time [22].

Fig. 2

(a) Illustration of entanglement distribution by propagation of entangled quasiparticles. Entangled quasiparticles spread through the system in opposite directions with group velocities ± v_g. Finite size effects become important when the fastest quasiparticles reach the boundary, here at time t^∗. This picture remains valid for relatively short-ranged interactions. (b) Quasiparticle propagation seen in the evolution of the mutual information I between distant spins i = 1 and j = 8 (here for a quench in a transverse Ising model with interactions decaying as a power law with distance $\sim \bar {J}/|i-j|{ }^\alpha$). For relatively short-ranged interactions (α = 2), the distant spins suddenly become entangled by a quasiparticle arrival at a time $t\overline {J} \sim 2$. For longer-ranged interactions α < 2, this picture breaks down. (c) Entanglement growth can be analyzed by means of quasiparticle spectra. Here, quasiparticle dispersion relations 𝜖(k) and the corresponding densities of states D(k) are shown for an exactly solvable long-range fermionic hopping model (power-law exponent α, see [23]). Shorter-range interactions (large α) lead to smooth 𝜖(k) and thus quasiparticles with well-defined group velocities. Long-range hoppings (small α) can lead to cusps and divergences in 𝜖(k). ((a) and (b) reproduced from [24], (c) reproduced from [23])

Importantly, the study of quasiparticle spectra can also be a useful approach for understanding entanglement growth in the presence of long-range interactions. While in general a Bogoliubov diagonalization is not possible for Hamiltonians such as (16), exceptions exist. For example in certain limits, linear spin-wave theories remain a valid approximation [23, 25, 26], or for related models with long-range fermionic hopping, also exact diagonalizations are sometimes possible [23, 27, 28].

We will exemplify the linear spin-wave approach for Hamiltonian (16), which is based on Holstein–Primakoff transformation. Traditionally defined for spin-S operators, this transformation reads

$$\displaystyle \begin{aligned} S_i^z &= a_i^\dag a_i - S \end{aligned} $$

(18)

$$\displaystyle \begin{aligned} S_i^- &= \sqrt{2S - a_i^\dag a_i} a_i \end{aligned} $$

(19)

$$\displaystyle \begin{aligned} S_i^+ &= a_i^\dag \sqrt{2S - a_i^\dag a_i}. \end{aligned} $$

(20)

Here, the spin operators for a spin at site i are expressed in terms of bosonic field operators $a_i^\dag$. We assume a quench setup, where the initial state is given by the fully polarized state with . For short enough times where the state remains sufficiently close to , one can linearize the Holstein–Primakoff transformation using the assumption of small occupation number of the bosonic modes, $\langle a_i^\dag a_i \rangle \ll 2 S$. Then,

$$\displaystyle \begin{aligned} S_i^- &\approx \sqrt{2S} a_i \end{aligned} $$

(21)

$$\displaystyle \begin{aligned} S_i^+ &\approx \sqrt{2S} a_i^\dag. {} \end{aligned} $$

(22)

Using $\sigma _i^z = 2 a_i^\dag a_i^\dag - 1$ and $\sigma _i^x \approx a_i+ a_i^\dag$ in this limit, Hamiltonian (16) becomes quadratic (constants are dropped):

$$\displaystyle \begin{aligned} H_{\mathrm{LRTI}} \approx \sum_{i<j} \frac{\bar{J}}{|i-j|{}^\alpha} \left(a_i a_j + a_i^\dag a_j + a_i a_j^\dag + a_i^\dag a_j^\dag\right) + 2 B \sum_i a_i^\dag a_i^\dag. \end{aligned} $$

(23)

A discrete Fourier transform into quasimomentum space for a spin chain with N spins, $b_q = \sum _j \mathrm {exp}(-\mathrm {i} q j) /{\sqrt {N}}$ for N discrete momentum values − π∕2 < q ≤ π∕2, leads to

$$\displaystyle \begin{aligned} H_{\mathrm{HP}} \approx \sum_{q} \mathcal{J}(q) \left(b_{-q} b_{q} + b_{q}^\dag b_{-q}^\dag\right) + \sum_{q} \left(\mathcal{J}(q) +\frac{B}{2}\right) \left(b_{q}^\dag b_{q} + b_{-q} b_{-q}^\dag\right). \end{aligned} $$

(24)

Here a crucial quantity is the Fourier transform of the power-law decaying function

$$\displaystyle \begin{aligned} \mathcal{J}(q) = \bar{J} \sum_d \frac{\mathrm{e}^{-\mathrm{i} d q}}{|d|{}^\alpha} \xrightarrow{N \to \infty} 2 \bar{J} \mathrm{Re}\left(\mathrm{Li}_\alpha(\mathrm{e}^{iq})\right), \end{aligned} $$

(25)

where in the first term the distance d runs over all pairwise distances from − N + 1 < d < N − 1 and the last term is an analytical expression in terms of the polylogarithm Li_n(z) of order n in the infinite system size limit N →∞.

Using a bosonic Bogolioubov transformation [23], the Hamiltonian can again be transformed into a diagonal form with new bosonic field operators that are a superposition of the Holstein–Primakoff bosons b_±q of opposite momenta. Crucially, the dispersion relation of the new quasiparticle excitations can be computed to be

$$\displaystyle \begin{aligned} \epsilon(q) = 2B \sqrt{1 + \frac{\mathcal{J}(q)}{B}}. {} \end{aligned} $$

(26)

It is important to re-emphasize that this quasiparticle dispersion result is only valid in the limit $\langle b_q^\dag b_q \rangle \ll 1$, which is true for sufficiently short times, i.e., sufficiently few quasiparticle excitations. It is clear that the timescale of validity increases with B since for B →∞ the initial state becomes an eigenstate and remains constant in time. The constraint of the validity of the Holstein–Primakoff ansatz is also visible in Eq. (26), which requires $B>\mathcal {J}(q)$ for 𝜖(q) to remain real.

In the limit of its validity, Eq. (26) allows to make statements about the quasiparticle nature of the entangling dynamics after the quench. For example, considering the limit of long-wavelength excitations |q|→ 0, one can derive that the limiting behavior of the dispersion relation for α < 0 is given by

$$\displaystyle \begin{aligned} \epsilon(q) \propto q^{\frac{\alpha-1}{2}}. \end{aligned} $$

(27)

The negative exponent implies that for α < 1, there are quasiparticle excitations with infinite group velocities that ultimately have to lead to a breakdown of the picture of propagating entangled quasiparticles. Furthermore, from this analytical ansatz, one can deduce that for 1 < α < 2 a cusp at q = 0 appears in the dispersion relation 𝜖(q). This means that the group velocity v_g = d𝜖(q)∕dq is already starting to diverge for $\alpha \lesssim 2$ [25]. In contrast, in general for α ≳ 2, the quasiparticle propagation picture remains to be valid, as e.g. demonstrated in Fig. 2b. There we show the propagation of correlations between spins at two distant sites i = 1 and j = 8 of a chain. Here this correlation is quantified by the mutual information I_i,j = S_VN(ρ_i) + S_VN(ρ_j) − S_VN(ρ_ij) with S_VN(ρ_i) and S_VN(ρ_ij) the von Neumann entropies of reduced density matrices on single- and two-spin Hilbert spaces, respectively. For the case of a clear entangled quasiparticle propagation (α = 2), the correlation between distant sites suddenly starts to establish at a “quasiparticle” arrival time of $t\bar J \sim 2$. In contrast, for α < 2, the distant sites become entangled immediately.

Finally, we want to point out that in a quasiparticle analysis, it is important to not only consider quasiparticle dispersion relations, but also to analyze the density of states at the respective quasimomenta. In Fig. 2c, we show the dispersion relation 𝜖(k) and the density of states D(k) for Bogoliubov excitations with quasimomentum k for a long-range fermionic hopping model [23] that can be computed exactly. Interestingly, qualitatively, this model has very similar features as the long-range interacting transverse Ising model in the linear spin-wave limit. Importantly, one finds that while the group velocity diverges for α < 2 and k → 0, here one also finds that D(k) → 0 is even more strongly suppressed, leading to an effective overall suppression of the correlation build-up.

2.4 Matrix Product States (MPS)

In one dimension, the study of entanglement growth in spin models can be assisted by very powerful numerical methods based on the so-called matrix product states (MPS). Let us consider the general time-evolved state of a chain with N spin-D particles and focus on pure Hamiltonian dynamics. The state at time t can be written in the basis of the local spin Hilbert spaces:

(28)

Here, i_n = 1, …, d are the local indices for an orthogonal basis of spin n, , with dimension d = 2S + 1. The difficulty of numerically simulating Hamiltonian dynamics of a spin chain on a classical computer stems from the exponential growth of the size of the complex states tensor $c_{i_1,i_2,\dots ,i_N}$ with system size N, $\dim (c_{i_1,i_2,\dots ,i_N})=d^{N}$. Importantly, the size of this state tensor can be drastically reduced by restricting the amount of entanglement. For example, let us consider the most extreme scenario and restrict the state tensor to product states only, which by definition excludes any entanglement. Then,

$$\displaystyle \begin{aligned} c^{\mathrm{PS}}_{i_1,i_2,\dots,i_N}(t) \approx c^{[1]}_{i_1}(t)c^{[2]}_{i_2}(t),\dots,c^{[N]}_{i_N}(t), {} \end{aligned} $$

(29)

and the state representation only requires Nd normalized complex amplitudes, $\sum _{i_n} |c^{[n]}_{i_n}(t)|=1$. Choosing for example some sub-system block A with indices {i₁, …, i_c}, the reduced density matrix is

(30)

This is a pure density matrix since $\mathrm {tr}\left \{{\left [\rho ^{\mathrm {PS}}_A(t)\right ]^2}\right \} = 1$, and therefore, the entanglement entropy (see Sect. 2.1) vanishes, $S_{\mathrm {VN}}(\rho ^{\mathrm {PS}}_A(t))=0$, for all times. Therefore, by choosing the product state ansatz (29), the numerical memory requirement is drastically reduced from $\mathcal {O}(d^N)$ to $\mathcal {O}(dN)$, which however comes at the cost of neglecting entanglement entropies entirely.

A matrix product state (MPS) can be thought of as a generalization of the product state ansatz (29) to states with finite entanglement. An MPS is a decomposition of the state tensor of the form

$$\displaystyle \begin{aligned} c^{\mathrm{MPS}}_{i_1,i_2,\dots,i_N} = \boldsymbol{\Gamma}_{i_1}^{[1]} \boldsymbol{\Gamma}_{i_2}^{[2]} \dots \boldsymbol{\Gamma}_{i_N}^{[N]} = \sum_{\alpha_1}^{\chi_1} \sum_{\alpha_2}^{\chi_2} \dots \sum_{\alpha_{N+1}}^{\chi_{N+1}} \Gamma_{i_1}^{[1];\alpha_1 \alpha_2} \Gamma_{i_2}^{[2];\alpha_2 \alpha_3} \dots \Gamma_{i_N}^{[N];\alpha_{N} \alpha_{N+1}}. {} \end{aligned} $$

(31)

Here we introduced N three-dimensional tensors, $\Gamma _{i_n}^{[n];\alpha _{n} \alpha _{n+1}}$, which can be thought of as χ_n × χ_n+1 matrices where the matrix elements are local kets on site n, $\boldsymbol {\Gamma }_{i_n}^{[n]}$. The state tensor is decomposed into a matrix multiplication of the $\boldsymbol {\Gamma }_{i_n}^{[n]}$ matrices on different sites, hence the name matrix product state. A common diagrammatic depiction of an MPS is shown in Fig. 3a: There, each colored box denotes an MPS tensor $\boldsymbol {\Gamma }_{i_n}^{[n]}$. Each line represents an index, and each line connecting the colored boxes implies a summation over that index. A tensor at site n connects to the tensors at sites n − 1 and n + 1, and the connecting indices α_n are also known as “bond indices.” Note that at the edge we kept two “dummy indices” for which (assuming the case of box boundary conditions) we will choose χ₁ = χ_N+1 = 1. Note that if we restrict all virtual “bond” indices to a dimension of χ_n = 1, the MPS decomposition (31) becomes equivalent to the product state form (29) and again neglects entanglement. The core idea behind MPS simulations of quantum states is to increase the matrix size to a manageable magnitude, thereby allowing for enough entanglement in the dynamics to keep the simulation of the system exact. In a key approximation step, we therefore can limit the bond dimensions of all bipartitions in the chain to a numerically manageable value, $\chi _n \lesssim \chi$. One can then show [29] that in an MPS with maximum bond dimension χ we can at most capture an entanglement entropy of

$$\displaystyle \begin{aligned} S_{\mathrm{VN}}(\rho_A^{\mathrm{MPS}, \chi}) \leq \mathrm{log}_2(\chi). \end{aligned} $$

(32)

Generalizing the result for the product state ansatz, an MPS with maximum bond dimension χ reduces the memory requirement for storing a quantum state from $\mathcal {O}(d^N)$ to $\mathcal {O}(Nd\chi ^2)$. This comes at the cost of limiting von Neumann entanglement entropy across any bipartition to log₂(χ). Note again that the product state ansatz is equivalent to χ = 1 for which $S_{\mathrm {VN}}(\rho _A^{\mathrm {MPS}, \chi =1} ) = 0$.

Fig. 3

(a) Sketch of an MPS decomposition of the state tensor in a system with N = 6 spins. Limiting the virtual indices α_n to a maximum bond dimension α_n ≤ χ, the von Neumann entanglement entropy for a bipartite splitting across the bond n is limited to log₂(χ). (b–d) Sketches of various algorithms for time-evolving an MPS. (b) The TEBD algorithm is a prescription for updating two tensors of the MPS after application of a gate. An approximation is made in the final step when after a singular value decomposition of the tensor Θ the new virtual index is truncated to α_n ≤ χ. Using a Trotter decomposition of the time-evolution operator $\mathrm {e}^{-\mathrm {i} \hat H \Delta t}$ into two-site gates in combination with swap gates can be used to simulate time evolution under Hamiltonians with long-range interactions. (b) Another class of MPS time-evolution algorithms makes use of a matrix product operator (MPO) description of the Hamiltonian, using, e.g., the time-dependent variational principle (TDVP) or Runge–Kutta. They rely on variational algorithms to find an MPS approximation for the state . (d) When the time-evolution operator can be constructed in MPO form, variational algorithms to find an MPS approximation for can be used

The MPS representation (31) has been an extremely useful tool for both analyzing ground states of quantum many-body systems, e.g., the famous density matrix renormalization algorithm (DMRG) [30] is based on MPS, and studying non-equilibrium dynamics. Focusing on quench dynamics, typically, the initial states of interest are either in a trivial product state form (e.g., the fully polarized state, ) or they are the ground state of a Hamiltonian that can be computed using DMRG. To then compute the time evolution of a many-body quantum state over a time step, Δt, one needs an algorithm to update the MPS tensors time dependently such that (ħ ≡ 1)

(33)

Several algorithms exist (for sketches of the concepts, see Fig. 3b–d).

For example, algorithms can be devised on the concept of “gate applications.” In particular, since most spin Hamiltonians of interest are based on two-body terms, i.e., Hamiltonians are of the form $\hat H = \sum _{i>j} \hat H_{i,j}$, one can use a Trotter decomposition of the full matrix exponential $\mathrm {e}^{-\mathrm {i} \hat H \Delta t}$ into two-site gates $\hat U_{i,j} = \mathrm {e}^{-\mathrm {i} \hat H_{i,j} \Delta t}$ up to an controllable error depending on a small time-step size Δt [31]. For example, commonly a 2-nd- or 4-th-order decomposition is used with errors $\mathcal {O}(\Delta t^3)$ or $\mathcal {O}(\Delta t^5)$, respectively. Then time evolution can be simulated by applying the two-site gates $\hat U_{i,j}$ to an MPS. Note that this approach is equivalent to the concept of digital quantum simulation [32], where the gates would be applied in a quantum circuit. An algorithm to apply two-site gates between neighboring spins is known as time-evolving block decimation algorithm (TEBD) [33] or time-dependent DMRG [34]. The scheme is sketched in Fig. 3b. It relies on straightforward tensor contraction, followed by a singular value decomposition. Crucially, the final step consists of a truncation of the bond dimension to χ, which introduces a gate error depending on the truncated weight, $\sum _{\alpha =\chi +1}^{d\chi } \lambda _{\alpha _{c+1}}^2$. One main disadvantage of the TEBD approach is that an error is made in each gate application. For treating systems with long-range couplings, it is also required to apply swap gates that interchange the physical indices between sites, which again result in an additional error for each swap operations.

To avoid such consecutive errors, it is also possible to construct the Hamiltonian in a matrix product form. In general, the matrix product operator (MPO) form is a full description of operators on a many-body Hilbert space analogous to MPS, but with two physical indices per site (see Fig. 3c, d for a sketch). There exist variational algorithms that, for an MPO ($\hat O$) and an MPS , find an optimal new MPS with bond dimension χ such that with a known minimal error . Typically, such algorithms make use of sweeps, consecutively updating the tensors on single or neighboring sites [29]. For nearest-neighbor Hamiltonians, it is straightforward to construct $\hat H$ in an exact MPO form. For systems with long-range interactions, this can usually be done approximately. In particular, systems with power-law interactions allow to approximation $\hat H$ with an MPO of moderate MPO bond dimension by utilizing an expansion of the power-law decay into a sum of exponentials (see, e.g., [35]). Having an algorithm that can apply a Hamiltonian MPO to a state (Fig. 3c) approximately, one can then rely on standard time-evolution algorithms making use of such Hamiltonian applications, such as Runge–Kutta. A popular algorithm making use of Hamiltonian applications is for example based on the time-dependent variational principle (TDVP), which in addition to the Hamiltonian application also relies on an application of a tangent space projection operator, see e.g., [36]. Lastly, an alternative way for simulating time evolution of an MPS is to directly compute an MPO expression of the time-evolution operator over a small time step $\hat U = \mathrm {e}^{-\mathrm {i} \hat H \Delta t}$ and to use an MPO application algorithm directly. Several ways have been proposed to construct a time-evolution MPO, e.g., based on Taylor expansions of the matrix exponential (e.g., notably the so-called W^{I, II} representations [37] or methods based on “MPO doubling” [38]). In general, the computational complexity for evolving an MPS in time with one of the algorithms described above is bottle-necked by the tensor constructions and in general the computational timescales as ∼ χ³. For a recent review summarizing MPS time-evolution algorithms, see e.g., [39].

Finally, let us emphasize again that MPSs provide an ideal tool to study entanglement growth after quenches. The eigenvalues of reduced density matrices of bipartitions, $\lambda _{\alpha _{n}}^2$, are readily available from an MPS, and entanglement entropies can be computed through Eqs. (3) and (4) (see Fig. 1 for an example MPS result of entanglement growth). MPS methods make it also possible to directly connect the entanglement entropy growth behavior after a quench to a numerical complexity for simulating the quench dynamics on a classical computer. For example, in the case of a linear entropy growth as shown in Fig. 1, we can conclude that since S_VN ∝ t and since for an MPS with bond dimension χ, S_VN ≤log₂(χ) as a function of time χ needs to grow as χ ∝exp(t), and therefore, this scenario is computationally hard to simulate with an MPS.

3 Power-Law Interacting Models

Here, we will focus on spin models with long-range interactions that decay as a function of the distance between spins with a power law, i.e., with interactions of the form

$$\displaystyle \begin{aligned} J_{ij} \propto \frac{1}{|{\mathbf{r}}_i-{\mathbf{r}}_j|{}^\alpha}. \end{aligned} $$

(34)

Here, r_i are the spin position vectors, and α ≥ 0 is the power-law exponent. The main motivation for considering such interactions is that they are realized in nature, e.g., in the case of electromagnetic interactions (Coulomb: α = 1, dipole–dipole: α = 3, van der Waals: α = 6). Furthermore, they allow to arrive at mathematical conclusions depending on only a single parameter, α. The fact that interactions always decay as a function of distance allows to also keep a notion of “dimensionality.” With respect to the dimensionality d, one can classify the range of interactions into “true” long-range interactions for α < d, in which case interaction energy of the system diverges in the infinite system limit, and to scenarios where α > d and the interaction energy remains finite.

In a very general form, we can define our power-law interacting spin models of interest as

$$\displaystyle \begin{aligned} \hat H &= \sum_{i>j} \left( J_{ij}^{x} S_i^x S_j^x + J_{ij}^{y} S_i^y S_j^y + J_{ij}^{z} S_i^z S_j^z \right) + \sum_i {\mathbf{h}}_i \cdot {\mathbf{S}}_i \quad \text{with} \quad J_{ij}^{x,y,z} = \frac{\bar{J}^{x,y,z}}{|{\mathbf{r}}_i-{\mathbf{r}}_j|{}^\alpha}. {} \end{aligned} $$

(35)

Here, ${\mathbf {S}}_i = (S^x_i,S^y_i,S^z_i)$ is a vector of the three spin-S operators $S^{x,y,z}_i$. The long-range coupling constants are denoted as $J_{ij}^{x,y,z}$, and they quantify the interaction energy of two spins at distance |r_i −r_j| when they are both aligned along the x, y, z direction, respectively. $\bar {J}_{ij}^{x,y,z}$ quantifies the energy at unit distance |r_i −r_j|≡ 1. In the following, we will focus on models on a lattice, for which we define a lattice constant a ≡ 1, and thus $\bar {J}_{ij}^{x,y,z}$ reduces to the nearest-neighbor coupling strengths. In addition, we allow for local “magnetic” fields along the different dimensions given by the vector ${\mathbf {h}}_i =(h_i^x, h_i^y, h_i^z)$.

The general Hamiltonian (35) includes for example a long-range Heisenberg model, for which $J_{ij}^x = J_{ij}^y=J_{ij}^z$ or a long-range XY model with $J_{ij}^z=0$. Both are special cases of an XXZ model with $J_{ij}^x = J_{ij}^y \neq J_{ij}^z$. XY couplings are, e.g., realized for systems interacting with dipole–dipole far-field interactions for which α = 3. Such a model describes pairwise coherent energy exchange between the spins since $(S_i^x S_j^x+S_i^y S_j^y) \propto (S_i^+ S_j^- + S_i^- S_j^+)$. Note that true dipole–dipole couplings typically also feature an interaction anisotropy, i.e., an interaction energy term depending on the relative dipole orientation; however, we will here be mostly interested in 1D scenarios and aligned dipoles. In ultra-cold atom physics, dipole–dipole couplings appear for example in systems with polar molecules [40] or with magnetic atoms [41, 42]. In the case where in Eq. (35) only the spin couplings for a single particular dimension remain finite, e.g., $J_{ij}^y = J_{ij}^z =0 \neq J_{ij}^x$, the model reduces to an Ising model. Since in this case all the interaction terms in the Hamiltonian commute with each other, the addition of a non-commuting transverse field typically leads to a richer quantum non-equilibrium entanglement dynamics and therefore long-range transverse Ising models of the form of (16), i.e., $J_{ij}^y = J_{ij}^z =0 \neq J_{ij}^x$ and $h_{i}^x = h_{i}^y =0 \neq h_{i}^z$ have been intensively studied [43, 44]. The Ising interaction is, e.g., relevant for van der Waals-type interactions for which α = 6. In ultra-cold atom physics, such interactions appear, e.g., for interacting Rydberg atom setups [45, 46]. They also play a crucial role in effective spin model implementations with trapped ions, which feature a unique possibility for Ising models with widely tunable interaction range, $\alpha \lesssim 2$ [47, 48]. Additionally, coupling to cavity modes allows to also realize spin models of the form of (35) with infinite range interactions (α = 0). See Sect. 5 for more details on experimental realizations.

The potential for harnessing long-range interactions of the form (35) to rapidly generate many-body entanglement between distant degrees of freedom has inspired a large body of the literature establishing fundamental bounds on the propagation of information in systems with power-law interactions [11,12,13, 49,50,51,52,53]. Recent work has established a hierarchy of Lieb–Robinson bounds in systems with power-law interactions [12] as well as concrete protocols for exploiting the resulting long-distance entanglement for quantum state transfer [54, 55].

In the following, we will summarize results for the entanglement growth dynamics in a long-range interacting transverse Ising model, as defined in Sect. 2.3:

$$\displaystyle \begin{aligned} H_{\mathrm{LRTI}} = \sum_{i<j} \frac{\bar{J}}{|i-j|{}^\alpha} \sigma^x_i \sigma_j^x + B \sum_i \sigma_i^z. {} \end{aligned} $$

(36)

We will focus on the results in a 1D chain of M spins. Note that the entanglement evolution is usually most interesting in lower-dimensional systems. For example, in equilibrium statistical physics, it is well known that mean-field theories that are equivalent to the product state ansatz from (29) become a very good approximation, as quantum fluctuations are typically argued to become less important if the spins couple to an increasing amount of neighbors. This is to some extent equivalent to a limit of very long-ranged interactions α → 0. In such a limit, the system can also be imagined as being high-dimensional since every spin couples equally to a very large number of “neighbors.” Below we will indeed see that with an increasing range of interactions the bipartite entanglement entropies in quench dynamics become generally suppressed when increasing the range of the power-law interactions.

We introduce three different regimes of power-law interaction ranges, for which one finds that entanglement growth exhibits qualitatively very different behavior: (i) The short-range regime for power-law exponents α > 2; (ii) the intermediate-range regime for power-law exponents 1 < α < 2; and (iii) the long-range regime for α < 1.

3.1 Short-Range Regime, α > 2

In the case of S = 1∕2 and in the limit of nearest-neighbor interactions, α →∞, Hamiltonians for Heisenberg, XY, XXZ or Ising models are generally integrable [56]. This means that they can be solved by Bethe ansatz solutions, which allows to understand the system dynamics in terms of elementary excitations. In some cases, easy analytical solutions for the dispersion relations and the shape of elementary excitations can be given, e.g., for the XY or transverse Ising model, where a Jordan–Wigner transformation can be used to map the chain to a quadratic fermionic Hamiltonian as shown above. As described in Sect. 2.3, in such a scenario, the dynamics of the quasiparticles after a quench leads to a linear growth of entanglement as a function of time until a saturation value depending on the system size. In particular, taking the fully polarized state as input state for the transverse Ising Hamiltonian (36) with α = ∞ (note that this corresponds to a quench of the field strength from ∞→ B since is the ground state for B →∞), one finds that [22]

$$\displaystyle \begin{aligned} S_{\mathrm{VN}}(\rho_A, t) = c_t t + M_A c_\infty {} \end{aligned} $$

(37)

with constants c_t and c_∞ and M_A the number of spins in the sub-system state ρ_A. The two constants c_t and c_∞ are largest for the scenario where $B=\bar J$ [22]. This means the entanglement growth is fastest for parameters that correspond to the transition point from a paramagnetic to an anti-ferromagnetic phase in the ground state of the Hamiltonian.

Remarkably, the same linear entanglement growth behavior is also observed for finite range interactions ∞ > α > 2 in the long-range transverse Ising model (36). This is for example shown in Fig. 4a that plots the time-dependent growth of the von Neumann entanglement entropy, S_VN, for half the chain as sub-system (from [24]). To compute dynamics, we utilize numerically exact MPS simulations of a chain with M = 50 spins and also compare them to an exact diagonalization simulation (ED) in a smaller system with M = 20 spins. Focusing on the results with α > 2, strikingly, while the entanglement growth rate is reduced with the range of interactions, the linear behavior persists. This hints to the conclusion that for α ≥ 2 the quasiparticle picture known for the nearest-neighbor case also survives for finite range interactions in the α > 2 regime. This conclusion is furthermore strengthened by the observation that the M = 50 and M = 20 simulations perfectly agree with each other. As explained in Sect. 2.3 (see Fig. 2), in the quasiparticle picture, the entanglement entropy growth is independent of the system size until entangled quasiparticles reach the edges of the chain. On the timescale considered in Fig. 4a (∼ five inverse spin interaction energies), quasiparticles cannot reach the boundary for both system sizes. It is also worth pointing out that in [24] it was shown that the linear growth rate of entanglement (constant c_t in Eq. 37) remains to be largest at the point of the ground-state phase transition, which with decreasing values of α shifts to values of B(J) < 1.

Fig. 4

(a) Time-dependent growth of the von Neumann entanglement entropy in a transverse Ising chain with M spins, for an initially fully polarized state, |ψ(t = 0)〉 =∏_i| ↓〉_i and $B=\bar {J}$. Shown are results for M = 20 (solid lines) and M = 50 (dashed lines), which are obtained from exact diagonalization and numerically exact MPS simulations, respectively. Various power-law exponents are compared (α = ∞, 3.0, 2.5, 2.0, 1.5). (b, c) Corresponding time evolution of the spin–spin correlation $C_d(t) = |\langle \sigma ^+_i \sigma ^-_{i+d} \rangle |$ as a function of distance d (the color scale corresponds to log₁₀[C_d(t)]). The three white markers correspond to log₁₀[C_d(t)] = −4, −3.5, −3 in (b) and to log₁₀[C_d(t)] = −3.25, −3, −2.75 in (c) (triangle, square, star, respectively). Panel (b) is for the short-range regime (α = 3), and panel (c) for the intermediate-range regime (α = 1.5). ((a) reproduced from [24], (b) and (c) reproduced from [23]))

To better analyze the quasiparticle picture, it is instructive to analyze the evolution of correlations between two distant spins (summarized, e.g., by the mutual information in Fig. 2b). In Fig. 4b, c, we analyze the time evolution of the spin–spin correlations $C_d(t) = |\langle \sigma ^+_i \sigma ^-_{i+d} \rangle |$, averaged over several starting sites i, as a function of the distance between spins, d (exact results from an MPS simulation, from [23]). Panel (b) shows the simulations for α = 3. The color-coded logarithmic scale shows that there is a clear linear lightcone effect, within which C_d evolves, whereas outside C_d is strongly suppressed.

Analytically, this lightcone behavior can be rationalized by the dispersion relation of the linearized Holstein–Primakoff quasiparticles from Eq. (26). As long as α > 2, this dispersion remains a smooth function of the quasimomentum, and therefore, elementary excitations with well-defined and maximum possible group velocities will be excited in the dynamics. It is however important to re-emphasize that the linearization of the Holstein–Primakoff transformation (22) only remains valid for states that fulfill $\langle a_i^\dag a_i \rangle \ll 2S$ and thus for low-energy quenches or for short times. In the low-energy quench limit, the quasiparticle dynamics can be verified [25]. Surprisingly also for high-energy quenches, one finds that the qualitative spreading of correlations is still very well captured when comparing the Holstein–Primakoff ansatz to exact MPS simulations [23]. We also want to note again that the Holstein–Primakoff dispersion has the same features as the quasiparticle dispersion of a fermionic long-range hopping shown in Fig. 2c that remains exact for arbitrary high-energy quenches and times. In this model, exact calculations of correlation functions in very large systems can be performed, which furthermore allows for a clear characterization of the lightcone boundaries for α > 2 [23]. Finally, it is worth remarking that while here we focused on results for a S = 1∕2 model, the same conclusions of the Holstein–Primakoff solution also hold for larger spins. In fact, one may expect that the validity of the model is extended to higher energies and longer times, since $\langle a_i^\dag a_i \rangle \ll 2S$ can be more easily fulfilled for larger S.

3.2 Intermediate Range Regime, 1 < α < 2

The dynamics of entanglement build-up starts to qualitatively change when the interactions become longer-ranged, i.e., for α < 2. For example, while for a large system simulation with M = 50 and α = 1.5 in Fig. 4a, the entanglement entropy growth still looks linear with additional small oscillations, now strikingly the growth dynamics strongly depends on the system size. Large differences in comparison with the M = 20 simulation appear, already at short times. This implies that distant parts of the chain must already become entangled at very short times, and thus in a quasiparticle picture, there must be entangling quasiparticle excitations with very large group velocities.

Analytically, this is justified by the fact that the dispersion relation for Holstein–Primakoff excitations (26) [25], or for the related fermionic long-range hopping model (Fig. 2c), starts to feature a cusp for α < 2, which implies the existence of elementary excitations with diverging group velocity. However, it is important to emphasize that whether such excitations can be created or not crucially depends on the initial state and on the density of states in the vicinity of the diverging group velocities in quasimomentum space (see Fig. 2c). There, one for example finds crucial differences in the correlation build-up between the long-range interacting transverse Ising model and the long-range fermionic hopping model [23]. For the Ising model, in Fig. 4c, we show the evolution of C_d(t) for α = 1.5. There, it is clearly visible that it becomes impossible to define a clear edge of the lightcone. Instead, the decay of the correlations as a function of the distance is significantly broadened and is not fully linear anymore.

To summarize, in the intermediate regime, entanglement and correlation build-up still exhibit certain features of a lightcone propagation leading to a linear long-time entanglement entropy growth, but on the other hand the existence of quasiparticles with diverging group velocity already leads to significant beyond lightcone features. It is important to note that those features have been experimentally measured in ion trap setups, both after single-spin flip quenches [47] and for fully polarized initial states [48].

3.3 Long-Range Regime, α < 1

Another drastic qualitative change in the entanglement growth dynamics can be observed when the power-law interaction decays more slowly than α < 1. Note that in this regime the overall interaction energy starts to diverge in the infinite system limit, and therefore, the bare interaction energy $\bar {J}$ has to be re-scaled with M for meaningful statements in the M →∞ limit. Strikingly, the change in behavior at α = 1 is displayed in the quasiparticle dispersion of the Holstein–Primakoff excitations (26) (or equivalently in the dispersion relation for the long-range fermionic hopping model in Fig. 2c). For q → 0, one finds that the energy of the elementary excitations is diverging. Therefore, for initial states where the quench excites significant excitations near q = 0, the dynamics of such quasiparticles dominates the entanglement spreading. This is for example seen in the evolution of the spin–spin correlations, which lose any type or lightcone features [23]. For example, in Fig. 2b, we find that the mutual information between distant spins is building up immediately after the quench, and any feature indicating a quasiparticle arrival at later times vanishes for α < 1.

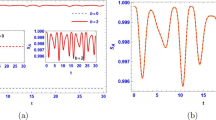
Also the time-dependent growth of the von Neumann entanglement entropy changes characteristically at α < 1. As shown in Fig. 5a, one finds in general (here α = 0.5) a sub-linear oscillatory growth, which for the fully polarized initial state exhibits a logarithmic increase. However, it is important to point out that the growth behavior now also strongly depends on the initial state, as shown in Fig. 5b. In particular, states that do not have permutation symmetry feature a faster increase rate of the entanglement entropy for $t\bar {J} >1$. On the one hand, this is again plausible since also excited quasiparticle states around q ∼ 0 do possess permutation symmetry and thus can be more directly excited in the dynamics. Another intuitive explanation of this observation can be made in the infinite-range limit of α → 0.

Fig. 5

(a) Time-dependent growth of the von Neumann entanglement entropy in a transverse Ising chain with M spins, for an initially fully polarized state, |ψ(t = 0)〉 =∏_i| ↓〉_i and $B=\bar {J}$. Shown are results for M = 20. Various power-law exponents are compared (α = ∞, 3.0, 2.0, 1.5). Rapid entropy at short times and sub-linear increase at later times are observed for α < 1. (b) Same plot as in (a) for α = 0.5 on a logarithmic timescale, and for various initial states. Initial states without full permutation symmetry lead to stronger entropy growth at later times. (c) Evolution for infinite-range interactions α = 0 and the fully polarized symmetric state (M = 50). S_VN remains bounded by the constant log₂(M∕4 + 1) due to the reduced dimension of the symmetric Hilbert subspace. ((a, b) reproduced from [23], (c) reproduced from [24])

For α = 0, Hamiltonian (36) becomes

$$\displaystyle \begin{aligned} H_{\mathrm{LRTI}}^{\alpha=0} &= \bar{J} \sum_{i<j} \sigma^x_i \sigma_j^x + B \sum_i \sigma_i^z \end{aligned} $$

(38)

$$\displaystyle \begin{aligned} &= \frac{J}{2} (S^x)^2 + B S^z - \frac{\bar{J}}{2} M. {} \end{aligned} $$

(39)

In the second line, we have defined the collective spin operators $S^{x,z} = \sum _i \sigma _i^{x,z}$. The collective model in Eq. (39) is also known as Lipkin–Meshkov–Glick (LMG) Hamiltonian, and its entanglement properties can be analytically studied [57]. Due to the permutation symmetry of the problem, a complete basis for Hamiltonian (39) can be constructed in terms of collective spin states, the M + 1 symmetric Dicke states:

(40)

These states are eigenstates of the collective operator spin-S = M∕2 operator S^z with quantum number m_S = −M∕2, …, M∕2, and they can be written as the symmetrized superposition of all states with a certain number of spins, n_↑, pointing “up.” Here, $\mathcal {S}$ denotes a symmetrization operator, and are all states with n_↑ spins in the state , and consequently M − n_↑ spins in the state . The bipartite von Neumann entropy for a sub-system density matrix containing half of the spins can be straightforwardly computed from simple combinatorial factors [24, 58]:

$$\displaystyle \begin{aligned} S_{\mathrm{VN}}^{\mathrm{LMG}} = - \sum_l p_l(n_\uparrow) \mathrm{log}_2[p_l(n_\uparrow)] \quad \text{with} \quad p_l(n_\uparrow) = \frac{{M/2 \choose l} {M/2 \choose n_\uparrow - l}}{ {M/2 \choose n_\uparrow}} {} \end{aligned} $$

(41)

with 0 ≤ l ≤ M∕2. Importantly, since the sum in (41) only features a maximum of M∕2 + 1 terms, the entanglement entropies in symmetric Dicke states are fundamentally limited to a quantity only growing logarithmic in the system size $S_{\mathrm {VN}}^{\mathrm {LMG}} \leq \mathrm {log}_2(M/2+1)$. It is therefore also easy to see that in our quench evolution on the small symmetric Hilbert space, entanglement entropies will remain limited to this bound. Note that since the quadratic term in S^x in (39) only couples Dicke states with m_S ↔ m_S ± 2, the bound can furthermore be tightened to $S_{\mathrm {VN}}^{\mathrm {LMG}}(t) \leq \mathrm {log}_2(M/4+1)$ [24]. In Fig. 5c, the evolution is demonstrated in an example simulation for M = 50. We again point out that for initial states that are outside of the symmetric Dicke manifold, a much larger Hilbert space can be accessed, which can lead to much larger von Neumann entanglement entropies, consistent with our observation of the initial-state dependence of the growth rate in Fig. 5c for α = 0.5.

4 Fast Scrambling and Sparse Models

In previous section, we explored how naturally occurring long-range interactions could be leveraged to generate many-body entanglement in spin chains. We now consider pushing this process of entanglement growth to its extremes. In particular, is there a “speed limit” on how rapidly entanglement can build up in any given system? The fast scrambling conjecture places a fundamental upper bound on the rate of entanglement growth in arbitrary quantum systems. Below we present explicit spin chain models that saturate this bound and highlight the central role played by nonlocal interactions. Systems that saturate these bounds and generate maximal entanglement in the shortest possible time are known as fast scramblers. Such systems share key properties with the dynamics of black holes [59] and show prospects for efficient entanglement generation in near-term experiments [60]. In studying these fast scrambling models, we will also find that the pattern of entanglement developed in these systems can determine the effective geometry of the underlying dynamics, which may differ substantially from the linear geometry of the original spin chain.

4.1 Sparse Nonlocal Interactions for Fast Scrambling

What kinds of physical systems are capable of generating such rapid entanglement growth? We can get a good handle on this question by first studying the Lieb–Robinson bounds derived in Sect. 2.2. Because these bounds are completely general, we can use them to characterize the growth of entanglement on any arbitrary coupling graph G. First, consider averaging Eq. (14) over all vertices i, j in the graph G,

$$\displaystyle \begin{aligned} \sum_{i,j} \frac{1}{N^2} \frac{\lVert [\mathcal{O}_j, \mathcal{O}_i(t)] \rVert}{2\lVert \mathcal{O}_j \rVert\lVert \mathcal{O}_i \rVert} \le \frac{1}{N} \mathrm{exp}\left[\frac{4ck_{\mathrm{max}}}{K} |t| \right], {} \end{aligned} $$

(42)

where k_max is the maximal degree in the graph. Whenever k_max∕K is finite, we see that operator growth is constrained to be exponentially fast. In particular, for chaotic systems that exhibit Lyapunov growth $\left \|[\mathcal {O}_{j},\mathcal {O}_{i}(t)]\right \|{ }^2 \sim \frac {1}{N} e^{\lambda _L t}$, the bound (42) establishes that the Lyapunov exponent λ_L can be no larger than

$$\displaystyle \begin{aligned} \lambda_L \leq \frac{4 c k_{\mathrm{max}}}{K}, \end{aligned} $$

(43)

thereby placing a bound on quantum many-body chaos at infinite temperature. Note that this bound on the Lyapunov exponent is distinct from the chaos bound of Maldacena et al, which places a bound on the Lyapunov exponent at finite temperature [61]. Moreover, since scrambling cannot occur until almost all OTOCs have grown to be order unity [6], the result (42) establishes that scrambling cannot occur before a time

$$\displaystyle \begin{aligned} t_* \geq \frac{K}{4 c k_{\mathrm{max}}} \mathrm{log} N. \end{aligned} $$

(44)

This therefore provides a proof of the fast scrambling conjecture on any graph for which k_max∕K is finite.

The generalized Lieb–Robinson bound also constrains which graphs G are capable of supporting fast scrambling. Further manipulations to (14) (see Appendix B of Ref. [17]) lead to

$$\displaystyle \begin{aligned} \mathrm{exp}\left[\frac{2c|t|}{K}(\mathcal{D}+\mathcal{A})\right]_{ij} < \mathrm{exp}\left[\frac{4\mathrm{e} ck_{\mathrm{max}}}{K} |t| - r_{ij}\right], {} \end{aligned} $$

(45)

where e ≈ 2.718 and the graph distance r_ij is the minimal path length between vertices i and j, i.e.,

$$\displaystyle \begin{aligned} r_{ij} = \min{\{n \in \mathbb{N} \quad \mathrm{s.t.} \quad [\mathcal{A}^n]_{ij} = 1 \}}. {} \end{aligned} $$

(46)

Equation (45) is the classic Lieb–Robinson bound [8]. From this expression, we see that the timescale required for an arbitrary operator to spread throughout the entire system is limited by the path length between the two most distant sites r ≡max_i,j(r_ij), or the graph diameter. We immediately conclude that only graphs with diameter $r \lesssim \mathrm {log} N$ can support fast scrambling [10, 17]. Fast scrambling is therefore impossible for all systems defined on a regular lattice in D dimensions, which have graph diameter r = N^1∕D.

4.2 Sparse Nonlocal Fast Scramblers

We argued above that nonlocal interactions are crucial to engineering fast scrambling; in particular, square lattices in any dimension D have diameter N^1∕D ≫logN and therefore are incapable of supporting fast scrambling dynamics even in principle. Here, we introduce sufficiently nonlocal spin models that feature a logarithmic graph diameter and are also sufficiently chaotic to generate strong scrambling dynamics. These models feature sparse couplings that can be implemented in near-term cold atom experiments employing trapped Rydberg atoms or neutral atoms coupled to an optical cavity, as we review in Sect. 5.

Here we consider sparse nonlocal Hamiltonians of the form

$$\displaystyle \begin{aligned} H = \frac{1}{2S}\sum_{i,j}J(i-j) S^+_i S^-_j, \end{aligned} $$

(47)

with translation-invariant couplings J(i − j) defined on a sparse graph where sites i, j are coupled if and only if they are separated by a power of two,

$$\displaystyle \begin{aligned} J(i-j) = \begin{cases} J_s 2^{\ell s} & \text{when}\,|i-j| = 2^\ell,\,\,\ell=0,1,2,3\dots \\ 0 & \text{otherwise}, \end{cases} \end{aligned} $$

(48)

as illustrated in Fig. 6a. The couplings in Eq. (48) are normalized by setting J_s = J₀ when s ≤ 0 and J_s = J₀(N∕2)^−s for s > 0, such that the largest coupling is always a constant J₀. Here, by tuning the exponent s from −∞ to + ∞, we interpolate between a linear limit (s →−∞) where the physics resembles a nearest-neighbor spin chain, and a treelike limit (s → +∞) in which the underlying geometry is radically reorganized as illustrated in Fig. 6b [62]. In between these two limits, with s = 0, all nonzero couplings are equal and the coupling graph is highly nonlocal. These nonlocal couplings permit information to spread exponentially quickly throughout the system because the number of pairwise interactions required for a particle to hop between any two sites i, j is never more than the Hamming distance $\left |i-j\right |{ }_{\mathrm {Hamming}} < \mathrm {log}_2 N$ when the site indices i, j are written in binary. The rapid spreading of information afforded by the nonlocal couplings at s = 0 allows this model to generate fast scrambling dynamics.

Fig. 6

Sparse nonlocal spin models with tunable geometry. (a) In the power-of-2 model, pairs of spins in a 1D chain are coupled if and only if they are separated by an integer power of 2. (b) By varying the envelope exponent s, we can tune the sparse model from a linear limit for s →−∞ to a treelike limit for s → +∞. Between these two limits s = 0, the sparse couplings form an “improved hypercube” graph that allows for fast scrambling. (c) The quasiparticle dispersion relation for s = −2, 0, 2 as a function of real-space momentum k (top) and as a function of Monna-mapped momentum $k_{\mathcal {M}}$ (bottom). (d) Quasiparticle density 〈n_j〉 in the power-of-2 model for s = −2, 0, 2 (i–iii). The clear lightcone present in the linear regime (i) breaks down in the fast scrambling and treelike regimes (ii, iii). A lightcone re-emerges when the system is organized either by graph distance (iv) or by 2-adic treelike distance (v). (Reproduced from [62])

The primary features of the model can already be observed by considering quasiparticle dynamics described by a nonlocally coupled harmonic Hamiltonian similar to the discussion in Sect. 2.3. Because the couplings J(i − j) are translation-invariant, we can easily diagonalize this harmonic model by performing a Fourier transform of the creation and annihilation operators a, a^†. This yields a single-particle dispersion relation

$$\displaystyle \begin{aligned} \epsilon_k = \sum_d J(d) e^{i k d} = 2 J_s \sum_{l=0}^{\mathrm{log}_2(N/2)} 2^{ls} \cos{}(2^l k). {} \end{aligned} $$

(49)

We plot this dispersion relation as a function of momentum k in Fig. 6c for exponents s = −2, 0, 2 (blue, black, red). For s < 0, the dispersion relation is smooth and resembles the dispersion relation for a free particle in a chain with nearest-neighbor interactions. By contrast, for s > 0, the dispersion relation becomes jagged and consists of features on the scale of the inverse lattice spacing 2π∕N. When s = 0, the dispersion relation appears to have a fractal structure.

Using the dispersion relation, we may immediately compute the particle density 〈n_j〉(t), which we plot in Fig. 6d. For s < 0, the system exhibits a clear linear lightcone as the initially localized excitation spreads ballistically through the system. By contrast, for s > 0, the excitation jumps discontinuously between distant sites, and a lightcone is not immediately apparent. It is tempting to interpret the absence of an obvious lightcone at s > 0, along with the discontinuities in the dispersion relation 𝜖_k, as indicating the absence of any notion of locality in this regime. Instead, we find that a new version of locality emerges in the limit s →∞ based on the treelike structure shown in Fig. 6b.

A dramatic reconception of geometry—where we significantly alter the definition of which spins are “close” to one another and which are “far apart”—allows us to recover a sense of locality from the apparently discontinuous hopping we observe for s > 0. Specifically, we may restore a sensible notion of spatial locality by defining distance in terms of the 2-adic norm |x|₂ = 2^−v(x), where 2^v(x) is the largest power of 2 that divides x. The distance |i − j|₂ between sites i and j is called ultrametric because the distance of the sum of two steps is never greater than the larger of the two steps’ distance; by contrast, the usual distance |i − j| is called Archimedean because many small steps can be combined into a large jump. We can understand the 2-adic norm as a treelike measure of distance because $|i-j|{ }_2 = 2^{d_{\text{tree}}(i,j)/2}/N$, where d_tree(i, j) is the number of edges between sites i and j along the regular tree in Fig. 6b. The leaves are numbered in order of increasing ${\mathcal {M}}(i)$, where the discrete Monna map ${\mathcal {M}}$ reverses the bit order in the site number. For example, for N = 8 sites, ${\mathcal {M}}(1) = 4$ because in binary, ${\mathcal {M}}(001_2) = 100_2$. Noting that Nk∕2π is an integer, we may likewise define a Monna-mapped wavenumber $k_{\mathcal {M}}$ by

$$\displaystyle \begin{aligned} N \frac{ k_{\mathcal{M}}}{2\pi} = {\mathcal{M}}\left( N \frac{k}{2\pi}\right) \,. \end{aligned} $$

(50)

For large positive s, we rearrange the spins according to the Monna map and find that a lightcone reappears (Fig. 6d(v)) and the dispersion relation is smoothed out (Fig. 6c, bottom), corroborating the transformation to the treelike geometry defined by the 2-adic norm.

At the crossover point s = 0 where all nonzero couplings are of equal strength, neither the linear nor the treelike geometries are suitable for describing the spread of quantum information. Instead, the sparse nonlocal couplings facilitate rapid spreading of information throughout the entire system on a logarithmic timescale t_∗∼logN, as demonstrated already in the single-particle dynamics shown in Fig. 6d(ii). In this limit, the coupling graph is equivalent to the “improved hypercube” illustrated in Fig. 6b, consisting of edges from a regular hypercube plus a few extra diagonal couplings to ensure the system is translationally invariant. The improved hypercube has graph diameter $\lceil {\frac {1}{2} \mathrm {log}_2 N}\rceil$ and is therefore capable of hosting fast scrambling dynamics by the graph-theoretic arguments presented in Sect. 4.1.

To examine the structure of entanglement naturally generated by the nonlocal power-of-2 couplings (48), we numerically simulate the evolution of the system using exact diagonalization for a system of N = 16 spins with S = 1∕2 and compute the resulting entanglement entropy between a variety of sub-systems. We initialize the system in a polarized state along S_x, evolve the system for a time t, then partition the system into (not necessarily sequential) sub-systems Q = A ∪ B, and compute the von Neumann entanglement entropy S_A of sub-system A.

Figure 7 shows the resulting entanglement entropy for bipartitions A, B as a function of the partition size L = |A| and time. We partition spins into sub-systems A, B either according to their physical position in the linear chain (top) or their Monna-mapped ordering (bottom). When |s| is large, we observe that there is a natural way to partition the system such that the entanglement entropy is low regardless of the length L of the partition. That is, for s < 0, we minimize the entanglement entropy by cutting the system between nearest neighbors in the linear chain, while for s > 0 we must cut the system between branches of the Bruhat–Tits tree. By contrast, if we use the “wrong” partitioning (e.g., Monna-mapped partition for s < 0), we find a very large entanglement entropy that depends sensitively on the region’s length L.

Fig. 7

Entanglement entropy as a probe of geometry. (a) Entanglement entropy for contiguous subregions of length L in the linear (top) or treelike (bottom) geometry. When s = −2, a linear partitioning of the system yields area-law entanglement at short times, whereas a treelike partitioning yields spurious volume-law entanglement; this suggests that a linear geometry is a suitable description for the dynamics. When s = 2, a treelike partitioning yields area-law entanglement, suggesting a treelike geometry. When s = 0, neither geometry produces area-law entanglement. In fact, at s = 0, every partition of the system has volume-law entanglement, as demonstrated in (b). This indicates that the s = 0 model is a fast scrambler. (Reproduced from [62])

At the crossover point s = 0, however, we find that entanglement entropy is large no matter how we partition the system. As shown in Fig. 7b, both the linear ordering (blue dotted) and the Monna-mapped ordering (red dash-dotted) give bipartitions with large entanglement entropy at s = 0. Moreover, we can consider the entanglement entropy across bipartitions A, B without regard to any sort of locality. In Fig. 7b, we also consider all possible bipartitions of size L = |A| and choose the bipartition with the smallest entanglement entropy at each value of s. Even so, we still find that the entanglement entropy is large at s = 0. In fact, at s = 0, we find that the entanglement entropy grows linearly with the partition size L, indicating a volume law in which entanglement extends into the bulk of the region A. These results indicate that there really is no notion of locality at the crossover point s = 0: all spins are equally “close” to one another, and there is entanglement between all pairs of spins.

5 Implementation in Experiments

Here, we briefly survey some of the state-of-the-art experimental platforms that can be used to explore entanglement growth in spin chains with structured long-range interactions using cold atoms and ions. This list is not exhaustive and represents only a small fraction of the experimental platforms available for controlled studies of entanglement growth.

5.1 Long-Range Interactions with Trapped Ions

Important motivation for studying information propagation with structured long-range interactions has come from experiments with trapped ions, in which the spin states are encoded on long-lived internal states of trapped ion chains in 1D Paul traps or 2D Penning traps [63]. In these experiments, controllable spin–spin interactions that decay algebraically with distance can be realized by using laser driving of spin transitions that couple also to the collective motional modes of the ions. Coupling off-resonantly to many motional modes produces effective Hamiltonians such as that in Eq. 16, with an algebraic decay exponent that can in principle vary from α = 0 to α = 3, and typically ranges in experiments from $0.5\lesssim \alpha \lesssim 2.5$.

There have been extensive experiments on information spreading [47, 48] and recent experimental work exploring the growth of entanglement and scrambling in these systems [64]. Future combinations with gate operations typical of quantum computing setups open the possibility for flexible programmable quantum simulation, which could access a broad variety of spin models with structured long-range interactions in these experiments [63].

5.2 Long-Range Interactions with Rydberg Atoms

Hydrogen-like alkali atoms whose outermost electron has been excited to a Rydberg state with very high principal quantum number n are extremely sensitive to external electric fields due to the Rydberg state’s large electric susceptibility. This sensitivity leads to long-range van der Waals forces between pairs of Rydberg atoms that decay as a power law $1/\left |{\mathbf {r}}_i-{\mathbf {r}}_j\right |{ }^6$; these interactions can be harnessed to process quantum information [65]. In modern experiments, an ensemble of atoms i = 0, …, N − 1 are typically prepared in a stable ground state and trapped in a lattice of optical tweezers as shown in Fig. 8a [66,67,68,69,70,71,72,73,74,75,76]. To generate interactions, the atoms are then optically excited by an applied drive laser to the Rydberg state . The pairwise Van der Waals interactions strongly shift the doubly excited Rydberg state , prohibiting nearby pairs of atoms i, j from being simultaneously excited (Fig. 8a). This “Rydberg blockade” effect yields an effective Hamiltonian

$$\displaystyle \begin{aligned} H = \sum_{i<j} J_{ij} n_i n_j - \sum_i \Delta_i \sigma_i^z + \sum_i \frac{\Omega_i}{2} \sigma_i^x, \end{aligned} $$

(51)

where Ω_i, Δ_i are the Rabi frequency and detuning of the drive laser from the Rydberg state , and where the couplings $J_{ij} = C / \left |{\mathbf {r}}_i - {\mathbf {r}}_j\right |{ }^6$ are naturally long-ranged. Additional optical and magnetic fields can be used to engineer a variety of additional non-commuting terms in this Hamiltonian or to simulate non-equilibrium (time-dependent) dynamics, and Rydberg dressing schemes or other state and field choices can be used to generate alternative long-range interaction models.

Fig. 8

Experimental platforms for studying entanglement growth in quantum spin chains with long-range interactions. (a) Rydberg atoms in 1D optical lattices interact via long-range Van der Waals forces that shift the doubly occupied Rydberg state |rr〉_ij for nearby atoms, leading to a Rydberg blockade effect. Repeated tweezer-assisted shuffling can be used to engineer effective pairwise interactions on a nonlocal hypercube coupling graph amenable to fast scrambling. (Reproduced from [60]). (b) Atoms coupled to the optical mode of a high-finesse cavity interact pairwise via a four-photon scattering process. Applying a linear magnetic field gradient along the cavity axis and driving the cavity with a multi-frequency drive field, we may engineer sparse nonlocal spin–spin interactions whose strengths are individually tuned by the relative strengths of the drive sidebands. Using this flexible drive scheme, we may engineer sparse interactions that either decay (i) or grow (ii) with distance. (Reproduced from [62])

While these Rydberg interactions are naturally long range, they are ultimately still constrained by the D-dimensional geometry of flat spacetime and are therefore incapable of executing fast scrambling dynamics by the arguments of Sect. 4.1. We can get around this problem by significantly altering the effective geometry of the interactions using tweezer-assisted shuffling [60]. Stretching and interleaving tweezer operations [77,78,79,80] can be used to rapidly shuffle the atom positions, as shown in Fig. 8b, thereby generating effective nonlocal interactions. For example, repeated interleaving of the atoms rapidly generates an m-regular hypercube graph Q_m [81, 82], a highly nonlocal, sparsely connected coupling graph shown in Fig. 8b. Many-body entanglement can be rapidly and efficiently built up on this graph using far fewer Rydberg interaction layers than would be needed in strictly 1D systems without shuffling.

5.3 Long-Range Interactions in Cavity Quantum Electrodynamics

Cavity QED systems can be engineered to mediate highly nonlocal spin–spin interactions between pairs of atoms trapped in the optical mode of the cavity [3, 83,84,85]. This coupling allows the atoms to exchange excitations with the cavity mode with an effective Hamiltonian:

(52)

where c is the annihilation operator for the cavity mode with resonance frequency ω_c and g_i is the atom–cavity coupling. Here, each atom i is a three-level system with ground states separated by a ground-state energy splitting ω_Z, and excited state with energy ω_a as illustrated in Fig. 8b.

By optically driving the cavity at a large detuning Δ = ω_c − ω_a ≫ g_i〈c^†c〉 from atomic resonance, the cavity mode c and the atomic excited state are unlikely to be populated and can be integrated out of the dynamics via standard perturbation theory [86]. In this case, the dominant processes are four-photon scattering transitions in which a pair of atoms i, j mutually flip their spins by exchanging a cavity photon as illustrated in Fig. 8b. These four-photon scattering processing generate effective spin–spin interactions between the atoms with effective Hamiltonian:

$$\displaystyle \begin{aligned} H_{\mathrm{eff}} \propto \sum_{ij} \xi_i \xi_j S_i^+ S_j^- + \mathrm{h.c.} {}, \end{aligned} $$

(53)

which describes all-to-all spin-exchange interactions between all pairs of atoms, where the coefficients ξ_i are determined by the local couplings g_i [3].

By applying a linear magnetic field gradient along the cavity axis and driving the cavity with multiple drive fields, as shown in Fig. 8b, it is possible to impose a further structure on the natural all-to-all couplings and realize sparse nonlocal interactions [62, 85, 87]. The linear magnetic field gradient along the length of the chain splits the energies of the spins in a staircase pattern, where the ground-state energy splitting ω_Z,i is now a function of atomic position i and increases linearly with atomic position. As a result of this energy splitting, the four-photon process introduced above is off-resonant and the interactions are shut off. However, by driving the cavity with two or more frequencies simultaneously, we may selectively reintroduce interactions between pairs of atoms that are separated by a particular distance d. That is, driving the system at the resonant frequency Δν_d = ω_i+d − ω_i generates pairwise spin flip processes only between spins that are separated by exactly d = j − i sites, and all other pairs are off-resonant to this drive. We can then build up additional interaction terms by adding more frequencies to our drive. As a result, we obtain a highly tunable set of distance-dependent interactions between atoms controlled by the spectrum of the drive light. With this flexible driving scheme in hand, we are able to implement a large class of nonlocal spin-exchange models including the translation-invariant sparse models (47) studied in Sect. 4.2. This drive scheme has recently been demonstrated in cavity experiments where it was used to engineer a variety of exotic coupling patterns that are not accessible in any other experimental system [85].

6 Outlook and Further Connections

In summary, experimental systems available in experiments with trapped ions, atoms in cavities, and tweezer arrays motivate an interesting new area where we can look at dynamics well beyond what we usually see in local interacting systems. In this chapter, we have only begun to introduce a wide range of possibilities to explore many-body physics in these systems, solely focusing on entanglement growth without disorder. There are large sub-fields discussing phenomena such as many-body localization [88, 89] in these systems, as well as topological effects. Long-range interactions occur in many systems in addition to those discussed here, including systems of polar molecules [40, 90], or harmonically trapped gases [91]. Dressed Rydberg excitations can also provide another way to generate controlled long-range interactions [65, 92].

The entanglement build-up discussed here can also be used as a building block for wider applications. Fast scrambling circuits like those described here can be leveraged to generate nearly random many-body matrices U, which are valuable resources in a variety of information processing contexts. For example, random matrices naturally generate random error-correcting codes, which can be used to protect quantum information from the effects of dissipation [93]. Random matrices can also be used to directly probe entanglement entropies in experiments without the need to introduce SWAP operators between multiple copies [64]. Finally, these fast scrambling circuits can be harnessed to teleport quantum information via Hayden–Preskill-type protocols, which rely on the fast scrambling dynamics to successfully teleport information [94,95,96].