The MNL-Bandit Problem

Abstract

In this chapter, we consider a dynamic assortment optimization problem where customers choose according to an unknown MNL choice model. In each period, we offer a subset (assortment) of products and observe the customer’s choice to learn the model parameters. We present two dynamic assortment selection approaches that optimally balances the exploration–exploitation trade-off and does not require any prior knowledge about the model parameters.

1 Introduction

One fundamental problem in revenue management that arises in many settings including retail and display-based advertising is assortment optimization. Here, the focus is on understanding how consumers select from a large number of substitutable items and identifying the optimal offer set to maximize revenues. Typically, for tractability, we assume a model that captures consumer preferences and focus on computing the optimal offer set. However, model selection and estimating the parameters is a challenging problem. In many e-commerce settings such as fast fashion retail, products have short selling seasons. Therefore, the data on consumer choices is either limited or nonexistent. The retailer needs to learn consumer preferences by offering different assortments and observing purchase decisions, but short selling seasons limit the extent of experimentation. There is a natural trade-off in these settings, where the retailer needs to learn consumer preferences and also maximizes cumulative revenues simultaneously. Finding the right balance between exploration and exploitation is a challenge. This chapter focuses on designing tractable robust algorithms for managing this trade-off in sequential decision-making under uncertainty for assortment optimization, which is a key component in many revenue management applications.

Organization

We first provide an overview of assortment planning and the multinomial logit model (MNL), which is the most popular predictive model for this application domain in Sect. 9.2. In Sect. 9.3, we introduce the “MNL-Bandit problem” (term first coined in Agrawal et al. (2019)) that formulates the problem of dynamic assortment optimization and learning under the MNL choice model. In Sect. 9.4, we discuss approaches based on the principle of optimism under uncertainty from Agrawal et al. (2016) that bridges the aforementioned gap between theory and practice. In Sect. 9.5, discuss the Thompson Sampling (TS)-based approach from Agrawal et al. (2017) with similar theoretical guarantees. This approach motivated by the growing popularity of TS approaches in practice due to their attractive empirical performance. In Sect. 9.6, we discuss fundamental limits on the performance of any dynamic learning algorithm for the MNL-Bandit problem which establishes that the algorithms discussed in this chapter are near-optimal. We conclude in Sect. 9.7 with some discussion on recent progress on the extensions of MNL-Bandit problem to settings involving contextual features and a large number of products.

2 Choice Modeling and Assortment Optimization

In many settings, a decision-maker is faced with the problem of identifying an optimal mix of items from a large feasible set. For example, an online retailer needs to select a subset (assortment) of products to display to its shoppers. Due to substitution effects, the demand for an individual product is influenced by other products in the assortment presented to the shopper. In display-based online advertising, a publisher needs to select a set of advertisements to display to its users, and due to competition between the ads, the click rates for an individual ad depends on the assortment of ads displayed. A movie recommendation system like the one used by Netflix or Amazon must determine a small subset of items to suggest to its users from a large pool of similar alternatives, and the user response may depend on the overall attractiveness of the recommended set. Furthermore, in all these settings, different items may be valued differently from the decision-maker’s perspective. Therefore, the assortment of items offered to users has significant impact on revenues. In order to identify the ideal set to offer, the decision-maker must understand the substitution patterns of users.

Choice models capture these substitution effects among items by specifying the probability with which a user selects an item from an offered set of items. More specifically, let $\mathcal {N} = \{1,\cdots ,N\}$ be the set of all available items for the decision-maker to choose from. For any subset $S \subset \mathcal {N}$ and any item i ∈ S, a choice model describes the probability of a random consumer preferring item i in the set S as

$$\displaystyle \begin{aligned} \pi(i,S) = \Pr(\text{customer selects item {$i$} from offer set {$S$}}). \end{aligned} $$

We refer to π(i, S) as choice probabilities. Using these choice probabilities, one can compute the expected revenue associated with an offer set as the weighted sum of revenues of items in the offer set and the choice probabilities. Specifically, if the value (revenue) associated with item $i \in \mathcal {N}$ is given by r_i, then the expected revenue R(S) of any assortment $S \subset \mathcal {N}$ can be written as

$$\displaystyle \begin{aligned} R(S) = \sum_{i \in S} r_i \cdot \pi(i,S). \end{aligned} $$

Then, the decision-maker can identify an optimal set by computing the set with highest expected revenue, resulting in an optimization problem commonly referred to as the assortment optimization problem and formulated as

$$\displaystyle \begin{aligned} \max \limits_{S \subseteq \mathcal{N}} R(S). \end{aligned} $$

(9.1)

More generally, assortment optimization problems also allow for constraints that arise in practice, e.g., budget for inventory, product purchasing, display capacity, etc.

A fundamental problem in assortment planning is (choice) model selection. There is a trade-off between working with models that have greater predictive power vs. simple models that allow greater tractability. Given a large number of alternatives, estimating choice probabilities from transactional data is a highly nontrivial task. As an extreme case, one may consider a choice model that makes no structural assumptions on the choice probabilities π(i, S) and therefore can represent any customer choice behavior. Learning and optimizing under such a choice model would require estimating 2^N parameters and solving an intractable combinatorial optimization problem. The trade-offs between the representation power and the tractability of a choice model are an important consideration for the decision-maker in its deployment, particularly in settings where one needs to constantly estimate and optimize the model.

The Multinomial Logit Model (MNL), owing primarily to its tractability, is one of the most widely used choice models for assortment selection problems. Recently, large-scale field experiments by Alibaba Feldman et al. (2021) have demonstrated the efficacy of the MNL model in boosting revenues. In this chapter, we use the MNL choice model to model customer preferences and develop efficient approaches that learn the model while simultaneously optimizing revenue.

Under the MNL model, the probability that a consumer purchases product i when offered an assortment S ⊂{1, …, N} is given by $\pi _{\mathsf {MNL}}(i,S) = \frac {v_i}{v_0+\sum _{j\in S}v_j},$ where v_i is the attraction parameter for product i in the MNL model. Without loss of generality, we can assume that v₀ = 1, and therefore, the choice probabilities can be reformulated as

$$\displaystyle \begin{aligned} \pi_{\textsf{MNL}}(i,S) = \frac{v_i}{1+\sum_{j\in S}v_j} , \end{aligned} $$

(9.2)

and the expected revenue for any assortment S is given by

$$\displaystyle \begin{aligned} \mathbb R(S,{\boldsymbol{v}}) = \sum_{i \in S} r_i\frac{v_i}{1+\sum_{j\in S}v_j}. \end{aligned} $$

(9.3)

From the choice probabilities, we can see that the ratio of choice probabilities of two items, π_MNL(i, S) and π_MNL(j, S), is independent of the offer set S. This property is known as the independent of irrelevant attributes (IIA) property (Ben-Akiva and Lerman, 1985) and is a limitation of the MNL model. Other random utility-based choice models like Nested Logit (NL) (Williams, 1977) and Mixed Logit model (mMNL) (McFadden and Train, 2000) generalize the MNL model and are not restricted by the IIA property. However, estimation of these models and the corresponding assortment planning problems involved are often intractable highlighting the challenges involved in model selection. See Désir et al. (2021) for further discussion on tractability of choice models. The closed-form expression of the choice probabilities makes the MNL model extremely tractable from estimation and optimization point of view (see Talluri and Van Ryzin (2004).) The tractability of the model in decision-making is the primary reason MNL has been extensively used in practice (Greene, 2003; Ben-Akiva and Lerman, 1985; Train, 2009).

Traditionally, assortment decisions are made at the start of the selling period based on a choice model that has been estimated from historical data; see (Kok and Fisher, 2007) for a detailed review. In many business applications such as fast fashion and online retail, new products can be introduced or removed from the offered assortments in a fairly frictionless manner, and the selling horizon for a particular product can be short. Therefore, the traditional approach of first estimating the choice model and then using a static assortment based on the estimates is not practical in such settings. Rather, it is essential to experiment with different assortments to learn consumer preferences, while simultaneously attempting to maximize immediate revenues. Suitable balancing of this exploration–exploitation trade-off is the focus of the remainder of this chapter.

3 Dynamic Learning in Assortment Selection

As alluded to above, many instances of assortment optimization problems commence with very limited or even no a priori information about consumer preferences. Traditionally, due to production considerations, retailers used to forecast the uncertain demand before the selling season starts and decide on an optimal assortment to be held throughout. There are a growing number of industries like fast fashion and online display advertising where demand trends change constantly and new products (or advertisements) can be introduced (or removed) from offered assortments in a fairly frictionless manner. In such situations, it is possible to experiment by offering different assortments and observing resulting purchases. Of course, gathering more information on consumer choice in this manner reduces the time remaining to exploit the said information.

Motivated by aforementioned applications, let us consider a stylized dynamic optimization problem that captures some salient features of the above application domain. The goal is to develop an exploration–exploitation policy that balances between gaining new information for learning the model and exploiting past information for optimizing revenue. In particular, consider a constrained assortment selection problem under the multinomial logit (MNL) model with N substitutable products and a “no purchase” option. The objective is to design a policy that adaptively selects a sequence of history-dependent assortments $(S_1, S_2, \ldots , S_T) \in \mathcal {S}^T$ so as to maximize the cumulative expected revenue,

$$\displaystyle \begin{aligned} \mathbb{E} \left(\sum_{t=1}^T R(S_t, \mathbf{v}) \right), \end{aligned} $$

(9.4)

where R(S, v) is the revenue corresponding to assortment S as defined as in (9.3). We measure the performance of a decision-making policy via its regret. The objective then is to design a policy that approximately minimizes the regret defined as

$$\displaystyle \begin{aligned} \mathsf{Reg}(T,{\boldsymbol{v}}) = \sum_{t=1}^T R(S^*,{\boldsymbol{v}}) - \mathbb{E}[R(S_t, \mathbf{v})], \end{aligned} $$

(MNL-Bandit)

where , with $\mathcal S$ being the set of feasible assortments. This exploration–exploitation problem, which is referred to as the MNL-Bandit problem, is the focus of this chapter.

Constraints Over Assortment Selection

The literature considers several naturally arising constraints over the assortments that the retailer can offer. The simplest form of constraints is cardinality constraints, i.e., an upper bound on the number of products that can be offered in the assortment. Other more general constraints include partition matroid constraints (where the products are partitioned into segments and the retailer can select at most a specified number of products from each segment) and joint display and assortment constraints (where the retailer needs to decide both the assortment and the display segment of each product in the assortment and there is an upper bound on the number of products in each display segment). More generally, consider the set of totally unimodular (TU) constraints on the assortments. Let x(S) ∈{0, 1}^N be the incidence vector for assortment S ⊆{1, …, N}, i.e., x_i(S) = 1 if product i ∈ S and 0 otherwise. The approaches discussed here extend to constraints of the form

$$\displaystyle \begin{aligned} \mathcal{S} = \left\{ S \subseteq \{1,\ldots,N\} \; \middle |\; A \; {\boldsymbol{x}}(S) \leq {\boldsymbol{b}}, \; {\boldsymbol{0}} \leq {\boldsymbol{x}} \leq {\boldsymbol{1}} \right\}, \end{aligned} $$

(9.5)

where A is a totally unimodular matrix and b is integral (i.e., each component of the vector b is an integer). The totally unimodular constraints model a rich class of practical assortment planning problems including the examples discussed above. We refer the reader to Davis et al. (2013) for a detailed discussion on assortment and pricing optimization problems that can be formulated under the TU constraints.

Algorithmic Approaches

Some initial works that consider the problem of minimizing regret under the MNL choice model include (Rusmevichientong et al., 2010; Sauré and Zeevi, 2013). Both these works present an “explore first and exploit later” approach. In particular, a selected set of assortments are explored until parameters can be estimated to a desired accuracy, and then the optimal assortment corresponding to the estimated parameters is offered for the remaining selling horizon. More specifically, when the expected revenue difference between the optimal and next best assortments is Δ, existing approaches uniformly explore all the products for $O(\log {T}/\Delta )$ time periods and use the obtained data to estimate the optimal assortment. The exploration period that depends on the knowledge of the revenue gap, Δ, is to ensure that the algorithm can identify the optimal assortment with “high probability.” Following this approach, (Sauré and Zeevi, 2013) show an asymptotic $O(N\log {T}/\Delta )$ regret bound, while (Rusmevichientong et al., 2010) establish an $O(N^2\log ^2{T}/\Delta )$ regret bound; recall N is the number of products and T is the time horizon. However, as highlighted above, their algorithm relies crucially on a priori knowledge of the revenue gap, Δ, which is not readily available in practice. In Sect. 9.4.4, we will highlight via numerical simulations how lack of this knowledge can result in settings where these algorithms perform quite poorly. In the remainder of the chapter, we focus on approaches that simultaneously explore and exploit demand information. Specifically, we discuss a UCB (upper confidence bound)-based approach from Agrawal et al. (2016, 2019) and a Thompson Sampling-based approach from Agrawal et al. (2017). An advantage of these adaptive approaches is that they do not require any a priori knowledge or assumptions, and their performance is in some sense best possible (matches the worst-case lower bound), thereby, making these approaches more universal in its scope.

4 A UCB Approach for the MNL-Bandit

In this section, we discuss an algorithm from Agrawal et al. (2016, 2019) that adapts the popular upper confidence bounds (UCBs) approach to the MNL-Bandit problem. After presenting the details of the algorithm, in Sect. 9.4.2, we present the regret analysis that shows that this algorithm achieves a worst-case regret bound of $O(\sqrt {NT \log {N}T})$ under a mild assumption, namely that the no purchase is the most “frequent” outcome. In Sect. 9.4.3, we also present the instance-dependent regret bounds that show that for “well separated” instances, the regret of the policy is bounded by $O\left (\min \left (N^2 \log {NT}/\Delta ,\sqrt {NT\log {NT}}\right )\right )$, where Δ is the “separability” parameter discussed in the previous section. This is comparable to the regret bounds, $O\left (N \log {T}/\Delta \right )$ and $O\left (N^2 \log ^2{T}/\Delta \right )$, established in Sauré and Zeevi (2013) and Rusmevichientong et al. (2010), respectively, even though the policy does not require any prior information on Δ unlike the aforementioned work. Finally, in Sect. 9.4.4, we present a computational study from Avadhanula (2019) that highlights several salient features of the UCB-based policy. In particular, the study tests the performance of the proposed algorithm over instances with varying degrees of separability between optimal and suboptimal solutions and observe that the performance is bounded irrespective of the “separability parameter.” In contrast, the approach of Sauré and Zeevi (2013) “breaks down” and results in linear regret for some values of the “separability parameter.”

Challenges and Overview

A key difficulty in applying standard multi-armed bandit techniques to this problem is that the response observed on offering a product i is not independent of other products in assortment S. Therefore, the N products cannot be directly treated as N independent arms. The algorithm presented here utilizes the specific properties of the dependence structure in MNL model to obtain an efficient algorithm with order $\sqrt {NT}$ regret.

The algorithm is based on a nontrivial extension of the UCB algorithm in Auer et al. (2002), which is predicated on Lai and Robbins (1985). It uses the past observations to maintain increasingly accurate upper confidence bounds for the MNL parameters {v_i, i = 1, …, N} and also uses these to (implicitly) maintain an estimate of expected revenue R(S, v) for every feasible assortment S. In every round, the algorithm picks the assortment S with the highest optimistic revenue. There are two main challenges in implementing this scheme. First, the customer response to being offered an assortment S depends on the entire set S and does not directly provide an unbiased sample of demand for a product i ∈ S. In order to obtain unbiased estimates of v_i for all i ∈ S, we offer a set S multiple times: specifically, it is offered repeatedly until a no purchase occurs. We show that proceeding in this manner, the average number of times a product i is purchased provides an unbiased estimate of the parameter v_i. The second difficulty is the computational complexity of maintaining and optimizing revenue estimates for each of the exponentially many assortments. To this end, we use the structure of the MNL model and define our revenue estimates such that the assortment with maximum estimated revenue can be efficiently found by solving a simple optimization problem. This optimization problem turns out to be a static assortment optimization problem with upper confidence bounds for v_i’s as the MNL parameters, for which efficient solution methods are available.

4.1 Algorithmic Details

The algorithm divides the time horizon into epochs, where in each epoch we offer an assortment repeatedly until a no purchase outcome occurs. Specifically, in each epoch , we offer an assortment repeatedly. Let denote the set of consecutive time steps in epoch . contains all time steps after the end of epoch , until a no purchase happens in response to offering , including the time step at which no purchase happens. The length of an epoch conditioned on is a geometric random variable with success probability defined as the probability of no purchase in . The total number of epochs L in time T is implicitly defined as the minimum number for which .

At the end of every epoch , we update our estimates for the parameters of MNL, which are used in epoch to choose assortment . For any time step , let c_t denote the consumer’s response to , i.e., c_t = i if the consumer purchased product , and 0 if no purchase happened. We define as the number of times a product i is purchased in epoch ,

(9.6)

For every product i and epoch , we keep track of the set of epochs before that offered an assortment containing product i and the number of such epochs. We denote the set of epochs by and the number of epochs by ; that is,

(9.7)

We compute as the number of times product i was purchased per epoch,

(9.8)

We show that for all , and are unbiased estimators of the MNL parameter v_i (see Corollary 6). Using these estimates, we compute the upper confidence bounds, , for v_i as

(9.9)

We establish that is an upper confidence bound on the true parameter v_i, i.e., , for all with high probability (see Lemma 1). The role of the upper confidence bounds is akin to their role in hypothesis testing; they ensure that the likelihood of identifying the parameter value is sufficiently large. We then offer the optimistic assortment in the next epoch, based on the previous updates as follows:

(9.10)

where $R(S,{\hat {\boldsymbol {v}}})$ is as defined in (9.3). We later show that the above optimization problem is equivalent to the following optimization problem:

(9.11)

where is defined as

(9.12)

We summarize the precise steps of this UCB-based algorithm in Algorithm 1.

Algorithm 1 Exploration–Exploitation algorithm for MNL-Bandit

Finally, we may remark on the computational complexity of implementing (9.10). The optimization problem (9.10) is formulated as a static assortment optimization problem under the MNL model with TU constraints, with model parameters being (see (9.11)). There are efficient polynomial time algorithms to solve the static assortment optimization problem under MNL model with known parameters (see Avadhanula et al. 2016; Davis et al. 2013; Rusmevichientong et al. 2010). We will now briefly comment on how Algorithm 1 is different from the existing approaches of Sauré and Zeevi (2013) and Rusmevichientong et al. (2010) and also why other standard “bandit techniques” are not applicable to the MNL-Bandit problem.

Remark 1 (Universality)

Note that Algorithm 1 does not require any prior knowledge/information about the problem parameters v (other than the assumption v_i ≤ v₀, refer to Avadhanula (2019) for discussion on designing algorithms for settings when v_i > v₀). This is in contrast with the approaches of Sauré and Zeevi (2013) and Rusmevichientong et al. (2010), which require the knowledge of the “separation gap,” namely, the difference between the expected revenues of the optimal assortment and the second best assortment. Assuming knowledge of this “separation gap,” both these existing approaches explore a predetermined set of assortments to estimate the MNL parameters within a desired accuracy, such that the optimal assortment corresponding to the estimated parameters is the (true) optimal assortment with high probability. This forced exploration of predetermined assortments is avoided in Algorithm 1, which offers assortments adaptively, based on the current observed choices. The confidence regions derived for the parameters v and the subsequent assortment selection ensure that Algorithm 1 judiciously maintains the balance between exploration and exploitation that is central to the MNL-Bandit problem.

Remark 2 (Estimation Approach)

Because the MNL-Bandit problem is parameterized with parameter vector (v), a natural approach is to build on standard estimation approaches like maximum likelihood (MLE), where the estimates are obtained by optimizing a loss function. However, the confidence regions for estimates resulting from such approaches are either asymptotic and are not necessarily valid for finite time with high probability or typically depend on true parameters, which are not known a priori. For example, finite time confidence regions associated with maximum likelihood estimates require the knowledge of (see Borovkov 1984), where I is the Fisher information of the MNL choice model and $\mathcal {V}$ is the set of feasible parameters (that is not known a priori). Note that using I(v^MLE) instead of for constructing confidence intervals would only lead to asymptotic guarantees and not finite sample guarantees. In contrast, in Algorithm 1, the estimation problem is resolved by a sampling method designed to give us unbiased estimates of the model parameters. The confidence bounds of these estimates and the algorithm do not depend on the underlying model parameters. Moreover, our sampling method allows us to compute the confidence regions by simple and efficient “book keeping” and avoids computational issues that are typically associated with standard estimation schemes such as MLE. Furthermore, the confidence regions associated with the unbiased estimates also facilitate a tractable way to compute the optimistic assortment (see (9.10), (9.11), and Step 4 of Algorithm 1), which is less accessible for the MLE estimate.

4.2 Min–Max Regret Bounds

For the regret analysis, we make the following assumptions.

Assumption 1

• 1. The MNL parameter corresponding to any product i ∈{1, …, N} satisfies v_i ≤ v₀ = 1.

• 2. The family of assortments $\mathcal {S}$ is such that $S \in \mathcal {S}$ and Q ⊆ S implies that $Q \in \mathcal {S}$.

The first assumption is equivalent to the “no purchase option” being the most likely outcome. We note that this holds in many realistic settings, in particular, in online retailing and online display-based advertising. The second assumption implies that removing a product from a feasible assortment preserves feasibility. This holds for most constraints arising in practice including cardinality and matroid constraints more generally. We would like to note that the first assumption is made for ease of presentation of the key results and is not central to deriving bounds on the regret. The main result is the following upper bound on the regret of the policy stated in Algorithm 1.

Theorem 1 (Performance Bounds for Algorithm 1)

For any instance v = (v₀, …, v_N) of the MNL-Bandit problem with N products, r_i ∈ [0, 1], and Assumption 1, the regret of the policy given by Algorithm 1 at any time T is bounded as

$$\displaystyle \begin{aligned} Reg_\pi(T,{\boldsymbol{v}}) \leq C_1\sqrt{NT\log{{N}T}} + C_2N\log^2{{N}T},\end{aligned} $$

where C₁ and C₂ are absolute constants (independent of problem parameters).

Proof Outline

In this section, we briefly discuss an outline of different steps involved in proving Theorem 1. We refer the interested readers to Agrawal et al. (2019) and Avadhanula (2019) for detailed proofs.

Confidence Intervals

The first step in the regret analysis is to prove the following two properties of the estimates computed as in (9.9) for each product i. Specifically, that v_i is bounded by with high probability and that as a product is offered an increasing number of times, the estimates converge to the true value with high probability. Specifically, we have the following result.

Lemma 1

For every , we have:

• 1. with probability at least for all i = 1, …, N.

• 2. There exist constants C₁ and C₂ such that

  

  with probability at least .

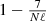Intuitively, these properties establish as upper confidence bounds converging to actual parameters v_i, akin to the upper confidence bounds used in the UCB algorithm for MAB in Auer et al. (2002). These properties follow from an observation that is conceptually equivalent to the IIA (independence of irrelevant alternatives) property of MNL and shows that in each epoch τ, $\hat {v}_{i,\tau }$ (the number of purchases of product i) provides independent unbiased estimates of v_i. Intuitively, $\hat {v}_{i,\tau }$ is the ratio of probabilities of purchasing product i to preferring product 0 (no purchase), which is independent of S_τ. This also explains why we choose to offer S_τ repeatedly until no purchase occurs. Given these unbiased i.i.d. estimates from every epoch τ before , we apply a multiplicative Chernoff–Hoeffding bound to prove concentration of .

Validity of the Optimistic Assortment

The product demand estimates were used in (9.12) to define expected revenue estimates for every set S. In the beginning of every epoch , Algorithm 1 computes the optimistic assortment as and then offers repeatedly until no purchase happens. The next step in the regret analysis is to leverage the fact that is an upper confidence bound on v_i to prove similar, though slightly weaker, properties for the estimates . First, we note that estimated revenue is an upper confidence bound on the optimal revenue, i.e., R(S^∗, v) is bounded by with high probability. The proof for these properties involves careful use of the structure of MNL model to show that the value of is equal to the highest expected revenue achievable by any feasible assortment, among all instances of the problem with parameters in the range $[0, v^{\textsf {UCB}}_i], i=1,\ldots , n$. Since the actual parameters lie in this range with high probability, we have that is at least R(S^∗, v) with high probability. In particular, we have the following result.

Lemma 2

Suppose $S^* \in \mathcal {S}$ is the assortment with highest expected revenue, and Algorithm 1 offers in each epoch . Then, for every epoch , we have

Bounding the Regret

The final part of the analysis is to bound the regret in each epoch. First, we use the fact that is an upper bound on R(S^∗, v) to bound the loss due to offering the assortment . In particular, we show that the loss is bounded by the difference between the “optimistic” revenue estimate, , and the actual expected revenue, . We then prove a Lipschitz property of the expected revenue function to bound the difference between these estimates in terms of errors in individual product estimates . Finally, we leverage the structure of the MNL model and the properties of to bound the regret in each epoch. Lemma 3 provides the precise statements of above properties.

Lemma 3

If r_i ∈ [0, 1], there exist constants C₁ and C₂ such that for every , we have

4.3 Improved Regret Bounds for “Well Separated” Instances

In this section, we consider the problem instances that are “well separated” and present an improved logarithmic regret bound. More specifically, we present an $O(\log {T})$ regret bound for Algorithm 1 for instances that are “well separated.” In Sect. 9.4.2, we established worst-case regret bounds for Algorithm 1 that hold for all problem instances satisfying Assumption 1. While the algorithm ensures that the exploration–exploitation trade-off is balanced at all times, we demonstrate that it quickly converges to the optimal solution for the problem instances that are “well separated,” leading to even better regret bounds. More specifically, we consider problem instances where the optimal assortment and “second best” assortment are sufficiently “separated” and derive an $O(\log {T})$ regret bound that depends on the parameters of the instance. Note that, unlike the regret bound derived in Sect. 9.4.2 that holds for all problem instances satisfying Assumption 1, the bound we derive here only holds for instances having certain separation between the revenues corresponding to optimal and second best assortments. In particular, let Δ(v) denote the difference between the expected revenues of the optimal and second best assortment, i.e.,

(9.13)

We have the following result.

Theorem 2 (Performance Bounds for Algorithm 1 in “Well Separated” Case)

For any instance v = (v₀, …, v_N) of the MNL-Bandit problem with N products, r_i ∈ [0, 1], and Assumption 1, the regret of the policy given by Algorithm 1 at any time T is bounded as

$$\displaystyle \begin{aligned} \textsf{Reg}(T,{\boldsymbol{v}}) \leq B_1\left(\frac{N^2\log{T}}{\Delta({\boldsymbol{v}})}\right) + B_2, \end{aligned}$$

where B₁ and B₂ are absolute constants.

Proof Outline

We provide a proof outline here. We refer the interested readers to Avadhanula (2019) for a detailed proof. In this setting, we analyze the regret by separately considering the epochs that satisfy certain desirable properties and the ones that do not. Specifically, we denote epoch as a “good” epoch if the parameters satisfy the following property:

and we call it a “bad” epoch otherwise, where C₁ and C₂ are constants as defined in Lemma 1. Note that every epoch is a good epoch with high probability , and we show that regret due to “bad” epochs is bounded by a constant (see Lemma 1). Therefore, we focus on “good” epochs and show that there exists a constant τ, such that after each product has been offered in at least τ “good” epochs, Algorithm 1 finds the optimal assortment. Based on this result, we can then bound the total number of “good” epochs in which a suboptimal assortment can be offered by our algorithm. Specifically, let

$$\displaystyle \begin{aligned} \tau = \frac{4{N}C\log{{N}T}}{\Delta^2({\boldsymbol{v}})}, \end{aligned} $$

(9.14)

where $C = \max \{{C^2_1},C_2\}$. Then, we have the following result.

Lemma 4

Let be a “good” epoch and be the assortment offered by Algorithm 1 in epoch . If every product in assortment is offered in at least τ “good epochs,” i.e., then we have .

The next step in the analysis is to show that Algorithm 1 will offer a small number of suboptimal assortments in “good” epochs. More specifically, we have the following result:

Lemma 5

Algorithm 1 cannot offer suboptimal assortments in more than Nτ “good” epochs.

It should be noted that the bound obtained in Theorem 2 is similar in magnitude to the regret bounds obtained by Sauré and Zeevi (2013) and is strictly better than the regret bound $O(N^2\log ^2{T})$ established by Rusmevichientong et al. (2010). Moreover, the algorithm does not require the knowledge of Δ(v), unlike the aforementioned papers that build on a conservative estimate of Δ(v) to implement their proposed policies.

4.4 Computational Study

In this section, we present insights from numerical experiments in Avadhanula (2019) that test the empirical performance of our policy and highlight some of its salient features. We study the performance of Algorithm 1 from the perspective of robustness with respect to the “separability parameter” of the underlying instance. In particular, we consider varying levels of separation between the revenues corresponding to the optimal assortment and the second best assortment and perform a regret analysis numerically. We contrast the performance of Algorithm 1 with the approach in Sauré and Zeevi (2013) for different levels of separation. We observe that when the separation between the revenues corresponding to optimal assortment and second best assortment is sufficiently small, the approach in Sauré and Zeevi (2013) breaks down, i.e., incurs linear regret, while the regret of Algorithm 1 only grows sub-linearly with respect to the selling horizon.

4.4.1 Robustness of Algorithm 1

Here, we present a study that examines the robustness of Algorithm 1 with respect to the instance separability. We consider a parametric instance (see (9.15)), where the separation between the revenues of the optimal assortment and the next best assortment is specified by the parameter 𝜖 and compare the performance of Algorithm 1 for different values of 𝜖.

Experimental Setup

We consider the parametric MNL setting with N = 10, K = 4, r_i = 1 for all i, and utility parameters v₀ = 1 and for i = 1, …, N,

$$\displaystyle \begin{aligned} v_i = \left\{ \begin{array}{ll} 0.25+ \epsilon, & \text{ if } i \in \{1,2,9,10\} \\ 0.25, & \text{ else }, \end{array}\right. \end{aligned} $$

(9.15)

where 0 < 𝜖 < 0.25, specifies the difference between revenues corresponding to the optimal assortment and the next best assortment. Note that this problem has a unique optimal assortment {1, 2, 9, 10} with an expected revenue of 1 + 4𝜖∕2 + 4𝜖 and the next best assortment has revenue of 1 + 3𝜖∕2 + 3𝜖. We consider four different values for 𝜖, 𝜖 = {0.05, 0.1, 0.15, 0.25}, where higher value of 𝜖 corresponds to larger separation and hence an “easier” problem instance.

Results

Figure 9.1 summarizes the performance of Algorithm 1 for different values of 𝜖. The results are based on running 100 independent simulations, and the standard errors are within 2%. Note that the performance of Algorithm 1 is consistent across different values of 𝜖, with a regret that exhibits sub-linear growth. Observe that as the value of 𝜖 increases, the regret of Algorithm 1 decreases. While not immediately obvious from Fig. 9.1, the regret behavior is fundamentally different in the case of “small” 𝜖 and “large” 𝜖. To see this, in Fig. 9.2, we focus on the regret for 𝜖 = 0.05 and 𝜖 = 0.25 and fit to $\log {T}$ and $\sqrt {T}$, respectively. (The parameters of these functions are obtained via simple linear regression of the regret vs $\log {T}$ and $\sqrt {T}$, respectively). It can be observed that the regret is roughly logarithmic when 𝜖 = 0.25 and in contrast roughly behaves like $\sqrt {T}$ when 𝜖 = 0.05. This illustrates the theory developed in Sect. 9.4.3, where we showed that the regret grows logarithmically with time, if the optimal assortment and the next best assortment are “well separated,” while the worst-case regret scales as $\sqrt {T}$.

Fig. 9.1

Performance of Algorithm 1 measured as the regret on the parametric instance (9.15). The graphs illustrate the dependence of the regret on T for “separation gaps” 𝜖 = 0.05, 0.1, 0.15, and 0.25, respectively

Fig. 9.2

Best fit for the regret of Algorithm 1 on the parametric instance (9.15). The graphs (a) and (b) illustrate the dependence of the regret on T for “separation gaps” 𝜖 = 0.05 and 0.25, respectively. The best $y = \beta _1 \log {T} + \beta _0$ fit and the best $y = \beta _1 \sqrt {T} + \beta _0$ fit are superimposed on the regret curve

4.4.2 Comparison with Existing Approaches

In this section, we present a computational study comparing the performance of our algorithm to that of Sauré and Zeevi (2013). To be implemented, their approach requires certain a priori information of a “separability parameter”; roughly speaking, measuring the degree to which the optimal and next best assortments are distinct from a revenue standpoint. More specifically, their algorithm follows an explore-then-exploit approach, where every product is offered for a minimum duration of time that is determined by an estimate of said “separability parameter.” After this mandatory exploration phase, the parameters of the choice model are estimated based on the past observations, and the optimal assortment corresponding to the estimated parameters is offered for the subsequent consumers. If the optimal assortment and the next best assortment are “well separated,” then the offered assortment is optimal with high probability, otherwise, the algorithm could potentially incur linear regret. Therefore, the knowledge of this “separability parameter” is crucial. For our comparison, we consider the exploration period suggested by Sauré and Zeevi (2013) and compare it with the performance of Algorithm 1 for different values of separation (𝜖). We will see that for any given exploration period, there is an instance where the approach in Sauré and Zeevi (2013) “breaks down” or in other words incurs linear regret, while the regret of Algorithm 1 grows sub-linearly ($O(\sqrt {T})$, more precisely) for all values of 𝜖 as asserted in Theorem 1.

Experimental Setup and Results

We consider the parametric MNL setting as described in (9.15) and for each value of 𝜖 ∈{0.05, 0.1, 0.15, 0.25}. Since the implementation of the policy in Sauré and Zeevi (2013) requires knowledge of the selling horizon and minimum exploration period a priori, we take the exploration period to be $20 \log {T}$ as suggested in Sauré and Zeevi (2013) and the selling horizon T = 10⁶. Figure 9.3 compares the regret of Algorithm 1 with that of Sauré and Zeevi (2013). The results are based on running 100 independent simulations with standard error of 2%. We observe that the regret for Sauré and Zeevi (2013) is better than the regret of Algorithm 1 when 𝜖 = 0.25 but is worse for other values of 𝜖. This can be attributed to the fact that for the assumed exploration period, their algorithm fails to identify the optimal assortment within the exploration phase with sufficient probability and hence incurs a linear regret for 𝜖 = 0.05, 0.1, and 0.15. Specifically, among the 100 simulations we tested, the algorithm in Sauré and Zeevi (2013) identified the optimal assortment for only 7%, 40%, 61%, and 97% cases, when 𝜖 = 0.05, 0.1, 0.15, and 0.25, respectively. This highlights the sensitivity to the “separability parameter” and the importance of having a reasonable estimate for the exploration period. Needless to say, such information is typically not available in practice. In contrast, the performance of Algorithm 1 is consistent across different values of 𝜖, insofar as the regret grows in a sub-linear fashion in all cases.

Fig. 9.3

Comparison with the algorithm of Sauré and Zeevi (2013). The graphs (a), (b), (c), and (d) compare the performance of Algorithm 1 to that of Sauré and Zeevi (2013) on problem instance (9.15), for 𝜖 = 0.05, 0.1, 0.15, and 0.25 respectively

5 Thompson Sampling for the MNL-Bandit

Motivated by the attractive empirical properties, in this section, we focus on a Thompson Sampling (TS)-based approach to the MNL-Bandit problem, first presented in Agrawal et al. (2017). In Sect. 9.5.1, we present the details of TS-based policy. In particular, we describe how to leverage the sampling technique introduced in Chap. 9.4 and design a prior distribution on the parameters of the MNL model such that the posterior update under the MNL-bandit feedback is tractable. In Sect. 9.5.4, we prove that the proposed algorithm achieves an $\tilde {O}(\sqrt {NT}\log {TK})$ regret upper bound. Here, we also highlight the key ingredient of the TS-based approach, a two-moment approximation of the posterior, and the ability to judicially correlate samples, which is done by embedding the two-moment approximation in a normal family. Section 9.5.5 demonstrates the empirical efficiency of our algorithm design.

5.1 Algorithm

In this section, we describe the posterior sampling (aka Thompson Sampling)-based algorithm for the MNL-Bandit problem. The basic structure of Thompson Sampling involves maintaining a posterior on the unknown problem parameters, which is updated every time new feedback is obtained. At the beginning of every round, a sample set of parameters is generated from the current posterior distribution, and the algorithm selects the best offer set according to these sample parameters. In the MNL-Bandit problem, there is one unknown parameter v_i associated with each item. To adapt the TS algorithm for this problem, we would need to maintain a joint posterior for (v₁, …, v_N). However, updating such a joint posterior is nontrivial since the feedback observed in every round is a choice sampled from the multinomial distribution. This depends on the subset S offered in that round. In particular, even if we initialize with an independent prior from a popular analytical family such as multivariate Gaussian, the posterior distribution after observing the MNL choice feedback will have a complex description. As a first step in addressing this challenge, we attempt to design a Thompson Sampling algorithm with independent priors. In particular, we leverage a sampling technique introduced in Sect. 9.4 that allows us to decouple individual parameters from the MNL choice feedback and provide unbiased estimates of these parameters. We can utilize these unbiased estimates to efficiently maintain independent conjugate Beta priors for the parameters v_i for each i. We present the details in Algorithm 1 below.

5.2 A TS Algorithm with Independent Beta Priors

Here, we present the first version of the Thompson sampling algorithm, which will serve as an important building block for the main algorithm in Sect. 9.5.3. In this version, we maintain a Beta posterior distribution for each item i = 1, …, N, which is updated as we observe users’ choice of items from the offered subsets. A key challenge here is to choose priors that can be efficiently updated on observing user choice feedback, to obtain increasingly accurate estimates of parameters {v_i}. To address this, we use the sampling technique introduced in the previous section to decouple estimates of individual parameters from the complex MNL feedback. The idea is to offer a set S multiple times; in particular, a chosen set S is offered repeatedly until the “outside option” is picked (in the online advertising application discussed earlier, this corresponds to displaying the same subset of ads repeatedly until we observe a user who does not click on any of the displayed ads). Proceeding in this manner, due to the structure of the MNL model, the average number of times an item i is selected provides an unbiased estimate of parameter v_i. Moreover, the number of times an item i is selected is also independent of the displayed set and is a geometric distribution with success probability 1∕(1 + v_i) and mean v_i. This observation is used as the basis for the epoch-based algorithmic structure and the choice of prior/posterior, as a conjugate to this geometric distribution.

Epoch-Based Offerings

Similar to the UCB approach, the algorithm proceeds in epochs An epoch is a group of consecutive time steps, where a set is offered repeatedly until the outside option is picked in response to offering . The set to be offered in epoch is picked at the beginning of the epoch based on the sampled parameters from the current posterior distribution; the construction of these posteriors and choice of is described in the next paragraph. We denote the group of time steps in an epoch as , which includes the time step at which an outside option was preferred. The following lemmas provide important building blocks for our construction. Refer to Avadhanula (2019) for detailed proofs.

Lemma 6 (Unbiased Estimate)

Let be the number of times an item is picked when the set is offered repeatedly until the outside option is picked. Then, for any and i, are i.i.d. geometric random variables with success probability $\frac {1}{1+v_i}$ and expected value v_i.

Lemma 7 (Conjugate Priors)

For any α > 3, β > 0, and Y_α,β ∼Beta(α, β), let $X_{\alpha ,\beta } = \frac {1}{Y_{\alpha ,\beta }-1}$ and f_α,β denote the probability distribution of random variable X_α,β. If the prior distribution of v_i is f_α,β, then after observing , a geometric random variable with success probability $\frac {1}{v_i+1}$, the posterior distribution of v_i is given by

Construction of Conjugate Prior/Posterior

From Lemma 6, we have that for any epoch and for any item , the estimate , the number of picks of item i in epoch is geometrically distributed with success probability 1∕(1 + v_i). Therefore, if we use the distribution of 1∕Beta(1, 1) − 1 as the initial prior for v_i, and then, in the beginning of epoch , from Lemma 7, we have that the posterior is distributed as , with being the number of epochs the item i has been offered before epoch (as part of an assortment) and being the number of times it was picked by the user.

Selection of Subset to be Offered

To choose the subset to be offered in epoch , the algorithm samples a set of parameters independently from the current posteriors and finds the set that maximizes the expected revenue as per the sampled parameters. In particular, the set to be offered in epoch is chosen as

(9.16)

The details of the above procedure are provided in Algorithm 2.

Algorithm 2 A TS algorithm for MNL-Bandit with Independent Beta priors

Algorithm 2 presents some unique challenges for theoretical analysis. A worst-case regret analysis of Thompson Sampling-based algorithms for MAB typically relies on showing that the best arm is optimistic at least once every few steps, in the sense that the parameter sampled from the posterior is better than the true parameter. Due to the combinatorial nature of our problem, such a proof approach requires showing that every few steps, all the K items in the optimal offer set have sampled parameters that are better than their true counterparts. However, Algorithm 2 samples the posterior distribution for each parameter independently in each round. This makes the probability of being optimistic exponentially small in K. In Sect. 9.5.3, we modify Algorithm 2 to address these challenges and in a manner amenable to theoretical analysis.

5.3 A TS Algorithm with Posterior Approximation and Correlated Sampling

In this section, we present a variant of TS with correlated sampling that achieves provably near-optimal regret bounds. We address the challenge associated with the combinatorial nature of the MNL-Bandit by employing correlated sampling across items. To implement correlated sampling, we find it useful to approximate the Beta posterior distribution by a Gaussian distribution with approximately the same mean and variance as the former, what was referred to in the introduction as a two-moment approximation. This allows us to generate correlated samples from the N Gaussian distributions as linear transforms of a single standard Gaussian random variable. Under such correlated sampling, we can guarantee that the probability that all K optimal items are simultaneously optimistic is constant, as opposed to being exponentially small (in K) in the case of independent sampling. However, such correlated sampling reduces the overall variance of the maximum of N samples severely, thus inhibiting exploration. We “boost” the variance by taking K samples instead of a single sample of the standard Gaussian. The resulting variant of Thompson Sampling, therefore, has three main modifications: posterior approximation through a Gaussian distribution, correlated sampling, and taking multiple samples (for “variance boosting”). We elaborate on each of these changes below.

Posterior Approximation

First, we present the following result that helps us in approximating the posterior.

Lemma 8 (Moments of the Posterior Distribution)

If X is a random variable distributed as Beta(α, β), then

$$\displaystyle \begin{aligned} \textstyle \mathbb{E}\left(\frac{1}{X}-1\right) &= \textstyle \frac{\beta}{\alpha-1},\;\;\;\mathit{\text{and}}\;\; \textstyle \textsf{Var}\left(\frac{1}{X}-1\right) & = \textstyle \frac{\frac{\beta}{\alpha-1}\left(\frac{\beta}{\alpha-1} + 1\right)}{\alpha-2}. \end{aligned}$$

We approximate the posterior distributions used in Algorithm 2 for each MNL parameter v_i, by a Gaussian distribution with approximately the same mean and variance given in Lemma 8. In particular, let

(9.17)

where is the number of epochs item i has been offered before epoch , and being the number of times it was picked by the user. We will use as the posterior distribution for item i in the beginning of epoch The Gaussian approximation of the posterior facilitates efficient correlated sampling from posteriors that plays a key role in avoiding the theoretical challenges in analyzing Algorithm 2.

Correlated Sampling

Given the posterior approximation by Gaussian distributions, we correlate the samples by using a common standard normal variable and constructing our posterior samples as an appropriate transform of this common standard normal. More specifically, in the beginning of an epoch , we generate a sample from the standard normal distribution, $\theta \sim \mathcal {N}\left (0,1\right )$, and the posterior sample for item i is generated as . Intuitively, this allows us to generate sample parameters for i = 1, …, N that are either simultaneously large or simultaneously small, thereby, boosting the probability that the sample parameters for all the K items in the best offered set are optimistic (i.e., the sampled parameter values are higher than the true parameter values).

Multiple (K) Samples

The correlated sampling decreases the joint variance of the sample set. More specifically, if θ_i were sampled independently from the standard normal distribution for every i, then for any epoch , we have that

In order to boost this joint variance and ensure sufficient exploration, we modify the procedure to generate multiple sets of samples. In particular, in the beginning of an epoch , we now generate K independent samples from the standard normal distribution, $\theta ^{(j)} \sim \mathcal {N}(0,1), j=1,\ldots , K$. And then for each j, a sample parameter set is generated as

Then, we use the largest valued samples

to decide the assortment to offer in epoch ,

We describe the algorithmic details formally in Algorithm 3.

Algorithm 3 TS algorithm with Gaussian approximation and correlated sampling

Intuitively, the second-moment approximation provided by Gaussian distribution and the multiple samples taken in Algorithm 3 may make the posterior converge slowly and increase exploration. However, the correlated sampling may compensate for these effects by reducing the variance of the maximum of N samples and therefore reducing the overall exploration. In Sect. 9.5.5, we illustrate some of these insights through numerical simulations. Here, correlated sampling is observed to provide significant improvements as compared to independent sampling and while posterior approximation by Gaussian distribution has little impact.

5.4 Regret Analysis

The following bound on the regret of Algorithm 3 was proven in Agrawal et al. (2017).

Theorem 3

For any instance v = (v₀, ⋯ , v_N) of the MNL-Bandit problem with N products, r_i ∈ [0, 1], and satisfying Assumption 1, the regret of Algorithm 3 in time T is bounded as

$$\displaystyle \begin{aligned} \textsf{Reg}{}(T,{\boldsymbol{v}}) \leq C_1\sqrt{NT}\log{TK} + C_2N\log^2{TK}, \end{aligned}$$

where C₁ and C₂ are absolute constants (independent of problem parameters).

Proof Outline

We provide a proof sketch for Theorem 3. We break down the expression for total regret

$$\displaystyle \begin{aligned} \textsf{Reg}(T,{\boldsymbol{v}}):=\mathbb{E}\left[\sum_{t=1}^T R(S^*, {\boldsymbol{v}}) - R(S_t, {\boldsymbol{v}})\right], \end{aligned}$$

into regret per epoch, and rewrite it as follows:

where is the number of periods in epoch , and is the set repeatedly offered by our algorithm in epoch . We bound the two terms: Reg₁(T, v) and Reg₂(T, v) separately.

Since is chosen as the optimal set for the MNL instance with parameters the first term Reg₁(T, v) is essentially the difference between the optimal revenue of the true instance and the optimal revenue of the sampled instance. This term contributes no regret if the revenues corresponding to the sampled instances are optimistic, i.e., if . Unlike optimism under uncertainty approaches such as UCB, this property is not directly ensured by the Thompson Sampling-based algorithm. To bound this term, we utilize the anti-concentration properties of the posterior, as well as the dependence between samples for different items. In particular, we use these properties to prove that at least one of the K sampled instances is optimistic “often enough.”

The second term Reg₂(T, v) captures the difference in reward from the offered set when evaluated on sampled parameters in comparison to the true parameters. We bound this by utilizing the concentration properties of the posterior distributions. It involves showing that for the sets that are played often, the posterior will converge quickly so that revenue on the sampled parameters will be close to that on the true parameters.

In what follows, we elaborate on the anti-concentration properties of the posterior distribution required to prove Theorem 3.

Anti-Concentration of the Posterior Distribution

The last and important component of our analysis is showing that revenues corresponding to the sampled instances are not optimistic, i.e., if only in a “small number” of epochs. We utilize the anti-concentration properties of the posterior to prove that one of the K sampled instances corresponds to higher expected revenue. We then leverage this result to argue that the Reg₁(T, v) is small.

We will refer to an epoch as optimistic if the expected revenue of the optimal set corresponding to the sampled parameters is higher than the expected revenue of the optimal set corresponding to true parameters, i.e., Any epoch that is not optimistic is referred to as a non-optimistic epoch. Since is an optimal set for the sampled parameters, we have Hence, for any optimistic epoch , the difference between the expected revenue of the offer set corresponding to sampled parameters and the optimal revenue R(S^∗, v) is bounded by zero. This suggests that as the number of optimistic epochs increases, the term Reg₁(T, v) decreases.

The central technical component of our analysis is showing that the regret over non-optimistic epochs is “small.” More specifically, we prove that there are only a “small” number of non-optimistic epochs. From the restricted monotonicity property of the optimal revenue (see Lemma 2), we have that an epoch is optimistic if every sampled parameter, , is at least as high as the true parameter v_i for every item i in the optimal set S^∗. Recall that each posterior sample, , is generated from a Gaussian distribution, whose mean concentrates around the true parameter v_i. We can use this observation to conclude that any sampled parameter will be greater than the true parameter with constant probability, i.e., . However, to show that an epoch is optimistic, we need to show that sampled parameters for all the items in S^∗ are larger than the true parameters. This is where the correlated sampling feature of our algorithm plays a key role. We use the dependence structure between samples for different items in the optimal set and variance boosting (by a factor of K) to prove an upper bound of roughly 1∕K on the number of consecutive epochs between two optimistic epochs. More specifically, we have the following result.

Lemma 9 (Spacing of Optimistic Epochs)

Let $\mathcal {E}^{\textsf {An}}(\tau )$ denote the set of consecutive epochs between an optimistic epoch τ and the subsequent optimistic epoch τ′. For any p ∈ [1, 2], we have

$$\displaystyle \begin{aligned} \mathbb{E}\left[ \left|\mathcal{E}^{\textsf{An}}(\tau) \right |{}^p \right] \leq \left(\frac{e^{12}}{K}+30^{1/p}\right)^p.\end{aligned}$$

5.5 Empirical Study

In this section, we test the various design components of the Thompson Sampling-based approach through numerical simulations. The aim is to isolate and understand the effect of individual features of our algorithm like Beta posteriors vs. Gaussian approximation, independent sampling vs. correlated sampling, and single sample vs. multiple samples, on the practical performance.

We simulate an instance of the MNL-Bandit problem with N = 1000, K = 10, and T = 2 × 10⁵, when the MNL parameters {v_i}_i=1,…,N are generated randomly from Unif[0, 1]. And, we compute the average regret based on 50 independent simulations over the randomly generated instance. In Fig. 9.4, we report the performance of the following different variants of TS:

• (i) Algorithm 2: Thompson Sampling with independent Beta priors, as described in Algorithm 2.

  Fig. 9.4

  

  Regret growth with T for various heuristics on a randomly generated MNL-Bandit instance with N = 1000, K = 10

• (ii) TS_{IID Gauss}: Algorithm 2 with Gaussian posterior approximation and independent sampling. More specifically, for each epoch and for each item i, we sample a Gaussian random variable independently with the mean and variance equal to the mean and variance of the Beta prior in Algorithm 2 (see Lemma 9.17).

• (iii) TS_{Gauss Corr}: Algorithm 3 with Gaussian posterior approximation and correlated sampling. In particular, for every epoch , we sample a standard normal random variable. Then, for each item i, we obtain a corresponding sample by multiplying and adding the preceding sample with the standard deviation and mean of the Beta prior in Algorithm 2 (see Step (a) in Algorithm 3). We use the values α = β = 1 for this variant of Thompson Sampling.

• (iv) Algorithm 3: Algorithm 1 with Gaussian posterior approximation with correlated sampling and boosting by using multiple (K) samples. This is essentially the version with all the features of Algorithm 3. We use the values α = β = 1 for this variant of Thompson Sampling.

For comparison, we also present the performance of UCB approach discussed in the previous section. The performance of all the variants of TS is observed to be better than the UCB approach in our experiments, which is consistent with the other empirical evidence in the literature.

Figure 9.4 shows the performance of the TS variants. Among the TS variants, the performance of Algorithm 2, i.e., Thompson Sampling with independent Beta priors is similar to TS_{IID Gauss}, the version with independent Gaussian (approximate) posteriors, indicating that the effect of posterior approximation is minor. The performance of TS_{Gauss Corr}, where we generate correlated samples from the Gaussian distributions, is significantly better than the other variants of the algorithm. This is consistent with our remark earlier that to adapt the Thompson sampling approach of the classical MAB problem to our setting, ideally, we would like to maintain a joint prior over the parameters {v_i}_i=1,…,N and update it to a joint posterior using the Bandit feedback. However, since this can be quite challenging, and intractable in general, we use independent priors over the parameters. The superior performance of TS_{Gauss Corr} demonstrates the potential benefits of considering a joint (correlated) prior/posterior in settings with a combinatorial structure. Finally, we observe that the performance of Algorithm 3, where an additional “variance boosting” is provided through K independent samples, is worse than TS_{Gauss Corr}. Note that while “variance boosting” facilitates theoretical analysis, it also results in a longer exploration period explaining the observed degradation of performance in comparison to the TS variant without “variance boosting.” However, Algorithm 3 performs significantly better than the independent Beta posterior version Algorithm 2. Therefore, significant improvements in performance due to the correlated sampling feature of Algorithm 3 compensate for the slight deterioration caused by boosting.

6 Lower Bound for the MNL-Bandit

In this section, we present the fundamental theoretical limits that any policy must incur a regret of $\Omega (\sqrt {NT})$. More precisely, (Chen and Wang, 2017) established the following result.

Theorem 4 (Lower Bound on Achievable Performance (Chen and Wang, 2017))

There exists a (randomized) instance of the MNL-Bandit problem with v₀ ≥ v_i , i = 1, …, N, such that for any N and K, and any policy π that offers assortment $\mathcal {S}_t^{{\pi }}$, $|{S}_t^{{\pi }}| \leq K$ at time t, we have for all T ≥ N that

where S^∗ is (at-most) K-cardinality assortment with maximum expected revenue, and C is an absolute constant.

Theorem 4 is proved by a reduction to a parametric multi-armed bandit (MAB) problem, for which a lower bound is known. We refer the interested readers to Chen and Wang (2017) for a detailed proof. Note that Theorem 4 establishes that Algorithms 1 and 3 achieve near-optimal performance without any a priori knowledge of problem parameters. Furthermore, these algorithms are adaptive in the sense that their performance is near-optimal in the “well separated” case.

7 Conclusions and Recent Progress

In this chapter, we studied the dynamic assortment selection problem under the widely used multinomial logit (MNL) choice model. Formulating the problem as a parametric multi-arm bandit problem, we discussed algorithmic approaches that learn the parameters of the choice model while simultaneously maximizing the cumulative revenue. We focused on UCB and Thompson Sampling-based algorithms that are universally applicable, and whose performance (as measured by the regret) is provably nearly optimal.

However, the approaches presented here only considered the settings where every product has its own utility parameter and has to be estimated separately. Such approaches can handle only a (small) finite number of products. Many real application settings involve a large number of products essentially described by a small of features, via what is often referred to as a factor model. Recently, several works (Chen et al., 2019, 2020, 2021; Cheung and Simchi-Levi, 2017; Saha and Gopalan, 2019; Feng et al., 2018; Miao and Chao, 2021, 2019; Oh and Iyengar, 2021, 2019) have considered extensions of the approaches presented here to those more complex settings.

The works of Chen et al. (2020); Miao and Chao (2019); Oh and Iyengar (2021) consider the more general contextual variant of the MNL-Bandit problem. These papers build upon (Agrawal et al., 2016, 2019) to develop UCB-based approaches and establish worst-case regret bounds of $\tilde {O}(d\sqrt {T}),$ where d is the dimension of contexts, with some additional dependencies on certain problem parameters.

The works of Cheung and Simchi-Levi (2017); Miao and Chao (2021); Oh and Iyengar (2019) developed Thompson Sampling-based approaches for contextual variations of the MNL-Bandit problem. These works achieve a Bayesian regret bound of $\tilde {O} (d\sqrt {T} )$ that are dependent on problem parameters. Feng et al. (2018) and Saha and Gopalan (2019) consider the best arm identification variant of the MNL-Bandit problem, where the focus is only on exploration to identify the best K items. Chen et al. (2019) consider a variant of the MNL-Bandit where feedback from a small fraction of users is not consistent with the MNL choice model. They present a near-optimal algorithm with a worst-case regret bound of $\tilde {O}(\epsilon K^2 T + \sqrt {NKT})$, where 𝜖 is the fraction of users for whom the feedback is corrupted.

Disclaimer

This work was done when Vashist (one of the authors) was at Columbia University.