On the Fine Interior of Three-Dimensional Canonical Fano Polytopes

Abstract

The Fine interior $\Delta ^{{{\mathrm{FI}\,}}}$ of a d-dimensional lattice polytope $\Delta$ is a rational subpolytope of $\Delta$ which is important for constructing minimal birational models of non-degenerate hypersurfaces defined by Laurent polynomials with Newton polytope $\Delta$. This paper presents some computational results on the Fine interior of all $674,\!688$ three-dimensional canonical Fano polytopes.

2.1 Introduction

Let $M \cong \mathbb {Z}^d$ be a free abelian group of rank d. We set $M_\mathbb {Q}:= M \otimes \mathbb {Q}$ and denote by N the dual group ${{\,\mathrm{Hom}\,}}(M, \mathbb {Z})$ in the dual $\mathbb {Q}$-linear vector space $N_\mathbb {Q}:= {{\,\mathrm{Hom}\,}}(M, \mathbb {Q})$. Let $\langle \cdot , \cdot \rangle : M_\mathbb {Q}\times N_\mathbb {Q}\rightarrow \mathbb {Q}$ be the natural pairing.

A convex compact d-dimensional polytope $\Delta \subseteq M_\mathbb {Q}$ is called lattice d-tope if all vertices of $\Delta$ belong to the lattice $M \subseteq M_\mathbb {Q}$, i.e., $\Delta$ equals the convex hull ${{\,\mathrm{conv}\,}}(\Delta \cap M)$ of all lattice points in $\Delta$. The usual interior $\Delta ^{\circ }$ of $\Delta$ is the complement $\Delta \setminus \partial \Delta$, where $\partial \Delta$ is the boundary of $\Delta$. Another interior of a lattice polytope $\Delta$ was introduced by Fine  [3, 13, 15, 20]:

Definition 1

Let $\Delta \subseteq M_\mathbb {Q}$ be a lattice d-tope. Denote by ${\text {ord}}_\Delta$ the piecewise linear function $N_\mathbb {Q}\rightarrow \mathbb {Q}$ with

$$\begin{aligned} {\text {ord}}_\Delta (y) := \min _{ x \in \Delta } \langle x, y \rangle \;\; (y \in N_\mathbb {Q}). \end{aligned}$$

Then the convex subset

$$ \Delta ^{{{\mathrm{FI}\,}}}:= \bigcap _{n \in N \setminus \{0 \}} \{ x \in M_\mathbb {Q}\, \mid \, \langle x, n \rangle \ge {\text {ord}}_\Delta (n) + 1 \} $$

is called the Fine interior of $\Delta$.

One can show that only finitely many linear inequalities $\langle x, n \rangle \ge {\text {ord}}_\Delta (n) + 1$ are necessary to define $\Delta ^{{{\mathrm{FI}\,}}}$. Therefore, $\Delta ^{{{\mathrm{FI}\,}}}$ is a convex hull of finitely many rational points $p \in M_\mathbb {Q}$. Moreover, any lattice point $p \in \Delta ^\circ \cap M$ in the usual interior of $\Delta$ is contained in $\Delta ^{{{\mathrm{FI}\,}}}$. Therefore, $\Delta ^{{{\mathrm{FI}\,}}}$ contains the convex hull of $\Delta \cap M$, i.e., we get the inclusion ${{\,\mathrm{conv}\,}}(\Delta ^{\circ } \cap M) \subseteq \Delta ^{{{\mathrm{FI}\,}}}$. In particular, $\Delta ^{{{\mathrm{FI}\,}}}$ is non-empty if $\Delta ^{\circ } \cap M$ is non-empty. Moreover, for any lattice polytope $\Delta$ of dimension $d \le 2$ one has the equality ${{\,\mathrm{conv}\,}}(\Delta ^{\circ } \cap M) = \Delta ^{{{\mathrm{FI}\,}}}$ [3]. The Fine interior $\Delta ^{{{\mathrm{FI}\,}}}$ of a lattice polytope $\Delta$ of dimension $d \ge 3$ may happen to be strictly larger than the convex hull ${{\,\mathrm{conv}\,}}(\Delta ^{\circ } \cap M)$. The simplest famous example of such a situation is due to M. Reid. Other similar examples based on hollow 3-topes can be found in Sect. 2.7:

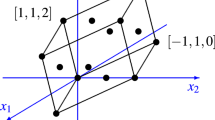
Example 2

([20, Example 4.15])   Let $M \subseteq \mathbb {Q}^4$ be 3-dimensional affine lattice defined by

$$ M := \left\{ ( m_1,m_2, m_3,m_4 ) \in \mathbb {Z}^4 \, \Big \vert \, \sum _{i=1}^4 m_i = 5, \; \sum _{i=1}^4 i m_i \equiv 0\ \left( \mathrm {mod}\ {5}\right) \right\} .$$

Consider the M-lattice 3-tope $\Delta \subseteq M_\mathbb {Q}$ defined as the convex hull of 4 lattice points

$$\begin{aligned} (5,0,0,0), \;(0,5,0,0), \;(0,0,5,0), \text { and}\; (0,0,0,5) \in M. \end{aligned}$$

Then ${{\,\mathrm{conv}\,}}(\Delta ^{\circ } \cap M) = \emptyset$, but $\Delta ^{{{\mathrm{FI}\,}}}$ is the 3-dimensional M-rational simplex

$$\begin{aligned} {{\,\mathrm{conv}\,}}\{(2,1,1,1), (1,2,1,1), (1,1,2,1), (1,1,1,2)\} \end{aligned}$$

and $\Delta ^{{{\mathrm{FI}\,}}} \cap M$ is empty.

In this paper, we are interested in lattice d-topes $\Delta \subseteq M_\mathbb {Q}$ obtained as Newton polytopes of Laurent polynomials $f_\Delta$ in d variables $x_1, \ldots , x_d$, i.e.,

$$\begin{aligned} f_\Delta (\mathbf{x}) = \sum _{m \in \Delta \cap M} a_m \mathbf{x}^m, \end{aligned}$$

where $a_m \in \mathbb {C}$ are sufficiently general complex numbers. The importance of the Fine interior is explained by the following theorem [3, 15, 20]:

Theorem 3

Let $\mathcal {Z}_\Delta \subseteq \mathbb {T}^d$ be a non-degenerate affine hypersurface in the d-dimensional algebraic torus $\mathbb {T}^d$ defined by a Laurent polynomial $f_\Delta$ with Newton d-tope $\Delta$. Then the following conditions are equivalent:

• 1. a smooth projective compactification $\mathcal {V}_\Delta$ of $\mathcal {Z}_\Delta$ has non-negative Kodaira dimension, i.e., $\kappa \ge 0$;

• 2.  $\mathcal {Z}_\Delta$ is birational to a minimal model ${\mathcal {S}}_\Delta$ with abundance;

• 3. the Fine interior $\Delta ^{{{\mathrm{FI}\,}}}$ of $\Delta$ is non-empty.

Remark 4

By well known results of Khovanskii [14], one has vanishing of the cohomology groups

$$\begin{aligned} h^{i}({\mathcal {O}}_{\mathcal {V}_\Delta }) = 0 \;\; (1 \le i \le d-2) \end{aligned}$$

and the equation $h^{d-1}({\mathcal {O}}_{\mathcal {V}_\Delta }) = | \Delta ^{\circ } \cap M|$. The numbers $h^{i}({\mathcal {O}}_{\mathcal {V}_\Delta })$ are birational invariants of $\mathcal {Z}_\Delta$; they do not depend on a smooth projective compactification $\mathcal {V}_\Delta$ of $\mathcal {Z}_\Delta$. In particular, the number $| \Delta ^{\circ } \cap M|$ is the geometric genus $p_g$ of the affine hypersurface $\mathcal {Z}_\Delta \subseteq \mathbb {T}^d$.

Smooth projective compactifications of non-degenerate hypersurfaces in $\mathbb {T}^d$ can be obtained using the theory of toric varieties [14].

Let $\Delta \subseteq M_\mathbb {Q}$ be a lattice d-tope. We consider the normal fan $\Sigma ^{\Delta }$ of $\Delta$ in the dual space $N_\mathbb {Q}$, i.e., $\Sigma ^{\Delta } := \{\sigma ^{\theta } \, | \, \theta \preceq \Delta \}$, where $\sigma ^{\theta }$ is the cone generated by all inward-pointing facet normals of facets containing the face $\theta \preceq \Delta$ of $\Delta$. One has $\dim (\sigma ^{\theta }) + \dim (\theta ) =d$ for any face $\theta \preceq \Delta$. We denote by $X_\Delta$ the normal projective toric variety constructed via the normal fan $\Sigma ^{\Delta }$. In particular, the above function ${\text {ord}}_\Delta :N_\mathbb {Q}\rightarrow \mathbb {Q}$ is a piecewise linear function with respect to this fan defining an ample Cartier divisor on $X_\Delta$. In particular, the cones $\sigma ^\theta \in \Sigma ^\Delta$ are defined as

$$ \sigma ^{\theta } = \left\{ y \in N_\mathbb {Q}\, \Big \vert \, {\text {ord}}_\Delta (y) = \langle x,y \rangle \; \text { for all } x \in \theta \right\} . $$

Remark 5

Using the normal fan $\Sigma ^\Delta$, one can compute the fundamental group $\pi _1(\mathcal {V}_\Delta )$ of a smooth projective birational model $\mathcal {V}_\Delta$ of a non-degenerate affine hypersurface $\mathcal {Z}_\Delta$ (given as in Theorem 3). The fundamental group $\pi _1(\mathcal {V}_\Delta )$ does not depend on the choice of the smooth birational model and it is isomorphic to the quotient of the lattice N modulo the sublattice $N'$ generated by all lattice points in $(d-1)$-dimensional cones $\sigma ^\theta$ of the normal fan $\Sigma ^\Delta$ [4].

Example 6

The minimal model ${\mathcal {S}_\Delta }$ of a non-degenerate affine surface $\mathcal {Z}_\Delta$ defined by a Laurent polynomial with the Newton polytope $\Delta$ from Example 2 is a  Godeaux surface. It is a surface of general type with $p_g = q=0$, $K^2 =1$, and $\pi _1({\mathcal {S}_\Delta }) \cong \mathbb {Z}/5 \mathbb {Z}$.

Definition 7

A lattice d-tope $\Delta$ is called canonical Fano d-tope if $| \Delta ^{\circ } \cap M| =1$. Up to a shift by a lattice vector, we will assume without loss of generality that $0 \in M$ is the single lattice point in the interior $\Delta ^{\circ }$ of the canonical Fano d-tope $\Delta$, i.e., $\Delta ^{\circ } \cap M = \{ 0 \}$.

All canonical Fano 3-topes have been classified [16]. There exists exactly $674,\!688$ canonical Fano 3-topes $\Delta$. The aim of this paper is to present computational results of their Fine interiors $\Delta ^{{{\mathrm{FI}\,}}}$ and some related combinatorial invariants. These data are important for computing minimal smooth projective surfaces $\mathcal {S}_\Delta$ with $p_g=1$ and $q =0$ which are birational to affine non-degenerate hypersurfaces $\mathcal {Z}_\Delta \subseteq \mathbb {T}^3 \cong (\mathbb {C}^\times )^3$.

The simplest description of the minimal surface $\mathcal {S}_\Delta$ has been obtained when $\Delta$ is a reflexive 3-tope [5].

Definition 8

A lattice d-tope $\Delta \subseteq M_\mathbb {Q}$ containing the origin $0 \in M$ in its interior is called reflexive if the dual polytope

$$\begin{aligned} \Delta ^* := \{ y \in N\, \vert \, \langle x, y \rangle \ge -1 \; \text { for all } x \in \Delta \} \subseteq N_\mathbb {Q}\end{aligned}$$

is a lattice polytope.

There exist $4,\!319$ reflexive 3-topes, classified by Kreuzer and Skarke [17]. They form a small subset in the list of all $674,\!688$ canonical Fano 3-topes [16]. Reflexive 4-topes are also classified by Kreuzer and Skarke [18]. There exist $473,\!800,\!776$ reflexive 4-topes, but the complete list of all canonical Fano 4-topes is unknown and expected to be much bigger.

If $\Delta$ is a reflexive d-tope, then $X_\Delta$ is a Gorenstein toric Fano d-fold and the Zariski closure $\overline{Z}_\Delta$ in $X_\Delta$ is a Gorenstein Calabi-Yau $(d-1)$-fold. If $d =3$, then $\overline{Z}_\Delta$ is a K3-surface with at worst finitely many Du Val singularities of type $A_k$. The minimal surface $\mathcal {S}_\Delta$ is a smooth K3-surface which is obtained as the minimal (crepant) desingularization of $\overline{Z}_\Delta$ [5].

One motivation for the present paper is due to Corti and Golyshev, who have found 9 interesting examples of canonical Fano 3-simplices $\Delta$ such that the affine surfaces $\mathcal {Z}_\Delta$ are birational to elliptic surfaces of Kodaira dimension $\kappa =1$ [11].

The computation of the Fine interior $\Delta ^{{{\mathrm{FI}\,}}}$ for all canonical Fano 3-topes $\Delta \subseteq M_\mathbb {Q}$ has shown that the dimension of the Fine interior $\Delta ^{{{\mathrm{FI}\,}}}$ has only three values: 0, 1, and 3. It is rather surprising that there are no canonical Fano 3-topes $\Delta$ with $\dim ( \Delta ^{{{\mathrm{FI}\,}}}) = 2$.

The condition $\dim (\Delta ^{{{\mathrm{FI}\,}}}) =0$ holds if and only if $\Delta ^{{{\mathrm{FI}\,}}}$ equals the lattice point $0 \in M$. There exist exactly $665,\!599$ canonical Fano 3-topes with $\Delta ^{{{\mathrm{FI}\,}}} = \{0 \}$, where $0 \in M$ is the only interior lattice point of $\Delta$. These polytopes are characterized in [3, Proposition 3.4] by the condition that $0 \in N$ is an interior lattice point of the lattice 3-tope

$$\begin{aligned}{}[\Delta ^*]:= {{\,\mathrm{conv}\,}}( \Delta ^* \cap N). \end{aligned}$$

Remark 9

If $\Delta$ is a canonical Fano 3-tope, then $\Delta ^{{{\mathrm{FI}\,}}} = \{0 \}$ if and only if the non-degenerate affine surface $\mathcal {Z}_\Delta$ is birational to a K3-surface [3, Theorem 2.26].

The case $\dim ( \Delta ^{{{\mathrm{FI}\,}}}) =1$ splits in two subcases. There exists exactly 20 canonical Fano 3-topes $\Delta$ such that $0 \in M$ is the midpoint of the Fine interior $\Delta ^{{{\mathrm{FI}\,}}}$. Therefore, we call this Fine interior symmetric. Canonical Fano 3-topes with 1-dimensional symmetric Fine interior are characterized by the condition that $[\Delta ^*]$ is a reflexive 2-tope. The Fine interior of the remaining $9,\!020~$ canonical Fano 3-topes with $\dim ( \Delta ^{{{\mathrm{FI}\,}}}) =1$ contains $0 \in M$ as a vertex. Therefore, we call this Fine interior asymmetric. Canonical Fano 3-topes with 1-dimensional asymmetric Fine interior are combinatorially characterized by the condition that $0 \in N$ is contained in the relative interior of a facet $\Theta \preceq [\Delta ^*]$ of the lattice 3-tope $[\Delta ^*]$. The minimal surfaces $\mathcal {S}_\Delta$ corresponding to canonical Fano 3-topes with 1-dimensional Fine interior (symmetric and asymmetric) are elliptic surfaces of Kodaira dimension $\kappa =1$.

There exist exactly 49 canonical Fano 3-topes with $\dim (\Delta ^{{{\mathrm{FI}\,}}}) =3$. These polytopes are characterized by the condition that $0 \in N$ is a vertex of the lattice 3-tope $[\Delta ^*]$. The surfaces $\mathcal {S}_\Delta$ corresponding to canonical Fano 3-topes $\Delta$ with 3-dimensional Fine interior $\Delta ^{{{\mathrm{FI}\,}}}$ are of general type (i.e., $\mathcal {S}_\Delta$ has maximal Kodaira dimension $\kappa =\dim (\mathcal {S}_\Delta )=2$).

Remark 10

The Fine interior computations were done using

$$ \Delta ^{{{\mathrm{FI}\,}}} = \bigcap _{\theta \preceq \Delta } \; \bigcap _{n \in \mathcal {H}(\sigma ^{\theta })} \left\{ x \in M_\mathbb {Q}\, \Big \vert \, \langle x,n \rangle \ge {\text {ord}}_\Delta (n) +1 \right\} , $$

where $\mathcal {H}(\sigma ^{\theta })$ denotes the set of all irreducible elements in the monoid $\sigma ^{\theta } \cap N$. It is the minimal generating set of the monoid $\sigma ^{\theta } \cap N$ and is called Hilbert basis of $\sigma ^{\theta } \cap N$.

In the next sections we consider examples and discuss additional properties of canonical Fano 3-topes $\Delta$ in dependence of their Fine interiors $\Delta ^{{{\mathrm{FI}\,}}}$. All computations were done using the Graded Ring Database [8], including the data of all $674,\!688$ canonical Fano 3-topes, and magma [7]. Therefore, all statements have been checked by computer calculations. The canonical Fano 3-topes used as examples in this paper appear with an ID that is the example’s ID in the Graded Ring Database.¹

2.2 Almost Reflexive Polytopes of Dimension 3 and 4

Definition 11

A canonical Fano d-tope $\Delta \subseteq M_\mathbb {Q}$ is called almost reflexive if the convex hull of all N-lattice points in the dual polytope $\Delta ^*$ is reflexive.

It is easy to show the following statement:

Proposition 12

If a canonical Fano d-tope $\Delta$ is almost reflexive, then

$$\begin{aligned} \Delta ^{FI} = \{0 \}. \end{aligned}$$

Proof

If $[ \Delta ^*]$ is reflexive, then $\Delta = (\Delta ^*)^*$ is contained in the dual reflexive polytope $[\Delta ^*]^*$. Therefore, the Fine interior of $\Delta$ is contained in the Fine interior of the reflexive polytope $[\Delta ^*]^*$ and $([\Delta ^*]^*)^\mathrm{FI} =\{ 0 \}$. Thus, $\Delta ^\mathrm{FI} = \{0 \}$.   $\square$

The converse statement is not true in general for $d \ge 5$, but there exist many equivalent characterizations of reflexive and almost reflexive d-topes among canonical Fano d-topes if $d =3$ or $d=4$.

Let us recall some combinatorial invariants of arbitrary lattice d-topes.

Definition 13

The Ehrhart power series of an arbitrary lattice d-tope $\Delta \subseteq M_\mathbb {Q}$ is defined as

$$ P_\Delta (t) := \sum _{k \ge 0} \left| k \Delta \cap M\right| t^k, $$

where $|k \Delta \cap M|$ denotes the number of lattice points in the k-th dilate $k \Delta$ of $\Delta$.

This Ehrhart series is a rational function of the form

$$ P_\Delta (t) = \frac{\psi _d (\Delta )t^ d + \cdots + \psi _1 (\Delta )t + \psi _0 (\Delta )}{(1 - t)^{d+1}}, $$

where $\psi _i(\Delta )$ are non-negative integers for all $0 \le i \le d$ [22] such that $\psi _0(\Delta ) =1$ and $\psi _1(\Delta ) = |\Delta \cap M| - d -1$. Moreover,  $\sum _{i=0}^d \psi _i(\Delta ) = v(\Delta )$, where  $v(\Delta ) := d! \cdot {{\,\mathrm{vol}\,}}(\Delta )$ denotes the normalized volume of $\Delta$.

One has the following characterization of reflexive d-topes:

Proposition 14

([6, Theorem 4.6]) A canonical Fano d-tope $\Delta$ is reflexive if and only if

$$\begin{aligned} \psi _i(\Delta ) = \psi _{d-i}(\Delta ) \; \; (0 \le i \le d). \end{aligned}$$

The Ehrhart reciprocity implies that the power series

$$ Q_\Delta (t) := \sum _{k \ge 1} \left| (k \Delta )^\circ \cap M\right| t^k $$

is a rational function

$$ Q_\Delta (t) = \frac{\varphi _{d+1}(\Delta )t^{d+1} + \cdots + \varphi _2 (\Delta )t + \varphi _1 (\Delta )t + \varphi _0 (\Delta )}{(1 - t)^{d+1}}, $$

where $\varphi _0 (\Delta )=0$ and $\varphi _1 (\Delta ) = |\Delta ^\circ \cap M|$. Using Serre duality, one obtains [12, Sect. 4, 5.11]

$$\begin{aligned} \varphi _i(\Delta ) = \psi _{d+1-i}(\Delta ) \; \; (1 \le i \le d+1), \end{aligned}$$

 i.e., in particular

$$\begin{aligned} \psi _d(\Delta )= \varphi _1(\Delta ) = |\Delta ^\circ \cap M| \end{aligned}$$

and

$$ \psi _{d-1}(\Delta ) =\varphi _2(\Delta ) = |2 \Delta ^\circ \cap M| - (d+1) |\Delta ^\circ \cap M|.$$

Therefore, the lattice d-tope $\Delta$ is a canonical Fano d-tope if and only if $\psi _d(\Delta ) =1$. Moreover,

$$\begin{aligned} \psi _{d-1}(\Delta ) = |(2 \Delta )^\circ \cap M| - (d+1) \end{aligned}$$

if $\Delta$ is a canonical Fano d-tope.

Applying the above equations, one immediately obtains the following criterion for reflexivity of canonical Fano d-topes in the case $d =3, 4$:

Proposition 15

Let $\Delta \subseteq M_\mathbb {Q}$ be a canonical Fano d-tope with $d \in \{ 3,4\}$. Then for $d =3$, one has

$$ P_\Delta (t) = \frac{t^ 3 + (|(2 \Delta )^\circ \cap M| -4)t^2 + ( |\Delta \cap M| - 4)t + 1}{(1 - t)^{4}} $$

and for $d =4$, one obtains

$$ P_\Delta (t) = \frac{t^ 4 + (|(2 \Delta )^\circ \cap M| -5)t^3 + \psi _2(\Delta ) t^2 + ( |\Delta \cap M| - 5)t + 1}{(1 - t)^{5}}. $$

In particular, $\Delta$ is reflexive if and only if

$$ \left| \Delta \cap M\right| = \left| (2 \Delta )^\circ \cap M\right| . $$

Proposition 16

Let $\Delta \subseteq M_\mathbb {Q}$ be a canonical Fano d-tope with $d \in \{3,4\}$ such that $0 \in N$ is an interior lattice point of $[\Delta ^*]$. Then $[\Delta ^*]$ is reflexive, i.e., $\Delta$ is almost reflexive.

Proof

Let $n \in N$ be an interior lattice point of $[\Delta ^*]$. Then  $\langle x, n \rangle \ge 0$ for all $x \in \Delta \cap M$ because

$$ \Delta ^* = \{ y \in N_\mathbb {Q}\; |\; \langle x, y \rangle \ge -1 \;\; \text { for all } x \in \Delta \} $$

and $\langle x, n \rangle$ is an integer. Since $0 \in \Delta ^\circ \cap M$, $M_\mathbb {Q}$ is the set of all non-negative $\mathbb {Q}$-linear combinations of all lattice points in $\Delta \cap M$. This implies $\langle x', n \rangle \ge 0$ for all $x' \in M_\mathbb {Q}$, i.e., $n =0$. Therefore, $[\Delta ^*]$ has only one interior lattice point $0 \in N$, i.e., $[\Delta ^*]$ is a canonical Fano d-tope.

It is clear that $[\Delta ^*]$ is contained in the interior of $2[\Delta ^*]$. Therefore, we have $[\Delta ^*] \cap N \subseteq (2[\Delta ^*])^\circ \cap N$. On the other hand, for any lattice point $n \in (2[\Delta ^*])^\circ$, $\langle x, n \rangle > -2~$ for all $x \in \Delta \cap M$. Since $\langle x, n \rangle ~$ is an integer, $n \in \Delta ^* \cap N$, i.e.,

$$\begin{aligned}{}[\Delta ^*] \cap N = (2[\Delta ^*])^\circ \cap N . \end{aligned}$$

Using Proposition 15, $[\Delta ^*]$ is reflexive.   $\square$

Corollary 17

Let $\Delta \subseteq M_\mathbb {Q}$ be a canonical Fano d-tope with $d \in \{3,4\}$ such that $0 \in N$ is an interior lattice point of $[\Delta ^*]$. Then $[\Delta ^*]^*$ is the smallest (referring to inclusion) reflexive polytope containing $\Delta$.

Proof

Let $\Delta ' \subseteq M_\mathbb {Q}$ be a reflexive d-tope such that  $\Delta \subseteq \Delta '$. Then $(\Delta ')^* \subseteq \Delta ^*$. Since $(\Delta ')^*$ is a lattice polytope, it is contained in $[\Delta ^*]$. Thus, $[\Delta ^*]^*$ is contained in $((\Delta ')^*)^* = \Delta '$.   $\square$

Remark 18

If $\Delta$ is a reflexive d-tope, then $[2\Delta ^\circ ] = \Delta$. If $\Delta$ is a canonical Fano d-tope with $d \in \{3,4\}$ such that $\Delta ^{{{\mathrm{FI}\,}}}=\{0\}$ and $\Delta$ is contained in a reflexive d-tope $\Delta '$, then $[2\Delta ^\circ ]$ is contained in $[(2\Delta ')^\circ ] = \Delta '$. Therefore, $[2\Delta ^\circ ]$ is contained in the smallest reflexive polytope $[\Delta ^*]^*$ containing $\Delta$, i.e.,

$$\begin{aligned}{}[2\Delta ^\circ ] \subseteq [\Delta ^*]^*. \end{aligned}$$

Computations showed that among all $665,\!599$ canonical Fano 3-topes $\Delta$ with $\Delta ^\mathrm{FI} = \{0 \}$ there exist exactly $211,\!941$ canonical Fano 3-tops such that $[2\Delta ^\circ ]$ is reflexive. For the remaining canonical Fano 3-topes $\Delta$ the lattice 3-topes $[2\Delta ^\circ ]~$ are larger than $\Delta$, but are not equal to the reflexive hull $[\Delta ^*]^*$.

Remark 19

Let $\Delta$ be an almost reflexive 3-tope. We denote by $\tau (\Delta )$ the lattice d-tope $[2\Delta ^\circ ]$ . If $\tau (\Delta )$ is not reflexive, then it is almost reflexive and we can consider the larger lattice d-tope $\tau ^2(\Delta ) := \tau (\tau (\Delta )) \subseteq [\Delta ^*]^*$. After at most five steps, $\tau ^k(\Delta )$ is equal to the reflexive hull $[\Delta ^*]^*$ of $\Delta$.

In dimension 4, the situation is comparable:

Example 20

Let $\Delta \subseteq \mathbb {R}^4$ be the almost reflexive 4-tope defined by the inequalities $x_i \ge -1$ $(1 \le i \le 4)$,  $x_1 \le 2$, and $x_1 + x_2 + x_3 + x_4 \le 1$. Then $\Delta ^{FI} = \{0\}$ and the smallest reflexive 4-tope containing $\Delta$ is the 4-simplex $[\Delta ^*]^*$ defined by the inequalities $x_i \ge -1$ $(1 \le i \le 4)$ and $x_1 + x_2 + x_3 + x_4 \le 1$. It is easy to see that $\tau (\Delta )$ is not the reflexive  4-tope $[\Delta ^*]^*$ because the vertex $(4,-1,-1,-1) \in \text {vert}([\Delta ^*]^*)$ is not in $2\Delta ^\circ$. However, $\tau ^2(\Delta ) = [\Delta ^*]^*$.

2.3 Canonical Fano 3-Topes with $\Delta ^{{{\mathrm{FI}\,}}} = \{0\}$

We note that the set of all reflexive 3-topes forms a rather small part of the set of all canonical Fano 3-topes. The majority of the canonical Fano 3-topes belong to the subset of almost reflexive 3-topes. The proof of the following statement is based on the result of Skarke [21] and the explanations in the previous section.

Proposition 21

A canonical Fano 3-tope $\Delta$ is almost reflexive if one of the following equivalent conditions is satisfied:

• 1.  $\Delta ^{{{\mathrm{FI}\,}}} =\{0\};$

• 2.  $0 \in N$ is an interior lattice point of $[\Delta ^* ]$;

• 3.  $\Delta$ is contained in some reflexive 3-tope;

• 4.  $\tau ^k(\Delta )$ is the reflexive 3-tope $[\Delta ^*]^*$ for some sufficiently large k $(1 \le k \le 5)$;

• 5. the lattice 3-tope $[2\Delta ^\circ ]$ has exactly one interior lattice point;

• 6. the non-degenerate affine hypersurface $\mathcal {Z}_\Delta$ defined by a Laurent polynomial with Newton polytope $\Delta$ is birational to a smooth K3-surface.

Computations show that there exist exactly $665,\!599$ almost reflexive canonical Fano 3-topes. The set of almost reflexive 3-topes includes all $4, \!319$ reflexive 3-topes. We have shown that for any almost reflexive 3-tope $\Delta$, the reflexive polytope $\Delta ^{{{\mathrm{ref}\,}}}:= [\Delta ^*]^*$ is the smallest reflexive 3-tope containing $\Delta$. We call $\Delta ^{{{\mathrm{ref}\,}}}$ the reflexive hull of $\Delta$. Thus we obtain a natural surjective map $\Delta \mapsto \Delta ^{{{\mathrm{ref}\,}}}$ from the set of almost reflexive 3-topes to the set of reflexive 3-topes, which is the identity on the set of reflexive 3-topes. The minimal surface $\mathcal {S}_\Delta$ is a K3-surface if and only if  $\Delta$ is an almost reflexive 3-tope. If $\Delta$ is an almost reflexive 3-tope, but not reflexive, then the minimal surface $\mathcal {S}_\Delta$ is a crepant desingularization of the Zariski closure of $\mathcal {Z}_\Delta$ in the Gorenstein toric Fano threefold $X_{\Delta ^{{{\mathrm{ref}\,}}}}$ defined by the reflexive hull of $\Delta$.

A generalization of the reflexive hull of almost reflexive 3-topes for arbitrary lattice d-topes with non-empty Fine interior can be obtained using the notion of the support of the Fine interior $\Delta ^{{{\mathrm{FI}\,}}}$.

Definition 22

Let $\Delta \subseteq M_\mathbb {Q}$ be a lattice d-tope with $\Delta ^{{{\mathrm{FI}\,}}} \ne \emptyset$. Then the set

$$ {{\,\mathrm{supp}\,}}(\Delta ^{{{\mathrm{FI}\,}}}) := \{ n \in N \, \vert \, \text { there exists }x \in \Delta ^{{{\mathrm{FI}\,}}} \; \mathrm{with }\; \langle x, n \rangle = {\text {ord}}_{\Delta }(n) +1 \} $$

is called support of the Fine interior of $\Delta$.

Example 23

If $\Delta$ is a reflexive d-tope, then the support of the Fine interior of $\Delta$ is the set of all non-zero lattice points in $\Delta ^* \cap N$.

Remark 24

It is easy to show that one always has

$$ \Delta ^{{{\mathrm{FI}\,}}} = \bigcap _{n \in {{\,\mathrm{supp}\,}}(\Delta ^{{{\mathrm{FI}\,}}})} \{ x \in M_\mathbb {Q}\, \vert \, \langle x, n \rangle \ge {\text {ord}}_{\Delta }(n) +1 \}. $$

Definition 25

Let $\Delta \subseteq M_\mathbb {Q}$ be a lattice d-tope with $\Delta ^{{{\mathrm{FI}\,}}} \ne \emptyset$. Then the rational polytope

$$ \Delta ^{{{\mathrm{can}\,}}}:= \bigcap _{n \in {{\,\mathrm{supp}\,}}(\Delta ^{{{\mathrm{FI}\,}}})} \{ x \in M_\mathbb {Q}\, \vert \, \langle x, n \rangle \ge {\text {ord}}_{\Delta }(n) \} $$

contains $\Delta$ and is called the canonical hull of $\Delta$.

Example 26

If $\Delta$ is an almost reflexive 3-tope, then ${{\,\mathrm{supp}\,}}(\Delta ^{{{\mathrm{FI}\,}}})$ is the set $(\Delta ^* \cap N) \setminus \{0\}$ of boundary lattice points in the reflexive 3-tope $[ \Delta ^*]$ and the canonical hull $\Delta ^{{{\mathrm{can}\,}}}$ equals the reflexive hull $\Delta ^{{{\mathrm{ref}\,}}}$ of the polytope $\Delta$, i.e., $\Delta ^{{{\mathrm{can}\,}}}=\Delta ^{{{\mathrm{ref}\,}}}=[\Delta ^*]^*$. In particular, in this case $\Delta ^{{{\mathrm{can}\,}}}$ is always a lattice 3-tope.

There exists a smooth projective toric variety $X_\Sigma$ defined by a fan $\Sigma$ whose 1-dimensional cones are generated by all lattice vectors from the finite set ${{\,\mathrm{supp}\,}}(\Delta ^{{{\mathrm{FI}\,}}})$. Then the minimal surface $\mathcal {S}_\Delta$ is a K3-surface which is the Zariski closure of $\mathcal {Z}_\Delta$ in $X_\Sigma$ [3].

Fig. 2.1

Canonical Fano 3-topes ${\boldsymbol{\Delta }}$ with ${\boldsymbol{\Delta }}^{\mathbf {FI}}\boldsymbol{{=}}\mathbf {\{0\}}$. Shaded faces are occluded and the Fine interior $\{0\}$ is shown in grey with a double border. The whole polytope is the canonical hull $\Delta ^{{{\mathrm{can}\,}}}$ as well as the reflexive hull $\Delta ^{{{\mathrm{ref}\,}}}$ and the grey coloured polytope is $\Delta$. a Reflexive polytope $\Delta = {{\,\mathrm{conv}\,}}\{v_1,v_2,v_3,v_4\}$ with $v_1=(1,0,0)$, $v_2=(0,1,0)$, $v_3=(0,0,1)$, $v_4= (-1,-1,-1)$, and $\Delta ^{{{\mathrm{ref}\,}}}=\Delta ^{{{\mathrm{can}\,}}}= \Delta$. All facets of $\Delta$ have lattice distance 1 to the origin. b Almost reflexive polytope $\Delta = {{\,\mathrm{conv}\,}}\{v_1,v_2,v_3,v_4\}$ with $v_1=(1,0,0)$, $v_2=(0,1,0)$, $v_3=(0,0,1)$, $v_4= (-1,-1,-2)$, and $\Delta ^{{{\mathrm{ref}\,}}}=\Delta ^{{{\mathrm{can}\,}}}= {{\,\mathrm{conv}\,}}\{v_1,v_2,v_3,v_4,v_5\}$ with $v_5=(0,0,-1)$ reflexive. The dark grey coloured facet of $\Delta$ has lattice distance 2 and all other facets have lattice distance 1 to the origin

Example 27

Let us consider the (almost) reflexive canonical Fano 3-tope $\Delta = {{\,\mathrm{conv}\,}}\{v_1,v_2,v_3,v_4\} \subseteq M_\mathbb {Q}$ (ID 547386, Fig. 2.1a) with vertices

$$ v_1 := (1,0,0), \, v_2 := (0,1,0), \, v_3 :=(0,0,1), \, \text {and } v_4 := (-1,-1,-1) $$

and ${\Delta }^{{{\mathrm{FI}\,}}}=\{0\}$. Moreover,

$$ \Delta ^{{{\mathrm{ref}\,}}}= {{\,\mathrm{conv}\,}}( 2\Delta ^\circ \cap M) = {{\,\mathrm{conv}\,}}(\Delta \cap M) = \Delta $$

and

$$ {\Delta }^{{{\mathrm{can}\,}}} =[{\Delta }^*]^* = ({\Delta }^*)^*={\Delta } $$

because ${\Delta }$ is reflexive, i.e., $\Delta ^{{{\mathrm{ref}\,}}}=\Delta ^{{{\mathrm{can}\,}}}= \Delta$ reflexive (Fig. 2.1a).

Example 28

Consider the almost reflexive canonical Fano 3-tope $\Delta \subseteq M_\mathbb {Q}$ (ID 547385, Fig. 2.1b) with vertices

$$ v_1 := (1,0,0), \, v_2 := (0,1,0), \, v_3 :=(0,0,1), \,\text {and } v_4 := (-1,-1,-2) $$

and ${\Delta }^{{{\mathrm{FI}\,}}}=\{0\}$. Moreover,

$$ \Delta ^{{{\mathrm{ref}\,}}}= {{\,\mathrm{conv}\,}}((\Delta \cap M) \cup \{v_5\}) = {{\,\mathrm{conv}\,}}\{v_1,v_2,v_3,v_4, v_5\} $$

and

$$ {\Delta }^{{{\mathrm{can}\,}}} =[{\Delta }^*]^* = {{\,\mathrm{conv}\,}}\{v_1,v_2,v_3,v_4, v_5\} $$

with $v_5:= (0, 0, -1)$ because ${\Delta }$ is almost reflexive, i.e., $\Delta ^{{{\mathrm{ref}\,}}}=\Delta ^{{{\mathrm{can}\,}}}= \Delta$ reflexive (Fig. 2.1b).

2.4 Asymmetric Fine Interior of Dimension 1

There exist exactly $9,\!020$ canonical Fano 3-topes $\Delta$ with 1-dimensional Fine interior such that $0 \in N$ belongs to a facet $\Theta \preceq [\Delta ^*]$ of the lattice 3-tope $[\Delta ^*]$. This class of canonical Fano 3-topes is characterized by the property that the lattice 3-tope $[2\Delta ^\circ ]$ has exactly 2 interior lattice points.

The corresponding minimal surfaces $\mathcal {S}_\Delta$ are  simply connected (i.e., have trivial fundamental group $\pi _1(\mathcal {S}_\Delta )$) elliptic surfaces of Kodaira dimension $\kappa =1$. We observed that the facet $\Theta \preceq [\Delta ^*]$ is a reflexive 2-tope corresponding to one of the three types pictured in Fig. 2.2. All N-lattice points on the boundary of $\Theta$ belong to ${{\,\mathrm{supp}\,}}(\Delta ^{{{\mathrm{FI}\,}}})$. It was checked that for all these 3-topes $\Delta$ the canonical hull $\Delta ^{{{\mathrm{can}\,}}}$ is again a lattice 3-tope. Moreover, the Fine interior $\Delta ^{{{\mathrm{FI}\,}}}$ is contained in the ray generated by the primitive lattice vector $v_\Delta \in M$ which is the primitive inward-pointing facet normal of $\Theta$, i.e., $\langle x , y \rangle =0$ for all $x \in \Delta ^{{{\mathrm{FI}\,}}}$, $y \in \Theta$. The lattice point $0 \in M$ is a vertex of $\Delta ^{{{\mathrm{FI}\,}}}$. More precisely, one has

$$\begin{aligned} \Delta ^{{{\mathrm{FI}\,}}} = {{\,\mathrm{conv}\,}}\{0, \lambda v_\Delta \}, \end{aligned}$$

where $\lambda \in \{ 1/2, 2/3\}$. The primitive lattice vector $v_\Delta$ is the unique interior lattice point on a reflexive facet $\theta _{+} \preceq \Delta$ of $\Delta$ of one of the three possible types pictured in Fig. 2.2. These three reflexive polygons $\theta _{+}$ are characterized by the condition that the dual reflexive polygons $\theta ^*_{+}$ are obtained from $\theta _{+}$ (Fig. 2.3) by enlarging the lattice $\mathbb {Z}^2$ in the following ways: $\mathbb {Z}^2 + \mathbb {Z}(1/3,2/3)$ (Fig. 2.3a), $\mathbb {Z}^2 + \mathbb {Z}(1/2, 0)$ (Fig. 2.3b), and $\mathbb {Z}^2 + \mathbb {Z}(1/2,1/2)$ (Fig. 2.3c). Moreover, the reflexive facet $\theta _{+}$ of $\Delta$ is isomorphic to the facet $\Theta$ of $[\Delta ^*]$. The projection $M \rightarrow M/\mathbb {Z}v_\Delta$ of $\Delta$ or of $\theta _{+}$ along $v_\Delta$ is a reflexive polygon of one of the three types pictured in Fig. 2.3, which is dual to $\theta _{+}$ and $\Theta$. The lattice vector $v_\Delta$ defines a character of the 3-dimensional torus $\chi : \mathbb {T}^3 \rightarrow \mathbb {C}^\times$. For almost all $\alpha \in \mathbb {C}^\times$, the fiber $\chi ^{-1} (\alpha )$ is an affine elliptic curve defined by a Laurent polynomial with the reflexive Newton polytope $\Theta ^* \cong \theta ^*_{+}$ of one of the three types pictured in Fig. 2.3 with the distribution shown in Table 2.1. So $\chi$ defines birationally an elliptic fibration.

Fig. 2.2

Reflexive Facets of $\Delta$ Containing $\pm v_\Delta$. Three types of reflexive facets $\theta _{\pm } \preceq \Delta$ of $\Delta$ containing $\pm v_\Delta$ for all $9,\!020+20$ canonical Fano 3-topes $\Delta$ with $\dim (\Delta ^{{{\mathrm{FI}\,}}})=1$. Vertices are coloured black, boundary points that are not vertices grey, and the origin light grey. a ${{\,\mathrm{conv}\,}}\{(1,0),(0,1),(-1,-1)\}$. b ${{\,\mathrm{conv}\,}}\{(1,0),(-1,1),(-1,-1)\}$. c ${{\,\mathrm{conv}\,}}\{(\pm 1,0),(0,\pm 1)\}$

Fig. 2.3

Reflexive Projection Polytopes. Three types of reflexive polytopes obtained via a projection of $\Delta$ along $\pm v_\Delta$ for all $9,\!020+20$ canonical Fano 3-topes $\Delta$ with $\dim (\Delta ^{{{\mathrm{FI}\,}}})=1$. Vertices are coloured black, boundary points that are not vertices grey, and the origin light grey. a ${{\,\mathrm{conv}\,}}\{(-1,2),(-1,-1),(2,-1)\}$. b ${{\,\mathrm{conv}\,}}\{(-2,-1),(0,1),$ $(2,-1)\}$. c ${{\,\mathrm{conv}\,}}\{(\pm 1,\pm 1)\}$

Table 2.1 Distribution of the Reflexive Facets of $\Delta$ Containing ${\boldsymbol{\pm }} {\mathbf {v}}_{\boldsymbol{\Delta }}$. Table contains: Type of the reflexive facet $\theta _{\pm }$ containing $\pm v_{\Delta }$, type of the dual reflexive facet $\theta ^*_{\pm }$, the enlarged lattice used to obtain $\theta ^*_{\pm }$ from ${\theta _{\pm }}$, the number of canonical Fano 3-topes $\Delta _{\text {asym}} := \{\Delta \, \vert \,~$1$\text {-dim. asym. } \Delta ^{{{\mathrm{FI}\,}}}\}$, and the number of canonical Fano 3-topes $\Delta _{\text {sym}} := \{\Delta \, \vert \,~$1$\text {-dim. sym. } \Delta ^{{{\mathrm{FI}\,}}}\}$ with respect to the facet type of $\theta _{\pm }$ pictured in Fig. 2.2

Fig. 2.4

Canonical Fano 3-topes with Asymmetric Fine Interior of Dimension 1 Shaded faces are occluded. The Fine interior and the origin are shown in grey, with a double border around the origin. The facet $\theta _{+}$ is grey dotted. a The whole polytope is $\Delta = {{\,\mathrm{conv}\,}}\{v_1,v_2,v_3,v_4\}$ with $v_1=(2,3,8)$, $v_2=(1,0,0)$, $v_3=(0,1,0)$, and $v_4= (-1,-1,-1)$. Moreover, $\Delta ^{{{\mathrm{FI}\,}}}= {{\,\mathrm{conv}\,}}\{(0,0,0), (1/2,1/2,1)\}$, $\theta _{+} = {{\,\mathrm{conv}\,}}\{v_1,v_2,v_3\}$, and $\Delta ^{{{\mathrm{can}\,}}} = {{\,\mathrm{conv}\,}}\{v_1, v_2, v_3, v_4, v_5\}$ with $v_5 = (0, 1,4)$. b The whole polytope is $\Delta = {{\,\mathrm{conv}\,}}\{v_1,v_2,v_3,v_4\}$ with $v_1=(-1,1,-2)$, $v_2=(1,-2,3)$, $v_3=(1,0,0)$, and $v_4= (-2,5,-3)$. Moreover, $\Delta ^{{{\mathrm{FI}\,}}}={{\,\mathrm{conv}\,}}\{(0,0,0), (0,2/3,0)\}$ and $\theta _{+}={{\,\mathrm{conv}\,}}\{v_2,v_3,v_4\}$, and $\Delta ^{{{\mathrm{can}\,}}} = {{\,\mathrm{conv}\,}}\{v_1, v_2, v_3, v_4, v_5\}$ with $v_5 = (-2, 4,-3)$

Example 29

Let $\Delta \subseteq M_\mathbb {Q}$ be a canonical Fano 3-tope given as the convex hull of

$$ v_1 := (2,3,8), \, v_2 := (1,0,0), \, v_3 := (0,1,0), \,\text {and } v_4 := (-1,-1,-1) $$

(ID 547324, Fig. 2.4a, Tables 2.2 and 2.4). Then

$$\begin{aligned} \Delta ^{{{\mathrm{FI}\,}}} = {{\,\mathrm{conv}\,}}\{(0,0,0), (1/2,1/2,1)\} = {{\,\mathrm{conv}\,}}\{0, 1/2 \cdot v_\Delta \}, \end{aligned}$$

where $v_\Delta = (1,1,2)$. One has $v_1 + 2v_2 + v_3 = 4 v_\Delta$. Therefore, $v_\Delta$ is the interior lattice point of the reflexive facet $\theta _{+}$ of $\Delta$ with vertices $v_1,v_2, v_3$ and the images $\overline{v}_1, \overline{v}_2, \overline{v}_3$ of $v_1,v_2,v_3$ in $M/\mathbb {Z}v_\Delta$ are vertices of the dual reflexive triangle $\theta ^*_{+}$ (Fig. 2.3b) satisfying the relation

$$\begin{aligned} \overline{v}_1 + 2 \overline{v}_2 + \overline{v}_3 =0. \end{aligned}$$

To compute the canonical hull $\Delta ^{{{\mathrm{can}\,}}}$ of $\Delta$, we obtain ${{\,\mathrm{supp}\,}}(\Delta ^{{{\mathrm{FI}\,}}}) = \{s_i \, \vert \, 1 \le i \le 18 \}$ with $s_1 := (-1, -1, 1)$, $s_2 := (-1, -1, 2)$, $s_3 := (-1, -1, 3)$, $s_4 := (-1, 0, 1)$, $s_5 := (-1, 0, 2)$, $s_6 := (-1, 1, 0)$, $s_7 := (-1, 1, 1)$, $s_8 := (-1, 2, 0)$, $s_9 := (-1, 3, -1)$, $s_{10} := (0, -1, 1)$, $\ldots$, $s_{18} := (-2, -2, 1)$, which leads to

$$ \Delta ^{{{\mathrm{can}\,}}} ={{\,\mathrm{conv}\,}}\{v_1,v_2,v_3,v_4, v_5\} $$

with $v_5:= (0, 1,4)$ (Fig. 2.4a).

Table 2.2 9 Canonical Fano 3-topes with Asymmetric Fine Interior of Dimension 1. Table contains: vertices $\text {vert}(\Delta )$ of $\Delta$, vertices $\text {vert}(\Delta ^{{{\mathrm{FI}\,}}})$ of the Fine interior $\Delta ^{{{\mathrm{FI}\,}}}$, unique primitive lattice point $v_{\Delta } \in \theta _+$ in the reflexive facet $\theta _+ \preceq \Delta$, and weights $(w_i)_{0 \le i \le 3}$ of the weighted projective 3-space $\mathbb {P}(w_0,\ldots ,w_3)$ appearing in [11]

Table 2.3 9 Canonical Fano 3-topes with Asymmetric Fine Interior of Dimension 1. Table contains: primitive inward-pointing facet normals $(n_{i})_{1 \le i \le 4}$ of $\Delta$, vertices $\text {vert}(\theta _{+})$ of the reflexive facet $\theta _{+}\preceq \Delta$, and primitive inward-pointing facet normal $n_{\theta _+}$ of the reflexive facet $\theta _+ \preceq \Delta$

Table 2.4 9 Canonical Fano 3-topes with Asymmetric Fine Interior of Dimension 1. Table contains: vertices $\text {vert}(\Theta )$ of the reflexive facet $\Theta \preceq [\Delta ^*]$, support ${{\,\mathrm{supp}\,}}(\Delta ^{{{\mathrm{FI}\,}}})$ of the Fine interior $\Delta ^{{{\mathrm{FI}\,}}}$, and vertices $\text {vert}(\Delta ^{{{\mathrm{can}\,}}})$ of the canonical hull $\Delta ^{{{\mathrm{can}\,}}}~$

Example 30

Let $\Delta \subseteq M_\mathbb {Q}$ be a canonical Fano 3-tope given as the convex hull of

$$ v_1 := (-1,1,-2), \, v_2 := (1,-2,3), \, v_3 := (1,0,0), \,\text {and } v_4 := (-2,5,-3) $$

(ID 547323, Fig. 2.4b, Tables 2.2 and 2.4). Then (Table 2.3)

$$\begin{aligned} \Delta ^{{{\mathrm{FI}\,}}} = {{\,\mathrm{conv}\,}}\{(0,0,0), (0,2/3,0)\} = {{\,\mathrm{conv}\,}}\{0, 2/3 \cdot v_\Delta \}, \end{aligned}$$

where $v_\Delta = (0,1,0)$. One has $v_2 + v_3 + v_4 = 3 v_\Delta$. Therefore, $v_\Delta$ is the interior lattice point of the reflexive facet $\theta _{+}$ of $\Delta$ with vertices $v_2,v_3, v_4$ and the images $\overline{v}_2, \overline{v}_3, \overline{v}_4$ of $v_2,v_3,v_4$ in $M/\mathbb {Z}v_\Delta$ are vertices of the dual reflexive triangle $\theta ^*_{+}$ (Fig. 2.3a) satisfying the relation

$$\begin{aligned} \overline{v}_2 + \overline{v}_3 + \overline{v}_4 =0. \end{aligned}$$

To compute the canonical hull $\Delta ^{{{\mathrm{can}\,}}}$ of $\Delta$, we obtain ${{\,\mathrm{supp}\,}}(\Delta ^{{{\mathrm{FI}\,}}}) = \{s_i \, \vert \, 1 \le i \le 20 \}$ with $s_1 := (-3, -3, -2)$, $s_2 := (-1, 0, 0)$, $s_3 := (-1,0,1)$, $s_4 := (-1,1,1)$, $s_5 := (-1,2,2)$, $s_6 := (-1,3,2)$, $s_7 := (-1,4,3)$, $s_8 := (-1,6,4)$, $s_9 := (0,1,1)$, $s_{10} := (0,2,1)$, $\ldots$, $s_{20} := (4,1,-1)$, which leads to

$$ \Delta ^{{{\mathrm{can}\,}}} ={{\,\mathrm{conv}\,}}\{v_1,v_2,v_3,v_4, v_5\} $$

with $v_5:= (-2,4,-3)$ (Fig. 2.4b).

Remark 31

The detailed information about a small selection of the $9,\!020$ canonical Fano 3-topes with $\dim (\Delta ^{{{\mathrm{FI}\,}}})=1$ and $0 \in \text {vert}(\Delta ^{{{\mathrm{FI}\,}}})$ can be found in Tables 2.2, 2.3, and 2.4.

2.5 Symmetric Fine Interior of Dimension 1

There exist exactly 20 canonical Fano 3-topes $\Delta$ such that 0 is the center of 1-dimensional Fine interior $\Delta ^{{{\mathrm{FI}\,}}}$. In this case,  $\mathcal {S}_\Delta$ is an elliptic surface of Kodaira dimension $\kappa = 1$ with non-trivial fundamental group $\pi _1(\mathcal {S}_\Delta )$ of order 2 or 3. Computations show that one always has  $\Delta =\Delta ^{{{\mathrm{can}\,}}}$ and

$$\begin{aligned} \Delta ^{{{\mathrm{FI}\,}}} = {{\,\mathrm{conv}\,}}\{-\lambda v_\Delta , \lambda v_\Delta \} \end{aligned}$$

with $\lambda = \frac{1}{2}~$ if and only if $\left| \pi _1(\mathcal {S}_\Delta ) \right| =2$ and

$$\begin{aligned} \Delta ^{{{\mathrm{FI}\,}}} = {{\,\mathrm{conv}\,}}\{-\mu v_\Delta , \mu v_\Delta \} \end{aligned}$$

with $\mu = \frac{2}{3}$ if and only if $\left| \pi _1(\mathcal {S}_\Delta ) \right| =3$. The primitive lattice vectors $\pm v_\Delta$ are the two unique interior lattice points in two reflexive facets $\theta _{\pm } \preceq \Delta$ of one of the three possible types pictured in Fig. 2.2. The reflexive facets $\theta _{\pm }$ of $\Delta$ are isomorphic to the facet $\Theta$ of $[\Delta ^*]$. The projections $M \rightarrow M/\mathbb {Z}(\pm v_\Delta )$ of $\Delta$ or of $\theta _{\pm }$ along $\pm v_\Delta$ reveal a reflexive polygon of one of the three types pictured in Fig. 2.3, which is dual to $\theta _{\pm }$ and $\Theta$. The lattice vector $v_\Delta$ defines a character of the 3-dimensional torus $\chi : \mathbb {T}^3 \rightarrow \mathbb {C}^\times$. For almost all $\alpha \in \mathbb {C}^\times$, the fiber $\chi ^{-1} (\alpha )$ is an affine elliptic curve defined by a Laurent polynomial with the reflexive Newton polytope $\Theta ^* \cong \theta ^*_{\pm }$ of one of the three types pictured in Fig. 2.3 with the distribution shown in Table 2.1. So $\chi$ defines birationally an elliptic fibration. The vertex sets of $\Delta$ and these reflexive facets are related via $\text {vert}(\Delta ) = \text {vert}(\theta _{+}) \cup \text {vert}(\theta _{-})$. Moreover, every edge of $\Delta$ is either an edge of $\theta _{+}$ or $\theta _{-}$ of these two facets or it is parallel to $v_\Delta$.

Fig. 2.5

Canonical Fano 3-topes with Symmetric Fine Interior of Dimension 1. Shaded faces are occluded. The Fine interior and the origin are shown in grey with a double border around the origin. The facets $\theta _{\pm }$ are grey dotted. a The whole polytope is $\Delta = {{\,\mathrm{conv}\,}}\{v_1,v_2,v_3,v_4\}$ with $v_1=(1,0,0)$, $v_2=(2,1,1)$, $v_3=(-2,-3,-5)$, and $v_4= (2,1,9)$. Moreover, $\Delta ^{{{\mathrm{FI}\,}}}= {{\,\mathrm{conv}\,}}\{(0,0,-1/2), (0,0,1/2)\}$, $\theta _{+} = {{\,\mathrm{conv}\,}}\{v_1,v_3,v_4\}$, $\theta _{-} = {{\,\mathrm{conv}\,}}\{v_1,v_2,v_3\}$, and $\Delta ^{{{\mathrm{can}\,}}} = \Delta$. b The whole polytope is $\Delta = {{\,\mathrm{conv}\,}}\{v_1,v_2,v_3,v_4\}$ with $v_1=(-4,2,9)$, $v_2=(1,0,0)$, $v_3=(0,1,0)$, and $v_4= (7,-6,-18)$. Moreover, $\Delta ^{{{\mathrm{FI}\,}}}= {{\,\mathrm{conv}\,}}\{(-2/3,2/3,2),(2/3,-2/3,-2)\}$, $\theta _{+} = {{\,\mathrm{conv}\,}}\{v_1,v_2,v_3\}$, $\theta _{-} = {{\,\mathrm{conv}\,}}\{v_1,v_3,v_4\}$, and $\Delta ^{{{\mathrm{can}\,}}} = \Delta$

Example 32

Let $\Delta \subseteq M_\mathbb {Q}$ be a canonical Fano 3-tope given as the convex hull

$$ v_1 := (0,1,0), \, v_2 := (2,1,1), \, v_3 := (-2,-3,-5), \,\text {and } v_4 := (2,1,9) $$

(ID 547393, Fig. 2.5b, Tables 2.5 and 2.6). Then

$$ \Delta ^{{{\mathrm{FI}\,}}} = {{\,\mathrm{conv}\,}}\{(0,0,-1/2), (0,0, 1/2)\} = {{\,\mathrm{conv}\,}}\{-\lambda v_\Delta , \lambda v_\Delta \} $$

with $\lambda = \frac{1}{2},~$ where $v_\Delta = (0,0,1)$. One has $2v_1 + v_3 + v_4 = 4 v_\Delta$ and $2v_1 + v_2 + v_3 = 4(- v_\Delta )$. Therefore, $v_\Delta$ is the interior lattice point of the reflexive facet $\theta _{+} = \theta _{134}$ of $\Delta$ and $-v_\Delta$ is the interior lattice point of the reflexive facet $\theta _{-}= \theta _{123}$ of $\Delta$ (Fig. 2.2b). The images $\overline{v}_1, \overline{v}_3, \overline{v}_4$ of $v_1,v_3,v_4$ in $M/\mathbb {Z}v_\Delta$ and the images $\overline{v}_1, \overline{v}_2, \overline{v}_3$ of $v_1,v_2,v_3$ in $M/\mathbb {Z}(-v_\Delta )$ are vertices of the dual reflexive triangle $\theta ^*_{\pm }$ (Fig. 2.3b) satisfying the relation

$$\begin{aligned} 2 \overline{v}_1 + \overline{v}_3 + \overline{v}_4 =0 \end{aligned}$$

and

$$\begin{aligned} 2 \overline{v}_1 + \overline{v}_2 + \overline{v}_3 =0, \end{aligned}$$

respectively.

To compute the canonical hull $\Delta ^{{{\mathrm{can}\,}}}$ of $\Delta$, we obtain ${{\,\mathrm{supp}\,}}(\Delta ^{{{\mathrm{FI}\,}}}) = \{s_i \, \vert \, 1 \le i \le 6 \}$ with $s_1 := (-1, -2, 2)$, $s_2 := (-1, 1, 0)$, $s_3 := (0, -1, 0)$, $s_4 := (1, -1, 0)$, $s_5 := (2, -1, 0)$, and $s_6 := (9, -2, -2)$, which leads to $\Delta ^{{{\mathrm{can}\,}}} = \Delta .$

Table 2.5 20 Canonical Fano 3-topes with Symmetric Fine Interior of Dimension 1. Table contains: vertices $\text {vert}(\Delta )$ of $\Delta$

Table 2.6 20 Canonical Fano 3-topes with Symmetric Fine Interior of Dimension 1. Table contains: vertices $\text {vert}(\Delta ^{{{\mathrm{FI}\,}}})$ of the Fine interior $\Delta ^{{{\mathrm{FI}\,}}}$, unique primitive lattice points $\pm v_{\Delta } \in \theta _\pm$ in the reflexive facets $\theta _\pm \preceq \Delta$, vertices $\text {vert}(\theta _{{\pm }})$ of the reflexive facets $\theta _{{\pm }} \preceq \Delta$, and support ${{\,\mathrm{supp}\,}}(\Delta ^{{{\mathrm{FI}\,}}})$ of the Fine interior $\Delta ^{{{\mathrm{FI}\,}}}$ (here: $\Delta ^{{{\mathrm{can}\,}}} = \Delta$)

Example 33

Let $\Delta \subseteq M_\mathbb {Q}$ be a canonical Fano 3-tope given as the convex hull

$$ v_1 := (-4,2,9), \, v_2 := (1,0,0), \, v_3 := (0,1,0), \,\text {and } v_4 := (7,-6,-18) $$

(ID 547409, Fig. 2.5b, Tables 2.5 and 2.6). Then

$$ \Delta ^{{{\mathrm{FI}\,}}} = {{\,\mathrm{conv}\,}}\{(-2/3, 2/3, 2),(2/3, -2/3, -2)\} = {{\,\mathrm{conv}\,}}\{ -\mu v_\Delta , \mu v_\Delta \} $$

with $\mu = \frac{2}{3},~$ where $v_\Delta = (1,-1,-3)$. One has $v_1+ v_2 +v_3 = -3 v_\Delta$ and $v_1 + v_3 + v_4 = -3(- v_\Delta )$. Therefore, $v_\Delta$ is the interior lattice point of the reflexive facet $\theta _{+} = \theta _{123}$ of $\Delta$ and $-v_\Delta$ is the interior lattice point of the reflexive facet $\theta _{-}= \theta _{134}$ of $\Delta$ (Fig. 2.2b). The images $\overline{v}_1, \overline{v}_2, \overline{v}_3$ of $v_1,v_2,v_3$ in $M/\mathbb {Z}v_\Delta$ and the images $\overline{v}_1, \overline{v}_3, \overline{v}_4$ of $v_1,v_3,v_4$ in $M/\mathbb {Z}(-v_\Delta )$ are vertices of the dual reflexive triangle $\theta ^*_{\pm }$ (Fig. 2.3b) satisfying the relation

$$\begin{aligned} \overline{v}_1 + \overline{v}_2 + \overline{v}_3 =0, \end{aligned}$$

and

$$\begin{aligned} \overline{v}_1 + \overline{v}_3 + \overline{v}_4 =0, \end{aligned}$$

respectively.

To compute the canonical hull $\Delta ^{{{\mathrm{can}\,}}}$ of $\Delta$, we obtain ${{\,\mathrm{supp}\,}}(\Delta ^{{{\mathrm{FI}\,}}}) = \{s_i \, \vert \, 1 \le i \le 5 \}$ with $s_1 := (-3,-3,-1)$, $s_2 := (-1, -1, 0)$, $s_3 := (-1,2, -1)$, $s_4 := (2, -1, 1)$, and $s_5 := (15,-3,7)$, which leads to $\Delta ^{{{\mathrm{can}\,}}} = \Delta$.

Remark 34

Information about all 20 canonical Fano 3-topes with $\dim (\Delta ^{{{\mathrm{FI}\,}}})=1$ and $0 \in {(\Delta ^{{{\mathrm{FI}\,}}})}^{\circ }$ can be found in Tables 2.5 and 2.6.

2.6 Fine Interior of Dimension 3

There exist 49 canonical Fano 3-topes $\Delta$ such that $\dim (\Delta ^{{{\mathrm{FI}\,}}}) = 3$. Exactly 3 of these polytopes $\Delta$ define minimal surface $\mathcal {S}_\Delta$ with non-trivial fundamental group of order 2 and $K^2 =2$. For these 3 polytopes one has $\Delta = \Delta ^{{{\mathrm{can}\,}}}$. The surfaces $\mathcal {S}_\Delta$ were investigated by Todorov [24] as well as Catanese and Debarre [10].

The remaining 46 canonical Fano 3-topes $\Delta$ define simply connected minimal surfaces $\mathcal {S}_\Delta$ with $K^2 =1$. These surfaces were investigated by Kanev [19], Catanese [9], and Todorov [23]. Among these 46 canonical Fano 3-topes there exist exactly 26 polytopes $\Delta$ such that $\Delta = \Delta ^{{{\mathrm{can}\,}}}$.

Example 35

([19]) Let $M \subseteq \mathbb {Q}^4$ be the 3-dimensional affine lattice defined by

$$ M := \{ ( m_1,m_2, m_3,m_4 ) \in \mathbb {Z}^4 \, \vert \, m_1 + m_2 + m_3 + 2 m_4 = 6, \; m_2 + 2 m_3 \equiv 0\ \left( \mathrm {mod}\ {3}\right) \} $$

and $\Delta ' \subseteq M_\mathbb {Q}$ be the convex hull of 4 lattice points

$$\begin{aligned} (6,0,0,0),\, (0,6,0,0), \,(0,0,6,0), \,\text {and }(0,0,0,3) \in M. \end{aligned}$$

Then $(\Delta ')^{{{\mathrm{FI}\,}}}$ is the 3-dimensional rational simplex

$$\begin{aligned} {{\,\mathrm{conv}\,}}\{(2,1,1,1), (1,2,1,1), (1,1,2,1), (1,1,1,3/2)\} \end{aligned}$$

and $(\Delta ')^{{{\mathrm{FI}\,}}} \cap M = \{ (2,1,1,1) \}$.

The canonical Fano 3-tope $\Delta '$ is the Newton polytope of the $\mu _3$-cyclic quotient $\overline{Z}_{\Delta '}$ of the projective surface of degree 6 defined by the polynomial $z_1^6 + z_2^6 + z_3^6 + z_4^3 =0$ in the weighted projective space $\mathbb {P}(1,1,1,2)$, where the cyclic group $\mu _3$ acts via $(z_1: z_2: z_3:z_4) \mapsto (z_1 : \varepsilon z_2: \varepsilon ^2 z_3: z_4)$. The single interior lattice point in $\Delta '$ corresponds to the monomial $z_1^2z_2z_3z_4$. The surface $\overline{Z}_{\Delta '}$ has 3 cyclic quotient singularities of type $A_2$. The minimal desingularization $\mathcal {S}_{\Delta '}$ of $\overline{Z}_{\Delta '}$ is a simply connected surface of general type with $K^2 =1$.

One can identify $\Delta '$ with the canonical Fano 3-simplex $\Delta$ given as the convex hull of

$$ v_1 := (1,0,0), \, v_2 := (-2,-4,-5), \, v_3 := (1,2,4), \,\text {and } v_4 := (1,4,2) $$

(ID 547444, Fig. 2.6a, Tables 2.7, 2.8, and 2.9). The primitive inward-pointing facet normals of the facets $\theta _{124}$, $\theta _{234}$, $\theta _{123}$, and $\theta _{134}\preceq \Delta$ of this simplex $\Delta$ are

$$ n_1 := (-2,-1,2), \, n_2 := (5,-1,-1), \, n_3 := (-1,2,-1), \,\text {and } n_4 := (-1,0,0), $$

respectively. They satisfy the relation

$$\begin{aligned} n_1 + n_2 + n_3 + 2n_4 = 0. \end{aligned}$$

To compute the canonical hull $\Delta ^{{{\mathrm{can}\,}}}$ of $\Delta$, we obtain ${{\,\mathrm{supp}\,}}(\Delta ^{{{\mathrm{FI}\,}}}) = \{s_i \, \vert \, 1 \le i \le 6 \}$ with $s_1 := (-2,-1,2)$, $s_2 := (-1, 0,0)$, $s_3 := (-1,2,-1)$, $s_4 := (1,1,-1)$, $s_5 := (3,0,-1)$, and $s_6 := (5,-1,-1)$, which leads to $\Delta ^{{{\mathrm{can}\,}}} = \Delta$.

Fig. 2.6

Canonical Fano 3-topes with Fine Interior of Dimension 3. Shaded faces are occluded. The Fine interior and the origin are shown in grey with a double border around the origin. a The whole polytope is $\Delta = {{\,\mathrm{conv}\,}}\{v_1,v_2,v_3,v_4\}$ with $v_1= (1,0,0)$, $v_2 = (-2,-4,-5)$, $v_3 = (1,2,4)$, and $v_4 = (1,4,2)$. Moreover, $\Delta ^{{{\mathrm{FI}\,}}}= {{\,\mathrm{conv}\,}}\{(0, 0, 0), (-1/2, -1, -3/2), (0, -1/3, -2/3), (0, 1/3, -1/3)\}$ and $\Delta ^{{{\mathrm{can}\,}}} = \Delta$. b The whole polytope is $\Delta = {{\,\mathrm{conv}\,}}\{v_1,v_2,v_3,v_4\}$ with $v_1 = (-3,-2,-2)$, $v_2 = (1,0,0)$, $v_3 = (1,3,1)$, and $v_4 = (1,1,3)$. Moreover, $\Delta ^{{{\mathrm{FI}\,}}}= {{\,\mathrm{conv}\,}}\{(0, 0, 0), (-1, -1/2, -1/2), (0, 3/4, 1/4), (0, 1/4, 3/4)\}$ and $\Delta ^{{{\mathrm{can}\,}}} = \Delta$

Table 2.7 49 Canonical Fano 3-topes with Fine Interior of Dimension 3 Table contains: vertices $\text {vert}(\Delta )$ of $\Delta$

Table 2.8 49 Canonical Fano 3-topes with Fine Interior of Dimension 3. Table contains: vertices $\text {vert}(\Delta ^{{{\mathrm{FI}\,}}})$ of the Fine interior $\Delta ^{{{\mathrm{FI}\,}}}$

Table 2.9 49 Canonical Fano 3-topes with Fine Interior of Dimension 3. Table contains: support ${{\,\mathrm{supp}\,}}(\Delta ^{{{\mathrm{FI}\,}}})$ of the Fine interior $\Delta ^{{{\mathrm{FI}\,}}}$, vertices $\text {vert}(\Delta ^{{{\mathrm{can}\,}}})$ of the canonical hull $\Delta ^{{{\mathrm{can}\,}}}$, and order of fundamental group $\left| \pi _1(\mathcal {S}_\Delta ) \right|$ of the minimal model $\mathcal {S}_{\Delta }$

Example 36

([24]) Let $M \subseteq \mathbb {Q}^4$ be the 3-dimensional affine lattice defined by

$$\begin{aligned} M:= \{ ( m_1,m_2,&m_3,m_4 ) \in \mathbb {Z}^4 \mid \\&m_1 + m_2 + 2m_3 + 2 m_4 = 8, \; 3m_2 + m_3 +3 m_4 \equiv 0\ \left( \mathrm {mod}\ {4}\right) \} \end{aligned}$$

and ${\Delta '} \subseteq M_\mathbb {Q}$ be the convex hull of 4 lattice points

$$\begin{aligned} (8,0,0,0), \, (0,8,0,0), \,(0,0,4,0), \,\text {and }(0,0,0,4) \in M. \end{aligned}$$

Then $({\Delta '})^{{{\mathrm{FI}\,}}}$ is the 3-dimensional rational simplex

$$\begin{aligned} {{\,\mathrm{conv}\,}}\{(3,1,1,1), (1,3,1,1), (1,1,2,1), (1,1,1,2)\} \end{aligned}$$

and $({\Delta '})^{{{\mathrm{FI}\,}}} \cap M = \{ (1,1,2,1) \}$.

The canonical Fano 3-tope ${\Delta '}$ is the Newton polytope of the $\mu _4$-cyclic quotient $\overline{Z}_{\Delta '}$ of the projective surface of degree 8 defined by the polynomial $z_1^8 + z_2^8 + z_3^4 + z_4^4 =0$ in the weighted projective space $\mathbb {P}(1,1,2,2)$, where the cyclic group $\mu _4$ acts via $(z_1: z_2: z_3:z_4) \mapsto (z_1 : i ^3z_2: i z_3: i ^3z_4)$. The single interior lattice point in this lattice simplex ${\Delta '}$ corresponds to the monomial $z_1z_2z^2_3z_4$. The projective surface $\overline{Z}_{\Delta '}$ has two Gorenstein cyclic quotient singularities of type $A_3$. The minimal desingularization $\mathcal {S}_{\Delta '}$ of $\overline{Z}_{\Delta '}$ is a surface of general type with $K^2=2$ and fundamental group $\pi _1(\mathcal {S}_\Delta )$ of order 2.

One can identify ${\Delta '}$ with the canonical Fano 3-simplex $\Delta$ given as the convex hull of

$$\begin{aligned} v_1 := (-3,-2,-2), \, v_2 := (1,0,0), \,v_3:=(1,3,1), \,\text {and } v_4:= (1,1,3) \end{aligned}$$

(ID 547465, Fig. 2.6b, Tables  2.7, 2.8, and 2.9). The primitive inward-pointing facet normals of the facets $\theta _{123}$, $\theta _{124}$, $\theta _{234}$, $\theta _{134} \preceq \Delta$ of this simplex $\Delta$ are

$$\begin{aligned} n_1 := (-1,-1, 3), \, n_2 := (-1,3,-1), \,n_3 := (-1,0,0 ), \,\text {and }n_4 := (2,-1,-1), \end{aligned}$$

respectively. They satisfy the relation

$$\begin{aligned} n_1 + n_2 + 2n_3 + 2n_4 = 0. \end{aligned}$$

To compute the canonical hull $\Delta ^{{{\mathrm{can}\,}}}$ of $\Delta$, we obtain ${{\,\mathrm{supp}\,}}(\Delta ^{{{\mathrm{FI}\,}}}) = \{s_i \, \vert \, 1 \le i \le 9 \}$ with $s_1 := (-1, -1, 3)$, $s_2 := (-1, 0,0)$, $s_3 := (-1,0,1)$, $s_4 := (-1,0,2)$, $s_5 := (-1,1,0)$, $s_6 :=(-1,1,1)$, $s_7 :=(-1,2,0)$, $s_8 :=(-1,3,-1)$, and $s_9 :=(2,-1,-1)$, which leads to $\Delta ^{{{\mathrm{can}\,}}} = \Delta$.

Remark 37

Information about all 49 canonical Fano 3-topes with $\dim (\Delta ^{{{\mathrm{FI}\,}}})=3$ can be found in Tables 2.7, 2.8, and 2.9.

2.7 Hollow 3-Topes with Non-empty Fine Interior

A lattice polytope $\Delta \subseteq M_\mathbb {Q}$ is called hollow if it has no interior lattice points in its relative interior, i.e., $\Delta ^\circ \cap M = \emptyset$. By [25, Theorem 1.3], any 3-dimensional hollow lattice polytope can be projected to the unimodular 1-simplex, to the double unimodular 2-simplex, or is an exceptional hollow 3-tope, whereas up to unimodular transformation there exist only a finite number of these. This theorem implies that a hollow 3-tope with non-empty Fine interior has to be exceptional because the unimodular 1-simplex and the double unimodular 2-simplex have empty Fine interior. Treutlein has found 9 maximal exceptional hollow polytopes, which was not an complete list. Averkov et al. [1, 2] have found the complete list consisting of 12 maximal exceptional hollow 3-topes $\Delta _i$ $(1 \le i \le 12)$ (Table 2.10, Fig. 2.7). Computations show that exactly 9 of 12 maximal exceptional hollow 3-topes $\Delta _i$ have non-empty Fine interior $\Delta _i^{{{\mathrm{FI}\,}}}$ (Table 2.10). Moreover, no one of these 9 polytopes contains a proper lattice 3-subpolytope with non-empty Fine interior. Thus, there exist exactly 9 hollow 3-topes $\Delta _i$ with non-empty Fine interior $\Delta _i^{{{\mathrm{FI}\,}}}$.

Table 2.10 12 Maximal Hollow 3-topes. Table contains: index i of the maximal hollow 3-tope $\Delta _i$, vertices $\text {vert}(\Delta _i)$ of $\Delta _i$, lattice width $\text {w}(\Delta _i)$ of $\Delta _i$, dimension $\dim (\Delta _i^{{{\mathrm{FI}\,}}})$ of Fine interior $\Delta _i^{{{\mathrm{FI}\,}}}$, vertices $\text {vert}(\Delta _i^{{{\mathrm{FI}\,}}})$ of $\Delta _i^{{{\mathrm{FI}\,}}}$, and order of fundamental group $\left| \pi _1(\mathcal {S}_\Delta ) \right|$ of the minimal model $\mathcal {S}_{\Delta _{i}}$

Fig. 2.7

12 Maximal Hollow 3-topes. Shaded faces are occluded. The Fine interior is shown in grey with double borders around its vertices

It is remarkable that all minimal surfaces $\mathcal {S}_{\Delta _i}$ corresponding to these 9 hollow 3-topes $\Delta _i$ have non-trivial fundamental group $\pi _1(\mathcal {S}_\Delta )$ of order 2, 3, or 5 (Table 2.10). There exist exactly 5 hollow 3-topes $\Delta _i$ with 0-dimensional Fine interior $\Delta _i^{{{\mathrm{FI}\,}}} = \{R\}$, where $R \in \frac{1}{2}M \setminus M$ is a rational point (Table 2.10). The normal fans $\Sigma ^{\Delta _i}$ of these 5 hollow polytopes $\Delta _i$ define 5 toric Fano threefolds $X_{\Sigma ^{\Delta _i}}$ with at worst canonical singularities (Table 2.11). These Fano threefolds can be obtained as quotients of Gorenstein toric Fano threefolds $X_{\Sigma _{\Delta ''}}$ in the following 5 ways:

Table 2.11 5 Hollow 3-topes with 0-dimensional Fine Interior. Table contains: index i of the maximal hollow 3-tope $\Delta _i$, rays of the normal fan $\Sigma ^{\Delta _i}$ corresponding to  $\Delta _i$, ID of the canonical Fano 3-tope  $\Delta '$ such that $\Sigma ^{\Delta _i} \cong \Sigma _{\Delta '}$, rays of the spanning fan $\Sigma _{\Delta '}$, ID of the reflexive canonical Fano 3-tope  $\Delta ''$ used to construct the Gorenstein toric Fano threefold $X_{\Sigma _{\Delta ''}}$ to obtain the toric Fano threefold $X_{\Sigma _{\Delta '}}$ with at worst canonical singularities as a $\mu _2$ quotient, and reference to the corresponding Gorenstein toric Fano threefold $X_{\Sigma _{\Delta ''}}$ including the precise $\mu _2$-action on Sect. 2.7

• 1.  $\mathbb {P}(1,1,2,4)$ with a $\mu _2$-action given by

  $$ (x_0,x_1,x_2,x_3) \mapsto (x_0,-x_1,-x_2,-x_3); $$

• 2.  $\mathbb {P}^3$ with a $\mu _4$-action given by

  $$ (x_0,x_1,x_2,x_3) \mapsto (x_0,ix_1,-x_2,-ix_3); $$

• 3.  $\{ x_1x_2 - x_3x_4 =0 \} \subseteq \mathbb {P}(2,1,1,1,1)$ with a $\mu _2$-action given by

  $$ (x_0,x_1,x_2,x_3,x_4) \mapsto (-x_0,-x_1,-x_2,x_3,x_4); $$

• 4.  $\mathbb {P}^1 \times \mathbb {P}(1,1,2)$ with a $\mu _2$-action given by

  $$ (x_0,x_1,y_0,y_1,y_2) \mapsto (x_0,-x_1,y_0,-y_1,-y_2); $$

• 5.  $\mathbb {P}^1 \times \mathbb {P}^1 \times \mathbb {P}^1$ with a $\mu _2$-action given by

  $$ (x_0,x_1,y_0,y_1, z_0,z_1) \mapsto (x_0,-x_1, y_0,-y_1, z_0, -z_1). $$

In addition, Table 2.12 contains the support ${{\,\mathrm{supp}\,}}(\Delta _i^{{{\mathrm{FI}\,}}})$ of the Fine interior $\Delta _i^{{{\mathrm{FI}\,}}}$ and the vertices of the canonical hull $\Delta _i^{{{\mathrm{can}\,}}}$ for all  9 hollow polytopes $\Delta _i$ with non-empty Fine interior $\Delta _i^{{{\mathrm{FI}\,}}}$.

Table 2.12 9 Hollow 3-topes with Non-empty Fine Interior. Table contains: index i of the maximal hollow 3-tope $\Delta _i$, support ${{\,\mathrm{supp}\,}}(\Delta _i^{{{\mathrm{FI}\,}}})$ of $\Delta _i^{{{\mathrm{FI}\,}}}$, and vertices $\text {vert}(\Delta _i^{{{\mathrm{can}\,}}})$ of the canonical hull $\Delta _i^{{{\mathrm{can}\,}}}$