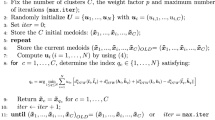On Some Fuzzy Clustering Algorithms for Time-Series Data

Abstract

Various fuzzy clustering algorithms have been proposed for vectorial data. However, these methods have not been applied to time-series data. This paper presents three fuzzy clustering algorithms for time-series data based on dynamic time warping (DTW). The first algorithm involves Kullback–Leibler divergence regularization of the DTW k-means objective function. The second algorithm replaces the membership of the DTW k-means objective function with its power. The third algorithm involves q-divergence regularization of the objective function of the first algorithm. Theoretical discussion shows that the third algorithm is a generalization of the first and second algorithms, which is substantiated through numerical experiments.

1 Introduction

Hard c-means (HCM) is the most commonly used type of clustering algorithm [1]. The fuzzy c-means (FCM) [2] approach is an extension of the HCM that allows each object to belong to all or some of the clusters to varying degrees. To distinguish the general FCM method from other proposed, such as entropy-regularized FCM (EFCM) [3], it is referred to as the Bezdek-type FCM (BFCM) in this work. The above mentioned algorithms may misclassify some objects that should be assigned to a large cluster as belonging to a smaller cluster if the cluster sizes are not balanced. To overcome this problem, some approaches introduce variables to control the cluster sizes [4, 5]. Such variables have been added to the BFCM and EFCM algorithms to derive the revised BFCM (RBFCM) and revised EFCM (REFCM) [6] algorithms, respectively.

In the aforementioned clustering algorithms, the dissimilariies between the objects and cluster centers are measured as the inner-product-induced squared distances. This measure cannot be used for time-series data because they vary over time. Dynamic time warping (DTW) is a representative dissimilarity with respect to time-series data. Hence, a clustering algorithm using the DTW is proposed [8] herein and referred to as the DTW k-means algorithm.

The accuracies that can be achieved with fuzzy clustered results are better than those using hard clustering. Various kinds of fuzzy clustering algorithms have been proposed in literature for vectorial data [2, 3]. However, this is not true for time-series data, which is the main motivation for this study.

In this work, we propose three fuzzy clustering algorithms for time-series data. The first algorithm involves the Kullback–Leibler (KL) divergence regularization of the DTW k-means objective function, which is referred to as the KL-divergence-regularized fuzzy DTW c-means (KLFDTWCM); this approach is similar to the REFCM obtained by KL divergence regularization of the HCM objective function. In the second algorithm, the membership of the DTW k-means objective function is replaced with its power, which is referred to as the Bezdek-type fuzzy DTW c-means (BFDTWCM); this method is similar to the RBFCM, where the membership of the HCM objective function is replaced with its power. The third algorithm is obtained by q-divergence regularization of the objective function of the first algorithm (QFDTWCM). The theoretical results indicate that the QFDTWCM approach reduces to the BFDTWCM under a specific condition and to the KLFDTWCM under a different condition. Numerical experiments were performed using artificial datasets to substantiate these observations.

The remainder of this paper is organized as follows. Section 2 introduces the notations used herein and the background regarding some conventional algorithms. Section 3 describes the three proposed algorithms. Section 4 presents the procedures and results of the numerical experiments demonstrating the properties of the proposed algorithms. Finally, Sect. 5 presents the conclusions of this work.

2 Preliminaries

2.1 Divergence

For two probability distributions P and Q, the KL divergence of Q from P, $D_{\mathsf {KL}}(P||Q)$ is defined to be

$$\begin{aligned} D_{\mathsf {KL}}(P||Q)=\sum _{k}P(k)\ln \left( \frac{P(k)}{Q(k)}\right) . \end{aligned}$$

(1)

KL divergence has been used to achieve fuzzy clustering [3] of vectorial data. KL divergence has been extended by using q-logarithmic function

$$\begin{aligned} \ln _{q}(x)=\frac{1}{1-q}(x^{1-q}-1)\quad (\text {for }x>0) \end{aligned}$$

(2)

as

$$\begin{aligned} D_{q}(P||Q)=&\frac{1}{1-q}\left( \sum _{k}P(k)^{q}Q(k)^{1-q}-1\right) , \end{aligned}$$

(3)

referred to as q-divergence [7]. In the limit $q\rightarrow {}1$, the KL-divergence is recovered. q-divergence has been implicitly used to derive fuzzy clustering only for vectorial data [6] although that is not indicated in the literature.

2.2 Clustering for Vectorial Data

Let $X=\{x_k\in \mathbb {R}^D\mid k\in \{1,\dots ,N\}\}$ be a dataset of D-dimensional points. The set of cluster centers is denoted by $v=\{v_i\in \mathbb {R}^D\mid i\in \{1,\dots ,C\}\}$. The membership of $x_k$ with respect to the i-th cluster is denoted by $u_{i,k}~(i\in \{1,\dots ,C\} k\in \{1,\dots ,N\})$ and has the following constraint:

$$\begin{aligned} \sum _{i=1}^C u_{i,k}=1. \end{aligned}$$

(4)

The variable controlling the i-th cluster size is denoted by $\alpha _i$, and has the constraint

$$\begin{aligned} \sum _{i=1}^C\alpha _i=1. \end{aligned}$$

(5)

The HCM, RBFCM, and REFCM clusters are respectively obtained by solving the following optimization problems:

$$\begin{aligned}&\mathop {\text {minimize}}\limits _{u,v}\sum _{i=1}^C\sum _{k=1}^Nu_{i,k}\Vert x_k-v_i\Vert _2^2,\end{aligned}$$

(6)

$$\begin{aligned}&\mathop {\text {minimize}}\limits _{u,v,\alpha }\sum _{i=1}^C\sum _{k=1}^N(\alpha _i)^{1-m}(u_{i,k})^m \Vert x_k-v_i\Vert _2^2, \end{aligned}$$

(7)

$$\begin{aligned}&\mathop {\text {minimize}}\limits _{u,v,\alpha }\sum _{i=1}^C\sum _{k=1}^Nu_{i,k} \Vert x_k-v_i\Vert _2^2+\lambda ^{-1}\sum _{i=1}^C\sum _{k=1}^Nu_{i,k}\log \left( \frac{u_{i,k}}{\alpha _i}\right) . \end{aligned}$$

(8)

where $m>1$ and $\lambda >0$ are the fuzzification parameters. When $m=1$, the RBFCM is reduced to HCM; the larger the value of m, the fuzzier are the memberships. When $\lambda \rightarrow +\infty$, the REFCM is reduced to HCM; the smaller the value of $\lambda$, the fuzzier are the memberships.

2.3 Clustering of Time-Series Data: DTW k-Means

Let $X=\{x_k\in \mathbb {R}^D\mid k\in \{1,\dots ,N\}\}$ be a time-series dataset and $x_{k,\ell }$ be its elements at time $\ell$. Let $v=\{v_i\in \mathbb {R}^D\mid i\in \{1,\dots ,C\}\}$ be the set of cluster centers set $v_{i,\ell }$ be its elements at time $\ell$. Let $\mathsf {DTW}_{i,k}$ be the dissimilarities between the objects $x_k$ and cluster centers $v_i$ as below, with $\mathsf {DTW}_{i,k}$ being defined as follows DTW [8]. Denoting $\varOmega _{i,k}\in \{0,1\}^{D\times D}$ as the warping path used to calculate $\mathsf {DTW}_{i,k}$, the membership of $x_k$ with respect to the i-th cluster is given by $u_{i,k}~(i\in \{1,\dots ,C\} k\in \{1,\dots ,N\})$. The DTW k-means is obtained by solving the following optimization problem

$$\begin{aligned}&\mathop {\text {minimize}}\limits _{u,v}\sum _{i=1}^C\sum _{k=1}^N u_{i,k}\mathsf {DTW}_{i,k}. \end{aligned}$$

(9)

in accordance with Eq. (4), where

$$\begin{aligned} \mathsf {DTW}_{i,k}=&\,\sqrt{ d(v_{i,D},x_{k,D}) }, \nonumber \\ d(v_{i,D},x_{k,D})=&\, ||x_{k,D}-v_{i,D}||^2 \end{aligned}$$

(10)

$$\begin{aligned}&\quad +\min \{ d(v_{i,D-1},x_{k,D-1}), d(v_{i,D},x_{k,D-1}), d(v_{i,D-1},x_{k,D})\}. \end{aligned}$$

(11)

In addition to DTW, we obtain the warping path that maps the pairs $(\ell ,m)$ for each element in the series to minimize the distance between them. Hence, the warping path is a sequence of pairs $(\ell ,m)$. Here, we consider matrices $\{\varOmega _{i,k}\in \{0,1\}^{D\times D}\}_{(i,k)=(1,1)}^{(C,N)}$ whose $(\ell ,m)$-th element is one if $(\ell ,m)$ is an element of the corresponding warping path and zero otherwise then, we have the cluster centers

$$\begin{aligned} v_i=\left( \sum _{x_k\in G_i}^N \varOmega _{i,k}x_k\right) \oslash \left( \sum _{x_k\in G_i} \varOmega _{i,k}\mathbf {1}\right) , \end{aligned}$$

(12)

where $\mathbf {1}$ is the D-dimensional vector with all elements equal to one, and $\oslash$ describes element-wise division. The DTW k-means algorithm can be summarized as follows.

Algorithm 1

(DTW k-means). [8]

• Step 1. Set the number of clusters C and initial membership $\{u_{i,k}\}_{(i,k)=(1,1)}^{(C,N)}$.

• Step 2. Calculate $\{v_i\}_{i=1}^C$ as

  $$\begin{aligned} v_i=\frac{\sum _{k=1}^Nu_{i,k}x_k}{\sum _{k=1}^Nu_{i,k}}. \end{aligned}$$

  (13)

• Step 3. Calculate $\{\mathsf {DTW}_{i,k}\}_{(i,k)=(1,1)}^{(C,N)}$ and update $\{v_i\}_{i=1}^C$ as

  • (a) Calculate $\mathsf {DTW}_{i,k}$ from Eq. (11).

  • (b) Update $v_i$ from Eq. (25).

  • (c) Check the limiting criterion for $v_i$. If the criterion is not satisfied, go to Step (a).

• Step 4. Update $\{u_{i,k}\}_{(i,k)=(1,1)}^{(C,N)}$ as

  $$\begin{aligned} u_{i,k}= {\left\{ \begin{array}{ll} 1 &{} (i={\mathop {\text {arg min}}\limits }_{1 \le j \le C}\{\mathsf {DTW}_{j,k}\}), \\ 0 &{} (\text {otherwise}). \end{array}\right. } \end{aligned}$$

  (14)

• Step 5. Check the limiting criterion for (u, v). If the criterion is not satisfied, go to Step 3

3 Proposed Algorithms

3.1 Concept

In this work, we propose three fuzzy clustering algorithms for time-series data.

The first algorithm is similar to the REFCM obtained by KL divergence regularization the DTW k-means objective function, which is referred to as KLFDTWCM. The optimization problem for this is given by

$$\begin{aligned} \mathop {\text {minimize}}\limits _{u,v,\alpha } \sum _{i=1}^C \sum _{k=1}^N u_{i,k}\mathsf {DTW}_{i,k}+\lambda ^{-1}\sum _{i=1}^C \sum _{k=1}^Nu_{i,k}\ln \left( \frac{u_{i,k}}{\alpha _i}\right) \end{aligned}$$

(15)

subject to Eqs. (4) and (5).

The second algorithm is similar to the RBFCM obtained by replacing the membership of the HCM objective function with its power, which is referred to as BFDTWCM. The optimization problem is then given by

$$\begin{aligned} \mathop {\text {minimize}}\limits _{u,v,\alpha } \sum _{i=1}^C \sum _{k=1}^N (\alpha _i)^{1-m}(u_{i,k})^m \mathsf {DTW}_{i,k} \end{aligned}$$

(16)

subject to Eqs. (4) and (5).

The third algorithm is obtained by q-divergence regularization of the BFDTWCM, which is referred to as QFDTWCM. The optimization problem in this case is given by

$$\begin{aligned} \mathop {\text {minimize}}\limits _{u,v,\alpha } \sum _{i=1}^C \sum _{k=1}^N (\alpha _i)^{1-m}(u_{i,k})^m \mathsf {DTW}_{i,k} + \frac{\lambda ^{-1}}{m-1}\sum _{i=1}^C \sum _{k=1}^N(\alpha _i)^{1-m}(u_{i,k})^m \end{aligned}$$

(17)

subject to Eqs. (4) and (5). This optimization problem relates the optimization problems for BFDTWCM and KLFDTWCM because Eq. (17) with $\lambda \rightarrow +\infty$ reduces to the BFDTWCM method and Eq. (17) with $m \rightarrow 1$ reduces to the KLFDTWCM approach. In the next subsection, we present derivation of the update equations for u, v, and $\alpha$ based on of the minimization problem in Eqs. (15), (16), and (17).

3.2 KLFDTWCM, BFDTWCM and QFDTWCM

The KLFDTWCM is obtained by solving the optimization problem in Eqs. (15), (4) and (5), where the Lagrangian $L(u, v, \alpha )$ is defined as

$$\begin{aligned} L(u, v, \alpha )=&\sum _{i=1}^C \sum _{k=1}^N u_{i,k}\mathsf {DTW}_{i,k}+\lambda ^{-1}\sum _{i=1}^C \sum _{k=1}^Nu_{i,k}\ln \left( \frac{u_{i,k}}{\alpha _i}\right) \nonumber \\&+\sum _{k=1}^N\gamma _k\left( 1-\sum _{i=1}^Cu_{i,k}\right) +\beta \left( 1-\sum _{i=1}^C\alpha _i\right) \end{aligned}$$

(18)

using Lagrangian multipliers $(\gamma _1, \cdots , \gamma _{N+1})$. The necessary conditions for optimality are given as

$$\begin{aligned} \frac{\partial {}L(u,v,\alpha )}{\partial {}u_{i,k}}=&\,0, \end{aligned}$$

(19)

$$\begin{aligned} \frac{\partial {}L(u,v,\alpha )}{\partial {}\alpha _i}=&\, 0, \end{aligned}$$

(20)

$$\begin{aligned} \frac{\partial {}L(u,v,\alpha )}{\partial {}\gamma _k}=&\,0, \end{aligned}$$

(21)

$$\begin{aligned} \frac{\partial {}L(u,v,\alpha )}{\partial {}\beta }=&\,0. \end{aligned}$$

(22)

The optimal membership is obtained from Eqs. (19) and (21) in a manner similar to that of the REFCM as

$$\begin{aligned} u_{i,k}=\left[ \sum _{j=1}^C\frac{\alpha _j}{\alpha _i}\exp (-\lambda (\mathsf {DTW}_{j,k}-\mathsf {DTW}_{i,k}))\right] ^{-1}. \end{aligned}$$

(23)

The optimal variable for controlling the cluster sizes is obtained from Eqs. (20) and (22) in a manner similar to that of the REFCM as

$$\begin{aligned} \alpha _i=\frac{\sum _{k=1}^Nu_{i,k}}{N}. \end{aligned}$$

(24)

Recall that in the DTW k-means approach, the cluster centers $v_i$ are calculated using $\varOmega _{i,k}$ and $x_k$ belonging to cluster $\#i$, as shown in Eq. (12), which can be equivalently written as

$$\begin{aligned} v_i=\left( \sum _{k=1}^N u_{i,k}\varOmega _{i,k}x_k\right) \oslash \left( \sum _{k=1}^N u_{i,k}\varOmega _{i,k}\mathbf {1}\right) . \end{aligned}$$

(25)

This form can be regarded as the $u_{i,k}$-weighted mean of $\varOmega _{i,k}x_k$. Similarly, the cluster centers for KLFDTWCM are calculated using Eq. (25). KLFDTWCM can be described as follows:

Algorithm 2

(KLFDTWCM). 

• Step 1. Set the number of clusters C, fuzzification parameter $\lambda >0$, and initial membership $\{u_{i,k}\}_{(i,k)=(1,1)}^{(C,N)}$.

• Step 2. Calculate $v_i$ from Eq. (13).

• Step 3. Calculate $\{\mathsf {DTW}_{i,k}\}_{(i,k)=(1,1)}^{(C,N)}$ and update $\{v_i\}_{i=1}^C$ as

  • (a) Calculate $\mathsf {DTW}_{i,k}$ from Eq. (11).

  • (b) Update $v_i$ from Eq. (25).

  • (c) Check the limiting criterion for $v_i$. If the criterion is not satisfied, go to Step (a).

• Step 4. Update u from Eq. (23)

• Step 5. Calculate $\alpha$ from Eq. (24)

• Step 6. Check the limiting criterion for $(u, v, \alpha )$. If the criterion is not satisfied, go to Step 3.

The BFDTWCM is obtained by solving the optimization problem in Eqs. (16), (4), and (5). Similar to the derivation of the KLFDTWCM, the optimal membership u, variable for controlling the cluster sizes $\alpha$, and cluster centers v are obtained as

$$\begin{aligned} u_{i,k}=&\frac{1}{\sum _{j=1}^C\frac{\alpha _j}{\alpha _i}\left( \frac{\mathsf {DTW}_{j,k}}{\mathsf {DTW}_{i,k}}\right) ^{1/(1-m)}}, \end{aligned}$$

(26)

$$\begin{aligned} \alpha _i=&\frac{1}{\sum _{j=1}^C\left( \frac{\sum _{k=1}^N(u_{j,k})^m\mathsf {DTW}_{j,k}}{\sum _{k=1}^N(u_{i,k})^m\mathsf {DTW}_{i,k}}\right) ^{1/m} }, \end{aligned}$$

(27)

$$\begin{aligned} v_i=&\left( \sum _{k=1}^N (u_{i,k})^m\varOmega _{i,k}x_k\right) \oslash \left( \sum _{k=1}^N (u_{i,k})^m\varOmega _{i,k}\mathbf {1}\right) , \end{aligned}$$

(28)

respectively. The BFDTWCM can be described as follows:

Algorithm 3

(BFDTWCM). 

• Step 1. Set the number of clusters C, fuzzification parameter $m>1$, and initial membership $\{u_{i,k}\}_{(i,k)=(1,1)}^{(C,N)}$.

• Step 2. Calculate $v_i$ from Eq. (13).

• Step 3. Calculate $\{\mathsf {DTW}_{i,k}\}_{(i,k)=(1,1)}^{(C,N)}$ and update $\{v_i\}_{i=1}^C$ as

  • (a) Calculate $\mathsf {DTW}_{i,k}$ from Eq. (11).

  • (b) Update $v_i$ from Eq. (28).

  • (c) Check the limiting criterion for $v_i$. If the criterion is not satisfied, go to Step. (a).

• Step 4. Update u from Eq. (26)

• Step 5. Calculate $\alpha$ from Eq. (27)

• Step 6. Check the limiting criterion for $(u, v, \alpha )$. If the criterion is not satisfied, go to Step. 3.

The QFDTWCM is obtained by solving the optimization problem in Eqs. (17), (4), and (5). Similar to the derivations of BFDTWCM and KLFDTWCM, the optimal membership u and variable for controlling the cluster sizes $\alpha$ are obtained as

$$\begin{aligned} u_{i,k}=&\frac{1}{\sum _{j=1}^C\frac{\alpha _j}{\alpha _i}\left( \frac{1-\lambda (1-m)\mathsf {DTW}_{j,k}}{1-\lambda (1-m)\mathsf {DTW}_{i,k}}\right) ^{1/(1-m)}}, \end{aligned}$$

(29)

$$\begin{aligned} \alpha _i=&\frac{1}{\sum _{j=1}^C\left( \frac{\sum _{k=1}^N(u_{j,k})^m(1-\lambda (1-m)\mathsf {DTW}_{j,k})}{\sum _{k=1}^N(u_{i,k})^m(1-\lambda (1-m)\mathsf {DTW}_{i,k})}\right) ^{1/m} }, \end{aligned}$$

(30)

respectively. The optimal cluster centers are defined by Eq. (28). The QFDTWCM can be described as follows:

Algorithm 4

(QFDTWCM). 

• Step 1. Set the number of clusters C, fuzzification parameter $m>1, \lambda >0$, and initial membership $\{u_{i,k}\}_{(i,k)=(1,1)}^{(C,N)}$.

• Step 2. Calculate $\{v_i\}_{i=1}^C$ from Eq. (13).

• Step 3. Calculate $\{\mathsf {DTW}_{i,k}\}_{(i,k)=(1,1)}^{(C,N)}$ and update $\{v_i\}_{i=1}^C$ as

  • (a) Calculate $\mathsf {DTW}_{i,k}$ from Eq. (11).

  • (b) Update $v_i$ from Eq. (28).

  • (c) Check the limiting criterion for $v_i$. If the criterion is not satisfied, go to Step (a).

• Step 4. Update u from Eq. (29).

• Step 5. Calculate $\alpha$ from Eq. (30).

• Step 6. Check the limiting criterion for $(u, v, \alpha )$. If the criterion is not satisfied, go to Step 4.

In the remainder of this section, we show that the QFDTWCM with $m-1 \rightarrow +0$ reduces to BFDTWCM and QFDTWCM with $\lambda \rightarrow +\infty$ reduces to KLFDTWCM.

The third step in the QFDTWCM approach is exactly equal to that of the BFDTWCM because Eq. (28) is identical to Eq. (28). In the fourth step of the QFDTWCM, the u value in Eq. (29) reduces to that in Eq. (26) of the BFDTWCM as

$$\begin{aligned}&\frac{1}{\sum _{j=1}^C\frac{\alpha _j}{\alpha _i}\left( \frac{1-\lambda (1-m)\mathsf {DTW}_{j,k}}{1-\lambda (1-m)\mathsf {DTW}_{i,k}}\right) ^{1/(1-m)}} \nonumber \\&=\frac{\alpha _i\left( 1/\lambda -(1-m)\mathsf {DTW}_{i,k}\right) ^{1/(1-m)}}{\sum _{j=1}^C\alpha _j\left( 1/\lambda -(1-m)\mathsf {DTW}_{j,k}\right) ^{1/(1-m)}}\nonumber \\&\rightarrow \frac{\alpha _i\left( -(1-m)\mathsf {DTW}_{i,k}\right) ^{1/(1-m)}}{\sum _{j=1}^C\alpha _j\left( -(1-m)\mathsf {DTW}_{j,k}\right) ^{1/(1-m)}} \nonumber \\&\quad (\text {with } \lambda \rightarrow +\infty ) \nonumber \\&=\frac{(m-1)\alpha _i\left( \mathsf {DTW}_{i,k}\right) ^{1/(1-m)}}{(m-1)\sum _{j=1}^C\alpha _j\left( \mathsf {DTW}_{j,k}\right) ^{1/(1-m)}} \nonumber \\&=\frac{\alpha _i\left( \mathsf {DTW}_{i,k}\right) ^{1/(1-m)}}{\sum _{j=1}^C\alpha _j\left( \mathsf {DTW}_{j,k}\right) ^{1/(1-m)}} \nonumber \\&=\frac{1}{\sum _{j=1}^C\frac{\alpha _j}{\alpha _i}\left( \frac{\mathsf {DTW}_{j,k}}{\mathsf {DTW}_{i,k}}\right) ^{1/(1-m)}}. \end{aligned}$$

(31)

In the fifth step of the QFDTWCM, the $\alpha$ value in Eq. (30) is reduces to that in Eq. (27) of the BFDTWCM as

$$\begin{aligned}&\frac{1}{\sum _{j=1}^C\left( \frac{\sum _{k=1}^N(u_{j,k})^m(1-\lambda (1-m)\mathsf {DTW}_{j,k})}{\sum _{k=1}^N(u_{i,k})^m(1-\lambda (1-m)\mathsf {DTW}_{i,k})}\right) ^{1/m}} \nonumber \\&=\frac{\left( \sum _{k=1}^N(u_{i,k})^m(1/\lambda -(1-m)\mathsf {DTW}_{i,k}) \right) ^{1/m}}{\sum _{j=1}^C \left( \sum _{k=1}^N(u_{j,k})^m(1/\lambda -(1-m)\mathsf {DTW}_{j,k}) \right) ^{1/m}} \nonumber \\&\rightarrow \frac{\left( \sum _{k=1}^N(u_{i,k})^m(-(1-m)\mathsf {DTW}_{i,k}) \right) ^{1/m}}{\sum _{j=1}^C \left( \sum _{k=1}^N(u_{j,k})^m(-(1-m)\mathsf {DTW}_{j,k}) \right) ^{1/m}} \nonumber \\&\quad (\text {with } \lambda \rightarrow +\infty ) \nonumber \\&=\frac{(m-1)^{1/m}\left( \sum _{k=1}^N(u_{i,k})^m(\mathsf {DTW}_{i,k}) \right) ^{1/m}}{(m-1)^{1/m}\sum _{j=1}^C \left( \sum _{k=1}^N(u_{j,k})^m(\mathsf {DTW}_{j,k}) \right) ^{1/m}} \nonumber \\&=\frac{\left( \sum _{k=1}^N(u_{i,k})^m(\mathsf {DTW}_{i,k}) \right) ^{1/m}}{\sum _{j=1}^C \left( \sum _{k=1}^N(u_{j,k})^m(\mathsf {DTW}_{j,k}) \right) ^{1/m}} \nonumber \\&=\frac{1}{\sum _{j=1}^C\left( \frac{\sum _{k=1}^N(u_{j,k})^m\mathsf {DTW}_{j,k}}{\sum _{k=1}^N(u_{i,k})^m\mathsf {DTW}_{i,k}}\right) ^{1/m}}. \end{aligned}$$

(32)

From the above discussion, we can conclude that the QFDTWCM with $\lambda \rightarrow +\infty$ reduces to the BFDTWCM.

The third step of the QFDTWCM with $m = 1$ is obviously equal to the third step of the KLFDTWCM because Eq. (28) with $m = 1$ is identical to Eq. (11). In the fourth step of the QFDTWCM, the u value in Eq. (29) reduces to that in Eq. (23) of the KLFDTWCM as

$$\begin{aligned}&\left( 1-\lambda (1-m)\mathsf {DTW}_{i,k} \right) ^{1/(1-m)} \nonumber \\&\rightarrow \exp (-\lambda (\mathsf {DTW}_{i,k}))\quad (\text {with } m=1). \end{aligned}$$

(33)

The fifth step of the QFDTWCM reduces to that of the KLFDTWCM because

$$\begin{aligned}&=\frac{1}{\sum _{j=1}^C\left( \frac{\sum _{k=1}^N(u_{j,k})^m(1-\lambda (1-m)\mathsf {DTW}_{j,k})}{\sum _{k=1}^N(u_{i,k})^m(1-\lambda (1-m)\mathsf {DTW}_{i,k})}\right) ^{1/m}} \nonumber \\&\rightarrow \frac{1}{\sum _{j=1}^C\sum _{k=1}^N\frac{u_{j,k}}{u_{i,k}}}\quad (\text {with } m=1) \nonumber \\&=\frac{\sum _{k=1}^N{u_{i,k}}}{\sum _{j=1}^C\sum _{k=1}^Nu_{j,k}} \nonumber \\&=\frac{\sum _{k=1}^Nu_{i,k}}{N}. \end{aligned}$$

(34)

From the above discussion, we can conclude that the QFDTWCM with $m-1 \rightarrow 0$ reduces to the KLFDTWCM.

As shown herein, the proposed QFDTWCM includes both the BFDTWCM and KLFDTWCM. Thus, the QFDTWCM is a generalization of the BFDTWCM as well as KLFDTWCM.

4 Numerical Experiments

This section presents some numerical examples based on one artificial dataset. The example compares the characteristic features of the proposed clustering algorithm (Algorithm 4) with those of other algorithms (Algorithms 2 and 3) for an artificial dataset, as shown in Figs. 1, 2, 3 and 4 for four clusters ($C = 4$), with each clusters containing five objects ($N=4 \times 5=20$).

Fig. 1.

Sample data group1

Fig. 2.

Sample data group2

Fig. 3.

Sample data group3

Fig. 4.

Sample data group4

The initialization step assigns the initial memberships according to the actual class labels. All three proposed methods with various fuzzification parameter values were able to classify the data adequately, and the obtained membership values are shown in Tables 1, 2, 3, 4, 5, 6, 7, 8 and 9. Tables 1 and 2 show that for the BFDTWCM, when the fuzzification parameter m is larger, the membership values are fuzzier. Tables 3 and 4 show that for the KLFDTWCM, when the fuzzification parameter $\lambda$ is smaller, the membership values are fuzzier. Tables 5 and 6 show that for the QFDTWCM, when the fuzzification parameter m is larger, the membership values are fuzzier. Tables 5 and 7 show that for the QFDTWCM, when the fuzzification parameter $\lambda$ is smaller, the membership values are fuzzier. Furthermore, Tables 6 and 8 show that the QFDTWCM with large values of $\lambda$ produces results similar to those of the KLFDTWCM, and Tables 7 and 9 show that the QFDTWCM with smaller values of m produces results similar to those of the BFDTWCM. These results indicate that the QFDTWCM combines the features of both BFDTWCM and KLFDTWCM.

Table 1. Sample data memberships of the BFDTWCM, $m=1.001$

Table 2. Sample data memberships of the BFDTWCM, $m=1.35$

Table 3. Sample data memberships of the KLFDTWCM, $\lambda =1.5$

Table 4. Sample data memberships of the KLFDTWCM, $\lambda =100$

Table 5. Sample data memberships of the QFDTWCM, $(m, \lambda )=(1.2, 3)$

Table 6. Sample data memberships of the QFDTWCM, $(m, \lambda )=(1.001, 3)$

Table 7. Sample data memberships of the QFDTWCM, $(m, \lambda )=(1.2, 100)$

Table 8. Sample data memberships of the KLFDTWCM, $\lambda =3$

Table 9. Sample data memberships of the BFDTWCM, $m=1.2$

5 Conclusion

This work, propose three fuzzy clustering algorithms for classifying time-series data. The theoretical results indicate that the QFDTWCM approach reduces to the BFDTWCM as $m - 1 \rightarrow +0$ and to the KLFDTWCM as $\lambda \rightarrow + \infty$. Numerical experiments were performed on an artificial dataset to substantiate these properties.

In the future work, these proposed algorithms will be applied to real datasets.