An Analysis to Treat the Degeneracy of a Basic Feasible Solution in Interval Linear Programming

Abstract

When coefficients in the objective function cannot be precisely determined, the optimal solution is fluctuated by the realisation of coefficients. Therefore, analysing the stability of an optimal solution becomes essential. Although the robustness analysis of an optimal basic solution has been developed successfully so far, it becomes complex when the solution contains degeneracy. This study is devoted to overcoming the difficulty caused by the degeneracy in a linear programming problem with interval objective coefficients. We focus on the tangent cone of a degenerate basic feasible solution since the belongingness of the objective coefficient vector to its associated normal cone assures the solution’s optimality. We decompose the normal cone by its associated tangent cone to a direct union of subspaces. Several propositions related to the proposed approach are given. To demonstrate the significance of the decomposition, we consider the case where the dimension of the subspace is one. We examine the obtained propositions by numerical examples with comparisons to the conventional techniques.

This work was supported by JSPS KAKENHI Grant Number JP18H01658.

1 Introduction

Linear programming addresses enormous real-world problems. The conventional LP techniques assume that all coefficients are precisely determined. However, this assumption cannot always be guaranteed. Sometimes the coefficients can only be imprecisely known with ranges or distributions due to measurement limitation, noise and insufficient knowledge. Since the imprecise coefficients may fluctuate the solution’s optimality, a decision-maker is usually interest in analysing its stability.

Researchers have studied the problem for decades. An approach called sensitivity analysis [1] that utilises shadow price can analyse the maximum variation on a single coefficient. To treat the case of multiple coefficients, Bradley, Hax, and Magnanti [1] solved a convex cone by the 100 Percent Rule, which is also called the optimality assurance cone in this paper. Then one only needs to check the belongingness of the imprecise coefficients to this convex cone. To represent the imprecise coefficients, researchers utilise several methods such as interval [5, 16], fuzzy [7, 9], and probability distribution [10, 11, 14, 15]. For example, the necessary optimality [9] is widely utilised in the interval case if a feasible solution is optimal for all realisations derived by the interval coefficients. The tolerance approach [2, 16, 17] can address it straightforwardly if the feasible set is constant.

Despite the usefulness of the optimality assurance cone, we cannot always solve it directly by the simplex method. When the feasible solution is non-basic or degenerate, it becomes problematic [6]. To handle it, researchers aim to separate the non-zero part of the solution instead of focusing on its basis. Some remarkable techniques have emerged, such as support set invariancy and optimal partition invariancy [6]. However, they only concentrate on the non-basic situation, which is called dual degeneracy in this paper. On the other hand, primal degeneracy is merely considered a particular case and treated by variational analysis [12] and convex analysis [13] theoretically. The reason is that the optimal solution and optimal value would not change even the basic index set varies. However, when solving the optimal assurance cone of a basic feasible solution, the variance of the basic index set causes troubles. If we list all combinations violently, the computational burden will become tremendous for a large-scale problem [6]. Hence, the study of the primal degeneracy is vital.

In this paper, we study the optimality assurance cone by its counterpart tangent cone [12, 13] in the view of linear algebra. We start by reviewing the interval linear programming and introduce the necessary optimality of a feasible solution in the next section. After identifying the difference between the primal and dual degeneracy, we focus on the primal one. We consider solving the tangent cone of a feasible basic solution and decompose the derived optimality assurance cone into a union of subspaces with equivalence. To simplify our analysis, we assume that the dimension of the subspace is only 1, i.e. the cardinality of the non-zero variable set is strictly 1 less than the basic index set. We finally give numerical examples to show that our approach can treat the problem with no loop or iteration.

2 Preliminaries

2.1 The Linear Programming

The linear programming (LP) problem in this paper follows the standard form as

$$\begin{aligned} \mathrm {minimize} \ {\boldsymbol{c}^\mathrm {T}\boldsymbol{x}}, \ \mathrm {subject~to} \ A\boldsymbol{x}=\boldsymbol{b}, \ \boldsymbol{x} \ge \boldsymbol{0}, \end{aligned}$$

(1)

where $\boldsymbol{x}\in \mathbb {R}^n$ is the decision variable vector, while $A\in \mathbb {R}^{m\times n}$, $\boldsymbol{b}\in \mathbb {R}^m$ and $\boldsymbol{c}\in \mathbb {R}^n$ are the coefficient matrix, right-hand-side coefficient vector and objective coefficient vector, respectively.

Since the simplex method needs a basic index set $\mathbb {I}_B$ with $\mathrm {Card}(\mathbb {I}_B)=m$, we have to consider basic feasible solutions. Therefore, let $\boldsymbol{x}_B^*\in \mathbb {R}^m$ and $\boldsymbol{x}_N^*\in \mathbb {R}^{n-m}$ denote the basic and non-basic sub-vectors of $\boldsymbol{x}^*$ separated by $\mathbb {I}_B$, respectively. Then we can also separate A with $A_B\in \mathbb {R}^{m\times m}$ and $A_N\in \mathbb {R}^{m\times (n-m)}$, and $\boldsymbol{c}$ with $\boldsymbol{c}_B\in \mathbb {R}^m$ and $\boldsymbol{b}_N\in \mathbb {R}^{n-m}$ accordingly.

Since $\mathbb {I}_B$ is solved by the simplex method, $A_B$ should be non-singular. Therefore, we have the proposition for the optimality of a basic feasible solution:

Proposition 1

A basic feasible solution $\boldsymbol{x}^*$ is optimal if and only if the following conditions are valid:

$$\begin{aligned} \boldsymbol{c}_N - A_N^\mathrm {T}A_B^{-\mathrm {T}} \boldsymbol{c}_B&\ \ge \ \boldsymbol{0}, \end{aligned}$$

(2)

$$\begin{aligned} A_B^{-1} \boldsymbol{b}&\ \ge \ \boldsymbol{0}, \end{aligned}$$

(3)

where the optimal solution is $\boldsymbol{x}_B^* = A_B^{-1}\boldsymbol{b}$, $\boldsymbol{x}_N^* = \boldsymbol{0}$ with the optimal value being $\boldsymbol{c}_B^\mathrm {T}A_B^{-1} \boldsymbol{b}$.

2.2 The Interval Linear Programming

Since the coefficients in an LP problem cannot always be guaranteed to be precise in reality, interval linear programming (ILP) considers utilising intervals to represent the imprecise coefficients. A typical ILP problem is written as

$$\begin{aligned} \mathrm {minimize} \ \boldsymbol{\gamma }^\mathrm {T}\boldsymbol{x}, \ \mathrm {subject~to} \ \varLambda \boldsymbol{x} = \boldsymbol{\varphi }, \ \boldsymbol{x}\ge \boldsymbol{0}, \end{aligned}$$

(4)

where $\boldsymbol{x}$ represents the decision variable vector, but $\varLambda \subseteq \mathbb {R}^{m \times n}$, $\boldsymbol{\varphi } \subseteq \mathbb {R}^m$ and $\boldsymbol{\gamma } \subseteq \mathbb {R}^n$ are the interval subsets composed of the imprecise A, $\boldsymbol{b}$ and $\boldsymbol{c}$, respectively. Therefore, an ILP problem can be regarded as a combination of multiple conventional LP problems, called scenarios [4]. Hence, the robustness analysis of a solution equals to analysing its all scenarios.

However, Proposition 1 only guarantees the invariance of $\mathbb {I}_B$ instead of the optimal solution $\boldsymbol{x}^*$ due to $\boldsymbol{x}^*_B = A_B^{-1} \boldsymbol{b}$. Since the imprecision in constraints is difficult (see [3, 4]) to study, we assume the ILP problem always has a constant feasible set, i.e. $\varLambda$ and $\boldsymbol{\varphi }$ are singletons containing A and $\boldsymbol{b}$, respectively. Hence, the ILP problem becomes

$$\begin{aligned} \mathrm {minimize} \ {\boldsymbol{\gamma }^\mathrm {T}\boldsymbol{x}}, \ \mathrm {subject~to} \ A\boldsymbol{x}=\boldsymbol{b}, \ \boldsymbol{x} \ge \boldsymbol{0}, \end{aligned}$$

(5)

where $\boldsymbol{\gamma }\in \varPhi := \{(c_1,\ldots ,c_n)^\mathrm {T}: c^\mathrm {L}_i \le c_i \le c^\mathrm {U}_i, \ i=1,\ldots , n\} \subseteq \mathbb {R}^n$. $c^\mathrm {L}_i$ and $c^\mathrm {U}_i$ are the lower and upper bounds of the interval $\varPhi _i$, $i=1,\ldots , n$, respectively.

To analyse the optimality of a feasible solution in an ILP problem (5), we utilise possible and necessary optimality [9]:

Definition 1 (possible and necessary optimality)

Let $\varPhi$ defined in Problem (5) denote an interval hyper-box composed of $\boldsymbol{\gamma }$ and let $\boldsymbol{x}^*$ be a feasible solution, then $\boldsymbol{x}^*$ is possibly optimal for $\varPhi$ if $\exists \,\boldsymbol{\gamma }\in \varPhi$ that $\boldsymbol{x}^*$ is optimal, and $\boldsymbol{x}^*$ is necessarily optimal for $\varPhi$ if $\forall \,\boldsymbol{\gamma }\in \varPhi$ that $\boldsymbol{x}^*$ is optimal.

To check the necessary optimality of $\boldsymbol{x}^*$, we use the optimality assurance cone [8] defined as

Definition 2 (optimality assurance cone)

Let $\boldsymbol{x}^*$ be a feasible solution. Then the optimality assurance cone, denoted as $\mathscr {S}^\mathrm {O}(\boldsymbol{x}^*)$, is defined by

$$\begin{aligned} \mathscr {S}^\mathrm {O}(\boldsymbol{x}^*):= \Big \{ \boldsymbol{c}\in \mathbb {R}^n: \boldsymbol{c}^\mathrm {T}\boldsymbol{x}^* = \min \{\boldsymbol{c}^\mathrm {T}\boldsymbol{x}: A \boldsymbol{x} = \boldsymbol{b}, \ \boldsymbol{x} \ge \boldsymbol{0}\} \Big \}. \end{aligned}$$

(6)

Since a decision-maker usually does not prefer a possibly optimal solution, we focus on the necessary optimality, which can be checked by the lemma below:

Lemma 1

A feasible solution $\boldsymbol{x}^*$ is necessarily optimal if and only if $\varPhi \subseteq \mathscr {S}^\mathrm {O}(\boldsymbol{x}^*)$.

However, Eq. (6) is not applicable for solving the optimality assurance cone. Fortunately, if $\boldsymbol{x}^*$ is a non-degenerate basic feasible solution, we can utilise Proposition 1 to get an equivalent result as the 100 Percent Rule [1] did:

Proposition 2

Let $\boldsymbol{x}^*$ be a non-degenerate basic feasible solution to the ILP Problem (5). Then a convex cone defined by $\boldsymbol{x}^*$, denoted as $\mathscr {M}^\mathrm {O}(\boldsymbol{x}^*)$, is equivalent to $\mathscr {S}^\mathrm {O}(\boldsymbol{x}^*)$. Namely,

$$\begin{aligned} \mathscr {M}^\mathrm {O}(\boldsymbol{x}^*) := \Big \{ \boldsymbol{c}\in \mathbb {R}^n: \boldsymbol{c}_N - A_N^\mathrm {T}A_B^{-\mathrm {T}} \boldsymbol{c}_B \ge \boldsymbol{0} \Big \} = \mathscr {S}^\mathrm {O}(\boldsymbol{x}^*). \end{aligned}$$

(7)

With the condition in Proposition 2, Lemma 1 equals to the following one:

Lemma 2

A non-degenerate basic feasible solution $\boldsymbol{x}^*$ is necessarily optimal if and only if $\varPhi \subseteq \mathscr {M}^\mathrm {O}(\boldsymbol{x}^*)$.

By Lemma 2, the necessary optimality can be checked straightforwardly by tolerance approach [2, 16, 17]. Since the only difference between Lemma 1 and 2 is whether $\boldsymbol{x}^*$ is non-degenerate and basic, the problem becomes difficult when there exists degeneracy. Hence, the key is how to correctly solve $\mathscr {S}^\mathrm {O}(\boldsymbol{x}^*)$ in an efficient way, which becomes the main topic in the following content.

3 Degeneracy and Optimality Assurance Cone

3.1 Difference Between Dual and Primal Degeneracy

Before proposing our approach, we need to illustrate what is the degeneracy that has been mentioned in previous sections by the following examples.

Example 1

Let us consider the following LP problem:

where $c_1 = -3$ and $c_2 = -4$. Solve this problem.

By the simplex method, we obtain the tabular as

Basis	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	RHS
$x_2$	0	1	1/3	$-1/3$	0	6
$x_1$	1	0	$-1/9$	4/9	0	6
$x_5$	0	0	$-1/3$	1/3	1	3
$-z$	0	0	1		0	42

where the optimal solution is $\boldsymbol{x}^* = (6,6,0,0,3)^\mathrm {T}$. However, since the last row of $x_4$ position being 0, we can re-pivot the tabular as:

Basis	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	RHS
$x_2$	0	1	0	0	1	9
$x_1$	1	0	1/3	0	$-4/3$	2
$x_4$	0	0	$-1$	1	3	9
$-z$	0	0	1	0		42

This time $\boldsymbol{x}^* = (2,9,0,9,0)^\mathrm {T}$, where the optimal value maintains to be $-42$. However, if we modify Example 1 as the following one:

Example 2

Reconsider Example 1, if $c_1 = -3$ and $c_2 = -2$ and there exists an extra constraint $x_1+x_2 + x_6 = 12$, solve this problem.

By the simplex method, we obtain the tabular as

Basis	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$x_6$	RHS
$x_2$	0	1	1/3	$-1/3$	0	0	6
$x_1$	1	0	$-1/9$	4/9	0	0	6
$x_5$	0	0	$-1/3$	1/3	1	0	3
$x_6$	0	0	$-2/9$	$-1/9$	0	1
$-z$	0	0	1/3	2/3	0	0	30

where the optimal solution is $\boldsymbol{x}^* = (6,6,0,0,3,0)^\mathrm {T}$. However, since $x_6 = 0$, we can also pivot the tabular as:

Basis	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$x_6$	RHS
$x_2$	0	1	0	$-1/2$	0	3/2	6
$x_1$	1	0	0	1/2	0	$-1/2$	6
$x_5$	0	0	0	2/3	1	$-3/2$	3
$x_3$	0	0	1	1/2	0	$-9/2$
$-z$	0	0	0	1/2	0	3/2	30

Unlike Example 1, both optimal solution and optimal value maintain to be the same even the basis changes, which means the situation of Example 2 is different even the basis in both examples change.

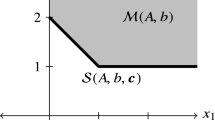
To explain both examples illustratively, we project them into $x_1$-$x_2$ coordinate in Fig. 1 since $c_i = 0, \ i\ne 1,2$. $\check{\mathscr {M}}^\mathrm {O}_i(\boldsymbol{x}^*_j)$ denotes the ith projection of the optimality assurance cone of $\boldsymbol{x}^*_j$.

Fig. 1.

Primal and dual degeneracy

Subfig. 1a shows the result of Example 1, where we find two optimal basic solutions. We show that the optimality assurance cones of $\boldsymbol{x}^*_1$ and $\boldsymbol{x}^*_2$ are independent, and can be solved once the optimal solution is determined. Moreover, it shows that any vertex on the line of $\boldsymbol{x}^*_1$ and $\boldsymbol{x}^*_2$ can be the optimal solution.

However, for the result of Example 2 shown in Subfig. 1b, the situation becomes different. At first, there exists only one optimal solution $\boldsymbol{x}^*$ with 3 active constraints on it, where only 2 of them are needed. Consequently, we have 3 potential optimality assurance cones as $\check{\mathscr {M}}^\mathrm {O}_1(\boldsymbol{x}^*)$, $\check{\mathscr {M}}^\mathrm {O}_2(\boldsymbol{x}^*)$ and $\check{\mathscr {M}}^\mathrm {O}_3(\boldsymbol{x}^*)$, where the union of them is what we want.

Example 1 and 2 show two different degeneracies. When considering them by the simplex method, we find that the degeneracy in Example 1 is connected with the objective coefficients, while in Example 2 is the right-hand-side coefficients. Hence, we identify them as dual degeneracy (Example 1) and primal degeneracy (Example 2) by Proposition 1, and state that for a basic feasible solution $\boldsymbol{x}^*$,

• there exists no dual degeneracy if $\boldsymbol{c}_N - A_N^\mathrm {T}A_B^{-\mathrm {T}} \boldsymbol{c}_B > \boldsymbol{0}$, and

• there exists no primal degeneracy if $A_B^{-1} \boldsymbol{b} > \boldsymbol{0}$,

and if $\boldsymbol{x}^*$ satisfies both, we define it as non-degenerate basic feasible.

Conventionally, dual and primal degeneracy are usually treated as the same question for both enabling the basic index set to change. Moreover, most of studies only focused on the dual one when a feasible solution is non-basic.

However, the rationales of dual and primal degeneracy are completely different. In the view of linear algebra, when the objective coefficient vector $\boldsymbol{c}$ is not independent from the rows of matrix A, dual degeneracy happens. On the other hand, primal degeneracy has no relation with the objective function, and is usually caused by the over-constraints on the solution. Therefore, it is necessary to do respective discussion.

Since the dual degeneracy only enables us to choose a non-basic solution, we can handle such trouble by simply choosing a basic one. Instead, the primal degeneracy does not diminish. Hence, we concentrate on the primal degeneracy.

3.2 Analysis of Primal Degeneracy

In Example 2, we show what is primal degeneracy by the simplex tabular and figure. We find that, despite with computational burden, the simplex method can always find the correct optimality assurance cone. Therefore, by utilising the support set [6] of a basic feasible solution $\boldsymbol{x}^*$, which is the index set $\mathbb {I}_P(\boldsymbol{x}^*):= \{i: x^*_i > 0\}$, we can treat the problem by the following theorem:

Theorem 1

Let $\mathbb {I}_P(\boldsymbol{x}^*) \subseteq \{1,2,\ldots ,n\}$ denote the support set of a basic feasible solution $\boldsymbol{x}^*$ in Problem (5) with $\mathrm {Card}(\mathbb {I}_P(\boldsymbol{x}^*)) \le m$, where m is the number of constraints. Then the optimality assurance cone of $\boldsymbol{x}^*$ is

(8)

where $\mathbb {I}_{B^i}$ with $\mathrm {Card}(\mathbb {I}_{B^i}) = m$ is the index set that determines $A_{B^i}$ and $\boldsymbol{c}_{B^i}$.

Proof

By the definition of support set, we have the result as

For any $\mathbb {I}_{B^i}$ satisfying $\mathbb {I}_{B^i} \supseteq \mathbb {I}_P(\boldsymbol{x}^*)$ and $A_{B^i}^{-1} \boldsymbol{b} \ge \boldsymbol{0}$, its counterpart normal cone calculated as $\{\boldsymbol{c}\in \mathbb {R}^n: \boldsymbol{c}_{N^i} - A_{N^i}^\mathrm {T}A_{B^i}^{-\mathrm {T}} \boldsymbol{c}_{B^i} \ge \boldsymbol{0}\}$ makes $\boldsymbol{x}^*$ optimal for any $\boldsymbol{c}$ belonging to it. Hence, we have the result by uniting all of them.    $\square$

The key of Theorem 1 is to list all situations where a feasible basic solution maintains to be optimal and unite them. However, since the calculation is linearly related to the combination of the basis, it becomes enormous when the system is in large-scale.

To treat the difficulty in Theorem 1, the following lemma is necessary for our approach:

Lemma 3

Let $\boldsymbol{x}^*$ be a basic feasible solution in the ILP Problem (5). Then the optimality assurance cone is normal to the tangent cone of the feasible set on $\boldsymbol{x}^*$.

Lemma 3 states the relation between the optimality assurance cone with its counterpart, i.e. tangent cone, which is significant since we can simply solve the tangent cone of a convex set on a point. By utilising the support set, we have the following proposition:

Proposition 3

The tangent cone of the feasible set on a basic feasible solution $\boldsymbol{x}^*$ in the ILP Problem (5) is

$$\begin{aligned} \mathscr {T}(\boldsymbol{x}^*)=\Big \{ \boldsymbol{x}\in \mathbb {R}^n: A_P \boldsymbol{x}_P + A_Z \boldsymbol{x}_Z = \boldsymbol{0}, \ \boldsymbol{x}_Z \ge \boldsymbol{0} \Big \}, \end{aligned}$$

(9)

where $\boldsymbol{x}_P$ and $\boldsymbol{x}_Z$ are separated by the support set $\mathbb {I}_P$ and its counterpart $\mathbb {I}_Z := \{1,2,\ldots ,n\}\backslash \mathbb {I}_P$.

Since $\mathscr {T}(\boldsymbol{x}^*)$ in Eq. (9) forms a convex cone, let us review the definition and some useful properties of it.

Definition 3 (Convex Cone)

A subset $\mathscr {C}$ of a vector space $\mathscr {V}$ over an ordered field $\mathscr {F}$ is a cone if for every vector $\boldsymbol{v}\in \mathscr {C}$ and any positive scalar $\alpha \in \mathscr {F}$, $\alpha \boldsymbol{v} \in \mathscr {C}$. Moreover, if for every $\boldsymbol{v}, \boldsymbol{w} \in \mathscr {C}$ and for any positive scalar $\alpha , \beta \in \mathscr {F}$ such that $\alpha \boldsymbol{v} + \beta \boldsymbol{w} \in \mathscr {C}$, then $\mathscr {C}$ is a convex cone.

Furthermore, the following lemma indicates that we can utilise convex techniques to analyse the tangent cone.

Lemma 4

The tangent cone of a convex set is convex.

Since it is known that a convex cone is not a vector space due to the non-negative scalar, we cannot utilise the basic space directly. However, we can still use the concept, where the convex cone is spanned by a series of vectors. We call these vectors as the basic vectors of the convex cone and note that, if the convex cone is polyhedral, e.g. the tangent cone, the number of the basic vectors is finite. Similar to the linear space, we call the left part as the null space.

The following theorem illustrates the relation between the basic vectors with the basis of the ILP problem (5).

Theorem 2

Given an ILP problem (5) with a non-degenerate basic feasible solution $\boldsymbol{x}^*$, then the null space of the tangent cone $\mathscr {T}(\boldsymbol{x}^*)$ corresponds to the basic index set $\mathbb {I}_B$ of $\boldsymbol{x}^*$.

Proof

Since $\boldsymbol{x}^*$ is non-degenerate and basic, $\boldsymbol{x}^*_B = A_B^{-1}\boldsymbol{b} > 0$ is always valid. Hence the tangent cone becomes

$$ \mathscr {T}(\boldsymbol{x}^*)=\Big \{ \boldsymbol{x}\in \mathbb {R}^n: A_B \boldsymbol{x}_B + A_N \boldsymbol{x}_N = \boldsymbol{0}, \ \boldsymbol{x}_N \ge \boldsymbol{0} \Big \}. $$

If we ignore $\boldsymbol{x}_N \ge \boldsymbol{0}$ and only consider the linear space $\{\boldsymbol{x}\in \mathbb {R}^n: A\boldsymbol{x} = \boldsymbol{0}\}$, it can be spanned by $(n-m)$ independent vectors due to $A\in \mathbb {R}^{m \times n}$. Since $\boldsymbol{x}^*$ is non-degenerate and basic, $\mathrm {Card}(\boldsymbol{x}_N) = n-m$. Hence, to cover the condition of $\boldsymbol{x}_N \ge \boldsymbol{0}$, we can utilise it directly as the basic vectors. Hence, the basic vectors of $\mathscr {T}(\boldsymbol{x}^*)$ corresponds to the non-basic part of $\boldsymbol{x}^*$, which is equivalent to the condition that the null space of $\mathscr {T}(\boldsymbol{x}^*)$ corresponds to $\mathbb {I}_B$ of $\boldsymbol{x}^*$    $\square$

Theorem 2 indicates the fact that, once we determine the basic vectors of the tangent cone of a basic feasible solution, the corresponding basis is known. Hence, we can extend this property to the following proposition:

Proposition 4

For the tangent cone $\mathscr {T}(\boldsymbol{x}^*)$ defined in Proposition 3, all combinations of choosing $(n-m)$ entries from $\mathbb {I}_Z$ can span the tangent cone.

By Theorem 1 and 2, Proposition 4 is obvious. However, the method in Proposition 4 has the same computational complexity as Theorem 1, indicating that our calculation speed would not improve with purely changing to the realm of convex cone.

To simplify the procedure, we only consider the dimension of the subspace to be 1, i.e. 1-dimensional degeneracy that $\mathrm {Card}(\mathbb {I}_P) = m - 1$. Therefore, there exist an extra entry in $\mathbb {I}_Z$, giving an extra constraint in spanning the tangent cone. It is because we need to choose $(n-m)$ basic vectors from $\mathbb {I}_Z$, but there exist $(n-m+1)$ entries should be non-negative. Hence, when $(n-m)$ basic vectors are chosen, there always leaves an entry in $\mathbb {I}_Z$ that should be non-negatively spanned by the chosen basic vectors.

However, to treat such problem, we can firstly use the following modification to make all coefficients in the extra constraint be non-negative:

Proposition 5

Let $\boldsymbol{x}^*$ be a basic feasible solution with 1-dimensional degeneracy for the ILP Problem (5) and let $\mathbb {I}_P$ denote its support set. Then there always exists an extra constraint that can be written with all coefficients non-negative:

$$\begin{aligned} \sum _{i\in \mathbb {I}^k_Z}k_i (\boldsymbol{x}_Z)_i = \sum _{j\in \mathbb {I}^l_Z}l_j (\boldsymbol{x}_Z)_j, \end{aligned}$$

(10)

where $\mathbb {I}^k_Z \cup \mathbb {I}^l_Z = \mathbb {I}_Z$ and $\mathrm {Card}(\mathbb {I}^k_Z) \le \mathrm {Card}(\mathbb {I}^l_Z)$. $k_i$ and $l_j$ are non-negative scalars.

It is easy to understand that when there exists no primal degeneracy, $\mathbb {I}^k_Z$ is empty by Theorem 2. Moreover, it also hints the following lemma:

Lemma 5

If $\mathrm {Card}(\mathbb {I}^k_Z) \le 1$ in Proposition 5, then $\mathbb {I}^l_Z$ is the index set that corresponds to the basic vectors of the tangent cone.

The rationality of Lemma 5 is that, once a variable can be expressed by other non-negative variables multiplied with non-negative scalars, it becomes non-negative. So it is no longer necessary to consider the non-negative constraint any more and hence can be abandoned.

To explain Lemma 5 more illustratively, let us use Example 2 again. In Example 2, we solve the optimal solution as $\boldsymbol{x}^* = (6,6,0,0,3,0)^\mathrm {T}$, which gives $\mathbb {I}_P = \{1,2,5\}$ and $\mathbb {I}_Z = \{3,4,6\}$. Hence we can write its tangent cone as

$$ \mathscr {T}(\boldsymbol{x}^*) = \Big \{ A\boldsymbol{x} = 0 \text { with } x_3,x_4,x_6 \ge 0 \Big \}. $$

Since $A\in \mathbb {R}^{4\times 6}$, there should only exist 2 entries in the basic space. Therefore, we need to pick out $v_1$ and $v_2$ from $x_3$, $x_4$ and $x_6$. As Proposition 5 indicates, we remove $x_1$, $x_2$ and $x_5$ from $A\boldsymbol{x} = 0$, which give the following extra constraint:

$$ x_4 = 9 x_6 - 2 x_3 \Rightarrow 9 x_6 = x_4 + 2 x_3 $$

After modification to make all scalars to be non-negative, it shows that $x_6$ should be removed. Hence, the correct basic space should be formed by $x_3$ and $x_4$, which indicates the correct basic index set $\mathbb {I}_B = \{1,2,5,6\}$. The result corresponds to the conventional analysis in Example 2.

However, if $\mathrm {Card}(\mathbb {I}^k_Z) \ge 2$, we cannot treat the problem simply by Lemma 5. Instead, we can pick every entry in $\mathbb {I}^k_Z$ as the one that should be removed, which results a series of basic vectors. Then we can form the tangent cone by their union. Mathematically, we have the following proposition:

Proposition 6

Let the extra constraint of $\boldsymbol{x}_Z$ be written in the form of Eq. (10) with $\mathrm {Card}(\mathbb {I}^k_Z) \le \mathrm {Card}(\mathbb {I}^l_Z)$ and $\mathbb {I}^k_Z \cup \mathbb {I}^l_Z = \mathbb {I}_Z$, and $k_i$ and $l_j$ are all non-negative scalars. Then the index of the basic vectors of the tangent cone is the union of the following sets:

$$\begin{aligned} \mathbb {I}_Z \backslash \{i\}, \ i\in \mathbb {I}^k_Z. \end{aligned}$$

(11)

It is easy to see that if $\mathrm {Card}(\mathbb {I}^k_Z) \le 1$, then Proposition 6 is equivalent to Lemma 5. To illustrate Proposition 6, let us consider a brief example.

Example 3

Let us consider the following LP problem:

where we assume $c_1 = 2, \ c_2 = 1, \ c_3 = -10$. Solve this problem.

By the simplex method with the following tabular, the degenerate optimal solutions is $\boldsymbol{x}^* = (3,3,2,0,0,0,0)^\mathrm {T}$, indicating that $\mathbb {I}_P=\{1,2,3\}$.

Basis	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$x_6$	$x_7$	RHS
$x_1$	1	0	0	$-1/2$	1/4	0	1/4	3
$x_3$	0	0	1	0	1/2	0	1/2	2
$x_6$	0	0	0	1	$-1$	1	$-1$
$x_2$	0	1	0	0	1/4	0	$-1/4$	3
$-z$	0	0	0	1	17/4	0	19/4	11

Hence, we can list 4 situations and take the union of them by Theorem 1. Since $c_i = 0, \ i = 4,5,6,7$, we can simply project the system to $\mathbb {R}^3$ and write the optimality assurance cone as

$$ \mathscr {M}^\mathrm {O}(\check{\boldsymbol{x}}^*) = \bigcup _{i=4,5,6,7}{ \big \{ \check{\boldsymbol{c}}\in \mathbb {R}^3: G^i\check{\boldsymbol{c}}\ge \boldsymbol{0} \big \}, } $$

where $\check{\boldsymbol{x}}^* = (x_1^*, x_2^*, x_3^*)^\mathrm {T}$ and $\check{\boldsymbol{c}}=(c_1,c_2,c_3)^\mathrm {T}$, and

$$\begin{aligned} G^4&= \left[ \begin{array}{ccc} 1/4 &{} -1/4 &{} -1/2 \\ -1/2 &{} 0 &{} 0 \\ 1/4 &{} 1/4 &{} -1/2 \end{array} \right] ,&G^5&= \left[ \begin{array}{ccc} 1/4 &{} -1/4 &{} -1/2 \\ -1/4 &{} -1/4 &{} -1/2 \\ 0 &{} 1/2 &{} 0 \end{array} \right] , \\ G^6&= \left[ \begin{array}{ccc} 1/2 &{} 0 &{} 0 \\ -1/4 &{} -1/4 &{} -1/2 \\ -1/4 &{} 1/4 &{} -1/2 \end{array} \right] ,&G^7&= \left[ \begin{array}{ccc} 1/4 &{} 1/4 &{} -1/2 \\ 0 &{} -1/2 &{} 0 \\ -1/4 &{} 1/4 &{} -1/2 \end{array} \right] , \end{aligned}$$

where $G^{i+3}$ denote the situation that ignore $(i_{th})$ constraint. However, in our approach by Proposition 5, we have the extra constraint as $x_4 + x_6 = x_5 + x_7$, which indicates that we only need to take the union of $G^4$ and $G^6$, or the union of $G^5$ and $G^7$, i.e.

$$\begin{aligned} \mathscr {M}^\mathrm {O}(\check{\boldsymbol{x}}^*) = \bigcup _{i=4,6}\big \{ \check{\boldsymbol{c}}\in \mathbb {R}^3: G^i\check{\boldsymbol{c}}\ge \boldsymbol{0} \big \} = \bigcup _{i=5,7}\big \{ \check{\boldsymbol{c}}\in \mathbb {R}^3: G^i\check{\boldsymbol{c}}\ge \boldsymbol{0} \big \} \end{aligned}$$

(12)

Moreover, if we draw the projection $\check{\boldsymbol{x}}$ in $x_1$-$x_2$-$x_3$ coordinate, we have Fig. 2, where the feasible set is the space in the tetrahedron. Then result shown by Eq. (12) is obvious.

Fig. 2.

Degeneracy in Example 3

4 Conclusion and Future Work

In this paper, we proposed a linear algebraic approach to treating the primal degeneracy in ILP problem with imprecise objective coefficients, since we always need to solve the optimality assurance cone explicitly when analysing the robustness of a basic feasible solution in the ILP problem.

In accomplishing our goal, we first consider the tangent cone of the basic feasible solution instead of listing all bases by the simplex method. Since the tangent cone is normal to the optimality assurance cone and is always polyhedral and convex, we modify the concept of basic space in linear subspace and apply it to the tangent cone. We show that once we can span the tangent cone by its basic space, we find the correct basis of the corresponding problem, which would lead to the correct optimality assurance cone. To illustrate and validate our technique, we give numerical examples.

However, since we assume that there exists only one degeneracy, the analysis is not complete. Moreover, when degeneracy becomes multiple, it is necessary to have some algorithms for forming the correct basic space. Another incomplete section is that we assume the feasible solution is basic even there exists dual degeneracy. Therefore, we would take dual degeneracy into consideration in our next step.