Optimal Subsystem Decomposition and Resilient Distributed State Estimation for Wastewater Treatment Plants

Abstract

The wastewater treatment plant (WWTP) is an important step in water recycling (Qu et al. 2013). WWTP is usually composed of several interconnected operation units. State estimation is a process of constructing system state based on output measurements and system model. State estimation is important for WWTP since many related states in WWTP cannot be measured or affected by significant noise. Cyber-physical systems (CPS) integrates communication network, engineering, computing, and physical process components and uses the network to realize the interaction between computing processes and physical processes (Zhang et al. 2021) and operate physical entities in a remote, reliable, real-time, secure (Wang et al. 2021), and cooperative way (Ding et al. 2020). When the distributed state estimation of sewage treatment system is carried out, in order to improve the efficiency, two or more computer equipment are often used for calculation and processing. That is, each computer processes a subsystem state estimation. Among the subsystems, the state information needs to be exchanged through the communication network. Therefore, WWTP can be regarded as an information physical system in which physical processes and networks are connected (Anter et al. 2020; Wei et al. 2020). In Barbu et al. (2011), deterministic and stochastic observers were developed. A univariate statistical technique was proposed in Baklouti et al. (2018) to enhance the monitoring of WWTP and the state estimation of two-time scale nonlinear systems was considered in (Kiss et al. (2011)). In Busch et al. (2013), a synthesis method based on optimization for design and estimation of sensor networks was proposed and was applied to the WWTP system.

12.1 Introduction

The wastewater treatment plant (WWTP) is an important step in water recycling (Qu et al. 2013). WWTP is usually composed of several interconnected operation units. State estimation is a process of constructing system state based on output measurements and system model. State estimation is important for WWTP since many related states in WWTP cannot be measured or affected by significant noise. Cyber-physical systems (CPS) integrates communication network, engineering, computing, and physical process components and uses the network to realize the interaction between computing processes and physical processes (Zhang et al. 2021) and operate physical entities in a remote, reliable, real-time, secure (Wang et al. 2021), and cooperative way (Ding et al. 2020). When the distributed state estimation of sewage treatment system is carried out, in order to improve the efficiency, two or more computer equipment are often used for calculation and processing. That is, each computer processes a subsystem state estimation. Among the subsystems, the state information needs to be exchanged through the communication network. Therefore, WWTP can be regarded as an information physical system in which physical processes and networks are connected (Anter et al. 2020; Wei et al. 2020). In Barbu et al. (2011), deterministic and stochastic observers were developed. A univariate statistical technique was proposed in Baklouti et al. (2018) to enhance the monitoring of WWTP and the state estimation of two-time scale nonlinear systems was considered in Kiss et al. (2011). In Busch et al. (2013), a synthesis method based on optimization for the design and estimation of sensor networks was proposed and was applied to the WWTP system. Extended Kalman filter (EKF) and unscented Kalman filter (UKF) were used to estimate the unmeasurable states in WWTP system in Wahab et al. (2012). In Yin and Liu (2018), EKF and the moving horizon estimator (MHE) estimators were proposed based on model reduction for improved computational efficiency. Also, there are some researches on distributed state estimation.

WWTP is considered critical infrastructure and their resiliency is vital. The resilience against natural disasters (storm and rain) as opposed to cyber-incidents is critical. Performing distributed state estimation is one of the effective ways to improve the resiliency of the system, compared to a centralized scheme applied to the whole system. There are some existing results on the distributed state estimation method for the WWTP system, i.e., in Zeng et al. (2016), distributed EKF (DEKF) was applied to WWTP system, and distributed MHE was studied in Yin et al. (2018). However, the existing distribution control and estimation usually assume that the system decomposition is available. A systematic approach to decompose the large-scale system into subsystems has not yet received enough attention and is crucial for distributed state estimation (Dunbar 2007). When applying the distributed state estimation, a good subsystem decomposition with weak inter-subsystem interactions can improve the resiliency of the system.

In Heo et al. (2015), there are some important results about the decomposition algorithm of distributed control system. In Yin et al. (2016), a subsystem decomposition method for distributed estimation was proposed and applied to WWTP system. In Yin and Liu (2019), the existing community discovery algorithm was extended to the common framework of distributed state estimation and control. However, the above subsystem partition based on community discovery algorithm only considers the correlation degree of the system and ignores the connection strength between different variables. In Zhang et al. (2019), a method of subsystem partition based on weighted edge group detection was proposed and was applied in distributed state estimation. However, the weighted community discovery algorithm for distributed control has not been investigated. Also, there are little results about subsystem decomposition method for WWTP system. Thus, community structure detection is used to decompose the WWTP into smaller groups, such that the intra-connection within each group is made much stronger than the interaction among different groups. Subsystem models that are appropriate for distributed state estimation are configured based on the variables assigned to the groups.

In this work, an optimal subsystem decomposition method is investigated for complex cyber-physical systems for the purpose of improving the resiliency under the distributed state estimation. The main contributions lie in the following: (1) a subsystem decomposition method based on community structure discovery algorithm is proposed for the WWTP system; (2) to deal with the natural disasters and the unreliable communication networks, a resilient distributed framework is proposed with information compensation strategy; (3) comparative study is carried out for WWTP system to show that the subsystem decomposition and resilient distributed state estimation scheme improves the resiliency of the system, compared to a centralized scheme applied to the whole system.

12.2 Model Description of Wastewater Treatment Plants

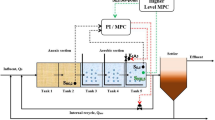
In this work, optimal subsystem decomposition and distributed EKF methods are designed. The theoretical results will be validated in a benchmark WWTP system (Alex et al. 2008). The benchmark WWTP system model will be reviewed in this part and the motivation for decomposing the WWTP system will be derived. The plant layout is shown in Fig. 12.1. In this process, the five activated sludge reactors are composed of two sections: (1) The anoxic section: reactor 1 and reactor 2, where the bacteria convert nitrate into nitrogen (i.e., denitrification biological reactions). (2) The aerated section: reactor 3, reactor 4, and reactor 5, where the bacteria oxidize ammonium to nitrate (i.e., nitrification reactions).

Fig. 12.1

General overview of the BSM1 plant

For each reactor, the following variables ($k=1$ to 5) are defined: flow rate: $Q_k$; concentration: $Z_{as,k}$; the volume of anoxic section: $V_{as,1}=V_{as,2}=1000\,\mathrm{m}^3$; the volume of aerobic section: $V_{as,3}=V_{as,4}=V_{as,5}=1333\,\mathrm{m}^3$; reaction rate: $r_i$. In this model, the general equation of mass balance of bioreactor (two anoxic reactors and three aerobic reactors) follows from Alex et al. (2008).

For reactor 1 ($k=1$),

$$\begin{aligned} \frac{dZ_{as,1}}{dt}=\frac{1}{V_{as,1}}(Q_{int}Z_{int}+Q_rZ_r+Q_iZ_i+r_{Z,1}V_{as,1}-Q_1Z_{as,1}), \end{aligned}$$

(12.1)

$$\begin{aligned} Q_1=Q_{int}+Q_r+Q_i. \end{aligned}$$

(12.2)

For reactor 2–5 ($k=2-5$),

$$\begin{aligned} \frac{dZ_{as,k}}{dt}=\frac{1}{V_{as,k}}(Q_{k-1}Z_{as,k-1}+r_{Z,k}V_{as,k}-Q_kZ_{as,k}), \end{aligned}$$

(12.3)

$$\begin{aligned} Q_k=Q_{k-1}. \end{aligned}$$

(12.4)

Special case for oxygen ($S_{O,k}$):

$$\begin{aligned} \frac{dS_{O,as,k}}{dt}=\frac{1}{V_{as,k}}(Q_{k-1}S_{O,as,k-1}+r_{Z,k}V_{as,k}+(K_{La})_kV_{as,k}(S_O^*-S_{O,as,k})-Q_kS_{O,as,k}), \end{aligned}$$

(12.5)

where the saturation concentration of oxygen is $S_O^*=8g\cdot m^3$, and $r_k$ denotes the conversion rate of different compounds in the reactor; the detailed calculation of $r_{Z,k}$ can be found in Alex et al. (2008). The flow rate of the reaction process in Fig. 12.1 satisfies the following:

$$\begin{aligned} Z_{int} &=Z_{as,5}, \nonumber \\ Z_{f} &=Z_{as,5}, \nonumber \\ Z_{w} &=Z_{r}, \nonumber \\ Q_{f} =Q_{e} + Q_{r} &+ \, Q_{w} =Q_{e}+Q_{u}. \end{aligned}$$

(12.6)

The solid flux caused by gravity is $J_s=v_s(X_{sc})X_{sc}$, where $X_{sc}$ denotes the total sludge concentration (i.e., including $X_I$, $X_S$, $X_{B,H}$, $X_{B,A}$, $X_P$, and $X_{ND}$). The double exponential settlement velocity function is selected:

$$\begin{aligned} v_s(X_{sc})=max\left[ 0,min\left\{ v_0^{'},v_0 \left( e^{-r_h(X_{sc}-X_{min})}-e^{-r_p(X_{sc}-X_{min})} \right) \right\} \right] , \end{aligned}$$

(12.7)

where $X_{min}=f_{ns}X_f$, $X_f$ is the total solids concentration from the bioreactor. The upward velocity ($v_{up}$) and the downward velocity ($v_{dn}$) are calculated as follows:

$$\begin{aligned}&v_{up}=\frac{Q_u}{A}=\frac{Q_r+Q_w}{A}, \nonumber \\&v_{dn}=\frac{Q_e}{A}. \end{aligned}$$

(12.8)

According to these symbols, the mass balance of sludge is written as follows:

$$\begin{aligned}&m=1:\frac{dX_{sc,m}}{dt}=\frac{v_{dn}(X_{sc,m+1}-X_{sc,m})+min(J_{s,m},J_{sc,m+1})}{z_m}\end{aligned}$$

(12.9a)

$$\begin{aligned}&m=2-5:\frac{dX_{sc,m}}{dt}=\frac{v_{dn}(X_{sc,m+1}-X_{sc,m})+min(J_{s,m},J_{sc,m+1})-min(J_{s,m},J_{sc,m-1})}{z_m}\end{aligned}$$

(12.9b)

$$\begin{aligned}&m=6: \frac{dX_{sc,m}}{dt}=\frac{\frac{Q_fX_f}{A}+J_{sc,m+1}-(v_{up}+v_{dn})X_{sc,m}-min(J_{s,m},J_{sc,m-1})}{z_m}\end{aligned}$$

(12.9c)

$$\begin{aligned}&m=7-9: \frac{dX_{sc,m}}{dt}=\frac{v_{up}(X_{sc,m-1}-X_{sc,m})+J_{sc,m+1}-J_{s,m}}{z_m}\end{aligned}$$

(12.9d)

$$\begin{aligned}&m=10: \frac{dX_{sc,m}}{dt}=\frac{v_{up}(X_{sc,m-1}-X_{sc,m})-J_{s,m}}{z_m}, \end{aligned}$$

(12.9e)

where the critical concentration is $X_t=3000 g/m^3$, and the detailed calculation of $J_{sc,m}$ can be found in Alex et al. (2008).

For soluble components (i.e., $S_I$, $S_S$, $S_O$, $S_{NO}$, $S_{NH}$, $S_{ND}$, and $S_{ALK}$), each layer represents the volume of complete mixing, and the concentration of soluble components is calculated accordingly.

$$\begin{aligned}&m=1-5:\frac{dZ_{sc,m}}{dt}=\frac{v_{dn}(Z_{sc,m+1}-Z_{sc,m})}{z_m}\end{aligned}$$

(12.10a)

$$\begin{aligned}&m=6:\frac{dZ_{sc,m}}{dt}=\frac{\frac{Q_fX_f}{A}-(v_{up}+v_{dn})Z_{sc,m}}{z_m}\end{aligned}$$

(12.10b)

$$\begin{aligned}&m=7-10:\frac{dZ_{sc,m}}{dt}=\frac{v_{up}(Z_{sc,m-1}-Z_{sc,m})}{z_m}, \end{aligned}$$

(12.10c)

where the concentration in the recycle and waste stream is equal to that in the first layer (bottom layer), that is, $Z_u=Z_{sc,1}$.

According to the concentration in compartment 5 of the activated sludge reactor, the sludge concentration can be calculated directly as follows:

$$\begin{aligned} X_f=\frac{1}{fr_{COD-SS}}(X_{S,as,5}+X_{P,as,5}+X_{I,as,5}+X_{B,H,as,5}+X_{B,A,as,5}), \end{aligned}$$

(12.11)

where the conversion coefficient $fr_{COD-SS}$ from COD to SS is equal to 4/3. The same principle applies $X-u$ (in the underflow of the secondary sedimentation tank) and $X-e$ (at the outlet of the secondary sedimentation tank).

Then, Eqs. (12.1)–(12.11) form the WWTP system model. Typically, there are 145 states in the system and it is difficult to design centralized controller or estimator for the WWTP system. Thus, distributed control/estimation method is necessary. To do this, we have to (1) decompose the whole system into subsystems and (2) design distributed controller/estimator.

12.3 Subsystem Decomposition

In this section, we will present a subsystem decomposition method for WWTP system. The existing decomposition method usually ignores the weights on the edges. We will present a weighted directed graph-based subsystem decomposition method for large-scale system. The whole system will be represented by a weighted directed graph, and the community structure detection method is derived for decomposition.

The dynamic model of WWTP system can be formulated as follows:

$$\begin{aligned}&\dot{x}(t) = f(x(t),u(t))\end{aligned}$$

(12.12a)

$$\begin{aligned}&y(t) = h(x(t)), \end{aligned}$$

(12.12b)

where $x \in \mathbb R^{n_x}$, $u \in \mathbb R^{n_y}$, and $y \in \mathbb R^{n_y}$, respectively, represent the state vector of the system, the vector of inputs, and the vector of measured outputs, and f and h are two vector fields describing the dynamics of the nonlinear system and the output relation, respectively. The objective is to decompose system (12.12) into subsystems with the form:

$$\begin{aligned}&\dot{x}_i(t) = f_i(x_i(t),X_i(t),u_i(t), U_i(t))\end{aligned}$$

(12.13a)

$$\begin{aligned}&y_i(t) = h_i(x_i(t)), \end{aligned}$$

(12.13b)

where $i=1,\ldots ,p$, with p being the number of subsystems, $x_i\in \mathbb R^{n_{x_i}}$ denotes the state vector of the ith subsystem, $u_i\in \mathbb R^{n_{u_i}}$ denotes the input vector of the ith subsystem, $y_i\in \mathbb R^{n_{y_i}}$ is the output vector of the ith subsystem, and $X_i$ and $U_i$ are the vector that comprises the states and input of all the subsystems that affect the dynamics of subsystem i directly.

The weighted subsystem decomposition method is extended from our early work (Zhang et al. 2019) to simultaneous state estimation and control (see Fig. 12.2). In the proposed approach, system (12.12) is characterized by a weighted directed graph. The graph characterizes the connectivity between the state, input, and measured output variables. When the entire system is not observable or not controllable, we have to adjust the system structure to get a observable or controllable system. For the observation, we can add more sensors to make sure that the observability matrix is full rank. Also, we can add more control variables to guarantee that the controllability matrix is full rank.

Fig. 12.2

The flowchart of the optimal subsystem decomposition

Specifically, the weighted directed graph is created based on the methods for generating unweighted directed graphs described. All the state, input, and measured output variables are considered as vertices of a graph, which are connected through directed edges. Let $f_i, i=1,\cdots , n_x$, denote the ith element of the vector field f, and $h_j, j=1,\ldots , n_y$, denote the jth element of the vector field h. In addition, let us denote $x_i, i = 1,\ldots ,n_x$, as the ith element of x, denote $u_k, k=1,\ldots ,n_u$, as the jth element of u, and denote $y_j, j=1,\ldots ,n_y$, as the jth element of y. The edges in a directed graph are constructed based on the following rules:

• State-to-state edge: there is a unidirectional edge from a state vertex $x_i$ to another state vertex $x_l$, if $\frac{\partial f_l(x,u)}{\partial x_i} \not = 0$, $l,i=1,\ldots , n_x$.

• State-to-input edge: there is a unidirectional edge from an output vertex $y_j$ to a state vertex $x_l$, if $\frac{\partial f_i(x,u)}{\partial u_k} \not = 0$, $i=1,\ldots , n_x, k=1,\ldots ,n_u$.

• State-to-output edge: there is a bidirectional edge from an output vertex $y_j$ to a state vertex $x_l$, if $\frac{\partial h_j(x)}{\partial x_l} \not = 0$, $l=1,\ldots , n_x, j=1,\ldots ,n_y$.

Then, the weighted directed graphs are constructed with $\mathscr {G}=(V,E)$, where $V=\{x_i,y_i,u_i\}$ is set of the vertices and E is the set of the edges. The edges are constructed as follows:

$$\begin{aligned} S(u_k,x_i)&= \frac{\partial f_i(x,u)}{\partial u_k} \big |_{(x_s,u_s)} \end{aligned}$$

(12.14a)

$$\begin{aligned} S(x_i,x_l)&= \frac{\partial f_l(x,u)}{\partial x_i} \big |_{(x_s,u_s)}\end{aligned}$$

(12.14b)

$$\begin{aligned} S(x_l,y_j)&= \frac{\partial h_j(x)}{\partial x_l}\big |_{x=x_s}, \end{aligned}$$

(12.14c)

where $S(x_i,x_l)$ is the sensitivity for a state-to-state pair $(x_i,x_j)$ and $S(x_l,y_j)$ is the sensitivity for a state-to-output pair $(x_l,y_j)$. A sensitivity matrix is constructed as follows:

$$\begin{aligned} S = \begin{bmatrix}\overline{A} &{} \overline{B} &{} \overline{C}^T &{} \\ 0_{n_u\times n_x} &{} 0_{n_u\times n_u} &{} 0_{n_u\times n_y}\\ \overline{C} &{} 0_{n_y\times n_u} &{} 0_{n_y\times n_y} \end{bmatrix}_{n_x+n_u+n_y}, \end{aligned}$$

(12.15)

where $\bar{A}$, $\bar{B}$, and $\bar{C}$ are obtained by taking the Jacobian of system (12.12) at $(x_s,u_s)$, respectively, as follows:

$$\begin{aligned} \overline{A}= \begin{bmatrix}\frac{\partial f_1}{\partial x_1} &{} \cdots &{} \frac{\partial f_1}{\partial x_{n_x}} \\ \vdots &{} \ddots &{} \vdots \\ \frac{\partial f_{n_x}}{\partial x_1} &{} \cdots &{} \frac{\partial f_{n_x}}{\partial x_{n_x}} \end{bmatrix}_{(x_s,u_s)},~\overline{B}= \begin{bmatrix}\frac{\partial f_1}{\partial u_1} &{} \cdots &{} \frac{\partial f_1}{\partial u_{n_u}} \\ \vdots &{} \ddots &{} \vdots \\ \frac{\partial f_{n_x}}{\partial u_1} &{} \cdots &{} \frac{\partial f_{n_x}}{\partial u_{n_u}} \end{bmatrix}_{(x_s,u_s)},~\overline{C}= \begin{bmatrix}\frac{\partial h_1}{\partial x_1} &{} \cdots &{} \frac{\partial h_1}{\partial x_{n_y}} \\ \vdots &{} \ddots &{} \vdots \\ \frac{\partial h_{n_y}}{\partial x_1} &{} \cdots &{} \frac{\partial h_{n_y}}{\partial x_{n_y}} \end{bmatrix}_{x=x_s}. \end{aligned}$$

(12.16)

The weights of the edges are defined as follows:

• Weight of state-to-state edge:

  $$\begin{aligned} w(x_i,x_l) = \left\{ \begin{aligned}&\frac{1}{| S(x_i,x_l)|},~\text {if}~\frac{\partial f_l(x,u)}{\partial x_i} \Big |_{(x_s,u_s)}\not =0,~l,i= 1,\ldots ,n_x \\&\infty ,~~\text{otherwise}. \end{aligned} \right. \end{aligned}$$

  (12.17)

• Weight of input-to-state edge:

  $$\begin{aligned} w(u_k,x_i) = \left\{ \begin{aligned}&\frac{1}{| S(u_k,x_i)|},~\text {if}~\frac{\partial f_i(x,u)}{\partial u_k} \Big |_{(x_s,u_s)}\not =0,~k=1,\ldots ,n_u,i= 1,\ldots ,n_x \\&\infty ,~~\text{otherwise}. \end{aligned} \right. \end{aligned}$$

  (12.18)

• Weight of state-to-output edge:

  $$\begin{aligned} w(x_l,y_j) =\left\{ \begin{aligned}&\frac{1}{ | S(x_l,y_j)|},~\text { if}~\frac{\partial h_j(x)}{\partial x_l}\Big |_{x_s}\not =0,~l= 1,\ldots , n_x,~j= 1,\ldots ,n_y \\&\infty ,~~\text{otherwise}. \end{aligned} \right. \end{aligned}$$

  (12.19)

The shortest paths can be identified for constructing the adjacency matrix. The lengths of the path $L_{il}(P_{il})$ from $x_i$ to $x_l$ and $x_l$ to an output vertex $y_j$ have been given in Zhang et al. (2019). Additionally, we need to take the connection from $u_k$ to a state vertex $x_i$ and path from a input vertex $u_k$ to an output vertex $y_j$ into account.

The length of the path $L_{ki}(P_{ki})$ from a input vertex $u_k$ to a state vertex $x_i$ is given as follows:

$$\begin{aligned} L_{ki}(P_{ki}) = w\left( {u_k,x_1^{(k,i)}}\right) +\cdots +w\left( {x_{N( P_{ki})}^{(k,i)},x_i}\right) . \end{aligned}$$

(12.20)

The corresponding shortest path $\underline{d}(u_k,x_i)$ is calculated as follows:

$$\begin{aligned} \begin{aligned} \underline{d}(u_k,x_i)&= \min \limits _{P_{ki} \in \mathbb P_{ki}} L_{ki}(P_{ki}) \\&=\min \limits _{P_{ki} \in \mathbb P_{ki}} \left\{ \frac{1}{ \Big | S\left( {u_k,x_1^{(k,i)}}\right) \Big |^{\alpha }}+\cdots +\frac{\mathrm {1}}{ \Big | S\left( {x_{N(P_{ki})}^{(k,i)},x_i}\right) \Big |^{\alpha }}\right\} , \end{aligned} \end{aligned}$$

(12.21)

where $k=1,\ldots ,n_u$, $i=1,\ldots ,n_x$, and $\mathbb P_{ki}$ and $P_{ki}$ represent the set of all the paths and one of path from a input vertex $u_k$ to a state vertex $x_i$, respectively.

The length of the path $L_{kj}(P_{kj})$ from a input vertex $u_k$ to an output vertex $y_j$ is given as follows:

$$\begin{aligned} L_{kj}(P_{kj}) = w\left( {u_k,x_1^{(k,j)}}\right) +\cdots +w\left( {x_{N( P_{kj})}^{(k,j)},y_j}\right) . \end{aligned}$$

(12.22)

The corresponding shortest path $\underline{d}(u_k,y_j)$ is calculated as follows:

$$\begin{aligned} \begin{aligned} \underline{d}(u_k,y_j)&= \min \limits _{P_{kj} \in \mathbb P_{kj}} L_{kj}(P_{kj}) \\&=\min \limits _{P_{kj} \in \mathbb P_{kj}} \left\{ \frac{1}{ \Big | S\left( {u_k,x_1^{(k,j)}}\right) \Big |^{\alpha }}+\cdots +\frac{\mathrm {1}}{ \Big | S\left( {x_{N(P_{kj})}^{(k,j)},y_j}\right) \Big |^{\alpha }}\right\} , \end{aligned} \end{aligned}$$

(12.23)

where $k=1,\ldots ,n_u$, $j=1,\ldots ,n_y$, and $\mathbb P_{kj}$ and $P_{kj}$ represent the set of all the paths and one of path from a input vertex $u_k$ to an output vertex $y_j$, respectively.

The length of the path $L_{jm}(P_{jm})$ from an output vertex $y_j$ to another output vertex $y_m$ is given as follows:

$$\begin{aligned} L_{jm}(P_{jm}) = w\left( {y_j,x_1^{(j,m)}}\right) +\cdots +w\left( {x_{N( P_{jm})}^{(j,m)},y_m}\right) . \end{aligned}$$

(12.24)

The corresponding shortest path $\underline{d}(y_j,y_m)$ is calculated as follows:

$$\begin{aligned} \begin{aligned} \underline{d}(y_j,y_m)&= \min \limits _{P_{jm} \in \mathbb P_{jm}} L_{jm}(P_{jm}) \\&=\min \limits _{P_{jm} \in \mathbb P_{jm}} \left\{ \frac{1}{ \Big | S\left( {y_j,x_1^{(j,m)}}\right) \Big |^{\alpha }}+\cdots +\frac{\mathrm {1}}{ \Big | S\left( {x_{N(P_{jm})}^{(j,m)},y_m}\right) \Big |^{\alpha }}\right\} , \end{aligned} \end{aligned}$$

(12.25)

where $j,m=1,\ldots ,n_y$, and $\mathbb P_{jm}$ and $P_{jm}$ represent the set of all the paths and one of path from an output vertex $y_j$ to another output vertex $y_m$, respectively.

An adjacency matrix $A_w\in \mathbb R^{n_a\times n_a}$ involving all the vertices is then constructed based on $\underline{d}(x_i,x_l)$, $\underline{d}(x_l,y_j)$, $\underline{d}(u_k,x_i)$, $\underline{d}(u_k,y_j)$, and $\underline{d}(y_j,y_m)$, $i,l = 1,\ldots ,n_x$, $k = 1,\ldots ,n_u$, $j,m = 1,\ldots ,n_y$:

$$\begin{aligned} \overline{A}_w = \begin{bmatrix}\overline{A}_{w,11} &{} \overline{A}_{w,12}&{}\overline{A}_{w,31}^T \\ 0_{n_u\times n_x} &{} 0_{n_u\times n_u} &{} 0_{n_u\times n_y}\\ \overline{A}_{w,31} &{} \overline{A}_{w,32} &{} \overline{A}_{w,33} \end{bmatrix}_{n_a \times n_a}, \end{aligned}$$

(12.26)

where $\overline{A}_{w,11}$, $\overline{A}_{w,12}$, $\overline{A}_{w,31}$, $\overline{A}_{w,32}$, and $\overline{A}_{w,33}$ are constructed as follows:

$$\begin{aligned} \begin{aligned}&\overline{A}_{w,11}=\begin{bmatrix}\frac{1}{\underline{d}(x_1,x_{1})} &{} \cdots &{} \frac{1}{\underline{d}(x_1,x_{n_x}) }\\ \vdots &{} \ddots &{} \vdots \\ \frac{1}{\underline{d}(x_{n_x},x_1)} &{} \cdots &{}\frac{1}{\underline{d}(x_{n_x},x_{n_x})}\end{bmatrix}, \overline{A}_{w,12}=\begin{bmatrix}\frac{1}{\underline{d}(u_1,x_{1})} &{} \cdots &{} \frac{1}{\underline{d}(u_1,x_{n_x}) }\\ \vdots &{} \ddots &{} \vdots \\ \frac{1}{\underline{d}(u_{n_u},x_1)} &{} \cdots &{}\frac{1}{\underline{d}(u_{n_u},x_{n_x})}\end{bmatrix},\\&\overline{A}_{w,31}=\begin{bmatrix}\frac{1}{\underline{d}(x_1,y_{1})} &{} \cdots &{}\frac{1}{\underline{d}(x_1,y_{n_y})} \\ \vdots &{} \ddots &{} \vdots \\ \frac{1}{\underline{d}(x_{n_x},y_{1})} &{} \cdots &{}\frac{1}{\underline{d}(x_{n_x},y_{n_y})}\end{bmatrix}, \overline{A}_{w,32}=\begin{bmatrix}\frac{1}{\underline{d}(u_1,y_{1})} &{} \cdots &{} \frac{1}{\underline{d}(u_1,y_{n_y}) }\\ \vdots &{} \ddots &{} \vdots \\ \frac{1}{\underline{d}(u_{n_u},y_1)} &{} \cdots &{}\frac{1}{\underline{d}(u_{n_u},y_{n_y})}\end{bmatrix},\\&\overline{A}_{w,33}=\begin{bmatrix}\frac{1}{\underline{d}(y_1,y_{1})} &{} \cdots &{} \frac{1}{\underline{d}(y_1,y_{n_y}) }\\ \vdots &{} \ddots &{} \vdots \\ \frac{1}{\underline{d}(y_{n_y},y_1)} &{} \cdots &{}\frac{1}{\underline{d}(y_{n_y},y_{n_y})}\end{bmatrix}. \end{aligned} \end{aligned}$$

(12.27)

The weighted adjacency matrix $A_w$ is constructed following (Zhang et al. 2019). The problem of subsystem decomposition is equivalent to performing community structure detection by finding a higher value of modularity Q. Community structure detection (Zhang et al. 2019) is used to decompose the network into smaller groups, such that the intra-connection within each group is made much stronger than the interaction among different groups. Subsystem models that are appropriate for distributed state estimation are configured based on the variables assigned to the groups. To this end, we have constructed the subsystem model for distributed state estimation. In the following section, we will present a resilient distributed estimator for WWTP system.

12.4 Resilient Distributed State Estimator Design

In distributed state estimation design, the distributed operation of each subsystem is usually carried out by multiple physical devices and the subsystem information needs to be exchanged. The physical equipment operation is supported by the communication network, and the subsystem information is transmitted through the communication network. Because the communication network may be unreliable, the data exchanged between subsystems may be altered, and they may be damaged by malicious network attacks. There are two common types of attacks, denial-of-service attack (DoS) and false data injection (FDI). DoS attack usually blocks the information flow between the sending device and the receiving device, thus increasing the packet loss rate in the communication process. FDI attack will hijack network nodes or physical devices and inject wrong or useless data information into the system, seriously endangering the safe and reliable operation of the system. To deal with the unreliable communication networks, a resilient distributed framework is proposed with information compensation strategy.

Based on the decomposed subsystems, distributed state estimator will be designed to show the improvement of the resiliency compared to the centralized state estimator. During the distributed state estimator design, the subestimators will work colorably to make a coordination. Denote $\hat{X}_i(t_{k-1})$ as the latest subsystem estimate information of $X_{(i)}(t)$ for time $t\in [t_{k-1},t_k]$ available to filter i. The communication network can be unreliable, i.e., $\hat{X}_i(t_{k-1})$ is attacked or lost. When the communication network is suffering FDI attack, the exchanged status will change to $\hat{X}_i(t_{k-1})=\hat{X}_i(t_{k-1})+X_a(t_{k-1})$. Thus, resilient distributed state estimator is necessary.

In the designed resilient DEKF, the attack is evaluated before each communication between subsystems with following strategy:

$$\begin{aligned} a =\left\{ \begin{aligned}&1,~\text { if}~\Vert y_i(t_{k-1})-C_i\hat{X}_i(t_{k-1})\Vert > \varDelta ~\text {or}~\hat{X}_i(t_{k-1})~\text {is~not~ received} \\&0,~\text { if}~\Vert y_i(t_{k-1})-C_i\hat{X}_i(t_{k-1})\Vert \le \varDelta . \end{aligned} \right. \end{aligned}$$

(12.28)

$$\begin{aligned} \hat{X}_i(t_{k-1}) =\left\{ \begin{aligned}&\hat{X}_i(t_{k-1}),~\text {if}~a=0 \\&\hat{X}_i(t_{k-2})+\int _{t_{k-2}}^{t_{k-1}} f_i(\hat{x}_i(t_{k-2}),\hat{X}_i(t),u_i(t), U_i(t)))dt,~\text { if}~a=1. \end{aligned} \right. \end{aligned}$$

(12.29)

In the resilient distributed EKF design, each local filter is designed as a continuous–discrete EKF. The resilient distributed EKF is implemented with the prediction step and update step.

(1) Prediction step:

$$\begin{aligned} \hat{x}_i (t_k|t_{k-1})=\hat{x}_i(t_{k-1})+\int _{t_{k-1}}^{t_k} f_i(\hat{x}_i(t),\hat{X}_i(t_{k-1}),u_i(t), U_i(t))dt, \end{aligned}$$

(12.30)

$$\begin{aligned} P_i(t_k|t_{k-1}) =A_i(t_{k-1})P_i(t_{k-1})A_i(t_{k-1})^T+Q_i. \end{aligned}$$

(12.31)

(2) Update step:

$$\begin{aligned} K_i(t_k) = P_i(t_k|t_{k-1})C_i^T\left[ C_iP_i(t_{k}|t_{k-1})C_i^T+R_i\right] ^{-1}, \end{aligned}$$

(12.32)

$$\begin{aligned} \hat{x}_i (t_k)=\hat{x}_i (t_k|t_{k-1})+K_i(t_k)\left[ y_i(t_k)-C_i\hat{x}_i(t_k|t_{k-1})\right] , \end{aligned}$$

(12.33)

$$\begin{aligned} P_i(t_k) = \left[ I-K_i(t_k)C_i\right] P_i(t_k|t_{k-1}), \end{aligned}$$

(12.34)

where $\hat{x}_i(t_k|t_{k-1})$ denotes the state prediction at time $t_k$, and, $P_i(t_{k-1})$ is used to denote the error covariance matrix of $x_{(i)}(t_{k-1})$. $P_i(t_k|t_{k-1})$ refer to the predicted error covariance matrix for time $t_k$. $Q_i$ and $R_i$ are the covariances of process noise and measurement noise of subsystem i, respectively; $A_i(t_{k-1})$ is the Jacobian of $f_{(i)}$ with respect to $x_{(i)}$ at time $t_{k-1}$; and $K_i(t_k)$ is the filter gain at $t_k$.

To show the derivation of the distributed EKF algorithm, the system is discretized at time interval $\varDelta$, such that $t_k=k\varDelta$:

$$\begin{aligned}&x_i(t_{k}) = f_i(x_i(t_{k-1}),X_i(t_{k-1}),u_i(t_{k-1}), U_i(t_{k-1}))+w_i(t_{k-1})\end{aligned}$$

(12.35a)

$$\begin{aligned}&y_i(t_k) = h_i(x_i(t_k))+v_i(t_k). \end{aligned}$$

(12.35b)

Assuming that the estimated error between the estimated value and the real value and the prediction error between the predicted value and the real value are $e_i(t_k)=x_i(t_k)-\hat{x}_i(t_k)$ and $e_i(t_k|t_{k-1})=x_i(t_k)-\hat{x}_i(t_k|t_{k-1})$, respectively, and the estimation error covariance matrix and the prediction error covariance matrix are $P_i(t_k)= E\{e_i(t_k)e_i^T(t_k)\}$ and $P_i(t_k|t_{k-1})= E\{e_i(t_k|t_{k-1})e_i^T(t_k|t_{k-1})\}$, respectively, where $E\{\cdot \}$ denotes mathematical expectation, then $\hat{x}_i(t_k|t_{k-1})$ and $\hat{x}_i(t_k)$ are

$$\begin{aligned} \begin{aligned}&\hat{x}_i (t_k|t_{k-1})=\hat{x}_i(t_{k-1})+\int _{t_{k-1}}^{t_k} f_i(\hat{x}_i(t),\hat{X}_i(t_{k-1}),u_i(t), U_i(t)dt\\&\hat{x}_i(t_k)= \hat{x}_i(t_k|t_{k-1})+ K_i(t_k)[y_i(t_k)-h_i(\hat{x}_i(t_k|t_{k-1}))], \end{aligned} \end{aligned}$$

(12.36)

where $K_i(t_k)$ is the filter gain at $t_k$. The Taylor expansion of $y_i(t_k)$ in Eq. (12.35) at $\hat{x}_i (t_k|t_{k-1})$

$$\begin{aligned} \begin{aligned}&y_i(t_k) = h_i(\hat{x}_i(t_k|t_{k-1}))+C_i(x_i(t_k)-\hat{x}_i (t_k|t_{k-1}))+v_i(t_k). \end{aligned} \end{aligned}$$

(12.37)

So the estimation error and the estimation error covariance matrix are

$$\begin{aligned} \begin{aligned}&e_i(t_k)=x_i(t_k)-\hat{x}_i(t_k)=x_i(t_k)-\hat{x}_i(t_k|t_{k-1})-K_i(t_k)[y_i(t_k)-h_i(\hat{x}_i(t_k|t_{k-1}))]\\&~~~~~~~~~=x_i(t_k)-\hat{x}_i(t_k|t_{k-1})-K_i(t_k)[C_i(x_i(t_k)-\hat{x}_i (t_k|t_{k-1}))+v_i(t_k)]\\&~~~~~~~~~=(I-K_i(t_k)C_i)(x_i(t_k)-\hat{x}_i (t_k|t_{k-1}))-K_i(t_k)v_i(t_k), \end{aligned} \end{aligned}$$

(12.38)

$$\begin{aligned} \begin{aligned}&P_i(t_k) = E\{e_i(t_k)e_i^T(t_k)\}\\&~~~~~~~~~~= E\{[(I-K_i(t_k)C_i)(x_i(t_k)-\hat{x}_i(t_k|t_{k-1}))-K_i(t_k)v_i(t_k)]\\&~~~~~~~~~~~~~~~~~~~[(I-K_i(t_k)C_i)(x_i(t_k)-\hat{x}_i(t_k|t_{k-1}))-K_i(t_k)v_i(t_k)]^T\}\\&~~~~~~~~~~=(I-K_i(t_k)C_i)E\{e_i(t_k|t_{k-1})e_i^T(k|t_{k-1})\}(I-K_i(t_k)C_i)^T+K_i(t_k)R_iK_i^T(t_k)\\&~~~~~~~~~~=(I-K_i(t_k)C_i)P_i(t_k|t_{k-1})(I-K_i(t_k)C_i)^T+K_i(t_k)R_iK_i^T(t_k).\\ \end{aligned} \end{aligned}$$

(12.39)

Because the diagonal element of $P_i(t_k)$ is the square of the estimation error, the trace of the matrix (expressed by $T[\cdot ]$) is the mean square deviation, that is,

$$\begin{aligned} \begin{aligned}&T[P_i(t_k)]=T[P_i(t_k|t_{k-1})]-2T[K_i(t_k)C_iP_i(t_k|t_{k-1})]\\&~~~~~~~~~~+T[K_i(t_k)(C_iP_i(t_k|t_{k-1})C_i^T+R_i)K_i^T(t_k)]. \end{aligned} \end{aligned}$$

(12.40)

To make the estimated value closer to the real value, the trace above must be as small as possible. Therefore, it is necessary to obtain an appropriate Kalman gain $K_i(t_k)$ to minimize the trace. The implication is to make the partial derivative of the trace to $K_i(t_k)$ is zero, that is,

$$\begin{aligned} \frac{dT[P_i(t_k)]}{dK_i(t_k)}=-2(C_iP_i(t_k|t_{k-1}))^T+2K_i(t_k)(C_iP_i(t_k|t_{k-1})C_i^T+R_i)=0. \end{aligned}$$

(12.41)

Furthermore, we have (12.32) and (12.34). The Taylor expansion of $x_i(t_k)$ in Eq. (12.35) at $(\hat{x}_i(t_{k}), \hat{X}_i(t_{k-1}))$:

$$\begin{aligned} \begin{aligned}&x_i(t_k) = f_i(\hat{x}_i(t_{k-1}),\hat{X}_i(t_{k-1}),u_i(t_{k-1}), U_i(t_{k-1}))\\&~~~~~~~~~~~~+A_i(t_{k-1})(x_i(t_{k-1})-\hat{x}_i(t_{k-1}))+w_i(t_{k-1}), \end{aligned} \end{aligned}$$

(12.42)

where $A_i(t_{k-1})$ is the Jacobian of $f_{(i)}$ with respect to $x_{(i)}$ at time $t_{k-1}$. Discretize $\hat{x}_i (t_k|t_{k-1})$ in Eq. (12.36):

$$\begin{aligned} \begin{aligned}&\hat{x}_i (t_k|t_{k-1})=f_i(\hat{x}_i(t_{k-1}),\hat{X}_i(t_{k-1}),u_i(t_{k-1}), U_i(t_{k-1})). \end{aligned} \end{aligned}$$

(12.43)

So the prediction error and its mathematical expectation are

$$\begin{aligned} \begin{aligned} e_i(t_k|t_{k-1})&=x_i(t_k)-\hat{x}_i(t_k|t_{k-1})\\&=A_i(t_{k-1})(x_i(t_{k-1})-\hat{x}_i(t_{k-1}))+w_i(t_{k-1}), \end{aligned} \end{aligned}$$

(12.44)

$$\begin{aligned} \begin{aligned}&E\{e_i(t_k|t_{k-1})e_i^T(t_k|t_{k-1})\}\\ =&E\{[A_i(t_{k-1})(x_i(t_{k-1})-\hat{x}_i(t_{k-1}))+w_i(t_{k-1})]\\&[A_i(t_{k-1})(x_i(t_{k-1})-\hat{x}_i(t_{k-1}))+w_i(t_{k-1})]^T\}\\ =&A_i(t_{k-1})E\{[x_i(t_{k-1})-\hat{x}_i(t_{k-1})][x_i(t_{k-1})-\hat{x}_i(t_{k-1})]^T)\}A_i^T(t_{k-1})+Q_i. \end{aligned} \end{aligned}$$

(12.45)

To this end, we get (12.31).

An algorithm is adopted for distributed EKFs to work collaboratively in this work. It is assumed that each local filter shares the state estimates with its interacting subsystem for each sampling periods. The resilient distributed EKF algorithm is implemented:

• Step 1: At $t_0 = 0$, initialize $x_i(0), P_i(t_0), i = 1,\ldots ,p$.

• Step 2: For time $t_k>0$, each local estimator i receives the measured output of the subsystem i, i.e., $y_i(t_k)$.

• Step 3: Each distributed EKF receives the state estimates of the interacting subsystems at the time $t_{k-1}$.

• Step 4: Check the communication network with (12.28) and set $\hat{X}_i(t_{k-1})$ using (12.29).

• Step 5: Based on the latest $\hat{X}_{(i)}(t_{ k-1})$, each EKF i calculates the state estimates $\hat{x}_i(t_k), i = 1,\ldots ,p$. The estimate of the entire system state is $\hat{x}(t_k)= \begin{bmatrix}\hat{x}_1(t_k)^T&\ldots&\hat{x}_p(t_k)^T\end{bmatrix}^T$.

• Step 6: At $k=k+1$, go to Step 2.

12.5 Simulation

In this section, the proposed subsystem decomposition method is validated by decomposing the subsystem model of WWTP system. The resilient distributed EKF under different subsystem methods is tested to show the efficiency of improving the resiliency of the system.

12.5.1 Subsystem Decomposition

In this section, the WWTP system will be divided into two subsystems for distributed state estimation. The input variables are $u=[Q_i, Q_{int}, K_{La3}, K_{La4}, K_{La5}, Q_r, Q_w]^T$. We use the initial conditions shown in Tables 12.1 and 12.2 and $u_s=[18446, 18446, 55338, 240, 240, 84, 18446, 385]^T$ as the working point $(x_s,u_s)$.

Table 12.1 Initial condition of the biological reactor

Table 12.2 Initial condition of the secondary clarifier

Table 12.3 Decomposition of WWTP

Two subsystem models are shown in Table 12.3, in which Decomposition 1 is directly divided according to the physical structure (Zeng et al. 2016) and Decomposition 2 is obtained by the proposed method in this work. As shown in Table 12.3, considering the circulating f low from the secondary clarifier to the first anoxic reactor, Decomposition 1 divides the secondary clarifier and and anoxic section (i.e., reactor 1 and reactor 2) into a subsystem and aerated section (i.e., reactor 3, reactor 4, and reactor 5) into another subsystem. It can be seen that when divided by structure, a reactor is considered as a whole, and the connections between internal states are not considered. While Decomposition 2 considers both the number and strength of connections between internal variables. In Decomposition 2, Reactor 1, concentration of $S_{ALK}$ in reactors 2–5, concentration of X, $S_I$, and $S_{ALK}$ in the secondary clarifier are configured as subsystem 1 and subsystem 2 includes the concentration of compounds except $S_{ALK}$ in reactors 2–5, concentration of $S_S$, $S_O$, $S_{NO}$, $S_{NH}$, and $S_{ND}$ in the secondary clarifier. It can be seen that the concentration of $S_{ALK}$ in all five reactors is taken out alone and put into subsystem 1 because it has little connection with other compounds in the same reactor.

12.5.2 Resilient Distributed State Estimator Design

WWTP is considered critical infrastructure and their resiliency is vital. In this section, the proposed subsystem decomposition and resilient distributed state estimation scheme is tested in the WWTP system to show the improvement of the resiliency compared to a centralized scheme applied to the whole system. We investigate the resiliency analysis under the storm and rain conditions, in which the unreliable communication networks are simultaneously considered.

The random process disturbance of the state equation and the noise in measurement are generated by the normal distribution values with mean value of zero and standard deviation of $w_Qx_0$ and $w_Ry_0$, respectively, where $w_Q$ and $w_R$ are parameters and the symbol $x_0$ represents the initial condition shown in Tables 12.1 and 12.2, and $y_0$ can be calculated by $y_0 = Cx_0$.The initial guess in different estimation schemes is set to be $1.1x_0$. The parameters used in the centralized EKF are $Q = diag ((w_Qx_0)^2)$, $R = diag ((w_Ry_0)^2)$, and $P(0)= Q = diag ((w_Qx_0)^2)$, where diag(V) is a diagonal matrix whose diagonal elements are elements of vector v. The parameters used in the distributed EKF are $Q_i = diag ((w_Qx_{0,i})^2)$, $R_i = diag ((w_Ry_{0,i})^2)$, and $P_i(0)= Q_i = diag ((w_Qx_{0,i})^2)$, where $x_{0,i}$ and $y_{0,i}$ are the corresponding portion in $x_0$ and $y_0$ to subsystem i.

In order to compare the performance of different state estimation schemes, we calculate the error. In order to explain the different magnitude of estimation error in different states, the error of each state is normalized according to the maximum estimation error of all estimation schemes. The Euclidean norm of the normalized estimation error is defined as follows:

$$\begin{aligned} e(t_k)=\sqrt{\sum _{i=1}^{145}(e_i(t_k))^2}, \end{aligned}$$

(12.46)

where $e(t_k)$ is the normalized error of 145 states at time instant $t_k$, and $e_i(t_k)$ is the normalized error of state i, $i = 1, 2,\ldots ,145$, defined as follows:

$$\begin{aligned} e_i(t_k)=\frac{\hat{x}_i(t_k)-x_i(t_k)}{max(\hat{x}_i-x_i)}, \end{aligned}$$

(12.47)

where the maximum error of given state i is the maximum error of state i in EKF and distributed EKF methods. This means that the error of each state is normalized based on the maximum estimation error given by two different schemes. The average and maximum value of the normalized estimation error can be defined as follows:

$$\begin{aligned}&Mean \vert e \vert =\frac{1}{K}\sum _{k=1}^K(e(t_k))\end{aligned}$$

(12.48a)

$$\begin{aligned}&Max \vert e \vert = max\{e(t_1),e(t_1),\cdots ,e(t_k)\}, \end{aligned}$$

(12.48b)

where K is the total number of samples over the simulation period.

Rain conditions. We adjust $w_Q$ and $w_R$ to test the performance under different interference and noise conditions. The average and maximum values of the estimation error calculated by the three schemes are shown in Table 12.4. Figure 12.3 shows the actual process state trajectories and the estimates given by the centralized EKF and the distributed EKF (see Zhang et al. 2019) under the Decomposition 1 and the Decomposition 2, and Fig. 12.4 shows the trajectories of the Euclidean norms of the normalized estimation errors given by the three different schemes when $w_Q=w_R=0.1$.

Fig. 12.3

Trajectories of the actual process state (black solid lines) and the estimates given by the centralized EKF (green dashed lines) and the distributed EKF under the Decomposition 1 (red solid lines)and the Decomposition 2 (blue dash-dotted lines) of reactor 5 under rain conditions

Fig. 12.4

Trajectories of the Euclidean norm of normalized estimation errors given by the EKF (green dashed lines) and the distributed EKF under the Decomposition 1 (red solid lines)and the Decomposition 2 (blue dash-dotted lines) under rain conditions

Table 12.4 Performance comparison for different schemes under rain conditions

Simulation results in Table 12.4 show that the average estimation error of distributed EKF under Decomposition 2 is always smaller than that of the distributed EKF under Decomposition 1, which shows that the proposed decomposition method makes the internal connection of subsystems closer, which can reduce the state estimation error under the same state estimation scheme. It also shows that when the noise is greater, the distributed EKF may have better performance. It is verified that the proposed subsystem decomposition with weak inter-subsystem interactions can improve the resiliency of the system when applying the distributed state estimation.

Furthermore, the condition with unreliable communication network is tested to show the resiliency of the system under the resilient distributed state estimator. The exchanged estimated stated is set as $\hat{X}_i(t)=\hat{X}_i(t)+0.5x_{init}$ during $t=3(\mathrm{days})$ to $t=3.05(\mathrm{days})$. This means that the exchange information could be attacked or modified. The proposed resilient distributed state estimator is used to construct the states under the reliable communication network. Trajectories of the actual process state and the resilient DEKF under the Decomposition 2 when $w_Q=w_R=0.1$ are shown in Fig. 12.5. The trajectories of the Euclidean norm of normalized estimation errors given by the Distributed EKF and the resilient distributed EKF under the Decomposition 2 are shown in Fig. 12.6. The results show that the proposed resilient distributed state estimation scheme can improve the resiliency of the system with unreliable communication network.

Fig. 12.5

Trajectories of the actual process state (black solid lines) and the DEKF (red dashed lines) and the resilient DEKF (blue solid lines) under the Decomposition 2 of reactor 1 under rain conditions with unreliable communication network $\hat{X}_i(t)=\hat{X}_i(t)+0.5x_{init}$ during $t=3(\mathrm{days})$ to $t=3.05(\mathrm{days})$

Fig. 12.6

Trajectories of the Euclidean norm of normalized estimation errors given by the DEKF (red dashed lines) and the resilient DEKF (blue solid lines) under the Decomposition 2 under rain conditions with unreliable communication network $\hat{X}_i(t)=\hat{X}_i(t)+0.5x_{init}$ during $t=3(\mathrm{days})$ to $t=3.05(\mathrm{days})$

Storm conditions. We further test the resilient distributed EKF under storm conditions. The average and maximum value of the estimation error calculated by the three schemes are shown in Table 12.5. Figure 12.7 shows the actual process state trajectories and the estimates given by the centralized EKF and the distributed EKF under the Decomposition 1 and the Decomposition 2 and Fig. 12.8 shows the trajectories of the Euclidean norms of the normalized estimation errors given by the three different schemes when $w_Q=w_R=0.1$.

Fig. 12.7

Trajectories of the actual state (black solid lines) and the estimated states given by the centralized EKF (green dashed lines) and the distributed EKF under the Decomposition 1 (red solid lines) and the Decomposition 2 (blue dash-dotted lines) of reactor 5 under storm conditions

Fig. 12.8

Trajectories of the Euclidean norm of normalized estimation errors given by the EKF (green dashed lines) and the distributed EKF under the Decomposition 1 (red solid lines)and the Decomposition 2 (blue dash-dotted lines) under storm conditions

Table 12.5 Performance comparison for different schemes under storm conditions

Simulation results in Table 12.5 show that the average estimation error of distributed EKF under Decomposition 2 is always smaller than that of the distributed EKF under Decomposition 1, which shows that the proposed decomposition method makes the internal connection of subsystems closer, which can reduce the state estimation error under the same state estimation scheme. It confirms that the proposed subsystem decomposition with weak inter-subsystem interactions can improve the resiliency of the system when applying the distributed state estimation.

Similarly, the condition with unreliable communication network is tested to show the resiliency of the system under the storm condition. The exchanged estimated stated is set as $\hat{X}_i(t)=\hat{X}_i(t)+0.5x_{init}$ during $t=3(\mathrm{days})$ to $t=3.05(\mathrm{days})$. Trajectories of the actual process state and the resilient DEKF under the Decomposition 2 when $w_Q=w_R=0.1$ are shown in Fig. 12.9. The trajectories of the Euclidean norm of normalized estimation errors are shown in Fig. 12.10. The results confirm that the proposed resilient distributed state estimation scheme can improve the resiliency of the system with unreliable communication network.

Fig. 12.9

Trajectories of the actual process state (black solid lines) and the DEKF (red dashed lines) and the resilient DEKF (blue solid lines) of reactor 1 under storm conditions with communicate attack which set $\hat{X}_i(t)=\hat{X}_i(t)+0.5x_{init}$, $t=3-3.05(\mathrm{days})$

Fig. 12.10

Trajectories of the Euclidean norm of normalized estimation errors given by the DEKF (red dashed lines) and the resilient DEKF (blue solid lines) under the Decomposition 2 under storm conditions with communicate attack which set $\hat{X}_i(t)=\hat{X}_i(t)+0.5x_{init}$, $t=3-3.05(\mathrm{days})$

12.6 Conclusion

In this work, an optimal subsystem decomposition algorithm is proposed based on the community discovery algorithm with weighted network graph and is applied to a benchmark WWTP system. A resilient distributed state estimator is designed and carried out under the subsystem models which are divided by the physical structure and the subsystem model obtained using the proposed decomposition method. The results show that the subsystem decomposition and distributed state estimation scheme improves the resiliency of the system, compared to a centralized scheme applied to the whole system.