Abstract
Key dependent message (KDM) security is a security notion that guarantees confidentiality of communication even if secret keys are encrypted. KDM security has found a number of applications in practical situations such as hard-disk encryption systems, anonymous credentials, and bootstrapping of fully homomorphic encryption. Recently, it also found an application in quantum delegation protocols as shown by Zhang (TCC 2019).
In this work, we investigate the KDM security of existing practical public-key encryption (PKE) schemes proposed in the quantum random oracle model (QROM). Concretely, we study a PKE scheme whose KEM is constructed by using Fujisaki-Okamoto (FO) transformations in the QROM. FO transformations are applied to IND-CPA secure PKE schemes and yield IND-CCA secure key encapsulation mechanisms (KEM). Then, we show the following results.
-
We can reduce the KDM-CPA security in the QROM of a PKE scheme whose KEM is derived from any of the FO transformations proposed by Hofheinz et al. (TCC 2017) to the IND-CPA security of the underlying PKE scheme, without square root security loss. For this result, we use one-time-pad (OTP) as DEM to convert KEM into PKE.
-
We can reduce the KDM-CCA security in the QROM of a PKE scheme whose KEM is derived from a single variant of the FO transformation proposed by Hofheinz et al. (TCC 2017) to the IND-CPA security of the underlying PKE scheme, without square root security loss. For this result, we use OTP-then-MAC construction as DEM to convert KEM into PKE. Also, we require a mild injectivity assumption for the underlying IND-CPA secure PKE scheme.
In order to avoid square root security loss, we use a double-sided one-way to hiding (O2H) lemma proposed by Kuchta et al. (EUROCRYPT 2020). In the context of KDM security, there is a technical hurdle for using double-sided O2H lemma due to the circularity issue. Our main technical contribution is to overcome the hurdle.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
1.1 Background
Post-quantum security is emerging as a de facto standard since quantum technology has been making rapid progress. In particular, since the NIST post-quantum cryptography standardization project started, IND-CCA security in the quantum random oracle model (QROM) have been extensively studied to design practical and post-quantum secure public-key encryption (PKE) [BHH+19, AHU19, HKSU20, JZM19a, HHK17, JZC+18, SXY18, TU16, KSS+20]. IND-CCA [RS92, DDN00] is the gold standard security notion for PKE since chosen-ciphertext attacks are realistic in many practical applications [Ble98]. The random oracle model (ROM) [BR93] is an idealized model where hash functions are modeled as ideal random functions in security proofs. This idealized model helps us to design extremely efficient cryptographic primitives. In the QROM [BDF+11], a random oracle query is a superposition query since adversaries are modeled as quantum polynomial-time algorithms and hash functions are locally computable.
Although IND-CCA is suitable for many practical applications, a stronger security goal than standard confidentiality is required in some settings. Key-dependent message (KDM) security [BRS03] is such an example. KDM security guarantees that adversaries cannot distinguish encryption of \(f_0(\mathsf {sk})\) from encryption of \(f_1(\mathsf {sk})\) where \(\mathsf {sk}\) is a secret key and \(f_0,f_1\) are arbitrary functions. The KDM situation is realistic in hard disk encryption systems like BitLocker [BHHO08] and bootstrapping fully homomorphic encryption [Gen09]. We also use KDM secure encryption as a building block of cryptographic primitives and protocols such as anonymous credentials [CL01]. In particular, (non-adaptive) KDM secure secret-key encryption (SKE) against quantum adversaries is used to achieve delegation of quantum computation [Zha19]. The KDM situation also naturally arises in formal verification of cryptographic protocols [AR02].
Thus, a natural question is:
Can we achieve practical KDM-CPA/CCA secure PKE in the QROM?
or
Do existing practical IND-CPA/CCA secure PKE satisfy KDM security in the QROM?
The difficulty of this question depends on what level of security and efficiency we achieve.
Security analysis in the QROM usually deviates from one in the classical ROM. One significant issue is that, in the QROM, we cannot directly use the observability of the classical ROM, which says reduction algorithms can observe input points where adversaries make random oracle queries. In the QROM, reduction algorithms need to measure superposition queries to observe random oracle queries, but this prevents reduction since adversaries can detect measurement. Superposition queries also prevent us from straightforwardly applying the adaptive programming technique. These problems make it more challenging to achieve CCA and KDM security in the QROM since each property is one of the crucial properties in the proofs for CCA and KDM [FO13, KMHT16]. New techniques have been proposed to solve the security-proof problems in the QROM. The one-way to hiding (O2H) lemma [Unr15] and its variants [AHU19, BHH+19, KSS+20] are the most well-known useful tools to solve the problem above and achieve secure encryption in the QROM.
Roughly speaking, the (original) O2H lemma is as follows. A quantum distinguisher
 is given oracle access to an oracle \(\mathcal {O}\), which is either a random function \(H: X \rightarrow Y\) or \(G:X \rightarrow Y\) such that \(\forall x \notin S\), \(H(x)=G(x)\). Let z be a random classical string or quantum state ((G, H, S, z) may have an arbitrary distribution). Let
is given oracle access to an oracle \(\mathcal {O}\), which is either a random function \(H: X \rightarrow Y\) or \(G:X \rightarrow Y\) such that \(\forall x \notin S\), \(H(x)=G(x)\). Let z be a random classical string or quantum state ((G, H, S, z) may have an arbitrary distribution). Let
 be a quantum algorithm that is given input z and oracle access to H, measures
be a quantum algorithm that is given input z and oracle access to H, measures
 ’s query, and outputs the result. The distinguishing advantage of
’s query, and outputs the result. The distinguishing advantage of
 ,
,
 , is bounded by the square root of the search advantage of
, is bounded by the square root of the search advantage of
 ,
,
 , that finds an element in S.Footnote 1 All O2H lemmas except the variant by Kuchta, Sakzad, Stehlé, Steinfeld, and Sun [KSS+20] incur a square root security loss. A square root security loss significantly degrades the performance of cryptographic primitives since we need to use much longer security parameters for building blocks to guarantee a reasonable security level, say, 128-bit security.Footnote 2 Thus, to achieve practical KDM secure PKE schemes, we should avoid a square root loss. When we focus on tight security, both security advantages and the running time of reductions are crucial factors. However, in most PKE schemes (and all our schemes), the overhead of running time of reductions is only additive and is not a dominant factor. Thus, we focus on security loss.
, that finds an element in S.Footnote 1 All O2H lemmas except the variant by Kuchta, Sakzad, Stehlé, Steinfeld, and Sun [KSS+20] incur a square root security loss. A square root security loss significantly degrades the performance of cryptographic primitives since we need to use much longer security parameters for building blocks to guarantee a reasonable security level, say, 128-bit security.Footnote 2 Thus, to achieve practical KDM secure PKE schemes, we should avoid a square root loss. When we focus on tight security, both security advantages and the running time of reductions are crucial factors. However, in most PKE schemes (and all our schemes), the overhead of running time of reductions is only additive and is not a dominant factor. Thus, we focus on security loss.
At first glance, the O2H lemma by Kuchta et al. [KSS+20] (denoted by O2H with MRM) seems to immediately answer our question since it does not incur a square root security loss. However, this is not the case. O2H with MRM is a variation of the double-sided O2H lemma by Bindel, Hamburg, Hövelmanns, Hülsing, and Persichetti [BHH+19], where
 is given oracle access to both H and G. Thus, in O2H with MRM,
is given oracle access to both H and G. Thus, in O2H with MRM,
 is given oracle access to a random oracle H and a modified random oracle G. This is not an issue for proving IND-CPA/CCA security. However, it is a serious issue for proving KDM security because correlated information about secret keys could remain in the modified random oracle G in known proofs for KDM in the classical ROM. See Sect. 1.4 for the detail. Kuchta et al. [KSS+20] left relaxing their double-sided O2H with MRM to a single-sided variant as an open question. However, that question remains elusive. In the KDM setting, we cannot directly apply a double-sided type O2H lemma. Achieving KDM security with a double-sided O2H lemma is of independent interest. Thus, our question is more precisely described as follows.
is given oracle access to a random oracle H and a modified random oracle G. This is not an issue for proving IND-CPA/CCA security. However, it is a serious issue for proving KDM security because correlated information about secret keys could remain in the modified random oracle G in known proofs for KDM in the classical ROM. See Sect. 1.4 for the detail. Kuchta et al. [KSS+20] left relaxing their double-sided O2H with MRM to a single-sided variant as an open question. However, that question remains elusive. In the KDM setting, we cannot directly apply a double-sided type O2H lemma. Achieving KDM security with a double-sided O2H lemma is of independent interest. Thus, our question is more precisely described as follows.
Can we achieve practical KDM-CPA/CCA secure PKE without a square root security loss in the QROM?
or
Do existing practical IND-CPA/CCA secure PKE satisfy KDM security without a square root security loss in the QROM?
1.2 Our Result
In this work, we affirmatively answer the question above. We prove the following.
-
We can obtain KDM-CPA secure PKE without a square root security loss by applying a Fujisaki-Okamoto transformation (denoted by FO) [FO13, HHK17] to IND-CPA secure PKE and combining one-time pad (OTP) as DEM.
-
We can obtain KDM-CCA secure PKE without a square root security loss by applying an FO [FO13, BHH+19] to IND-CPA secure PKE and combining OTP and strong one-time MACFootnote 3 (that is, OTP-then-MAC) as DEM.
Note that our goal is PKE (not KEM) since we can consider the KDM setting only in PKE. We need OTP to achieve PKE since FO yields KEM [FO13, HHK17]. Our results are extremely versatile since we can convert IND-CPA secure PKE to KDM-CPA/CCA secure PKE by the well-known general transformations. FO yields practical KEM/PKE schemes and is employed in many candidates of the NIST PQC standardization to achieve CCA security. Note that we do not need the perfect correctness of the building block PKE. However, for the result on KDM-CCA secure PKE, we require that a derandomized version of the building block PKE is injective as in the CCA schemes in some previous works [BHH+19, KSS+20]. Bindel et al. argue that injectivity is commonly satisfied by many practical IND-CPA secure lattice based schemes [BHH+19]. We also note that we use PKE in the multi-user setting [BBM00] as the building block PKE in the transformation since the KDM setting is the multi-user setting by default.Footnote 4
To explain our result more precisely, we recall that an FO can be decomposed into two transformations \(\mathsf {T}\) and \(\mathsf {U}\). This was first observed by Hofheinz, Hövelmanns, and Kiltz [HHK17]. In this work, we adopt variants of \(\mathsf {T}\) and \(\mathsf {U}\) defined by Bindel et al. [BHH+19]. The only difference between the transformations by Hofheinz et al. and those by Bindel et al. is that the validity check by encryption in the decryption algorithm is performed as a part of \(\mathsf {T}\) in the former while it is performed as a part of \(\mathsf {U}\) in the latter. Thus, the resulting FO is the same regardless of which definitions of \(\mathsf {T}\) and \(\mathsf {U}\) we use.
\(\mathsf {T}\) transformation transforms an IND-CPA secure PKE scheme into an OW-CPA secure deterministic PKE scheme. \(\mathsf {U}\) transformation transforms an OW-CPA secure deterministic PKE scheme into an IND-CCA secure KEM. Regarding \(\mathsf {U}\), there are six variants, \(\mathsf {U}^{\bot }\), \(\mathsf {U}^{\not \bot }\), \(\mathsf {U}^{\bot ,\mathtt {keyconf}}\), \(\mathsf {U}^{\bot }_{m}\), \(\mathsf {U}^{\not \bot }_m\), and \(\mathsf {U}^{\bot ,\mathtt {keyconf}}_m\). Here, \(\bot \) and \(\not \perp \) mean explicit and implicit rejection in decryption, respectively, and no subscript and subscript m mean a hash function takes a ciphertext as a part of the input or not. Superscript \(\mathtt {keyconf}\) (key confirmation) means that we add a hash value of a plaintext to a ciphertext and check the hash value in decryption. Bindel et al. [BHH+19] prove that \(\mathsf {U}^{\bot }\), \(\mathsf {U}^{\not \bot }\), and \(\mathsf {U}^{\bot ,\mathtt {keyconf}}\) yield IND-CCA KEM if and only if \(\mathsf {U}^{\bot }_{m}\), \(\mathsf {U}^{\not \bot }_m\), and \(\mathsf {U}^{\bot ,\mathtt {keyconf}}_m\) yield IND-CCA KEM, respectively. It does not matter whether a hash function takes a ciphertext as the input or not. This is also the case in the context of KDM security since the prove can be done via simple mappings between random functions. Thus, in this work, we focus on \(\mathsf {U}^{\bot }_{m}\), \(\mathsf {U}^{\not \bot }_m\), and \(\mathsf {U}^{\bot ,\mathtt {keyconf}}_m\).
To solve the correlated information problem above, we introduce a new security notion called seed-dependent message one-wayness against related seed attacks (SDM-OW-RSA). This notion is a technical contribution and plays a crucial role in this work (defined in Sect. 2.3). Then, we show that if we apply the \(\mathsf {U}^{\bot }_{m}\) transformation to SDM-OW-RSA deterministic PKE, the resulting scheme is KDM-CPA secure by combining OTP as DEM. We also show that if we apply \(\mathsf {U}^{\bot ,\mathtt {keyconf}}_m\) to SDM-OW-RSA secure deterministic PKE with injectivity, the resulting scheme is KDM-CCA secure by combining OTP-then-MAC as DEM. Although we need O2H with MRM in this part to avoid a square root security loss, we can overcome the double-sided oracle issue due to SDM-OW-RSA security.
In order to complete the proof for the KDM security of FO transformations, we go to the following path. We first introduce a variant of \(\mathsf {T}\) that we call \(\mathsf {T}\) transformation with hash key generation \(\mathsf {T}_{\mathtt {HKG}}\), and show that if we apply \(\mathsf {T}_{\mathtt {HKG}}\) to IND-CPA PKE, the resulting deterministic PKE scheme satisfies SDM-OW-RSA without square root security loss. Combined with the above, we see that \(\mathsf {U}^{\bot }_{m}\) (resp. \(\mathsf {U}^{\bot ,\mathtt {keyconf}}_m\)) together with \(\mathsf {T}_{\mathtt {HKG}}\) can be used to obtain a KDM-CPA (resp. KDM-CCA) secure PKE scheme from an IND-CPA secure PKE scheme without square root loss. Finally, we show that \(\mathsf {T}_{\mathtt {HKG}}\) in those constructions can be replaced with \(\mathsf {T}\), thus prove the KDM security of FO transformations.
Although we omit in this paper, we can see that we can prove the KDM-CPA security without a square root security loss even if we use \(\mathsf {U}^{\not \bot }_m\) instead of \(\mathsf {U}^{\bot }_{m}\). Interestingly, if we use \(\mathsf {U}^{\not \bot }_m\) instead of \(\mathsf {U}^{\bot ,\mathtt {keyconf}}_m\), it is not clear whether we can prove the KDM-CCA security without a square root loss. In the IND-CCA case, \(\mathsf {U}^{\not \bot }_m\) provides us with IND-CCA security without a square root security loss [KSS+20, BHH+19]. See Sect. 1.4 for the detail. We summarize these results in Table 1.
1.3 Related Work
Our work is the first study on KDM secure PKE in the QROM. Our work also focuses on tighter reductions. Zhang constructs a non-adaptive KDM-CPA SKE scheme in the QROM to achieve delegation of quantum computation [Zha19].
Backes, Dürmuth, and Unruh [BDU08] study the KDM security of the OAEP transformation [BR95] in the classical ROM. They prove that OAEP is KDM-secure in the classical ROM if the underlying trapdoor permutation is partial-domain one-way. Note that there is no post-quantum secure trapdoor permutation so far. Davies and Stam [DS14] study the KDM security in the KEM/DEM framework. They prove that if a key derivation function (KDF) is used in between the KEM and DEM part and the KDF function is modelled as a classical random oracle, the resulting PKE scheme is KDM-secure. See the reference for security requirements. Kitagawa, Matsuda, Hanaoka, and Tanaka [KMHT16] prove that the FO transformation [FO13] satisfies KDM-CCA security in the classical ROM.Footnote 5 These works studied KDM security in the classical ROM basically prove KDM security by eliminating key dependency of plaintexts by random oracle programming.
We also briefly introduce previous works on IND-CCA secure PKE/KEM in the QROM. Let \(\epsilon \) and \(\epsilon _\mathsf {bb}\) be the advantages of IND-CCA PKE/KEM and the building block, respectively. Let \(q_H\) be the number of random oracle queries (and we set \(d_H := q_H\) for simplicity). Below, we omit “IND-CCA” and “in the QROM” since all results are about them. We also ignore the differences between FO and FO variants.
Boneh et al. [BDF+11] use a KEM variant of Bellare-Rogaway transformation [BR93] to obtain their KEM from trapdoor functions and \(\epsilon \approx q_H \sqrt{\epsilon _\mathsf {bb}}\). Targhi and Unruh [TU16] use FO to obtain their PKE from OW-CPA PKE and \(\epsilon \approx q_H^{1.5} \root 4 \of {\epsilon _\mathsf {bb}}\). They also use an OAEP variant to obtain their PKE from partial domain trapdoor injective OWFs and \(\epsilon \approx {\mathrm {poly}}(q_H) \root 8 \of {\epsilon _\mathsf {bb}}\). Hofheinz et al. [HHK17] present modular analysis for FO, but their KEM does not improve the construction by Targhi and Unruh. Saito et al. [SXY18] use FO to obtain their KEM from disjoint simulatable deterministic PKE and \(\epsilon \approx \epsilon _\mathsf {bb}\). They also obtain their KEM from IND-CPA PKE with perfect correctness and \(\epsilon \approx q_H \sqrt{\epsilon _\mathsf {bb}}\). Jiang, Zhang, Chen, Wang, and Ma [JZC+18] use FO and obtain their KEM from OW-CPA PKE and \(\epsilon \approx q_H \sqrt{\epsilon _\mathsf {bb}}\). Jiang, Zhang, and Ma [JZM19a] achieve the same bound as those by Jiang et al. [JZC+18] and Saito et al. [SXY18] by using the same assumptions and FO with explicit rejection. Ambainis, Hamburg, and Unruh [AHU19] prove an improved variant of the original O2H lemma (semi-classical O2H lemma) and its bound is
 (the query loss is improved). The semi-classical O2H lemma leads to KEM with improved bounds in the query part [AHU19, HKSU20, JZM19b]. Bindel et al. [BHH+19] prove the double-sided O2H lemma whose bound is
(the query loss is improved). The semi-classical O2H lemma leads to KEM with improved bounds in the query part [AHU19, HKSU20, JZM19b]. Bindel et al. [BHH+19] prove the double-sided O2H lemma whose bound is
 . They use FO to obtain their KEM from IND-CPA PKE with injectivity, but its bound is essentially the same as that of schemes using the semi-classical O2H lemma. Kuchta et al. [KSS+20] prove O2H with MRM and obtain their KEM from IND-CPA PKE with injectivity via FO, and \(\epsilon \approx q_H^2\epsilon _\mathsf {bb}\).
. They use FO to obtain their KEM from IND-CPA PKE with injectivity, but its bound is essentially the same as that of schemes using the semi-classical O2H lemma. Kuchta et al. [KSS+20] prove O2H with MRM and obtain their KEM from IND-CPA PKE with injectivity via FO, and \(\epsilon \approx q_H^2\epsilon _\mathsf {bb}\).
1.4 Technical Overview
We provide the technical overview of this work. Our goal here is to show that the KDM security in the QROM of the PKE scheme \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}(\mathsf {T}(\mathsf {PKE},G_{\mathtt {enc}}),H)\)Footnote 6 can be reduced to the IND-CPA security of the underlying \(\mathsf {PKE}\) without square root security loss. Roughly speaking, the difficulty is that in the setting of KDM security, double-sided O2H lemmas [BHH+19, KSS+20] cannot be applied straightforwardly, which is currently the only tool that enables us to circumvent square root security loss in the QROM.
We first explain how we circumvent square root security loss and prove the KDM security in the QROM of the PKE scheme \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}=\mathsf {U}^{\bot }_{m,\mathtt {OTP}}(\mathsf {d}\mathsf {PKE},H)\) whose ciphertext is described as
where \(\mathsf {dEnc}\) is the encryption algorithm of a deterministic PKE scheme \(\mathsf {d}\mathsf {PKE}\) with the message space \(\mathcal {M}\), \(s\leftarrow \mathcal {M}\), and H is a random oracle. We identify that the KDM security in the QROM of \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}\) can be reduced without square root loss to the security notion of \(\mathsf {d}\mathsf {PKE}\) that we call seed-dependent message one-wayness (SDM-OW security). Then, we explain that the SDM-OW security in the QROM of a tweaked version of \(\mathsf {T}=\mathsf {T}(\mathsf {PKE},G_{\mathtt {enc}})\) can be reduced to the IND-CPA security of the underlying PKE scheme \(\mathsf {PKE}\) without square root security loss. We call the tweaked version \(\mathsf {T}\) transformation with hash key generation \(\mathsf {T}_{\mathtt {HKG}}=\mathsf {T}_{\mathtt {HKG}}(\mathsf {PKE},(G_{\mathtt {kg}},G_{\mathtt {enc}}))\) where \(G_{\mathtt {kg}}\) and \(G_{\mathtt {enc}}\) are random oracles. From these facts, we see that the KDM security in the QROM of \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}(\mathsf {T}_{\mathtt {HKG}}(\mathsf {PKE},(G_{\mathtt {enc}},G_{\mathtt {kg}})),H)\) can be reduced to the IND-CPA security of \(\mathsf {PKE}\) without square root security loss. Finally, we state that the KDM security of \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}(\mathsf {T}(\mathsf {PKE},G_{\mathtt {enc}}),H)\) immediately follows from the KDM security of \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}(\mathsf {T}_{\mathtt {HKG}}(\mathsf {PKE},(G_{\mathtt {enc}},G_{\mathtt {kg}})),H)\).
Below, we start with how to prove the KDM security of \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}\) in the classical ROM. For simplicity, in this overview, we consider the following simplified KDM security. Given a ciphertext of \(f_{b}(\mathsf {sk})\), any adversary cannot predict b correctly better than random guessing, where \(b\leftarrow \{0,1\}\) is the challenge bit and \(f_{0}\) and \(f_{1}\) are any a-priori fixed two functions. The actual KDM security requires indistinguishability holds for multiple pairs of functions adaptively chosen by an adversary under multiple public and secret key pairs.
KDM Security of \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}\) in the Classical ROM. Let
 be an adversary.
be an adversary.
 is given the challenge ciphertext and the random oracle access, which are described as
is given the challenge ciphertext and the random oracle access, which are described as
We first make a conceptual change to the security game so that the challenge ciphertext and the random oracle are described as
where u is a uniformly chosen value independent of H and \(f_{b}(\mathsf {sk})\). We can confirm that this is a purely conceptual change since V behaves as a random function and the challenge ciphertext is computed as \((\mathsf {dEnc}(\mathsf {pk},s), V(s)\oplus f_{b}(\mathsf {sk}))=(\mathsf {dEnc}(\mathsf {pk},s),u)\). Therefore, it does not change
 ’s advantage. Then, we further change the security game so that
’s advantage. Then, we further change the security game so that
 gets access to H instead of V, but the challenge ciphertext is still generated using V. Thus, the challenge ciphertext is not changed from \((\mathsf {dEnc}(\mathsf {pk},s), u)\). In other words, except for the generation of the challenge ciphertext, we program the output value of the random oracle at point s from \(V(s)=u\oplus f_{b}(\mathsf {sk})\) into H(s). The view of
gets access to H instead of V, but the challenge ciphertext is still generated using V. Thus, the challenge ciphertext is not changed from \((\mathsf {dEnc}(\mathsf {pk},s), u)\). In other words, except for the generation of the challenge ciphertext, we program the output value of the random oracle at point s from \(V(s)=u\oplus f_{b}(\mathsf {sk})\) into H(s). The view of
 is now
is now
We see that in the final game, the challenge bit b is completely hidden from the view of
 , and thus
, and thus
 ’s advantage is 0. Therefore, we must estimate how much the advantage of
’s advantage is 0. Therefore, we must estimate how much the advantage of
 is changed by the above programming of the random oracle. From the difference lemmaFootnote 7, this can be bounded by the probability that
is changed by the above programming of the random oracle. From the difference lemmaFootnote 7, this can be bounded by the probability that
 queries s to H in the final security game. In the final game, information of \(f_{b}(\mathsf {sk})\) is completely eliminated from the view of
queries s to H in the final security game. In the final game, information of \(f_{b}(\mathsf {sk})\) is completely eliminated from the view of
 . Thus, we can use the security of \(\mathsf {d}\mathsf {PKE}\) in order to estimate the probability. Concretely, the probability is estimated by using the OW-CPA security of \(\mathsf {d}\mathsf {PKE}\). This completes the proof. Of course, square root security loss does not occur in this proof.
. Thus, we can use the security of \(\mathsf {d}\mathsf {PKE}\) in order to estimate the probability. Concretely, the probability is estimated by using the OW-CPA security of \(\mathsf {d}\mathsf {PKE}\). This completes the proof. Of course, square root security loss does not occur in this proof.
KDM Security of \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}\) in the QROM? When we try to prove KDM security of \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}\) in the QROM, we need a different tool from the difference lemma. This is because “the probability that
 queries s to H” is not well-defined in this case since
queries s to H” is not well-defined in this case since
 can make a query to the random oracle in super-position. In the QROM, in many cases, we can use one-way to hiding (O2H) lemma [Unr15] and its variants [AHU19, BHH+19, KSS+20] as drop-in replacements of the difference lemma in the security proof done in the classical ROM. Roughly speaking, the O2H lemma guarantees that there exists an extractor
can make a query to the random oracle in super-position. In the QROM, in many cases, we can use one-way to hiding (O2H) lemma [Unr15] and its variants [AHU19, BHH+19, KSS+20] as drop-in replacements of the difference lemma in the security proof done in the classical ROM. Roughly speaking, the O2H lemma guarantees that there exists an extractor
 such that the distinguishing gap caused by a programming of a quantumly-accessible random oracle can be bounded by the probability that
such that the distinguishing gap caused by a programming of a quantumly-accessible random oracle can be bounded by the probability that
 extracts the programmed point. O2H lemma is classified into two categories. The first one is a single-sided O2H lemma where
extracts the programmed point. O2H lemma is classified into two categories. The first one is a single-sided O2H lemma where
 gets access to either pre-programmed or post-programmed random oracles. The other one is a double-sided O2H lemma where
gets access to either pre-programmed or post-programmed random oracles. The other one is a double-sided O2H lemma where
 gets access to both of them. In order to circumvent the square root security loss, we currently need to use double-sided O2H lemma proposed in [KSS+20] called O2H with measure-rewind-measure (MRM) lemma.
gets access to both of them. In order to circumvent the square root security loss, we currently need to use double-sided O2H lemma proposed in [KSS+20] called O2H with measure-rewind-measure (MRM) lemma.
Suppose to prove KDM security of \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}\) in the QROM, we follow the same strategy as the case of the classical ROM (i.e., make a conceptual change and program V into H) and use O2H lemma instead of the difference lemma. Since our goal here is to prove the KDM security of \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}\) in the QROM without square root security loss, we use O2H lemma with MRM. By doing so, we can say that there exists a QPT extractor
 such that
such that

where \(z=(\mathsf {dEnc}(\mathsf {pk},s),u)\) and d is the query depth of
 to the random oracle.Footnote 8 Thus, if we can in turn bound the probability
to the random oracle.Footnote 8 Thus, if we can in turn bound the probability
 by using the security of the underlying \(\mathsf {d}\mathsf {PKE}\), we can complete the entire security proof. However, it turns out that it cannot be done straightforwardly using the OW-CPA security of \(\mathsf {d}\mathsf {PKE}\) as before. The reason is that since
by using the security of the underlying \(\mathsf {d}\mathsf {PKE}\), we can complete the entire security proof. However, it turns out that it cannot be done straightforwardly using the OW-CPA security of \(\mathsf {d}\mathsf {PKE}\) as before. The reason is that since
 has access to not only H but also V that has information of \(f_{b}(\mathsf {sk})\), it is not clear whether we can use the OW-CPA security of \(\mathsf {d}\mathsf {PKE}\). Recall that in the proof in the classical ROM case, when estimating “the probability that
has access to not only H but also V that has information of \(f_{b}(\mathsf {sk})\), it is not clear whether we can use the OW-CPA security of \(\mathsf {d}\mathsf {PKE}\). Recall that in the proof in the classical ROM case, when estimating “the probability that
 queries s to H” using the OW-CPA security of \(\mathsf {d}\mathsf {PKE}\), information of \(f_{b}(\mathsf {sk})\) is eliminated from the view of
queries s to H” using the OW-CPA security of \(\mathsf {d}\mathsf {PKE}\), information of \(f_{b}(\mathsf {sk})\) is eliminated from the view of
 since
since
 does not have access to V.
does not have access to V.
In summary, in the proof in the classical ROM, we can successfully reduce the KDM security of \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}\) to the OW-CPA security of \(\mathsf {d}\mathsf {PKE}\) by eliminating information of \(f_{b}(\mathsf {sk})\) using programming of the random oracle. However, in the case of the QROM, if we use O2H with MRM lemma, it seems difficult to eliminate the information of \(f_{b}(\mathsf {sk})\) by programming the random oracle. This is because we finally need to handle the extractor
 who gets access to both pre-programmed and post-programmed random oracles.
who gets access to both pre-programmed and post-programmed random oracles.
Note that even if V does not have information of \(f_{b}(\mathsf {sk})\), it might not be clear whether an OW-CPA adversary can simulate two random oracles V and H at the same time for
 . The reason is that the differing point s of the two random oracles is the solution of the OW-CPA game itself. This problem can be handled by using the correctness of \(\mathsf {d}\mathsf {PKE}\). As shown by [LW21], the correctness of \(\mathsf {d}\mathsf {PKE}\) implies that under a randomly generated key \((\mathsf {pk},\mathsf {sk})\), a randomly generated message m does not have a collision, that is another message \(m'\) such that \(\mathsf {dEnc}(\mathsf {pk},m)=\mathsf {dEnc}(\mathsf {pk},m')\), with overwhelming probability. If \(\mathsf {ct}=\mathsf {dEnc}(\mathsf {pk},s)\) has unique pre-image s, the OW-CPA adversary can check the condition “if \(x=s\)” by checking “if \(\mathsf {dEnc}(\mathsf {pk},x)=\mathsf {ct}\)” (in super-position), thus can simulate V and H at the same time if V does not have information of \(f_{b}(\mathsf {sk})\).
. The reason is that the differing point s of the two random oracles is the solution of the OW-CPA game itself. This problem can be handled by using the correctness of \(\mathsf {d}\mathsf {PKE}\). As shown by [LW21], the correctness of \(\mathsf {d}\mathsf {PKE}\) implies that under a randomly generated key \((\mathsf {pk},\mathsf {sk})\), a randomly generated message m does not have a collision, that is another message \(m'\) such that \(\mathsf {dEnc}(\mathsf {pk},m)=\mathsf {dEnc}(\mathsf {pk},m')\), with overwhelming probability. If \(\mathsf {ct}=\mathsf {dEnc}(\mathsf {pk},s)\) has unique pre-image s, the OW-CPA adversary can check the condition “if \(x=s\)” by checking “if \(\mathsf {dEnc}(\mathsf {pk},x)=\mathsf {ct}\)” (in super-position), thus can simulate V and H at the same time if V does not have information of \(f_{b}(\mathsf {sk})\).
Reduction to SDM-OW Security. Although it seems difficult to bound the probability
 using the OW-CPA security of \(\mathsf {d}\mathsf {PKE}\), we show that it can be bounded if \(\mathsf {d}\mathsf {PKE}\) satisfies SDM-OW security introduced in this work. Hereafter, we assume that the message space \(\mathcal {M}\) of \(\mathsf {d}\mathsf {PKE}\) is an abelian group with the operation “\(+\)” and the random coin space of the key generation algorithm \(\mathsf {d}\mathsf {KG}\) of \(\mathsf {d}\mathsf {PKE}\) is contained in \(\mathcal {M}\). Then, SDM-OW security is a security notion that guarantees that given \((s,\mathsf {dEnc}(\mathsf {pk},r+ s))\), an adversary cannot compute \(r+ s\), where \(s\leftarrow \mathcal {M}\), and \(r\in \mathcal {M}\) is the random coin used to generate \((\mathsf {pk},\mathsf {sk})\) (i.e., \((\mathsf {pk},\mathsf {sk})\leftarrow \mathsf {d}\mathsf {KG}(1^\lambda ;r)\)).
using the OW-CPA security of \(\mathsf {d}\mathsf {PKE}\), we show that it can be bounded if \(\mathsf {d}\mathsf {PKE}\) satisfies SDM-OW security introduced in this work. Hereafter, we assume that the message space \(\mathcal {M}\) of \(\mathsf {d}\mathsf {PKE}\) is an abelian group with the operation “\(+\)” and the random coin space of the key generation algorithm \(\mathsf {d}\mathsf {KG}\) of \(\mathsf {d}\mathsf {PKE}\) is contained in \(\mathcal {M}\). Then, SDM-OW security is a security notion that guarantees that given \((s,\mathsf {dEnc}(\mathsf {pk},r+ s))\), an adversary cannot compute \(r+ s\), where \(s\leftarrow \mathcal {M}\), and \(r\in \mathcal {M}\) is the random coin used to generate \((\mathsf {pk},\mathsf {sk})\) (i.e., \((\mathsf {pk},\mathsf {sk})\leftarrow \mathsf {d}\mathsf {KG}(1^\lambda ;r)\)).
The estimation is done after adding the following changes to z and V that do not affect the view of
 . First, we replace s in z and V with \(r+ s\), where \(r\in \mathcal {M}\) is the random coin used to generate \((\mathsf {pk},\mathsf {sk})\). Namely, we change z and V as
. First, we replace s in z and V with \(r+ s\), where \(r\in \mathcal {M}\) is the random coin used to generate \((\mathsf {pk},\mathsf {sk})\). Namely, we change z and V as
This change does not affect the view of
 since s is chosen uniformly at random and independently of r. Then, we further replace V with the following
since s is chosen uniformly at random and independently of r. Then, we further replace V with the following
where \(\widehat{f}_{b}\) is a function that is given x as an input, computes \((\mathsf {pk},\mathsf {sk})\leftarrow \mathsf {KG}(1^\lambda ;x- s)\), and outputs \(f_{b}(\mathsf {sk})\). We can check that V in Eq. (1) and V in Eq. (2) are functionally equivalent. Thus, this change also does not affect the view of
 . Moreover, we finally replace the condition “if \(x=s+r\)” in V with “if \(\mathsf {dEnc}(\mathsf {pk},x)=\mathsf {dEnc}(\mathsf {pk},r+ s)\)”. As noted before, this can be justified from the correctness of \(\mathsf {d}\mathsf {PKE}\).
. Moreover, we finally replace the condition “if \(x=s+r\)” in V with “if \(\mathsf {dEnc}(\mathsf {pk},x)=\mathsf {dEnc}(\mathsf {pk},r+ s)\)”. As noted before, this can be justified from the correctness of \(\mathsf {d}\mathsf {PKE}\).
We see that by the above changes, z and V (i.e., the entire view of
 ) can now be simulated by an SDM-OW adversary
) can now be simulated by an SDM-OW adversary
 who is given \((s,\mathsf {dEnc}(\mathsf {pk},r+ s))\). Moreover,
who is given \((s,\mathsf {dEnc}(\mathsf {pk},r+ s))\). Moreover,
 can break the SDM-OW security if the simulated
can break the SDM-OW security if the simulated
 successfully extracts the differing point of V and H, that is, \(r+ s\). This means that
successfully extracts the differing point of V and H, that is, \(r+ s\). This means that
 can be bounded by using the SDM-OW security of \(\mathsf {d}\mathsf {PKE}\).
can be bounded by using the SDM-OW security of \(\mathsf {d}\mathsf {PKE}\).
From the above arguments, we see that the KDM security of \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}\) in the QROM can be reduced to the SDM-OW security of \(\mathsf {d}\mathsf {PKE}\) without square root security loss.
SDM-OW Security of a Variant of \(\mathsf {T}\). We next explain the SDM-OW security of \(\mathsf {T}_{\mathtt {HKG}}=\mathsf {T}_{\mathtt {HKG}}(\mathsf {PKE},(G_{\mathtt {kg}},G_{\mathtt {enc}}))\) can be reduced to the IND-CPA security of the underlying PKE scheme \(\mathsf {PKE}\) without square roof security loss, where \(G_{\mathtt {kg}}\) and \(G_{\mathtt {enc}}\) are random oracles. \(\mathsf {T}_{\mathtt {HKG}}\) is a tweaked version of \(T=T(\mathsf {PKE},G_{\mathtt {enc}})\) transformation. T transformation converts a (randomized) IND-CPA secure PKE scheme into an OW-CPA secure deterministic PKE scheme. The encryption algorithm of \(\mathsf {T}\) is described as \(\mathsf {Enc}(\mathsf {pk},m;G_{\mathtt {enc}}(m))\), where \(\mathsf {Enc}\) is the encryption algorithm of the underlying \(\mathsf {PKE}\). The key generation and decryption algorithms of \(\mathsf {T}\) are those of \(\mathsf {PKE}\) themselves. In \(\mathsf {T}_{\mathtt {HKG}}\), we also generate a key pair \((\mathsf {pk},\mathsf {sk})\) by using a random coin generated by the random oracle \(G_{\mathtt {kg}}\), that is, \((\mathsf {pk},\mathsf {sk})\leftarrow \mathsf {KG}(1^\lambda ;G_{\mathtt {kg}}(r))\), where \(r\leftarrow \mathcal {M}\).
Bindel et al. [BHH+19] showed that the OW-CPA security of \(\mathsf {T}\) can be reduced to the IND-CPA security of \(\mathsf {PKE}\) without square root security loss. The important thing is that the target security notion is one-wayness (not indistinguishability) here. Essentially, Bindel et al. avoided the square root security loss by relying on the fact that if the target security notion is one-wayness and the starting security notion is indistinguishability, we can avoid square root security loss by using single-sided O2H lemma called semi-classical O2H lemma [AHU19]. In this work, we show that such a reduction to IND-CPA security without square root loss is possible even when we prove \(\mathsf {T}_{\mathtt {HKG}}\)’s SDM-OW security, which can be seen as one-wayness for a kind of key dependent messages. In fact, there is no difficulty based on the circularity issue as before since we use single-sided O2H lemma in this step, not double-sided one. Roughly speaking, when we use single-sided O2H lemma, we can eliminate correlations between keys, encryption random coins, and plaintexts by random oracle programming in the security proof even in the context of QROM. We give the overview of this proof in Sect. 5.2. More specifically, we provide a high-level idea of how to solve the correlations after we describe a few hybrid games for the proof, and complete the proof.
The KDM Security of \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}(\mathsf {T}(\mathsf {PKE},G_{\mathtt {enc}}), H)\). From the discussions so far, we see that the KDM security of \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}(\mathsf {T}_{\mathtt {HKG}}(\mathsf {PKE},(G_{\mathtt {kg}},G_{\mathtt {enc}})),H)\) can be reduced to the IND-CPA security of \(\mathsf {PKE}\) without square root security loss. This immediately implies the same holds for \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}(\mathsf {T}(\mathsf {PKE},G_{\mathtt {enc}}),H)\). This is because adversaries cannot detect whether the public and secret key pair is generated using a random oracle or not. The KDM security of \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}(\mathsf {T}(\mathsf {PKE},G_{\mathtt {enc}}),H)\) can be reduced to that of \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}(\mathsf {T}_{\mathtt {HKG}}(\mathsf {PKE},(G_{\mathtt {kg}},G_{\mathtt {enc}})),H)\).
Remarks.
-
In the actual security game of KDM security, an adversary can choose a pair of functions \((f_{0},f_{1})\) adaptively and obtain a ciphertext of \(f_{b}(\mathsf {sk})\) multiple times under the existence of multiple key pairs. Also, to capture a wide range of usage scenarios, we allow those functions to get access to random oracles. We handle these issues by using the adaptive reprogramming technique for QROM [Unr14] and introducing a security notion we call SDM-OW-RSA security which is an extension of SDM-OW security.
-
Our proof technique is also compatible with KDM-CCA security. Concretely, we can prove the KDM-CCA security of a PKE scheme constructed by using \(\mathsf {U}^{\bot ,\mathtt {keyconf}}_m=\mathsf {U}^{\bot ,\mathtt {keyconf}}_m(\mathsf {d}\mathsf {PKE},H)\) [BHH+19] as KEM and OTP-then-MAC as DEM without square root security loss. We assume the underlying \(\mathsf {d}\mathsf {PKE}\) is SDM-OW-RSA secure and additionally satisfies injectivity. The security proof is a combination of our proof for the KDM security of \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}\) and the proof for the IND-CCA security of \(\mathsf {U}^{\bot ,\mathtt {keyconf}}_m\) by [BHH+19, KSS+20]. Thus, we mainly focus on KDM-CPA security in this version, and we provide the results on KDM-CCA security in [KN21].
As shown by [BHH+19], \(\mathsf {U}^{\bot ,\mathtt {keyconf}}_m\) and \(\mathsf {U}^{\not \bot }_m\) are IND-CCA secure KEMs that are compatible with double-sided O2H lemma such as O2H lemma with MRM. To use \(\mathsf {U}^{\bot ,\mathtt {keyconf}}_m\) as the KEM part in the above construction is essential. If we use \(\mathsf {U}^{\not \bot }_m\) as the KEM part, it seems difficult to prove the KDM-CCA security of the construction. \(\mathsf {U}^{\not \bot }_m\) returns a random value generated by using pseudo-random functions (PRF) if the decryption algorithm detects a given ciphertext is not valid to make it possible to simulate the decryption oracle without using secret keys. In the KDM-CCA security game of a PKE scheme whose KEM part is \(\mathsf {U}^{\not \bot }_m\), the keys of PRF are also encrypted. In that case, we cannot use the security of PRF and cannot simulate the decryption oracle. It is an interesting open problem to prove KDM-CCA security of a PKE scheme whose KEM part is \(\mathsf {U}^{\not \bot }_m\) without square root security loss.
-
Our proof strategy explained so far can be realized more easily for SKE where the secret key is used for encryption. A ciphertext of a simple SKE scheme is \((s, H(\mathsf {sk}\Vert s)\oplus m)\), where H is a random oracle. The simple scheme has a good structure to apply our proof strategy because the secret key \(\mathsf {sk}\) can be recovered from the differing point \(\mathsf {sk}\Vert s\) when programming the random oracle in the security proof. Zhang [Zha19] showed the non-adaptive KDM security of the SKE scheme with security bound \(\sqrt{\frac{{\mathrm {poly}}(q,q_{\mathtt {kdm}},{q_f},\ell )}{2^\lambda }}\), where q is the number of random oracle queries, \(q_{\mathtt {kdm}}\) is the number of KDM queries, \({q_f}\) is the number of random oracle queries by KDM functions, \(\ell \) is the number of secret keys, and \(\lambda \) is the length of \(\mathsf {sk}\). Using our proof strategy, we can prove the non-adaptive KDM security of the SKE scheme with security bound roughly \(\frac{{\mathrm {poly}}(q,q_{\mathtt {kdm}},{q_f},\ell )}{2^\lambda }\). We formally prove it in [KN21]. The proof of this is much easier than the proof of our main construction \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}\). The former can be a warming-up for the latter.
-
We do not directly prove the KDM security of \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}(\mathsf {T}(\mathsf {PKE},G_{\mathtt {enc}}), H)\), and first prove that of \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}(\mathsf {T}_{\mathtt {HKG}}(\mathsf {PKE},(G_{\mathtt {kg}},G_{\mathtt {enc}})),H)\). If we directly prove the former in a modular way, we think we would need to introduce a more complicated security notion for deterministic PKE schemes. We believe that the introduction of \(\mathsf {T}_{\mathtt {HKG}}\) makes our presentation simpler and more modular.
-
In this work, we focus on PKE schemes whose DEM is OTP for a technical reason. As we saw above, for our strategy, it is important that DEM has a non-committing property in the sense that we can move an encrypted plaintext from the ciphertext to the key. Although our technique can be used to not only OTP but also any DEM with non-committing property, it is an interesting open question to prove KDM security of FO transformation with any DEM without square root security loss.
2 Preliminaries
2.1 Notations
In this paper, for a finite set X and a distribution D, \(x \leftarrow X\) denotes selecting an element from X uniformly at random, \(x \leftarrow D\) denotes sampling an element x according to D. Let \(y \leftarrow \mathsf {A}(x)\) denotes assigning to y the output of a probabilistic or deterministic algorithm \(\mathsf {A}\) on an input x. When we explicitly show that \(\mathsf {A}\) uses randomness r, we write \(y \leftarrow \mathsf {A}(x;r)\). When \(\mathsf {A}\) is allowed to get access to an oracle O, we write \(y \leftarrow \mathsf {A}^{O}(x)\). Let [a] and [a, b] denote the sets of integers \(\{1, \cdots , a \}\) and \(\{a,\cdots ,b\}\), respectively. \(\lambda \) denote a security parameter. PPT and QPT algorithms stand for probabilistic polynomial-time algorithms and polynomial-time quantum algorithms, respectively. Let \({\mathsf {negl}}\) denote a negligible function.
2.2 Public-Key Encryption
A public-key encryption (PKE) scheme \(\mathsf {PKE}\) is a three tuple \((\mathsf {KG}, \mathsf {Enc}, \mathsf {Dec})\) of PPT algorithms. Let \(\mathcal {M}\) be the message space of \(\mathsf {PKE}\). The key generation algorithm \(\mathsf {KG}\), given a security parameter \(1^\lambda \), outputs a public key \(\mathsf {pk}\) and a secret key \(\mathsf {sk}\). The encryption algorithm \(\mathsf {Enc}\), given a public key \(\mathsf {pk}\) and message \(m \in \mathcal {M}\), outputs a ciphertext \(\mathsf {CT}\). The decryption algorithm \(\mathsf {Dec}\), given a secret key \(\mathsf {sk}\) and ciphertext \(\mathsf {CT}\), outputs a message \(\tilde{m} \in \{ \bot \} \cup \mathcal {M}\).
Definition 2.1
(Correctness of PKE). We say that \(\mathsf {PKE}\) is \(\delta \)-correct if
where \(\mathcal {R}\) is the random coin space of \(\mathsf {Enc}\). If \(\mathsf {PKE}\) is constructed in the random oracle model, the expectation is taken over the choice of \((\mathsf {pk},\mathsf {sk})\leftarrow \mathsf {KG}(1^\lambda )\) and the random oracle.
We say that \(\mathsf {PKE}\) is deterministic PKE if \(\mathsf {Enc}(\mathsf {pk},\cdot )\) is a deterministic function. We introduce the correctness notion that is specific to deterministic PKE. In addition to the ordinary correctness above, it requires that under a randomly generated key \((\mathsf {pk},\mathsf {sk})\), a randomly generated message m does not have a collision, that is another message \(m'\) such that \(\mathsf {dEnc}(\mathsf {pk},m)=\mathsf {dEnc}(\mathsf {pk},m')\). This correctness notion is useful when we use double-sided O2H lemmas [BHH+19, KSS+20].
Definition 2.2
(Correctness of deterministic PKE). We say that a deterministic PKE scheme \(\mathsf {d}\mathsf {PKE}=(\mathsf {d}\mathsf {KG},\mathsf {dEnc},\mathsf {d}\mathsf {Dec})\) with the message space \(\mathcal {M}\) is \((\delta _1,\delta _2)\)-correct if it is \(\delta _1\)-correct and it holds that
If \(\mathsf {d}\mathsf {PKE}\) is constructed in the random oracle model, the probability is taken over the choice of \((\mathsf {pk},\mathsf {sk})\leftarrow \mathsf {d}\mathsf {KG}(1^\lambda )\), \(m\leftarrow \mathcal {M}\), and the random oracle.
We introduce a multi-instance and multi-challenge version of IND-CPA security for PKE that we denote as IND-m-CPA security.
Definition 2.3
(IND-m-CPA security for PKE). Let \(\mathsf {PKE}=(\mathsf {KG},\mathsf {Enc},\)\(\mathsf {Dec})\) be a PKE scheme. We define
 for an adversary
for an adversary
 as follows.
as follows.
-
Initialize: First, the challenger chooses a challenge bit \(b \leftarrow \{0,1\}\). Next, the challenger generates \((\mathsf {pk}^{k},\mathsf {sk}^{k}) \leftarrow \mathsf {KG}(1^{\lambda })\) for every \(k\in [\ell ]\). The challenger executes
 .
. -
\(O_{\mathtt {IND}}\): On the i-th call with input \((k_{i},\mathsf {m}_{i,0},\mathsf {m}_{i,1})\), where \(k_{i}\in [\ell ]\) and \(\left|\mathsf {m}_{i,0} \right|=\left|\mathsf {m}_{i,1} \right|\), it returns \(\mathsf {ct}_{i} \leftarrow \mathsf {Enc}(\mathsf {pk}^{k_{i}}, \mathsf {m}_{i,b})\).
-
Finalize: The challenger outputs 1 if \(b=b'\) and 0 otherwise.
We say that \(\mathsf {PKE}\) is IND-m-CPA secure if for any polynomial \(\ell =\ell (\lambda )\) and QPT adversary
 , we have
, we have
 .
.
We introduce the definition of KDM-CPA security for PKE.
Definition 2.4
(KDM-CPA security for PKE). Let \(\mathsf {PKE}=(\mathsf {KG},\mathsf {Enc},\mathsf {Dec})\) be a PKE scheme. We define
 for an adversary
for an adversary
 as follows.
as follows.
-
Initialize: First, the challenger chooses a challenge bit \(b \xleftarrow {\mathsf {r}}\{0,1\}\). Next, the challenger generates \((\mathsf {pk}^{k},\mathsf {sk}^{k}) \leftarrow \mathsf {KG}(1^{\lambda })\) for every \(k\in [\ell ]\). The challenger sets \(\mathbf {sk}:=(\mathsf {sk}^{1}, \ldots , \mathsf {sk}^{\ell })\), and executes
 .
. -
\(O_{\mathtt {KDM}}\): On the i-th call with input \((k_{i},f_{i,0},f_{i,1})\), where \(k_{i}\in [\ell ]\) and \(f_{i,0}\) and \(f_{i,1}\) are efficiently computable functions with the same output length, it returns \(\mathsf {ct}_{i} \leftarrow \mathsf {Enc}(\mathsf {pk}^{k_{i}}, f_{i,b}(\mathbf {sk}))\).
-
Finalize: The challenger outputs 1 if \(b=b'\) and 0 otherwise.
We say that \(\mathsf {PKE}\) is KDM-CPA secure if for any polynomial \(\ell =\ell (\lambda )\) and QPT adversary
 , we have
, we have

Remark 2.1
(KDM security in QROM). In order to capture a wide variety of situations, we allow KDM functions to get access to random oracles if the scheme is constructed in the (quantum) random oracle model. We allow only classical access random oracles for KDM functions, while adversaries get access to random oracles in super-position. This setting is sufficient when honest entities are classical.
2.3 \(\text {SDM-OW-RSA}\) Security
We introduce a new security notion seed-dependent message one-wayness against related seed attacks (SDM-OW-RSA security). This notion plays a crucial role in achieving KDM security from IND-m-CPA security in the QROM without square roof security loss.
Definition 2.5
(SDM-OW-RSA security for PKE). Let \(\mathsf {PKE}=(\mathsf {KG},\)\(\mathsf {Enc},\mathsf {Dec})\) be a PKE scheme such that the message space \(\mathcal {M}\) is an abelian group with the operation \(+\), and the random coin space of \(\mathsf {KG}\) is \(\mathcal {M}\). We define
 for an adversary
for an adversary
 as follows.
as follows.
-
Initialize: The challenger first generates \(r\leftarrow \mathcal {M}\). The challenger then generates \(\varDelta ^{k}\leftarrow \mathcal {M}\) and \((\mathsf {pk}^{k},\mathsf {sk}^{k}) \leftarrow \mathsf {KG}(1^{\lambda };r+\varDelta ^{k})\) for every \(k\in [\ell ]\). Next, for every \(k\in [\ell ]\) and \(i\in [{q_{\mathtt {sdm}}}]\), the challenger generates \(s_{i,k}\leftarrow \mathcal {M}\) and computes \(\mathsf {ct}_{i,k} \leftarrow \mathsf {Enc}\left( \mathsf {pk}^{k}, r+s_{i,k}\right) \). Finally, the challenger executes
 .
. -
Finalize:The challenger outputs 1 if and only if T contains \(r'\) such that \(r'=r+s_{i,k}\) holds for some \(i\in [{q_{\mathtt {sdm}}}]\) and \(k\in [\ell ]\).
We say that \(\mathsf {PKE}\) is \(\text {SDM-OW-RSA}\) secure if for any polynomial \(\ell =\ell (\lambda )\) and \({q_{\mathtt {sdm}}}={q_{\mathtt {sdm}}}(\lambda )\) and QPT adversary
 , we have
, we have

3 Quantum Random Oracle and Useful Lemmas
Given a function \(H:X\rightarrow Y\), a quantum-accessible oracle O of H is modeled by a unitary transformation \(U_H\) operating on two registers in and out, in which \(\left|x\right>\left|y\right>\) is mapped to \(\left|x\right>\left|y\oplus H(x)\right>\), where \(\oplus \) denotes XOR group operation on Y. Following [AHU19, BHH+19, KSS+20], we model a quantum algorithm
 making parallel queries to a quantum oracle O as a quantum algorithm making \(d\le q\) queries to an oracle \(O^{\otimes n}\) consisting of \(n=q/d\) parallel copies of oracle O. Given an input state of n pairs of in/out registers \(\left|x_1\right>\left|y_1\right>\cdots \left|x_n\right>\left|y_n\right>\), the oracle \(O^{\otimes n}\) maps it to the state \(\left|x_1\right>\left|y_1\oplus H(x_1)\right>\cdots \left|x_n\right>\left|y_n\oplus H(x_n)\right>\). We call d the algorithm’s query depth, n the parallelization factor, and \(q=n\cdot d\) the total number of oracle queries. We write
making parallel queries to a quantum oracle O as a quantum algorithm making \(d\le q\) queries to an oracle \(O^{\otimes n}\) consisting of \(n=q/d\) parallel copies of oracle O. Given an input state of n pairs of in/out registers \(\left|x_1\right>\left|y_1\right>\cdots \left|x_n\right>\left|y_n\right>\), the oracle \(O^{\otimes n}\) maps it to the state \(\left|x_1\right>\left|y_1\oplus H(x_1)\right>\cdots \left|x_n\right>\left|y_n\oplus H(x_n)\right>\). We call d the algorithm’s query depth, n the parallelization factor, and \(q=n\cdot d\) the total number of oracle queries. We write
 to denote that the algorithm
to denote that the algorithm
 ’s oracle O is a quantum-accessible oracle.
’s oracle O is a quantum-accessible oracle.
Simulation of Quantum Random Oracles. In this paper, following many previous works in the QROM, we give quantum-accessible random oracles to reduction algorithms if needed. This is just a convention. We can efficiently simulate quantum-accessible random oracles perfectly by using 2q-wise independent hash function [Zha12], where q is the number of queries to the quantum-accessible random oracles by an adversary.
3.1 One-Way to Hiding (O2H) Lemma
Definition 3.1
(Punctured oracle). Let \(F:X\rightarrow Y\) be any function, and \(S\subset X\) be a set. The oracle \(F\setminus S\)(“F punctured by S”) takes as input a value \(x\in X\). It first computes whether \(x\in S\) into an auxiliary register and measures it. Then it computes F(x) and returns the result. Let \(\mathtt {Find}\) be the event that any of the measurements returns 1.
Lemma 3.1
(Semi-classical O2H [AHU19, Theorem 1]). Let \(G,H:X\rightarrow Y\) be random functions, z be a random value, and \(S\subseteq X\) be a random set such that \(G(x)=H(x)\) for every \(x\notin S\). The tuple (G, H, S, z) may have arbitrary joint distribution. Furthermore, let
 be a quantum oracle algorithm. Let \(\mathtt {Ev}\) be any classical event. Then we have
be a quantum oracle algorithm. Let \(\mathtt {Ev}\) be any classical event. Then we have

where d is the query depth of
 for G and \(H\setminus S\).
for G and \(H\setminus S\).
Lemma 3.2
(Search in semi-classical oracle [AHU19, Theorem 2]). Let \(H:X\rightarrow Y\) be a random function, let z be a random value, and let \(S\subset X\) be a random set. (H, S, z) may have arbitrary joint distribution. Let
 be a quantum oracle algorithm. If for each \(x\in X\), \(\Pr [x\in S]\le \epsilon \) (conditioned on H and z), then we have
be a quantum oracle algorithm. If for each \(x\in X\), \(\Pr [x\in S]\le \epsilon \) (conditioned on H and z), then we have

where q is the number of queries to \(H\setminus S\) by
 .
.
Note that the above lemma is originally introduced in [AHU19], but we use a variant that is closer to Lemma 4 in [BHH+19].
Lemma 3.3
(Adapted version of O2H with MRM [KSS+20, Lemma 3.3]). Let \(G,H:X\rightarrow Y\) be functions, and \(S\subseteq X\) be a set such that \(G(x)=H(x)\) for every \(x\notin S\). Also, let z be a value and \(O_{\mathtt {aux}}\) be a function. The tuple \((G,H,S,z,O_{\mathtt {aux}})\) may have arbitrary joint distribution. Furthermore, let
 be a quantum oracle algorithm. Then we can construct an algorithm
be a quantum oracle algorithm. Then we can construct an algorithm
 such that
such that
-
The running time of
 is roughly three times longer than that of
is roughly three times longer than that of
 . Moreover, if
. Moreover, if
 makes at most q queries to G and H with query depth d,
makes at most q queries to G and H with query depth d,
 makes at most O(q) queries to each of those oracles with query depth O(d), and outputs a list \(T\subseteq X\) of size at most O(q).
makes at most O(q) queries to each of those oracles with query depth O(d), and outputs a list \(T\subseteq X\) of size at most O(q). -
It holds that

where d is the query depth of
 for the first oracle.
for the first oracle.
Remark 3.1
(On the difference from the original version). There are some differences between Lemma 3.3 and the original O2H lemma with MRM [KSS+20, Lemma 3.3]. First, in Lemma 3.3, we allow the algorithm
 to get access to an additional oracle \(O_{\mathtt {aux}}\), which is not explicitly appeared in the original version. Second, in Lemma 3.3, we explicitly state the size of
to get access to an additional oracle \(O_{\mathtt {aux}}\), which is not explicitly appeared in the original version. Second, in Lemma 3.3, we explicitly state the size of
 ’s output T is at most O(q) while the original lemma does not refer to the size of T. For the first one, it is easy to see that even if we introduce such an additional oracle, the lemma still holds. (This extension is used in also [LW21].) For the second, the concrete extractor
’s output T is at most O(q) while the original lemma does not refer to the size of T. For the first one, it is easy to see that even if we introduce such an additional oracle, the lemma still holds. (This extension is used in also [LW21].) For the second, the concrete extractor
 constructed in [KSS+20] satisfies this condition. Since we need the upper bound on the size of T in order to estimate the security bound in our proof, we place the requirement.
constructed in [KSS+20] satisfies this condition. Since we need the upper bound on the size of T in order to estimate the security bound in our proof, we place the requirement.
3.2 Additional Lemma
The following lemma is a multi-point version of adaptive reprogramming of QRO used in the proof of adaptive O2H lemma [Unr14, Lemma 14 in the eprint version]. We need it to handle KDM queries that are adaptively made. We provide the proof of it in [KN21].
Lemma 3.4
(Adaptive reprogramming of QRO). We consider the following
 .
.
-
Initialization: The challenger first generates the challenge bit \(b\leftarrow \{0,1\}\) and a fresh random oracle \(V_{0}:X\rightarrow Y\). Then, the challenger executes
 , where \(O_{\mathtt {prog}}\) is defined as follows.
, where \(O_{\mathtt {prog}}\) is defined as follows. -
\(O_{\mathtt {prog}}\): On the i-th call, it first generates \(s_{i}\leftarrow X\). If \(b=0\), it just returns \((s_{i},V_{0}(s_{i}))\). Otherwise, it generates \(u_{i}\leftarrow Y\), updates the random oracle
 gets access into \(V_{i}\) defined as $$\begin{aligned} V_{i}(x)= {\left\{ \begin{array}{ll} u_{j} &{} (\text {if}~~x=s_{j}~~\text {holds for some}~~j\le i)\\ H(x) &{} (\text {otherwise}), \end{array}\right. } \end{aligned}$$
gets access into \(V_{i}\) defined as $$\begin{aligned} V_{i}(x)= {\left\{ \begin{array}{ll} u_{j} &{} (\text {if}~~x=s_{j}~~\text {holds for some}~~j\le i)\\ H(x) &{} (\text {otherwise}), \end{array}\right. } \end{aligned}$$and returns \((s_{i},V_{i}(s_{i}))=(s_{i},u_{i})\).
-
Finalization: The challenger outputs 1 if \(b=b'\) and 0 otherwise.
Then, for any integer \({q_{\mathtt {prog}}}\) and an oracle algorithm
 that makes at most q queries to \(O_{\mathtt {b}}\), we have
that makes at most q queries to \(O_{\mathtt {b}}\), we have
 .
.
4 KDM-CPA Security of \(\mathsf {U}^{\bot }_{m}\) with OTP as DEM
In this section, we show that the KDM-CPA security in the QROM of a PKE scheme \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}=\mathsf {U}^{\bot }_{m,\mathtt {OTP}}(\mathsf {d}\mathsf {PKE},H)\) can be reduced to the \(\text {SDM-OW-RSA}\) security of the underlying \(\mathsf {d}\mathsf {PKE}\) without square root security loss. \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}\) is constructed by using \(\mathsf {U}^{\bot }_{m}(\mathsf {d}\mathsf {PKE},H)\) [BHH+19] as KEM and OTP as DEM. Since we focus on KDM-CPA security here, \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}\) omits the ciphertext validity check by re-encryption in the decryption algorithm, which is performed in \(\mathsf {U}^{\bot }_{m}\).
4.1 Construction
Construction 4.1. Let \(\mathsf {d}\mathsf {PKE}=(\mathsf {d}\mathsf {KG},\mathsf {dEnc},\mathsf {d}\mathsf {Dec})\) be a deterministic PKE scheme whose message space is \(\mathcal {M}\). We assume that \(\mathcal {M}\) is an abelian group and denote the operation in \(\mathcal {M}\) as \(+\). Let \(H:\mathcal {M}\rightarrow \{0,1\}^*\) be a hash function. We construct \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}=(\mathsf {KG},\mathsf {Enc},\mathsf {Dec})\) as follows.
-
\(\mathsf {KG}(1^\lambda )\): Return \((\mathsf {pk},\mathsf {sk}) \leftarrow \mathsf {d}\mathsf {KG}(1^\lambda )\).
-
\(\mathsf {Enc}(\mathsf {pk},\mathsf {m})\): Generate \(s\leftarrow \mathcal {M}\) and compute \(\mathsf {ct}\leftarrow \mathsf {dEnc}(\mathsf {pk},s)\) and \(t=H(s)\oplus \mathsf {m}\). Return \(\mathsf {CT}=(\mathsf {ct},t)\).
-
\(\mathsf {Dec}(\mathsf {sk},\mathsf {CT}')\): Parse \(\mathsf {CT}'=(\mathsf {ct}',t')\), compute \(s'\leftarrow \mathsf {d}\mathsf {Dec}(\mathsf {sk},\mathsf {ct}')\), and return \(\bot \) if \(s'=\bot \). Otherwise, return \(t'\oplus H(s')\).
We see that if \(\mathsf {d}\mathsf {PKE}\) is \((\delta _1,\delta _2)\)-correct, then \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}\) is \(\delta _1\)-correct for any \(\delta _1\).
4.2 Security Proof
We prove the following theorem.
Theorem 4.2
Let \(\ell =\ell (\lambda )\) be a polynomial and \(\mathsf {d}\mathsf {PKE}\) be a \((\delta _1,\delta _2)\)-correct deterministic PKE. Let
 be a QPT adversary against the \(\text {KDM}\text {-}\text {CPA}\) security of \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}=\mathsf {U}^{\bot }_{m,\mathtt {OTP}}(\mathsf {d}\mathsf {PKE},H)\) making q (superposition) random oracle queries to H with query depth d and \(q_{\mathtt {kdm}}\) (classical) queries to \(O_{\mathtt {KDM}}\). Also, let \({q_f}\) be the upper bound of the total number of (classical) random oracle queries made by KDM functions. Then, there exists a QPT adversary
be a QPT adversary against the \(\text {KDM}\text {-}\text {CPA}\) security of \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}=\mathsf {U}^{\bot }_{m,\mathtt {OTP}}(\mathsf {d}\mathsf {PKE},H)\) making q (superposition) random oracle queries to H with query depth d and \(q_{\mathtt {kdm}}\) (classical) queries to \(O_{\mathtt {KDM}}\). Also, let \({q_f}\) be the upper bound of the total number of (classical) random oracle queries made by KDM functions. Then, there exists a QPT adversary
 such that
such that

Proof. We complete the proof using hybrid games. Let \(\mathtt{SUC}_X\) be the event that the final output is 1 in Game X. We assume that
 makes at least one KDM query before the first set of random oracle queries and between \(d^*\)-th set of random oracle queries and \((d^*+1)\)-th set of random oracle queries for every \(d^*\in [d-1]\). This assumption is without loss of generality in the sense that any adversary can be transformed into one satisfying this condition without changing the number and depth of random oracle queries.
makes at least one KDM query before the first set of random oracle queries and between \(d^*\)-th set of random oracle queries and \((d^*+1)\)-th set of random oracle queries for every \(d^*\in [d-1]\). This assumption is without loss of generality in the sense that any adversary can be transformed into one satisfying this condition without changing the number and depth of random oracle queries.
-
Game 1: This is
 .
.-
Initialize: First, the challenger chooses a challenge bit \(b \leftarrow \{0,1\}\). The challenger also generates a fresh random oracle H. Next, the challenger generates \((\mathsf {pk}^{k},\mathsf {sk}^{k}) \leftarrow \mathsf {d}\mathsf {KG}(1^{\lambda })\) for every \(k\in [\ell ]\). The challenger sets \(\mathbf {sk}:=(\mathsf {sk}^{1}, \ldots , \mathsf {sk}^{\ell })\) and \(\mathbf {pk}:=(\mathsf {pk}^{1}, \ldots , \mathsf {pk}^{\ell })\), and executes
 . \(O_{\mathtt {KDM}}\) behaves as follows.
. \(O_{\mathtt {KDM}}\) behaves as follows. -
\(O_{\mathtt {KDM}}\): On the i-th call with input \((k_{i}, f_{i,0},f_{i,1})\), it returns \(\mathsf {CT}_{i}\) generated as follows.
-
1.
Generate \(s_{i}\leftarrow \mathcal {M}\) and compute \(\mathsf {ct}_{i}\leftarrow \mathsf {dEnc}(\mathsf {pk}^{k_{i}},s_{i})\).
-
2.
Compute \(t_{i}=H(s_{i})\oplus f_{i,b}^{H}(\mathbf {sk})\).
-
3.
Set \(\mathsf {CT}_{i}\leftarrow (\mathsf {ct}_{i},t_{i})\).
-
1.
-
Finalize: The challenger outputs 1 if \(b=b'\) and 0 otherwise.
-
-
Game 2: This is the same as Game 1 except the behavior of \(O_{\mathtt {KDM}}\). In this game, \(O_{\mathtt {KDM}}\) adaptively reprograms the random oracle that
 (and functions queried by
(and functions queried by
 ) gets access every time it is invoked. The detailed description is as follows.
) gets access every time it is invoked. The detailed description is as follows.-
\(O_{\mathtt {KDM}}\): On input \((k_{i}, f_{i,0},f_{i,1})\), it returns \(\mathsf {CT}_{i}\) generated as follows.
-
1.
Generate \(s_{i}\leftarrow \mathcal {M}\) and compute \(\mathsf {ct}_{i}\leftarrow \mathsf {dEnc}(\mathsf {pk}^{k_{i}},s_{i})\).
-
2.

-
3.
Set \(\mathsf {CT}_{i}\leftarrow (\mathsf {ct}_{i},t_{i})\).
Also, it updates the random oracle into

-
1.
-
From Lemma 3.4, we have \(\left|\Pr [\mathtt{SUC}_1]-\Pr [\mathtt{SUC}_2] \right|=\frac{4(q+{q_f})q_{\mathtt {kdm}}}{\sqrt{\mathcal {M}}}\).
-
Game 3: This game is the same as Game 2 except that \(u_{i}\) is replaced with \(u_{i}\oplus f_{i,b}^{V_{i-1}}(\mathbf {sk})\) for every \(i\in [q_{\mathtt {kdm}}]\). More concretely, the behavior of \(O_{\mathtt {KDM}}\) is changed as follows.
-
\(O_{\mathtt {KDM}}\): On input \((k_{i}, f_{i,0},f_{i,1})\), it returns \(\mathsf {CT}_{i}\) generated as follows.
-
1.
Generate \(s_{i}\leftarrow \mathcal {M}\) and compute \(\mathsf {ct}_{i}\leftarrow \mathsf {dEnc}(\mathsf {pk}^{k_{i}},s_{i})\).
-
2.
Generate \(u_{i}\leftarrow \{0,1\}^*\) and
 .
. -
3.
Set \(\mathsf {CT}_{i}\leftarrow (\mathsf {ct}_{i},t_{i})\).
Also, it updates the random oracle into
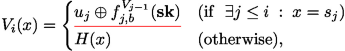
-
1.
-
This change does not affect the view of
 since \(u_{i}\) is chosen uniformly at random and independently of \(f_{i,b}^{V_{i-1}}(\mathbf {sk})\) for every \(i\in [q_{\mathtt {kdm}}]\). Thus, we have \(\left|\Pr [\mathtt{SUC}_2]-\Pr [\mathtt{SUC}_3] \right|=0\).
since \(u_{i}\) is chosen uniformly at random and independently of \(f_{i,b}^{V_{i-1}}(\mathbf {sk})\) for every \(i\in [q_{\mathtt {kdm}}]\). Thus, we have \(\left|\Pr [\mathtt{SUC}_2]-\Pr [\mathtt{SUC}_3] \right|=0\).
-
Game 4: This game is the same as Game 3 except for the following. The challenger first generates \(r\leftarrow \mathcal {M}\). The challenger then generates \(\varDelta ^{1},\ldots ,\varDelta ^{\ell }\leftarrow \mathcal {M}\) and generates \((\mathsf {pk}^{k},\mathsf {sk}^{k}) \leftarrow \mathsf {d}\mathsf {KG}(1^{\lambda };r+\varDelta ^{k})\) for every \(k\in [\ell ]\).
The above change does not affect the view of
 since the distribution of \((\mathsf {pk}^{k},\mathsf {sk}^{k})_{k\in [\ell ]}\) does not change. Thus, we have \(\left|\Pr [\mathtt{SUC}_3]-\Pr [\mathtt{SUC}_4] \right|=0\).
since the distribution of \((\mathsf {pk}^{k},\mathsf {sk}^{k})_{k\in [\ell ]}\) does not change. Thus, we have \(\left|\Pr [\mathtt{SUC}_3]-\Pr [\mathtt{SUC}_4] \right|=0\).
-
Game 5: This game is the same as Game 4 except that \(s_{i}\) is replaced with \(r+s_{i}\). More concretely, the challenger generates
 for every \(i\in [q_{\mathtt {kdm}}]\). Also, the challenger sets \(V_{i}\) as
for every \(i\in [q_{\mathtt {kdm}}]\). Also, the challenger sets \(V_{i}\) as 
for every \(i\in [q_{\mathtt {kdm}}]\).
We have \(\left|\Pr [\mathtt{SUC}_4]-\Pr [\mathtt{SUC}_5] \right|=0\) since this change also does not affect the view of
 .
.
From the next game, we use the function \(\widehat{f}_{i,b}\) described in Fig. 1. \(\widehat{f}_{i,b}\) is designed so that it computes \(f_{i,b}^{V_{i-1}}(\mathbf {sk})\) if it has oracle access to H and is given \(r+s_{i}\) as an input. For this aim, \(\widehat{f}_{i,b}^H\) sequentially computes \(V_j\) from \(V_1, V_2,...,V_{i-1}\) using H. They are denoted as \(\widehat{V}_j\) in the description of \(\widehat{f}^H_{i,b}\). Here, the computation of \(\widehat{V}_j\) by \(\widehat{f}^H_{j,b}\) is local, and thus \(\widehat{f}^H_{j,b}\) does not perform the updates of the random oracle that
 gets access.
gets access.
-
Game 6: For every \(i\in [q_{\mathtt {kdm}}]\), we define a function . Then, Game 6 is the same as Game 5 except that the challenger sets \(V_{i}\) as

for every \(i\in [q_{\mathtt {kdm}}]\).
Since \(\widehat{f}_{i,b}\) correctly computes \(f_{i,b}^{V_{i-1}}(\mathbf {sk})\) if it has oracle access to H and is given \(r+s_{i}\) as an input for every \(i\in [q_{\mathtt {kdm}}]\), the functionality of \(V_{i}\) does not change between Game 5 and 6 for every \(i\in [q_{\mathtt {kdm}}]\). Therefore, we have \(\left|\Pr [\mathtt{SUC}_5]-\Pr [\mathtt{SUC}_6] \right|=0\).
-
Game 7: This game is the same as Game 6 except that for every \(i\in [q_{\mathtt {kdm}}]\), \(V_{i}\) is defined as

If \(\mathsf {ct}_{i}\) has a unique pre-image \(r+s_{i}\) under \(\mathsf {pk}^{k_{i}}\) for every \(i\in [q_{\mathtt {kdm}}]\), the functionality of \(V_{i}\) does not change for every \(i\in [q_{\mathtt {kdm}}]\) between Game 6 and 7. Thus, from the correctness of \(\mathsf {d}\mathsf {PKE}\), we have \(\left|\Pr [\mathtt{SUC}_6]-\Pr [\mathtt{SUC}_7] \right|\le q_{\mathtt {kdm}}\cdot \delta _2\).
At Game 7,
 can obtain information of the challenge bit b only through d sets of random oracle queries. Below, we use d more hybrid games and remove information of b from those d sets of random oracle queries one by one.
can obtain information of the challenge bit b only through d sets of random oracle queries. Below, we use d more hybrid games and remove information of b from those d sets of random oracle queries one by one.
-
Game \(7+{d^*}~({d^*}=1,\ldots ,d)\): This is the same game as Game 7 except \(O_{\mathtt {KDM}}\) defers updating the random oracle. Concretely, \(O_{\mathtt {KDM}}\) does not update the random oracle until
 makes the \({d^*}\)-th set of random oracle queries. The detailed description of \(O_{\mathtt {KDM}}\) is as follows.
makes the \({d^*}\)-th set of random oracle queries. The detailed description of \(O_{\mathtt {KDM}}\) is as follows.-
\(O_{\mathtt {KDM}}\): On input \((k_{i}, f_{i,0},f_{i,1})\), it returns \(\mathsf {CT}_{i}\) generated as follows.
-
1.
Generate \(s_{i}\leftarrow \mathcal {M}\) and compute \(\mathsf {ct}_{i}\leftarrow \mathsf {dEnc}(\mathsf {pk}^{k_{i}},r+s_{i})\).
-
2.
Generate \(u_{i}\leftarrow \{0,1\}^*\) and set \(t_{i}\leftarrow u_{i}\).
-
3.
Set \(\mathsf {CT}_{i}\leftarrow (\mathsf {ct}_{i},t_{i})\).
Also,
 it updates the random oracle into $$\begin{aligned} V_{i}(x)= {\left\{ \begin{array}{ll} u_{j}\oplus \widehat{f}_{j,b}^{H}(x) &{} (\text {if}~~\exists j\le i {\;\; : \;\;}\mathsf {dEnc}(\mathsf {pk}^{k_{j}},x)=\mathsf {ct}_{j})\\ H(x) &{} (\text {otherwise}). \end{array}\right. } \end{aligned}$$
it updates the random oracle into $$\begin{aligned} V_{i}(x)= {\left\{ \begin{array}{ll} u_{j}\oplus \widehat{f}_{j,b}^{H}(x) &{} (\text {if}~~\exists j\le i {\;\; : \;\;}\mathsf {dEnc}(\mathsf {pk}^{k_{j}},x)=\mathsf {ct}_{j})\\ H(x) &{} (\text {otherwise}). \end{array}\right. } \end{aligned}$$ -
1.
-
We have \(\left|\Pr [\mathtt{SUC}_{7+d}]-\frac{1}{2} \right|=0\) since in Game \(7+d\), the view of
 is completely independent of b. In order to estimate \(\left|\Pr [\mathtt{SUC}_{7+{d^*}-1}]-\Pr [\mathtt{SUC}_{7+{d^*}}] \right|\) for every \({d^*}\in [d]\), we consider the following procedure \(\mathsf {Setup}_{{d^*}}\).
is completely independent of b. In order to estimate \(\left|\Pr [\mathtt{SUC}_{7+{d^*}-1}]-\Pr [\mathtt{SUC}_{7+{d^*}}] \right|\) for every \({d^*}\in [d]\), we consider the following procedure \(\mathsf {Setup}_{{d^*}}\).
-
\(\mathsf {Setup}_{{d^*}}\): First, the challenger chooses a challenge bit \(b \leftarrow \{0,1\}\). The challenger also generates a fresh random oracle H. Next, the challenger generates \((\mathsf {pk}^{k},\mathsf {sk}^{k}) \leftarrow \mathsf {d}\mathsf {KG}(1^{\lambda };r+\varDelta ^{k})\), where \(r\leftarrow \mathcal {M}\) and \(\varDelta ^{k}\leftarrow \mathcal {M}\) for every \(k\in [\ell ]\). The challenger sets \(\mathbf {pk}:=(\mathsf {pk}^{1}, \ldots , \mathsf {pk}^{\ell })\), and executes
 just before
just before
 makes the \({d^*}\)-th set of random oracle queries. \(O_{\mathtt {KDM}}\) behaves as follows.
makes the \({d^*}\)-th set of random oracle queries. \(O_{\mathtt {KDM}}\) behaves as follows.-
\(O_{\mathtt {KDM}}\): On input \((k_{i}, f_{i,0},f_{i,1})\), it returns \(\mathsf {CT}_{i}\) generated as follows.
-
1.
Generate \(s_{i}\leftarrow \mathcal {M}\) and compute \(\mathsf {ct}_{i}\leftarrow \mathsf {dEnc}(\mathsf {pk}^{k_{i}},r+s_{i})\).
-
2.
Generate \(u_{i}\leftarrow \{0,1\}^*\) and set \(t_{i}\leftarrow u_{i}\).
-
3.
Set \(\mathsf {CT}_{i}\leftarrow (\mathsf {ct}_{i},t_{i})\).
-
1.
Let
 makes \(i^{*}\) KDM queries before \({d^*}\)-th set of random oracle queries. Then, the challenger sets \(V_{i^{*}}\) as $$\begin{aligned} V_{i^{*}}(x)= {\left\{ \begin{array}{ll} u_{j}\oplus \widehat{f}_{j,b}^{H}(x) &{} (\text {if}~~\exists j\le i^{*}{\;\; : \;\;}\mathsf {dEnc}(\mathsf {pk}^{k_{j}},x)=\mathsf {ct}_{j})\\ H(x) &{} (\text {otherwise}) \end{array}\right. } \end{aligned}$$
makes \(i^{*}\) KDM queries before \({d^*}\)-th set of random oracle queries. Then, the challenger sets \(V_{i^{*}}\) as $$\begin{aligned} V_{i^{*}}(x)= {\left\{ \begin{array}{ll} u_{j}\oplus \widehat{f}_{j,b}^{H}(x) &{} (\text {if}~~\exists j\le i^{*}{\;\; : \;\;}\mathsf {dEnc}(\mathsf {pk}^{k_{j}},x)=\mathsf {ct}_{j})\\ H(x) &{} (\text {otherwise}) \end{array}\right. } \end{aligned}$$and \(S_{i^{*}}=\{x|\exists j\in [i^{*}]{\;\; : \;\;}\mathsf {dEnc}(\mathsf {pk}^{k_{j}},x)=\mathsf {ct}_{j}\}\). The challenger also generates \(s_{i,k}\leftarrow \mathcal {M}\) and generates \(\mathsf {ct}_{i,k}\leftarrow \mathsf {dEnc}(\mathsf {pk}^{k},r+s_{i,k})\) for every \(i\in [i^{*}+1,q_{\mathtt {kdm}}]\) and \(k\in [\ell ]\). The challenger then sets
$$\begin{aligned} z=(\left|st\right>,b,\mathbf{pk} , ({\varDelta }^{k})_{k\in [\ell ]},({k}_{i},{f}_{i,b},{s}_{i},{\textsf {ct}}_{i},{u}_{i})_{i\in [i^{*}]}, ({s}_{i,k},{\textsf {ct}}_{i,k})_{i\in [i^{*}+1,{q_{\texttt {kdm}}}],k\in [\ell ]}), \end{aligned}$$(4)where \(\left|st\right>\) is the internal state of
 at this point. The challenger outputs \((V_{i^{*}},H,S_{i^{*}},z,O_{\mathtt {aux}}=H)\).
at this point. The challenger outputs \((V_{i^{*}},H,S_{i^{*}},z,O_{\mathtt {aux}}=H)\). -
Also, we consider the following QPT algorithm
 that has oracle access to \(O_{\mathtt {}}\in \{V_{i^{*}},H\}\) and \(O_{\mathtt {aux}}=H\).
that has oracle access to \(O_{\mathtt {}}\in \{V_{i^{*}},H\}\) and \(O_{\mathtt {aux}}=H\).
-
 : Given an input z,
: Given an input z,
 parse it as Eq. (4) and executes
parse it as Eq. (4) and executes
 from
from
 ’s \({d^*}\)-th set of random oracle queries using \(\left|st\right>\) as the internal state of
’s \({d^*}\)-th set of random oracle queries using \(\left|st\right>\) as the internal state of
 at that point.
at that point.
 simulates \(O_{\mathtt {KDM}}\) as follows.
simulates \(O_{\mathtt {KDM}}\) as follows.-
\(O_{\mathtt {KDM}}\): On input \((k_{i}, f_{i,0},f_{i,1})\), it returns \(\mathsf {CT}_{i}\) generated as follows.
-
1.
Set \(\mathsf {ct}_{i}\leftarrow \mathsf {ct}_{i,k_{i}}\) (and set \(s_{i}\leftarrow s_{i,k_{i}}\)).
-
2.
Generate \(u_{i}\leftarrow \{0,1\}^*\) and set \(t_{i}\leftarrow u_{i}\).
-
3.
Set \(\mathsf {CT}_{i}\leftarrow (\mathsf {ct}_{i},t_{i})\).
Also, it updates the random oracle that
 gets access into $$\begin{aligned} V_{i}(x)= {\left\{ \begin{array}{ll} u_{j}\oplus \widehat{f}_{j,b}^{H}(x) &{} (\text {if}~~\exists j\le i {\;\; : \;\;}\mathsf {dEnc}(\mathsf {pk}^{k_{j}},x)=\mathsf {ct}_{j})\\ H(x) &{} (\text {otherwise}). \end{array}\right. } \end{aligned}$$
gets access into $$\begin{aligned} V_{i}(x)= {\left\{ \begin{array}{ll} u_{j}\oplus \widehat{f}_{j,b}^{H}(x) &{} (\text {if}~~\exists j\le i {\;\; : \;\;}\mathsf {dEnc}(\mathsf {pk}^{k_{j}},x)=\mathsf {ct}_{j})\\ H(x) &{} (\text {otherwise}). \end{array}\right. } \end{aligned}$$ -
1.
When
 terminates with output \(b'\),
terminates with output \(b'\),
 outputs 1 if \(b=b'\) and 0 otherwise.
outputs 1 if \(b=b'\) and 0 otherwise. -
Suppose we execute \(\mathsf {Setup}_{{d^*}}\) and
 successively. They simulate the view of
successively. They simulate the view of
 in Game \(7+{d^*}-1\) (resp. Game \(7+{d^*}\)) if \(O_{\mathtt {}}=V_{i^{*}}\) (resp. \(O_{\mathtt {}}=H\)). Also,
in Game \(7+{d^*}-1\) (resp. Game \(7+{d^*}\)) if \(O_{\mathtt {}}=V_{i^{*}}\) (resp. \(O_{\mathtt {}}=H\)). Also,
 outputs 1 if and only if the output of the simulated games is 1. Thus, we have
outputs 1 if and only if the output of the simulated games is 1. Thus, we have
 and
and
 . From Lemma 3.3, there exists a QPT algorithm
. From Lemma 3.3, there exists a QPT algorithm
 such that
such that

Note that
 makes queries to \(O_{\mathtt {}}\in \{V_{i^{*}},H\}\) with depth 1 by the following reason.
makes queries to \(O_{\mathtt {}}\in \{V_{i^{*}},H\}\) with depth 1 by the following reason.
 is supposed to simulate Game \(7+d^*-1\) (resp. Game \(7+d^*\)) for
is supposed to simulate Game \(7+d^*-1\) (resp. Game \(7+d^*\)) for
 from the point that
from the point that
 makes \(d^*\)-th set of random oracle queries when
makes \(d^*\)-th set of random oracle queries when
 gets access to \(O_{\mathtt {}}=V_{i^*}\) (resp. \(O_{\mathtt {}}=H\)). The answers to
gets access to \(O_{\mathtt {}}=V_{i^*}\) (resp. \(O_{\mathtt {}}=H\)). The answers to
 ’s \((d^*+1)\) to d-th set of random oracle queries are identical between Game \(7+d^*-1\) and \(7+d^*\). (Here,
’s \((d^*+1)\) to d-th set of random oracle queries are identical between Game \(7+d^*-1\) and \(7+d^*\). (Here,
 makes at least one KDM query between the \(d^*\)-th and \((d^*+1)\)-th set of random oracle queries due to the assumption. Thus, they are answered using an updated random oracle.)
makes at least one KDM query between the \(d^*\)-th and \((d^*+1)\)-th set of random oracle queries due to the assumption. Thus, they are answered using an updated random oracle.)
 can simulate them by using \(O_{\mathtt {aux}}=H\) and information included in z. Therefore,
can simulate them by using \(O_{\mathtt {aux}}=H\) and information included in z. Therefore,
 uses its oracle \(O_{\mathtt {}}\) only for answering to
uses its oracle \(O_{\mathtt {}}\) only for answering to
 ’s \(d^*\)-th set of random oracle queries, and thus
’s \(d^*\)-th set of random oracle queries, and thus
 ’s query depth to \(O_{\mathtt {}}\) is 1.
’s query depth to \(O_{\mathtt {}}\) is 1.
We bound the right-hand side probability. Using
 , we construct the following adversary
, we construct the following adversary
 against the \(\text {SDM-OW-RSA}\) security of \(\mathsf {d}\mathsf {PKE}\).
against the \(\text {SDM-OW-RSA}\) security of \(\mathsf {d}\mathsf {PKE}\).
-
 : Given \(\mathbf {pk}=(\mathsf {pk}^{1},\ldots ,\mathsf {pk}^{\ell })\), \((\varDelta ^{k})_k\), and \((s_{i,k},\mathsf {ct}_{i,k})_{i\in [q_{\mathtt {kdm}}],k\in [\ell ]}\),
: Given \(\mathbf {pk}=(\mathsf {pk}^{1},\ldots ,\mathsf {pk}^{\ell })\), \((\varDelta ^{k})_k\), and \((s_{i,k},\mathsf {ct}_{i,k})_{i\in [q_{\mathtt {kdm}}],k\in [\ell ]}\),
 first simulates \(\mathsf {Setup}_{{d^*}}\).
first simulates \(\mathsf {Setup}_{{d^*}}\).
 chooses a challenge bit \(b \leftarrow \{0,1\}\) and prepares a fresh random oracle H.
chooses a challenge bit \(b \leftarrow \{0,1\}\) and prepares a fresh random oracle H.
 then executes
then executes
 just before
just before
 makes the \({d^*}\)-th set of random oracle queries, where \(O_{\mathtt {KDM}}\) is simulated as follows.
makes the \({d^*}\)-th set of random oracle queries, where \(O_{\mathtt {KDM}}\) is simulated as follows.-
\(O_{\mathtt {KDM}}\): On input \((k_{i}, f_{i,0},f_{i,1})\), it returns \(\mathsf {CT}_{i}\) generated as follows.
-
1.
Set \(\mathsf {ct}_{i}\leftarrow \mathsf {ct}_{i,k_{i}}\) (and set \(s_{i}\leftarrow s_{i,k_{i}}\)).
-
2.
Generate \(u_{i}\leftarrow \{0,1\}^*\) and set \(t_{i}\leftarrow u_{i}\).
-
3.
Set \(\mathsf {CT}_{i}\leftarrow (\mathsf {ct}_{i},t_{i})\).
-
1.
Let
 makes \(i^{*}\) KDM queries before \({d^*}\)-th set of random oracle queries. Then,
makes \(i^{*}\) KDM queries before \({d^*}\)-th set of random oracle queries. Then,
 sets \(V_{i^{*}}\) as $$\begin{aligned} V_{i^{*}}(x)= {\left\{ \begin{array}{ll} u_{j}\oplus \widehat{f}_{j,b}^{H}(x) &{} (\text {if}~~\exists j\le i^{*}{\;\; : \;\;}\mathsf {dEnc}(\mathsf {pk}^{k_{j}},x)=\mathsf {ct}_{j})\\ H(x) &{} (\text {otherwise}) . \end{array}\right. } \end{aligned}$$
sets \(V_{i^{*}}\) as $$\begin{aligned} V_{i^{*}}(x)= {\left\{ \begin{array}{ll} u_{j}\oplus \widehat{f}_{j,b}^{H}(x) &{} (\text {if}~~\exists j\le i^{*}{\;\; : \;\;}\mathsf {dEnc}(\mathsf {pk}^{k_{j}},x)=\mathsf {ct}_{j})\\ H(x) &{} (\text {otherwise}) . \end{array}\right. } \end{aligned}$$ also sets $$\begin{aligned} z=( \left|st\right>,b,\mathbf{pk} , (\varDelta ^{k})_{k\in [\ell ]},(k_{i},f_{i,b},s_{i},\textsf {ct}_{i},u_{i})_{i\in [i^{*}]}, (s_{i,k},\textsf {ct}_{i,k})_{i\in [i^{*}+1,{q_{\texttt {kdm}}}],k\in [\ell ]} ), \end{aligned}$$
also sets $$\begin{aligned} z=( \left|st\right>,b,\mathbf{pk} , (\varDelta ^{k})_{k\in [\ell ]},(k_{i},f_{i,b},s_{i},\textsf {ct}_{i},u_{i})_{i\in [i^{*}]}, (s_{i,k},\textsf {ct}_{i,k})_{i\in [i^{*}+1,{q_{\texttt {kdm}}}],k\in [\ell ]} ), \end{aligned}$$where \(\left|st\right>\) is the internal state of
 at this point. Finally,
at this point. Finally,
 outputs
outputs
 .
. -
 perfectly simulates a successive execution of \(\mathsf {Setup}_{{d^*}}\) and
perfectly simulates a successive execution of \(\mathsf {Setup}_{{d^*}}\) and
 . Also, in the simulated execution, if \(T\cap S_{i^{*}}\ne \emptyset \) occurs and \(\mathsf {ct}_{i}\) has a unique pre-image \(r+s_{i}\) under \(\mathsf {pk}^{k_{i}}\) for every \(i\in [q_{\mathtt {kdm}}]\),
. Also, in the simulated execution, if \(T\cap S_{i^{*}}\ne \emptyset \) occurs and \(\mathsf {ct}_{i}\) has a unique pre-image \(r+s_{i}\) under \(\mathsf {pk}^{k_{i}}\) for every \(i\in [q_{\mathtt {kdm}}]\),
 wins. Thus, we have
wins. Thus, we have

By setting
 as
as
 such that
such that
 for every \({d^*}\in [d]\), we see that there exists a QPT
for every \({d^*}\in [d]\), we see that there exists a QPT
 that satisfies Eq. (3). \(\Box \) (Theorem 4.2)
that satisfies Eq. (3). \(\Box \) (Theorem 4.2)
5 \(\text {SDM-OW-RSA}\) Secure Deterministic PKE
In this section, we show that the \(\text {SDM-OW-RSA}\) security in the QROM of a tweaked version of \(\mathsf {T}\) transformation [BHH+19] can be reduced to the IND-CPA security of the underlying PKE scheme.
5.1 Construction
Construction 5.1. Let \(\mathsf {PKE}=(\mathsf {KG},\mathsf {Enc},\mathsf {Dec})\) be a PKE scheme whose message space is an abelian group \(\mathcal {M}\) with the operation \(+\). We also let the random coin space of \(\mathsf {KG}\) and \(\mathsf {Enc}\) be \(\mathcal {R}_{\mathtt {kg}}\) and \(\mathcal {R}_{\mathtt {enc}}\), respectively. Let \(G=(G_{\mathtt {kg}},G_{\mathtt {enc}})\) be a pair of hash functions, where \(G_{\mathtt {kg}}:\mathcal {M}\rightarrow \mathcal {R}_{\mathtt {kg}}\) and \(G_{\mathtt {enc}}:\mathcal {M}\rightarrow \mathcal {R}_{\mathtt {enc}}\). We construct \(\mathsf {T}\) transformation with hash key generation \(\mathsf {T}_{\mathtt {HKG}}=\mathsf {T}_{\mathtt {HKG}}(\mathsf {PKE},G)=(\mathsf {d}\mathsf {KG},\mathsf {dEnc},\mathsf {d}\mathsf {Dec})\) as follows.
-
\(\mathsf {d}\mathsf {KG}(1^\lambda ;r)\): Return \((\mathsf {pk},\mathsf {sk}) \leftarrow \mathsf {KG}(1^\lambda ;G_{\mathtt {kg}}(r))\).
-
\(\mathsf {dEnc}(\mathsf {pk},\mathsf {m})\): Return \(\mathsf {ct}\leftarrow \mathsf {Enc}(\mathsf {pk},\mathsf {m};G_{\mathtt {enc}}(\mathsf {m}))\).
-
\(\mathsf {d}\mathsf {Dec}(\mathsf {sk},\mathsf {CT})\): Return \(\mathsf {m}\leftarrow \mathsf {Dec}(\mathsf {sk},\mathsf {ct})\).
Recall that we define a deterministic PKE scheme is \((\delta _1,\delta _2)\)-correct if it is \(\delta _1\)-correct, and under a randomly generated key \((\mathsf {pk},\mathsf {sk})\), the probability that a randomly generated message m has a collision, that is, another message \(m'\) such that \(\mathsf {dEnc}(\mathsf {pk},m)=\mathsf {dEnc}(\mathsf {pk},m')\) is bounded by \(\delta _2\). Under this definition, as shown by [LW21, Lemma 4], \(T(\mathsf {PKE},G_{\mathtt {enc}})\) is \((\delta ,2\delta )\)-correct if \(\mathsf {PKE}\) is \(\delta \)-correct for any \(\delta \). We can easily see that the correctness of \(\mathsf {T}_{\mathtt {HKG}}(\mathsf {PKE},G)\) can be reduced to that of \(\mathsf {T}(\mathsf {PKE},G_{\mathtt {enc}})\), and thus \(\mathsf {T}_{\mathtt {HKG}}(\mathsf {PKE},G)\) is \((\delta ,2\delta )\)-correct if \(\mathsf {PKE}\) is \(\delta \)-correct for any \(\delta \).
5.2 Security Proof
We prove the following theorem.
Theorem 5.2
Let \(\ell =\ell (\lambda )\) and \({q_{\mathtt {sdm}}}={q_{\mathtt {sdm}}}(\lambda )\) be polynomials and \(\mathsf {PKE}\) be a PKE scheme. Let
 be a QPT adversary against \(\text {SDM-OW-RSA}\) security of \(\mathsf {T}_{\mathtt {HKG}}=\mathsf {T}_{\mathtt {HKG}}(\mathsf {PKE},G)\) making total q (superposition) random oracle queries to \(G_{\mathtt {kg}}\) and \(G_{\mathtt {enc}}\) with query depth d, and outputs a list of size at most t as the final output. Then, there exists a QPT adversary
be a QPT adversary against \(\text {SDM-OW-RSA}\) security of \(\mathsf {T}_{\mathtt {HKG}}=\mathsf {T}_{\mathtt {HKG}}(\mathsf {PKE},G)\) making total q (superposition) random oracle queries to \(G_{\mathtt {kg}}\) and \(G_{\mathtt {enc}}\) with query depth d, and outputs a list of size at most t as the final output. Then, there exists a QPT adversary
 such that
such that

Proof. Without loss of generality, we assume that
 makes random oracle queries to a single random oracle \(G=G_{\mathtt {kg}}\times G_{\mathtt {enc}}\) instead of separate two random oracles \(G_{\mathtt {kg}}\) and \(G_{\mathtt {enc}}\) in the security games. Let
makes random oracle queries to a single random oracle \(G=G_{\mathtt {kg}}\times G_{\mathtt {enc}}\) instead of separate two random oracles \(G_{\mathtt {kg}}\) and \(G_{\mathtt {enc}}\) in the security games. Let
 be a QPT adversary that runs in the same way as
be a QPT adversary that runs in the same way as
 except that before it terminates,
except that before it terminates,
 computes and discards \(G(r')\) for all \(r'\) contained in
computes and discards \(G(r')\) for all \(r'\) contained in
 ’s final output \(\mathsf {T}\). Then,
’s final output \(\mathsf {T}\). Then,
 makes at most \(q+t\) queries to G with query depth \(d+1\), and we have
makes at most \(q+t\) queries to G with query depth \(d+1\), and we have
 . We estimate the latter using hybrid games. Let \(\mathtt{SUC}_X\) be the event that the final output is 1 in Game X.
. We estimate the latter using hybrid games. Let \(\mathtt{SUC}_X\) be the event that the final output is 1 in Game X.
-
Game 1: This is
 .
.-
Initialize: The challenger generates \(r\leftarrow \mathcal {M}\) and generates \((\mathsf {pk}^{k},\mathsf {sk}^{k}) \leftarrow \mathsf {KG}(1^{\lambda };G_{\mathtt {kg}}(r+\varDelta ^{k}))\), where \(\varDelta ^{k}\leftarrow \mathcal {M}\) for every \(k\in [\ell ]\). Then, for every \(k\in [\ell ]\) and \(i\in [{q_{\mathtt {sdm}}}]\), the challenger generates \(s_{i,k}\leftarrow \mathcal {M}\) and computes \(\mathsf {ct}_{i,k} \leftarrow \mathsf {Enc}(\mathsf {pk}^{k}, r+s_{i,k};G_{\mathtt {enc}}(r+s_{i,k}))\). The challenger executes
 .
. -
Finalize: The challenger outputs 1 if and only if \(\mathsf {T}\) contains \(r'\) such that \(r'=r+s_{i,k}\) holds for some \(i\in [{q_{\mathtt {sdm}}}]\) and \(k\in [\ell ]\).
-
-
Game 2: This game is the same as Game 1 except the followings. First, if there exists a pair \((s_{i,k},s_{i',k'})\) such that \(s_{i,k}=s_{i',k'}\), the challenger immediately outputs 0 as the final output of the game. Also, \(G=G_{\mathtt {kg}}\times G_{\mathtt {enc}}\) is replaced with

where \(u^{k},v_{i,k}\leftarrow \mathcal {R}_{\mathtt {kg}}\times \mathcal {R}_{\mathtt {enc}}\) for every \(k\in [\ell ]\) and \(i\in [q_{\mathtt {kdm}}]\).
We have \(\left|\Pr [\mathtt{SUC}_1]-\Pr [\mathtt{SUC}_2] \right|=\frac{\ell {q_{\mathtt {sdm}}}(\ell {q_{\mathtt {sdm}}}-1)}{2\left|\mathcal {M} \right|}\) since Game 1 and 2 are identical unless there exists a pair \((s_{i,k},s_{i',k'})\) such that \(s_{i,k}=s_{i',k'}\). Below, we let \(S=\{r+\varDelta ^{k}\}_{k\in [\ell ]}\cup \{r+s_{i,k}\}_{i\in [{q_{\mathtt {sdm}}}],k\in [\ell ]}\).
Before proceeding the hybrid games, We provide the high level overview of the rest of games. In Game 2, the key generation randomness \(G_{\mathtt {kg}}(r+\varDelta ^{k})\) and encryption randomness \(G_{\mathtt {enc}}(r+s_{i,k})\) correlate with the encrypted plaintexts \(r+s_{i,k}\). Thus, next, at transition from Game 2 to 3, we eliminate the correlation by programming the random oracle. Concretely, in Game 3, the above randomnesses are generated by using V, but
 gets access to only the punctured oracle \(G\setminus S\), not V. In order to justify the programming, we use semi-classical O2H lemma (Lemma 3.1). By doing so, we can justify the programming without square root security loss, and obtain \(\Pr [\mathtt{SUC}_2]\le (d+2)\Pr [\mathtt {Find}_3]\), where \(\mathtt {Find}_X\) be the event that the punctured oracle \(G\setminus S\) returns 1 in Game X. Thus, all we have to do is to bound \(\Pr [\mathtt {Find}_3]\). At Game 3, from the view of
gets access to only the punctured oracle \(G\setminus S\), not V. In order to justify the programming, we use semi-classical O2H lemma (Lemma 3.1). By doing so, we can justify the programming without square root security loss, and obtain \(\Pr [\mathtt{SUC}_2]\le (d+2)\Pr [\mathtt {Find}_3]\), where \(\mathtt {Find}_X\) be the event that the punctured oracle \(G\setminus S\) returns 1 in Game X. Thus, all we have to do is to bound \(\Pr [\mathtt {Find}_3]\). At Game 3, from the view of
 , the key generation randomness and encryption randomness are uniformly random strings that are independent of r, that is, \(u^k\) and \(v_{i,k}\). Namely, the correlation issue above are solved. Thus, at transition from Game 3 to 4, we use the IND-m-CPA security of \(\mathsf {PKE}\), and eliminate information of r from \(\mathsf {ct}_{i,k}\). In Game 4, except the punctured oracle \(G \setminus S\), r is completely hidden from the view of
, the key generation randomness and encryption randomness are uniformly random strings that are independent of r, that is, \(u^k\) and \(v_{i,k}\). Namely, the correlation issue above are solved. Thus, at transition from Game 3 to 4, we use the IND-m-CPA security of \(\mathsf {PKE}\), and eliminate information of r from \(\mathsf {ct}_{i,k}\). In Game 4, except the punctured oracle \(G \setminus S\), r is completely hidden from the view of
 . Therefore, by using Lemma 3.2, we can bound \(\Pr [\mathtt {Find}_4]\) and complete the proof.
. Therefore, by using Lemma 3.2, we can bound \(\Pr [\mathtt {Find}_4]\) and complete the proof.
-
Game 3: This game is the same as Game 2 except that
 gets access to the
gets access to the
 . \((\mathsf {pk}^{k},\mathsf {sk}^{k})\) and \(\mathsf {ct}_{i,k}\) are still generated using V for every \(k\in [\ell ]\) and \(i\in [{q_{\mathtt {sdm}}}]\).
. \((\mathsf {pk}^{k},\mathsf {sk}^{k})\) and \(\mathsf {ct}_{i,k}\) are still generated using V for every \(k\in [\ell ]\) and \(i\in [{q_{\mathtt {sdm}}}]\).
Let \(\mathtt {Find}_X\) be the event that the punctured oracle \(G\setminus S\) returns 1 in Game X. From the definition of
 , we have \(\Pr \left[ \mathtt{SUC}_3\wedge \lnot \mathtt {Find}_3\right] =0\). Thus, we have
, we have \(\Pr \left[ \mathtt{SUC}_3\wedge \lnot \mathtt {Find}_3\right] =0\). Thus, we have
By applying Lemma 3.1, we obtain
Therefore, we also obtain \(\Pr [\mathtt{SUC}_2]\le (d+2)\Pr [\mathtt {Find}_3]\).
-
Game 4: This game is the same as Game 3 except that \(\mathsf {ct}_{i,k}\) is generated as
 for every \(k\in [\ell ]\) and \(i\in [{q_{\mathtt {sdm}}}]\).
for every \(k\in [\ell ]\) and \(i\in [{q_{\mathtt {sdm}}}]\).
In order to estimate \(\left|\Pr [\mathtt {Find}_3]-\Pr [\mathtt {Find}_4] \right|\), using
 , we construct the following QPT adversary
, we construct the following QPT adversary
 against the IND-m-CPA security of \(\mathsf {PKE}\). In the description, a function \(\mathsf {Test}\) takes a value x and a set X as inputs and outputs 1 if \(x\in X\) and 0 otherwise.
against the IND-m-CPA security of \(\mathsf {PKE}\). In the description, a function \(\mathsf {Test}\) takes a value x and a set X as inputs and outputs 1 if \(x\in X\) and 0 otherwise.
-
Initialize: Given \((\mathsf {pk}^{k})_k\),
 first generates \(r\leftarrow \mathcal {M}\).
first generates \(r\leftarrow \mathcal {M}\).
 then generates \(\varDelta ^{k}\leftarrow \mathcal {M}\) for every \(k\in [\ell ]\), \(s_{i,k}\leftarrow \mathcal {M}\) for every \(i\in [{q_{\mathtt {sdm}}}]\) and \(k\in [\ell ]\), and a fresh random oracle G. If there exists a pair \((s_{i,k},s_{i',k'})\) such that \(s_{i,k}=s_{i',k'}\),
then generates \(\varDelta ^{k}\leftarrow \mathcal {M}\) for every \(k\in [\ell ]\), \(s_{i,k}\leftarrow \mathcal {M}\) for every \(i\in [{q_{\mathtt {sdm}}}]\) and \(k\in [\ell ]\), and a fresh random oracle G. If there exists a pair \((s_{i,k},s_{i',k'})\) such that \(s_{i,k}=s_{i',k'}\),
 outputs 0 and terminates. Next, for every \(i\in [{q_{\mathtt {sdm}}}]\) and \(k\in [\ell ]\),
outputs 0 and terminates. Next, for every \(i\in [{q_{\mathtt {sdm}}}]\) and \(k\in [\ell ]\),
 queries \((k,r+s_{i,k},0)\) to its oracle \(O_{\mathtt {IND}}\) and obtains \(\mathsf {ct}_{i,k}\). Finally,
queries \((k,r+s_{i,k},0)\) to its oracle \(O_{\mathtt {IND}}\) and obtains \(\mathsf {ct}_{i,k}\). Finally,
 sets \(b'=0\) and executes
sets \(b'=0\) and executes
 , where \(G\setminus S\) is simulated as follows.
, where \(G\setminus S\) is simulated as follows. -
\(G\setminus S\):When
 makes a (superposition) query \(\left|x\right>\left|y\right>\) to \(G\setminus S\),
makes a (superposition) query \(\left|x\right>\left|y\right>\) to \(G\setminus S\),
 first computes \(\left|x\right>\left|y\right>\left|\mathsf {Test}(x,S)\right>\) and measures \(\left|\mathsf {Test}(x,S)\right>\). If the result is 0,
first computes \(\left|x\right>\left|y\right>\left|\mathsf {Test}(x,S)\right>\) and measures \(\left|\mathsf {Test}(x,S)\right>\). If the result is 0,
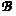 just returns \(\left|x\right>\left|y\oplus G(x)\right>\) to
just returns \(\left|x\right>\left|y\oplus G(x)\right>\) to
 . Otherwise,
. Otherwise,
 set the value of \(b'\) to 1, and returns \(\left|x\right>\left|y\oplus G(x)\right>\) to
set the value of \(b'\) to 1, and returns \(\left|x\right>\left|y\oplus G(x)\right>\) to
 .
. -
Finalize: If
 terminates,
terminates,
 terminates with output \(b'\).
terminates with output \(b'\).
Let the challenge bit in
 be b.
be b.
 perfectly simulates Game 3 and 4 for
perfectly simulates Game 3 and 4 for
 when \(b=0\) and \(b=1\), respectively. Also,
when \(b=0\) and \(b=1\), respectively. Also,
 outputs \(b'=1\) if and only if \(\mathtt {Find}_3\) and \(\mathtt {Find}_4\) occur in the simulated Games. Thus, we have
outputs \(b'=1\) if and only if \(\mathtt {Find}_3\) and \(\mathtt {Find}_4\) occur in the simulated Games. Thus, we have

Finally, we bound \(\Pr [\mathtt {Find}_4]\). In Game 4, conditioned on \((\mathsf {pk}^{k},\varDelta ^{k})_{k\in [\ell ]}\) and \((s_{i,k},\mathsf {ct}_{i,k})_{i\in [{q_{\mathtt {sdm}}}],k\in [\ell ]}\), we have \(\Pr _{r\leftarrow \mathcal {M}}[m\in S]\le \frac{\ell ({q_{\mathtt {sdm}}}+1)}{\left|\mathcal {M} \right|}\) for any \(m\in \mathcal {M}\). Thus, from Lemma 3.2, we obtain \(\Pr [\mathtt {Find}_4]\le \frac{4(q+t)\ell ({q_{\mathtt {sdm}}}+1)}{\left|\mathcal {M} \right|}\).
Overall, we see that there exists a QPT
 that satisfies Eq. (5). \(\Box \) (Theorem 5.2)
that satisfies Eq. (5). \(\Box \) (Theorem 5.2)
6 Conclusion: KDM Security of FO Transformations
In the conclusion, we show that the KDM security in the QROM of FO transformations can be reduced to the IND-CPA security of the underlying PKE scheme without square root security loss.
We first provide the security bound for the KDM-CPA security of the PKE scheme \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}(\mathsf {T}_{\mathtt {HKG}}(\mathsf {PKE},G),H)\) in terms of the IND-m-CPA security of the underlying \(\mathsf {PKE}\). In order to capture the most general setting, we allow adversaries for the KDM-CPA security of \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}(\mathsf {T}_{\mathtt {HKG}}(\mathsf {PKE},G),H)\) and KDM functions queried by them to get access to not only H but also G. The access to G by an adversary does not affect the security proof provided in Sect. 4.2 since H and G are independent random oracles. Then, the following theorem holds.
Theorem 6.1
Let \(\ell =\ell (\lambda )\) be a polynomial and \(\mathsf {PKE}\) be a \(\delta \)-correct PKE scheme. Let
 be an adversary for the KDM-CPA security of \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}(\mathsf {T}_{\mathtt {HKG}}(\mathsf {PKE},G),H)\) making \(q_{\mathtt {kdm}}\) KDM queries. Suppose
be an adversary for the KDM-CPA security of \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}(\mathsf {T}_{\mathtt {HKG}}(\mathsf {PKE},G),H)\) making \(q_{\mathtt {kdm}}\) KDM queries. Suppose
 makes at most \(q^G\) (resp. \(q^H\)) super-position random oracle queries to G (resp. H) with query depth \(d^G\) (resp. \(d^H\)). Also, suppose KDM functions queried by
makes at most \(q^G\) (resp. \(q^H\)) super-position random oracle queries to G (resp. H) with query depth \(d^G\) (resp. \(d^H\)). Also, suppose KDM functions queried by
 makes at most \(q_f^G\) (resp. \(q_f^H\)) classical random oracle queries to G (resp. H). Then, there exists a QPT adversary
makes at most \(q_f^G\) (resp. \(q_f^H\)) classical random oracle queries to G (resp. H). Then, there exists a QPT adversary
 such that
such that

Proof. We estimate the number of queries to G made by
 appeared in the proof of Theorem 4.2 when
appeared in the proof of Theorem 4.2 when
 is used inside of it. First,
is used inside of it. First,
 make \(O(q^G)\) queries with depth \(O(d^G)\) in order to simulate queries to G made by
make \(O(q^G)\) queries with depth \(O(d^G)\) in order to simulate queries to G made by
 . Also, every time
. Also, every time
 makes a query to \(V_{i^{*}}\),
makes a query to \(V_{i^{*}}\),
 needs to make at most \(O(\ell +q_f^G)\) queries to G with depth \(O(q_f^G)\) in order for the computation of \(\widehat{f}_{i,b}\). Since
needs to make at most \(O(\ell +q_f^G)\) queries to G with depth \(O(q_f^G)\) in order for the computation of \(\widehat{f}_{i,b}\). Since
 makes at most \(O(q^H)\) queries to \(V_{i^{*}}\) with depth \(O(d^H)\), to simulate
makes at most \(O(q^H)\) queries to \(V_{i^{*}}\) with depth \(O(d^H)\), to simulate
 ’s queries to \(V_{i^{*}}\),
’s queries to \(V_{i^{*}}\),
 needs to make at most \(O(q^H\cdot (\ell +q_f^G))\) queries to G with query depth \(O(d^H\cdot q_f^G)\). Therefore,
needs to make at most \(O(q^H\cdot (\ell +q_f^G))\) queries to G with query depth \(O(d^H\cdot q_f^G)\). Therefore,
 makes at most \(O(q^G+q^H\cdot (\ell +q_f^G))\) queries to G with query depth \(O(d^G+d^H\cdot q_f^G)\). This holds for every \({d^*}\in [d]\). Also, Since
makes at most \(O(q^G+q^H\cdot (\ell +q_f^G))\) queries to G with query depth \(O(d^G+d^H\cdot q_f^G)\). This holds for every \({d^*}\in [d]\). Also, Since
 outputs a list of size \(O(q^H)\), so does
outputs a list of size \(O(q^H)\), so does
 for every \({d^*}\in [d]\). From this fact and Theorem 4.2 and 5.2, we see that there exists a QPT
for every \({d^*}\in [d]\). From this fact and Theorem 4.2 and 5.2, we see that there exists a QPT
 that satisfies Eq. (6).
that satisfies Eq. (6).
\(\Box \) (Theorem 6.1)
Remark 6.1
(On the value of \(q_f^G\) and \(q_f^H\).). Note that the values of \(q_f^G\) and \(q_f^H\) are determined depending on usage scenarios and independent of the adversary’s behavior. For example, in the usage scenario where we need only circular security such as anonymous credential [CL01], we can set \(q_f^G=q_f^H=0\). In that case, the multiplicative term of
 in Eq. (6) is roughly the square of the query depth of
in Eq. (6) is roughly the square of the query depth of
 to the random oracles. It is asymptotically the same as the multiplicative term appeared in the proof of IND-CCA secure KEM using O2H lemma with MRM [KSS+20]. In order to capture a wide range of applications, we allow KDM functions to get access to the random oracles in this work, but we think \(q_f^G\) and \(q_f^H\) are not large in many applications.
to the random oracles. It is asymptotically the same as the multiplicative term appeared in the proof of IND-CCA secure KEM using O2H lemma with MRM [KSS+20]. In order to capture a wide range of applications, we allow KDM functions to get access to the random oracles in this work, but we think \(q_f^G\) and \(q_f^H\) are not large in many applications.
Let \(\mathsf {FO}^{\bot }_{m,\mathtt {OTP}}(\mathsf {PKE},G_{\mathtt {enc}},H)\) be a PKE scheme constructed by combining the KEM \(\mathsf {U}^{\bot }_{m}(\mathsf {T}(\mathsf {PKE},G_{\mathtt {enc}}),H)\) with OTP as DEM. From Theorem 6.1, we can show that \(\mathsf {FO}^{\bot }_{m}(\mathsf {PKE},G_{\mathtt {enc}},H)\) satisfies KDM-CPA security with asymptotically the same security loss with respect to the underlying IND-m-CPA secure \(\mathsf {PKE}\) as Eq. (6). Concretely, we have the following theorem.
Theorem 6.2
Let \(\ell =\ell (\lambda )\) be a polynomial and \(\mathsf {PKE}\) be a PKE scheme. Let
 be an adversary for the KDM-ATK security of \(\mathsf {FO}^{\bot }_{m,\mathtt {OTP}}(\mathsf {PKE},G_{\mathtt {enc}},H)\) where \(\text {ATK}\in \{\text {CPA},\text {CCA}\}\). Then, for \(\mathsf {atk}\in \{\mathsf {cpa},\mathsf {cca}\}\), there exists an adversary
be an adversary for the KDM-ATK security of \(\mathsf {FO}^{\bot }_{m,\mathtt {OTP}}(\mathsf {PKE},G_{\mathtt {enc}},H)\) where \(\text {ATK}\in \{\text {CPA},\text {CCA}\}\). Then, for \(\mathsf {atk}\in \{\mathsf {cpa},\mathsf {cca}\}\), there exists an adversary
 such that
such that

Proof. Suppose we modify the security game
 so that the k-th key pair \((\mathsf {pk}^{k},\mathsf {sk}^{k})\) is generated by using \(G_{\mathtt {kg}}(r^{k})\) as the random coin for \(\mathsf {KG}\) for every \(k\in [\ell ]\), where \(G_{\mathtt {kg}}:\mathcal {M}\rightarrow \mathcal {R}_{\mathtt {kg}}\) is a random oracle and \(r^{k}\leftarrow \mathcal {M}\) for every \(k\in [\ell ]\). If \(r^{1},\ldots ,r^{\ell }\) are mutually different, then the distribution of \(\ell \) key pairs does not change from the view of
so that the k-th key pair \((\mathsf {pk}^{k},\mathsf {sk}^{k})\) is generated by using \(G_{\mathtt {kg}}(r^{k})\) as the random coin for \(\mathsf {KG}\) for every \(k\in [\ell ]\), where \(G_{\mathtt {kg}}:\mathcal {M}\rightarrow \mathcal {R}_{\mathtt {kg}}\) is a random oracle and \(r^{k}\leftarrow \mathcal {M}\) for every \(k\in [\ell ]\). If \(r^{1},\ldots ,r^{\ell }\) are mutually different, then the distribution of \(\ell \) key pairs does not change from the view of
 by this modification. We emphasize that
by this modification. We emphasize that
 does not have access to \(G_{\mathtt {kg}}\). By the modification,
does not have access to \(G_{\mathtt {kg}}\). By the modification,
 ’s advantage is changed at most \(\frac{\ell (\ell -1)}{2\left|\mathcal {M} \right|}\). We can see that we can easily construct an adversary
’s advantage is changed at most \(\frac{\ell (\ell -1)}{2\left|\mathcal {M} \right|}\). We can see that we can easily construct an adversary
 such that
such that
 is exactly the same as
is exactly the same as
 ’ advantage in the modified game. Therefore, we obtain the theorem. \(\Box \) (Theorem 6.2)
’ advantage in the modified game. Therefore, we obtain the theorem. \(\Box \) (Theorem 6.2)
Thus, we see that the KDM-CPA security of \(\mathsf {FO}^{\bot }_{m,\mathtt {OTP}}(\mathsf {PKE},G_{\mathtt {enc}},H)\) is reduced to that of \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}(\mathsf {T}_{\mathtt {HKG}}(\mathsf {PKE},G),H)\) with additional security loss \(\frac{\ell (\ell -1)}{2\left|\mathcal {M} \right|}\) which is absorbed by the additive term of Eq. (6).
Extension to KDM-CCA Security. In the main body of this paper, we focused on KDM-CPA security. Our proof technique is also compatible with KDM-CCA security. Concretely, we can prove the KDM-CCA security of a PKE scheme constructed by using a variant of \(\mathsf {U}^{\bot }_{m}\) called \(\mathsf {U}^{\bot ,\mathtt {keyconf}}_m=\mathsf {U}^{\bot ,\mathtt {keyconf}}_m(\mathsf {d}\mathsf {PKE},H)\) as KEM and OTP-then-MAC as DEM without square root security loss if the underlying \(\mathsf {d}\mathsf {PKE}\) is \(\text {SDM-OW-RSA}\) secure and additionally satisfies injectiveness. The security proof is a combination of our proof for the KDM-CPA security of \(\mathsf {U}^{\bot }_{m,\mathtt {OTP}}\) and the proof for the IND-CCA security of \(\mathsf {U}^{\bot ,\mathtt {keyconf}}_m\) by [BHH+19, KSS+20]. We provide the formal description of this construction and security proof for the KDM-CCA security of it in [KN21].
By following a similar argument as the case of KDM-CPA security, we can show that the KDM-CCA security of the KEM \(\mathsf {FO}^{\bot ,\mathtt {keyconf}}_{m}(\mathsf {PKE},G_{\mathtt {enc}},H)=\mathsf {U}^{\bot ,\mathtt {keyconf}}_m(T(\mathsf {PKE},G_{\mathtt {enc}}),H)\) combined with OTP-then-MAC as DEM, can be reduced to the IND-CPA security of \(\mathsf {PKE}\). The multiplicative term in the security bound with respect to the underlying \(\mathsf {PKE}\) is roughly the same as Eq. (6) though some additive terms are added to the security bound.
Notes
- 1.
Here, we ignore security loss by the number of queries and constants for simplicity.
- 2.
- 3.
Strong one-time MAC unconditionally exists.
- 4.
We can achieve PKE in the \(\ell \)-user setting with advantage \(\epsilon ^\prime \) from standard PKE with advantage \(\epsilon \) such that \(\epsilon ^\prime \approx \ell \cdot \epsilon \).
- 5.
Precisely speaking, the FO transformations studied in the context of QROM are somewhat different from the original FO transformation [FO13].
- 6.
We again note that we use variants of \(\mathsf {T}\) and \(\mathsf {U}\) transformations defined by [BHH+19] in this work.
- 7.
The lemma states that if \(\Pr [A\wedge \lnot C]=\Pr [B \wedge \lnot C]\), \(\left|\Pr [A]-\Pr [B] \right| \le \Pr [C]\) holds for any events A,B, and C.
- 8.
The notation
 indicates that
indicates that
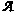 is allowed to make a query to O in super-position. Also, for the definition of query depth, see Sect. 3.
is allowed to make a query to O in super-position. Also, for the definition of query depth, see Sect. 3.
References
Ambainis, A., Hamburg, M., Unruh, D.: Quantum security proofs using semi-classical Oracles. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11693, pp. 269–295. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26951-7_10
Abadi, M., Rogaway, P.: Reconciling two views of cryptography (the computational soundness of formal encryption). J. Cryptol. 15(2), 103–127 (2002)
Bellare, M., Boldyreva, A., Micali, S.: Public-key encryption in a multi-user setting: security proofs and improvements. In: Preneel, B. (ed.) EUROCRYPT 2000. LNCS, vol. 1807, pp. 259–274. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-45539-6_18
Boneh, D., Dagdelen, Ö., Fischlin, M., Lehmann, A., Schaffner, C., Zhandry, M.: Random Oracles in a quantum world. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 41–69. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25385-0_3
Backes, M., Dürmuth, M., Unruh, D.: OAEP is secure under key-dependent messages. In: Pieprzyk, J. (ed.) ASIACRYPT 2008. LNCS, vol. 5350, pp. 506–523. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-89255-7_31
Bindel, N., Hamburg, M., Hövelmanns, K., Hülsing, A., Persichetti, E.: Tighter proofs of CCA security in the quantum random Oracle model. In: Hofheinz, D., Rosen, A. (eds.) TCC 2019. LNCS, vol. 11892, pp. 61–90. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-36033-7_3
Boneh, D., Halevi, S., Hamburg, M., Ostrovsky, R.: Circular-secure encryption from decision Diffie-Hellman. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 108–125. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_7
Bleichenbacher, D.: Chosen ciphertext attacks against protocols based on the RSA encryption standard PKCS #1. In: Krawczyk, H. (ed.) CRYPTO 1998. LNCS, vol. 1462, pp. 1–12. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0055716
Bellare, M., Rogaway, P.: Random Oracles are practical: a paradigm for designing efficient protocols. In ACM CCS 93, 62–73 (1993)
Bellare, M., Rogaway, P.: Optimal asymmetric encryption. In: De Santis, A. (ed.) EUROCRYPT 1994. LNCS, vol. 950, pp. 92–111. Springer, Heidelberg (1995). https://doi.org/10.1007/BFb0053428
Black, J., Rogaway, P., Shrimpton, T.: Encryption-scheme security in the presence of key-dependent messages. In: Nyberg, K., Heys, H. (eds.) SAC 2002. LNCS, vol. 2595, pp. 62–75. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36492-7_6
Camenisch, J., Lysyanskaya, A.: An efficient system for non-transferable anonymous credentials with optional anonymity revocation. In: Pfitzmann, B. (ed.) EUROCRYPT 2001. LNCS, vol. 2045, pp. 93–118. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44987-6_7
Dolev, D., Dwork, C., Naor, M.: Nonmalleable cryptography. SIAM J. Comput. 30(2), 391–437 (2000)
Davies, G.T., Stam, M.: KDM security in the hybrid framework. In: Benaloh, J. (ed.) CT-RSA 2014. LNCS, vol. 8366, pp. 461–480. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-04852-9_24
Fujisaki, E., Okamoto, T.: Secure integration of asymmetric and symmetric encryption schemes. J. Cryptol. 26(1), 80–101 (2011). https://doi.org/10.1007/s00145-011-9114-1
Gentry, C.: A fully homomorphic encryption scheme. Ph.D. thesis, Stanford University (2009). crypto.stanford.edu/craig
Hofheinz, D., Hövelmanns, K., Kiltz, E.: A modular analysis of the Fujisaki-Okamoto transformation. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10677, pp. 341–371. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_12
Hövelmanns, K., Kiltz, E., Schäge, S., Unruh, D.: Generic authenticated key exchange in the quantum random Oracle model. In: Kiayias, A., Kohlweiss, M., Wallden, P., Zikas, V. (eds.) PKC 2020. LNCS, vol. 12111, pp. 389–422. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45388-6_14
Jiang, H., Zhang, Z., Chen, L., Wang, H., Ma, Z.: IND-CCA-secure key encapsulation mechanism in the quantum random Oracle model, revisited. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10993, pp. 96–125. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96878-0_4
Jiang, H., Zhang, Z., Ma, Z.: Key encapsulation mechanism with explicit rejection in the quantum random Oracle model. In: Lin, D., Sako, K. (eds.) PKC 2019. LNCS, vol. 11443, pp. 618–645. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17259-6_21
Jiang, H., Zhang, Z., Ma, Z.: Tighter security proofs for generic key encapsulation mechanism in the quantum random Oracle model. In: Ding, J., Steinwandt, R. (eds.) PQCrypto 2019. LNCS, vol. 11505, pp. 227–248. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-25510-7_13
Kitagawa, F., Matsuda, T., Hanaoka, G., Tanaka, K.: On the key dependent message security of the Fujisaki-Okamoto constructions. In: Cheng, C.-M., Chung, K.-M., Persiano, G., Yang, B.-Y. (eds.) PKC 2016. LNCS, vol. 9614, pp. 99–129. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49384-7_5
Kitagawa, F., Nishimaki, R.: KDM Security for the Fujisaki-Okamoto Transformations in the QROM. IACR Cryptol. ePrint Arch., p. 1200 (2021)
Kuchta, V., Sakzad, A., Stehlé, D., Steinfeld, R., Sun, S.-F.: Measure-rewind-measure: tighter quantum random Oracle model proofs for one-way to hiding and CCA security. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020. LNCS, vol. 12107, pp. 703–728. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45727-3_24
Liu, X., Wang, M.: QCCA-secure generic key encapsulation mechanism with tighter security in the quantum random Oracle model. In: Garay, J.A. (ed.) PKC 2021. LNCS, vol. 12710, pp. 3–26. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-75245-3_1
Rackoff, C., Simon, D.R.: Non-interactive zero-knowledge proof of knowledge and chosen ciphertext attack. In: Feigenbaum, J. (ed.) CRYPTO 1991. LNCS, vol. 576, pp. 433–444. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-46766-1_35
Saito, T., Xagawa, K., Yamakawa, T.: Tightly-secure key-encapsulation mechanism in the quantum random Oracle model. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10822, pp. 520–551. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78372-7_17
Targhi, E.E., Unruh, D.: Post-quantum security of the Fujisaki-Okamoto and OAEP transforms. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9986, pp. 192–216. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53644-5_8
Unruh, D.: Quantum position verification in the random Oracle model. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8617, pp. 1–18. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44381-1_1
Unruh, D.: Revocable quantum timed-release encryption. J. ACM 62(6), 49:1–49:76 (2015)
Zhandry, M.: Secure identity-based encryption in the quantum random Oracle model. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 758–775. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_44
Zhang, J.: Delegating quantum computation in the quantum random Oracle model. In: Hofheinz, D., Rosen, A. (eds.) TCC 2019. LNCS, vol. 11892, pp. 30–60. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-36033-7_2
Acknowledgments
The authors thank Takashi Yamakawa for helpful comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 International Association for Cryptologic Research
About this paper
Cite this paper
Kitagawa, F., Nishimaki, R. (2022). KDM Security for the Fujisaki-Okamoto Transformations in the QROM. In: Hanaoka, G., Shikata, J., Watanabe, Y. (eds) Public-Key Cryptography – PKC 2022. PKC 2022. Lecture Notes in Computer Science(), vol 13178. Springer, Cham. https://doi.org/10.1007/978-3-030-97131-1_10
Download citation
DOI: https://doi.org/10.1007/978-3-030-97131-1_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-97130-4
Online ISBN: 978-3-030-97131-1
eBook Packages: Computer ScienceComputer Science (R0)





 .
. .
. .
.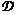 is roughly three times longer than that of
is roughly three times longer than that of
 . Moreover, if
. Moreover, if
 makes at most q queries to G and H with query depth d,
makes at most q queries to G and H with query depth d,
 makes at most O(q) queries to each of those oracles with query depth O(d), and outputs a list
makes at most O(q) queries to each of those oracles with query depth O(d), and outputs a list 
 for the first oracle.
for the first oracle. , where
, where  gets access into
gets access into  .
. .
.  (and functions queried by
(and functions queried by
 ) gets access every time it is invoked. The detailed description is as follows.
) gets access every time it is invoked. The detailed description is as follows.

 .
.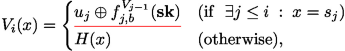
 for every
for every 



 makes the
makes the  it updates the random oracle into
it updates the random oracle into  just before
just before
 makes the
makes the  makes
makes  at this point. The challenger outputs
at this point. The challenger outputs  : Given an input z,
: Given an input z,
 parse it as Eq. (
parse it as Eq. ( from
from
 ’s
’s  at that point.
at that point.
 simulates
simulates  gets access into
gets access into  terminates with output
terminates with output  outputs 1 if
outputs 1 if  : Given
: Given  first simulates
first simulates  chooses a challenge bit
chooses a challenge bit  then executes
then executes
 just before
just before
 makes the
makes the  makes
makes  sets
sets  also sets
also sets  at this point. Finally,
at this point. Finally,
 outputs
outputs
 .
. .
. .
.
 gets access to the
gets access to the
 .
.  for every
for every  first generates
first generates  then generates
then generates  outputs 0 and terminates. Next, for every
outputs 0 and terminates. Next, for every  queries
queries  sets
sets  , where
, where  makes a (superposition) query
makes a (superposition) query  first computes
first computes  just returns
just returns  . Otherwise,
. Otherwise,
 set the value of
set the value of  .
. terminates,
terminates,
 terminates with output
terminates with output  indicates that
indicates that
 is allowed to make a query to O in super-position. Also, for the definition of query depth, see Sect.
is allowed to make a query to O in super-position. Also, for the definition of query depth, see Sect. 