A Survey on Chaos-Based Cryptosystems: Implementations and Applications

Abstract

Chaos theory is considered as a tool for studying the systems that show divergence and disorder. After having used discrete mathematics to deduce non-convergence situations, these theories are modeled in the form of a dynamic system and are applied in several domains such as electronic, mechanic, network security, etc. In network security domain, the development of new cryptosystems based on chaos is a relatively new area of research and is increasingly relevant. The essence of the theoretical and practical efforts in this field derive from the fact that these cryptosystems are faster than conventional methods, while ensuring performance of security, at least similar. In this paper, we discuss several proposals about chaos-based cryptosystem and pseudo-random number generator (PRNG). Moreover, topology and architecture of the proposed chaos systems are detailed. Finally, in order to show the more suitable system for encryption and secure communication, a synthesis comparison is presented and considered.

1 Introduction

Nowadays, network communication is vulnerable to many threats and cyber-attacks and it becomes more important for network experts to safeguard the network access [1]. Among the available security mechanisms, chaos-based cryptosystems are considered one of the most effective solution that provides the integrity, the authentication and the confidentiality. Recently, the development of new cryptosystems based on chaos is a relatively new area of research and is increasingly relevant.

In [2], an Field-Programmable-Gate-Array (FPGA) implementation of image encryption purpose using two chaotic discrete time systems. The proposed two phases algorithm is executed by using the well known Arnold Cat map and the generalized logistic map, respectively. Authors in [3] initiate a systematic methodology for securing real-time video communication. The proposed chaos-based cryptosystem have been implemented on an FPGA hardware platform via Verilog Hardware Description Language (Verilog HDL). Sreenath and Narayanan [4] presents a Hardware implementation of a Pseudo chaos signal generator using three reconfigurable discrete time systems with a linear feedback shift registers (RLFSR). The proposed technique was implemented using Verilog HDL codes, then analyzed using Xilinx Plan Ahead compiler and Model-sim software. In terms of network security protocols, [5] proposed a novel chaos-based mechanism that includes Pseudo-Random Key-Generator which can be used to secure a socket-based communication. The proposed key-generator, created by solving the Lorenz chaos-system, has the main task of delivering at each opened channel a new 32-bit key that is used for encrypting/decryption the exchanged data.

In this paper, we discuss several proposals about chaos-based cryptosystem and pseudo-random number generator (PRNG). Moreover, topology and architecture of the proposed chaos systems are detailed. Finally, in order to show the more suitable system for encryption and secure communication, a synthesis comparison is presented and considered.

The remainder of this paper is structured as follows. Section 2 describes the classification of the most used chaotic systems. Section 3 shows the hardware implementations of these chaotic systems as well as their purposes. Section 4 concludes this paper.

2 Background and Description of Chaotic Systems

Due to the sensitivity and periodicity properties, chaotic systems have been involved mainly in key generation of the recently proposed cryptography schemes. Regarding their topology and mathematical model, we can classify all existing and newly proposed chaos systems in two main categories: continuous-time systems and discrete-time systems.

2.1 Continuous Time Systems

The continuous-time systems are described by a set of linear differential equation. Moreover, in order to ensure that the dynamical systems to be chaotic, the dimensions of the system’s phase space must be at least equal to three (3). In the literature, there are several well known continuous-time systems such as Lorenz [6], Chen [7], Lu [8], etc.

Lorenz System The basic form of the Lorenz 3-D system is described by the following set of equation:

$$\begin{aligned}&\dot{x}= a(y-x)\\&\dot{y}= y+bx-xz\\&\dot{z}= xy-cz \end{aligned}$$

where x, y and z are the state variables. a, b and c are the system parameters. The chaotic behaviour (see Fig. 1) appears for a = 10, b = 28 and c = 8/3 with the initial conditions $x_0=0$, $y_0=5$ and $z_0=25$ [8].

Fig. 1

Trajectory graph of the Lorenz system

Van-der-Pol System The Van-der-Pol oscillator as given in [9], is described in two dimensions as follows:

$$\begin{aligned}&\dot{x}= a(x-(1/3)x^{3}-y)\\&\dot{y}= (1/a)x \end{aligned}$$

where x, y are the state variables, and a is the system controller. The phase portrait of the 2-D system is illustrated in Fig. 2.

Fig. 2

Phase plan projection of the Van-der-Pol system

Chen System Based on the 3-D Lorenz system, Chen 3-D system is proposed and described by the following set of equations:

$$\begin{aligned}&\dot{x}= a(y-x)\\&\dot{y}= (b-a)x+by-xz\\&\dot{z}= xy-cz \end{aligned}$$

where x, y and z are the state variables. a, b and c are the system parameters. The chaotic behaviour appears for a = 35, b = 28 and c = 8/3 [10], while the phase plan projection is shown in Fig. 3.

Fig. 3

Phase plan X−Y projection of the 3-D Chen system

Lu System The Lu system is known as the bridge between Lorenz system and Chen system [8]. Thereby, the mathematical model is given as follows:

$$\begin{aligned}&\dot{x}= a(y-x)\\&\dot{y}= by-xz\\&\dot{z}= xy-cz \end{aligned}$$

where x, y and z are the state variables. a, b and c are the system parameters. The trajectory graph of the proposed system is given in Fig. 4.

Fig. 4

Trajectory X−Y−Z of the 3-D Lu system

Linz-Sprott System Trying to simplify the formula of a chaotic system, Linz and Sprott [10] have proposed a new system which is defined as follows:

$$\begin{aligned}&\dot{x}= y\\&\dot{y}= z\\&\dot{z}= -az-y-1+|x |\end{aligned}$$

where x, y and z are the state variables and a is the system’s parameter. As shown in Fig. 5, the chaotic behaviour of the proposed system is achieved for a = 0.6.

Fig. 5

Trajectory X−Y−Z of the Linz-Sprott system

Four-Wing memristive hyperchaotic System Looking for higher dimensional chaotic system, authors in [11] have proposed a novel 4-D system which is described as follows:

$$\begin{aligned}&\dot{x}= ax+byz\\&\dot{y}= cy+dxz-pyW(w)-Q\\&\dot{z}= ez+fxy+gxw\\&\dot{w}= -y\\&W(w)= m+3nw^{2} \end{aligned}$$

where x, y, z, w are the state variables. a, b, c, d, e, f, g, m, n, p, Q are the controllers of the proposed system. In order to ensure the chaotic behaviour, the controllers parameters are defined as follows: a = 0.35, b = −10, c = −0.6, d = 0.3, e = −1.6, f = 2, g = 0.1, m = 0.1, n = 0.01, p = 0.2 and Q = 0.01. The trajectory graphs corresponding to the proposed system with the associated parameters, are shown in Fig. 6.

Fig. 6

Trajectory graphs of the proposed 4-Wing system

New 3-D Continuous Time System Getting inspired from the Lorenz system [12], with only two (02) controllers, a novel 3-D system is proposed and defined as follows:

$$\begin{aligned}&\dot{x}= y-x-az\\&\dot{y}= xz-x\\&\dot{z}= -xy-y+b \end{aligned}$$

where x, y and z are the state variables. a and b are the system parameters. The chaotic behaviour of the proposed system is observed for the values a = 0.5 and b = 1 while the initial conditions are $x_0=y_0=z_0=0$ (see Fig. 7).

Fig. 7

Phase plan projections of the proposed 3-D system

New 4-D Continuous Time System In [13], another new 4-D chaotic system is proposed based on the Rossler system, and defined by the following set of equations:

$$\begin{aligned}&\dot{x}= -y-z+dw\\&\dot{y}= x+ay\\&\dot{z}= b+z(x-c)-a(y-w)\\&\dot{w}= az-w \end{aligned}$$

where x, y, z and w are the state variables. a, b, c and d are the system parameters. By choosing a = 0.4, b = 0.6, c = 3 and d = 0.8, the chaotic behaviour of the proposed system is showed by phase plan projection (see Fig. 8).

Fig. 8

Phase plan projection of the proposed system

2.2 Discrete Time Systems

The discrete time chaos system is a dynamic system which works in increments and takes the conditions at a given time t to change these conditions at a later time $t+\Delta {t}$. Hence, unlike the mathematical model of the continuous time systems, discrete time maps are described mathematically by an iterated function. Moreover, the dimension of the system’s phase space could be only equal to one (01) to show chaos behaviour.

Logistic Map In the literature, many proposals have used the well known logistic map such as in [14] for PRNG, [2] for image encryption,[15] for chaotic signal generating, etc. The mathematical description of this map is given as follows:

$$\begin{aligned}&x_{i+1}= ax_{i}(1-x_{i}) \end{aligned}$$

where $x_{i}$ is the state variable and a is the system controller.

To ensure the chaotic behaviour (see Figs. 9 and 10) of this system, a should be in the interval $[3.57-4]$.

Fig. 9

Trajectory graph of the logistic map

Fig. 10

Signal graph of the logistic map

Hénon Map A simple 2-D with quadratic non-linearity, Hénon system was the first map to show strange attractor with a fractal structure [16]. The mathematical description of this map is given as follows:

$$\begin{aligned}&x_{i+1}= a+y_{i}- x_{i}^{2}\\&y_{i+1}= bx_{i} \end{aligned}$$

where $x_{i}$ and $y_{i}$ are the state variables and a, b are the system controllers.

The obtained strange attractor of this map, is shown in Fig. 11 while the controllers are a = 1.4 and b = 0.3.

Fig. 11

Trajectory graph of the Hénon map

Rene-Lozi Map By introducing the absolute value in the Hénon map, the Rene-Lozi map used in [17] for stream cipher purpose, is described as follows:

$$\begin{aligned}&x_{i+1}= 1+y_{i}-a|x_{i}|\\&y_{i+1}= bx_{i} \end{aligned}$$

where $x_{i}$ and $y_{i}$ are the state variables and a, b are the system controllers.

Similarly to the Hénon map, it has been shown that for a = 1.4 and b = 0.3, chaotic behaviour of this map can appear (see Fig. 12).

Fig. 12

Trajectory graph of the Rene-Lozi map

Bernoulli Map Unlike all the discrete time maps, Bernoulli map is composed of two piece-wise linear parts which are separated by a discontinue space of points [11] (see Fig. 13).

Mathematically, the Bernoulli map is defined as follows:

$$\begin{aligned} x_{i+1} = {\left\{ \begin{array}{ll} ax_{i}+0.5 &{} \text {if}\, x < 0\\ ax_{i}-0.5 &{} \text {if}\, x \ge 0, \end{array}\right. } \end{aligned}$$

where $x_{i}$ is the state variable and a is the control parameter.

The chaotic status of this map is ensure for all the values of the parameter a inside the interval $]1.4 - 2]$ (see Fig. 14).

Fig. 13

Trajectory graph of the Bernoulli map

Fig. 14

Signal graph of the Bernoulli map

Sine Map The sine map is qualitatively similar to the logistic map, and the superficial similarity has resulted in a much deeper connection.

As indicated by its name, the sine map is defined by a sine function as follows:

$$\begin{aligned}&x_{i+1}= a\sin (\pi x_{i}),\quad 0 \le x_{i} \le 1, \,a>0 \end{aligned}$$

where $x_{i}$ is the state variable and a is the system parameter. The projection graph which proves the behaviour of this map is shown in Fig. 15.

Fig. 15

Trajectory graph of the sine map

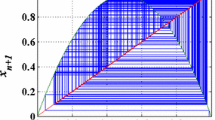
Tent Map Regarding the slope of its mathematical function, tent map with only one state variable, is considered as a slope of two (02) model. Without any control parameter, the tent map is defined as follows:

$$\begin{aligned} x_{i+1} = {\left\{ \begin{array}{ll} 2x_{i} &{} \text {if}\, 0 \le x_{i} < 1/2\\ 2(1-x_{i}) &{} \text {if}\, 1/2 \le x_{i} \le 1 \end{array}\right. } \end{aligned}$$

where $x_{i}$ is the state variable. Moreover, the trajectory graph of the tent map is shown in Fig. 16.

Fig. 16

Trajectory graph of the tent map

All these systems have been used mainly for either generating random numbers, cipher keys or chaotic signals. They differ from each other in terms of dimension, control parameters and the purpose of use. In Table 1 we summarize all these differences obtained regarding our study.

Table 1 Summary of the chaotic systems: description and purpose of application

3 Hardware Implementations and Applications

FPGA-based prototyping is specifically geared toward meeting the design and verification demands created by the complexities of low and constrained resources devices. Moreover, FPGA-based prototyping allows designers to develop and test their systems and provides software developers early access to a fully functioning hardware platform long before silicon is available. In order to be implemented on FPGA, the continuous time systems need to be discredited numerically using some popular methods such as Euler and Runge-Kutta (RK) methods. Euler’s method is a straight-forward method that estimates the next point based on the rate of change at the current point and it is easy to code [19]. It is called also a single step method. While RK methods are actually a family of schemes derived in a specific style. Higher order accurate RK methods are multi-stage because they involve slope calculations at multiple steps at or between the current and next discrete time values [20]. The next value of the dependent variable is calculated by taking a weighted average of these multiple stages based on a Taylor series approximation of the solution. The weights in this weighted average are derived by solving non-linear algebraic equations which are formed by requiring cancellation of error terms in the Taylor series. Developing higher order RK methods is tedious and difficult without using symbolic tools for computation. The most popular RK method is RK4 since it offers a good balance between order of accuracy and cost of computation. RK4 is the highest order explicit Runge-Kutta method that requires the same number of steps as the order of accuracy (i.e. RK1 = 1 stage, RK2 = 2 stages, RK3 = 3 stages, RK4 = 4 stages, RK5 = 6 stages, $\ldots$). Beyond fourth order the RK methods become relatively more expensive to compute. Among all the studied proposals, we have synthesised a brief comparison that includes mainly the used FPGA technology and the consumed resources. Table 2 summarizes the difference between different proposals regarding the chosen system as well as the resource consumption. However, we found that in the single-precision and the double-precision operations, there are more than $10^{-6}$ differences in less than 100 iterations, and the difference reaches more than one digit after 1000 iterations [21]. This is because the binary has a round-off error, so the binary cannot strictly obey the commutative law or the distribution law in floating-point operations.

Table 2 Summary of the FPGA implementations

4 Conclusion

In this paper, we discuss several proposals about chaos-based cryptosystem and pseudo-random number generator (PRNG). Moreover, topology and architecture of the proposed chaos systems are detailed. Finally, in order to show the more suitable system for encryption and secure communication, a synthesis comparison is presented and considered.