Universality of Boltzmann Statistical Mechanics, Thermodynamics, Quantum Mechanics, and Shannon Information Theory

Abstract

Universal nature of Boltzmann statistical mechanics, generalized thermodynamics, quantum mechanics, spacetime, black hole mechanics, Shannon information theory, Faraday lines of force, and Banach-Tarski paradox (BTP) are studied. The nature of matter and Dirac anti-matter are described in terms of states of compression and rarefaction of physical space, Aristotle fifth element, or Casimir vacuum identified as a compressible tachyonic fluid. The model is in harmony with perceptions of Plato who believed that the world was formed from a formless primordial medium that was initially in a state of total chaos or “Tohu Vavohu” (Sohrab in Int J Mech 8:73–84, [1]). Hierarchies of statistical fields from photonic to cosmic scales lead to universal scale-invariant Schrödinger equation thus allowing for new perspectives regarding connections between classical mechanics, quantum mechanics, and chaos theory. The nature of external physical time and its connections to internal thermodynamics time and Rovelli thermal time are described. Finally, some implications of renormalized Planck distribution function to economic systems are examined.

1 Introduction

The universal nature of turbulence and mathematical similarities amongst transport laws shared by stochastic quantum fields [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18] and classical hydrodynamic fields [19,20,21,22,23,24,25,26,27,28,29,30,31] resulted in introduction of a scale-invariant model of Boltzmann statistical mechanics and its applications to the fields of thermodynamics [32, 33], fluid mechanics [34, 35], and quantum mechanics [36,37,38] at intermediate, large, and small scales.

The present study begins with a brief description of invariant model of Boltzmann statistical mechanics and the invariant forms of conservation equations. Next, generalized thermodynamics and Helmholtz decomposition of energy and momentum, and definitions of dark-energy, dark-matter, and dark-momentum are discussed. The concept of internal spacetime versus external independent space and time and their connection to Rovelli thermal time are presented. Invariant Schrödinger equation recently derived from invariant Bernoulli equation [38] and some of its implications to a new paradigm for physical foundation of quantum mechanics are described next. In particular, the nature of wave function, wave-particle duality, and hierarchies of quantum mechanics wave functions and particles as de Broglie wave-packets [4] are studied. Also, the implication of the model to entropy and the problem of information loss in black hole is addressed. A universal hydrodynamic model of Faraday line of force applicable from very small scale of stochastic chromodynamics to the exceedingly large cosmic scale is presented. Finally, some implications of the model to Banach-Tarski paradox are examined.

2 Scale–Invariant Model of Boltzmann Statistical Mechanics

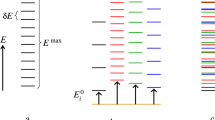
The scale-invariant model of statistical mechanics for equilibrium galactic-, planetary-, hydro-system-, fluid-element-, eddy-, cluster-, molecular-, atomic-, subatomic-, kromo-, and tachyon-dynamics corresponding to the scale β = g, p, h, f, e, c, m, a, s, k, and t is schematically shown on the left hand side of Fig. 1.

Fig. 1

A scale-invariant model of statistical mechanics. Equilibrium-β-dynamics on the left-hand-side and non-equilibrium laminar-β-dynamics on the right-hand-side for scales β = g, p, h, f, e, c, m, a, s, k, and t as defined in [37]. Characteristic lengths of (system, element, “atom”) are $(\text{L}_\upbeta ,\lambda_\upbeta ,\ell_\upbeta )$ and λ_β is the mean-free-path

For each statistical field, one defines particles that form the background fluid and are viewed as point-mass or “atom” of the field. Next, the elements of the field are defined as finite-sized composite entities composed of an ensemble of “atoms”. Finally, ensemble of a large number of “elements” is defined as the statistical “system” at that particular scale. The most-probable element of scale β defines the “atom” (system) of the next higher β + 1 (lower β − 1) scale.

Following the classical methods [20, 39,40,41,42,43], the invariant definitions of the density ρ_β, and the velocity of atom u_β, element v_β, and system w_β at the scale β are given as [37]

$${\uprho }_\upbeta = \text{n}_\upbeta {{\text{m}}}_\upbeta = \text{m}_\upbeta \int {\text{f}_\upbeta {{\text{du}}}_\upbeta } ,\quad {\mathbf{u}}_\upbeta = {\mathbf{v}}_{{\text{w}}\upbeta - 1}$$

(1)

$${{\mathbf{v}}}_\upbeta = \uprho_\upbeta^{ - 1} \text{m}_\upbeta \int {{\mathbf{u}}_\upbeta f_\upbeta {\text{du}}_\upbeta } ,\quad {\mathbf{w}}_\upbeta = {\mathbf{v}}_{{\text{w}}\upbeta + 1}$$

(2)

Similarly, the invariant definitions of the peculiar and diffusion velocities are introduced as

$${{\mathbf{V}^{\prime}}}_\upbeta = {\mathbf{u}}_\upbeta - \mathbf{v}_\upbeta ,\quad {\mathbf{V}}_\upbeta = {\mathbf{v}}_\upbeta - \mathbf{w}_\upbeta ,\quad {\mathbf{V}}_\upbeta = {{{\mathbf{V}}^{\prime}}}_{\upbeta + 1}$$

(3)

A magnified view of part of hierarchy of statistical fields in Fig. 1 is shown in Fig. 2 where atomic, element, and system velocities of stochastic fields are better revealed.

Fig. 2

Hierarchy of embedded statistical fields from LAD to LED scales with atom ${\mathbf{u}}_\upbeta$, element ${\mathbf{v}}_\upbeta$, and system ${\mathbf{w}}_\upbeta$ velocity

Following the classical methods [20, 39,40,41], the scale-invariant forms of mass, thermal energy, linear and angular momentum conservation equations at scale β are given as [34, 35]

$$\frac{{\partial {\uprho }_{{{\text{i}}\upbeta }} }}{{\partial t_{\upbeta } }} + {{\nabla }}.({\uprho }_{{{\text{i}}\upbeta }} {{\mathbf{v}}}_{\upbeta } ) = \Re_{{{\text{i}}\upbeta }}$$

(4)

$$\frac{{\partial {\upvarepsilon }_{{{\text{i}}\upbeta }} }}{{\partial t_{\upbeta } }} + {{\nabla }}.{{(\upvarepsilon }}_{{{\text{i}}\upbeta }} {{\mathbf{v}}}_{\upbeta } ) = 0$$

(5)

$$\frac{{\partial {{\mathbf{p}}}_{{{\text{i}}\upbeta }} }}{{\partial t_{\upbeta } }} + {{\nabla }}.({{\mathbf{p}}}_{{{\text{i}}\upbeta }} {{\mathbf{v}}}_{\upbeta } ) = - {{\nabla }}.\mathbf{P}_{{\text{{ij}}\upbeta }}$$

(6)

$$\frac{{\partial {\varvec{\uppi }}_{{{{\text{i}}\upbeta }}} }}{{\partial t_{\upbeta } }} + {{\nabla }}.({\varvec{\uppi }}_{{{{\text{i}}\upbeta }}} {{\mathbf{v}}}_{\upbeta } ) = {\uprho }_{{{{\text{i}}\upbeta }}} {\varvec{\upomega }}_{\upbeta } .\nabla {{\mathbf{v}}}_{\upbeta }$$

(7)

involving the volumetric density of thermal energy $\upvarepsilon_{{\text{i}}\upbeta } = {\uprho }_{{\text{i}}\upbeta } \tilde{h}_{{\text{i}}\upbeta }$, linear momentum ${{\mathbf{p}}}_{{\text{i}}\upbeta } = {\uprho }_{{\text{i}}\upbeta } {{\mathbf{v}}}_{{\text{i}}\upbeta }$, and angular momentum ${\varvec{\uppi }}_{{\text{i}}\upbeta } = {\uprho }_{{{\text{i}}}\upbeta } {\varvec{\upomega }}_{{{\text{i}}}\upbeta }$ (since $\text{r}_{{\text{a}}\upbeta - 1} = 1$). Also, $\Re_{{\text{i}}\upbeta }$ is the chemical reaction rate and $\tilde{h}_{{\text{i}}\upbeta } = \hat{h}_{{\text{i}}\upbeta } /{\text{m}}_\upbeta$ is the absolute enthalpy [37]. It is noted that the time coordinates in (4–7) also have a scale subscript β.

3 Generalized Thermodynamics, Helmholtz Decomposition of Thermal Energy and Momentum

To arrive at scale-invariant model of Boltzmann statistical mechanics with (atom, element, system) velocities $({\mathbf{u}}_{{\text{i}}\upbeta } ,{{\mathbf{v}}}_{{\text{i}}\upbeta } ,{\mathbf{w}}_{{\text{i}}\upbeta } )$, one requires a stable “atom” stabilized by an external pressure acting as Poincaré stress [36, 37]. Next, atoms with different energy $\upvarepsilon_\text{j} = {\text{h}}\upnu_{\text{j}}$ are grouped in atomic-clusters or elements (energy levels) of various sizes. Atoms of various energy are under constant motion and allowed to make transition between elements by emitting/absorbing sub-particles. The question is, given the total number of atoms N of an ideal gas and the total energy H, with mean atomic enthalpy $\hat{h}_\text{w} = 4{\text{k}}T$ hence $H = 4N\text{k}T$ [33], what distribution of element sizes corresponding to various atomic energy, speed, and momenta leads to stochastically stationary field. Such state of thermodynamic equilibrium corresponds to energy, speed, and velocity of particles being governed by invariant Planck, Maxwell–Boltzmann, and Gauss (Maxwell) distribution functions [37].

$$\frac{\upvarepsilon_\upbeta {\text{dN}}_\upbeta }{\text{{V}}} = \frac{8\uppi \text{h}}{{{\text{u}}_\upbeta^3 }} \frac{\upnu_\upbeta^3 }{{{\text{e}}^{{{\text{h}}}\upnu_\upbeta /{\text{kT}}} - 1}} {{\text{d}}}\upnu_\upbeta$$

(8)

$$\frac{{{\text{dN}}_{{{\text{u}}}\upbeta } }}{\text{N}} = 4\uppi \left( {\frac{{\text{m}}_\upbeta }{{2\uppi {{\text{kT}}}_\upbeta }}} \right)^{3/2} {\text{u}}_\upbeta^2 \text{e}^{ - {\text{m}}_\upbeta {\text{u}}_\upbeta^2 /2\text{kT}_\upbeta } {{\text{du}}}_\upbeta$$

(9)

$$\text{f}_\upbeta ({{\text{v}}}_\upbeta ) = \left( {\frac{{{\text{m}}}_\upbeta }{{2\uppi {{{\text{kT}}}}_\upbeta }}} \right)^{3/2} {{{\text{e}}}}^{ - {{\text{m}}}_\upbeta {{{\text{u}}}}_\upbeta^2 /2{{{\text{kT}}}}_\upbeta }$$

(10)

Also, due to the closure of the gap between photon gas in Planck equilibrium radiation theory and ideal gas in Boltzmann kinetic theory, just like photon gas, the potential and internal energy of ideal gas are related as [38]

$$p_{\upbeta } V_{\upbeta } = \frac{{U_{\upbeta } }}{3} = \frac{{3N{\text{k}}T_{\upbeta } }}{3} = N{\text{k}}T_{\upbeta }$$

(11)

Hence, Sommerfeld [44] “total thermal energy” or enthalpy $H_{\upbeta }$ for an ideal gas is the sum of internal energy and potential energy [33]

$$H_{\upbeta } = U_{\upbeta } + p_{\upbeta } V_{\upbeta } = U_{\upbeta } + U_{\upbeta } /3 = \frac{4}{3}U_{\upbeta } = 4N_{\upbeta } {\text{k}}T_{\upbeta }$$

(12)

By (11)–(12), enthalpy could also be expressed as

$$\begin{aligned} H_{\upbeta }& = U_{\upbeta } + \frac{{U_{\upbeta } }}{3} = U_{\upbeta } + \frac{{H_{\upbeta } }}{4} = U_{\upbeta } + \frac{1}{4}\left( {U_{\upbeta } + \frac{{U_{\upbeta } }}{3}} \right) = \cdots \\ & = U_{\upbeta } \left( {{1} + \frac{1}{4} +\frac{1}{4^2 } + \frac{1}{4^3 } + \cdots } \right) = \frac{4}{3}U_{\upbeta } \end{aligned}$$

(13)

involving Archimedes [45] theorem on the area under a parabolic segment

$$1 + \frac{1}{4} +\frac{1}{4^2 } + \frac{1}{4^3 } + \cdots = \sum_{\text{n} = 0}^\infty {\frac{1}{4^{{\text{n}}} }} = \frac{4}{3}$$

(14)

With frequency made dimensionless through division by the most probable or Wien frequency ν_w, re-normalized Planck [46] distributions at two adjacent scales appear as shown in Fig. 3.

Fig. 3

Re-normalized Planck energy distributions as a function of $\nu /\nu_w$

It is known that precisely 3/4 and 1/4 of the total thermal energy under Planck distribution curve in Fig. 3 fall on $\nu > \nu_w$ and $\nu < \nu_w$ sides of Wien frequency $\nu_w$ [33]. In his pioneering study, Helmholtz [47] decomposed the total thermal energy or enthalpy H into what he called free-heat and latent-heat that were recently identified as internal energy U and potential energy pV [33]

$$H_{\upbeta } = U_{\upbeta } + p_{\upbeta } V_{\upbeta }$$

(15)

Hence, the result in (14) is in exact agreement with the pioneering prediction by Hasenöhrl [48, 49] of the relation between total energy and electromagnetic energy or dark-energy expressed as

$$H_{\upbeta } = \text{M}_{{\text{t}}} {{{\text{c}}}}^2 = \frac{{4}}{3}\text{M}_{{{{\text{EM}}}}} {\text{c}}^2$$

(16)

such that total mass relates to electro-magnetic mass by [38]

$$\text{M}_{{{\text{t}}}} = \frac{{4}}{3}\text{M}_{{{{\text{EM}}}}}$$

(17)

Since in equilibrium radiation within enclosures photons are at “stationary state”, their speed is Wien speed

$${\text{v}}_{{{{\text{kw}}}}}^2 = {\text{v}}_{{{{\text{kw}}}}^+ }^2 + {\text{v}}_{{{{\text{kw}}}}^- }^2 = 2{\text{v}}_{{{{\text{kw}}}} + }^2$$

(18)

that is related to the root-mean square speed by [33]

$${\text{c}}^2 = {\text{c}}_{{{{\text{rk}}}}}^2 = 3{\text{v}}_{{{{\text{kw}}}} + }^2$$

(19)

Therefore, Lorentz [50] relativistic mass also leads to prediction of Hasenöhrl [48, 49]

$$\text{M}_{{\text{t}}} = \frac{{\text{M}_{{{{\text{EM}}}}} }}{{(1 - \text{v}_{{{{\text{kw}}}}}^2 /{{\text{c}}}^2 )^{1/2} }} \simeq \text{M}_{{{{\text{EM}}}}} \left( {1 + \frac{{\text{v}_{{{{\text{kw}}}}}^2 }}{2{\text{c}}^2 }} \right) = \text{M}_{{{\text{EM}}}} \left( {1 + \frac{1}{3}} \right) = \frac{4}{3}\text{M}_{{{{\text{EM}}}}}$$

(20)

As discussed in [32], if potential energy is identified as dark-matter or gravitational mass

$$p_{\upbeta } V_{\upbeta } = \text{M}_{{{\text{DM}}}{\upbeta }} {\text{c}}^2 = \frac{{{1 }}}{3}{\text{M}}_{{{{\text{EM}}}}{\upbeta }} {\text{c}}^2 = \frac{{{1 }}}{4}{\text{M}}_{{{{\text{t}}}}_{\upbeta } } {\text{c}}^2 = {\text{N}}_{\upbeta } {{{\text{kT}}}}_{\upbeta }$$

(21)

total mass becomes the sum of dark energy or electromagnetic mass M_EM, and dark matter or gravitational mass M_GM [32, 51,52,53,54]

$${\text{M}}_{{{{\text{t}}}\upbeta }} = {\text{M}}_{{{{\text{EM}}}}{\upbeta }} + {\text{M}}_{{{{\text{GM}}}}{\upbeta }} = \frac{3}{4}{\text{M}}_{{{\text{t}}}{\upbeta }} + \frac{1}{4}{\text{M}}_{{{\text{t}}}{\upbeta }}$$

(22)

It is most interesting to note that, as discussed in [32], Helmholtz [47] decomposition of system thermal energy at thermodynamic equilibrium in (19) also extends to cosmological scale (Fig. 1) and is in accordance with predictions of general theory of relativity [55, 56] as described by Pauli [56]

The energy of a spatially finite universe is three-quarters electromagnetic and one-quarter gravitational in origin

In addition, predicted fractions 3/4 and 1/4 for dark energy and dark matter in (19) are in good agreement with recent cosmological observations [57,58,59,60].

On the other hand, according to Planck [46] energy distribution (Fig. 3) and (18), dark matter of scale β is the total energy or enthalpy of the next lower scale β − 1.

$$(Dark\,Matter)_{\upbeta}=(Total\,Energy)_{\upbeta - 1}$$

Also, it is known that when particles form “cooper pairs” and behave as composite bosons [61, 62], one can derive Schrödinger equation from invariant Bernoulli equation for potential incompressible flow [38]. Hence, following classical methods [63, 64], quantum mechanics wave function may be expressed as products of translational, rotational, vibrational, and potential (internal) wave functions as [62]

$$\varvec{\Psi}_{\varvec{\upbeta }} = \varvec{\Psi}_{{{\mathbf{t}{\varvec{\upbeta}} }}} \varvec{\Psi}_{{{\mathbf{r}\varvec{\upbeta} }}} \varvec{\Psi}_{{{\mathbf{v}\varvec{\upbeta} }}} \varvec{\Psi}_{{{\mathbf{p}\varvec{\upbeta }}}} = \varvec{\Psi}_{{{\mathbf{t}\varvec{\upbeta} }}} \varvec{\Psi}_{{{\mathbf{r}\varvec{\upbeta} }}} \varvec{\Psi}_{{{\mathbf{v}\varvec{\upbeta }}}} \varvec{\Psi}_{{{\varvec{\upbeta} - 1}}} = \cdots$$

(23)

At cosmological scale $\Psi _{\text{g}}$, the wave-particle duality of galaxies is evidenced by their observed quantized red-shifts [65]. Therefore, the scale-invariance of the model (Fig. 1) and (23) lead to hierarchy of embedded statistical fields with translational TKE, rotational RKE, vibrational VKE kinetic energy (dark energy) and potential energy PE (dark matter) resulting in energy cascade from cosmic to photonic scales shown in Fig. 4.

Fig. 4

Cascades of kinetic energy TKE, RKE, VKE (dark energy), and potential energy PE (dark matter) from cosmic to photonic scales

Following Helmholtz [47], one can consider decomposition of momentum in Normalized Maxwell–Boltzmann (NMB) distribution as a function of dimensionless speed with respect to the most-probable or Wien speed $\text{v}/{{\text{v}}}_{{{\text{w}}}} = \uplambda_{{{\text{w}}}} /\uplambda$ shown in Fig. 5.

Fig. 5

Normalized Maxwell–Boltzmann distribution as a function of dimensionless speed ${{\text{v}}}/{{{\text{v}}}}_w = \lambda_w /\lambda$ [37]

As compared with (3/4, 1/4) division of energy in Planck curve in Fig. 3, the division of momentum on either side of Wien speed in Fig. 5 is (2/3, 1/3). In view of the equality of translation kinetic and potential energy due to Boltzmann equipartition principle, $m_{\upbeta } {\text{v}}_{wx+{\upbeta - 1}}^2 = m_{\upbeta } {\text{V}}^{\prime2}_{x\upbeta }$ [38], three components of momentum are equal due to what is called principle of equipartition of translational momenta

$$\overline{{\text{p}}}_{{{\text{x}}}^+ } = {\text{mv}}_{{{\text{x}}}^+ } = \overline{{{\text{p}}}}_{{{\text{x}}}^- } = {\text{mv}}_{{{\text{x}}} - } = \overline{{{\text{p}}}}^{\prime}_{{\text{x}}} = {\text{mV}}^{\prime}_{{\text{x}}}$$

(24a)

Therefore, for an ideal gas, of the total dimensionless translational momentum ${\overline{{{\text{P}}}}}_x = ({\overline{{{\text{p}}}}}_{x^+ } + {\overline{{{\text{p}}}}}_{x^- } + {\overline{{{\text{p}}}}^{\prime}}_x )/{\overline{{{\text{p}}}}}_{xw} = 3$ under NMB curve in Fig. 5, 2/3 is on ${{{\text{v}}}} > {{{\text{v}}}}_w$ side of the Wien speed and is associated with root-mean-square momenta due to atomic translational velocity in ${({{\text{x}}}}_+ ,{{\text{x}}}_- )$ directions, and 1/3 is on ${{{\text{v}}} < {{\text{v}}}}_w$ side of the Wien speed and is associated with peculiar translational momentum hence,

$$\overline{{{\text{p}}}}_{{\text{x}}} = \overline{{{\text{p}}}}_{{{\text{x}}}^+ } + \overline{{{\text{p}}}}_{{{\text{x}}}^- } + \overline{{{\text{p}}}}^{\prime}_{{\text{x}}} = \frac{2}{3}\overline{{{\text{P}}}}_{{\text{x}}} + \frac{1}{3}\overline{{{\text{P}}}}_{{\text{x}}}$$

(24b)

Parallel to the concept of dark-matter in Helmholtz energy decomposition, for decomposition of momentum the second part of (24b) may be referred to as dark-momentum.

As discussed in a recent study [66], once physical variables are made dimensionless, particular problems of physics become universal problems of mathematics and the nature of the specific physical entities being studied no longer matters. As an example, the distribution of annual personal income in economic systems is considered. In a recent study by Roper [67], it is suggested that the log-Verhulst distribution function fits the data better than does the lognormal distribution function. In view of random nature of economic systems, in some economic literature Gauss normal distribution is considered as “ideal” or optimal income distribution. However, typical data of annual personal income distribution [68] shown in Fig. 6 clearly indicate the non-Gaussian character of actual income distribution.

Fig. 6

Comparison between annual income distributions in 1971 and 2015 [68]

If the income in Fig. 6 is made dimensionless by division with the most probable income I_mp, the distribution will become similar to Planck energy distribution since I/I_mp is in the range (1–4) in Fig. 3 rather than the range (1–3) in Fig. 5. Hence, with dimensionless personal annual income (I/I_mp) viewed as dimensionless frequency (ν/ν_w), renormalized Planck distribution could be considered as the optimum or “ideal” income distribution because it corresponds to an equilibrium i.e., maximum entropy state as discussed below. It is reasonable to anticipate that Gauss normal distribution will govern the vector field corresponding to “velocity” of money flow between various income levels (energy levels), in analogy to kinetic theory of ideal gas [37]. Rather than individuals, at larger scales of companies (corporations), one expects similar normalized Planck distribution of income (like Fig. 3) with thousands (millions) of dollars instead of dollars as “atomic” units exchanging between various income-levels of companies (corporations).

As discussed in [32, 33, 37, 38], in accordance with Boltzmann kinetic theory of ideal gas and Planck theory of photon gas [46], one asks the question: given a total amount of money M and total number of income earners N, what is the distribution of number of income earners N_j with income I_j that results in stochastically stationary i.e., equilibrium economic system. On the other hand, entropy of an ideal gas was recently identified [32, 33] as the maximum number of Heisenberg-Kramers [69] virtual oscillators S = 4Nk, given the total system energy or Hamiltonian i.e., enthalpy TS = H = 4NkT. Therefore, maximization of entropy in Planck [46] distribution ensures that the total energy (total monitory wealth) is distributed amongst maximum number of oscillators (income levels). In such quantum mechanical economic model, the transfer of energy (money) between different energy levels (income levels) will be governed by Schrödinger equation such that at equilibrium all income levels will be in “stationary states”.

In Fig. 6, one notes the shifting of income from middle-class to upper-class from 1971 to 2015 that constitutes a departure from equilibrium thus having a destabilizing effect on the socio-economic system. The unfortunate delta function at the maximum income level in Fig. 6 is even more embarrassing departure from Planck optimal distribution thus further enhancing economic instabilities that may lead to future revolutionary (quantum) change in the socio-economic system.

4 Thermodynamic Definition of Spacetime and the Nature of Rovelli Thermal Time

Since Aristotle [70] and St Augustine [71], the nature of physical time has remained a mysterious problem of physics. The central insight of Aristotle namely “the concept of time without change is meaningless”, although correct remained puzzling and circular since the concept of change itself involves the notion of time. The hierarchy of time durations encountered from cosmic to photonic scales (Fig. 1) is described in an excellent recent book by ‘t Hooft and Vandoren [72]. Although the pioneering insights of Poincaré [73,74,75,76], Lorentz [50], Einstein [77], and Minkowski [78] resulted in introduction of the concept of spacetime as a 4-dimentional manifold, the exact physical nature of such mathematical concept remained obscure. Also, even though Einstein [79] general theory of relativity (GTR) attributed a dynamic character to spacetime, the very notion of existence of time was questioned in what is known as the “time problem” of GTR [80,81,82,83,84,85,86,87,88,89,90].

In a recent study [91], the nature of physical space and time was investigated and the concepts of internal spacetime versus external space and time were introduced. Assuming that a statistical field at scale β is in thermodynamic equilibrium with the physical space at scale (β − 1) within which it resides, both fields will have a homogenous constant temperature $T_\upbeta = T_{\upbeta - 1}$ defined in terms of Wien wavelength of particle thermal oscillations as [33]

$${\text{m}}_\upbeta {\text{u}}_\upbeta^2 = {\text{m}}_{\upbeta - 1} {\text{v}}_{{\text{w}}\upbeta - 1}^2 = {\text{kT}}_{\upbeta - 1} = {\text{k}}\lambda_{{\text{w}}\upbeta - 1}$$

(25)

Hence, by definition of most-probable or Wien speed $\text{v}_{{{\text{ws}}}} = \uplambda_{{{\text{ws}}}} \upnu_{{{\text{ws}}}} = \uplambda_{{{\text{ws}}}} /\uptau_{{{\text{ws}}}}$, one can associate constant internal measures of (extension, duration)

$$\left\{ \begin{gathered} \uplambda_{{{\text{ws}}}} {\text{ Internal measure of extension}} \hfill \\ \uptau_{{{\text{ws}}}} {\text{ Internal measure of duration}} \hfill \\ \end{gathered} \right.$$

(26)

with every “point” or “atom” of space in a universe at constant temperature $T_\upbeta = T_{\upbeta - 1}$. Next, external space and time that are independent of each other are defined in terms of the internal spacetime in (26). For example, at cosmic scale $\upbeta = {\text{g}}$, one employs internal (ruler, clock) of the lower scale of astrophysics β = s to define external space and time coordinates defined as [91]

$$({\text{x}}_\upbeta ,{\text{y}}_\upbeta ,{\text{z}}_\upbeta ) = (N_{{\text{x}}\upbeta } ,N_{{\text{y}}\upbeta } ,N_{{\text{z}}\upbeta } )\uplambda_{{\text{wx}}\upbeta - 1} ,\quad t_\upbeta = N_{{\text{t}}\upbeta } \uptau_{{\text{w}}\upbeta - 1}$$

(27)

with the four numbers $(N_{{\text{x}}\upbeta } ,N_{{\text{y}}\upbeta } ,N_{{\text{z}}\upbeta } ,N_{{\text{t}}\upbeta } )$ being independent numbers. Whereas internal spacetime in (26) provides local structure of spacetime, the external space and time in (27) describe global dynamics of the system and are irreversible. Also, according to (26–27) both internal and external space and time are quantized. The four dimensions $({\text{x}}_\upbeta ,{\text{y}}_\upbeta ,{\text{z}}_\upbeta ,t_\upbeta )$ with three real space and one imaginary time coordinates represent Poincaré [75] and Minkowski [78] four-dimensional spacetime manifold.

Recently, the author became aware of a number of wonderful books and articles by Rovelli [92,93,94,95,96] and consequently learned about his much earlier pioneering contributions to the understanding of the nature of time in general and what he called thermal time in particular. Clearly, the definition of spacetime in (26) is in accordance with the perceptions of Rovelli [95]

The theory seems to indicate that there is no explanation for the peculiar properties of the time variable at the mechanical level. We suggest that such an explanation should be searched at the thermodynamical level. We propose the idea that the very concept of time is meaningful only in the thermodynamic context.

It is emphasized that the definition of internal spacetime in (26) is based on thermodynamic equilibrium corresponding to stochastically stationary thus time-reversible state. The objective is to define what the variable called physical time represents as noted by Rovelli [95]

It may seem strange that time is determined by an equilibrium state, since in an equilibrium state the system loses track of the direction (the versus, the arrow) of time. However, we are not concern here with versus of the time flow: we are concerned with definition of a variable that represents time, which is a very different problem.

Therefore, the external or physical time quantitatively defined in (27) is called Rovelli thermal time. Of course, because entropy generation due to various dissipations in all real systems lead to change in temperature, the internal measures of spacetime in (26) will also change. For example, in cosmology, the internal measure of spacetime change extremely slowly (eons) due to dissipations and the expansion of universe.

In another recent investigation by Rovelli [96] concerning general relativistic statistical mechanics, thermodynamic temperature was related to the ratio between the thermal time $\uptau$ and physical time t as

$$T = \frac{\uptau }{{\text{t}}}$$

(28)

Since dimension of absolute temperature is meters $T = \uplambda_{\text{w}}$, (28) appears to be dimensionally non-homogeneous. To reveal the nature of dimensional homogeneity of (28) we consider the velocity ratio

$$\frac{{{\text{v}}}}{{\text{v}_{{{\text{w}}}} }} = \frac{{\text{x}}/{{\text{t}}}}{\uplambda_{\text{w}} /\uptau_{\text{w}} } = \frac{\uptau_{\text{w}} }{{\text{t}}}\frac{\text{x}}{\uplambda_{\text{w}} } = {\text{N}}$$

(29)

When the external spatial extension or length is defined as $x = {\text{N}}\ell_{{\text{x}}} {\text{m}}$, (29) simplifies as

$$\frac{\uptau_{\text{w}} }{{{\text{t}}}} = \frac{{\text{N}}\uplambda_{{{\text{w}}}} }{{\text{x}}} = \frac{{\text{N}}\uplambda_{{{\text{w}}}} }{{{\text{N}}\ell_{{\text{x}}} }} = \frac{\uplambda_{\text{w}} }{{\ell_{\text{x}} }} = \uplambda_{{{\text{w}}}} = T$$

(30)

Equation (30) that is dimensionally homogeneous becomes identical to (28) because of the choice of the metric or unit of length $\ell_{\text{x}} = 1\,{\text{m}}$. Therefore, (30) in effect requires that the unit of length (say meters) for external spatial coordinate x be identical to the internal unit employed to express absolute temperature $T = \uplambda_{\text{w}} {\text{m}}$.

According to (27), since external (ruler, clock) = (x_β, t_β) at scale β within the hierarchy (Fig. 1) are always defined in terms of internal (ruler, clock) = (λ_wβ−1, τ_wβ−1) at the next lower scale β − 1, the definition of (extension, duration) = (space, time) could be relegated to lower scales ad infinitum. This is because infinite divisibility of both extension and duration must follow the philosophy of Anaxagoras [97]

Neither is there a smallest part of what is small, but there is always a smaller, for it is impossible that what is should ever cease to be

Therefore, both absolute zero and absolute infinite (extension, duration) are singularities as ideal Aristotle potential limits never actualized as discussed in [66]. The fundamental and quantum nature of both space and time and their role in constitution of matter in quantum field theory and GTR will be further discussed in the following section.

5 Universality of Quantum Mechanics and the Nature of Wave-Particle Duality

The fact that Boltzmann anticipated quantum mechanics by about three decades is evidenced by the following quotation taken from his pioneering and often neglected 1872 paper [98]

We wish to replace the continuous variable x by a series of discrete values ε, 2ε, 3ε … pε. Hence, we must assume that our molecules are not able to take up a continuous series of kinetic energy values, but rather only values that are multiples of a certain quantity ε. Otherwise, we shall treat exactly the same problem as before. We have many gas molecules in a space R. They are able to have only the following kinetic energies:

$$\upvarepsilon,2\upvarepsilon,3\upvarepsilon,4\upvarepsilon,\ldots,{\text{p}}\upvarepsilon$$

No molecule may have an intermediate or greater energy. When two molecules collide, they can change their kinetic energies in many different ways. However, after the collision the kinetic energy of each molecule must always be a multiple of ε. I certainly do not need to remark that for the moment we are not concerned with a real physical problem. It would be difficult to imagine an apparatus that could regulate the collisions of two bodies in such a way that their kinetic energies after a collision are always multiples of ε. That is not a question here.

Although more recent theoretical understanding of quantum mechanics based on fundamental contributions of its founders Planck [46, 99], Einstein [100], Bohr [101], de Broglie [2,3,4], Heisenberg [102], Dirac [103], Schrödinger [104], Pauli [101], and Born [105] is fully established, its physical and intuitive understanding encounter difficulties due to abstract nature of its mathematical foundation. As a result, the theory confronts many problems associated with its physical interpretation such as

• 1. The nature of wave function and its probabilistic interpretation.

• 2. Wave-particle-duality.

• 3. Particle–particle entanglement.

• 4. Double-slit experiment.

• 5. EPR and problem of action-at-a-distance.

• 6. Quantum-jumps and trajectory problems.

• 7. Schrödinger cat.

among others.

The problem of lack of intuitive understanding of quantum mechanics mentioned above extends to Newton [106] law of gravitation, Einstein [79] general theory of relativity, and Dirac [107] equation of quantum field theory. This is because, similar to quantum mechanics, such mathematical theories were based on certain desired mathematical properties, such as the inverse square law, the equivalence principle, or relativistic wave equation with positive probability, rather than derivation from the first principles. As a result, in spite of excellent predictive power of the theories, the exact connection between abstract mathematical models and the physical phenomena they aim to reveal remain obscure.

Recent investigations [36, 37] were focused on connections between energy spectrum of photon gas given by Planck [99] distribution and both energy and dissipation spectrum of isotropic stationary turbulence. Thus, the gap between the problems of quantum mechanics and hydrodynamics was closed through connections between Cauchy, Euler, Bernoulli equations of hydrodynamics, Hamilton–Jacobi equation of classical mechanics, and finally Schrödinger equation of quantum mechanics. This resulted in recent derivation of invariant time-independent and time-dependent Schrödinger equations from invariant Bernoulli equation for potential incompressible flow [38]

$$\frac{\hbar^2 }{{2{\text{m}}_\upbeta }}\nabla_\upxi^2 {\uppsi }_\upbeta + (\tilde{H}_\upbeta - \tilde{V}_\upbeta ){\uppsi }_\upbeta = 0$$

(31)

$$i\hbar \frac{{\partial {\Psi }_\upbeta }}{\partial t_\upbeta } + \frac{\hbar^2 }{{2{\text{m}}_\upbeta }}\nabla_\upxi^2 {\Psi }_\upbeta - \tilde{V}_\upbeta {\Psi }_\upbeta = 0$$

(32)

The quantum mechanics wave function is defined as [38]

$${\Psi }_{\upbeta } (\upxi ,t) = \uprho^{1/2} \Phi^{\prime}_\upbeta (\upxi ,t) = \uprho^{1/2} {\text{e}}^{ik_{\text{r}} \upxi } {\text{e}}^{ - {\text{i}}\tilde{H}t_\upbeta /\hbar }$$

(33)

such that ${\Psi }_\upbeta {\Psi }_\upbeta^\ast = \uprho_{\upbeta }$ accounts for particle localization in accordance with classical results [108]. The velocity potential $\Phi^{\prime}_\upbeta$ of peculiar velocity that is complex accounts for normalization and hence the success of Born [105] probabilistic interpretation of ${\Psi }_\upbeta$. In the following, some implications of the model to the resolution of problems in the list (1–7) above concerning interpretation of quantum mechanics will be briefly examined.

According to the invariant model of Boltzmann statistical mechanics, each equilibrium statistical field (Fig. 1) is composed of a spectrum of cluster or wave-packet sizes containing “atoms” with velocity, speed, and energy respectively following Gauss, Maxwell–Boltzmann, and Planck distribution functions. As discussed in [38], the conventional field of fluid dynamics does not correspond to equilibrium molecular dynamics EMD β = m but rather to the next higher scale of equilibrium cluster-dynamics ECD β = c. Hence, in stationary fluid at ECD scale, Maxwell–Boltzmann distribution function governs the spectrum of cluster sizes that are stochastically stationary. Random motion of clusters accounts for the Brownian motion of small suspensions that is known to be a non-dissipative stationary phenomenon [36]. Transition of a cluster from a small fast-oscillating “eddy” (high energy-level-j) to a large slowly-oscillating “eddy” (low energy-level-i) results in emission of a “sub-particle” that is a molecule to carry away the excess energy in harmony with Bohr [101] frequency formula $\Delta \varepsilon_{{\text{ji}}\upbeta } = {\text{h}}(\upnu_{{{{\text{j}}}}\upbeta } - \upnu_{{{{\text{i}}}}\upbeta } )$ as schematically shown in Fig. 7a.

Fig. 7

a Transition of cluster c_ij from eddy-j to eddy-i leading to emission of molecule m_ij. b Electron transitions with emission of photon γ_ji [38]

Similarly, but at the much smaller scale of ESD β = s or stochastic electrodynamics (SED), transition of an electron from high to low energy atoms lead to emission of a sub-particle namely photon γ_ji as shown in Fig. 7b.

As described in [38], derivation of invariant Schrödinger equation from invariant Bernoulli equation results in a new paradigm of physical foundation of quantum mechanics. Considering the case of stationary fluid or equilibrium cluster-dynamics ECD β = c, the quantum mechanics wave function ${\Psi }_{\text{c}}$ relates to the velocity potential of particle peculiar velocity. However, particle or “atom” of ECD field namely cluster is the most-probable molecular cluster by definition ${\mathbf{u}}_{\text{c}} = {\mathbf{v}}_{{\text{wm}}}$ in (1). Therefore, particle of scale β is identified as the most probable wave-packet of the lower scale β − 1. Hence, each statistical field will have a quantum mechanics wave function ${\Psi }_\upbeta$ and particle ${{\text{P}}}_\upbeta$ that is stationary wave-packet of the lower scale

$$\left\{ \begin{gathered} \Psi_\upbeta = ({\text{Wave Function)}} = {\text{WF}}_\upbeta \hfill \\ {\text{P}}_\upbeta = ({\text{Particle}})_\upbeta = ({\text{Wave Packet)}}_{\upbeta - 1} = {\text{WP}}_{\upbeta - 1} \hfill \\ \end{gathered} \right.$$

(34)

In harmony with de Broglie [2,3,4] picture of quantum mechanics, motion of “particle” P_β as local singularity identified as wave-packet = WP_β−1 of lower scale is guided by a global external quantum mechanics wave function ${\Psi }_\upbeta$ as schematically shown in Fig. 8.

Fig. 8

Macroscopic wave functions Ψ_β or de Broglie guidance waves at (ECD), (EMD), and (EAD) scales that guide particles identified as wave-packets (WP)_β−1 or de Broglie matter-waves [38]

Hence, at any scale within the hierarchy of statistical fields in Fig. 1, the solution of Schrödinger equation gives the energy spectrum of “atomic” clusters that represent Bohr [101] stationary states or energy levels of the field.

When one moves to the next lower scale of equilibrium molecular dynamics EMD β = m, derivation of Schrödinger equation [38] involves a stationary coordinate moving with velocity ${\mathbf{v}}_{{\text{wa}}}$ since ${\mathbf{v}}_{\text{m}} = {\mathbf{u}}_{\text{m}} - \upvarepsilon {{\mathbf{V}^{\prime}}}_{\text{m}} = {\mathbf{v}}_{{\text{wa}}} - \upvarepsilon {{\mathbf{V}^{\prime}}}_{\text{m}}$ by (1–2). Because by (33) ${\Psi }_{\text{m}}$ relates to the velocity potential of molecular peculiar velocity ${{\mathbf{V}^{\prime}}}_{\text{m}}$, under thermodynamic equilibrium ${\mathbf{v}}_{{\text{wm}}} = {\mathbf{u}}_{\text{c}}$ will also be related to ${{\mathbf{V}^{\prime}}}_{\text{m}}$ thus connecting ${\Psi }_{\text{m}}$ with P_c. As a result, particle P_β of the upper scale is identified as quantum mechanics wave function of the lower scale ${\Psi }_{\upbeta - 1}$ and one arrives at a hierarchy of embedded wave functions expressed as

$$\left\{ \begin{gathered} {\text{P}}_\upbeta = \Psi_{\upbeta - 1} = ({\text{Wave Function)}}_{\upbeta - 1} = {\text{WF}}_{\upbeta - 1} \hfill \\ {\text{P}}_{\upbeta - 1} = ({\text{Wave Packet)}}_{\upbeta - 2} = {\text{WF}}_{\upbeta - 2} \hfill \\ \end{gathered} \right.$$

(35)

According to (35) and Figs. 1 and 6, the universe is composed of hierarchies of embedded waves suggesting that the entire universe was formed when the Almighty decided to make some waves!

The results in (34–35) and Fig. 8 may help in the understanding of the first and second problems in the list 1–7 above. The wave-particle duality problem is understood in terms of wave function ${\Psi }_\upbeta$ that globally guides motion of particles identified as wave-packet of lower scale in accordance with the perceptions of de Broglie [4]. New perspectives provided by the results in (34–35) and Fig. 8 concerning problems 1–2 are also expected to facilitate the resolution of the remaining problems 3–7. For example, problem number 6 namely absence of particle trajectories in quantum mechanics becomes understandable because as shown in Fig. 7, any particle from cluster j can make a transition to cluster i through any arbitrary trajectory with exactly the same final results, thus accounting for success of Feynman method of sum-over-paths. Regarding number 7 problem concerning Schrödinger cat, in view of probabilistic aspect of $\Phi^{\prime}_\upbeta$ hence ${\Psi }_\upbeta$ by (33), it is clear that any interference with the field due to a measuring instrument will disturb the velocity potential thus leading to collapse of the wave function ${\Psi }_\upbeta$.

Schrödinger cat problem is more challenging since it involves the phenomenon of life and death that are not understood. Since as discussed in [1] all living systems are composed of living elements, and living elements are in turn composed of living cells, one may speculate if such infinite regression leads to an “atom of life” or Leibniz “living Monad”! Although at present such questions are metaphysical and hence outside of jurisdiction of science, some aspects of the problem may be considered within the framework of quantum mechanics.

To introduce the required concepts, we need to consider an example from cosmology. It is well known that sometimes around 380,000 years after the explosion of Lemaître [109] “atom” of our universe, the Big Bang, there was decoupling of radiation field from the baryonic matter field and the present Penzias-Wilson [110] cosmic background microwave radiation temperature of 2.73 [m] is remnant of the cooling of Casimir [111] vacuum. It is also reasonable to anticipate that a living system will involve complex dynamics at EMD, EAD, ESD, EKD, END, ETD, … scales (Fig. 1) with END denoting equilibrium-neutrino-dynamics at scale β = n (not shown in Fig. 1). By invariant Schrödinger (31) and (35), hierarchies of wave functions and particles will be associated with such fields. Therefore, due to the well-known decoupling of radiation from matter field in cosmology, one cannot rule out possible decoupling of some fields say neutrino-dynamics (END) or lower scale of tachyon-dynamics (ETD) from the baryonic field of molecular-dynamics of living systems at the moment of death t = t_f. In view of the hierarchies of wave functions in (23), there will be a critical sub-photonic decoupling scale $\upbeta = \upbeta_{\text{d}}$ at which the cascade of wave functions in (23) will be broken

$$\ldots \Psi_{{{{\varvec{\upbeta}}}} = \mathbf{d} + \mathbf{2}} \Psi_{{{\varvec{\upbeta}}} = \mathbf{d} + \mathbf{1}} \Leftarrow \Rightarrow \Psi_{{{\varvec{\upbeta}}} = \mathbf{d}}\Psi_{{{\mathbf{d} - \mathbf{1}}}} \Psi_{{{\mathbf{d} - \mathbf{2}}}} \ldots$$

(36)

Such an event may correspond to what Hegel referred to as the moment in which the spirit transcends temporality [94]. It is ironic that according to such a model, death or decoupling of Schrödinger cat corresponds to the collapse of wave function of cat’s life! Of course, strictly speaking, according to the present model (Fig. 1), complete decoupling hence total isolation of any part of the universe from the rest should be impossible as noted by Boltzmann [37].

Interestingly, Feynman [112] suggested that Schrödinger equation might in fact explain life

Often people in some unjustified fear of physics say you cannot write an equation for life. Well, perhaps we can. As a matter of fact, we very possibly already have the equation to a sufficient approximation when we write the equation of quantum mechanics:

$$\text{{H}}\Psi = - \frac{{{\hbar }}}{{\text{i}}}\frac{{{{\partial {\Psi} }}}}{{{{\partial \text{t}}}}}$$

Although decoupling of sub-photonic statistical fields from living system at molecular-dynamic scale is plausible, regarding its connection to the mind–body problem of Descartes or Hegel’s transcendence of spirit from corporal temporality, I respond by borrowing a quotation from Rovelli [93] about Plato’s account of a statement by Socrates: “I am not sure”.

At the important scale of LKD (Fig. 1) physical space or Casimir vacuum [111] is identified as a compressible fluid, Planck compressible ether [113], as discussed in [114]. A schematic diagram of physical space as states of a compressible fluid from infinite rarefaction (white hole WH) to infinite compression (black hole BH) is shown in Fig. 9.

Fig. 9

Different degrees of rarefaction and compression of Casimir vacuum identified as a compressible fluid. (−3) White hole $\uprho_{{\text{WH}}} = 0$(−2, −1) Anti-matter $\uprho_{{\text{AM}}} < \uprho_{\text{v}}$ (0) Casimir vacuum $\uprho = \uprho_{\text{v}}$ (1, 2) Matter $\uprho_{{\text{MA}}} > \uprho_{\text{v}}$ (3) Black hole $\uprho_{{\text{BH}}} = \infty$ [38]

Compressibility of physical space was recently shown [115] to account for relativistic effects when Michelson number Mi = v/c approaches unity thus revealing the causal [56] nature of Lorentz-FitzGerald contraction in accordance with Poincaré-Lorentz dynamic theory of relativity as opposed to Einstein kinematic theory of relativity in harmony with ideas of Darrigol [116] and Galison [117].

When physical space or Casimir [111] vacuum is identified as superfluid photon or Bose–Einstein condensate, it is reasonable to anticipate that when heated to a critical vaporization or boiling temperature $T_{\text{b}}$, the vacuum or space will nucleate what could be called photon gas bubbles that following Dirac could be also referred to as holes or anti-matter particles. Similarly, if space or Casimir vacuum cools below certain critical fusion or melting temperature $T_{\text{m}}$ liquid photon undergoes phase transition and becomes solidified thus forming solid-light that was defined as black hole [118]. Therefore, in such a model, Hawking evaporation of BH will instead correspond to Hawking melting or sublimation of BH. Loss of mass due to melting of black hole could be caused by heating due to absorption of photon gas bubbles, anti-matter particles, that give their excess energy to melt part of BH and convert it to Casimir vacuum, i.e., space. This is in accordance with absorption of negative curvature energy in classical model of quantum gravity described by ‘t Hooft [119]

When a black hole loses energy, it is primarily because it absorbs negative amounts of ‘curvature energy’. Clearly, our primordial model must allow for the presence of negative amounts of energy. Actually, this is obviously true for quantum mechanical energy, because, after diagonalization, the total Hamiltonian has zero eigenvalue. Prior to diagonalization of the total H, the Hamiltonian density $\mathcal{H}(\text{x})$ must have negative eigenstates. We now see that, since the black hole must lose weight, the primordial model must also have local fluctuations with negative ‘curvature energy’. Black holes absorb negative amounts of energy, allowing positive energy to scape to infinity.

It is due to the postulated thermodynamical stability that the fluctuations surviving at spatial infinity may only have positive energy. Since the total energy balances out, the black hole will therefore receive net amounts of negative energy falling in. Hence it loses weight and decays.

It is reasonable to expect two surfaces of event-horizon (BHH, WHH) to surround (BH, WH) with the corresponding surface temperatures $(T_{\text{m}} ,T_{\text{b}} )$. Under such a paradigm of physical space, Casimir vacuum with constant density $\uprho = \uprho_{\text{v}}$ will correspond to constant measure (zero curvature) Euclidean space, colder and denser $\uprho_{\text{m}} > \uprho_{\text{v}}$ regions correspond to matter (positive curvature) called Riemannian space, and finally hotter and lighter $\uprho_{{\text{am}}} < \uprho_{\text{v}}$ regions correspond to Dirac anti-matter (negative curvature) and called Lobachevskian space [38].

The new perspectives concerning the nature of physical space described in Fig. 9 as well and the identification of dimension of absolute thermodynamic temperature as length [m] associated with Wien wavelength of thermal oscillation will have a major impact on cosmology in general and physical interpretation of Einstein [79] GTR in particular. Compressible nature of physical space (Fig. 9) with “atomic” or quantum volume $\hat{{\text{v}}} = T^3 = \uplambda_{\text{w}}^3$ may facilitate bridging the gap between QM and GTR since it is harmonious with modern paradigms of quantum gravity [119,120,121]. For example, it is reasonable to anticipate that gravitational forces will be associated with gradient of Casimir [111] vacuum density (scalar curvature) hence pressure of physical space.

In a recent study [33] it was shown that entropy of black hole is S = 4Nk in exact agreement with prediction of Major and Setter [122]. The entropy of black hole according to Rovelli and Vidotto [123] is

$$S = {\text{k}}\frac{4}{3}\sqrt[4]{{\frac{\uppi^2 {\text{L}}^3 {{{\text{E}}}}^3 }{{15({\text{c}}\hbar )^3 }}}}$$

(37)

However, one notes that the power of four in the expression

$$\tilde{N}^4 = \frac{\uppi^2 {\text{L}}^3 {{{\text{E}}}}^3 }{{15({\text{c}}\hbar )^3 }}$$

(38)

is due to the four degrees of freedom per oscillator associated with its translational, rotational, vibrational, and potential energy such that the actual number of oscillators is

$$\tilde{N} = \frac{\uppi^2 {\text{L}}^3 {{{\text{E}}}}^3 }{{15({\text{c}}\hbar )^3 }}$$

(39)

From a recent study [37] on closure of the gap between photon gas in Planck equilibrium radiation and Boltzmann kinetic theory of ideal monatomic gas, the number of photons in volume V of Casimir [111] vacuum is

$$N = \frac{8\uppi^5 V}{{45}}\left( {\frac{{{{\text{kT}}}}}{{\text{hc}}}} \right)^3 = \frac{{\uppi^2 \text{L}^3 }}{45}\left( {\frac{{\text{E}}}{{{\text{c}}\hbar }}} \right)^3$$

(40)

The results in (37), (39), and (40) give

$$S = 4N{\text{k}}$$

(41)

in exact agreement with [33, 122].

The result in (41) is also in agreement with general relativistic statistical mechanics of Rovelli [96]

$$S = - \int\limits_\Gamma \rho_\upbeta ( \upbeta \ln\rho - \ln Z) = \upbeta E + \ln Z$$

(42)

when mean value of energy

$$h = - \int\limits_\Gamma \ln\rho$$

(43)

is identified as the internal energy U that is related to Hamiltonian (enthalpy) H as

$$E = h = \frac{3}{4}H = U = 3N{\text{k}}T$$

(44)

Substituting for $\beta = 1/{\text{k}}T = 1/T$, with the assumption k = 1 [96], the translational partition function $Z_{\text{t}} = {{{\text{e}}}}^N$, and the mean energy E from (44) into (42) gives the black hole entropy in (41).

Alternatively, the partition function Z in [96]

$$Z(\upbeta ) = \int {{\text{e}}^{ - \upbeta H} } ={\text{e}}^{ - \upbeta F}$$

(45)

is the translational partition function $Z_{\text{t}} = {{{\text{e}}}}^{ - \upbeta F}$ and $F = - N{\text{k}}T$ is Helmholtz free energy of ideal gas [32]. Inclusion of translational, rotational, and vibrational degrees of freedom gives $Z = Z_{\text{t}} Z_{{{\text{r}}}} Z_{\text{v}} = {{{\text{e}}}}^{ - 3\upbeta F} = {{{\text{e}}}}^{ \upbeta U}$ such that the mean energy E [96]

$$E = - \frac{1}{\upbeta }\frac{{\text{d}}\ln Z}{{{\text{d}}\upbeta }}$$

(46)

becomes the internal energy $U = - 3F = {3}N{{\text{k}}}T$ as in (40). Therefore, the result in (41) is also in exact agreement with entropy given by Rovelli [96] formula

$$S = \upbeta E - \upbeta F$$

(47)

after substitution for $\upbeta = 1/T$, $F = - N{\text{k}}T$, and $E = U = {3}N{{\text{k}}}T$ from (46).

An outstanding problem regarding connection between thermodynamics and black hole mechanics [124,125,126,127,128,129,130] concerns Shannon information theory [131]

$$I = - {\text{K}}\sum\limits_{{{\text{j}}}} {\text{p}_{{{\text{j}}}} } \ln \text{p}_{{{\text{j}}}}$$

(48)

and what happens to the information as matter crosses the event horizon into a black hole. For ideal monatomic gas with four degrees of freedom namely translational, rotational, vibrational, and potential, $Z = Z_{\text{r}} Z_{{{\text{r}}}} Z_{{{\text{v}}}} Z_{{{\text{p}}}} = {{{\text{e}}}}^{4N}$, the atomic, element, and system entropy relate to the number of Heisenberg-Kramers [69] virtual oscillators as [33]

$$\hat{{\text{s}}} = - {\text{k}}\ln {\hat{{\text{p}}}},\quad {\hat{{\text{p}}}} = {{{\text{e}}}}^{ - 4}$$

(49a)

$$S_{\text{j}} = - {\text{k}}\sum\limits_{{{\text{j}}}} {\ln {\hat{{\text{p}}}}} = - {\text{k}}\ln {{\text{p}}}_{{{\text{j}}}} ,\quad {{\text{p}}}_{{\text{j}}} = {{\text{e}}}^{ - 4N_{\text{j}} }$$

(49b)

$$S = \sum_{\text{j}} {S_{{\text{j}}} } = - {\text{k}}\sum_{{{\text{j}}}} {\ln \text{p}_{{{\text{j}}}} } = -{\text{k}}\ln {{\text{p}}},\quad \text{p} = {{\text{e}}}^{ - 4N}$$

(49c)

For a multicomponent mixture, the atomic mixture entropy is [1]

$$\hat{s}_{{\text{mix}}} = \frac{S}{N} = - {\text{k}}\sum {\text{p}_{{{\text{j}}}} \ln \text{p}_{{{\text{j}}}} }$$

(50)

Therefore, Shannon formula in (48) becomes identical to (50) of thermodynamics if one defines Shannon measure K in terms of Boltzmann constant as K = Nk and (48) gives “atomic” information as

$$\hat{{\text{i}}} = \frac{I}{N} = - {\text{k}}\sum_{\text{j}} {\text{p}_{{\text{j}}} } \ln \text{p}_{{\text{j}}}$$

(51)

With entropy identified as the number of Heisenberg-Kramers [69] virtual oscillators, the problem of information loss in black hole is resolved since loss of number of oscillators could be attributed to coarse-graining as photons freeze from liquid to solid phase when they cross black hole event-horizon BHH. In other words, as temperature decreases, atoms of space i.e., photons collect in larger and larger clusters, thus decreasing the number of oscillators leading to loss of entropy by (41) [1]. On the other hand, when anti-matter bubbles enter the black hole, their excess thermal energy leads to melting of part of black hole from solid into liquid photon at BHH increasing entropy and producing more Casimir [111] vacuum that accounts for observed accelerative expansion of the universe [57,58,59,60].

In view of the model of physical space in Fig. 9 and entropy of black hole in (41), it is reasonable to assume that Lemaître [109] primordial “atom” of our universe was in a state of solid light extremely close to absolute zero temperature hence having nearly zero entropy as Planck perfect crystal [46, 99]. This is in harmony with perceptions of Plato who believed that the world was formed from a formless state of total chaos or “Tohu Vavohu” [1]. Since according to Fig. 9 matter and anti-matter annihilate each other leaving Casimir [111] vacuum of a flat universe, in harmony with perceptions of Aristotle there is no “void” except the singularity called white hole (Fig. 9).

6 Universal Hydrodynamic Model of Faraday Line of Force from Cosmic to Photonic Scales

Because of the scale-invariant nature of the model (Fig. 1) the physical insights available at ordinary scales can help in the understanding of nature at much larger or much smaller scales that are less accessible to ordinary human intuition. For example, it is known that a rotating sphere in an otherwise quiescent fluid causes polar inflow jets (IJ) and equatorial outflowing disk (OD) [132] as shown in Fig. 10.

Fig. 10

Direct photograph of swirling equatorial disc outflow (DO) created by a rotating rigid sphere in otherwise stationary silicon oil with aluminum powder illuminated by laser sheet light [132]

However, if the rigid sphere is stationary but instead the surrounding fluid is rotating, Huygens centrifugal forces will reverse direction resulting in accretion by inflowing disk (ID) and polar outflowing jets (OJ). Occurrence of outflow jets (OJ) from black holes is well established in cosmology.

The flow fields in otherwise stationary background fluid induced by rotating spherical particles are shown in Fig. 11.

Fig. 11

Schematic model (a) flow near a spinning particle (b) locally conserved flow streamlines (c) formation of Faraday line of force from a row of co-spinning particles and the associated vortex field within the subquantum background fluid [132]

Because of finite available energy and momentum, such flows cannot extend to infinity and instead form a finite spherical volume by outflowing equatorial disk turning around and joining the inflowing polar jets as shown in Fig. 11b resembling magnetic field lines in electrodynamics. When multiple spinning spheres are present, the hydrodynamic forces cause spinning particles to form a chain of alternating particle and “anti-particle” also called “hole” that is spherical regions of rarefaction, called hydrodynamic model of Faraday line of force [114] schematically shown in Fig. 12.

Fig. 12

Faraday line of force as electron (black) and positron (white) string with inflow jet (IJ) of one matching the outflow jet (OJ) of its neighbor. Also shown are alternating outflow (OD) and inflow discs (ID) [114]

In a pioneering study, Dirac [133] introduced the mathematical concept of Faraday line of force as a directional line with an electron at one end and a positron at the other,

This leads us to a picture of discrete Faraday lines of force, each associated with a charge, −e or +e. There is a direction attached to each line, so that the ends of a line that has two ends are not the same, and there is a charge −e at one end and a charge +e at the other. We may have lines of force extending to infinity, of course, and then there is no charge.

The fluid or Casimir vacuum between two spinning spherical particles is expected to cavitate, because of strong equatorial outflowing disks from spinning particles (Figs. 11 and 12), thus forming a spherical region of vapor called “hole” or Dirac “anti-matter” particle. For example, the Faraday line of force in stochastic electro-dynamics at ESD scale (Fig. 1) will be composed of an alternating chain of electron–positron as shown in Fig. 12. The breakage of such stable vortex lines is analogous to the following description of Dirac [133] concerning the breaking of Faraday line of force:

This process - the breaking of the line of force - would be the picture for creation of an electron (e−) and a positron (e+). It would be quite a reasonable picture, and if one could develop it, it would provide a theory in which e appears as a basic quantity. I have not yet found any reasonable system of equations of motion for these lines of force, and so I just put forward the idea as a possible physical picture we might have in the future.

Similarly, but at much smaller chromodynamics (SU3) or EKD scale, the chromodynamic Faraday line of force will be identified as strings of quark-antiquark as described by ‘t Hooft [134]

It took several years before it became clear that these are exactly the expressions obtained if each of these mesons is viewed as being a kind of rope with quark at one end and an antiquark at the other. The ropes can be stretched ad infinitum, because stretching them adds energy to them, which will be turned into more matter: that is, more rope.

At large hydrodynamic scales turbulent eddies are known to form vortex tubes. By Kelvin circulation theorem, it is known that such vortex lines cannot abruptly end within potential flows and instead must be either pinned to a solid boundary or else close on themselves thus forming a closed vortex “loop” in harmony with LQG [120, 121] models of quantum gravity. Such behavior is well known in superfluid helium-3 experiments revealing “quantized” vortex lines discussed in [132].

An example at molecular-dynamics scale is combustion of acetylene that results in large amounts of soot or carbon particles that form many centimeters long chains. At the much larger scale of astrophysics, it has recently been observed that our galaxy the Milky Way contains large numbers of very long star streams [135, 136]. Finally, at exceedingly large scale of cosmology, it is well known that rotating galaxies form very long streams that could be called cosmic Faraday lines of force.

7 Implication to Banach-Tarski Paradox

In this section, application of invariant model of Helmholtz vorticity equation [34, 35] to the interesting mathematical problem of Banach-Tarski [137] paradox (BTP) is examined. To begin, let us consider a spherical flow within a fluid droplet located at the stagnation point of axisymmetric gaseous counterflow jets as shown in Fig. 13. As seen in this figure, induced by the outer flow, two cylindrically closed recirculation flows, or two tori, form in the upper and lower hemispheres of the spherical droplet.

Fig. 13

Flow in liquid droplet composed of two semi-spherical Hill vortices at stagnation point of gaseous axisymmetric counterflow [34]

The streamlines for such a flow (Fig. 14a) obtained from solution of modified Helmholtz vorticity equation [34].

$$\text{w}_{{\text{r}}} \frac{{\partial {{\varvec{\upomega}}}_\uptheta }}{\partial \upxi } + \text{w}_{{\text{z}}} \frac{{\partial {{\varvec{\upomega}}}_\uptheta }}{\partial \upzeta } = \frac{{{\varvec{\upomega }}_\uptheta \text{v}_{{\text{r}}} }}{\upxi } + \frac{{\partial^2 {{\varvec{\upomega}}}_\uptheta }}{\partial \upxi^2 } + \frac{1}{\upxi }\frac{{\partial {{\varvec{\upomega}}}_\uptheta }}{\partial \upxi } - \frac{{{{\varvec{\upomega}}}_\uptheta }}{\upxi^2 } + \frac{{\partial^2 {{\varvec{\upomega}}}_\uptheta }}{\partial \upzeta^2 }$$

(52)

Fig. 14

a Streamlines from (53). Turning a sphere from (54) inside out: b 1-1 and 2-2 as outer tori, c 1-1 and 2-2 as inner tori [34]

is given by the stream function

$$\Psi = \upzeta \upxi^2 (1 - \upxi^2 /{\text{R}}^2 - \upzeta^2 /{\text{R}}^2 )$$

(53)

Because of linearity of Helmholtz vorticity (52), one can apply the superposition principle and introduce product solutions for flow within two immiscible liquid droplets given by the stream function

$$\Psi = \upzeta^2 \upxi^4 (1 - \upxi^2 /{\text{R}}^2 - \upzeta^2 /{\text{R}}^2 )(3 - \upxi^2 /{\text{R}}^2 - \upzeta^2 /{\text{R}}^2 )$$

(54)

leading to the flow configurations shown in Fig. 14b.

First, the problem of turning a sphere inside-out is considered by looking at flow fields within two concentric spherical flows shown in Fig. 14b. Each hemisphere is composed of two semi-spherical tori, the outer toros 1-1 and the inner toros 3-3 in Fig. 14b. It is easy to imagine that one could compress the inner toros 3-3 towards vertical axis and move it upwards, while the outer toros 1-1 is stretched outwards and pushed down. When one imagines each toros as a cylindrical balloon, the above procedure changes the position of outer 1-1 and inner 3-3 tori thus turning the sphere 14b inside out as shown in Fig. 14c.

A flow configuration that results in fusion of two spheres into one sphere of identical volume is shown in Fig. 15.

Fig. 15

a Hill spherical vortex. b Fusion of two Hill spherical vortices into c a spherical flow composed of two semi-spherical Hill vortices [35]

As two spherical Hill vortices (S₁, S₂) in uniform flow (Fig. 15a) in opposing cylindrically-symmetric jets approach each other (Fig. 15b), they form two semi-spherical Hill vortices [35] and merge into a single spherical flow S₃ at the stagnation point as shown in Fig. 15c. It is possible to adjust the flow conditions such that spheres (S₁, S₂) containing N₁ = N₂ molecules of ideal gas $p_1 V_1 = N_1 {\text{k}}T_1$ and $p_2 V_2 = N_2 {\text{k}}T_2$ form sphere S₃ at temperature T₃

$$T_3 = T_1 /2 = T_2 /2,\quad N_3 = N_1 + N_2 = 2N_1$$

(55)

such that,

$$p_1 V_1 = p_2 V_2 = p_3 V_3 = N_3 {\text{k}}T_3 = E_1$$

(56)

In the above fusion process, density is doubled, temperature is halved, and energy of S₃ is half that of the original two spheres

$$E_3 = p_3 V_3 = E_1 {,}\quad p_1 V_1 { + }p_2 V_2 = E_1 + E_2 = 2E_3$$

(57)

Hence, conservation of energy requires that energy E₁ be removed from the system (exothermic). The inverse process of “fission”, namely S₃ splitting into two spheres (S₁, S₂) will be endothermic and require absorption of energy E₁.

The above transformations of spherical geometry, though related, do not correspond to the mathematical problem of Banach-Tarski paradox (BTP) [137] since in BTP problem a sphere is shown to transform to two spheres with identical volume and density as the original. Hence, BTP constitutes a clear violation of rational foundation of mathematics in the spirit emphasized by Nelson [138]. As a result, some mathematicians have raised objection, and justifiably so, against the assumptions underlying the set theoretical foundation of BTP. It is important to emphasize that the two spheres generated in BTP are known to be “measureless”. In the following, some implications of invariant model of Boltzmann statistical mechanics (Fig. 1) and the associated laws of generalized thermodynamics to BTP are examined.

In the above fusion of spherical objects, whereas the role of number of particles N and volume V as mathematically concepts are clear, that of temperature is not. According to (25) and (26), absolute temperature is the most-probable or Wien wavelength of particle thermal oscillation thus constituting a “measure” of spatial extension. It is most interesting that in his description of hyperbolic geometry, Poincaré [139] anticipated absolute thermodynamic temperature as a “measure” or metric of physical space:

Suppose, for example, a world enclosed in a large sphere and subject to the following laws: The temperature is not uniform; it is greatest at the center, and gradually decreases as we move towards the circumference of the sphere, where it is absolute zero. The law of this temperature is as follows: If R be the radius of the sphere, and r the distance of the point considered from the center, the absolute temperature will be proportional to $R^2 - r^2$. Further, I shall suppose that in this world all bodies have the same coefficient of dilatation, so that the linear dilatation of any body is proportional to its absolute temperature. Finally, I shall assume that a body transported form one point to another of different temperature is instantaneously in thermal equilibrium with its new environment. There is nothing in these hypotheses either contradictory or unimaginable. A moving object will become smaller and smaller at it approaches the circumference of the sphere. Let us observe, in the first place, that although from the point of view of our ordinary geometry this world is finite, to the inhabitants it will appear infinite. As they approach the surface of the sphere, they become colder and at the same time smaller and smaller. The steps they take are therefore smaller and smaller, so that they can never reach the boundary of the sphere. If to us geometry is only the study of the laws according to which invariable solids move, to these imaginary beings it will be the study of the laws of motion of solids deformed by the differences of temperature alluded to.

Therefore, $T_\upbeta = \uplambda_{{\text{w}}\upbeta }$ is called Poincaré thermal measure of extension.

To address BTP problem, we begin with the following thought experiment concerning geometry. Let us consider a circle with 360 m circumference and at spacings of 1-m around the circumference, let straight lines of equal and uniform thickness t = 1 mm be drawn to the origin of the circle as schematically shown in Fig. 16.

Fig. 16

Formation of black-core due to coalescence of radial lines

Clearly, due to their finite thickness, adjacent lines will coalesce on a circle with approximate circumference of 360 mm beyond which the merged lines form a “black core” around the origin as shown in Fig. 16. This thought experiment suggests that there exists a circle with critical minimum radius corresponding to maximum number density even in the limit of infinitesimal thickness of radial lines. Clearly, the diameter of such a “black core” could be used as a measure of maximum resolution of printers.

Therefore, the question is what happens if the above procedure (Fig. 16) is considered in the limits of a circle of infinite radius when infinite number of radial lines of zero thickness are drawn to the origin. For example, at cosmological scale (Fig. 1) the problem corresponds to infinite radial lines from circumference of a spherical universe converging on a galaxy as “atom” at the center like a hologram. As discussed in a recent study on the gap between physics and mathematics [66], the invariant model of statistical mechanics leads to coordinates shown in Fig. 17.

Fig. 17

Hierarchy of normalized coordinates associated with embedded statistical fields [37]

According to this figure, interval $x_\upbeta = (0_\upbeta ,1_\upbeta )$ of upper (outer) scale corresponds to interval $x_{\upbeta - 1} = (1_{\upbeta - 1} ,\infty_{\upbeta - 1} )$ of next lower (inner) scale (Fig. 17). The location of the new origin $x_{\upbeta - 1} = 0_{\upbeta - 1}$ is defined by the new unit of length or measure at the lower scale.

According to Fig. 5, invariant Maxwell–Boltzmann distribution when re-normalized with respect to the most-probable state leads to transformation ${\text{(x}}_{{{\text{mp}}}} \to 1,{\text{x}}_\infty \to 4/\sqrt {\uppi } = 2.567)$. For example, three consecutive scales within the hierarchy of coordinates with ${(0}_{\upbeta } = 10^{ - 120} , 1_{\upbeta } = (4/\sqrt {\uppi } )10^{ - 100} , {\infty }_{\upbeta } = (4/\sqrt {\uppi } )^{2} {10}^{ - 80} )$ and the size of zero and infinity relative to unity taken as ${(10}^{{ - 20}} , 1 , 10^{{20}} )$ is shown in Fig. 18 from the previous study [66].

Fig. 18

Hierarchy of coordinates for hierarchy of embedded statistical fields [66]

Applying the hierarchy of normalized coordinates $x_\upbeta = (0_\upbeta ,1_\upbeta ,\infty_\upbeta )$, results in circular geometry corresponding to three generation as shown in Fig. 19.

Fig. 19

Formation of hierarchy of embedded black holes due to infinite number of compactified statistical fields at the origin [118]

In Fig. 19, three generations covering the range of radii $(0_\upbeta ,1_\upbeta )$, $(0_{\upbeta + 1} ,1_{\upbeta + 1} )$, $(0_{\upbeta + 2} ,1_{\upbeta + 2} )$ are revealed. Following Aristotle, it is assumed that potentially infinite statistical fields are compactified within the black hole singularity at the origin. According to (25) and Fig. 18, since temperature is Wien wavelength or Poincaré thermal measure $T_\upbeta = \uplambda_{{\text{w}}\upbeta }$, absolute zero of adjacent scales relate as $0_\upbeta = 1_{\upbeta - 1} = \infty_{\upbeta - 2}$.

As a second thought experiment, let us consider a spherical volume S₁ at scale $\upbeta$ composed of two semi-spherical tori as shown in Fig. 14a. The central singularity or black hole is at “absolute zero” $r_\upbeta = 0_\upbeta$ and located at the origin. Let the sphere S₁ contain total of $N_1$ atoms of ideal gas ($N_1 /2$ in each toros) at the average temperature $T_{\text{ave}} = \overline{T}$, thus the total energy or enthalpy $E_1 = H_1 = 4N_1 {\text{k}}\overline{T}$ [33]. Let thermal energy $E_1$ be added to S₁ resulting in $N_1$ new atoms being decompactified from “black hole” singularity, due to phase transition such as melting, forming a smaller internal spherical volume (tori 3-3 and 4-4 in Fig. 14b) at temperature $T_3 = T_4 = T_L$. It is assumed that half of the added energy $E_1$ is absorbed by gases in original sphere S₁ (tori 1-1 and 2-2 in Fig. 14b) raising their temperature from $T_{{\text{ave}}} = \overline{T}$ to $T_1 = T_2 = T_{\text{H}}$. Finally, let the two embedded spheres in Fig. 14b undergo fission and split into two spheres S₂ = Tori (1-1)-(3-3) and S₃ = Tori (2-2)-(4-4). It is assumed that during the fission process the heat exchange between tori (1-1) and (3-3) results in their temperatures being respectively lowered and raised to the average temperature $(T_{{\text{H}}} + T_{{\text{L}}} )/2 = T_{\text{ave}} = \overline{T}$. Exactly similar heat exchange is assumed between (2-2) and (4-4) tori also leading to the same final average temperature $\overline{T}$.

Therefore, the original sphere S₁ has undergone an endothermic fission process (absorbed energy E₁) creating two identical spheres S₂ and S₃ with exactly the same number of atoms N₁, volume V₁, pressure p₁, and temperature $\overline{T}$. This process could be repeated ad infinitum, as long as energy E₁ is added to the system each time, due to Aristotle potentially infinite statistical fields that are compactified in the central black hole singularity [118]. Satisfaction of energy conservation principle as well as clarification of “measureless” nature of generated spheres in BTP problem, through introduction of what is called Poincaré thermal measure $T_\beta = \uplambda_{{\text{w}}\upbeta }$, may help in resolution of the paradoxical aspect of Banach-Tarski problem [137].

In connection to BTP problem, it is further noted that due to Poincaré thermal measure $T_\upbeta = \uplambda_{{\text{w}}\upbeta }$, macroscopic (extensive) system volume $V_\upbeta$ and microscope (intensive) most probable atomic volume ${\hat{\text{v}}}_{{{\text{w}}}\upbeta }$ are related as

$$V_\upbeta = N_\upbeta \hat{{\text{v}}}_{{\text{w}}\upbeta } = N_\upbeta \uplambda_{{\text{w}}\upbeta }^3 = N_\upbeta T_\upbeta^3$$

(58)

Also, at thermodynamic equilibrium, by NMB distribution in Fig. 5 and in view of speed versus wavelength ratio relation [37]

$${\text{v}}_{{{\text{j}}}} /{{{\text{v}}}}_w = \lambda_w /\lambda_{\text{j}}$$

(59)

the statistical field is composed of a spectrum of cluster or “element” volumes

$$V_{{\text{j}}\upbeta } = \sum\limits_{\text{i}} {\hat{{\text{v}}}_{{{{\text{ij}}}}\upbeta } } = \sum\limits_{\text{i}} {\uplambda_{{{{\text{ij}}}}\upbeta }^3 }$$

(60)

such that

$$V_\upbeta = \sum_{{{\text{j}}}} {{{{V}}}_{{\text{j}}\upbeta } }$$

(61)

The quantum nature of physical space with spectrum of “atomic” volumes ${\hat{{{\text{v}}}}}_{{\text{ij}}\upbeta }$ forming a spectrum of cluster volumes $V_{{\text{j}}\upbeta }$ is in harmony with modern concepts of quantum gravity [119,120,121,122,123].

8 Concluding Remarks

Some implications of a scale-invariant model of Boltzmann statistical mechanics to generalized thermodynamics, Helmholtz decomposition of energy and momentum, and definitions of dark-energy, dark- matter, and dark-momentum were investigated. The model resulted in internal spacetime and external space and time having quantum nature in accordance with thermodynamic thermal time of Rovelli [95]. Invariant Schrödinger equation resulted in introduction of hierarchies of quantum mechanics wave functions and particles as de Broglie wave-packets from cosmic to photonic scales.

Physical space, Casimir [111] vacuum, was identified as a compressible fluid with density ρ_v varying from infinite rarefaction $\uprho_{{\text{WH}}} = 0$ (white hole) to infinite compression $\uprho_{{\text{BH}}} = \infty$ (black hole) as its two singularities. With space curvature viewed as deviation of density from density of Casimir vacuum $\kappa = \uprho_\upbeta - \uprho_{\text{v}}$, the states $(\kappa > 0, \kappa = 0, \kappa < 0)$ of (matter, vacuum, anti-matter) fields were associated with (Riemannian, Euclidean, Lobachevskian) geometry. An invariant hydrodynamic model of Faraday line of force was introduced and shown to be in harmony with observations from cosmic to photonic scales. Finally, some implications of the model to black hole entropy and information loss as well as Banach-Tarski paradox were examined. The results were found to be in harmony with quantum gravity considered as dissipative deterministic dynamic system [119].