Formulation Space Search Metaheuristic

Abstract

Many methods for solving discrete and continuous global optimization problems are based on changing one formulation to another, which is either equivalent or very close to it. These types of methods include dual, primal-dual, Lagrangian, linearization, surrogation, convexification methods, coordinate system change, discrete/continuous reformulations, to mention a few. However, in all those classes, the set of formulations of one problem are not considered as a set having some structure provided with some order relation among formulations. The main idea of Formulation Space Search (FSS) is to provide the set of formulations with some metric or quasi-metric relations, used for solving a given class or type of problem. In that way, the (quasi) distance between formulations is introduced, and the search space is extended to the set of formulations as well. This chapter presents the general methodology of FSS, and gives an overview of several applications taken from the literature that fall within this framework. We also examine a few of these applications in more detail.

1 Introduction

Many methods for solving discrete and continuous global optimization problems are based on changing one formulation to another, which is either equivalent or very close to it, so that by solving the reformulated problem we can easily get the solution of the original one. These types of methods include

• i. dual methods,

• ii. primal-dual methods,

• iii. Lagrange methods,

• iv. linearization methods,

• v. convexification methods,

• vi. (nonlinear) coordinate system change methods (e.g., polar, Cartesian, projective transformations, etc.),

• vii. discrete/continuous reformulation methods,

• viii. augmented methods,

to mention a few. However, in all those classes, the set of formulations of one problem are not considered as a set having some structure provided with some order relation among formulations. The usual conclusion in papers oriented to a new formulation is that a given formulation is better than another or the best among several. The criteria for making such conclusions are typically the duality or integrality gap provided (difference between upper and lower bounds), precision, efficiency (the CPU times spent by the various methods applied to different formulations of the same instances), and so on.

Formulation space search (FSS) is a metaheuristic first proposed in 2005 by Mladenović et al. [37]. Since then, many algorithms for solving various optimization problems have been proposed that apply this framework. The main idea is to provide the set of formulations used for solving a given class or type of problem with some metric or quasi-metric. In that way, the distance between formulations can be induced from those (quasi) metric functions, and thus, the search space is extended to the set of formulations as well. Therefore, the search space becomes a pair ($\mathcal {F}, \mathcal {S}$), consisting of formulation space $\mathcal {F}$ and solution space ${\mathcal {S}}$. Most importantly, in all of the above mentioned method classes (i)–(viii), the discrete metric function between any two formulations can easily be defined. For example, in Lagrange methods, the distance between any two formulations can be defined as the difference between their relaxed constraints (the number of multipliers used); in coordinate change methods the distance between formulations could be the difference between the number of entities (points) presented in the same coordinate system, etc.

The work of Mladenović et al. [37] is also motivated by the following important observation: when solving continuous nonlinear programs (NLPs) with the aid of a solver that uses first-order information, the solution obtained may be a stationary point that is not a local optimum. Stationary points may be induced by the objective function (F) or the constraints. In the first case, they are found at points in the solution space where the first-order partial derivatives of F are all equal to zero. In the second case, they may occur at points on the boundary of one or more constraints where the derivatives of F are not all zero, but no feasible and improving direction of search can be found because of the imposed constraints. Unfortunately, these stationary points are often neither local minima nor local maxima. Checking the second-order conditions may help to identify these artificial local optima and escape them, but may also be computationally expensive, since the number of stationary points can be huge. Alternatively, different formulations of the same problem may have different characteristics that can be exploited in order to move in an efficient manner from these stationary points to better solutions. That is, while the improving search is stuck at a stationary point in one formulation, this solution may not be a stationary point in another formulation.

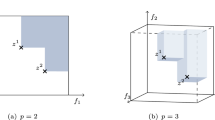
To illustrate the fact that a local solution in one formulation may behave differently in another, consider the following simple problem in the plane ($\mathbb {R}^2$):

$$\begin{aligned} \min F(x, y) = x + y, \end{aligned}$$

(12.1)

subject to

$$\begin{aligned} \begin{aligned}&x^2 + y^2 \ge 1,\\&x \ge 0, y \ge 0. \end{aligned} \end{aligned}$$

The objective function is linear, and therefore convex, but the feasible region is not a convex set, resulting in a nonconvex program. This problem may be reformulated from Cartesian coordinates in (12.1) to Polar coordinates to obtain an equivalent model:

$$\begin{aligned} \min G(r, \theta ) = r (\cos \theta + \sin \theta ), \end{aligned}$$

(12.2)

subject to

$$\begin{aligned} r \ge 1, 0 \le \theta \le \pi / 2. \end{aligned}$$

Interestingly, in (12.2), the objective function is nonconvex, while the constraints are linear, and therefore define a convex feasible set. Referring to Fig. 12.1(a) for model (12.1) with (x, y) coordinates, we see that a local solution occurs at the point $(1/\sqrt{2}, 1/\sqrt{2})$. This is because no feasible move direction exists at this point that will improve the solution (i.e., there is an immediate increase in the objective function or no improvement at all). Hence, any (local) improving search would be stuck at this point, even though the iso-contours of F show that this solution is not a local minimum. Referring to Fig. 12.1(b) for model (12.2), we find that the situation is not the same at the corresponding point in $(r, \theta )$ space, $(r, \theta ) = (1, \pi / 4)$. Moving down (or up) along the vertical line $r = 1$ is a feasible direction that immediately improves the solution. Continuing down (or up) along this vertical line eventually leads to an optimal solution at $(r, \theta ) = (1, 0)$ (or $(r, \theta ) = (1, \pi /2))$. This is equivalent to moving clockwise (or counter clockwise) along the circumference of the circle in Fig. 12.1(a) from the local solution at $(x, y) = (1/\sqrt{2}, 1/\sqrt{2})$ to the optimal solution at $(x, y) = (1, 0)$ (or (0, 1)). Thus, this small example illustrates that a local solution in one coordinate system may not be one in another coordinate system.

Fig. 12.1

Illustrative example

The FSS approach was first applied to the circle packing problem (Mladenović et al. [37]), which is a highly nonconvex NLP due to the imposed constraints, and as a result, contains a large number of stationary points. Here the authors used the nonlinear transformation demonstrated in the example above, where the mathematical formulation of the problem switches back and forth between Cartesian and Polar coordinate systems when convergence to a stationary point is detected, and proceeds in this manner until no further improvement is possible in either coordinate system. This simple application of FSS produced excellent results, and several successful applications of FSS have appeared since. The rest of this chapter is organized as follows. In the next section, we do a brief literature review of several papers that examine a range of optimization problems, continuous and discrete, and that have applied FSS in different ways. This is followed in Sect. 12.3 by a discussion of the general procedure or methodology at the base of FSS. Section 12.4 examines in detail how the steps of FSS have been incorporated in solution methods used to solve the circle packing problem, and the graph coloring problem (Hertz et al. [23]). We also examine in this section the reformulation local search methodology proposed in Brimberg et al. [6], which is closely related to FSS and was developed to solve continuous location problems. Section 12.5 provides some conclusions.

2 Literature Review

A sample of papers using FSS and related ideas is presented here, and briefly discussed.

• Circle Packing - Reformulation Descent  (Mladenović et al. [37]). Several years ago, classical Euclidean geometry problems of densest packing of circles in the plane were formulated as nonconvex optimization problems, allowing to find heuristic solutions by using any available NLP solver. The faster NLP solvers use first-order information only, and so may stop at stationary points which are not local optima. A simple switch from Cartesian coordinates to polar, or vice versa, can destroy this stationarity, and thus allow the solver to move further to better solutions. Such formulation switches may of course be iterated. For densest packing of equal circles into a unit circle, this simple feature turns out to yield results close to the best known, while beating second-order methods by a time-factor well over 100. This technique is formalized as a general reformulation descent (RD) procedure, which iterates among several formulations of the same problem until the applied local searches obtain no further improvement.

• Circle Packing (Mladenović et al. [38]). This paper extends the RD idea by using several formulations instead of only two. This is formalized as a general search in formulation space. The distance between two formulations is defined as the number of centers whose coordinates are expressed in different systems in each formulation. Therefore, the search is performed through the formulation space as well. Results with up to 100 circles compare favorably with the RD method.

• Packing Unequal Circles Using Formulation Space Search  (López and Beasley [30]). This paper presents a heuristic algorithm for the problem of packing unequal circles in a fixed size container such as the unit circle, the unit square or a rectangle. The problem is viewed as scaling the radii of the unequal circles so that they can all be packed into the container. The presented algorithm has an optimization phase and an improvement phase. The optimization phase is based on the formulation space search method, while the improvement phase creates a perturbation of the current solution by swapping two circles. The instances considered are categorized into two groups: instances with large variations in radii, and instances with small variations. Six different containers: circle, square, rectangle, right-angled isosceles triangle, semicircle, and circular quadrant are investigated. Computational results show improvements over previous work in the literature.

• Packing Unequal Circles in a Fixed Size Circular Container (López and Beasley [32]). This paper considers the problem of packing unequal circles in a fixed size circular container, where the objective is to maximize the value of the circles packed. Two different objectives are examined: maximize the number of circles packed; maximize the area of the circles packed. For the particular case where the objective is to maximize the number of circles packed, the authors prove that the optimal solution has a particular form. A heuristic is developed for the general problem based upon formulation space search. Computational results are given for a number of publicly available test problems involving the packing of up to 40 circles. Computational results are also provided for test problems taken from the literature, relating to packing both equal and unequal circles.

• Mixed Integer Nonlinear Programming Problem (López and Beasley [31]). An approach based on FSS to solve mixed-integer nonlinear (zero-one) programming problems is presented. Zero-one variables are presented by a well-known single nonlinear constraint, and an iterative method which adds a single nonlinear inequality constraint of increasing tightness to the original problem, is proposed. Computational results are presented on 51 standard benchmark problems taken from MINLPLib and compared against the Minotaur and minlp_bb nonlinear solvers, as well as against the RECIPE algorithms [28].

• Timetabling Problem  (Kochetov et al. [26]). This paper examines a well-known NP-hard teacher/class timetabling problem. Variable neighborhood search and tabu search heuristics are developed based on the idea of formulation space search. Two types of solution representation are used in the heuristics. Each representation considers two families of neighborhoods. The first uses swapping of time periods for the teacher (class) timetable. The second is based on the idea of large Kernighan-Lin neighborhoods. Computational results for difficult random test instances show that the proposed approach is highly efficient.

• Multi-item Capacitated Lot-Sizing Problem  (Erromdhani et al. [16]). This paper proposes a new variant of Variable neighborhood search (VNS) designed for solving Mixed integer programming problems. The procedure is called Variable neighborhood formulation search (VNFS), since the neighborhoods and formulations are both changed during the search. The VNS part is responsible for the integer variables, while an available (commercial) solver is responsible for the continuous variables and the objective function value. The procedure is applied to the multi-item capacitated lot-sizing problem with production time windows and setup times, under the non-customer specific case. This problem is known to be NP-hard and can be formulated as a mixed 0-1 program. Neighborhoods are induced from the Hamming distance in 0-1 variables, while the objective function values in the corresponding neighborhoods are evaluated using different mathematical programming formulations of the problem. The computational experiments show that the new approach is superior to existing methods from the literature.

• Graph Coloring  (Hertz et al. [23]). This paper studies the k-coloring problem. Given a graph $G = (V, E)$ with vertex set V, and edge set E, the aim is to assign a color (a number chosen in $\{1, \dots , k\}$) to each vertex of G so that no edge has both endpoints with the same color. A new local search methodology, called Variable Space Search is proposed and then applied to this problem. The main idea is to consider several search spaces, with various neighborhoods and objective functions, and to move from one to another when the search is blocked at a local optimum in a given search space. The k-coloring problem is thus solved by combining different formulations of the problem which are not equivalent, in the sense that some constraints are possibly relaxed in one search space and always satisfied in another. The authors show that the proposed heuristic is superior to each local search used independently (i.e., with a unique search space). It was also found to be competitive with state-of-the-art coloring methods, which consisted of complex hybrid evolutionary algorithms at the time.

• Cutwidth Minimization Problem  (Pardo et al. [41]). This paper proposes different parallel designs for the VNS schema. The performance of these general strategies is examined by parallelizing a new VNS variant called variable formulation search (VFS). Six different variants are proposed, which differ in the VNS stages to be parallelized as well as in the communication mechanisms among processes. These variants are grouped into three different templates. The first one parallelizes the whole VNS method; the second parallelizes the shake and the local search procedures; the third parallelizes the set of predefined neighborhoods. The resulting designs are tested on the cutwidth minimization problem (CMP). Experimental results show that the parallel implementation of the VFS outperforms previous state-of-the-art methods for the CMP.

• Maximum Min-Sum Dispersion Problem  (Amirgaliyeva et al. [1]). The maximum min-sum dispersion problem aims to maximize the minimum accumulative dispersion among the chosen elements. It is known to be a strongly NP-hard problem. In Amirgaliyeva et al. [1], the objective functions of two different problems are shifted. Though this heuristic can be seen as an extension of the variable formulation search approach (Pardo et al. [41]) that takes into account alternative formulations of one problem, the important difference is that it allows using alternative formulations of more than one optimization problem. Here it uses one alternative formulation that is of a max-sum type of the originally max-min type, maximum diversity problem. Computational experiments on benchmark instances from the literature show that the suggested approach improves the best-known results for most instances in a shorter computing time.

• Continuous Location Problems  (Brimberg et al. [6]). This paper presents a new approach called Reformulation local search (RLS), which can be used for solving continuous location problems. The main idea is to exploit the relation between the continuous model and its discrete counterpart. The RLS switches between a local search in the continuous model and a separate improving search in a discrete relaxation in order to widen the search. In each iteration new points obtained in the continuous phase are added to the discrete formulation making the two formulations equivalent in a limiting sense. Computational results on the multi-source Weber problem (a.k.a. the continuous or planar p-median problem) show that the RLS procedure significantly outperforms the continuous local search by itself, and is even equivalent to state-of-the-art metaheuristic-based methods.

3 Methodology

The general methodology of FSS and related ideas are presented here. We first analyze two usual types of search methodologies, stochastic and deterministic. Then we present FSS methods that combine both stochastic and deterministic elements.

3.1 Stochastic FSS

Let us denote with ($\varphi , x$) an incumbent formulation-solution pair, and with $f_{{\text {opt}}}=f(\varphi ,x)$ the current objective function value. One can alternate between formulation space ${\mathcal F}$ and solution space ${\mathcal S}$ in the following ways:

• i. Monte-Carlo FSS. This is the simplest search heuristic through ${\mathcal F}$:

  • a. take formulation - solution pair $(\varphi ',x') \in ({\mathcal F}, {\mathcal S})$ at random and calculate the corresponding objective function value $f'$;

  • b. keep the best solution and value;

  • c. repeat previous two steps p (a parameter) times.

• ii. Random walk FSS. For a random walk procedure we need to introduce neighborhoods of both, the formulation and the solution: ($N(\varphi ),\mathcal{N}(x)$), $\varphi \in {\mathcal F}$ and $x \in {\mathcal S}$. Then we simply walk through the formulation-solution space by taking a random solution from such a defined neighborhood in each iteration.

• iii. Reduced FSS. This technique for searching through ${\mathcal F}$ has already been successfully applied in [37]. It represents a combination of Monte-Carlo and random walk stochastic search strategies. Here we take a formulation-solution pair from a given neighborhood as in the random walk. However, we do not move to that solution if it is not better than the current one. We rather return, and take a two-step walk move (in other words, we jump to a random point in the formulation-solution neighborhood of the current solution, and then jump to a random point in the formulation-solution neighborhood of that point (two jumps)). If a better solution is found, we move there and restart the process; otherwise we return and perform a three-step walk, etc. Once we unsuccessfully perform $k_{{\text {max}}}$ (a parameter) steps, we return to the one-step move again.

In all three FSS routines above, we choose $(\varphi ',x')$ at random and then simply calculate the objective function value. However, $(\varphi ',x')$ could be used as an initial point for any usual descent (ascent) optimization method through $({\mathcal F}, {\mathcal S})$. Moreover, as an improvement method, one can use a Reformulation descent procedure described below. The final results should be of better quality in that case, but require much more computing time. Thus, some problem specific strategy in balancing the number of calls to an optimization routine is worth considering.

3.2 Deterministic FSS

• i. Local FSS. One can  perform local search through ${\mathcal F}$ as well. That is, find local solution $x'$ for any $\varphi ' \in N(\varphi )$ (starting from x as an initial solution) and keep the best; repeat this step until there is a formulation in the neighborhood that gives an improvement. Local FSS is probably not as efficient and effective as LS in the solution space, since it is not very likely that many solutions will be different in the neighboring formulations. Moreover, local FSS is a very time-consuming procedure since for each neighboring formulation, some optimization method is applied. Therefore, we do not give detailed pseudo code for local FSS here.

• ii. Reformulation Descent (RD). Up to now, we choose the next formulation in the search at random. A procedure that changes the formulation in a deterministic way is called Reformulation descent. The following procedure describes in more detail how we propose to exploit the availability of several formulations of a problem. We assume that at least two ($\ell _{{\text {max}}} \ge 2$) not linearly related formulations of the problem are constructed ($\varphi _\ell , \ell = 1,\dots ,\ell _{{\text {max}}}$), and that initial solution x and formulation ($\ell =1$) are found. Our RD performs the following steps:

  • a. Using Formulation $\varphi _\ell$ and an optimization code, find a stationary or local optimum point $x'$ starting from x;

  • b. If $x'$ is better than x, move there ($x \leftarrow x'$) and start again from the first formulation ($\ell \leftarrow 1$); otherwise change the formulation ($\ell \leftarrow \ell +1$);

  • c. Repeat the steps above until $\ell > \ell _{max}$.

  This algorithm was used for solving the circle packing problem in Mladenović et al. [37]. Results obtained were comparable with the best-known values. Moreover, the RD was 150 times faster than a Newton type method.

• iii. Steepest Descent FSS. If objective functions $f_i$ of all formulations $\varphi _i$, $i = 1,\dots ,\ell _{{\text {max}}}$ are smooth, then, after finding an initial solution x, the Steepest descent FSS may be constructed as follows:

  • a. Find descent search directions $-\nabla f_i(x)$.

  • b. Perform a line search along all directions (i.e., find $\lambda _i^* > 0$) to get a set of new solutions

    $$x^{(i)} \leftarrow x^{(i)} - \lambda _i^* \nabla f_i(x).$$

  • c. Let $f_i \leftarrow f_i(x^{(i)})$, and let $i^*$ be the index where $f_i$ is a minimum. Set $x \leftarrow x^{(i^*)}$ and $f_{{\text {opt}}} \leftarrow f_{i^*}$.

  • d. Repeat the previous three steps until $f_{{\text {opt}}} \ge f_{i^*}$.

For constrained optimization, replace $\nabla f_i(x)$ by feasible move direction $\Delta _i(x)$ in the formula in step (b), such that the inner product $\nabla f_i(x) \cdot \Delta _i(x) \ge 0$.

3.3 Variable Neighborhood FSS and Variants

• i. Variable Neighborhood Formulation Space Search (VNFSS). As in Variable neighborhood search (VNS), we can combine stochastic and deterministic searches, to get VNFSS. Traditional ways to tackle an optimization problem consider a given formulation, and search in some way through its feasible set X. The fact that the same problem may often be formulated in different ways allows to extend search paradigms to include jumps from one formulation to another. Each formulation should lend itself to some traditional search method, its “local search” that works totally within this formulation, and yields a final solution when started from some initial solution. Any solution found in one formulation should be easily transformed to its equivalent solution in any other formulation. We may then move from one formulation to another using the solution resulting from the former’s local search as the initial solution for the latter’s local search. Such a strategy will of course only be useful when local searches in different formulations behave differently. This idea was first investigated in [37] while examining the circle packing problem. Only two formulations of the circle packing problem (one with Cartesian coordinates, and the other with polar coordinates) were used. The nonlinear solver used by the authors alternates between these two formulations, each time starting from the solution reached in the previous iteration (but transformed into the corresponding solution (point) in the other formulation) until there is no further improvement. This approach was named Reformulation Descent. The same paper also introduced the idea of Formulation space search (FSS) where more than two formulations could be used. In [38], the collection of formulations is enlarged by presenting a subset of circles in Cartesian coordinates, while the rest are presented in polar coordinates. Also, the distance between any two formulations is introduced, and neighborhoods are defined as collections of formulations based on this distance. So, neighborhood $\mathcal {N}_k(\varphi )$ of formulation $\varphi$ contains all formulations $\varphi '$ that are at distance k from formulation $\varphi$. The basic idea behind FSS is to continue the search in one of the given formulations $\varphi$ until it gets trapped at a stationary point, then choose a new formulation $\varphi '$ belonging to the current neighborhood of $\varphi$, then transform the stationary point in $\varphi$ to the corresponding solution in $\varphi '$, and continue the search in $\varphi '$ from that point. An improved version of FSS for solving the circle packing problem is proposed in [29]. One methodology that uses the variable neighborhood idea in searching through the formulation space is given in Algorithms 1 and 2. Here $\varphi$ ($\varphi '$) denotes a formulation from given formulation space ${\mathcal F}$, x ($x'$) denotes a solution in the feasible set defined with that formulation, and $\ell \le \ell _{{\text {max}}}$ is the formulation neighborhood index. Note that Algorithm 2 uses a reduced VNS strategy [19] in ${\mathcal F}$.

We can extend to the full VNFSS with the following changes:

• a. the shake step involves only the random selection of formulation $\varphi '\in {\mathcal N}_{\ell }(\varphi )$; then set $x'\in \varphi '$ to the same solution as $x\in \varphi$;

• b. in between the shake and formulation change steps, add a local search to map $x'$ onto a stationary point under formulation $\varphi '$: $x'\leftarrow LS_{\varphi '}(x')$.

• ii. Variable Objective Search (VOS). Butenko et al. [10] propose a variant they call Variable Objective Search (VOS). Their idea uses the fact that many combinatorial optimization problems have different formulations (e.g. the maximum clique problem with more than twenty formulations, traveling salesman with more than 40 formulations, quadratic assignment problem, max-cut problem, etc). They assume that all formulations share the same feasible region, but have different objective functions. Also, all formulations have the same neighborhood structures. However,

  • a stationary point for one formulation may not correspond to a stationary point with respect to another formulation;

  • a global optimum of the considered combinatorial optimization problem should correspond to a global optimum for any formulation of this problem.

  Based on the previous assumptions, Butenko et al. [10] propose the following method (named Basic Variable Objective Search):

  • Arrange formulations in prespecified order: $\varphi _1, \varphi _2, ..., \varphi _n$. Denote with $f_i$ the objective function for formulation $\varphi _i$.

  • Choose an initial feasible solution, and perform a local search in a proposed neighborhood ${\mathcal N}$, yielding local optimum $x^{(1)}$ with respect to formulation $\varphi _1$.

  • Perform a local search starting from the previous local optimum $x^{(1)}$ in neighborhood ${\mathcal N}$, but with respect to formulation $\varphi _2$. In other words the neighbors of current local optimum $x^{(1)}$ are mapped into corresponding points in formulation $\varphi _2$, and checked to see if a better solution can be obtained according to formulation $\varphi _2$ (and according to objective function $f_2$). This local search produces a local optimum with respect to formulation $\varphi _2$, and this local optimum will be presented (remembered) as a point in the solution space of formulation $\varphi _1$.

  • After performing local search with respect to formulation $\varphi _i$ ($i<n$), local search starting from the last obtained local optimum with respect to formulation $\varphi _{i+1}$ is performed.

  • After performing local search with respect to formulation $\varphi _n$, the complete procedure repeats until there is no improvement with respect to all formulations.

  A Variable Objective Search is demonstrated on the Maximal Independent Set Problem. A so-called Uniform Variable Objective Search is also proposed in [10]. Instead of local search with respect to a single formulation, this method performs simultaneous local search by exploring the complete neighborhood ${\mathcal N}$ of the current solution, thereby determining a collection of local optima with respect to all formulations. The move is then made to the best of all obtained local optima.

• iii. Variable Formulation Search (VFS). Many optimization problems in the literature, for example, min–max types, present a flat landscape. This means that, given a formulation of the problem, there are many neighboring solutions with the same value of the objective function. When this happens, it is difficult to determine which neighborhood solution is a more promising one to continue the search. To address this drawback, the use of alternative formulations of the problem within VNS is proposed in [36, 39, 41]. In [41] this approach is named Variable Formulation Search (VFS). It combines the change of neighborhood within the VNS framework, with the use of alternative formulations. In particular, the alternative formulations will be used to compare different solutions with the same value of the objective function, when considering the original formulation.

  Let us assume that, beside the original formulation and the corresponding objective function $f_0(x)$, there are p other formulations denoted as $f_1(x),\dots ,f_p(x), x \in X$. Note that two formulations are equivalent if the optimal solution of one is the optimal solution of the other, and vice versa. Without loss of clarity, we will denote different formulations as different objectives $f_i(x), i = 1,\dots , p$. The idea of VFS is to add the procedure Accept$(x, x', p)$, given in Algorithm 3 in all three steps of Basic VNS (BVNS): Shaking, LocalSearch and NeighborhoodChange. Clearly, if a better solution is not obtained by any formulation among the p pre-selected, the move is rejected. The next iteration in the loop of Algorithm 3 will take place only if the objective function values according to all previous formulations are equal.

If Accept ($x, x', p$) is included in the LocalSearch subroutine of BVNS, then it will not stop the first time a non-improved solution is found. In order to stop LocalSearch, and thus claim that $x'$ is a local minimum, $x'$ should not be improved by any among the p different formulations. Thus, for any particular problem, one needs to design different formulations of the problem considered and decide the order they will be used in the Accept subroutine. Answers to those two questions are problem specific and sometimes not easy. The Accept ($x, x', p$) subroutine can obviously be added to the NeighborhoodChange and Shaking steps of BVNS as well.

In Mladenović et  al. [39], three evaluation functions, or acceptance criteria, within the Neighborhood Change step are used in solving the bandwidth minimization problem. This min-max problem consists in finding permutations of rows and columns of a given square matrix such that the maximal distance of a nonzero element from the main diagonal in the corresponding row, is a minimum. Solution x may be presented as a labeling of a graph and the move from x to $x'$ as $x \leftarrow x'$. The three criteria used are:

• 1. the simplest one which is based on the objective function value $f_0(x)$ (bandwidth length);

• 2. the total number of critical vertices $f_1(x)$ (if $f_0(x') = f_0(x)$ and $f_1(x') < f_1(x)$);

• 3. $f_3(x,x') = \rho (x,x') - \alpha$ (if $(f_0(x') = f_0(x)$ and $f_1(x') = f_1(x)$), but x and $x'$ are relatively far from each other; that is, the distance between solutions x and $x'$, $\rho (x,x') > \alpha$, where $\alpha$ is an additional parameter).

The idea for a move to a mildly worse solution if it is very far, is used within Skewed VNS [19]. However, a move to a solution with the same value is performed in [39] only if its Hamming distance from the incumbent is greater than $\alpha$.

In [36], a different mathematical programming formulation of the original problem is used as a secondary objective within the Neighborhood Change function of VNS. Two combinatorial optimization problems on graphs are considered here: the Metric dimension problem and the Minimal doubly resolving set problem.

• iv. Variable Space Search (VSS). Hertz et al. [23] developed this variant of FSS to solve the graph coloring problem (GCP). Their solution method exploits the relation between the k-coloring problem and the GCP. Three solution spaces are defined as follows: $S_1$ containing all k-colorings of a given graph G, $S_2$ containing all partially legal k-colorings of G, and $S_3$ containing all cycle-free orientations of the edges of G. The VSS procedure cycles through these spaces in an empirically determined sequence. We will examine their VSS procedure in more detail in a later section.

• (v) Reformulation Local Search (RLS) was originally proposed for solving continuous location problems (Brimberg et al. [6]). This approach differs from FSS in that the different formulations used are not equivalent to each other. There is a base model, which is a single formulation of a given continuous location problem, and a series of discrete formulations, which are improving approximations of the continuous model.

  The RLS switches between the continuous model (the original problem) and a discrete approximation in order to expand the search. In each iteration, new facility locations obtained by the improving search in the continuous phase are added to the discrete formulation. Thus, the two formulations become equivalent in a limiting sense. As in FSS, the solution found using the current formulation becomes the starting point for the next formulation.

  There are many ways to construct an RLS-based algorithm (e.g. choice of: rules for inserting promising points or removing non-promising points in the discrete phase, improving searches for both phases, the initial discrete model, and so on). RLS can be applied not only to continuous location problems, but also other types of problems having continuous and discrete formulations. More details are given in the next section.

4 Some Applications

4.1 Circle Packing Problem

The circle packing problem can be stated in the following way. Given a number n of circular disks of equal radius r, determine how to place them within a unit circle without any overlap in order to maximize the radius r.

i. Circle Packing Problem Formulation in Cartesian Coordinates. The circular container is the unit radius circle with center (0, 0). The circles to be packed within it are given by their centers $(x_i,y_i)$ ($i=1,\dots ,n$), and their common radius r, which is to be maximized. This may be formulated as:

$$\begin{aligned} \max r \end{aligned}$$

(12.3)

subject to

$$\begin{aligned} \begin{aligned}&(x_i-x_j)^2+(y_i-y_j)^2-4r^2 \ge 0,&\forall \; i,j \; (1\le i < j \le n)\\&x_i^2+y_i^2\le (1-r)^2,&\forall \; i \; (1 \le i \le n)\\&r \ge 0, \ \ x_i, y_i \in R,&\forall \; i\; (1\le i \le n). \end{aligned} \end{aligned}$$

The first set of inequalities expresses that any two disks should be disjoint: the squared Euclidean distance between their centers must be at least $(2r)^2$. The second set states that the disks must fully lie within the unit circle. This smoother quadratic form is preferred to the more standard constraint

$$\sqrt{x_i^2 + y_i^2} + r \le 1.$$

ii. Circle Packing Problem Formulation in Polar Coordinates. The circular container is centered at the pole and has unit radius. The disks to be packed within it are given by their centers at polar coordinates $(\rho _i, \theta _i)$ ($i= 1, 2, \dots , n$), and their common radius r, which is to be maximized. The equivalent problem may be formulated as:

$$\begin{aligned} \max r \end{aligned}$$

(12.4)

subject to

$$\begin{aligned} \begin{array}{ll} \rho _i^2+\rho _j^2-2\rho _i\rho _j\cos (\theta _i-\theta _j) -4r^2\ge 0, &{} \forall \; i,j \; (1 \le i < j \le n) \\ \rho _i+r\le 1, &{} \forall \; i \; (1 \le i \le n)\\ r \ge 0, &{} \\ \rho _i \ge 0, \quad \theta _i\in [0,2\pi ], &{} \forall \; i \; (1 \le i \le n).\\ \end{array} \end{aligned}$$

Note that, unlike the Cartesian formulation, the second constraint set, expressing inclusion of the disks inside the container, is now linear.

4.1.1 Reformulation Descent

These two formulations are used to solve the circle packing problem in [37], using MINOS (an off-the-self nonlinear program solver). The starting solution is a set of randomly chosen points within the container acting as centers of the circles. The radius of the circles is a maximal number r such that the corresponding circles do not overlap and each circle is completely inside the unit circle. The centers of the circles are first expressed in Cartesian coordinates. As already noted, MINOS is applied to the current solution, in this case, the selected initial solution. After MINOS finishes at some stationary point, the coordinates of the obtained centers are converted to polar coordinates, and MINOS is applied on the optimization problem written in polar coordinates with the set of current centers and current value of r as the initial solution. If MINOS is unable to increase the radius of the circles, the method finishes, and the final solution is the corresponding solution. Otherwise, if MINOS is able to increase r, the centers of the obtained circles are converted in Cartesian coordinates and a new iteration begins using the current solution as the initial solution.

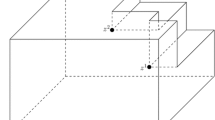
This procedure, referred to as Reformulation Descent (RD), is illustrated in Fig. 12.2 for $n=35$ equal circles. As can be seen, seven executions are applied until the final (which is also optimal) solution is obtained.

Fig. 12.2

Illustration of reformulation descent applied on packing 35 circles in the unit circle ([37])

Reformulation Descent (RD) is implemented in [37] on packing n ($n = 10, 15,$ $20, \dots , 100$) circles in the unit circle. For each value of n, RD is executed 50 times. The same problem is also executed 50 times using Cartesian coordinates only from the same set of initial solutions, and again in Polar coordinates only from the same set of initial solutions. Initial solutions are generated by choosing at random Polar coordinates $\rho$ and $\theta$ and converting them into Cartesian coordinates (if it is necessary). The value of radius $\rho$ is set to $(1-1/\sqrt{n})\cdot \sqrt{rnd}$ where rnd is uniformly distributed on [0, 1]. The value of angle $\theta$ is uniformly distributed on $[0,2\pi ]$.

Summary results are given in Table 12.1. The first column contains the value of n (number of circles). Column 2 contains the best-known result (radius of the circle) for the corresponding value of n. Columns 3–5 contain the percentage deviation of best results obtained respectively by MINOS with RD, MINOS with Cartesian coordinates only, and MINOS with Polar coordinates only, from the best-known results (radius). Columns 6–8 contain the percentage deviation of average results obtained by RD, Cartesian coordinates, and Polar coordinates, respectively, from the best-known results (radius). Columns 9–11 contain the average running time respectively for RD, Cartesian coordinates, and Polar coordinates.

Table 12.1 Summary results of 50 executions of RD, Cartesian coordinates only, and Polar coordinates only [37]

iii. Mixed formulation of Circle Packing Problem. There are many possible formulations obtained by expressing the locations of some centers in Cartesian coordinates, and the remaining centers in Polar coordinates. Suppose that centers of circles are numbered $1, 2, 3, \dots , n$. Then the pair of disjoint sets $C_{\varphi }$ and $P_{\varphi }$, whose union is the set $\{1, 2, 3, \dots , n\}$, determines one formulation ($\varphi$) as follows:

$$\begin{aligned} \max r \end{aligned}$$

(12.5)

subject to

$$\begin{aligned} \begin{array}{ll} (x_i-x_j)^2+(y_i-y_j)^2-4r^2 \ge 0, &{}\forall \; i,j \in C_{\varphi } (i< j)\\ \rho _i^2+\rho _j^2-2\rho _i\rho _j\cos (\theta _i-\theta _j) -4r^2\ge 0, &{} \forall \; i,j \in P_{\varphi } (i < j) \\ (x_i-\rho _j\cos (\theta _j))^2+(y_i-\rho _j\sin (\theta _j))^2-4r^2 \ge 0, &{}\forall \; i \in C_{\varphi }, \forall \; j \in P_{\varphi } \\ x_i^2+y_i^2\le (1-r)^2, &{}\forall \; i \in C_{\varphi } \\ \rho _i+r\le 1, &{} \forall \; i \in P_{\varphi } \\ r \ge 0, &{} \\ x_i, y_i \in \mathbb {R}, &{} \forall i \in C_{\varphi }\\ \rho _i \ge 0, \quad \theta _i\in [0,2\pi ], &{} \forall \; i \in P_{\varphi }. \\ \end{array} \end{aligned}$$

A general reformulation descent procedure could be constructed by replacing the two pure formulations (Cartesian and polar) used above by a specified sequence of mixed and pure formulations.

4.1.2 Formulation Space Search

We will call the set of all possible formulations Formulation Space ${\mathcal F}$. Each of these formulations can be used by MINOS (or any other NLP solver) for solving the circle packing problem. In Mladenović et al. [38], a distance function in the formulation space is introduced as the cardinality of the symmetric difference of sets representing the subsets of circles which are in Cartesian coordinates:

$$d(\varphi _1, \varphi _2) = |C_{\varphi _1} \Delta C_{\varphi _2}| = |P_{\varphi _1} \Delta P_{\varphi _2}|.$$

The defined distance allows the definition of neighborhoods in the Formulation space:

$${\mathcal N}_k(\varphi ) = \{\varphi '| d(\varphi ,\varphi ')=k\},$$

and introduces Formulation Space Search for the circle packing problem. A pseudo code for FSS is given in Algorithm 4 ([38]).

Execution of FSS for $n=50$ circles is shown in Fig. 12.3. The starting solution is not randomly selected, but is instead a solution obtained after applying Reformulation Descent. Each picture shows an improved solution obtained by execution of function MinosMix. Below each picture we see the value of circle radius (r) as well as the neighborhood in the Formulation Space in which the improved solution is obtained.

In Mladenović et al. [38], $k_{{\text {min}}}$ and $k_{{\text {step}}}$ are both set to 3, and $k_{{\text {max}}}$ is set to $n = 50$. Note that the first improvement was obtained for $k_{{\text {curr}}}=12$. This implies that no improvement was found with $k_{{\text {curr}}} = 3, 6$ and 9. Since the initial formulation is all Cartesian, this also means that a mixed formulation with 12 polar and 38 Cartesian coordinates was used ($|C_F| = 38$, $|P_F| = 12$). In the next round, a formulation with 3 randomly chosen circle centers ($k_{{\text {curr}}}=3$), was unsuccessful, but a better solution was found with 6, and so on. After 10 improvements, the algorithm ends up with a solution with radius $r_{{\text {max}}} = 0.125798$.

Fig. 12.3

Illustration of execution of formulation space search applied on packing 50 circles in the unit circle. Starting solution is a solution obtained by Reformulation Descent ([38])

A comparison of results obtained by 50 executions of Reformulation Descent and Formulation Space Search for the circle packing problem is given in Table 12.2. The first column in Table 12.2 contains the number of circles n. The second column contains the value of the best-known solution for the corresponding value of n. Columns 3–5 contain results for Reformulation Descent: percentage deviation of best solution from best-known solution, percentage deviation of the average of solutions and average running time. Columns 6–8 contain the corresponding values for solutions obtained by Formulation Space Search.

The table shows that the average error of the FSS heuristic is smaller, i.e., solutions obtained by FSS are more stable than those obtained with RD.

Table 12.2 Comparison of reformulation descent and formulation space search on circle packing problem [38]

4.2 Graph Coloring Problem

A graph $G = (V, E)$ with vertex set V and edge set E, and an integer k are given. A k-coloring of G is a mapping $c : V \rightarrow \{1, \dots , k\}$. The value c(x), where x is a vertex is called the color of x. The vertices which have color i ($1 \le i \le k$) represent a color class, denoted $V_i$. If two adjacent vertices x and y have the same color i, vertices x and y, the edge (x, y) and color i are said to be conflicting. A k-coloring without conflicting edges is a legal coloring and its color classes are called stable sets.

The Graph Coloring Problem (GCP for short) requires that the smallest integer k be determined, such that a legal k-coloring of G exists. Number k is also called the chromatic number of G, and is denoted as $\chi (G)$. Given a fixed integer k, the optimization problem k-GCP is to determine a k-coloring of G which has the minimal number of conflicting edges. If the optimal value of the k-GCP is zero then graph G has a legal k-coloring. A local search algorithm for the GCP can be used to solve the k-GCP by simply stopping the search as soon as a legal k-coloring is found. Also, an algorithm that solves the k-GCP can be used to solve the GCP, by starting with an upper bound k on $\chi (G)$, and then decreasing k as long as a legal k-coloring can be found.

Hertz et al. [23] define three solution spaces for solving the GCP and k-GCP problems. Note that a solution of the k-GCP should satisfy two conditions if possible: there are no edges where both endpoints have the same color, and all vertices must be colored. The first two solution spaces relax one of these two conditions; the third search space satisfies both conditions.

The first proposed solution space $S_1$ consists of all (not necessarily legal) k-colorings of graph G. In solution space $S_1$, objective function $f_1(s)$ (for $s\in S_1$) is defined as the number of conflicting edges in coloring s. In solution space $S_1$, neighborhood $N_1(s)$ consists of all k-coloring $s'$ obtained by changing the color of exactly one vertex. Based on the proposed neighborhood, Hertz and de Werra [22] developed a Tabu search algorithm, also called TabuCol, for solving the k-coloring problem.

The second solution space $S_2$ consists of all partially legal k-colorings. More precisely each solution is a partition of the set of vertices into $k+1$ disjoint sets $V_1, V_2, \dots , V_k, V_{k+1}$, where sets $V_1, V_2, \dots , V_k$ are stable sets, while $V_{k+1}$ is a set of non-colored vertices. In solution space $S_2$, the objective function $f_2$ is defined, such that $f_2(s)$ is the cardinality of subset $V_{k+1}$. Morgenstern [40] proposed the objective function $f_2'(s) = \sum _{v\in V_{k+1}} d(v)$, where d(v) denotes the number of edges incident to vertex v. Neighborhood $N_2(s)$ consists of all solutions obtained by moving a vertex $v\in V_{k+1}$ in the set (color class) $V_i$, and moving to $V_{k+1}$ all vertices $u\in V_i$ adjacent to vertex v. Bloechliger and Zufferey [2] obtained very good results by using reactive tabu search and the number of non-colored vertices as the objective function. Solution space $S_3$ consists of the cycle-free orientations of the edges of graph G. Gallai [18], Roy [43], and Vitaver [46] independently proved in the sixties that the length of a longest path in an orientation of graph G is at least equal to the chromatic number of G. As a corollary, the problem of orienting the edges of a graph so that the resulting digraph $\overrightarrow{G}$ is cycle-free, and the length $\lambda (\overrightarrow{G})$ of a longest path in $\overrightarrow{G}$ is minimum, is equivalent to the problem of finding the chromatic number of G.

Indeed, given a $\chi (G)$-coloring c of a graph G, one can easily construct a cycle-free orientation $\overrightarrow{G}$ with $\lambda (\overrightarrow{G}) \le \chi (G)$ by simply orienting each edge [u, v] from u to v if and only if $c(u) < c(v)$. Conversely, given a cycle-free orientation $\overrightarrow{G}$ of G, one can build a $\lambda (\overrightarrow{G})$-coloring of G by assigning to each vertex v a color c(v) equal to the length of a longest path ending at v in $\overrightarrow{G}$.

So, objective function $f_3$ can be defined, such that $f_3(s)$ is the length of the longest oriented path. Many local searches can be defined in $S_3$. One of them is removing all arcs (oriented edges) not contained in the longest path, choosing vertex u and changing the orientation of all arcs ending at vertex u or beginning at vertex u. It can be proved that the length of a longest path in the so obtained graph is bigger by at most one than the length of the longest path in the starting graph.

Translators can be constructed that translate the solution belonging to one of the three solution spaces into the corresponding solution belonging to another solution space. After some preliminary experiments, Hertz et al. [23] found that the sequence $S_1 \rightarrow S_3 \rightarrow S_2 \rightarrow S_1$ of search spaces, called a cycle, appears to be a good choice, each translation from an $S_i$ to its successor being easy to perform.

A variable space search (VSS) algorithm (Hertz et al. [23]) is executed on 16 graphs from the DIMACS Challenge. After a preliminary set of experiments, the following graphs were selected as representative of the most challenging ones.

• Six DSJCn.d graphs: the DSJCs are random graphs with n vertices and a density of $\frac{d}{10}$. It means that each pair of vertices has a probability of $\frac{d}{10}$ to be adjacent. Hertz et al. [23] use the DSJC graphs with $n \in \{500, 1000\}$ and $d \in \{1, 5, 9\}$

• Two DSJRn.r graphs: the DSJRs are geometric random graphs. They are constructed by choosing n random points in the unit square and two vertices are connected if the distance between them is less than $\frac{r}{10}$. Graphs with an added end letter “c” are the complementary graphs. The authors use two graphs with $n = 500$ and, respectively, $r = 1$ and $r = 5$.

• Four flatn_$\chi$_0 graphs: the flat graphs are constructed graphs with n vertices and a chromatic number $\chi$. The end number “0” means that all vertices are incident to the same number of vertices.

• Four len_$\chi$x graphs: the Leighton graphs are graphs with n vertices and a chromatic number $\chi$ equal to the size of the largest clique (i.e., the largest number of pairwise adjacent vertices). The end letter “x” stands for different graphs with similar settings.

Detailed results of the VSS coloring algorithm are presented in Table 12.3. The first column contains the name of the graph. The second column contains the chromatic number (“*” when it is not known), and the third column contains the best-known upper bound. The VSS algorithm was run 10 times on each graph with different values of k. The fourth column reports various values of k ranging from the smallest number for which they had at least one successful run, to the smallest number for which they had 10 successful runs. The next columns respectively contain the number of successful runs and the number of tries, the average number of iterations in thousands (i.e., the total number of moves performed using the 3 neighborhoods, divided by 1000) on successful runs, and the average CPU time used (in seconds).

Table 12.3 Detailed results of VSS coloring with a time limit of 1 hour ([23])

The VSS algorithm is compared with TabuCol [22], PartialCol [2] as well as with three graph coloring algorithms which are among the most effective ones: the GH algorithm in [17], the MOR algorithm in [40], and the MMT algorithm in [34]. A detailed comparison is given in Table 12.4.

Table 12.4 Comparisons between VSS-Col and five other algorithms ([23])

4.3 Continuous Location Problems

4.3.1 Preliminaries

Location models in the literature typically determine where to place a given number of new facilities in order to serve a given set of demand points (also called existing facilities, fixed points, or customers) in the best way. Continuous models, also known as site-generating models (Love et al. [33]), allow the new facilities to be located anywhere in N-dimensional Euclidean space ($E^N$) or a sub-region thereof. A specified distance function is required in practical applications in order to measure the distances between new facilities and the customers they will serve. Most applications in the literature occur in the plane ($N = 2$), and use the Euclidean norm as the distance function.

Consider the unconstrained planar p-median problem with Euclidean distances (also known as the multi-source Weber problem (MWP)), which may be written as:

$$\begin{aligned} (\min )\ \ f (X_1, X_2,\dots , X_p) = \sum _{j\in [n]} w_j \min \{d(X_i, A_j): i\in [p]\}, \end{aligned}$$

(12.6)

where n denotes the number of demand points; p denotes the number of new facilities to be opened; $[t] = \{1, 2, \dots , t\}$ for any positive integer t; $w_j$ is a positive weight equivalent to the demand at given point $A_j = (a_j, b_j)$, $j \in [n]$; $X_i = (x_i, y_i)$ denotes the unknown location of new facility $i \in [p]$; and $d(X_i, A_j)$ is the Euclidean distance between $X_i$ and $A_j$, for all pairs $(X_i, A_j)$.

The objective function f in (12.6) is a weighted sum of distances between the demand points and their closest facilities. Since the minimum of a set of convex functions is nonconvex, the function f is itself nonconvex and may contain several stationary points. This was recognized by Cooper [11, 12], who was also the first to propose this continuous location–allocation problem. Among the methods proposed by Cooper to solve (12.6), one became quite famous, and is referred in the literature as Cooper’s algorithm. It is based on the following simple observation. When the facility locations are fixed, the problem reduces to allocating each demand point to its closest facility. Then when the resulting partition of the set of demand points is fixed, the problem reduces to p independent and convex single facility location problems, which are easily solved by gradient descent methods such as the well-known Weiszfeld procedure (Weiszfeld [47]). Cooper’s algorithm iterates between location and allocation steps until a local minimum is reached.

Solving the planar p-median problem is equivalent to enumerating the Voronoi partitions of the set of demand points, which is NP-hard (Megiddo and Supowit [35]). The complexity of the problem has been demonstrated in the literature. For example, Brimberg et al. [5] test the well-studied 50-customer problem in Eilon et al. [14] by running Cooper’s algorithm from 10,000 randomly generated starting solutions for each $p \in \{5, 10, 15\}$. They obtain 272, 3008, and 3363 different local minima, respectively. The worst deviation from the best solution found (later shown to be optimal by Krau [27]) was, respectively, $47\%, 66\%$ and $70\%$. The best-found solution was obtained 690 times for $p = 5$, 34 times for $p = 10$, and only once for $p = 15$. Considering that $n = 50$ is a small instance by today’s standard, these results demonstrate quite dramatically the complex topology of the objective function. For further reading, see e.g., Brimberg and Salhi [9].

4.3.2 Reformulation Local Search for Continuous Location

Any continuous location model can be formulated as a discrete problem by restricting the potential sites of the new facilities to a finite set of given points in the continuous space. The distance between any pair of points is measured by the same distance function used in the continuous model. For example, the continuous p-median problem in (12.6) becomes the classical discrete p-median problem when the facility locations are restricted to the n given demand points. Exploiting the relation between these two formulations was suggested in the original work of Cooper [11, 12]. Hansen et al. [20] proposed an effective heuristic that first solves the discrete p-median exactly using a primal-dual algorithm by Erlenkotter [15], and then completes one iteration of “continuous-space adjustment” by solving the p continuous single facility minisum problems identified by the partition of the set of demand points found in the discrete phase. The excessive computation time needed to solve larger instances of the discrete model limits the size of instances that can be considered (Brimberg et al. [4]). A similar approach is proposed in Salhi and Gamal [44], but this time a heuristic is used to solve the discrete p-median approximately. Kalczynski et al. [25] describe a greedy, random approach to construct good discrete starting solutions. They go on to show the rather counter-intuitive result that using good discrete starting solutions can be more effective and efficient than the optimal discrete solution.

A general procedure known as reformulation local search (RLS) that iterates between the continuous location problem under consideration and discrete approximations of this problem was proposed in [6]. The RLS procedure may be viewed as a special case of formulation space search (FSS), i.e., its extended Reformulation descent variant. In the latter case, two or more equivalent formulations of a given problem are combined in the search process. Meanwhile, in RLS we have the original continuous location model coupled with a series of discrete approximations. Each succeeding discrete formulation presents a better approximation of the original (continuous) problem until the algorithm terminates at a local optimum in both spaces. We will also see later that the series of approximations can be made to converge in an asymptotic sense to an equivalent formulation of the original problem. The general steps of RLS are examined next (see [6] for further details).

Consider a continuous location problem of the following general form:

$$\begin{aligned} \min \ \ (\text {or }\max )\; f (X_1, X_2, \dots , X_p), \end{aligned}$$

(12.7)

requiring p new facility sites $X_i \in \mathbb {R}^N$, $i \in [p]$, to be found. The multi-source Weber problem (MWP) given in (12.6) is an example. Another important, but less-studied class of location problems is given by the continuous p-centre problem,

$$\begin{aligned} \min g(X_1, X_2, \dots , X_p) = \max \{\min \{d(X_i, A_j): i \in [p]\}: j \in [n]\}, \end{aligned}$$

(12.8)

where the objective is to minimize the furthest distance from a demand point to its closest facility, and which is used when quality of service (e.g., emergency response) is the main goal. (Note that the unweighted version of MWP, where $w_j = 1$, for all j, minimizes the average distance from a demand point to its closest facility.) The continuous p-dispersion problem is used to locate obnoxious facilities. Here we have a $\max \min \min$ objective:

$$\begin{aligned} \max h(X_1, X_2,\dots , X_p) = \min \{\min \{d(X_i, A_j): i \in [p]\}: j \in [n]\}. \end{aligned}$$

(12.9)

In this case, constraints are required to limit the locations of the new facilities to a closed sub-region of $\mathbb {R}^N$. Constraints specifying a minimum separation distance between the new facilities may also be included. Other types of constraints, such as limits on the capacities of the facilities, may be added to the general model in (12.7) without affecting the discussion below. We will refer to (12.7) ($+$ any required constraints) as (GLP) for the general location problem in continuous space.

Using the notation in Brimberg et al. [6], let $(GLP)'$ denote the current discrete approximation of (GLP), and S the finite set of potential sites specified in $(GLP)'$. The discrete approximation of the unconstrained (GLP) in (12.7) may be written as:

$$\begin{aligned} \min \ (\text {or }\max )_{X \subset S,\; |X| = p}\; f (X). \end{aligned}$$

(12.10)

For the case of p homogeneous facilities, and where no constraints are included in (GLP), there are $\left( {\begin{array}{c}M\\ p\end{array}}\right)$ possible solutions to $(GLP)'$. When constraints are included in (GLP), they must also be respected in $(GLP)'$, and so to be effective, the constructed set S should contain several feasible solutions. To complete the preliminaries, let $L_C$ and $L_D$ denote the selected improving searches for (GLP) and $(GLP)'$, respectively. These searches stop at a current solution, if and only if, a better solution cannot be found in the respective neighborhood of the search. The framework for reformulation local search (RLS) is now presented assuming that (GLP) is a minimization problem (see [6]).

Referring to Algorithm 5, we can note the following useful features of RLS:

• The initial set S is not restricted to the set of demand points as in other methods that combine a discrete approximation of the original continuous problem. For example, S can include some “attractive” demand points combined with a sufficient number of “attractive” sites obtained by local search from several random initial solutions. The choice of initial solution $X^0$ is also left up to the analyst. It can be, for example, a randomly generated solution or one obtained by a constructive method (e.g. [8]).

• The analyst also selects the algorithms, $L_C$ and $L_D$ for improving the solution in the continuous and discrete spaces, respectively. These can be the simplest of local searches, metaheuristic based methods, and in the case of $L_D$, even an exact method. Thus, the RLS framework is very flexible.

• Step 3 (augmenting S) is an important feature. It allows new, attractive facility sites to be added to the discrete model. For example, referring to the continuous p-median problem (12.6), new median points found by $L_C$ in the continuous space allow new partitions of the set of demand points to be investigated in the discrete phase by $L_D$, which in turn may give improved solutions of the original problem (12.6). We demonstrate this in the following example. (Also see [6] for a different example.)

4.3.2.1 An Illustration

Consider the small example in Fig. 12.4 with five demand points arranged to form two equilateral triangles, a small one with sides of length = 1, and a large one with sides of length = 3. The two triangles share a common vertex $A_3$ located at the origin (0, 0), and the large one is symmetrically inverted above the small one with the vertical axis bisecting the two triangles. The weights at the demand points are all equal to 1; $w_j = 1$, $j = 1, \dots , 5$, and three facilities are to be located ($p = 3$). The initial set S (step 1) comprises the complete set of demand points. Suppose also that the initial solution consists of p randomly selected demand points (a commonly used procedure), and this time $X^0 = \{A_1, A_2, A_4\}$. Assigning demand points to their nearest facilities, with ties broken arbitrarily, results in the following partition:

$$\begin{aligned} \{A_1, A_3\},\ \{A_2\},\ \{A_4, A_5\} \end{aligned}$$

Fig. 12.4

Illustration of RLS

The objective value for this solution is $f = d(A_1, A_3) + d(A_4, A_5) = 1 + 3 = 4$. Since the facilities are optimally located with respect to their assigned demand points, the current solution is a local minimum, and $L_C$ (Cooper’s algorithm is chosen) cannot improve it in step 2. As a result, no new points are added to S in step 3. Using the common single vertex swap move for $L_D$ in step 4 (where only one facility can move from its current vertex to any unoccupied vertex) leads to an improved solution where $X_2$ moves from $A_2$ to $A_5$, and a better partition of the demand points is achieved:

$$\begin{aligned} \{A_1, A_2, A_3\},\ \{A_5\},\ \{A_4\} \end{aligned}$$

The objective value is reduced to $f = d(A_1, A_3) + d(A_1, A_2) = 1 + 1 = 2$. In the next iteration of the continuous phase, $X_1$ moves from $A_1$ to the median point of its assigned cluster $\{A_1, A_2, A_3\}$, $X_m = (0, -1/\sqrt{3})$, with new $f = d(X_m, A_1) + d(X_m, A_2) + d(X_m, A_3) = 3 \times \frac{1}{\sqrt{3}} = \sqrt{3}$. The new point $X_m$ is added to S. The next iteration of the discrete phase cannot improve this solution; so the algorithm terminates with final solution, $X_1 = X_m$, $X_2 = A_5$, and $X_3 = A_4$, which is also the optimal solution. The summary of RLS moves is as follows:

$$\begin{aligned} \begin{aligned} X^0 =\{A_1, A_2, A_4\} \overset{L_C}{\longrightarrow }&X^1 = X^0 \overset{L_D}{\longrightarrow } X^2 =\{A_1, A_5, A_4\} \overset{L_C}{\longrightarrow } \\&X^3 =\{X_m, A_5, A_4\} \overset{L_D}{\longrightarrow } X^4 = X^3. \end{aligned} \end{aligned}$$

4.3.2.2 A Small Instance (n = 50) from the Literature

Brimberg et al. [6] carry out a detailed computational experiment on the well-studied 50-customer problem from [14]. The aim of the experiment is to compare RLS to Cooper’s classical algorithm, which is referred to as MALT to signify multi-start alternating (locate–allocate), and which is used as a basis of comparison to this day for heuristics developed to solve the multi-source Weber problem (12.6). Note that MALT was originally developed for MWP, but can also be adapted to many other classes of location problems, continuous or discrete, such as the p-centre problem, by simply changing the objective function. Five different values of p are tested ($p = 5, 10, 15, 20, 25$). Each of these five instances is run 100 times from random starting solutions generated within the smallest rectangle containing the set of demand points, for both MALT and RLS. The most basic form of RLS is used, where the improving search in the continuous phase ($L_C$) is the same Cooper algorithm used in MALT, and the improving search in the discrete phase ($L_D$) is the standard single vertex exchange (Teitz and Bart [45]) discussed above in the illustrative example. The number of distinct local minima (LM), the number of occurrences of the 1st, 2nd, and 3rd best solutions, and the number of solutions within given fractional deviations of the optimal solution (from Krau [27]) are tabulated. Sample results are provided here in Table 12.5.

Table 12.5 Sample results comparing MALT and RLS on 50-customer problem (Brimberg et al. [6])

Some interesting observations are noted.

• The number of distinct local minima is much smaller for RLS than MALT. For $p = 5$, this number = 50 for MALT and only 4 for RLS. For $p = 15$, all 100 runs in MALT produce different local minima, while RLS only produces two different local minima. We may attribute the small number of local minima found by RLS to the much larger search neighborhood compared to MALT obtained by adding the discrete phase.

• The first best solution obtained by RLS turns out to be the optimal solution in all five instances tested. However, MALT finds the optimal solution only for the smallest instance, $p = 5$.

• The quality of the few local minima obtained by RLS is very good. Considering the poor quality of the random starting solutions, this would indicate that RLS is able to descend deep down along the surface (or landscape) of the objective function, and certainly avoid many of the local optima traps that MALT gets stuck in. As a result, the quality of the solutions found by RLS is vastly superior to MALT. The improvement for the smallest instance with $p = 5$ is not as dramatic as the larger instances. For example, for $p = 15$ (see Table 12.5), 70 out of 100 runs of RLS produce the optimal solution compared to 0 for MALT. The remaining 30 runs of RLS produce its second best solution, which is within 0.05 (5%) of the optimal, while MALT produces only 4 solutions out of 100 within 0.05 of optimal.

Further analysis (see [6] for details) also reveals that the augmentation step in RLS (step 3), where new median points from the continuous phase are added to the set S containing the nodes of the discrete model, is a useful feature. This step enhances the algorithm by increasing the number of iterations between continuous and discrete phases; i.e., more descent moves and better solutions are obtained.

4.3.2.3 Computational Results on Large Instances

Three other data sets commonly used for the MWP (e.g., see [4]) are also examined in [6]. These are the 287 - customer problem from Bongartz et al. [3], and the 654- and 1060 - customer problems from the TSP library (Reinelt [42]). Values of p were taken from $\{2, 3, 4, \dots , 15, 20, 25, \dots , 100\}$ for $n = 287$, and $\{5, 10, 15, \dots , 150\}$ for $n = 654$ and 1060, giving a total of 91 instances tested. CPU time for each instance and each algorithm was set at 20, 120, and 300 sec, respectively, for $n = 287$, 654, and 1060. The average percentage deviation from the best-known result over all instances run for the specified data set is given in Table 12.6 for MALT and RLS (see [6] for detailed results for each instance). Note that these best-known solutions were shown to be optimal for the $n = 287$ instances (Krau [27]). As we might expect, Table 12.6 shows that RLS significantly outperforms MALT. It is also noteworthy that despite the simple RLS procedure used in Brimberg et al. [6], this algorithm was able to improve on two best-known solutions for $n = 654$, obtained by a much more sophisticated metaheuristic-based method. These results are quite encouraging. They also demonstrate that simple algorithm designs can be as effective (or nearly so) as more complicated ones, in support of the “less is more” (LIMA) philosophy discussed in a separate chapter of this book.

Table 12.6 Summary of results on larger instances, MALT and RLS (see [6] for details)

4.3.2.4 Injection Points

Brimberg et al. [7] suggest that injection points be added to set S once the basic RLS procedure terminates. The idea here is to add “attractive” points to the discrete model in order to improve the discrete approximation of the original model. In that way, the improving search $L_D$ may find a better solution, and hence, jump out of the current local optimum trap. The steps of the new procedure, called augmented reformulation local search (ARLS), are shown in Algorithm 6 below for convenience. Note the new parameter K in step 1 denoting the total number of injection points that will be added. Otherwise, the procedure is the same as basic RLS (Algorithm 5) until step 5 where the algorithm starts to add the injection points ($Y_j$) once the basic RLS cannot improve the solution any further. The injection points are added one at a time, and each time one is added, the search in the discrete phase (step 4) is resumed. If a better solution is found than the current best ($X^0$), the algorithm returns to the continuous phase (step 2) with this new solution, and resumes the basic RLS. The algorithm ends when all K injection points are added, and the solution cannot be improved further.

The injection points can be determined in different ways. In Brimberg et al. [7], two strategies are specified. The first requires the injection points to be convex combinations of two or more demand points (or facilities, or combinations of the two). The second strategy involves the use of a local search in the continuous problem that can be different from $L_C$, and that can generate local optima with new and attractive points to add to the set S. However, in the computational experiments, they only use the first strategy with pairs of randomly selected demand points, e.g.,

$$\begin{aligned} Y_j = A_{j_1}/2 + A_{j_2}/2, \end{aligned}$$

where $Y_j$ is placed at the midpoint of the line segment joining $A_{j_1}$ and $A_{j_2}$. The computational results are comparable to basic RLS, suggesting this is only a preliminary study, and more work is needed to develop effective strategies for inserting injection points.

Some interesting features of ARLS are noted:

• A small example in [6] demonstrates that a multi-start version of basic RLS is not guaranteed to be globally convergent. In this case, the starting solution is a randomly selected combination of p demand points, and Cooper’s algorithm is used to improve the solution in the continuous phase. They show that the optimal solution of the MWP is unattainable under these conditions. On the other hand, injecting median points into the discrete approximation easily fixes this issue.

• Adding injection points, for example, median points for the MWP, makes the discrete model a better approximation of the original (continuous) model. By generating all possible local solutions, and adding the obtained facility sites to the set S, the discrete model becomes an equivalent formulation of the continuous one. That is, solving one model automatically solves the other. Thus, we may view the RLS approach as falling within the FSS framework in an asymptotic sense.

5 Conclusions

Many methods for solving global optimization problems are based on changing one formulation to another. These types of methods include dual, primal-dual, Lagrangian, linearization, surrogation, convexification methods, coordinate system change, discrete/continuous reformulations, to mention a few. The main idea of Formulation Space Search (FSS) is to provide the set of formulations for a given problem with some metric or quasi-metric functions. In that way, the (quasi) distance between formulations is introduced, and the search space is extended to the set of formulations as well. Most importantly, in all solution method classes mentioned, the discrete metric function between any two formulations can easily be defined. Those simple facts open an avenue to a new approach where heuristics are developed within the FSS framework. Instead of a single formulation with corresponding solution space, as in the traditional approach, there are now multiple formulations and solution spaces to explore in a structured way. This opens up immense possibilities in designing new and powerful heuristics. For example, it may be that new types of distances in the formulation space will make some hard problems easier to solve.

Computational results demonstrate that the FSS framework can produce simple and effective heuristics that support the less is more (LIMA) philosophy discussed in a separate chapter of this book. The authors hope they have convinced the reader that FSS is an exciting direction for future research.