The L-shape search method for triobjective integer programming

Abstract

We present a new criterion space search method, the L-shape search method, for finding all nondominated points of a triobjective integer program. The method is easy to implement, and is more efficient than existing methods. Moreover, it is intrinsically well-suited for producing high quality approximate nondominated frontiers early in the search process. An extensive computational study demonstrates its efficacy.

1 Introduction

Multiobjective optimization is one of the earliest fields of study in operations research. Many real world-problems involve multiple objectives. Due to conflict between objectives, finding a feasible solution that simultaneously optimizes all objectives is usually impossible. Consequently, in practice, decision makers want to understand the trade off between objectives before choosing a suitable solution. Thus, generating many or all efficient solutions, i.e., solutions in which it is impossible to improve the value of one objective without a deterioration in the value of at least one other objective, is the primary goal in multiobjective optimization.

It has been shown that even for the simplest optimization problems, e.g., the minimum spanning tree problem, the shortest path problem, and the matching problem, and even for just two objective functions, determining whether a point in the criterion space is associated with an efficient solution is NP-hard [31]. This “negative” result may have contributed to the fact that multiobjective optimization has received relatively little attention from the mathematical programming community, but enormous attention from the evolutionary computing community. For example, the evolutionary multiobjective optimization (EMOO) website maintained by Carlos A Coello Coello (http://delta.cs.cinvestav.mx/~ccoello/EMOO/) lists close to 4000 journal papers and more than 3000 conference papers on the topic. For an introduction to and a recent survey of evolutionary methods for multiobjective optimization see [11, 37] and for surveys on their use in different domains see [28] (engineering), [8] (economics and finance), [25] (production scheduling), [18] (combinatorial optimization), and [27] (traveling salesman problem). Many of the problems considered in these domains can be modeled as multiobjective (mixed) integer programs (MOIPs), but because of the absence of powerful and easy-to-use software for solving such problems, researchers and practitioners alike resort to using readily available evolutionary methods, e.g., NSGA and NSGA II [14].

The apparent lack of interest and effort in multiobjective optimization by the mathematical programming community is unfortunate, as multiobjective optimization poses many interesting theoretical as well as algorithmic challenges. The ubiquitous use of evolutionary methods for multiobjective optimization in a large number of application domains also exposes the huge opportunity that has been missed. However, all is not lost. Mathematical programming methods can provide performance guarantees where evolutionary methods cannot. This is an accepted and recognized weakness of evolutionary methods and as such still provides an opportunity for alternatives that can do better. We hope that the work discussed in this paper illustrates the challenges and richness of multiobjective integer programming and that it will stimulate further research in the area.

The work discussed in this paper also demonstrates that, in part due to the availability of cheap computing power and powerful single-objective commercial solvers, such as IBM ILOG CPLEX Optimizer (http://www-01.ibm.com/software/info/ilog), FICO Xpress Optimizer (http://www.fico.com), and Gurobi Optimizer (http://www.gurobi.com), solving certain MOIPs, i.e., computing the complete nondominated frontier, has become possible. Others have recognized this as well, which has led to an upswing of interest in the last few years, with a focus on developing efficient algorithms that can solve practical-sized instances in a reasonable amount of time.

Exact algorithms for MOIPs can be divided into decision space search algorithms, i.e., methods that search in the space of feasible solutions, and criterion space search algorithms, i.e., methods that search in the space of objective function values. Because there can be multiple solutions with the same objective function values, it has long been argued (see for example Benson et al. [3]) that criterion space search algorithms have an advantage over decision space search algorithms and are likely to be more successful. Therefore, in the remainder of the paper, we focus on criterion space search algorithms. Readers interested in recent advances in the area of decision space search algorithms are referred to [2, 34, 36].

The simplest form of a MOIP has only two objectives and is known as a biobjective integer program (BOIP). The earliest algorithms only generated a subset of all nondominated points, the so-called extreme supported nondominated points, e.g., Aneja and Nair [1]. But not long after, algorithms were developed that generated the complete nondominated frontier. The most popular of these are the $\epsilon$-constraint, Tchebycheff and perpendicular search methods [6, 9, 10, 12, 33]. Interested readers may refer to Boland et al. [5] and Ehrgott [17] for an overview of recent advances in solving BOIPs using criterion search space algorithms, including discussions of the box algorithm [20] and the balanced box method [5].

The situation is quite different when the number of objectives is greater than two; few methods have been proposed for generating the complete nondominated frontier in these settings. There are two main reasons why it is significantly more challenging to generate the complete nondominated frontier of a MOIP with more than two objectives.

• 1. The number of nondominated points tends to grow with the number of objective functions (see Brunsch et al. [7] for recent theoretical results that support this empirical observation). Since at least one search operation has to be performed to find a nondominated point, and searching for a nondominated point in (current) criterion space search methods involves solving a single-objective IP, the number of single-objective IPs that needs to be solved in order to solve even relatively small MOIP instances becomes quite large as the number of objectives grows.

• 2. Developing effective strategies for decomposing the criterion search space is much more difficult, because such strategies need to balance the number and shape of the elements in the decomposition with the difficulty of the single-objective IP used to explore an element of the decomposition. As a result, many more single-objective IP solves or very expensive single-objective IP solves are unavoidable.

Algorithmically, a trade off between solving a small number, but increasingly difficult single-objective IPs (e.g. [35]) and solving a large number, but manageable size single-objective IPs (e.g. [13, 22, 29, 30]) has to be made.

The main contribution of our research is the development of the L-shape search method (LSM) for solving triobjective integer programs (TOIPs). LSM is designed with practical computation in mind and balances the number of single-objective IPs solved with the size of the single-objective IPs solved. (Theoretically, the performance of LSM, in terms of the number of the single-objective IPs that may have to be solved, is worse than the performance of the algorithm of Dächert and Klamroth [13].) Each of the single-objective IPs solved in LSM has the same feasible set as the original IP with either two or three additional objective constraints (each enforcing an upper bound on one of the objective function values), or with one additional binary variable and two additional constraints to model a disjunctive constraint on the objective function values of two of the objectives.

The performance of LSM in practice shows that it has two desirable characteristics:

• it generates the complete nondominated frontier more efficiently than any existing criterion space search method; and

• it produces high-quality approximate nondominated frontiers early on in the search.

LSM is the only method to date that provides both benefits. In practice, the ability to rapidly produce high-quality approximate nondominated frontiers is critical. The quality of an approximate nondominated frontier depends on the number and variety of its nondominated points. Thus, to rapidly produce high-quality approximate nondominated frontiers, a method has to generate many nondominated points in a short amount of time and these nondominated points have to come from different parts of criterion space. As far as we know, LSM is the only method which achieves this while retaining the ability to provably produce the complete frontier.

To demonstrate the efficacy of LSM, an extensive computational study has been conducted using four sets of publicly available instances of triobjective optimization problems. The study investigates the performance of LSM, and compares it with that of two recent methods: those of Özlen et al. [30] and Kirlik and Sayın [22], using the implementations made available by their respective authors. The results show conclusively that LSM provides the best performance in terms of both overall solution time and early approximation of the nondominated frontier.

The rest of paper is organized as follows. In Sect. 2, we introduce important concepts and notation. In Sect. 3, we review existing methods for solving TOIPs. In Sect. 4, we detail the logic of LSM. In Sect.  5, we investigate enhancements that can improve LSM’s efficiency. In Sect. 6, we illustrate the workings of LSM on a small instance. In Sect. 7, we analyze the results of a comprehensive computational study. Finally, in Sect. 8, we give some concluding remarks.

2 Preliminaries

A multiobjective optimization problem can be stated as follows

$$\begin{aligned} \min _{x \in \mathcal {X}}\ z(x) = (z_1(x),\ldots ,z_p(x)) \end{aligned}$$

(1)

where $\mathcal {X} \subseteq \mathbb {R}^n$ represents the feasible set in the decision space and the image $\mathcal {Y}$ of $\mathcal {X}$ under the vector-valued function $z:\mathbb {R}^n\rightarrow \mathbb {R}^p$ represents the feasible set in the criterion space, i.e., $\mathcal {Y} := z(\mathcal {X}) := \{y\in \mathbb {R}^p: y=z(x)$ for some $x\in \mathcal {X} \}$. For convenience, we also define the following sets: $\mathbb {R}^p_{\ge } := \{y \in \mathbb {R}^p: y \ge 0\}$, the nonnegative orthant of $\mathbb {R}^p$, and $\mathbb {R}^p_{>} := \{y \in \mathbb {R}^p: y > 0\}$, the positive orthant of $\mathbb {R}^p$.

When $\mathcal {X}$ is defined by a set of linear constraints and $z_1, \ldots , z_p$ are linear functions, then (1) is a multiple objective linear program (MOLP), and is a multiple objective integer program (MOIP) when $\mathcal {X} \subseteq \mathbb {Z}^n$.

Definition 1

A feasible solution $x'\in \mathcal {X}$ is called weakly efficient, if there is no other $x\in \mathcal {X}$ such that $z_k(x)< z_k(x')$ for $k=1,\ldots ,p$. If $x'$ is weakly efficient, then $z(x')$ is called a weakly nondominated point.

Definition 2

A feasible solution $x'\in \mathcal {X}$ is called efficient or Pareto optimal, if there is no other $x\in \mathcal {X}$ such that $z_k(x)\le z_k(x')$ for $k=1,\ldots ,p$ and $z(x) \ne z(x')$. If $x'$ is efficient, then $z(x')$ is called a nondominated point. The set of all efficient solutions in $\mathcal {X}$ is denoted by $\mathcal {X}_E$. The set of all nondominated points in $\mathcal {Y}$ is denoted by $\mathcal {Y}_N$ and referred to as the nondominated frontier or efficient frontier.

Observation 3

Let $y \in \mathcal {Y}$. If there is no $y' \in \mathcal {Y}$ such that $y' \ne y$ and $y \in y' + \mathbb {R}^p_{\ge }$, then $y \in \mathcal {Y}_N$.

Next, we introduce concepts and notation that will facilitate the presentation and discussion of the methods proposed in the literature for solving TOIPs, as well as of the LSM. Some of the methods, including the LSM, operate in a 2-dimensional projected space rather than the 3-dimensional criterion space itself. Without loss of generality, we assume that the 2-dimensional space on which points in the criterion space are projected is defined by the first two objectives, i.e., by $z_1(x)$ and $z_2(x)$. We thus define the projection of a point $y \in \mathbb {R}^3$ to be $(y_1,y_2)$, which we denote by $\overline{y}$.

LSM makes use of two shapes in the projected space (i.e. in $\mathbb {R}^2$): the rectangle and the L-shape, defined as follows. Given $u^1$ and $u^2$ in the projected space, we define the (closed) rectangle $R(u^1,u^2) = \{u\in \mathbb {R}^2\ :\ u^1 \le u \le u^2\}$. Note that $R(u^1,u^2) = \emptyset$ unless $u^1 \le u^2$ (i.e. unless $u^1_1 \le u^2_1$ and $u^1_2 \le u^2_2$). We refer to $u^1$ as the lower bound of rectangle $R(u^1,u^2)$ and to $u^2$ as the upper bound of rectangle $R(u^1,u^2)$. The area of rectangle $R(u^1,u^2)$ is denoted by $a(R(u^1,u^2))$. Given $u^1$, $u^2$ and $u^*$ in the projected space, we define the L-shape $L(u^1,u^*,u^2) = R(u^1,u^2){\setminus } R(u^*,u^2)$ and denote its area by $a(L(u^1,u^*,u^2))$. Note that we normally use the L-shape $L(u^1,u^*,u^2)$ in situations where $u^1 \le u^* \le u^2$. The following observation will be useful.

Observation 4

If $v\in L(u^1,u^*,u^2)$ for some $u^1, u^*, u^2\in \mathbb {R}^2$ then $R(u^1,v)\subseteq L(u^1,u^*,u^2)$.

Other criterion-space search methods make use of the box shape in criterion space: given $y^1$ and $y^2$ in $\mathbb {R}^3$, we define the (closed) box $B(y^1,y^2) = \{y\in \mathbb {R}^3\ :\ y^1 \le y \le y^2\}$. We also assume the availability of two points in criterion space, $z^B$ and $z^T$, for which the box $B(z^B,z^T)$ contains the set of nondominated points $\mathcal {Y}_N$. If $\mathcal {X}$ is bounded, which we will assume, then $z^B$ and $z^T$ can readily be calculated by solving single-objective ($\min$ or $\max$) IPs over $\mathcal {X}$, or alternatively by solving single-objective LPs over the LP relaxation of $\mathcal {X}$, which we denote by $\mathcal {X}_{LP}$.

Note that in some cases it is convenient to extend $\mathbb {R}^2$ and $\mathbb {R}^3$ to include infinite-valued vectors, and in particular to refer to rectangles, L-shapes or boxes in which the lower bound point is $(-\infty ,-\infty )$ in the case of the former two and $(-\infty ,-\infty ,-\infty )$ in the case of the latter. In such cases the interpretation of the shape is the natural one, and we will write the lower bound point simply as $-$, for example, we will write $R(-,u)$ to indicate $R((-\infty ,-\infty ),u)$.

Searching for an as yet unknown nondominated point is a core operation in any method for generating the nondominated frontier of a TOIP. Below, we discuss three relevant methods (or scalarization techniques) for doing so.

• 1. A nondominated point $z^n = z(x^n)$ with the property that $z^n \leqslant u$ for a given point u in the criterion space, if one exists, can be found by solving the following IP

  $$\begin{aligned} x^n \in \hbox {arg min}\left\{ \sum _{k=1}^{3} z_k(x)\ :\ x \in \mathcal {X}\ \text{ and }\ z_k(x) \le u_k, \ k \in \{1,2,3\}\right\} . \end{aligned}$$

  We denote this type of search by 3D-NDP-Search(u). (Note that this search combines ideas from the weighted sum method and the $\epsilon$-constraint method, and is known as the hybrid method, see, e.g., Chankong and Haimes [10].) By Proposition 5 below, we have that in criterion space this search returns $z^n \in \mathcal {Y}_N\cap B(-,u)$.

Proposition 5

If $x^n$ exists, then $z(x^n)$ is a nondominated point, i.e. $z(x^n)\in \mathcal {Y}_N$.

Proof

Suppose $x^n$ exists, but that $z(x^n)$ is not a nondominated point, i.e., there exists a point $\hat{z} \in \mathcal {Y}$ with $\hat{z}_k \le z_k(x^n)$ for all $k \in \{1,2,3\}$ and $\hat{z} \ne z(x^n)$. This implies that for some $x\in \mathcal {X}$, $z(x) = \hat{z}$ and $\sum _{k=1}^{3}z_k(x) = \sum _{k=1}^{3} \hat{z}_k < \sum _{k=1}^{3}z_k(x^n)$, which contradicts the optimality of $x^n$.

• 2. A nondominated point $z^n = z(x^n)$ with the property that its projection $\overline{z^n}$ satisfies $\overline{z^n} \le u$ for a given point u in the projected space, if one exists, can be found by solving two IPs. First, an intermediate point $x^i\in \mathcal {X}$ with minimal third objective value over those for which $z(x^i)$ has the desired property is found via

  $$\begin{aligned} x^i \in \hbox {arg min}\{ z_3(x)\ :\ x \in \mathcal {X}\ \text{ and }\ z_k(x) \le u_k, \ k \in \{1,2\} \}. \end{aligned}$$

  If this IP is feasible, it is followed by the second IP

  $$\begin{aligned} x^n \in \hbox {arg min}\left\{ \sum _{k=1}^{3} z_k(x)\ :\ x \in \mathcal {X}\ \text{ and }\ z_k(x) \le z_k(x^i), \ k \in \{1,2,3\}\right\} . \end{aligned}$$

  We denote this search by 2D-NDP-Search(u). (Note that this search is, and is sometimes referred to as, a two-stage method [22].) If the first IP is infeasible, we say 2D-NDP-Search(u) returns Null and $x^i$ does not exist. Otherwise, i.e., if $x^i$ exists, the second IP must be feasible (as per Proposition 7 below) and 2D-NDP-Search(u) returns $x^n$. Observe that as a consequence of the results below, in criterion space this search returns $z^n$ with $z^n_3$ minimal over those $z^n\in \mathcal {Y}_N$ with $\overline{z^n}\in R(-,u)$, i.e., 2D-NDP-Search(u) searches the rectangle with upper bound u for a nondominated point with minimal third objective value.

Proposition 6

If $x^i$ exists, then $z(x^i)$ is a weakly nondominated point.

Proof

Suppose $x^i$ exists, but that $z(x^i)$ is not a weakly nondominated point, i.e., there exists a point $\hat{z} \in \mathcal {Y}$ with $\hat{z}_k < z_k(x^i)$ for $k \in \{1,2,3\}$. So for some $x\in \mathcal{X}$, $z(x) = \hat{z}$ and $z_k(x) < z_k(x^i)$ for $k \in \{1,2,3\}$. Thus $z_k(x) < z_k(x^i) \le u_k$ for $k=1,2$ and $z_3(x) < z_3(x^i)$, contradicting the optimality of $x^i$. $\square$

Proposition 7

If $x^i$ exists, then $x^n$ exists and $z(x^n)$ is a nondominated point, i.e., $z(x^n)\in \mathcal {Y}_N$.

Proof

If $x^i$ exists, then it is feasible for the second IP, and hence $x^n$ exists. In this case, suppose $z(x^n) \notin \mathcal {Y}_N$. Then there must exist some $y \in \mathcal {Y}_N$ which dominates $z(x^n)$, i.e. there must exist $x\in \mathcal {X}$ with $z(x) = y \le z(x^n)$ and with $y \ne z(x^n)$. Thus $z_k(x) = y_k \le z_k(x^n) \le z_k(x^i)$ for $k=1,2,3$ and $\sum _{k=1}^{3} z_k(x) = \sum _{k=1}^{3} y_k < \sum _{k=1}^{3} z_k(x^n)$, contradicting the optimality of $x^n$. $\square$

Proposition 8

If 2D-NDP-Search(u) returns $x^n$, then $z(x^n)$ dominates any $y \in \mathcal {Y}$ with $\overline{y}\in R(\overline{{z}(x^n)}, u)$ and $y\ne z(x^n)$.

Proof

Suppose 2D-NDP-Search(u) returns $x^n$ and let $y \in \mathcal {Y}$ with $\overline{y}\in R(\overline{{z}(x^n)}, u)$ and $y\ne z(x^n)$. By definition, $x^n$ has the minimum possible value for $z_3(x)$ among all $x\in \mathcal {X}$ with z(x) having projection $\overline{z(x)}\le u$, and hence among all $x\in \mathcal {X}$ with $\overline{z(x)}\in R(\overline{z(x^n)},u)$. Thus $y_3 \ge z_3(x^n)$. Moreover, $\overline{y}\in R(\overline{{z}(x^n)}, u)$ implies $\overline{y}\ge \overline{{z}(x^n)}$. Thus $y \ge z(x^n)$. Since $y\ne z(x^n)$, $z(x^n)$ must dominate y. $\square$

Corollary 9

If 2D-NDP-Search(u) returns $x^n$, then $\mathcal {Y}_N \cap \{y \in \mathcal {Y}{:}\overline{y}\in R(\overline{{z}(x^n)}, u)\} = \{z(x^n)\}$.

Proof

The result follows immediately from Propositions 7 and 8.

• 3. A nondominated point $z^n = z(x^n)$ with the property that its projection $\overline{z^n}$ satisfies $\overline{z^n} \le u$ and $\overline{z^n} \not \ge u^*$ for two given points $u, u^*\in \mathbb {R}^2$ with $u^* \le u$, if one exists, can be found by solving two IPs. First, an intermediate point $x^i\in \mathcal {X}$ with third objective value minimal over all those with the desired property is found via

  $$\begin{aligned}&x^i \in \hbox {arg min}\{ z_3(x)\ : \ x \in \mathcal {X},\ w \in \{0,1\}^2,\ z_k(x) \le (u^*_k- \epsilon )\\&\quad + (u_k - u^*_k + \epsilon ) (1 - w_k),\ k \in \{1,2\},\\&\quad \text{ and } \ w_1 + w_2 \ge 1 \}, \end{aligned}$$

  where $\epsilon$ is a small positive constant. If this IP is feasible, it is followed by the second IP

  $$\begin{aligned} x^n \in \hbox {arg min}\left\{ \sum _{k=1}^{3} z_k(x)\ :\ x \in \mathcal {X}\ \text{ and }\ z_k(x) \le z_k(x^i), \ k \in \{1,2,3\}\right\} . \end{aligned}$$

The constraints in the first IP ensure that either $z_1(x^i) < u^*_1$ or $z_2(x^i) < u^*_2$, so $\overline{z(x^i)}\in L(-,u^*,u)$. Thus by Observation 4 and the constraints for the second IP, it must be that $\overline{z(x^n)}\in L(-,u^*,u)$ also. We denote this search by 2D-NDP-L-Search $(u^*, u)$. (Note that this search uses some of the ideas introduced in Sylva and Crema [35], which we discuss in more detail in the next section.) If the first IP is infeasible, we say 2D-NDP-L-Search $(u^*, u)$ returns Null and $x^i$ does not exist. Otherwise the second IP must be feasible, as per Proposition 11 below, in which case 2D-NDP-L-Search $(u^*, u)$ returns $x^n$. Observe that as a consequence of the results below, in criterion space this search returns $z^n$ with $z^n_3$ minimal over those $z^n\in \mathcal {Y}_N$ with $\overline{z^n}\in L(-,u^*,u)$, i.e., 2D-NDP-L-Search $(u^*,u)$ searches the L-shape with upper bound u and “elbow” $u^*$ for a nondominated point with minimal third objective value.

Before discussing useful properties of $x^n$ returned by 2D-NDP-L-Search $(u^*,u)$, we first make some comments about the choice of formulation for the IPs. For 2D-NDP-Search(u), the constraints $z(x)\le z(x^i)$ in the second IP, which ensure $\overline{z(x^n)}$ is in the rectangle $R(-,\overline{z(x^i)})$ and hence in $R(-,u)$, could equally well have been replaced by $z_k(x)\le u_k$ for $k=1,2$ and $z_3(x)\le z_3(x^i)$; all the subsequent propositions would still hold. In the case of 2D-NDP-L-Search $(u^*,u)$, however, the use of $z(x)\le z(x^i)$ in the second IP allow us to guarantee (via Observation 4) that $\overline{z(x^n)}$ is in the L-shape $L(-,u^*,u)$ without resorting to any additional binary variables and associated disjunctive constraints. This is helpful for efficiency of the second IP solution. The choice of model presented for the second IP of 2D-NDP-Search(u) maintains consistency between the two 2D search methods, and is furthermore consistent with the use of this search method in the current literature. Finally, we observe that the first IP in 2D-NDP-L-Search $(u^*,u)$ can be formulated with only one binary variable rather than two, via the observation that $w_1 + w_2 = 1$, rather than $w_1 + w_2 \ge 1$, gives a valid model. Our computational tests with the former showed only very small improvements in run time over the latter, on average, with many instances showing no difference at all. Furthermore the latter form of model is used in other methods in the literature (discussed in the next section). Thus to be consistent we present the model and computational results for the latter form of model.

Proposition 10

If $x^i$ exists, then $z(x^i)$ is a weakly nondominated point.

Proof

Similar to the proof of Proposition 6.

Proposition 11

If $x^i$ exists then $x^n$ exists and $z(x^n)$ is a nondominated point, i.e. $z(x^n)\in \mathcal {Y}_N$.

Proof

Similar to the proof of Proposition 7.

The following proposition mirrors Proposition 8 in the case that the search is performed over the L-shape $L(-,u^*,u)$. Note that in general for $v\in L(u^1,u',u^2)$ for some $u^1, u',u^2\in \mathbb {R}^2$, either $R(v,(u'_1,u^2_2)) = \emptyset$, which occurs if $v_1 > u'_1$, (v is in the horizontal part of the L but not in its corner rectangle), or $R(v,(u^2_1,u'_2)) = \emptyset$, which occurs if $v_2 > u'_2$, (v is in the vertical part of the L but not in its corner rectangle), or $R(v,(u'_1,u^2_2)) \ne \emptyset$ and $R(v,(u^2_1,u'_2)) \ne \emptyset$, which occurs if $v \le u'$, (v is in the corner rectangle of the L). In the latter case, $R(v,(u'_1,u^2_2))\cup R(v,(u^2_1,u'_2))$ form a (fully closed) L-shape, nested in the closure of $L(u^1,u',u^2)$. In the former two cases, $R(v,(u^2_1,u'_2)) \ne \emptyset$ and $R(v,(u'_1,u^2_2)) \ne \emptyset$ respectively, with the rectangles contained in the closure of the L-shape. In any of the three cases we may safely say that $R(v,(u'_1,u^2_2))\cup R(v,(u^2_1,u'_2))$ is contained in the closure of the L-shape $L(u^1,u',u^2)$, so for positive $\epsilon$, $R(v,(u'_1-\epsilon ,u^2_2))\cup R(v,(u^2_1,u'_2-\epsilon ))\subseteq L(u^1,u',u^2)$.

Proposition 12

If 2D-NDP-L-Search $(u^*, u)$ returns $x^n$ then $z(x^n)$ dominates any $y\in \mathcal {Y}$ with $\overline{y}\in R(\overline{z(x^n)},(u^*_1-\epsilon ,u_2))\cup R(\overline{z(x^n)},(u_1,u^*_2-\epsilon ))$ and $y\ne z(x^n)$.

Proof

Suppose 2D-NDP-L-Search $(u^*, u)$ returns $x^n$ and let $y\in \mathcal {Y}$ with $\overline{y}\in R(\overline{z(x^n)},(u^*_1-\epsilon ,u_2))\cup R(\overline{z(x^n)},(u_1,u^*_2-\epsilon ))$ and $y\ne z(x^n)$. By definition of the two IPs, $x^n$ has the minimum possible $z_3(x)$ value among all $x\in \mathcal {X}$ with $\overline{z(x)}\in L(-,u^*,u)$. Now $y= z(x)$ for some $x\in \mathcal {X}$ and it must be that

$$\begin{aligned} \overline{z(x)} = \overline{y} \in R(\overline{z(x^n)},(u^*_1-\epsilon ,u_2))\cup R(\overline{z(x^n)},(u_1,u^*_2-\epsilon )) \subseteq L(-,u^*,u) \end{aligned}$$

by the discussion above. Thus $y_3 = z_3(x) \ge z_3(x^n)$. Moreover $\overline{y}\in R(\overline{z(x^n)}, (u^*_1-\epsilon ,u_2)) \cup R(\overline{z(x^n)}$, and $(u_1,u^*_2-\epsilon ))$ implies that $\overline{y}\ge \overline{z(x^n)}$. Thus $y\ge z(x^n)$. Since $y\ne z(x^n)$ it must be that $z(x^n)$ dominates y. $\square$

Corollary 13

If 2D-NDP-L-Search $(u^*, u)$ returns $x^n$ then

$$\begin{aligned} \mathcal {Y}_N\cap \{y\in \mathcal {Y}\; :\;\overline{y}\in R(\overline{z(x^n)},(u^*_1-\epsilon ,u_2))\cup R(\overline{z(x^n)},(u_1,u^*_2-\epsilon ))\} = \{z(x^n)\}. \end{aligned}$$

Proof

This follows directly from Propositions 11 and 12.

3 Review of existing criterion space search algorithms

LSM method employs several algorithmic ideas for solving MOIPs that have been explored and embedded in existing methods. In this section, we describe these algorithmic ideas in the context of TOIPs. All these algorithmic ideas focus on the exploration of the (3-dimensional) criterion space. In some cases, the exploration takes place in the criterion space itself, in other cases the exploration takes place in the 2-dimensional projected space.

3.1 Sylva and Crema’s method

Sylva and Crema’s method [35] directly employs the definition of efficiency (Definition 2). (Note that the method is based on the method of Klein and Hannan [23].) The method finds the nondominated points one by one, with each subsequent, distinct, nondominated point found by solving an IP. Denote the distinct nondominated point obtained in iteration t by $z^t = (z^t_1,z^t_2,z^t_3)$ and its corresponding efficient solution by $x^t$. In the first iteration, the algorithm solves the IP

$$\begin{aligned} x^1 \in \hbox {arg min}_{x \in \mathcal {X}} \ \sum _{i=k}^{3}\&\lambda _kz_k(x), \end{aligned}$$

where $\lambda _k > 0$ for $k \in \{1,2,3\}$ to guarantee that $x^1$ is efficient. The corresponding criterion space iterate is $z^1 = z(x^1)$. At iteration $t\ge 2$ of the method, a nondominated point that is distinct from $z^1,\dots ,z^{t-1}$ is sought. Thus, by Definition 2, a point in $\mathcal {X}$ with at least one objective value strictly better than the corresponding element of $z^i$ for each $i=1,\dots ,t-1$ is required. This requirement can be enforced in the IP by adding three binary variables and corresponding disjunctive constraints for each $i=1,\dots ,t-1$, i.e., the following IP is solved

$$\begin{aligned}&x^t \in \hbox {arg min}_{x \in \mathcal {X}} \ \sum _{k=1}^{3} \ \lambda _kz_k(x) \\ \text{ subject } \text{ to }&z_k(x) \le (z^i_k - \epsilon ) + M (1 - w^i_k), \quad k \in \{1,2,3\}, \ i \in \{1,2,\ldots ,t-1\}\\&\sum _{k=1}^{3} w^i_k \ge 1, \quad \ i \in \{1,2,\ldots ,t-1\}\\&w^i \in \{0,1\}^3, \quad \ i \in \{1,2,\ldots ,t-1\} \end{aligned}$$

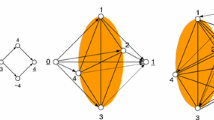
where M is an appropriately chosen large constant. (Note that the IP presented is slightly simpler than the IP presented by Sylva and Crema [35] and that the IP is still valid if we replace the constraints $\sum _{k=1}^{3} w^i_k \ge 1$ with $\sum _{k=1}^{3} w^i_k=1$.) The disjunctive constraints remove the dominated part of the criterion space identified and defined by $z^1,\dots ,z^{t-1}$. An illustration of the part of the criterion space that may still contain as yet unknown nondominated points after two nondominated points have been found is shown in Fig. 1, i.e. $B(z^B,z^T) {\setminus } (B(z^1,z^T) \bigcup B(z^2,z^T))$. Obviously, as soon as the IP becomes infeasible, all nondominated points have been found. The obvious weakness of the method is that the IPs get harder and harder to solve in each iteration, with the number of additional binary variables and (weak) disjunctive constraints increasing in proportion to the number of iterations completed.

Fig. 1

Area in the criterion space where as yet known nondominated points may be found after finding nondominated points $z^1$ and $z^2$

To avoid having too many disjunctive constraints in the IPs that need to be solved, the methods discussed in the remainder of this section all decompose the criterion space into boxes or rectangles (depending on the dimension of the criterion space in which they operate) after finding a new nondominated point and explore each box or rectangle separately.

3.2 The recursive method

This recursive method [29, 30] is a generalization of the well-known $\epsilon$-constraint method for solving biobjective IPs [10]. The basic idea is the following. In each iteration of the algorithm, the nondominated frontier of a biobjective IP is determined by solving

$$\begin{aligned} \begin{array}{rll} \mathcal {Y}^{2D}(U) := &{} \displaystyle \min _{x \in \mathcal {X}} &{} (z_1(x), z_2(x)) \\ &{} \text{ subject } \text{ to } &{} z_3(x) \le U - \epsilon , \end{array} \end{aligned}$$

with $U = z^T_3$ in the first iteration. The points in the 2-dimensional nondominated frontier are then translated into nondominated points in the original 3-dimension criterion space, for example, by solving, for each point $y \in \mathcal {Y}^{2D}(U)$, the following IP, which minimizes the value of the third objective

$$\begin{aligned}&\min _{x\in \mathcal {X}} z_3(x) \\ \text{ subject } \text{ to }&z_k(x) \le y_k \quad \ k \in \{1,2\}. \end{aligned}$$

The translated points form a subset of the nondominated frontier in the original 3-dimensional criterion space. In each iteration, the maximum value $z^{max}_3$ of the third objective function over all nondominated points generated in that iteration is computed and used as the upper bound U in the next iteration. The method terminates as soon as updating the upper bound U results in an infeasible biobjective IP.

A few comments about the recursive method follow. (1) The idea to convert a TOIP to a sequence of BOIPs can, of course, also be used to convert a BOIP to a sequence of single-objective IPs. The lexicographic method [30] combines these two ideas into a single method. (2) Solving an IP to translate a point in $\mathcal {Y}^{2D}(U)$ to a nondominated point in the original 3-dimensional criterion space can be avoided by adding $z_3(x)$ to the other objective functions with a small, appropriately chosen weight. This is referred to as an augmented approach and is used by Özlen and Azizoğlu [29].

3.3 The full p-split method

The full p-split method [13, 15] maintains a priority queue of boxes, each of which may still contain as yet unknown nondominated points. The priority queue is initialized with $B(z^B,z^T)$ and the method terminates when the priority queue is empty.

We will outline a simple version of the full p-split method and then comment on how its efficiency can be improved. In the simple version, the lower bound of all boxes in the priority queue is equal to $z^B$, i.e., the boxes are all of the form $B(z^B,u)$ with $u\in \mathcal {Y}$. Moreover, a nondominated point, if one exists, is found by using an arbitrary scalarization method (e.g., 3D-NDP-Search(u)). After finding a nondominated point $z^n\in \mathcal {Y}_N$, the boxes in the priority queue are examined and, if necessary, split into smaller boxes. Observe that $B(z^n,u) \cap \mathcal {Y}_N = \{z^n\}$ for any box $B(z^B, u)$ with $z^n \le u$. This observation suggests a decomposition scheme that splits a box in the priority queue into at most three boxes [15]: if a box $B(z^B, u)$ in the priority queue has $z^n \le u-\epsilon$, where $z^n$ is the most recently found nondominated point, then the box is removed from the priority queue, and for each $i \in \{1,2,3\}$, if $z^n_i\ge z^B_i+\epsilon$, then $B(z^B,\hat{u})$ with $\hat{u}_i = z^n_i -\epsilon$ and $\hat{u}_j = u_j$ for $j \in \{1,2,3\} {\setminus } \{i\}$ is added to the priority queue. An illustration of the three boxes created after the first nondominated point $z^n$ is found, i.e., $B(z^1,u')$, $B(z^1,u'')$, and $B(z^1,u''')$, is shown in Fig.  2.

Fig. 2

Upper bounds $u'$, $u''$ and $u'''$ of each of the three boxes create after finding the first nondominated point $z^n$

The decomposition may result in redundancy. If there are two boxes $B(z^B,u)$ and $B(z^B,u')$ in the priority queue with $u' \ge u$, then box $B(z^B,u)$ can be removed from the priority queue. Dächert and Klamroth [13] present a version of the full p-split method that is designed to efficiently avoid redundancy.

Assuming that the ideal point is known, Dächert and Klamroth [13] prove that the full 3-split method solves at most $3|\mathcal {Y}_N|- 2$ subproblems, where a subproblem is any scalarization that should be solved. Thus, if 3D-NDP-Search is used as the scalarization, the algorithm solves $3|\mathcal {Y}_N|-2$ IPs (at most $2|\mathcal {Y}_N|-2$ of which are infeasible).

3.4 The full $(p-1)$-split method

The full $(p-1)$-split method is a special case of the full p-split method [13, 22, 24, 26]. Like the Recursive Method, it operates in a projected 2-dimensional criterion space. To be able to work in the projected space, searching for a nondominated point must be done by a special operation, for instance by $\textsc {2D-NDP-}\textsc {Search}$.

Since we have used the variant of the full $(p-1)$-split method introduced by Kirlik and Sayın [22] in our computational study, we will explain that one in more detail. Their variant maintains a priority queue of rectangles, each of which may still contain as yet unknown nondominated points. The priority queue is initialized with $R(\overline{z^B},\overline{z^T})$ and the method terminates when the priority queue is empty. A nondominated point in a rectangle is found, if one exists, by calling (a slight modification of) $\textsc {2D-NDP-}\textsc {Search}$. After finding a nondominated point $z^n\in \mathcal {Y}_N$, the rectangles in the priority queue are examined and split if one of the components of $z^n$ intersects the corresponding side of the rectangle. More specifically, any rectangle $R(u^1, u^2)$ with $u^1_1 < z^n_1 < u^2_1$ is split into two rectangles: $R(u^1, (z^n_1 - \epsilon ,u^2_2)) \simeq \{y \in R(u^1,u^2) : y_1 < z^n_1 \}$ and $R((z^n_1,u^1_2), u^2) = \{y \in R(u^1,u^2): y_1 \ge z^n_1\}$, both immediately added to the priority queue. Then any rectangle $R(u^1, u^2)$ with $u^1_2 < z^n_2 < u^2_2$ is split into two rectangles $R(u^1,(u^2_1,z^n_2 - \epsilon ))$ and $R((u^1_1,z^n_2),u^2)$. Any new rectangles created by splitting may be split again, until no rectangle $R(u^1,u^2)$ in the priority queue has $u^1_i < z^n_i < u^2_i$ for any $i\in \{1,2\}$.

Fig. 3

Three iterations of the variant of the full $(p-1)$-split method introduced by Kirlik and Sayın [22]

To avoid redundant computations when exploring $R(u^1,u^2)$ three ideas are employed. (1) The priority queue uses $a(R(\overline{z^B}, u^2))$ as the priority for a rectangle $R(u^1,u^2)$, i.e., the rectangle with the largest area is always chosen to be explored next. This implies that $R(u^1,u^2)$ cannot be dominated by any other as yet unexplored rectangle. (2) After finding a nondominated point $z^n$ while exploring $R(u^1,u^2)$ and after applying the decomposition scheme, any rectangle $R(u^3, u^4)$ in the priority queue with $R(u^3, u^4) \subseteq R(z^n,u^2)$ is removed (correctness follows from Proposition 8). (3) Similarly, after determining that $R(u^1,u^2)$ contains no nondominated points, any rectangle $R(u^3,u^4)$ in the priority queue with $R(u^3,u^4) \subseteq R(\overline{z^B},u^2)$ is removed.

An illustration of the first three iterations of the variant of the full $(p-1)$-split method introduced by Kirlik and Sayın [22] can be found in Fig. 3. The rectangle being investigated in an iteration is shown in bold, the nondominated point found is shown as a solid circle, and the resulting split rectangles and the dominated area are shaded (in green). Observe that in the third iteration, the nondominated point found lies outside the rectangle being investigated. After splitting, the hatched rectangle is dominated and can be removed from the priority queue.

Note that working in the projected space has some advantages. For example, whereas in the full p-split method many IPs solved are infeasible, this rarely happens in the full $(p-1)$-split method; instead of the IP being infeasible, it returns a previously obtained nondominated point. This is important from an efficiency point of view, because IP solvers tend to struggle with infeasible IPs.

4 The L-shape search method

4.1 High-level description

The LSM maintains a priority queue of rectangles, each of which still has to be explored, i.e., may still contain as yet unknown nondominated points. The rectangles are maintained in nonincreasing order of their area. The priority queue is initialized with $R(\overline{z^B},\overline{z^T})$. The method also maintains an ordered list of nondominated points (and their corresponding solutions) $L_N$, which is updated after finding a new nondominated point. The nondominated points are maintained in nondecreasing order of their third objective value. If two different nondominated points have the same third objective value, the one that LSM finds first has a higher priority in $L_N$.

The method explores a rectangle by finding all nondominated points with a projection in the rectangle, other than those lying within a set of disjoint subrectangles identified during the search procedure. The disjoint subrectangles are added to the priority queue to be explored later. A high-level overview of the process for exploring a rectangle is given below; more detail is provided later.

The method explores a rectangle by searching for a nondominated point with projection in the rectangle. In the process, known nondominated points (already in $L_N$) with projection outside the rectangle may be found, in which case the rectangle is “shrunk”. The search either determines that the rectangle contains no nondominated points with projection in the rectangle and that therefore the rectangle can be discarded, or it finds a nondominated point with projection in the rectangle. This point induces an L-shape contained in the rectangle, which is then searched for a nondominated point with projection in the L-shape. Again, known nondominated points with projection outside the L-shape may be found, in which case the L-shape is shrunk. Either the L-shape is shown to contain no nondominated point with projection in the L-shape and can be discarded, or a nondominated point with projection in the L-shape is identified. This point induces a new rectangle, one of the set of disjoint subrectangles, which is added to the priority queue, and the L-shape is shrunk. The process of searching an L-shape continues until it is proved that all nondominated points with projection in the rectangle have been identified and added to $L_N$, or must have their projection in one of the subrectangles added to the priority queue.

The critical factors for LSM’s success are that it (1) keeps the size of the single-objective IPs small by working with rectangles and L-shapes only, and (2) “fully” explores a rectangle, i.e., does not decompose a rectangle as soon as a nondominated point is found. The latter ensures that different parts of the criterion space are explored early in the search (e.g., by fully exploring the first rectangle $R(\bar{z}^B, \bar{z}^T)$).

4.2 Detailed description

We now give the details of LSM. The first important operation in LSM, denoted by $\textsc {Find-NDP}(u^1,u^2,L_N)$, searches for an as yet unknown nondominated point with projection in a given rectangle $R(u^1,u^2)$ by repeated calls to $\textsc {2D-NDP-}\textsc {Search}$. The operation starts by calling $\textsc {2D-NDP-}\textsc {Search}(u^2)$. This can either return Null or an efficient solution $x^n$. Since $\textsc {2D-NDP-}\textsc {Search}(u^2)$ searches $R(-,u^2)$ it is possible that $\overline{z(x^n)}\not \in R(u^1,u^2)$. Four cases need to be considered:

• 1. $\textsc {2D-NDP-}\textsc {Search}(u^2)$ returns an efficient point $x^n$ and $\overline{z(x^n)} \in R(u^1,u^2)$. In this case, $x^n$ is returned.

• 2. $\textsc {2D-NDP-}\textsc {Search}(u^2)$ fails to find an efficient point (returns Null). This implies that there does not exist a nondominated with its projection in $R(u^1,u^2)$. In this case, Null is returned.

• 3. $\textsc {2D-NDP-}\textsc {Search}(u^2)$ returns an efficient point $x^n$, $\overline{z(x^n)} \notin R(u^1,u^2)$, and $z_1(x^n) < u^1_1$ and $z_2(x^n) < u^1_2$. In this case, by Proposition 8 and since $R(\overline{z(x^n)},u^2){\setminus }\{\overline{z(x^n)}\} \supset R(u^1,u^2)$, all points in $\mathcal {Y}$ that have their projection in $R(u^1,u^2)$ are dominated by $z(x^n)$. Thus there cannot exist any nondominated point with its projection in $R(u^1,u^2)$ and Null is returned.

• 4. $\textsc {2D-NDP-}\textsc {Search}(u^2)$ returns an efficient point $x^n$, $\overline{z(x^n)} \notin R(u^1,u^2)$, and either $z_1(x^n) \ge u^1_1$ or $z_2(x^n) \ge u^1_2$, or equivalently $z_2(x^n) < u^1_2$ or $z_1(x^n) < u^1_1$. In this case, by Proposition 8, all points in $\mathcal {Y}$ that have their projection in $R(\overline{z(x^n)},u^2){\setminus }\{\overline{z(x^n)}\}$ are dominated by $z(x^n)$. Thus we can safely ignore either the top part of $R(u^1,u^2)$, in the case that $z_2(x^n) \ge u^1_2$ (equivalently $z_1(x^n) < u^1_1$), or the right part of $R(u^1,u^2)$, in the case that $z_1(x^n) \ge u^1_1$ (equivalently $z_2(x^n) < u^1_2$). Specifically, we know that any nondominated point with its projection in $R(u^1,u^2)$ must have its projection within $R(u^1,(u^2_1,z_2(x^n)-\epsilon ))$ if $z_1(x^n) < u^1_1$ and within $R(u^1,(z_1(x^n)-\epsilon ,u^2_2))$ if $z_2(x^n) < u^1_2$. The former case is illustrated in Fig. 4, where the (green) shaded rectangle shows the part of the criterion space dominated by $z(x^n)$. In this case, the search is continued, with $\textsc {2D-NDP-}\textsc {Search}$ applied again, to the updated upper bound (either $(u^2_1,z_2(x^n)-\epsilon )$ or $(z_1(x^n)-\epsilon ,u^2_2)$, depending on the case).

Note that as long as Case 4 applies, $\textsc {2D-NDP-}\textsc {Search}$ is repeated, each time searching a rectangle that is a strict subset of the rectangle before. The process finishes as soon as one of Cases 1–3 is encountered. A precise description of $\textsc {Find-NDP}(u^1,u^2,L_N)$ is given in Algorithm 1. Note that by Proposition 7, a point $x^n$ returned by $\textsc {2D-NDP-}\textsc {Search}(u^2)$ must be efficient, and therefore the list of known efficient points is updated each time $\textsc {2D-NDP-}\textsc {Search}(u^2)$ returns a point $x^n$, i.e., it is added to $L_N$ if it is not already in $L_N$.

Next, we discuss how rectangles are explored (treated). The exploration of a rectangle $R(u^1,u^2)$ starts by calling $\textsc {Find-NDP}(u^1,u^2,L)$ to find a nondominated point $z^n$ with projection inside the rectangle. If $z^n = Null$ or $\overline{z^n} = u^1$, then (using Proposition 8) there do not exist as yet unknown nondominated points with projection in the rectangle, and no further exploration of the rectangle is required. If $z^{n} \ne Null$ and $\overline{z^n} \ne u^1$, then $\overline{z^n}$ must be a point in the rectangle that is not in either of the two lower side boundaries (the left and the bottom sides). In this case, we convert the rectangle to the L-shape $L(u^1, \overline{z^n}, u^2)$ and the LSM continues by exploring the L-shape. Note that during $\textsc {Find-NDP}(u^1,u^2,L_N)$ $u^2$ may have been updated.

Fig. 4

$\overline{z(x^n)}$ lies outside $R(u^1,u^2)$

An L-shape $L(u^1,u^*,u^2)$ is explored by calling $\textsc {2D-NDP-L-}\textsc {Search}(u^*,u^2)$ repeatedly to find a new nondominated point $z^{new}$ with projection inside the L-shape, or show that no such point exists. Four possible cases need to be considered.

• 1. $\textsc {2D-NDP-L-}\textsc {Search}(u^*,u^2)$ fails to find a nondominated point. In this case, the exploration of the L-shape is complete.

• 2. $\textsc {2D-NDP-L-}\textsc {Search}(u^*,u^2)$ returns an efficient point $x^n$, $\overline{z(x^n)}\not \in L(u^1,u^*,u^2)$ and $z_1(x^n) \le u^1_1$ and $z_2(x^n) \le u^1_2$. This implies, by Proposition 12 and since in this case the region dominated by $z(x^n)$ contains all points with projection in $L(u^1,u^*,u^2)$, that there does not exist a nondominated point with its projection in $L(u^1,u^*,u^2)$, other than $z^n$ itself if $\overline{z^n} = u^1$. In this case, too, the exploration of the L-shape is complete.

• 3. $\textsc {2D-NDP-L-}\textsc {Search}(u^*,u^2)$ returns an efficient point $x^n$, $\overline{z^n} \not \in L(u^1,u^*,u^2)$, and either $z^n_1 < u^1_1$ and $z^n_2 \ge u^1_2$, or $z^n_2 < u^1_2$ and $z^n_1 \ge u^1_1$, where $z^n=z(x^n)$. In this case, by Proposition 12, $\overline{z^n}$ dominates either a rectangle at the top of the vertical part of the L or dominates a rectangle at the right of the horizontal part of the L. The L-shape can thus be “shrunk”: if $z^n_1 < u^1_1$ and $z^n_2 \ge u^1_2$ then the only part of the L-shape that may still contain nondominated points is $L(u^1,u^*,(u^2_1,z^n_2 - \epsilon ))$; if $z^n_2 < u^1_2$ and $z^n_1 \ge u^1_1$ then the only part of the L-shape that may still contain nondominated points is $L(u^1,u^*,(z^n_1 - \epsilon ,u^2_2))$. An illustration of this case is shown in Fig. 5. Note that the remaining L-shape may degenerate to a rectangle (e.g. if $z^n_1 < u^1_1$ and $u^*_2 \ge z^n_2 \ge u^1_2$ it becomes the rectangle $R(u^1,(u^2_1,z^n_2 - \epsilon ))$), in which case the rectangle is searched using $\textsc {2D-NDP-}\textsc {Search}$; otherwise the search is continued with $\textsc {2D-NDP-L-}\textsc {Search}$.

• 4. $\textsc {2D-NDP-L-}\textsc {Search}(u^*,u^2)$ returns an efficient point $x^n$, and $\overline{z^n} \in L(u^1,u^*,u^2)$ where $z^n = z(x^n)$. In this case, we create a new point $u^{b} = (\min (z^n_1, u^*_1), \min (z^n_2, u^*_2))$ (see Fig. 6a). Now by Proposition 12, all points with projections in $R(\overline{z^n},(u^*_1-\epsilon ,u^2_2)) \cup R(\overline{z^n},(u^2_1,u^*_2-\epsilon ))$ are dominated by $z^n$, other than $z^n$ itself. There are two sub-cases to consider.

  • (a) If $u^b = \overline{z^n}$, then $z^n_1 \le u^*_1$ and $z^n_2 \le u^*_2$, ($\overline{z^n}$ is in the corner rectangle of the L), and removing the projected region known to be dominated by $z^n$ from the L-shape causes it to be “shrunk” to $L(u^1,\overline{z^n},u^2)$.

  • (b) Otherwise, removing the projected region known to be dominated by $z^n$ from the L-shape results in a kind of “step” shape, formed by the intersection of $L(u^1,u^*,u^2)$ and $L(u^1,z^n,u^2)$. Rather than handle such a shape directly, we partition it into the rectangle $R(u^{b},u^t)$ where $u^t = (\max (z^n_1,u^*_1)-\epsilon , \max (z^n_2,u^*_2)-\epsilon )$ (indicated by R in Fig. 6b) and the L-shape $L(u^1,u^b,u^2)$. The rectangle is added to the priority queue.

  Note that in both of these subcases, there is a “remaining” L-shape given by $L(u^1,u^b,u^2)$ that may still contain the projections of nondominated points; this revised L-shape is again searched with $\textsc {2D-NDP-L-}\textsc {Search}$.

Fig. 5

$\overline{z^n}$ lies outside $L(u^1,u^*,u^2)$ with $z^n_1 < u^1_1$ and $z^n_2>u^*_2 \ge u^1_2$ after a call to $\textsc {2D-NDP-L-}\textsc {Search}(u^*,u^2)$ (Case 3)

Fig. 6

$\overline{z^n}$ lies inside $L(u^1,u^*,u^2)$ after a call to $\textsc {2D-NDP-L-}\textsc {Search}(u^*,u^2)$ (Case 4)

A precise description of LSM is shown in Algorithm 2. Next, we prove that LSM solves at most $O(|\mathcal {Y}_N|^2)$ single-objective IPs when solving a TOIP.

Theorem 14

The number of single-objective IPs solved by LSM to generate the nondominated frontier of a TOIP is bounded below by $2|\mathcal {Y}_N|+1$ and above by $(|\mathcal {Y}_N|-1)^2+3|\mathcal {Y}_N|$.

Proof

Each nondominated point will be obtained at least once as the solution to either $\textsc {2D-NDP-}\textsc {Search}$ or 2D-L-NDP-Search, each requiring the solution of two IPs. This, together with the fact that at least one IP has to be solved to recognize that there are no other nondominated points, shows that the number of IPs that must be solved is at least $2|\mathcal {Y}_N|+1$. After finding a nondominated point, LSM adds at most one rectangle to the priority queue. For LSM to terminate, the rectangles in the priority queue must not contain any as yet unknown nondominated points. Establishing that a rectangle does not contain as yet unknown nondominated points requires the solution of one IP. It is clear that the first nondominated point is found at most once. Next, consider any other nondominated point generated by LSM. The point might be generated again when investigating any of the other $|\mathcal {Y}_N|-1$ rectangles. However, when that happens, it is recognized after one IP is solved. Consequently, the IPs solved is bounded by $2|\mathcal {Y}_N| + |\mathcal {Y}_N| + (|\mathcal {Y}_N|-1)^2$. $\square$

We note that the method by Dächert and Klamroth [13] has a better worst-case behavior than LSM as the number of single-objective IPs solved can be bounded by a linear function of $|\mathcal {Y}_N|$.

5 Implementation issues and enhancements

LSM starts by exploring rectangle $R(\bar{z}^B, \bar{z}^T)$, with the projection of the upper bound $z^T$ passed as the argument of $\textsc {2D-NDP-}\textsc {Search}$ and $\textsc {2D-NDP-L-}\textsc {Search}$. The initial choice of $z^T$ can be important to the performance of the algorithm. One possibility, which we use in our implementation of LSM, is to take $z^T_i = \max _{x \in \mathcal {X}_{LP}} z_i(x)$ for each $i=1,2,3$, where $\mathcal {X}_{LP}$ is the LP-relaxation of $\mathcal {X}$, assumed throughout to be bounded. Another, more expensive, option is to take $z^T_i = \max _{x\in \mathcal {X}}z_i(x)$ for each $i=1,2,3$.

Note that the lower bound $z^B$ is not used in $\textsc {2D-NDP-}\textsc {Search}$ or$\textsc {2D-NDP-L-}\textsc {Search}$. Thus, the choice of $z^B$ is not important for the efficiency of LSM but only for its correctness. In our implementation, we set $z^B_i = \min _{x\in \mathcal {X}_{LP}}z_i(x)$ for each $i=1,2,3$.

As LSM relies heavily on solving single-objective IPs, it is important that these IPs are solved as efficiently as possible. Therefore, high-quality initial feasible solutions are provided to the solver whenever possible. This is done by exploiting the list of known nondominated points. In many cases, one or more of the known solutions in $L_N$ are feasible for the first IP solved in $\textsc {2D-NDP-}\textsc {Search}$ or $\textsc {2D-NDP-L-}\textsc {Search}$. Furthermore, if the first IP solved in $\textsc {2D-NDP-}\textsc {Search}$ or $\textsc {2D-NDP-L-}\textsc {Search}$ is feasible, then its optimal solution is obviously feasible for the second IP. Note that the list of known nondominated points $L_N$ is maintained in nondecreasing order of their third objective values. Therefore, the first feasible solution encountered in the list is that with the best objective value for the first IP in $\textsc {2D-NDP-}\textsc {Search}$ and $\textsc {2D-NDP-L-}\textsc {Search}$.

We also make sure that we avoid solving IPs unnecessarily. For example, if we provide a feasible solution x from $L_N$ to the first IP in $\textsc {2D-NDP-}\textsc {Search}$ or $\textsc {2D-NDP-L-}\textsc {Search}$ and we find that x is optimal, then, because x is efficient, x will be optimal for the second IP as well and there is no need to solve it.

Propositions 15–18 presented below provide additional opportunities to avoid solving IPs unnecessarily. The propositions rely on the fact that solving an IP may be unnecessary if a relaxation (with respect to the objective function constraints that have been added) has been solved previously. Similar ideas have been used in several other methods (e.g., Lokman and Köksalan [26], Özlen et al. [30]). Since in all cases the proofs are straightforward, we omit them.

Proposition 15

Let $R(u^1,u^2)$ and $R(v^1,v^2)$ be two rectangles such that $u^2\ge v^2$. If $\textsc {2D-NDP-}\textsc {Search}(u^2)$ is infeasible, then $\textsc {2D-NDP-}\textsc {Search}(v^2)$ is also infeasible. Otherwise, let $x^n$ be an optimal solution of $\textsc {2D-NDP-}\textsc {Search}(u^2)$. If $\overline{z(x^n)}\le v^2$ then $x^n$ is also optimal for $\textsc {2D-NDP-}\textsc {Search}(v^2)$.

Proposition 16

Let $R(u^1,u^2)$ and $L(v^1,v^*,v^2)$ be a rectangle and an L-shape such that $u^2\ge v^2$. If $\textsc {2D-NDP-}\textsc {Search}(u^2)$ is infeasible, then $\textsc {2D-NDP-L-}\textsc {Search}(v^*,v^2)$ is also infeasible. Otherwise, let $x^n$ be an optimal solution of 2D-NDP-Search $(u^2)$. If $\overline{z(x^n)}\le v^2$ and $\overline{z(x^n)}\notin R(v^*,v^2)$, then $x^n$ is also optimal for $\textsc {2D-NDP-L-}\textsc {Search}(v^*,v^2)$.

Proposition 17

Let $L(u^1,u^*,u^2)$ and $R(v^1,v^2)$ be an L-shape and a rectangle such that $u^2\ge v^2$ and $v^2\notin R(u^*,u^2)$. If $\textsc {2D-NDP-L-}\textsc {Search}(u^*,u^2)$ is infeasible, then $\textsc {2D-NDP-}\textsc {Search}(v^2)$ is also infeasible. Otherwise, let ${x}^n$ be an optimal solution of $\textsc {2D-NDP-L-}\textsc {Search}(u^*,u^2)$. If $\overline{z(x^n)}\le v^2$ then $x^n$ is also optimal for $\textsc {2D-NDP-}\textsc {Search}(v^2)$.

Proposition 18

Let $L(u^1,u^*,u^2)$ and $L(v^1,v^*,v^2)$ be two L-shapes such that $u^2 \ge v^2$ and either $v^* \le u^*$ or $v^2\not \in R(u^*,u^2)$ or both. If $\textsc {2D-NDP-L-}\textsc {Search}(u^*,u^2)$ is infeasible, then $\textsc {2D-NDP-L-}\textsc {Search}(v^*,v^2)$ is also infeasible. Otherwise, let $x^n$ be an optimal solution to $\textsc {2D-NDP-L-}\textsc {Search}(u^*,u^2)$. If $z(x^n)\le v^2$ and $\overline{z(x^n)}\notin R(v^*,v^2)$, then $x^n$ is also optimal for $\textsc {2D-NDP-L-}\textsc {Search}(v^*,v^2)$.

We note that a careful analysis of the logic of LSM reveals that the conditions of Propositions 16 and 18 never hold in LSM, which implies that solving the first IP in 2D-NDP-L-Search cannot be avoided. To be able to exploit these propositions, information about every call to $\textsc {2D-NDP-}\textsc {Search}$ and 2D-NDP-L-Search is recorded. Specifically, two data structures are employed, the first to record information about every call to 2D-NDP-Search and $\textsc {2D-NDP-L-}\textsc {Search}$ that returned Null, i.e. that was infeasible, and the second to record information about calls that resulted in an efficient solution in $L_N$. In the former case, every value of u for which $\textsc {2D-NDP-}\textsc {Search}(u)$ was found to be infeasible and every pair of values $u^*, u$ for which $\textsc {2D-NDP-L-}\textsc {Search}(u^*,u)$ was found to be infeasible are recorded. Before solving the first IP in any new call to $\textsc {2D-NDP-}\textsc {Search}$ or $\textsc {2D-NDP-L-}\textsc {Search}$, we check this stored information to see whether any of the above propositions can be applied to deduce a priori that infeasibility will result. The second data structure is used to record, for each efficient solution in $L_N$, the parameters of any calls to either $\textsc {2D-NDP-}\textsc {Search}$ or $\textsc {2D-NDP-L-}\textsc {Search}$ that returned this solution. Because a nondominated point can be “discovered” multiple times, we keep track of the information for each discovery. This information is sufficient to check whether the conditions of any of the propositions hold. More specifically, before solving the first IP in any new call to $\textsc {2D-NDP-}\textsc {Search}$ or $\textsc {2D-NDP-L-}\textsc {Search},$ we go through the known efficient solutions in $L_N$ and find the first feasible point for this IP, if it exists. If a feasible point is found, we check the stored information regarding its discovery to see whether one of the propositions can be applied. If unsuccessful, then we check any other points in $L_N$ with the same third objective function value, since the existence of the feasible point with this value is assurance that the optimal value of the first IP cannot be higher than this (and recall the list is kept in nondecreasing order of the third objective value). Note that we check for feasible points in $L_N$ first and only if that fails check the data recorded on infeasible calls to $\textsc {2D-NDP-}\textsc {Search}$ and $\textsc {2D-NDP-L-}\textsc {Search}$.

6 An example

We illustrate the workings of LSM on a $5\times 5$ instance of an assignment problem with three objectives introduced by Özlen and Azizoğlu [29]. The objective function coefficients can be found in Table 1. The instance has 15 nondominated points shown in Fig. 7.

Table 1 Objective function coefficients of a $5 \times 5$ instance of an assignment problem with three objectives

Fig. 7

Nondominated points of a $5\times 5$ instance of an assignment problem with three objectives with their projections

Table 2 Demonstration of LSM on a $5\times 5$ AP instance taken from Özlen and Azizoğlu [29]

The steps of the search performed by LSM on this instance are represented in Table 2, where we refer to the exploration of a rectangle as an “Iteration” and the search for a nondominated point as a “Step”. Column $z^n$ shows the nondominated point found in each step, or $\infty$ in case no nondominated was found (i.e., no nondominated point with projection in the rectangle or L-shape existed). When a nondominated point is found for the first time, it is shown in bold font; when a nondominated point is found again, it is shown in regular font. LSM terminates after 12 iterations, but found all 15 nondominated points in the first three iterations. Columns $u^1, u^*$ and $u^2$, define the rectangle or L-shape being searched in each step. If $u^*$ is blank, then LSM searches a rectangle (using $\textsc {2D-NDP-}\textsc {Search}$), otherwise it searches an L-shape (using $\textsc {2D-NDP-L-}\textsc {Search}$). For presentational convenience, the upper bound points $u^2$ have integer coordinates, whereas in reality, a small constant $\epsilon$ has been subtracted from each component. Columns A-IP1 and A-IP2 show whether the first IP or second IP is avoided, due to the use of enhancements. For instance, because of the results of iterations 9 and 10, no IP is solved in iterations 11 and 12.

7 A computational study

To assess the performance of LSM, we have carried out an extensive computational study. Based on our review of the recent literature, two of the fastest existing methods for solving TOIPs are the enhanced recursive method (ERM) of Özlen et al. [30], where the enhancements are based on propositions similar to those discussed in Sect. 5, and the full $(p-1)$-split method of Kirlik and Sayın [22] (which we denote by KSA). In our computational study, we have used the implementations of ERM and KSA made available by their authors (at https://bitbucket.org/melihozlen/moip_aira/ and http://home.ku.edu.tr/~moolibrary/, respectively). KSA is coded in C++ and ERM is coded in C. LSM has been coded in C++. To ensure that our performance comparison is fair, we made all codes use CPLEX 12.5.1 as the integer programming solver and we carried out all computational experiments on the same hardware, a Dell PowerEdge R710 with dual hex core 3.06 Gz Intel Xeon X5675 processors and 96 GB RAM, running the RedHat Enterprise Linux 6 operating system, and using a single thread.

We note that the method with the best known theoretical performance is the full $(p-1)$-split method of Dächert and Klamroth [13], because the number of subproblems solved by their method is linearly bounded. Unfortunately, no C or C++ implementation of their method is (publicly) available, and, as a result, we were unable to include their method in our computational study.

In our computational study, we use two publicly available sets of instances, Set I and Set II, used in previous studies of methods for solving TOIPs. The first set has been used by Özlen et al [30] and contains 19 instances with different sizes, including 10 instances of the triobjective assignment problem (AP), 6 instances of the triobjective 3-dimensional knapsack problem (3DKP), and 3 instances of the triobjective traveling salesman problem (TSP). The second set has been used by Kirlik and Sayın [22] and has a class of AP instances and a class of 1DKP instances. Each class contains 10 subclasses, each with 10 instances. A subclass is characterized by the size of the instances it contains (in terms of the number of agents and tasks in AP and in terms of the number of items in 1DKP). The subclasses of AP have instances of size 5, 10, 15, 20, 25, 30, 35, 40, 45, and 50. The subclasses of 1DKP have instances of size 10, 20, 30, 40, 50, 60, 70, 80, 90, and 100. (Note that the size of an instance of 1DKP and 3DKP gives the number of binary variables in the formulation; the size of instance of AP to the power two gives the number of binary variables in the formulation, the size of an instance of TSP is in terms of the number of cities and thus the size to the power of two gives the number of binary variables in the formulation.) In our computational study, each instance was solved five times and averages over the five instances are reported in the result tables.

7.1 Performance

We start by comparing the performance of LSM, ERM, and KSA on the instances in Set I. Table 3 shows instance information, namely the class, the size, and the number of points in the nondominated frontier, as well as result information, namely for each method the number of single-objective IPs solved and the time taken to generate the nondominated frontier, and the percent improvement in number of IPs solved and time taken to generate the nondominated frontier of LSM over ERM and KSA. (In these experiments, LSM is initialized with $z^T_i = \max _{x \in \mathcal {X}_{LP}} z_i(x)$ and $z^B_i = \min _{x\in \mathcal {X}_{LP}} z_i(x)$ for $i = 1, 2, 3$.)

Table 3 Performance comparison of LSM, ERM, and KSA on Set I

We observe that LSM outperforms both ERM and KSA. It is, on average, 32 % faster than ERM and 17 % faster than KSA, primarily because it solves fewer IPs, namely on average 42 % fewer than ERM and 8 % fewer than KSA.

Detailed performance statistics of LSM on instances of Set I can be found in Table 4, where, in addition to the number of single-objective IPs solved and the time taken to generate the nondominated frontier, we also report the number of rectangles processed (#Rec), the number of IPs solved (#S), and the number of times the solution of an IP was avoided because of one of the propositions in Sect. 5 (#A). These counts are grouped by $\textsc {2D-NDP-}\textsc {Search}$ and $\textsc {2D-NDP-L-}\textsc {Search}$ as well as by whether it is the first or the second of the IPs solved in these operations. Where appropriate, we give the number of IPs that were infeasible in parentheses. Note that if solving the first IP in $\textsc {2D-NDP-}\textsc {Search}$ or $\textsc {2D-NDP-L-}\textsc {Search}$ can be avoided because of one of the propositions and corollaries in Sect. 5, we automatically avoid solving the second IP too. Therefore, we only report the number of times the solution of the second IP was avoided when the first IP was solved.

Table 4 Detailed results of the LSM on Set I

We observe that the enhancements are critical to the performance, because the solution of many IPs is avoided. (Recall that the conditions of Propositions 16 and 18 never hold in LSM and therefore no first IP solves of $\textsc {2D-NDP-L-}\textsc {Search}$ are avoided; the related column is included only for aesthetics and completeness sake.)

The importance of the enhancements is illustrated in a different way in Fig. 8, which shows the ratio of the number of IPs solved when all enhancements are enabled and the number of IPs solved when all enhancements are disabled. (The instances are presented along the horizontal axis in nondecreasing order of their number of nondominated points.) Again, we see that the number of IPs actually solved reduces substantially (by a factor of about 0.35) when the enhancements are enabled.

Fig. 8

Ratio of number of IPs solved by LSM with enhancements to the number of IPs solved by LSM without enhancements

Fig. 9

Ratio of the IP solve time to the total solve time

The importance of the enhancements becomes more obvious when we look at a breakdown of the solution time. Figure 9 shows the fraction of time taken up by solving $\textsc {2D-NDP-}\textsc {Search}$ and $\textsc {2D-NDP-L-}\textsc {Search}$ as well as the fraction of time taken up by solving the first and second IPs of $\textsc {2D-NDP-}\textsc {Search}$ and $\textsc {2D-NDP-L-}\textsc {Search}$. We see that more than 90 % of the solution time is consumed by solving single-objective IPs and, not surprisingly, that the largest fraction of that time is solving first IPs.

We have mentioned earlier, that one of the critical factors for LSM’s success is that it “fully” explores a rectangle, i.e., that it does not decompose a rectangle as soon as a nondominated point is found. This ensures that different parts of the criterion space are explored early in the search (e.g., by fully exploring the first rectangle $R(z^B, z^T)$). Figure 10 illustrates this aspect of LSM by showing the area of the 2nd through 20th rectangles explored by LSM for instance AP50 as a fraction of the area of the initial rectangle $R(z^B, z^T)$. The figure clearly shows that the area of the rectangles explored decreases sharply in the first few iterations.

Fig. 10

Area of the rectangles 2 through 20 as a fraction of the area of $R(\bar{z}^B,\bar{z}^T)$ for instance AP50

Fig. 11

Performance profile of the run time of the algorithms on 1DKP instances in Set II

Fig. 12

Performance profile of the run time of the algorithms on AP instances in Set II

Because the number of instances in Set II is much larger than the number of instances in Set I, we present performance profiles rather than result tables. A performance profile is a graph with along the horizontal axis the ratio of the run time of an instance to the minimum run time for that instance among all methods and along the vertical axis the fraction of instances that achieved a ratio that is less than or equal to the ratio on the horizontal axis [16]. (This implies that values in the upper left-hand corner of the graph indicate the best performance.)

The performance profile of run time of LSM, ERM, and KSA for the 1DKP and AP instances in Set II can be found in Figs. 11 and 12, respectively. We observe that LSM clearly outperforms ERM and KSA (and that KSA clearly outperforms ERM).

7.2 Approximate frontiers

In practice, finding approximate nondominated frontiers, especially if this can be done quickly, is of premium importance. LSM is designed, in part, to enable the efficient generation of approximate frontiers. We have conducted a number of computational experiments to assess whether LSM, ERM, and KSA are capable of generating a high-quality approximate frontier early in the search. We start our investigation using one of the best-known measures for assessing and comparing approximate frontiers: the hypervolume indicator (or S-metric), which is the volume of the dominated part of the criterion space with respect to a reference point [38, 40]. As the reference point impacts the value of the hypervolume indicator, we have used the nadir point, i.e., $z^N_i := \max \{z_i(x): z \in \mathcal {Y}_N\}$ for $i = 1,2,3$, as the reference point, which is the best possible choice for the reference point. (Note that computing the nadir point is not easy in general, but trivial once the nondominated frontier is known.) The effort required to compute the hypervolume indicator is a function of both the number of nondominated points and the dimension of the criterion space; for more information on computing the hypervolume indicator see [4]. Several public domain codes for calculating the hypervolume indicator are available. We have used the one at http://www.tik.ee.ethz.ch/~sop/download/supplementary/weightedHypervolume.

Let the hypervolume of a given set of nondominated points S be denoted by h(S) and let the hypervolume gap of an approximate frontier with nondominated points $\mathcal {Y}^A_N \subseteq \mathcal {Y}_N$ be defined as $\frac{h(\mathcal {Y}_N) - h(\mathcal {Y}^A_N)}{h(\mathcal {Y}_N)}$. (Note that the hypervolume gap can only be computed once the nondominated frontier is known.)

In Fig. 13, we show the number of nondominated points (as a fraction of the total number of nondominated points) that must be generated to achieve a hypervolume gap of less than 20 % for LSM, ERM, and KSA on the instances from Set I and Set II with at least 500 nondominated points. We have chosen to restrict the set of instances in this way, because computing approximate frontiers is of interest primarily when it is too costly to compute the complete nondominated frontier, which is more likely to be the case when the number of points in the nondominated frontier is large. In each figure, the instances (represented on the horizontal axis) are ordered by the number of points in their nondominated frontier, from small to large.

Fig. 13

Fraction of nondominated points that needs to be generated to achieve a hypervolume gap of less than 20 %

We observe that LSM has to generate fewer nondominated points to reach a hypervolume gap of less than 20 % than both ERM and KSA, in general. Moreover, these figures suggest that for the instances with a larger number of points in the nondominated frontier, LSM needs to generate, on average, around 5 % of the points to reach a hypervolume gap of less than 20 %, KSA has to generate, on average, around 25 % of the points, and ERM has to generate, on average, around 50 % of the points.

In Fig. 14, we show the time (as a fraction of the total time required to obtain the complete nondominated frontier by LSM) needed to achieve a hypervolume gap of less than 20 % for LSM, ERM, and KSA on the instances from Set I and Set II with at least 500 nondominated points. The patterns are similar to those of Fig. 13, which demonstrates that algorithms that need to find more nondominated points to reach a hypervolume gap of less than 20 % require more computational time.

Fig. 14

Fraction of time needed to achieve a hypervolume gap of less than 20 %

Even though the hypervolume indicator provides meaningful insights in the quality of an approximation, many researchers have argued that the quality of an approximation must be assessed using multiple (or orthogonal) indicators. There are at least three dimensions of interests when assessing the quality of an approximation, including cardinality, coverage, and uniformity [32]. For each of these dimensions several indicators have been proposed in the literature (mostly to be able to evaluate the quality of approximations obtained by evolutionary methods). We refer the interested reader to Zitzler et al. [39] for further information about quality indicators. Therefore, to complement our initial assessment of the capability of LSM, ERM, and KSA to produce high-quality approximate frontiers quickly, we will also investigate measures related to cardinality, coverage, and uniformity.

Note that our setting is quite different from the typical setting encountered when evaluating the quality of approximate frontiers produced by evolutionary methods. We have a finite nondominated frontier and an approximate frontier that consists of a subset of the nondominated points of the frontier. As a consequence, we can introduce indicators that make use of this information.

Let $t_i$ be time required by LSM to compute the nondominated frontier of instance i. To assess the capability of LSM, ERM, and KSA to produce a high-quality approximate frontier quickly for instance i, we give each method a run time limit of $\frac{t_i}{10}$.

To present the quality indicators used for evaluation, we have to introduce some new notation. Let the nondominated frontier of an instance be $\mathcal {Y}_N$ and the approximate frontier be $\mathcal {Y}^A_N$. Furthermore, denote the Euclidean distance between two points y and $y'$ by $d(y,y')$. Define $k_1(y)$ and $k_2(y)$ to be the closest and second closest nondominated point in the approximate frontier to a nondominated point $y \in \mathcal {Y}_N$, respectively. Finally, for each $y \in \mathcal {Y}^A_N$, define n(y) to be the number of nondominated points $y' \in \mathcal {Y}_N {\setminus } \mathcal {Y}^A_N$ with $k_1(y') = y$.

Cardinality We define the cardinality of an approximate frontier simply as the fraction of the points of the nondominated points it contains, i.e., $\frac{|\mathcal {Y}^A_N|}{|\mathcal {Y}_N|}$. Figure 15 shows the cardinality for the approximate frontiers obtained by LSM, ERM, and KSA. None of the methods clearly dominates the others, although we see that LSM does better than ERM and KSA for the 1DKP instances of Set II and for the AP instances of Set II with larger nondominated frontiers, and KSA does better than ERM and LSM for the AP instances of Set II with smaller nondominated frontiers.

Fig. 15

Cardinality of approximate frontiers after 10 % of total CPU time of LSM

Coverage We define two coverage indicators: max coverage and average coverage. Let $\hat{f}^m$, $\hat{f}^a$, and $f^a$ be

$$\begin{aligned} \hat{f}^m = \max _{y\in \mathcal {Y}_N\backslash \mathcal {Y}^A_N}d(k_1(y),y), \end{aligned}$$

i.e., the maximum distance from any nondominated point not contained in the approximate frontier to the closest point in the approximate frontier,

$$\begin{aligned} \hat{f}^a=\frac{\sum _{y\in \mathcal {Y}_N\backslash \mathcal {Y}^A_N}d(k_1(y),y)}{|\mathcal {Y}_N\backslash \mathcal {Y}^A_N|}, \end{aligned}$$

i.e., the average distance from any nondominated point not contained in the approximate frontier to the closest point in the approximate frontier, and

$$\begin{aligned} f^a=\frac{\sum _{y\in \mathcal {Y}_N}d(k_2(y),y)}{|\mathcal {Y}_N|}, \end{aligned}$$

i.e., the average distance to the closest point (other than the point itself) in the nondominated frontier, respectively. Observe that $f^a$ can be viewed as a measure of dispersion of the points in the nondominated frontier. Smaller values of $\hat{f}^m$ and $\hat{f}^a$ indicate that the nondominated points in the approximate frontier are in different parts of the criterion space. As a consequence, an algorithm has a better coverage if $\hat{f}^m$ or $\hat{f}^a$ are smaller. To make these indicators scale invariant, we divide them by $f^a$. We refer to $\frac{\hat{f}^a}{f^a}$ as average coverage and to $\frac{\hat{f}^m}{f^a}$ as max coverage. Figures 16 and 17 show the average coverage and the max coverage indicators for the approximate frontiers obtained by LSM, ERM, and KSA. It is clear that LSM significantly outperforms both ERM and KSA in both coverage indicators.

Fig. 16

Average coverage of the approximate frontiers after 10 % of total CPU time of LSM

Fig. 17

Max coverage of the approximate frontiers after 10 % of total CPU time of LSM

Uniformity A uniformity indicator should capture how well the points in an approximate frontier are spread out. Points in a cluster do not increase the quality of an approximate frontier. Let $\tilde{\mu }$ and $\tilde{\sigma }$ be

$$\begin{aligned} \tilde{\mu }=\frac{\sum _{y\in \mathcal {Y}^A_N}n(y)}{|\mathcal {Y}^A_N|}, \end{aligned}$$

and

$$\begin{aligned} \tilde{\sigma }=\frac{\sum _{y\in \mathcal {Y}^A_N} (n(y)-\tilde{\mu })^2}{|\mathcal {Y}^A_N|}, \end{aligned}$$

respectively. We define the uniformity indicator to be $\frac{\tilde{\sigma }}{\tilde{\mu }}$; the smaller the value of this indicator, the better the uniformity of an approximate frontier. Figure 18 shows the uniformity of the approximate frontiers obtained by LSM, ERM, and KSA. It is clear that the approximate frontiers produced by LSM have a significantly better spread than those produced by ERM and KSA.

Fig. 18

Uniformity of the approximate frontiers after 10 % of total CPU time of LSM

8 Conclusion

We have introduced a new criterion space search method, the LSM, for general triobjective integer programs. The method cleverly combines and enhances ideas of many of the approaches that have been proposed and discussed in the literature. The method is highly effective and, equally if not more important, allows the generation of high-quality approximate frontiers in a reasonable amount of time; in practice, being able to compute high-quality approximate frontiers efficiently is critical.

We hope that the simplicity, versatility, and performance of the LSM method encourages (more) practitioners to consider using exact methods for solving triobjective integer programs.

In regard to future research, there remain many opportunities to develop and improve algorithms for multiobjective integer programming. Two directions we believe hold particular promise are as follows. (1) Even though some fundamental results regarding approximate frontiers exist, e.g., [31] show that for any multiobjective optimization problem and any $\epsilon > 0$, there is always an $\epsilon$-approximate Pareto set consisting of a number of solutions that is polynomial in the input size of the problem and $\frac{1}{\epsilon }$, there have been few, if any, attempts to exploit this algorithmically. (2) There have been exciting advances in the development of a duality theory for multiobjective linear programming, e.g., [19, 21], and again, this theory may be useful in the design of new algorithms for multiobjective integer programming.