Resonance Dynamics of the Non-ideal System Having the Pendulum as Absorber of Elastic Vibrations

Abstract

The resonance behavior of the 3-DOF system with a limited power supply (non-ideal system) having the pendulum-type absorber is analyzed by the multiple scales method. Comparison of the obtained analytical solution with corresponding numerical simulation demonstrates a good exactness of the analytical construction. It is shown that amplitudes of the elastic sub-system resonance vibrations can be essentially reduced by some choosing of the system parameters.

1 Introduction

The system with a limited power supply (or non-ideal system, NIS) is characterized by interaction of source of energy and elastic sub-system which is under action of the source. For the non-ideal systems the external applied excitation depends on displacements of the excited elastic sub-system. The most interesting effect appearing in such systems is the Sommerfeld effect [1], when in the elastic sub-system it is appeared the stable resonance regime with large amplitudes, and the big part of the vibration energy passes from the energy source to these resonance vibrations. Resonance dynamics of the non-ideal systems was first analytically described by V.O. Kononenko [2]. Then investigations on the subject were continued as by Kononenko [3], as well by other authors [4,5,6,7]. Reviews on numerous studies of the NIS dynamics can be found in papers [8, 9] and in the book [10]. We can note that different kinds of the NIS behavior were considered, including forced and parametric vibrations, self-oscillations, transient, including transfer to chaotic vibrations, interaction of the NIS with the energy supplies of the different physical characters, etc.

It is known that nonlinear vibration absorbers permit to reduce essentially amplitudes of the resonance elastic vibrations. Reduction of the vibration amplitudes and elimination or reduction of the Sommerfeld effect in NIS coupled with different type nonlinear absorbers and dampers, are studied in [11,12,13].

In the paper the resonance behavior of the 3-DOF non-ideal system having the pendulum-type absorber is considered by the multiple scales method. The basic model is presented in Sect. 2. Then the construction of the system solution in the region of the first resonance is presented in Sect. 3. Numerical simulation is shown in Sect. 4. Besides, it is shown in the Sect. 4 that amplitudes of the elastic sub-system resonance vibrations in the system can be reduced by changing some system parameters.

2 The Basic Model

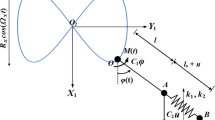
The non-ideal system under consideration contains the limited power supply (or the motor), the elastic sub-system with the Duffing type nonlinear elastic characteristic, which vibrations take place under the motor excitation. Besides, the system contains the pendulum as absorber. Models under consideration are shown in Fig. 1. The motor (source of energy) acts to the elastic sub-system having a mass $M$ by the crank shaft of the radius $r$. The pendulum having a mass $m$ is attached to the elastic sub-system. Here L is the driving moment of the source of energy.

Fig. 1

The non-ideal systems with the pendulum absorber

Kinetic and potential energies of the system without the driving moment are the following:

$$\begin{aligned} T & = \frac{1}{2}I\dot{\varphi }^{2} + \frac{1}{2}M\dot{x}^{2} + \frac{1}{2}m\left[ {\left( {\dot{x} + l\dot{\theta }\cos \theta } \right)^{2} + l^{2} \dot{\theta }^{2} \sin^{2} \theta } \right]; \\ V & = \frac{1}{2}c_{0} x^{2} + \frac{1}{2}c_{1} \left( {x - r\sin \varphi } \right)^{2} + mgl\left( {1 - \cos \theta } \right). \\ \end{aligned}$$

(1)

The small parameter ε in relations (1) characterizes a smallness of the absorber mass with respect to the mass of elastic part of the system. Using the Lagrange equations, one obtains the following equations of motion:

$$\left\{ {\begin{array}{*{20}l} {\left( {M + m} \right)\ddot{x} + \left( {c_{0} + c_{1} } \right)x = c_{1} r\sin \varphi - ml\left( {\ddot{\theta }\cos \theta - \dot{\theta }^{2} \sin \theta } \right);} \hfill \\ {I\ddot{\varphi } = a - b\dot{\varphi } + c_{1} r\left( {x - r\sin \varphi } \right)\cos \varphi ;} \hfill \\ {ml\left( {l\ddot{\theta } + g\sin \theta + \ddot{x}\cos \theta } \right) = 0.} \hfill \\ \end{array} } \right.$$

(2)

In relations (1) and Eq. (2) $I$ is a moment of inertia of rotating masses; $\left( {c_{0} + c_{1} } \right)$ is a stiffness of the elastic sub-system having the mass $M$, $L = a - b\dot{\varphi }$ is the driving moment of the source of energy, that is the motor characteristic. We can see from the Eq. (2) that the moment $c_{1} rx\cos \varphi$ is such part of the motor excitation, which depends on the elastic sub-system vibrations.

3 Construction of the Analytical Solution

To describe the system behavior in the neighborhood of the resonance some asymptotic approach, namely the multiple scales method [14] is used. To apply the method one has the following transformations. First of all, we use expansions of the functions $\cos \theta$ and $\sin \theta$ in the system (2) to the Maclaurin series, and save terms up to third degree. The small parameter ε introduced in the equations of motion characterizes a smallness of the absorber mass with respect to the mass of elastic part of the system, $m \to \varepsilon m$, and a smallness of vibration components in variability in time of angle φ velocity with respect to the main constant component. The small terms εh $\dot{x}$ and εh $\dot{\theta }$ describe a dissipation which is proportional to velocities of variables. Considering a region of the resonance between frequencies of the motor rotation and the elastic sub-system vibrations, we introduce the small detuning as εΔ = $\omega^{2} - \dot{\varphi }^{2}$, where $({c}_{0}+{c}_{1})/M={\omega }^{2}$. We also suppose that in a region of the resonance the external excitation to the elastic sub-system is small. The relatively not large nonlinear response of the elastic sub-system is presented by the term $\varepsilon \tau x^{3}$. It is included to the first equation of the system (2). Thus, the equations of motion (2) are transformed to the following equations, containing the small parameter:

$$\left\{ {\begin{array}{*{20}l} {\left( {M + \varepsilon m} \right)\ddot{x} + \omega ^{2}M x + \varepsilon h\dot{x} + \varepsilon \tau x^{3} = \varepsilon c_{1} r\sin \varphi - \varepsilon ml\left( \begin{gathered} \ddot{\theta }\left( {1 - \frac{1}{2}\theta ^{2} } \right) \hfill \\ - \left( {\theta - \frac{{\theta ^{3} }}{6}} \right)\dot{\theta }^{2} \hfill \\ \end{gathered} \right)~~~} \hfill \\ {I\ddot{\varphi } = \varepsilon \left( {a - b\dot{\varphi } + c_{1} r\left( {x - r\sin \varphi } \right)\cos \varphi } \right)} \hfill \\ {\varepsilon ml\left( {l\ddot{\theta } + g\left( {\theta - \frac{{\theta ^{3} }}{6}} \right) + \ddot{x}\left( {1 - \frac{1}{2}\theta ^{2} } \right)} \right) + \varepsilon h\dot{\theta } = 0} \hfill \\ \end{array} } \right.$$

(3)

Later the following notations will be used:

$$\frac{a}{{I\Omega^{2} }} = K,\frac{b}{{I\Omega }} = N,\frac{{c_{1} r}}{{I\Omega^{2} }} = q$$

(4)

According to the multiple scales method one uses the following presentations for the unknown variables:

$$\begin{aligned} x\left( {t,\varepsilon } \right) & = x\left( {t,\varepsilon t,\varepsilon ^{2} t,...;\varepsilon } \right);{\text{ }}\varphi \left( {t,\varepsilon } \right) = \varphi \left( {t,\varepsilon t,\varepsilon ^{2} t,...;\varepsilon } \right);{\text{ }} \\ \theta \left( {t,\varepsilon } \right) & = \theta \left( {t,\varepsilon t,\varepsilon ^{2} t,...;\varepsilon } \right) \\ \end{aligned}$$

(5)

Besides, the next transformations are also used:

$$\begin{aligned} \frac{d}{dt} & = \frac{\partial }{{\partial T_{0} }} + \varepsilon \frac{\partial }{{\partial T_{1} }} + \varepsilon^{2} \frac{\partial }{{\partial T_{2} }} + ... \\ \frac{{d^{2} }}{{dt^{2} }} & = \frac{{\partial^{2} }}{{\partial T_{0}^{2} }} + 2\varepsilon \frac{\partial }{{\partial T_{0} }}\frac{\partial }{{\partial T_{1} }} + \varepsilon^{2} \left( {\frac{{\partial^{2} }}{{\partial T_{1}^{2} }} + 2\frac{\partial }{{\partial T_{0} }}\frac{\partial }{{\partial T_{2} }}} \right) + ... \\ \end{aligned}$$

(6)

Here ${T}_{0}=\omega t; {T}_{1}=\varepsilon t,$ etc. Solutions for variables $x$, $\varphi$ and $\theta$ are presented as the following power series by the small parameter:

$$x = x_{0} + \varepsilon x_{1} + \varepsilon^{2} x_{2} + ...,\;\varphi = \varphi_{0} + \varepsilon \varphi_{1} + \varepsilon^{2} \varphi_{2} + ...,\;\theta = \theta_{0} + \varepsilon \theta_{1} + \varepsilon^{2} \theta_{2} + ...$$

(7)

Substituting the expansions (5)–(7) to the system (3) one extracts terms of the zero and first power by the small parameter. As a result, the following system of differential equations can be obtained:

$$\varepsilon^{0} :\frac{{\partial^{2} x_{0} }}{{\partial T_{0}^{2} }} + \Omega^{2} x_{0} = 0$$

(8)

$$\frac{{\partial^{2} \varphi_{0} }}{{\partial T_{0}^{2} }} = 0$$

(9)

$$\begin{array}{*{20}l} {\varepsilon^{1} :2M\frac{{\partial^{2} x_{0} }}{{\partial T_{0} \partial T_{1} }} + M\frac{{\partial^{2} x_{1} }}{{\partial T_{0}^{2} }} + m\frac{{\partial^{2} x_{0} }}{{\partial T_{0}^{2} }} + \Delta Mx_{0} + } \hfill \\ { + M\Omega^{2} x_{1} + h\frac{{\partial x_{0} }}{{\partial T_{0} }} + r\tau x_{0}^{3} = c_{1} rsin\left( {\Omega T_{0} } \right) - } \hfill \\ { - ml\frac{{\partial^{2} \theta_{0} }}{{\partial T_{0}^{2} }} + \frac{1}{2}ml\frac{{\partial^{2} \theta_{0} }}{{\partial T_{0}^{2} }} \cdot \theta_{0}^{2} + ml\theta_{0} \left( {\frac{{\partial \theta_{0} }}{{\partial T_{0} }}} \right)^{2} - ml\frac{{\theta_{0}^{3} }}{6} \cdot \left( {\frac{{\partial \theta_{0} }}{{\partial T_{0} }}} \right)^{2} } \hfill \\ \end{array}$$

(10)

$$2\frac{{\partial^{2} \varphi_{0} }}{{\partial T_{0} \partial T_{1} }} + \frac{{\partial^{2} \varphi_{1} }}{{\partial T_{0}^{2} }} = K - N \frac{{\partial \varphi_{0} }}{{\partial T_{0} }} + qx_{0} \cos \varphi_{0} - 0.5{qr}\sin 2\varphi_{0}$$

(11)

$$l \frac{{\partial^{2} \theta_{0} }}{{\partial T_{0}^{2} }} + g\theta_{0} - g\frac{{\theta_{0}^{3} }}{6} + \frac{{\partial^{2} x_{0} }}{{\partial T_{0}^{2} }} - \frac{{\theta_{0}^{2} }}{2}\frac{{\partial^{2} x_{0} }}{{\partial T_{0}^{2} }} + (h/ml)\frac{{\partial \theta_{0} }}{{\partial T_{0} }} = 0$$

(12)

One has the solution of the Eqs. (8) and (9) as

$$\left\{ {\begin{array}{*{20}l} {x_{0} = A\cos \left( {\Omega T_{0} } \right) + B\sin \left( {\Omega T_{0} } \right) } \hfill \\ {\varphi_{0} = \Omega T_{0} } \hfill \\ \end{array} } \right.$$

(13)

We assume that in the resonance under consideration between frequencies of the motor rotation and the elastic sub-system vibrations, amplitudes of the pendulum vibrations are not large. Thus, one assumes that in the system (12) all terms having a power more than one, have an order of the small parameter ε. Hence one has from the Eq. (12) that

$$\theta_{0} = C\cos \Omega T_{0} + D\sin \Omega T_{0} \,,\,\,where\,\, C = \frac{{A\Omega^{2} }}{{g - l\Omega^{2} }},D = \frac{{B\Omega^{2} }}{{g - l\Omega^{2} }}$$

(14)

The solution of the zero approximation by the small parameter is substituted to the Eq. (10). To avoid an appearance the secular terms in solution, coefficients at $\sin \left( {\Omega T_{0} } \right),\cos \left( {\Omega T_{0} } \right)$ in the right side of the equation are equated to zero. As a result one obtains so-called modulation equations in the following form:

$$2\frac{\partial A}{{\partial T_{1} }}\Omega + \mu B\Omega^{2} - \Delta B + \frac{hA\Omega }{M} - \frac{{3\tau A^{2} B}}{4M} - \frac{{3\tau B^{3} }}{4M} + \sigma + \mu lD\Omega^{2} = 0$$

(15)

$$- 2\frac{\partial B}{{\partial T_{1} }}\Omega + \mu A\Omega^{2} - \Delta A - \frac{hB\Omega }{M} - \frac{{3\tau AB^{2} }}{4M} - \frac{{3\tau A^{3} }}{4M} + \mu lC\Omega^{2} = 0$$

(16)

$$\left( {\mu = \frac{m}{M},\sigma = \frac{{c_{1} r}}{M}} \right)$$

Then, to avoid an appearance of the secular terms in solution of the Eq. (11), one has the following relation:

$$2\frac{\partial \Omega }{{\partial T_{1} }} + N\Omega^{2} =K+ \frac{qA}{2},$$

(17)

where K, N, q are determined by the relations (4). The Eqs. (14) and (15) represent a dependence of functions A and B on the excitation frequency Ω. The Eq. (16) is the so-called “system characteristic”. Together all three Eqs. (15)–(17) give values of the variables A, B and Ω corresponding to the resonance state under consideration.

Considering the stationary solution we assume that values A, B and Ω are constant. In this case the Eqs. (15)–(17) are converted to the system of nonlinear algebraic equations with respect to these values, which is solved by the numerical Newton method in the pocket Matlab. Thus, the constant values $A_{0} ,B_{0} ,\Omega_{0}$ for the stationary regime can be obtained. In particular, we have from the Eq. (17) that

$$\Omega_{0} = \pm \sqrt {\frac{{2a + c_{1} rA_{0} }}{2b}}$$

(18)

Note that in the resonance region the frequencies Ω and ${\omega }$ differ for the value of the order of the small parameter ε. Thus, if we change in the coefficients K, N the variable frequency Ω for ${\omega }$, we can find the following solution of the Eq. (17):

$$\Omega = \Omega_{0} + \rho e^{{ - 0.5NT_{1} }}$$

(19)

Here the constant ρ is determined by the initial value of Ω. The last relation presents a tending of the motor frequency to the stationary value ${\Omega }_{0}$ with an increase of time.

4 Numerical Simulation. Influence of the System Parameters to Resonance Dynamics of the System

Here we consider an influence of the system parameters to the elastic vibration amplitudes in the resonance region. Namely, a change of the parameter of the driving moment a, the pendulum mass m and the parameter of the nonlinearity in elastic force τ is considered. Simultaneously the obtained analytical solution is compared with numerical simulation which is realized for the basic system (2) by use of the Runge–Kutta method of the 4-th order. Note that an increase of the pendulum length l leads to the insignificant decrease of the elastic vibration amplitude, thus, results corresponding to change of the parameter are not presented here.

Based on the numerical simulation we can conclude that amplitudes of the resonance elastic vibrations can be essentially reduced when the mass m and the parameter τ increase. Some change of the parameter a, permits to reduce essentially the elastic vibration amplitude. Note that values of the parameter a are chosen near the value corresponding to maximal resonance amplitudes. We can note that only a small part of obtained numerical results are presented.

In Fig. 2 the analytical and numerical solutions are shown for the following parameters: a = 0.3815, l = 0.5, τ = 0.05 when the pendulum mass m is changing. In Fig. 2a the parameter m = 0.04 (here $A_{0} = 0.506$, $B_{0} = - 0.836$), and in Fig. 2b the parameter m = 0.1 (here $A_{0} = - 0.07$, $B_{0} = 0.489$). We can see here the noticeable decrease of the resonance vibration amplitude with increase of the absorber mass. In Fig. 3 the analytical and numerical solutions are presented for the following parameters: l = 1, a = 0.3728, m = 0.05 when the parameter of nonlinearity τ is changing. Figure 3a represents calculations made for τ = 0.01, and in Fig. 3b the parameter τ = 0.03. In Fig. 4 the analytical and numerical solutions are shown for the following parameters: m = 0.05, l = 1, τ = 0.05 when the parameter a is changing. In Fig. 4a the calculations are made for a = 0.3728, and in Fig. 4b the parameter a = 0.3778. We can see the essential decrease of the resonance vibration amplitude for considered change of the parameters τ and a, where such effect is observed even for insignificant change of the parameter characterizing the driving moment a. Note that in all presented variants the admissible coincidence of the analytical solution and the numerical simulations is observed. Here the numerical solution is calculated with initial values obtained from the approximate analytical solution.

Fig. 2

Change of the variables x, φ, θ in time for different values of the pendulum mass m

Fig. 3

Change of the variables x, φ, θ in time for different values of the parameter of nonlinearity τ

Fig. 4

Change of the variables x, φ, θ in time for different values of the parameter a

5 Conclusion

In the paper the system with a limited power supply (or non-ideal system) having the pendulum as absorber, is considered. The analytical solution in the region of the first resonance is obtained by the multiple scales method. Numerical simulation shows a good exactness of the analytical results. It is shown that an essential reduction of the system resonance vibration amplitudes can be obtained by choose of the system parameters, namely, of the pendulum mass m, the parameter τ characterizing the nonlinear response of the elastic sub-system, and the parameter of the driving moment a. We suppose that the presented results can help in the future as in more precise analysis of the steady states of the non-ideal system, as well in analysis of transient in such systems.