Control of the Dynamics of Mechanical Structures Supporting DC Motors with Limited Power Supply

Abstract

The present Chapter presents on its entirety the dynamics of mechanical structures such as beam and rectangular plate when they are subjected to one or more DC motors with limited power supply. Attention is paid on the various applications of such study in civil and mechanical engineering. To deal with this topic, we developed two main approaches with the purpose to give a good insight on vibration control and stability of the studied system. The first step consists on the use of some electric transducers and tuned mass damper to reduce the amplitudes of vibration of a plate. An adequate choice of the physical parameters of the control device enhances the efficiency of the control strategy. A stability analysis using the Routh-Hurwitz criteria confirms the pertinence of the control strategy. The second method is rather based on the synchronization with and without delay between the external sources (DC motors) working on the structure. Here, the physical parameters of the structure enable to present the phase and anti-phase or rapid and late synchronization phenomena between the motors. This difference of phase or the input delay between the motors and the voltage applied on the motors lead to situations where the amplitude vibrations of the mechanical structure are considerably reduced.

1 Introduction

The study of thin plate vibrations displays a rich and complex dynamics that ranges from linear to strongly nonlinear regimes when increasing the vibration amplitude with respect to the thickness. A plate is a continuous system, and thus, in the language of Mechanical Engineering, it possesses an infinite number of degrees of freedom. Truncating the degrees of freedom from an infinite number to a finite one can lead nonetheless to a faithful reproduction of the dynamics. When a rectangular plate vibrates in a weakly nonlinear regime, modal couplings produce amplitude dependent vibrations, internal resonances, instabilities, jumps and bifurcations. In the case where it vibrates in a strongly nonlinear regime, the most appropriate description of the dynamics is given in terms of the statistical properties of the system, because of the large number of interacting degrees-of-freedom.

The range of applications of plates is quite large, thus thin vibrating structures are found very often in musical instruments. For example, plates are fundamental components of the piano and the guitar, serving as soundboards; they have been extensively used as analog reverb units before the advent of digital systems. Instruments such as bells, gongs or cymbals are, roughly speaking, curved plates. In old theatres, large metallic plates were used at times to simulate the powerful sounds of thunders and storms.

The scientific interest of studying mechanical structures such as rectangular plates is really broad, and comprises domains that are apparently very different. Many applications are found in common engineering problems, such as panel flutter in aeronautics, energy harvesting of fluttering flexible plates, piezoelectric and laminated plates, and others.

Several engineering structures such as buildings, airplanes wings, helicopter blades, bridges are usually subjected to various types of vibrations. These vibrations may result from wind gusts, high speeding cars, rotating machines and some environmental disturbances. The dynamic response of mechanical and civil structures prone to high-amplitude motions is often undesirable and dangerous. These vibrations often lead to material fatigue, structural damage and failure, deterioration of system performance, and increased noise level.

Frequently we encounter in civil and mechanical engineering situations where a rectangular plate is excited by one or more DC motors leading to high amplitude of vibration. However, there are two principal types of rotating machines, each of them is composed by a fixed part called stator and another one mobile around a fixed axes named rotor. These motors can be powered either by direct current (DC motors) or by alternative current (AC motors). In DC motors, the rotational speed is proportional to the applied voltage and the normal method of speed control is by varying the input voltage. This speed is however also inversely proportional to the flux in the air gap. This means that the speed increases as the flux provided by the coils decreases.

Analysis of the response of structures subjected to non-ideal excitations is of fundamental importance for their implementation in industry and civil engineering. For such an analysis to be able to predict the realistic behavior of a structure during an actual non-ideal motion, certain information is necessary. First, the nature of the Non-ideal excitation must be specified, and secondly the mechanical behavior of the structure (thin plate) should be modeled within a reasonable accuracy. Since 1956, there exist numerous analytical and numerical techniques for the modeling and dynamics predictions of linear and nonlinear thin plate. Platforms, quay, flagstone and bridges are some examples of rectangular thin plates currently present in our environment (Ashour 2001, Shafic 1999). The mastery of this dynamics helps to prevent some catastrophe and disaster during the construction or the functioning of such structures. Among the perturbations which can cause mechanical vibration in structure, one can note wind, rotating machines, static and moving charges. In the case of rotating machines which can be divided in two principals groups, AC and DC motors one can note some situations currently encountered in civil and mechanical engineering. Usually, these motors are mounted on structure in industry to function alone or in series. In this last case, the synchronization phenomenon can probably appear between them when they are coupled. This phenomenon has been well studied in the last decades.

Sometimes DC motors are capable of limited power supply and in a situation where they are fixed on a mechanical structure, the system is named a non ideal one because the excitation source will be influenced by the response of the main system [1]. In industry we note the presence of some electrical machines mounted on elastic structure and during their works they will certainly interact. This interaction may be profitable or not to the firm, in the last case one has to take some care to avoid damage. Thus, it is well recommend to study the vibration control theory to predict some unpredictable behaviors.

The second section will be devoted to the presentation of the generalities on interaction of DC motors with limited power supply with mechanical structures. Section 3 deals with mathematical formalism for the vibration control of a rectangular plate where both techniques are presented. The fourth section presents recent results on the topic and the last section concludes the chapter.

2 Generalities on Interaction of DC Motor with Limited Power Supply and Mechanical Structures

In the manufacturing process in industry, it is common to have a DC motor resting on a mechanical structure. However, motors will inevitably induce vibrations to the structure. Depending on the running speed of the motor, we may face a situation where the resulting vibrations of the mechanical structure will influence that of the DC motor which initially acts as an exciter. In the literature, it is known that when the excitation of a vibrating system is not influenced by its response, it is said to be an ideal excitation or an ideal source of energy. On the other hand, when the excitation is influenced by the response of the system, it is said to be non-ideal one.

The behavior of ideal vibrating systems is well known in the current literature [2, 3] but there are few results on non ideal ones. Laval is probably the first one to work with non-ideal problems. He built, in 1889, a one single-stage turbine and demonstrated that in the case of rapid passage through resonance with enough power; the maximum vibration amplitude may be reduced significantly compared with that obtained in the steady state resonant vibration. Balthazar [1] and his research group present the progress of this kind of problem. It is also known for non ideal systems that sometimes the passage through resonance requires more input power than the dynamical system driven has available. The consequence is the so-called Sommerfeld Effect which means that the dynamical system cannot pass the resonance or requires an intensive interaction between the dynamical system and the motor to do it. Kononenko [4] has devoted an entire text to this subject. Nayfeh and Mook [5] gave a comprehensive and complete review of different approaches to the problem up to 1979. More recently, De Mattos [6] presented experimental results of the vibrations excited by a rotating mass at the end of a cantilever beam. They observed that the extent of the associated jump could be increased by increasing the unbalanced mass. Also, they observed that, in some cases, the amplitude and frequency of the motion became and remained modulated. Contrary to their counterpart, non-ideal vibrating systems have one more degree of freedom.

As application of such systems, one can have a mechanical structure (beam, rectangular plate, etc.…) supporting an unbalanced direct-current (DC) motor with limited power supply. A sample of schematic presentation of non idealsystem is given in Fig. 1, where the DC motor is mounted on a hinged-hinged beam.

Fig. 1

A DC motor mounted on a hinged-hinged beam

The general form of dynamical equations of a non ideal system is presented as follow:

$$\left\{ {\begin{array}{*{20}c} {Dynamic\;Equation\;of\;the\;supporting\;structure = Interaction\;terms} \\ {J\frac{{d^{2} \varphi }}{{dt^{2} }} + F\left( {\frac{d\varphi }{{dt}}} \right) = OtherInteractionterms} \\ \end{array} } \right.$$

where J, H and $(\frac{d\varphi }{dt})$ represent respectively the inertia moment of the rotating mass, the driving torque of the DC motor and the angular velocity of the rotor. The previous equations can take into account damping and the resisting torque of the motor. Others details will depend on the particular problem studied the properties of the supported structure and the characteristics of the used rotor.

Another characteristic of non ideal excitation is that it is always limited in two senses:

• The characteristic curves of the energy source (DC source)

• The dependence of the motion of the dynamical system on the motion of the energy source, that is, the coupling between the governing equations of motion of the dynamical system and the energy source

3 Mathematical Formalism of the Vibration Control of Rectangular Plate

The present section gives some information about the different control approaches which could be used to control the vibration amplitude of a rectangular plate, beginning by the used of some electric transducers in Sect. 3.1. Section 3.2 used the coupling between DC sources and the plate. Each section gives some details about the mathematical formalism used. The equations of motion of a rectangular plate submitted to a non ideal excitation can be derived following the Hamilton’s principle. This principle is based on the knowledge of the kinetic, the elastic potential and the external energy of the system under consideration.

3.1 Rectangular Plate Connected to an Electric Transducer as Controller

The active control is based on the use of secondary sources of noise or vibrations which by superposition with the primary sources leads to a minimize signal. For thus control strategy, the actuator applies a force on a structure using for their functioning an external energy source [7] (Bravo 2000, Ottersten 2003, Tchokuegno 2003, Le 2009, Deng 2012, Jamula 2012, Yan 2013). This control method uses two main strategies. The first consists to identify the perturbation creating the excitation and to cancel it by adding another source of excitation inverse to it. The second one consist of indentifying the response of the structure instead of the excitation, thus it needs the modeling of the dynamics behavior of the structure. One can use smart materials like piezoelectric, ceramics or electric transducers as device to reduce the amplitude of vibration of mechanical structures. Today, we have some new control techniques like opto-electromechanical control, saturation control [3], magnetorheological control [8].

In the case of electric transducers, we have to add another differential equation to the one obtained without the transducer. Thus the system will have a new degree of freedom, which can be the electric charge or the electric current of the studied system. The dynamical equation of the plate will have an additional term related to the coupling with the electric transducer; this term is usually connected to the control parameter of the system. Its variation leads to appreciate the control of the amplitude of vibration in considered structure. The dynamical equation of the controller have too a term coupled to the mechanical structure which is responsible to the energy balance between the external source and the controller.

Sometimes the form of the coupling terms leads to some phenomenon as saturation one [9]. When we display analytically the dynamical equation of the system, one can denote the influence of these terms in the energy transfer between the external excitation and the absorber.

The usual form of the dynamic equation of a rectangular plate supporting a DC motor with limited power supply connected to an electric transducer is given as follow:

$$\left\{ {\begin{array}{*{20}c} {Dynamic\;equation\;of\;the\;structure = Interactions\;terms + Coupling\;term} \\ {J\frac{{d^{2} \varphi }}{dt} + L\left( {\frac{d\varphi }{{dt}}} \right) = Other\;interaction\;terms} \\ {Dynamic\;equation\;of\;the\;controller = Another\;Coupling\;term} \\ \end{array} } \right.$$

where J, L and $(\frac{d\varphi }{dt})$ represent respectively the inertia moment of the rotating mass, the driving torque of the DC motor and the angular velocity of the rotor.

The obtained dynamical equations are explored by taking into account the boundary conditions of the plate. The solutions of the PDE of the system are supposed to be a superposition of a spatial and a temporal term expressed as follow:

Inserting this solution in the PDE and using the orthogonal properties of the spatial function, one obtains the normalized equation in the first mode denoted modal equation of the system. This modal equation can be analyzed by a number of different methods such as the asymptotic methods, the multiples scales method and the method of normal forms.

3.2 DC Motors Mounted on a Rectangular Plate

In this subsection, we present mechanical systems, with rotating parts, which are typical in engineering applications and subject of intensive studies. Problem of scientific interest, which among others occurs in those systems, is the phenomenon of synchronization of different rotating parts. Such situations are currently encountered in industry where on the same mechanical structure are mounted two or more DC motors with limited power supply. This is usually done in order to increase the output, to avoid human physical effort and to realize easily some tasks. The coupling between the external sources is assured by the rectangular plate where they are fixed.

Balthazar et al. [10] investigated the self-synchronization of a vibrating system composed of two rotating unbalanced motors with limited power supply, mounted on a simple portal frame. Their obtained results lead to conclude that we can denote self-synchronization and absence of synchronization between the two motors for specific characteristics. This phenomenon has been studied before in the literature in other ideal problems, distinct from the present one by [11, 12], among others.

In seventeenth century Huygens reported his discovery of tendency of two pendulums (of the clocks) coupled through elastic structure (beam) to synchronize [13]. It was the first observation, which has an application in physics, of phenomenon of coupled harmonic oscillators. Kanunnikov and Lamper prove that accurate antiphase motion of pendulums with different masses cannot occur. Pogromsky created a controller which solves the synchronization problem. Pendulums reach required level of energy and move synchronously in opposite directions. More recently, others works have been implemented in the same sense. Between them, we can note those of Czolczynski et al. [14, 15] who studied the synchronization phenomenon appearing between a numbers of rotating pendulums mounted on a horizontal beam which can roll on the parallel surface. They showed that after the initial transient, different states of pendulums synchronization occurs. Additionally, it is shown in [16], that two motors mounted on the same plate can enter into synchronization with a phase difference equal to 0, π or 2π depending on the physical characteristics of the motors and the plate, and that a reduction of vibration in a plate is obtained when the motors phase difference is equal to π.

The number of the PDE describing the dynamic of a rectangular plate supporting some DC motors with limited power supply depends on the number of non ideal sources fixed on the plate. Their usual form is obtained by using the Hamilton principle and is given as follow:

$$\left\{ {\begin{array}{*{20}c} {Dynamic\;equation\;of\;the\;structure = Interactions\;term\;(equal\;to} \\ {the\;number\;of\;DCsources)} \\ {Ji\frac{{d^{2} \varphi i}}{dt} + Li\left( {\frac{d\varphi i}{{dt}}} \right) = Other\;interaction\;terms} \\ \end{array} } \right.$$

where J_i, Li and $(\frac{d\varphi i}{dt})$ represent respectively the inertia moment of the rotating mass, the driving torque and the angular velocity of the rotor of each DC motor.

4 Recent Results

The present section is devoted to the recent published results on the vibration control of rectangular plate supporting some DC motors. The presented results are obtained by the authors on the use of electric transducers and tuned mass damper as controller device where we paid an attention on the stability analysis of the controlled system and self-synchronization with and without delay of the DC sources mounted on the rectangular plate.

4.1 Electromechanical Control of Vibration on a Plate Submitted to a Non-ideal Excitation

Nonlinear vibration of rectangular plates has been investigated by a number of authors [17]. Subjected to various types of excitation they can lead to high amplitude of vibration which is not always necessary for the human being.

The topic of vibration control is one of the most relevant in the civil and mechanical engineering domain. However, the attenuation of vibration remains a problem of primary importance in many engineering fields. In the past, the reduction of the amplitude of vibration in a mechanical system was pursued by increasing the stiffness and the mass of the structure with respect to the initial scheme in order to increase the damping effect. To deal with vibrations in mechanical structure, various configurations of devices have been proposed until now. Thus, in the literature we can note that they are range from simple archaic solutions to more modern one using new techniques of vibration control. The new one presents the advantage that they are less costly and more effective. Moreover, some control techniques used electric transducers such as electromechanical devices to come through natural vibration in mechanical structures. However in 2006, Kitio Kwuimy et al. showed the optimization of the electromechanical control of a beam submitted to transversal and axial loads.

In this subsection, we present an electromechanical device used to control the vibration of a rectangular plate submitted to a DC motor with an unbalanced mass acting on a particular surface of the plate. After the modeling of the studied system, we analyze analytically and numerically the condition for the effectiveness of the control strategy. The reader should keep in their mind that in our previous works [9, 18], the dynamics of a beam was studied. There, we have used an electrostatic device as a controller coupled with the notion of saturation to determine the effect of control on the vibration amplitude.

4.1.1 Presentation of the Device and Mathematical Modeling of the Studied Problem

The studied system consists of a mechanical structure represent here by a rectangular plate with edges simply supported, on which a DC motor with an unbalanced mass is fixed. In order to perform the modeling of the studied system, the surface on which the motor is fixed is taken into account through the step function. The acting force provided by the mechanical part of the electromechanical system acts under the plate by various stings regularly spaced and connected to the plate. Figure 2 presents an overview of the studied system.

Fig. 2

An overview of the system under control (the top of figure is composed by a rectangular plate where is resting a DC motor and the bottom is composed by a RL circuit with a magnet connected to the structure by stings)

Fig. 3

Stability card of the controlled system around the chosen fixed point

The angular displacement of the motor is denoted by φ. The DC motor is composed by a rotor with a moment of inertia J which carries an unbalanced mass m₀ situated at a distance r from the axis. In order to pursue the theoretical study, the driving torque characteristic of the motor is considered to be a type frame 284. This indication is a reference which is well known either by the manufacturer or the experimenters.

The dynamical equations of motions are derived using the Hamilton Principle where is taken into account the total potential energy of the controlled system, the kinetic energy of the system and the sum of the non conservative forces.

According to the Hamilton Principle we obtained the coupled partial differential equations of the motion for the plate under control (of length a, wide b and thickness h) with the DC motor are given as follows:

$$\begin{aligned}&\left( {\rho h + \frac{{m_0 }}{{ab}}} \right)\frac{{\partial ^2 W}}{{\partial t^2 }} + \lambda \frac{{\partial W}}{{\partial t}} + D\left[ {\frac{{\partial ^4 W}}{{\partial x^4 }} + 2\frac{{\partial ^2 W}}{{\partial x^2 }}\frac{{\partial ^2 W}}{{\partial y^2 }} + \frac{{\partial ^4 W}}{{\partial y^4 }}} \right] \\ & \quad = \frac{{m_0 r}}{{a_1 b_1 }}\left( {\dot{\varphi }^2 \sin \varphi - \ddot{\varphi }\cos \varphi } \right)\left[ {H(x - x_0 ) - H(x - x_0^{\prime} )} \right] \\ & \quad \quad \times \left[ {H(y - y_0 ) - H(y - y_0^{\prime} )} \right] - \frac{{l_b B}}{{NM}}\sum_{i = 1}^N {\sum_{j = 1}^M {I\delta (x - x_i )\delta (y - y_i )} } \\ & \quad \quad \left[ {\left( {J + m_0 r^2 } \right)\ddot{\varphi } - L\left( {\dot{\varphi }} \right) + m_0 rg\cos \varphi } \right] + \frac{{m_0 r}}{2}\frac{{\partial ^2 W}}{{\partial t^2 }}\cos \varphi = 0 \\ & \quad \quad L\left( {\left( {1 + \zeta } \right) - \zeta \tanh ^2 \left( {\frac{I}{{I_0 }}} \right)} \right)\frac{{\partial I}}{{\partial t}} + RI = l_b B\sum_{i = 1}^N {\sum_{j = 1}^M {\frac{{\partial W}}{{\partial t}}\delta (x - x_i )\delta (y - y_i )} } \\ \end{aligned}$$

(1)

where W, ρ, D and h are respectively transversal displacement, density, flexural rigidity and thickness of the plate, L(φ^.) is the difference between the generated and frictional torque of the motor, λ is the damping coefficient, r and m₀ are the excentricity and the mass of the unbalanced shaft of the electric motor, g the intensity of the gravity field. B, L, l_b, ς and R are respectively the magnetic field, inductance, length, saturation parameter of the coil and resistance of the electric circuit. a_1 =x’_0 −x₀ and b_1 =y’_0 −y₀ the position of the electric motor on the plate, where x₀, x’₀, y₀, y’₀ are coordinates of the boundary of the surface occupy by the DC motor respectively in x and y directions, I the electric current. H, δ are respectively the Heaviside and Dirac delta functions. x_i and y_j are the coordinates of the stings acting under the plate. The characteristic curve of the energy source (DC motor) is considered as a straight line (for more details see Warminski [19]): In this case the constant u₁ and u₂ refer respectively to the voltage and a physical characteristic of the corresponding motor.

$$L\left( {\dot{\varphi }} \right) = u_{1} - u_{2} \dot{\varphi }$$

(2)

In this case the constants u₁ and u₂ refer respectively to the voltage and a physical characteristic of the corresponding motor.

Taking in account the boundary conditions of the plate (simply supported one) and according to the orthogonality of the eigenfunctions (Peeters, 2010), the following modal equations are derived as:

$$\begin{gathered} \left( {\rho h + \frac{{m_{0} }}{ab}} \right)\ddot{Y}_{n,m} (t) + \lambda \dot{Y}_{n,m} (t) + D\left[ {\left( {\frac{n\pi }{a}} \right)^{2} + \left( {\frac{m\pi }{b}} \right)^{2} } \right]^{2} Y_{n,m} (t)\hfill \\ = \frac{{4m_{0} r}}{{\pi^{2} a_{1} b_{1} }}\left( {\dot{\varphi }^{2} \sin \varphi - \ddot{\varphi }\partial \cos \varphi } \right)\left[ {\cos \left( {\frac{n\pi }{a}x_{0} } \right) - \cos \left( {\frac{n\pi }{a}x^{\prime}_{0} } \right)} \right] \hfill \\ \times \left[ {\cos \left( {\frac{m\pi }{b}y_{0} } \right) - \cos \left( {\frac{m\pi }{b}y^{\prime}_{0} } \right)} \right] - \frac{{4l_{b} B}}{abNM}I\sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{M} {\sin \left( {\frac{n\pi }{a}x_{i} } \right)\sin \left( {\frac{m\pi }{b}y_{j} } \right)} } \hfill \\ \left[ {\left( {J + m_{0} r^{2} } \right)\ddot{\varphi } - L\left( {\dot{\varphi }} \right) + m_{0} rg\cos \varphi } \right] + \frac{{\pi^{2} m_{0} r}}{{8\left( {1 - \cos \left( {n\pi } \right)} \right)\left( {1 - \cos \left( {m\pi } \right)} \right)}}\ddot{Y}_{n,m} (t)\cos \varphi = 0 \hfill \\ L\left( {\left( {1 + \zeta } \right) - \zeta \tanh^{2} \left( {\frac{I}{{I_{0} }}} \right)} \right)\frac{dI}{{dt}} + RI = l_{b} B\dot{Y}_{nm} (t)\sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{M} {\sin \left( {\frac{n\pi }{a}x_{i} } \right)\sin \left( {\frac{m\pi }{b}y_{j} } \right)} } \hfill \\ \end{gathered}$$

(3)

Where

$$\dot{Y}_{n,m} (t) = \frac{{dY_{n,m} }}{dt},\;\dot{\varphi } = \frac{d\varphi }{{dt}},\;\ddot{\varphi } = \frac{{d^{2} \varphi }}{{dt^{2} }},\;\ddot{Y}_{n,m} = \frac{{d^{2} Y_{n,m} }}{{dt^{2} }},$$

For the n and m mode in each direction we derive the normalized equations:

$$\begin{gathered} \ddot{U}_{n,m} (t) + \gamma \dot{U}_{n,m} (t) + \omega_{n,m}^{2} U_{n,m} (t) = \frac{{4m_{0} r}}{{a\pi^{2} a_{1} b_{1} \left( {\rho h + \left( {m_{0} /ab} \right)} \right)}}\left( {\dot{\varphi }^{2} \sin \varphi - \ddot{\varphi }\cos \varphi } \right)\hfill \\ \times \left[ {\cos \left( {\frac{n\pi }{a}x_{0} } \right) - \cos \left( {\frac{n\pi }{a}x^{\prime}_{0} } \right)} \right] \hfill \\ \times \left[ {\cos \left( {\frac{m\pi }{b}y_{0} } \right) - \cos \left( {\frac{m\pi }{b}y^{\prime}_{0} } \right)} \right] - \frac{{4l_{b} BI_{0} \omega_{0}^{2} }}{{a^{2} bNM\left( {\rho h + \left( {m_{0} /ab} \right)} \right)}}V_{n,m} \hfill \\ \times\sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{M} {\sin \left( {\frac{n\pi }{a}x_{i} } \right)\sin \left( {\frac{m\pi }{b}y_{j} } \right)} } \hfill \\ \ddot{\varphi } = L^{\prime}\left( {\dot{\varphi }} \right) + \chi \cos \varphi + \sigma_{n,m} \ddot{U}_{n,m} (t)\cos \varphi \hfill \\ \left( {1 - \varepsilon \tanh^{2} \left( {V_{n,m} } \right)} \right)\frac{{dV_{n,m} }}{dt} + \omega_{\varepsilon } V_{n,m} (t) = \frac{{al_{b} B}}{{I_{0} L}}\dot{U}_{nm} (t)\sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{M} {\sin \left( {\frac{n\pi }{a}x_{i} } \right)\sin \left( {\frac{m\pi }{b}y_{j} } \right)} } \hfill \\ \end{gathered}$$

(4)

with the dimensionless variables given by: V_nm =(I/I0); U_nm =(Y_nm/a); τ = (t/ω0);

Here I₀, ν, N and M are respectively the characteristic current of the electrical circuit, Poisson ratio, number of stings acting in x and y direction respectively.

4.1.2 Performance of the Control Strategy

• (a) Stability analysis of the controlled system

Instead of reinforcing the structure, active control strategies could destabilize the structure due to the forces acting on the system. It is therefore primordial to focus on the stability of the system in autonomous case. Thus, the Jacobian matrix related to the dynamics equations is extracted and explored. Four fixed points are derived from the dynamics equations with a condition but only two are physically possible [20]. The characteristic polynomial is derived from this Jacobian and according to the Routh–Hurwitz criterion [21], the system is stable if some conditions are satisfied. In order to get the real domain where the controlled system will be stable in the space parameter, we display the following diagram, where the region with dark points is the stable region of the controlled system. The stability card obtained is validated by carrying out the eigenvalues of the Jacobian matrix of the controlled system in the both regions [20].

• (b) Effect of the control on the amplitude of vibration of the plate

The equations of motion of the system under control are solved analytically by using the harmonic balance method. After some algebraic analytical manipulation, we obtained strongly non-linear and coupled amplitude equations. A good accordance between our analytical results with the numerical one is observed since it is quite impossible to plot separately the amplitude of the structure, angular velocity and the current as function of the motor velocity (see [20] for more details).

To show the effect of the control strategy used, we display in Fig. 4 the evolution of amplitude when the control is on and off. We observed from this figure that the amplitude response of the plate is well reduced for these set of parameters.

Fig. 4

Amplitude curve of the plate when the control is off (points with dashed line) and on (points with line) for N = 5 and M = 3

Fig. 5

Maximum amplitude of the plate as function of the number of stings acting in each direction

By increasing the number of stings acting under the plate in each direction, we observe in Fig. 5 that the amplitude response of the plate is more and more reduced.

The effect of the saturation parameters of the inductance has been explored and we can observe that the reduction of amplitude may lead to the production of an important quantity of energy in the electromechanical device. It is also proved [20] that the amplitude of vibration of the plate decreases as the number of the stings increases and as the intensity of the magnetic field increases.

4.2 Vibration Control a Rectangular Plate Submitted to a Non-ideal Excitation with a TLCD

4.2.1 Description of the Control Device and Mathematical Modeling of the Studied Problem

The schematic of the studied system consists on simply supported edges rectangular plate under the excitation of an unbalanced DC motor with limited power supply coupled with a TLCD. Both the motor and the damper are fixed to the plate. The plate and the DC motor system form a non-ideal system, meaning that the excitation created by the DC motor is influenced by the response of the supporting structure and that the applied voltage has a limited power supply.

The present device is different from the others commonly seen in the literature [3] in the sense that the orifice is placed vertically. Once the system is excited by the motor, there arise transversal vibrations of the plate. As a result, the liquid inside the columns of TLCD starts vibrating by passing through the vertical orifice and try to stabilize the plate. This allows us to distinguish the vertical column L_v to the horizontal column L_h as shown in Fig. 6.

Fig. 6

Rectangular plate supporting an unbalanced DC motor and a TLCD: a perspective view and b front view

Fig. 7

Numerical results of the responses of the rectangular plate and phase diagrams with and without TLCD device obtained with the parameters’ values u₁ = 2.1; α₀ = 0.42; α₁ = 0.201; g₀ = 7.9; g₁ = 1; β₀ = 0.1; λ₁ = 0.001; ξ = 0.6; ω₁ = 2; β₁ = 1.25; and v₁ = 0.02

Fig. 8

Rectangular plate supporting two DC motors

The dynamic equations of the system are obtained by combining the kinetic, potential and external energies of the plate, the motor, and the TLCD. Then after determining the respective derivatives and substituting in the Lagrangian equations, we get the following system of equations:

$$\left\{ {\begin{array}{*{20}l} {\left[ {\rho_{p} h + \frac{{m_{0} }}{{a_{0} b_{0} }}\left( {H\left( {x - x_{1} } \right) - H\left( {x - x_{2} } \right)} \right)\left( {H\left( {y - y_{1} } \right) - H\left( {y - y_{2} } \right)} \right) + \frac{{\rho_{c} L}}{{a_{1} b_{1} }}\left( {H\left( {x - x^{\prime}_{1} } \right) - H\left( {x - x^{\prime}_{2} } \right)} \right)\left( {H\left( {y - y^{\prime}_{1} } \right) - H\left( {y - y^{\prime}_{2} } \right)} \right)} \right]\ddot{W}_{s} } \hfill \\ {\frac{\lambda }{ab}\dot{W}_{s} + D\left[ {\frac{{\partial^{4} W_{s} }}{{\partial x^{4} }} + 2\frac{{\partial^{4} W_{s} }}{{\partial x^{2} \partial y^{2} }} + \frac{{\partial^{4} W_{s} }}{{\partial y^{4} }}} \right] = \frac{{m_{0} r_{0} }}{{a_{0} b_{0} }}\left( {\ddot{\varphi }\sin \varphi + \dot{\varphi }^{2} \cos \varphi } \right)\left( {H\left( {x - x_{1} } \right) - H\left( {x - x_{2} } \right)} \right)\left( {H\left( {y - y_{1} } \right) - H\left( {y - y_{2} } \right)} \right)} \hfill \\ { - \frac{{\rho_{c} A}}{{a_{1} b_{1} }}\left( {2\dot{W}_{f}^{2} + 2W_{f} \ddot{W}_{f} } \right)\left( {H\left( {x - x^{\prime}_{1} } \right) - H\left( {x - x^{\prime}_{2} } \right)} \right)\left( {H\left( {y - y^{\prime}_{1} } \right) - H\left( {y - y^{\prime}_{2} } \right)} \right)} \hfill \\ {\left( {J + m_{0} r^{2} } \right)\ddot{\varphi } - \frac{1}{2}m_{0} r\ddot{W}_{s} \sin \varphi - \frac{1}{2}m_{0} gr\cos \varphi = \hat{a} - b\dot{\varphi }} \hfill \\ {2L_{v} \ddot{W}_{f} + \frac{1}{2L}\xi \left| {\dot{W}_{f} } \right|\dot{W}_{f} + gW_{f} = - 2W_{f} \ddot{W}_{s} } \hfill \\ \end{array} } \right.$$

(5)

with L_v and L_h the vertical and horizontal length of the liquid inside the tube, ρ_c the density of the fluid inside the columns of the TLCD, a₁ = x₂ − x₁ and b₁ = y₂ − y₁ are the dimensions occupied by the TLCD along the x- and y-axes of the plate, respectively, with x₁, x₂, y₁, and y₂ the coordinates of the boundaries of the areas occupied by the TLCD, respectively, in the x and y directions. A_v and A_h are the cross-sectional areas, respectively, of the vertical and the horizontal columns of the tube, and H represents the Heaviside function. The movement of the system is characterized by two generalized coordinates W_f and W_s, respectively, the response of the liquid damper (TLCD) and the response of the plate in the transversal motion. The plate has the following dimensions: the length a, the width b, and the thickness h. Concerning the motor, a mass m₀ is fixed on the shaft of the rotor with an eccentricity r.

4.2.2 Optimization of the Control Strategy

Taking into account the boundary conditions of the plate and the Galerking approach we displayed the orthogonality of the obtained spaced function and we derived the following algebraic modal dimensionless equations:

$$\left\{ {\begin{array}{*{20}l} {\ddot{T}_{nm} + \lambda \dot{T}_{nm} + \omega_{nm}^{2} T_{nm} = \alpha_{0} \left( {\ddot{\varphi }\sin \varphi + \dot{\varphi }^{2} \cos \varphi } \right) - \alpha_{1} \left( {2\dot{Z}_{f}^{2} + 2Z_{f} \ddot{Z}_{f} } \right)} \hfill \\ {\ddot{\varphi } - \beta_{0} \ddot{T}_{nm} \sin \varphi - g_{0} \cos \varphi = u_{1} - v_{1} \dot{\varphi }} \hfill \\ {\ddot{Z}_{f} + \frac{1}{4L}\xi \left| {\dot{Z}_{f} } \right|\dot{Z}_{f} + g_{1} Z_{f} = - \beta_{1} Z_{f} \ddot{T}_{nm} } \hfill \\ \end{array} } \right.$$

(6)

This system of ODE’s has been displayed analytically and numerically to perform the control strategy used (Feulefack 2021). Thus, it has been proved that some physical parameters of the studied system have a great effect on the vibration control of the rectangular plate.

Modeling of the studied system here takes more details into account such as the spaces occupied by the DC motor and TLCD under and over the rectangular plate respectively. Physical and mechanical parameters used for numerical simulations are chosen according to a common situation in civil or mechanical engineering. Accordance observed between numerical and analytical results lead to conclude that one can predict the influence of some physical or mechanical parameters of the system on the plate amplitude of vibration. Consequently, the results obtained will, therefore, encourage engineers to use a TLCD concept as a control system for tall buildings and structures due to its multiple advantages.

4.3 Self-synchronization of DC Motors on a Rectangular Plate and Reduction of Vibration

In industry, several rotating machines inevitably exhibit nonlinear behaviors when they are mounted on flexible structures. In general, the excitation of this type of vibrating system is considered to be always a limited power supply since the response of the structure influences the rotating moving of the motors [1, 9]. The Mathematical formalism leading to the modeling of a non-ideal system includes an additional equation compared to that of the corresponding ideal system, to describe the interaction between the energy source and the rest of the system.

In order to optimize the output in industry or to carry out many tasks at the same time, synchronization or desynchronization of machines can be necessary to optimize the production. Thus, it may be possible for two or more machines having each a motor to self-synchronize. Balthazar et al. [1, 22] investigated the self-synchronization of a vibrating system composed of two rotating unbalanced motors with limited power supply mounted on a simple portal frame. They reached to the conclusion that we can denote self-synchronization and absence of synchronization between the two motors for specific characteristics.

The results presented here are divided in two parts where the first one is devoted to the synchronization of two DC motors supported by the same plate and on the analysis of plate vibration control when the motors enter into synchronization. The second one focuses on the synchronization of three DC motors supported by the same plate when they are rotating in the same or in the opposite direction. The plate vibration control analysis is studied when the motors enter into synchronization or not. Using numerical simulation, one can show the influence of the main frequency structure on synchronization, and the impact of rotating direction of the DC motors on the plate displacement.

4.3.1 Self-synchronization of Two DC Motors Mounted on a Rectangular Plate

• (a) Description of the model

The studied system consists of a rectangular plate with simply supported edges, on which two DC motors with an unbalanced mass are fixed. The surface on which the motors are fixed is taken into account by considering the area a₁b₁ and a₂b₂.

The angular displacements of the motors are denoted φ₁ and φ₂. The rotors have respectively the inertia moment J₁, J₂ and carry the same unbalanced mass m₀ at a distance r from their axis. The physical characteristics of the motors such as the characteristic driving torque of the motor for each is assumed to be well known, either from the manufacturer or from experiments [10].

According to the Hamilton principle, the PDE describing the dynamics of the system is given as follow:

$$\begin{array}{*{20}c} {\left( {\rho h + \frac{m_1 + m_2 }{{ab}}} \right)\frac{\partial^2 w}{{\partial t^2 }} + \lambda \frac{\partial w}{{\partial t}} + D\left[ {\frac{\partial^4 w}{{\partial x^4 }} + 2\frac{\partial^4 w}{{\partial x^2 \partial y^2 }} + \frac{\partial^4 w}{{\partial y^4 }}} \right] = } \\ {{\sum\limits_i=1^2} {\frac{ - m_i r_i }{{a_i b_i }}\left( {\dot{\varphi }_i^2 \sin \varphi_i - \ddot{\varphi }_i \cos \varphi_i } \right)\left[ {H\left( {x - x_i } \right) - H\left( {x - x_i^{\prime} } \right)} \right]\left[ {H\left( {y - y_i } \right) - H\left( {y - y_i^{\prime} } \right)} \right]} } \\ {\ddot{\varphi }_i = \frac{ - m_i r_i }{{2\left( {J + m_i r_i^2 } \right)}}\frac{\partial^2 w}{{\partial t^2 }}\cos \varphi_i - \frac{m_i r_i g}{{\left( {J + m_i r_i^2 } \right)}}\cos \varphi_i + L_i \left( {\dot{\varphi }_i } \right)} \\ \end{array}$$

(7)

Taking in account the boundary conditions of the plate (simply supported one), and using the orthogonality of the eigenfunctions obtained, the following normalized modal equations are derived as:

$$\begin{aligned} \ddot{y} + \delta \,\dot{y} + \omega^2 y & = \alpha_1 \left( {\dot{\varphi }_1^2 \sin \varphi_1 - \ddot{\varphi }_1 \cos \varphi_1 } \right) + \alpha_1^{\prime} \left( {\dot{\varphi }_2^2 \sin \varphi_2 - \ddot{\varphi }_2 \cos \varphi_2 } \right) \\ \ddot{\varphi }_1 & = \beta_1 \ddot{y}\cos \varphi_1 + \varepsilon_1 \cos \varphi_1 + \tilde{L}_1 \left( {\dot{\varphi }_1 } \right) \\ \ddot{\varphi }_2 & = \beta_2 \ddot{y}\cos \varphi_2 + \varepsilon_2 \cos \varphi_2 + \tilde{L}_2 \left( {\dot{\varphi }_2 } \right) \\ \end{aligned}$$

wherey represent the normalized plate amplitude.

Considering the two non ideal sources acting on the structure and taking into account their physical characteristics, we can distinguish four situations for which the dynamics can be explored:

. 1st case: a_01 =a₀₂, b_01 =b₀₂, meaning that the DC motors are identical and have the same applied voltages.

. 2nd case: a_01 ≠a₀₂, b_01 ≠b₀₂, meaning that the DC motors are different and have different applied voltages.

. 3rd case: a_01 =a₀₂, b_01 ≠b₀₂, meaning that the DC motors have the same applied voltages and are different.

. 4th case: a_01 ≠a₀₂, b_01 =b₀₂, meaning that the DC motors are identical and have different applied voltages.

We assume first that the both non ideal sources are identical with the same source of voltage apply, that the both non ideal sources have a source voltage, Fig. 9 shows the (a) variation of the velocity, (b) velocity difference, (c) phase difference between the two motors (d) and plate amplitude as a function of the time.

Fig. 9

Self-synchronization of the non ideal sources with b_01 =b_02 =1.624 and a_01 =3.209, a₀₂ = 3.207

Observation of these curves let appears that curves that the two DC motors enter into synchronization in the first case mentioned above with a phase difference of Δφ=2π. This synchronization appears with time because of the energy transfer between the two rotors (Kapitaniak 2012). This synchronization phenomenon appears with time because of the energy transfer between the two rotors (Kapitaniak 2012). It is also found that the amplitude of vibration of the plate increases. Still in the first case, one notice that for some values of the frequencies, the phases difference can be equal to π, 2π or equal to 0(see Fig. 10).

Fig. 10

Phase difference between the DC sources as function of frequency structure for identical sources

Fig. 11

Amplitude of the plate for Δφ= π (dash lines) ω = 0.78, Δφ = 2π (solid lines) ω = 2.21

However, there is a domain where the phase difference is different to the previous values (see Fig. 10). This domain is situated between the domains where the phase differences are π and 2π or 0. In this domain we note high amplitude of vibration in the plate [16]. On the base of these results, we can note that self-synchronization of non ideal sources may lead to reduction of amplitude vibration of the plate when they have a phase difference Δφ=π.

Due to the fact that, the frequency of the structure ω is a parameter which contributes to get synchronization with phase difference of π or 2π, the density of the structure and its thickness are parameters that can be chosen to reduce the amplitude of the plate. For instance, with two identical DC motors, a concrete plate having the following characteristics:

. Dimensions: 800 mm × 600 mm × 4 mm;

. Density: 2500 kg/m³;

. Young modulus: 3.0× 10¹⁰ N.m⁻²;

. Poisson ratio: 0.20.

leads to a structure frequency of ω = 2.21 when the thickness is h = 4 mm, meaning that we can get self-synchronization with Δφ = 2π.and when the thickness is h = 1.4 mm we have ω = 0.77 leading to self-synchronization with Δφ = π. With a thickness of h = 2.4 mm, the phase difference is between] π, 2π [.

• (b) Influences of voltage sources on amplitude vibration of the plate for different motor

For identical motors (b_01 =b₀₂), we display in Fig. 11 the amplitude of vibration of the plate when the voltage applied to one DC source varies and for the other one we fix as a₀₂ = 3.201. Observation of this curve shows that the transition to the resonance leads to less amplitude of vibration when the two DC sources are synchronized with a phase difference of 2π or 0 compared to the synchronization with phase difference of π. In the region where we have ω = 0.78 and ω = 1.3 (synchronization with Δφ = π and self-synchronization with Δφ ϵ] π, 2π [) Figs. 12 and 13 show a global view of the plate amplitude in a 3D plot for identical DC motors (b_01 =b₀₂), while each applied voltage is varied. The associated color bars showing different regions, indicating values of the amplitude vibration of the plate as it increases from minimum (blue) to maximum (brown) are clearly identified. The blue color denotes regions in space parameters (a₀₁, a₀₂) where the amplitude vibration of the plate is less than amplitude in the region where we have brown color. Through the diagonal (a_01 =a₀₂), we note less amplitude of vibration in the plate whether in resonant regions or not.

Fig. 12

Amplitude of the plate as function of a₀₁ and a₀₂ for ω = 0.78 and identical motor. a Space representation in 3D; b projection in the plan

Figure 13 Amplitude of the plate as function of a01 and a02 for ω = 1.3 and identical motor. a: Space representation in 3D; b projection in the plan

Fig. 13

Amplitude of the plate as function of a₀₁ and a₀₂ for ω = 1.3 and identical motor. a: Space representation in 3D; b projection in the plan

• (iii) Influences of voltage sources on amplitude vibration of the plate for different motor

When the two non ideal sources are different (b_01 ≠b₀₂), we represent the amplitude vibration of the plate when varying the voltage applied to one DC motor and setting the other at a₀₂ = 3.201. The curves in Fig. 14 are obtained with two values of structure frequency (ω = 0.78, ω = 2.5). We note that, the amplitude of vibration in the structure is reduced for ω = 2.5 compare with the value ω = 0.78 at the resonance.

Fig. 14

Plate amplitude as function of voltage apply to one DC motor a ω = 0.78 dashed curve with stars and ω = 2.5 solid lines with points

Comparison between the both figures let appears that the amplitude of vibration of the plate is more reduced when the frequency structure is increasing. Thus for different DC motors, plate thickness and his density are parameters to be chosen carefully so as to avoid high amplitude of vibration in the structure. It is also important to know the physical characteristics of one motor which will self-synchronize (in phase or in antiphase) with a different one whose characteristics are well known [16].

4.3.2 Self-synchronization of Three DC Motors Mounted on a Rectangular Plate

• (a) Description of the studied system

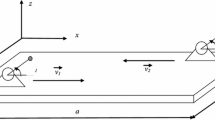
Here, the studied system consists of a rectangular plate with simply supported edges, on which three DC motors with an unbalanced mass are fixed and are capable to rotate in the same or in the opposite direction. The surface on which the motors are fixed is taken into account by considering the area a₁b₁, a₂b₂ and a₃b₃. A schematic of the set-up is shown in Fig. 15. The rotors have each the moment of inertia J_i carrying an unbalanced mass m_i at a distance r from their axis. The angular displacements of the motors are denoted φ_i. The characteristic driving torque of the motor for each given power level is assumed to be well known, either from the manufacturer or from experiments [19].

Fig. 15

Schematic of a rectangular plate supporting three DC motors rotating in opposite direction

On the base of the Hamilton principle, the obtained PDE describe the dynamics of the system is similar to the one obtained in the case of two DC motors but the number of PDE correspond to the number of DC motors mounted on the plate. The main structure equation has additional external term equal to the number of the DC sources mounted on the structure.

The rotating opposite direction of the DC sources is taken in account in the characteristics equations by taken negative the voltage apply to the DC sources. This characteristics curve of the energy source is assumed to be a straight line as in Warminski [19]. The boundary condition of the studied plate is a simply supported one.

• (b) Self-synchronization and amplitude vibration of the plate when the DC motors rotate in the same direction

In this subsection, we assume that the non-ideal sources have a same source voltage and the same physical characteristics. It is quite important to note that the values of the coupling terms are different because of different position occupied by the motors on the structure. We denote self-synchronization between the DC sources [23] by observing the behavior of the phase difference between the DC motors as the structure frequency is varied. We note that for small frequency of vibration of the structure the phase difference between motors 2 (DC2) and 3 (DC3) is equal to 0while the phase difference between motor 1 (DC1) and motor 2 (DC2) is π. When the plate frequency is high there is a perfect synchronization between motor 2 and motor 3 and anti phase synchronization between motor 1 and motor 2 or motor 3.

Through numerical simulation, we observe that by comparing the plate amplitude for small and high value of the frequency, anti-phase synchronization is quite recommended to get small amplitude of vibration of the plate.

Substituting DC motor 2 by another one, we note that for small frequency of the plate, the phase differences ϕ_2 −ϕ₃ and ϕ_1 −ϕ₂ are equal to 4π/5 and represent the half of ϕ_1 −ϕ₃, while for high frequency, all the DC motors synchronize in phase. Looking and comparing the plate amplitude, one can note that these amplitudes are small when one motor synchronizes in phase with the others even if one of them is out of phase. It is also possible to substitute a DC motor with another one capable of creating and in-phase synchronization.

As we note that the natural frequency of the structure is a relevant parameter which contributes to get synchronization with phase difference of π, 4π/5, 8π/5 or 2π we can conclude that the density of the structure and its thickness are parameters that can be well chosen in order to more reduce the amplitude vibration of the plate.

• (iii) Self-synchronization and amplitude vibration of the plate when the DC motors rotate in different directions

This subsection is related to the situation presented in Fig. 15, however according to the rotating direction of DC motor 2, the control parameter a₂ will be count negatively. Thus, when we considered identical motors (b_01 =b_02 =b₀₃), we display in Fig. 16 the phase differences between the DC motors while the plate frequency is varied.

Fig. 16

Phase difference between DC motors as function of structure frequency, DC1-DC3 (black points), DC2-DC3 (red stars), DC1-DC2 (green points)

Fig. 17

Representation of velocity difference (a) and phase difference (b) between the two DC motors as function of dimensionless time computed with α₁ = α₂ = 0.201 when the main frequency of the structure is ω₁₁ = 0.873

The corresponding plate amplitude show low amplitude of vibration for less value of the frequency and high amplitude in the other case. This means that when two of the three DC sources are synchronized in phase the amplitude of vibration is inevitably high even if the structure frequency is high.

By displaying the corresponding plate amplitude, the obtained figures [23], it is shown that for identical motors rotating in the same direction compare to the case of different motors rotating in the opposite direction both obtained for a small value of the structure frequency.

However, it is noted that for a high value of the structure frequency the amplitude of vibration of the plate is identical when the motors are identical or not and rotating in the same direction or in the opposite directions.

In the case where the three non-ideal sources are different (b_01 ≠b_02 ≠b₀₃), we denote small amplitude of vibration when one of the motors rotate in the opposite direction.

4.3.3 Effect of Time Delay of DC Motors on Their Self-synchronization When Mounted on a Rectangular Plate

It has been already proved before that two or three DC motors supported by a rectangular plate can easily enter in a self-synchronized dynamics with different phase differences. However, up to now we do not yet pay enough attention about the effect of the switching delay which could be imposed to one or two DC motors when others are already switch on [24].

The mathematical formalism of such system follows the same rules as presented before thus, we obtained the following dynamical equations:

$$\begin{array}{*{20}l} {\ddot{Y}_{k,l} \left( \tau \right) + 2\delta \dot{Y}_{k,l} \left( \tau \right) + \omega_{k,l}^{2} Y_{k,l} \left( \tau \right) = \alpha_{i} \left( {\tau - \tau_{i} } \right)\left( {\dot{\varphi }_{i}^{2} \sin \varphi_{i} - \ddot{\varphi }_{i} \cos \varphi_{i} } \right) + \beta_{i} \left( {\tau - \tau_{i} } \right)} \hfill \\ {\ddot{\varphi }_{i} = \sigma_{i,kl} \ddot{Y}_{k,l} \left( \tau \right)\cos \varphi_{i} + \varepsilon_{i} \cos \varphi_{i} + \tilde{L}_{i} \left( {\dot{\varphi }_{i} } \right)} \hfill \\ \end{array}$$

where i = 1;2 or 3, τ_i the functioning delay imposed to the DC motors, k and l refer nodal lines along the x- and the y- directions, respectively.

• (a) Case of two DC motors

Here we display a situation where two DC motors are mounted on a rectangular plate and one is switch on with a delay τ_i when the second one is already working on the plate. The study is restricted here to the first mode of vibration in each direction of the plate because it has been proven that it is the place of high amplitude of vibration in the system. Based on numerical simulations done, It is observed that when the second DC motor starts to function with a delay τ₂, both DC motors quickly synchronize, the faster for an increased delay. Hence, this leads us to conclude firstly that late switching on of the second motor reduces the time to reach to a synchronous state between DC motors.

However from Fig. 18, we observe that whatever the value of the starting delay imposed to the second DC motor, it doesn’t have any effect on the plate amplitude of vibration in the case of the high natural frequency of the plate. Nevertheless, we denote the presence of high amplitude of plate vibration when the phase difference φ₂-φ₁ = 2π compared to the situation of an anti-phase (φ₂-φ₁ = π obtained with low value of the natural frequency) synchronization between the sources which is in accordance with previous results [16].

Fig. 18

Representation of plate amplitude vibration for two values of the main frequency of the plate ω₁₁ = 2.73 (a) and ω₁₁ = 0.873 (b) in view of their comparison

• (b) Case of three DC motors

The situation presented here consists of three motors resting and acting on a rectangular plate. However, the starting delay imposed to the DC motors can be introduced in different ways. To show the impact of the starting delay of the DC motors on the time required for synchronization, we focus our attention on the case where the DC motors are synchronized (identical motor characteristics and same voltage supply). Note that numerical solutions have been provided for the fundamental mode in each direction of the plate and motors rotate in the same direction.

However, when the natural frequency of the plate is ω₁₁ = 0.873(Fig. 19) the starting time of the third motor affects the time required to achieve synchronization of the three DC motors. Thus, from the start of the third DC motor, the three DC motors are caused to synchronize more sooner. This can be explained by the fact that the third DC starts when the two others are already synchronized. Thus, we could conclude that the natural frequency of the plate (by its physical and mechanical characteristics) contributes efficiently to the rapid self-synchronization between the DC motors. Moreover, we can denote that energy transfer is quickly realized between the sources for a high of the value natural frequency of the plate.

Fig. 19

Representation of phase difference (a, b, c) between the three motors and velocity difference between the DC1 and DC3 (d) for a main frequency of the structure of ω₁₁ = 0.873. The first and the second DC motors start at the same moment τ₁ = τ₂ = 0 while the third starts with a delay τ₃ = 100 (red);τ₃ = 200 (black); τ₃ = 300 (blue)

5 Conclusions

In this chapter, the dynamics and vibration control of mechanical structures submitted to the vibrations of rotating machines with limited power supply is treated. Such systems are usually called non ideal systems because they are systems for which the external source is influenced by the response of main system. This kind of system is regularly encountered in industry, civil and mechanical engineering.

The first section presents a large number of applications of rectangular plate, following by history and some information about rotating machines especially the DC motor. The vibration control problem is approached by the presentation of some control techniques. Some examples/applications and details on the dynamics on non-ideal systems are presented in the following section.

The mathematical formalism of the vibration control of the mechanical structure is presented in two steps. The first one concerns the used of electric transducer and a tuned mass damper as controller device and the second the synchronization phenomenon with and without delay appearing between the external excitation. A brief review of each techniques of control is well presented.

The recent results on the subject are divided in two parts, they concern the electromechanical control of the rectangular plate where we paid an attention on the stability of the control system and the self synchronization of the DC sources mounted on the rectangular plate.

In the first case studied, after modeling of the proposed device, the implementation of the control strategy leads to obtain the condition for which the control is effective, the effect of some control parameters on the reduction of the amplitude are displayed and the stability condition of all the system is established in order to enhance the efficiency of the control strategy used.

In the second set of results, the dynamics of two and three DC sources with limited power supply mounted on a rectangular plate is studied; the sources are capable to rotate in the same or in the opposite direction. The main phenomenon observes is the self-synchronization appearing between the DC sources with time. It is shown that the structure frequency is a relevant factor allowing synchronization between the sources with a phase difference of zero, π, 2π, 2π/5, 4π/5, 8π/5. The effects of the control parameter (voltage apply to the DC sources), physical and mechanical characteristics of the plate are displayed and the impact on the control strategy of the direction of rotation of the sources is also shown. It is conclude that the rectangular plate will less vibrate when the two sources are antiphase synchronizing, or when one of the sources are rotate in the opposite direction than the two others. The phase synchronization will be profitable only in the case of resonance.

This work leads to some prospective works which could be to get vibration control device which do not need more energy for functioning and to evaluate eventually damage on the structure when it is connected to the controlled device during his functioning. In addition, it will be preferable to adapt the DC motors before or during his functioning to the mechanical structure in order to get early energy balance between the both and to avoid early high amplitude of vibration of the system. We can also study the stability of the system, while the DC motors are synchronized on the mechanical structure and look for experimental verification of the synchronization of DC motors fixed on a plate usually encountered in building site.