On the Stability and Long-Term Behaviour of Structural Systems Excited by Nonideal Power Sources

Abstract

This chapter investigates the problem of an unbalanced motor attached to a fixed frame by means of a nonlinear spring and a linear damper. The proposed mathematical model is simple enough to allow for an analytical treatment of the equations, while sufficiently complex to preserve the main nonlinear phenomena that can be observed in real unbalanced rotating machinery. The primary focus is on the bidirectional interaction that in general exists between the excitation provided by the motor and the response of the vibrating structure. By combining various mathematical tools (Averaging, Singular Perturbation Theory, classification of Hopf bifurcations, Poincaré-Bendixson Theorem), the long-term behaviour of the system is investigated in detail. The analytical results are verified numerically. It should be noted that the study presented in this Chapter was originally published in [1, 2].

1 Introduction

The motion of unbalanced rotors constitutes one of the most common vibration sources in mechanical engineering [3, 4]. Vibrations due to unbalance may occur in any kind of rotating systems, such as turbines, flywheels, blowers or fans [5]. Actually, in practice, rotors can never be completely balanced because of manufacturing errors such as porosity in casting, non-uniform density of the material, manufacturing tolerances, etc. [6]. Even a subsequent balancing process will never be perfect due to the tolerances of the balancing machines.

Usually, rotor unbalance has a harmful effect on rotating machinery, since vibration may damage critical parts of the machine, such as bearings, seals, gears and couplings [6]. However, there are applications where unbalanced rotors are used to generate a desired vibration. Some examples are the feeding, conveying and screening of bulk materials, or the vibrocompaction of quartz agglomerates, which makes use of unbalanced motors to compact a quartz-resin mixture. Actually, our interest in this vibrocompaction process has been the motivation for the presented study.

A simple model to analyse the dynamic response of a structure to the excitation produced by an unbalanced motor is sketched in Fig. 1. The simplest approach to this problem consists in assuming the rotor speed to be either constant or a prescribed function of time. In the constant speed case, the centrifugal force on the unbalance produces a harmonic excitation on the vibrating system, whose amplitude grows with the square of the rotating speed and whose frequency coincides with the rotating speed [5, 7].

Fig. 1

Simple 2-DOF model of a structure excited by an unbalanced motor

Note that, with this approach, it is implicitly being assumed that the rotational motion of the motor is independent of the vibration of the structure. This property is what defines an ideal excitation: it remains unaffected by the vibrating system response. Thus, the amplitude and frequency of an ideal excitation are known a priori, before solving the vibration problem. Obviously, this notion of ideality is applicable to any kind of excitation, and not only to the one produced by an unbalanced motor.

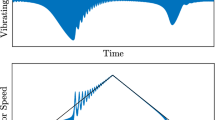
The ideality assumption is valid, with good approximation, in many real problems. However, there are situations where it is not. In 1904, Sommerfeld [8], whose pioneering work inspired many subsequent investigations, found experimentally kinds of behaviour that could not be explained upon the ideality hypothesis. He mounted an unbalanced electric motor on an elastically supported table and monitored the input power as well as the frequency and amplitude of the response [9]. The experiment consisted in increasing continuously the power input in order to make the rotor speed pass through the resonance frequency of the table, and then conduct the inverse process by decreasing the input power. The results obtained by Sommerfeld are qualitatively depicted in Fig. 2. When the rotor speed was close to resonance, an increment of the input power produced only a very slight increase of the rotor speed, while the oscillation amplitude increased considerably. This means that, in this part of the experiment, the increasing input power was not making the motor rotate faster, but was giving rise to larger oscillations. With further increasing of the input power, the rotor speed jumped abruptly to a frequency above resonance and, at the same time, the vibration amplitude jumped to a much smaller quantity than measured in the resonance region. When the process was reversed, by decreasing the motor input power, a jump phenomenon in the resonance region was also observed (see Fig. 2). However, this jump was found to be different from the one occurring for increasing rotor speed. This anomalous behaviour is usually referred to as ‘The Sommerfeld Effect’.

Fig. 2

Sommerfeld effect

In 1969 [10], Kononenko published a book entirely devoted to the study of nonideal excitations. He considered different configurations of vibrating systems excited by nonideal motors and applied the Averaging Method to the equations of motion. By taking into account the two-way interaction between the motor and the vibrating structure, he was able to explain the nonlinear phenomena found by Sommerfeld. According to Kononenko, the Sommerfeld effect is produced by the torque on the rotor due to vibration of the unbalanced mass.

Rand et al. [11] reported the detrimental effect of a nonideal energy source in dual spin spacecrafts, which could endanger a particular manoeuvre of the spacecraft once placed in orbit.

Although most studies use averaging procedures to obtain approximate solutions to the equations of motion, Blekhman [12] proposed an alternative approach, based on the method of ‘Direct Separation of Motions’.

Several authors, like El-Badawi [13] and Bolla et al. [14], analysed models where the vibrating system included an intrinsic cubic nonlinearity, in addition to the nonlinearity associated to the nonideal coupling between exciter and structure.

Balthazar et al. [15] published an extensive exposition of the state of the art concerning nonideal excitations.

The contents of this chapter are organized as follows. The analytical developments needed to understand the long-term behaviour of the system are presented in Sect. 2. Section 3 contains the results of a number of significant simulations with a twofold purpose: investigate some bifurcations of limit cycles that are too complex for an analytical treatment and serve as a numerical validation of the analytical procedures of Sect. 2. Finally, Sect. 4 presents the major conclusions of the study.

2 Analytical Approach

In this section, several analytical techniques are used to investigate the dynamics of a 2-DOF system consisting in an unbalanced motor attached to the fixed frame by a nonlinear spring and a linear damper.

2.1 Problem Statement and Assumptions

Consider the system depicted in Fig. 3. It consists in an unbalanced motor attached to a fixed frame by a nonlinear spring –whose force has linear and cubic components– and a linear damper. The cubic component of the spring gives the possibility to model a nonlinear behaviour for the structure supporting the motor [16]. The effect of gravity can be shown to have no relevance [17] and, therefore, it will not be included in the model.

Fig. 3

Model

Variable $x$ stands for the linear motion, $\phi$ is the angle of the rotor, ${m}_{1}$ is the unbalanced mass with eccentricity $r$, $m_{0}$ is the rest of the vibrating mass, ${I}_{0}$ is the rotor inertia (without including the unbalance), $b$ is the viscous damping coefficient and $k$ and $\lambda$ are, respectively, the linear and cubic coefficients of the spring. The equations of motion for the coupled 2-DOF system are [13]

$$\begin{array}{*{20}c} {m\ddot{x} + b\dot{x} + kx + \lambda x^{3} = m_{1} r\left( {\dot{\phi }^{2} \cos \phi + \ddot{\phi }\,\sin \,\phi } \right)} \\ {I\ddot{\phi } = L_{m} \left( {\dot{\phi }} \right) + m_{1} r\ddot{x}\,\sin \,\phi ,} \\ \end{array}$$

(1)

where $m={m}_{0}+{m}_{1}$, $I={I}_{0}+{m}_{1}{r}^{2}$ and an overdot represents differentiation with respect to time, ${t}$.

Function ${L}_{\mathrm{m}}\left(\dot{\phi }\right)$ is the driving torque produced by the motor –given by its torque-speed curve, also known as static characteristic– minus the losses torque due to friction at the bearings, windage, etc. We assume this net torque to be a linear function of the rotor speed:

$${L}_{m}\left(\dot{\phi }\right)=A+D\dot{\phi }.$$

(2)

Although ${L}_{\mathrm{m}}\left(\dot{\phi }\right)$ includes the damping of rotational motion, we will usually refer to it shortly as ‘the motor characteristic’.

As will be seen later, it is convenient for the purpose of this chapter to write the driving torque in an alternative way. Then, denoting by ${\omega }_{{n}}$ the linear natural frequency of the oscillator, given by ${\omega }_{{n}}=\sqrt{{k}/{m}}$, the motor torque can be written as

$${L}_{m}\left(\dot{\phi }\right)=C+D\left(\dot{\phi }-{\omega }_{n}\right),$$

(3)

where $C$ represents the driving torque at resonance $\left({L}_{m}\left({\omega }_{n}\right)=C\right)$. From Eqs. (2) and (3), the relation between constants $A$ and $C$ can be directly deduced:

$$C=A+D{\omega }_{n}.$$

(4)

Along the whole chapter, the motor characteristic will be written as (3) or (4), depending on the situation. It should be kept in mind that these two expressions are totally equivalent. The important point is that the driving torque is assumed to follow a linear relation with the rotor speed. It is further assumed that ${D}<0$ –the driving torque decreases with the rotor speed–, as is usual for most kinds of motor. This assumption will prove to be of major importance.

As an example, the static characteristic of an induction motor is depicted in Fig. 4. Note that such a motor is usually designed to work on the region $\dot{\phi }>{\omega }_{{peak}}$, where the curve could be reasonably approximated by a straight line with negative slope. The simplified motor characteristic given at (3) is represented in Fig. 5.

Fig. 4

Typical static characteristic for an asynchronous motor

Fig. 5

Static characteristic corresponding to Eq. (3)

In the second of Eq. (1), which imposes the equilibrium of the rotor, the last term is of great significance, since it accounts for the torque on the rotor caused by linear motion of the system. Its physical interpretation can be readily understood with the aid of Fig. 6. Due to displacement ${x}\left({t}\right)$, a horizontal inertial force acts on the unbalanced mass and generates a torque with respect to the rotor axis. This particular term of the equations of motion is what makes the excitation nonideal, for it takes into account how vibration influences rotation. If this torque due to vibration did not exist –or if it was negligible–, the rotor equilibrium equation would reduce to ${I}\ddot{\phi }={{L}}_{{m}}\left(\dot{\phi }\right)$, and it could be solved for $\phi \left({t}\right)$ regardless of the linear motion. Then, this solution $\phi \left({t}\right)$ could be introduced in the first of Eq. (1) as a prescribed excitation.

Fig. 6

Torque on the rotor due to vibration

By defining

$$\begin{array}{*{20}c} {R_{m} = m_{1} /m,\quad R_{I} = m_{1} r^{2} /I,\quad \xi = \frac{b}{{2\sqrt {km} }},\quad \alpha = \frac{{R_{I} R_{m} }}{2\xi }} \\ {c = \frac{C}{{I\omega_{n}^{2} }},\quad d = \frac{D}{{I\omega_{n} }},\quad \tau = \omega_{n} t,\quad u = \frac{x}{r}\frac{2\xi }{{R_{m} }},\quad \rho = \frac{{\lambda r^{2} }}{k}\left( {\frac{{R_{m} }}{2\xi }} \right)^{2} ,} \\ \end{array}$$

(5)

the equations of motion can be written in a more convenient dimensionless form

$$\begin{array}{*{20}c} {\ddot{u} + u = - 2\xi \dot{u} - \rho u^{3} + 2\xi \left( {\dot{\phi }^{2} \,\cos\,\phi + \ddot{\phi }\,\sin\,\phi } \right)} \\ {\ddot{\phi } = c + d\left( {\dot{\phi } - 1} \right) + \alpha \ddot{u}\,\sin\,\phi ,} \\ \end{array}$$

(6)

where a dot now represents differentiation with respect to dimensionless time, $\tau$.

In order to apply perturbation techniques to system (6), some assumptions on the order of magnitude of the system parameters have to be made. Thus, we assume the damping, the unbalance and the nonlinearity to be small. This is expressed by making the corresponding coefficients proportional to a sufficiently small, positive and dimensionless parameter $\epsilon$:

$$\xi = \epsilon \xi_{0} ,\quad \alpha = \epsilon \alpha_{0} ,\quad \rho = \epsilon \rho_{0} ,$$

(7)

where parameters with subscript ‘0’ are $\epsilon$-independent. It is also assumed that the torque generated by the motor at resonance $\left(\dot{\phi }=1\right)$ is sufficiently small:

$$c=\epsilon {c}_{0}$$

(8)

Finally, the slope of the motor characteristic is assumed to be of the order of unity, i.e. independent of $\epsilon$:

$$d={d}_{0}$$

(9)

This last statement deserves some attention. Two possible assumptions with respect to the order of magnitude of parameter $d$ are particularly relevant: $d={d}_{0}$ (large slope of the motor characteristic) and $d=\epsilon {d}_{0}$ (small slope of the motor characteristic). It will be seen in Sect. 2.4 that the particular choice made in this chapter (large slope) implies that the slope of the motor torque curve is comparable to the slope of the curve representing the torque on the rotor due to vibration. On the other hand, the assumption of small slope of the motor characteristic corresponds to a situation where the motor torque is nearly constant around the resonance region of the system. Both the required mathematical approach and the dynamics exhibited by the system are very different depending on whether the slope of the motor characteristic is large or small. References [18, 19] are examples of investigations based on the assumption of small slope of the motor characteristic, while [9, 10, 12, 14, 17] correspond to the assumption of large slope.

Taking the proposed scaling (7)–(9) into account and dropping the subscript ‘$0$’ for convenience, system (1) takes the form

$$\begin{array}{*{20}c} {\ddot{u} + u = \epsilon \left[ { - 2\xi \dot{u} - \rho u^{3} + 2\xi \left( {\dot{\phi }^{2} \,\cos\,\phi + \ddot{\phi }\,\sin\,\phi } \right)} \right]} \\ {\ddot{\phi } = d\left( {\dot{\phi } - 1} \right) + \epsilon \left[ {c + \alpha \ddot{u}\,\sin\,\phi } \right].} \\ \end{array}$$

(10)

2.2 First Order Averaging

Before turning to the treatment of (10), a specific averaging technique is developed in this section. The reader might wonder why there is a need to develop any new averaging procedures, instead of relying on the well-established averaging theorems for dynamical systems that can be found, for example, in [18]. The reason is that averaging theorems are usually valid for systems where the state variables can be split-up into two groups: a set of slow variables and one or more fast rotating phases over which the averaging is performed. It will be seen in Sect. 2.3 that the system under study does not take this form, but has one additional non-angular fast variable that makes conventional averaging theorems not applicable.

In order to make the procedure as general as possible, consider a system of the form

$$\left\{\begin{array}{c}\dot{{\varvec{x}}}=\epsilon \left[{\varvec{A}}{\varvec{y}}+{\varvec{X}}\left({\varvec{x}},\phi \right)\right]+O\left({\epsilon }^{2}\right)\\ \dot{{\varvec{y}}}={\varvec{B}}{\varvec{y}}+{\varvec{Y}}\left({\varvec{x}},\phi \right)+O\left(\epsilon \right)\\ \dot{\phi }=\Omega +O\left(\epsilon \right)\end{array}\right\}, \begin{array}{c}{\varvec{x}}\in D\subset {\mathbb{R}}^{n}\\ {\varvec{y}}\in R\subset {\mathbb{R}}^{m}\\ \phi \in {S}^{1},\end{array}$$

(11)

where ${\varvec{A}}$ and ${\varvec{B}}$ are matrices of constant coefficients and $\Omega$ is a scalar constant, bounded away from zero. It will be shown in the next section that system (10) can be written in the form (11).

First, we define the averaged variables as

$$\overline{\user2{x}}(t) \equiv \frac{1}{T}\mathop \int \limits_{t - T/2}^{t + T/2} {\varvec{x}}(s)ds,\quad \overline{\user2{y}}(t) \equiv \frac{1}{T}\mathop \int \limits_{t - T/2}^{t + T/2} {\varvec{y}}(s)ds$$

(12)

where $T=2\pi /\Omega$. As illustrated in Fig. 7, the effect of the operator defined in (12) is to smooth out the short-term fluctuations of each variable, while retaining the long-term behavior.

Fig. 7

Definition of the averaged variables

Suppose we are interested in the evolution of the averaged variables $\overline{{\varvec{x}} }\left(t\right)$ and $\overline{{\varvec{y}} }\left(t\right)$. Then, we can average the first two equations in (11), which yields

$$\left\{\begin{array}{c}\dot{\overline{{\varvec{x}}} }=\epsilon \left[{\varvec{A}}\overline{{\varvec{y}} }+\frac{1}{T}\underset{t-T/2}{\overset{t+T/2}{\int }}{\varvec{X}}\left({\varvec{x}}\left(s\right),\phi \left(s\right)\right)ds\right]+O\left({\epsilon }^{2}\right)\\ \dot{\overline{{\varvec{y}}} }={\varvec{B}}\overline{{\varvec{y}} }+\frac{1}{T}\underset{t-T/2}{\overset{t+T/2}{\int }}{\varvec{Y}}\left({\varvec{x}}\left(s\right),\phi \left(s\right)\right)ds+O\left(\epsilon \right)\end{array}\right\},$$

(13)

where it has been used that the average, as defined in (12), is a linear operator (the average of the sum is the sum of the averages).

The next step consists in transforming the integrals in (13). Since the process is exactly the same for both integrals, we only focus on the first of them.

First, we can write

$$\frac{1}{T}\underset{t-T/2}{\overset{t+T/2}{\int }}{\varvec{X}}\left({\varvec{x}}\left(s\right),\phi \left(s\right)\right)ds=\frac{1}{T}\underset{t-T/2}{\overset{t+T/2}{\int }}{\varvec{X}}\left({\varvec{x}}\left(t\right),\phi \left(s\right)\right)ds+O\left(\epsilon \right),$$

(14)

where it has been used the property that, in one period $T$, ${\varvec{x}}\left(t\right)$ can only change by ${O}\left(\epsilon \right)$, according to (11). Thus, we can write ${\varvec{x}}\left(s\right)={\varvec{x}}\left(t\right)+O\left(\epsilon \right)$. Changing the integration variable from $\mathrm{s}$ to $\phi$ yields

$$\frac{1}{T}\underset{t-T/2}{\overset{t+T/2}{\int }}{\varvec{X}}\left({\varvec{x}}\left(t\right),\phi \left(s\right)\right)ds+O\left(\epsilon \right)=\frac{1}{2\pi }\underset{\phi \left(t-T/2\right)}{\overset{\phi \left(t+T/2\right)}{\int }}{\varvec{X}}\left({\varvec{x}}\left(t\right),\phi \right)d\phi +O\left(\epsilon \right),$$

(15)

where the last of relations (11) has been used $\left(d\phi =\mathrm{\Omega ds}+O\left(\epsilon \right)\right)$. The integration limits can also be transformed by using again $\dot{\phi }=\Omega +O\left(\epsilon \right)$:

$$\frac{1}{2\pi }\underset{\phi \left(t-T/2\right)}{\overset{\phi \left(t+T/2\right)}{\int }}{\varvec{X}}\left({\varvec{x}}\left(t\right),\phi \right)d\phi +O\left(\epsilon \right)=\frac{1}{2\pi }\underset{\phi \left(t\right)-\pi }{\overset{\phi \left(t\right)+\pi }{\int }}{\varvec{X}}\left({\varvec{x}}\left(t\right),\phi \right)d\phi +O\left(\epsilon \right).$$

(16)

Finally, as function ${\varvec{X}}$ is $2\uppi$-periodic in $\phi$, we can write

$$\frac{1}{2\pi }\underset{\phi \left(t\right)-\pi }{\overset{\phi \left(t\right)+\pi }{\int }}{\varvec{X}}\left({\varvec{x}}\left(t\right),\phi \right)d\phi +O\left(\epsilon \right)=\frac{1}{2\pi }\underset{0}{\overset{2\pi }{\int }}{\varvec{X}}\left({\varvec{x}}\left(t\right),\phi \right)d\phi +O\left(\epsilon \right).$$

(17)

Thus, system (13) can be rewritten as

$$\left\{\begin{array}{c}\dot{\overline{{\varvec{x}}} }=\epsilon \left[{\varvec{A}}\overline{{\varvec{y}} }+\overline{{\varvec{X}} }\left(\overline{{\varvec{x}} }\right)\right]+O\left({\epsilon }^{2}\right)\\ \dot{\overline{{\varvec{y}}} }={\varvec{B}}\overline{{\varvec{y}} }+\overline{{\varvec{Y}} }\left(\overline{{\varvec{x}} }\right)+O\left(\epsilon \right)\end{array}\right\},$$

(18)

where

$$\overline{{\varvec{X}}} ( \cdot ) \equiv \frac{1}{2\pi }\mathop \int \limits_{0}^{2\pi } {\varvec{X}}\left( { \cdot ,\phi } \right)d\phi ,\quad \overline{{\varvec{Y}}} ( \cdot ) \equiv \frac{1}{2\pi }\mathop \int \limits_{0}^{2\pi } {\varvec{Y}}\left( { \cdot ,\phi } \right)d\phi$$

(19)

We have been able to derive an autonomous system for the averaged variables, where the fast angle no longer appears –except in the higher order terms of (18). Note that the proposed approach exploits a particular property of system (11), namely the fact that the vector of fast variables ${\varvec{y}}$ only appears linearly on the r.h.s. of the equations. This feature, together with the linearity of the averaging operator, allows applying an averaging technique to system (11), despite it containing fast variables (in addition to the fast rotating phase $\phi$).

Finally, it is convenient to remark the difference between the original and averaged variables. From Eq. (11), variations of ${\varvec{x}}$ and ${\varvec{y}}$ in one period $T$ are $O\left(\epsilon \right)$ and $O\left(1\right)$, respectively. Therefore, we can write

$${\varvec{x}}(t) = \overline{\user2{x}}(t) + O\left( \epsilon \right),\quad {\varvec{y}}(t) = \overline{\user2{y}}(t) + O(1).$$

(20)

2.3 Perturbation Approach: Derivation of the Reduced System

Going back to the mechanical system under study, Eq. (10) constitute an autonomous dynamical system of dimension 4, with state variables $\left\{u, \dot{u}, \phi , \dot{\phi }\right\}$. A perturbation approach is proposed in this section, whereby (10) is transformed into an approximate 2D system.

First, it is convenient to perform a change of variables, from $\left\{u, \dot{u}\right\}$ to polar coordinates [18]:

$$\begin{array}{*{20}c} {u = a\,\cos\,\left( {\phi + \beta } \right)} \\ {\dot{u} = - a\,\sin\,\left( {\phi + \beta } \right).} \\ \end{array}$$

(21)

This step does not include any approximation, since it consists in just replacing the pair of variables $\left\{u\left(\tau \right), \dot{u}\left(\tau \right)\right\}$ with the pair of amplitude-phase variables $\left\{a\left(\tau \right), \beta \left(\tau \right)\right\}$.

By differentiating the first of relations (21) we obtain

$$\dot{u} = \dot{a}\,\cos\,\left( {\phi + \beta } \right) - a\left( {\dot{\phi } + \dot{\beta }} \right)\,\sin\,\left( {\phi + \beta } \right).$$

(22)

Comparing (22) with the second of relations (21) yields

$$\dot{a}\,\cos\left( {\phi + \beta } \right) - a\left( {\dot{\phi } - 1 + \dot{\beta }} \right)\,\sin\,\left( {\phi + \beta } \right) = 0.$$

(23)

On the other hand, if (21) is introduced into the first of Eq. (10), we have

$$\begin{array}{*{20}c} { - \dot{a}\,\sin\,\left( {\phi + \beta } \right) - a\left( {\dot{\phi } - 1 + \dot{\beta }} \right)\,\cos\,\left( {\phi + \beta } \right) = } \\ { = \epsilon \left[ {2\xi a\,\sin\,\left( {\phi + \beta } \right) - \rho a^{3} \,\cos\,^{3} \left( {\phi + \beta } \right) + 2\xi \left( {\dot{\phi }^{2} \,\cos\,\phi + \ddot{\phi }\,\sin\,\phi } \right)} \right]} \\ \end{array}$$

(24)

Equations (23) and (24) together form a linear system for $\dot{a}$ and $\dot{\beta }$ that can be readily solved:

$$\begin{array}{*{20}c} {\dot{a} = - \epsilon \,\sin\,\left( {\phi + \beta } \right)\left[ {2\xi a\,\sin\,\left( {\phi + \beta } \right) - \rho a^{3} \,\cos\,^{3} \left( {\phi + \beta } \right) + 2\xi \left( {\dot{\phi }^{2} \,\cos\,\phi + \ddot{\phi }\,\sin\,\phi } \right)} \right]} \\ {\dot{\beta } = 1 - \dot{\phi } - \epsilon \frac{{\cos\,\left( {\phi + \beta } \right)}}{a}\left[ {2\xi a\,\sin\,\left( {\phi + \beta } \right) - \rho a^{3} \,\cos^{3} \left( {\phi + \beta } \right) + 2\xi \left( {\dot{\phi }^{2} \,\cos\,\phi + \ddot{\phi }\,\sin\,\phi } \right)} \right]} \\ \end{array}$$

(25)

It is also suitable to define a new variable for the rotor speed:

$$\Omega \equiv \dot{\phi }.$$

(26)

Then, the dynamical system, written in terms of the new variables, becomes

$$\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\dot{a} = - \epsilon \,\sin\left( {\phi + \beta } \right)F_{1} \left( {a,\beta ,\phi ,\Omega } \right) + O\left( { \epsilon^{2} } \right)} \\ {\dot{\beta } = 1 - \varOmega - \epsilon \frac{{\cos\left( {\phi + \beta } \right)}}{a}F_{1} \left( {a,\beta ,\phi ,\Omega } \right) + O\left( { \epsilon^{2} } \right)} \\ \end{array} } \\ {\begin{array}{*{20}c} {{\dot{\Omega }} = d\left( {\varOmega - 1} \right) + \epsilon \left( {c - \alpha a\,\sin\,\phi\, \cos\,\left( {\phi + \beta } \right)} \right) + O\left( { \epsilon^{2} } \right)} \\ {\dot{\phi } = {\Omega },} \\ \end{array} } \\ \end{array} } \right\},$$

(27)

where

$$F_{1} = 2\xi a\,\sin\,\left( {\phi + \beta } \right) - \rho a^{3} \,\cos^{3} \left( {\phi + \beta } \right) + 2\xi \left[ {{\Omega }^{2} \,\cos\,\phi + d\left( {{\Omega } - 1} \right)\,\sin\,\phi } \right].$$

(28)

A new 4D autonomous dynamical system (27) has been derived, with state variables $\left\{ {a, \beta , \phi , \varOmega } \right\}$, which is fully equivalent to (10).

Consider now a general set of initial conditions $\left\{ {a_{0} , \beta_{0} , \phi_{0} , \varOmega_{0} } \right\}$ and let us investigate how the variables evolve with time. In the next subsections, it will be shown that the dynamics of (27) is composed of three consecutive stages of time, with different qualitative behaviours.

First stage

For the moment, consider only the evolution equations for variables $\beta$ and $\Omega$, which can be written as

$$\left\{ {\begin{array}{*{20}c} {\dot{\beta } = 1 - {\Omega } + O\left( \epsilon \right)} \\ {\dot{\varOmega } = d\left( {{\Omega } - 1} \right) + O\left( \epsilon \right)} \\ \end{array} } \right\}.$$

(29)

It is clear that, to first order of approximation, the evolution of $\beta$ and $\Omega$ only depends on $\Omega$. This first order approximation corresponds to neglecting the $O\left(\epsilon \right)$ terms in (29).

$$\left\{\begin{array}{c}\dot{\beta }=1-\Omega \\ \dot{\Omega }=d\left(\Omega -1\right)\end{array}\right\}.$$

(30)

The relation between exact system (29) and (30) is established by the Regular Perturbation Theory [18], which assures that solutions of (30) are $O\left(\epsilon \right)$–approximations to solutions of (29), for $\tau =O\left(1\right)$. Thus, we proceed to solve system (30):

$$\left\{\begin{array}{c}\beta ={\beta }_{0}^{*}+\frac{1-{\Omega }_{0}}{d}{e}^{d\tau }\\\Omega =1+\left[{\Omega }_{0}-1\right]{e}^{d\tau }\end{array}\right\},$$

(31)

with

$${\beta }_{0}^{*}\equiv {\beta }_{0}+\frac{{\Omega }_{0}-1}{d}.$$

(32)

It is clear from (31) that both variables tend exponentially to constant values:

$$\beta \to \beta_{0}^{*} ,\quad \Omega \to 1.$$

(33)

This is due to the assumption $d<0$ (otherwise, the exponentials in (31) would be divergent). Taking into account the approximation made when transforming (29) into (30), it can be stated that, after a time interval $\tau =O\left(1\right)$, we have

$$\beta = \beta_{0}^{*} + O\left( \epsilon \right),\quad \Omega = 1 + O\left( \epsilon \right).$$

(34)

Once $\beta$ and $\Omega$ are at an $O\left(\epsilon \right)$–distance from ${\beta }_{0}^{*}$ and $1$, respectively, the first stage of the motion is over. Note that, during this stage, the rotor speed evolves monotonically towards the resonance region.

During this first phase, variable $a$ remains nearly constant. Since $\dot{a}=O\left(\epsilon \right)$—see (27), variable $a$ needs a time length $\tau =O\left(1/\epsilon \right)$ to evolve significantly. Thus, at the end of the first stage, we have

$$a={a}_{0}+O\left(\epsilon \right).$$

(35)

In summary, the first stage corresponds to a time length $\tau =O\left(1\right)$. It starts at $\tau =0$ and it ends when $\beta$ and $\Omega$ have reached an $O\left(\epsilon \right)$–distance to ${\beta }_{0}^{*}$ and $1$, respectively.

Second stage

At the beginning of the second stage, the rotor speed is already in the vicinity of resonance. Consequently, it can be naturally expanded as

$$\Omega =1+\epsilon \sigma .$$

(36)

A new variable $\sigma$ has been introduced in (36), which will be very widely used throughout the chapter. Notice that $\sigma$ is a detuning coordinate, which measures how much the rotor speed deviates from the system natural frequency.

If system (27) is written using variable $\sigma$ instead of $\Omega$, it becomes

$$\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\dot{a} = - \epsilon \,\sin \,\left( {\phi + \beta } \right)F_{2} \left( {a,\beta ,\phi } \right) + O\left( { \epsilon^{2} } \right)} \\ {\dot{\beta } = - \epsilon \sigma - \epsilon \frac{{\cos \,\left( {\phi + \beta } \right)}}{a}F_{2} \left( {a,\beta ,\phi } \right) + O\left( { \epsilon^{2} } \right)} \\ \end{array} } \\ {\begin{array}{*{20}c} {\dot{\sigma } = c + d\sigma - \alpha a\,\sin \,\phi \,\cos \left( {\phi + \beta } \right) + O\left( \epsilon \right)} \\ {\dot{\phi } = 1 + \epsilon \sigma } \\ \end{array} } \\ \end{array} } \right\},$$

(37)

where

$$F_{2} = 2\xi a\sin \left( {\phi + \beta } \right) - \rho a^{3} \cos^{3} \left( {\phi + \beta } \right) + 2\xi \cos \phi .$$

(38)

Notice that the closeness between the rotor speed and the natural frequency of the system has transformed $\beta$ into a slow variable. Note also that system (37) is of the form (11), with $\left\{a, \beta \right\}$ playing the role of vector ${\varvec{x}}$ and $\sigma$ that of vector ${\varvec{y}}$. Therefore, the averaging technique presented in Sect. 2.2 can be readily applied to (37), in order to obtain the evolution of the averaged variables.

The averaged system, which in the general case is given by (18), takes in the present case the form

$$\left\{ {\begin{array}{*{20}c} {\dot{\overline{a}} = - \epsilon \xi \left( {\overline{a} + \sin \overline{\beta }} \right) + O\left( { \epsilon^{2} } \right)} \\ {\dot{\overline{\beta }} = - \epsilon \left( {\overline{\sigma } + \xi \frac{{\cos \overline{\beta }}}{{\overline{a}}} - \frac{3}{8}\rho \overline{a}^{2} } \right) + O\left( { \epsilon^{2} } \right)} \\ {\dot{\overline{\sigma }} = c + d\overline{\sigma } + \frac{\alpha }{2}\overline{a}\sin \overline{\beta } + O\left( \epsilon \right)} \\ \end{array} } \right\},$$

(39)

where the averaged variables $\left\{ {\overline{a},\overline{\beta },\overline{\sigma }} \right\}$ are defined as in (12). System (39) has dimension 3, since variable $\phi$ no longer appears.

It is convenient to highlight the relation between the original and the averaged variables. Particularizing the general expression (20) to the system under analysis, we find

$$\begin{array}{*{20}c} {a = \overline{a} + O\left( \epsilon \right)} \\ {\beta = \overline{\beta } + O\left( \epsilon \right)} \\ {\sigma = \overline{\sigma } + O\left( 1 \right).} \\ \end{array}$$

(40)

Observe that, even with an $O\left(1\right)$ error in $\sigma$, the rotor speed is still known with $O\left(\epsilon \right)$ precision, according to (36). From now on, the overbars will be omitted, unless otherwise stated.

The task now is to investigate system (39). As pointed out before, this is a fast-slow system, with two slow variables $a$ and $\beta$ and one fast variable $\sigma$. This difference in the time scales allows exploiting the Singular Perturbation Theory [20,21,22].

According to the SPT, a system with the form of (39) displays two qualitatively different behaviors at two sequential time scales, which correspond to the second and third stages of the original system (27). With the aim of studying the first of them –second stage of (27), consider a time interval $\tau =O\left(1\right)$ for system (39). Since $\mathrm{a}$ and $\upbeta$ evolve with rate $O\left(\epsilon \right)$, it is clear that we have

$$\begin{array}{*{20}c} {a = a_{0} + O\left( \epsilon \right)} \\ {\beta = \beta_{0}^{*} + O\left( \epsilon \right)} \\ {\dot{\sigma } = c + d\sigma + \frac{\alpha }{2}a_{0} \sin \beta_{0}^{*} + O\left( \epsilon \right),} \\ \end{array}$$

(41)

where we have taken into account that, at the beginning of stage 2, $a={a}_{0}+O\left(\epsilon \right)$ and $\beta ={\beta }_{0}^{*}+O\left(\epsilon \right)$.

Then, the only variable that changes considerably during this stage is $\sigma$. From a direct analysis of the last of Eq. (41), it can be deduced that $\sigma$ tends exponentially to the following value

$$\sigma \to - \frac{c}{d} - \frac{\alpha }{2d}a_{0} \sin \beta_{0}^{*} ,$$

(42)

which is the only fixed point for the last of Eq. (41). The assumption $d<0$ guarantees that the fixed point is globally attracting.

Expression (42), generalized to any values of $a$ and $\beta$, gives what is called ‘the Slow Manifold’:

$$\sigma^{*} \left( {a,\beta } \right) = - \frac{c}{d} - \frac{\alpha }{2d}a\sin \beta .$$

(43)

Thus, (42) can be rewritten as

$$\sigma \to {\sigma }^{*}\left({a}_{0},{\beta }_{0}^{*}\right).$$

(44)

Thereby, at this stage, the slow variables remain almost constant, while the fast variable evolves until reaching the vicinity of the slow manifold.

Summing up, the second stage corresponds to a time length $\tau =O\left(1\right)$, just as the first one. It ends once variable $\sigma$ has reached an $O\left(\epsilon \right)$–distance to ${\sigma }^{*}\left({a}_{0},{\beta }_{0}^{*}\right)$. During this phase of the motion, $a$ and $\beta$ do not change significantly.

Third stage

The third stage of the original system (27) –which is the second stage of the averaged system (39)—occurs at a time scale $\tau =O\left(1/\epsilon \right)$. This can be easily understood by noticing that, once the system is near the slow manifold, variable $\sigma$ becomes slow (introducing (43) in (39) leads to $\dot{\sigma }=O\left(\epsilon \right)$). Therefore, near the slow manifold, all variables are slow and, as a consequence, the system natural time scale is $\tau =O\left(1/\epsilon \right)$.

Obviously it still needs to be proved that, once the system is near the slow manifold, it remains in its neighborhood for all subsequent time. In other words, we have to verify that the manifold is always attracting. Although the proof is beyond the scope of this book and will not be displayed here, it can be shown that the attractiveness of the slow manifold is guaranteed as long as $d<0$.

By introducing the expression of the slow manifold in (39), the equations corresponding to the third phase of the motion are obtained:

$$\left\{ {\begin{array}{*{20}c} {\dot{a} = - \epsilon \xi \left( {a + \sin\,\beta } \right) + O\left( { \epsilon^{2} } \right)} \\ {\dot{\beta } = - \epsilon \left( {\sigma^{*} \left( {a,\beta } \right) + \xi \frac{\cos\,\beta }{a} - \frac{3}{8}\rho a^{2} } \right) + O\left( { \epsilon^{2} } \right)} \\ {\sigma = \sigma^{*} \left( {a,\beta } \right) + O\left( \epsilon \right).} \\ \end{array} } \right\}$$

(45)

As usual, higher order terms in (45) can be eliminated, giving rise to an $O\left(\epsilon \right)$ approximation for a time length $\tau =O\left(1/\epsilon \right)$:

$$\left\{ {\begin{array}{*{20}c} {\dot{a} = - \epsilon \xi \left( {a + \sin\,\beta } \right)} \\ {\dot{\beta } = - \epsilon \left( {\sigma^{*} \left( {a,\beta } \right) + \xi \frac{\cos\,\beta }{a} - \frac{3}{8}\rho a^{2} } \right)} \\ {\sigma = \sigma^{*} \left( {a,\beta } \right).} \\ \end{array} } \right\}$$

(46)

It is convenient to observe that, although (46) contains three equations, only two of them are differential equations. Thus, (46) represents a 2D autonomous dynamical system. The evolution of $a$ and $\beta$ no longer depends on $\sigma$, once $\sigma$ is written as a function of $a$ and $\beta$. The last equation is written with the only purpose of tracking the evolution of variable $\sigma$.

In summary, the third stage corresponds to a time length $\tau =O\left(1/\epsilon \right)$. At this phase of the motion, the averaged system evolves along the slow manifold given by (43). Variables $a$, $\beta$ and $\sigma$ obey Eq. (46), with $O\left(\epsilon \right)$ precision.

Figure 8 shows a schematic representation of the three different stages of the system dynamics, summing up the results obtained in the present section. Note that, in Fig. 8, the use of overbars for the averaged variables is recovered. The most relevant result is that, once the initial transient corresponding to the first two stages has finished, the evolution of variables $a$ and $\beta$ is governed by Eq. (46)—within an $O\left(\epsilon \right)$ error–.

Fig. 8

Overview of the system dynamics, with $\left\{{{a}}_{{R}}, {\beta }_{{R}}\right\}$ being the solution of system (46) with appropriate initial conditions

From Fig. 8, it is clear that suitable initial conditions for system (46) are $\left\{{a}_{0},{\beta }_{0}^{*}\right\}$. Recalling definition (32), this can be written as $\left\{{a}_{0},{\beta }_{0}+\left({\Omega }_{0}-1\right)/d\right\}$, where $\left\{{a}_{0}, {\beta }_{0}, {\phi }_{0}, {\Omega }_{0}\right\}$ is the set of initial conditions for system (27).

However, we may be interested in a particular set of initial conditions for system (10), given as $\left\{{u}_{0}, {\dot{u}}_{0}, {\phi }_{0}, {\dot{\phi }}_{0}\right\}$. It is, then, convenient, to express the initial conditions for (46) as functions of the initial conditions for (10):

$$\begin{array}{c}{a}_{0}=\sqrt{{u}_{0}^{2}+{\dot{u}}_{0}^{2}}\\ {\beta }_{0}^{*}={\mathit{tan}}^{-1}\left(\frac{-{\dot{u}}_{0}}{{u}_{0}}\right)-{\phi }_{0}+\frac{{\dot{\phi }}_{0}-1}{d},\end{array}$$

(47)

as can be readily deduced from relations (21), (26) and (32).

Recapitulating, we have been able to eliminate from the formulation variable $\phi$ by Averaging, and variable $\sigma$ by applying the Singular Perturbation Theory.

2.4 Analysis of the Reduced System

This section focuses on the behaviour of system (46), once it has been shown to capture, with $O\left(\epsilon \right)$ precision, the dynamics of the original system (10) during the third stage of the motion.

Firstly, it is useful to make a comparison between the system under study and its ideal counterpart, where the rotor speed is constant. Clearly, for this ideal case, the equation of motion of the system shown in Fig. 3 is given by

$$m\ddot{x} + b\dot{x} + kx + \lambda x^{3} = m_{1} r\dot{\phi }^{2} \cos\,\phi ,$$

(48)

with $\dot{\phi }$ fixed. Equation (48) describes a Duffing oscillator, subjected to harmonic excitation. This is a very well-known problem, which has been widely studied in the literature [9, 19, 23, 24]. Under the assumptions of small damping, small nonlinearity, small unbalance and near-resonant excitation $\left(\dot{\phi }=1+\epsilon {\sigma }_{0}\right)$, the Averaging Method can be applied to system (48), leading to

$$\left\{ {\begin{array}{*{20}c} {\dot{a} = - \epsilon \xi \left( {a + \sin\,\beta } \right)} \\ {\dot{\beta } = - \epsilon \left( {\sigma_{0} + \xi \frac{\cos\,\beta }{a} - \frac{3}{8}\rho a^{2} } \right)} \\ \end{array} } \right\},$$

(49)

where all the parameters and variables are defined as in Sects. 2.1 and 2.3. It is easy to verify that system (49) is exactly the same as (46), with the only difference of replacing ${\sigma }^{*}\left(a,\beta \right)$ by the constant value ${\sigma }_{0}$. This is a clear illustration of the concept of nonideal excitation. In the ideal case, the rotor speed appears in Eq. (49) as a constant value ${\sigma }_{0}$, externally imposed by the motor. However, in the nonideal case, the rotor speed enters Eq. (46) as a function of the system vibratory motion, ${\sigma }^{*}\left(a,\beta \right)$.

It is also important to observe that an ideal motor displays a vertical static characteristic, corresponding to the limit case $d\to -\infty$. The motor is, then, able to generate any torque for the same rotor speed. This suggests the idea that a real motor with a static characteristic of very large slope (in absolute value) is more likely to behave in an ideal manner than another one with a smaller slope.

Fixed points

Going back to the objective of analyzing system (46), it is first convenient to look for its fixed points, $\left\{{a}_{eq},{\beta }_{eq},{\sigma }_{eq}\right\}$:

$$\begin{array}{*{20}c} {a_{eq} = - \sin\,\beta_{eq} } \\ {\sigma^{*} \left( {a_{eq} ,\beta_{eq} } \right) = \frac{3}{8}\rho a_{eq}^{2} - \xi \frac{{\cos\,\beta_{eq} }}{{a_{eq} }}} \\ {\sigma_{eq} = \sigma^{*} \left( {a_{eq} ,\beta_{eq} } \right).} \\ \end{array}$$

(50)

From the first of Eq. (50), we have

$$\cos\,\beta_{eq} = - z\sqrt {1 - a_{eq}^{2} } ,\;\;z = \pm 1.$$

(51)

Combining (43), (50) and (51) yields

$$-\frac{c}{d}+\frac{\alpha }{2d}{a}_{eq}^{2}=\frac{3}{8}\rho {a}_{eq}^{2}+z\xi \frac{\sqrt{1-{a}_{eq}^{2}}}{{a}_{eq}}.$$

(52)

Solutions of (52), for both values of $z$, give ${a}_{eq}$ for all the fixed points of (46). This can be done analytically, but the expressions become cumbersome and difficult to interpret. An alternative procedure is proposed, which leads to the fixed points of (46) in a graphical way. To this end, the last of Eq. (46) can be rewritten as

$$c + d\sigma = - \frac{\alpha }{2}a\,\sin\,\beta ,$$

(53)

where definition (43) has been used. Now, recall the last of Eq. (39), which governs the evolution of the rotor speed for the averaged system:

$$\dot{\sigma } = c + d\sigma + \frac{\alpha }{2}a\,\sin\,\beta + O\left( \epsilon \right).$$

(54)

In the light of (54), (53) can be interpreted as an equilibrium between two torques on the rotor. The left hand term in (53) represents the driving torque produced by the motor, while the right hand term represents the resisting torque due to vibration. Thus, the fact that the averaged system is on the slow manifold –which is expressed in Eq. (53)—can be understood as a torque equilibrium condition.

Equation (53), particularized for the fixed point $\left\{{a}_{eq},{\beta }_{eq},{\sigma }_{eq}\right\}$, takes the form

$$c+d{\sigma }_{eq}=\frac{\alpha }{2}{a}_{eq}^{2},$$

(55)

where (50) has been used. We now define the following functions:

$$\begin{array}{c}{T}_{m}\left(\sigma \right)\equiv c+d\sigma \\ {T}_{v}\left(a\right)\equiv \frac{\alpha }{2}{a}^{2}.\end{array}$$

(56)

Clearly, according to the comments below Eq. (54), ${T}_{m}$ represents the driving torque produced by the motor, while ${T}_{v}$ corresponds to the resisting torque due to vibration. Then, (55) can be rewritten as

$${T}_{m}\left({\sigma }_{eq}\right)={T}_{v}\left({a}_{eq}\right),$$

(57)

which is the torque equilibrium condition, particularized for the fixed point.

In order to solve (57) in a graphical way, it would be desirable to write both torques explicitly in terms of ${\sigma }_{eq}$. However, this would in turn need explicitly writing ${a}_{eq}$ in terms of ${\sigma }_{eq}$, which produces long and complicated expressions. Thus, an implicit procedure for the graphical representation is proposed. Combining (50) and (51) results in

$${\sigma }_{eq}={\sigma }_{v}\left(z,{a}_{eq}\right),$$

(58)

where function ${\sigma }_{v}\left(z,a\right)$ is defined as

$${\sigma }_{v}\left(z,a\right)\equiv \frac{3}{8}\rho {a}^{2}+z\xi \frac{\sqrt{1-{a}^{2}}}{a}.$$

(59)

The proposed representation can be constructed as follows: first, graph ${T}_{m}$ versus $\sigma$ according to (56). Then, graph on the same plot the parametric curve given by $\left\{{\sigma }_{v}\left(z,a\right),{T}_{v}\left(a\right)\right\}$, for $z=\pm 1$ and $a\in \left(\left.\mathrm{0,1}\right]\right.$. The fact that ${a}$ is strictly positive comes from the definition of $\mathrm{a}$ as the radius of a polar coordinate transformation –see (21)–(20). On the other hand ${a}_{eq}$ cannot be greater than 1, according to the first of Eq. (50).

The above procedure gives rise to a plot like that shown in Fig. 9. Considering Eq. (57), the fixed points can be found as the intersections of the two torque curves. In the particular case displayed in Fig. 9, there are three equilibrium points, marked with circles. Note that the curve associated to the vibration torque is composed of two branches, which collide at the maximum of the curve. They correspond to the two possible values of parameter $z$, as specified in Fig. 9.

Fig. 9

Fixed points of system (46)

We note that the ‘Sommerfed effect’, which was described in the introduction, can be readily explained by using Fig. 9. For such an explanation, the interested reader can refer to [9, 10, 12, 17].

Stability Analysis

Once the fixed points of the reduced system have been obtained, it is convenient to investigate their stability. For a 2D system, this reduces to calculating the trace and determinant of the jacobian matrix, evaluated at the equilibrium point of interest:

$${{\varvec{J}}}_{eq}=\epsilon \left[\begin{array}{cc}-\xi & z\xi {R}_{eq}\\ \left(-\frac{\alpha }{2d}+\frac{3\rho }{4}\right){a}_{eq}-\frac{z\xi {R}_{eq}}{{a}_{eq}^{2}}& -\frac{z\alpha {a}_{eq}{R}_{eq}}{2d}-\xi \end{array}\right],$$

(60)

where ${R}_{eq}$ stands for $\sqrt{1-{a}_{eq}^{2}}$.

The conditions for a fixed point to be asymptotically stable are

$${\mathbf{C}}{\mathbf{1}}.\quad tr\left( {J_{eq} } \right) < 0$$

(61)

$${\mathbf{C}}{\mathbf{2}}.\quad det\left( {J_{eq} } \right) > 0.$$

(62)

After some algebra, these conditions can be expressed as

$${\mathbf{C}}{\mathbf{1}}.\quad \frac{{z\alpha a_{eq} R_{eq} }}{4d} + \xi > 0$$

(63)

$${\mathbf{C}}{\mathbf{2}}.\quad \left\{ {\begin{array}{*{20}c} {\frac{1}{\eta } - \frac{1}{d} < 0,\;\;if\;z = 1} \\ {\frac{1}{\eta } - \frac{1}{d} > 0,\;\;if\;z = - 1} \\ \end{array} } \right\},$$

(64)

where $\eta$ denotes the slope of the ${T}_{v}$ curve at the considered equilibrium point (see Figs. 10 and 11), and has the expression

Fig. 10

Stability regions for $z=-1$. S and U label the stable and unstable regions, respectively. a $\eta >0$, b $\eta <0$

Fig. 11

Stability regions for $z=1$. S and U label the stable and unstable regions, respectively. a $\eta >0$, (b.1) $\eta <{d}_{H}<0$, (b.2) ${d}_{H}<\eta <0$

$$\frac{1}{\eta }=-\frac{z\xi }{\alpha {a}_{eq}^{3}{R}_{eq}}+\frac{3\rho }{4\alpha },$$

(65)

as can be deduced from (56), (59).

Conditions (63) and (64)are now applied to evaluate stability regions in different scenarios. The procedure is as follows. Consider parameters $\alpha , \xi , \rho$ fixed, so that the ${T}_{v}$ curve –see Fig. 9– is fixed too. Consider a pair of values $\left(c,d\right)$ that gives a particular curve ${T}_{m}\left(\sigma \right)$. The intersections between the two curves represent the equilibrium points of the system. Select one of them –if there are more than one– and let parameters $\left(c,d\right)$ vary in such a way that the selected equilibrium point remains an equilibrium point. In other words, let parameters $\left(c,d\right)$ vary so as to make the curve ${T}_{m}\left(\sigma \right)$ rotate around the selected equilibrium point, satisfying restriction $d<0$. Finally, use conditions (63) and (64) to analyze how the stability of the fixed point is affected by the slope ${d}$ of the motor characteristic.

Figure 10 displays the outcome of applying the above procedure for a fixed point located at the left branch of the vibration torque curve $\left(z=-1\right)$. Two scenarios are considered, depending on the sign of slope $\eta$, evaluated at the fixed point under consideration. It is observed that a change of stability occurs when both torque curves become tangent $\left(d=\eta \right)$. This can be shown to correspond to a transcritical bifurcation. Note that, in Fig. 10, the motor curve corresponding to $d=\eta$ has been directly labeled as $d=\eta$, instead of ${T}_{m}\left(d=\eta \right)$. This shortened notation will be widely used in the figures of the document.

Figure 11 shows analogous results for a fixed point located at the right branch of the vibration torque curve $\left(z=1\right)$. The system behavior is richer in this case, since stability may change in two different ways, depending on the comparison $\eta \lessgtr {d}_{H}$ where ${{d}}_{{H}}$ is defined below.

We define critical slope ${d}_{H}$ as the value of ${d}$ that makes $tr\left({J}_{eq}\right)=0$. Recall that the stability condition $tr\left({J}_{eq}\right)<0$ was written as (63). Therefore, ${d}_{H}$ takes the form

$${d}_{H}\left(\alpha ,\xi ,{a}_{eq}\right)=-\frac{\alpha {a}_{eq}{R}_{eq}}{4\xi }.$$

(66)

Below, the different possibilities for $z=1$ are considered.

• If $\eta >0$ (Fig. 11a), condition C2 is never fulfilled, so the fixed point is unstable regardless the value of slope $d$.

• If $\eta <{d}_{H}<0$ (Fig. 11b.1), the critical condition –i.e. the one that produces the stability change– is C2. In this case, a transcritical bifurcation can be shown to occur when both torque curves are tangent $\left(d=\eta \right)$. Note that this result is analogous to that obtained for the left branch (Fig. 10).

• If ${{d}}_{{H}}<\eta <0$ (Fig. 11b.2), the critical condition is C1. In this case, the stability change occurs at $d={d}_{H}$ through a Hopf bifurcation, after which parameter ${d}_{H}$ was named.

To better understand the nature of the different bifurcations, notice the following correspondence between conditions C1 and C2, and the eigenvalues of ${{\varvec{J}}}_{eq}$, according to (61), (62):

• C1 is the critical condition $\to \left\{ {\begin{array}{*{20}c} {{\text{tr}}\left( {J_{eq} } \right) = 0} \\ {{\text{det}}\left( {J_{eq} } \right) > 0} \\ \end{array} } \right\}$ both eigenvalues of ${{\varvec{J}}}_{eq}$, being complex conjugates, cross the imaginary axis.

• C2 is the critical condition $\to \left\{ {\begin{array}{*{20}c} {{\text{tr}}\left( {J_{eq} } \right) < 0} \\ {{\text{det}}\left( {J_{eq} } \right) = 0} \\ \end{array} } \right\}$ a single, real eigenvalue of ${{\varvec{J}}}_{eq}$ crosses the imaginary axis.

It is worth stressing that most of the literature on nonideal excitations maintains that stability changes when the torque curves become tangent [9, 10, 12, 17]. This is consistent with our results, with the important exception of case $z=1, {d}_{H}<\eta <0$ (Fig. 11b.2). Thus, one of the major findings presented in this chapter consists in having found a case where the usual rule of thumb for stability is not valid. In this scenario, the stable region is in fact smaller than predicted by usual theories (see Fig. 11b.2). Not taking this into account may be dangerous in real applications, since it could lead to unexpected instabilities.

Finally, the conditions for the existence of a Hopf bifurcation in the linear case $\left(\rho =0\right)$ are investigated in more detail. As stated above, a Hopf bifurcation exists if

$$z = 1,\quad d_{H} < \eta < 0.$$

(67)

By substituting expression (65) and (66) into (67), for $\rho =0$, we have

$$z = 1,\quad - \frac{{\alpha a_{eq} R_{eq} }}{4\xi } < - \frac{{\alpha a_{eq}^{3} R_{eq} }}{\xi } < 0.$$

(68)

Simplifying (68) yields

$$z = 1,\quad a_{eq} < 0.5.$$

(69)

Therefore, if the system under study has no structural nonlinearity $\left(\rho =0\right)$, it is particularly easy to predict the existence of a Hopf bifurcation, by simply checking condition (69).

2.5 Classification of the Hopf Bifurcations

Clearly, it would be of great interest to characterize the Hopf bifurcation encountered in last section as subcritical or supercritical. In the former case, an unstable limit cycle coexists with the stable fixed point, while in the latter case there is a stable limit cycle coexisting with the unstable fixed point, as represented in Fig. 12.

Fig. 12

Classification of Hopf bifurcations. a Supercritical b Subcritical. Thick (thin) lines represent stable (unstable) solutions

Characterizing the bifurcations requires several transformations of system (46) that are detailed below.

Transformation to Cartesian Coordinates

We assume the system parameters are such that there exists a fixed point on the right branch of curve ${T}_{v}$ $\left(z=1\right)$, satisfying condition (67) and, thereby, undergoing a Hopf bifurcation. By defining change of variables

$$\left\{ {\begin{array}{*{20}c} {\tilde{x} = a\,\cos\,\beta } \\ {\tilde{y} = a\,\sin\,\beta } \\ \end{array} } \right\},$$

(70)

system (46), particularized for the bifurcation point $\left(d={d}_{H}\right)$, can be rewritten as

$$\left\{\begin{array}{c}\dot{\tilde{x }}=-\epsilon \left[\xi \tilde{x }+\frac{c}{{d}_{H}}\tilde{y }+\frac{\alpha }{2{d}_{H}}{\tilde{y }}^{2}+\frac{3}{8}\rho \tilde{y }\left({\tilde{x }}^{2}+{\tilde{y }}^{2}\right)\right]\\ \dot{\tilde{y }}=\epsilon \left[-\xi -\xi \tilde{y }+\frac{c}{{d}_{H}}\tilde{x }+\frac{\alpha }{2{d}_{H}}\tilde{x }\tilde{y }+\frac{3}{8}\rho \tilde{x }\left({\tilde{x }}^{2}+{\tilde{y }}^{2}\right)\right]\end{array}\right\}.$$

(71)

Displacement of the origin

In order to characterize the bifurcation, it is convenient to locate the origin of the coordinate system at the fixed point under investigation. Then, we define change of variables

$$\left\{ {\begin{array}{*{20}c} {x = \tilde{x} - a_{eq} \,\cos\,\beta_{eq} } \\ {y = \tilde{y} - a_{eq} \,\sin\,\beta_{eq} } \\ \end{array} } \right\}.$$

(72)

Using the new coordinates, system (71) takes the form

$$\left\{\begin{array}{c}\dot{x}=\epsilon \left[-\left[\xi +\frac{3}{4}\rho {a}^{3}R\right]x-\left[\frac{3}{4}\rho {a}^{4}+\xi \left(\frac{2a}{R}-\frac{R}{a}\right)\right]y+\frac{3}{8}\rho {a}^{2}{x}^{2}+\left[\frac{2\xi }{aR}+\frac{9}{8}\rho {a}^{2}\right]{y}^{2}+\frac{3}{4}\rho aRxy-\frac{3}{8}\rho y\left[{x}^{2}+{y}^{2}\right]\right]\\ \dot{y}=\epsilon \left[\left[\frac{3}{4}\rho {a}^{2}{R}^{2}-\xi \frac{R}{a}\right]x+\left[\xi +\frac{3}{4}\rho {a}^{3}R\right]y-\frac{9}{8}\rho aR{x}^{2}-\frac{3}{4}\rho aR{y}^{2}-\left[\frac{2\xi }{aR}+\frac{3}{4}\rho {a}^{2}\right]xy+\frac{3}{8}\rho x\left[{x}^{2}+{y}^{2}\right]\right]\end{array}\right\}.$$

(73)

where ${a}_{eq}$ and ${R}_{eq}$ are shortly written as $a$ and $R$, respectively, in order to make the expression more manageable. This abbreviated notation will also be used in the Appendix. Note that system (73) is of the form

$$\left[\begin{array}{c}\dot{x}\\ \dot{y}\end{array}\right]=\epsilon \left({\varvec{A}}\left[\begin{array}{c}x\\ y\end{array}\right]+{\varvec{h}}\left(x,y\right)\right)$$

(74)

where matrix ${\varvec{A}}$ is given by

$${\varvec{A}}=\left[\begin{array}{cc}-\left(\xi +\frac{3}{4}\rho {{a}}_{{eq}}^{3}{{R}}_{{eq}}\right)& -\left[\frac{3}{4}\rho {{a}}_{{eq}}^{4}+\xi \left(\frac{2{{a}}_{{eq}}}{{{R}}_{{eq}}}-\frac{{{R}}_{{eq}}}{{{a}}_{{eq}}}\right)\right]\\ \frac{3}{4}\rho {{a}}_{{eq}}^{2}{{R}}_{{eq}}^{2}-\upxi \frac{{{R}}_{{eq}}}{{{a}}_{{eq}}}&\xi +\frac{3}{4}\rho {{a}}_{{eq}}^{3}{\mathrm{R}}_{{eq}}\end{array}\right]$$

(75)

and vector ${\varvec{h}}\left(x,y\right)$ contains the nonlinear terms of the system.

Transformation to the real eigenbasis of matrix ${\varvec{A}}$

A new change of variables, using the real eigenbasis of matrix ${\varvec{A}}$, is defined:

$$\left[\begin{array}{c}x\\ y\end{array}\right]={\varvec{T}}\left[\begin{array}{c}{z}_{1}\\ {z}_{2}\end{array}\right],$$

(76)

where the columns of matrix ${\varvec{T}}$ are the real and imaginary parts of the complex conjugate eigenvectors of ${\varvec{A}}$, denoted by ${{\varvec{v}}}_{\mathrm{1,2}}$:

$${{\varvec{v}}}_{{1,2}}=\left[\begin{array}{c}{{c}}_{1}\\ {{c}}_{2}\end{array}\right]\pm \mathrm{i}\left[\begin{array}{c}{\omega }_{0}\\ 0\end{array}\right]\to {\varvec{T}}=\left[\begin{array}{cc}{{c}}_{1}& {\omega }_{0}\\ {{c}}_{2}& 0\end{array}\right],$$

(77)

with

$$\begin{array}{c}{c}_{1}=\xi +\frac{3}{4}\rho {a}_{eq}^{3}{R}_{eq}\\ {c}_{2}=\xi \frac{{R}_{eq}}{{a}_{eq}}-\frac{3}{4}\rho {a}_{eq}^{2}{R}_{eq}^{2}\\ {\omega }_{0}=\sqrt{\left(\frac{1-4{a}_{eq}^{2}}{{a}_{eq}^{2}}\right){\xi }^{2}-\frac{3}{4}\rho \xi {a}_{eq}{R}_{eq}}.\end{array}$$

(78)

System (73), written in terms of the new variables, takes the form

$$\left[\begin{array}{c}\dot{{z}_{1}}\\ \dot{{z}_{2}}\end{array}\right]=\epsilon \left(\left[\begin{array}{cc}0& -{\omega }_{0}\\ {\omega }_{0}& 0\end{array}\right]\left[\begin{array}{c}{z}_{1}\\ {z}_{2}\end{array}\right]+\left[\begin{array}{c}f\left({z}_{1},{z}_{2}\right)\\ g\left({z}_{1},{z}_{2}\right)\end{array}\right]\right),$$

(79)

where functions $f$ and $g$, containing the nonlinear terms of the system, can be written as Taylor series:

$$\begin{array}{c}f\left({z}_{1},{z}_{2}\right)=\sum\limits_{i+j=2}^{3}\frac{1}{i!j!}{f}_{ij}{z}_{1}^{i}{z}_{2}^{j}\\ g\left({z}_{1},{z}_{2}\right)=\sum\limits_{i+j=2}^{3}\frac{1}{i!j!}{g}_{ij}{z}_{1}^{i}{z}_{2}^{j}\end{array}$$

(80)

Coefficients ${f}_{ij}$ and ${g}_{ij}$ are specified in the Appendix.

Transformation to normal form

The final step to characterize the bifurcation includes transformation in complex form, near-identity transformation and transformation in polar coordinates [25]. This is a standard procedure whose details can be found in [26, 27]. After these last transformations, system (79) can be written in its Normal Form

$$\dot{r}=\epsilon \delta {r}^{3},$$

(81)

which governs the radial dynamics at the bifurcation. As shown in [27], coefficient $\delta$ can be computed as

$$16\delta =\left\{\begin{array}{c}{f}_{30}+{f}_{12}+{g}_{21}+{g}_{03}\\ \begin{array}{c}+\frac{1}{{\omega }_{0}}\left[{f}_{11}\left({f}_{20}+{f}_{02}\right)-{g}_{11}\left({g}_{20}+{g}_{02}\right)\right]\\ +\frac{1}{{\omega }_{0}}\left[{f}_{02}{g}_{02}-{f}_{20}{g}_{20}\right]\end{array}\end{array}\right\}.$$

(82)

In summary, we can say that, after a large number of variable transformations, system (46) can be written as (81), from which we deduce that the bifurcation is supercritical (subcritical) if $\delta <0 \left(\delta >0\right)$.

Despite the fact that coefficients ${{f}}_{{ij}}$ and ${{g}}_{{ij}}$ are of rather complicated form, we find –with the aid of the symbolic computation toolbox in Matlab– that the condition for supercriticality or subcriticality can be expressed in a surprisingly simple manner:

$$\begin{array}{c}\mathrm{Supercritical}\Rightarrow \delta <0\Rightarrow \rho <-\frac{8\xi }{3{a}_{eq}{R}_{eq}}\\ \mathrm{Subcritical}\Rightarrow \delta >0\Rightarrow \rho >-\frac{8\xi }{3{a}_{eq}{R}_{eq}}\end{array}$$

(83)

From (83), it is clear that a nonlinearity of the softening type $\left(\rho <0\right)$ is needed to have a supercritical bifurcation.

It is also worth noting that conditions (83) admit a very clear graphical interpretation. Consider a curve ${T}_{m}$ which intersects ${T}_{v}$ at the equilibrium point under consideration and also at the peak of curve ${T}_{v}$. Let ${d}_{P}$ denote the slope of this particular motor characteristic, as depicted in Fig. 13.

Fig. 13

Definition of slope ${{d}}_{{P}}$

In order to obtain ${d}_{P}$, the coordinates of the two points defining the straight line are defined below. First, the highest peak of curve ${T}_{v}$ can be shown to correspond to $a=1$. Substituting this condition into (56) and (59) yields

$$\sigma = \frac{3}{8}\rho ,\quad T = \frac{\alpha }{2}$$

(84)

On the other hand, the $\left(\sigma ,T\right)$ coordinates of the equilibrium point under study are directly given in (56) and (59):

$$\sigma = \frac{3}{8}\rho a_{eq}^{2} + \xi \frac{{R_{eq} }}{{a_{eq} }},\quad T = \frac{\alpha }{2}a_{eq}^{2}$$

(85)

Then, from (84) and (85), the expression of ${d}_{P}$ can be readily obtained:

$$\frac{1}{{d}_{P}}=\frac{3\rho }{4\alpha }-\frac{2\xi }{\alpha {a}_{eq}{R}_{eq}},$$

(86)

By comparing (86) and (66) conditions (83) can be expressed as

$$\begin{array}{c}\mathrm{Supercritical}\Rightarrow {d}_{H}<{d}_{P}\\ \mathrm{Subcritical}\Rightarrow {d}_{H}>{d}_{P}.\end{array}$$

(87)

This last manner of characterizing the bifurcation is certainly appealing from a graphical point of view, since the essential information about the bifurcation can be directly observed from the torque–speed curves, as shown in Fig. 14 for two particular examples.

Fig. 14

Examples of a subcritical and b supercritical bifurcations. a $\xi =1, \alpha =1, \rho =-2, {a}_{eq}=0.3$ b $\xi =1, \alpha =1, \rho =-15, {a}_{eq}=0.4$

2.6 Conditions Under Which All System Trajectories are Attracted Towards a Limit Cycle

In Sect. 2.5, a simple condition has been obtained to ascertain whether the Hopf bifurcation under study is subcritical or supercritical, which in turn allows predicting the kind of limit cycle generated by the bifurcation (see Fig. 12). Although this distinction is relevant, it is based on a local analysis and, consequently, it only gives local information about the system behaviour. This is so in two senses: the analysis of Sect. 2.5 provides insight into the system dynamics.

• for values of $d$ close enough to ${d}_{H}$ (results are local in the parameter space) and

• for trajectories close enough to the investigated fixed point (results are local in the phase plane).

In view of the aforementioned limitations, this section addresses a new global result that complements those of Sect. 2.5. First, let us briefly recall the Poincaré-Bendixson theorem, which is an essential result from the global theory of nonlinear systems [28]. The theorem can be stated, in short terms, as follows.

Consider a 2D dynamical system and a closed, bounded region $R$ of the phase plane that does not contains any equilibrium points. Then, every trajectory that is confined in $R$ –it starts in $R$ and remains in $R$ for all future time– is a closed orbit or spirals towards a closed orbit as $t\to \infty$. For a more rigorous and detailed exposition of the theorem, see [28].

Let us show that, under certain circumstances, the P-B theorem can be used to prove that all trajectories of the system under study are attracted towards a limit cycle.

First, it can be easily deduced from (46) that

$$a>1\Rightarrow \dot{a}<0.$$

(88)

Let ${a}$ and $\beta$ represent polar coordinates on the phase plane, according to (70), and let $D$ denote a circle centred at the origin of the phase plane with a radius slightly greater than $1$, say $1.01$. From (88), it can be said that every trajectory starting outside region $D$ will enter $D$ and remain inside for all subsequent time. Obviously, trajectories starting inside $D$ will also remain inside forever. This kind of behavior would present $D$ as a suitable candidate for the role of region $R$ in the P-B theorem, if it were not for the presence of fixed points inside $D$.

Consider now the following particular situation:

$$\left\{ {\begin{array}{*{20}c} {{\text{The}}\;{\text{system}}\;{\text{has}}\;{\text{only one }}\;{\text{fixed}}\;{\text{point}}} \\ {z = 1,\;\;d_{H} < d < \eta < 0} \\ \end{array} } \right\},$$

(89)

whose torque curves are depicted in Fig. 15. We suppose that the only fixed point of the system is on the right branch of curve ${T}_{v}$ and undergoes a Hopf bifurcation. It is also assumed that the actual slope of the motor characteristic is $d>{d}_{H}$ and, therefore, the equilibrium is unstable.

Fig. 15

Schematic view of the torque curves corresponding to conditions (89)

First, let us prove that the fixed point is a repeller. Since the equilibrium is already known to be unstable, we only need to prove that it is not a saddle. Let ${{\varvec{J}}}_{eq}$ be the jacobian matrix of system (46), evaluated at the equilibrium point. Taking into account that a saddle point has two real eigenvalues ${\lambda }_{1}, {\lambda }_{2}$ with different signs, we can state

$${\text{If}}\;det\left( {{\varvec{J}}_{eq} } \right) = \lambda_{1} \lambda_{2} > 0,\quad {\text{then}}\;{\text{the}}\;{\text{equilibrium}}\;{\text{is}}\;{\text{not}}\;{\text{a}}\;{\text{saddle}}.$$

(90)

With some simple algebra, it can be shown that, for $z=1$, condition $det\left({{\varvec{J}}}_{eq}\right)>0$ can be written as $d<\eta$. Then, it is clear that, for a fixed point satisfying (89), we have $det\left({{\varvec{J}}}_{eq}\right)>0$. Thus, the equilibrium is a repeller.

A new region $Q$ is now defined as $D$ minus a circle of infinitesimal radius around the equilibrium point. From the above considerations –all trajectories enter $D$ and the fixed point is a repeller–, it is clear that the flow on the boundary of $Q$ is directed inwards, as depicted in Fig. 16.

Fig. 16

Flow on the boundary of region $Q$ (dashed), under conditions (89)

In summary, a closed, bounded region $Q$ of the phase plane has been obtained, which contains no fixed points and such that all trajectories of the system enter $Q$ and remain inside forever. Then, all conditions of the P-B theorem are fulfilled, and it can be assured that any trajectory of the system is attracted towards a closed orbit as $t\to \infty$, if it is not a closed orbit itself.

Finally, it should be noted that, although the P-B theorem does not guarantee that all trajectories tend to the same closed orbit, all the numerical experiments conducted show the presence of only one stable limit cycle, namely that created by the Hopf bifurcation. This suggests that, for a system verifying (89), all the system dynamics is attracted towards a unique limit cycle.

2.7 Discussion

Time validity

A crucial point in any perturbation analysis is the time scale for which the obtained approximate solution is valid. It has been shown in Sect. 2.3 that the solution given by the reduced system is valid, at least, for a time scale $\tau =O\left(1/\epsilon \right)$ –see Fig. 8–.

However, the situation is even better than that. From the Averaging Theory, it is known [18], that the asymptotic approximations attained through averaging are valid for all time, whenever they are attracted by a stable fixed point or a stable limit cycle. In the latter case, the uniform validity holds for all variables except the angular one, i.e. the variable measuring the flow on the limit cycle. As will be seen later, all the numerical solutions obtained in this chapter fulfil the above condition of attraction.

Comparison with other authors’ results

In this subsection, the presented approach and results are compared to some proposed by other authors.

First of all, as far as the authors know, there has been no attempt in the literature to use the SPT for the analysis of nonideally excited systems. Thus, the analytical procedure addressed in this Chapter appears to be a novel approach to the problem.

On the other hand, the possibility of a Hopf bifurcation on the right branch of the vibration torque curve (Fig. 11b.2) has been addressed. An important implication of this result is that the stability of the stationary solutions near resonance does not only depends on the comparison between the slopes of the two torque curves $\left(\eta \lessgtr d\right)$, as commonly stated in the literature [9, 10, 12, 17]. Let us try to explain this divergence in the results.

Kononenko’s book [10] is one of the most relevant references in the subject. He considered several linear and nonlinear systems excited by nonideal motors. By using the averaging method, he was able to analytically investigate the stationary motions of the motor and their stability. His approach was as follows. Considering the rotor speed to be in the vicinity of resonance, he expanded it as

$$\dot{\phi } = 1 + \varDelta ,\quad \varDelta = \epsilon \sigma .$$

(91)

Thus, he found equations of motion of the form

$$\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\dot{a} = O\left( \epsilon \right)} \\ {\dot{\beta } = - \epsilon \sigma + O\left( \epsilon \right)} \\ \end{array} } \\ {\begin{array}{*{20}c} {\dot{\varDelta } = O\left( \epsilon \right)} \\ {\dot{\phi } = 1 + \varDelta } \\ \end{array} } \\ {\varDelta = \epsilon \sigma } \\ \end{array} } \right\},$$

(92)

which is a system analogous to (37). Then, he averaged (92) over the fast angle $\phi$, obtaining an averaged system of the form

$$\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\dot{\overline{a}} = O\left( \epsilon \right)} \\ {\dot{\overline{\beta }} = - \epsilon \overline{\sigma } + O\left( \epsilon \right)} \\ \end{array} } \\ {\begin{array}{*{20}c} {\dot{\overline{\varDelta }} = O\left( \epsilon \right)} \\ {\overline{\varDelta } = \epsilon \overline{\sigma }} \\ \end{array} } \\ \end{array} } \right\}.$$

(93)

This averaged system is completely analogous to system (39), obtained in the present chapter. The only difference lies in the fact that Kononenko used the evolution equation for $\overline{\varDelta }$, instead of that for $\overline{\sigma }$. This has an important consequence. From (39), it is clear that $\overline{\sigma }$ is a fast variable, while $\overline{a}$ and $\overline{\beta }$ are slow. This property was exploited in Sect. 2.3 to obtain a reduced 2D system (46), by using the SPT. The analysis of the fixed points of this reduced system and their stability has revealed the possibility of Hopf bifurcations, and conditions for their appearance have been derived in Sect. 2.4. However, the form of the averaged Eq. (93), used by Kononenko, doesn’t evidence so clearly the fact that $\overline{\sigma }$ is a fast variable. Then, instead of taking advantage of this separation in the time scales through the SPT, he directly investigated system (93), which did not allow him to obtain analytical conditions for the existence of Hopf bifurcations.

While several authors followed Kononenko’s approach [9, 17], Blekhman proposed a completely different one, based on the ‘method of direct separation of motions’ [12]. With this procedure, he came to the conclusion that the system dynamics is governed by equation

$$I\ddot{\phi }={L}_{m}\left(\dot{\phi }\right)+V\left(\dot{\phi }\right)$$

(94)

where dimensional variables have been used. In (94), $V\left(\dot{\phi }\right)$ represents the torque on the rotor due to vibration. Based on this equation, Blekhman deduced the same result as Kononenko regarding the stability of stationary solutions, namely, that stability changes when the driving torque curve and the vibration torque curve are tangent.

It is worth noting that Blekhman’s approach is not applicable under the assumptions of the present chapter. The reason is that, in general, the torque on the rotor due to vibration depends on the linear motion of the system, as observed in the second of Eq. (1). This feature is maintained in the averaged system (39) obtained in this Chapter, where the vibration torque appears as a function of $a, \beta$.

On the contrary, in [12], the vibration torque is written as a function of the rotor speed –see (94), which implies neglecting the dynamics associated to variables $a$ and $\beta$. This would only be valid if the rotor speed was a much slower variable than those associated to the linear vibration $\left(a, \beta \right)$. To better understand this point, suppose that, in system (1), the rotor inertia was $O\left(1/\epsilon \right)$, with the rest of the parameters being $O\left(1\right)$. Then, writing $I=\tilde{I }/\epsilon$, system (1) would take the form

$$\left\{ {\begin{array}{*{20}c} {m\ddot{x} + b\dot{x} + kx + \lambda x^{3} = m_{1} r\dot{\phi }^{2} \,\cos\,\phi + O\left( \epsilon \right)} \\ {\tilde{I}\ddot{\phi } = \epsilon \left[ {A + D\dot{\phi } + m_{1} r\ddot{x}\,\sin\,\phi } \right]} \\ \end{array} } \right\}.$$

(95)

With this particular scaling of the parameters, Blekhman’s approach would be valid because the dynamics of linear motion would be much faster than that of the rotor speed. Then, as predicted by the SPT, the variables associated to the linear motion would be slaved to the rotor speed. This would in turn allow writing the vibration torque as a function of the rotor speed, as in (94).

As pointed out above, the assumptions of the present chapter (7)–(9)are not compatible with the results in [12], because the required difference in the time scales of the different variables is not satisfied. This can be observed in the averaged system (39), where we find $\left\{\dot{a}=O\left(\epsilon \right), \dot{\beta }=O\left(\epsilon \right), \dot{\sigma }=O\left(1\right)\right\}$.

More recently, Bolla et al. [14] used the Multiple Scales method to solve the same problem studied in this Chapter, under the same assumptions. However, after obtaining system (39), they conducted the stability analysis considering only the first two equations in (39) and taking $\sigma$ as a fixed parameter. As explained at the beginning of Sect. 2.4, this corresponds to studying the ideal case, where the rotor speed is externally imposed. Consequently, they did not find the Hopf bifurcations that have been identified within this work. In fact, Bolla et al. explicitly stated the impossibility of Hopf bifurcations: ‘This fact eliminates the possibility of a pair eigenvalue pure imaginary, so this eliminates Hopf bifurcation kind’. Thus, the present Chapter can be envisaged as an extension of [14], where new bifurcations are encountered due to the nonideal interaction between motor and vibrating system.

3 Numerical Simulations

This section presents two main purposes. First, a numerical investigation of the reduced system (46) is conducted in order to analyse the global bifurcations of limit cycles. While Sect. 2.5 studies how the Hopf bifurcations give rise to the appearance of limit cycles, Sect. 3.1 gives some insight about the dynamical mechanisms whereby the limit cycles are destroyed. A second subsection is presented where, by comparing numerical solutions of the original and reduced systems (10) and (46), respectively the proposed approach is validated. The objective is to demonstrate that the conclusions attained for the reduced system are also valid for the original system.

3.1 Global Bifurcations of the Limit Cycles

In Sect. 3.1, the creation of limit cycle oscillations (LCOs) through Hopf bifurcations has been investigated. Now, the opposite question is examined: once a limit cycle is born, does it exist for every $d>{d}_{H}$ in the supercritical case –for every $d<{d}_{H}$ in the subcritical case–, or is it destroyed at any point? In the latter case, it would also be interesting to know the dynamical mechanism which makes the limit cycle disappear.

The aim of this Section is to analyse the global dynamics of the system, tracking the evolution of the limit cycles in order to find out how they are destroyed –if they are destroyed at all–. Since this task is in general too difficult to be carried out analytically, we resort to numerical computation.

The Subcritical Case

Consider the following set of dimensionless parameters:

$$\xi = 1,\quad \alpha = 1,\quad \rho = 0,\quad a_{eq} = 0.3,\quad z = 1,$$

(96)

which might be associated to dimensional parameters

$$\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {m = 1\,kg } \\ {k = 1\,N/m} \\ {b = 0.002\,Ns/m} \\ \end{array} } \\ {\begin{array}{*{20}c} {m_{1} = 0.001\,kg} \\ {\lambda = 0\,N/m^{3} } \\ \end{array} } \\ {\begin{array}{*{20}c} {r = 0.1\,m} \\ {I = 5 \cdot 10^{ - 3} m^{2} kg} \\ \end{array} } \\ \end{array} } \right\},$$

(97)

with $\epsilon =0.001$. Obviously, (97) s only one of the many possible sets of dimensional parameters giving rise to (96).

By using Eqs. (66) and (86), slopes ${d}_{H}$ and ${d}_{P}$ can be obtained, as depicted in Fig. 17.

$$d_{H} = - 0.0715,\quad d_{P} = - 0.1431$$

(98)

Fig. 17

Torque curves corresponding to parameters (96)

According to criterion (87), the Hopf bifurcation is found to be subcritical. Thus, as represented in Fig. 12, an unstable limit cycle is known to exist for $d<{d}_{H}$, within a certain neighborhood of ${d}_{H}$. We are interested in tracking the evolution of this limit cycle as slope $\mathrm{d}$ decreases. By numerically integrating system (46), using embedded Runge-Kutta formulae of orders 4 and 5, for different values of $d$, the limit cycle is found to disappear at $d={d}_{C}$ –see Fig. 17, with

$${d}_{C}=-0.0795$$

(99)

The dynamical mechanism whereby the limit cycle is destroyed, which turns out to be a homoclinic bifurcation [26], is shown in Figs. 18 and 19 Let us follow the evolution of the phase portrait. From Fig. 18a, b, the Hopf bifurcation takes place: the focus becomes stable, while an unstable limit cycle is born around it. In Fig. 19a, the cycle has swelled considerably and passes close to saddle point $S$. The homoclinic bifurcation occurs when the cycle touches the saddle point $\left(d={d}_{C}\right)$, becoming a homoclinic orbit. In Fig. 19b, we have $d<{d}_{C}$ and the loop has been destroyed.

Fig. 18

Phase portraits corresponding to parameters (96). The fixed points are marked with dots. The dashed loop represents the unstable limit cycle a $d=-0.070$, b $d=-0.073$

Fig. 19

Phase portraits corresponding to parameters (96). The fixed points are marked with dots. The dashed loop represents the unstable limit cycle a $d=-0.078$, b $d=-0.081$

It is worth noting that, when the unstable limit cycle exists –namely, for ${d}_{C}<d<{d}_{H}$–, it acts as a frontier between the domains of attraction of the two stable equilibrium points of the system –see Figs. 18b, 19a.

Many other cases exhibiting a subcritical bifurcation, which are not shown here, have also been numerically solved. In all of them, the unstable limit cycle has been found to disappear through a homoclinic bifurcation.

The Supercritical Case

Consider the following set of dimensionless parameters:

$$\xi = 1,\quad \alpha = 2,\quad \rho = - 10,\quad a_{eq} = 0.5,\quad z = 1,$$

(100)

which might be associated to dimensional parameters

$$\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {m = 1\,kg } \\ {k = 1\,N/m} \\ {b = 0.002\,Ns/m} \\ \end{array} } \\ {\begin{array}{*{20}c} {m_{1} = 0.001\,kg} \\ {\lambda = - 4\,N/m^{3} } \\ \end{array} } \\ {\begin{array}{*{20}c} {r = 0.1\,m} \\ {I = 2.5 \cdot 10^{ - 3} m^{2} kg} \\ \end{array} } \\ \end{array} } \right\},$$

(101)

with $\epsilon =0.001$. Equations (66) and (86) yield the values of slopes ${d}_{H}$ and ${d}_{P}$, depicted in Fig. 20.

$$d_{H} = - 0.2165,\quad d_{P} = - 0.1650$$

(102)

Fig. 20

Torque curves corresponding to parameters (100)

Criterion (87) allows characterizing the bifurcation as supercritical. Then, as represented in Fig. 12, it can be assured that a stable limit cycle encircles the unstable equilibrium for $d>{d}_{H}$, within a certain neighborhood of ${d}_{H}$. As a matter of fact, the results of Sect. 2.6 can be used here to investigate the range of slopes $d$ for which the limit cycle exists.

Consider the curve ${T}_{m}$ which intersects ${T}_{v}$ at the fixed point under study and is tangent to curve ${T}_{v}$ at some other point close to the peak. Let ${d}_{T}$ stand for the slope of that particular torque curve, as displayed in Fig. 20. Then, it is straightforward to show that, for ${d}_{H}<d<{d}_{T}$, conditions (89) are fulfilled and, consequently, it can be assured that all system trajectories tend to a periodic orbit. In the case under analysis, we have

$${d}_{T}=-0.1697$$

(103)

Note that the Poincaré-Bendixson Theorem gives sufficient, but not necessary, conditions for the existence of a stable periodic orbit. Thus, it cannot be deduced from the Theorem whether the limit cycle survives or not when $d>{d}_{T}$. To the end of answering this question, we resort again to a numerical resolution of system (46), for increasing values of $d$. The results are displayed in Figs. 21 and 22.

Fig. 21

Phase portraits corresponding to parameters (100). The fixed points are marked with dots. The solid loop represents the stable limit cycle. a ${d}=-0.22$, b ${d}=-0.19$

Fig. 22

Phase portraits corresponding to parameters (100), for $d=-0.169$. The fixed points are marked with dots

Let us track the evolution of the phase portrait. In Fig. 21a we have $d<{d}_{H}$ and all system trajectories are attracted towards the only fixed point of the system. It may seem from Fig. 21a that trajectories are actually attracted towards a limit cycle surrounding the fixed point. The reason for this false impression is that the attraction of the fixed point is very weak, as it is close to becoming unstable ($d$ is close to ${d}_{H}$). Hence the required time for trajectories to approach the equilibrium is extremely long.

Figure 21b corresponds to ${d}_{H}<d<{d}_{T}$. The Hopf bifurcation has occurred and, therefore, the focus has lost its stability at the same time that a stable limit cycle has appeared around it. Note that, in Fig. 21b, conditions (89) hold. Consequently, all system trajectories are attracted towards a periodic orbit. Actually, Fig. 21b can be observed as a particular example of the general picture shown in Fig. 16.

The numerical results mentioned above are only useful to confirm the analytical developments of previous sections. By contrast, Fig. 22 does provide new information about the global dynamics of the system. It shows that the stable limit cycle is destroyed through a saddle-node homoclinic bifurcation [26], which occurs at $d={d}_{T}$. This means that the cycle disappears exactly when conditions (89) are not fulfilled anymore. The mechanism is as follows. At $d={d}_{T}$ a new fixed point, which immediately splits into a saddle and a node, is created through a saddle-node bifurcation. This new equilibrium appears precisely on the limit cycle, transforming it into a homoclinic orbit. What is found at $d>{d}_{T}$, as observed in Fig. 22, is that the limit cycle has been replaced by a couple of heteroclinic orbits connecting the saddle and the node.

It has been shown that, for the particular set of parameters (100), conditions (89) are necessary and sufficient for the existence of a stable limit cycle. Thus, the periodic orbit never coexists with any other attractor of the system. Nevertheless, it should be stressed that this is not always the case. In fact, cases have also been found where the stable limit cycle is destroyed through a homoclinic bifurcation, just like in the subcritical case. In these situations, the global bifurcation occurs at certain slope ${d}_{C}>{d}_{T}$ and, therefore, the limit cycle coexists with a stable equilibrium for ${d}_{T}<d<{d}_{C}$.

As an example, consider a case with ${d}_{H}$ satisfying ${d}_{T}<{d}_{H}<{d}_{P}$. Clearly, according to (87), the Hopf bifurcation is supercritical. However, it is not possible for the limit cycle to be destroyed through a saddle-node homoclinic bifurcation, because the saddle and the node are created before the limit cycle. In fact, in these cases, the closed orbit has been found to die in the same way as the unstable limit cycle shown in Fig. 19., i.e. through a homoclinic bifurcation due to the presence of a saddle point.

In summary, the simulations carried out suggest that, while unstable limit cycles are destroyed by homoclinic bifurcations, the stable ones can disappear either through homoclinic bifurcations or saddle-node homoclinic bifurcations.

3.2 Numerical Validation of Analytical Results

A Subcritical Case

Consider again the set of parameters given at (96), which gives rise to a subcritical Hopf bifurcation, as depicted in Figs. 18 and 19. Two different scenarios are studied, corresponding to the following slopes of the motor characteristic:

$$d_{1} = - 0.078,\quad d_{2} = - 0.070.$$

(104)

By comparing (104) with Figs. 18 and 19, it can be verified that, for $d={d}_{1}$, the system has a stable focus surrounded by an unstable limit cycle, while, at $d={d}_{2}$, the focus has become unstable through a Hopf bifurcation. As pointed out in Sect.  3.1, the unstable limit cycle for $d={d}_{1}$ is the boundary which separates the basins of attraction of the two attracting fixed points present in the system–see Fig. 19a.

For ${d}={{d}}_{1}$, two sets of initial conditions, I.C. (1) and I.C. (2), are selected, outside and inside the limit cycle, respectively:

$${\text{I}}.{\text{C}}.(1)\left\{ {\begin{array}{*{20}c} {a_{0} = 0.2} \\ {\beta_{0}^{*} = - 2.8} \\ \end{array} } \right\},\quad {\text{I}}.{\text{C}}.(2)\left\{ {\begin{array}{*{20}c} {a_{0} = 0.1} \\ {\beta_{0}^{*} = - 2.8} \\ \end{array} } \right\}.$$

(105)

Then, by using relations (47), corresponding initial conditions for the original system can be computed:

$${\text{I}}.{\text{C}}.(1)\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {u_{0} = 0.2{ }} \\ {{ }\dot{u}_{0} = 0} \\ \end{array} } \\ {\begin{array}{*{20}c} {\phi_{0} = 2.8} \\ {\dot{\phi }_{0} = 1} \\ \end{array} } \\ \end{array} } \right\},\quad {\text{I}}.{\text{C}}.(2)\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {u_{0} = 0.1{ }} \\ {{ }\dot{u}_{0} = 0} \\ \end{array} } \\ {\begin{array}{*{20}c} {\phi_{0} = 2.8} \\ {\dot{\phi }_{0} = 1} \\ \end{array} } \\ \end{array} } \right\}.$$

(106)

Note that this step has not a unique solution, because different sets of original initial conditions can produce the same reduced initial conditions.

The obtained numerical solutions are shown in Fig. 23, for $\epsilon ={10}^{-3}$. A good agreement between solutions of both systems is observed. Clearly, the two considered sets of initial conditions lead the system to different attractors.

Fig. 23

Comparison of numerical solutions of the original (solid line) and reduced (dashed line) systems for parameters (96), $\epsilon ={10}^{-3}$ and $d={d}_{1}=-0.078$. a Displacements b Rotor Speed

It is convenient to make here an observation about the size of parameter $\epsilon$. The procedure used in Sect.  2 to transform the original system into a simpler reduced system is based on perturbation methods. These techniques are useful for dynamical systems containing a small parameter $\epsilon$, and they explain how such systems behave for a sufficiently small $\epsilon$. This means that the smaller $\epsilon$ is, the more accurate perturbation predictions are. Figure 23 shows that, for the case under consideration, a value of $\epsilon ={10}^{-3}$ gives a remarkable accordance between solutions of the original and reduced system. As an illustrative example, the same numerical computation is done, for initial conditions I.C. (2) and $\epsilon ={10}^{-2}$. This larger $\epsilon$ gives rise to a less accurate prediction, as displayed in Fig. 24. The required $\epsilon$ to have an accurate result depends on the case under study. For instance, in the following simulation (Fig. 25), it was necessary to take $\epsilon ={10}^{-4}$ for a good matching between solutions of the exact and approximate systems. However, in the majority of simulations conducted within this work, $\epsilon ={10}^{-3}$ proved to be small enough.

Fig. 24

Comparison of numerical solutions of the original (solid line) and reduced (dashed line) systems for parameters (96), initial conditions I. C. (2), $\epsilon ={10}^{-2}$ and $d={d}_{1}=-0.078$. a Displacements b Rotor Speed

Fig. 25

Comparison of numerical solutions of the original (solid line) and reduced (dashed line) systems for parameters (96), $\epsilon ={10}^{-4}$ and $d={d}_{2}=-0.070$. a Displacements b Rotor speed

Consider now the case ${d}={{d}}_{2}$ where, according to Fig. 18a, the focus is unstable and there is a unique attracting fixed point in the system. Initial conditions

$$\mathrm{I}.\mathrm{C}. \left(3\right)\left\{\begin{array}{c}{a}_{0}=0.25\\ {\beta }_{0}^{*}=-2.65\end{array}\right\}$$

(107)

are selected for the reduced system, from which corresponding initial conditions for the original system can be obtained:

$$\mathrm{I}.\mathrm{C}. \left(3\right)\left\{\begin{array}{c}\begin{array}{c}{u}_{0}=0.25 \\ { \dot{u}}_{0}=0\end{array}\\ \begin{array}{c}{\phi }_{0}=2.65\\ {\dot{\phi }}_{0}=1\end{array}\end{array}\right\}.$$

(108)

The original and reduced systems are numerically solved with $\epsilon ={10}^{-4}$ and initial conditions (108) and (107) respectively. The results are displayed in Fig. 25, where it is clearly observed how the system moves away from the unstable focus, as the oscillation amplitude increases, until it is attracted to the stable node.

A Supercritical Case

In order to observe limit cycle oscillations in the original system, we need to consider a case where a supercritical Hopf bifurcation occurs, giving birth to a stable limit cycle. Thus, consider again the set of parameters given at (100) and a motor characteristic with slope $d=-0.19$, which corresponds to the phase portrait exhibited in Fig. 21b. With these parameters, the original system of Eq. (10) is numerically solved for $\epsilon ={10}^{-3}$ and initial conditions

$$\left\{\begin{array}{c}\begin{array}{c}{u}_{0}=0.1 \\ { \dot{u}}_{0}=0\end{array}\\ \begin{array}{c}{\phi }_{0}=0\\ {\dot{\phi }}_{0}=0\end{array}\end{array}\right\}.$$

(109)

The reduced system (46) is numerically integrated as well for comparison. The associated initial conditions for the reduced system can be computed with the aid of relations (47):

$$\left\{\begin{array}{c}{a}_{0}=0.1\\ {\beta }_{0}^{*}=5.263\end{array}\right\}.$$

(110)

With these sets of initial conditions, the obtained results for both systems are represented in Figs. 26 and 27, exhibiting very good agreement.

Fig. 26

Comparison of displacements obtained by numerical resolution of the original (solid line) and reduced (dashed line) systems for parameters (100), $\epsilon ={10}^{-3}$ and $d=-0.19$

Fig. 27

Comparison of the rotor speed obtained by numerical resolution of the original (solid line) and reduced (dashed line) systems for parameters (100), $\epsilon ={10}^{-3}$ and $d=-0.19$ a Full view b Close-up around resonance

It is worth stressing that, as depicted in Figs. 26 and 27, a new kind of behaviour has been found for the mechanical system under study, which consists in a vibratory motion of the structure with slowly oscillating amplitude, due to the nonideal interaction between exciter and vibrating system. The periodic solutions of the averaged system correspond to quasiperiodic solutions of the original one.

This type of motion had not been addressed before, to the authors’ knowledge, in the literature about nonideal excitations. Note that the LCOs give rise, in this case, to very large variations of the amplitude. Thus, the effect of the studied instability may be of great importance in real applications.

4 Summary and Conclusions

The present chapter contains a detailed analytical and numerical investigation of the dynamics of a 2-DOF mechanical system, consisting in an unbalanced motor connected to a fixed frame through a nonlinear spring and a linear damper. This model intends to constitute a simplified representation of a general unbalanced rotating machine, with the purpose of analyzing the kinds of nonlinear behavior that might be found in real applications.

In addition to the nonlinearity of the spring, a peculiar type of nonlinearity appears if the excitation is nonideal, i.e. if there is a significant bidirectional interaction between the system vibration and the rotation of the motor. The combination of these two types of nonlinearity gives rise to a rich dynamic behavior that can be studied analytically and numerically.

The main contributions presented in this chapter are summarized below.

• A novel analytical approach to the problem, which combines an averaging procedure with the Singular Perturbation Theory (SPT), has been proposed. It is worth stressing that, although both the SPT and the Averaging Method are actually classical in nonlinear dynamics, they had not been used together before in the context of nonideal excitations. Thanks to this novel combination of perturbation techniques, the original 4D system is transformed into a reduced 2D system, much easier to analyse.

• The conditions for stability of equilibria of the reduced system have been analytically derived. Transcritical and Hopf bifurcations have been found. The Hopf bifurcation is particularly relevant, for it gives rise to a smaller stable region than predicted by conventional theories. Consequently, not taking it into account may be perilous for real applications, since unexpected instabilities could occur.

• The Hopf bifurcations have been analytically investigated, in order to characterize them as subcritical or supercritical. A very simple criterion, with clear graphical interpretation, has been obtained to distinguish both types of bifurcations.

• The Poincaré-Bendixson Theorem has been used to find conditions under which all trajectories in the averaged system are attracted towards a periodic orbit, corresponding to a quasiperiodic solution of the original system.

• The global bifurcations destroying the stable and unstable limit cycles have been numerically investigated. These simulations suggest that unstable LCOs are destroyed through homoclinic bifurcations, while stable LCOs can be destroyed either through homoclinic bifurcations or through saddle-node homoclinic bifurcations.

• When an unstable limit cycle exists, the system exhibits two stable equilibrium points, whose domains of attraction are clearly delimited by the periodic orbit.

• The presence of LCOs in the problem under study has been confirmed by numerically solving the original system of equations. An excellent agreement between the solutions of the original and reduced systems has been found. In addition, numerical results show that LCOs can produce very significant variations in the vibration amplitude, which suggests that the addressed instability might be of great relevance in real applications.

• All the analytical developments presented here have been validated by comparing numerical solutions of the original and reduced systems. In particular, the Hopf bifurcation existence has been numerically proved, not only for the reduced system, but, more importantly, also for the original system of equations.

Appendix

This section provides the expressions of parameters ${f}_{ij}$ and ${g}_{ij}$ in Eq. (80). These are simply the coefficients of the nonlinear terms of system (79), which result when system (73) is transformed according to change of variables (76),

$${f}_{20}=-\frac{3\rho aR}{4{c}_{2}}\left(3{c}_{1}^{2}+{c}_{2}^{2}\right)-2{c}_{1}\left(\frac{2\xi }{aR}+\frac{3}{4}\rho {a}^{2}\right)$$

(A.1)

$${f}_{02}=-\frac{9\rho aR{\omega }_{0}^{2}}{4{c}_{2}}$$

(A.2)

$${f}_{11}=-\frac{3}{4}\rho {\omega }_{0}a\left(a+3R\frac{{c}_{1}}{{c}_{2}}\right)-\frac{2\xi {\omega }_{0}}{aR}$$

(A.3)

$${f}_{30}=\frac{9\rho {c}_{1}}{4{c}_{2}}\left({c}_{1}^{2}+{c}_{2}^{2}\right)$$

(A.4)

$${f}_{03}=\frac{9\rho {\omega }_{0}^{3}}{4{c}_{2}}$$

(A.5)

$${f}_{21}=\frac{3\rho {\omega }_{0}}{4{c}_{2}}\left(3{c}_{1}^{2}+{c}_{2}^{2}\right)$$

(A.6)

$${f}_{12}=\frac{9{c}_{1}\rho {\omega }_{0}^{2}}{4{c}_{2}}$$

(A.7)

$${g}_{20}=\frac{\left({c}_{1}^{2}+{c}_{2}^{2}\right)}{{\omega }_{0}}\left[\frac{9\rho a}{4}\left(R\frac{{c}_{1}}{{c}_{2}}+a\right)+\frac{4\xi }{aR}\right]$$

(A.8)

$${g}_{02}=\frac{3\rho {\omega }_{0}a}{4}\left(a+3R\frac{{c}_{1}}{{c}_{2}}\right)$$

(A.9)

$${g}_{11}=\frac{3}{2}\rho {a}^{2}{c}_{1}+\frac{3\rho aR}{4{c}_{2}}\left(3{c}_{1}^{2}+{c}_{2}^{2}\right)+\frac{2\xi {c}_{1}}{aR}$$

(A.10)

$${g}_{30}=-\frac{9\rho }{4{\omega }_{0}{c}_{2}}{\left({c}_{1}^{2}+{c}_{2}^{2}\right)}^{2}$$

(A.11)

$${g}_{03}=-\frac{9{c}_{1}\rho {\omega }_{0}^{2}}{4{c}_{2}}$$

(A.12)

$${g}_{21}=-\frac{9{c}_{1}\rho }{4{c}_{2}}\left({c}_{1}^{2}+{c}_{2}^{2}\right)$$

(A.13)

$${g}_{12}=-\frac{3\rho {\omega }_{0}}{4{c}_{2}}\left(3{c}_{1}^{2}+{c}_{2}^{2}\right),$$

(A.14)

where ${a}_{eq}$ and ${R}_{eq}$ have been shortly written as $a$ and $R$, respectively.